VizNav: A Modular Off-Policy Deep Reinforcement Learning Framework for Vision-Based Autonomous UAV Navigation in 3D Dynamic Environments

Abstract

Unmanned aerial vehicles (UAVs) provide benefits through eco-friendliness, cost-effectiveness, and reduction of human risk. Deep reinforcement learning (DRL) is widely used for autonomous UAV navigation; however, current techniques often oversimplify the environment or impose movement restrictions. Additionally, most vision-based systems lack precise depth perception, while range finders provide a limited environmental overview, and LiDAR is energy-intensive. To address these challenges, this paper proposes VizNav, a modular DRL-based framework for autonomous UAV navigation in dynamic 3D environments without imposing conventional mobility constraints. VizNav incorporates the Twin Delayed Deep Deterministic Policy Gradient (TD3) algorithm with Prioritized Experience Replay and Importance Sampling (PER) to improve performance in continuous action spaces and mitigate overestimations. Additionally, VizNav employs depth map images (DMIs) to enhance visual navigation by accurately estimating objects’ depth information, thereby improving obstacle avoidance. Empirical results show that VizNav, by leveraging TD3, improves navigation, and the inclusion of PER and DMI further boosts performance. Furthermore, the deployment of VizNav across various experimental settings confirms its flexibility and adaptability. The framework’s architecture separates the agent’s learning from the training process, facilitating integration with various DRL algorithms, simulation environments, and reward functions. This modularity creates a potential to influence RL simulation in various autonomous navigation systems, including robotics control and autonomous vehicles.

1. Introduction

The advent of autonomous unmanned aerial vehicles (UAVs) has led to significant advancements due to their diverse applicability ranging from package delivery to military operations, traffic collision response, search and rescue missions, and communication network support [1,2]. However, training these autonomous UAVs for navigation poses significant challenges, primarily due to their limited computational resources, power supply, and the economic implications of component replacements resulting from collisions [1].

Research attempts have predominantly focused on applying deep reinforcement learning (DRL) within 3D virtual environments for UAV navigation training, leveraging Markov decision processes (MDP) or partially observable MDP (POMDP) to manage dynamic decision-making [3,4]. MDP, being fully observable [3], offers a practical alternative to POMDP, which, while enabling planning in complex problems, faces challenges, including the high computational cost [5] and the curse of ambiguity arising from difficulties in quantifying exact transition probabilities [4]. Using MDP thus reduces complexity, accelerating the learning process [3,4,6,7].

RL-based autonomous UAV navigation methods frequently resort to oversimplifications of the environment, such as navigating flat terrain or avoiding obstacles represented as simple geometric shapes, compromising the realism and practical applicability of the navigation model [8,9,10,11,12,13,14,15]. Furthermore, conventional environment representations like grid-cell or 1D/2D formats fail to accurately portray the intricate characteristics of real-world environments, including complex terrains, diverse obstacles, and dynamic elements. The discordance between training and application conditions can consequently lead to a performance gap.

Moreover, restrictions are often imposed on UAVs’ maneuverability, such as limiting the UAV to operate within a fixed plane or to adhere to predefined waypoints [16,17,18,19,20]. Such restrictions significantly curb the UAV’s potential for genuine autonomy, as they do not accurately reflect the dynamic and unpredictable scenarios encountered in real-world operations.

Navigating environments without accurate object depth estimation constitutes an inherent challenge in UAV visual navigation, often leading to collisions [21]. This issue remains largely unaddressed in numerous existing UAV navigation methodologies, particularly those reliant on RGB images [10,16,18]. Although existing research proposed defining depth information through techniques such as range finders or LiDAR [16,20,22], these methodologies encounter their respective limitations. Despite their utility, range finders provide object distance only in specific directions, requiring multiple range finders for a comprehensive spatial overview. Conversely, LiDAR, albeit providing depth information, has high energy consumption and exhibits susceptibility to environmental conditions, including light and weather [23]. Depth map images (DMIs) present a promising technique to overcome these constraints by offering pixel-wise depth-enhancing object perception in 3D environments characterized by complex visual textures and features [24,25].

In the realm of training UAVs in complex environments, the choice of the learning algorithm is paramount and hinges on the specific nature of the environment and the task at hand. UAV navigation in highly stochastic environments using a continuous action space is time-consuming and could extend over several days depending on the chosen RL algorithm and technique. In this context, the policy type is essential in stabilizing UAV training. On-policy algorithms have been known to be sensitive to hyperparameters and require extensive training time due to their reliance on the current policy to make decisions [26,27].

Conversely, off-policy algorithms have shown significant promise for such tasks. Unlike on-policy methods, off-policy algorithms can learn from past experiences and adjust future actions based on these experiences [27,28]. This inherent ability allows them to handle highly stochastic or non-stationary environments more effectively, improving training, especially when combined with techniques such as Experience Replay (ER) [29] and Prioritized ER with Importance Sampling (PER) [30]. Twin Delayed Deep Deterministic Policy Gradient (TD3) [31], an off-policy RL algorithm, has emerged as an appropriate selection, given its compatibility with the continuous action space and unlimited states integral to UAV navigation [32].

To overcome the limitations posed by oversimplified environmental representations and the imposed restrictions on UAV maneuverability while leveraging depth images, this paper proposes a modular RL-based navigation framework, VizNav, which leverages the TD3 algorithm with DMIs obtained from a front-facing camera while adopting PER. The DMIs are processed and interpreted by VizNav to provide the agent with a more accurate and comprehensive depth perspective, improving navigation in complex environments. Moreover, VizNav incorporates PER with TD3, introducing a bias towards critical experiences during the learning process for improved UAV navigation results.

The modular design of the VizNav framework allows each module to execute specific tasks independently, ensuring adaptability and enabling seamless modifications or enhancements to individual modules without affecting others. Components, including the RL algorithms, can be replaced with new ones as they become available, without changing other components.

By decoupling the training and learning processes, VizNav streamlines the training of various RL agents. Moreover, it allows straightforward adjustment of reward functions and hyperparameters via configuration files and integrates seamlessly with various navigation environments. Thus, VizNav not only addresses the specific navigation problem examined in this study but also positions itself as a versatile platform for various RL-based navigation challenges.

This paper’s main contributions are as follows:

• VizNav trains the agent to navigate complex environments using depth map images (DMIs) from a front-facing camera, providing a more accurate and comprehensive depth perspective. This approach enhances the realism of training environments and promotes genuine autonomous capabilities, overcoming the limitations of traditional models.
• VizNav utilizes TD3, an off-policy algorithm known for its stability and efficiency in handling continuous actions and reducing overestimations in value functions, making it a robust choice for the proposed navigation task.
• VizNav incorporates Prioritized Experience Replay (PER) to enhance TD3’s performance by focusing the agent’s learning process on key transitions, enabling improved training results and faster model convergence.
• VizNav is a modular and adaptable framework that can train different RL agents seamlessly, facilitate easy hyperparameter tuning, and that can integrate with various navigation environments.

The remainder of the paper is organized as follows: Section 2 introduces various RL concepts, Section 3 discusses the related work, Section 4 formulates the navigation problem, Section 5 presents the proposed framework and its modules, Section 6 describes experiments and discusses findings, and, finally, Section 7 concludes the paper.

2. Background

This section introduces the concepts and algorithms based on the proposed framework.

2.1. MDP and Deterministic Policy

Reinforcement learning (RL), elucidated through a Markov decision process (MDP), can complete various tasks without prior knowledge. MDP uses an agent that receives a state s from the environment, performs an action a according to the state, and then receives a reward r, which is used to judge the success or failure of the action. The performed action causes a change in the environment’s current state, resulting in a new state $s^{\prime }$. The MDP objective described in Equation (1) is to maximize the reward R obtained from actions performed over several time steps, focusing on the reward received from the current time step and decreasing the weight of rewards gained from future time steps using a discounted factor ${\gamma }^k$, where $\gamma \in [0,1]$, and k denotes the time step.

$$G_t=E\left[\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}\right]$$

(1)

In general, RL agent behavior, known as policy $\pi$, explains how the agent acts (select actions a) in different situations (states s). The policy can be either stochastic $\pi$—described in Equation (2), which returns the probability distribution across actions for the same state, or it can be deterministic $\mu$, which is similar to stochastic policy but always delivers the same action for a given state.

$$Q_{\pi }(s,a)=E_{\pi }\left[\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}|S_t=s,A_t=a\right]$$

(2)

Silver et al. [33] prove that the deterministic policy gradient of MDPs exists and is a special case of the stochastic policy gradient if the stochastic policy satisfies certain conditions. Deterministic policies are typically more efficient and easier to implement than stochastic policies. Moreover, the objective of autonomous UAV navigation is frequently to determine a safe and efficient route between a starting point and a destination, where the surroundings may be dynamic and the UAV must avoid obstacles. Therefore, the UAV must make consistent, predictable decisions in such situations to explore the environment safely and effectively.

2.2. Off-Policy vs. On-Policy RL

The RL agent learns two policies; the first is the target policy $\theta \left(a\right|s)$, wherein the agent learns through the value function to determine the expected return [32]. In contrast, the second policy is the behavior policy $\beta \left(a\right|s)$ that the agent uses to select actions when interacting with the environment [1]. Based on these two policies, an RL algorithm can be classified as either an off-policy or an on-policy RL algorithm.

In an on-policy algorithm, the behavior policy follows the target policy $\theta \left(a\right|s)$: the same policy is used to collect the training samples and to determine the expected return. In contrast, an off-policy algorithm collects the training samples in accordance with the behavior policy $\beta \left(a\right|s)$, whereas the expected reward is generated using the target policy $\theta \left(a\right|s)$ [1].

In general, off-policy algorithms use various Experience Replay (ER) techniques to improve the stability and efficiency of learning. ER [29] is a technique where the agent stores the generated experiences over time in a replay buffer, then uses the replay buffer to uniformly sample a batch of experiences for agent training. Prioritized Experience Replay (PER) [30] extends ER by associating each experience with a priority value determined according to the magnitude of the temporal difference error that regulates the probability of sampling the experiences. PER uses importance sampling to reduce the contribution of high-priority experiences, since the model is more likely to sample experiences with high priorities, which might result in overestimating their actual importance, allowing the model to acquire knowledge more precisely [30]. On the other hand, on-policy algorithms do not require ER because the agent learns directly from the actions it takes in the environment [1].

Although on-policy algorithms are more efficient and easier to implement than off-policy algorithms, they require more training time and are sensitive to the learning rate and other hyperparameters [26,27]. Consequently, VizNav promotes off-policy algorithms because they perform better in highly stochastic or non-stationary environments [27,28], which makes them a better fit for autonomous UAV navigation in dynamic environments.

2.3. DDPG vs. TD3

Actor–critic (AC) algorithms employ deterministic off-policy RL compared to other policy gradient methods, which often utilize on-policy RL. Overall, actor-critic approaches offer a more efficient and stable learning algorithm than policy gradient methods, and they are commonly employed in DRL [27,34,35,36,37,38].

Actor–critic often utilizes two networks, the actor and the critic [34]. The actor network is responsible for determining the optimal deterministic policy $\mu \left(s\right)$, whereas the critic network applies an action-value function $Q_w^{\pi }(s_t,a_t)$ parameterized by w and the temporal-difference (TD) approach [33] to evaluate the actor-selected action and the quality of the new state [1].

Deep Deterministic Policy Gradient (DDPG) [39] is a deterministic off-policy AC algorithm that can operate over continuous action spaces. DDPG is based on the Deterministic Policy Gradient (DPG) algorithm [33], where it employs experience replay techniques and the target networks (doubling technique) for the actor and critic to prevent the overestimation problem.

On the other hand, the Twin Delayed Deep Deterministic (TD3) algorithm [31] extends DDPG by incorporating the following improvements: (1) it employs two critics to compute the temporal difference error (TD-error) and considers the minimum value between the critics to reduce overestimation bias, and (2) it applies delayed policy updates to reduce per-update error and improve the performance. Therefore, VizNav adopts TD3 for UAV autonomous navigation and compares the results to DDPG.

3. Related Work

Autonomous navigation of unmanned aerial vehicles (UAVs) through RL hinges on three fundamental factors: the mechanism governing UAV movement (action), the input types formulated as environment states (e.g., front-facing camera, range finder, LiDAR), and the specific RL technique used to train the agent [1]. Existing methodologies vary based on these parameters, creating different strategies for maneuvering UAVs while avoiding obstacles or selecting necessary waypoints to reach a destination.

3.1. Navigation Using 1D/2D Environments or Restricted Actions

Approaches in this category simplify either the environment or action representation. For instance, Wang et al. [16] employed an improved Recurrent Deterministic Policy Gradient (RDPG) [40] called Fast-RDPG, which is designed for handling continuous states and action spaces. The model uses range finders to estimate the distance to the UAV’s surroundings. However, it restricts UAV movement to the x and y planes without considering camera images for training. Other research [17,18,19] applied a grid world and discrete actions to simplify the environment. Anwar and Raychowdhury [41] simplified action representation by dividing the scene into $(N\times N)$ squares/cells, restricting the UAV movement to one of the scene cells.

Despite the advancements in autonomous UAV navigation through DRL presented in these studies [16,17,18,19,41], they impose limitations such as operating in a fixed plane, using restricted UAV movement, or simplifying the environment. Furthermore, their action spaces do not align with actions employed to control UAVs in real-world scenarios.

3.2. UAV Navigation Using Front-Facing Cameras

In this category, approaches rely on front-facing camera images to guide navigation and evade obstacles. Depth map images (DMIs) enable the agent to perceive depth in its environment, a critical aspect of autonomous navigation. For example, He et al. [42] constructed DMIs from two frames produced by a monocular camera, supporting UAV navigation in a fixed plane by controlling the velocity and yaw angle.

Boiteau et al. [43] addressed UAV navigation in environments lacking GPS and visibility through a POMDP framework tested in cluttered indoor settings. While this is pivotal for search and rescue operations, VizNav extends these capabilities by incorporating continuous action spaces and enhanced depth map imaging, thus improving UAVs’ navigation in dynamic and unstructured environments.

Singla et al. [44] utilized conditional generative adversarial networks (cGANs) to generate DMIs. They employed deep recurrent Q-networks (DRQN) [45] with a temporal attention mechanism, thereby introducing a time-aware component to process DMIs. This approach allowed the recurrent network to retain depth information across multiple time steps and learn temporal dependencies, while the temporal attention mechanism weighs the importance of recent observations. However, the use of DRQN permitted UAV movement control through discrete actions only, thus imposing a limitation on the UAV movement.

In contrast, Bouhamed et al. [10] used DDPG to control UAV movement in a continuous action space with no DMI employed, lacking objects’ depth information. Furthermore, the action space allowed the UAV to travel a radial distance using inclination and elevation angles, which do not reflect the commands used to fly UAVs in real-life situations (pitch, roll, and yaw).

Despite the varied methodologies employed in the aforementioned studies [10,42,44], common limitations persist. Some methods do not leverage DMIs, thereby lacking depth information about objects, while others impose restrictions on UAV maneuverability.

3.3. UAV Navigation Frameworks

This category encompasses frameworks facilitating RL agent training in navigating physical or virtual environments. These frameworks employ RL algorithms combined with other methods and techniques, enabling agents to navigate the environment and reach a specific goal.

Walker et al. [46] proposed a modular framework in which modules communicate with each other. However, while controlling the yaw angle, the framework confines UAV movement to a fixed plane in the x and y directions. Another framework suggested by Bouhamed et al. [47] uses spatiotemporal scheduling to accommodate the maximum number of prescheduled events spread spatially and temporally across a specific geographical region over a given time horizon. Unlike other frameworks, this framework [47] did not employ images, focusing instead on selecting different locations in an area of interest.

Camci et al. [48] suggested a two-stage training process where, in the initial phase, the agent learns motion primitives for various scenarios and, in the second stage, applies these primitives for swiftly planning maneuvers such as waypoint navigation, take-off, and landing. Although this framework enables the UAV to navigate using roll, pitch, and yaw rate, it assumes prior knowledge of the environment. Therefore, the UAV operates along a predetermined path and does not use images for training.

Exploring the limitations of traditional navigation frameworks in forest environments, Lee et al. [49] focus on color segmentation to identify navigable spaces using discrete action space. In contrast, VizNav introduces a more flexible approach utilizing continuous action space and depth map images.

Advancements in object detection for drone-to-drone interactions presented by Ye et al. [50] aim to enhance detection capabilities using adjacent frame fusion techniques. However, this approach does not integrate simulation and UAV control. VizNav addresses these gaps by emphasizing spatial awareness and incorporating continuous action mechanisms, significantly enhancing UAV adaptability and operational performance in dynamic environments. Moreover, Wang et al. [51] proposed a DRL system focusing on simulated environments for UAV obstacle avoidance using static object detection techniques and discrete action space. In contrast, VizNav extends these concepts by employing depth map images and continuous actions, providing a more adaptable navigation solution capable of handling complex environmental dynamics.

Addressing resource-constrained platform challenges, Zhang et al. [52] utilize lightweight CNNs for depth estimation on nano-drones in static environments and discrete action space. In contrast, VizNav uses dynamic simulations to enable adaptive decision-making, transcending the limitations inherent in static dataset-driven methods.

Another framework suggested by Yang et al. [8] proposed a UAV navigation with Double DQN and PER to circumvent obstacles in a dynamic environment, enabling the collaborative control of multiple UAVs. However, the environment representation was oversimplified to a vector of raw pixels, and discrete actions influenced the UAV movement, hence using Double DQN.

While existing frameworks [8,46,47,48,49,50,51,52] have made noticeable strides in autonomous UAV navigation, they also harbor some limitations. Among these, the most prominent is the neglect of depth map images (DMIs), thereby lacking comprehensive depth information. Coupled with oversimplifications of environment representations and restrictions on UAV maneuverability, these drawbacks compromise their real-world applicability. Moreover, the predominance of methodologies that favor discrete action spaces over continuous ones further widens the gap. Thus, a critical need exists for a more robust framework that seamlessly integrates DMIs, promotes continuous action spaces, and alleviates assumptions of prior environment knowledge.

3.4. RL Algorithm for UAV Navigation

In UAV navigation, the stochastic nature of the task and environment necessitates a strategic choice of the RL algorithm. The preference often leans towards off-policy algorithms because they learn from past experiences to adjust future actions, optimizing the exploration–exploitation trade-off, which is beneficial for UAV navigation in complex environments [10,16].

Within the realm of off-policy algorithms, actor–critic methods stand out due to their inherent structure and ability to handle continuous action spaces. They employ an actor for decision-making based on the policy and a critic for evaluating decisions via estimated value functions. This dual approach improves the learning process and ensures a balanced exploration–exploitation trade-off.

In a recent study, AlMahamid and Grolinger [1] proposed a process for algorithm selection according to the problem formulation. This leads us to a subset of off-policy, single-threaded, actor–critic algorithms that support unlimited states and continuous actions, such as DDPG [39], TD3 [31], SAC [38], DAC [53], and ACE [54].

Each of these algorithms exhibits unique characteristics influencing their suitability for UAV navigation tasks using DMIs. For example, SAC employs entropy regularization, enhancing exploration–exploitation balance, but its inherent stochasticity could limit its application in time-critical tasks such as UAV navigation [38]. ACE and DAC hold promise but may impose additional computational requirements, potentially slowing decision-making in real-time continuous environments [53,54].

Considering these factors, the Twin Delayed Deep Deterministic Policy Gradient (TD3) algorithm emerges as a suitable choice for UAV navigation. TD3 offers robust performance in continuous action spaces, reduced sensitivity to hyperparameters, and mitigation of overestimations [31]. Its ability to provide more stable learning makes it particularly suited for navigating complex 3D environments using DMIs.

4. Problem Formulation

This section formulates the UAV navigation in 3D dynamic environments using MDP, provides state and action space specifications, and describes the engineered rewards.

4.1. VizNav Navigation

VizNav conducts UAV navigation training in a 3D dynamic environment with the main objective of the UAV to move from a starting point $A(X_{start},Y_{start},Z_{start})$ to a destination point $B(X_{dest},Y_{dest},Z_{dest})$ while avoiding obstacles using RGB images and DMI, along with other UAV-related information such as velocity and orientation.

UAV maneuverability is controlled by employing continuous flight control commands based on Euler angles—(1) pitch ($angl{e}_{\Theta }$), (2) roll ($angl{e}_{\Phi }$), and (3) yaw ($angl{e}_{\Psi }$)—that control the rotation around the three axes, as shown in Figure 1. The flight command also uses the throttle (${\mathit{Throttle}}_{\Omega }$) value, which contains the engines’ thrust.

4.2. State and Action Space Specifications

VizNav formulates the navigation problem as MDP. The states might look similar in a 3D dynamic environment, impacting the agent’s learning. Thus, VizNav uses a complex state to describe the UAV’s unique conditions and status, which improves the agent’s learning. The state contains the following:

• RGB Image $I_{RGB}$ is produced by the UAV front-facing camera capturing the UAV current scene.
• Depth Information $I_{Depth}$ is a 2D array that contains the estimated distance between all the points from the captured scene and the current UAV position. The 2D array is converted to a single-channel gray-scale image.
• Angular Velocity $V(X_{\Theta },Y_{\Phi },Z_{\Psi })$ is the rate of rotation of a rigid body (here, UAV) relative to its center of rotation and independently of its origin, which is provided by the inertial measurement unit (IMU).
• Linear Acceleration $A(X_{\Theta },Y_{\Phi },Z_{\Psi })$, also measured by IMU, refers to the rate of change in velocity without a change in direction.
• Orientation $O(W_q,X_q,Y_q,Z_q)$ measures the UAV’s orientation relative to the NED (North, East, Down) coordinate system using quaternion instead of Euler angles.
• Current Position $P_{current}(X,Y,Z)$ measures the current UAV position using the NED coordinate system.
• Destination Position$P_{dest}(X,Y,Z)$ refers to the destination point using the NED coordinate system.
• Remaining Distance $D_{remain}$ is the remaining distance from the current position $P_{current}(X,Y,Z)$ to the destination point $P_{dest}(X,Y,Z)$ measured in meters.
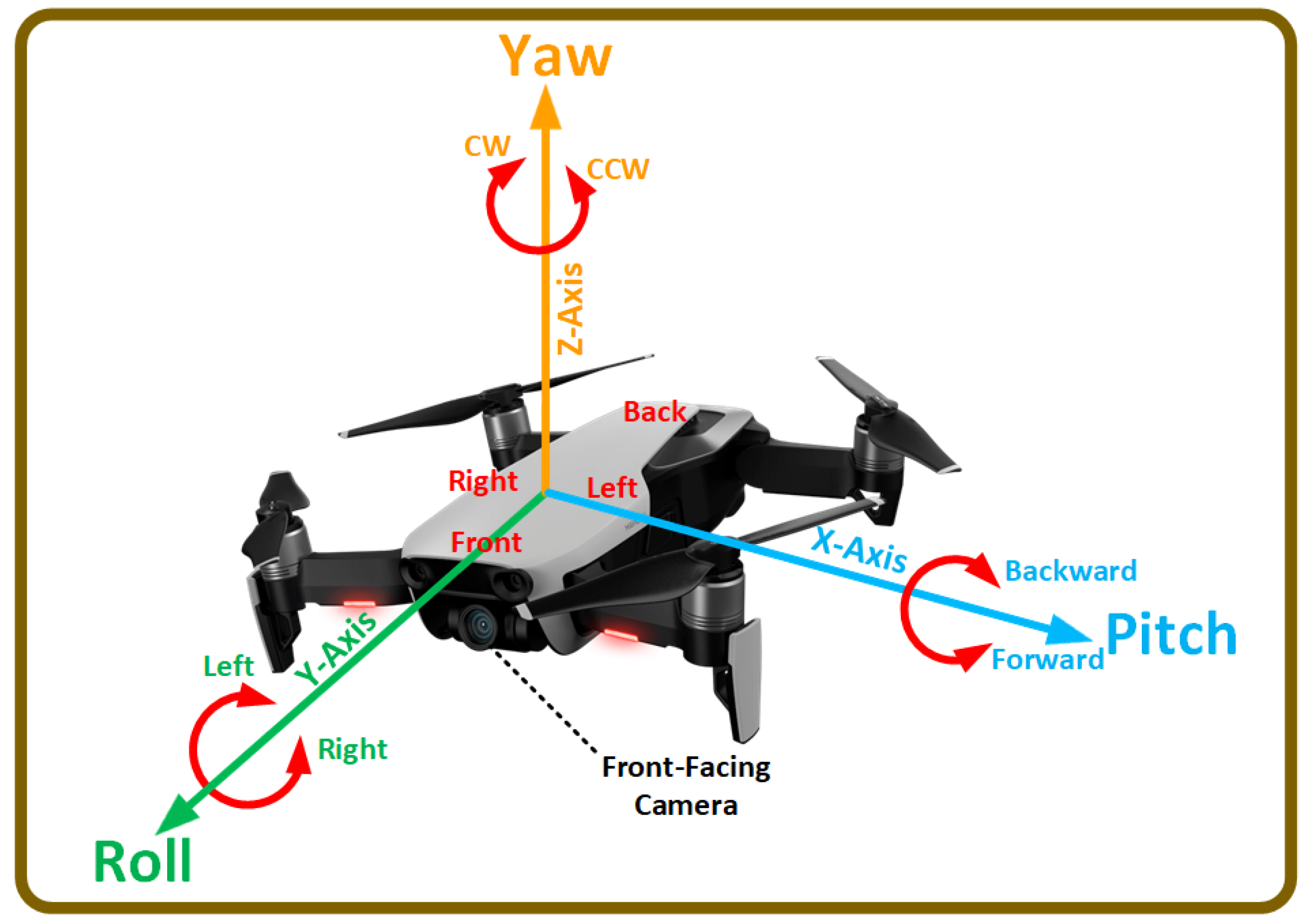
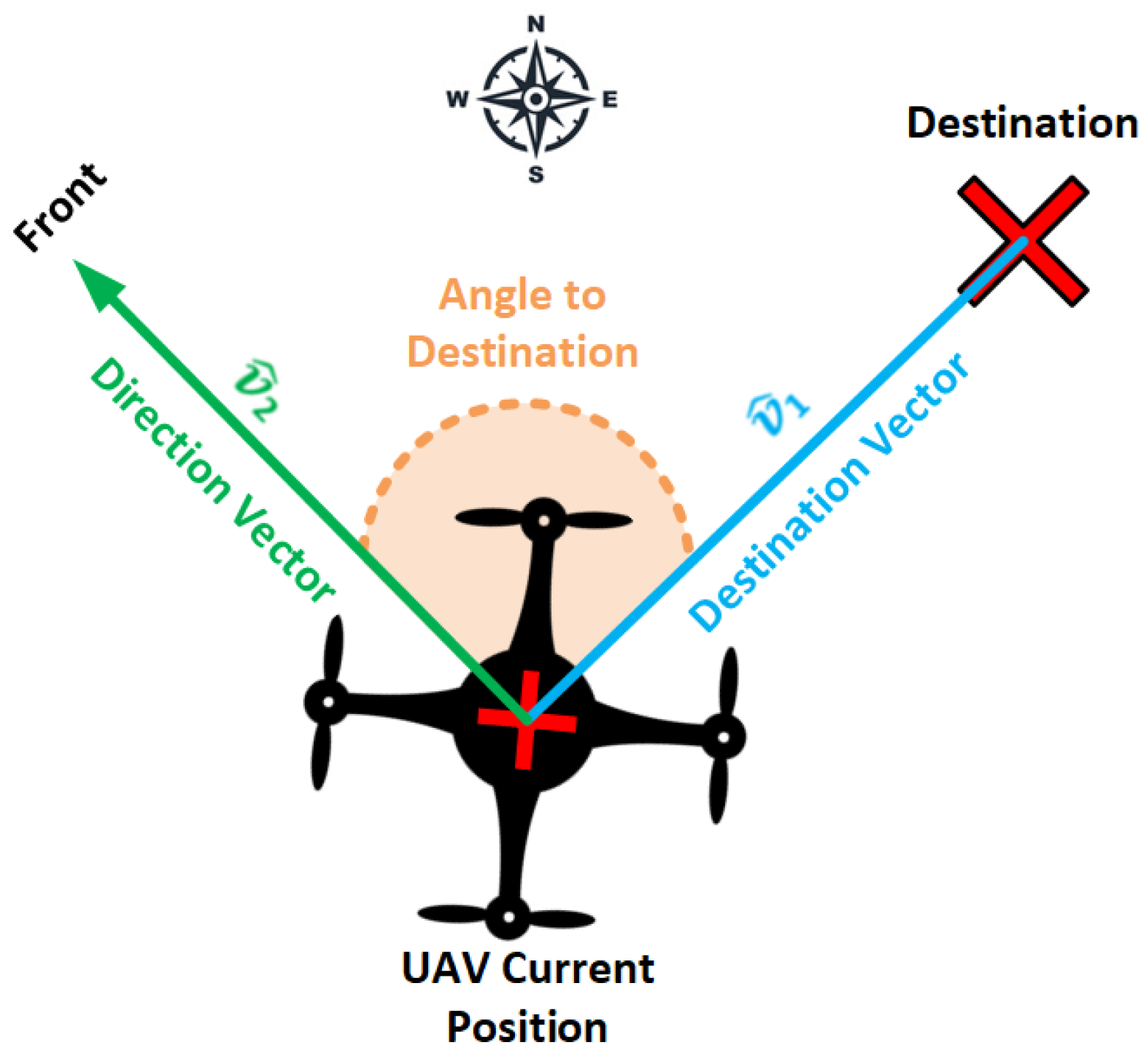
• Angle to Destination $D_{angle}$ measures the angle between the UAV’s current orientation $O(W_q,X_q,Y_q,Z_q)$ and the destination point $P_{dest}(X,Y,Z)$. As shown in Figure 2, the angle is computed by defining two unit vectors, $\widehat{{\upsilon }_1}$ and $\widehat{{\upsilon }_2}$. The first unit vector $\widehat{{\upsilon }_1}$ from the UAV’s current position $P_{current}(X,Y,Z)$ to the destination point $P_{dest}(X,Y,Z)$ defines the destination direction, whereas $\widehat{{\upsilon }_2}$ defines the unit vector of the UAV’s facing direction $O(W_q,X_q,Y_q,Z_q)$ with respect to the NED coordinate system. Equation (3) shows how the unit vector, also known as a normalized vector, is computed by dividing the direction vector ($\overrightarrow{V}$) by its norm/magnitude ($\parallel V\parallel$), whereas Equation (4) shows how the angle $D_{angle}$ between the UAV’s current position and destination point is computed.

  Figure 1. The UAV control mechanism demonstrates regulating the UAV’s movement through the rotation angle around three axes—pitch, roll, and yaw—while the throttle adjusts the engines’ thrust. Rotation around the roll axis, highlighted in green, directs the UAV left or right. Rotation around the pitch axis, shown in blue, moves the UAV forward or backward. Rotation around the yaw axis, depicted in orange, enables clockwise (CW) or counterclockwise (CCW) rotation.

  Figure 1. The UAV control mechanism demonstrates regulating the UAV’s movement through the rotation angle around three axes—pitch, roll, and yaw—while the throttle adjusts the engines’ thrust. Rotation around the roll axis, highlighted in green, directs the UAV left or right. Rotation around the pitch axis, shown in blue, moves the UAV forward or backward. Rotation around the yaw axis, depicted in orange, enables clockwise (CW) or counterclockwise (CCW) rotation.

  $$\widehat{\upsilon }=\frac{\overrightarrow{V}}{\parallel V\parallel }$$

  (3)

  $$\begin{array}{cc}\hfill D_{angle}& =arccos(\frac{\overrightarrow{V_1}}{\parallel V_1\parallel }·\frac{\overrightarrow{V_2}}{\parallel V_2\parallel })\hfill \\ \hfill & =arccos({\widehat{\upsilon }}_1·{\widehat{\upsilon }}_2)\hfill \end{array}$$

  (4)

Figure 2. UAV orientation angle with respect to the destination point. The angle is measured using two vectors: the destination vector ${\widehat{\upsilon }}_1$, which points from the UAV’s current location to the destination point, and the direction vector ${\widehat{\upsilon }}_2$, which points in the forward direction of the UAV.

Figure 2. UAV orientation angle with respect to the destination point. The angle is measured using two vectors: the destination vector ${\widehat{\upsilon }}_1$, which points from the UAV’s current location to the destination point, and the direction vector ${\widehat{\upsilon }}_2$, which points in the forward direction of the UAV.

The features/scalars are combined in a single vector $I_{Features}$ as follows:

$$\begin{array}{cc}\hfill I_{Feature{s}_t}=\{& V_t(X_{\Theta },Y_{\Phi },Z_{\Psi }),\hfill \\ \hfill & A_t(X_{\Theta },Y_{\Phi },Z_{\Psi }),\hfill \\ \hfill & O_t(W_q,X_q,Y_q,Z_q),\hfill \\ \hfill & P_{current}(X,Y,Z),\hfill \\ \hfill & P_{dest}(X,Y,Z),D_{remain},D_{angle}\}.\hfill \end{array}$$

(5)

Vector $I_{Features}$ is combined with $I_{RGB}$ and $I_{Depth}$ to form the state

$$\begin{array}{c}\hfill S_t=\left\{I_{RG{B}_t},I_{Dept{h}_t},I_{Feature{s}_t}\right\}.\end{array}$$

(6)

On the other hand, the action space $A_t\{\Delta angl{e}_{\Theta },\Delta angl{e}_{\Phi },$ $\Delta angl{e}_{\Psi },\Delta Throttl{e}_{\Omega }\}\in A$ represents the amount of change in pitch, roll, and yaw angles, as well as the throttle value. Therefore, the flight command represents the agent’s selected action $A_t$ added to the current pitch, roll, yaw, and throttle values, as shown in Equation (7).

$$\begin{array}{cc}\hfill angl{e}_{{\Theta }_t}& =angl{e}_{{\Theta }_{t-1}}+\Delta angl{e}_{{\Theta }_t}\hfill \\ \hfill angl{e}_{{\Phi }_t}& =angl{e}_{{\Phi }_{t-1}}+\Delta angl{e}_{{\Phi }_t}\hfill \\ \hfill angl{e}_{{\Psi }_t}& =angl{e}_{{\Psi }_{t-1}}+\Delta angl{e}_{{\Psi }_t}\hfill \\ \hfill Throttl{e}_{{\Omega }_t}& =Throttl{e}_{{\Omega }_{t-1}}+\Delta Throttl{e}_{{\Omega }_t}\hfill \end{array}$$

(7)

4.3. Reward Engineering

Reward engineering plays a vital role in the agent’s learning. The reward can be sparse or non-sparse. A sparse reward used commonly [8,46,55,56] in navigation tasks has a simple formalization that awards the agent with a constant reward depending on the failure or success of the action causing long convergence times [16]. Alternatively, a non-sparse reward incorporates domain knowledge and considers even slight changes in the state, assuring policy invariance. Nevertheless, the non-sparse reward must be engineered to support the learning objective.

Therefore, VizNav employs an engineered complex and compound non-sparse reward that incorporates domain knowledge to control UAV navigation. The award consists of the following sub-rewards: (1) Collision Reward $r_{collision}$, (2) Distance Reward $r_{distance}$, (3) Orientation Reward $r_{orient}$, and (4) Time-Step Reward $r_{step}$.

The Collision Reward $r_{collision}$ encourages the UAV to avoid obstacles, utilizing mainly the depth images $I_{Depth}$, by keeping a safe distance from objects. If the UAV collides, the collision reward function awards a constant penalty ${\rho }_c$. However, if no collision occurs, the reward function finds the minimum distance to the obstacles using $I_{Depth}$ and compares it to a safe distance threshold ${\xi }_c$. If the minimum distance is less than ${\xi }_c$, the reward function generates a reward equal to $-(1/min\left(I_{Depth}\right))$, and if it is greater or equal to the threshold ${\xi }_c$, it grants a positive reward ${\lambda }_c$, as described in Equation (8).

$$r_{collision}=\left\{\begin{array}{cc}{\rho }_c\hfill & ,collided=True\hfill \\ -\left(\frac{1}{min\left(I_{Depth}\right)}\right)\hfill & ,min\left(I_{Depth}\right)<{\xi }_c\hfill \\ {\lambda }_c\hfill & ,min\left(I_{Depth}\right)\ge {\xi }_c\hfill \end{array}\right.$$

(8)

The Distance Reward $r_{distance}$ awards a constant positive ${\lambda }_d$ if the UAV’s remaining distance $D_{remain}$ to the destination is less than or equal to the ${\gamma }_d$ threshold. This means that the UAV is considered to have reached the destination if it is within a radius equal to ${\gamma }_d$ from the destination point. On the other hand, if the UAV gets closer to the destination, which is defined by finding if the new remaining distance $D_{remai{n}_{t+1}}$ is smaller than the previous remaining distance $D_{remai{n}_t}$, the reward is generated as ${\alpha }_d\times e^{({\beta }_d\times D_{remain})}$, where ${\alpha }_d$ and ${\beta }_d$ are defined constants. Finally, a negative reward is generated if the UAV gets away from the destination point, as described in Equation (9). Providing a negative reward if the UAV gets away from the destination point helps the agent not to alternate between the forward and backward movement to maximize the reward.

$$r_{distance}=\left\{\begin{array}{cc}{\lambda }_d\hfill & ,D_{remain}\le {\gamma }_d\hfill \\ {\alpha }_d\times e^{({\beta }_d\times D_{remain})}\hfill & ,D_{remai{n}_{t+1}}<D_{remai{n}_t}\hfill \\ -{\alpha }_d\times e^{({\beta }_d\times D_{remain})}\hfill & ,\mathrm{Otherwise}\hfill \end{array}\right.$$

(9)

The Orientation Reward $r_{orient}$ encourages the UAV to reach the destination point while front-facing, which helps the UAV capture the images required to find the obstacles as it moves towards the destination. This reward computes the orientation angle $D_{angle}$ in degrees (as explained in Section 4.2) and applies a penalty/reward according to Equation (10) if the $D_{angle}$ is bigger/smaller than the angle threshold ${\xi }_o$.

$$r_{orient}=\left\{\begin{array}{cc}{\alpha }_{o1}\times e^{({\beta }_{o1}\times D_{angle})}\hfill & ,D_{angle}\le {\xi }_o\hfill \\ -{\alpha }_{o2}\times e^{({\beta }_{o2}\times D_{angle})}\hfill & ,\mathrm{Otherwise}\hfill \end{array}\right.$$

(10)

Finally, the Time-Step Reward $r_{step}$ encourages the UAV to reach the destination faster by applying a penalty that increases at each episodic time step $ste{p}_t$, as described in Equation (11).

$$r_{step}={\alpha }_s\ast log\left(ste{p}_t\right)$$

(11)

The final reward r at step t is the summation of all rewards, as shown in Equation (12).

$$r_t=r_{collision}+r_{distance}+r_{orient}+r_{step}$$

(12)

5. VizNav Framework

This section discusses the VizNav framework modules, their interactions, the deep neural network architecture, and the UAV navigation training. VizNav is explicitly designed to support UAV visual navigation training in a 3D environment by facilitating the interactions between the DRL agent, UAV Controller, the 3D environment, and the flight simulator.

5.1. Framework Modules

The VizNav framework depicted in Figure 3 adopts MDP for UAV navigation training in a 3D environment using deterministic off-policy DRL with experience replay techniques such as Prioritized Experience Replay (PER). The framework has the following modules.

5.1.1. Training Manager

The Training Manager represents the core module of the framework. It is responsible for loading the experiment configurations, initializing all other modules using the loaded configurations, and starting the 3D environment with the flight simulator software. The experiment configurations are stored in a configuration file, which defines the various parameters related to the UAV, DRL agent, replay buffer, 3D environment, and reward function. For example, the DRL agent settings stored in the configuration file are the learning rate, the maximum steps allowed for each episode, and the update interval for the TD3 algorithm. Other settings contained in the configuration file are the UAV settings, such as the start location, the destination point, initial UAV orientation, and the maximum and minimum allowed values (thresholds) of the pitch, roll, yaw, and throttle rates.

Once the environment is fully loaded and all the modules are initialized, the training manager starts the agent’s main training block (agent trainer), where it either explores or exploits the environment according to the $ϵ$-greedy strategy. The environment exploration is created by generating random actions, collecting the states and rewards, and then saving the learned experiences to the replay buffer. On the other hand, environment exploitation is formed by initiating the learn function of the DRL agent, which utilizes the replay buffer to stabilize the training. Environment exploration/exploitation requires executing actions and collecting the new UAV state to/from the UAV Controller, respectively, and collecting the generated reward from the Reward Generator based on the new state.

5.1.2. Replay Buffer Manager

The Replay Buffer Manager is responsible for storing and sampling experiences according to the selected memory replay technique specified in the configurations. The Replay Buffer Manager supports two types of memory replay techniques: (1) Experience Replay (ER) and (2) Prioritized Experience Replay with importance sampling (PER).

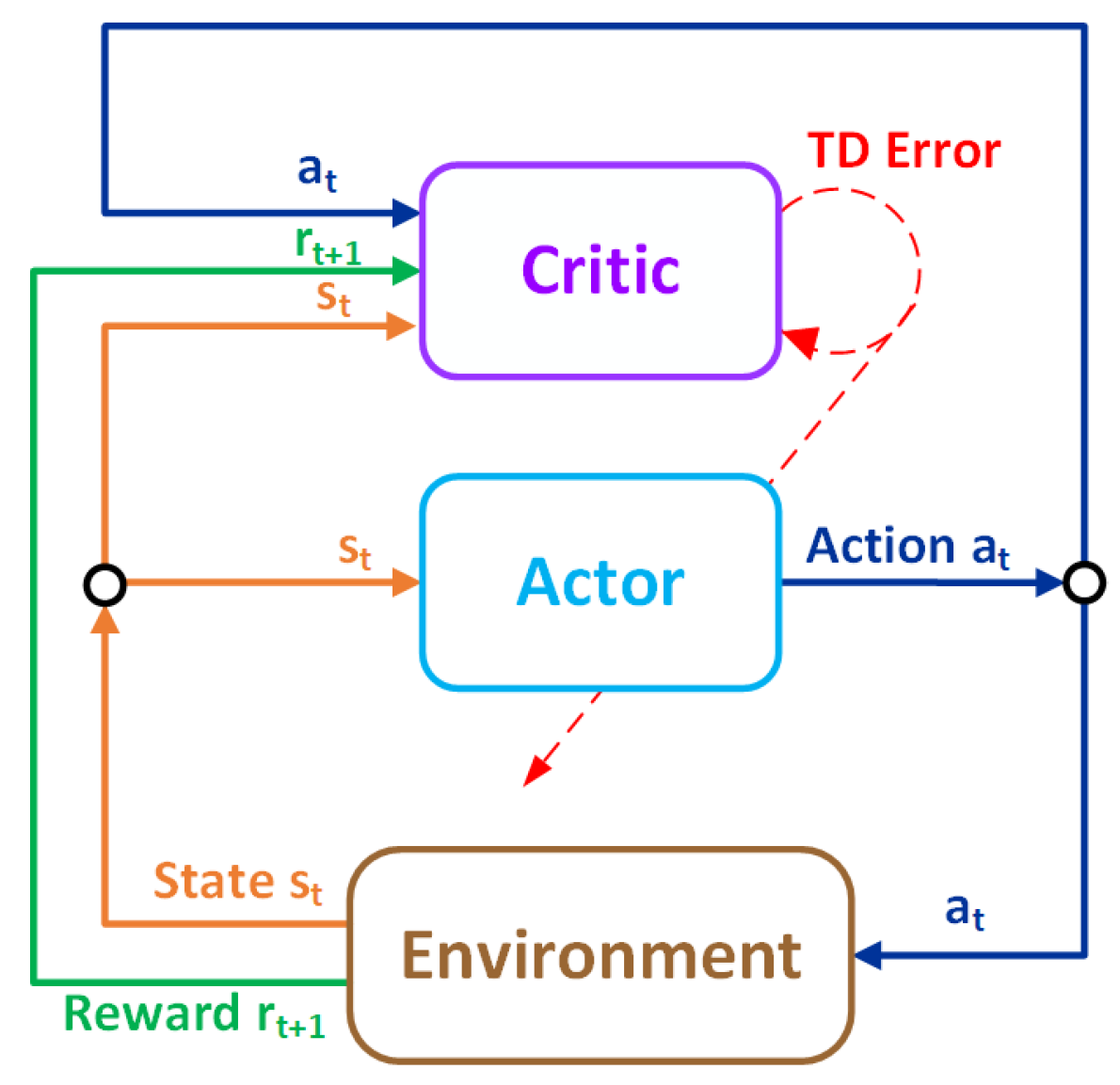
5.1.3. DRL Agent

The DRL Agent denotes the off-policy RL algorithm that uses mini-batches sampled from the replay buffer to train the agent every time step that the Training Manager explores/exploits the environment. The DRL Agent instantiates the neural network architecture defined in the Neural Network module, which defines the neural network (NN) architecture adopted by the actor/critic.

Additionally, the DRL Agent provides the Training Manager with the exploitation/ exploration actions required to build experiences, receives a mini-batch of experiences required for training from the Replay Buffer Manager, and updates the priorities of the experiences in the replay buffer if PER is employed.

5.1.4. UAV Controller

The UAV Controller is responsible for controlling the UAV movements by transferring the agent’s action to a flight command $(angl{e}_{{\Theta }_t},angl{e}_{{\Phi }_t},angl{e}_{{\Psi }_t},Throttl{e}_{{\Omega }_t})$, as explained in Equation (7). Furthermore, the UAV Controller is responsible for providing all the information related to the current UAV state, including collision information and other information required by the Reward Generator to generate the reward. The UAV Controller uses the AirSim APIs to control and collect information regarding the UAV from the 3D environment.

5.1.5. Reward Generator

The Reward Generator is responsible for generating a reward after each time step the Training Manager explores/exploits the environment. The final reward $r_t$ is the summation of four different rewards: (1) Orientation Reward, (2) Time-Step Reward, (3) Distance Reward, and (4) Collision Reward, which are explained in Section 4.3. To perform the reward calculation, the Reward Generator inquires UAV Controller about the UAV state, such as collision information, current position, and orientation.

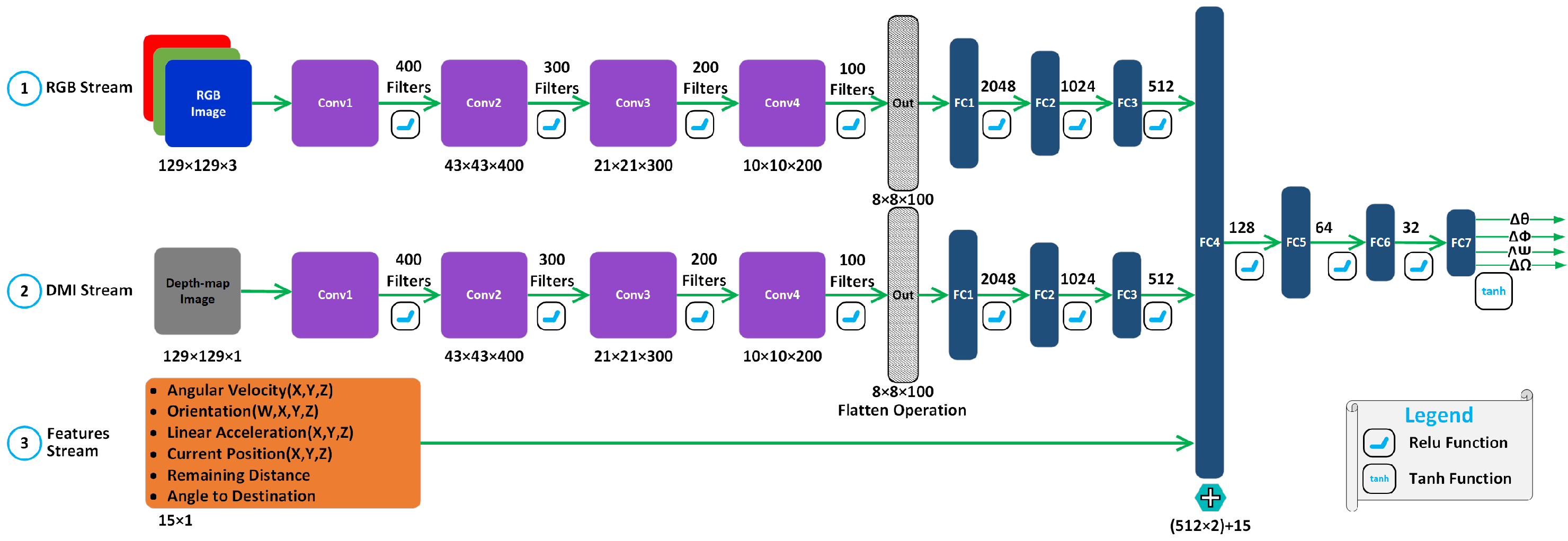
5.2. Deep Agent Architecture

The neural network (NN) plays a vital role in RL agent training. Actor–critic algorithms mainly have two networks: the actor network receives the state and produces the action values, while the critic network receives the state and the actions produced by the actor and produces a state value to criticize the action made by the actor, as illustrated in Figure 4.

Figure 5 shows the actor NN architecture using three streams: (1) RGB stream, (2) DMI stream, and (3) features stream. RGB and DMI streams both use four 2D convolutional layers and seven fully connected layers. The NN first processes the RGB image, depth map image, and the linear features as separate steams. Then, the fourth linear layer (FC4) performs a concatenation between the scene’s convolved images (RGB & DMI) and other linear inputs of the UAV state information. The concatenated information is then passed through fully connected layers, as shown in Figure 5.

The critic shares a very similar architecture as the described actor NN, except that the critic has extra linear inputs denoting the actions produced by the actor. Also, the critic has a single output: the Q-value (state value). The actor and critic NNs’ architectures are instantiated while initializing the DRL Agent module.

Figure 4. Actor–critic architecture showing that the actor receives the state and produces the actions. The critic network receives the state and the actions produced by the actor and produces a state value to criticize the action made by the actor.

Figure 4. Actor–critic architecture showing that the actor receives the state and produces the actions. The critic network receives the state and the actions produced by the actor and produces a state value to criticize the action made by the actor.

Figure 5. DRL neural network architecture showing three streams for processing state information: (1) RGB stream, (2) DMI stream, and (3) features stream. The concatenation layer FC4 fuses the data received from the three streams.

Figure 5. DRL neural network architecture showing three streams for processing state information: (1) RGB stream, (2) DMI stream, and (3) features stream. The concatenation layer FC4 fuses the data received from the three streams.

5.3. VizNav Navigation Training

In addressing the challenges of UAV navigation in dynamic environments, Algorithm 1 (VizNav Training) introduces several key innovations that distinguish it from existing methods. Notably, it decouples the learning processes from UAV control execution, enhancing the system’s robustness by allowing updates to learning algorithms without affecting flight operations. Additionally, the algorithm features advanced configuration management, enabling smooth integration and straightforward adaptation of experimental settings, reward functions, and control parameters. This flexibility ensures that changes to the UAV’s operational goals or methods can be implemented without altering the core learning algorithm. Together, these features improve the adaptability and scalability of the UAV navigation training, making it well-suited for real-world applications in simulation environments where experimental conditions and operational controls frequently change. The following outlines the key steps involved in executing Algorithm 1:

1.

Initialization (Lines 1–8):

1.1

Experiment Configurations (Line 2): The algorithm starts by loading predefined settings that detail the UAV’s operating parameters and environmental setup.

1.2

3D Environment Launch (Line 3): A simulated 3D environment is initialized using Unreal Engine, creating a realistic navigation space.

1.3

UAV Initialization (Line 4): The UAV’s starting position and control commands—pitch, roll, yaw, and throttle—are initialized according to the predefined settings in the configuration file to ensure a standardized baseline for each training session.

1.4

DRL Agent Initialization (Lines 5–8): The replay buffer is initialized to store experiences of size M (Line 5), the reward generator is initialized to start calculating the reward (Line 6), and the DRL agent’s neural networks, i.e., policy and target networks, are initialized for both the actor and critic networks (Lines 7–8).

2.

Main Training Loop (Lines 9–24):

2.1

Episode Initialization (Lines 10–12):

2.1.1

Reset UAV (Lines 10–11): At the start of each episode, the UAV is reset to its initial position and orientation. Following the reset, the UAV’s initial state is captured, including its position, orientation, and sensor data, to establish the starting point for the episode. This ensures that each episode begins under consistent conditions.

2.1.2

Reset Collision Status (Line 12): The collision status is reset at the beginning of each episode. If a collision has occurred in a previous episode, the UAV status is reset to enable learning from mistakes without carrying over error states.

2.2

Episode Processing (Lines 13–23): For each step in the episode, the following tasks are performed. The episode will end either by reaching the terminal state (i.e., target reached or collision occurred) or upon reaching a limit of $\tau$ number of steps:

2.2.1

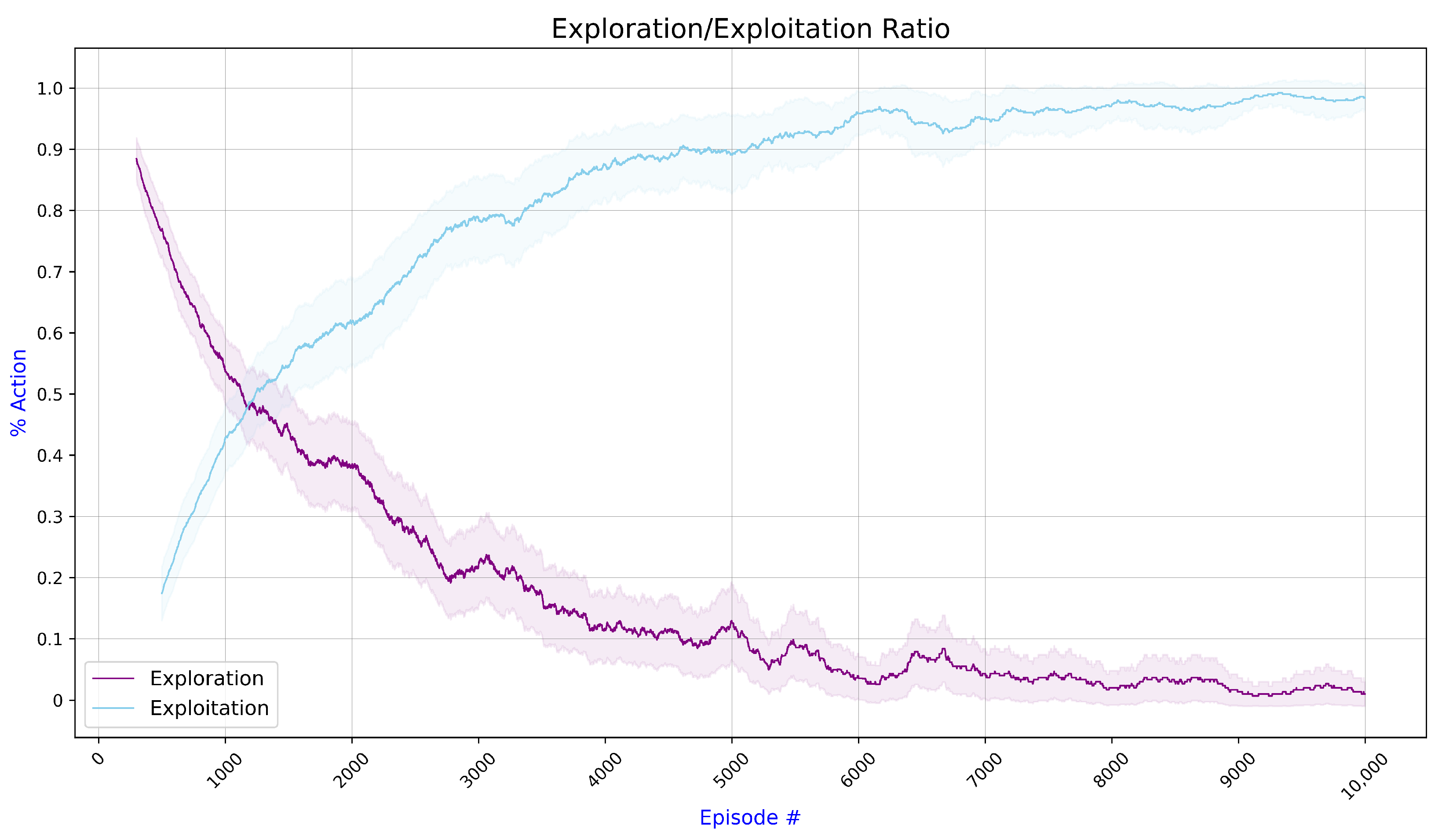
Exploration and Exploitation (Lines 14–16):

• Action Selection (Line 14): Actions are selected using a decaying $ϵ$-greedy strategy, which helps the UAV balance exploring new actions and exploiting known beneficial ones.
• Noise Addition and Clipping (Lines 15–16): To encourage exploration, random noise $\mathcal{N}(0,\sigma )$ is added to the selected actions (Line 15), then the actions are clipped at Line 16 according to the configured threshold values $[a_{min},a_{max}]$ to ensure they remain related and safe for execution.

2.2.2

Action Execution and Feedback (Lines 17–19):

• Flight Command Execution and State Observation (Lines 17–18): The selected action is converted into UAV flight commands (i.e., adjustments in pitch, roll, yaw, and throttle) and executed, which moves the UAV in the simulated environment. After executing the action, the agent observes the new state, including the image captured using the front-facing camera, position, orientation, and environmental interactions.
• Reward Calculation (Line 19): A reward is generated based on the observed new state, influencing future actions.

2.2.3

Learning from Experience (Lines 20–21):

• Experience Storage (Line 20): The experience (comprising the previous state, action taken, reward received, and new state) is stored in the replay buffer. These data are crucial for learning, as they provide a historical record of actions and outcomes.
• State Update (Line 21): After executing the action and observing the new state, the new state becomes the current state for the next step in the episode.

2.2.4

Agent’s Learning (Line 22): At each training step, the DRL agent refines its decision-making model by learning from a batch of experiences sampled from the replay buffer, progressively improving its action selection (policy) based on accumulated knowledge.

Building upon the training framework established by Algorithm 1, Algorithm 2 commences its execution at Line 22 of Algorithm 1. This transition initiates the deep reinforcement learning phase for the UAV agent. Algorithm 2 primarily employs the TD3 method [31] suited for environments with continuous action spaces. Nevertheless, the algorithm’s structure allows for substituting TD3 with other off-policy algorithms such as DDPG, providing flexibility based on specific needs or preferences. The main operations in Algorithm 2 include:

Algorithm 1 VizNav Training

1: function train(Configurations $\mathcal{C}$) 2:     Load Experiment Configurations $\mathcal{C}$ 3:     Launch 3D Environment 4:     Initialize UAV $\mathcal{U}$ 5:     Initialize Replay Buffer $\mathcal{B}$ according to the Experience Replay type Experience Replay type 6:     Initialize Reward Generator $\mathcal{R}$ 7:     Initialize DRL Agent: Actor ${\mu }_{\theta }$, Critics $Q_{{\omega }_1}$, $Q_{{\omega }_2}$ 8:     Initialize Target Networks: ${\mu }_{\theta }^{\prime }$, $Q_{{\omega }_1}^{\prime }$, $Q_{{\omega }_2}^{\prime }$ 9:     for $i=1$to N do 10:         Reset $\mathcal{U}$ 11:         $s_t\leftarrow \mathrm{State}(\mathcal{U})$ 12:         $collision\leftarrow False$ 13:         while ($t\le \tau$) and ($s_t\notin$ terminal state) do 14:            Select exploration/exploitation action $a_t$ using       decaying $ϵ$-greedy 15:            Add noise $\mathcal{N}(0,\sigma )$ to action $a_t$ 16:            Clip action $a_t$ according to ${\displaystyle {a_t}_{\top a_{min}}^{\perp a_{max}}}$ 17:            Transform $a_t$ to a flight-command            $({\Theta }_t,{\Phi }_t,{\Psi }_t,{\Omega }_t)$ 18:            Execute flight-command action $a_t$ and observe        the new state $s_{t+1}$ 19:            Generate the reward $r_t$ using $\mathcal{R}(a_t,s_{t+1})$ 20:            Store experience $e(a_t,s_t,r_t,s_{t+1})$ in $\mathcal{B}$ 21:            Update $s_t$ to $s_{t+1}$ 22:            Call the agent’s learning method learn() 23:         end while 24:     end for 25: end function

1.

Check for Adequate Experiences (Line 2): The algorithm first checks if the replay buffer contains enough experiences to form a batch of size N. If it does, it proceeds to the sampling step; otherwise, it waits until there are enough experiences to form a batch of size N.

2.

Sampling from Replay Buffer (Line 3): Extracts a mini-batch of N experiences from the replay buffer.

3.

Importance Sampling for PER (Lines 4–6): If PER [30] is employed, the algorithm retrieves importance sampling weights (Line 5) to focus on significant experiences.

4.

Target Action and Q-value Calculations (Lines 7–10): The algorithm computes the target actions using the policy network of the target model (Line 7), adds exploration noise (Line 8), and clips the actions to ensure they are within acceptable bounds (Line 9). It then calculates the target Q-values from the target critic network.

5.

Policy and Critic Network Updates (Lines 11–20): The critic networks are updated based on the loss between computed Q-values and the target Q-values (Lines 11–15), adjusting the model to predict value estimates better. This includes updating priorities in the replay buffer if PER is used (Lines 14–15).

6.

Policy Network Update (Lines 21–22): The policy network is periodically updated using a deterministic policy gradient approach.

7.

Soft Update of Target Networks (Lines 23–26): This step applies a soft update rule to gradually merge the trained network weights into the target networks, ensuring the stability of learning updates.

Algorithm 2 leverages a configuration management system initiated in Algorithm 1 at Line 7 to load essential DRL settings, such as learning rate, action noise thresholds, update intervals, and batch sizes. This mechanism standardizes initialization and operational parameters and facilitates adjustments to varying training conditions without necessitating modifications to the algorithm itself. The integration of Algorithms 1 and 2 forms a strategy for UAV training that merges direct environmental interaction (Algorithm 1) with reinforcement learning mechanisms (Algorithm 2). This combination addresses challenges such as adapting to new environments and optimizing responses to varied simulation conditions, providing a flexible framework for UAV navigation.

Algorithm 2 TD3 Agent Learning

1: function learn( ) ▹${\mu }_{\theta },Q_{{\omega }_1}$, $Q_{{\omega }_2},{\mu }_{\theta }^{\prime },Q_{{\omega }_1}^{\prime },Q_{{\omega }_2}^{\prime }$ networks are initialized in the train method, Algorithm 1 2:     if $len\left(\mathcal{B}\right)\ge N$ then 3:         Sample mini-batch of N experiences from $\mathcal{B}$ 4:         if PER is used then 5:               Retrieve Importance Sampling Weights $\lambda$ 6:         end if 7:         Extract all experiences $(a,s,r,s^{\prime })\in E$ 8:         Compute target actions $\tilde{a}$ using ${\mu }_{\theta }^{\prime }\left(s^{\prime }\right)$ 9:         Add noise $\mathcal{N}(0,\sigma )$ to $\tilde{a}$ 10:        Clip target actions $\tilde{a}$ according to ${\displaystyle {\tilde{a}}_{\top a_{min}}^{\perp a_{max}}}$ 11:        Compute target critics Q-value ${\tilde{q}}^{\prime }$ using        $min\left(Q_{{\omega }_1}^{\prime }(s^{\prime },\tilde{a}),Q_{{\omega }_2}^{\prime }(s^{\prime },\tilde{a})\right)$ 12:         Find target critics optimal Q-value $q_{*}^{\prime }$ for       all non-terminal states using $r+\gamma .{\tilde{q}}^{\prime }$ 13:         Compute critics expected Q-value ${\tilde{q}}_1$ & ${\tilde{q}}_2$ for        $Q_{{\omega }_1}(s,a)$ and $Q_{{\omega }_2}(s,a)$, respectively 14:         if PER is used then 15:                Update Critic 1 ${\nabla }_{{\omega }_1}J\left({\omega }_1\right)$ using             ${\mathrm{argmin}}_{{\omega }_1}{N}^{-1}\sum \lambda {(q_{*}^{\prime }-{\tilde{q}}_1)}^2$ 16:            Update $\mathcal{B}$ priorities using $|q_{*}^{\prime }-{\tilde{q}}_1|$ 17:            Update Critic 2 ${\nabla }_{{\omega }_2}J\left({\omega }_2\right)$ using             ${\mathrm{argmin}}_{{\omega }_2}{N}^{-1}\sum \lambda {(q_{*}^{\prime }-{\tilde{q}}_2)}^2$ 18:         else 19:            Update Critic 1 ${\nabla }_{{\omega }_1}J\left({\omega }_1\right)$ using            ${\mathrm{argmin}}_{{\omega }_1}{N}^{-1}\sum {(q_{*}^{\prime }-{\tilde{q}}_1)}^2$ 20:            Update Critic 2 ${\nabla }_{{\omega }_2}J\left({\omega }_2\right)$ using            ${\mathrm{argmin}}_{{\omega }_2}{N}^{-1}\sum {(q_{*}^{\prime }-{\tilde{q}}_2)}^2$ 21:         end if 22:         if $t\%d$ then 23:            Update ${\nabla }_{\theta }J\left(\theta \right)$ deterministic policy gradient            using $-N^{-1}\sum Q_{{\omega }_1}(s,{\mu }_{\theta }\left(s\right))$ 24:            Soft update all target networks: 25:                  ${\theta }^{\prime }\leftarrow \tau \theta +(1-\tau ){\theta }^{\prime }$ 26:                  ${\omega }_1^{\prime }\leftarrow \tau {\omega }_1+(1-\tau ){\omega }_1^{\prime }$ 27:                  ${\omega }_2^{\prime }\leftarrow \tau {\omega }_2+(1-\tau ){\omega }_2^{\prime }$ 28:         end if 29:     end if 30: end function

6. Evaluation

This section describes the experimental setup, presents the results with performance analysis, and discusses the findings.

6.1. Experimental Setup

Simulation environments are described in this subsection, followed by data collection methodology and configuration.

6.1.1. Simulation Environment

UAV training typically requires virtual 3D environments due to constraints such as limited computational resources, power supply limitations, and the high costs associated with UAV damage from collisions. This study conducted simulations using Microsoft AirSim flight simulator [11] and the Unreal 3D graphics engine [57]. For a clear demonstration of the environments used in the simulations, Figure 6 presents two types of visual representations:

• 3D View Snapshot provides a sample view of the UAV in the environment, captured from a third-person perspective.
• Voxel Grid offers a simplified 3D view of the environment, where the environment is divided into a 3D grid of cubes (voxels), with each voxel representing whether the space is occupied. These grids provide a view of the complete environment, showcasing the complexity of the environment; nevertheless, the realistic 3D rendering (as in 3D view) is employed in simulations.

These two visual representations are used in Figure 6 to illustrate the two distinct outdoor environments designed using the Unreal Engine for UAV navigation experiments:

• Neighborhood Environment features a small neighborhood block including residential buildings, roads, and vegetation. This is a static environment used for basic UAV navigation.
• City Environment captures a complex urban setting with high-rise buildings, moving cars, and pedestrians. The dynamic nature of this environment poses advanced challenges for UAV navigation, requiring strategies that adapt to moving obstacles.

6.1.2. Data Collection Methodology

Data are collected directly from the simulation in real-time, including recording UAV positional data, sensor outputs (from the onboard camera and IMU), and outcomes of the interaction with environmental objects. The DRL agent learns from these data as they arrive, continuously improving knowledge through episodes. For each episode, the data are collected and recorded in CSV files, allowing for detailed post-simulation analysis to assess learning progress and algorithmic performance over time. This structured data capture, which includes timestamps, control inputs, sensor readings, and navigation outcomes, facilitates a thorough performance analysis.

Moreover, the reward structure is standardized across all experiments to establish comparable performance metrics. The reward parameters, outlined in Section 4.3 and detailed in Section 6.1.3, were consistently applied in all test scenarios. This uniform application of reward calculations ensures that differences in UAV behavior and learning progress can be attributed to the intended changes of the experimental setup, such as changes in the replay buffer strategy or the use of depth imaging.

Figure 6. An overview of the two simulation environments used for the UAV navigation experiments summarizing spatial layout and obstacle distribution for illustrative purposes. Panels (a,b) show the neighborhood’s 3D view and voxel grid, respectively. Panels (c,d) show the city block’s 3D view and voxel grid, respectively.

Figure 6. An overview of the two simulation environments used for the UAV navigation experiments summarizing spatial layout and obstacle distribution for illustrative purposes. Panels (a,b) show the neighborhood’s 3D view and voxel grid, respectively. Panels (c,d) show the city block’s 3D view and voxel grid, respectively.

Similarly, a uniform DRL neural network architecture ensures comparability across all experiments, as shown in Figure 5. This architecture processes both RGB and depth information, along with scalar inputs. However, depth information is omitted in RGB-only experiments. Maintaining the same network structure across all trials increases the similarity of experiments and enables the focus on variables under consideration, such as algorithm choice or the use of experience replay.

Adhering to a consistent neural network architecture and reward system controls these variables, allowing for a fair comparison of results across different setups. This methodological consistency supports the integrity and reliability of our findings and enhances the validity of our conclusions.

6.1.3. Experiment Configurations

The ultimate goal of all experiments is for the UAV to reach the destination point with the fewest required steps while the UAV is front-facing the destination. The destination point is selected at 100 m from the start point, and no restrictions are imposed on the direction or orientation of the UAV’s movement. The DRL agent used a decaying $ϵ$-greedy strategy for action selection where, at the initial 1500 episodes, the agent is primarily exploring the environment. In contrast, exploiting actions are dominant in the later stages, as shown in Figure 7.

The DRL agent adopts episodic RL training with a maximum of 10 steps per trajectory, as configured in the configuration file. Achieving one of the following is considered a terminal state and results in resetting the UAV/agent to its initial settings: (1) reaching the destination, (2) colliding with the objects in the environment, and (3) reaching the maximum number of episodes.

Configuration files are employed to specify each experiment setting. The following values are used to generate various reward parts described in Section 4: the Collision Reward $r_{collision}({\lambda }_c=1, {\rho }_c=-100, {\xi }_c=2)$, the Distance Reward $r_{distance}$$({\lambda }_d=200,$ ${\alpha }_d=100$, ${\beta }_d=0.1, {\gamma }_d=15.0)$, the Orientation Reward $r_{orient}({\alpha }_{o1}=10, {\beta }_{o1}=1,$${\alpha }_{o2}=10,$${\beta }_{o2}=0.01,$${\xi }_o=0.349066)$, and the Time-Step Reward $r_{step}({\alpha }_s=10)$. These values have been determined through experiments.

The UAV settings restrict the UAV to fly at a maximum altitude of 10 m to stay within the virtual environment boundaries. The maximum/minimum value of pitch, roll, and yaw angles in radians are: $angl{e}_{\Theta }=\pm 0.785398,$$angl{e}_{{\Phi }_t}=\pm 0.785398,$$angl{e}_{{\Psi }_t}=\pm 0.785398$, and the throttle value between 0 and 1 $Throttl{e}_{{\Omega }_t}=[0,1]$. The selected values help to stabilize the UAV maneuvers, as moving without limiting the angles can cause the UAV to flip and crash, as we have observed in the experiments. However, these values can be changed in the configuration files to support different experiment requirements and goals.

6.2. Performance Analysis

This section examines TD3 and DDPG algorithms for training the DRL agent using two different environments (neighborhood and city), employing two types of replay buffer techniques: Experience Replay (ER) and Prioritized Experience Replay with Importance Sampling technique (PER). Moreover, two imaging techniques are considered: color images (RGB) and depth map images (DMI) combined with RGB images (DRGB). Therefore, there are four different experiments for each combination of the algorithm and environment:

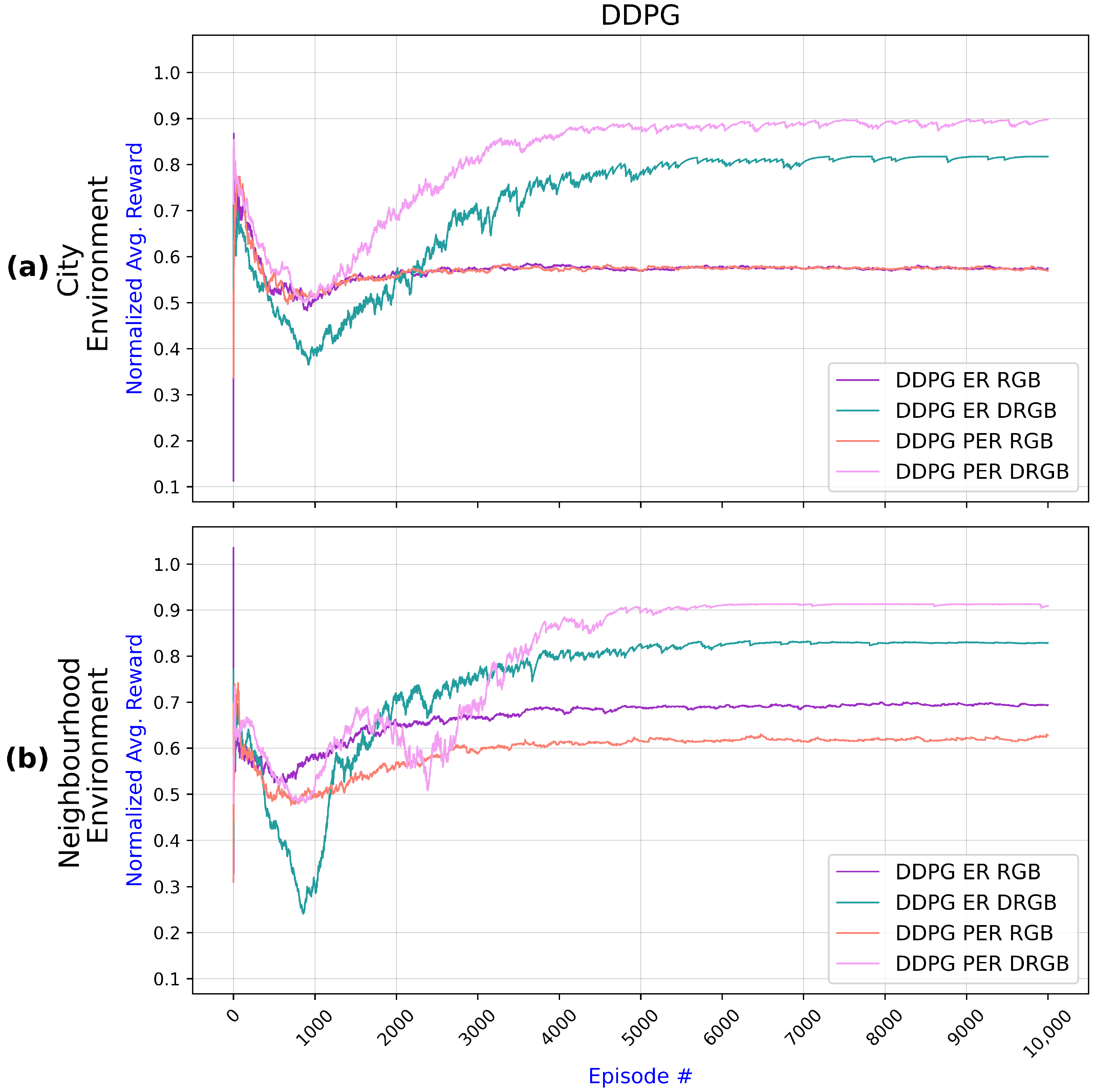
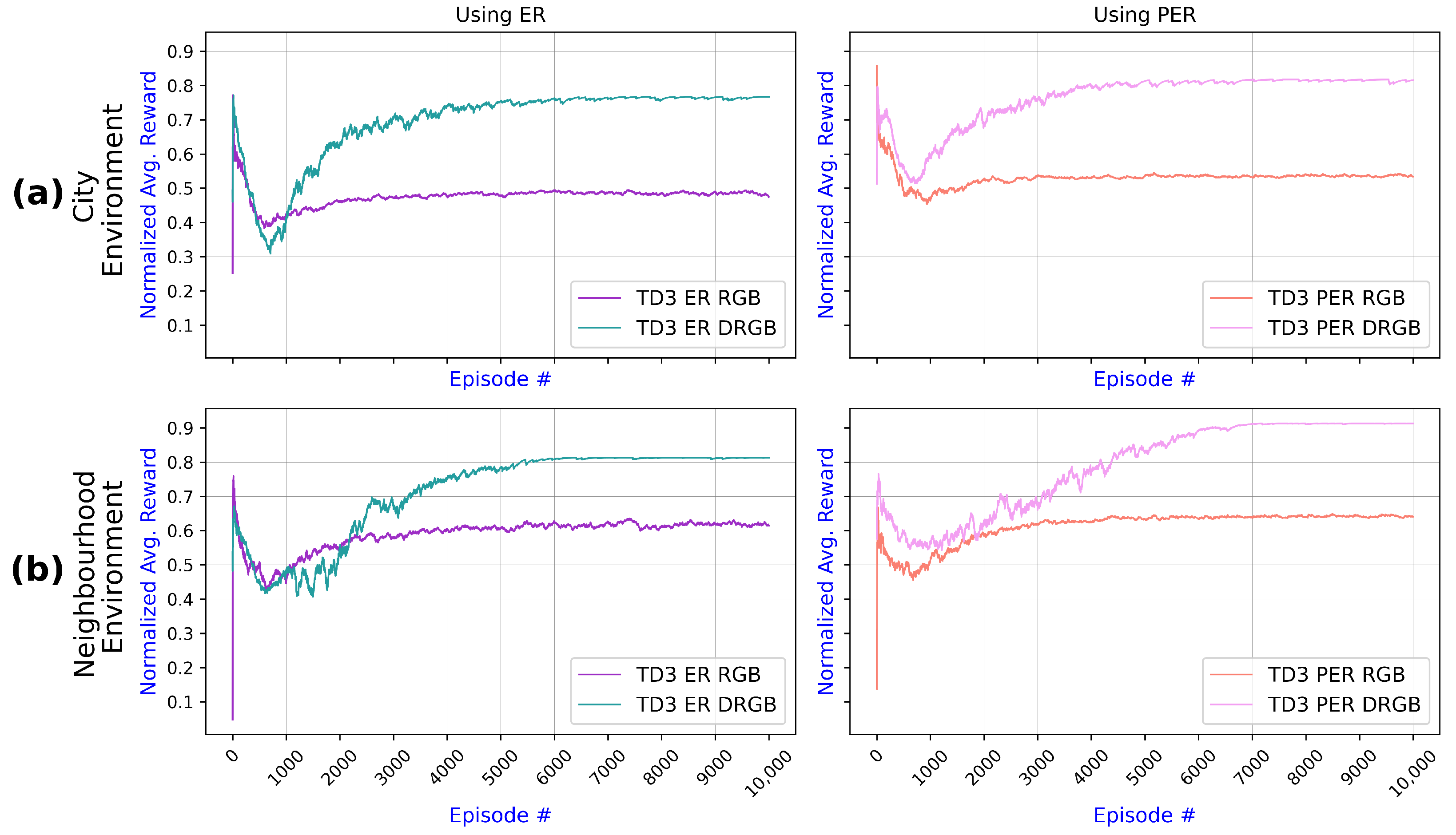
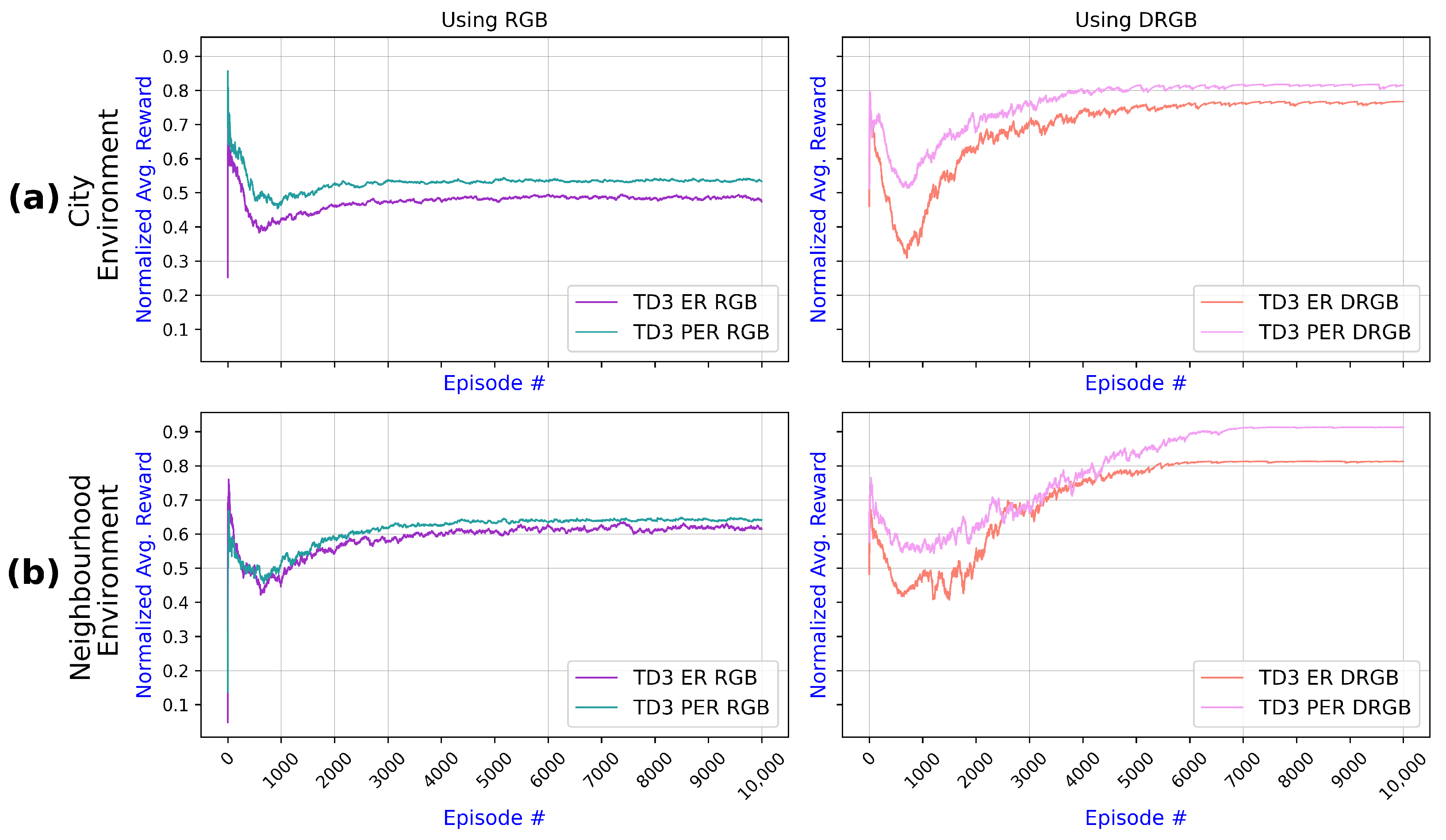
• Using ER and RGB images (ER RGB);
• Using PER and RGB images (PER RGB);
• Using ER with RGB and DMI (PER DRGB);
• Using PER with RGB and DMI (PER DRGB).

Evaluations are based on the average discounted reward Equation (1), which quantifies the total expected reward a UAV can collect over time, adjusted by a factor that decreases the value of future rewards.

All experiments, including different algorithms, different buffering and imaging techniques, are examined in two environments, to introduce environment diversity and to consider static and dynamic environments. A direct comparison with reported performance metrics in other studies is not feasible because, as noted by AlMahamid and Grolinger [1], there is a lack of standardized benchmarking approaches in RL-based UAV navigation. Nevertheless, the two environments introduce varying levels of navigation complexities, and consideration of different algorithms and variants shows the contributions of various improvements. Moreover, we compare TD3 with the DDPG algorithm to demonstrate the impact of the algorithm selection on the overall navigation. The two algorithms were selected because they support unlimited states and continuous actions and, as discussed in Section 3.4, are suitable for UAV navigation.

The following subsections examine the overall behavior of the TD3 and DDPG algorithms. Next, they discuss the algorithm variants and investigate the impact of the replay buffer type and depth images.

6.2.1. TD3 and DDPG Results

The comparative analysis of the TD3 and DDPG algorithms is detailed in Figure 8, illustrating how these algorithms perform under different experimental conditions. The first row of the graphs depicts results obtained using the city environment, while the second row depicts results obtained using the neighborhood environment. This figure compares the algorithms’ (DDPG vs. TD3) performance in the static neighborhood environment and the dynamic city environment, exploring the impact of varying data input techniques (RGB vs. DRGB) and experience replay strategies (ER vs. PER).

As shown in Figure 8, TD3 outperformed DDPG in all experiments for both environments. TD3 achieved noticeably better results for all experiments in all environments, except for ER using RGB only, where TD3 slightly outstrips DDPG.

Comparing the two environments, TD3 achieved slightly higher rewards operating in the neighborhood environment compared to its performance in the city environment. The city environment is more challenging because humans and cars move dynamically in the city, and the agent needs to accommodate this.

Furthermore, the comparative results presented in Figure 8 illustrate that, while TD3 and DDPG achieve similar outcomes with ER and RGB images (as shown in the first column of graphs), distinct performance differences emerge when DMI is utilized (refer to the second and fourth columns) or when ER is substituted with PER (visible in the third and fourth column). Notably, TD3 consistently surpasses DDPG, particularly when combining PER and DMI, indicating its superior efficacy in these configurations.

6.2.2. Examining Variants of TD3 and DDPG

All TD3 experiments for the two environments are compared in Figure 9. Using PER with DMI outperformed all other methods for both environments and yielded a better reward. Changing from ER to PER resulted in an increased reward; however, adding depth images produces a larger improvement, as observed from the two top lines corresponding to the approaches with DMI. While PER helped the agent learn significant experiences, using DMI enabled the agent to understand the surroundings’ depth better and improved obstacle avoidance, resulting in a higher reward. However, TD3 required more convergence time when employing DMI than RGB images.

While Figure 9 presents results for TD3, Figure 10 does the same for DDPG. Generally, DDPG results follow the same patterns as the TD3 results, with PER and DMI improving the UAV training. An exception is when using ER versus PER with RGB images only: for the city environment, DDPG achieved very similar results with ER and PER. Furthermore, like TD3, DDPG requires more time to converge when using DMI than when using RGB images.

6.2.3. Examining the Impact of DMI and PER

This subsection focuses on examining the impact of DMI and PER using TD3, as TD3 overall achieved better results than DDPG, as discussed in Section 6.2.1. Moreover, the results for DDPG follow the same patterns as those for TD3.

Figure 11 compares TD3 variants with and without depth information to examine the impact of the depth information. The experiments reveal that DMI considerably enhanced UAV training compared to utilizing RGB images alone, regardless of the environment or the replay buffer type (ER vs. PER). Nevertheless, the agent took around 4000 episodes to converge utilizing DMI compared to around 2000 episodes using RGB images. The significant increase in the convergence time is reasonable owing to the knowledge the agent must acquire about the object depth information.

The impact of PER on TD3 in the two environments is examined in Figure 12. It can be observed that employing PER compared to using ER enhanced the UAV training for both environments and was irrelevant if RGB or depth images were employed because PER prioritizes experiences and reuses more relevant experiences, which assists the agent in learning and leading to a higher reward. The improvement in PER reward is more evident when using DMI in the city environment. Comparing Figure 11 and Figure 12, it can be observed that introducing depth images has a more significant impact on the reward than changing from ER to PER.

6.3. Discussion

The presented results demonstrate that the proposed VizNav framework can train the agent to navigate to the destination point while avoiding obstacles using the TD3 algorithm. The proposed approach does not simplify the environment as demonstrated through two complex simulated environments: the neighborhood and the city. Moreover, the agent employs continuous action space with unlimited states, resulting in realistic UAV movements and enabling navigation in complex environments. Using an off-policy algorithm in experiments TD3 and DDPG enables the agent to employ experience replay strategies to improve the stability of learning [30].

The VizNav framework, as shown in Figure 3, enables an easy change of the RL algorithms and changes to the framework modules. Moreover, the use of configuration files supports straightforward experiment setup without changes to the framework itself. The presented experiments have taken advantage of this modularity to examine different RL algorithms, experience buffer strategies, depth images, and behavior in various environments. Moreover, such a modular approach will enable substituting the currently used DRL algorithms with new ones as they emerge, supporting the fast adaptation of the latest RL research in UAV navigation.

Experiments, as shown in Figure 8, demonstrated that the TD3 algorithm outperformed DDPG in all experiments irrelevant to the environment, confirming the work of Fujimoto et al. [31], which demonstrated that TD3 improves DDPG by employing two critics and applying delayed policy updates. While TD3 performed better than DDPG, the difference between the two algorithms varied depending on the type of replay buffer and the use of depth information.

When TD3 was used with PER and DMI, the results were better than when TD3 was used with ER or RGB images, as seen in Figure 9. The same was observed for DDPG in Figure 10, demonstrating the need to employ experience replay and depth images. Figure 11 and Figure 12 further examined the impact of DMI and PER and showed that the DMI has a more significant effect on the improvement of the navigation than PER.

While the evaluation demonstrated that depth information improves UAV navigation, it is vital to notice that this requires different cameras and may be prohibitive based on cost, the type of drone, or other reasons. Still, the proposed VizNav framework can operate without such information. Moreover, depth information results in a longer convergence time, as shown in Figure 9 and Figure 10, which can be explained by the need to learn from more complex data.

Experiments presented in this study employed DRL neural network architecture shown in Figure 5: this structure captures RGB, depth information, and scalar information. Depth information is not used in RGB-based experiments. The same network structure is employed for all experiments. It is important to note that tuning this structure for each algorithm and each environment could potentially improve the overall results; however, we have kept the network architecture fixed to analyze the performance of the algorithms and the impact of depth images and experience replay. Similarly, the reward structure presented in Section 4.3 with parameters described in Section 6.1.1 was consistent throughout the experiments to facilitate the comparison of results.

Overall, the presented experiments demonstrated that the proposed VizNav provides a flexible approach to navigation in dynamic environments. Moreover, the experiments showed that TD3 outperforms DDPG and that using DMI and PER improves navigation.

7. Conclusions

This paper proposes the VizNav framework, a novel approach to UAV navigation that utilizes deterministic off-policy deep reinforcement learning (DRL) with Prioritized Experience Replay (PER). The framework facilitates vision-based autonomous navigation in dynamic environments with continuous action space by leveraging a front-facing camera that provides depth map images (DMI) to augment RGB scenery images with detailed depth information. The evaluation in dynamic environments demonstrated that integrating TD3 with PER and DMIs outperforms navigation with TD3 and improves upon the DDPG algorithm. While adding depth information had a more significant impact than employing PER, it resulted in longer convergence times.

Unlike conventional navigation methods, VizNav does not impose restrictions on UAV maneuverability nor simplifies the training environment, thereby reflecting more realistic and complex operational scenarios. The control scheme employed using pitch, roll, yaw, and throttle closely mimics real-world UAV controls, enhancing the practical applicability of our approach.

The modular and adaptable design of the VizNav architecture allows for the separation of learning and training processes, the customization of simulation environments and reward functions, and the ability to update and tailor the controller managing the UAV. This flexibility enhances the framework’s utility not only for UAV navigation but also for broader applications in RL simulations for autonomous systems, including robotics control, autonomous vehicles, and operations in industrial and agricultural sectors.

It is essential to recognize the difficulties of transitioning from simulations to the real world. To start with, obtaining accurate depth images is not only difficult, but the specialized equipment also increases cost, and the added weight reduces the battery life. Moreover, the generalization of RL algorithms to unseen environments is still limited and could result in crashes and damage to the drone. Nevertheless, the presented study represents a step towards autonomous RL-driven UAV navigation.

Future work will expand the VizNav framework’s capabilities by incorporating additional sensor information, such as LiDAR, to enrich environmental data inputs. We also aim to explore the framework’s generalization and sensitivity to various parameters. These steps will pave the way toward autonomous RL navigation and deployments on real-world drones and other autonomous robotic platforms, pushing the boundaries of what is possible in autonomous navigation and control.