Research on Improvement Methods for Driven System of Bio-Inspired Aircraft to Increase Flight Speed

Abstract

The flapping-wing ornithopter is an aircraft that imitates the flight of birds in nature. It has significant potential and value in various fields such as surveying, search and rescue, military reconnaissance, and unmanned warfare, due to its biomimetic stealth and high efficiency in low Reynolds number flight. However, the cruising speed of current flapping-wing ornithopters is generally lower than that of birds of the same size, which seriously affects biomimicry, mission capability, and wind resistance. Increasing the cruising speed can make the aircraft fly more like a bird, improve the efficiency of reconnaissance missions and wind resistance per unit time, and has important research significance. However, the methods to increase the cruising speed of flapping-wing ornithopters are currently lacking. Firstly, this paper presents improvements to the propulsion system based on the team’s “Dove” aircraft to meet the speed requirements. The actual flapping frequency and rocking arm end torque of the “Dove” aircraft under different voltages are tested. To select and match the motor and gearbox in the propulsion system, a method for matching and selection among the motor, gearbox, and load is proposed. Finally, wind tunnel experiments and flight validations are conducted on the improved flight prototype. The wind tunnel experiments show that the increase in flapping frequency has a significant impact on thrust. The trimmed states at different speeds are obtained. The flight validation demonstrates the sustained high-speed flight capability of the aircraft. At a flapping frequency of approximately 15 Hz, the average flight speed of the aircraft is 13.3 m/s within a 15 min duration, which is close to the actual flight speed of pigeons. The duration of high-speed flight is tripled compared to the initial duration. The speed improvement successfully enhances the biomimicry and efficiency of reconnaissance missions per unit time for the aircraft.

1. Introduction

The initial human flight dreams originated from the imitation of flying creatures in nature, such as birds and insects. Humans have long had a fascination with the flight of living organisms and have made numerous attempts to replicate it. Extensive research has shown that birds possess exceptional maneuverability and energy efficiency [1,2,3,4,5,6,7,8,9]. Bio-inspired flight vehicles typically operate at Reynolds numbers below 10⁵, where fixed-wing and rotary-wing aircraft exhibit lower flight efficiency. In contrast, bio-inspired flight vehicles generate high lift and thrust through wing flapping [10,11], offering wide-ranging applications in military and civilian sectors [12,13,14,15,16].

In recent years, flapping-wing aircraft have attracted increasing attention and research. Nguyen et al. [17] designed a tailless flapping wing micro air vehicle (NUS-Roboticbird). Currently, the aircraft weighs 31 g and has a wingspan of 22 cm. It is capable of flying rapidly forward at a speed of approximately 5 m/s and can sustain flight for 3.5 min with a payload of a 4.5 g onboard camera. The flight speed of the RoboBee, a bee-inspired flapping-wing aircraft developed by Harvard University in the United States, is about 1 m/s, while the flight speed of bees in nature is approximately 6 m/s [18]. The Nano Hummingbird, a hummingbird-inspired flapping-wing aircraft developed by AeroVironment in the United States, has a flight speed of 4.7 m/s, whereas the actual flight speed of hummingbirds is around 8.3 m/s [19]. The SmartBird, a seagull-inspired flapping-wing aircraft developed by Festo in Germany, achieves a flight speed of 7 m/s, while the real seagull’s flight speed is approximately 14 m/s [18]. The “Dove”, a pigeon-inspired flapping-wing aircraft developed by Northwestern Polytechnical University in China, has a flight speed of 10 m/s, whereas the actual flight speed of pigeons is around 16 m/s [18]. The differences in flight speeds between these typical bio-inspired flapping-wing aircraft and real-life organisms are summarized in

Table 1. Comparison between the flight speeds of bio-inspired flapping-wing aircraft and real organisms.

Bio-Inspired Aircraft	Flight Speed (m/s)	Real Organism Flight Speed (m/s)	Bio-Inspired Aircraft Image
RoboBee	1	6
Nano Hummingbird	4.7	8.3
SmartBird	7	14
Dove	10	16

. These bio-inspired flapping-wing aircraft are developed based on the characteristics of organisms in the natural world. However, they share a common characteristic, which is that the flight speed of bio-inspired aircraft differs from that of real organisms.

According to Table 1, it can be observed that the current flight speeds of flapping-wing aircraft are generally lower than those of birds of similar size. This makes them easily detectable and reduces the inherent bio-inspired camouflage and deception of these aircraft. Additionally, low flight speeds in flapping-wing aircraft can lead to the following drawbacks:

• Low mission efficiency: Flapping-wing aircraft typically have lower mission efficiency during low-speed flight. This is because, at low speeds, the distance covered by the aircraft per unit of time is relatively small, resulting in lower mission efficiency.
• Weak wind resistance: Flapping-wing aircraft exhibit weaker resistance to wind during low-speed flight. If the flight speed of a flapping-wing aircraft is low and it has a small inertia, it becomes more susceptible to disturbances from gusts or crosswinds in the atmospheric environment. This can cause the aircraft to deviate from its intended trajectory or even disrupt normal flight, limiting the application of flapping-wing aircraft in complex environments and adverse weather conditions.

Therefore, in order to improve the mission efficiency, wind resistance, and bio-inspired camouflage of bio-inspired flapping-wing aircraft, it is important to develop aircraft that can achieve higher speeds or speeds closer to those of real birds.

Currently, in order to improve the speed of bio-inspired flapping wing aircraft, most researchers focus on optimizing the wing design to increase the aircraft’s thrust and, consequently, its flight speed. Li et al. [20] studied the effect of wing parameters on aerodynamic forces and used an optimized wing design to construct a 30 g flapping wing aircraft, which underwent outdoor flight testing. The aircraft was able to fly for 6.5 min with a payload of 4.5 g. Within a certain range, increasing the flapping frequency will increase the thrust. Shkarayev et al. [21] investigated the influence of flapping frequency on lift and thrust and found that thrust increases with increasing flapping frequency, while lift shows less significant variation with increasing flapping frequency in the absence of angle of attack. Wu et al. [22] studied the relationship between passive deformation of flexible wings and generated thrust and found that within a certain range, increasing the flapping frequency leads to nearly linear increase in thrust. The researchers in these studies generally focus on improving the speed and performance of flapping-wing aircraft to achieve more efficient task execution and better biomimetic effects. They explore different design methods, including optimizing wing profiles, increasing flapping frequencies, and enhancing the design of propulsion systems. However, increasing the flapping frequency imposes higher demands on the flapping mechanism. Therefore, this study will focus on investigating methods to improve flight speed by increasing the flapping frequency.

To improve the flight speed of the ornithopter to the level of birds, the first problem to be solved is to ensure that the flapping aircraft’s propulsion system can generate sufficient driving force to obtain the required lift and thrust for fast flight. However, there is currently a lack of systematic research on how to design a flapping propulsion system that possesses rapid forward propulsion capabilities. Moreover, the design improvements need to address issues such as the selection of motors and reducers, as well as the matching of the flapping mechanism with the new motors and reducers.

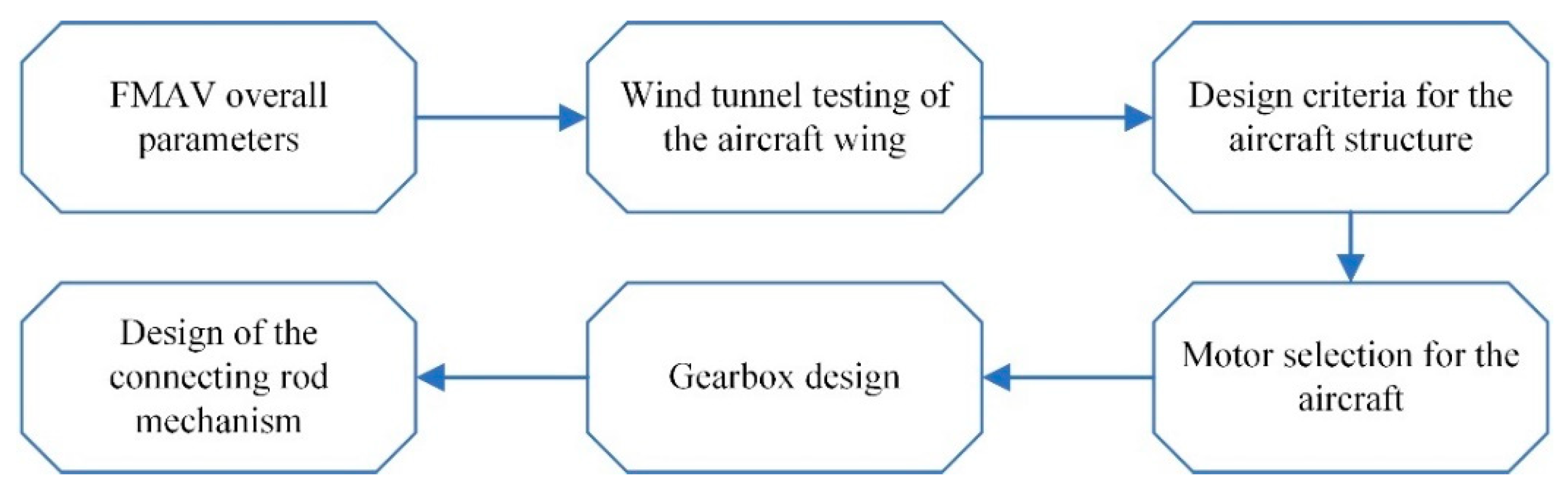
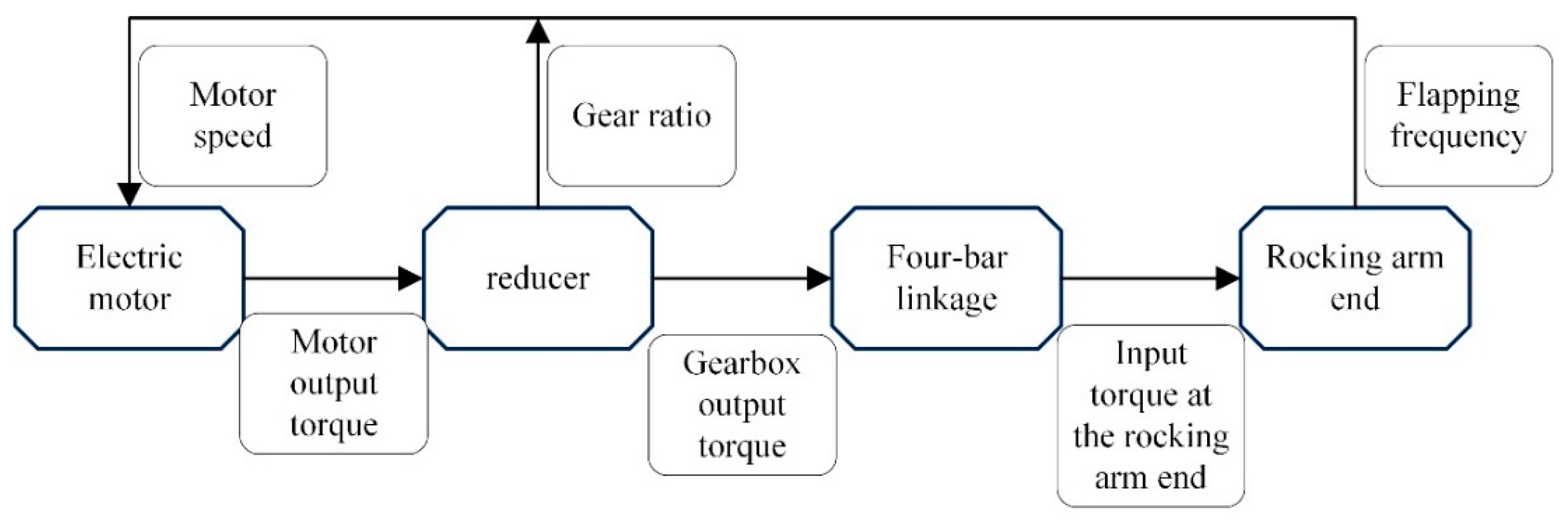
For the same type of mechanism design, in order to meet the requirements for increased speed, a complete drive system needs to be redesigned separately. This will increase the design cost and extend the product development time. Currently, there are not many researchers who have conducted detailed studies on the matching design of various subsystems in the propulsion system. Li et al. [23] conducted comprehensive research on the design methodology of mechanical transmission flapping mechanisms for conventional motor-driven ornithopters and summarized the general process of mechanical transmission flapping mechanism design, as shown in Figure 1. Han et al. [24] introduced the bio-inspired design and manufacturing of small-scale winged micro aerial vehicles. Jones et al. [25] provided an introduction to the design methods of various subsystems in flapping wing aircraft and successfully designed a flapping wing aircraft weighing as light as 11 g, with a wingspan of 23 cm and a length of 18 cm. This aircraft utilizes a rechargeable battery and can fly for approximately 20 min. Furthermore, it is capable of stable flight at speeds ranging from 2 to 5 m per second. These studies present design methodologies for individual subsystems of flapping-wing aircraft but do not provide detailed discussions on the matching design between these subsystems. Therefore, the main objective of this paper is to propose a set of design methods for improving the propulsion system of flapping aircraft, specifically targeting the need for increased speed. The proposed methods will be validated through wind tunnel experiments and flight tests.

2. Research on Matching Methods between Motor and Reducer in the Propulsion System

2.1. Actual Flapping Frequency Testing of “Dove” Aircraft at Different Voltages

The cruising speed of the “Dove” aircraft is 10 m/s, while the typical flight speed of a real pigeon ranges from 13 to 16 m/s. There is a significant difference between the flight speed of the aircraft and that of real birds. The other parameters are shown in

Table 2. Main Parameters of “Dove” Aircraft.

Parameter	Value
Weight/g	230~280
Wingspan/cm	60
Cruising Speed/(m/s)	10
Flapping Frequency/Hz	10
Maximum Flight Time/min	185

[26]. The propulsion system of the “Dove” aircraft is shown in Figure 2. A low flight speed reduces the biomimicry of the ornithopter, decreases its operational range, and compromises its wind resistance. Therefore, this paper focuses on improving the speed based on the “Dove” aircraft platform.

According to the limit testing of the “Dove “ aircraft, when equipped with a 3S battery (13.05 V), it can briefly achieve a flight speed of 15 m/s under a flapping frequency of 15 Hz. However, this leads to severe motor overheating, and gear teeth are prone to strength failure.

In order to obtain the voltage of the “Dove” mechanism at a flapping frequency of 15 Hz, this study conducted actual wing-flapping frequency tests on the “Dove” mechanism at different voltages, as shown in Figure 3. The voltage of the motor was adjusted by adjusting the value of the voltage regulator power supply. During each test, the throttle of the remote controller was set to the maximum to ensure that the input voltage of the motor matched the voltage value of the voltage regulator power supply. The current of the motor and the input power of the motor were simultaneously recorded during the testing process. The test results are shown in Figure 4. Based on the test results, it can be determined that the “Dove” mechanism has a wing-flapping frequency of 14.9 Hz at a voltage of 12.5 V, with an input power of 60 W for the motor.

2.2. Calculation of Load Torque at the Rocker Arm End

The no-load current of the MN1804 motor was measured by supplying it with power from a voltage regulator while the motor was under no load. The measured no-load current (I₀) is 0.49 A.

The internal resistance and back electromotive force constant (K_e) of the MN1804 motor are calculated using the measured voltage, current, and flapping frequency. The first-order motor model provides the relationship between motor voltage, current, and motor speed [27,28,29].

$$\begin{array}{c}{E}_m=R_m{I}_m+K_e{\omega }_m\end{array}$$

(1)

• E_m—Motor voltage;
• R_m—Motor internal resistance;
• I_m—Motor current;
• ω_m—Motor speed, (rad/s).

The data in

Table 3. Parameters of the three motors.

Motor Model	KV Value (RPM/V)	No-Load Current (A)	Resistance (Ω)	Weight (g)
MN1804	2400	0.49	0.78	16
Aeolus 2105.5	3600	1.4	0.07	21
GTS V3 2104	3000	0.9	0.11	16

were fitted using a linear regression analysis method, and the fitting result is shown in Figure 5. The fitted curve can be represented by the following equation:

$$\begin{array}{c}\left\{\begin{array}{c}{E}_m=0.7768I_m+0.00377{\omega }_m\\ R^2=0.9983\end{array}\right.\end{array}$$

(2)

Based on the analysis, the MN1804 motor has an internal resistance of 0.78 Ω and a back electromotive force constant (K_e) of 0.00377.

According to the first-order motor model (3) and the current and voltage of the motor at a wing-flapping frequency of 15 Hz, the motor speed and torque can be determined.

$$\begin{array}{c}\left\{\begin{array}{c}{T}_m=\left(I_m-I_0\right)K_m\\ E_m=R_m{I}_m+K_e{\omega }_m\end{array}\right.\end{array}$$

(3)

• T_m—Motor torque;
• K_m—Motor torque constant.

In engineering applications, it is common to assume K_e to be equal to K_m. The transmission ratio of the flapping mechanism to the load can be approximately determined by the ratio of the rocker arm length (l₃) to the crank-connecting rod length (l₁) [30].

$$\begin{array}{c}\left\{\begin{array}{c}{T}_{load}=\frac{1}{2}\frac{l_3}{l_1}{i}_{ori}{T}_m\\ \frac{l_3}{l_1}=2\\ i_{ori}=24.9\end{array}\right.\end{array}$$

(4)

• i_ori—Original reduction ratio;
• T_load—Load torque at the rocker arm end when the flapping frequency is 15 Hz.

The calculation yields that at flapping frequency of 15 Hz, T_load = 0.40 N·m, and ${\omega }_m=2346 \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$.

2.3. Study on Drive System Matching Methods

2.3.1. Calculation of Motor Efficiency

The power transmission flowchart of the drive system is shown in Figure 6. The output power of the battery is transmitted through the electronic speed controller (ESC), motor, reducer, and four-bar linkage to the end of the rocker arm. The overall efficiency of the system is given by

$$\begin{array}{c}{\eta }_{total}=\frac{P_O}{P_T}={\eta }_1{\eta }_2{\eta }_3{\eta }_4\end{array}$$

(5)

• η₁—ESC efficiency;
• η₂—Motor efficiency;
• η₃—Reducer efficiency;
• η₄—Four-bar linkage efficiency;
• P_O—Input power at the end of the rocker arm;
• P_T—Output power of the battery.

In the improvement of the drive system in this study, in order to minimize the improvement cycle and keep the size and materials of the original ESC and four-bar linkage unchanged, it is assumed that the effect of fine-tuning the gear size on the efficiency of the reducer is negligible. Therefore, the change in efficiency of the drive system is only related to the motor efficiency. Here, we assume that η₁, η₃, and η₄ are constant and can be represented by a constant value, denoted as k. Therefore, the overall efficiency of the drive system is related to the motor efficiency, which in turn is related to the output power of the battery and the output power of the motor.

For different types of motors, while keeping the wing type unchanged, the power required at the end of the rocker arm at a flapping frequency of 15 Hz is a constant value. Based on the motor’s output speed and average output torque obtained from the “Dove” at a flapping frequency of 15 Hz, the power required for motor output can be calculated.

$$\begin{array}{c}{P}_{OUT}=T_m\times {\omega }_m=0.0162\times 2346=38 \mathrm{W}\end{array}$$

(6)

The motor efficiency is calculated using the following equation:

$$\begin{array}{c}{\eta }_2=\frac{P_{OUT}}{UI}\times \%\end{array}$$

(7)

• U—Battery voltage;
• I—Battery current.

According to the first-order motor model, the current I of the motor can be determined under different voltages. Due to the requirement of the same output power, for different motors and different voltages, the efficiency of the motor obtained from Equation (8) is also different.

$$\begin{array}{c}\left\{\begin{array}{c}{T}_m=\left(I-I_0\right)K_m\\ E_m=R_{m}I+K_e{\omega }_m\\ T_m\times {\omega }_m=P_{OUT}\end{array}\right.\end{array}$$

(8)

2.3.2. Calculation of Gear Ratio

The gear ratio is calculated using the following equation:

$$\begin{array}{c}i=\frac{{\omega }_m}{2\pi f_{set}}\end{array}$$

(9)

The motor speed ${\omega }_m$ calculated based on the first-order motor model can be used to calculate the gear ratio at a flapping frequency of 15 Hz. The calculated gear ratio serves as a preliminary selection criterion, but the final choice should consider factors such as the size of the reducer, the ease of gear machining and manufacturing, and the suitable operating range of the motor.

2.4. Selection of Motor and Gear Ratio

2.4.1. Selection of Motor

In general, for pigeon-scale biomimetic bird-like aircraft, the power input multiplier factor $K_p$, which represents the ratio of the input power of the propulsion system to the cruising power during flight, is typically around 4 to 5. The overall lift-to-drag ratio of the aircraft is around 3 to 4 [30].

$$\begin{array}{c}{P}_{in}=K_p{P}_{cruise}\end{array}$$

(10)

$$\begin{array}{c}{P}_{cruise}=D{V}_{cruise}\end{array}$$

(11)

$$\begin{array}{c}D=\frac{W_{to}}{\raisebox{1ex}{$L$}\!\left/ \!\raisebox{-1ex}{$D$}\right.}\end{array}$$

(12)

• P_in—Total input power of the propulsion system;
• K_p—Power input multiplier factor;
• P_cruise—Power during cruise flight;
• W_to—Takeoff weight;
• D—Drag;
• L—Lift.

Assuming an initial takeoff weight of 2.5 N, based on the lift-to-drag ratio, the range of cruise drag can be determined as D = 0.625 N~0.82 N. Assuming a flight speed of 15 m/s, the range of cruise power can be determined as $P_{cruise}$ = 9.375 W~12.3 W. Based on the multiplier factor, the final range of total input power of the propulsion system is approximately 37.5 W~61.5 W. The ground flapping experiment in Section 2.1, with a flapping frequency of 15 Hz, yielded a motor input power of 60 W, which falls within the estimated range mentioned earlier. This result further supports the correctness of the two methods for calculating the total required power.

Based on the calculated preliminary selection of the drive system input power, commonly available motors on the market that meet the power requirements can be chosen. The detailed parameters of the motors are shown in Table 3. The Aeolus 2105.5 motor and GTS V3 2104 motor have their no-load current and internal resistance values provided by the manufacturer.

In Equation (13), the motor efficiency can be calculated based on the motor’s no-load current $I_0$, internal resistance $R_m$, motor back electromotive force constant $K_e$, and motor output power $P_{OUT}$, for different voltages.

$$\begin{array}{c}\left\{\begin{array}{c}{T}_m=\left(I-I_0\right)K_m\\ E_m=R_{m}I+K_e{\omega }_m\\ T_m\times {\omega }_m=P_{OUT}\end{array}\right.\end{array}$$

(13)

When the voltage of the motor varies, the calculated motor current, motor output speed, and motor output torque differ, resulting in different motor efficiencies and gear ratios. For the convenience of ground testing, the motor voltage is typically controlled through the throttle on the remote controller. Therefore, at a voltage of 3S (13.05 V), the motor efficiencies at different voltages are compared for the three motors at throttle settings of 100%, 90%, 80%, 70%, and 60%. The results are shown in

Table 4. Motor efficiency and gear ratio with a flapping frequency of 15 Hz of MN1804 at different voltages.

Voltage (V)	Output Torque (N∙m)	Output Speed (rad/s)	Current (A)	Motor Efficiency (%)	Gear Ratio
13.05	$0.01497$	$2539$	4.46	65.3	$27.0$
12.38	$0.01682$	$2259$	4.95	62.0	$24.0$
11.67	$0.02009$	$1892$	5.82	56.0	$20.1$
11.30	$0.02445$	$1554$	7.00	48.2	$16.5$
10.11	——	——	——	——	——

,

Table 5. Motor efficiency and gear ratio with a flapping frequency of 15 Hz of Aeolus 2105.5 at different voltages.

Voltage (V)	Output Torque (N∙m)	Output Speed (rad/s)	Current (A)	Motor Efficiency (%)	Gear Ratio
13.05	$0.007897$	$4812$	4.38	66.5	$51.1$
12.38	$0.008348$	$4552$	4.55	67.5	$48.3$
11.67	$0.008878$	$4280$	4.75	68.5	$45.4$
10.92	$0.009540$	$3983$	5.00	69.7	$42.3$
10.11	$0.010330$	$3677$	$5.30$	$70.9$	$39.0$

and

Table 6. Motor efficiency and gear ratio with a flapping frequency of 15 Hz of GTS V3 2104 at different voltages.

Voltage (V)	Output Torque (N∙m)	Output Speed (rad/s)	Current (A)	Motor Efficiency (%)	Gear Ratio
13.05	$0.00957$	$3970$	3.91	74.5	$42.1$
12.38	$0.01014$	$3746$	4.09	75.1	$39.8$
11.67	$0.01081$	$3515$	4.30	75.8	$37.3$
10.92	$0.01161$	$3274$	4.55	76.5	$34.8$
10.11	$0.01262$	$3010$	$4.87$	$77.2$	$32.0$

.

The motor efficiency comparison at different voltages for the three motors is shown in Figure 7. From the calculation results, it can be observed that the MN1804 motor’s efficiency gradually increases with higher motor voltage. On the other hand, the Aeolus 2105.5 and GTS V3 2104 motors experience a gradual decrease in efficiency with increasing motor voltage. At 75% throttle, the equation has no solution for the MN1804 motor, indicating that the flapping frequency of the mechanism cannot reach 15 Hz when the voltage is below 11.3 V. Among the three motors, the MN1804 motor exhibits the lowest efficiency at different voltages, while the GTS V3 2104 motor demonstrates the highest efficiency. Therefore, based on the calculation results of motor efficiency at different voltages, the GTS V3 2104 motor performs better in terms of motor efficiency compared to the other two motors.

The discharge range of a single cell battery voltage in the “Dove” mechanism is 3.0~4.35 V. To ensure optimal battery utilization and increase battery cycling efficiency, a design reference voltage of 9.6 V for the drive system is determined. During the complete discharge period, the MN1804 motor experiences a voltage range where it cannot achieve a flapping frequency of 15 Hz, while the Aeolus 2105.5 and GTS V3 2104 motors do not have this problem. The GTS V3 2104 motor exhibits higher motor efficiency than the Aeolus 2105.5 motor at the same voltage, and the calculated gear ratio for the GTS V3 2104 motor is smaller than that of the Aeolus 2105.5 motor at the same voltage. A larger gear ratio results in a larger size and weight of the gearbox. Additionally, the current of the GTS V3 2104 motor is lower than that of the Aeolus 2105.5 motor at the same voltage. A lower motor current corresponds to a lower input power for the motor at the same voltage. Therefore, based on the considerations mentioned above, the GTS V3 2104 motor is the most suitable choice.

2.4.2. Selection Gear Ratio

The motor output torque is transmitted from the gearbox and flapping mechanism to the end of the rocker arm, as shown in Figure 8.

At a flapping frequency of 15 Hz, the rotational speed transmitted to the motor end is

$$\begin{array}{c}{\omega }_m=15\times 2\pi \times i\end{array}$$

(14)

The relationship between motor output torque and speed is

$$\begin{array}{c}\left\{\begin{array}{c}{\omega }_m=a{T}_m+b\\ a<0\\ b>0\end{array}\right.\end{array}$$

(15)

The driving torque transmitted to the single-side of the rocker arm from the motor can be expressed as

$$\begin{array}{c}{T}_{drive}=\frac{\frac{l_3}{l_1}i{T}_m}{2}\end{array}$$

(16)

• T_drive—Torque transmitted to the single-side of the rocker arm from the motor.

The remaining torque transmitted to the end of the rocker arm from the motor can be expressed as

$$\begin{array}{c}{T}_{remain}=T_{drive}-T_{load}\end{array}$$

(17)

• T_remain—Remaining torque.

According to Section 2.2, the torque $T_{load}$ at the end of the rocker arm is obtained. During the motion parameter-power system matching of the flapping wing, it is necessary to ensure that the remaining torque is not less than zero, which means fulfilling the design requirements for the driving torque of the flapping wing.

$$\begin{array}{c}{T}_{drive}>T_{load}\end{array}$$

(18)

Therefore, in order to achieve a flapping frequency of 15 Hz, it is necessary to solve for constraints on motor speed and motor torque. The constraints are as follows:

$$\begin{array}{c}\left\{\begin{array}{c}{\omega }_m\ge 15\times 2\pi \times i\\ T_{drive}\ge T_{load}\\ \frac{l_{roc}}{l_{cra}}=2\end{array}\right.\end{array}$$

(19)

The relationship expression between output torque and speed of the GTS V3 2104 motor obtained from a first-order motor model at a battery cut-off voltage of 9.6 V is as follows:

$$\begin{array}{c}{\omega }_m=-10878T_m+2988\end{array}$$

(20)

Substituting Equation (20) into Equation (19), the constraint relationship between motor torque and gear ratio can be obtained according to the constraints.

$$\begin{array}{c}\left\{\begin{array}{c}{T}_m\le -\frac{30\pi }{10878}i+\frac{2988}{10878}\\ T_m\ge \frac{T_{load}}{i}\end{array}\right.\end{array}$$

(21)

The feasible range of motor torque and gear ratio for the GTS V3 2104 motor at a voltage of 9.6 V is obtained, as shown in Figure 9. In order to achieve a flapping frequency of 15 Hz, the selection of motor output torque and gear ratio should fall within the shaded region in the figure. To further select the appropriate gear ratio, while satisfying the flapping frequency of 15 Hz ($i={\omega }_m/(15\times 2\pi )$), the motor output power is calculated based on Equation (20) for different gear ratios.

$$\begin{array}{c}{P}_G=-0.8157i^2+25.875i\end{array}$$

(22)

• P_G—Motor output power at different gear ratios.

The motor efficiency at different gear ratios is expressed by Equation (23) as follows:

$$\begin{array}{c}{\eta }_G=\frac{P_G}{9.6I}\end{array}$$

(23)

• η_G—Motor efficiency at different gear ratios.

The relationship between motor output torque and motor current for the GTS V3 2104 motor at 9.6 V is given by the following equation:

$$\begin{array}{c}{T}_m=\left(I-0.9\right)\times 0.00318\end{array}$$

(24)

By substituting Equations (14), (20), and (24) into Equation (23), the efficiency of the motor can be obtained.

$$\begin{array}{c}{\eta }_G=\frac{-0.8157i^2+25.875i}{-26.142i+837.87}\times 100\%\end{array}$$

(25)

In order to maximize the efficiency of the GTS V3 2104 motor at a voltage of 9.6 V, according to Figure 9, it can be determined that the maximum efficiency of the motor is achieved when the gear ratio is 28.8 (C). Therefore, to achieve a flapping frequency of 15 Hz and maximize the efficiency of the GTS V3 2104 motor at a design reference voltage of 9.6 V, the gear ratio is chosen as 28.8.

3. Wind Tunnel Experiments the Flight Test Prototype

In the second section, the motor and gear ratio were matched and selected, and the new drive system of the flight test prototype is shown in Figure 10. The new drive system is installed on the “Dove” aircraft, with a total weight of 279.4 g, as shown in Figure 11.

The wind tunnel experimental control system used in this section was specifically developed by the research team for flapping-wing aircraft. The external shape of the wind tunnel is shown in Figure 12. The wind tunnel adopts a DC open jet configuration, with a test section of circular cross-section with a diameter of 1.6 m. The designed wind speed ranges from 5 m/s to 15 m/s, and the angle of attack can be adjusted from −10° to 20°. The turbulence intensity in the test section is not greater than 0.5%, and the dynamic pressure stability is not greater than 0.5%.

From a macroscopic perspective, the average values of parameters such as lift, thrust, and pitching moment generated by the flight test prototype throughout the entire flapping cycle are crucial for assessing flight performance. However, the data obtained from wind tunnel testing consist of a series of instantaneous values within the flapping cycle. Therefore, when analyzing the flight performance of the test prototype, it is necessary to calculate the average values over the entire sampled flapping cycle. For a discrete set of data over several cycles, the calculation method is as follows:

$$\begin{array}{c}{F}_{mean}=\frac{1}{n-2}\left({\displaystyle \sum _{n=1}^m}F\left(n\right)-F_{min}-F_{max}\right)\end{array}$$

(26)

• F_mean—Mean force over the cycle;
• m—Number of samples taken during the entire flapping cycle.

In the experiment, each sampling duration was 1 s, and a total of 10 samples were taken. By processing the instantaneous forces measured by the balance within 10 s, the time-averaged lift and thrust of the flight test prototype were obtained. The specific method for processing the balance data can be found in the referenced literature [30,31].

In the wind tunnel experiment, a current sampling system is used to visually display the flapping frequency of the flight test prototype. The interface of the current sampling system is shown in Figure 13, and the flapping frequency of the flight test prototype can be directly obtained from the current frequency displayed in the bottom right corner.

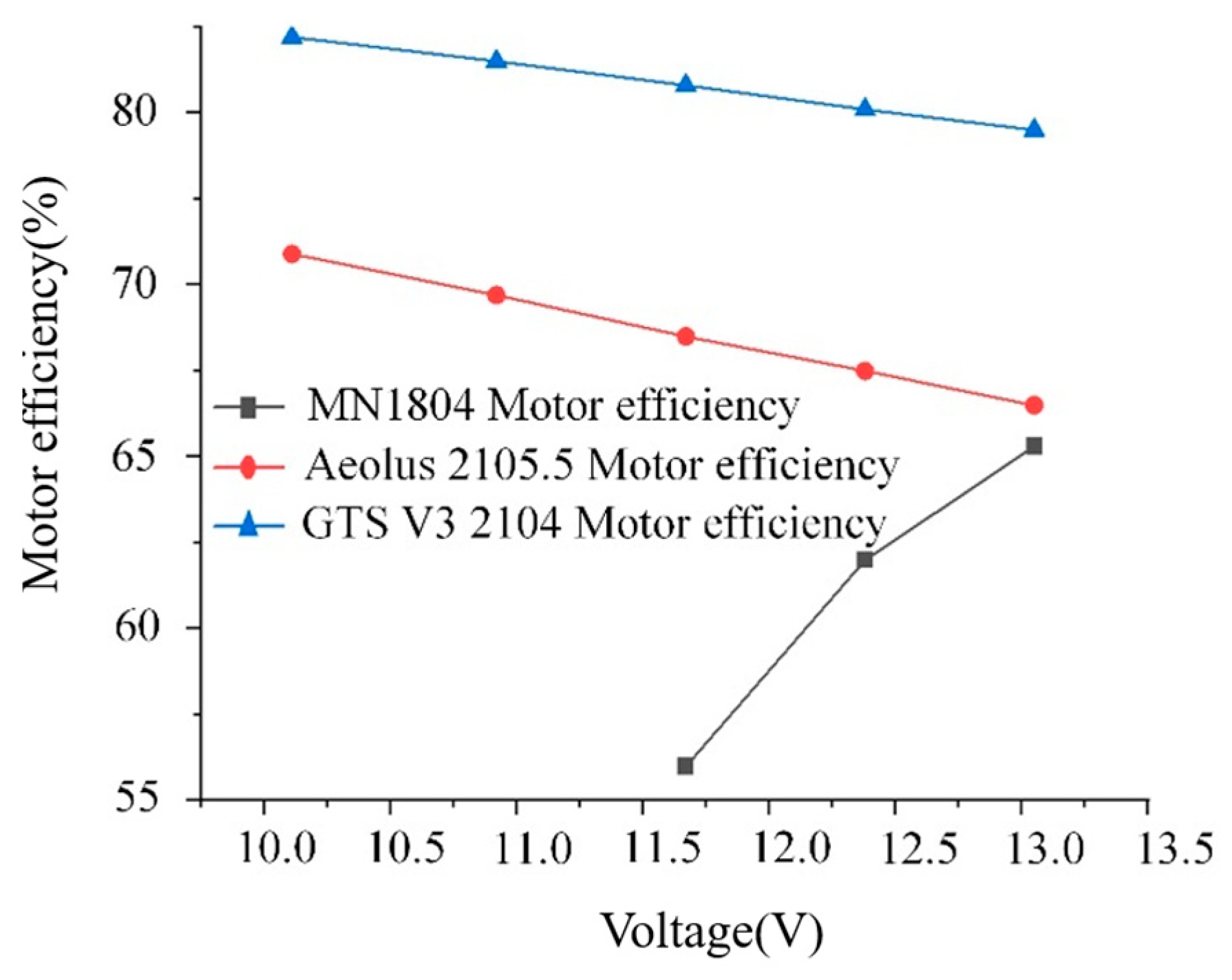
To further compare the performance differences between the Aeolus 2105.5 motor and the GTS V3 2104 motor on the flight test prototype, wind tunnel load tests were conducted on the flight test prototypes equipped with the GTS V3 2104 motor and the Aeolus 2105.5 motor, as shown in Figure 14.

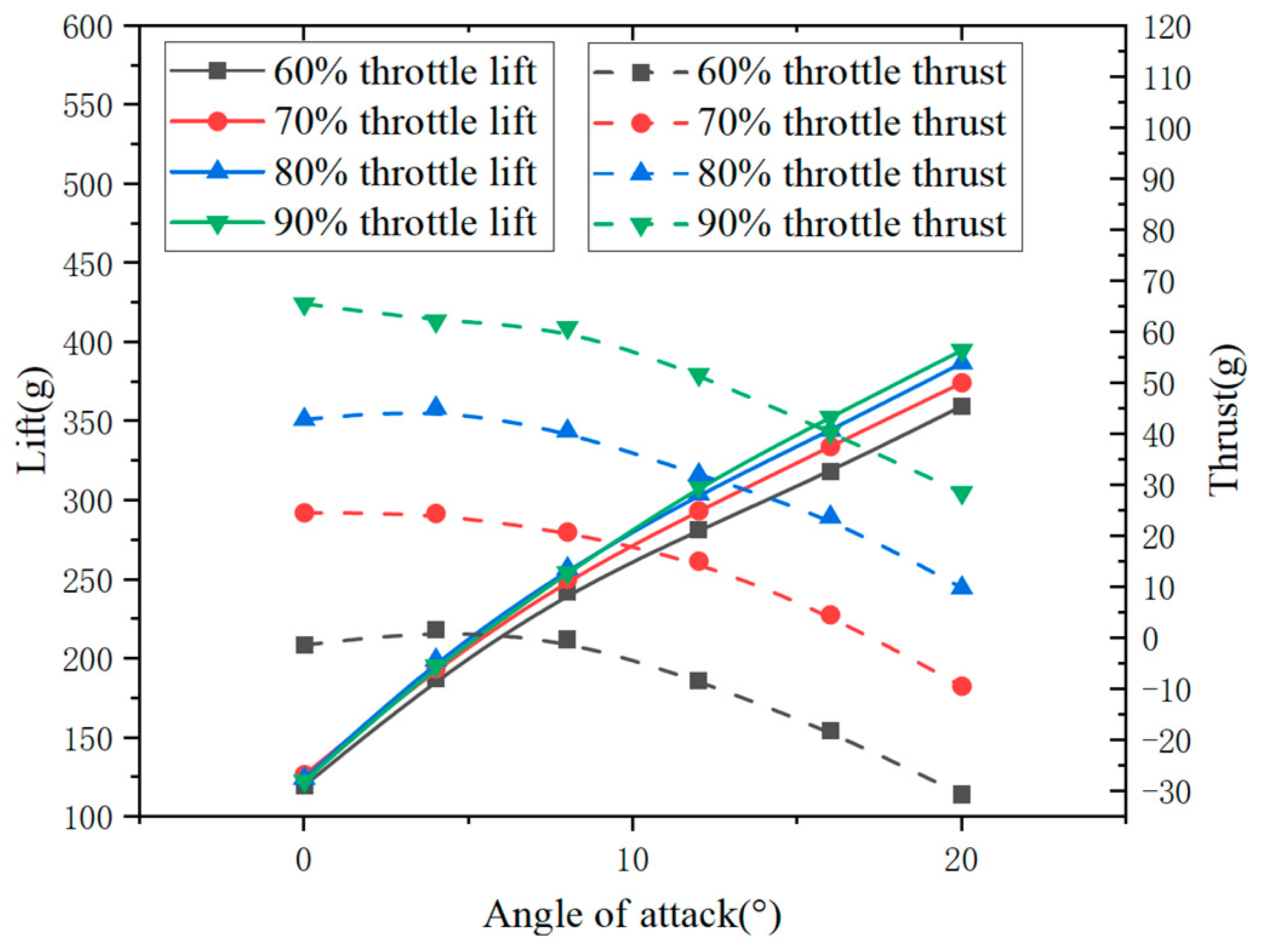
In order to obtain the range of parameters in the wind tunnel experiment, based on the flight test prototype with the GTS V3 2104 motor, the lift and thrust of the flight test prototype were obtained at a wind speed of 10 m/s and angle of attack of 0°, 4°, 8°, 12°, 16°, and 20°, respectively, at throttle settings of 60%, 70%, 80%, and 90%, as shown in Figure 15.

At a specific throttle setting, the trim state of the aircraft can be determined by analyzing the angle of attack at zero thrust. When the throttle is set to 60%, the angle of attack at zero thrust is 7.3°, and the corresponding lift is 232.5 g. Since the total weight of the flight test prototype is 279.4 g, the aircraft cannot achieve a trim state at a wind speed of 10 m/s and throttle setting of 60%. When the throttle is set to 70%, the angle of attack at zero thrust is 17.5°, and the corresponding lift is 348.3 g. Therefore, at a wind speed of 10 m/s and throttle setting of 70%, the aircraft can achieve a trim state.

In order to obtain the actual flapping frequencies of the flight test prototypes with different motors at different throttle settings, tests were conducted on the flight test prototypes equipped with the Aeolus 2105.5 motor and the GTS V3 2104 motor. The results of the flapping frequency tests are shown in

Table 7. Flapping frequencies of different motors at different throttle settings.

Throttle (%)	GTS V3 2104 Motor Flight Test Prototype Flapping Frequency (Hz)	Aeolus 2105.5 Motor Flight Test Prototype Flapping Frequency (Hz)
60	11	13
70	13	15
80	15	17
90	17	19
100	19	21

.

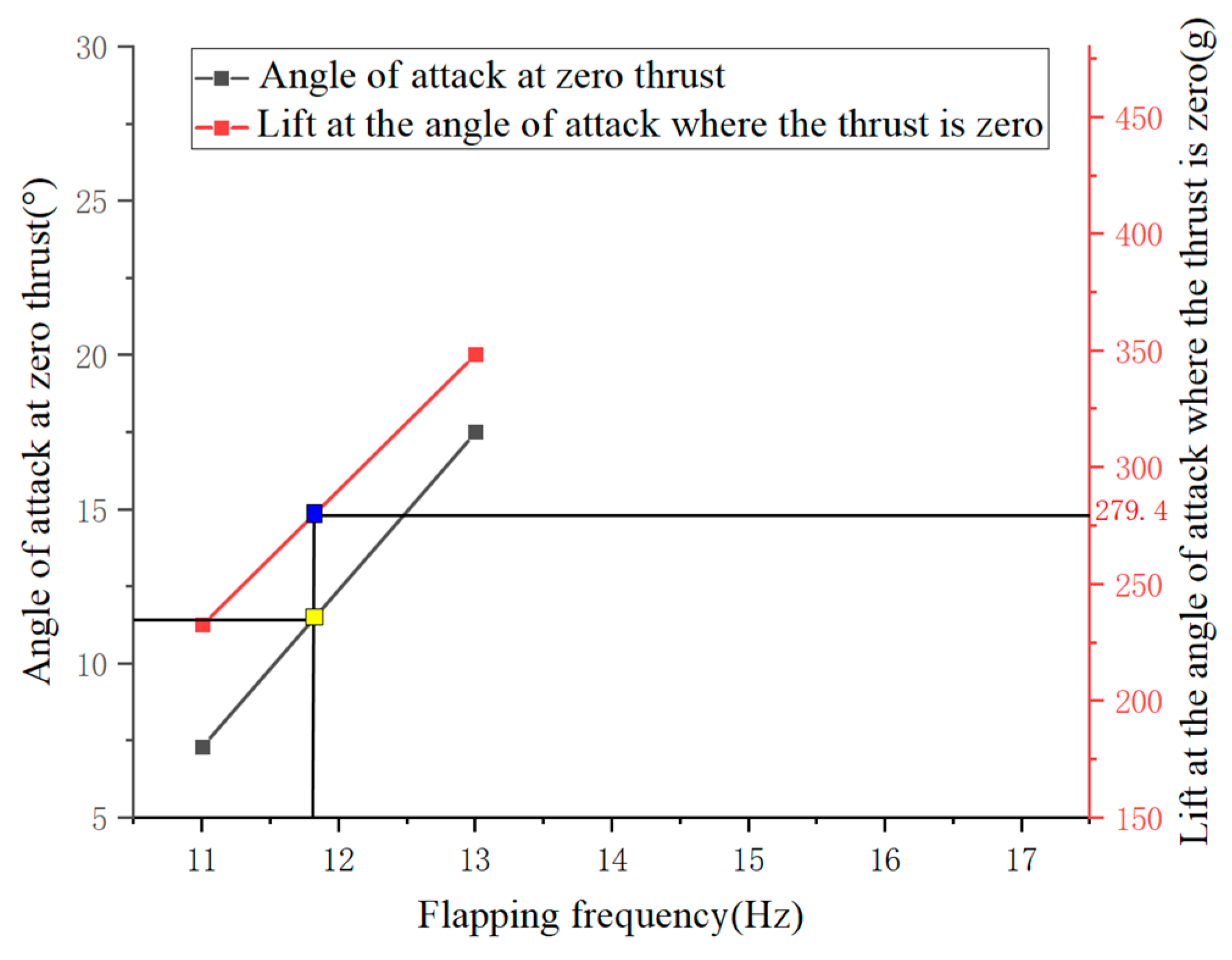
At a wind speed of 10 m/s, the trim angle of the flight test prototype with the GTS V3 2104 motor ranges from 7.3° to 17.46°. Therefore, the experimental parameter range for the angle of attack is selected as 0° to 20°. From

Table 8. Wind tunnel experimental design variables.

Parameters	Values
Motor Type	GTS V3 2104, Aeolus 2105.5
Angle of Attack	0°, 5°, 10°, 15°, 20°
Flapping Frequency	12 Hz, 13 Hz, 14 Hz, 15 Hz, 16 Hz
Wind Speed	10 m/s, 12.5 m/s

, it is found that at 60% throttle, the flapping frequency is 11 Hz, and at 70% throttle, the flapping frequency is 13 Hz. Considering that the total weight of the prototype is 279.4 g, the trim flapping frequency of the flight test prototype is between 11 Hz and 13 Hz, as shown in Figure 16. Since the designed flapping frequency criterion in this study is 15 Hz and considering the significant impact of high-frequency flapping on the lifespan of the mechanism, the selected range for the flapping frequency is 12 Hz to 16 Hz. At a wind speed of 10 m/s, a flapping frequency between 11 Hz and 13 Hz can achieve a trim state for the flight test prototype. Considering that the wind tunnel’s designed wind speed range is between 10 m/s and 15 m/s, the experimental setup is conducted at wind speeds of 10 m/s and 12.5 m/s.

The Aeolus 2105.5 motor is 5 g heavier than the GTS V3 2104 motor. However, at the same throttle setting, the flight test prototype with the Aeolus 2105.5 motor has a flapping frequency that is 2 Hz higher than the flight test prototype with the GTS V3 2104 motor. Therefore, the experimental parameter range for the flight test prototype with the Aeolus 2105.5 motor is consistent with that of the flight test prototype with the GTS V3 2104 motor.

The wind tunnel experimental design variable parameters are shown in Table 8.

4. Results and Discussion of Wind Tunnel Testing

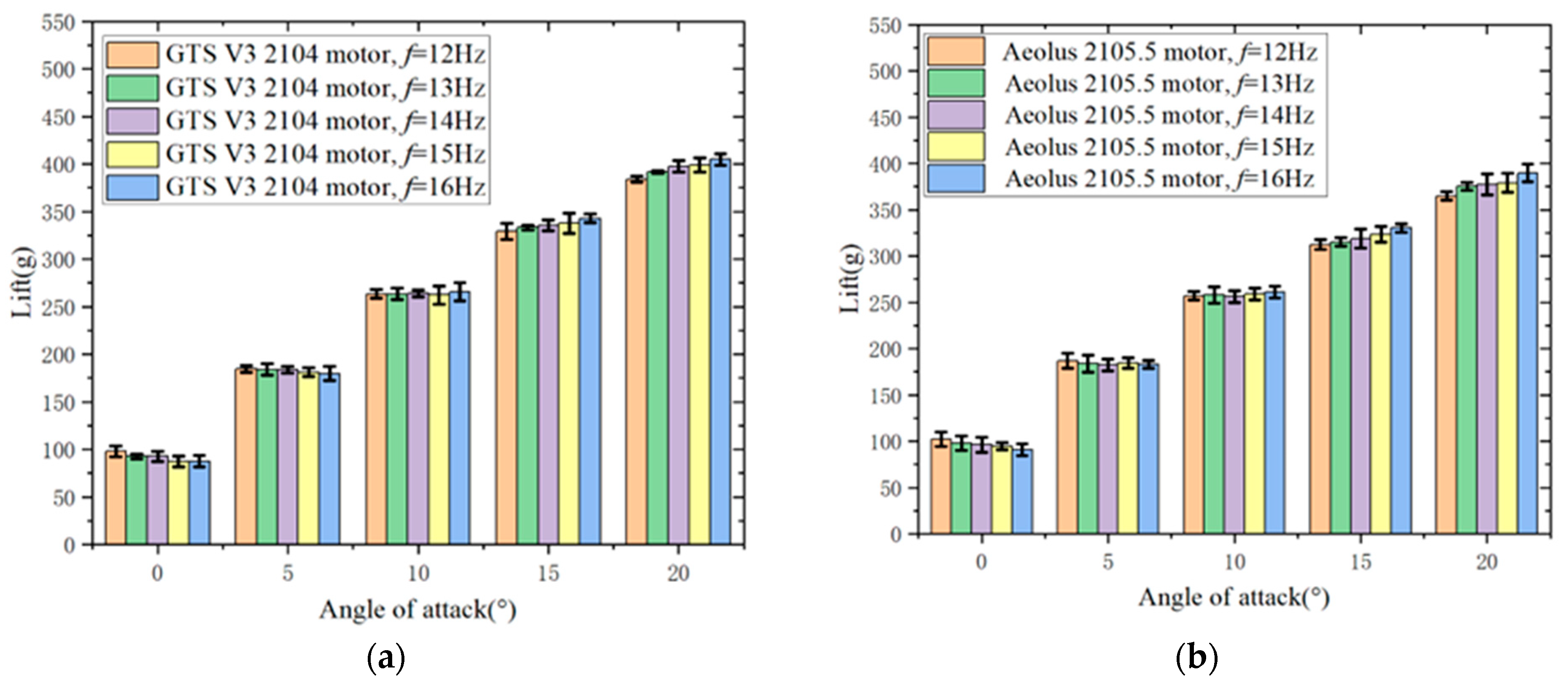
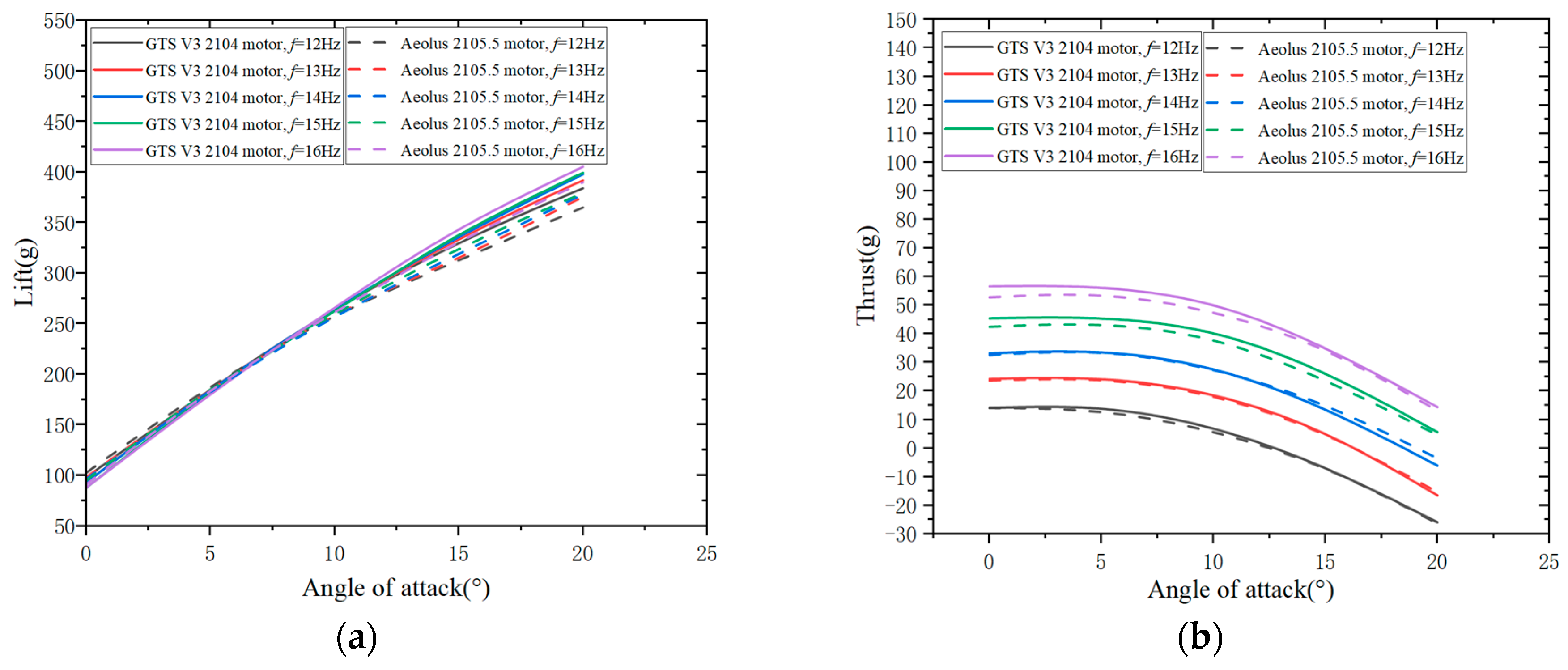
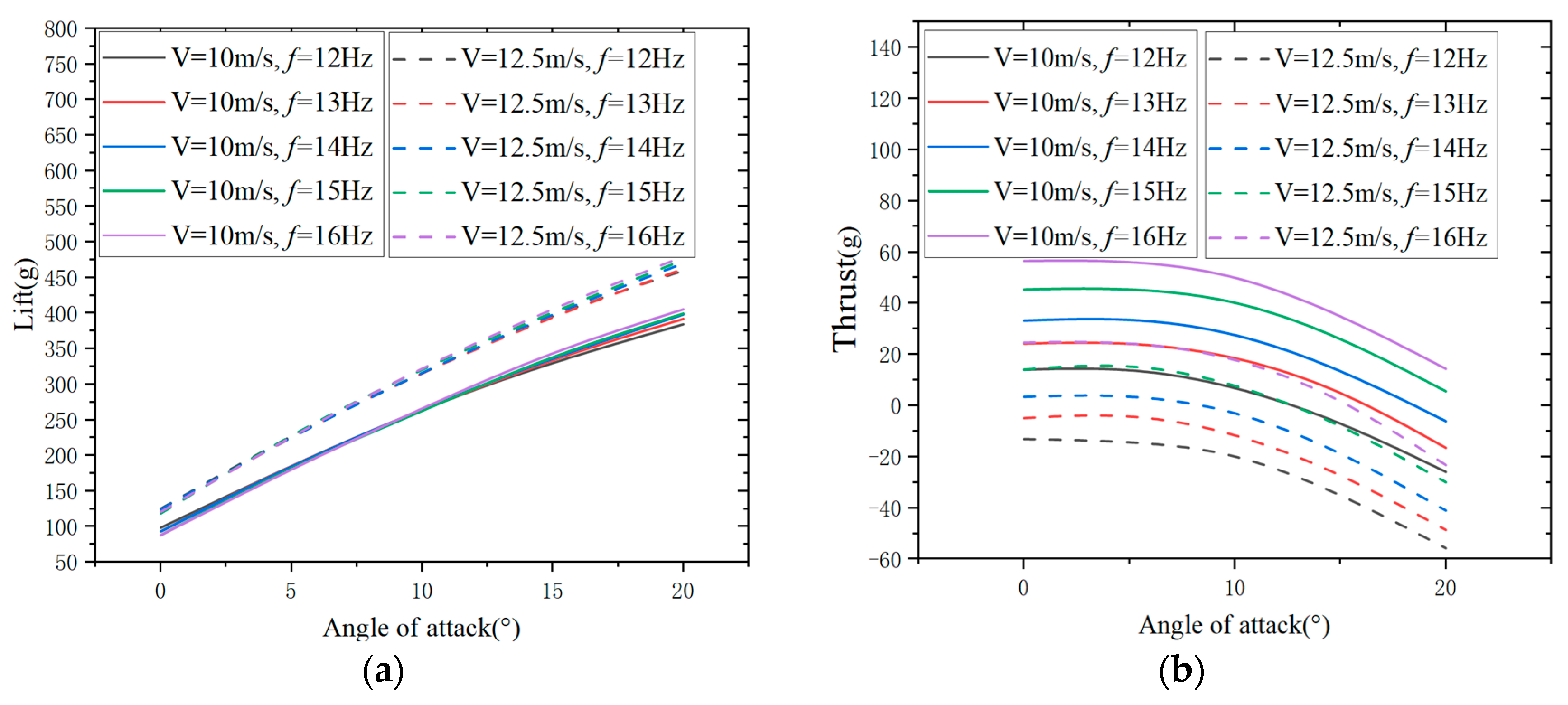
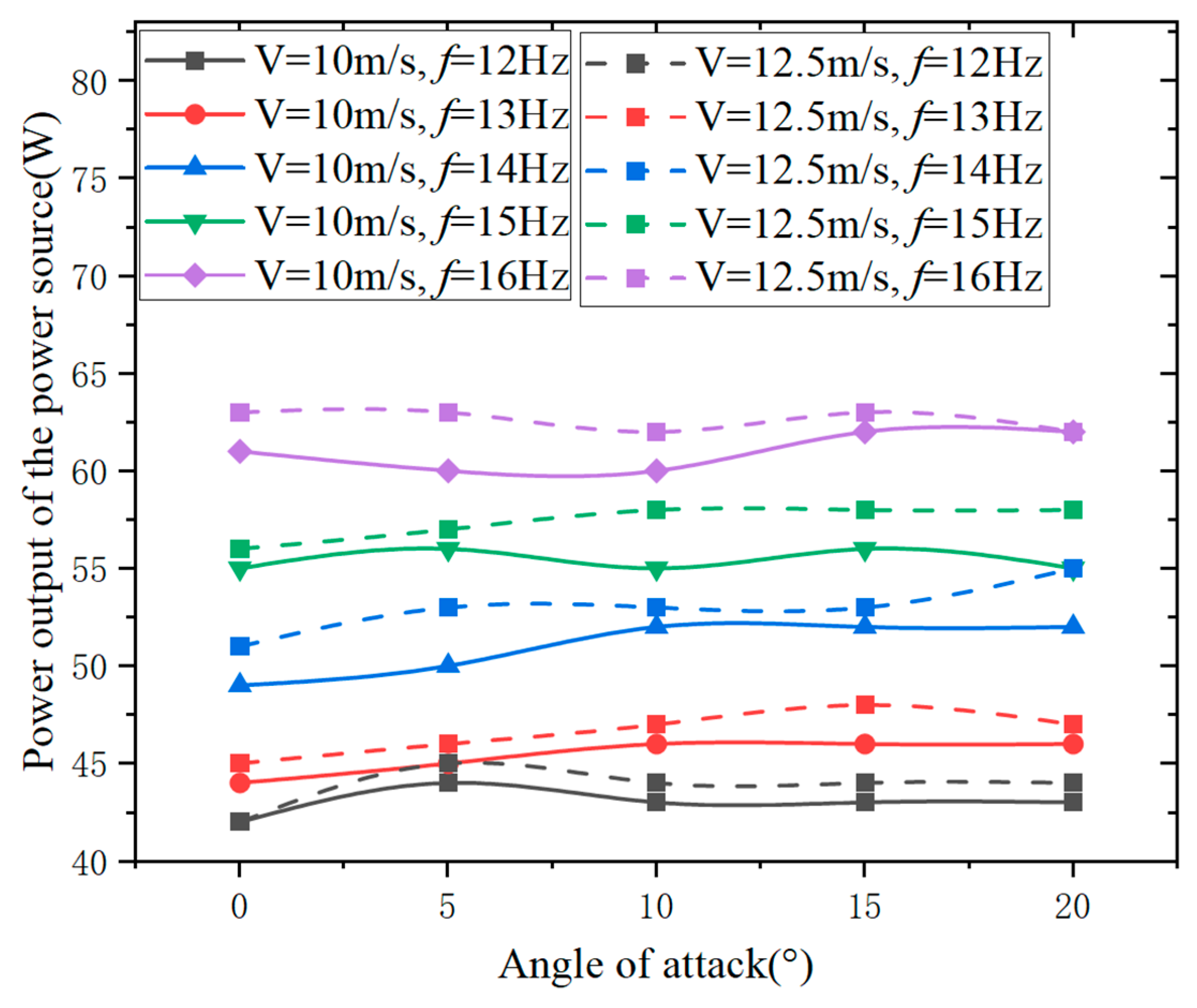
The lift and thrust of the flight test prototypes with the Aeolus 2105.5 motor and the GTS V3 2104 motor at different angles of attack and flapping frequencies at a wind speed of 10 m/s are analyzed. In Figure 17 and Figure 18, both the GTS V3 2104 motor and the Aeolus 2105.5 motor flight test prototypes show an increase in lift with an increase in angle of attack, while the thrust initially increases and then decreases with an increase in angle of attack.

In Figure 17, at 0° angle of attack, the lift of both the Aeolus 2105.5 motor and the GTS V3 2104 motor flight test prototypes decreases with an increase in flapping frequency. At 5° and 10° angles of attack, the lift variation with flapping frequency is not significant for both motor flight test prototypes. At 15° and 20° angles of attack, the lift of both motor flight test prototypes increases with an increase in flapping frequency. In summary, the variation of lift with flapping frequency is not significant.

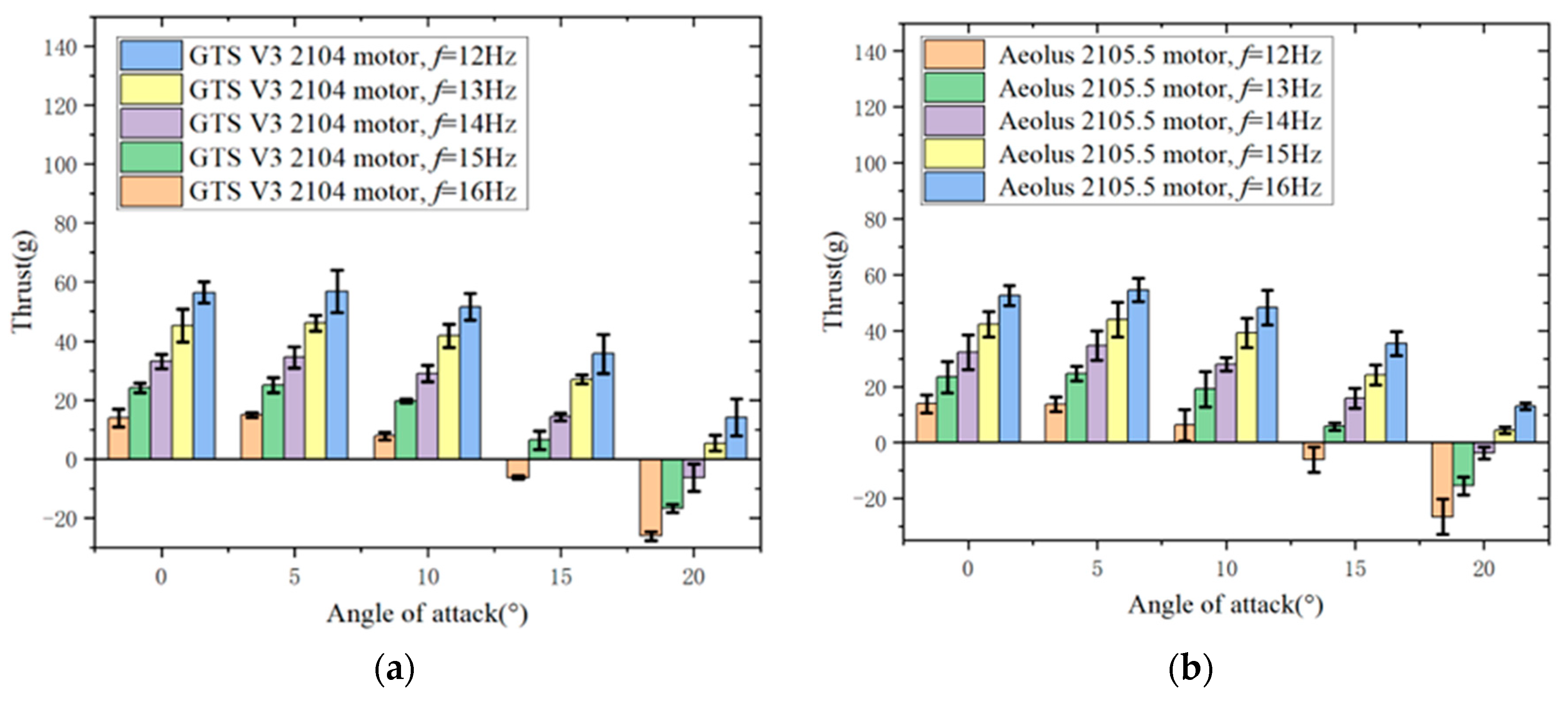
In Figure 18, the thrust of both the Aeolus 2105.5 motor and the GTS V3 2104 motor flight test prototypes increases with an increase in flapping frequency. At 0°, 5°, and 10° angles of attack, both motor flight test prototypes generate positive thrust at any flapping frequency between 12 Hz and 16 Hz. At a 15° angle of attack, except for a negative thrust generated at a flapping frequency of 12 Hz, positive thrust is generated at all other flapping frequencies. At a 20° angle of attack, positive thrust is generated at flapping frequencies of 15 Hz and 16 Hz, while negative thrust is generated at all other flapping frequencies. Zakaria et al. [32] analyzed “Lift and drag of flapping membrane wings at high angles of attack”. They found that increasing the flapping frequency generally leads to an increase in lift and thrust at a given flight speed and positive angle of attack, which is consistent with the findings of this study.

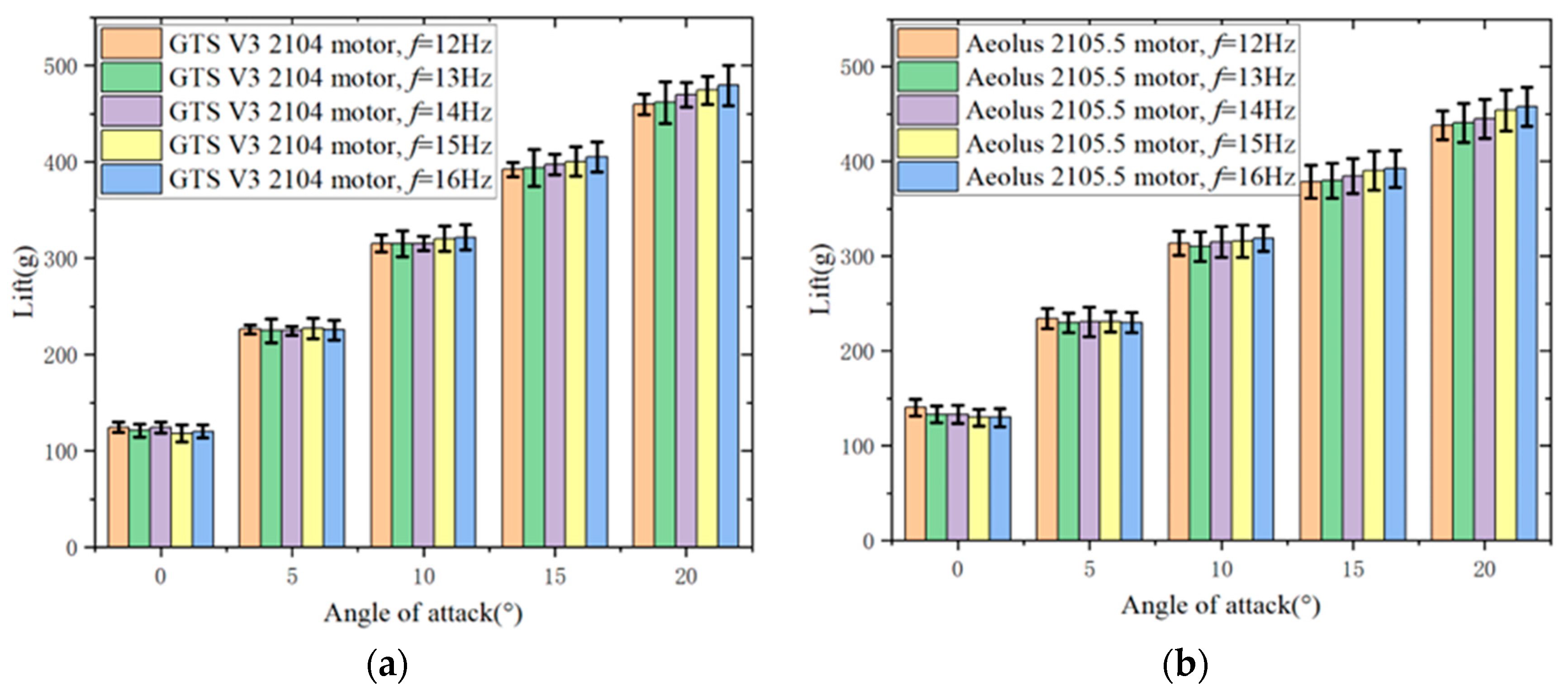
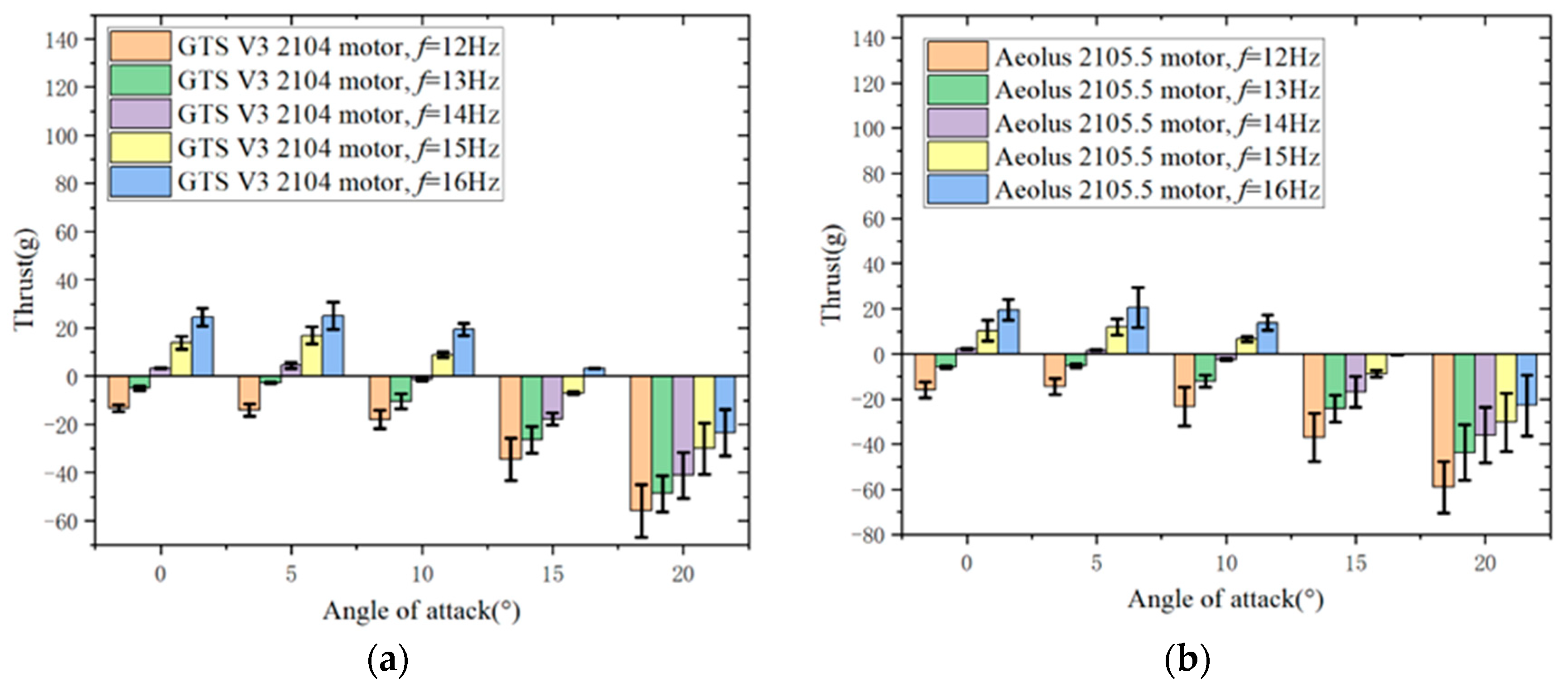
In Figure 19, at specific flapping frequencies and angles of attack, there is not much difference in lift and thrust between the Aeolus 2105.5 motor and the GTS V3 2104 motor flight test prototypes. This is because the generation of lift and thrust is only related to the state of the flapping wing. As long as the angle of attack, wind speed, flapping frequency, and flapping wing are the same, the lift and thrust should be the same. The slight discrepancies observed in the figures may be due to the accumulated zero drift error in the balance data, control errors in wind tunnel experimental wind speed, and other factors.

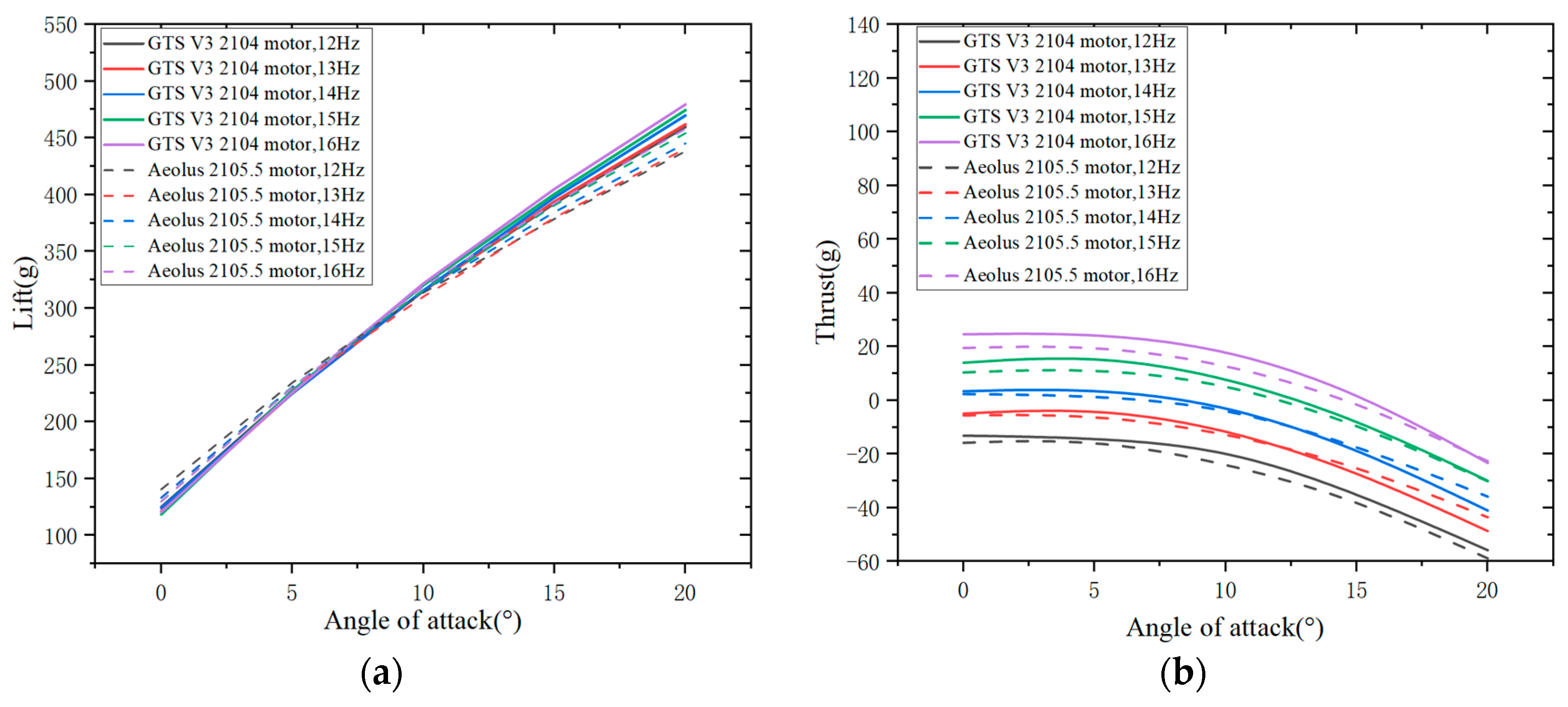
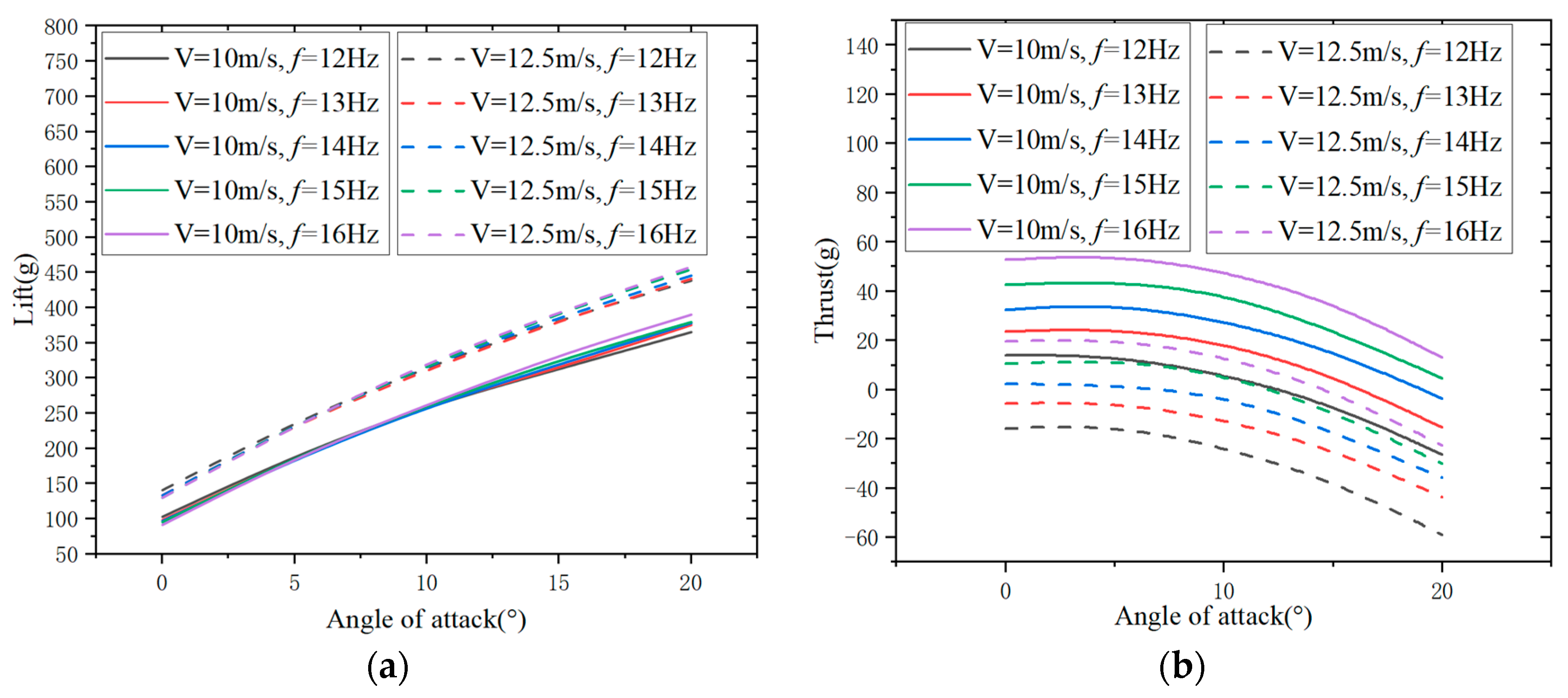
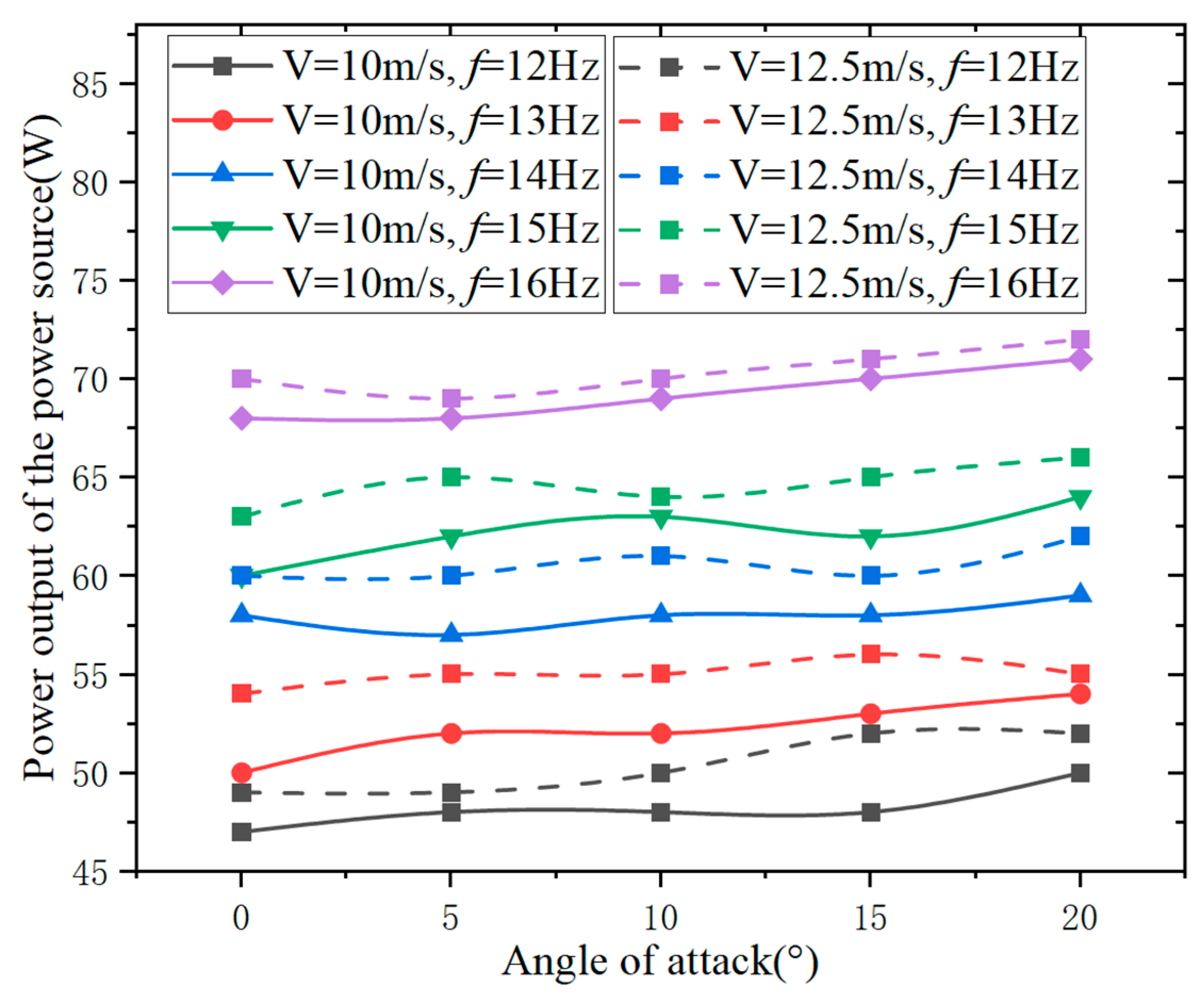
At a wind speed of 12.5 m/s and different flapping frequencies, the lift and thrust of the flight test prototypes with the Aeolus 2105.5 motor and the GTS V3 2104 motor are analyzed at various angles of attack. In Figure 20, the lift of both the Aeolus 2105.5 motor and the GTS V3 2104 motor flight test prototypes increases with an increase in angle of attack. At 0°, 5°, and 10° angles of attack, the variation of lift with increasing flapping frequency is not significant. However, at 15° and 20° angles of attack, the lift increases with an increase in flapping frequency.

In Figure 21, at specific flapping frequencies, the thrust of the flight test prototypes with the Aeolus 2105.5 motor and the GTS V3 2104 motor initially increases and then decreases with an increase in angle of attack. At specific angles of attack, the thrust of both motor flight test prototypes increases with an increase in flapping frequency. At a 15° angle of attack and a flapping frequency of 16 Hz, the GTS V3 2104 motor flight test prototype generates positive thrust, while the Aeolus 2105.5 motor flight test prototype generates negative thrust. At a 20° angle of attack, both motor flight test prototypes generate negative thrust at any flapping frequency between 12 Hz and 16 Hz.

In Figure 22, the lift does not differ significantly between the Aeolus 2105.5 motor and the GTS V3 2104 motor flight test prototypes at the same flapping frequency and angle of attack. However, there is a significant difference in thrust between the two motor flight test prototypes at low angles of attack and high flapping frequencies.

In Figure 23, a comparison is made between the lift of the GTS V3 2104 motor flight test prototype at wind speeds of 10 m/s and 12.5 m/s. Under the same flapping frequency and angle of attack, the lift generated at a wind speed of 12.5 m/s is higher than the lift generated at a wind speed of 10 m/s. However, the thrust generated at a wind speed of 10 m/s is higher than the thrust generated at a wind speed of 12.5 m/s. This is because an increased wind speed leads to a greater pressure difference around the aircraft, resulting in increased lift. However, the increased wind speed also leads to higher drag, causing the thrust to decrease.

In Figure 24, a comparison is made between the lift and thrust of the Aeolus 2105.5 motor flight test prototype at wind speeds of 10 m/s and 12.5 m/s. Under the same flapping frequency and angle of attack, the lift generated at a wind speed of 12.5 m/s is higher than the lift generated at a wind speed of 10 m/s. However, the thrust generated at a wind speed of 12.5 m/s is smaller than the thrust generated at a wind speed of 10 m/s.

Both the Aeolus 2105.5 motor flight test prototype and the GTS V3 2104 motor flight test prototype experience an increase in lift as the wind speed increases. However, the thrust decreases with an increase in wind speed. Additionally, at high angles of attack, the difference in lift between wind speeds of 10 m/s and 12.5 m/s is greater than the difference in lift at low angles of attack.

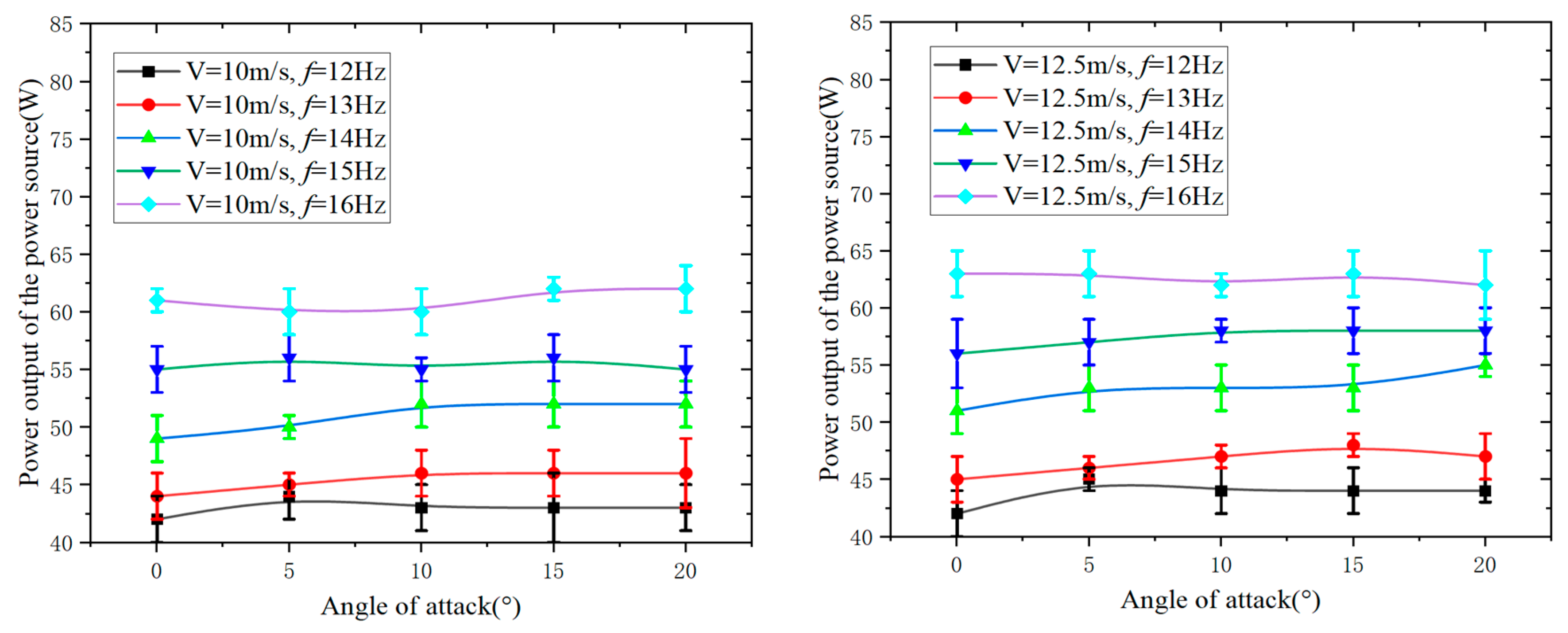
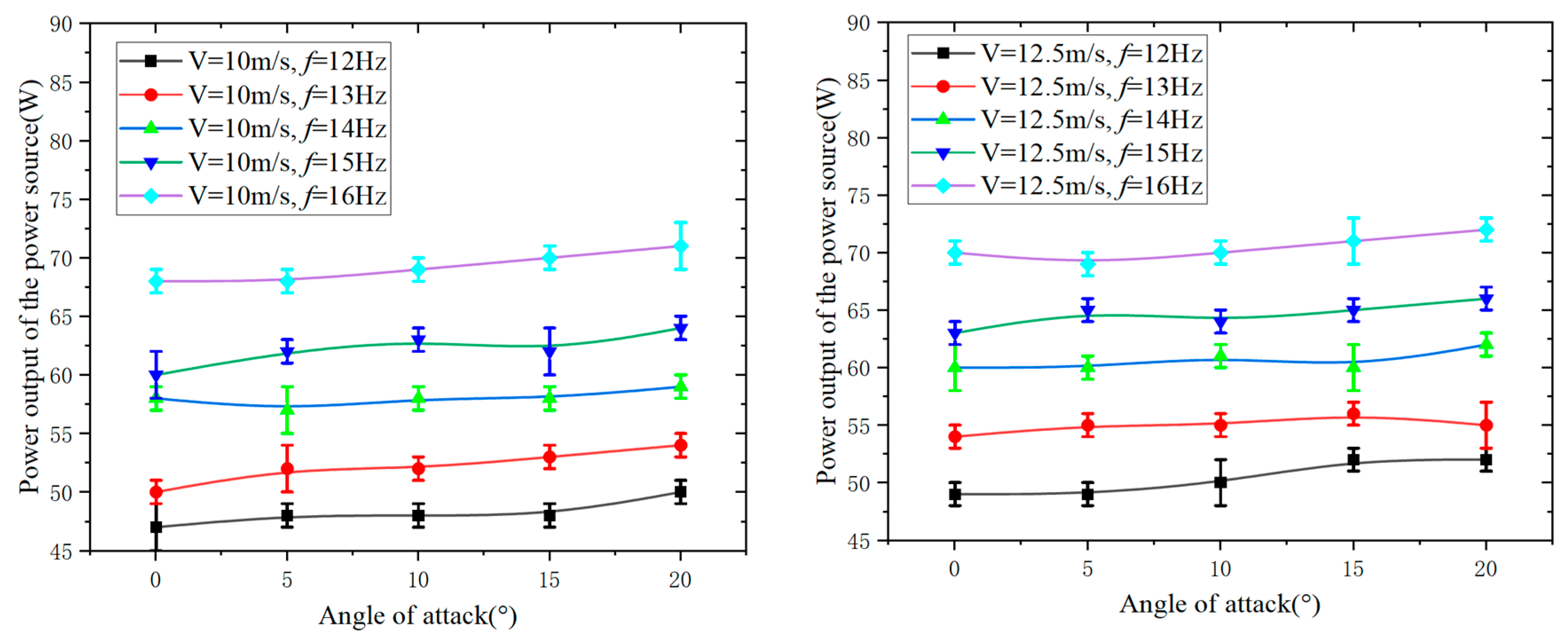
In order to obtain the input power of two different motor flight test prototypes at various wind speeds, flapping frequencies, and angles of attack, the input power of the voltage regulator was recorded simultaneously during the wind tunnel force measurements. Figure 25 and Figure 26 represent the power input curves of the GTS V3 2104 motor and the Aeolus 2105.5 motor, respectively, under different wind speeds and flapping frequencies as a function of the angle of attack. In Figure 27, at specific wind speeds and flapping frequencies, the input power of the GTS V3 2104 motor flight test prototype shows little variation with an increase in angle of attack. At specific wind speeds and angles of attack, the input power increases with an increase in flapping frequency. Similarly, at specific flapping frequencies and angles of attack, the input power increases with an increase in wind speed. In Figure 28, at specific wind speeds and flapping frequencies, the input power of the Aeolus 2105.5 motor flight test prototype also shows little variation with an increase in angle of attack. At specific wind speeds and angles of attack, the input power increases with an increase in flapping frequency. Likewise, at specific flapping frequencies and angles of attack, the input power increases with an increase in wind speed.

Comparing with Figure 4, at a flapping frequency of 15 Hz, the MN1804 motor requires an input power of 60 W, the GTS V3 2104 motor requires an input power of 55.4 W, and the Aeolus 2105.5 motor requires an input power of 62.2 W. Additionally, under the same flapping frequency and angle of attack, there is little difference in lift and thrust between the Aeolus 2105.5 motor and the GTS V3 2104 motor flight test prototypes. Therefore, in order to maximize the aircraft’s endurance, the GTS V3 2104 motor is superior to the other two motors.

From the wind tunnel experimental results, it can be observed that the lift of the flight test prototype increases with an increase in angle of attack, while the thrust decreases with an increase in angle of attack. Angle of attack has a significant influence on both lift and thrust. Within a certain range, as the angle of attack increases, the lift coefficient increases, leading to an increase in lift. However, an increase in angle of attack also results in increased drag, which reduces the thrust.

At angles of attack of 15° and 20°, the lift increases with an increase in flapping frequency, but the increment is relatively small. For other angles of attack, the variation of lift with flapping frequency is not significant. This is because the increase in lift is primarily influenced by the velocity and angle of attack, while the flapping frequency can only enhance the peak instantaneous lift but has little effect on the average lift.

Regardless of the angle of attack, the thrust increases with an increase in flapping frequency, and the increment is significant. This indicates that the flapping frequency has a smaller impact on lift but a larger impact on thrust. This is because when the flapping frequency increases, the interaction between the object and the fluid occurs more frequently within a unit of time, resulting in a greater transfer of momentum to the fluid.

An increase in wind speed leads to a significant increase in lift but also a significant decrease in thrust. This is because an increase in wind speed results in a larger pressure difference between the upper and lower surfaces of the wing, thereby increasing lift. However, the faster fluid velocity generates greater momentum loss and increased drag, which reduces thrust.

Angle of attack has a minor impact on the input power of the power supply. Under different angles of attack, the difference in input power is minimal. On the other hand, flapping frequency and wind speed have a significant influence on the input power of the power supply. As the wind speed and flapping frequency increase, the input power of the power supply increases noticeably.

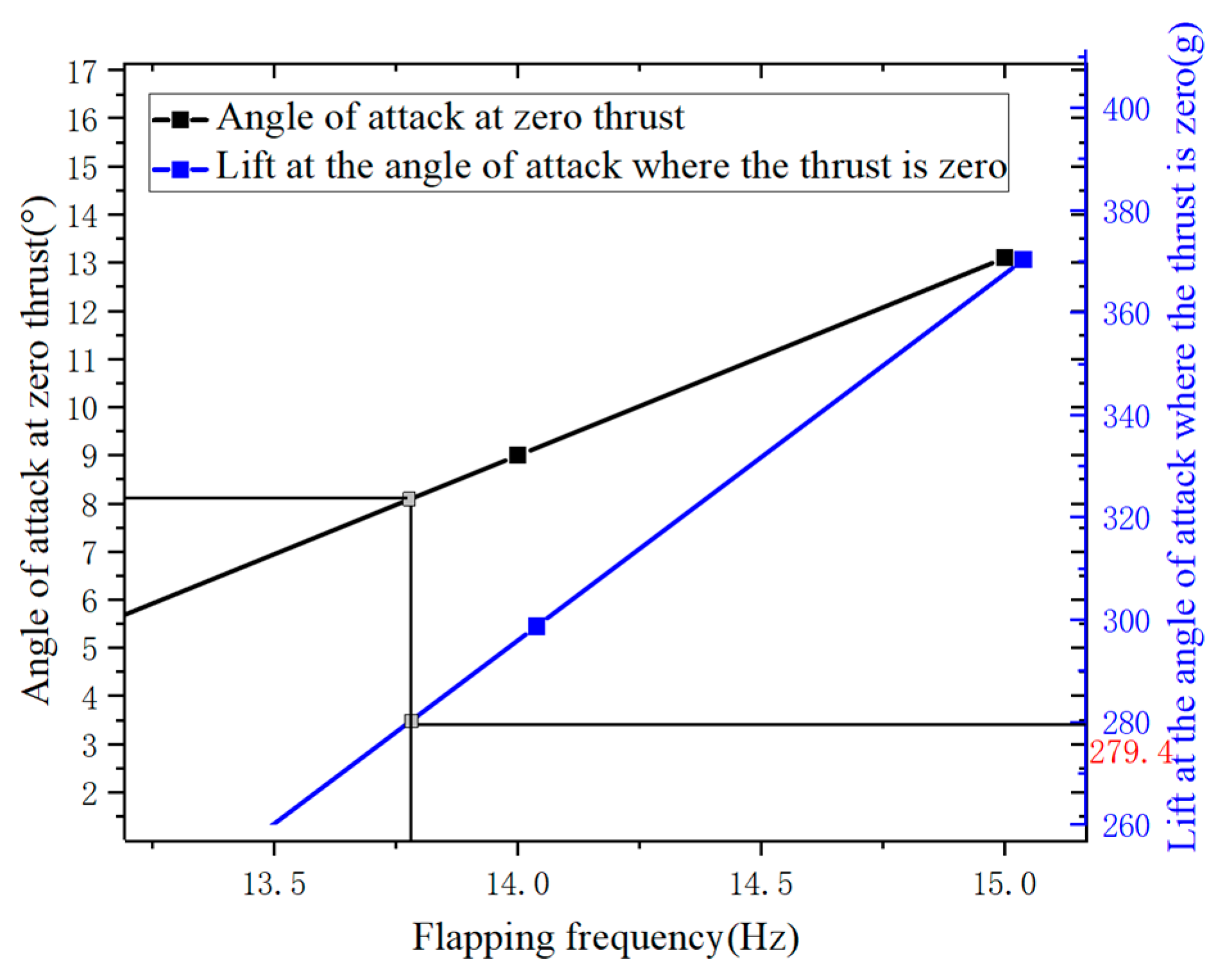
According to the wind tunnel experimental results, the variation of the angle of attack at zero thrust and the corresponding lift at a wind speed of 12.5 m/s and flapping frequencies of 14 Hz and 15 Hz are shown in Figure 29. When the flapping frequency is 13 Hz, the thrust is non-zero at all angles of attack. Therefore, based on the results at flapping frequencies of 14 Hz and 15 Hz, a fitting extrapolation is performed, yielding a trimmed flapping frequency of 13.7 Hz and an angle of attack of 7.9° for a lift of 279.4 g.

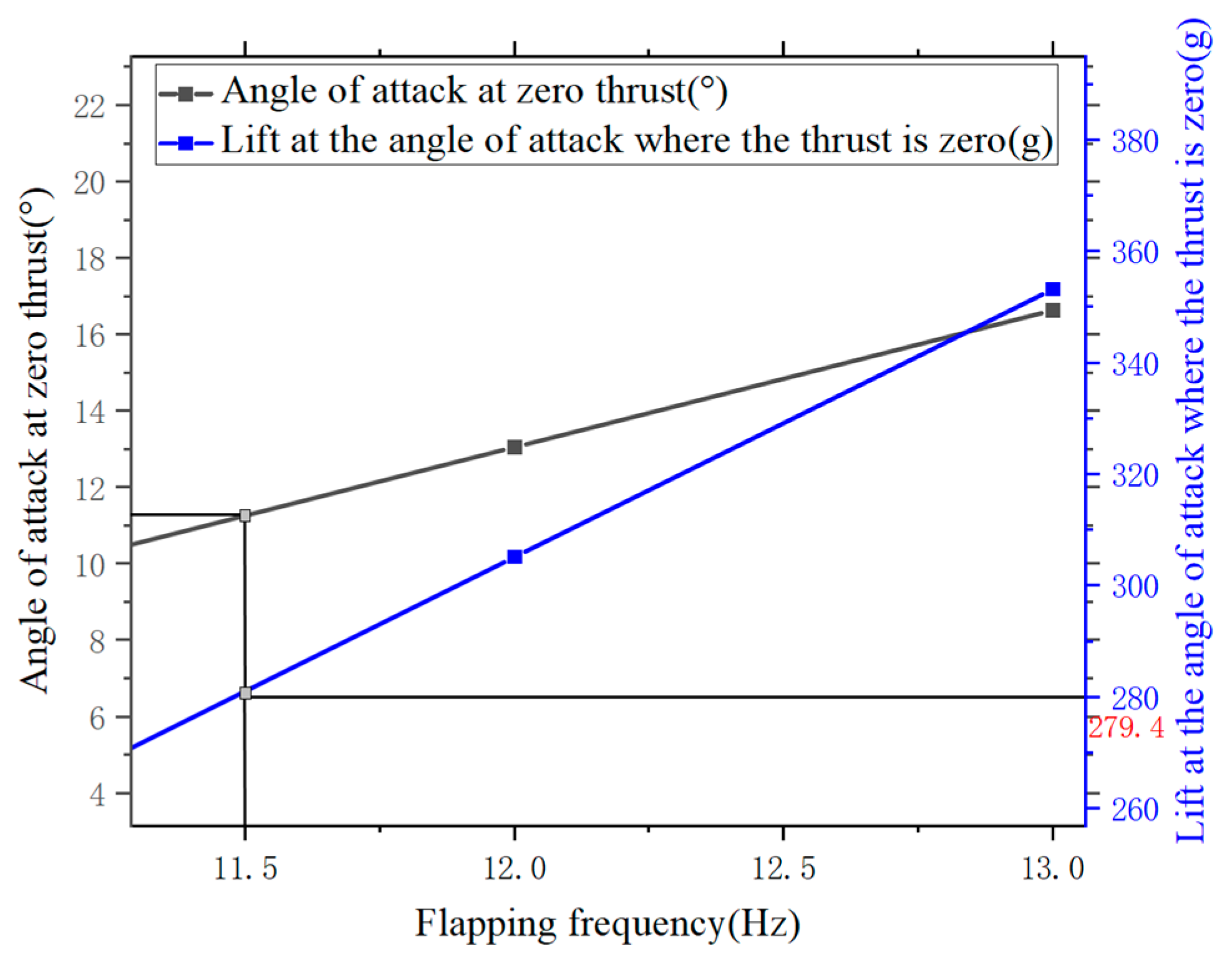
Similarly, for a wind speed of 10 m/s and flapping frequencies of 12 Hz and 13 Hz, the variation of the angle of attack at zero thrust and the corresponding lift are shown in Figure 30. A fitting extrapolation yields a trimmed flapping frequency of 11.5 Hz and an angle of attack of 11.1° for a lift of 279.4 g.

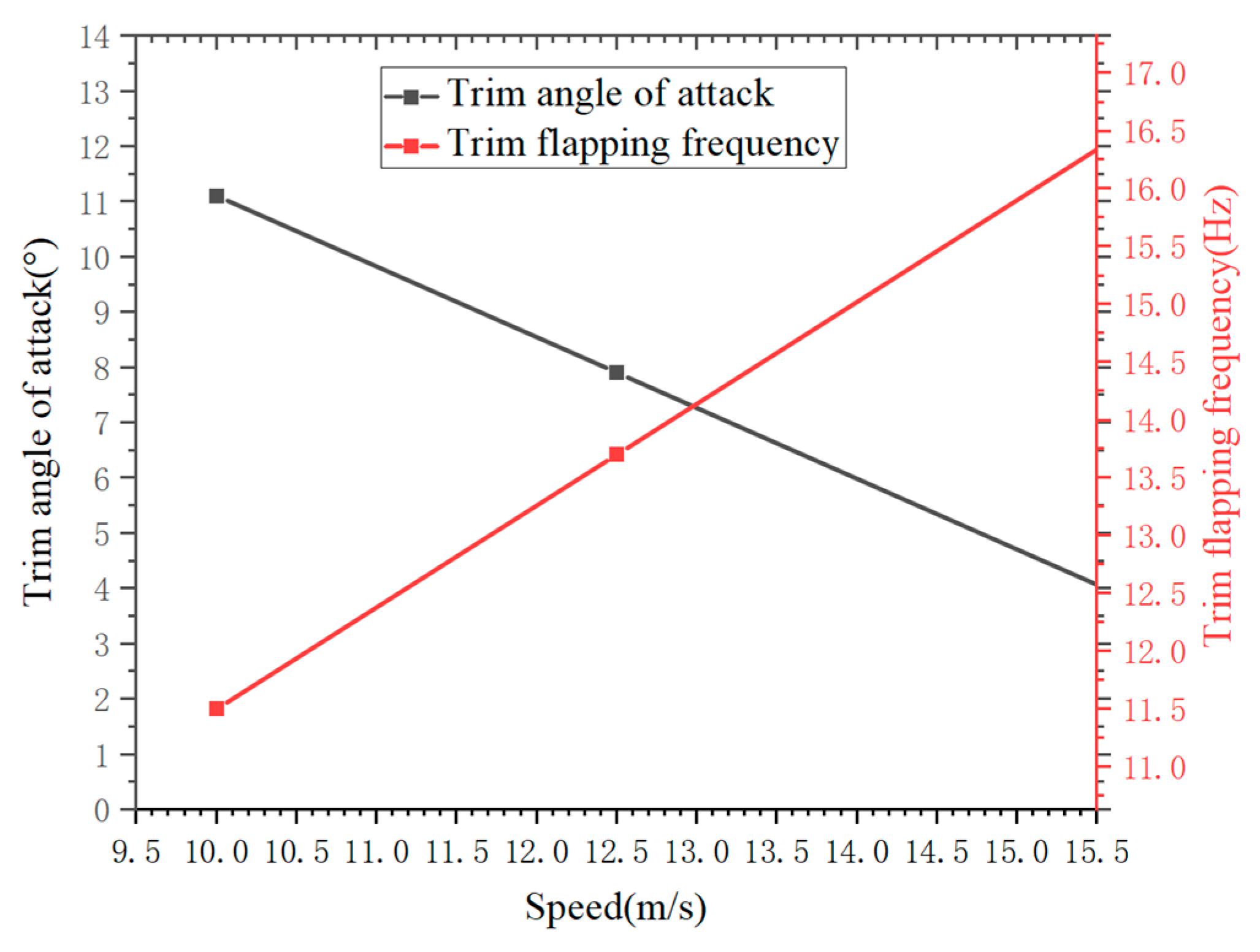
The curves depicting the trimmed flapping frequency and angle of attack as a function of velocity are shown in Figure 31. From the graph, a fitting extrapolation can be performed to obtain the trimmed pitch angle and trimmed flapping frequency for various wind speeds in the wind tunnel experiments.

5. Results and Discussion of Flight Validation

Actual flight tests were conducted on the prototype aircraft with the GTS V3 2104 motor. The test prototype designed in this study achieved stable flight.

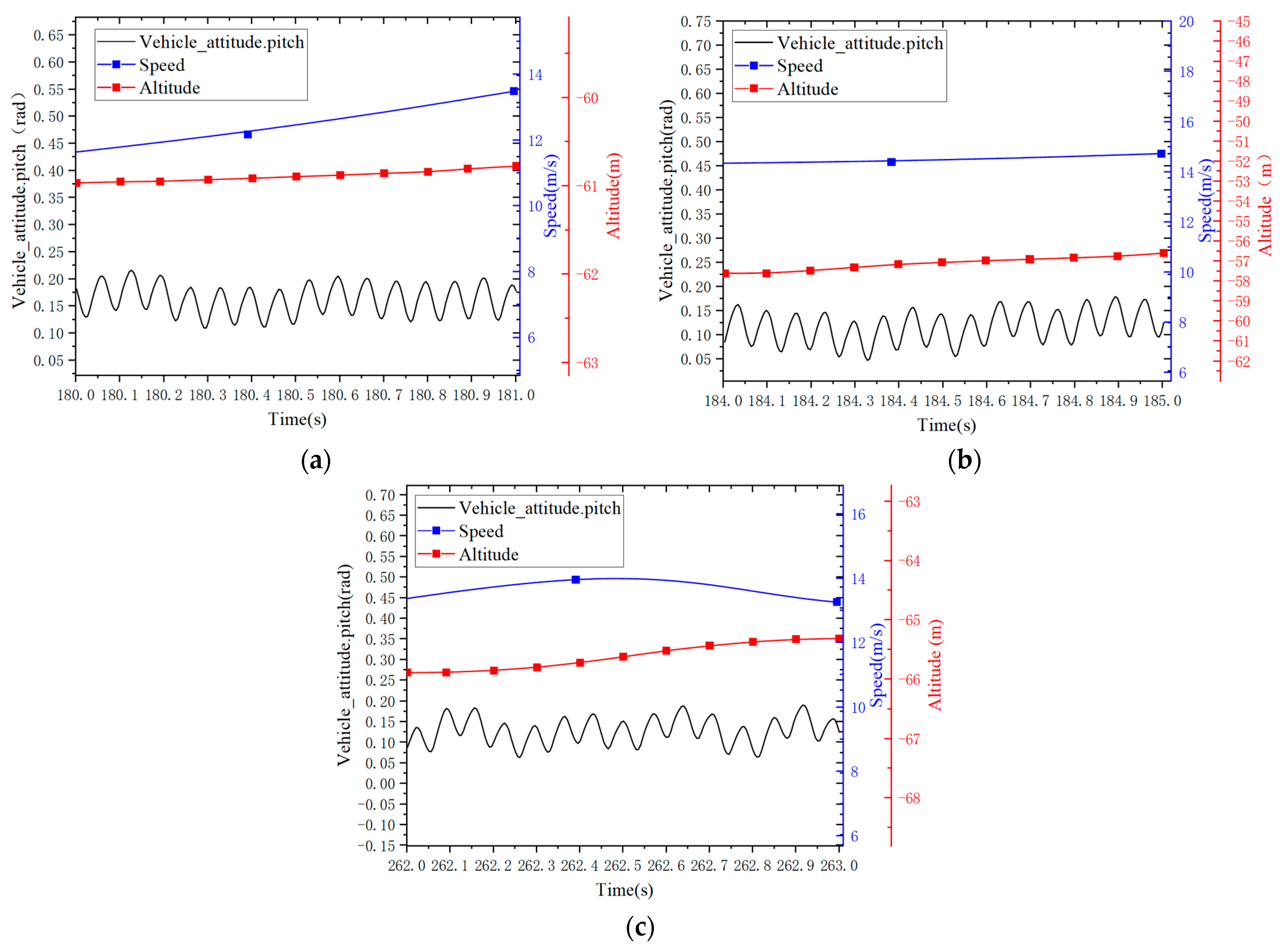
After the flight, the flight log files are converted for analysis of the flight process. The flapping aircraft exhibits a pitching frequency that corresponds to the flapping frequency. Therefore, the pitching frequency of the aircraft can be extracted from the flight log files to obtain the actual flapping frequency during flight. The initial pitch angle of the aircraft on level ground is 2.0°, as shown in Figure 32. Three time intervals with minimal changes in altitude were selected during the flight process (180 s~181 s, 184 s~185 s, and 262 s~263 s). The average pitch angle, average flight speed, and flapping frequency for each of these intervals are presented in

Table 9. Pitch angle, flight speed, and flapping frequency of the aircraft in different time intervals.

Time (s)	Pitch Angle (°)	Average Flight Speed (m/s)	Flapping Frequency (Hz)
180~181	7.3	12.8	14.9
184~185	4.9	14.6	14.5
262~263	7.5	13.6	14.5

. The speeds, altitudes, and pitch angles of three different time periods of the aircraft are shown in Figure 33.

Based on the fitting results of the trimmed flapping frequency and angle of attack with respect to velocity in Section 3, the errors of the trimmed flapping frequency, pitch angle, and flight data relative to wind tunnel experiments during the three time intervals (180 s~181 s, 184 s~185 s, 262 s~263 s) are shown in

Table 10. Trimmed pitch angle, flapping frequency, and errors for different time intervals in wind tunnel experiments.

Time (s)	Pitch Angle (°)	Average Flight Speed (m/s)	Flapping Frequency (Hz)	Trimmed Pitch Angle from Wind Tunnel (°)	Trimmed Flapping Frequency from Wind Tunnel (Hz)	Pitch Angle Error (%)	Flapping Frequency Error (%)
180~181	7.3	12.8	14.9	7.5	14.0	3	7
184~185	4.9	14.6	14.5	5.2	15.5	6	6
262~263	7.5	13.6	14.5	6.5	14.7	15	1

. From the table, it can be observed that the error between the measured flapping frequency and the trimmed flapping frequency from wind tunnel experiments is within 10%. The error between the average pitch angle of the aircraft and the trimmed pitch angle from wind tunnel experiments is within 15%. These small errors further demonstrate that the obtained trimmed states from wind tunnel experiments can provide a reliable basis for setting the trim angle of attack in flight tests.

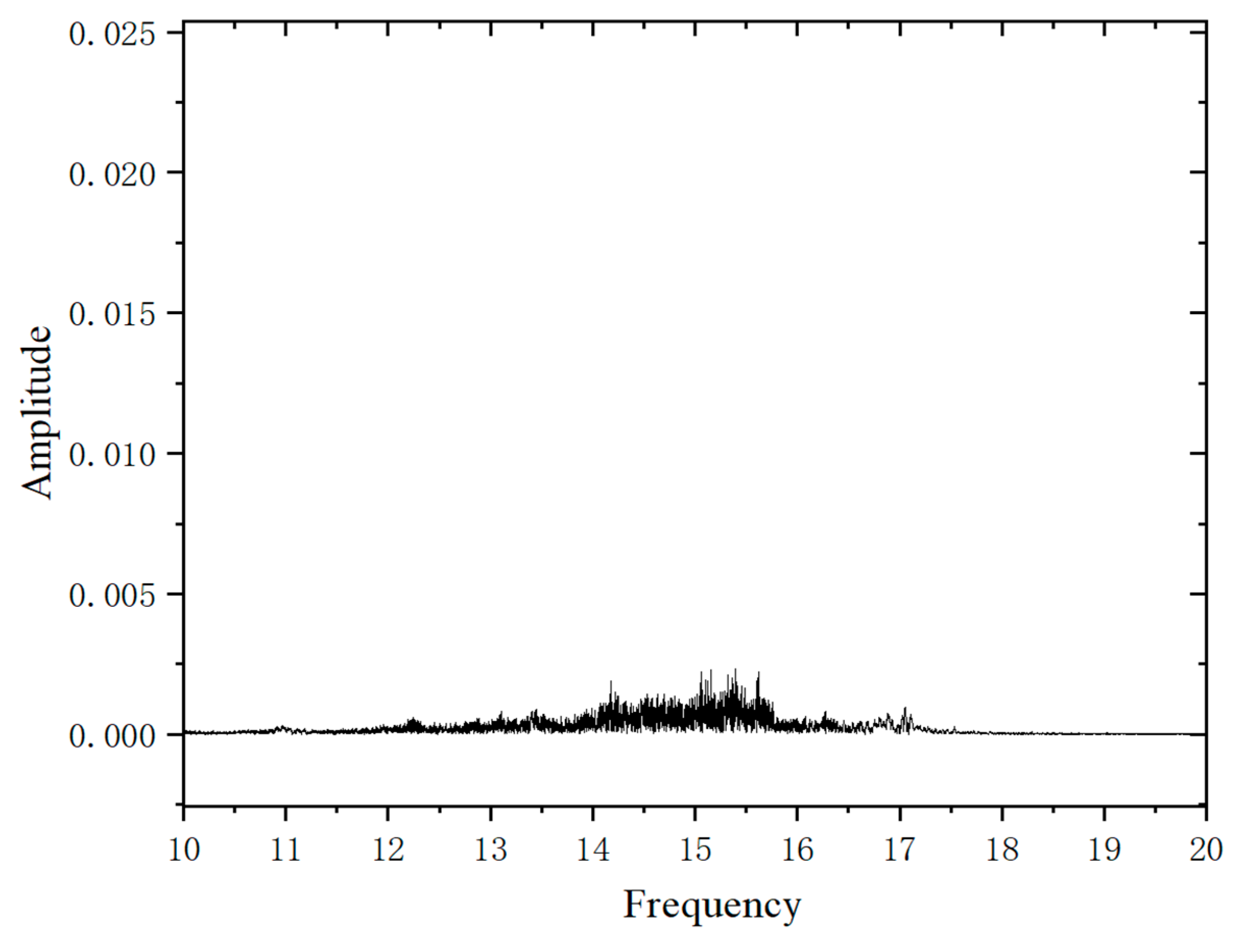
Based on the actual test results, the flapping frequency of the aircraft can reach 15 Hz only when the motor voltage is above 11.2 V. Therefore, during the entire flight phase, the flight is stopped when the battery voltage drops below 11.2 V. In Figure 34, based on the obtained flight data, the frequency spectrum was obtained using Fast Fourier Transform, as shown in the figure. According to the analysis of the frequency spectrum, the flapping frequency of the aircraft during flight is mainly concentrated between 14 Hz and 16 Hz. 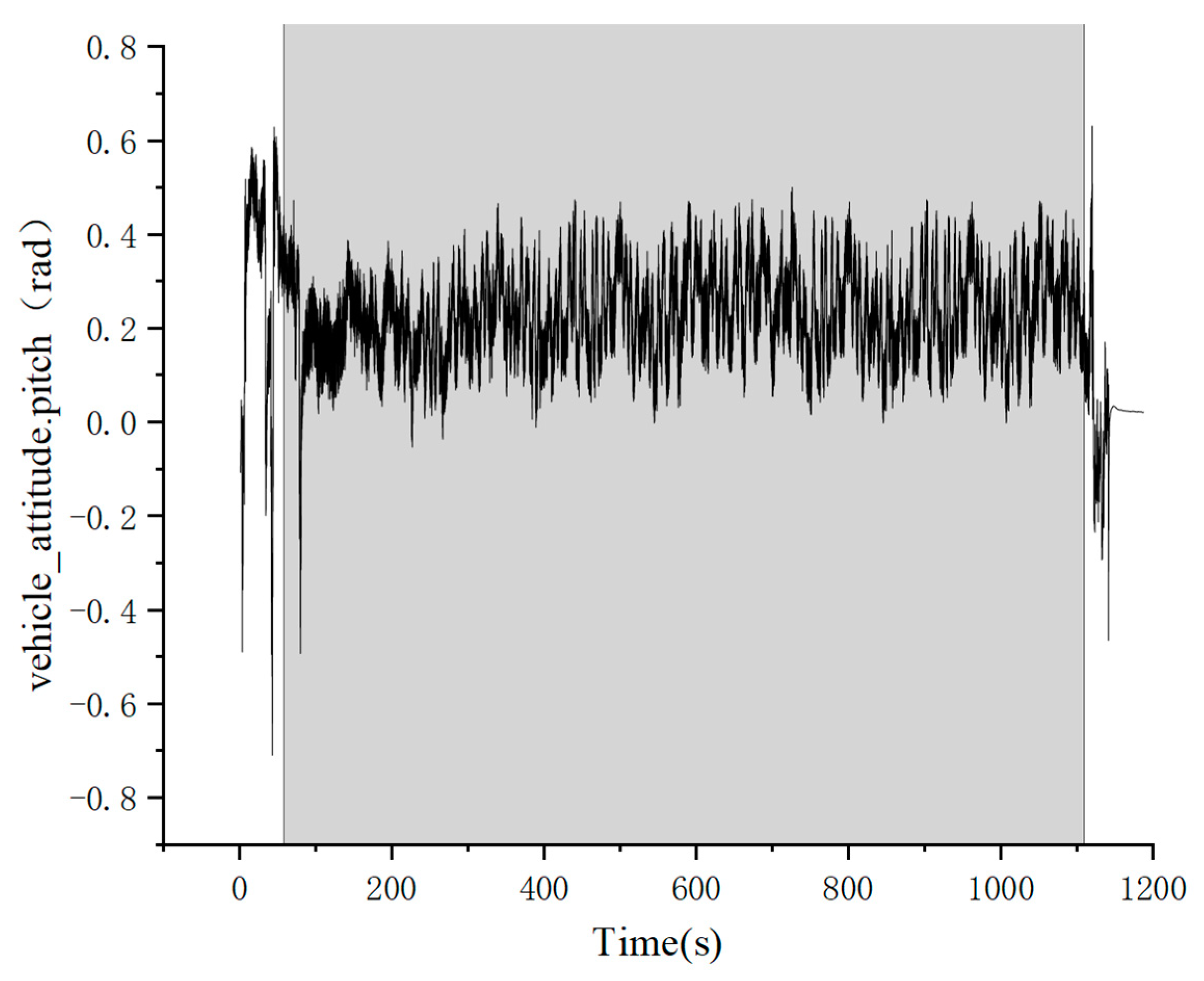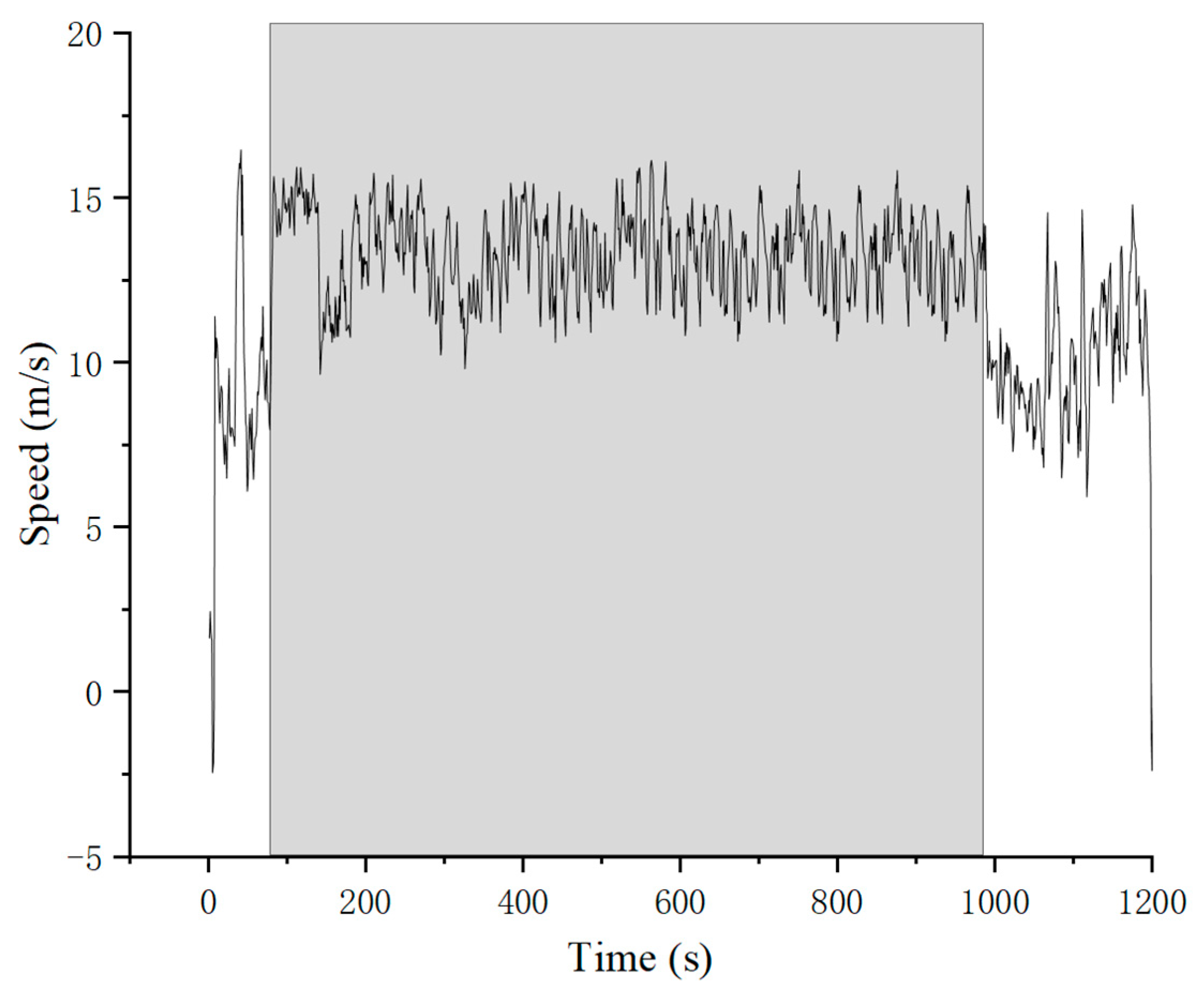Figure 35 shows the variation of the aircraft’s pitch angle with time throughout the flight phase, where the battery voltage is maintained above 11.2 V to sustain a flapping frequency of approximately 15 Hz. The shaded area in the figure represents the stable flight phase of the aircraft (80 s–1110 s).

During the flight phase, a time interval (80 s–980 s) was selected where the flapping frequency was approximately 15 Hz and the flight speed remained relatively constant, as shown in Figure 36. Within the 15 min flight duration, the average flight speed was calculated by taking the mean of the flight speeds, resulting in an average speed of 13.3 m/s. The average speed of the aircraft increased from the initial 10 m/s to 13.3 m/s, representing a 33% improvement. Furthermore, the maximum flight speed reached 16 m/s, which is close to the flight speed of pigeons in nature. The duration of high-speed flight increased from the initial 5 min to 15 min, tripling the previous duration.

6. Conclusions

Firstly, based on the foundation of the team’s “Dove” aircraft, this paper presents improvements to the propulsion system to meet the speed requirements. A matching and selection method for the motor, gearbox, and load is proposed. The appropriate motor is selected based on the input power of the propulsion system, and the matching between the motor and gearbox is determined using the motor efficiency and gear ratio calculation method provided in this paper. Finally, a flight test prototype is designed using the proposed matching method, and wind tunnel experiments and flight validations are conducted.

• The wind tunnel experiments show that at an angle of attack of 15° and 20°, the lift increases with the increase in flapping frequency, but the increase is relatively small. At other angles of attack, the change in lift with increasing flapping frequency is not significant. The thrust, on the other hand, increases significantly with the increase in flapping frequency at any angle of attack.
• The flight validation demonstrates that at a flapping frequency of approximately 15 Hz, the average flight speed of the aircraft is 13.3 m/s within a 15 min duration, which is close to the actual flight speed of pigeons. The duration of high-speed flight (15 Hz) is tripled compared to the initial duration.