A Novel Attitude Control Strategy for a Quadrotor Drone with Actuator Dynamics Based on a High-Order Sliding Mode Disturbance Observer
Abstract
1. Introduction
- A novel state feedback control incorporating HOSMDO is proposed to increase the robustness and accuracy of the attitude control system under matched and mismatched disturbances as well as actuator dynamics. The control strategy was designed with a holistic mindset for the whole system, rather than a recursive design using back-stepping methods.
- The HOSMDO is proposed to achieve exact robust estimation of matched/mismatched disturbances and their higher-order derivatives in finite time. To the best of our knowledge, the HOSMDO modified from the non-recursively formed HOSM differentiator is utilized here for the first time.
- By comparing the stability of the controller designed with and without considering actuator dynamics, it was found that the control parameter range of the latter is limited by actuator dynamics, and the closed-loop tracking accuracy is also affected.
2. Preliminaries and Problem Formulation
2.1. Preliminaries
2.2. Problem Formulation
2.2.1. Attitude Motion Model of a Quadrotor Drone
2.2.2. Problem Statement
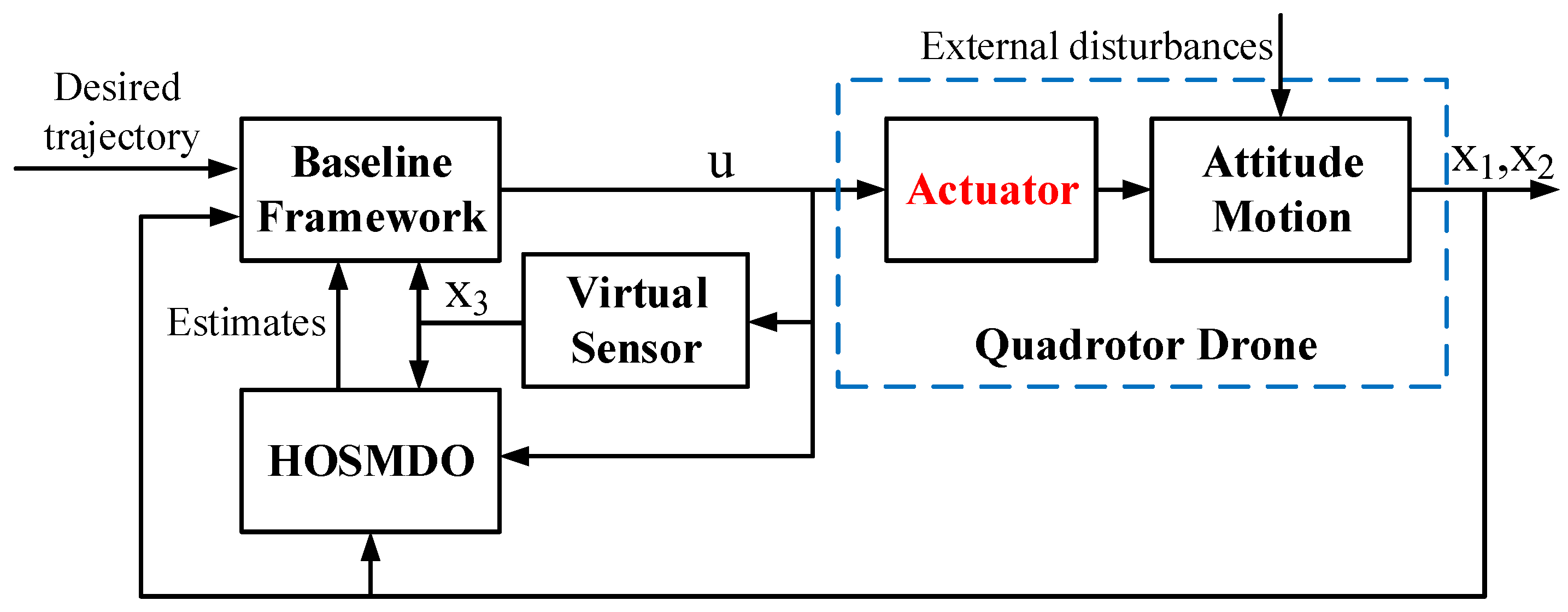
3. The HOSMDO-Based Control Strategy
3.1. The Baseline Control Framework Design
3.2. The High-Order Sliding Mode Disturbance Observer
3.3. The Proposed Control Strategy
- construct a baseline framework in the ideal scenario where all disturbance information is known;
- replace the disturbances and relevant derivatives required for the baseline framework with the corresponding estimates generated by the HOSMDOs to obtain the overall control scheme.
4. Stability Analysis
4.1. Analysis of HOSMDO
4.2. Analysis of the Proposed Controller
4.3. Analysis of the Reduced Controller
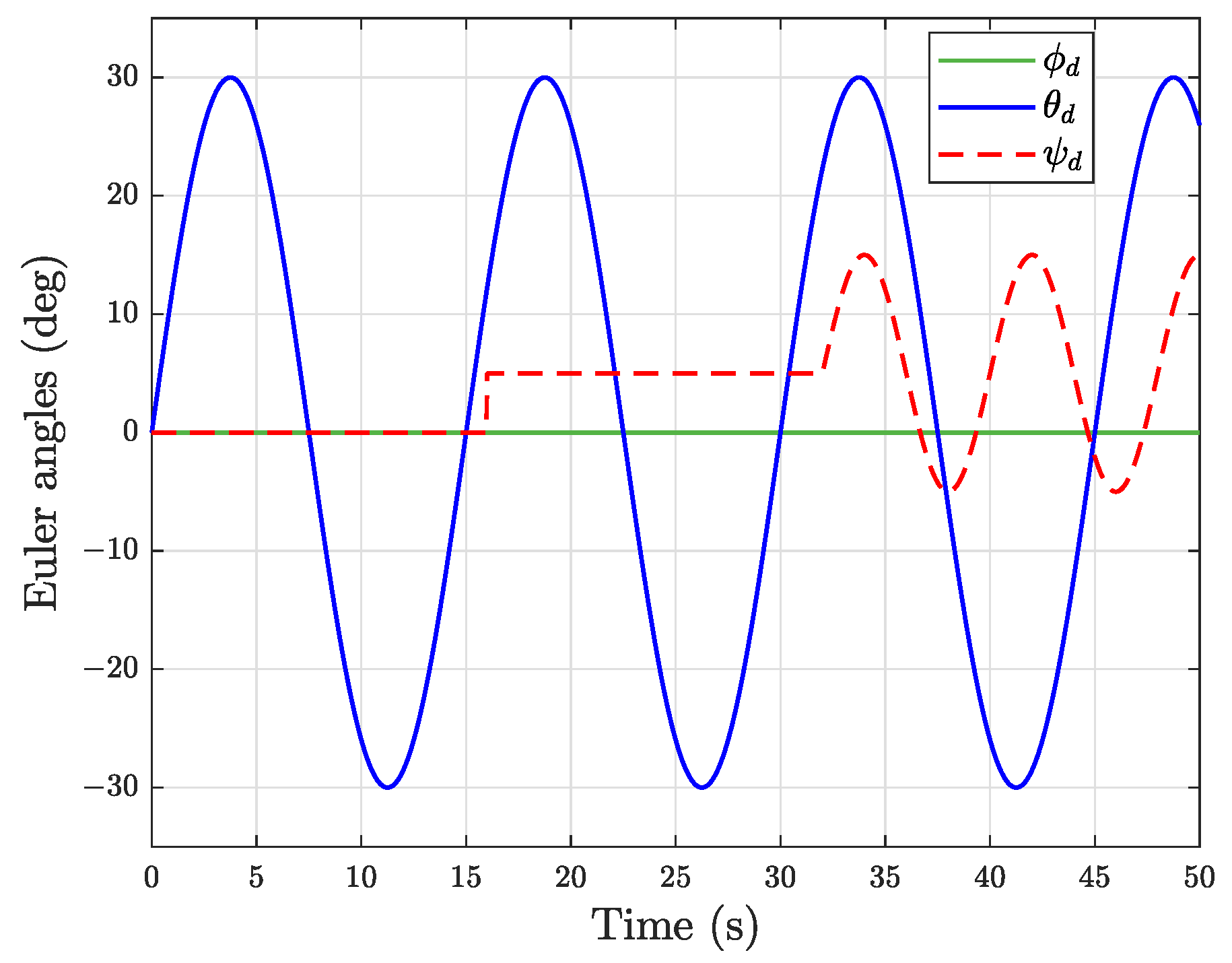
5. Simulation Results
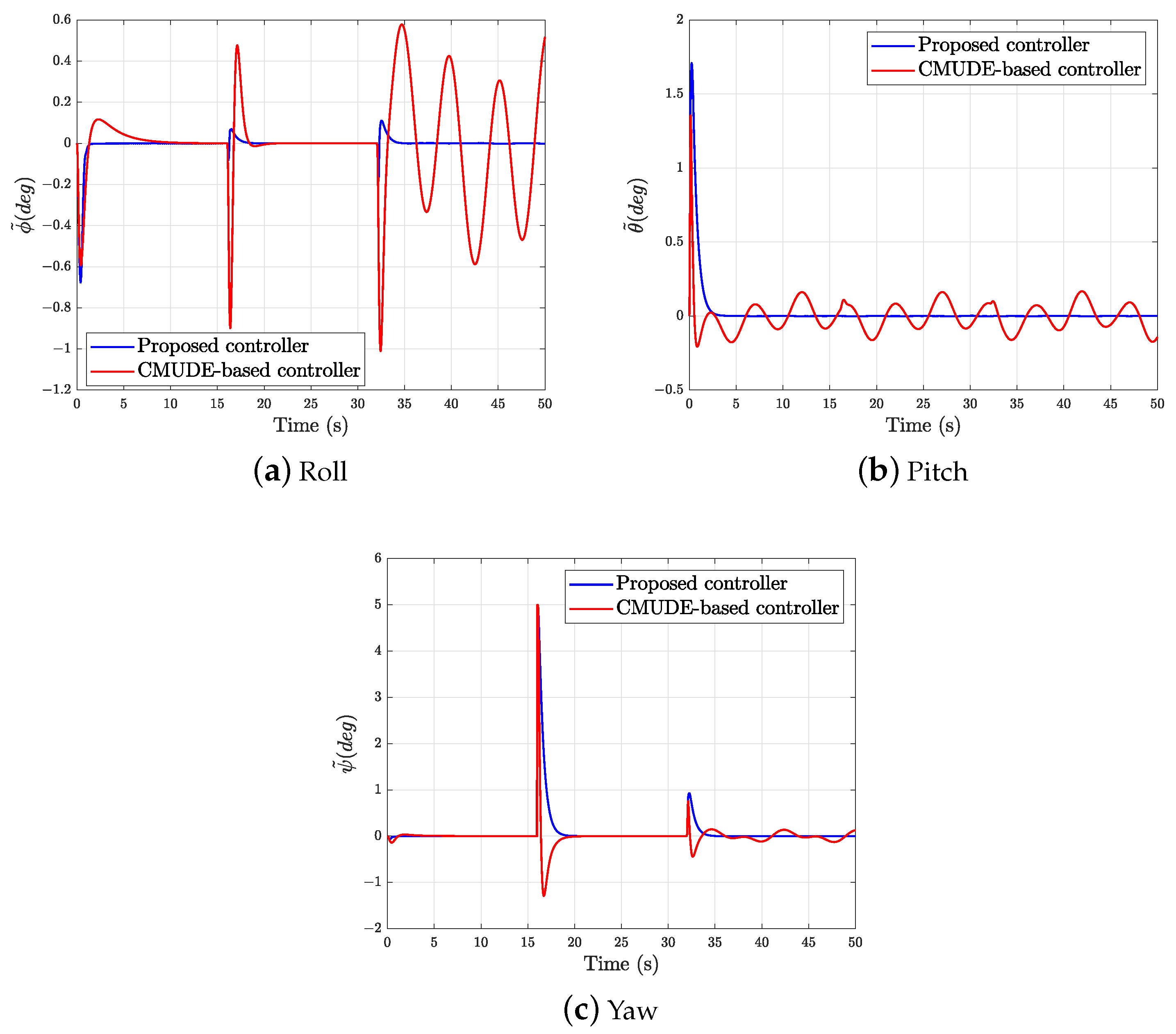
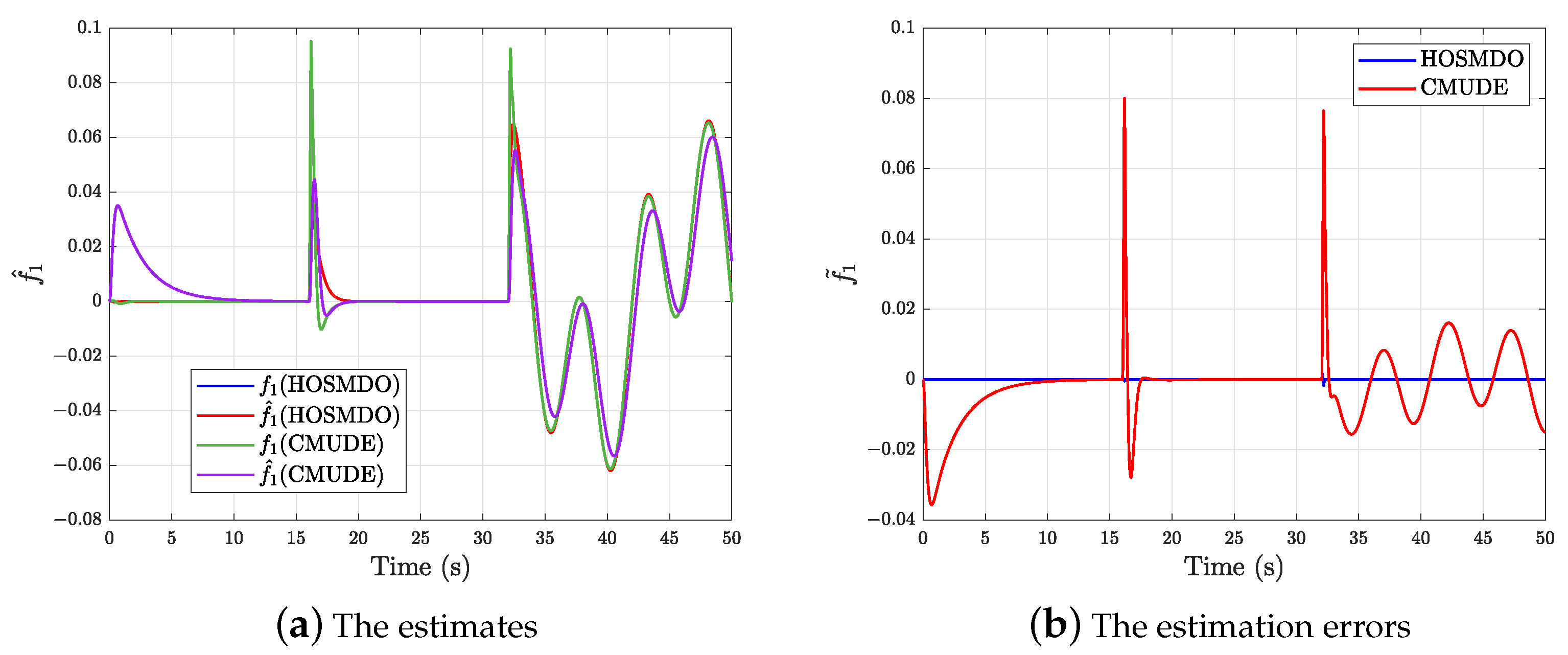
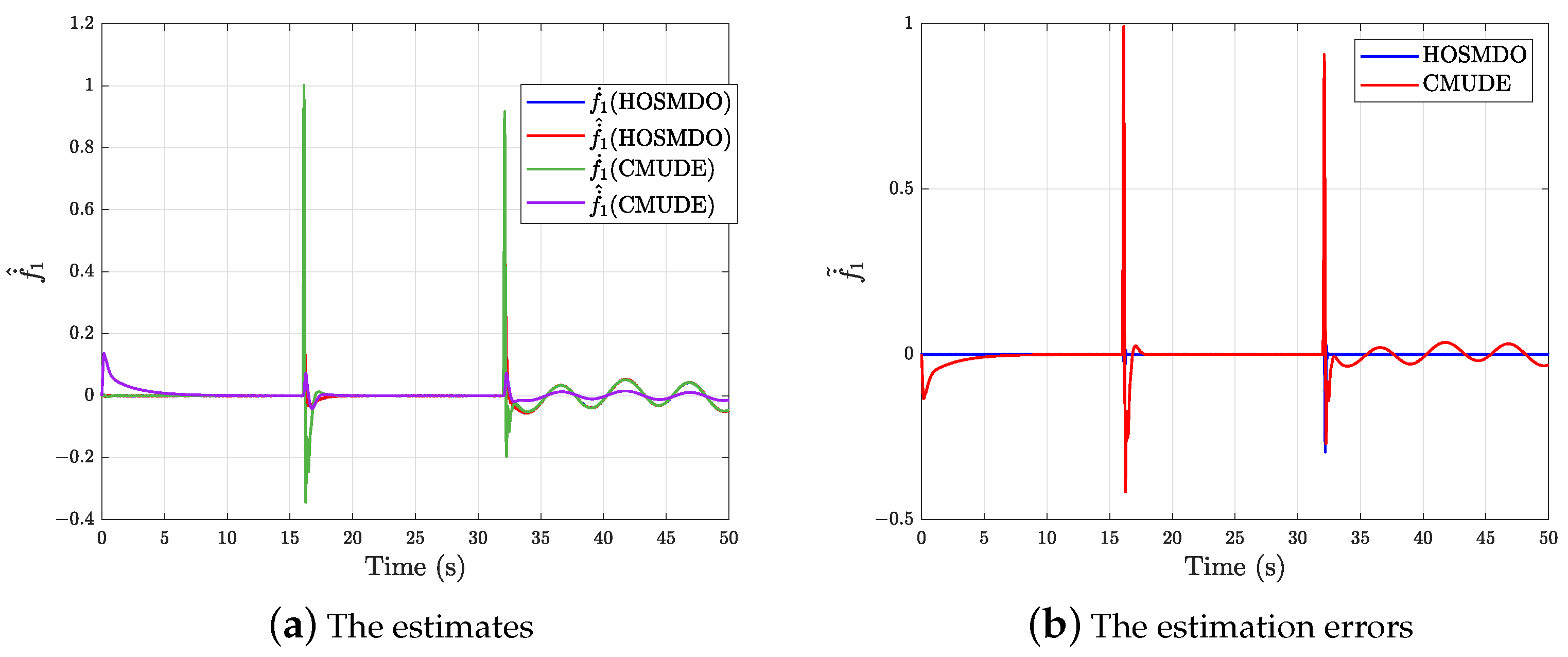
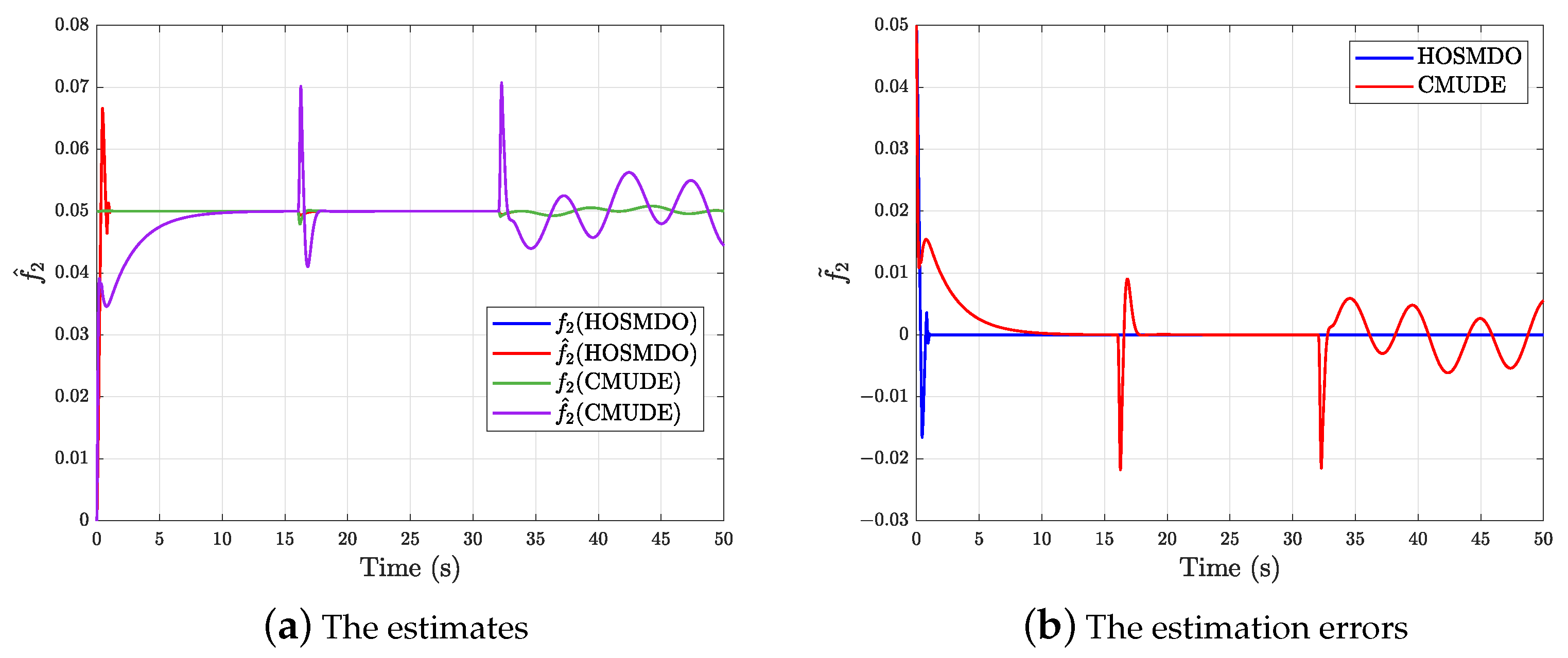
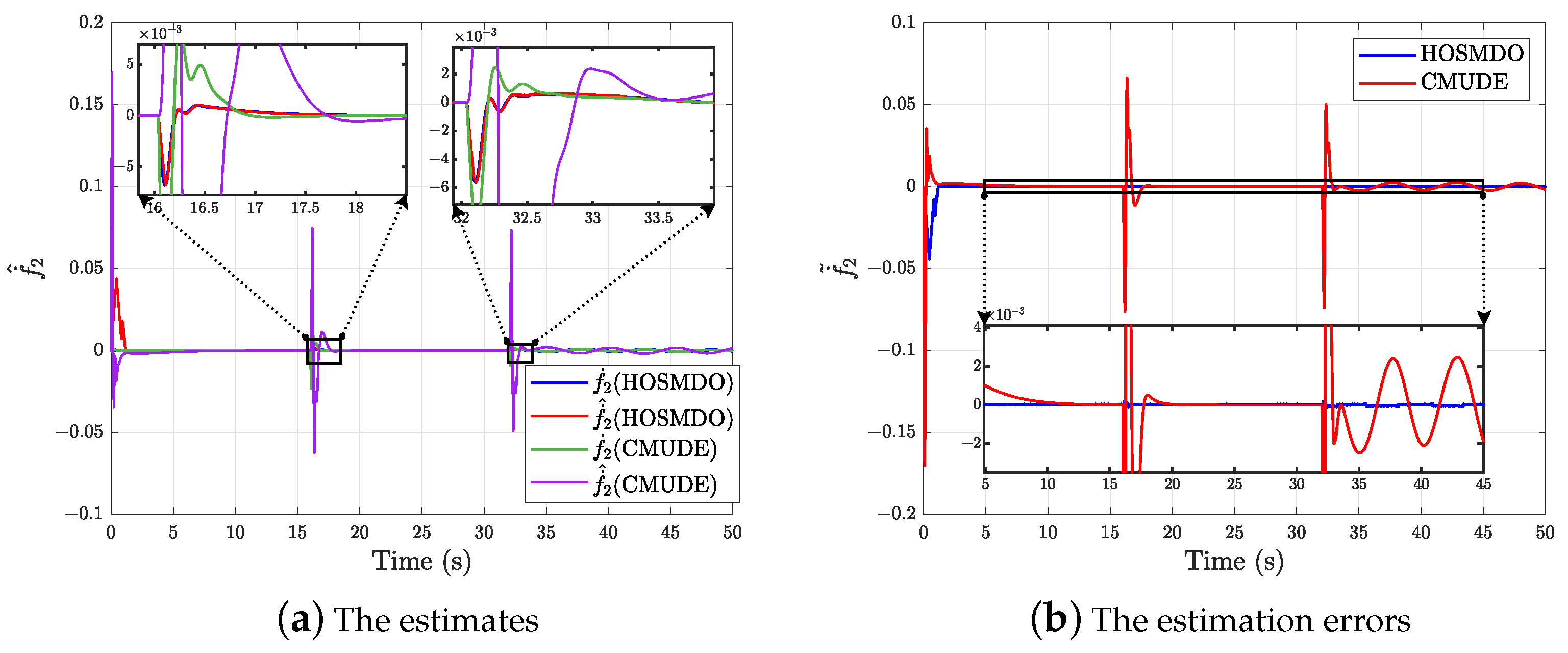
5.1. Comparison Results for the Proposed Controller and the CMUDE-Based Controller
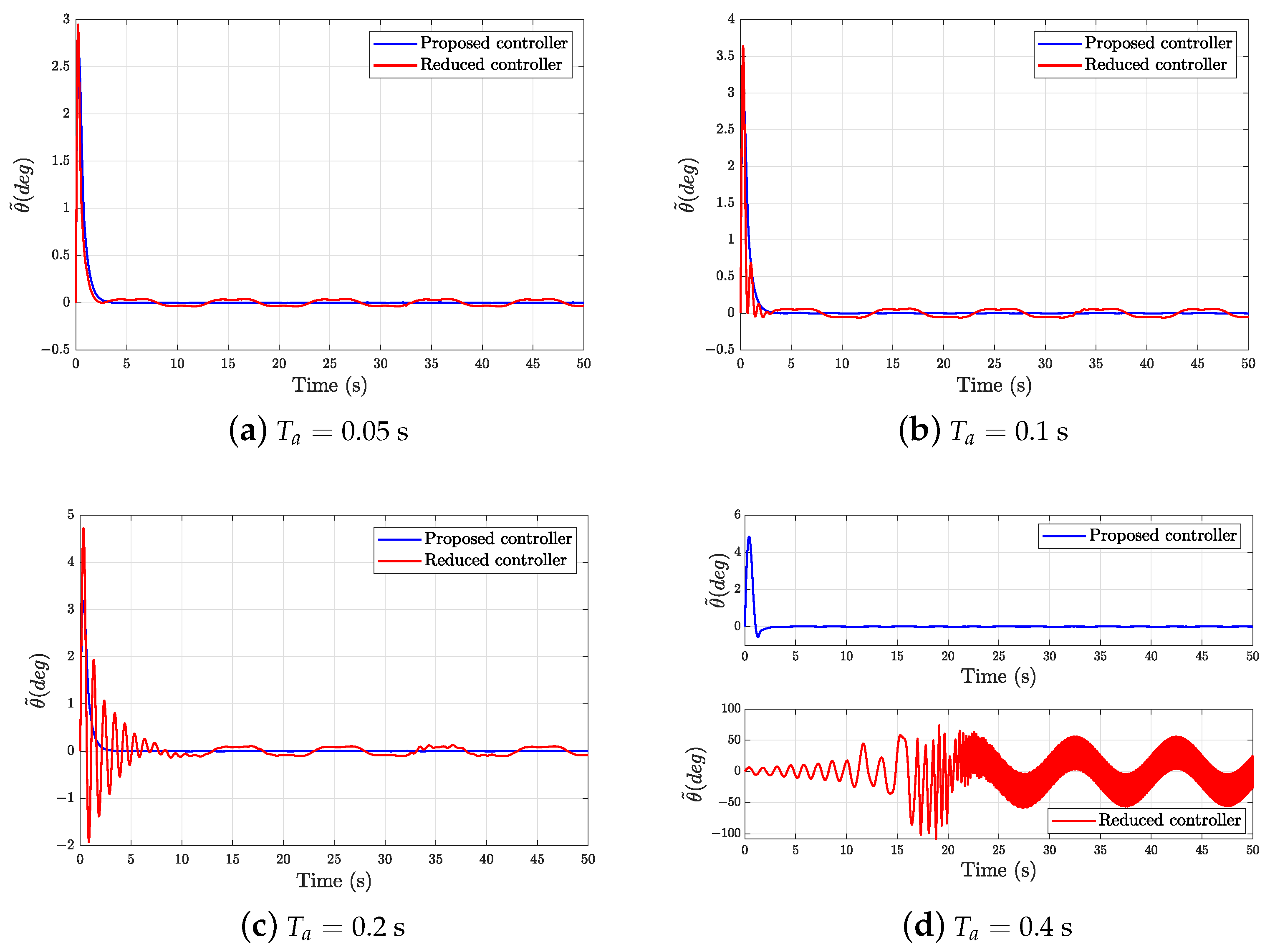
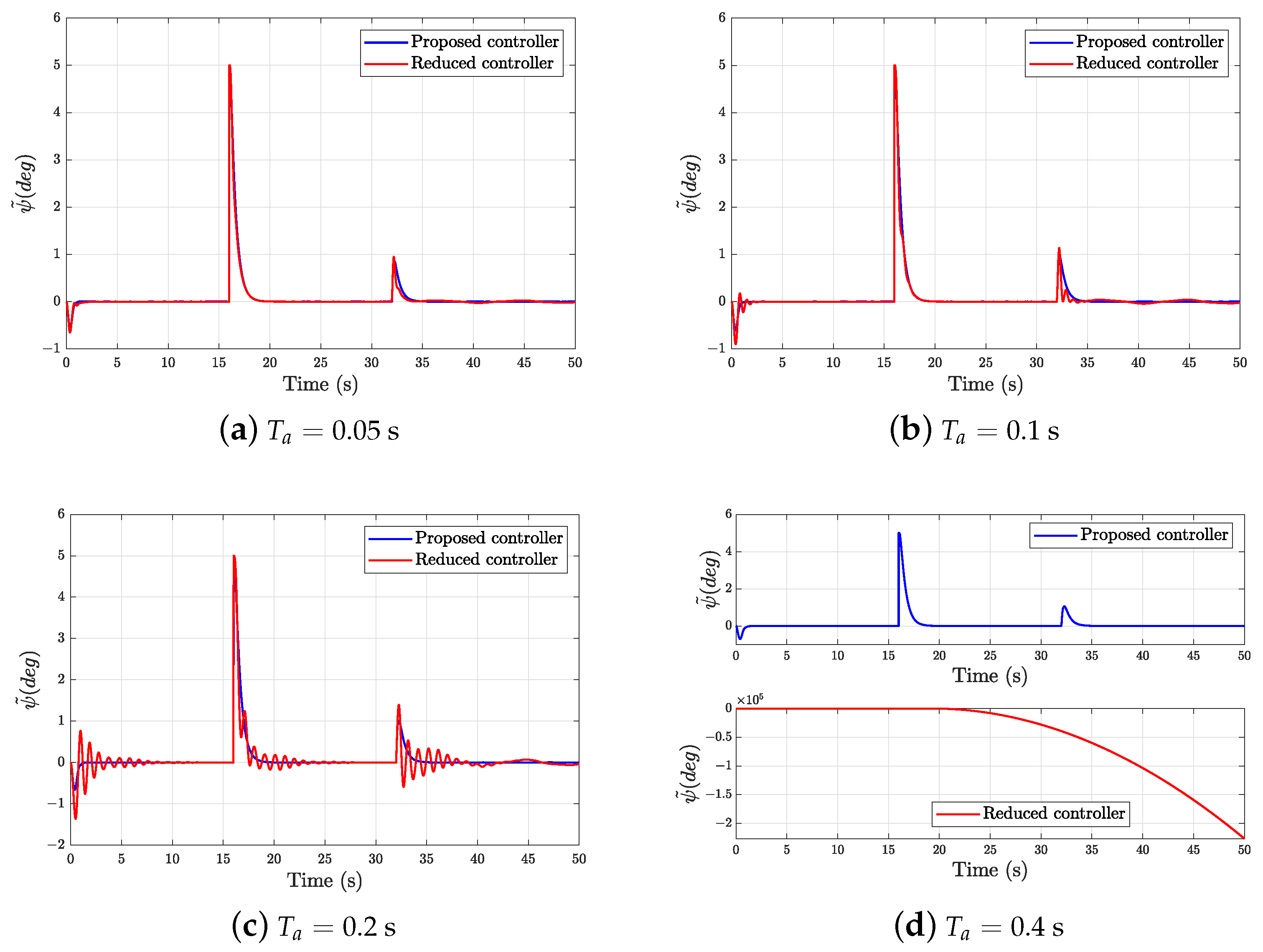
5.2. Comparison Results for the Proposed Controller and the Reduced Controller
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mahony, R.; Kumar, V.; Corke, P. Multirotor aerial vehicles: Modeling, estimation, and control of quadrotor. IEEE Robot. Autom. Mag. 2012, 19, 20–32. [Google Scholar] [CrossRef]
- Gupte, S.; Mohandas, P.I.T.; Conrad, J.M. A survey of quadrotor unmanned aerial vehicles. In Proceedings of the 2012 IEEE Southeastcon, Orlando, FL, USA, 15–18 March 2012; pp. 1–6. [Google Scholar]
- Giannetti, F.; Chirici, G.; Gobakken, T.; Naesset, E.; Travaglini, D.; Puliti, S. A new approach with DTM-independent metrics for forest growing stock prediction using UAV photogrammetric data. Remote Sens. Environ. 2018, 213, 195–205. [Google Scholar] [CrossRef]
- Sonugür, G. A Review of quadrotor UAV: Control and SLAM methodologies ranging from conventional to innovative approaches. Robot. Auton. Syst. 2023, 161, 104342. [Google Scholar] [CrossRef]
- Budiharto, W.; Irwansyah, E.; Suroso, J.S.; Chowanda, A.; Ngarianto, H.; Gunawan, A.A.S. Mapping and 3D modelling using quadrotor drone and GIS software. J. Big Data 2021, 8, 48. [Google Scholar] [CrossRef]
- Fernández-Guisuraga, J.M.; Sanz-Ablanedo, E.; Suárez-Seoane, S.; Calvo, L. Using unmanned aerial vehicles in postfire vegetation survey campaigns through large and heterogeneous areas: Opportunities and challenges. Sensors 2018, 18, 586. [Google Scholar] [CrossRef]
- Liu, H.; Xi, J.; Zhong, Y. Robust attitude stabilization for nonlinear quadrotor systems with uncertainties and delays. IEEE Trans. Ind. Electron. 2017, 64, 5585–5594. [Google Scholar] [CrossRef]
- Garcia, R.A.; Rubio, F.R.; Ortega, M.G. Robust PID control of the quadrotor helicopter. IFAC Proceedings Volumes 2012, 45, 229–234. [Google Scholar] [CrossRef]
- Noordin, A.; Mohd Basri, M.A.; Mohamed, Z. Position and Attitude Tracking of MAV Quadrotor Using SMC-Based Adaptive PID Controller. Drones 2022, 6, 263. [Google Scholar] [CrossRef]
- Fei, Y.; Sun, Y.; Shi, P. Robust Hierarchical Formation Control of Unmanned Aerial Vehicles via Neural-Based Observers. Drones 2022, 6, 40. [Google Scholar] [CrossRef]
- Mechali, O.; Xu, L.; Xie, X.; Iqbal, J. Fixed-time nonlinear homogeneous sliding mode approach for robust tracking control of multirotor aircraft: Experimental validation. J. Frank. Inst. 2022, 359, 1971–2029. [Google Scholar] [CrossRef]
- Kang, B.; Miao, Y.; Liu, F.; Duan, J.; Wang, K.; Jiang, S. A second-order sliding mode controller of quad-rotor UAV based on PID sliding mode surface with unbalanced load. J. Syst. Sci. Complex. 2021, 34, 520–536. [Google Scholar] [CrossRef]
- Falcón, R.; Ríos, H.; Dzul, A. Comparative analysis of continuous sliding-modes control strategies for quad-rotor robust tracking. Control Eng. Pract. 2019, 90, 241–256. [Google Scholar] [CrossRef]
- Chen, W.H.; Yang, J.; Guo, L.; Li, S. Disturbance-observer-based control and related methods—An overview. IEEE Trans. Ind. Electron. 2015, 63, 1083–1095. [Google Scholar] [CrossRef]
- Wei, X.; Guo, L. Composite disturbance-observer-based control and H∞ control for complex continuous models. Int. J. Robust Nonlinear Control IFAC-Affil. J. 2010, 20, 106–118. [Google Scholar] [CrossRef]
- Yang, J.; Chen, W.H.; Li, S. Non-linear disturbance observer-based robust control for systems with mismatched disturbances/uncertainties. IET Control Theory Appl. 2011, 5, 2053–2062. [Google Scholar] [CrossRef]
- Davila, J. Exact tracking using backstepping control design and high-order sliding modes. IEEE Trans. Autom. Control 2013, 58, 2077–2081. [Google Scholar] [CrossRef]
- Yang, J.; Chen, W.H.; Li, S. High-order mismatched disturbance compensation for motion control systems via a continuous dynamic sliding-mode approach. IEEE Trans. Ind. Inform. 2013, 10, 604–614. [Google Scholar] [CrossRef]
- De Loza, A.F.; Bejarano, F.J.; Fridman, L. Unmatched uncertainties compensation based on high-order sliding mode observation. Int. J. Robust Nonlinear Control 2013, 23, 754–764. [Google Scholar] [CrossRef]
- Zhou, C.; Dai, C.; Yang, J.; Li, S. Disturbance observer-based tracking control with prescribed performance specifications for a class of nonlinear systems subject to mismatched disturbances. Asian J. Control 2023, 25, 359–370. [Google Scholar] [CrossRef]
- Dai, J.; Ren, B.; Zhong, Q.C. Uncertainty and disturbance estimator-based backstepping control for nonlinear systems with mismatched uncertainties and disturbances. J. Dyn. Syst. Meas. Control 2018, 140, 121005. [Google Scholar] [CrossRef]
- Moulay, E.; Léchappé, V.; Bernuau, E.; Defoort, M.; Plestan, F. Fixed-time sliding mode control with mismatched disturbances. Automatica 2022, 136, 110009. [Google Scholar] [CrossRef]
- Qi, Y.; Zhu, Y.; Wang, J.; Shan, J.; Liu, H.H. MUDE-based control of quadrotor for accurate attitude tracking. Control Eng. Pract. 2021, 108, 104721. [Google Scholar] [CrossRef]
- Qin, Z.; Wang, H.; Liu, K.; Zhu, B.; Zhao, X.; Zheng, W.; Dang, Q. Cascade-modified uncertainty and disturbance estimator–based control of quadrotors for accurate attitude tracking under exogenous disturbance. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2023, 237, 2312–2330. [Google Scholar] [CrossRef]
- Wang, J.; Alattas, K.A.; Bouteraa, Y.; Mofid, O.; Mobayen, S. Adaptive finite-time backstepping control tracker for quadrotor UAV with model uncertainty and external disturbance. Aerosp. Sci. Technol. 2023, 133, 108088. [Google Scholar] [CrossRef]
- Mofid, O.; Mobayen, S.; Zhang, C.; Esakki, B. Desired tracking of delayed quadrotor UAV under model uncertainty and wind disturbance using adaptive super-twisting terminal sliding mode control. ISA Trans. 2022, 123, 455–471. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Sun, M.; Chen, Z.; Sun, Q. Super-twisting sliding mode control for aircraft at high angle of attack based on finite-time extended state observer. Nonlinear Dyn. 2020, 99, 2785–2799. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of homogeneous systems. In Proceedings of the American Control Conference (Cat. No. 97CH36041), Albuquerque, NM, USA, 6 June 1997; pp. 2513–2514. [Google Scholar]
- Levant, A. Higher-order sliding modes, differentiation and output-feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Perruquetti, W.; Floquet, T. Homogeneous finite time observer for nonlinear systems with linearizable error dynamics. In Proceedings of the 2007 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 390–395. [Google Scholar]
- Angulo, M.T.; Moreno, J.A.; Fridman, L. Robust exact uniformly convergent arbitrary order differentiator. Automatica 2013, 49, 2489–2495. [Google Scholar] [CrossRef]
- Reichhartinger, M.; Spurgeon, S. An arbitrary-order differentiator design paradigm with adaptive gains. Int. J. Control 2018, 91, 2028–2042. [Google Scholar] [CrossRef]
- Castillo, A.; Sanz, R.; Garcia, P.; Qiu, W.; Wang, H.; Xu, C. Disturbance observer-based quadrotor attitude tracking control for aggressive maneuvers. Control Eng. Pract. 2019, 82, 14–23. [Google Scholar] [CrossRef]
- Wang, Y.; Ren, B.; Zhong, Q.C. Bounded UDE-based controller for input constrained systems with uncertainties and disturbances. IEEE Trans. Ind. Electron. 2020, 68, 1560–1570. [Google Scholar] [CrossRef]
- Falanga, D.; Kleber, K.; Mintchev, S.; Floreano, D.; Scaramuzza, D. The foldable drone: A morphing quadrotor that can squeeze and fly. IEEE Robot. Autom. Lett. 2018, 4, 209–216. [Google Scholar] [CrossRef]
- Ji, R.; Ma, J.; Ge, S.S. Modeling and control of a tilting quadcopter. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 2823–2834. [Google Scholar] [CrossRef]
- Ji, R.; Ma, J.; Ge, S.S.; Ji, R. Adaptive second-order sliding mode control for a tilting quadcopter with input saturations. IFAC-PapersOnLine 2020, 53, 3910–3915. [Google Scholar] [CrossRef]
- Xu, L.; Qin, K.; Zhu, Y.; Li, W.; Shi, M. Parameter Design Constraints of UDE-Based Control under Non-ideal Actuators. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Heifei, China, 25–27 July 2022; pp. 1078–1083. [Google Scholar]
- Cruz-Zavala, E.; Moreno, J.A. Lyapunov functions for continuous and discontinuous differentiators. IFAC-PapersOnLine 2016, 49, 660–665. [Google Scholar] [CrossRef]
- Şahin, H.; Kose, O.; Oktay, T. Simultaneous autonomous system and powerplant design for morphing quadrotors. Aircr. Eng. Aerosp. Technol. 2022, 94, 1228–1241. [Google Scholar] [CrossRef]
- Chovancová, A.; Fico, T.; Chovanec, L’.; Hubinský, P. Mathematical modelling and parameter identification of quadrotor (a survey). Procedia Eng. 2014, 96, 172–181. [Google Scholar] [CrossRef]
- Chaturvedi, N.A.; Sanyal, A.K.; McClamroch, N.H. Rigid-body attitude control. IEEE Contr. Syst. Mag. 2011, 31, 30–51. [Google Scholar]
- Ozgoren, M.K. Comparative study of attitude control methods based on Euler angles, quaternions, angle–axis pairs and orientation matrices. Trans. Inst. Meas. Control. 2019, 41, 1189–1206. [Google Scholar] [CrossRef]
- Huo, X.; Huo, X.; Karimi, H.R. Attitude stabilization control of a quadrotor UAV by using backstepping approach. Math. Probl. Eng. 2014, 2014, 749803. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Q.; Wang, Y. Distributed cooperative control for multiple quadrotor systems via dynamic surface control. Nonlinear Dyn. 2014, 75, 513–527. [Google Scholar] [CrossRef]
- Khalil, H.K.; Grizzle, J.W. Nonlinear Systems; Prentice-Hall: Upper Saddle River, NJ, USA, 2002; Volume 3, pp. 134–180. [Google Scholar]





| Proposed Controller | CMUDE-Based Controller | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | −10 | −1 | −1 | 2 | 0.5 | ||||||
| 8 | −100 | −1 | −0.1 | 1 | 0.2 | ||||||
| 10 | −100 | −0.1 | −0.01 | 1 | 0.05 | ||||||
| −30 | |||||||||||
| Proposed controller | 0.0024 | 0.0010 | 0.0015 | |
| CMUDE-based controller | 0.3338 | 0.0947 | 0.0793 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Qin, K.; Tang, F.; Shi, M.; Lin, B. A Novel Attitude Control Strategy for a Quadrotor Drone with Actuator Dynamics Based on a High-Order Sliding Mode Disturbance Observer. Drones 2024, 8, 131. https://doi.org/10.3390/drones8040131
Xu L, Qin K, Tang F, Shi M, Lin B. A Novel Attitude Control Strategy for a Quadrotor Drone with Actuator Dynamics Based on a High-Order Sliding Mode Disturbance Observer. Drones. 2024; 8(4):131. https://doi.org/10.3390/drones8040131
Chicago/Turabian StyleXu, Linxi, Kaiyu Qin, Fan Tang, Mengji Shi, and Boxian Lin. 2024. "A Novel Attitude Control Strategy for a Quadrotor Drone with Actuator Dynamics Based on a High-Order Sliding Mode Disturbance Observer" Drones 8, no. 4: 131. https://doi.org/10.3390/drones8040131
APA StyleXu, L., Qin, K., Tang, F., Shi, M., & Lin, B. (2024). A Novel Attitude Control Strategy for a Quadrotor Drone with Actuator Dynamics Based on a High-Order Sliding Mode Disturbance Observer. Drones, 8(4), 131. https://doi.org/10.3390/drones8040131






