HiFly-Dragon: A Dragonfly Inspired Flapping Flying Robot with Modified, Resonant, Direct-Driven Flapping Mechanisms
Abstract
1. Introduction
2. System Design and Fabrication
2.1. Wing Design and Manufacturing
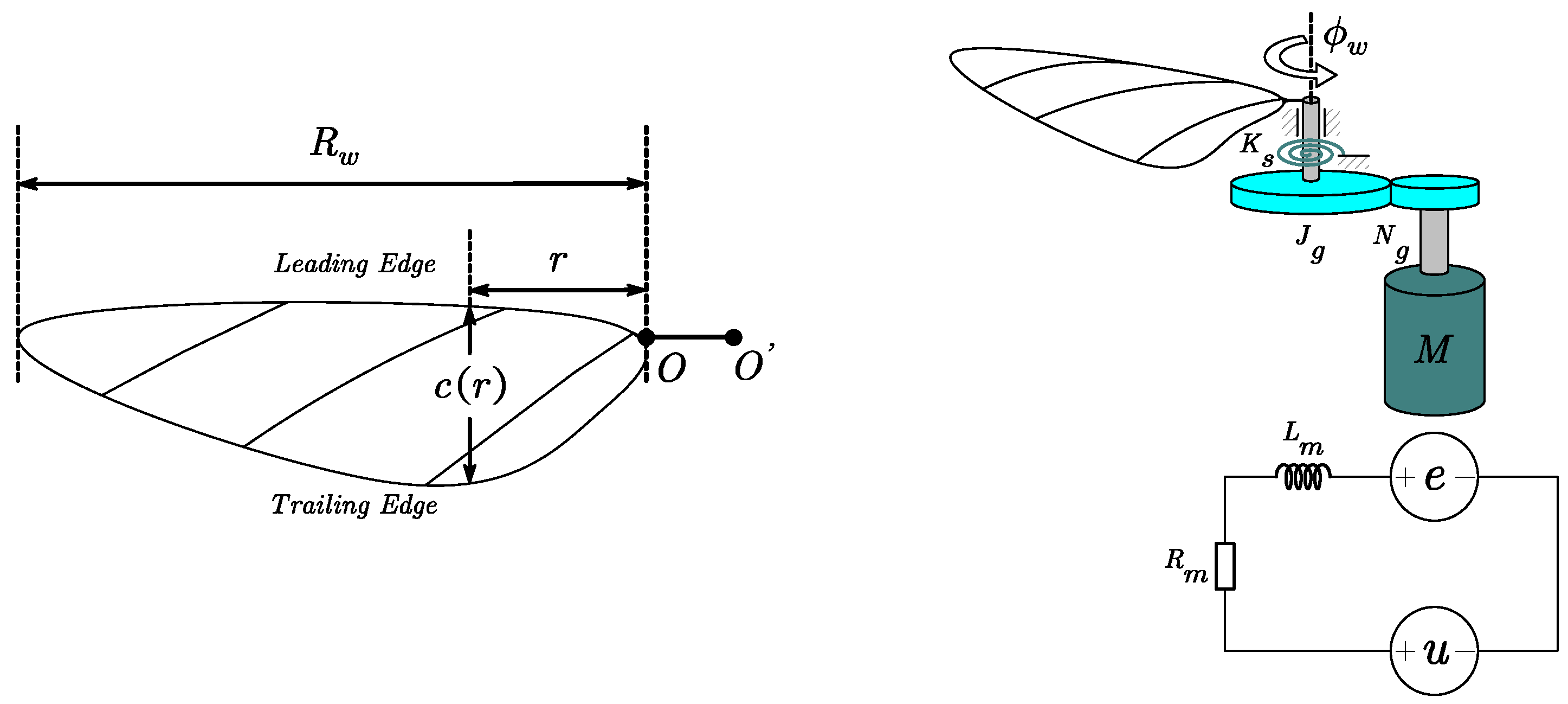
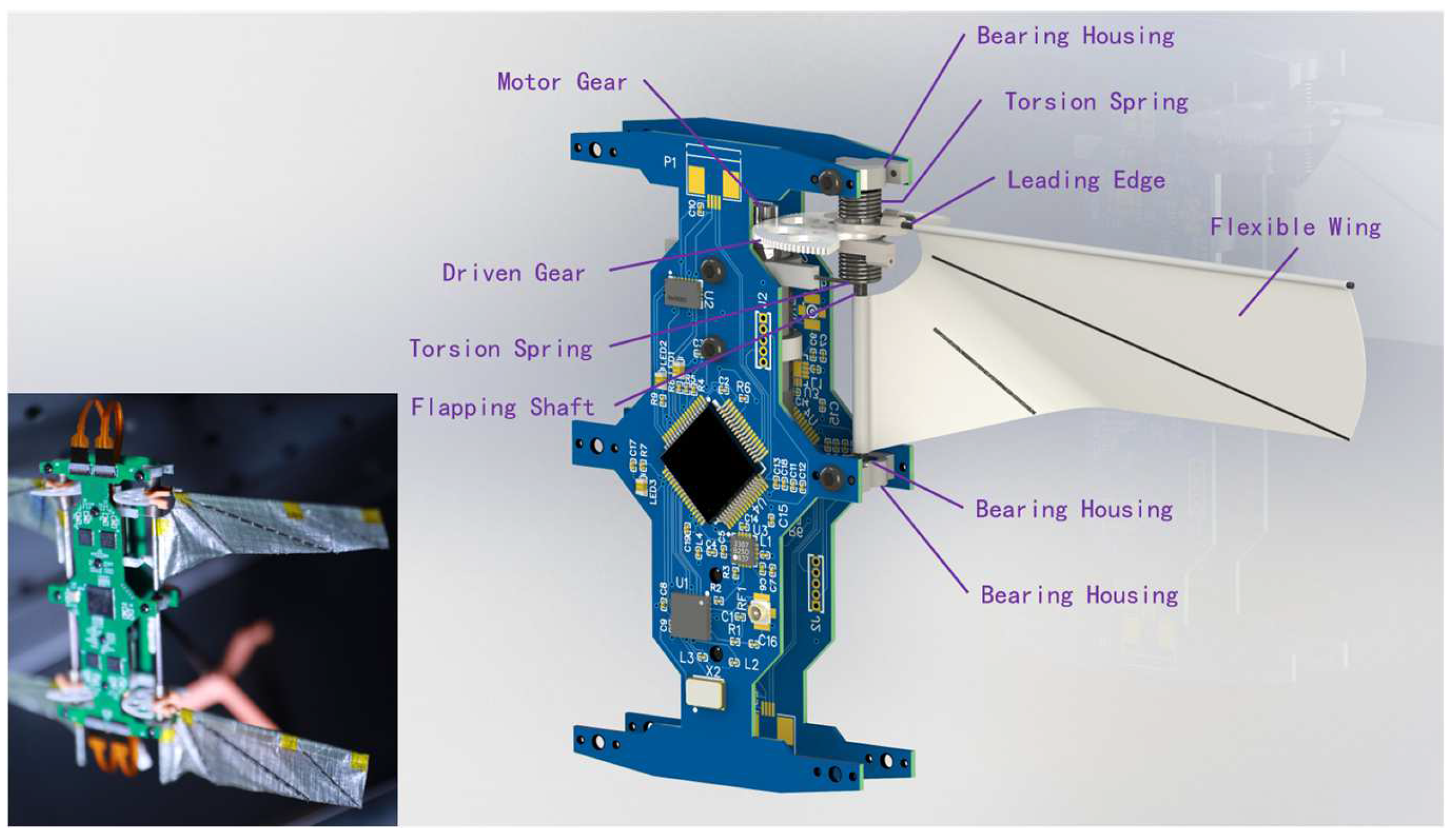
2.2. Resonant, Direct-Driven Flapping System
2.2.1. Modeling and Analysis of the Resonant, Direct-Driven Flapping Wing System
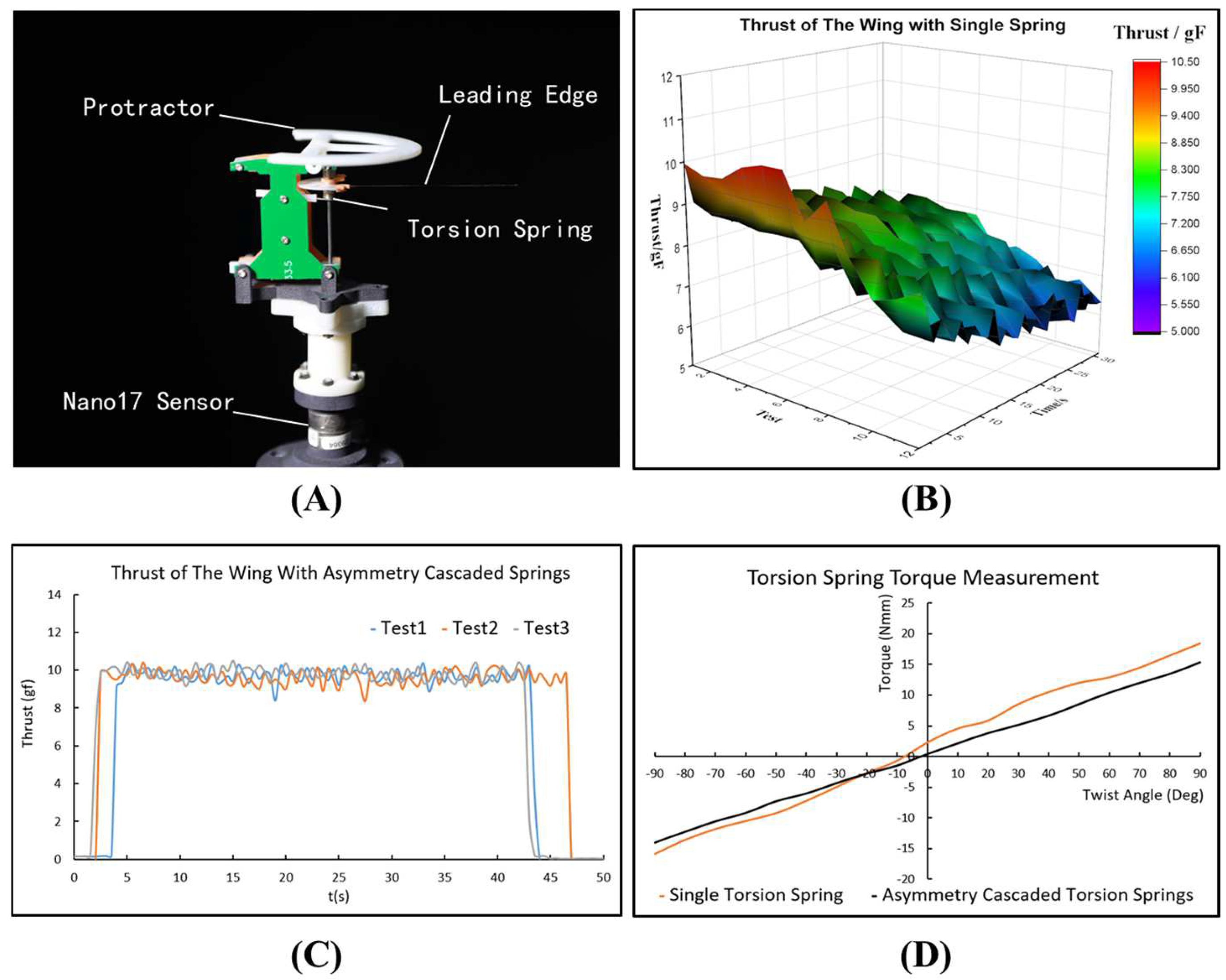
2.2.2. Resonant, Direct-Driven Flapping System Design and Fabrication
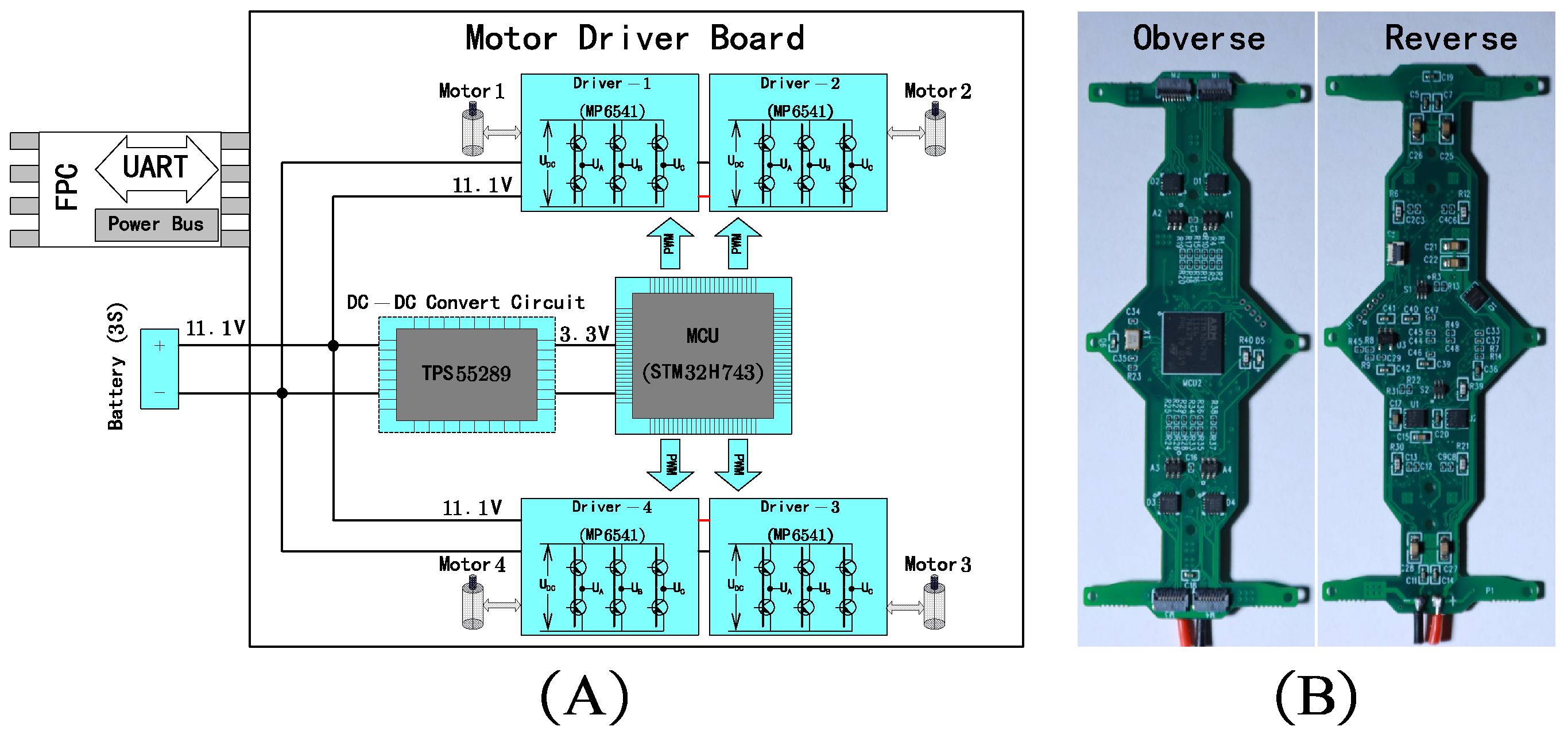
2.2.3. The BLDC Motor Controller Design and Fabrication
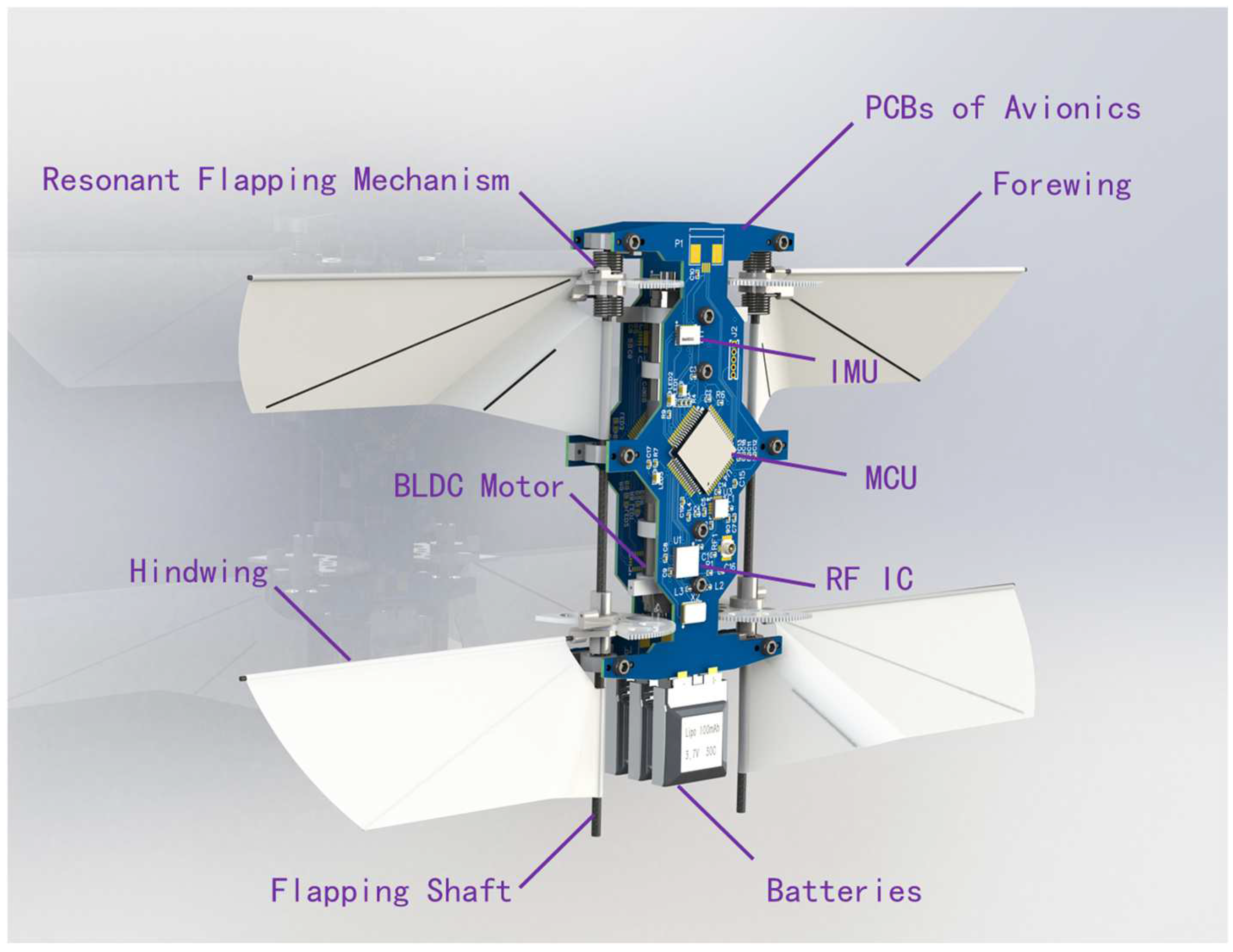
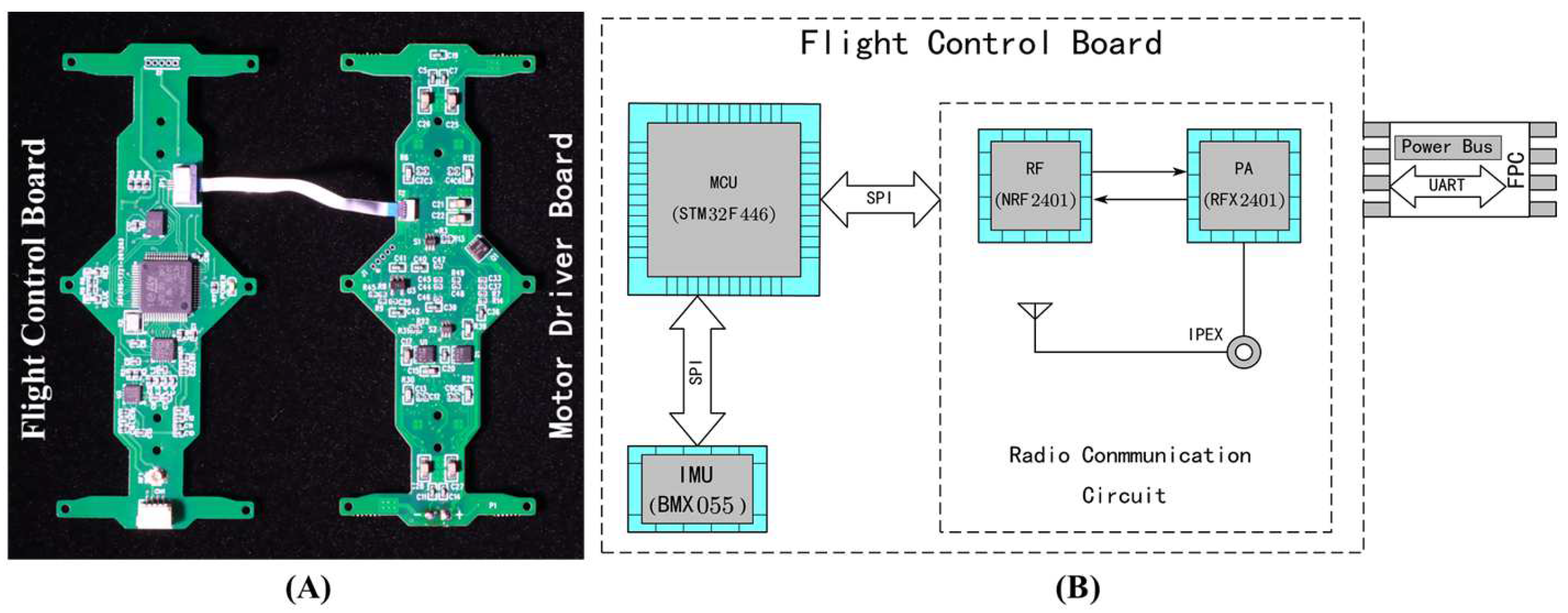
2.3. Onboard Avionics
2.3.1. Design of Onboard Avionics Hardware
2.3.2. Onboard Attitude Estimation
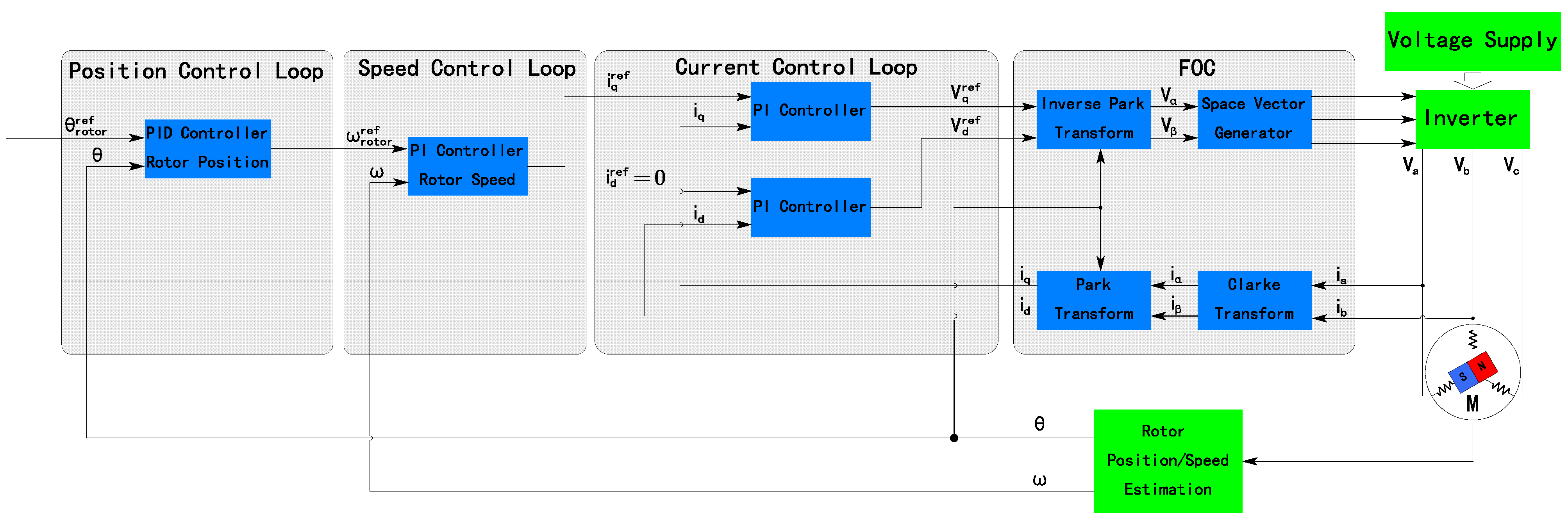
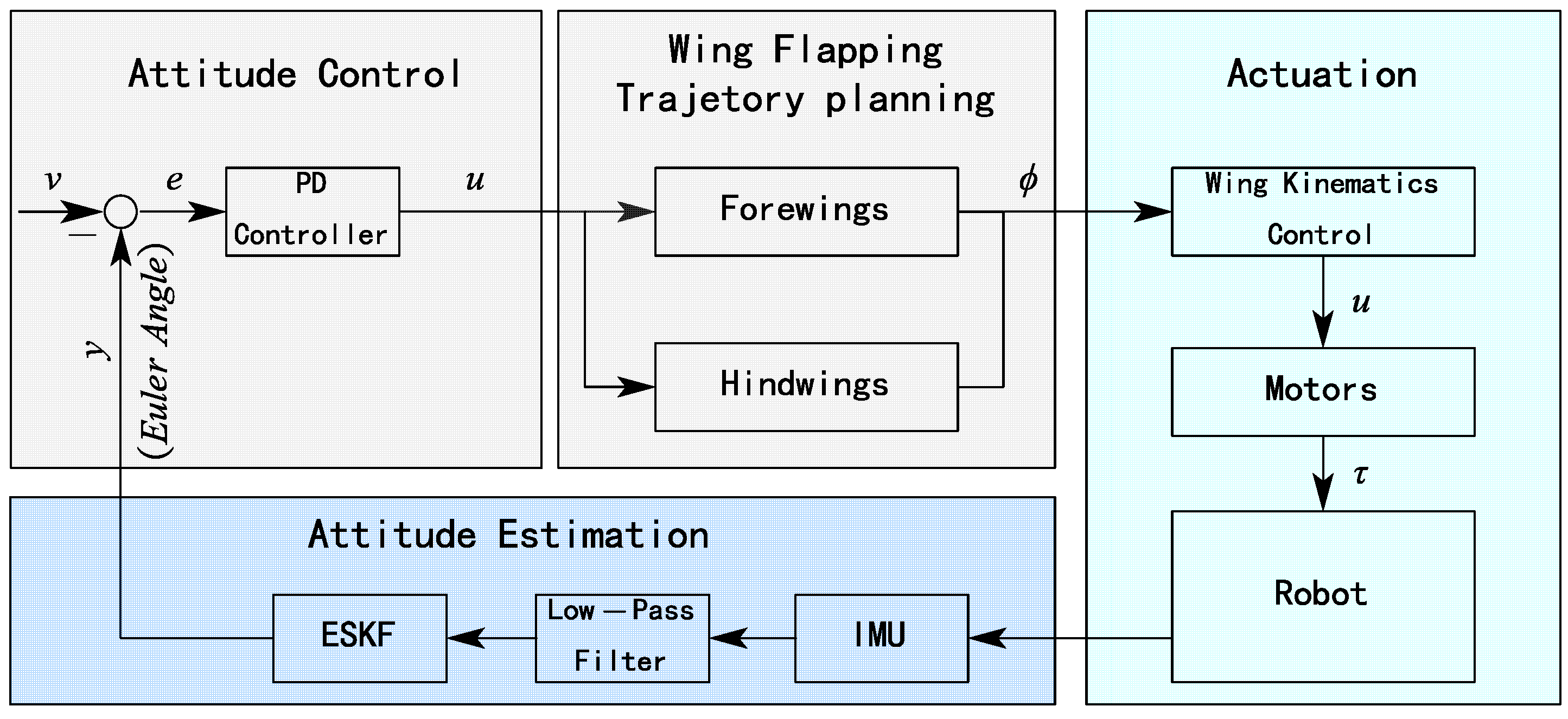
2.3.3. Onboard Flight Attitude Control Algorithm
2.4. System Integration of HiFly-Dragon
3. Flight Control of HiFly-Dragon
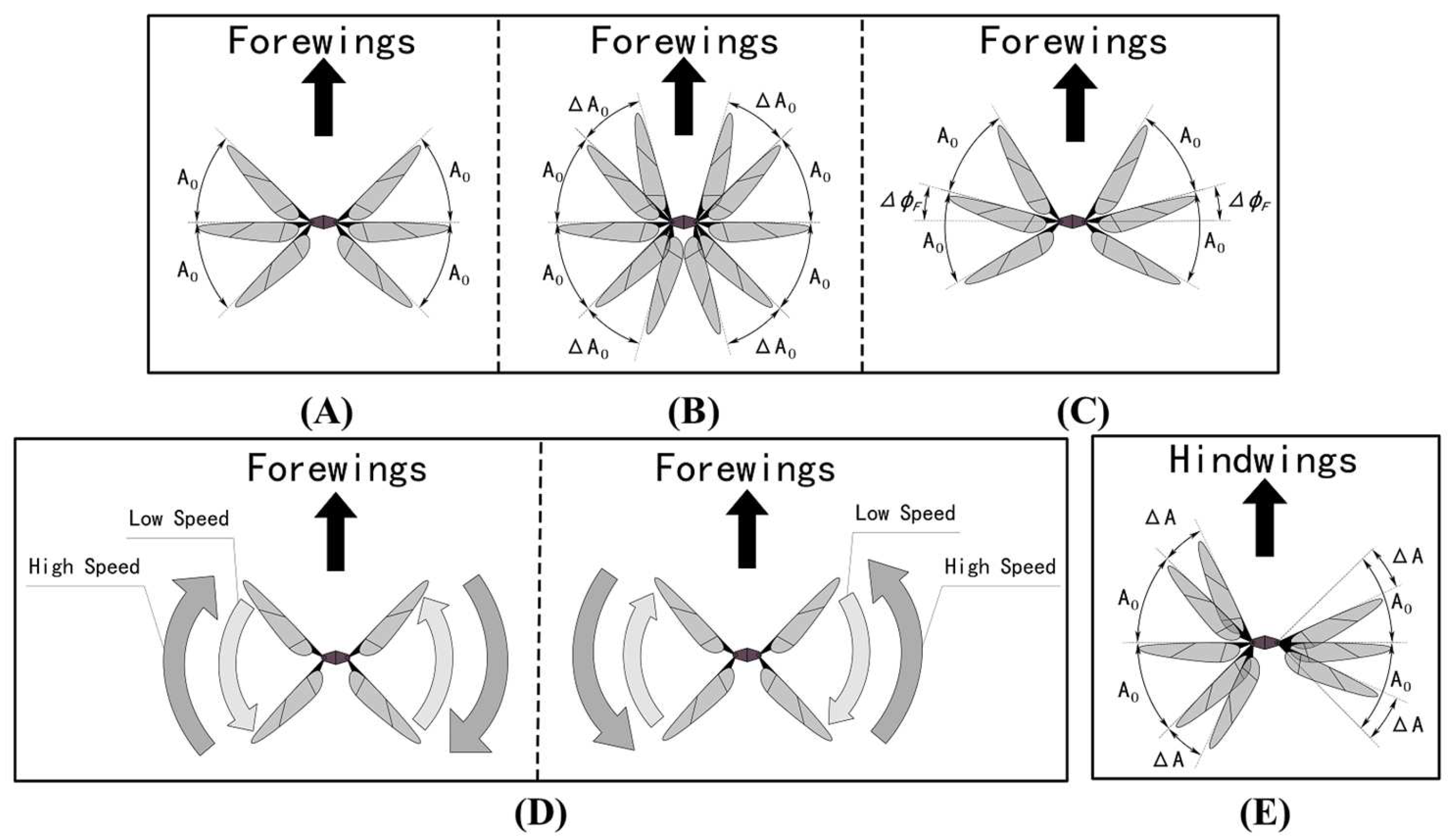
Control Torque Generation
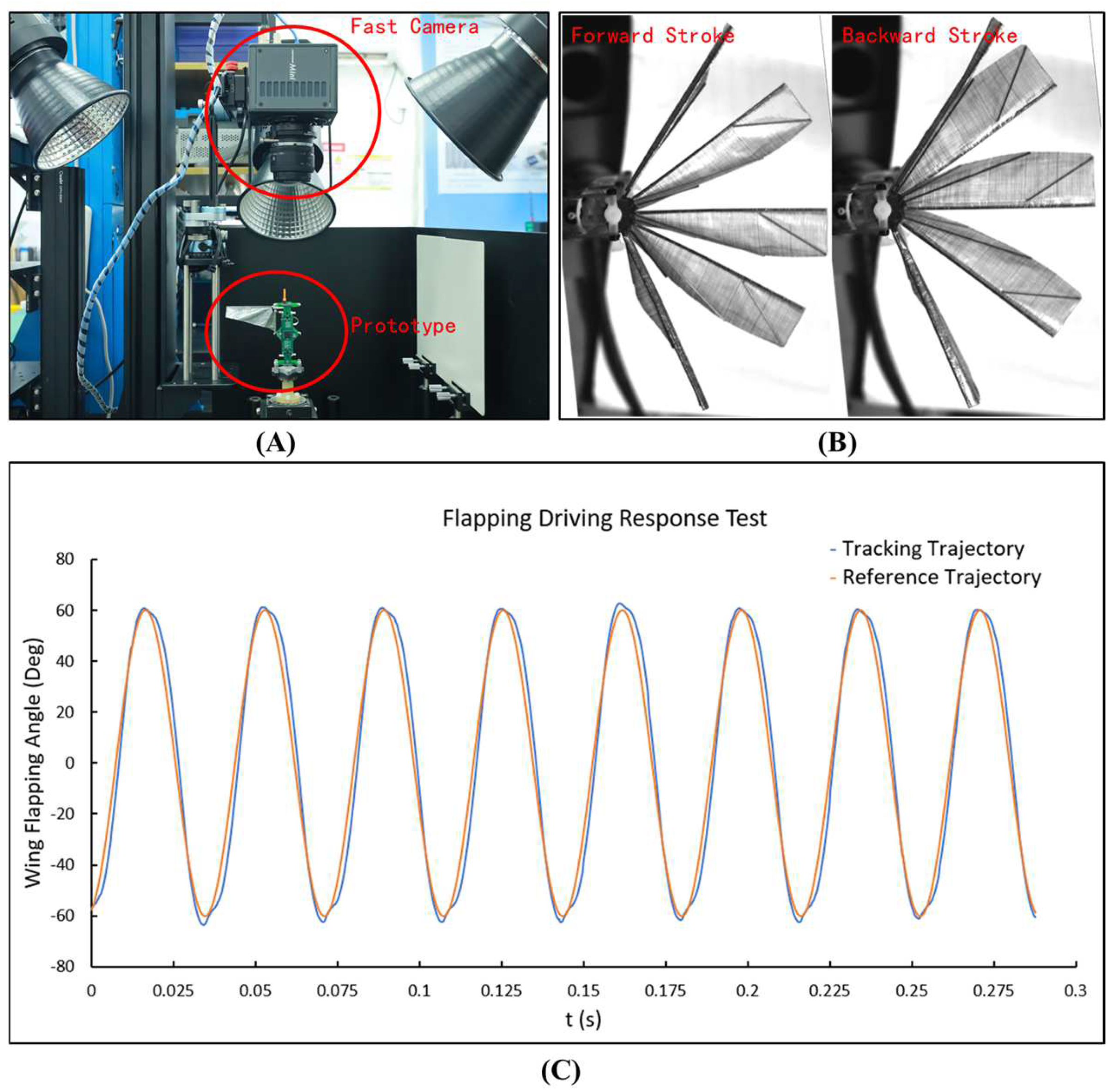
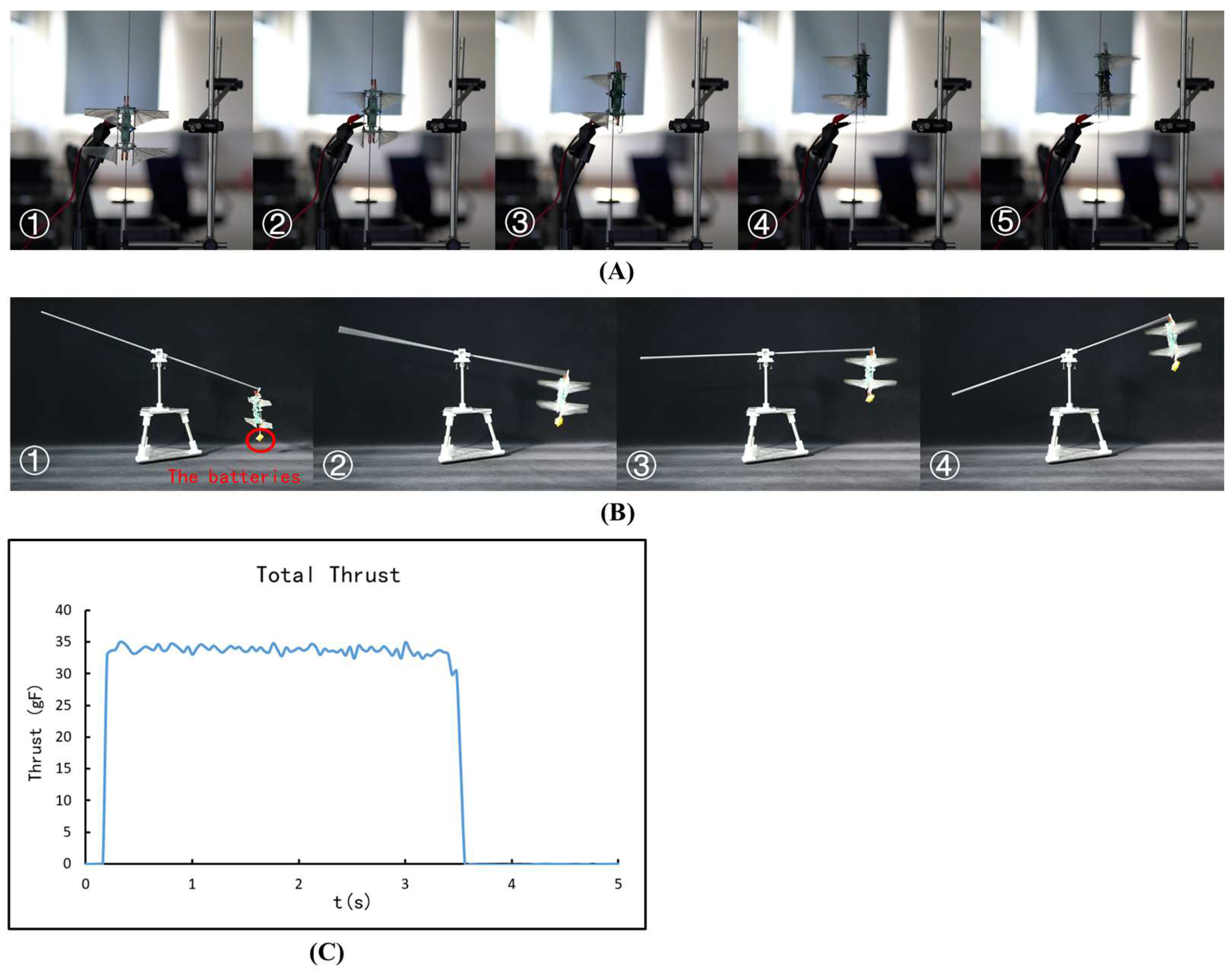
4. Tracked Flight Tests
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hassanalian, M.; Abdelkefi, A. Towards Improved Hybrid Actuation Mechanisms for Flapping Wing Micro Air Vehicles: Analytical and Experimental Investigations. Drones 2019, 3, 73. [Google Scholar] [CrossRef]
- Cote, B.; Weston, S.; Jankauski, M. Modeling and Analysis of a Simple Flexible Wing—Thorax System in Flapping-Wing Insects. Biomimetics 2022, 7, 207. [Google Scholar] [CrossRef] [PubMed]
- Shyy, W.; Kang, C.; Chirarattananon, P.; Ravi, S.; Liu, H. Aerodynamics, Sensing and Control of Insect-Scale Flapping-Wing Flight. Proc. R. Soc. A 2016, 472, 20150712. [Google Scholar] [CrossRef] [PubMed]
- Chirarattananon, P.; Chen, Y.; Helbling, E.F.; Ma, K.Y.; Cheng, R.; Wood, R.J. Dynamics and Flight Control of a Flapping-Wing Robotic Insect in the Presence of Wind Gusts. Interface Focus 2017, 7, 20160080. [Google Scholar] [CrossRef] [PubMed]
- Karásek, M.; Muijres, F.T.; De Wagter, C.; Remes, B.D.W.; De Croon, G.C.H.E. A Tailless Aerial Robotic Flapper Reveals That Flies Use Torque Coupling in Rapid Banked Turns. Science 2018, 361, 1089–1094. [Google Scholar] [CrossRef] [PubMed]
- Keennon, M.; Klingebiel, K.; Won, H. Development of the Nano Hummingbird: A Tailless Flapping Wing Micro Air Vehicle. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012; American Institute of Aeronautics and Astronautics: Nashville, TN, USA, 2012. [Google Scholar]
- Phan, H.V.; Aurecianus, S.; Kang, T.; Park, H.C. KUBeetle-S: An Insect-like, Tailless, Hover-Capable Robot That Can Fly with a Low-Torque Control Mechanism. Int. J. Micro Air Veh. 2019, 11, 175682931986137. [Google Scholar] [CrossRef]
- Gaissert, N.; Mugrauer, R.; Mugrauer, G.; Jebens, A.; Jebens, K.; Knubben, E.M. Inventing a Micro Aerial Vehicle Inspired by the Mechanics of Dragonfly Flight. In Proceedings of the Towards Autonomous Robotic Systems: 14th Annual Conference, TAROS 2013, Oxford, UK, 28–30 August 2013. [Google Scholar]
- Riyaz, M. Dragonflies: The Apex Predators of the Insect World. Acad. Lett. 2021, 2, 1365. [Google Scholar] [CrossRef]
- Bechly, G.; Brauckmann, C.; Zessin, W.; Groning, E. New Results Concerning the Morphology of the Most Ancient Dragonflies (Insecta: Odonatoptera) from the Namurian of Hagen-Vorhalle (Germany). J. Zool. Syst. 2001, 39, 209–226. [Google Scholar] [CrossRef]
- Silsby, J. Dragonflies of the World; CSIRO Publishing: Clayton, VIC, Canada, 2001; ISBN 978-0-643-10087-9. [Google Scholar]
- Chahl, J.; Chitsaz, N.; McIvor, B.; Ogunwa, T.; Kok, J.-M.; McIntyre, T.; Abdullah, E. Biomimetic Drones Inspired by Dragonflies Will Require a Systems Based Approach and Insights from Biology. Drones 2021, 5, 24. [Google Scholar] [CrossRef]
- Vargas, A.; Mittal, R.; Dong, H. A Computational Study of the Aerodynamic Performance of a Dragonfly Wing Section in Gliding Flight. Bioinspir. Biomim. 2008, 3, 026004. [Google Scholar] [CrossRef]
- Wakeling, J.M.; Ellington, C.P. Dragonfly Flight: I. Gliding Flight and Steady-State Aerodynamic Forces. J. Exp. Biol. 1997, 200, 543–556. [Google Scholar] [CrossRef]
- Wakeling, J.M.; Ellington, C.P. Dragonfly Flight: II. Velocities, Accelerations and Kinematics of Flapping Flight. J. Exp. Biol. 1997, 200, 557–582. [Google Scholar] [CrossRef] [PubMed]
- DiLeo, C.; Deng, X. Design and Experiments of a Dragonfly-Inspired Robot. J. Adv. Robot. 2009, 23, 1003–1021. [Google Scholar] [CrossRef]
- Ratti, J.; Vachtsevanos, G. A Biologically-Inspired Micro Aerial Vehicle: Sensing, Modeling and Control Strategies. J. Intell. Robot. Syst. 2010, 60, 153–178. [Google Scholar] [CrossRef]
- Zhang, Y.-L.; Li, J.-C.; Zhou, H.; Liu, Y.-Q.; Han, D.-D.; Sun, H.-B. Electro-Responsive Actuators Based on Graphene. Innovation 2021, 2, 100168. [Google Scholar] [CrossRef] [PubMed]
- Ozaki, T.; Ohta, N.; Jimbo, T.; Hamaguchi, K. A Wireless Radiofrequency-Powered Insect-Scale Flapping-Wing Aerial Vehicle. Nat. Electron. 2021, 4, 845–852. [Google Scholar] [CrossRef]
- Salami, E.; Ward, T.A.; Montazer, E.; Ghazali, N.N.N. A Review of Aerodynamic Studies on Dragonfly Flight. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 6519–6537. [Google Scholar] [CrossRef]
- Sun, X.; Gong, X.; Huang, D. A Review on Studies of the Aerodynamics of Different Types of Maneuvers in Dragonflies. Arch. Appl. Mech. 2017, 87, 521–554. [Google Scholar] [CrossRef]
- Hamamoto, M.; Ohta, Y.; Hara, K.; Hisada, T. Free-Flight Analysis of Dragonfly Hovering by Fluid–Structure Interaction Analysis Based on an Arbitrary Lagrangian–Eulerian Method. Adv. Robot. 2013, 27, 657–666. [Google Scholar] [CrossRef]
- Ratti, J.; Jones, E.; Vachtsevanos, G. Fixed Frequency, Variable Amplitude (FiFVA) Actuation Systems for Micro Aerial Vehicles. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; IEEE: Shanghai, China, 2011; pp. 165–171. [Google Scholar]
- Azhar, M.; Campolo, D.; Lau, G.-K.; Hines, L.; Sitti, M. Flapping Wings via Direct-Driving by DC Motors. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; IEEE: Karlsruhe, Germany, 2013; pp. 1397–1402. [Google Scholar]
- Nabawy, M.R.A.; Marcinkeviciute, R. Scalability of Resonant Motor-Driven Flapping Wing Propulsion Systems. R. Soc. Open Sci. 2021, 8, 210452. [Google Scholar] [CrossRef]
- Zhang, J.; Deng, X. Resonance Principle for the Design of Flapping Wing Micro Air Vehicles. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; IEEE: Daejeon, Republic of Korea, 2016; pp. 2412–2418. [Google Scholar]
- Jeong, S.; Kim, J.; Choi, S.; Park, J.; Kang, T. Platform Design and Preliminary Test Result of an Insect-like Flapping MAV with Direct Motor-Driven Resonant Wings Utilizing Extension Springs. Biomimetics 2022, 8, 6. [Google Scholar] [CrossRef] [PubMed]
- Roshanbin, A.; Abad, F.; Preumont, A. Kinematic and Aerodynamic Enhancement of a Robotic Hummingbird. AIAA J. 2019, 57, 4599–4607. [Google Scholar] [CrossRef]
- Tu, Z.; Fei, F.; Deng, X. Untethered Flight of an At-Scale Dual-Motor Hummingbird Robot with Bio-Inspired Decoupled Wings. IEEE Robot. Autom. Lett. 2020, 5, 4194–4201. [Google Scholar] [CrossRef]
- Lane, P.; Throneberry, G.; Fernandez, I.; Hassanalian, M.; Vasconcellos, R.; Abdelkefi, A. Towards Bio-Inspiration, Development, and Manufacturing of a Flapping-Wing Micro Air Vehicle. Drones 2020, 4, 39. [Google Scholar] [CrossRef]
- Roshanbin, A.; Altartouri, H.; Karásek, M.; Preumont, A. COLIBRI: A Hovering Flapping Twin-Wing Robot. Int. J. Micro Air Veh. 2017, 9, 270–282. [Google Scholar] [CrossRef]
- Nan, Y. An Experimental Study on Effect of Wing Geometry of Hummingbird-like Flapping Wing in the Hover. In Proceedings of the International Micro Air Vehicles Conference and Flight Competition 2015 (IMAV 2015), Aachen, Germany, 15–18 September 2015. [Google Scholar]
- Roll, J.A.; Cheng, B.; Deng, X. An Electromagnetic Actuator for High-Frequency Flapping-Wing Microair Vehicles. IEEE Trans. Robot. 2015, 31, 400–414. [Google Scholar] [CrossRef]
- Doman, D.B.; Oppenheimer, M.W.; Sigthorsson, D.O. Wingbeat Shape Modulation for Flapping-Wing Micro-Air-Vehicle Control During Hover. J. Guid. Control. Dyn. 2010, 33, 724–739. [Google Scholar] [CrossRef]
- Zhu, J.; Zhou, C. Aerodynamic Performance of a Two-Dimensional Flapping Wing in Asymmetric Stroke. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2014, 228, 641–651. [Google Scholar] [CrossRef]
- Oppenheimer, M.; Doman, D.; Sigthorsson, D. Dynamics and Control of a Biomimetic Vehicle Using Biased Wingbeat Forcing Functions: Part I—Aerodynamic Model. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition; American Institute of Aeronautics and Astronautics, Orlando, FL, USA, 4–7 January 2010. [Google Scholar]
- Oppenheimer, M.W.; Doman, D.B.; Sigthorsson, D.O. Dynamics and Control of a Biomimetic Vehicle Using Biased Wingbeat Forcing Functions. J. Guid. Control. Dyn. 2011, 34, 204–217. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, B.; Deng, X. Instantaneous Wing Kinematics Tracking and Force Control of a High-Frequency Flapping Wing Insect MAV. J. Micro-Bio Robot. 2016, 11, 67–84. [Google Scholar] [CrossRef]
- Rafiq, M.A.; Sarwer, M.G.; Datta, M.; Ghosh, B.C. Fast Speed Response Field-Orientation Control of Induction Motor Drive with Adaptive Neural Integrator. In Proceedings of the 2005 IEEE International Conference on Industrial Technology, Hong Kong, China, 14–17 December 2005; IEEE: Hong Kong, China, 2005; pp. 610–614. [Google Scholar]
- Zhang, J.; Tu, Z.; Fei, F.; Deng, X. Geometric Flight Control of a Hovering Robotic Hummingbird. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; IEEE: Singapore, 2017; pp. 5415–5421. [Google Scholar]





| Component | Weight (g) | PCT (%) |
|---|---|---|
| Power-Driven Board | 3.502 | 10.62 |
| Flight Control Board | 2.693 | 8.17 |
| Batteries | 7.551 | 22.90 |
| Nylon Screws | 0.156 | 0.47 |
| BLDC Motors | 10.132 | 30.73 |
| Ball Bearings | 0.504 | 1.53 |
| Wings | 0.14 | 0.42 |
| Torsional Spring | 1.312 | 3.98 |
| Others | 6.98 | 21.17 |
| Total | 32.97 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, H.; Gong, P.; Tian, Y.; Wu, Q.; Pan, M.; Yin, H.; Liu, Y.; Chen, C. HiFly-Dragon: A Dragonfly Inspired Flapping Flying Robot with Modified, Resonant, Direct-Driven Flapping Mechanisms. Drones 2024, 8, 126. https://doi.org/10.3390/drones8040126
Ma H, Gong P, Tian Y, Wu Q, Pan M, Yin H, Liu Y, Chen C. HiFly-Dragon: A Dragonfly Inspired Flapping Flying Robot with Modified, Resonant, Direct-Driven Flapping Mechanisms. Drones. 2024; 8(4):126. https://doi.org/10.3390/drones8040126
Chicago/Turabian StyleMa, He, Peiyi Gong, Yuqiang Tian, Qingnan Wu, Min Pan, Hao Yin, Youjiang Liu, and Chilai Chen. 2024. "HiFly-Dragon: A Dragonfly Inspired Flapping Flying Robot with Modified, Resonant, Direct-Driven Flapping Mechanisms" Drones 8, no. 4: 126. https://doi.org/10.3390/drones8040126
APA StyleMa, H., Gong, P., Tian, Y., Wu, Q., Pan, M., Yin, H., Liu, Y., & Chen, C. (2024). HiFly-Dragon: A Dragonfly Inspired Flapping Flying Robot with Modified, Resonant, Direct-Driven Flapping Mechanisms. Drones, 8(4), 126. https://doi.org/10.3390/drones8040126





