1. Introduction
Recently, the focus on heterogeneous multi-agent collaborative systems has intensified, attributed to their diverse capabilities, broad applicability, and strong adaptability [
1]. As a specific form of heterogeneous systems, the air–ground collaborative system not only has the wide field of view and high mobility of multi-unmanned aerial vehicles (UAVs), but also has the meticulous search capability and long-lasting endurance of multi-unmanned vehicles (UGVs). It is used in patrol [
2], rescue [
3], reconnaissance attack [
4], express delivery [
5], and other military or civilian fields.
In actual application scenarios, UAVs and UGVs are often required to go to certain designated areas to complete related tasks, which involve task assignment and path planning. UAVs and UGVs are intelligent bodies with different kinematic parameters, and there are also large differences in functions. To solve such optimization problems so that they more closely represent reality, it is necessary to fully consider commonality and uniqueness when constructing the model.
The Traveling Salesman Problem (TSP), as one of the most typical models of task assignment, was initially used in scenarios where only UAVs or only UGVs are operational. Cities in the TSP are viewed as target points that need to perform tasks, and the connections between cities can be viewed as paths. Murry and Chu [
5] proposed the Flying Partner Traveling Salesman Model (FSTSP) and the Parallel Drone Dispatching Traveling Salesman Model (PDSTSP), which are theoretical models for solving the last-mile problem in the air–ground collaborative express delivery scenario. Mara [
6] proposed the Traveling Salesman Problem with Drone (TSP-D), similar to the FSTSP, and added the limitation of operating mileage for UAVs. In [
7,
8,
9], variants of the above model and various solutions are proposed.
The Vehicle Routing Problem (VRP), which is similar to the TSP, is also applied and developed in the air–ground coordination problem. Wang [
10] proposed the vehicle routing problem with drones (VRPD), which is similar to the FSTSP and used to describe the scenario where UAVs are delivered with trucks. The literature [
11] introduced multiple UAVs, extended the model to the VRPD-MD, and realized the collaborative path planning of UAVs and UGVs. In addition, refs. [
12,
13] adopted effective inequality (VIEQ) and variable neighborhood descent processes (ILS-VND) to speed up the solution of such problems, improving the availability of the model in practical application.
However, TSP and VRP and their variants are limited by the basic model, so it is difficult to expand into a model with many constraints. That is the main reason that most TSP and VRP models can only focus on the express delivery problem. Unlike the above two models, Mixed Integer Linear Programming (MILP) does not have an initial basic model, and as long as linear or integer constraints are satisfied, they can become part of the MILP model. Therefore, the strong expansibility of the MILP model makes it widely used for solving multi-target optimization problems.
In addition, the above works can be transformed into the MILP model; refs. [
14,
15,
16] added UAV collision avoidance constraints and mission event constraints to the MILP model, making this type of mathematical model more realistic. Afterwards, in [
5], a variety of heterogeneous UAVs suitable for anti-radar operations were added to the MILP model, and the task completion time was limited by time window constraints. In [
17], UGVs were added to provide energy supplies for UAV constraints, effectively prolonging the operating time of UAVs.
From the above analysis, we know that the MILP is extremely suitable for describing air–ground coordination problems. However, the applicability of the model is relatively narrow, there is a relatively complete model only in the scenario of unmanned vehicles carrying drones for delivery, and a model with wide applicability is desperately needed. Therefore, the following contributions are made in this paper:
(1) A novel air–ground collaborative multi-target detection task model based on MILP, considering kinematic constraints, dynamic collision avoidance constraints, task allocation constraints, and obstacle avoidance constraints, is constructed to describe the air–ground collaborative environmental coverage problem more realistically and reasonably.
(2) A more comprehensive objective function, which comprehensively considers the time spent on task completion, the energy consumption during operation, and the smoothness of the path trajectory, is proposed to obtain the optimal solution of air–ground collaborative multi-target detection task assignment and path planning.
(3) A Branch-and-Bound method combined with the Improved Genetic Algorithm (IGA-B&B) is proposed to solve the objective function, and the optimal task assignment and optimal path of air–ground collaborative multi-target detection can be obtained. In this method, we adjust the chromosome attributes and genetic operations in the Genetic Algorithm to make the Improved Genetic Algorithm more suitable for the model and speed up the operation.
(4) A simulation environment with multi-agent, multi-obstacle, and multi-task points and several other elements is constructed to validate the effectiveness and progressiveness of the proposed method in this work. The simulation results show that the proposed IGA-B&B method can reduce the running time by 30% compared with the traditional B&B method. In addition, the practicality and feasibility are also verified through experiments in outdoor environments.
The rest of this paper is organized as follows. Related work is introduced in
Section 2. The proposed method is described in detail in
Section 3 and
Section 4, including the task assignment and path optimization model for air–ground collaborative multi-target detection based on MILP, the comprehensive establishment of the objective function, and the optimization function solution method based on the IGA-B&B method. In
Section 5, the simulation and experimental environment are introduced, and the guidelines and experimental results are analyzed and compared, which verify the rationality and feasibility of the proposed method. Finally, this work is concluded in
Section 6.
4. Optimal Solution Method of Mathematical Model
After establishing the mathematical model, it is necessary to design a corresponding solution method to solve the model to obtain a solution with appropriate accuracy. The model designed in this article can be solved by traditional optimization methods or heuristic algorithms, but the original algorithm still needs to be appropriately modified to ensure that the calculation can converge and speed up the calculation as much as possible.
4.1. Branch-and-Bound
The branch and bound (B&B) method was proposed by Land [
27] in the 1960s to solve integer programming problems and then extended by [
28] to solve MILP problems. The core idea of this method lies in branching, delimiting, and pruning.
Specifically, suppose a Mixed Integer Linear Programming problem
to find the minimum solution, and suppose its corresponding linear programming problem
. Starting from solving problem
, if the optimal solution does not meet the integer condition of
, then the optimal objective function value
must be the lower bound of the optimal objective function value
of
, denoted as
. Furthermore, the value of the objective function for any feasible solution of
will be the upper bound of
, denoted as
. The Branch-and-Bound method divides the feasible region into several sub-regions, and this process is called branching. After that, each sub-region will solve the new upper bound
and lower bound
as the boundary of the region, which is called delimitation. If the new lower bound
is greater than the known optimal solution
, it means that the region has been searched and no further branching is required, and its subset may not be considered, which is called pruning. In short, the Branch-and-Bound method needs to gradually reduce
and increase
in the iterative process, and finally find
. The algorithm framework of B&B is shown in Algorithm 1.
| Algorithm 1 Branch-and-Branch |
| Input: A mixed integer programming problem , the upper bounds of the current solution , the lower bounds of the current solution , is the corresponding linear programming problem of , is a branch of |
| Output: The optimal solution |
- 1:
while solution of is not empty do - 2:
if is feasible then - 3:
Let be optimal solution of - 4:
if then - 5:
Cut the branch - 6:
end if
|
- 7:
if satisfies integral solution of then - 8:
if then - 9:
- 10:
end if - 11:
else - 12:
- 13:
end if - 14:
end if - 15:
end while - 16:
return
|
4.2. Improved Genetic Algorithm and A* Algorithm
The Genetic Algorithm has a faster solution speed in task allocation and path planning, but in this paper, task planning and path planning have a strong coupling relationship, which makes it difficult for traditional Genetic Algorithms to effectively solve this type of problem by designing simple chromosomes and genetic operators. Therefore, in this paper, the Genetic Algorithm is used to assign tasks, the A* algorithm is used to obtain the path planning results, and the objective function value obtained as a whole is used as the fitness value of the Genetic Algorithm. The specific process is described in Algorithm 2.
| Algorithm 2 Genetic Algorithm Process |
- 1:
Initialize the population - 2:
Coding chromosome - 3:
while the number of iterations is not reached do - 4:
Calculate fitness - 5:
Select operation - 6:
Crossover operation - 7:
if chromosomes need to be adjusted then - 8:
Adjust operation - 9:
end if - 10:
Mutate operation - 11:
Generate a new generation - 12:
end while
|
The population size , selection probability, crossover probability, mutation probability, and maximum evolutionary algebra need to be determined for initialization of the population.
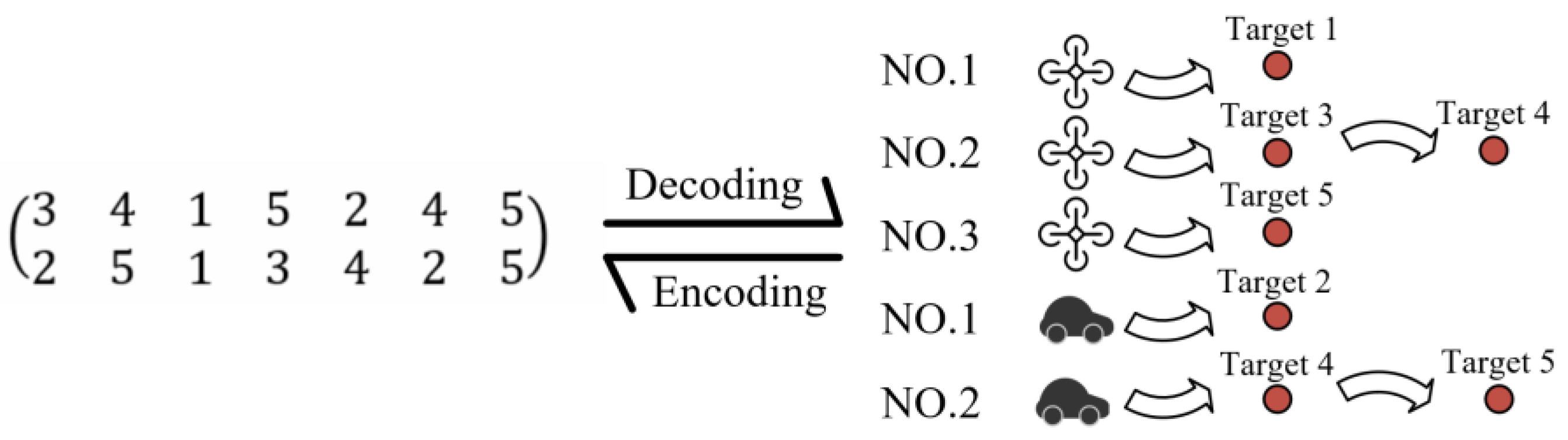
To encode the chromosome, we take the chromosome as a two-layer code. Among them, the first layer of the chromosome code represents the execution order of all target points, and the second layer represents the ID number of the agent required for detection of the corresponding target point. If the total number of target points is
, and the number of target points that need to be detected by both UAV and UGV is
, then the length of the chromosome is
. For instance, if there are three UAVs and two UGVs—a total of 5 target points, including 2 target points that need to be detected by both UAVs and UGVs and 3 target points that need to be detected by UAVs or UGVs—then the encoded chromosome can be described as in
Figure 6.
From
Figure 6, we know that UAV No. 1 performs the detection task of target point No. 1, UAV No. 2 performs the detection task of target point No. 3 and No. 4 in turn, UAV No. 3 performs the detection task of target point No. 5, UGV No. 1 performs the detection task of target point No. 2, and UGV No. 2 performs the detection task of target point No. 4 and No. 5 in turn. Chromosomes encoded by this method can meet the constraints of assignment of task points.
In this step, according to the target points that need to be detected by the corresponding agent after decoding the individual
, the planned path of each agent can be obtained through the A* algorithm. After that, the optimization solution calculated by the above objective function is the original fitness
. In order to facilitate the selection of population individuals later, the final fitness
is set as
The magnitude of fitness implies the length of the path and, consequently, the resource consumption. A higher fitness value indicates a lower resource consumption.
The selection phase adopts elitism, that is, individuals with higher fitness are more likely to be retained in the genetic process. Therefore, the selection probability for an individual is
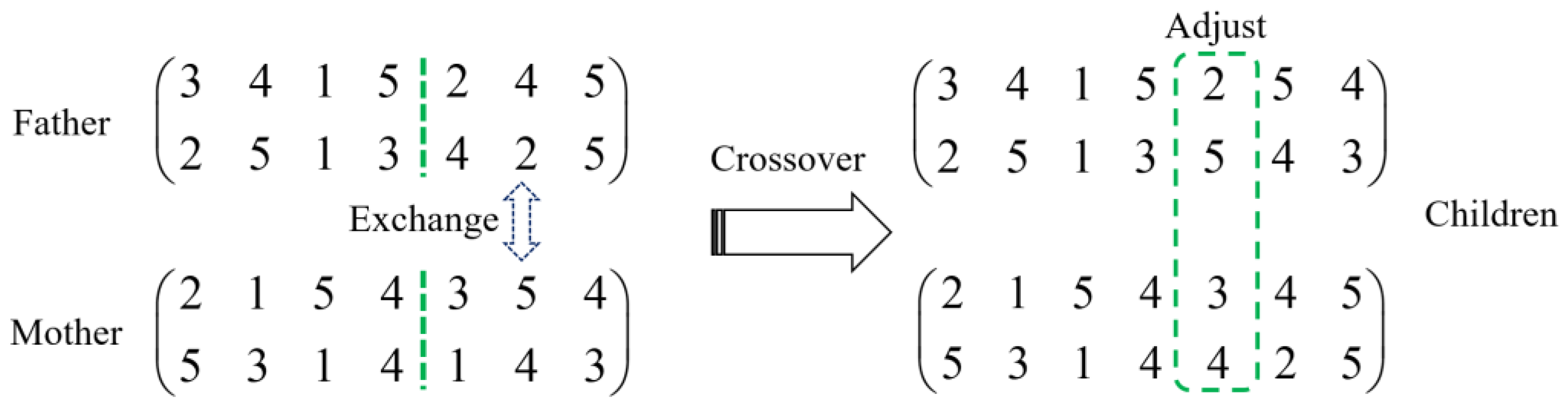
According to the crossover probability, we can select two chromosomes from the population, randomly determine the crossover position on the chromosome, and perform crossover operation on the gene codes. For example, after selecting two individuals to cross at the fifth position, the specific effect can be obtained as shown in
Figure 7. The chromosome is divided into two parts by a green line, and the parent and mother generations cross over on the right half of the green line.
Unless the genes of the crossover position of the two individuals of the parent are identical, the offspring generated by this method will have the phenomenon of missing target points and repeated target points at the same time, and the number of missing target points will be the same as that of repeated target points. Therefore, a one-step adjustment operation is required to replace redundant task points with missing target points. After that, it is necessary to check whether the agent distribution of the offspring meets the requirements. The adjusted individual is shown in
Figure 8, and the two offspring can meet the coding requirements and can further participate in the subsequent evolution.
According to the mutation probability, the individual that needs to be mutated is randomly selected in the population, two mutation positions are also randomly selected from the chromosome of the individual, and the two mutation positions are exchanged. The specific implementation of the proposed method is shown in
Figure 9. The genes in the green and blue boxes meet the model requirements through reasonable mutation.
The selected parent chromosomes and the offspring chromosomes generated after crossover and mutation operations are merged to form a new generation of populations.
The fitness value of the new population is calculated, and it is determined whether the contemporary optimal result satisfies the iteration termination condition. If not, we skip to step 4 to select a new generation and start a new generation of evolutionary iteration. If the maximum number of iterations has been reached, the Genetic Algorithm ends.
4.3. Branch-and-Bound with Improved Genetic Algorithm (IGA-B&B)
The hot start method for the B&B algorithm is commonly used to solve small-scale MILP problems. It requires pre-provision of a set of feasible solutions to limit the bounds. In this paper, we pre-provide a set of feasible solutions, which can be obtained by the proposed Improved Genetic Algorithm to limit the upper bound of the problem, thereby improving the efficiency of pruning and the speed of the overall operation.
The specific implementation involves initially disregarding the kinematic parameters of UAVs and UGVs, reducing the problem under study to a simplified single-agent path planning problem. An Improved Genetic Algorithm is then employed to find an initial solution. Since it is certain that this solution is not better than the optimal solution, it can serve as an upper bound for the B&B algorithm.
Furthermore, by initializing the B&B algorithm with the upper bound obtained, it effectively partitions the explored space, significantly enhancing the search speed and algorithm efficiency. The algorithm framework of this specific algorithm is shown in Algorithm 3.
| Algorithm 3 Branch-and-Branch combined with Improved Genetic Algorithm |
- 1:
Employ Improved Genetic Algorithm to find initial solution - 2:
Set as the upper bound for - 3:
Initialize Branch-and-Bound algorithm with the upper bound - 4:
while solution of is not empty do - 5:
Select a branch from - 6:
if is feasible then - 7:
Let be optimal solution of - 8:
if then - 9:
cut the branch - 10:
else - 11:
Update - 12:
end if - 13:
end if
|
- 14:
if satisfies integral solution of then - 15:
- 16:
Break - 17:
end if - 18:
end while - 19:
return
|
5. Simulation Comparison and Experimental Verification
In order to increase the contrast and minimize the impact of environmental changes on the model, a grid map with the same environmental scene is used in our simulation test and the kinematic constraints are limited to the maximum speed and maximum acceleration. Each agent can only move in 8 directions. There are three UAVs and two UGVs, a total of eight mission points, two no-fly zones for UAVs, and two no-go zones for UGVs in the simulation maps.
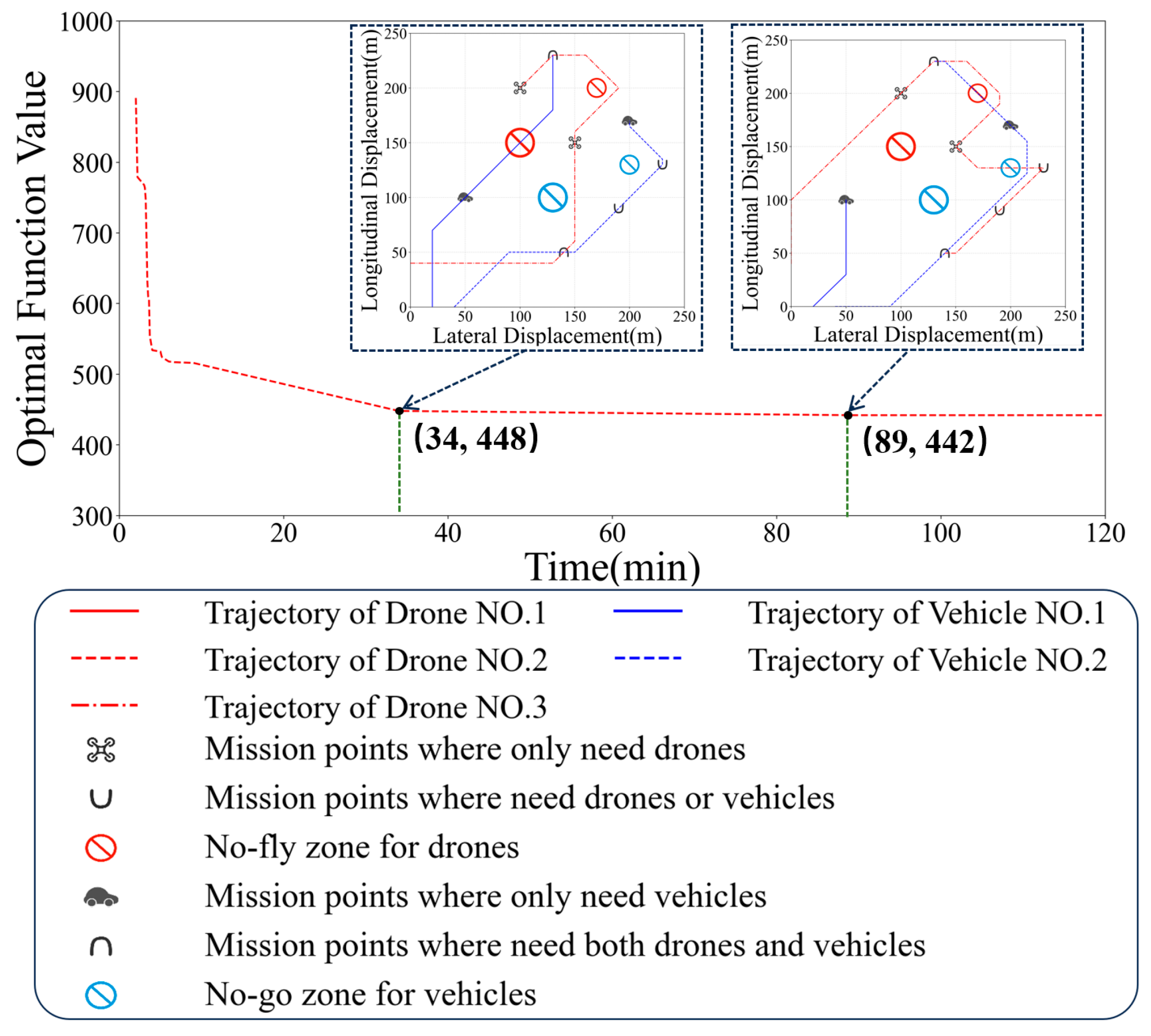
Although the Branch-and-Bound method has the ability to solve the global optimization problem, the excessive running time is unacceptable. It can be seen from the curve in
Figure 10 that after 34 min, as the running time increases, the value of the objective function barely changes and the final generated trajectory hardly improves. Therefore, in the subsequent simulation experiments, the running time is set as 34 min.
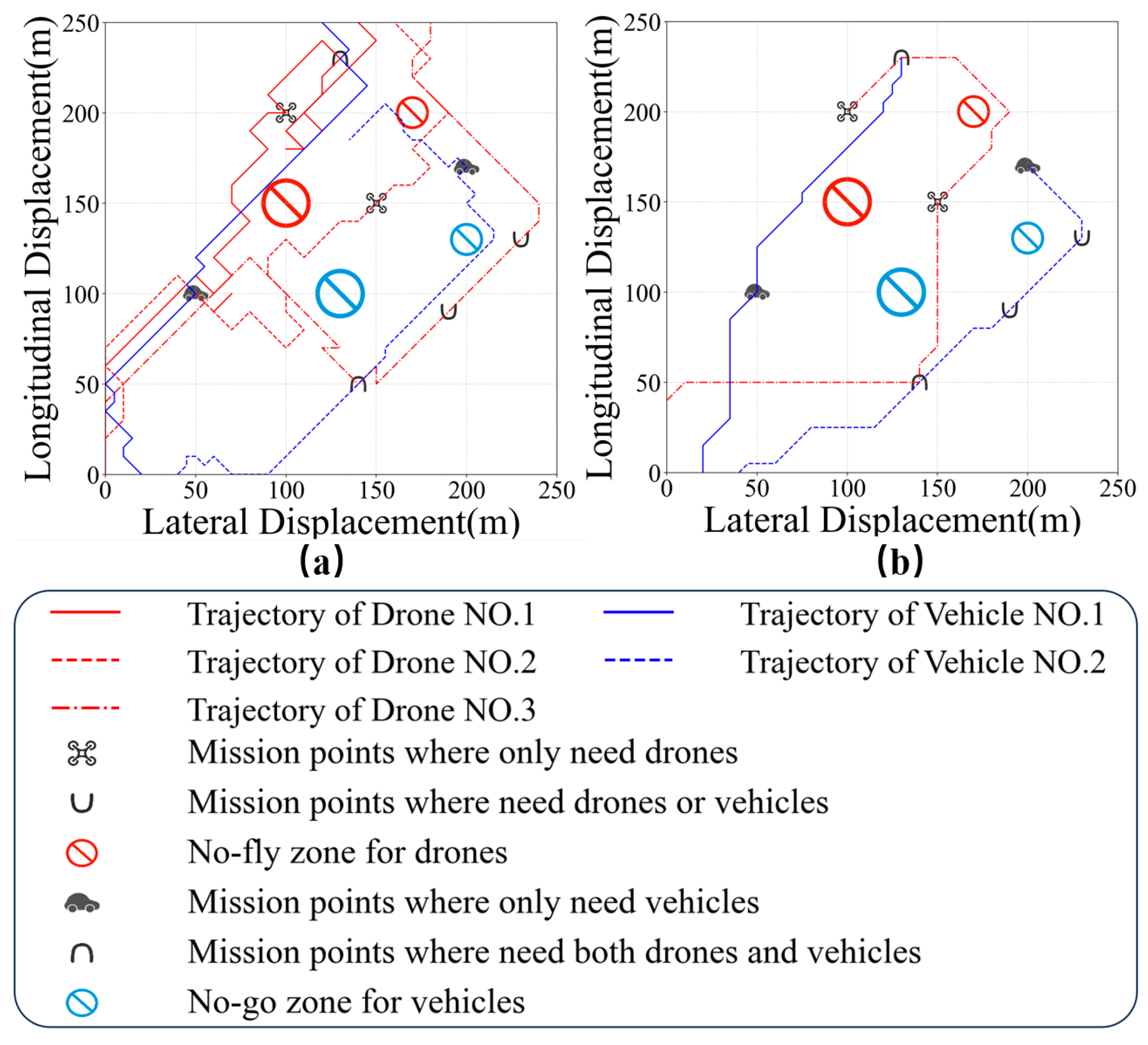
In the model with only the shortest time as the objective function, due to the lack of constraints on the running mileage, there are two bad results: one is that the agent with a task will not stop after completing the task; the other is the behavior of the agent without a task is not guided and constrained by the objective function, resulting in trajectory chaos, as shown in
Figure 11a. These problems can be effectively solved after adding energy consumption constraints, as shown in
Figure 11b.
After adding the trajectory smoothness constraint to the objective function, compared with the model with only time and energy consumption constraints, the problem of continuous direction changes of each agent can be greatly improved, thereby reducing the difficulty of path following controlling and unnecessary energy consumption, as shown in
Figure 12.
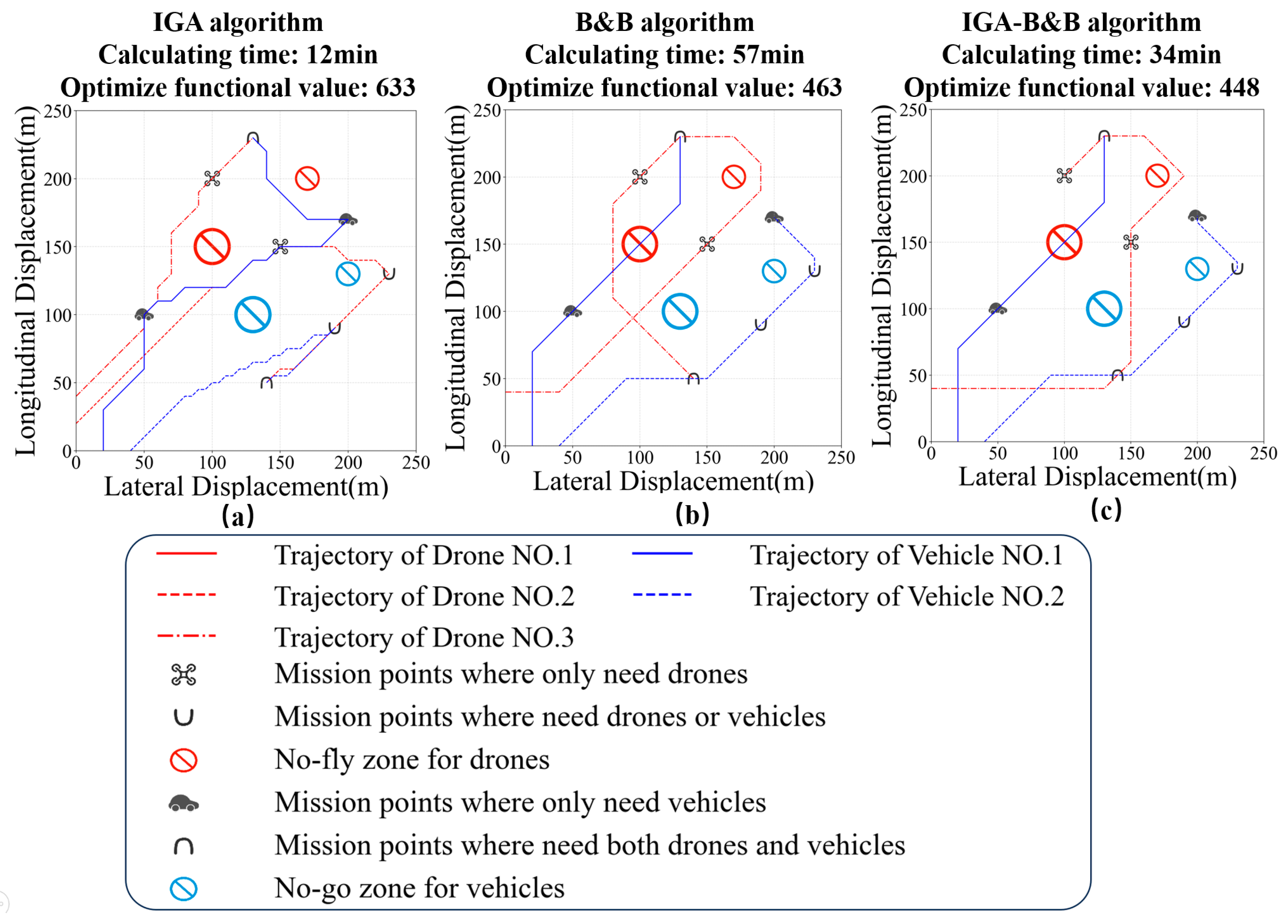
To verify the superiority of the proposed IGA-B&B algorithm, we compared simulation results by using several different objective-function-solving methods, as shown in
Figure 13. From
Figure 13a, we know that the Genetic Algorithm has a faster calculation time, but due to the lack of dynamic constraints of the A* algorithm, the final path is relatively discontinuous and the final optimal value of the objective function is lower. The final value of the objective function is 633 by using the Genetic Algorithm method and this value barely reduces with the increase in calculation time. Although the traditional B&B method can effectively obtain the optimal solution, the traversal search speed is slow and high computation memory is needed, resulting in slow running speed and even memory overflow, as shown in
Figure 13b. The proposed IGA-B&B method can fully take advantage of the Genetic Algorithm and B&B methods, which means that the calculation time is effectively reduced by 30% and a relatively good allocation result can also be obtained, as shown in
Figure 13c.
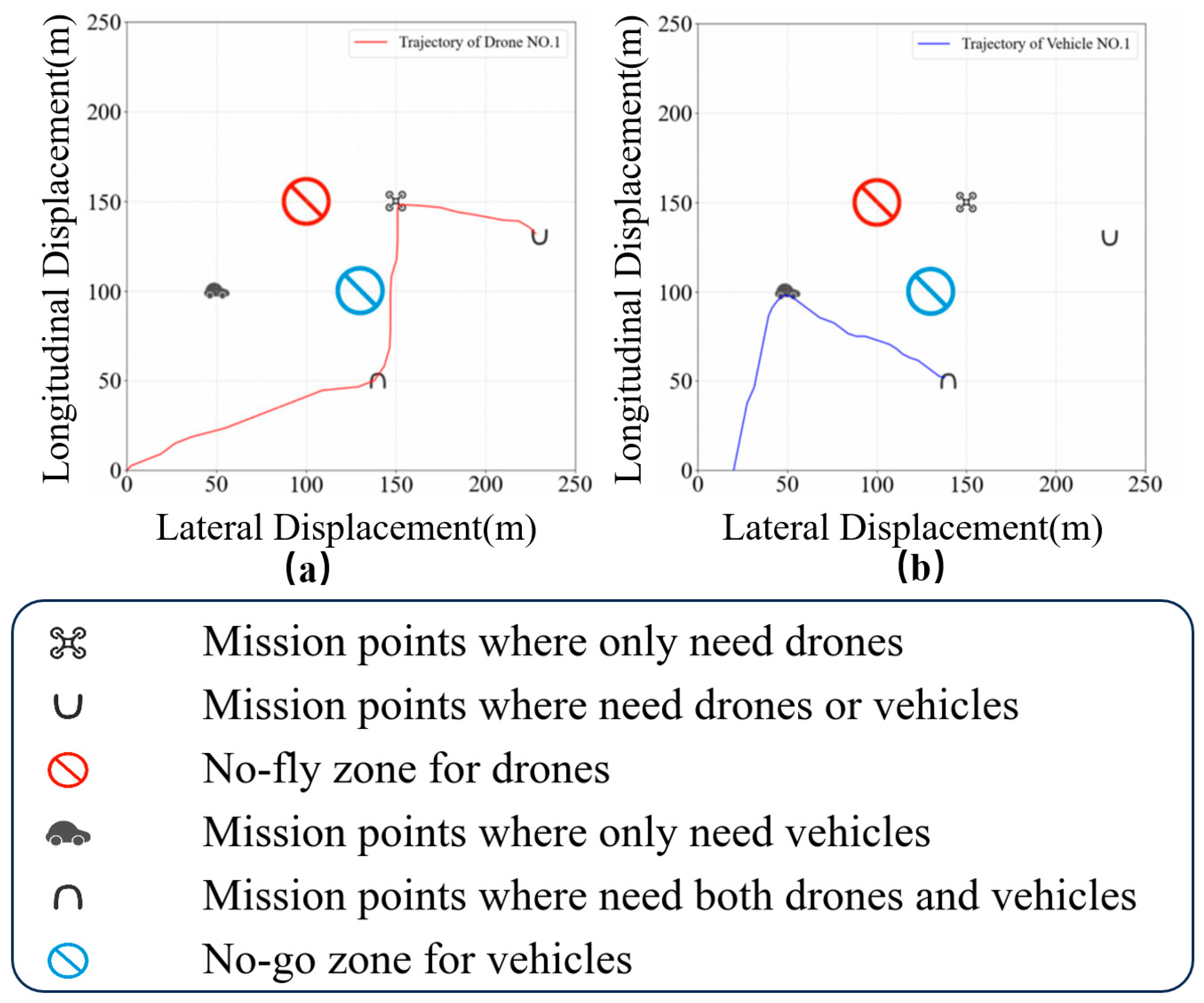
In order to verify the feasibility of the proposed model, experiments are carried out in the outdoor environment. The relevant testing equipment used in this work is shown in
Figure 14.
There are one UAV and one UGV, a total of four mission points, one simulated no-fly zone for UAVs, and one simulated no-go zone for UGVs in our experimental scene, which is located in a square area with a side length of 250 m in the Southeast University campus, as shown in
Figure 15.
Using our proposed method, the target point detection tasks of UAVs and UGVs are assigned, and the optimal paths are also planned. Under the action of their respective path tracking controller, the UAVs and UGVs move along the planned paths. They are able to closely follow the planned trajectories and successfully complete tracking of all path points within 3 min. Their respective trajectories are shown in
Figure 16a,b. It can be seen that UAVs and UGVs effectively reach the target points and successfully avoid their respective prohibited areas, further demonstrating the effectiveness and practicability of the proposed method.
6. Conclusions
In this paper, an air–ground collaborative multi-target detection task model based on Mixed Integer Linear Programming (MILP) is proposed. In this model, kinematic constraints of the UAVs and UGVs, dynamic collision avoidance constraints, task allocation constraints, and obstacle avoidance constraints are considered. In addition, an objective function with optimization directions of time consumption, energy consumption, and trajectory smoothness is established. To solve this objective function, a Branch-and-Bound method combined with the Improved Genetic Algorithm (IGA-B&B) is proposed and the optimal task assignment and optimal path of air–ground collaborative multi-target detection can be obtained. A simulation environment with multi-agents, multi-obstacles, and multi-task points is established. The simulation and experimental results show the effectiveness and feasibility of the proposed method.
In order to facilitate calculation and simplify the problem, many assumptions were set during our model construction process, which to some extent lost the authenticity of the model. For example, we ignore the energy loss caused by the ascent and descent of the drone. In addition, when facing extremely complex environmental conditions, such as scenes with a large number of UAVs and UGVs, and a significant number of target task points and no-go or no-fly zones, the proposed method may not be able to find a feasible solution within the specified time. Therefore, in order to further broaden the application range of the proposed model, we will focus on designing a novel objective-function-solving algorithm to achieve fast and approximate solutions in our following work.