MoNA Bench: A Benchmark for Monocular Depth Estimation in Navigation of Autonomous Unmanned Aircraft System
Abstract
1. Introduction
- We design a real-time monocular MAV-based unmanned aircraft system. Our system accomplishes efficient path planning to enable the effective implementation of autonomous obstacle avoidance and safe target tracking.
- We introduce MoNA Bench, a benchmark for monocular depth estimation in autonomous navigation for unmanned aircraft systems. We develop a series of deployable performance evaluation experiments for monocular depth estimation and identify significant attributes that MDE algorithms should possess for efficient trajectory and path planning.
- To benefit the community, we release the complete source code of the proposed benchmark at: https://github.com/npu-ius-lab/MoNA-Bench (accessed on 31 December 2023).
2. Related Work
2.1. Monocular Depth Estimation
2.2. Efficient Flight Trajectory Planning
2.3. Target Detection and Pose Estimation
2.4. Monocular Vision-Based Autonomous Obstacle Avoidance
3. Approach
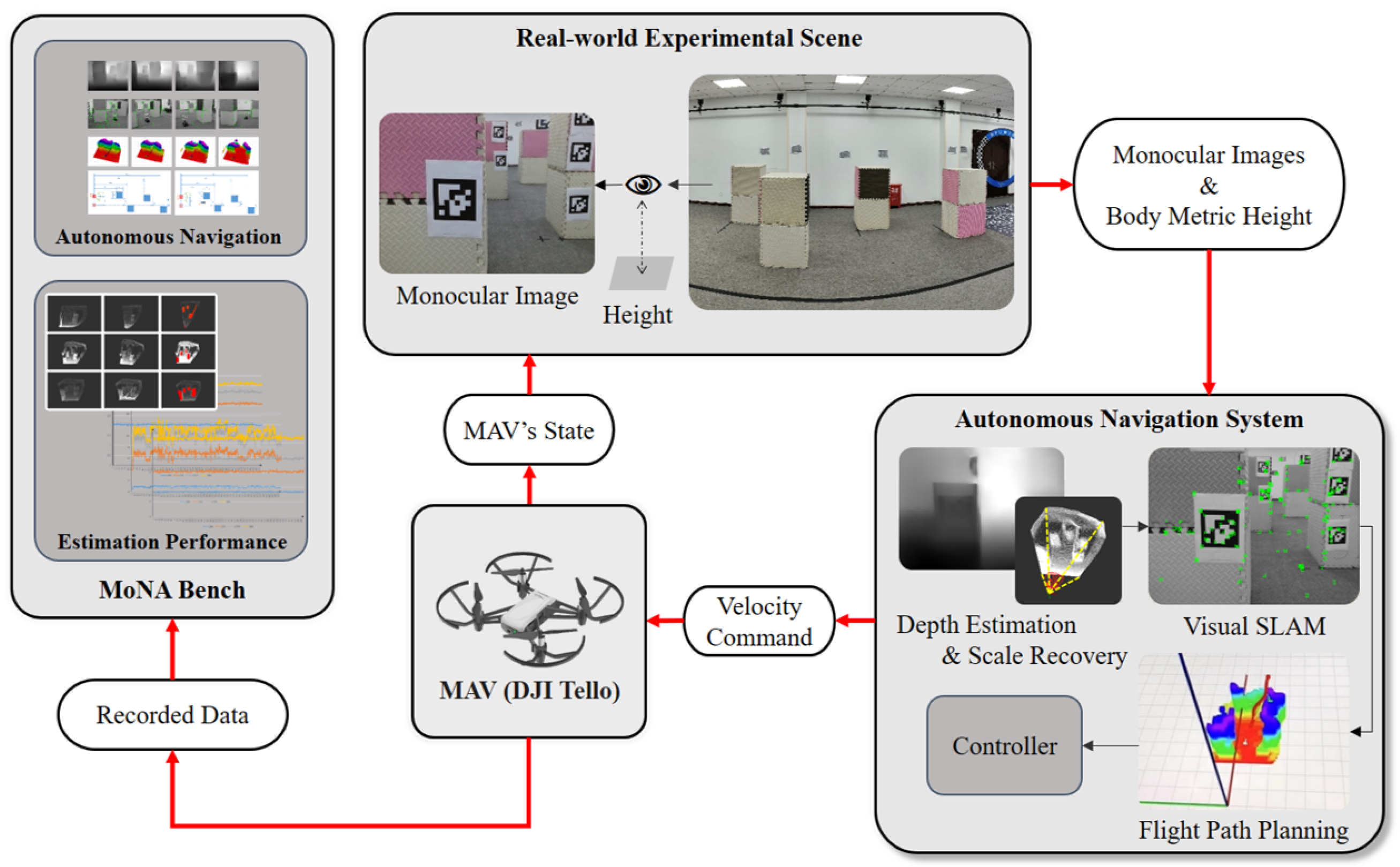
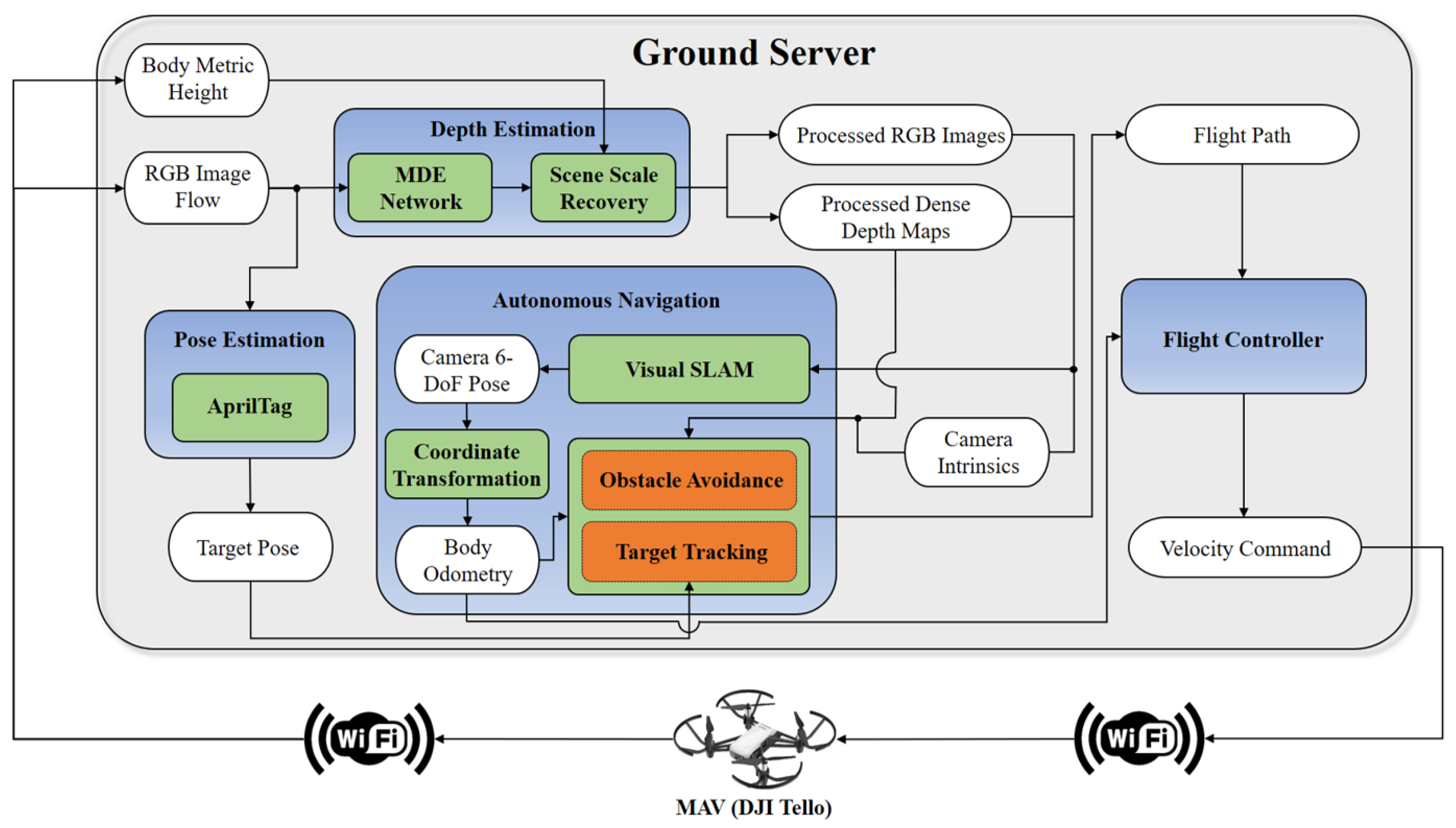
3.1. Overview
- System Connection. The MAV establishes a wireless connection with the ground server through WiFi, transmitting a continuous stream of RGB images. Upon receiving the activation command, the MAV initiates takeoff and maintains a stable hover at an altitude of approximately 0.9 m.
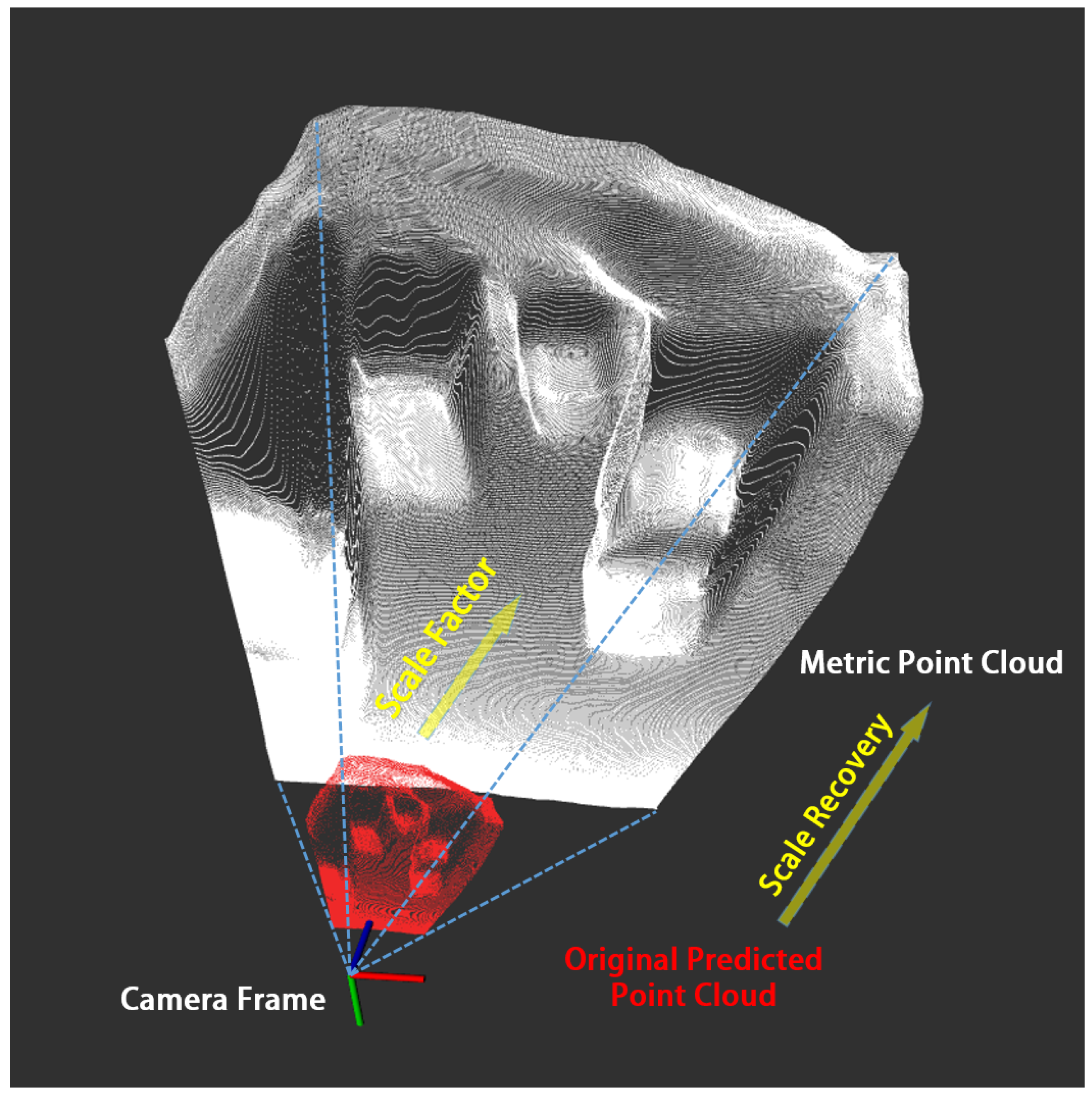
- Depth Estimation. The depth estimation network operates on the ground server, integrating extensively validated networks like MonoDepth, MiDaS, and SC-DepthV2. To recover metric information from the physical world for subsequent navigation, a novel scene scale recovery submodule is developed. This submodule incorporates MAV height information and executes recovery through four steps: depth map to point cloud conversion, point cloud ground segmentation, point cloud coordinate transformation, and scale factor calculation. Additionally, to facilitate subsequent computations, both RGB images and dense depth maps are resized to a resolution of .
- Autonomous Navigation. To enable autonomous MAV navigation, a visual SLAM (Simultaneous Localization and Mapping) submodule localizes the camera’s 6 degrees of freedom (DoF) pose through processed RGB images, dense depth maps, and camera intrinsics. Subsequently, the coordinate transformation submodule converts the estimated camera pose to MAV body odometry. Following this, the flight trajectory is generated with two distinct options:
- Obstacle Avoidance. In this mode, the system employs RGB images, predicted dense depth maps, camera intrinsics, and MAV body odometry to generate a 3D occupancy grid map. This map serves as the foundation for constructing a local trajectory and establishing a front tracking point when a flying target is specified.
- Target Tracking. In this mode, alongside RGB images, predicted dense depth maps, camera intrinsics, and MAV body odometry, the system requires a subscription to the target position obtained from the 6-DOF pose estimation module to generate the specialized trajectory for tracking the designated target.
- Pose Estimation. Accurate target tracking hinges on determining the real-world positions of designated targets. In our system, AprilTag has been selected as the tracking target due to its reliable and distinctive visual features. The target’s pose estimation is accomplished by analyzing RGB image sequences, allowing the system to precisely locate and track the designated target throughout its movements.
- Velocity Control. Upon generating the flight trajectory, the system provides adaptability by offering a choice between two controllers to calculate the MAV’s velocity command: a PID controller and a path-following controller. This flexibility ensures efficient control and responsiveness tailored to the specific requirements of the mission or task at hand.
3.2. Monocular Depth Estimation
3.2.1. MDE Algorithms
3.2.2. Scale Recovery
| Algorithm 1: RANSAC-based Point Cloud Ground Plane Segmentation |
 |
3.3. Autonomous Navigation
3.3.1. Visual SLAM
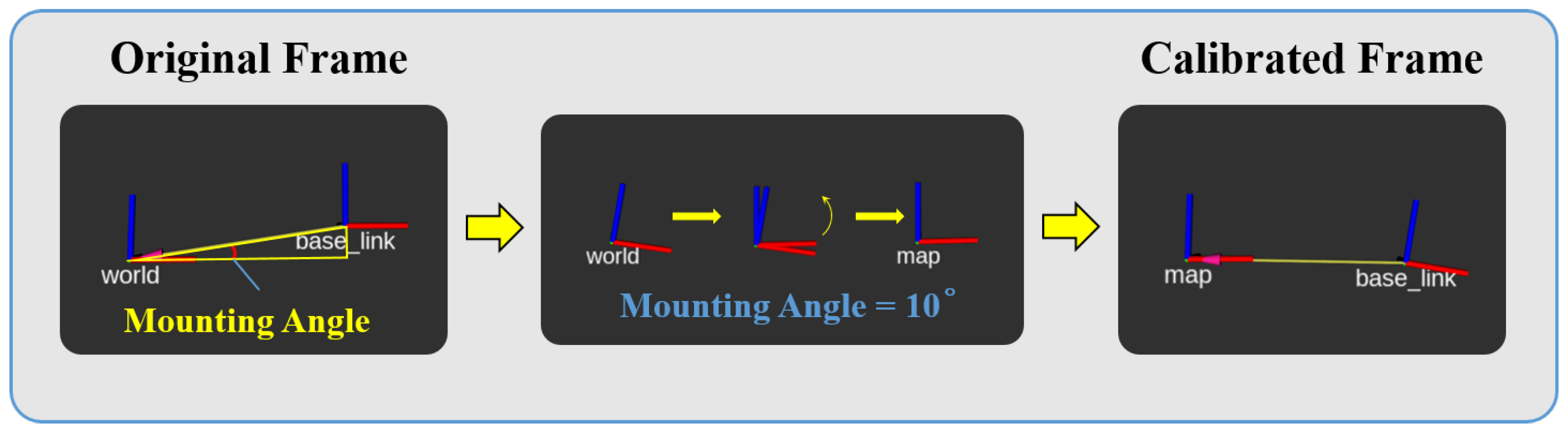
3.3.2. Pose Estimation
3.3.3. Path Planning
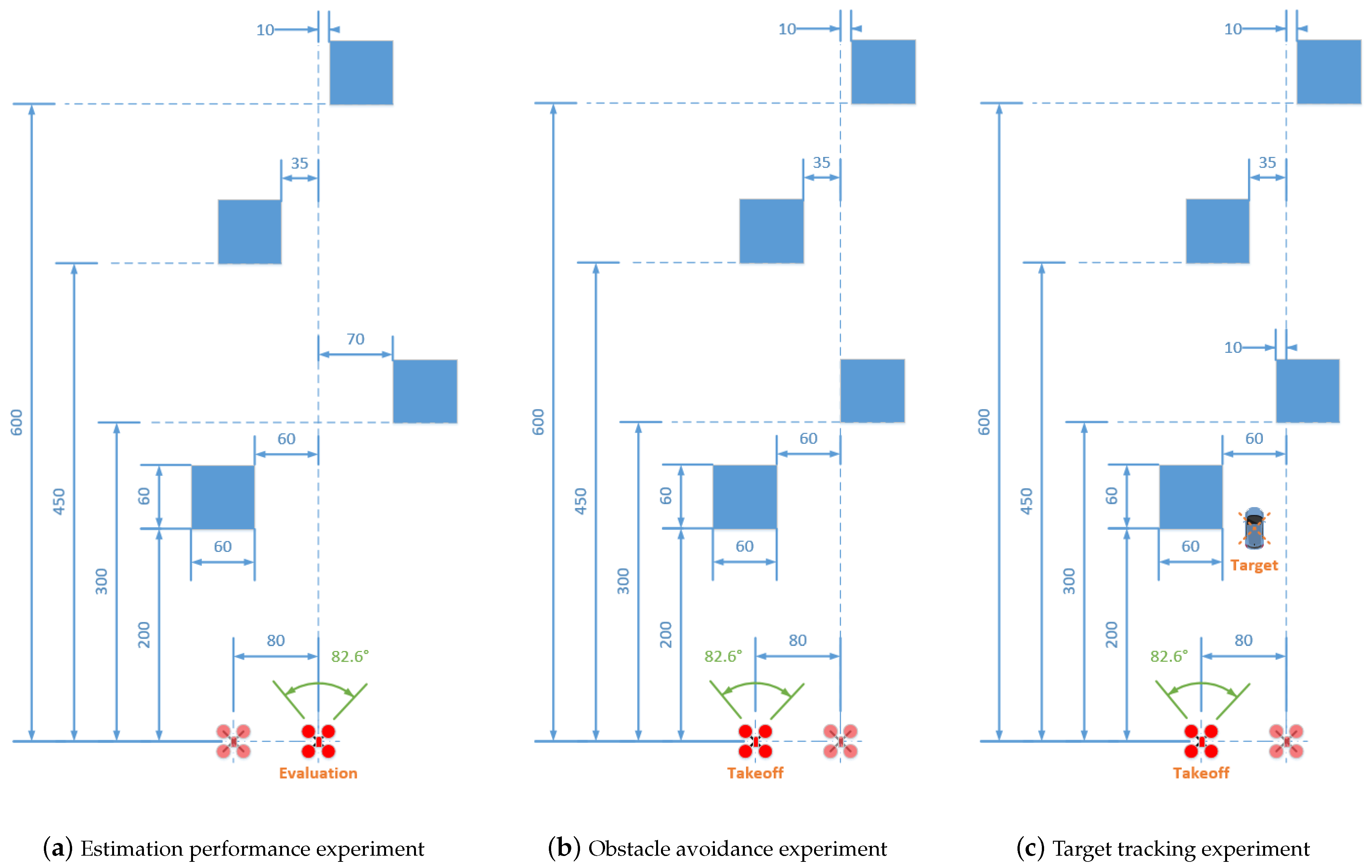
4. Experiments
4.1. Experimental Configurations
4.2. Depth Estimation Experiments
4.3. Autonomous Navigation Experiments
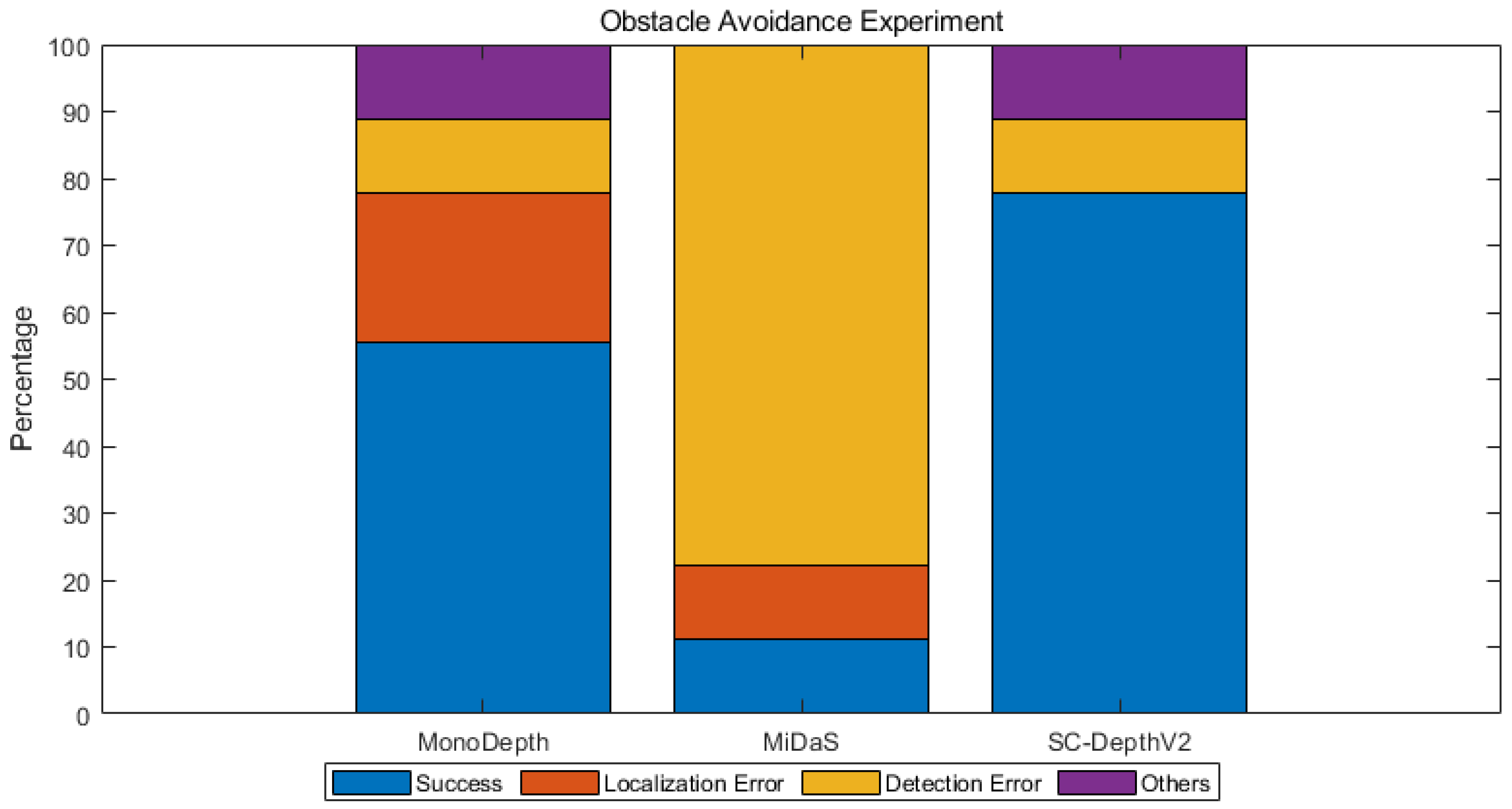
4.3.1. Obstacle Avoidance
- Localization Error. Due to the high computing resource demand, certain MDE algorithms encountered challenges in processing received image data continuously and sequentially in real-time when the ground server reached its performance limits. This discrepancy led to the loss of feature points and, subsequently, localization failure.
- Detection Error. Discrepancies between the predicted depth map of spatial obstacles and the actual distribution of obstacles in space contributed to collisions between the MAV and obstacles. Detection errors were also observed when the depth map failed to clearly distinguish the boundaries of obstacles, such as the top part of an obstacle and the gap between obstacles.
- Others. This category includes unexpected wobbling or instability of the MAV during the experiments.
4.3.2. Safe Target Tracking
4.3.3. Navigation Performance
4.4. MoNA Bench
5. Discussions and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TPP | Trajectory and Path Planning |
| UAS | Unmanned Aircraft System |
| MAV | Micro-aerial Vehicles |
| MDE | Monocular Depth Estimation |
References
- Pan, Y.; Wang, J.; Chen, F.; Lin, Z.; Zhang, S.; Yang, T. How Does Monocular Depth Estimation Work for MAV Navigation in the Real World? In Proceedings of the 2022 International Conference on Autonomous Unmanned Systems (ICAUS 2022), Xi’an, China, 23–25 September 2022; pp. 3763–3771. [Google Scholar]
- Eigen, D.; Puhrsch, C.; Fergus, R. Depth map prediction from a single image using a multi-scale deep network. In Proceedings of the 27th International Conference on Neural Information Processing Systems (NIPS’14), Montreal, QC, Canada, 8–13 December 2014; pp. 2366–2374. [Google Scholar]
- Alhashim, I.; Wonka, P. High quality monocular depth estimation via transfer learning. arXiv 2018, arXiv:1812.11941. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Silberman, N.; Hoiem, D.; Kohli, P.; Fergus, R. Indoor segmentation and support inference from rgbd images. In Proceedings of the 12th European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 746–760. [Google Scholar]
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Vision meets robotics: The kitti dataset. Int. J. Robot. Res. 2013, 32, 1231–1237. [Google Scholar] [CrossRef]
- Ranftl, R.; Lasinger, K.; Hafner, D.; Schindler, K.; Koltun, V. Towards robust monocular depth estimation: Mixing datasets for zero-shot cross-dataset transfer. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 1623–1637. [Google Scholar] [CrossRef]
- Guizilini, V.; Ambrus, R.; Pillai, S.; Raventos, A.; Gaidon, A. 3d packing for self-supervised monocular depth estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2485–2494. [Google Scholar]
- Bian, J.W.; Zhan, H.; Wang, N.; Li, Z.; Zhang, L.; Shen, C.; Cheng, M.M.; Reid, I. Unsupervised scale-consistent depth learning from video. Int. J. Comput. Vis. 2021, 129, 2548–2564. [Google Scholar] [CrossRef]
- Bian, J.W.; Zhan, H.; Wang, N.; Chin, T.J.; Shen, C.; Reid, I. Auto-Rectify Network for Unsupervised Indoor Depth Estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 9802–9813. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Gao, F.; Wang, L.; Liu, C.; Shen, S. Robust and efficient quadrotor trajectory generation for fast autonomous flight. IEEE Robot. Autom. Lett. 2019, 4, 3529–3536. [Google Scholar] [CrossRef]
- Han, Z.; Zhang, R.; Pan, N.; Xu, C.; Gao, F. Fast-tracker: A robust aerial system for tracking agile target in cluttered environments. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 328–334. [Google Scholar]
- Kato, H.; Billinghurst, M. Marker tracking and hmd calibration for a video-based augmented reality conferencing system. In Proceedings of the 2nd IEEE and ACM International Workshop on Augmented Reality (IWAR’99), San Francisco, CA, USA, 20–21 October 1999; pp. 85–94. [Google Scholar]
- Olson, E. AprilTag: A robust and flexible visual fiducial system. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3400–3407. [Google Scholar]
- Krogius, M.; Haggenmiller, A.; Olson, E. Flexible layouts for fiducial tags. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 1898–1903. [Google Scholar]
- Zhang, Z.; Xiong, M.; Xiong, H. Monocular depth estimation for UAV obstacle avoidance. In Proceedings of the 2019 4th International Conference on Cloud Computing and Internet of Things (CCIOT), Changchun, China, 6–7 December 2019; pp. 43–47. [Google Scholar]
- Liu, Q.; Zhang, Z.; Xiong, M.; Xiong, H. Obstacle Avoidance of Monocular Quadrotors with Depth Estimation. In Proceedings of the International Conference on Autonomous Unmanned Systems, Changsha, China, 24–26 September 2021; pp. 3194–3203. [Google Scholar]
- Yonchorhor, J. (The) Development of the Scale-Aware Monocular Depth Estimation Aided Monocular Visual SLAM System for Real-Time Robot Navigation. Master’s Thesis, Korea Advanced Institute of Science & Technology (KAIST), Daejeon, Republic of Korea, 2021. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Mur-Artal, R.; Tardós, J.D. Orb-slam2: An open-source slam system for monocular, stereo, and rgb-d cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]

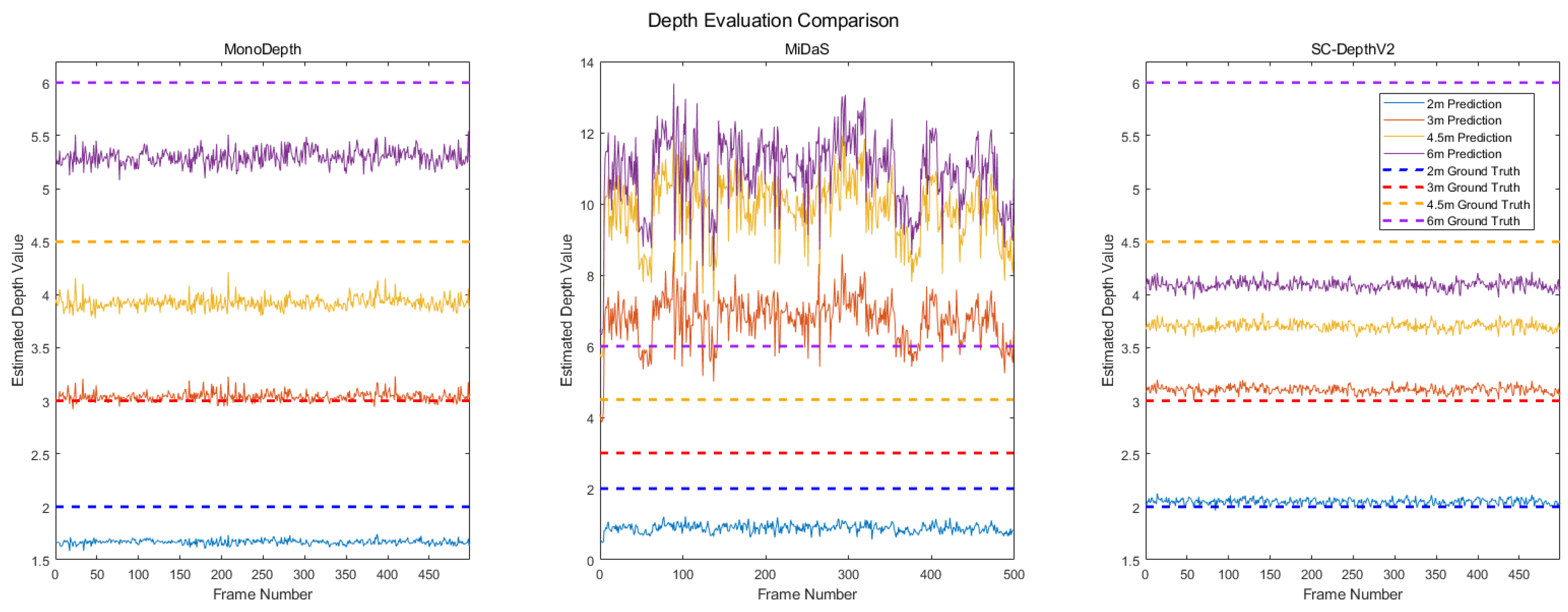


| Algorithms | GPU Occupancy (%) | CV Estimation * (%) | 2 m ARE (%) | 3 m ARE (%) | 4.5 m ARE (%) | 6 m ARE (%) |
|---|---|---|---|---|---|---|
| MonoDepth | 81–89 | 1.5 | 16.6 | 1.5 | 12.8 | 11.7 |
| MiDaS | 31–35 | 9.7 | 55.7 | 124.6 | 117.8 | 81.9 |
| SC-DepthV2 | 32–34 | 1.0 | 2.5 | 3.5 | 17.7 | 31.8 |
| Algorithms | APF * (Hz) | DUR ** (%) | CV Navigation *** (%) | Success Rate (%) | Safe Tracking |
|---|---|---|---|---|---|
| MonoDepth | 8.2 | 26.67 | 6.3 | 55.6 | False |
| MiDaS | 30.0 | 100 | 39.4 | 11.1 | False |
| SC-DepthV2 | 30.0 | 100 | 5.0 | 77.8 | True |
| MoNA Bench | |||||||
|---|---|---|---|---|---|---|---|
| MDE Efficiency | MDE Accuracy | Scale Consistency | Navigation Capability | ||||
| GPU Occupancy | APF | DUR | Distance AREs * | CV Estimation | CV Navigation | Success Rate | Safe Tracking |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, Y.; Liu, B.; Liu, Z.; Shen, H.; Xu, J.; Fu, W.; Yang, T. MoNA Bench: A Benchmark for Monocular Depth Estimation in Navigation of Autonomous Unmanned Aircraft System. Drones 2024, 8, 66. https://doi.org/10.3390/drones8020066
Pan Y, Liu B, Liu Z, Shen H, Xu J, Fu W, Yang T. MoNA Bench: A Benchmark for Monocular Depth Estimation in Navigation of Autonomous Unmanned Aircraft System. Drones. 2024; 8(2):66. https://doi.org/10.3390/drones8020066
Chicago/Turabian StylePan, Yongzhou, Binhong Liu, Zhen Liu, Hao Shen, Jianyu Xu, Wenxing Fu, and Tao Yang. 2024. "MoNA Bench: A Benchmark for Monocular Depth Estimation in Navigation of Autonomous Unmanned Aircraft System" Drones 8, no. 2: 66. https://doi.org/10.3390/drones8020066
APA StylePan, Y., Liu, B., Liu, Z., Shen, H., Xu, J., Fu, W., & Yang, T. (2024). MoNA Bench: A Benchmark for Monocular Depth Estimation in Navigation of Autonomous Unmanned Aircraft System. Drones, 8(2), 66. https://doi.org/10.3390/drones8020066







