Research on Cooperative Arrival and Energy Consumption Optimization Strategies of UAV Formations
Abstract
1. Introduction
1.1. Literature Review
1.2. Motivations and Contributions
2. Method and Material
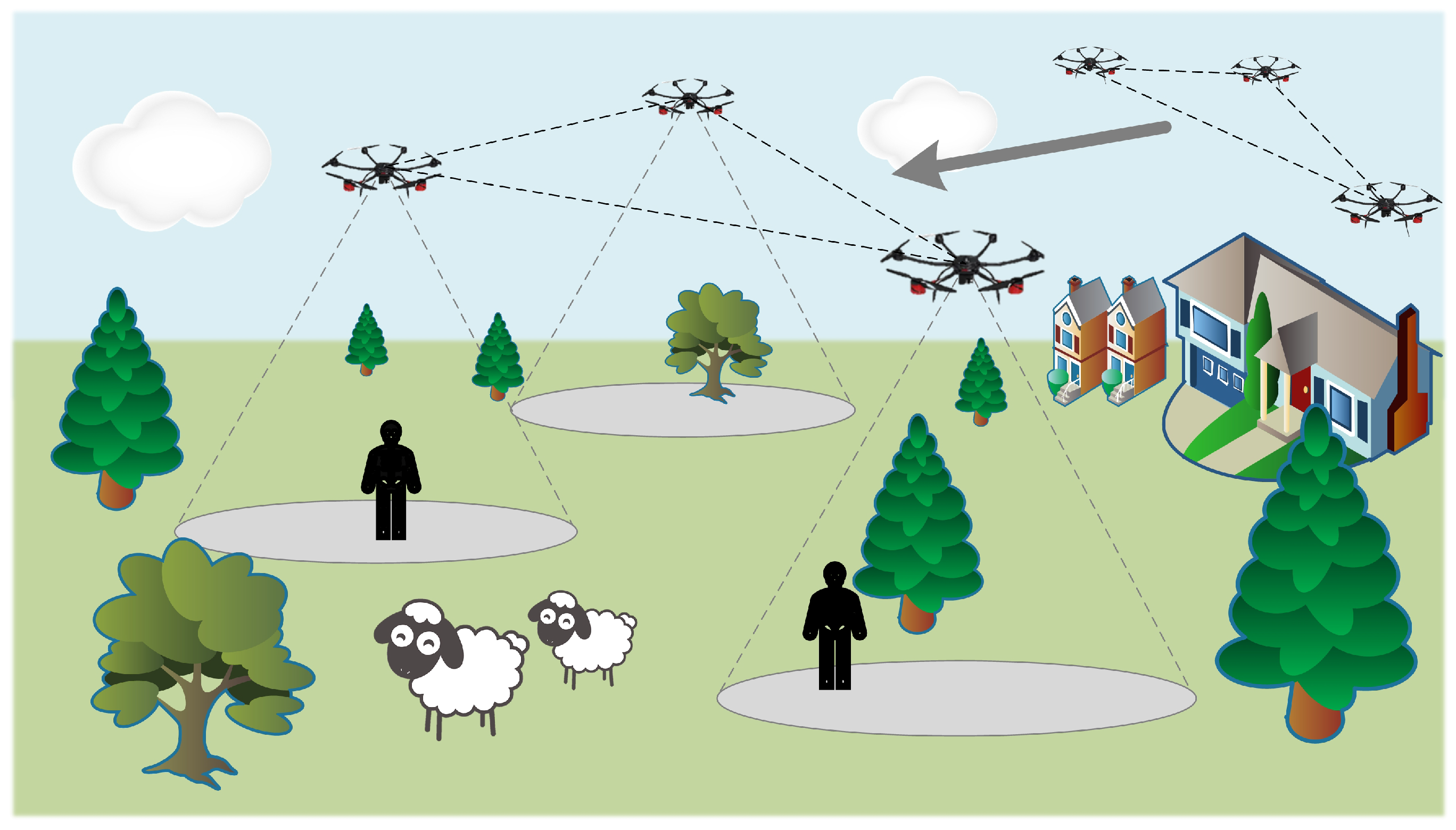
2.1. System Overview
2.2. UAV Energy Consumption Model
2.3. Energy Consumption Optimization and Coordinated Arrival Model for UAV Formation
2.4. Model Processing
3. Algorithm Design for Solution
| Algorithm 1 Optimization Algorithm Based on Model Reconstruction and IPM |
|
4. Simulation Experiment
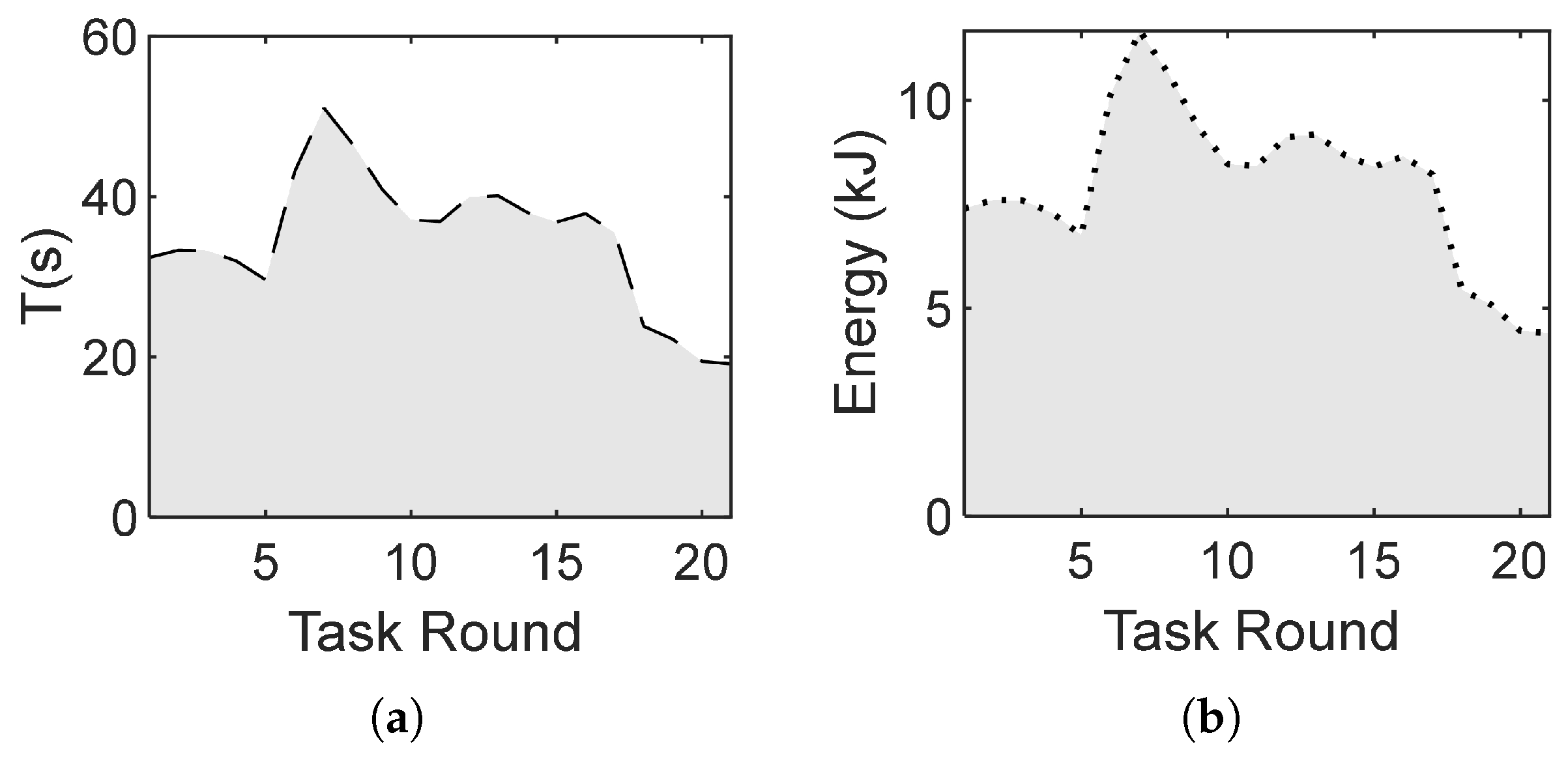
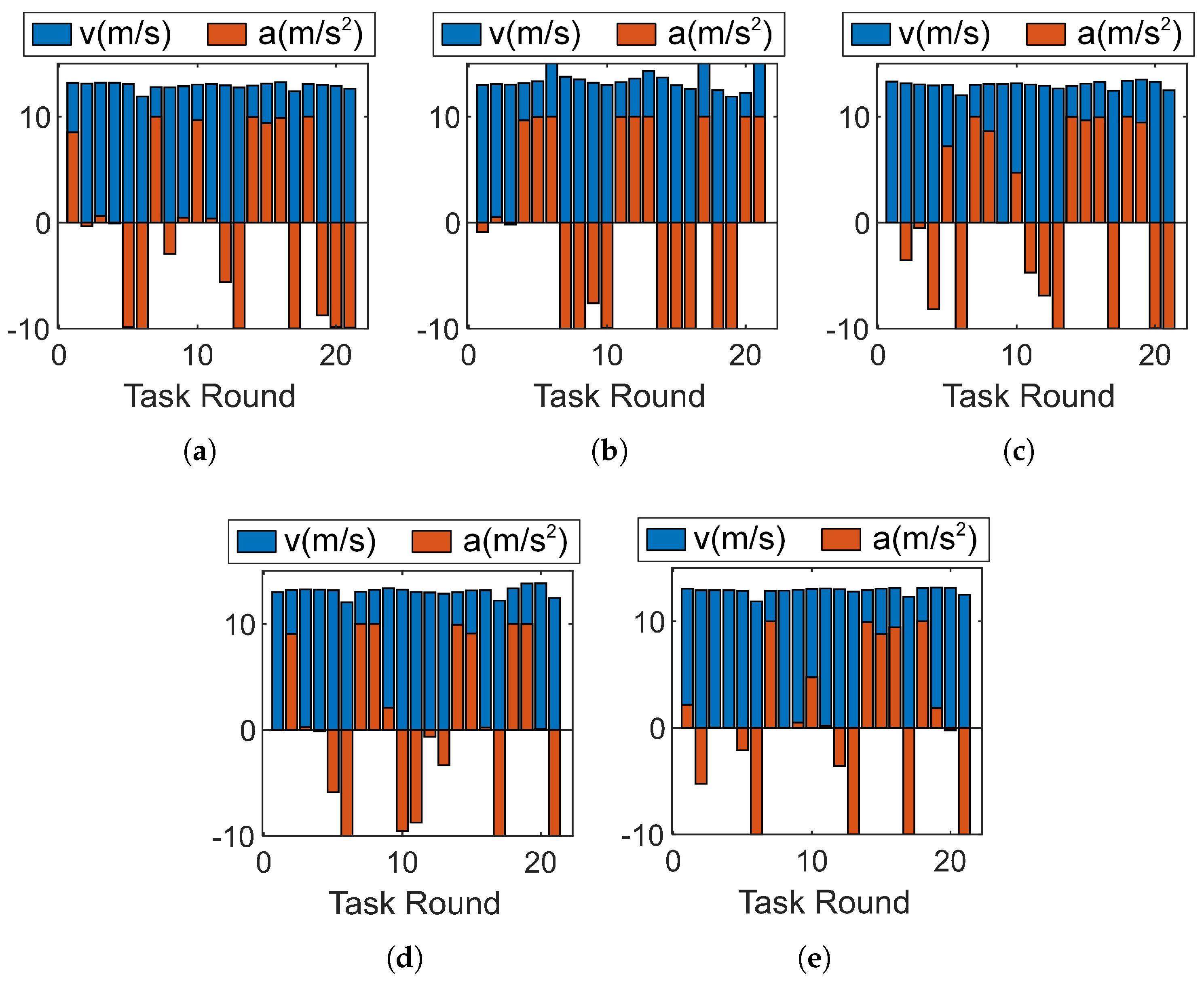
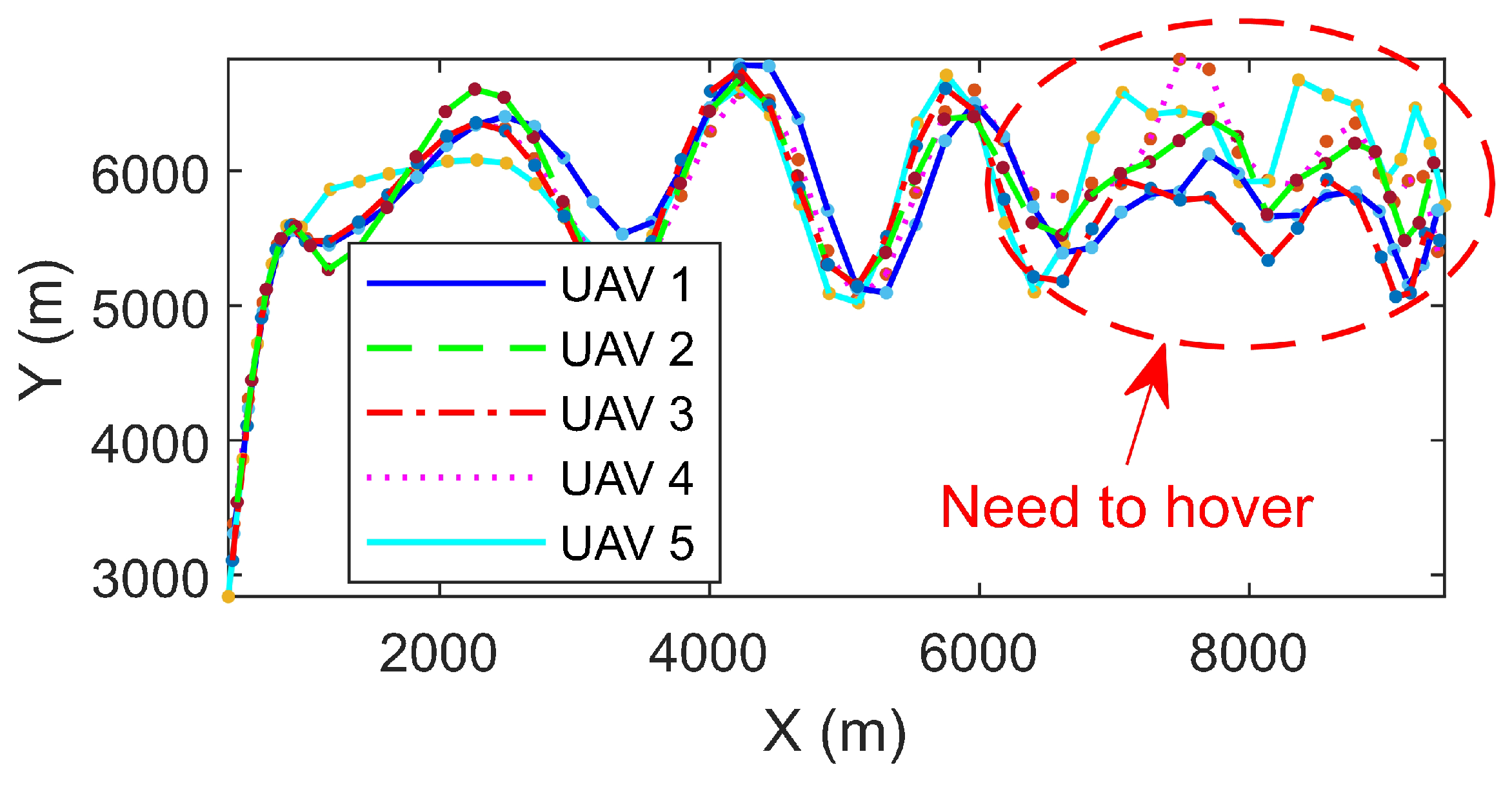
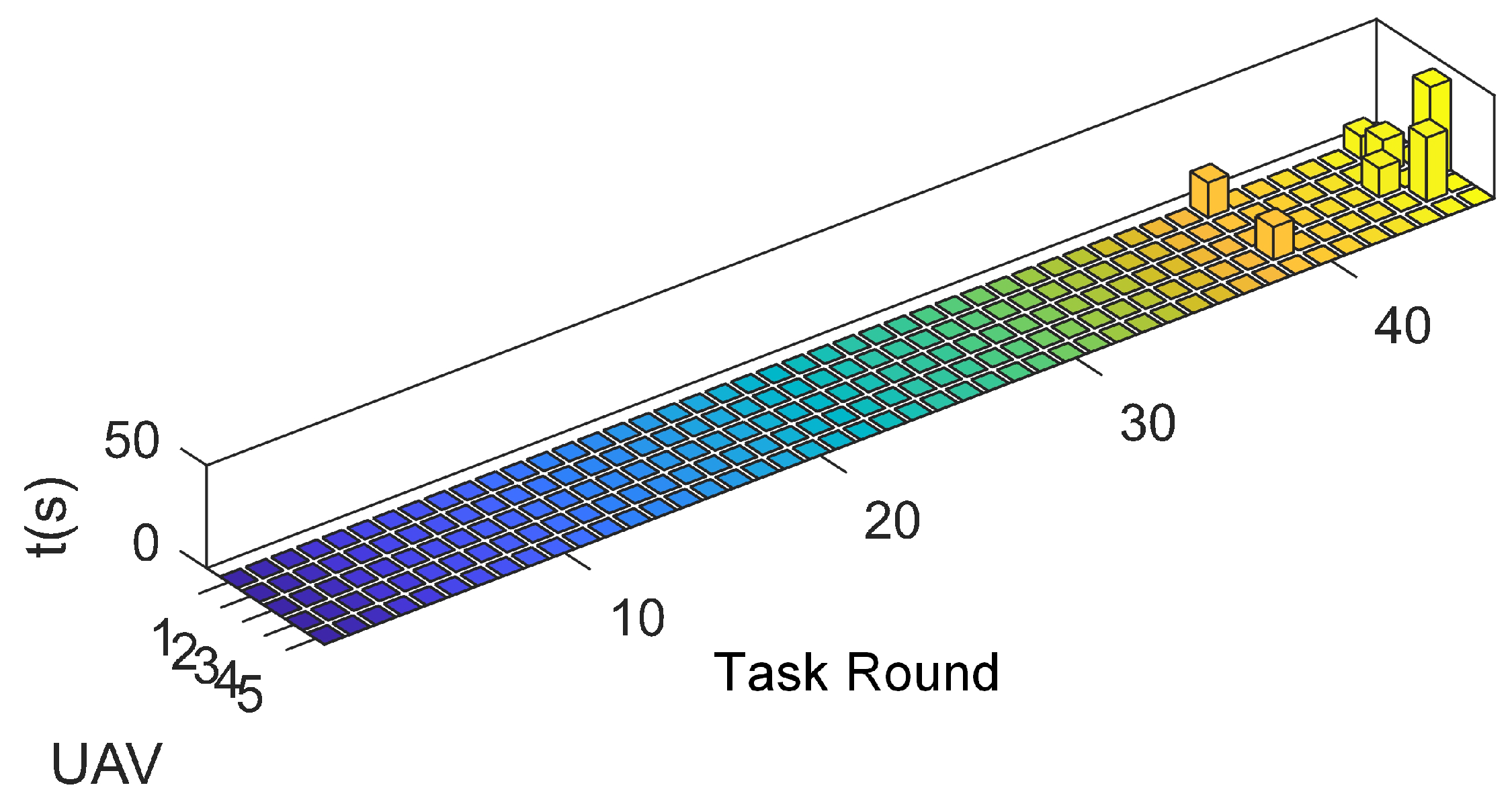
4.1. Experiment Scenario 1
4.2. Experiment Scenario 2
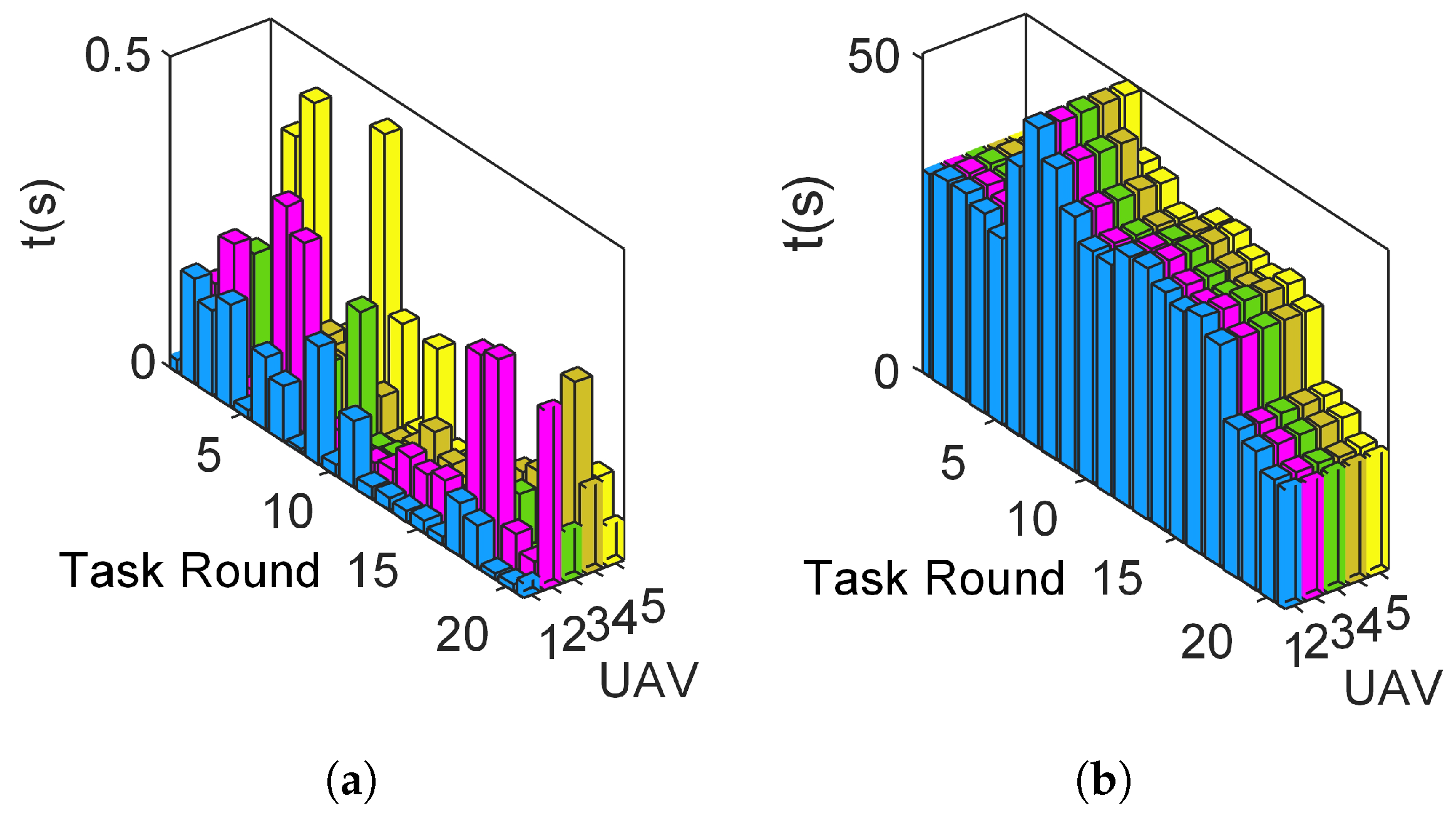
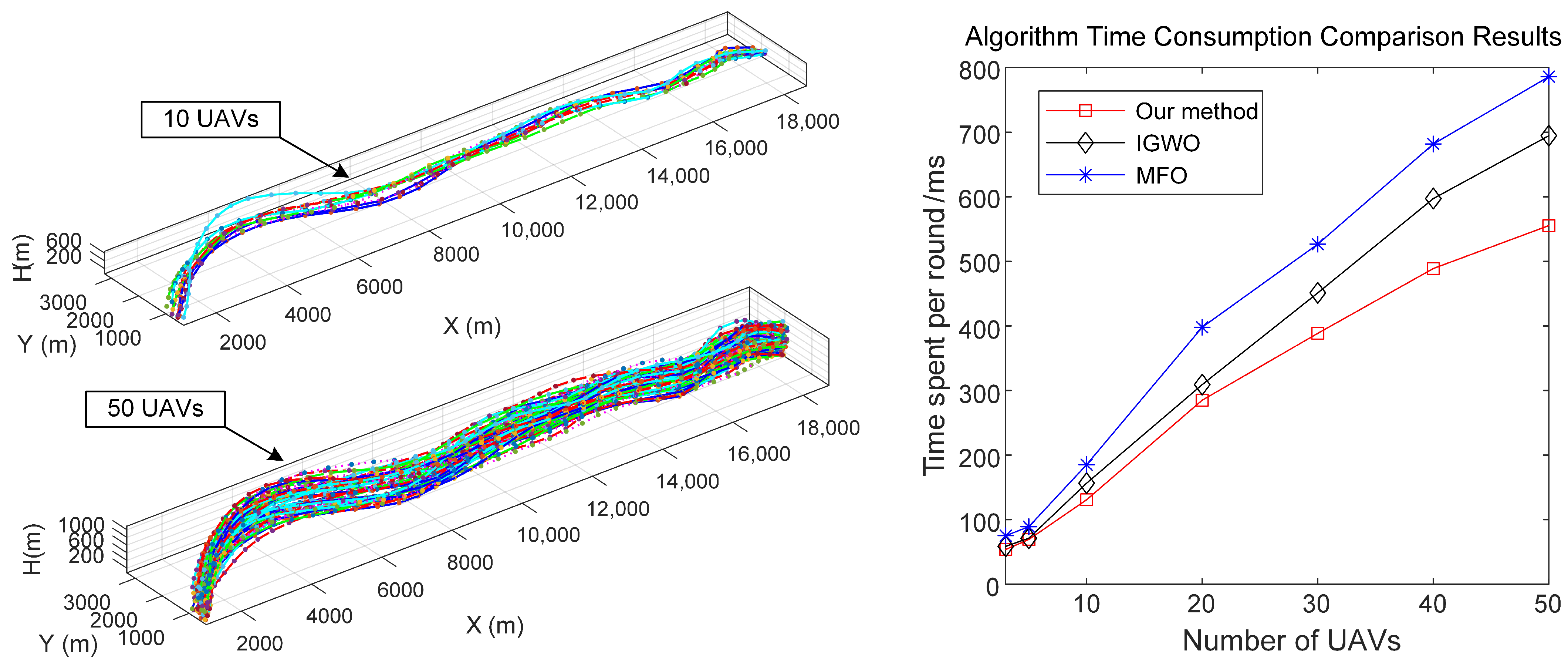
4.3. Algorithm Performance Test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ouyang, Q.; Wu, Z.; Cong, Y.; Wang, Z. Formation control of unmanned aerial vehicle swarms: A comprehensive review. Asian J. Control 2023, 25, 570–593. [Google Scholar] [CrossRef]
- Liu, Z.; Li, J. Application of unmanned aerial vehicles in precision agriculture. Agriculture 2023, 13, 1375. [Google Scholar] [CrossRef]
- Cheng, N.; Wu, S.; Wang, X.; Yin, Z.; Li, C.; Chen, W.; Chen, F. AI for UAV-assisted IoT applications: A comprehensive review. IEEE Internet Things J. 2023, 10, 14438–14461. [Google Scholar] [CrossRef]
- Luo, Q.; Luan, T.H.; Shi, W.; Fan, P. Edge computing enabled energy-efficient multi-UAV cooperative target search. IEEE Trans. Veh. Technol. 2023, 72, 7757–7771. [Google Scholar] [CrossRef]
- Yasin, J.N.; Mohamed, S.A.S.; Haghbayan, M.H.; Heikkonen, J.; Tenhunen, H.; Yasin, M.M.; Plosila, J. Energy-efficient formation morphing for collision avoidance in a swarm of drones. IEEE Access 2020, 8, 170681–170695. [Google Scholar] [CrossRef]
- Falkowski, K.; Duda, M. Dynamic models identification for kinematics and energy consumption of rotary-wing UAVs during different flight states. Sensors 2023, 23, 9378. [Google Scholar] [CrossRef]
- Chen, L.; Xiao, J.; Lin, R.C.H.; Feroskhan, M. Angle-constrained formation maneuvering of unmanned aerial vehicles. IEEE Trans. Control Syst. Technol. 2023, 31, 1733–1746. [Google Scholar] [CrossRef]
- Shao, X.; Liu, H.; Zhang, W.; Zhao, J.; Zhang, Q. Path driven formation-containment control of multiple UAVs: A path-following framework. Aerosp. Sci. Technol. 2023, 135, 108168. [Google Scholar] [CrossRef]
- Gao, Y.; Qiao, Z.; Pei, X.; Wu, G.; Bai, Y. Design of energy-management strategy for solar-powered UAV. Sustainability 2023, 15, 14972. [Google Scholar] [CrossRef]
- Ma, B.; Liu, Z.; Jiang, F.; Zhao, W.; Dang, Q.; Wang, X.; Zhang, J.; Wang, L. Reinforcement learning based UAV formation control in GPS-denied environment. Chin. J. Aeronaut. 2023, 36, 281–296. [Google Scholar] [CrossRef]
- Wu, Y.; Liang, T.; Gou, J.; Tao, C.; Wang, H. Heterogeneous mission planning for multiple UAV formations via metaheuristic algorithms. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 3924–3940. [Google Scholar] [CrossRef]
- Hu, W.; Yu, Y.; Liu, S.; She, C.; Guo, L.; Vucetic, B.; Li, Y. Multi-UAV coverage path planning: A distributed online cooperation method. IEEE Trans. Veh. Technol. 2023, 72, 11727–11740. [Google Scholar] [CrossRef]
- Li, J.; Xiong, Y.; She, J. UAV path planning for target coverage task in dynamic environment. IEEE Internet Things J. 2023, 10, 17734–17745. [Google Scholar] [CrossRef]
- Gong, S.; Wang, M.; Gu, B.; Zhang, W.; Hoang, D.T.; Niyato, D. Bayesian optimization enhanced deep reinforcement learning for trajectory planning and network formation in multi-UAV networks. IEEE Trans. Veh. Technol. 2023, 72, 10933–10948. [Google Scholar] [CrossRef]
- Na, Y.; Li, Y.; Chen, D.; Yao, Y.; Li, T.; Liu, H.; Wang, K. Optimal energy consumption path planning for unmanned aerial vehicles based on improved particle swarm optimization. Sustainability 2023, 15, 12101. [Google Scholar] [CrossRef]
- Souto, A.; Alfaia, R.; Cardoso, E.; Araújo, J.; Francês, C. UAV path planning optimization strategy: Considerations of urban morphology, microclimate, and energy efficiency using Q-learning algorithm. Drones 2023, 7, 123. [Google Scholar] [CrossRef]
- Abubakar, A.I.; Ahmad, I.; Omeke, K.G.; Ozturk, M.; Ozturk, C.; Abdel-Salam, A.M.; Imran, M.A. A survey on energy optimization techniques in UAV-based cellular networks: From conventional to machine learning approaches. Drones 2023, 7, 214. [Google Scholar] [CrossRef]
- Liang, Z.; Li, Q.; Fu, G. Multi-UAV Collaborative Search and Attack Mission Decision-Making in Unknown Environments. Sensors 2023, 23, 7398. [Google Scholar] [CrossRef]
- Bu, Y.; Yan, Y.; Yang, Y. Advancement Challenges in UAV Swarm Formation Control: A Comprehensive Review. Drones 2024, 8, 320. [Google Scholar] [CrossRef]
- Alhafnawi, M.; Salameh, H.A.B.; Masadeh, A.E.; Al-Obiedollah, H.; Ayyash, M.; El-Khazali, R.; Elgala, H. A survey of indoor and outdoor UAV-based target tracking systems: Current status, challenges, technologies, and future directions. IEEE Access 2023, 11, 68324–68339. [Google Scholar] [CrossRef]
- Pan, Y.; Li, L.; Qin, J.; Chen, J.J.; Gardoni, P. Unmanned aerial vehicle–human collaboration route planning for intelligent infrastructure inspection. Comput. Civ. Infrastruct. Eng. 2024, 39, 2074–2104. [Google Scholar] [CrossRef]
- Zeng, Y.; Xu, J.; Zhang, R. Energy minimization for wireless communication with rotary-wing UAV. IEEE Trans. Wirel. Commun. 2019, 18, 2329–2345. [Google Scholar] [CrossRef]
- Rao, Y.; Su, J.; Kheirfam, B. A Full-Newton Step Interior-Point Method for Weighted Quadratic Programming Based on the Algebraic Equivalent Transformation. Mathematics 2024, 12, 1104. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Kumar, S.; Mohapatra, S.S.; Mistry, K. Moth Flame Optimization: Theory, Modifications, Hybridizations, and Applications. Arch. Comput. Methods Eng. 2023, 30, 391–426. [Google Scholar] [CrossRef] [PubMed]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An Improved Grey Wolf Optimizer for Solving Engineering Problems. Expert Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- Reddy, M.R.; Kumar, K.; Narayana, K. Energy-Efficient Cluster Head Selection in Wireless Sensor Networks Using an Improved Grey Wolf Optimization Algorithm. Computers 2023, 12, 35. [Google Scholar] [CrossRef]
- Vashishtha, G.; Kumar, R. An Amended Grey Wolf Optimization with Mutation Strategy to Diagnose Bucket Defects in Pelton Wheel. Measurement 2022, 187, 110272. [Google Scholar] [CrossRef]






| Symbol | Meaning |
|---|---|
| Optimal flight speed of UAV | |
| Initial velocity of UAV-i | |
| Acceleration of UAV-i | |
| Time for the UAV to accelerate from to | |
| Time for UAV to fly at speed | |
| UAV hovering time | |
| Flight time of UAV-i in each round of tasks | |
| Energy consumption during flight at | |
| Energy consumption during acceleration | |
| UAV hovering energy consumption | |
| Total time spent by UAV in each task cycle | |
| Total energy consumption of the UAV-i | |
| Total task rounds | |
| k | Task round index |
| Symbol | Meaning | Value |
|---|---|---|
| W | UAV weight/N | 18 |
| Rotor radius/m | 0.4 | |
| Air density/kg/m2 | 1.225 | |
| A | Rotor disk area/m2 | 0.503 |
| Average rotor-induced velocity in hovering/m/s | 4.03 | |
| Rotor tip speed m/s | 120 | |
| Profile resistance coefficient | 0.012 | |
| Rotor speed rad/s | 300 | |
| Inductive power correction coefficient | 0.1 | |
| b | Number of blades | 4 |
| c | Blade chord length/m | 0.0157 |
| Equivalent plane area of fuselage/m2 | 0.151 | |
| Airframe drag ratio | 0.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Chen, R.; Yan, X.; Zhang, J.; Nian, Y. Research on Cooperative Arrival and Energy Consumption Optimization Strategies of UAV Formations. Drones 2024, 8, 722. https://doi.org/10.3390/drones8120722
Liu H, Chen R, Yan X, Zhang J, Nian Y. Research on Cooperative Arrival and Energy Consumption Optimization Strategies of UAV Formations. Drones. 2024; 8(12):722. https://doi.org/10.3390/drones8120722
Chicago/Turabian StyleLiu, Hao, Renwen Chen, Xiaohong Yan, Junyi Zhang, and Yongjia Nian. 2024. "Research on Cooperative Arrival and Energy Consumption Optimization Strategies of UAV Formations" Drones 8, no. 12: 722. https://doi.org/10.3390/drones8120722
APA StyleLiu, H., Chen, R., Yan, X., Zhang, J., & Nian, Y. (2024). Research on Cooperative Arrival and Energy Consumption Optimization Strategies of UAV Formations. Drones, 8(12), 722. https://doi.org/10.3390/drones8120722






