Joint Optimization Strategy of Task Migration and Power Allocation Based on Soft Actor-Critic in Unmanned Aerial Vehicle-Assisted Internet of Vehicles Environment

Abstract

In recent years, the unmanned aerial vehicle-assisted internet of vehicles has been extensively studied to enhance communication and computation services in vehicular environments where ground infrastructures are limited or absent. However, due to the limited-service range and battery life of unmanned aerial vehicles, along with the high mobility of vehicles, an unmanned aerial vehicle cannot continuously cover and serve the same vehicle, leading to interruptions in vehicular application services. Therefore, this paper proposes a joint optimization strategy for task migration and power allocation based on soft actor-critic (JOTMAP-SAC). First, communication models, computational resource allocation models, and computation models are established sequentially based on the computational resource and dynamic coordinate of each node. The joint optimization problem of task migration and power allocation is then formulated. Considering the dynamic nature of the unmanned aerial vehicle-assisted internet of vehicles environment and the continuity of the action space, a soft actor-critic based algorithm for task migration and power allocation is designed. This algorithm iteratively finds the optimal solution to the joint optimization problem, thereby reducing the processing delay in unmanned aerial vehicle-assisted internet of vehicles and ensuring the continuity of internet of vehicles task processing.

1. Introduction

Alongside the dynamic evolution of Unmanned Aerial Vehicles (UAVs), as well as the new generation of wireless communication technologies [1], the Internet of Vehicles (IoV) enables seamless integration with the internet, connecting moving pedestrians, vehicles, and roadside units (RSUs) with cloud servers. This concept is often referred to as Vehicles to Everything (V2X) [2]. V2X includes various communication scenarios such as Vehicle-to-Vehicle (V2V), Vehicle-to-Infrastructure (V2I), Vehicle-to-Pedestrian (V2P), and Vehicle-to-Network (V2N). The Internet of Vehicles has a powerful computing node, which provides real-time traffic information, security communication, and entertainment services through vehicle interconnection, significantly enhancing driving safety and travel experience [3,4]. Although there has been significant advancement in the computing power of nodes, the IoV still faces the dilemma that computing capabilities of individual vehicles cannot meet the low latency requirements of vehicle applications, as well as needing to overcome limited network coverage. Continuous service in the IoV system cannot be sustained with insufficient network coverage.

To address this, unmanned aerial vehicle (UAV)-assisted vehicle networking architecture has been widely adopted, as shown in Figure 1. In this architecture, UAVs have the advantages of small size, low cost, flexible mobility, wide coverage, and rapid deployment [5,6,7] UAVs, as the air mobile base stations, mobile relays, and other types of air communication platforms, provide necessary communication services for vehicles [8,9]. Meanwhile, UAVs can also provide computing services for constrained-resource vehicles. When integrated into the IoV system, UAVs can significantly enhance the Quality of Service (QoS).

However, the limited coverage range and high energy consumption of UAVs, combined with the high mobility of vehicles, make it challenging to maintain continuous service to the same vehicle [10,11]. Thus, effectively managing task migration for vehicular services and enhancing UAVs energy efficiency effectively to improve the continuity of service at computational nodes are critical issues in UAV-assisted vehicular networks. As illustrated in Figure 2, the novelty of the paper is that a novel method to jointly optimize task offloading and power allocation in a UAV-assisted IoV system is proposed, considering the task generated by the vehicle to be divisible. The goal is to minimize the response delay of vehicles and the energy consumption of UAVs with computation-intensive and latency-sensitive applications, while concurrently enhancing continuous service.

In conclusion, the main contributions of this paper are summarized as follows.

(1)

In the UAV-assisted vehicular network, a mathematical model is established to jointly optimize task migration and power allocation. This model considers the time-sensitive nature of tasks in the system. To minimize task processing delay and energy consumption while ensuring service continuity, a non-convex optimization problem is formulated.

(2)

An SAC-based joint optimization algorithm for task migration and power allocation (SAC-JOTMP) is proposed to solve this complex optimization problem. The algorithm dynamically adjusts the task migration and power allocation strategies to optimize the network performance in real-time.

(3)

Comprehensive simulation experiments are conducted to validate the effectiveness and advantages of the proposed algorithm. The simulation results demonstrate that the SAC-JOTMP algorithm significantly reduces task processing delay and energy consumption while enhancing system performance and service continuity.

The rest of this paper is organized as follows. The related work is summarized in Section 2. In Section 3, the system model, consisting of the several derivation types of computation, is constructed. In Section 4, the optimization problem is formulated. In Section 5, a SAC-based algorithm is proposed to solve the problem. The conducted simulations and system performance results are then reported in Section 6. Section 7 concludes the article and puts forward the future work.

2. Relate Work

Noferi A et al. [12] mentioned that existing task migration efforts primarily focus on reducing latency and migration costs. Zhao F and Li Z et al. [13,14] proposed using an MDP framework to predict potential user mobility, enabling the derived migration decisions to minimize task transmission latency. However, they did not investigate the collaboration between edge servers, treating them as independent entities. In contrast, our work is designed to address this gap by proposing a collaborative framework for edge server interactions. Farhoudi M et al. [15] applied deep learning techniques to predict user mobility. However, their approach did not consider the varying vehicular service demands, making it challenging to apply in real-world scenarios. In contrast, the method proposed in this paper requires only knowledge of the states of edge servers and UAVs, as well as the user’s position during each time period, thereby reducing the waiting latency for information acquisition.

Ghosh S et al. [16] proposed an efficient one-dimensional search algorithm that achieves a migration strategy with minimal average latency. However, it only considers a full offloading mode, where each task can only be completely offloaded to one node, without accounting for the possibility and benefits of partial offloading. Heidarpour A R et al. [17] considered the impact of latency and reliability on user quality of service and proposed a novel network design. However, their paper discusses task types, indicating that not all tasks can be migrated, which limits its applicability in universal environments. Peng K et al. [18] addressed task migration latency and costs, ultimately formulating a multi-objective optimization problem; however, it lacks the collaborative relationship between users and edge servers, which may lead to inefficient resource allocation.

The aforementioned papers primarily focus on latency issues while overlooking other metrics, and they rarely consider the simultaneous aspects of resource allocation and energy consumption for edge servers. In contrast, Arshed J U et al. [19] researched methods to enhance migration efficiency for mobile devices, eliminating task migration time and improving prediction accuracy. Wei Qin et al. [20] proposed a mobile computing offloading and task migration method based on trajectory and resource prediction (MCOTM), aiming at minimizing task turnaround time and system energy consumption.

The comparison of the above-mentioned works is demonstrated in

Table 1. Comparison of related works.

Reference	Environment	Objective	Method	Considering Factors
[12]	Mobile edge computing	Helping researchers of ETSI MEC to evaluate the performance of products	Provide an architecture based on Simu5G and improve the performance of ETSI MEC	The number of edge servers
[13]	Satellite edge computing	Minimize the task process delay within the migration cost constraint	Propose the online satellite service deployment scheme based on Convolutional Proximal Policy Optimization	Steps, time, deployment location
[14]	Multiple access edge computing	Maximize the task process quality	Use the Knapsack Potential Game to obtain the optimal offloading ratio	High-priority task accessibility and performance deviation
[16]	UAV assisted edge computing	Minimize delay, energy consumption and load	Propose a computation offloading method based on Gravity search algorithm	The number of tasks, iteration times
[17]	Mobile edge computing	Maximize the network life within given the length of task queue	Propose a deep reinforcement learning life cycle maximization method based on soft actor-critic	Interval, bandwidth, CPU
[18]	Mobile edge computing	Minimize the task process time, energy consumption; Maximize the resource utilization rate of edge servers	Propose computation offloading method within terminal-edge-cloud collaboration	The number of users, edge servers and applications
[19]	Mobile edge computing	Predict the current location of users	Propose migration algorithm based on logistic regression	Data distribution, task numbers
[20]	Edge computing	Minimize the task process time and energy consumption	Propose a mobility-aware computation offloading and task migration method based on trajectory and resource prediction	The number of mobile terminals, the edge server distribution, the different migration decision
Ours	UAV assisted edge computing	Minimize the total task process delay and energy consumption of UAVs	Propose a joint optimization algorithm of task migration and power allocation based on SAC	The number of vehicles, the steps, the task size, the computation capacity of UAVs

. Different from these existing works, we investigate the joint optimization strategy for task migration and power allocation based on SAC, aimed at minimizing total task processing latency and UAV energy consumption. In contrast, while studies have proposed various optimization methods in different edge computing environments, such as cooperative evolutionary migratory bird optimization algorithms based on online learning policy gradients, convolutional proximal policy optimization, and backpack potential games, these approaches exhibit limitations in terms of applicability and optimization objectives. For example, the cooperative evolutionary migratory bird optimization algorithm is effective for resource allocation in dynamic environments but may underperform in optimizing UAV energy consumption. Convolutional proximal policy optimization excels in large-scale task scheduling but may struggle with tasks requiring high real-time performance. In comparison, the SAC-based joint optimization strategy proposed in this paper offers a more comprehensive solution for optimizing task latency and energy consumption issues in UAV-assisted edge computing.

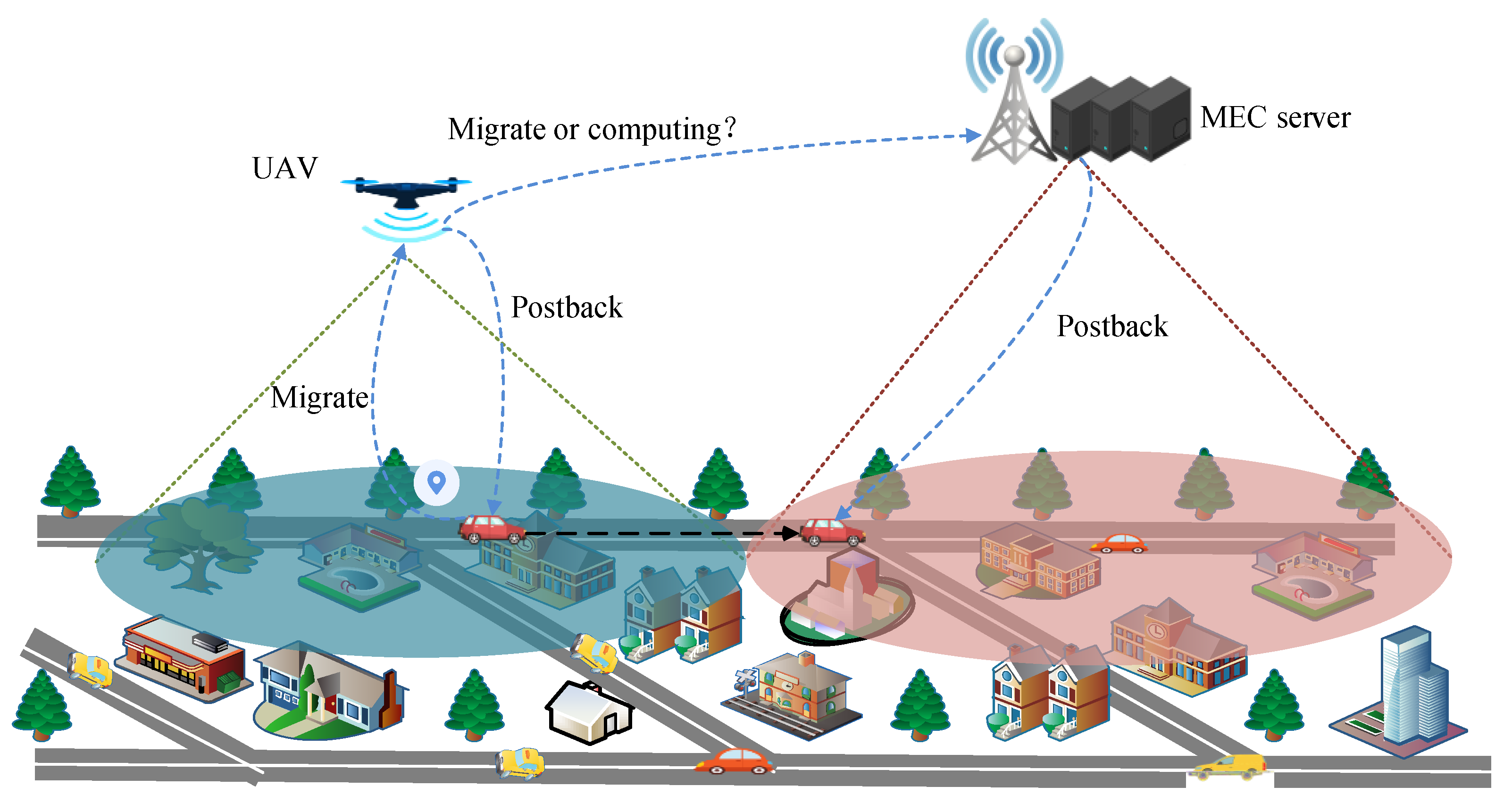
3. System Model

Consider a multi-UAV assisted IoV environment, which contains a Base Station (BS) equipped with a MEC, $U$ UAVs, and $V$ vehicles. The vehicles have limited computation resources, and they can communicate with each other. Since UAVs are all equipped with the computation and communication units, UAVs can provide computation and communication services to multiple vehicles, which can improve the communication efficiency. $U$ UAVs are indexed by $\mathcal{U}=\{1,\mathrm{\dots },u,\mathrm{\dots },U\}$. The set of vehicles is denoted by $\mathcal{V}=\{1,\mathrm{\dots },v,\mathrm{\dots },V\}$. In this system, edge nodes ${\mathcal{U}}^{\prime }=\{1,2,\mathrm{3\dots },u,u+1\}$ including UAVs and a single MEC server, where $u+1=M$ is MEC server. Task characteristics can be represented by $A_v=\{W_v,D_v,{\tau }_v\}$, where $W_v$ denotes the number of CPU cycles required to process task $A_v$, $D_v$ denotes the size of $A_v$, and ${\tau }_v$ denotes the maximal tolerable latency of task process for the vehicle $v$. A vehicle can generate a migration task in a certain time slot and without loss of generality, assuming that the task can be divided into several subtasks.

3.1. Communication Model

During transmission, we assume that channel $B$ denotes bandwidth, $p_v$ denotes the transmission power of the vehicle, ${\rho }_{los}$ is the shadow fading component ${\mathrm{d}}_{v,u}$ denotes the distance between the vehicle $v$ and UAV $u$, and $\epsilon$ denotes the channels gain. $N_0$ is the additive white Gaussian noise.

Due to the dynamic characteristics of vehicles, there will be interference between vehicles; the interference of other vehicles with vehicle $v$ is defined as ${\displaystyle {\sum }_{v^{\prime }=1,v^{\prime }\ne i}^V{p}_{v^{\prime }}{\rho }_{los}{d}_{v,u}^{-\epsilon }}$. The uplink data transmission rate between $v$ and $u$ is defined as [21,22]:

$$r_{v,u}^t=B{\log }_2(1+{\displaystyle \frac{p_v{\rho }_{los}{d^{-\epsilon }}_{v,u}}{{\displaystyle \sum _{v^{\prime }=1,v^{\prime }\ne v}^V{p}_{v^{\prime }}{\rho }_{los}}{d^{-\epsilon }}_{v^{\prime },u}+N_0}})$$

(1)

where the uplink data transmission rate between the vehicle $v$ and MEC is defined as:

$$r_{v,M}^t=B{\log }_2(1+{\displaystyle \frac{p_v{\rho }_{los}{d^{-\epsilon }}_{v,M}}{{\displaystyle \sum _{v^{\prime }=1,v^{\prime }\ne v}^V{p}_{v^{\prime }}{\rho }_{los}}{d^{-\epsilon }}_{v^{\prime },M}+N_0}})$$

(2)

The uplink data transmission rate between the UAV $u$ and MEC is defined as:

$$r_{u,M}^t=B{\log }_2(1+{\displaystyle \frac{z_u^t{p}_u{\rho }_{los}{d^{-\epsilon }}_{u,M}}{{\displaystyle \sum _{u^{\prime }=1,u^{\prime }\ne u}^U{z}_u^t{p}_{u^{\prime }}{\rho }_{los}}{d^{-\epsilon }}_{u\prime ,ES}+N_0}})$$

(3)

where $z_u^t$ is UAV $u$ power allocation decision at time $\mathrm{t}$. The downlink data transmission rate between the MEC and UAV $u$ is defined as:

$$r_{M,u}^t=B{\log }_2(1+{\displaystyle \frac{p_M{\rho }_{los}{d^{-\epsilon }}_{M,u}}{N_0}}).$$

(4)

The data transmission rate between UAVs is defined as:

$$r_{u,u^{\prime }}^t=B{\log }_2(1+{\displaystyle \frac{z_u^t{p}_u{\rho }_{los}{d^{-\epsilon }}_{u,u^{\prime }}}{{\displaystyle \sum _{u^{″}=1,u^{″}\ne u}^U{z}_{u^{″}}^t{p}_{u^{″}}{\rho }_{los}}{d^{-\epsilon }}_{u^{″},u^{\prime }}+N_0}})$$

(5)

3.2. Resource Allocation Model

For each computing node, its computing resources will be allocated based on the size of each computing task. The computing resource coefficient allocated by edge node $v$ for migration task $j$ is defined as.

$${\eta }_{v,j}={\displaystyle \frac{x_{v,j}^t{D}_v}{{\displaystyle \sum _{v=1}^{\mathcal{V}}{x}_{v,j}^t{D}_v}+{\displaystyle \sum _{v^{\prime }\in {\mathcal{K}}_j^t}(1-{\displaystyle \sum _{j^{\prime }\in {\mathcal{U}}^{\prime }}{x}_{v^{\prime },j^{\prime }}^t})D_{v^{\prime }}}}}.$$

(6)

where $x_{v,j}^t$ represents the ratio of migration task $v$ to node $j$. Therefore, the computing resources allocated to the edge node $j$ for migration task $v$ are defined as.

$$f_{v,j}={\eta }_{v,j}{f}_j,$$

(7)

where $f_v$ represents the computing resources of edge node $j$. Similarly, when the unmigrated part of the task $v$ is transferred to the local edge node, the computing resource allocation coefficient of the local edge node to the unmigrated part of the task $v$ is defined as:

$${\eta }_v={\displaystyle \frac{(1-{\displaystyle \sum _{j^{\prime }\in {\mathcal{U}}^{\prime }}{x}_{v,j^{\prime }}^t})D_v}{{\displaystyle \sum _{v=1}^{\mathcal{V}}{x}_{v,s_v^t}^t{D}_v}+{\displaystyle \sum _{v^{\prime }\in {\mathcal{K}}_{s_v^t}^t}(1-{\displaystyle \sum _{j^{\prime }\in {\mathcal{U}}^{\prime }}{x}_{v^{\prime },j^{\prime }}^t})D_{v^{\prime }}}}}.$$

(8)

The computing resources allocated to the local edge node for migration task $v$ are defined as:

$$f_v={\eta }_v{f}_{s_v^t}$$

(9)

3.3. Computing Model

3.3.1. Local Model

The calculation task of the vehicle is partially calculated on the local edge node and is partially migrated to the edge node. The task processing delay of the local edge node is defined as [21,23]:

$${{\mathrm{t}}^{exe}}_v={\displaystyle \frac{w_v(1-{\displaystyle \sum _{j\in {\mathcal{U}}^{\prime }}{x}_{v,j}^t})}{f_v}},$$

(10)

The delay for transmitting the vehicular task to the local edge node is defined as:

$$t_v^{tra}={\displaystyle \frac{D_v(1-{\displaystyle \sum _{j\in {\mathcal{U}}^{\prime }}{x}_{v,j}^t})}{r_{v,s_v^t}}}.$$

(11)

Therefore, the total processing delay the local edge node is defined as:

$$T_v^{local}={{\mathrm{t}}^{exe}}_v+t_v^{tra}.$$

(12)

3.3.2. Migration Model

To alleviate the situation of limited local computing resources in vehicles, some vehicular tasks are offloaded to edge nodes. The task processing delay of the migration to the edge node $j$ is defined as:

$${t^{exe}}_{v,j}={\displaystyle \frac{w_v{x}_{v,j}}{f_{v,j}}}.$$

(13)

The delay for transmitting the vehicular task to the edge node is defined as:

$$t_{v,j}^{tra}={\displaystyle \frac{D_v{x}_{v,j}}{r_{s_v^t,j}}}.$$

(14)

Therefore, the total processing delay at the edge node is defined as:

$$T_{v,j}^{mig}={{\mathrm{t}}^{exe}}_{v,j}+t_{v,j}^{tra}.$$

(15)

The latency for users to download processed data from the BS is negligible since the processed data have a much smaller size compared to the offloaded raw data and the BS has more power to transmit with a higher data rate [24]. Thus, the total delay is the maximum value between the local edge node delay and the delay of offloading to the edge node, which is:

$$T_{v,j}^t=MAX(T_v^{local},t_v^{tra}+T_{v,j}^{mig}).$$

(16)

3.4. Energy Model

In our system, the energy consumption of UAVs is divided into three parts: local execution energy consumption of UAVs, local UAVs transmission energy consumption, and execution energy consumption when migrating to the UAVs. The energy consumption for local UAVs execution is defined as [25]:

$$e_{v,u}^{t,local,exe}=z_u^t{p}_{u}I(s_v^t){\displaystyle \frac{(1-{\displaystyle \sum _{j\in {\mathcal{U}}^{\prime }}{x}_{v,j}^t})w_v}{f_{v,u}}},$$

(17)

where $I(s_v^t)$ represents the vehicle $v$ at time slot $t$ and whether the initially connected edge node is a UAV. If the initial connected edge node is a UAV, then $I(s_v^t)=1$; otherwise $I(s_v^t)=0$. It can be expressed as:

$$I(s_v^t)=\left\{\begin{array}{l}1,s_v^t\in U\\ 0,otherwise\end{array}\right..$$

(18)

The local UAVs transmission energy consumption is defined as:

$$e_{v,u,j}^{t,tra}=z_u^t{p}_{u}I(s_v^t){\displaystyle \frac{x_{v,j}^t{D}_v}{r_{u,j}}}.$$

(19)

Thus, the energy consumption of local UAVs is defined as:

$$e_{v,u,j}^{t,local}=e_{v,u}^{t,local,exe}+e_{v,u,j}^{t,tra}.$$

(20)

The purpose of the migration UAV execution energy consumption is defined as:

$$e_{v,j}^{\mathrm{t},\mathrm{mig}}=O(v,j),$$

(21)

$$O(v,j)=\left\{\begin{array}{l}{z}_j^t{p}_j{\displaystyle \frac{x_{v,j}^t{w}_v}{f_{v,j}}},j\in U\\ 0,otherwise\end{array}\right.,$$

(22)

where $O(v,j)$ represents that the migration destination is a UAV, and there will be energy consumption for the execution of the migration destination UAV. If the migration destination is not a UAV, then $O(v,j)=0$. Therefore, the total energy consumption of UAVs is expressed as:

$$E^{total}={\displaystyle \sum _{v=1}^{\mathcal{V}}{\displaystyle \sum _{u=1}^{\mathcal{U}}{\displaystyle \sum _{j=1}^{{\mathcal{U}}^{\prime }}(e_{v,u,j}^{\mathrm{t},local}+e_{v,\mathrm{j}}^{t,mig}}}}).$$

(23)

The system overhead function is defined by the sum of all user’s value on the local edge nodes and migration edge nodes. Then, the joint power allocation and task migration is described as a system overhead minimization problem, which is represented as:

$$\mathbf{P}\mathbf{1}:\underset{X,Z}{MIN}{\displaystyle \sum _{v=1}^{\mathcal{V}}{\displaystyle \sum _{j=1}^{{\mathcal{U}}^{\prime }}\frac{T^t-T_{v,j,\min }^t}{T_{v,j,\max }^t-T_{v,j,\min }^t}}}+{\displaystyle \frac{E^{total}-E_{\min }^{total}}{E_{\max }^{total}-E_{\min }^{total}}},$$

(24)

s.t.

$$x_{v,j}^t=[0,1],j\in {\mathcal{U}}^{\prime },j\ne s_v^t,$$

(25)

$$z_j^t\in [0,1],\forall j\in \mathcal{U},$$

(26)

$${\displaystyle \sum _{j=1}^{{\mathcal{U}}^{\prime }}{T}_{v,j}^t}\le {\tau }_v,$$

(27)

$${\displaystyle \sum _{v=1}^{\mathcal{V}}{\displaystyle \sum _{j=1}^{{\mathcal{U}}^{\prime }}{e}_{v,u,j}^{t,local}}}\le E_u^{\max },$$

(28)

$${\displaystyle \sum _{v=1}^{\mathcal{V}}{\displaystyle \sum _{j=1}^{\mathcal{U}}{E}_{v,j}^{t,mig}}}\le E_u^{\max },$$

(29)

where migration decision vector is $X$, $Z$ is power allocation decision vector. $T_{v,j,\min }^t$ represents the minimum latency for vehicle $v$ to migrate to node $j$ at time $t$, $T_{v,j,\max }^t$ represents the maximum latency for vehicle $v$ to migrate to node $j$ at time $t$, $E_{\min }^{total}$ represents the minimum total energy consumption of the UAV, and $E_{\min }^{total}$ represents the maximum total energy consumption of the UAV. Here, the constraint (27) represents that the total processing delay of computing task cannot exceed the maximum tolerant delay. Constraints (28) and (29) constrain the available UAV energy.

In this form, the migration decision variables and power allocation decision variables are optimized while minimizing the total tasks delay and UAV energy consumption.

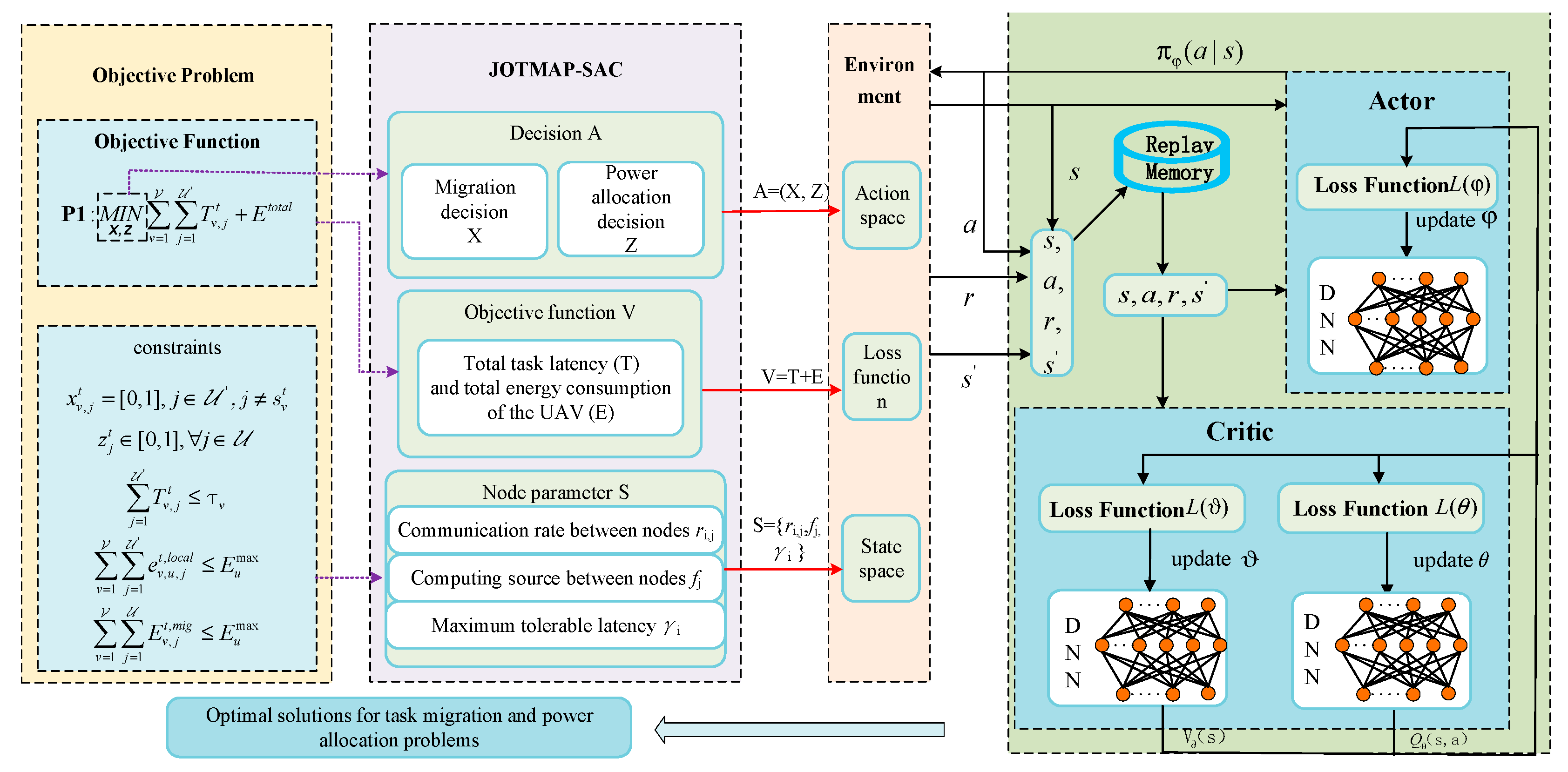
4. Algorithm Design

The SAC algorithm was proposed by Haarnoja et al. [26] in 2018 based on the concept of Actor-Critic in reinforcement learning. The core idea is to enhance the original reward by incorporating entropy information to encourage exploration, thereby training a behavior policy that maximizes rewards with entropy. This approach maximally retains the randomness of the behavior policy, which improves the agent’s ability to perceive the environment. It enables the agent to adaptively adjust its strategy in the dynamically changing channel conditions of UAV-assisted vehicular networks, facilitating reasonable task migration and power allocation decisions [27]. The task migration and power allocation joint optimization problem proposed in this paper is a non-convex problem that cannot be solved using naive algorithms. Accordingly, this paper presents a joint optimization algorithm for task migration and power allocation based on SAC, as shown in Figure 2.

This paper uses a joint optimization algorithm based on SAC for task migration and power allocation to solve problem P1. The SAC algorithm includes two Q-critic networks ($Q_{{\beta }_1}(s_n,a_n)$, $Q_{{\beta }_2}(s_n,a_n)$) and two target Q-critic network (${\widehat{Q}}_{{\beta }_1}(s_n,a_n)$, ${\widehat{Q}}_{{\beta }_2}(s_n,a_n)$). At time slot $t$, the agent interacts with the environment and then learns an optimal policy ${\pi }_{\alpha }$. If the agent takes an action $a_n$ in state $s_n$, the environment will turn to the next state. Parameters ${\beta }_1$ and ${\beta }_2$ are used to generate the Q-values $Q_{{\beta }_1}(s_n,a_n)$, $Q_{{\beta }_2}(s_n,a_n)$, with two Q networks utilized during the gradient descent process.

In the UAV-assisted IoV, the optimization objective P1 operates in a multi-time-slot environment, where each time slot has equal duration. Within each time slot, migration and power allocation decisions are generated based on the current state, leading to the next state. Therefore, the problem is framed as a Markov Decision Process (MDP), represented by a tuple $\{S,A,P,R\}$, where $S$ is the state space, $A$ is the action space, $P$ is the state transition matrix of the model, and $R$ is the reward function. The optimization problem based on SAC is illustrated in Figure 2.

(1)

Define State Space

The state space is composed of $V$ vehicles, $U$ UAVs, and an ES. In accordance with the MDP assumption that the next state depends on the current one, we define the state representation based on this dependency. Consequently, the state space $\mathrm{s}$ at time slot $t$ is given by:

$$S=\left\{s\right|s=<v,{\tau }_v,p>\}.$$

(30)

(2)

Define Action Space

In this system, the agent’s decisions encompass the selection of target nodes for task migration, the formulation of power allocation strategies, the distribution of computation resources across nodes, and the management of communication bandwidth. Thus, the action space at time slot $t$ can be expressed as:

$$A=\left\{a\right|a=<X,Z>\}.$$

(31)

(3)

Define Reward Function

The reward function represents the reward the system receives after executing an action. In the UAV-assisted IoV system, for any given state $s_t$, the task processing delay at time step $t$ can be determined. Upon taking action $a^t$, the system transitions from state $s^t$ to state $s^{t+1}$. If this action violates constraints (25) to (29), the reward value will be very small. The reward function is defined as the negative change in the average task processing delay, specifically:

$$r(s,a)=-({\displaystyle \sum _{v=1}^{\mathcal{V}}{\displaystyle \sum _{j=1}^{{\mathcal{U}}^{\prime }}\frac{T^t-T_{v,j,\min }^t}{T_{v,j,\max }^t-T_{v,j,\min }^t}}}+{\displaystyle \frac{E^{total}-E_{\min }^{total}}{E_{\max }^{total}-E_{\min }^{total}}}).$$

(32)

The objective function of the JOTMAP-SAC algorithm seeks to maximize the combined sum of the reward and policy entropy, which is expressed as:

$$J(\pi )={\displaystyle \sum _{n=1}^N{E}_{(s_n,a_n)~{\rho }_{\pi }}[r(s_n,a_n)-\partial \log (\pi (|s_n))]},$$

(33)

where $\pi (a_n|s_n)$ represents the probability of taking action $a_n$ in state $s_n$. A larger value of $a$ indicates a higher degree of randomness in the policy, while a smaller value makes the policy more deterministic. At each interval, the JOTMAP-SAC algorithm performs gradient descent on the Q network’s neural network to update the parameters, which can be expressed as:

$$\begin{array}{ll}\hfill J_Q({\beta }_i)=& E_{(s_n,a_n)~D}[\frac{1}{2}(Q_{{\beta }_i}(s_n,a_n)-(r(s_n,a_n)\\ & +{\rm Y}({\min }_{j=1,2}{Q}_{{\beta }_j}(s_{n+1},a_{n+1})\\ & -\partial \log \pi {(a_{n+1}|s_{n+1})))}^2{]}_{n+1})\\ & -\wp \log {\pi }_{\Phi }{(a_{n+1}|s_{n+1})))}^2],\end{array}$$

(34)

where $D$ represents the sampling status and action. Meanwhile, the parameters of the policy function are also updated:

$$\begin{array}{l}{J}_{\pi }(\alpha )=E_{s_n~D}[\partial \log {\pi }_{\alpha }(f_{\alpha }(s_n)|s_n)\\ -{\min }_{j=1,2}{Q}_{{\beta }_j}(s_n,f_{\alpha }(s_n))],\end{array}$$

(35)

where ${\pi }_{\alpha }(f_{\alpha }(s_n)|s_n)$ is the probability of taking action $f_{\alpha }(s_n)$ in state $s_n$, $\alpha$ a hyperparameter that balances the weight between reward and strategy entropy [28].

According to the above analysis, the pseudocode of the proposed SAC-JO3C algorithm is shown as below (Algorithm 1).

Algorithm 1: The joint optimization algorithm of task migration and power allocation based on SAC (JOTMAP-SAC)

Input: The parameter $\alpha$$,{\beta }_i,i=1,2$, $\mathrm{the}\mathrm{objective}\mathrm{network}\mathrm{parameter}{{\beta }^{\prime }}_i,i=1,2$, the size $H$ of experience pool, the randomly sampling parameter $m$

Output: The optimal value of $\alpha$, ${\beta }_i$, ${{\beta }^{\prime }}_i$ 1: for each episode do 2:     for time step n = 1, 2, …, N do 3:     The initial state $s_n$ 4:     Achieving the initial state and the action $a_n\sim {\pi }_{\alpha }(a_n|s_n)$ by actor network 5:     Executing action and achieving the reward $r_n(a_n,s_n)$ and next state $s_{n+1}$ 6:     Storing the current experience $(s_n,a_n,r_n,s_{n+1})$ into the experience pool $7:\mathrm{if}n>H\mathrm{then}$ 8:         Randomly sampling $m$ $\mathrm{experience}(s_n,a_n,r_n,s_{n+1})$ $9:\mathrm{Updating}{\beta }_i,i=1,2$ by Equation (34) $10:\mathrm{Updating}\mathrm{parameter}\alpha$ by Equation (35) 11:     Updating the objective network parameter ${\beta }_i^{\prime }\leftarrow \tau {\beta }_i+(1-\tau ){\beta }_i^{\prime },i=1,2$ 12:   end 13: end

The computational complexity of the proposed JOTMAP-SAC algorithm is primarily determined by the number and structure of the neural networks in the SAC system. The dimensions of the DNN for the actor’s input and output are $2(V+U)+3$ and $4\left(V+U\right)+4$, respectively, where $V$ is the number of vehicles and $K$ is the total number of subtasks. For the critic, the input dimensions are $4(V+U)+5$ and the output dimension is 1, where $U$ is the number of UAVs. Both the actor and the critic networks share the same number of hidden layers, denoted as $L$, and $B$ is the batch size. Therefore, the computational complexity for the gradient descent of the actor and critic can be estimated as $O\left(BLK{\left(V+U\right)}^2\right)$ and $O\left(BL\left(V+U\right)\right)$, respectively. Consequently, the overall complexity of the JOTMAP-SAC algorithm is estimated as $O\left(EBL{\left(V+U\right)}^2\right)$, where EEE represents the number of episodes [29].

5. Use Case

As shown in Figure 3, during vehicle movement, when local computing resources are insufficient, the vehicle’s high-precision map navigation task is offloaded to the current edge node that covers the vehicle. However, due to the limited coverage of edge nodes, as the vehicle moves out of range, the algorithm must decide whether to migrate the task to another edge node or to forward the results after computation at the current edge node. The proposed algorithm aims to minimize both delay and energy consumption by selecting the optimal strategy between task migration and task forwarding. The decision-making process is based on a comparison of the delay and energy cost for both strategies. The algorithm selects the strategy that minimizes these costs while maintaining system performance.

In the case of fixed power allocation, the system cannot adjust power dynamically based on real-time conditions, which may result in suboptimal performance. The fixed power allocation might not be efficient enough to handle varying network demands, leading to higher energy consumption and potentially increased delays. This lack of adaptability could hinder the system’s ability to perform well in dynamic vehicular environments, particularly when the vehicle moves quickly or the network conditions change.

When implementing full task migration, the algorithm would transfer the entire task to a new edge node once the vehicle leaves the current coverage area. While this reduces the computational burden on the current edge node, it introduces a significant communication overhead. Migrating the full task increases both delay and energy consumption, especially in cases where the vehicle moves rapidly or edge nodes are geographically dispersed. In contrast, the proposed algorithm dynamically decides between task migration and forwarding based on a comparison of delay and energy costs, optimizing performance while minimizing the impact of task migration overhead and power allocation constraints.

6. Numerical Simulation and Analysis

6.1. Experiment Environment

The experiment was conducted in a numerical simulation environment, and the entire process was validated on a personal computer with the following configuration: Intel^® Core™ i7-12700f CPU @ 2.10 GHz, 16.0 GB RAM, 1024 GB DISK (Santa Clara, CA, USA), and Windows 10 operating system. The programming language used is Python, version 3.8, with the Python Integrated Development Environment (IDE) being PyCharm 2020. The virtual environment was built using Anaconda 4.10.1. The training and prediction processes were carried out using TensorFlow 2.3. The main parameters of the simulations are listed in

Table 2. Experimental parameter.

Parameter	Value	Parameter	Value
$o_{v,k}$	[0.5, 1] Mb	${\rho }_{los}$	−80 dBm [30]
$H_v$	−80 dBm	$\epsilon$	2 [31]
$p_{ES}$	40 W [31]	$f_v$	[1, 2] Ghz [30]
$H_{ES}$	100 MB	$B_{ES}^{down}$	1000 Mhz
$p_u$	0.2 w	$B_u^{down}$	−10 Mhz
$H_u$	80 MB	$N_0$	−114 dBm [30]
$f_{uav}$	[6, 8] Ghz [30]	$B$	30 Mhz [30]
${\omega }_{v,k}$	[10, 1000] cycles/bit [30]	$p_v$	1.3 w

.

In the proposed JOTMAP-SAC algorithm, both the actor and critic networks are based on a multi-layer perceptron (MLP) structure. Each network consists of 2 hidden layers, with each hidden layer having 256 units. The activation function used in the hidden layers is ReLU, while the output layers of both the actor and critic networks do not use any activation function.

6.2. Benchmark Algorithms

(1)

A DQN-based joint optimization of task migration and power allocation algorithm (JOTMAP-DQN): This algorithm utilizes Deep Q-Network (DQN) to make migration decisions and determine power allocation strategies within a single time slot. By combining Q-learning with deep neural networks, DQN allows the agent to learn optimal policies based on the current state, which is crucial in dynamic environments like UAV-assisted vehicular networks. The deep neural network is employed to approximate the Q-function, representing the expected future rewards for a given state-action pair, facilitating efficient decision-making within the constraints of a single time slot [32].

(2)

A DDPG-based joint optimization of task migration and power allocation algorithm (JOTMAP-DDPG): This algorithm utilizes Deep Deterministic Policy Gradient (DDPG), based on the Actor-Critic architecture, to make migration and power allocation decisions. By combining deep learning with the policy gradient method, DDPG efficiently handles continuous action spaces, enabling real-time decision-making in UAV-assisted vehicular networks within a single time slot [33].

(3)

Task Migration Optimization with Fixed Power Allocation based on SAC (OTMFPA-SAC): This algorithm assigns a fixed power value to the UAV. When there are vehicular tasks that cannot be processed at the local node, a portion of these tasks will be migrated to edge nodes for execution based on optimal migration decisions.

(4)

Power Allocation Optimization with Full Task Migration and based on SAC (OFTMPA-SAC): This algorithm migrates all tasks to edge nodes. For the tasks that are migrated to the UAV, we implement an optimal power allocation decision to ensure that all tasks are processed at the edge nodes.

6.3. Metrics

In the experiments, the following metrics are used: reward, total UAV energy consumption, total task delay, and average migration delay. The reward represents the negative sum of the total task processing delay and total UAV energy consumption. Total UAV energy consumption includes the energy used by the UAV for both communication and computation. Total task delay refers to the average latency for processing all tasks. The average migration delay is the combined communication and computation delay incurred when migrating a task to an edge node.

6.4. Numerical Results

In the validation experiments, the number of vehicles, step size, computational task size, and UAV computing frequency are set to 20, 10 G, (100, 300) KB, and (6, 8) GHz [29,34,35].

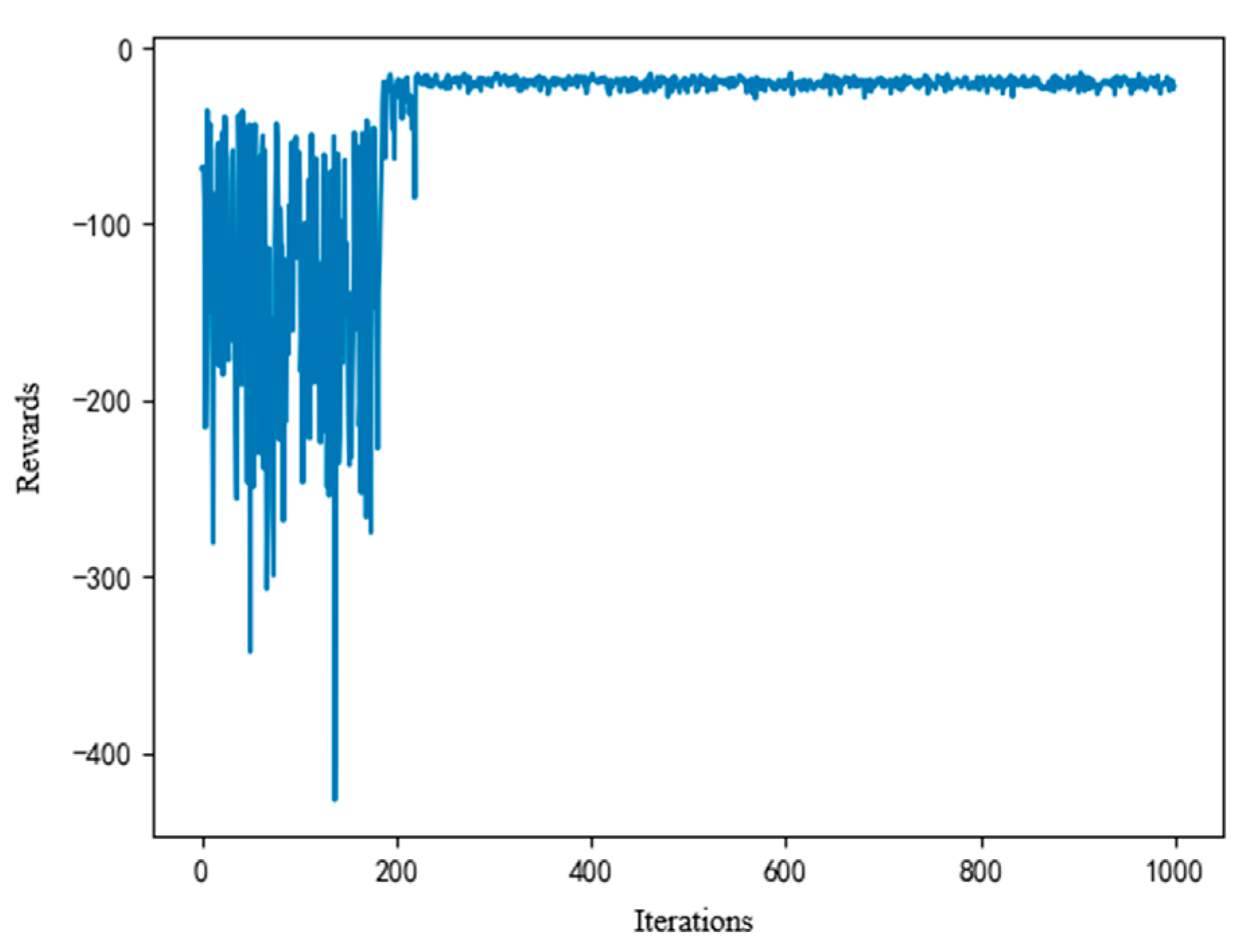
(1)

Feasibility of JOTMAP-SAC Algorithm

The convergence of the proposed algorithm is shown in Figure 4. As the number of iterations increases, the algorithm progressively converges, and the parameters approach the global optimum, allowing for the determination of the optimal migration and power allocation strategies.

(2)

The impact of the number of vehicles on the experimental results

To discuss the impact of the number of vehicles on the performance of the joint optimization algorithm for task migration and power allocation based on SAC, the change curve of reward of completing all tasks in different vehicles numbers (5, 10, 15, 20, 25) is represented in Figure 5.

As shown in Figure 5, with the increasing number of vehicles, the total UAV energy consumption, total task delay, and average migration delay tend to rise, while the reward curve declines. This is because as the number of vehicles grows, the number of tasks requiring processing also increases. Due to the limited computing capacity of the UAVs, some tasks cannot be executed at the initial node and must be offloaded to edge nodes. In cases where tasks cannot be processed locally, they are migrated to edge nodes to ensure the continuity of vehicular services.

From Figure 5, the JOTMAP-SAC algorithm performance is the best. Since the DQN algorithm is designed for discrete action spaces, while DDPG is suitable for continuous action spaces, it is important to note that DDPG can suffer from stability issues and may easily converge to a local optimum. The OFTMPA-SAC algorithm performs poorly due to complete task migration; it can lead to imbalanced resource allocation. Additionally, the OTMFPA-SAC algorithm faces challenges with its fixed power allocation strategy, which fails to adapt to fluctuations in vehicle numbers, resulting in suboptimal resource distribution and task scheduling in varying environments.

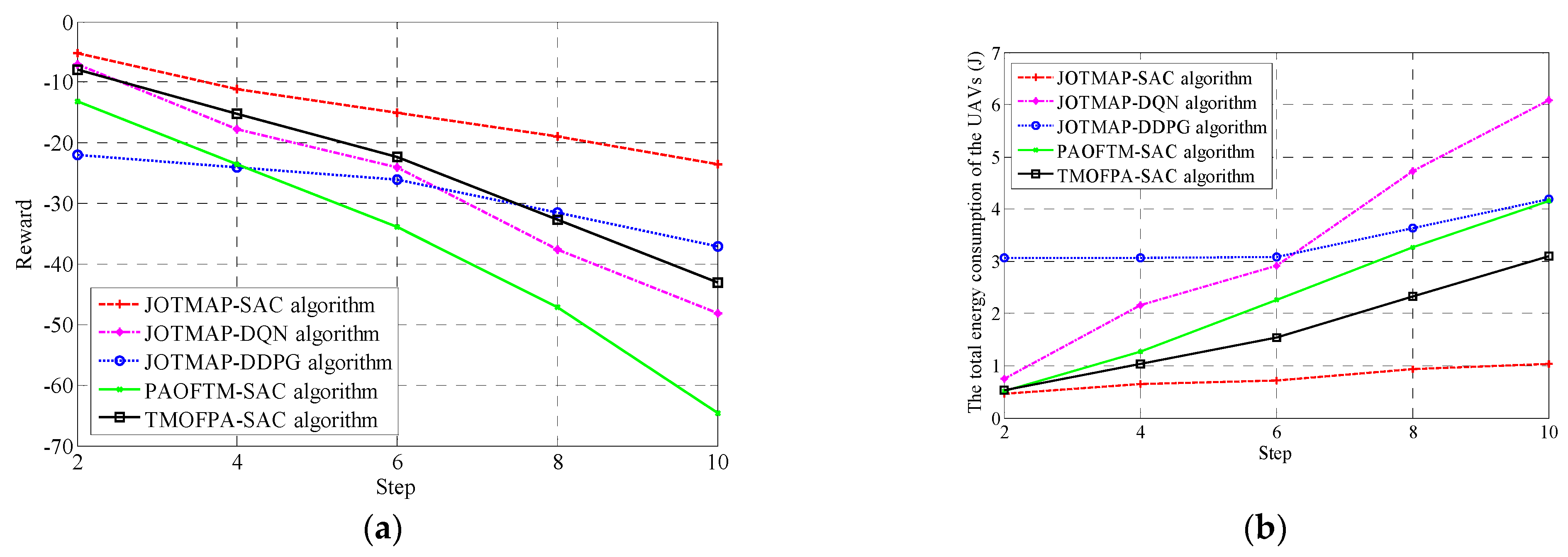
(3)

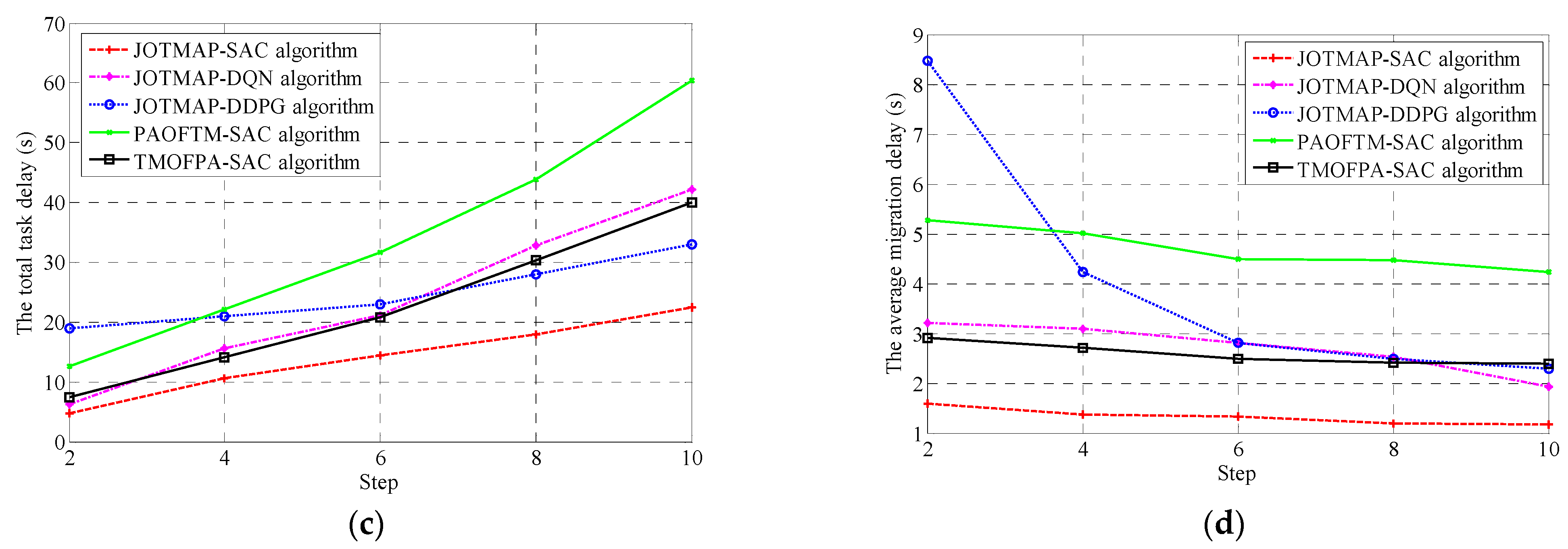
The impact of the step size on the experimental results

To analyze the impact of the step size on algorithm performance, the step sizes were set sequentially to 2, 4, 6, 8, and 10. The number of vehicles was set to 20, the computing task size was set to (100, 300) KB, and the computing frequency of the UAV was set to (6, 8) GHz. The experimental results are shown in Figure 6.

As shown in Figure 6, as the number of vehicles increases, total UAV energy consumption, total task delay, and average migration delay tend to rise, while the reward curve decreases. This is because the growing number of vehicles leads to an increase in the number of tasks requiring processing. Due to the limited computing capacity of UAVs, some tasks cannot be executed at the initial node and must be offloaded to edge nodes. To ensure the continuity of vehicular services, tasks that cannot be processed locally are migrated to edge nodes.

From Figure 6, it is clear that the JOTMAP-SAC algorithm performance is the best. This is because the DQN algorithm is applicable to discrete action space and DDPG is only suitable for continuous action space. In addition, DDPG is not stable, and may obtain the local optimal solution easily. The OFTMPA-SAC algorithm performs poorly due to complete task migration; it can lead to imbalanced resource allocation. Additionally, the OTMFPA-SAC algorithm faces challenges with its fixed power allocation strategy, which fails to adapt to fluctuations in vehicle numbers, resulting in suboptimal resource distribution and task scheduling in varying environments.

(4)

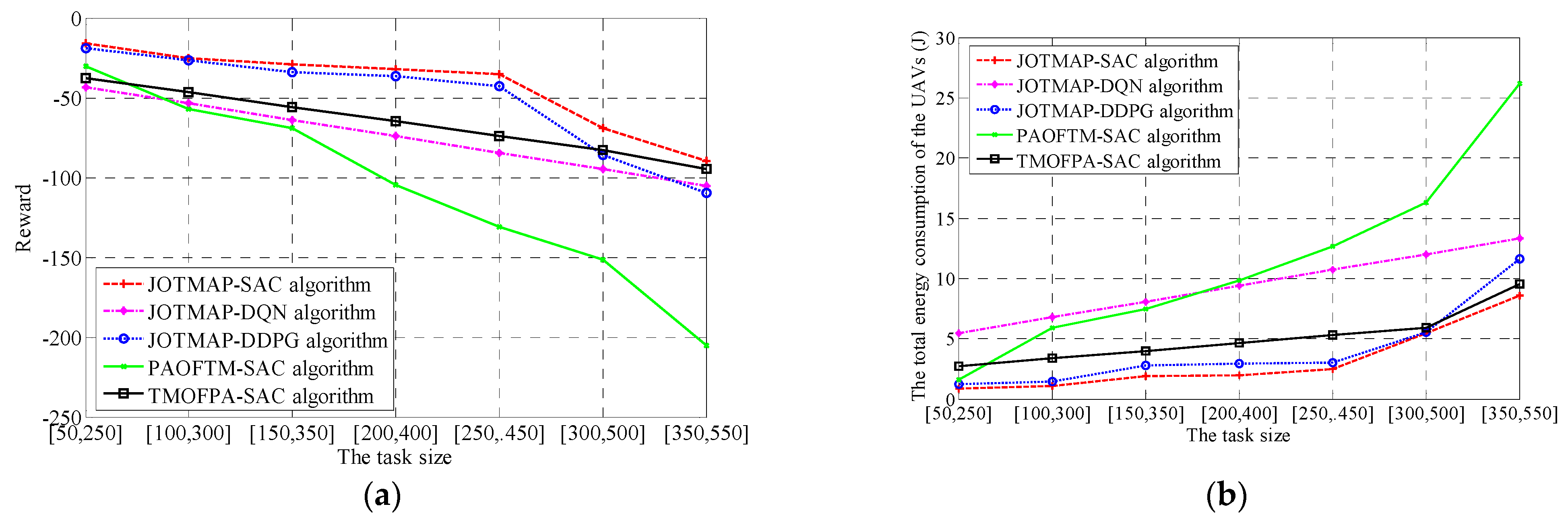
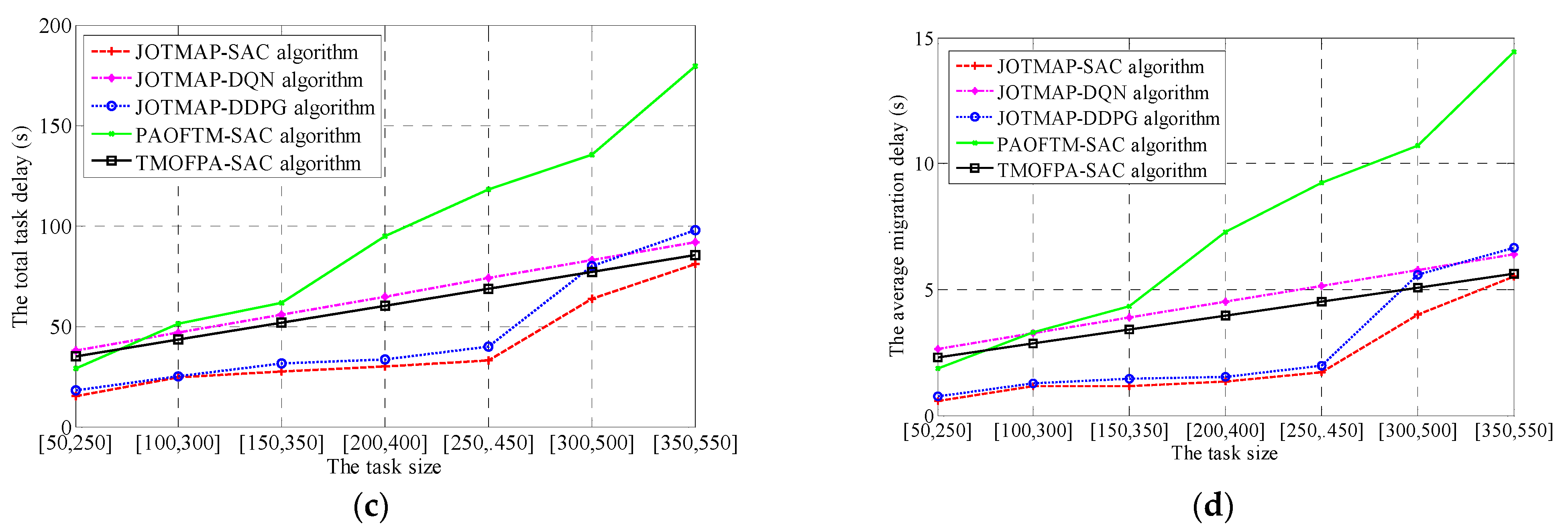
The impact of the task size on the experimental results

Figure 7 shows the impact of different task sizes on algorithm performance. The computational task sizes are sequentially set to (50, 250) KB, (100, 300) KB, (150, 350) KB, (200, 400) KB, (250, 450) KB, (300, 500) KB, and (350, 550) KB. Simultaneously, the step size is fixed at 10, the number of vehicles is set to 20, and the UAV’s computing frequency is configured to (6, 8) GHz.

As shown in Figure 7, we observe that as the task size increases, the total UAV energy consumption, total task delay, and average migration delay rise, while the reward shows a downward trend. This is primarily due to the increasing task size, which causes the nodes to struggle with processing tasks within a short time, given the limited computing capacities of the edge nodes. To maintain the continuity of vehicular task services, tasks that cannot be processed locally are migrated to edge nodes.

From Figure 7, it is evident that the JOTMAP-SAC algorithm consistently outperforms other algorithms, achieving the lowest average processing latency and energy consumption. The DDPG algorithm, which is designed for continuous action spaces, faces challenges in convergence, training instability, and adapting to various environments, whereas DQN is limited to discrete action spaces. In comparison, the JOTMAP-SAC algorithm demonstrates superior performance, with better convergence and stability.

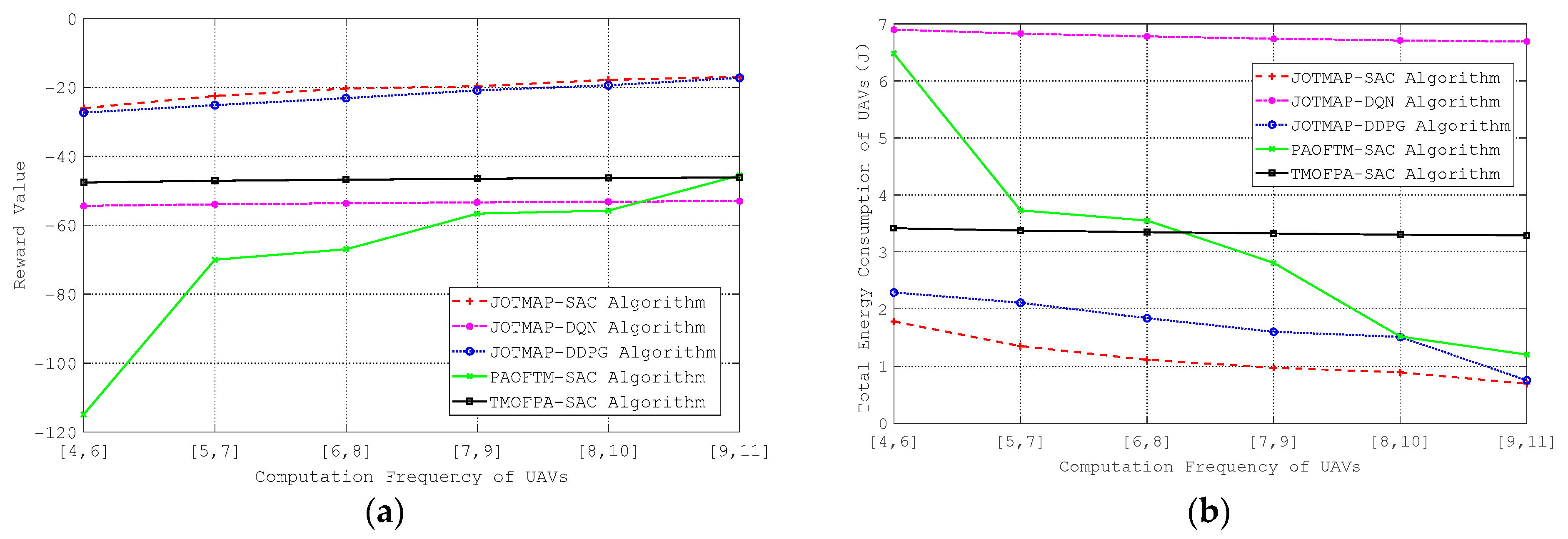
(5)

The impact of the UAVs computing frequency on the experimental results

Figure 8 demonstrates the impact of UAV local computing resources on algorithm performance. The UAV’s computing frequency is sequentially set to (4, 6) GHz, (5, 7) GHz, (6, 8) GHz, (7, 9) GHz, (8, 10) GHz, and (9, 11) GHz. The number of vehicles is fixed at 20, the computational task size is set to (100, 300) KB, and the step size is fixed at 10.

As the computing frequency of UAVs increases, the total UAV energy consumption, total task delay, and average migration delay gradually decrease, while the reward curve, defined as the negative sum of task delays, gradually increases. This is due to the improved computing resources, which increase the computing frequency of the nodes. As a result, tasks can be processed more efficiently by the associated UAVs, enhancing execution efficiency.

Furthermore, compared to other algorithms, the superiority of the proposed JOTMAP-SAC algorithm is evident. The primary advantage lies in the entropy-based approach and the use of double Q-networks, which enable the algorithm to achieve a more reliable global optimal solution than DDPG. Additionally, while DQN is restricted to discrete problems, the JOTMAP-SAC algorithm can handle both discrete and continuous problems effectively.

7. Discussion

In this paper, we propose a UAV-assisted MEC system designed to ensure coverage for vehicles in scenarios where infrastructures are limited or absent. When the onboard computing resources of vehicles are insufficient to handle certain tasks, the system facilitates task migration to nearby UAVs or edge servers within the coverage area. However, due to the dynamic nature of vehicle movements, it is challenging to guarantee that tasks will be completed before the vehicle exits the coverage area of the current edge node. As a result, we must assess whether tasks should be migrated to other edge nodes for continued processing or transferred after completion at the current node. We introduce the JOTMAP-SAC algorithm as a solution for optimizing task migration and resource allocation in UAV-assisted IoV systems. Although this algorithm demonstrates potential in reducing latency and energy consumption, several challenges remain. These include issues of scalability in large-scale systems, the complexity of real-world deployment, high computational demands, and battery constraints of UAVs.

The reward values decrease as the number of vehicles increases or as task sizes grow larger. This is due to the increased number of tasks requiring processing, which the UAVs cannot fully handle due to their limited computing capacity. Consequently, tasks must be migrated to edge nodes, resulting in higher delays and energy consumption. The JOTMAP-SAC algorithm excels here due to its ability to balance task migration and power allocation. By optimizing both, it achieves better performance and rewards. The SAC algorithm uses an entropy-based approach and a double Q-network that helps to stabilize the learning process and find the global optimum solution. This allows it to better manage task offloading and power distribution, reducing unnecessary migrations and ensuring more efficient processing. In contrast, the JOTMAP-DQN algorithm struggles with scalability due to its discrete action space, which limits its ability to adjust quickly to dynamic task migration requirements. The JOTMAP-DDPG algorithm, while suited for continuous spaces, faces stability challenges, particularly when the number of vehicles increases, making it less effective in adapting to the dynamic nature of task migration and power reallocation.

As the number of vehicles increases, total UAV energy consumption rises due to more frequent task migrations and power reallocation decisions. JOTMAP-SAC algorithm minimizes energy consumption by efficiently distributing power and offloading tasks to the edge nodes only when necessary. It adapts to fluctuations in vehicle numbers and computational demand, ensuring that energy usage is optimized. Both JOTMAP-DQN algorithm and JOTMAP-DDPG algorithm consume more energy as they are less efficient in managing task migrations and power allocation. JOTMAP-DQN algorithm discrete action space makes it inefficient at handling continuous power adjustments, while JOTMAP-DDPG algorithm suffers from instability, leading to suboptimal power distribution and frequent task offloading, which increases overall energy use.

As task size and the number of vehicles grow, total task latency increases across all algorithms, since larger tasks and more vehicles lead to more frequent task migrations. However, the JOTMAP-SAC algorithm shows the lowest task latency due to its optimized approach to task migration and power allocation. By continuously updating the power and migration strategies, it ensures tasks are processed in a timely manner, minimizing delays. In comparison, the JOTMAP-DQN algorithm experiences slower task processing times as it is less effective at managing the increased complexity of task migrations. JOTMAP-DDPG algorithm also faces delays due to challenges with power allocation and frequent task offloading, which prolongs task execution.

The average migration latency increases as the number of vehicles or task size grows. The JOTMAP-SAC algorithm handles this well by carefully balancing task offloading and power distribution. Its stable learning process allows for faster decision-making, which reduces the migration delay. In contrast, the JOTMAP-DQN algorithm experiences higher migration delays because it struggles with adapting to continuous changes in the environment and cannot efficiently manage task migration in a dynamic system. Similarly, the JOTMAP-DDPG algorithm may suffer from instability, resulting in slower migration decisions and higher average migration latency compared to the JOTMAP-SAC algorithm.

In this section, we compare the performance of two algorithms: the JOTMAP-DQN algorithm and the JOTMAP-DDPG algorithm. We analyze the impact of key parameters, including the number of vehicles, step size, task size, UAV computation frequency, UAV battery lifetime, and vehicle dynamics, on the performance of both algorithms.

Number of vehicles: As the number of vehicles increases, the system’s complexity grows, making it harder for algorithms to handle large state-action spaces. JOTMAP-SAC algorithm is particularly well-suited for such environments because it efficiently balances exploration and exploitation, which allows it to adapt more effectively in large, dynamic systems. While the JOTMAP-DQN algorithm and the JOTMAP-DDPG algorithm may struggle with increased computational demands and decision-making complexity, the JOTMAP-SAC algorithm is designed to handle such challenges with improved stability and faster convergence in large-scale systems. When the number of vehicles is small, the environment becomes simpler, with fewer interactions and task migrations. The JOTMAP-DQN algorithm benefits from this reduced complexity, as the smaller state space allows it to learn Q-values more quickly and efficiently. The JOTMAP-DDPG algorithm also performs well in this case because the reduced computational burden allows for more efficient decision-making. However, in such simple scenarios, both algorithms may lack sufficient challenges, which means their scalability and performance in larger, more complex systems may not be fully tested.

Step size: The JOTMAP-SAC algorithm offers greater stability compared to the JOTMAP-DQN algorithm and the JOTMAP-DDPG algorithm when adjusting the step size. A small step size leads to slow adaptation in the JOTMAP-DQN algorithm and the JOTMAP-DDPG algorithm. Despite this, the JOTMAP-SAC algorithm can still maintain stable learning and gradual policy updates, avoiding the instability that large step sizes introduce in both other algorithms. This makes the JOTMAP-SAC algorithm a better choice when there is a need for controlled learning. A large step size accelerates learning but can cause instability. For the JOTMAP-DQN algorithm, large step sizes lead to erratic Q-value updates, making the agent prone to incorrect decisions and suboptimal performance. The JOTMAP-DDPG algorithm also faces instability with large step sizes, causing rapid fluctuations in policy updates, which can negatively impact task migration and power allocation decisions.

Task size: When task size increases, the computational load on the UAV grows, and more frequent task migrations are required. The JOTMAP-SAC algorithm handles larger tasks more effectively than the JOTMAP-DQN algorithm and the JOTMAP-DDPG algorithm because it leverages continuous action spaces to make smoother decisions for task migration and power allocation. The JOTMAP-DQN algorithm struggles with larger state-action spaces, while the JOTMAP-DDPG algorithm can become inefficient due to the frequent need for power reallocation. The JOTMAP-SAC algorithm, on the other hand, maintains performance by optimizing both the policy and the value functions simultaneously, which allows it to adapt better in more complex settings. When the task size is small, the computational load on the UAV is reduced, and the decision-making process becomes simpler. The JOTMAP-DQN algorithm can efficiently learn and update Q-values, and the JOTMAP-DDPG algorithm faces fewer migration decisions, leading to faster and more efficient performance. However, the environment may not be complex enough to challenge the algorithms’ full potential, making them less likely to optimize well for more complex tasks.

Computation frequency: A higher UAV computation frequency accelerates decision-making but can lead to faster battery depletion. The JOTMAP-SAC algorithm benefits from higher computation frequencies without the instability seen in the JOTMAP-DDPG algorithm, which may exhaust its battery too quickly under similar conditions. Moreover, SAC’s ability to balance exploration and exploitation helps mitigate the risk of rapid overfitting and instability in environments with frequent updates, whereas the JOTMAP-DQN algorithm may experience overestimation of Q-values with too many rapid updates. When the UAV’s computation frequency is low, both algorithms struggle with slow decision-making and learning. The JOTMAP-DQN algorithm updates Q-values more slowly, which leads to inefficient learning and delayed responses. The JOTMAP-DDPG algorithm suffers similarly, as low computation frequency makes it harder to update its policy in a timely manner, negatively affecting its real-time decision-making capabilities.

Battery lifetime: When battery lifetime is short, both the JOTMAP-DQN algorithm and then JOTMAP-DDPG algorithm can struggle with frequent task migrations or power reallocation decisions, leading to inefficiencies. The JOTMAP-SAC algorithm, with its continuous action space and stable learning, is better equipped to make optimized decisions regarding task migration and power distribution, even with limited resources. The JOTMAP-SAC algorithm can focus on long-term rewards, which helps extend the UAV’s operational life by reducing unnecessary task migrations and minimizing power wastage. Longer battery life allows for extended task processing and more opportunities for both algorithms to learn and make decisions. With longer battery life, the JOTMAP-DQN algorithm benefits from more time to update Q-values and optimize decision-making. The JOTMAP-DDPG algorithm also performs better, as it can make better-informed decisions regarding task migration and power allocation over a longer period, improving performance and efficiency.

The JOTMAP-SAC algorithm excels in handling complex, dynamic environments due to its efficient use of continuous action spaces, stability during learning, and ability to balance exploration and exploitation. While the JOTMAP-DQN algorithm and the JOTMAP-DDPG algorithm have their strengths in specific contexts, the JOTMAP-SAC algorithm is better suited for real-time decision-making in high-complexity scenarios, where both computational efficiency and effective resource utilization are critical.

8. Conclusions

In this work, to provide and ensure real-time, efficient processing for IoV devices, we establish a flexible and widely covered UAV-assisted vehicular network system. This system optimizes the UAV’s power allocation and task migration strategy, formulating an optimization problem aimed at minimizing total task delay and energy consumption. In this context, we propose a SAC-based joint optimization strategy for task migration and power allocation in UAV-assisted vehicular networks. The strategy effectively optimizes system resource utilization and overall performance while considering constraints such as UAV battery levels and communication bandwidth. By offloading computation-intensive tasks from UAVs to edge servers and comparing with other algorithms, we significantly improve computational efficiency and reduce energy consumption. Through reasonable power allocation and task migration strategies, we optimize communication quality and ensure the continuity and stability of network coverage. In future work, we will consider additional efficient analysis of parameters such as battery lifetime, vehicle dynamics, and the limited computing capacity of edge nodes on the proposed algorithm performance. We also plan to test the performance of the proposed algorithm in real-world scenarios.