Cooperative Path Planning for Multi-UAVs with Time-Varying Communication and Energy Consumption Constraints

Abstract

In the field of Unmanned Aerial Vehicle (UAV) path planning, designing efficient, safe, and feasible trajectories in complex, dynamic environments poses substantial challenges. Traditional optimization methods often struggle to address the multidimensional nature of these problems, particularly when considering constraints like obstacle avoidance, energy efficiency, and real-time responsiveness. In this paper, we propose a novel algorithm, Dimensional Learning Strategy and Spherical Motion-based Particle Swarm Optimization (DLS-SMPSO), specifically designed to handle the unique constraints and requirements of cooperative path planning for Multiple UAVs (Multi-UAVs). By encoding particle positions as motion paths in spherical coordinates, the algorithm offers a natural and effective approach to navigating multidimensional search spaces. The incorporation of a Dimensional Learning Strategy (DLS) enhances performance by minimizing particle oscillations and allowing each particle to learn valuable information from the global best solution on a dimension-by-dimension basis. Extensive simulations validate the effectiveness of the DLS-SMPSO algorithm, demonstrating its capability to consistently generate optimal paths. The proposed algorithm outperforms other metaheuristic optimization algorithms, achieving a feasibility ratio as high as 97%. The proposed solution is scalable, adaptable, and suitable for real-time implementation, making it an excellent choice for a broad range of cooperative multi-UAV applications.

1. Introduction

Unmanned Aerial Vehicles (UAVs) have become increasingly prevalent in a variety of applications, ranging from environmental monitoring [1] and agricultural surveillance [2] to search and rescue operations [3] and military missions [4]. The ability to deploy multi-UAVs in a coordinated manner significantly enhances the efficiency and effectiveness of these missions. However, the complexity of ensuring cooperation among multi-UAVs introduces several challenges, particularly in terms of path planning [5,6,7] and maintaining reliable communication [8].

In dynamic and unpredictable environments, the communication links between UAVs can fluctuate significantly due to factors such as obstacles, interference, and the mobility of the UAVs themselves. These time-varying communication [9] constraints present a major challenge for effective path planning, as UAVs must continuously adapt their trajectories to maintain connectivity while still accomplishing their mission objectives. Research on communication constraints in multi-UAV systems has primarily focused on ensuring reliable data exchange [10] and maintaining network connectivity [11]. Techniques such as relay placement [12] and network topology optimization [13] have been explored to enhance communication reliability. However, these methods often assume static or predictable environments, which is not always the case in real-world applications. Several studies have proposed integrating communication models with path planning algorithms [14,15,16] to address time-varying communication constraints. These approaches generally involve real-time evaluation of communication link quality and dynamic adjustments to UAV paths to ensure continuous connectivity. However, despite these advancements, there is still a need for more robust and adaptive methods capable of addressing the complexities of real-time, dynamic environments.

The field of cooperative path planning for multi-UAV systems has been widely explored, with numerous approaches developed to tackle various facets of the problem. Traditional methods like A* and Dijkstra’s algorithms have been commonly applied to path planning in static environments [17], but they struggle to perform effectively in dynamic settings where time-varying constraints play a significant role. More recent methods have employed heuristic and metaheuristic approaches, including Genetic Algorithms (GA) [18,19], Ant Colony Optimization (ACO) [20,21,22], Grey Wolf Optimizer (GWO) [23,24,25], and Artificial Bee Colony (ABC) [26,27,28] to enhance path planning capabilities under dynamic conditions. Particle Swarm Optimization (PSO) [29,30,31,32] has emerged as a powerful tool for optimization problems, including path planning for UAVs. Its capability to discover near-optimal solutions in complex search spaces makes it well-suited for multi-UAV path planning [33]. However, the standard PSO algorithm lacks the intrinsic ability to manage communication constraints, which are crucial for the coordination and effective operation of UAVs in collaborative missions.

Traditional path-planning algorithms often struggle to address the complexities of time-varying communication constraints, highlighting the need for advanced methods that can handle dynamic network conditions [34] while ensuring robust communication among UAVs. PSO [35], a nature-inspired optimization technique, has demonstrated considerable potential in path planning applications due to its simplicity and effectiveness in navigating complex search spaces. However, standard PSO algorithms require modifications to adequately handle the challenges posed by time-varying communication constraints in multi-UAV systems, ensuring both connectivity and optimal path planning.

To tackle these challenges, various enhanced PSO variants have been developed. These improvements generally fall into several key areas: adaptive parameter control, hybridization with other optimization techniques, the introduction of multi-swarm or cooperative strategies, and the incorporation of novel operators. Ref. [36] presents an Adaptive Quantum-behaved PSO (AQPSO) algorithm, which is applied to UAV path planning tasks, demonstrating notable improvements in both convergence speed and solution quality. Ref. [37] introduces a Cooperative Multiple Swarm PSO (CMSPSO) method, integrating traditional PSO with a cooperative strategy among multiple swarms, resulting in enhanced convergence efficiency and superior solution quality for UAV path planning applications. Ref. [38] proposes an Adaptive Mutation PSO (AMPSO) algorithm, which integrates mutation operators to prevent premature convergence and improve solution diversity, particularly in challenging UAV path planning scenarios. Ref. [39] introduces a Chaotic PSO (CPSO), incorporating chaos theory into the standard PSO algorithm, thereby enhancing global search capabilities and avoiding local minima in UAV path optimization. Ref. [40] proposes a Multi-Objective PSO (MOPSO) approach specifically tailored for UAV path planning, efficiently optimizing multiple conflicting objectives. Meanwhile, Ref. [41] presents a Quantum-behaved PSO (QPSO) algorithm designed for dynamic environments. By incorporating quantum mechanics principles, QPSO significantly enhances the swarm’s exploration capabilities, leading to more robust and adaptive path planning under uncertain and fluctuating conditions. Ref. [42] investigates the application of Angle-encoded PSO (APSO) for optimizing UAV deployment in search and rescue missions. This approach encodes the search area using angular parameters, allowing UAVs to swiftly adjust their search patterns in response to changing environmental conditions, which enhances the efficiency and speed of rescue operations. Additionally, Ref. [43] introduces a hybrid PSO-GA method designed to optimize the coverage and connectivity of UAV ad hoc networks. By combining the strengths of PSO and GA, this hybrid algorithm improves network performance, specifically in terms of coverage and communication latency. Refs. [44,45,46] combine different metaheuristic algorithms to enhance performance in UAV path planning. The above UAV path planning algorithm is summarized as shown in

Table 1. The classification of UAV path planning algorithms.

Algorithms	Example
Heuristic	$A^{\ast }$, Dijkstra’s, and so on
Metaheuristic	GA, ACO, PSO, ABC, GWO, and so on
Hybrid Metaheuristic	PSO-GA, PSO-GWO, and so on
PSO variants	AQPSO, CMSPSO, AMPSO, CPSO, MOPSO, and so on

.

To address the challenge of multi-UAV collaborative path planning under communication constraints, Ref. [47] proposed the Comprehensive Learning and Dynamic Multi-swarm PSO (CL-DMSPSO) algorithm. This approach facilitates the effective planning of high-quality paths for UAVs, ensuring optimized performance in constrained environments. However, it primarily addresses communication constraints alone. In real-world UAV missions, communication and energy consumption constraints are often interdependent. For instance, maintaining stable communication may require the UAV to follow a path that increases energy consumption, while conserving energy might force the UAV to operate in areas with weaker communication links.

Thus, an effective path-planning algorithm must strike a balance between these constraints, optimizing both communication reliability and energy efficiency. Given the limitations in communication and energy consumption, certain UAVs may be unable to independently perform path planning. Consequently, effective coordination among all UAVs becomes crucial in the path-planning process. In this paper, we introduce the DLS-SMPSO algorithm, specifically designed for cooperative path planning in multi-UAV systems with time-varying communication and energy consumption constraints. The DLS-SMPSO algorithm tackles the complex challenges of UAV path planning by encoding each particle’s position as a motion path in spherical coordinates, enabling efficient exploration of the search space. By incorporating a DLS into velocity updates, the algorithm minimizes oscillations, allowing particles to learn from the global best solution dimension by dimension. Simulation results validate the algorithm’s feasibility and effectiveness, showcasing its superior performance in handling these constraints.

The key contributions of our work are outlined as follows:

(1) A novel DLS-SMPSO algorithm is proposed to address the challenges of collaborative path planning for multi-UAVs. By simply adjusting the angles in spherical coordinates, the particle’s orientation can be modified directly without the need to decompose these changes into cartesian components. As a result, the DLS-SMPSO algorithm can explore the search space more naturally, facilitating smoother transitions and more precise adjustments in particle positions.

(2) In the DLS-SMPSO algorithm, particle positions are encoded as motion paths using spherical coordinates, rather than the conventional cartesian coordinates employed in standard PSO. This spherical encoding is particularly advantageous for UAV path planning, as it allows for more intuitive and direct manipulation of trajectories, resulting in more efficient optimization and improved path generation.

(3) The integration of DLS minimizes particle oscillation during the evolutionary process by enabling each particle to learn from the global best solution in a dimension-by-dimension manner. This strategy helps prevent premature stagnation, leading to a more stable and efficient optimization process. In addition, the algorithm seamlessly incorporates constraint handling mechanisms, such as obstacle avoidance and boundary enforcement, within the optimization process. This guarantees that the generated solutions are not only optimal but also feasible and safe for practical real-world applications.

The rest of this paper is organized as follows: Section 2 offers a comprehensive overview of the multi-UAV path planning problem formulation and reviews related work on objective function design. Section 3 introduces the PSO variant algorithms and details the proposed DLS-SMPSO approach. Section 4 presents the simulation setup and results, demonstrating the effectiveness of our approach. Finally, Section 5 concludes the paper and outlines potential directions for future research.

2. Problem Formulation

In this section, we begin by outlining the cooperative path planning problem for multi-UAVs, incorporating various essential constraints in Section 2.1. Following that, we provide a detailed explanation of the path representation in Section 2.2. Building on this foundation, we formulate the objective function for the specified path planning problem in Section 2.3.

2.1. Problem Description

The UAV path planning problem involves determining optimal paths for n UAVs, each starting from a specific location and aiming to reach Unmanned Ground Vehicle 0 (UGV0). The goal is to minimize various factors such as path length, energy consumption, and collision risks while ensuring that the paths are feasible within the UAV’s kinematic and dynamic constraints. Additionally, the paths must avoid both static and dynamic obstacles in the environment. In more detail, the UAV path planning problem entails finding the most efficient trajectories for five UAVs to travel from their respective starting points to UGV0. The cost function to be minimized typically includes critical aspects such as total distance traveled, energy consumption, and the risk of collisions with obstacles or other UAVs. The planned paths must adhere to each UAV’s physical limitations, including speed, acceleration, and turning radius, ensuring that the maneuvers are both possible and safe. Obstacle avoidance plays a central role, requiring the UAVs to navigate around static obstacles like buildings and trees, as well as dynamic obstacles such as other moving UAVs or changing environmental factors. The problem also demands consideration of communication constraints [9,48], especially in scenarios where UAVs must maintain connectivity with ground stations or other UAVs. Ultimately, the challenge lies in balancing these multiple objectives achieving paths that are not only optimal in terms of minimizing costs but also robust, feasible, and safe for real-world operations.

The path planning problem for multi-UAV systems can be defined as determining the optimal routes for a fleet of UAVs to travel from their respective starting points to UGV0. These routes must minimize specific cost functions while satisfying constraints such as obstacle avoidance, communication range, and the UAV’s dynamic capabilities.

(1) The UAV must avoid collision obstacles in the environment.

(2) The UAV’s path must adhere to its turning angle constraints to ensure feasible and safe flight.

(3) The UAV must maintain communication with a UGV0 or other UAVs, which may impose constraints on its path.

(4) The UAV’s path must minimize energy consumption to ensure that the mission can be completed within the available battery capacity.

2.2. Path Representation

In the context of multi-UAV path planning, where there are n UAVs and m waypoints, the path representation becomes a more complex but structured task. Each UAV’s trajectory is defined by a series of waypoints, where each waypoint represents a specific coordinate in 3D space.

For n UAVs, the paths can be represented as:

$$P_i=\left[\left(x_{i1},y_{i1},z_{i1}\right),\left(x_{i2},y_{i2},z_{i2}\right),\dots ,\left(x_{im},y_{im},z_{im}\right)\right]$$

(1)

where $i=1,2,\dots ,n$ denotes the UAV index, and $(x_{ij},y_{ij},z_{ij})$ denotes the j-th waypoint for the i-th UAV. Here, m represents the total number of waypoints that each UAV must navigate through from its starting position to UGV0.

The sequence of waypoints forms a trajectory that the UAV must follow from its start position to UGV0. The challenge lies in ensuring that these waypoints are chosen to minimize a predefined cost function in Equation (1) while satisfying the UAV’s operational constraints, avoiding obstacles, and coordinating with other UAVs to prevent collisions. For a UAV’s path to be considered feasible, it must meet several essential constraints. These include complying with the UAV’s kinematic and dynamic limits, such as maximum speed, acceleration, and turning radius. The path must also guarantee the safe avoidance of obstacles in the environment. Additionally, UAVs must maintain adequate separation to avoid mid-air collisions. The chosen waypoints should facilitate smooth transitions between different path segments, avoiding sharp turns or abrupt maneuvers that could compromise the UAV’s stability. Furthermore, the path must accommodate communication requirements, ensuring the UAVs remain within the necessary communication range to maintain control and receive mission updates. By satisfying these conditions, the planned paths will ensure safe, efficient, and successful mission execution.

2.3. Objective Function

The objective function in UAV path planning is a key mathematical tool that defines the mission’s goals, such as minimizing total path length, reducing energy consumption, and avoiding collisions with obstacles. It incorporates various criteria affecting the UAV’s performance, including kinematic and dynamic constraints, environmental terrain, and static obstacle avoidance. By optimizing this function, the path planning process aims to identify the most efficient and safe routes for all UAVs, ensuring they successfully reach UGV0 while meeting all mission-specific requirements.

In the cooperative path planning problem for multi-UAV systems with time-varying communication constraints, the objective function is crafted to optimize multiple criteria simultaneously. The aim is to determine a set of paths that minimize the overall mission cost while adhering to all constraints. Key factors include path length, safety, energy consumption, communication connectivity, turning angle limitations, and obstacle collision avoidance, ensuring that the mission is both efficient and feasible.

The objective function J can be formulated as a weighted sum of these criteria:

$$J=w_1{J}_{\mathrm{length}}+w_2{J}_{\mathrm{safety}}+w_3{J}_{\mathrm{energy}}+w_4{J}_{\mathrm{communication}}+w_5{J}_{\mathrm{turning}}+w_6{J}_{\mathrm{obstacle}}$$

(2)

where $w_1$, $w_2$, $w_3$, $w_4$, $w_5$, and $w_6$ are weighting factors that balance the relative importance of each criterion. Each component of the objective function is detailed below:

(1) Path length

The path length component aims to minimize the total distance traveled by all UAVs. It is defined as the sum of the lengths of the paths [31] of all UAVs:

$$J_{\mathrm{length}}=\sum _{i=1}^n\sum _{j=1}^{m_i-1}\sqrt{{\left(x_{i(j+1)}-x_{ij}\right)}^2+{\left(y_{i(j+1)}-y_{ij}\right)}^2+{\left(z_{i(j+1)}-z_{ij}\right)}^2}$$

(3)

where n is the number of UAVs, $m_i$ is the number of waypoints for UAV i, and $(x_{ij},y_{ij},z_{ij})$ are the coordinates of the j-th waypoint for UAV i.

The cost of path length Equation (3) in UAV path planning is a critical element of the overall Objective Function Value (OFV), which serves as a comprehensive measure for evaluating the efficiency and feasibility of a given path. The path length cost reflects the total distance a UAV must travel from its starting point to UGV0, passing through the necessary waypoints. A shorter path length typically results in reduced energy consumption, shorter travel times, and overall more efficient mission execution, which is especially important when UAVs have limited battery life or must operate within strict time constraints. However, focusing solely on path length may not yield the best solution, as other critical mission factors must also be considered. To account for this, the OFV often incorporates a penalty function alongside the path length cost. This penalty function adds terms that impose additional costs for violating specific constraints, such as proximity to obstacles, entering no-fly zones, or straying from predefined safe routes. For example, if a UAV’s path passes too close to a hazardous area or another UAV, the penalty function increases the OFV, discouraging such risky paths during the optimization process. By integrating the path length cost in Equation (3) and penalty functions, the objective function becomes more robust, guiding the path planning algorithm not only to minimize the distance traveled but also to adhere to safety, regulatory, and operational constraints. This approach ensures that the resulting paths are not only efficient but also safe and compliant with mission requirements. By balancing various factors, the optimization process delivers paths that are both effective and practical, enhancing the UAV’s overall performance in complex and dynamic environments.

(2) Safety

In UAV path planning, safety and feasibility constraints such as Equation (4) are paramount to ensuring secure and effective operations. Safety constraints include avoiding collisions with both static obstacles (e.g., buildings, trees) and dynamic obstacles (e.g., other UAVs and UGV0), adhering to no-fly zones, and maintaining altitude and speed within operational limits. Additionally, UAVs must monitor battery life to ensure mission completion and a safe return while remaining within the communication range of control systems. Feasibility constraints involve navigating diverse terrains, managing payload weight and size, adhering to airspace regulations and local laws, and ensuring that the path planning algorithm is computationally efficient and scalable. These constraints collectively guarantee that UAVs operate safely, efficiently, and in compliance with relevant regulations. This can be represented as [42]:

$$J_{\mathrm{safety}}=\sum _{i=1}^{n-1}\left(\mathbb{I}\left[v\left(m_i,m_i+1\right)<v_{min}\right]+\mathbb{I}\left[v\left(m_i,m_i+1\right)>v_{max}\right]\right.$$

$$\left.+\mathbb{I}\left[W_i>W_{max}\right]\right)$$

(4)

where $v\left(m_i,m_i+1\right)$ is the speed between waypoints $m_i$ and $m_i+1$. $v_{min}$ and $v_{max}$ are the minimum and maximum allowable speeds, respectively. $W_i$ is the weight of the UAV’s payload. $W_{max}$ is the maximum allowable payload weight.

(3) Energy consumption

Energy consumption is a critical factor in UAV path planning, particularly for missions requiring long endurance or operations in environments where recharging opportunities are limited. Several factors influence a UAV’s energy consumption, including path length, speed, altitude, and maneuvering requirements. Therefore, incorporating and minimizing energy consumption is essential in the objective function, as seen in Equation (5) of the UAV path planning problem. The energy consumption component aims to minimize the energy used by UAVs and can be approximated by the total distance traveled, changes in altitude, and the number of turns along the path. This ensures that the UAVs can complete their missions efficiently while conserving energy. It is defined as:

$$J_{\mathrm{energy}}=\sum _{i=1}^n\left(\sum _{j=1}^{m_i-1}\sqrt{{\left(x_{i(j+1)}-x_{ij}\right)}^2+{\left(y_{i(j+1)}-y_{ij}\right)}^2+{\left(z_{i(j+1)}-z_{ij}\right)}^2}\right.$$

$$\left.+\alpha \sum _{j=1}^{m_i-1}\left|z_{i(j+1)}-z_{ij}\right|+\beta \sum _{j=1}^{m_i-2}\left|{\theta }_{i(j+2)}-{\theta }_{i(j+1)}\right|\right)$$

(5)

where $\alpha$ and $\beta$ are weighting factors for altitude changes and turns, respectively, and ${\theta }_{ij}$ represents the heading angle at waypoint j for UAV i.

(4) Time-varying communication

Time-varying communication constraints in UAV path planning refer to the dynamic nature of communication between UAVs and between UAVs and UGV0. These constraints can fluctuate due to several factors, including environmental changes (such as obstacles or weather conditions), UAV positions, and varying network conditions. As UAVs navigate their paths, the quality of communication links may change [48], leading to periods of reliable communication interspersed with periods of limited or no communication. To ensure smooth operations, the path planning algorithm must account for these time-varying constraints by optimizing routes to maximize communication reliability, ensuring critical data are transmitted during periods of strong communication, as outlined in Equation (6). This often involves adjusting the UAV’s positions and flight paths to maintain connectivity while meeting the mission objectives and environmental challenges. The communication component of the path planning model penalizes paths where communication constraints are violated, ensuring that UAVs maintain stable links throughout their mission. It is defined as [9,49]:

$$J_{\mathrm{communication}}=\sum _{k=1}^T\sum _{i=1}^n\sum _{k=1,j\ne i}^n\left({\displaystyle \frac{1}{d_{ij}\left(k\right)-d_{max}}}·\mathbb{I}\left(d_{ij}\left(k\right)>d_{max}\right)\right)$$

(6)

where T is the total number of time steps, $d_{ij}\left(k\right)$ is the distance between UAV i and UAV j at time k, $d_{max}$ is the maximum allowable communication range, and $\mathbb{I}$ is the indicator function that is 1 if the condition is true and 0 otherwise.

(5) Turning angle limitation

The turning angle limitation is a critical constraint in UAV path planning, restricting the maximum angle at which a UAV can change its direction between consecutive waypoints, as expressed in Equation (7). This constraint ensures that UAV trajectories remain smooth and feasible, avoiding abrupt maneuvers that could compromise stability or lead to increased energy consumption. By integrating this limitation into the path planning algorithm, the resulting flight paths are more realistic and aligned with the UAV’s physical capabilities, enhancing both safety and overall mission performance. The turning angle limitation component penalizes large deviations in the heading angle between consecutive waypoints, ensuring UAVs avoid sharp turns that could be challenging to execute and potentially destabilizing. This can be represented as [33]:

$$J_{\mathrm{turning}}=\sum _{i=1}^n\sum _{j=1}^{m_i-2}{\left({\theta }_{i(j+1)}-{\theta }_{ij}\right)}^2$$

(7)

where ${\theta }_{ij}$ is the heading angle at waypoint j for UAV i. The objective is to minimize the sum of squared differences between consecutive heading angles.

(6) Obstacle collision avoidance

Each obstacle is represented as a predefined area or volume within the environment, and the UAV’s path must be designed to avoid entering these restricted zones. This constraint is typically enforced by calculating the minimum distance between the UAV and each obstacle at every point along its path, ensuring that this distance stays above a predetermined safety margin throughout the flight. This is achieved by defining each obstacle as a fixed region and imposing the condition that the UAV’s coordinates never fall within these regions, thereby maintaining a collision-free trajectory. Additionally, paths that come too close to obstacles are penalized, as described in Equation (8), ensuring safe navigation throughout the mission. This can be represented as [49]:

$$J_{\mathrm{obstacle}}=\sum _{i=1}^n\sum _{j=1}^{m_i}\left(\sum _{k=1,k\ne i}^n\sum _{l=1}^{m_k}{\displaystyle \frac{1}{{∥\left(x_{ij},y_{ij},z_{ij}\right)-\left(x_{kl},y_{kl},z_{kl}\right)∥}^2+ϵ}}\right.$$

$$\left.+\sum _{o=1}^O{\displaystyle \frac{1}{{∥\left(x_{ij},y_{ij},z_{ij}\right)-\left(x_o,y_o,z_o\right)∥}^2+ϵ}}\right)$$

(8)

where O is the number of obstacles, $(x_0,y_0,z_0)$ are the coordinates of the obstacles, and $ϵ$ is a small positive constant to avoid division by zero.

Equation (2) highlights several important aspects of the UAV path planning problem. It demonstrates that the problem is a multi-objective optimization task, where the overall objective function comprises multiple weighted cost terms, such as path length, energy consumption, collision risk, and turning angle limitations. Furthermore, the inclusion of penalty functions underscores that constraints like obstacle avoidance and UAV kinematic limitations are integrated into the optimization process. These penalties ensure that the generated paths are not only optimal concerning the objective function but also feasible and safe in real-world applications. Moreover, Equation (2) incorporates constraints such as obstacle avoidance and turning angle limitations via penalty functions, ensuring that the planned paths maintain both optimality and feasibility. The use of weighted sums enables flexibility in prioritizing different mission objectives, making the approach adaptable to real-world scenarios where multiple objectives and constraints must be addressed simultaneously.

3. UAV Path Planning Method

In this part, we first review the standard PSO and its variants, including ASPSO and QPSO, in Section 3.1, Section 3.2, Section 3.3. Then, we introduce a new DLS-SMPSO algorithm in Section 3.4. Finally, the detailed implementation of the path planning method using DLS-SMPSO is proposed in Section 3.5.

3.1. PSO Algorithm

The PSO Algorithm [50,51] is an optimization technique inspired by the social behavior of animals like birds flocking or fish schooling. In this algorithm, a swarm of particles, each representing a potential solution to an optimization problem, moves through the search space to find the best solution. Each particle through Equations (9) and (10) has a position vector $x_i\left(k\right)$ and a velocity vector $v_i\left(k\right)$, where i is the particle index and k is the iteration number. The movement of each particle is influenced by its own experience (personal best position $p_i\left(k\right)$) and the experience of the entire swarm (global best position $g\left(k\right)$).

The velocity of each particle is updated using the formula:

$$v_i(k+1)=\omega v_i\left(k\right)+c_1{r}_1·\left(p_i\left(k\right)-x_i\left(k\right)\right)+c_2{r}_2·\left(g\left(k\right)-x_i\left(k\right)\right)$$

(9)

where $\omega$ is the inertia weight that controls the influence of the previous velocity, balancing exploration and exploitation. $c_1$ and $c_2$ are cognitive and social coefficients that weigh the particle’s personal best position and the global best position, respectively. $r_1$ and $r_2$ are random numbers between 0 and 1, introducing stochastic variability.

The new position of each particle is then calculated by updating its current position with the new velocity:

$$x_i(k+1)=x_i\left(k\right)+v_i(k+1).$$

(10)

At each iteration, the fitness of the new position is evaluated. The personal best position $p_i(k+1)$ is updated if the current position $x_i(k+1)$ offers a better fitness value. Similarly, the global best position $g(k+1)$ is updated if any particle achieves a better fitness than the current global best.

3.2. APSO Algorithm

In APSO [42], each particle’s position and velocity are represented by an angle or a set of angles in Equations (11) and (12), rather than by cartesian coordinates or other conventional representations. The position of a particle is encoded as an angle ${\theta }_i$ within a certain range, typically between 0 and 2$\pi$. This angle can represent directions, phases, or any other cyclic variables. The velocity and position updates are conducted in angular space, which requires modifications to the standard PSO in Equations (9) and (10).

The velocity $v_i\left(k\right)$ in APSO is an angular velocity that determines how quickly and in which direction the particle’s angle ${\theta }_i\left(k\right)$ will change:

$$v_i(k+1)=\omega v_i\left(k\right)+c_1{r}_1·\left({\theta }_{pbest,i}-{\theta }_i\left(k\right)\right)+c_2{r}_2·\left({\theta }_{gbest}-{\theta }_i\left(k\right)\right)$$

(11)

$${\theta }_i(k+1)={\theta }_i\left(k\right)+v_i(k+1)$$

(12)

where ${\theta }_{pbest,i}$ is the angle corresponding to the personal best position, ${\theta }_{gbest}$ is the angle of the global best position, and $\omega$, $c_1$, $c_2$ are the inertia and acceleration coefficients as in standard PSO.

3.3. QPSO Algorithm

In QPSO [41], particles do not have fixed trajectories determined by velocity. Instead of being directly influenced by velocity and position updates, as in traditional PSO, each particle’s position in QPSO is governed by a probability distribution derived from quantum mechanics. This allows particles to have a probabilistic range of positions, enabling a broader and more diverse exploration of the search space. In QPSO, each particle is attracted to an “attractor” point, which is a combination of its personal best position and the global best position. This attractor guides the particle’s probabilistic position updates, allowing for more flexible and efficient searching within the solution space.

The attractor $P_i\left(k\right)$ for a particle i is typically defined as:

$$P_i\left(k\right)=[p_i\left(k\right)+g_i\left(k\right)]/2$$

(13)

where $p_i\left(k\right)$ is the personal best position of particle i at time k. $g_i\left(k\right)$ is the global best position at time k.

Instead of updating the velocity and position directly, QPSO updates the position using a random number generated from the particle’s probability distribution. The position of a particle $x_i(k+1)$ is updated according to:

$$x_i(k+1)=P_i\left(k\right)\pm \beta ·\left|m\left(k\right)-x_i\left(k\right)\right|·ln\left({\displaystyle \frac{1}{u}}\right)$$

(14)

where $m\left(k\right)$ is the mean best position of all particles at time k. $\beta$ is a parameter controlling the convergence speed. u is a uniformly distributed random number in the interval (0, 1). The ± sign indicates that the particle can move towards or away from the attractor, introducing exploration.

The mean best position $m\left(k\right)$ is calculated as:

$$m\left(k\right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N{p}_i\left(k\right)$$

(15)

where N is the number of particles in the swarm. This position helps determine the overall direction of the swarm’s movement. The particles evolve according to Equations (13)–(15) to converge to the optimal path.

3.4. The Proposed DLS-SMPSO Algorithm

The DLS-SMPSO algorithm extends the traditional PSO by encoding the position of each particle as a series of motion paths, with each path represented by a set of directional vectors. Specifically, if a path consists of waypoints $w_1,w_2,\dots ,w_n$, then the motion vector $V_k$ for the k-th segment of the path is defined as:

$$V_k=w_{k+1}-w_k$$

(16)

where $k=1,2,\dots ,n-1$. Each waypoint in the path is defined by spherical coordinates: $w_k=(r_k,{\theta }_k,{\varphi }_k)$. Radial distance from the origin $r_k\in (0,pat{h}_{length})$, azimuthal angle ${\theta }_k\in (-\pi ,\pi )$ in the xy-plane from the x-axis and polar angle ${\varphi }_k\in (-\pi /2,\pi )$ from the z-axis.

From Equation (16), one gets that

$$V_k=(\Delta r_k,\Delta {\theta }_k,\Delta {\varphi }_k).$$

(17)

According to Equation (17), we can deduce velocity update Equations (18)–(20):

$$v_{r_k}^i(k+1)=w·v_{r_k}^i\left(k\right)+c_1·r_1·(p_{r_k}^i-w_{r_k}^i\left(k\right))+c_2·r_2·(g_{r_k}-w_{r_k}^i\left(k\right))+d_{r_k}^i\left(k\right)$$

(18)

$$v_{{\theta }_k}^i(k+1)=w·v_{{\theta }_k}^i\left(k\right)+c_1·r_1·(p_{{\theta }_k}^i-w_{{\theta }_k}^i\left(k\right))+c_2·r_2·(g_{{\theta }_k}-w_{{\theta }_k}^i\left(k\right))+d_{{\theta }_k}^i\left(k\right)$$

(19)

$$v_{{\varphi }_k}^i(k+1)=w·v_{{\varphi }_k}^i\left(k\right)+c_1·r_1·(p_{{\varphi }_k}^i-w_{{\varphi }_k}^i\left(k\right))+c_2·r_2·(g_{{\varphi }_k}-w_{{\varphi }_k}^i\left(k\right))+d_{{\varphi }_k}^i\left(k\right).$$

(20)

The DLS adjustment is:

$$d_{d_k}^i\left(k\right)=\lambda ·(g_{d_k}-w_{d_k}^i\left(k\right))$$

(21)

where $d_k$ represents each spherical component $(r_k,{\theta }_k,{\varphi }_k)$. w is the inertia weight, controlling exploration and exploitation. $c_1$ and $c_2$ are cognitive and social coefficients. $r_1$ and $r_2$ are random values between 0 and 1. $p^i$ is the personal best position of particle i. g is the global best position among all particles. $\lambda$ is the DLS learning rate influencing the degree of adjustment.

Updated velocities are used to compute new positions:

$$w_{r_k}^i(k+1)=w_{r_k}^i\left(k\right)+v_{r_k}^i(k+1)$$

(22)

$$w_{{\theta }_k}^i(k+1)=w_{{\theta }_k}^i\left(k\right)+v_{{\theta }_k}^i(k+1)$$

(23)

$$w_{{\varphi }_k}^i(k+1)=w_{{\varphi }_k}^i\left(k\right)+v_{{\varphi }_k}^i(k+1).$$

(24)

To evaluate the associated costs, we will convert Equations (22)–(24) to cartesian coordinates:

$$x_k=w_{r_k}^i·sin\left(w_{{\varphi }_k}^i\right)·cos\left(w_{{\theta }_k}^i\right)$$

(25)

$$y_k=w_{r_k}^i·sin\left(w_{{\varphi }_k}^i\right)·sin\left(w_{{\theta }_k}^i\right)$$

(26)

$$z_k=w_{r_k}^i·cos\left(w_{{\varphi }_k}^i\right).$$

(27)

The DLS-SMPSO algorithm is an advanced optimization technique that enhances traditional PSO by encoding particle positions as motion paths, making it particularly effective for trajectory optimization problems like UAV path planning. By incorporating spherical vector-based representation and the DLS, the algorithm significantly improves exploration capabilities, convergence speed, and overall solution quality. Algorithm 1 provides a summary of the implementation details for the DLS-SMPSO algorithm.

3.5. Implementation of the UAV Path Planning Method Using DLS-SMPSO

The encoding process in the DLS-SMPSO algorithm is crucial for representing and manipulating the paths or trajectories in the solution space. Here, we present a detailed description of how the search trajectory is encoded as a series of motion paths and how each path is further encoded as a set of vectors. In DLS-SMPSO, each solution is interpreted as a path or trajectory that, like a UAV, follows through the environment. This path is encoded as a series of motion vectors, each of which represents a movement from one waypoint to another. Additionally, the DLS is incorporated to address the oscillation of particles during the evolution process. By using DLS, each particle assimilates advantageous information from the global optimal solution on a dimension-by-dimension basis. This approach helps to minimize the degradation of particles throughout the evolution and ensures a more robust optimization process.

Algorithm 1 Pseudo code of DLS-SMPSO for UAV path planning.

Initialize: Dimension (f); inertia weight (w); acceleration coefficients ($c1,c2$); max iterations ($ite{r}_{max}$); swarm size (nPop); nonupdating number ($c_i$); position ($x_i$); velocity ($v_i$); Iterate:   1: for each particle in swarm do   2:  Create random motion-encoded paths $w_k$;   3:  Get a set of directional vectors $V_k$;   4:  The fitness value of $x_i$ is calculated by Equation (2);   5:  Calculate $p^i$ based on current fitness values;   6: end for   7: Set g to the best fit particle;   8: for $i=1:ite{r}_{max}$ do   9:  for each particle in swarm do 10:    Compute velocity $v_i$ using Equations (18)–(20); 11:    Compute new position $x_i$ using Equations (25)–(27); 12:    Calculate the fitness value J by Equation (2); 13:    Update personal best position $p^i$; 14:  end for 15:  if $J\left(x_i\right)>p^i$ then 16:    $c_i=c_i+1$; 17:    if $c_i>d$ then 18:     $c_i$ = 0; 19:    else 20:     for j = 1 : f do 21:       Substitute the the j-th dimension of $x_i$ with the corresponding j-th 22:       dimension of g, referred to as S; 23:       if $J\left(S\right)$ < J($x_i$) then 24:         $S=x_i$; 25:       end if 26:     end for 27:    end if 28:  end if 29:  Update global best position g; 30: end for

The encoding process in the DLS-SMPSO algorithm plays a critical role in representing and optimizing paths or trajectories in the solution space. Specifically, the algorithm encodes each search trajectory as a series of motion paths, where each path is represented by a set of vectors. These vectors correspond to movements from one waypoint to another. To further enhance the optimization process, the DLS is incorporated, addressing the common issue of particle oscillation during evolution. DLS allows each particle to assimilate beneficial information from the global best solution on a dimension-by-dimension basis. This method reduces the risk of particle degradation during evolution and ensures a more robust and effective optimization process.

Step 1: Randomly generate initial positions and velocities for all particles in spherical coordinates. Evaluate initial fitness and set personal and global bests.

Step 2: Compute new velocities using the above Equations (18)–(20), integrating DLS adjustments (Equation (21)). Update particle positions based on new velocities. Adjust positions and velocities to satisfy all constraints in Equation (2), compute fitness for updated positions in Equations (25)–(27). Update personal and global bests based on new fitness evaluations.

Step 3: Repeat iteration until convergence criteria are met (e.g., maximum iterations, acceptable fitness level).

Step 4: The global best position represents the optimal or near-optimal solution to the optimization problem.

4. Experiments and Analysis

In this section, we begin by introducing the experimental setups for UAV path planning in Section 4.1. Following this, Section 4.2 presents the performance evaluation criteria. Finally, Section 4.3 provides a comparative analysis based on the planned paths within the experimental setups. This is followed by further discussion in Section 4.4.

4.1. Experimental Setups

In the designed scenario for UAV path planning, several key parameters are established to ensure the simulation closely mirrors real-world conditions. Each UAV is set to operate within a speed range of 5 m/s to 25 m/s, balancing agility with stability. The UAVs are constrained by a minimal turning radius of 50 m, which corresponds to a maximal turning angle $\theta$ of 45 degrees, ensuring that maneuvers are smooth and within safe limits. The environment is modeled using a Digital Elevation Model (DEM), accurately representing terrain features. All five UAVs depart simultaneously from point (200, 100, 150) and proceed toward the UGV0 at point (800, 800).

Additionally, communication limitations are considered, as noted in Ref. [9]. The path planning algorithm is configured with specific values for the DLS-SMPSO method, including a population size of 50 particles, a maximum of 200 iterations, and parameter settings such as an inertia weight w of 1 and both cognitive $c_1$ and social $c_2$ coefficients set to 1.5. For consistency in comparison, all algorithms are implemented using the same set of parameters. The simulation environment is divided into two parts, Case 1 and Case 2, and the parameters are shown in

Table 2. Environment parameter setting: simple environment.

NO.	x/m	y/m	z/m	r/m
1	400	500	100	80
2	600	200	150	70
3	500	350	150	80
4	350	200	150	70
5	700	550	150	70
6	650	750	150	80

and

Table 3. Environment parameter setting: complex environment.

NO.	x/m	y/m	z/m	r/m
1	450	550	100	80
2	500	350	150	80
3	300	200	150	50
4	650	650	150	70
5	200	300	150	70
6	300	450	150	70
7	450	150	150	70
8	650	250	150	55
9	750	400	150	75
10	850	650	150	70

, respectively.

4.2. Performance Evaluation Criteria

When assessing the performance of UAV path planning algorithms, several essential criteria are typically taken into account to evaluate the effectiveness and efficiency of the proposed solutions. These criteria include the following:

Feasibility Ratio (FR): FR measures the proportion of solutions produced by a UAV path planning algorithm that satisfies all specified constraints, such as obstacle avoidance, compliance with turning angle restrictions, and adherence to energy consumption limits. A higher FR indicates that the algorithm is more effective in generating feasible paths that meet mission-critical requirements.

Best Cost: The best cost metric is a critical evaluation criterion in optimization algorithms, especially for UAV path planning. It reflects the most optimal solution found during the search process, representing the path with the lowest possible cost. This metric is often presented alongside the “Optimal”, “Worst”, and “Mean” values for a more holistic assessment of the algorithm’s performance. The “Worst” cost highlights the least favorable solution encountered, offering valuable insights into the algorithm’s robustness and its ability to consistently generate high-quality solutions.

4.3. Comparison Analysis

(1) Case 1: In this section, we present the experimental results obtained from testing the proposed UAV path planning algorithm in a simple and complex flight environment. The aim is to validate the feasibility and effectiveness of the path planning method under controlled conditions with limited obstacles and forward terrain.

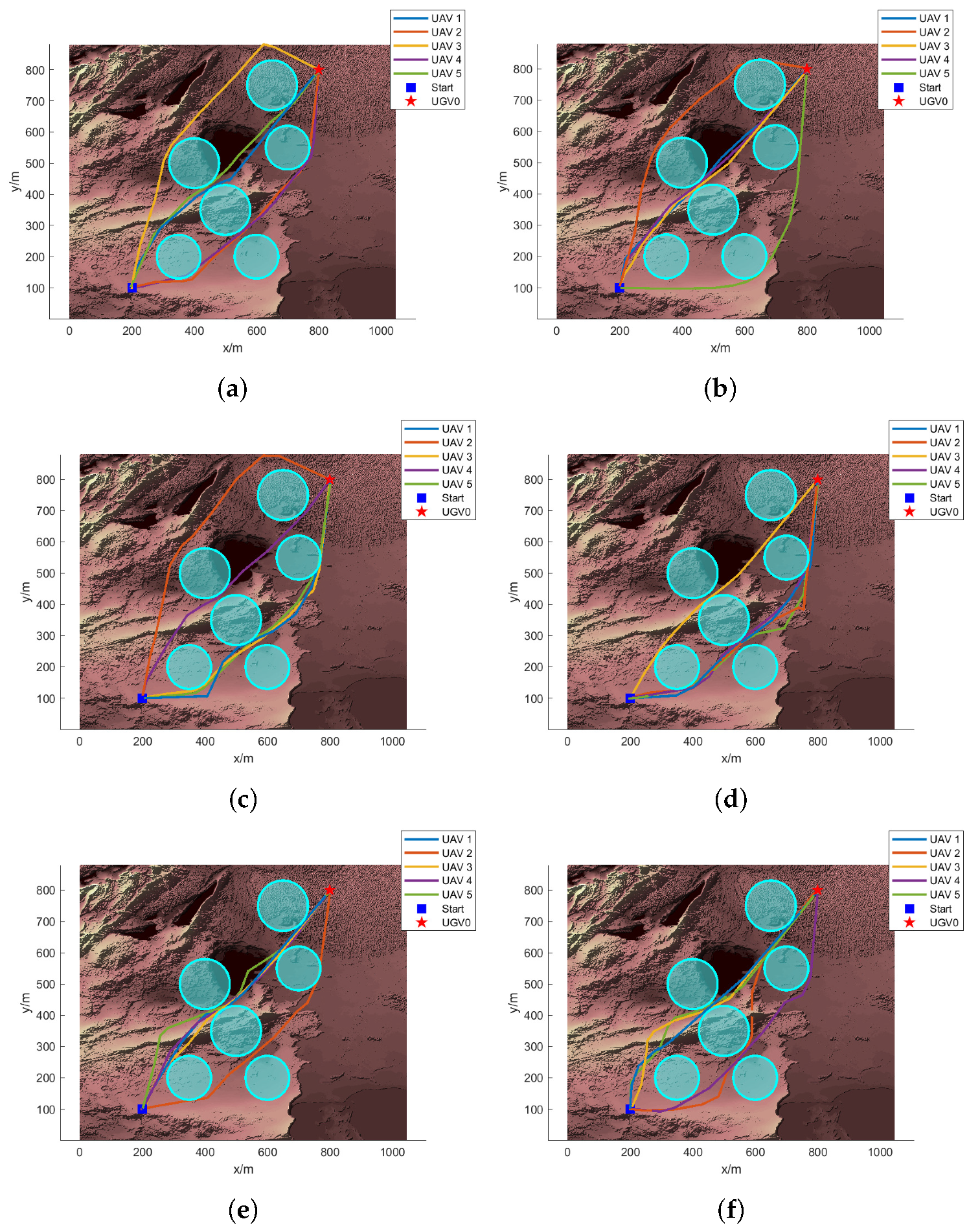
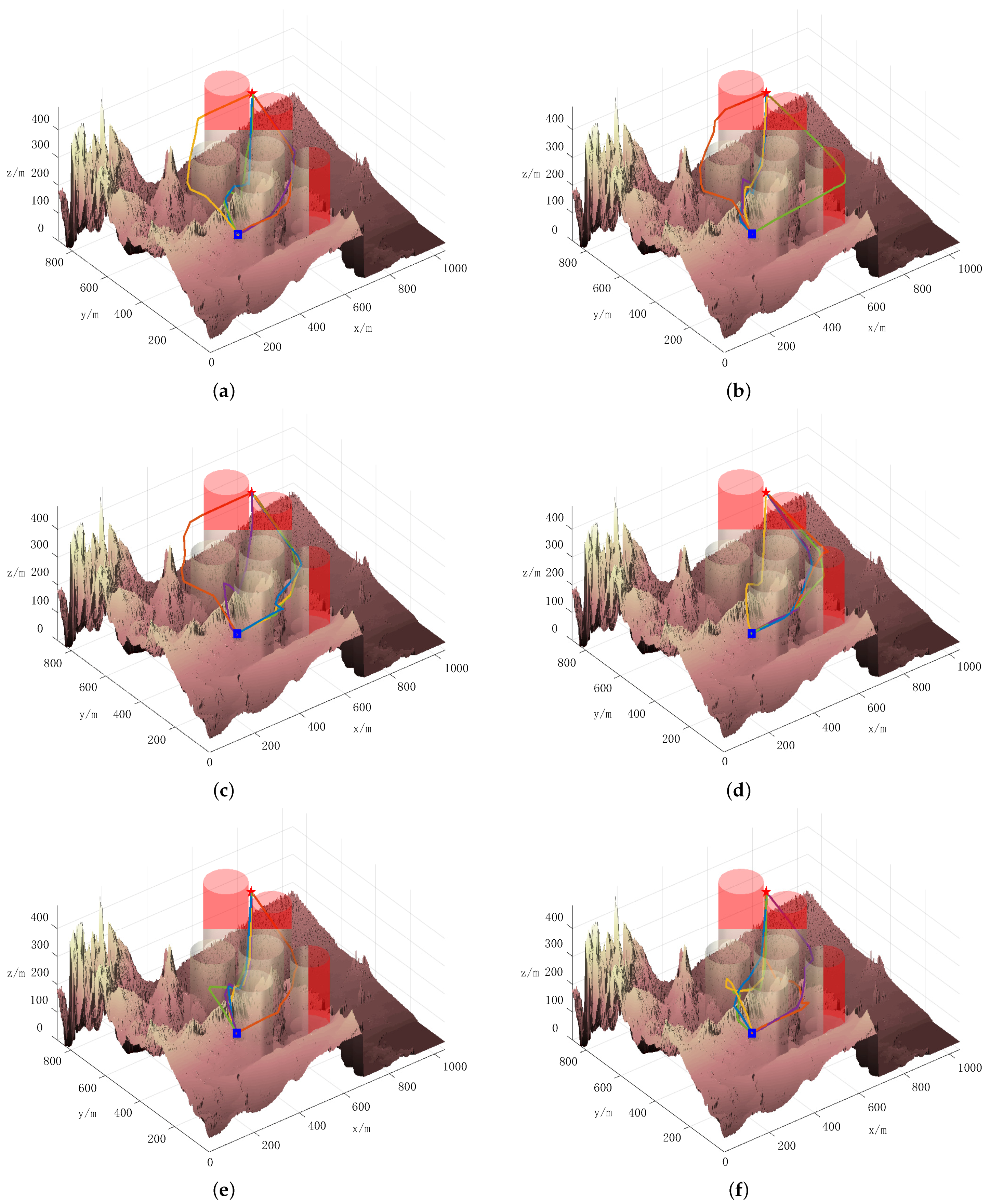
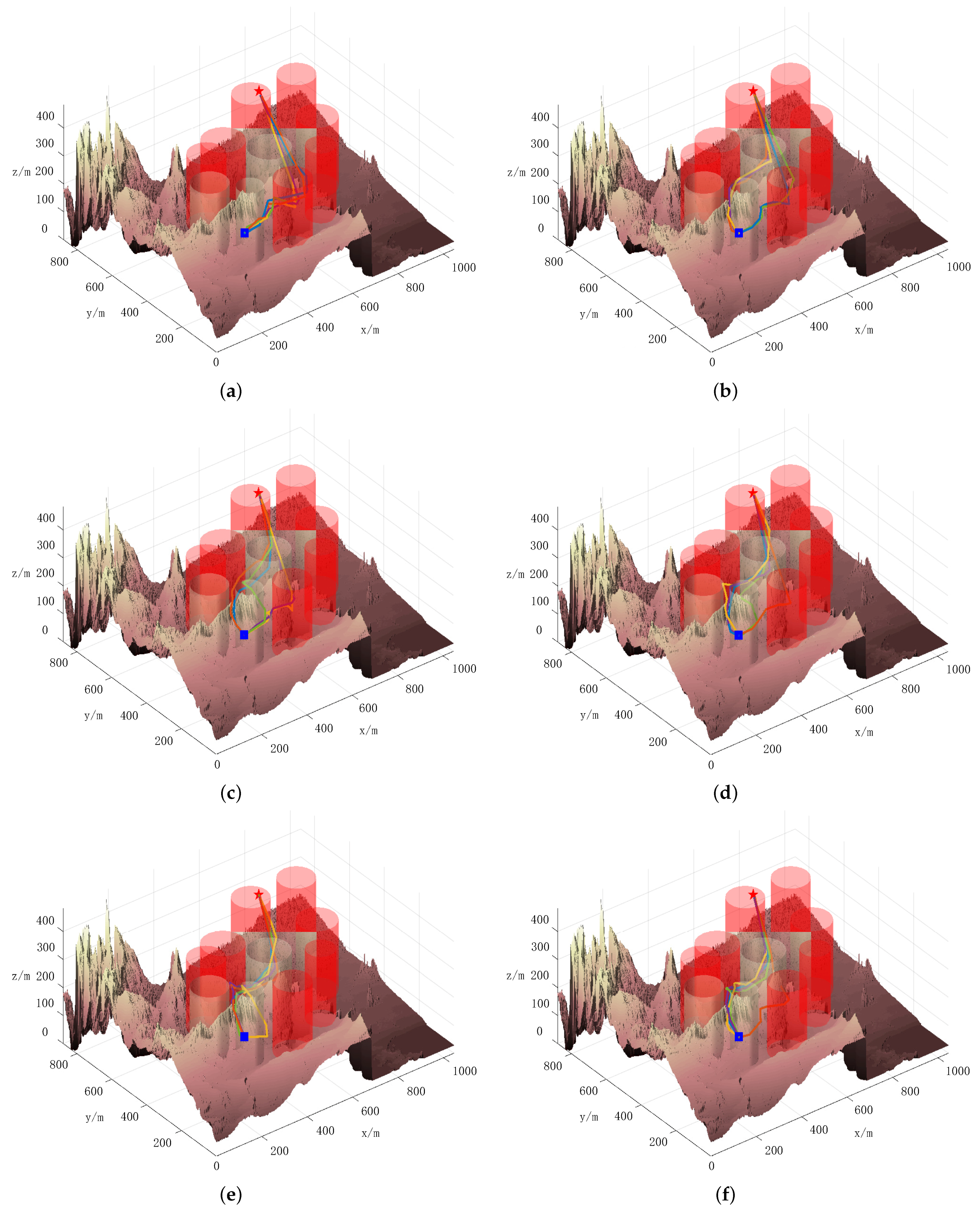
Figure 1 and Figure 2 present the top and three-dimensional views, respectively, of the flight path for Case 1. From these images, it is evident that the DLS-SMPSO algorithm effectively designed a path that minimizes the risk of collision and ensures the safety of each UAV by avoiding potential threats. In contrast, the paths generated by the PSO, APSO, QPSO, GWO, and ABC algorithms exhibit shortcomings in terms of safety and communication interference, highlighting the superior performance of DLS-SMPSO in these aspects.

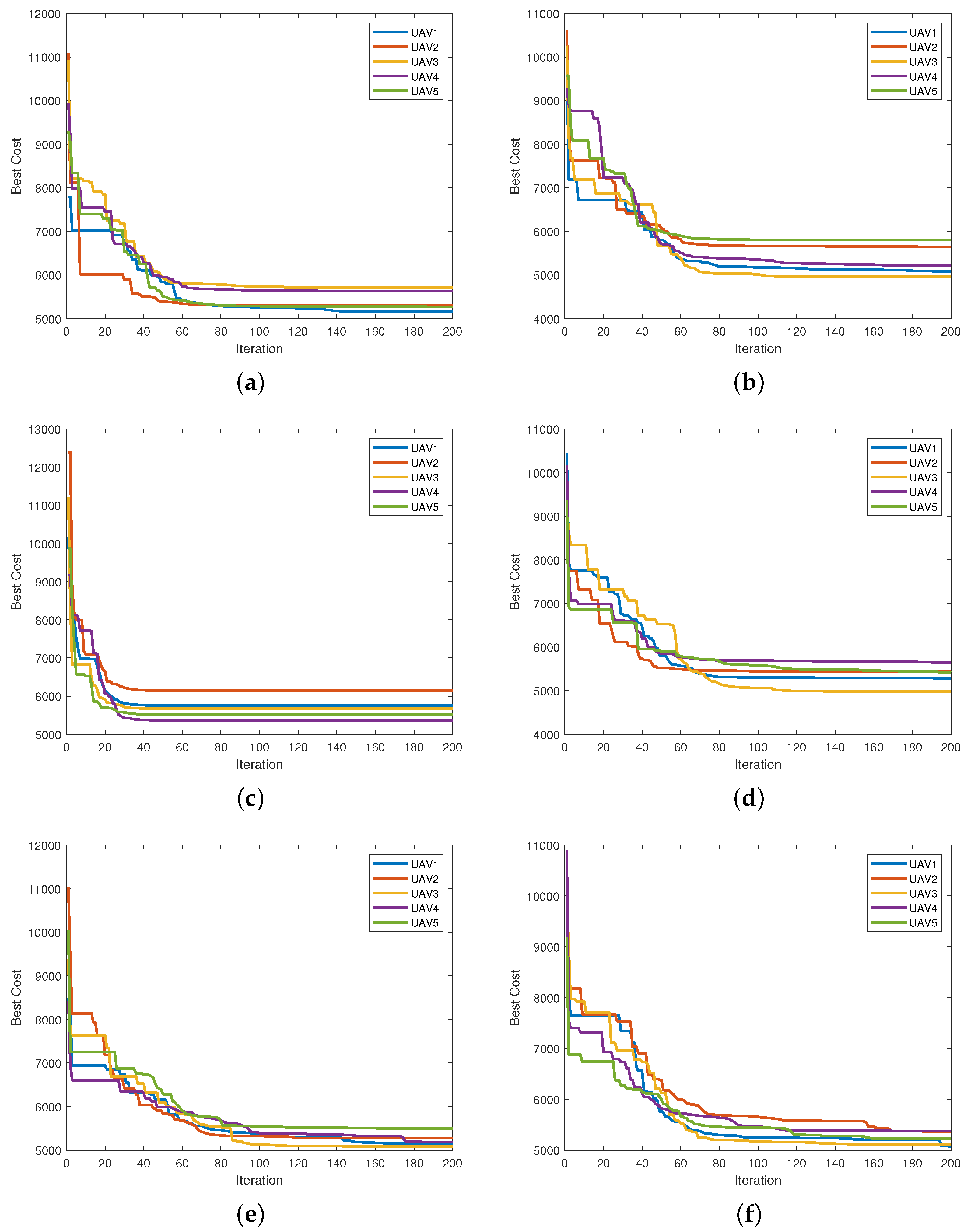
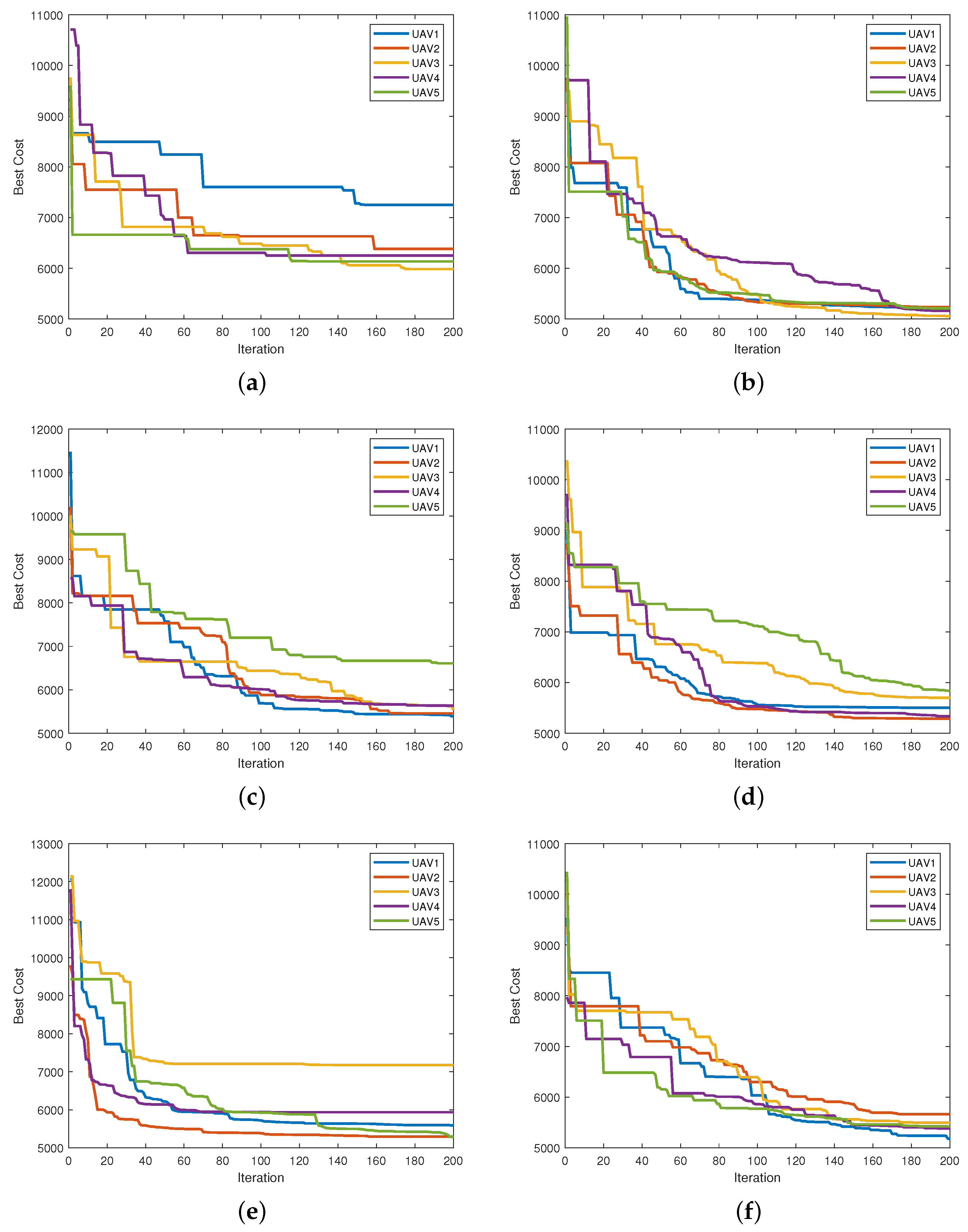
In addition, Figure 3 illustrates the convergence curves of the six algorithms in Case 1. The convergence curve reveals that the DLS-SMPSO algorithm quickly identifies an optimal solution in the early stages. As the search progresses, the DLS-SMPSO algorithm adapts to stricter constraints and gradually converges toward the feasible region, demonstrating excellent convergence performance and the ability to find superior paths. Although it may not appear advantageous compared to the PSO, APSO, QPSO, GWO, and ABC algorithms at first glance, a closer examination of Figure 1a–f in Figure 3 reveals a key distinction: most of the optimizations in Figure 1a–e involve the continuous refinement of a single UAV’s path. In contrast, the DLS-SMPSO algorithm, depicted in Figure 1f, excels in collaborative path planning. Notably, in Figure 1f, it can be observed that UAV2 is able to maintain a stable flight path with the assistance of other UAVs, even when communication is interrupted. This underscores the significant advantages of the DLS-SMPSO algorithm in fostering cooperation among UAVs.

Table 4. Result comparison after 200 repetitions in a simple environment.

NO.	1	2	3	4
Indicators	Worst	Optimal	Mean	FR(%)
QPSO	5.4316 × 103	5.2311 × 103	5.3968 × 103	93
GWO	6.1404 × 103	5.3821 × 103	5.8103 × 103	88
ABC	6.0464 × 103	5.4693 × 103	5.7223 × 103	89
PSO	5.8903 × 103	5.1473 × 103	5.8103 × 103	90
APSO	5.8136 × 103	5.2198 × 103	5.8103 × 103	92
DLS-SMPSO	5.3804 × 103	5.1142 × 103	5.2286 × 103	97

presents the statistical results of all algorithms under Case 1, with boldface indicating the results of our algorithm. As observed in Table 4, the DLS-SMPSO algorithm outperformed other algorithms in terms of average, worst, and best values; it achieved the highest FR. This suggests that the DLS-SMPSO algorithm is more effective in finding feasible solutions. However, it is important to note that the path selected by UAVs using the DLS-SMPSO algorithm may not always be optimal regarding cooperative cost. This observation leads us to infer that cooperative path planning for multi-UAVs prioritizes relatively optimal flight decisions that align with coordination constraints rather than focusing on achieving an individually optimal path for each UAV.

The experimental results show that the proposed path-planning algorithm successfully guided all UAVs to their targets in a simple environment. The total path length was optimized for each UAV, with the algorithm achieving a high FR across all test cases. The execution time remained within acceptable limits, even as the number of UAVs increased, demonstrating the scalability of the method.

(2) Case 2: In this section, we present the experimental results obtained from testing the proposed UAV path planning algorithm in a complex flight environment. The objective is to evaluate the algorithm’s performance under more challenging conditions, which include a higher density of obstacles and elements that simulate real-world scenarios.

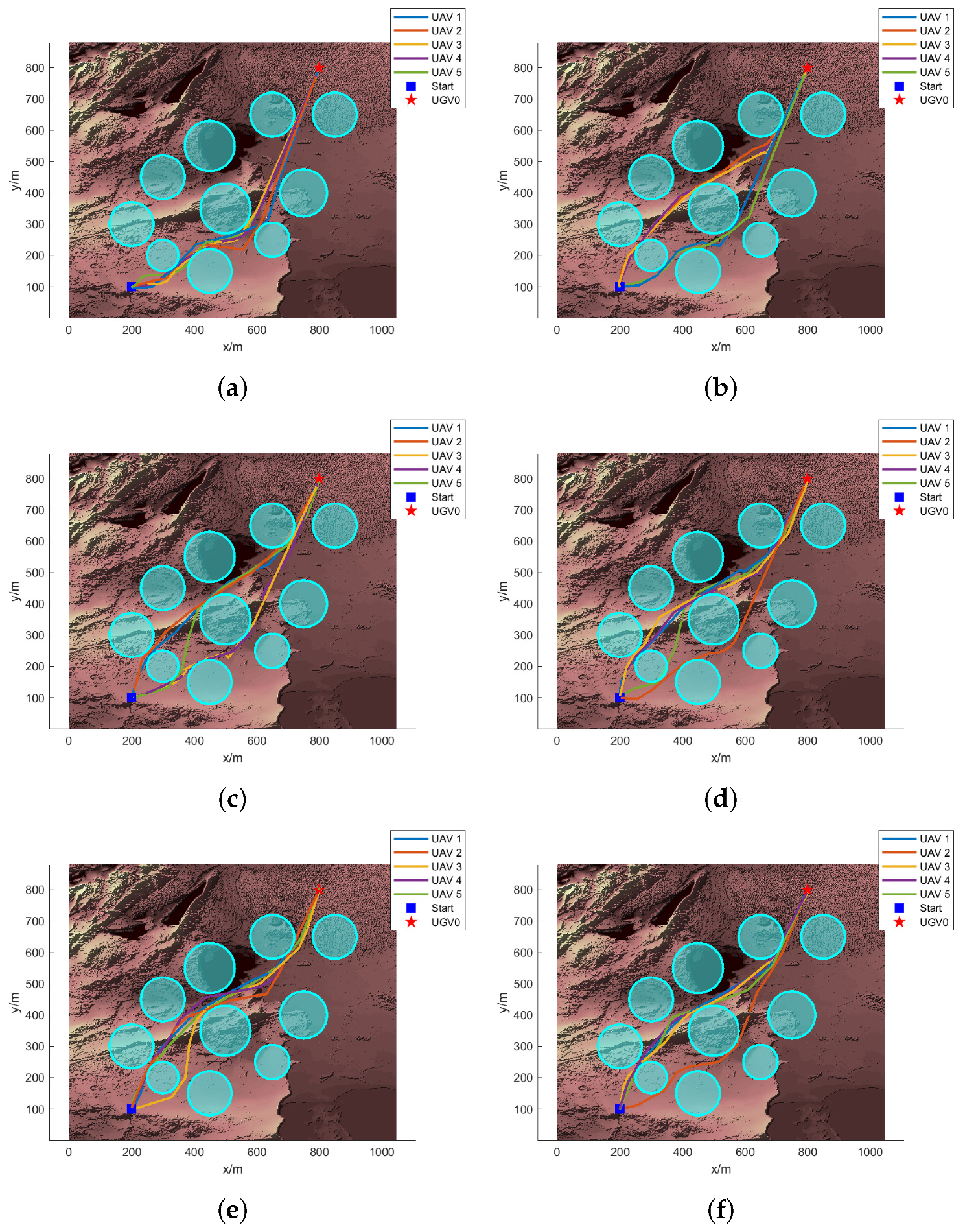
Figure 4 provides a detailed 3D view of the best flight paths achieved by the various algorithms in operation, while Figure 5 offers a top view of these corresponding paths. As observed in Figure 4 and Figure 5, when the flight environment becomes more complex, the DLS-SMPSO algorithm enables the UAV to successfully avoid obstacles and complete the path planning task. The convergence curve depicted in Figure 6 indicates that, although the convergence speed of the DLS-SMPSO algorithm may be slower at times, its performance remains consistent with the results obtained in simpler environments. Notably, our algorithm demonstrates a significant advantage in collaborative path planning. Furthermore, the DLS-SMPSO algorithm leverages DLS to learn beneficial information dimension by dimension from the global optimal solution, thereby improving the feasible ratio of the paths. As shown in

Table 5. Result comparison after 200 repetitions in a simple environment.

NO.	1	2	3	4
Indicators	Worst	Optimal	Mean	FR(%)
PSO	5.9557 × 103	5.4611 × 103	5.7140 × 103	88
QPSO	5.5405 × 103	5.3727 × 103	5.4199 × 103	91
APSO	5.8203 × 103	5.6814 × 103	5.7140 × 103	90
GWO	7.4486 × 103	6.0255 × 103	6.8329 × 103	85
ABC	6.1732 × 103	5.5040 × 103	5.8287 × 103	87
DLS-SMPSO	5.3878 × 103	5.1790 × 103	5.2391 × 103	96

, the FR of the DLS-SMPSO algorithm is the best, which verifies the feasibility and superiority of the algorithm.

The experimental results revealed that the proposed path planning algorithm was able to effectively navigate the UAVs through challenging scenarios. The algorithm maintained a high FR, with most UAVs successfully reaching their targets while avoiding obstacles. The results suggest that the proposed UAV path planning algorithm is robust and adaptable to real-world scenarios.

4.4. Discussion

Extensive simulations and comparative analyses demonstrate that DLS-SMPSO excels in generating safe, feasible, and optimal paths for multi-UAV operations. The proposed algorithm performs exceptionally well in complex environments with numerous obstacles, as evidenced by its consistently low fitness values. This effectiveness is driven by the transformation of the search space from cartesian to spherical coordinates, enabling more intuitive and flexible exploration. Furthermore, constraints on UAV dynamics, such as turning and climbing angles, are seamlessly integrated into the DLS-SMPSO variables, refining the search space and yielding high-quality solutions.

However, this paper encounters challenges with complex wind patterns and intricate obstacle geometries, which may delay UAV progress or cause them to miss waypoints. Refs. [52,53] explore the modeling of wind and obstacle disturbances to assess UAV swarm resilience, emphasizing performance and adaptability under challenging environmental conditions. These studies offer valuable insights into how dynamic environmental factors impact UAV swarm behavior, which may aid in addressing the issues posed by complex wind patterns and obstacle geometries.

5. Conclusions

In this paper, we tackled the complex issue of cooperative path planning for multi-UAV systems under time-varying communication constraints using the DLS-SMPSO algorithm. The DLS-SMPSO method provides a robust solution by introducing an innovative approach that encodes particle positions as motion paths in spherical coordinates. This, coupled with the DLS, significantly enhances the algorithm’s ability to plan cooperative paths, minimizes oscillations during the optimization process, and improves overall stability. The simulation results confirm the feasibility and effectiveness of the proposed approach, demonstrating its potential for real-world applications.

While the proposed approach demonstrates effective path planning capabilities, several limitations highlight opportunities for future enhancement. First, this study evaluates the algorithm with a limited number of agents (five UAVs), constraining the assessment of scalability and collaborative effectiveness in larger, multi-agent scenarios. Future work will focus on extending the algorithm to accommodate a greater number of UAVs, enabling a comprehensive evaluation of its robustness and scalability in more complex swarm configurations.

Furthermore, this study does not account for environmental factors such as complex wind patterns and diverse obstacle geometries, both of which could significantly impact path feasibility and necessitate adaptive re-planning to maintain safe and efficient trajectories. For instance, intricate wind dynamics may alter UAV paths and demand continuous adjustments, while complex obstacle geometries could trap UAVs in confined spaces, testing the limits of the pathfinding strategy. Future research will incorporate these dynamic environmental variables to enhance the algorithm’s resilience. Additionally, embedding comprehensive UAV dynamics and considering aspects like inertia and aerodynamics directly into the optimization framework will allow for a more realistic representation of physical constraints, enabling adaptable and accurate path planning. Addressing these factors will help validate and refine the algorithm for a wider range of applications, thereby improving its efficacy in dynamic and unpredictable environments.