Abstract
As an essential application of unmanned aerial vehicle (UAV) systems, payload transportation has garnered significant attention in recent years. Collaborative payload transportation utilizing multiple UAVs can effectively increase the payload capacity of the transportation system. Nevertheless, the incorporation of multiple UAVs makes the dynamic model of the transportation system more complex due to the coupled UAV and payload states. In the immediate disaster relief response, the collaborative system is often required to promptly deliver supplies to the target site while avoiding obstacles to ensure the system’s safety. Consequently, devising fast delivery trajectories that avoid collisions for such complicated systems poses a considerable challenge. To this end, a novel trajectory planning method is presented for collaborative transportation systems. Specifically, the dynamic model of the collaborative transportation system is derived by utilizing the Euler–Lagrange method. Then, the trajectory planning problem is formulated as an optimization problem with considerations of dynamics, actuation, safety, and formation constraints. To expedite the optimization process, the collision avoidance safety constraint is constructed using dual variables. The efficacy of this trajectory planning approach is confirmed through multiple real-world flight experiments involving collaborative aerial transportation systems of two and three UAVs.
1. Introduction
Thanks to their low cost and high maneuverability, unmanned aerial vehicles (UAVs) have been extensively applied in military and civilian fields, such as inspection, search and rescue, and fire detection [1,2,3,4]. As one of the most active and important applications, payload transportation emerges as a particularly active and significant focus of research in recent years.
At present, there exist two general approaches for payload transportation: delivery via a suspended cable [5,6,7] and grasping-based transportation. Grasping-based transportation is further divided into fixed gripper grasping [8,9] and robotic arm manipulation [10,11]. Each method presents unique advantages in terms of cost, dexterity, and the complexity of modeling and control. Specifically, the low-cost method of cable suspension, discussed in this paper, maintains high maneuverability of the UAVs. However, it typically requires operator intervention for autonomous payload deployment, particularly in hazardous environments. Conversely, the integration of a robotic arm enhances dexterity for transport tasks but introduces challenges related to energy consumption and mechanical design.
Trajectory planning is pivotal in payload transportation, attracting growing attention within the research community. This interest has yielded two primary trajectory planning strategies: continuous-time polynomials and discrete-time representations. As for the first approach, some exciting studies have been performed by exploiting the differentially flat property [12,13]. Based on the differentially flat outputs, the trajectory generation method could deal with the case when the cable tension became zero [12]. A trajectory planning method was designed in [13] for a multi-robot system, where the robot’s trajectory was refined into a higher-order segmented polynomial. However, the trajectories were moderately conservative, failing to maximize actuator performance within physical constraints.
On the other hand, discrete-time trajectory generation methods for cable-suspended aerial transportation systems have been explored through various approaches, including search-based [14,15], optimization-based [16,17], and reinforcement learning techniques [18]. For instance, a cable-suspended payload transportation system was modeled as a quadrotor linked by three passive, constrained joints [16]. This model facilitated trajectory optimization as a mathematical program with complementarity constraints (MPCC). In [17], the trajectory generation problem for a quadrotor with a suspended payload was formulated as a nonlinear optimization problem, incorporating a variety of constraints from the robot, task, environment, and user-defined guidance. Experimental results across various tasks demonstrated that the method achieved short computational times and satisfactory performance. A real-time, time-optimal trajectory strategy using convex optimization and reinforcement learning was proposed for the cable-suspended transportation system [18].
The aforementioned studies predominantly focus on payload transportation using a single UAV. However, these approaches are often inadequate for collaborative aerial transportation involving multiple UAVs. The dynamics in collaborative transportation systems are significantly more complex due to factors such as inter-UAV interactions and payload sharing, which introduce substantial challenges in trajectory planning. Consequently, techniques effective for single-UAV systems cannot be directly applied to multi-UAV collaborative transport. Therefore, research on trajectory planning for collaborative transportation systems remains limited, leaving a significant gap in the literature. Aimed at this issue, the property of differential flatness in multi-quadrotor cooperative payload delivery was established in [19], leading to the generation of smooth trajectories by optimizing flat outputs. In [20], the trajectory for the collaborative aerial transportation system was obtained by optimizing the cable tensions while considering the tension constraints and collision avoidance among UAVs. A trajectory generation method was proposed for the collaborative aerial transportation system in [21], capable of simultaneously planning payload trajectories and cable tensions while adhering to tension constraints and minimizing tension disparities. In [22], a trajectory planning algorithm based on value function approximation was developed, consisting of two independent phases: parameter learning and trajectory generation. However, the above studies focus solely on trajectory planning for collaborative transportation systems in open environments, making them unsuitable for complex, obstacle-filled environments, which greatly limits their range of applications. To address this challenge, the optimization problem was formulated in [23] to minimize trajectory jerk, while a modified A* algorithm was employed to ensure collision avoidance in collaborative transportation systems with a fixed number of UAVs. In [24], a scalable approach was presented that utilized distributed optimization to deal with the nonlinear dynamics and nonconvex constraints. Nevertheless, travel time, a critical factor in payload transportation, was not adequately considered in these studies. This limitation makes it challenging to apply these methods in time-sensitive scenarios, such as disaster response and logistics delivery. To this end, this paper aims to enhance system safety and expedite payload delivery in collaborative aerial transportation while also improving scalability for systems with varying numbers of UAVs. Specifically, the dynamic model of the collaborative transportation system is established using the Euler–Lagrange method. The dynamics constraint is then integrated into the optimization problem through the application of the multiple shooting method. Moreover, actuation, safety, and formation constraints are taken into consideration in the optimization problem. To accelerate the solution of the optimization problem, collision-avoidance constraints are constructed using dual variables. By addressing the optimization problem, a rapid payload transportation trajectory solution with collision avoidance can be achieved. The main contributions of this paper lie in two aspects:
- Unlike previous research on trajectory planning for collaborative transportation systems in open environments [19,20,21,22], this study focuses on developing methods for obstacle avoidance in collaborative transportation systems operating in complex, obstacle-filled environments, aiming to enhance safety in challenging scenarios. Although some studies [23,24] have addressed trajectory planning in such environments, they did not consider transportation time as a critical factor. Additionally, the approach in [23] lacked scalability for systems with different numbers of UAVs. To bridge these gaps, this paper presents a unified obstacle avoidance trajectory planning method that integrates transportation time as a key objective and is designed for systems with two or more UAVs. Real-world experiments are conducted on a self-built collaborative transportation platform to assess the effectiveness and scalability of the proposed method across systems with varying numbers of UAVs.
- In the trajectory planning problem for the transportation system, system dynamics, actuation, safety, and formation constraints are taken into account to obtain the quick delivery trajectory for reaching the target point. The resulting optimization problem, formed by these constraints, is inherently non-convex, thus imposing a significant computational burden. To accelerate the solution of the optimization problem, the collision avoidance constraints are established using dual variables.
This paper is organized as follows: the dynamics model of the collaborative aerial transportation system is given in Section 2. The trajectory optimization problem is formulated by considering system dynamics, actuation, safety, and formation constraints in Section 3. Subsequently, simulation and experimental results are detailed in Section 4. Finally, Section 5 provides a summary of the entire paper.
2. Dynamic Model of the Collaborative Aerial Transportation System
As illustrated in Figure 1, the point-mass payload is suspended by cables from three UAVs. The inertial frame is denoted as o-; and represent the masses of the ith UAV and the payload, respectively. is the center of mass position of the ith UAV. represents the payload position, and is the rope length between the center of mass position of the ith UAV and the payload position. and are the payload swing angles, with denoting the angle between the ith cable’s projection in the o- plane and the positive x-axis, and representing the angle between the ith cable and its projection in the o- plane. For brevity in subsequent discussions, the abbreviations and are introduced.
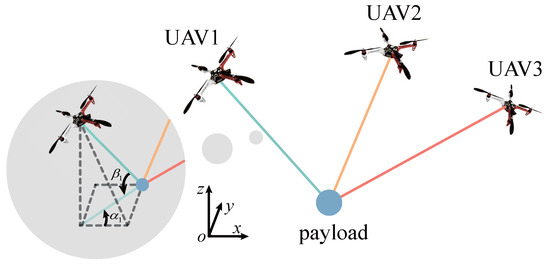
Figure 1.
Schematic of collaborative aerial transportation with three UAVs.
Thus, the following relationships are available:
where denotes the unit vector of each rope. Taking the time derivative of , the following result can be obtained:
To achieve the construction of the dynamic model, the generalized state of the aerial transportation system is chosen as . Then, based on the Euler–Lagrange method, the dynamic model of the system can be derived [19,25]:
where the Lagrangian L is the sum of the kinetic energy T and the potential energy U, represents the generalized force. It is noted that the rotations of UAVs are not included in the kinetic energy of the system since the payload motion is directly determined by the UAV’s translation. The specific expressions of T and U are provided as follows:
where g denotes the gravity constant, .
Utilizing (1)–(6) and doing some calculations, the following equations can be obtained:
where represents the inertia matrix, denotes the centripetal-Coriolis matrix, is the gravity matrix, is the control input of the system and denotes the control input of the ith UAV.
By generalizing the dynamics model of the transportation system involving three UAVs, we can derive a unified dynamics model for the multi-UAV collaborative transportation system, including the dynamics regarding the payload position and swing angle. The dynamics concerning the payload position can be formulated as
where , with being the number of UAVs.
The dynamics concerning the swing angle can be expressed as:
3. Discrete Trajectory Optimization Problem Formulation
The optimization variables encompass the travel time and the state , where the state includes the system state and the control input at node k. The introduction of aims to facilitate rapid payload delivery. A node represents a time point. The time interval between adjacent nodes is , and the time at node k is . Consequently, the optimization variable can be organized as .
In order to generate a dynamically feasible and safe trajectory for payload transport, the following constraints are considered in this paper: dynamics, actuation, safety, and formation. Subsequently, the aforementioned constraints will be introduced individually.
- (1)
- Dynamics constraint
The dynamics constraint is utilized to describe the evolution and progress of the collaborative transportation system. By employing the Euler method, the relationship between and can be articulated as follows:
where represents the discrete time step. The system state is defined as , and the detailed dynamic equations for the system can be found in Equations (8)–(12).
- (2)
- Actuation constraint
Given the constrained nature of actuator performance and the safety hazards entailed by operating at performance boundaries, establishing safety margins to limit the input range of UAVs is crucial for ensuring actuator safety, which is expressed as follows:
where and respectively represent the allowable minimum and maximum control efforts. Moreover, excessive flight speed can result in payload swing, thereby impeding stable payload transportation. Restricted system responses may arise from large attitude angles, hindering timely adjustments to UAV attitudes. Additionally, UAV instability can be induced, thereby increasing the risk of loss of control. Consequently, it becomes imperative to confine both the attitude and speed of the ith UAV within a reasonable range, namely,
where represents the attitude of the ith UAV in Euler angles, denotes the allowable maximum values, and and are the allowable minimum and maximum velocities of the ith UAV, respectively.
- (3)
- Safety constraint
To ensure the safety of the collaborative transportation system during task execution, the safety constraint is designed with two primary considerations. The first consideration concerns collisions among UAVs, which is mitigated by ensuring a certain safe distance between them, i.e.,
where denotes the Euclidean norm, and represents the prescribed minimum safety distance between UAVs.
On the other hand, the collaborative transportation system, denoted as , is expected to avoid potential collisions with obstacle , representing the second facet of the safety constraint. This necessitates ensuring the satisfaction of the following condition:
where denotes the number of the obstacles, is the allowable safety margin.
In this paper, it is assumed that the shape of and can be approximated by a union of bounded polyhedra, whose mathematical expressions are as follows:
As illustrated in Figure 2, the geometry of the collaborative aerial transportation system can be bounded with a union of square cuboids. Each payload attached to the ith UAV and its corresponding rope can be modeled as a cuboid. Consequently, the following relationship can be derived:
where the initial convex set represents a cuboid formed by the vertical connection of the UAV and the payload, is the convex set described in the inertia frame, , , and are employed to define the size of the cuboid, is the rope length, and can be calculated with the Rodrigues’ rotation formula.
where denotes the three-dimensional identity matrix, and represents the hat operator, defined such that for any vectors and in , . It should be noted that the values for the rotation axis and rotation angle are not unique. In this paper, we adopt and , where .
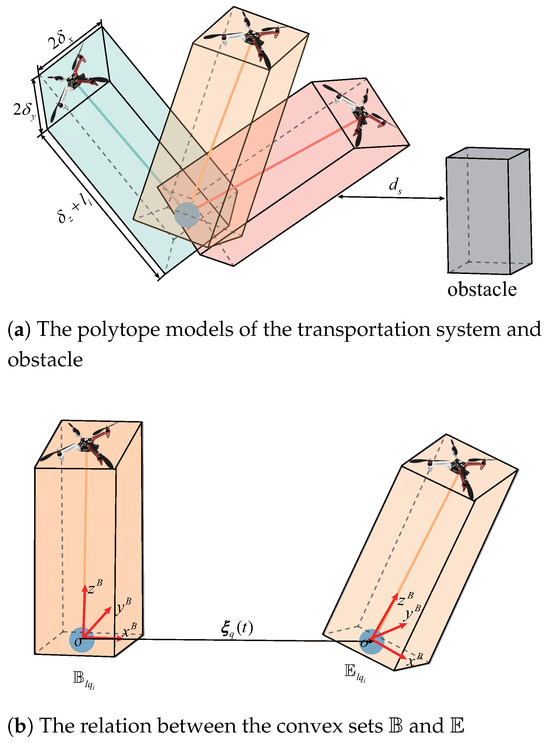
Figure 2.
Collision avoidance constraint between the system and environmental obstacles.
To ensure the safety of payload transportation, a specified safe distance from obstacles must be maintained by the system, as indicated by the inequality . Here, represents the minimum distance between and , which is determined by solving the following optimization problem:
Based on Equation (21) and the Weak Duality Theorem [26], the safety constraint between the system and obstacles can be reformulated as [27,28]:
Based on Equation (22), the dual variables should be integrated into in the optimization variable, i.e., The safety constraints consist of two parts: collision avoidance between UAVs and collision avoidance between the system and environmental obstacles. To ensure collision avoidance between UAVs, the safe distance should account for the size of the UAVs, including the dimensions of their arms and propellers. For collision avoidance between the system and environmental obstacles, the system contour can be represented by the polyhedral model shown in Figure 2. Ideally, collisions with environmental obstacles are avoided if the safe distance remains greater than zero. However, to account for tracking controller inaccuracies and external disturbances, an additional safety margin should be added to both and .
- (4)
- Formation constraint
Performing force analysis of the payload, one has
where . Based on Equation (23), it is evident that the z-directional component of the rope tension is responsible for counterbalancing the payload’s gravity. However, even a slight swing angle of the payload can exert a substantial horizontal force component on the UAV, potentially destabilizing the UAV’s attitude loop control. Hence, to maintain UAV stability, should be confined to a specific range. Furthermore, to ensure a relative relationship between UAVs, should be constrained within an acceptable range. Consequently, the formation constraint can be articulated as follows:
where and represent the initial angles of and , respectively, while and are the allowable angle ranges for these variables. Given that the swing angles are constrained to a narrow range, it can be deduced that the values of and are small. Moreover, by utilizing the velocity relationship between the ith UAV and the payload as defined in Equation (2), the speed constraint of UAVs can be translated into a velocity limit on the payload, which can be expressed as
where and are the permissible velocities of the payload.
Based on the above representations, the optimization problem can be formulated as:
where and are the initial and final positions of the ith UAV, and , denote the value of the corresponding variable at node k. The optimization problem presented in Equation (26) is solved using CasADi [29,30], which is an open-source tool for nonlinear optimization.
4. Simulation and Experimental Results
To validate the effectiveness of the proposed method, comparative tests are conducted. Specifically, the comparative method, namely the relative distance-based approach, constructs collision avoidance constraints by calculating the distance between the system and obstacles. Other constraints, including dynamics, actuation, and formation constraints, remain consistent with the proposed method. Subsequently, simulations are conducted to compare the planned trajectories of a two-UAV transportation system and a three-UAV transportation system using the two methods. Additionally, experiments of the proposed method are carried out.
Remark 1.
It should be noted that a discrete trajectory sequence, which includes UAV position, velocity, and time information, is obtained by solving the optimization problem (26). In the actual experiment, this sequence serves as the raw data, from which the desired UAV position and velocity at any given time are determined through data fitting based on the transmission frequency of the UAV trajectory. The desired trajectory is then transmitted to the UAV via Wi-Fi to perform the payload transportation task.
4.1. Simulation
Simulation 1: In this simulation, a comparative test is conducted on a collaborative aerial transportation system with two UAVs. The safety distance is set as , and the initial and the desired payload positions are respectively set as . The initial and final payload swing angles are chosen as , . The actuation constraints are set as . It should be noted that obstacles are modeled as cylinders in this paper, whose locations are known and predefined as
where is the position of the obstacle, which is the projection of the cylindrical centerline on the o- plane, r is the base radius of the cylinder, and h is the height of the cylinder.
Simulation 2: In this simulation, a comparative test is implemented on a three-UAV transportation system. The safety distance is set as , the initial and desired positions of the payload are chosen as . The initial and final states of the swing angles are given as , , . The actuation constraints are set as . The parameters of the obstacles are taken as:
The comparison test results in Simulation 1 and Simulation 2 are depicted in Figure 3 and Figure 4, where the planned trajectories for the two-UAV and three-UAV transportation systems are presented using both the proposed method and the comparative method, respectively. The solid line represents the trajectory obtained by solving the optimization problem with dual variables, while the dashed line represents the comparison method. In the comparative method, the obstacle is represented as a cylinder , while each UAV and the payload is modeled as a cylinder . The obstacle collision avoidance constraint, based on relative distance, is formulated as , where is the distance between the cylinders and and is the safety distance. The remaining constraints, including the dynamics constraint (13), actuation constraint (14) and (15), UAV collision avoidance constraint (16), and formation constraint (24), are consistent with the proposed method in this paper. It can be observed from the figures that both the proposed method and the comparison method can generate collision-free transport trajectories for the systems. The computation and trajectory times for Simulation 1 and Simulation 2 are provided in Table 1 and Table 2, respectively. Notably, for both the two-UAV collaborative and three-UAV collaborative transportation systems, the trajectory times obtained using the proposed and comparative methods show no significant differences. However, in terms of computation time, the proposed method significantly improves the efficiency of solving the optimization problem compared to the comparative method. The primary difference between the proposed and comparative methods lies in the construction of obstacle avoidance constraints. Both optimization problems are solved using the same solver. In other words, the use of dual variables in constructing obstacle avoidance constraints in the proposed method effectively enhances the efficiency of the optimization problem-solving process. The constraint in (21) between the system and environmental obstacles is reformulated as its corresponding dual constraint. According to [27,28], the dual problem corresponding to Equation (21) is convex, offering better solution characteristics. Analyzing Equation (21) reveals that the original problem focuses on ensuring that the minimum distance between the robot and the obstacles is greater than the safety distance . In the dual formulation, however, the objective shifts to finding a set of appropriate Lagrange multipliers, and , that satisfy the corresponding dual conditions and constraints. This transformation leverages the convexity of the dual problem, thereby enhancing computational efficiency.
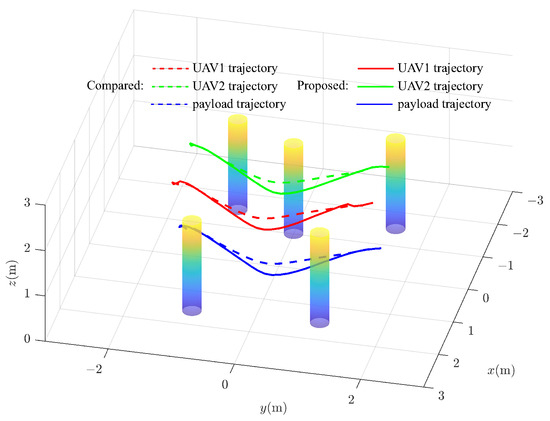
Figure 3.
Comparison test in Simulation 1.
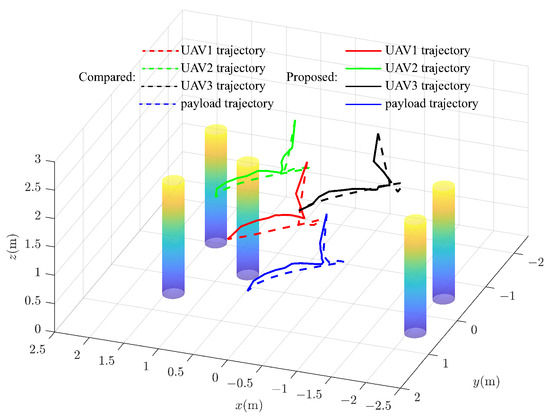
Figure 4.
Comparison test in Simulation 2.

Table 1.
Comparison with relative distance-based method for collaborative aerial transportation system with two UAVs.

Table 2.
Comparison with relative distance-based method for collaborative aerial transportation system with three UAVs.
4.2. Experiment
Subsequently, hardware experiments are carried out on the self-built platform to further validate the effectiveness of the proposed method. As depicted in Figure 5, multiple UAVs collaboratively deliver a spherical payload, which is connected to each quadrotor by a tether. The frame of each quadrotor is DJI-F330, with a motor-to-motor distance of . Raspberry Pi 4B serves as the onboard computer, facilitating communication between the ground station and the Pixhawk 4. Data communication between the ground station and the onboard computer utilizes Robot Operation System (ROS) via WiFi, while communication between the onboard computer and Pixhawk employs the MAVLink protocol. The ground station transmits planned trajectories to the Pixhawk, including UAV positions and velocities, which is achieved through ROS message subscription and publishing mechanisms. Throughout the planned trajectories transfer process, the autopilot Pixhawk should be in offboard mode, which is activated using a MAVLink message sent through the Radiolink AT98 remote control. It is important to note that the RC radio receiver is installed on the UAV and connected to the Pixhawk to receive the signal from the remote control. The control input calculation for each UAV is performed on the Pixhawk based on the desired positions and velocities of each UAV. The Qualisys motion capture system, equipped with fourteen cameras, identifies reflective markers on the quadrotors and payload to record their positions. The computer configuration utilized in the optimization problem solving is as follows: The processor is Intel(R) Core(TM) i7-8700 CPU, and the memory is 16 GB. The parameters of the three-UAV transportation system are given as . The parameters of the two-UAV transportation system, including the rope length and mass of the UAV, are kept consistent with those of the three-UAV transportation system. The payload mass is set as .
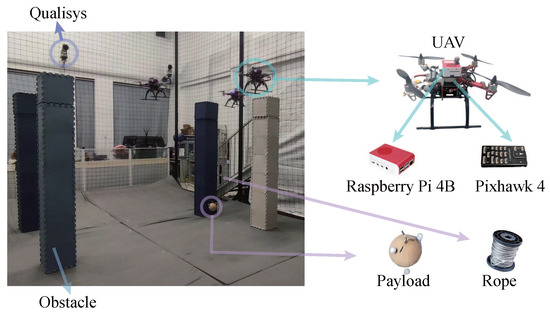
Figure 5.
Experimental platform.
Experiment 1: The parameter settings are the same as in Simulation 1. The obtained experimental results are presented in Figure 6, Figure 7, Figure 8 and Figure 9, including the trajectories of the two UAVs and the payload, along with a 3D visualization of the scene. The entire flight lasts for . At first, the UAV hovers at the starting position. At , the payload delivery task is initiated, and the UAV reaches the target position at about . Thereafter, the UAV hovers until the land command is received. The time required for the system to travel from the initial to the target position is . The planned trajectories are tracked by the cascade PID controller of the Pixhawk. More specifically, the positions and velocities of the two UAVs are presented in Figure 6a,b. The red desired trajectories can be accurately tracked by the blue real flight trajectories, which demonstrates the feasibility of the planning algorithm. The feasibility of the trajectory is achieved by fully considering the dynamics of the collaborative transportation system in the planning algorithm. On the other hand, the satisfactory tracking performance of the controller can be obtained from Figure 6a,b. During the experiment, the desired position and velocity of each UAV are transmitted to the Pixhawk, with velocity serving as a feedforward signal in the position control loop. The distance between the UAVs is shown in Figure 6c, where the red dashed line represents the minimum safety distance. As can be seen from the figure, the UAVs are able to maintain a safe distance throughout the entire delivery process, demonstrating that the planned trajectory ensures collision avoidance safety between the UAVs. The distances from the current payload position to the target position are illustrated in Figure 7a. Here, , , and represent the absolute deviations in three directions between the current payload position and the target. As evident from the figure, these deviations tend towards zero, affirming that the proposed method effectively achieves precise payload delivery to the intended position. The payload velocity is shown in Figure 7b. It can be observed from the figure that the planned trajectory ensures the velocity remains in the given range. The payload swing angles are depicted in Figure 8, which demonstrates that the planned trajectory maintains the system’s formation constraint. Figure 6a,b show that before , both UAVs remain in a stable hovering state, resulting in a constant inter-UAV distance, as depicted in Figure 6c. The delivery task begins at , causing variations in the distance between the UAVs. The distance reaches its minimum around , primarily due to position tracking deviations observed in the trajectory plots of Figure 6a,b. After the payload is delivered to the target location at (as shown in Figure 7), the UAVs return to a hovering state with a relatively stable distance between them. However, Figure 7 reveals significant fluctuations in payload velocity, primarily due to the payload swing effect. This swing phenomenon poses substantial challenges to system safety, potentially causing payload velocities to exceed prescribed limits and introducing hazards. This effect becomes especially pronounced during high-speed operations or complex flight maneuvers, significantly increasing the risk of collisions with environmental obstacles. Future research will focus on developing payload swing suppression control strategies to mitigate these dynamic effects effectively. Furthermore, to illustrate the collision avoidance trajectory generated by the proposed method, the snapshot of the experiment is depicted in Figure 9. This visualization reveals the collaborative aerial transportation system successfully avoiding collisions with environmental obstacles during real flight. In addition, the UAVs are kept a safe distance from each other, which means that the safety constraint is ensured by the proposed planning scheme.
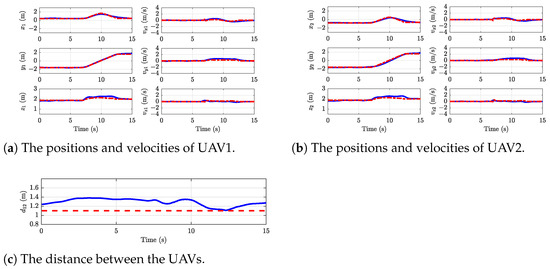
Figure 6.
The UAV trajectories results in Experiment 1. (Blue solid line): experiment results; (Red dashed line): desired values/minimum safety distance.
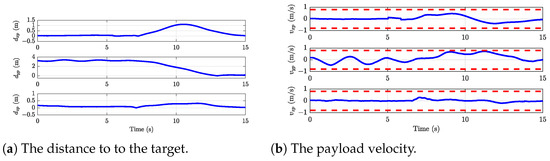
Figure 7.
The position and velocity results of the payload in Experiment 1.
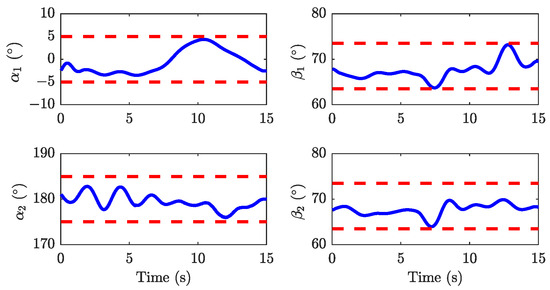
Figure 8.
Payload swing angles in Experiment 1. (Red dashed line): swing angle limit.

Figure 9.
Snapshot of Experiment 1. The trajectories of UAVs are depicted by solid lines, while the payload trajectory is indicated by the dashed line.
Figure 6c and Figure 10a present a comparison of the distances between the two UAVs in Experiment 1 and Simulation 1, respectively. During the initial phase (), both UAVs remain in a hovering state, and the simulation results closely align with the experimental data. After , the distance between the UAVs begins to decrease; however, a significant reduction is observed in the experimental results only around , likely due to tracking delays and controller precision. Figure 7a and Figure 10b compare the distances from the payload to the target in the simulation and experiment, demonstrating a high degree of consistency. This suggests that the proposed method effectively ensures accurate payload delivery in both scenarios. Figure 7b and Figure 10c illustrate the comparison of payload velocity. While both the simulation and experiment maintain the velocity within the predefined range, noticeable payload swings are observed in the experimental data. Figure 8 and Figure 10d compare the payload swing angles. Although the swing angles remain within the specified limits in both cases, significant discrepancies are evident. These differences indicate substantial inaccuracies in the theoretical model’s ability to describe the payload swing. Furthermore, the use of the Euler method to represent dynamic constraints is likely to have contributed to these discrepancies.
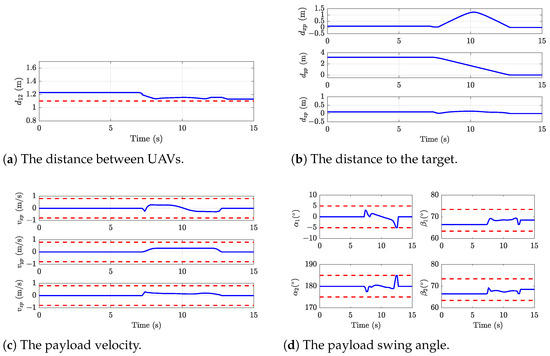
Figure 10.
The results of the proposed method in Simulation 1. (Blue solid line): simulation results; (Red dashed line): constraint boundaries.
Experiment 2: The parameter settings are the same as in Simulation 2. The experimental results of the proposed method are recorded in Figure 11, Figure 12, Figure 13 and Figure 14. The entire trajectory lasts for 15 seconds. The UAV starts moving at around and reaches the target position at approximately . The expected positions and velocities of each UAV in Figure 11 are closely tracked with high precision. The distance among the UAVs is demonstrated in Figure 11d, where the distance is kept in the safe range. According to Figure 12, it is found that the payload is accurately and quickly transported to the desired position and the payload velocity is limited in the allowable range. The payload angles are shown in Figure 13. The snapshot of Experiment 2, shown in Figure 14, confirms the maintenance of a safe distance between the transportation system and obstacles. Figure 15 presents the top view of the UAVs and payload trajectories in Experiment 2. The dashed lines represent the desired trajectories of the UAVs, obtained by solving the optimization problem (26). The solid lines indicate the actual trajectories of the UAVs. The cylinders represent obstacles, and the shaded gray area indicates the instance where UAV2 moves in the negative x-direction to avoid potential collisions. This move causes all other UAVs to shift right as well to maintain formation. This behavior demonstrates the effectiveness of the proposed method in preventing system-environment collisions. Figure 12a–c show that before , all UAVs maintain a hovering state, with the distance between them remaining nearly constant, as seen in Figure 10d. Once , the delivery task begins, and the distance between the UAVs starts to increase. The UAVs then follow the desired task trajectory, adjusting their positions and velocities accordingly, as depicted in Figure 12a–c. After about , the payload is successfully delivered to the target location (shown in Figure 12), and the UAVs return to a hovering state, with the distance between them stabilizing once again. However, during this phase, fluctuations in both payload velocity and the distance between the UAVs are evident. These fluctuations are primarily caused by the payload swing, as illustrated in Figure 13. Furthermore, due to the imposed collision avoidance between UAVs and formation constraints, both the payload and other UAVs exhibit varying degrees of displacement in the x-direction when UAV2 enters the shaded region. The collision avoidance performance between the transportation system and obstacles, as well as among the UAVs themselves, underscores the effectiveness of the safety constraint.
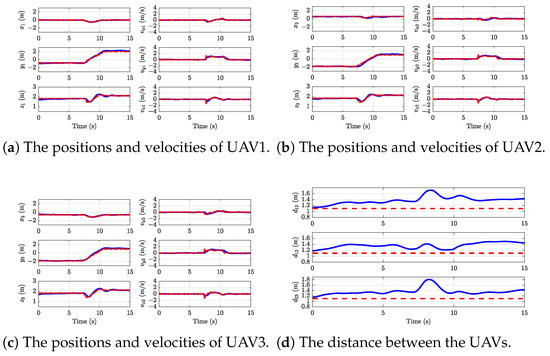
Figure 11.
The UAV trajectories results in Experiment 2. (Blue solid line): experiment results; (Red dashed line): desired values/minimum safety distance.
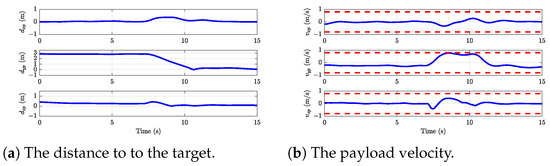
Figure 12.
The position and velocity results of the payload in Experiment 2. (Red dashed line): velocity limit.
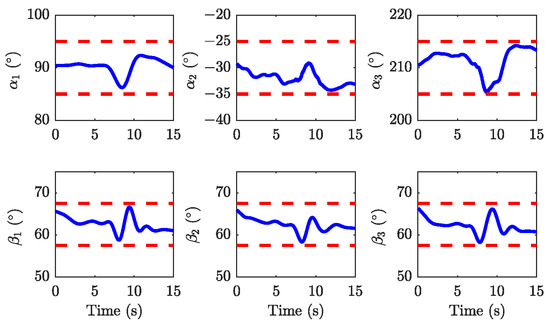
Figure 13.
Payload swing angles in Experiment 2. (Red dashed line): swing angle limit.
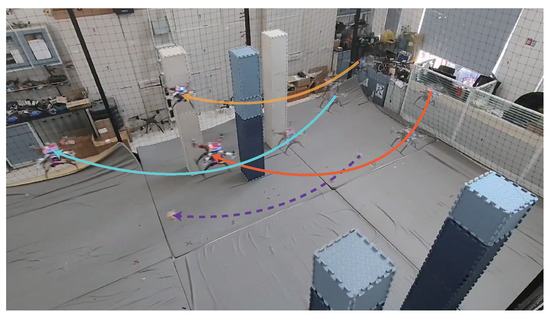
Figure 14.
Snapshot of Experiment 2. The trajectories of UAVs are depicted by solid lines, while the payload trajectory is indicated by the dashed line.
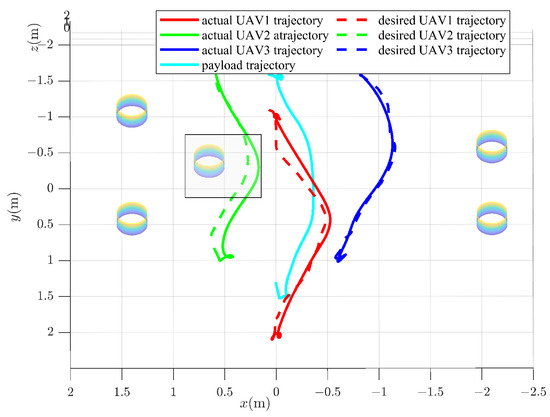
Figure 15.
The top view of the trajectories in Experiment 2. Dotted line: desired value; solid line: actual value.
A comparative analysis of the distances between UAVs in Experiment 2 and Simulation 2 is presented in Figure 11d and Figure 16a. During the initial phase (), both UAVs maintain a stable hovering position, with the simulation results closely matching the experimental data. After , the distance between the UAVs starts to increase, and the system successfully completes the payload delivery task by , after which the UAVs return to hovering state. While the distance between the UAVs remains consistent in both the simulation and experimental scenarios, the experimental results show notable fluctuations, primarily due to payload swing effects. The comparison of payload velocity is illustrated in Figure 12b and Figure 16c. Although both the simulation and experimental data indicate that payload velocities remain within the specified constraints, the experimental results exhibit more pronounced velocity variations. Figure 13 and Figure 16d compare the payload swing angles in the experimental and simulation cases. Despite the swing angles staying within the designated limits in both scenarios, significant disparities are observed. These discrepancies can be attributed to two main factors: the theoretical model’s inability to precisely capture payload swing dynamics and the approximations inherent in using the Euler method for representing dynamics constraint.
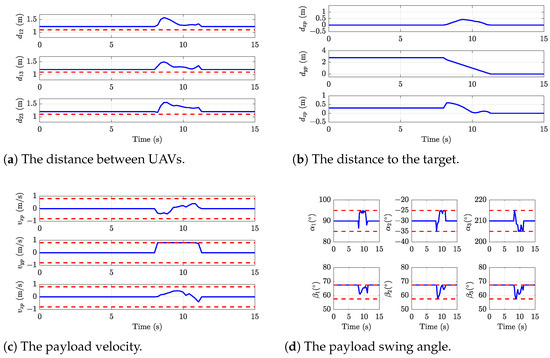
Figure 16.
The results of the proposed method in Simulation 2. (Blue solid line): simulation results; (Red dashed line): constraint boundaries.
In summary, the trajectories generated by the proposed method for the collaborative transportation system ensure swift payload delivery to the target location while mitigating collisions with obstacles and among UAVs.
Remark 2.
The planned trajectory can be disrupted by external disturbances, resulting in deviations that hinder accurate tracking. These deviations significantly increase the risk of collisions, either between UAVs or with environmental obstacles, thus posing a considerable threat to overall system safety. Future work will focus on extending the current framework to develop obstacle avoidance trajectory planning methods that account for external influences.
5. Conclusions
A unified collision avoidance trajectory planning algorithm is presented for collaborative aerial transportation systems in this paper. Specifically, the trajectory planning problem is formulated as an optimization problem, and the traveling time is chosen as the optimization objective while considering the dynamics, actuation, safety, and formation constraints. To expedite the solution speed of optimization problems, collision avoidance constraints between the system and environmental obstacles are established using dual variables. Comprehensive simulations and real-world experiments are conducted to demonstrate the effectiveness of the proposed method. The results show that the method can generate optimized trajectories that simultaneously satisfy system dynamics, actuation, safety, and formation constraints. This ensures not only the precise delivery of the payload to the target location but also effectively prevents collisions between UAVs and between systems with environmental obstacles. Moreover, the proposed method achieves comparable trajectory times to the compared method while significantly reducing the computation time. This demonstrates the clear advantage of utilizing dual variables for obstacle avoidance in complex environments. These capabilities significantly enhance the system’s safety and reliability in complex environments, offering an efficient and robust solution for collaborative UAV transportation tasks. The method’s potential is further highlighted in real-world applications requiring accurate and safe trajectory planning, such as logistics delivery and disaster relief operations. Future research will explore more complex environments, including scenarios with moving obstacles in the planning problem.
Author Contributions
Conceptualization, Y.C.; methodology, Y.C. and X.L.; software, Y.C.; validation, Y.C.; formal analysis, Y.C.; investigation, Y.C.; resources, Y.C.; data curation, Y.C.; writing—original draft preparation, Y.C. and X.L.; writing—review and editing, Y.C. and X.L.; visualization, Y.C.; supervision, X.L. and J.H.; project administration, J.H.; funding acquisition, Y.C. and X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by Postdoctoral Fellowship Program of CPSF under Grant GZC20231173, in part by National Natural Science Foundation of China under Grant 62273187, and in part by the Natural Science Foundation of Tianjin under Grant 23JCQNJC01930.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Harikumar, K.; Senthilnath, J.; Sundaram, S. Multi-UAV oxyrrhis marina-inspired search and dynamic formation control for forest firefighting. IEEE Trans. Autom. Sci. Eng. 2019, 16, 863–873. [Google Scholar] [CrossRef]
- Wang, J.; Wang, P.; Tian, B. Hyperbolic tangent function-based fixed-time event-triggered control for quadrotor aircraft with prescribed performance. J. Frankl. Inst. 2022, 359, 6267–6285. [Google Scholar] [CrossRef]
- Zhang, J.; Sheng, H.; Chen, Q.; Zhou, H.; Yin, B.; Li, J.; Li, M. A four-dimensional space-time automatic obstacle avoidance trajectory planning method for multi-UAV cooperative formation flight. Drones 2022, 6, 192. [Google Scholar] [CrossRef]
- Shan, L.; Li, H.B.; Miura, R.; Matsuda, T.; Matsumura, T. A novel collision avoidance strategy with D2D communications for UAV systems. Drones 2023, 7, 283. [Google Scholar] [CrossRef]
- Xian, B.; Yang, S. Robust tracking control of a quadrotor unmanned aerial vehicle-suspended payload system. IEEE/ASME Trans. Mechatronics 2020, 26, 2653–2663. [Google Scholar] [CrossRef]
- Li, H.; Zhong, H.; Gao, J.; Lv, Y.; Sha, J.; Liang, J.; Zhang, H.; Wang, Y. A nonlinear trajectory tracking control strategy for quadrotor with suspended payload based on force sensor. IEEE Trans. Intell. Veh. 2024, 9, 704–714. [Google Scholar] [CrossRef]
- Peng, X.; Zhang, Z.; Zhang, A.; Yuen, K.V. Antisaturation backstepping control for quadrotor slung load system with fixed-time prescribed performance. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 1–12. [Google Scholar] [CrossRef]
- Pounds, P.E.; Dollar, A. Hovering stability of helicopters with elastic constraints. In Proceedings of the Dynamic Systems and Control Conference, Cambridge, MA, USA, 12–15 September 2010; Volume 44182, pp. 781–788. [Google Scholar]
- Backus, S.B.; Odhner, L.U.; Dollar, A.M. Design of hands for aerial manipulation: Actuator number and routing for grasping and perching. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 34–40. [Google Scholar]
- Suarez, A.; Jimenez-Cano, A.; Vega, V.; Heredia, G.; Rodriguez-Castaño, A.; Ollero, A. Lightweight and human-size dual arm aerial manipulator. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems, Miami, FL, USA, 13–16 June 2017; pp. 1778–1784. [Google Scholar]
- Kim, H.; Seo, H.; Choi, S.; Tomlin, C.J.; Kim, H.J. Incorporating safety into parametric dynamic movement primitives. IEEE Robot. Autom. Lett. 2019, 4, 2260–2267. [Google Scholar] [CrossRef]
- Sreenath, K.; Michael, N.; Kumar, V. Trajectory generation and control of a quadrotor with a cable-suspended load-A differentially-flat hybrid system. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 4888–4895. [Google Scholar]
- Tang, S.; Thomas, J.; Kumar, V. Hold or take optimal plan (hoop): A quadratic programming approach to multi-robot trajectory generation. Int. J. Robot. Res. 2018, 37, 1062–1084. [Google Scholar] [CrossRef]
- Kim, H.; Seo, H.; Kim, J.; Kim, H.J. Sampling-based motion planning for aerial pick-and-place. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems, Macau, China, 3–8 November 2019; pp. 7402–7408. [Google Scholar]
- Silveira, J.; Givigi, S.N.; Freire, E.O.; Molina, L.; Carvalho, E. Aggressive motion planning for a quadrotor system with slung load based on RRT. In Proceedings of the 2020 IEEE International Systems Conference, Montreal, QC, Canada, 24 August–20 September 2020; pp. 1–7. [Google Scholar]
- Foehn, P.; Falanga, D.; Kuppuswamy, N.; Tedrake, R.; Scaramuzza, D. Fast trajectory optimization for agile quadrotor maneuvers with a cable-suspended payload. In Proceedings of the Robotics: Science and Systems, Cambridge, MA, USA, 12–16 July 2017. [Google Scholar]
- Zeng, J.; Kotaru, P.; Mueller, M.W.; Sreenath, K. Differential flatness based path planning with direct collocation on hybrid modes for a quadrotor with a cable-suspended payload. IEEE Robot. Autom. Lett. 2020, 5, 3074–3081. [Google Scholar] [CrossRef]
- Hua, H.; Fang, Y.; Zhang, X.; Qian, C. A time-optimal trajectory planning strategy for an aircraft with a suspended payload via optimization and learning approaches. IEEE Trans. Control. Syst. Technol. 2022, 30, 2333–2343. [Google Scholar] [CrossRef]
- Sreenath, K.; Kumar, V. Dynamics, control and planning for cooperative manipulation of payloads suspended by cables from multiple quadrotor robots. Proc. Robot. Sci. Syst. 2013, 1, r3. [Google Scholar]
- Liu, Y.; Zhang, F.; Huang, P.; Zhang, X. Analysis, planning and control for cooperative transportation of tethered multi-rotor UAVs. Aerosp. Sci. Technol. 2021, 113, 106673. [Google Scholar] [CrossRef]
- Geng, J.; Singla, P.; Langelaan, J.W. Load-distribution-based trajectory planning and control for a multilift system. J. Aerosp. Inf. Syst. 2022, 19, 366–381. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.; Han, J. Trajectory planning of load transportation with multi-quadrotors based on reinforcement learning algorithm. Aerosp. Sci. Technol. 2021, 116, 106887. [Google Scholar] [CrossRef]
- Pei, C.; Zhang, F.; Huang, P.; Yu, H. Trajectory planning for collaborative transportation by tethered multi-UAVs. In Proceedings of the 2021 IEEE International Conference on Real-time Computing and Robotics, Xining, China, 15–19 July 2021; pp. 769–775. [Google Scholar]
- Jackson, B.E.; Howell, T.A.; Shah, K.; Schwager, M.; Manchester, Z. Scalable cooperative transport of cable-suspended loads with UAVs using distributed trajectory optimization. IEEE Robot. Autom. Lett. 2020, 5, 3368–3374. [Google Scholar] [CrossRef]
- Alothman, Y.; Guo, M.; Gu, D. Using iterative LQR to control two quadrotors transporting a cable-suspended load. IFAC-PapersOnLine 2017, 50, 4324–4329. [Google Scholar] [CrossRef]
- Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Zhang, X.; Liniger, A.; Borrelli, F. Optimization-based collision avoidance. IEEE Trans. Control Syst. Technol. 2020, 29, 972–983. [Google Scholar] [CrossRef]
- Thirugnanam, A.; Zeng, J.; Sreenath, K. Safety-critical control and planning for obstacle avoidance between polytopes with control barrier functions. In Proceedings of the 2022 International Conference on Robotics and Automation, Philadelphia, PA, USA, 23–27 May 2022; pp. 286–292. [Google Scholar]
- Foehn, P.; Romero, A.; Scaramuzza, D. Time-optimal planning for quadrotor waypoint flight. Sci. Robot. 2021, 6, eabh1221. [Google Scholar] [CrossRef] [PubMed]
- Andersson, J.A.E.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi – A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).