Joint Optimization Control Algorithm for Passive Multi-Sensors on Drones for Multi-Target Tracking
Abstract
1. Introduction
2. Problem Description and Mathematical Model
2.1. Multi-Target Tracking Model for Distributed APBR Networks
2.2. Multi-Node Optimal Control Model for Distributed APBR Networks
3. Multi-Target Density Fusion Method Under Limited FOV
3.1. AA Fusion Based on LMB Density
| Algorithm 1: The flow of the LMB-AA fusion algorithm based on the flooding strategy |
3.2. AA Fusion Based on PLMB Density
4. Multi-Node Joint Optimization Control Algorithm
4.1. Task Adaptive Switching Mechanism
4.2. Optimization Objective Function for Different Tasks
4.2.1. Derivation of the Objective Function for Tracking Tasks
4.2.2. Derivation of the Objective Function for Searching Tasks
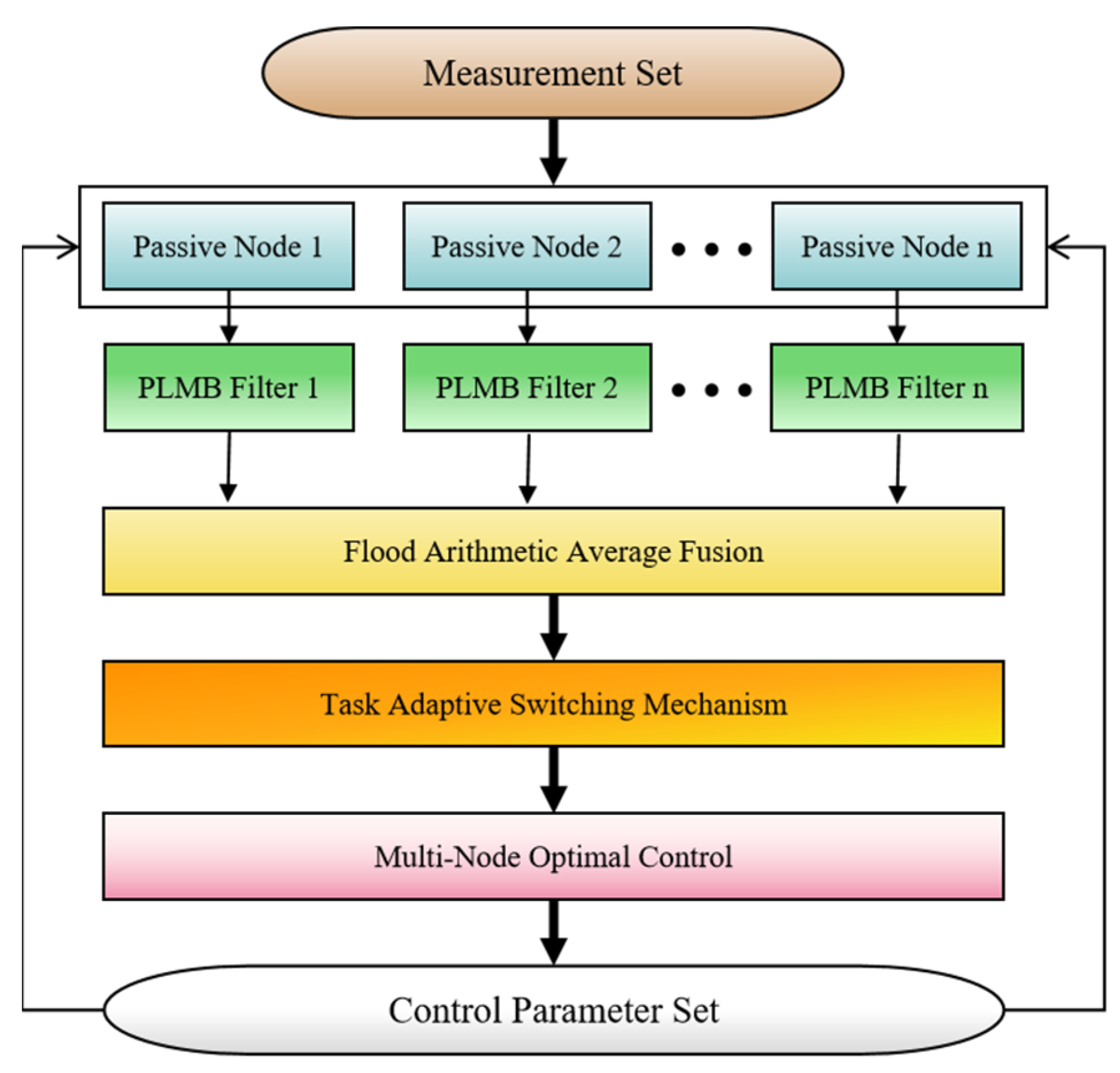
4.3. Joint Optimization Control Algorithm Flow
5. Simulation Verification and Result Analysis
5.1. Experimental Scenario Setting
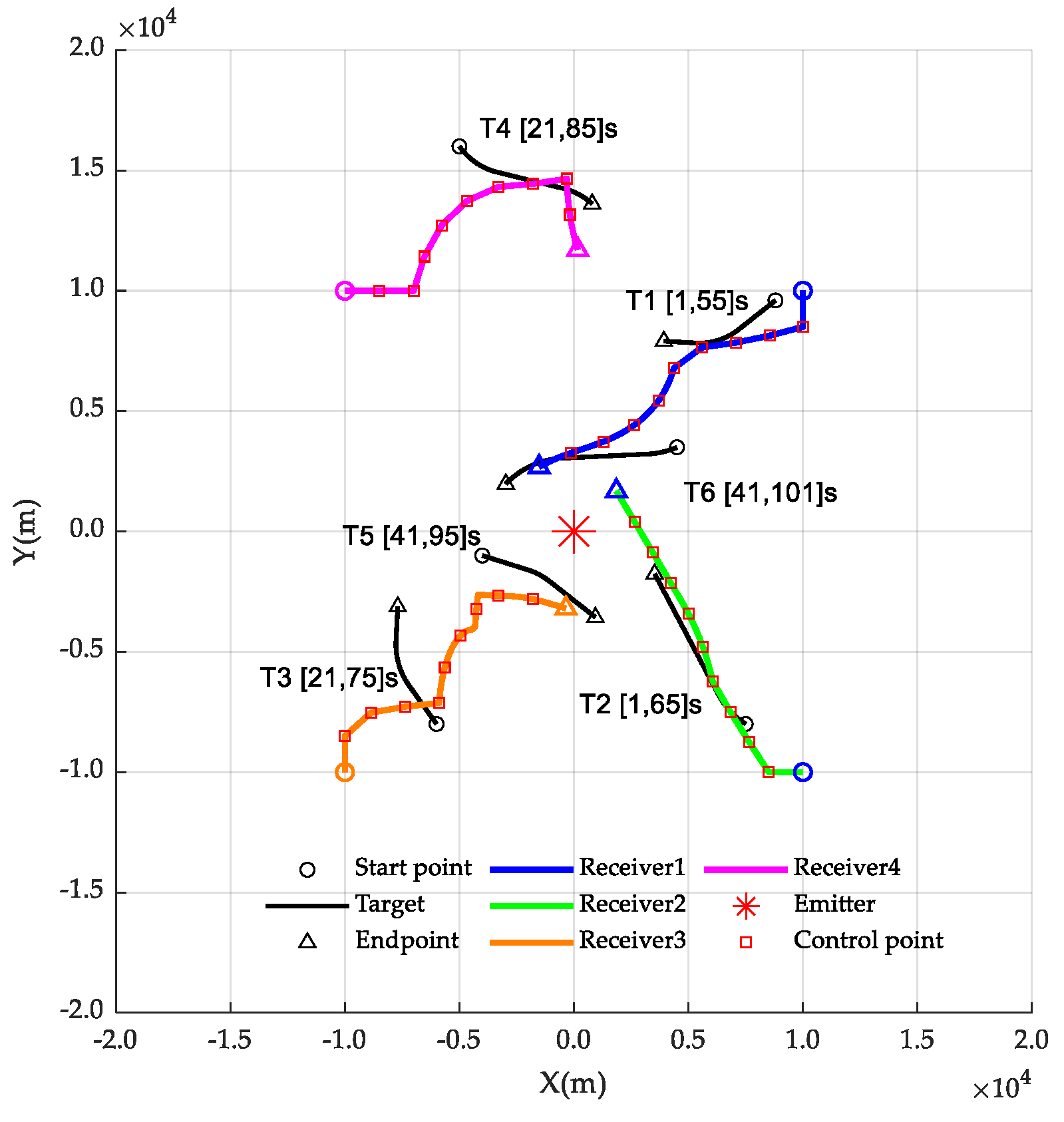
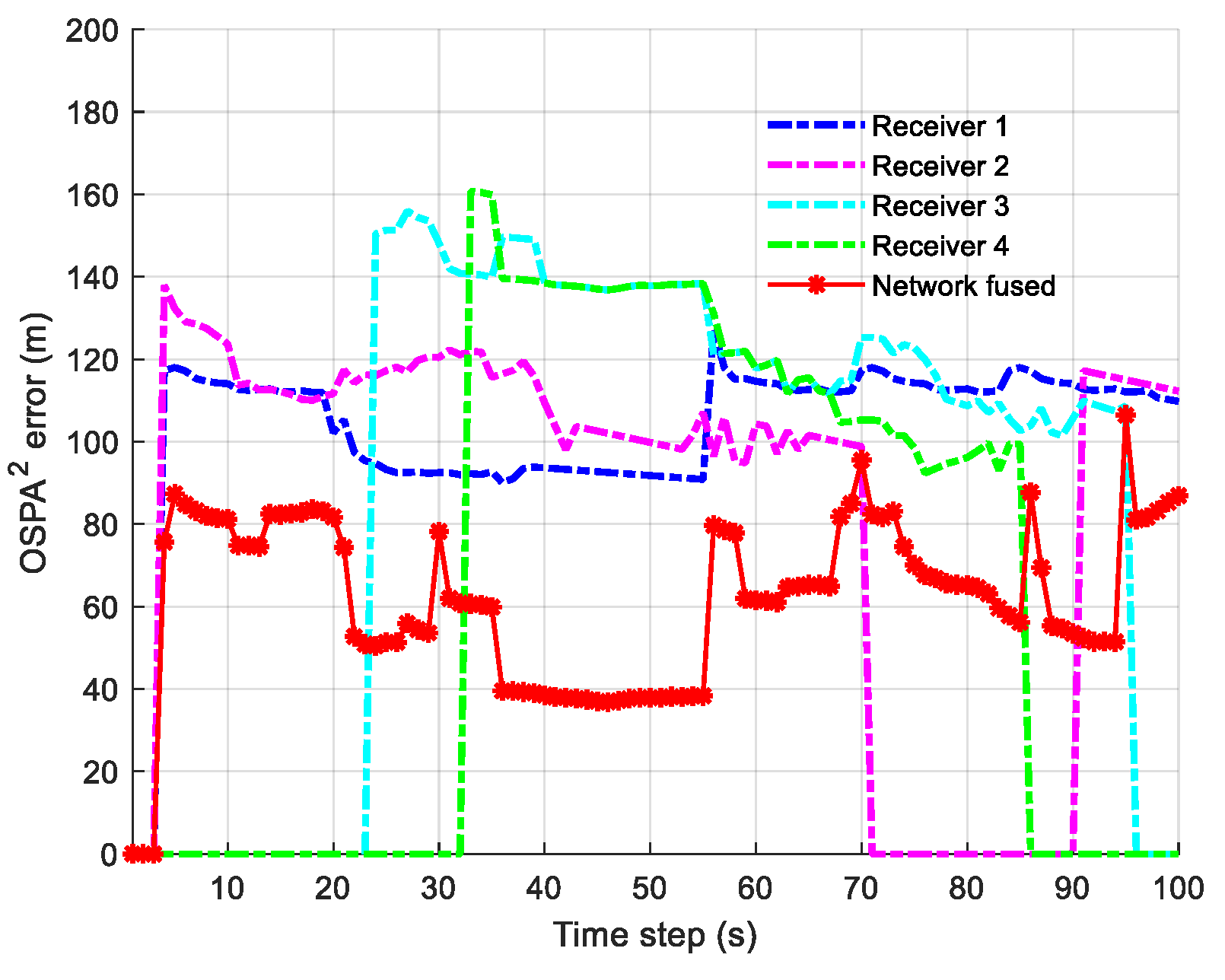
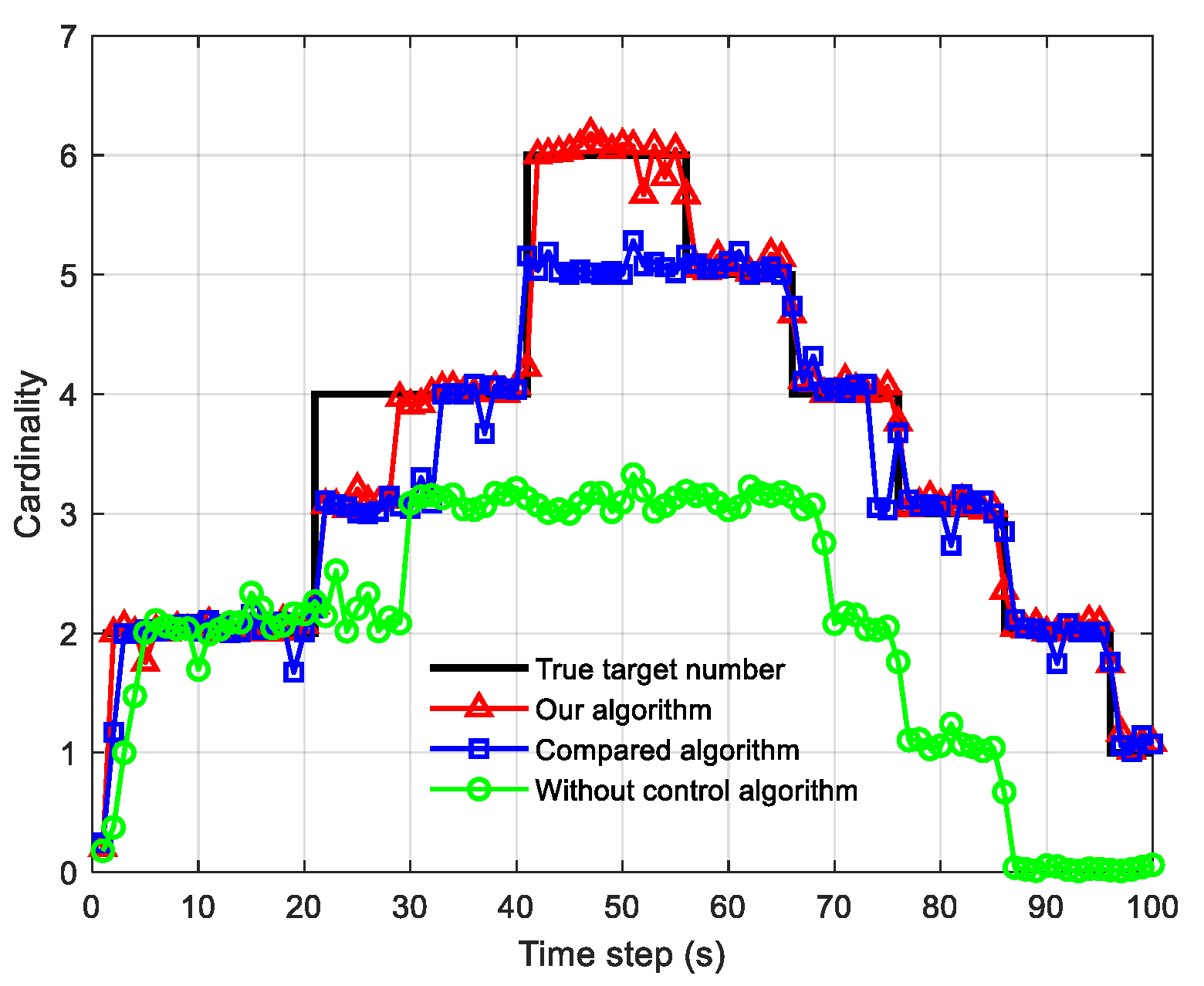
5.2. Analysis of Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hu, S.; Yi, J.; Wan, X.; Cheng, F.; Hu, Y.; Hao, C. Illuminator of Opportunity Localization for Digital Broadcast-Based Passive Radar in Moving Platforms. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 3539–3549. [Google Scholar] [CrossRef]
- Gabard, B.; Wasik, V.; Rabaste, O.; Deloues, T.; Poullin, D.; Jeuland, H. Airborne Targets Detection by UAV-Embedded Passive Radar. In Proceedings of the 2020 17th European Radar Conference (EuRAD), Utrecht, The Netherlands, 10–15 January 2021; pp. 346–349. [Google Scholar]
- Malanowski, M.; Rytel-Andrianik, R.; Kulpa, K.; Stasiak, K.; Ciesielski, M.; Kulpa, J. Geometric Clutter Analysis for Airborne Passive Coherent Location Radar. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Zhao, Z.; Cao, Y.; Wang, Y.; Zhou, H. Transmitted-Signal-Free Target Information Extraction for OFDM-Based Passive Radar with Time-Varying Sparse Model. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Colone, F.; Filippini, F.; Pastina, D. Passive Radar: Past, Present, and Future Challenges. IEEE Aerosp. Electron. Syst. Mag. 2023, 38, 54–69. [Google Scholar] [CrossRef]
- Sun, Z.; Wu, J.; Yen, G.G.; Lu, Z.; Yang, J. Performance Analysis and System Implementation for Energy-Efficient Passive UAV Radar Imaging System. IEEE Trans. Veh. Technol. 2023, 72, 9938–9955. [Google Scholar] [CrossRef]
- Mahler, R.P.S. Multitarget Bayes filtering via first-order multitarget moments. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1152–1178. [Google Scholar] [CrossRef]
- Vo, B.; Vo, B.; Cantoni, A. Bayesian Filtering with Random Finite Set Observations. IEEE Trans. Signal Process. 2008, 56, 1313–1326. [Google Scholar] [CrossRef]
- Saucan, A.; Coates, M.J.; Rabbat, M. A Multisensor Multi-Bernoulli Filter. IEEE Trans. Signal Process. 2017, 65, 5495–5509. [Google Scholar] [CrossRef]
- García-Fernández, Á.F.; Williams, J.L.; Granström, K.; Svensson, L. Poisson Multi-Bernoulli Mixture Filter: Direct Derivation and Implementation. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1883–1901. [Google Scholar] [CrossRef]
- Boström-Rost, P.; Axehill, D.; Hendeby, G. Sensor Management for Search and Track Using the Poisson Multi-Bernoulli Mixture Filter. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2771–2783. [Google Scholar] [CrossRef]
- Vo, B.; Vo, B.; Phung, D. Labeled Random Finite Sets and the Bayes Multi-Target Tracking Filter. IEEE Trans. Signal Process. 2014, 62, 6554–6567. [Google Scholar] [CrossRef]
- Reuter, S.; Vo, B.; Vo, B.; Dietmayer, K. The Labeled Multi-Bernoulli Filter. IEEE Trans. Signal Process. 2014, 62, 3246–3260. [Google Scholar] [CrossRef]
- Vo, B.; Vo, B.; Hoang, H.G. An Efficient Implementation of the Generalized Labeled Multi-Bernoulli Filter. IEEE Trans. Signal Process. 2017, 65, 1975–1987. [Google Scholar] [CrossRef]
- Cament, L.; Correa, J.; Adams, M.; Pérez, C. The histogram Poisson, labeled multi-Bernoulli multi-target tracking filter. Signal Process. 2020, 176, 107714–107729. [Google Scholar] [CrossRef]
- Li, G.; Battistelli, G.; Yi, W.; Kong, L. Distributed multi-sensor multi-view fusion based on generalized covariance intersection. Signal Process. 2020, 166, 107246. [Google Scholar] [CrossRef]
- Li, G.; Battistelli, G.; Chisci, L.; Gao, L.; Wei, P. Distributed Joint Detection, Tracking, and Classification via Labeled Multi-Bernoulli Filtering. IEEE Trans. Cybern. 2024, 54, 1429–1441. [Google Scholar] [CrossRef]
- Shen, K.; Dong, P.; Jing, Z.; Leung, H. Consensus-Based Labeled Multi-Bernoulli Filter for Multitarget Tracking in Distributed Sensor Network. IEEE Trans. Cybern. 2022, 52, 12722–12733. [Google Scholar] [CrossRef]
- Yi, W.; Li, G.; Battistelli, G. Distributed Multi-Sensor Fusion of PHD Filters with Different Sensor Fields of View. IEEE Trans. Signal Process. 2020, 68, 5204–5218. [Google Scholar] [CrossRef]
- Li, T.C.; Song, Y.; Song, E.B.; Fan, H.Q. Arithmetic average density fusion—Part I: Some statistic and information-theoretic results. Inf. Fusion 2024, 104, 102199. [Google Scholar] [CrossRef]
- Li, T. Arithmetic Average Density Fusion—Part II: Unified Derivation for Unlabeled and Labeled RFS Fusion. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 3255–3268. [Google Scholar] [CrossRef]
- Li, T.; Yan, R.; Da, K.; Fan, H. Arithmetic Average Density Fusion—Part III: Heterogeneous Unlabeled and Labeled RFS Filter Fusion. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 1023–1034. [Google Scholar] [CrossRef]
- Li, T.C.; Hlawatsch, F. A distributed particle-PHD filter using arithmetic-average fusion of Gaussian mixture parameters. Inf. Fusion 2021, 73, 111–124. [Google Scholar] [CrossRef]
- Battistelli, G.; Chisci, L.; Fantacci, C.; Farina, A.; Graziano, A. Distributed multitarget tracking for passive multireceiver radar systems. In Proceedings of the 2013 14th International Radar Symposium (IRS), Dresden, Germany, 19–21 June 2013; pp. 337–342. [Google Scholar]
- Li, S.; Yi, W.; Hoseinnezhad, R.; Battistelli, G.; Wang, B.; Kong, L. Robust Distributed Fusion with Labeled Random Finite Sets. IEEE Trans. Signal Process. 2018, 66, 278–293. [Google Scholar] [CrossRef]
- Li, S.; Battistelli, G.; Chisci, L.; Yi, W.; Wang, B.; Kong, L. Computationally Efficient Multi-Agent Multi-Object Tracking with Labeled Random Finite Sets. IEEE Trans. Signal Process. 2019, 67, 260–275. [Google Scholar] [CrossRef]
- Gostar, A.K.; Hoseinnezhad, R.; Bab-Hadiashar, A. Multi-bernoulli sensor control via minimization of expected estimation errors. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 1762–1773. [Google Scholar] [CrossRef]
- Gostar, A.K.; Hoseinnezhad, R.; Bab-Hadiashar, A.; Liu, W. Sensor-Management for Multitarget Filters via Minimization of Posterior Dispersion. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2877–2884. [Google Scholar] [CrossRef]
- Ristic, B.; Vo, B.; Clark, D. A Note on the Reward Function for PHD Filters with Sensor Control. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1521–1529. [Google Scholar] [CrossRef]
- Beard, M.; Vo, B.T.; Vo, B.N.; Arulampalam, S. Sensor control for multi-target tracking using Cauchy-Schwarz divergence. In Proceedings of the 2015 18th International Conference on Information Fusion (Fusion), Washington, DC, USA, 6–9 July 2015; pp. 937–944. [Google Scholar]
- Zhu, Y.; Liang, S.; Gong, M.; Yan, J. Decomposed POMDP Optimization-Based Sensor Management for Multi-Target Tracking in Passive Multi-Sensor Systems. IEEE Sens. J. 2022, 22, 3565–3578. [Google Scholar] [CrossRef]
- LeGrand, K.A.; Zhu, P.; Ferrari, S. A Random Finite Set Sensor Control Approach for Vision-based Multi-object Search-While-Tracking. In Proceedings of the 2021 IEEE 24th International Conference on Information Fusion (FUSION), Sun City, South Africa, 1–4 November 2021; pp. 1–8. [Google Scholar]
- Nguyen, H.V.; Vo, B.N.; Vo, B.T.; Rezatofighi, H.; Ranasinghe, D.C. Multi-Objective Multi-Agent Planning for Discovering and Tracking Multiple Mobile Objects. IEEE Trans. Signal Process. 2024, 72, 3669–3685. [Google Scholar] [CrossRef]
- Li, T.; Corchado, J.M.; Prieto, J. Convergence of Distributed Flooding and Its Application for Distributed Bayesian Filtering. IEEE Trans. Signal Inf. Process. Netw. 2017, 3, 580–591. [Google Scholar] [CrossRef]
- Chen, X.; Tharmarasa, R.; Pelletier, M.; Kirubarajan, T. Integrated Clutter Estimation and Target Tracking Using Poisson Point Processes. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 1210–1235. [Google Scholar] [CrossRef]
- Wei, J.; Luo, F.; Qi, J.; Luo, X. Distributed Fusion of Labeled Multi-Bernoulli Filters Based on Arithmetic Average. IEEE Signal Process. Lett. 2024, 31, 656–660. [Google Scholar] [CrossRef]
- Boström-Rost, P.; Axehill, D.; Hendeby, G. PMBM Filter with Partially Grid-Based Birth Model with Applications in Sensor Management. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 530–540. [Google Scholar] [CrossRef]
- Verma, J.K.; Chhabra, J.K.; Ranga, V. Track Consensus-Based Labeled Multi-Target Tracking in Mobile Distributed Sensor Network. IEEE Trans. Mob. Comput. 2024, 23, 7351–7362. [Google Scholar] [CrossRef]
- Chen, K.; Chai, L.; Yi, W. Multi-Sensor Control for Jointly Searching and Tracking Multi-Target Using the Poisson Multi-Bernoulli Mixture Filter. In Proceedings of the 2022 11th International Conference on Control, Automation and Information Sciences (ICCAIS), Hanoi, Vietnam, 21–24 November 2022; pp. 240–247. [Google Scholar]
- Rahmathullah, A.S.; García-Fernández, Á.F.; Svensson, L. Generalized optimal sub-pattern assignment metric. In Proceedings of the 2017 20th International Conference on Information Fusion (Fusion), Xi’an, China, 10–13 July 2017. [Google Scholar]
- Beard, M.; Vo, B.T.; Vo, B.N. OSPA(2): Using the OSPA metric to evaluate multi-target tracking performance. In Proceedings of the 2017 International Conference on Control, Automation and Information Sciences (ICCAIS), Chiang Mai, Thailand, 31 October–1 November 2017; pp. 86–91. [Google Scholar]

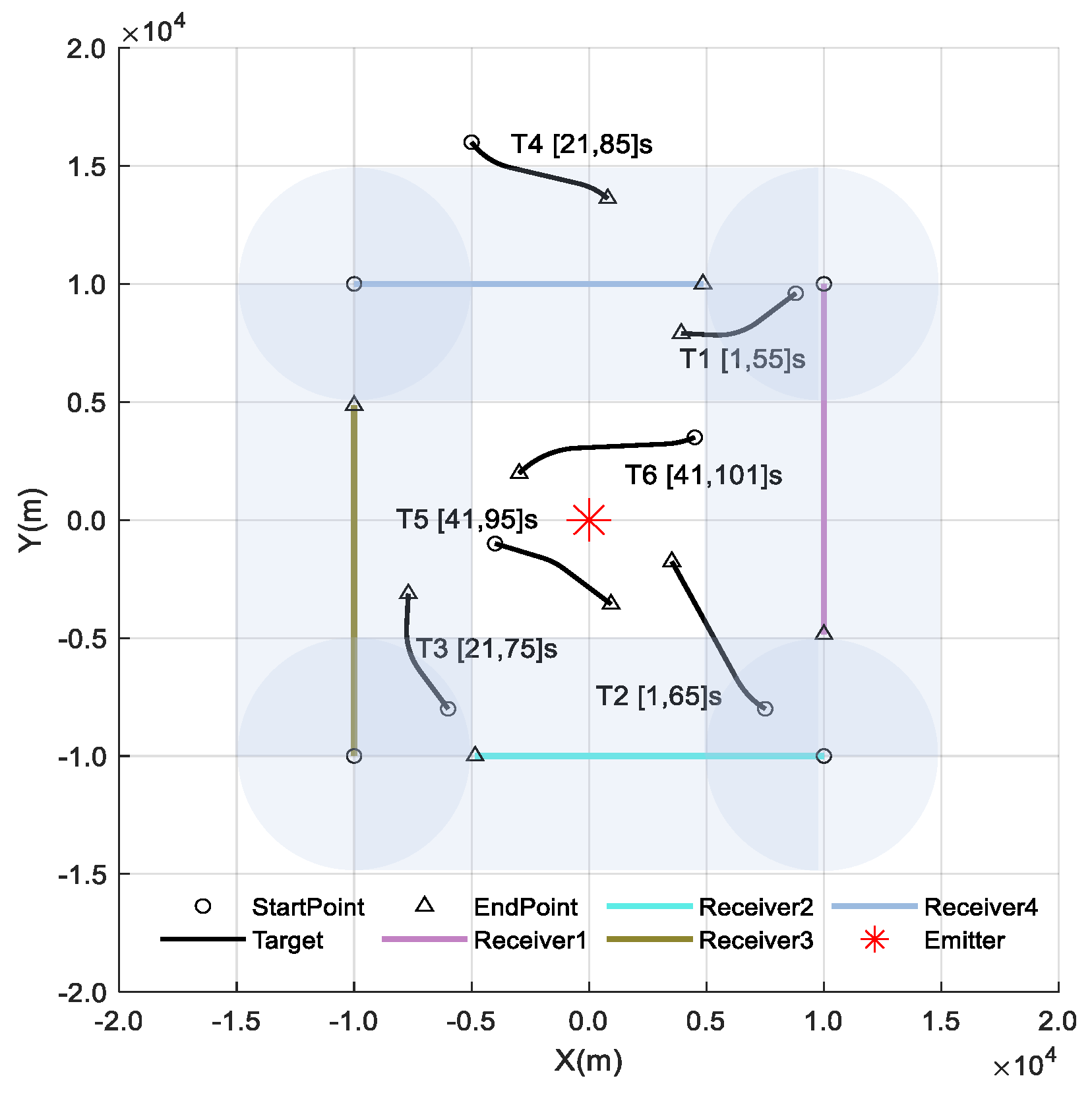


| Simulated Entity | ||
|---|---|---|
| Target 1 | [8800; −80; 9600; −60] | [1, 55] |
| Target 2 | [7500; −100; −8000; 60] | [1, 65] |
| Target 3 | [−6000; −60; −8000; 80] | [21, 75] |
| Target 4 | [−5000; 60; 16,000; −80] | [21, 85] |
| Target 5 | [−4000; 100; −1000; −30] | [41, 95] |
| Target 6 | [4500; −120; 3500; −50] | [41, 101] |
| Emitter | [0; 0; 0; 0] | - |
| Receiver 1 | [10,000; 0; 10,000; −150] | - |
| Receiver 2 | [10,000; −150; −10,000; 0] | - |
| Receiver 3 | [−10,000; 0; −10,000; 150] | - |
| Receiver 4 | [−10,000; 150; 10,000; 0] | - |
| Simulation Parameters | Specific Values |
|---|---|
| Detection radius of the node FOV | 5000 m |
| Probability of detection within node FOV | 0.95 |
| Target Track Confirmation Time | 3 |
| 5 | |
| 0.99 | |
| Target Extraction Threshold | 0.5 |
| 10−5 | |
| GM merging threshold ThGMm | 10 |
| Survival probability of newborn BCs | 0.01 |
| 10−5 | |
| 30 |
| Control Moments/s | Receiver 1 | Receiver 2 | Receiver 3 | Receiver 4 |
|---|---|---|---|---|
| 1 | S | S | S | S |
| 11 | T | T | S | S |
| 21 | T | T | T | S |
| 31 | T | T | T | T |
| 41 | T | T | T | T |
| 51 | T | T | T | T |
| 61 | T | T | T | T |
| 71 | T | T | T | T |
| 81 | T | T | T | T |
| 91 | T | T | T | S |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, X.; Lu, Y.; Ruan, L. Joint Optimization Control Algorithm for Passive Multi-Sensors on Drones for Multi-Target Tracking. Drones 2024, 8, 627. https://doi.org/10.3390/drones8110627
Guan X, Lu Y, Ruan L. Joint Optimization Control Algorithm for Passive Multi-Sensors on Drones for Multi-Target Tracking. Drones. 2024; 8(11):627. https://doi.org/10.3390/drones8110627
Chicago/Turabian StyleGuan, Xin, Yu Lu, and Lang Ruan. 2024. "Joint Optimization Control Algorithm for Passive Multi-Sensors on Drones for Multi-Target Tracking" Drones 8, no. 11: 627. https://doi.org/10.3390/drones8110627
APA StyleGuan, X., Lu, Y., & Ruan, L. (2024). Joint Optimization Control Algorithm for Passive Multi-Sensors on Drones for Multi-Target Tracking. Drones, 8(11), 627. https://doi.org/10.3390/drones8110627






