Abstract
The rapid advancement of unmanned aerial vehicles (UAVs) has introduced new challenges in overseeing and managing their flight operations due to their diverse flight dynamics and performance metrics. To address these complexities, this study introduces a concept of trajectory conformity aimed at enhancing the supervision and control of UAV flights. Trajectory conformity, from a regulatory perspective, is defined as the distribution of deviations between a UAV’s actual flight path and its intended trajectory, offering a measure of system-wide operational error. The concept of conformity is hoped to simplify and strengthen the monitoring process to ensure conflict-free drone flying. The present work is also concerned with the development of a comprehensive UAV collision risk model grounded in trajectory conformity analysis. The normality and homogeneity of UAV trajectory deviations are validated by evaluating the trajectory data obtained from real-world UAV flights. Well clear thresholds between two UAVs operating in three orthogonal directions within the same airspace have been established by the developed model. The results obtained demonstrate the effectiveness in omni-encounter scenarios, underscoring the potential to strengthen safety measures. The present work is expected to enhance UAV safety systems, such as detect and avoid (DAA) and unmanned aircraft system traffic management (UTM), by enabling real-time collision warnings within predefined safety thresholds, supporting proactive risk mitigation. Furthermore, the model’s versatility allows it to be applied to various UAV operational aspects in future works, including route planning, flight procedure design, airspace capacity assessments, and establishment of separation minima.
1. Introduction
As the Beyond Visual Line of Sight (BVLOS) operation of UAVs is gradually integrated into the existing airspace system, the potential operational risks of UAVs have gained significant attention [1,2,3,4,5,6,7,8]. Accurately assessing the collision risk of UAVs, whether managed via autonomous airborne detect and avoid (DAA) systems or ground-based unmanned aircraft system traffic management (UTM), is essential for ensuring the safe and efficient operation of UAVs in various scenarios. The design of urban low-altitude airspace structures has an impact on the safe operation of UAVs, with methods such as airspace discretization and zonal or layer separation [9,10,11,12,13]. However, in free-flight airspace, UAVs can fly directly from the takeoff point to the destination, significantly enhancing operational efficiency. Therefore, studying the collision risks in free-flight airspace is of great importance [14,15]. Position uncertainty is one of the key factors considered in the evaluation of the UAV collision risk. However, this uncertainty can be caused by multiple factors, such as the electromagnetic environment, UAV control errors, and tracking delays, which complicates the supervision and monitoring of UAVs in practice.
To tackle the above-mentioned issues, this research introduces the concept of trajectory conformity, inspired by performance-based navigation (PBN) [16], as a measure of the total tracking error that occurs in the “human-machine-management-environment” system. Trajectory conformity is defined as the stochastic deviation between a UAV’s intended trajectory and its actual flight path. By applying this concept, we develop a UAV collision risk model that can serve as a tool for monitoring dynamic collision risks between UAVs. In addition, civil aviation authorities can utilize trajectory conformity to establish a framework that simplifies the evaluation of UAV operational safety.
This paper concerns UAV collision risk assessment, and is organized as follows: first, we provide a review of the literature in Section 2; in Section 3, we emphasize trajectory conformity to capture the inherent uncertainty in UAV flight paths; Section 4 presents a formulation of UAV dynamic collision risk based on trajectory conformity; Section 5 validates the potential of the proposed model in determining well clear thresholds; and, finally, Section 6 summarizes our initial findings and discusses prospective applications of the model developed.
2. Literature Review
Position uncertainty is one of the major factors contributing to the collision risk of UAVs. Therefore, investigating the UAVs’ tracking performance during flight is the key to evaluating and monitoring the collision risk [17,18], followed by research focusing on modeling the collision risk in different scenarios [19,20,21,22,23]. Many researchers have conducted in-depth studies on the collision probability generated by the uncertainty of the position during UAV movement. Zhang et al. [19] proposed a risk assessment model based on the flight trajectories of unmanned and manned aircraft in restricted areas of airports. Lee et al. [20] established a UAV collision risk model based on a 3D Gaussian distribution and validated the model with airport surveillance radar data. McFadyen and Martin [24] investigated the risk of vertical collisions between UAVs and crewed aircraft by analyzing airport surveillance data and UAV altitude-holding capabilities. La Cour-Harbo and Schiøler [25] established a collision risk model for UAV BVLOS flights by analyzing the encounter process between UAVs and general aviation aircraft. Bijjahalli et al. [21] formulated the UAV collision risk in free airspace, considering the CNS performance and wind uncertainty. Zhang et al. [26] modeled the collision of two UAVs in free airspace based on the positioning error obeying a three-dimensional Gaussian distribution and recommended the safety separation for UAV operation.
A further application of UAV’s collision model is to determine separation minima corresponding to the target level of safety (TLOS). A risk-based autonomous spacing approach was proposed by Weibel et al. [27] to monitor the near mid-air collision (NMAC) risk for encounters with varying initial separations via Monte Carlo simulation. Subsequently, Weinert et al. [28] constructed a mission-oriented flight trajectory model for small UAVs and investigated the autonomous spacing of UAVs in low-altitude non-terminal area airspace. Munoz et al. [29] proposed four UAV autonomous separation models based on the TCAS II collision resolution logic and analyzed the characteristics of these models from the perspectives of time-based separation and conflict area prediction. Wang et al. [17] investigated the 3D spatial deviation of UAVs from the standard trajectory under VLOS and BVLOS via a data-driven approach. Johnson et al. [22] cited UAV autonomy spacing models in RTCA SC-228 to derive the UAV autonomy separation in Class E airspace, which provides the technical support for developing the minimum operational performance standards (MOPS) for UAV DAA systems. Mullins et al. [30] investigated the dynamic spacing for UAV airborne DAA systems based on the time-based well clear threshold, considering UAV dynamics.
More recently, several scholars have applied the concept of civil aviation performance-based navigation (PBN) to the trajectory estimation of UAVs, that the random motion process of UAVs follows a stable Gaussian distribution. The total system error (TSE) represents the probability of the UAV deviating from the expected trajectory, which can be classified into path definition error (PDE), navigation system error (NSE), and flight technical error (FTE) [31]. Dai and Deng [32] proposed the concept of PBN to predict communication, navigation, and surveillance performances in the UAV’s operational airspace. Pang et al. [18] investigated the deviation of UAVs from their expected routes by analyzing UAV flight data. They also examined the effect of altitude change on UAV navigation performance [33]. Deng et al. [34] investigated the impact of the UAV approach to different types of urban obstacles on UAV horizontal navigation performance. Kallinen et al. [35] fitted UAV flight deviation data to analyze the static TSE of the UAV.
3. Trajectory Conformity
3.1. Definition
Ensuring a UAV’s adherence to the specified flight plan is essential in determining its ability to stay within the predefined airspace boundaries and thereby reduce collision risks to an acceptable level. From this perspective, trajectory conformity, related to the total tracking error, represents a three-dimensional (3D) stochastic distribution of the UAV’s actual track deviation from its intended path. This conformity can be established by comparing historical data of actual and desired flight paths. The field testing is typically tailored to specific operational scenarios (as shown in Figure 1). From the perspective of overseeing and monitoring the UAV operation, the trajectory conformity closely aligns with the regulatory goals for UAVs while also adapting to the diversity and flexibility of UAV technology systems, beneficial for promoting the safe, efficient, and smooth integration of UAVs into the national airspace system [33,36]. Moreover, utilizing trajectory conformity allows us to ascertain the boundary of the protected area for UAV routes and flight procedures [37], assess the capacity of low-altitude airspace [38], and establish suitable separations between UAVs in operational airspace [39].
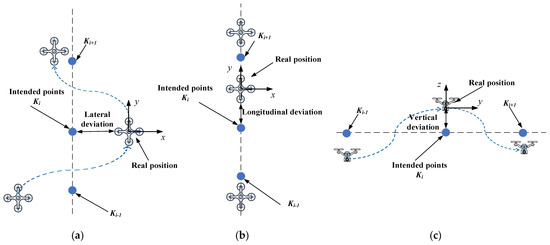
Figure 1.
Track deviation of UAV in three directions: (a) Lateral deviation. (b) Longitudinal deviation. (c) Vertical deviation.
This study uses trajectory conformity as the parameter to assess the UAV collision risk, as opposed to the traditional aircraft collision risk model in which the total system error (TSE), which is the deviation of an aircraft’s measuring position from its actual position, builds the collision risk. Furthermore, UAV trajectory conformity can be utilized as a metric to approve the designated airspace safety qualifications for UAVs by comparing their actual trajectory conformity to the required trajectory conformity. In cases where UAVs fail to meet the required trajectory conformity for the designated airspace, operators can enhance UAV’s trajectory conformity by incorporating additional ground Real-time kinematics (RTKs) [40], improving UAV flight control accuracy, and implementing other relevant methods. Failure by UAV operators to improve trajectory conformity through enhancements in communication, navigation, flight control, and other areas may result in operation restrictions or prohibitions. In UAV airspace management, trajectory conformity can also be employed to determine the UAV route’s semi-width, assess the capacity of a UAV operational airspace, and evaluate the separation minima.
3.2. Data Acquisition and Analysis
To obtain real track data of the UAVs, we established a ground RTK system and enhanced two UAVs with RTK transponders, ensuring a tracking error of less than 5 cm. As such, we regard the GPS + RTK track as authentic, leveraging it to calculate the UAV’s trajectory conformity. Subsequently, we acquired datasets on track deviations through experiments conducted in operational airspace on different days.
We conducted the field tests at a flight altitude of 200 m above the ground, with the same experimental procedure followed on every flight day. We next define datasets in three orthogonal directions, by statistically compiling track deviations of the UAV (as defined by Equations (1)–(3)), where , and denote the subsets of the UAV’s track deviations on flight day , as given by
where
where , , and represent the deviation data of the drone at the data collection point j on fight day , M represents the number of experiment days, and N represents the number of data collection point.
To determine UAV trajectory conformity (as demonstrated in Appendix A), we conducted normality tests individually on each day’s subset of the 3D track deviations. Furthermore, we conduct hypothesis tests to investigate the track deviations across different subsets. Following the successful normality tests of all sample data in the three datasets, we performed an analysis of variance (ANOVA) on the datasets that exhibited normal distribution. We formulated the null hypothesis H0 (indicating that the mean deviations of all test days are statistically equal) and the alternative hypothesis H1 (indicating that not all datasets have the same means). By denoting and as the sample mean and variance, respectively, for day i, the hypothesis test can be summarized as follows:
(i) Hypothesis test of sample means
(ii) Hypothesis test of sample variances
If H0 is accepted, it indicates that all flight experiment datasets have the same standard deviation at a certain confidence level. If H0 is rejected, we perform a post-hoc test on the abnormal dataset, then remove the abnormal data and continue to repeat the above.
4. Collision Risk Assessment
As previously stated, the collision risk is the probability of two UAVs’ 3D positions to overlap, which varies depending on their dynamic relative positions and velocities.
To model the encounter process, we establish both a ground coordinate system and an airframe coordinate system (Figure 2). The global coordinate system features an origin point chosen arbitrarily on the ground, where the Y-axis aligns with the magnetic north, the X-axis extends eastward, and the right-hand rule determines the Z-axis. On the other hand, the origin of a local coordinate system is positioned at the center of the UAV, with the Y-axis oriented towards the UAV’s forward direction, the X-axis perpendicular to the airframe’s symmetry plane, pointing towards the right side of the airframe, and the right-hand rule determining the Z-axis [41,42].
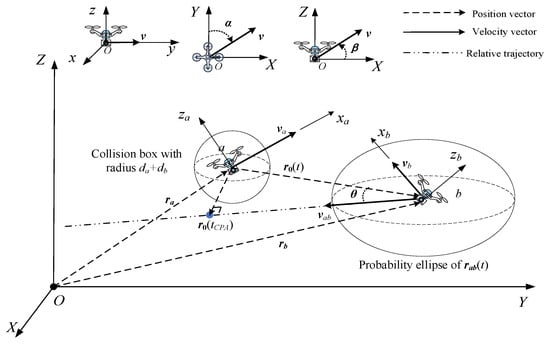
Figure 2.
Encounter process of two UAVs.
For the host UAV a and the intruder UAV b at time t with their respective actual position vectors , velocity vectors and desired position vectors and , we have
where and , the trajectory conformity of UAV a and UAV b, can be obtained through the approach developed in Section 3.2.
The relative actual position vector between UAV a and UAV b is then
while the relative desired position vector between UAV a and UAV b is
and the relative velocity vector is
where and denote the disired position of UAV a and UAV b at time t. Then
where
and
are the rotation matrices that represent the transformation from the airframe coordinate system to the global coordinate system, where is the heading of the UAV and is the climb angle of UAV (Figure 2).
In assessing the collision risk between UAVs, a simplified approach is adopted by considering each UAV’s collision box as a sphere with radius d. The trajectory conformity of the two UAVs is factored onto UAV b, and the collision box sizes of both UAVs are accounted for by adding them onto UAV a. In this case, the collision risk of the two UAVs can be simplified as the probability of UAV b falling into the UAV a’s collision box. Figure 2 depicts the spatial relationship between UAV a and UAV b, highlighting the concept of UAV b potentially intersecting or entering the collision box of UAV a.
We assume the trajectory conformity of UAV a and b each separately follows
and
where
Before initiating collision avoidance maneuvers, the positions of two UAVs are considered independent, leading to the expression of the relative actual position vector at time t.
The collision probability can be interpreted as the likelihood of a stochastic event occuring. Therefore,
where , .
Note that can be utilized to monitor two UAVs’ time-varying collision risk by either DAA or UTM. Further, if the collision risk at the closest proximity position (CPA), which represents the peak risk during the encounter, is lower than the predefined target level of safety (TLOS), the encounter can be declared collision-free.
To determine the position of the closest proximity position (CPA) between two UAVs, we need to calculate the angle θ between the relative desired position vector and the relative velocity vector, which is
therefore
During the approach of two UAVs, the angle θ between them serves as a directional indicator. When two UAVs approach closer to each other, . Vice versa, when two UAVs move apart, In this case, Equation (17) holds at CPA.
The time at the CPA is
Then, the closest distance between two UAVs during the encounter process can be derived by
and can be obtained by substituting into Equation (18). If > TLOS, then the two UAVs will be deemed as not meeting the TLOS criteria which can be calculated by
In determining separation minima, TLOS serves as a crucial benchmark for assessing the safety of aircraft operations. TLOS is widely recognized as the standard safety level, calculated based on the number of accidents per flight hour across various operational scenarios, considering factors such as traffic flow density and airspace topology [43,44,45]. Rather than relying solely on traditional accident rates and flight hour metrics, this study emphasizes the importance of positional overlap probability as a key indicator of acceptable safety levels (as illustrated in Figure 3) [46,47,48].
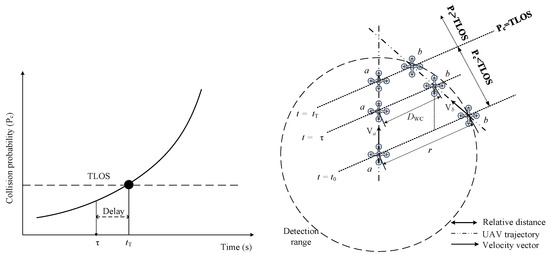
Figure 3.
Schematics of time threshold and relative distance.
Considering the UAV’s delay in communication, mechanic transmission, and collision avoidance maneuvering, the well clear thresholds before shall be determined to avoid collisions. Well clear ensures safe separation between UAVs through a combination of spatial and temporal elements, including minimum horizontal and vertical distances, and the latest maneuvering time (τ) required to avoid a collision [29,48,49], which is given by
Constrained by DAA’s maximum detection range , the well clear spatial distance of the UAV in a conflict scenario can then be obtained as
As shown in Figure 3, the relative distance between the two UAVs during the encounter continues to decrease until the collision avoidance threshold is reached by the relative distance.
5. Simulation and Results
5.1. Scenario Setting
We took medium-sized rotary-wing UAV H703-NG, small-sized rotary-wing UAV H723-200, and composite-wing UAV H713-400 as candidates operating in free airspace to analyze their dynamic collision risk in free airspace using our proposed UAV collision risk model. The historical UAV tracks and the related flight plans of a company mainly operated in Hainan province of China were collected and analyzed to generate the trajectory conformity of three UAVs. For simplicity, we set the initial position of the host UAV at the origin of the ground coordinate system and randomly generated the position of the intruder UAVs. Table 1 lists the UAV flight parameters of H703-NG, H723-200, and H713-400. We considered an encountering scenario in which the intruder infringes the detection range of the host UAV from omni azimuths, as shown in Figure 4. Let be the horizontal azimuth of the intruder from the host and be the elevation of the intruder from the horizontal profile (XOY profile). The horizontal intruding bearing ranges from −180° to 180°, where positive values indicate a clockwise bearing and negative values represent the opposite direction. Similarly, the vertical intruding bearing ranges from −90° to 90°, with positive values indicating the intruder is positioned higher than the host and negative values denoting the reverse scenario.

Table 1.
UAV flight performance parameters.
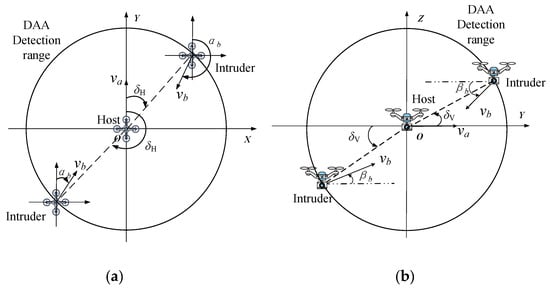
Figure 4.
Schematic of the UAV being detected in different horizontal and elevations of intruder UAV from host UAV: (a) XOY profile. (b) YOZ profile.
It is assumed in the two simulation scenarios that the heading of the host UAV is magnetic north, and its velocity direction is the same as the heading, so the heading angle and climb angle of the main UAV are both 0°. Similarly, the heading of the intruder, which ranges from 0° to 360°, increases in a clockwise direction, and the climb angle of intruder ranges from −90° to 90°.
When two UAVs approach, their positional overlapping probability and collision risk increase. We set the TLOS of two UAVs’ collision risk to be 5% [50,51], implying that an overlapping probability larger than 5% is unacceptable in our experiments.
5.2. Simulation and Results
Two scenarios are considered in our simulation on the two UAVs approaching each other at different velocities and altitudes, as well as from omni-azimuths: (1) A fast intruder approaching the slower host UAV, and (2) A slow intruder approaching the faster host UAV. We identify the heading of intruder with the maximum collision risks for each azimuth of the intruder and calculate the horizontal relative position at which TLOS is unsatisfied by using Equation (24). We then calculate the well clear thresholds for the host UAV to avoid a collision safely using Equation (26).
Figure 5 depicts how the heading of intruder, with maximum collision risk not satisfying the specified TLOS, varies with the intruding azimuth. Figure 5a relates to the scenario where the fast intruder UAV c approaches the slow host UAV a, while Figure 5b,c represent the slow intruder UAV a approaching the fast host UAV b and c. Similarly, Figure 6a–c depict the vertical relative bearing at which the maximum collision risk does not satisfy the specified TLOS, varying with the intruding elevation when the two aircraft are flying on reverse tracks.
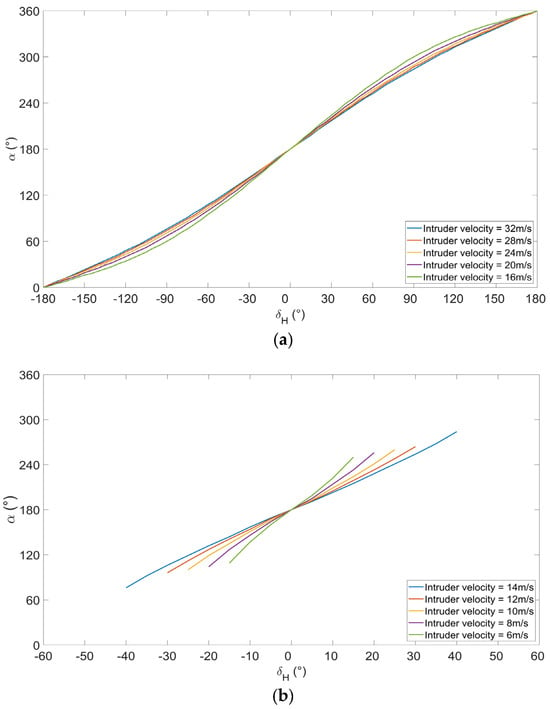
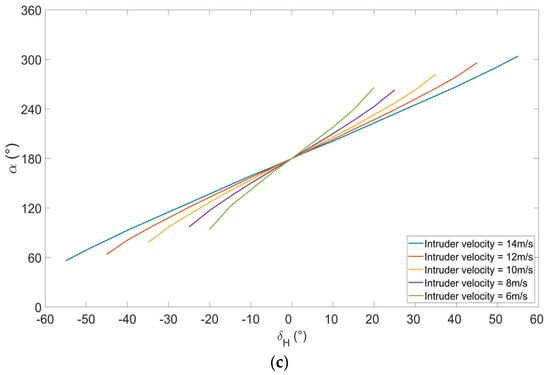
Figure 5.
The intruding azimuth vs. the heading angle: (a) Fast UAV c approaching slow UAV a. (b) Slow UAV a approaching fast UAV c. (c) Slow UAV a approaching fast UAV b.
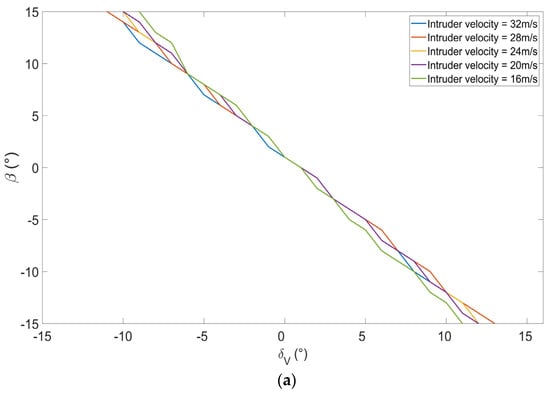
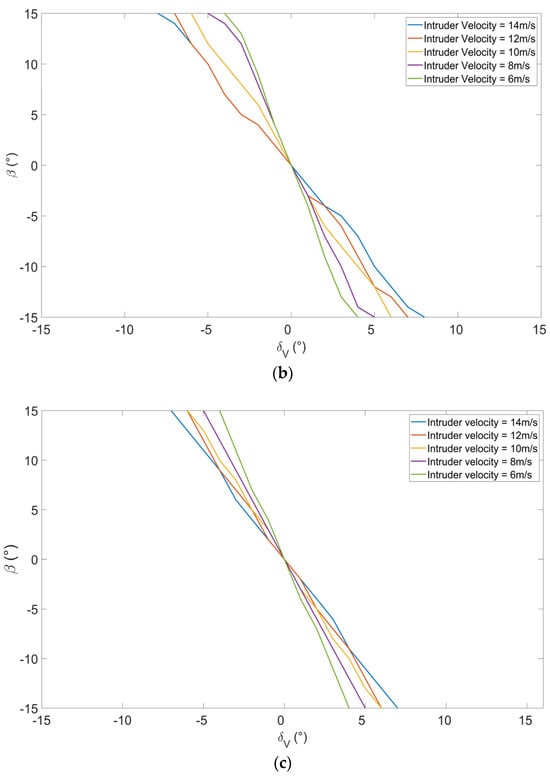
Figure 6.
The intruding azimuth vs. the climb angle: (a) Fast UAV c approaching slow UAV a. (b) Slow UAV a approaching fast UAV c. (c) Slow UAV a approaching fast UAV b.
As for the fast UAV approaching the slow UAV, the intruding horizontal azimuth with collision risk not satisfying TLOS varies from −180° to 180°. This means that when a fast UAV approaches a slow UAV, there always exists a heading not satisfying TLOS for omni-intruding azimuths of the host, and this will trigger collision-avoidance maneuvering. However, for a slow UAV approaching a fast UAV, the intruding azimuth with a heading not satisfying TLOS ranges far less than when a fast UAV approaches a slow UAV. Additionally, when the slow UAV approaches a fast UAV, the intruding azimuth with a heading not satisfying TLOS ranges increases as the velocity of the host UAV decreases.
Further, the larger velocity of the intruder yields a larger intruding azimuth range for the host to maneuver to avoid the intruder, as seen in Figure 5. Similarly, Figure 6 depicts the variation in climb angle corresponding to the maximum collision risk when the intruder’s elevation changes while flying on a reverse track compared to the host UAV. Due to the limitation of the maximum climb angle, is restricted to a value between −15° and 15°.
Figure 7 depicts a sample scenario where the fast intruder UAV c and the slow host UAV a are flying on reverse tracks. We demonstrate how the detection range affects the collision probability and the well clear thresholds. Figure 7a–d show that, as the UAV detection distance decreases, the range of intruding headings unsatisfying the TLOS increases. Moreover, a nearly flat section of the curve depicted in Figure 7a illustrates the scenario where the collision boxes of two UAVs intersect and pass through each other.
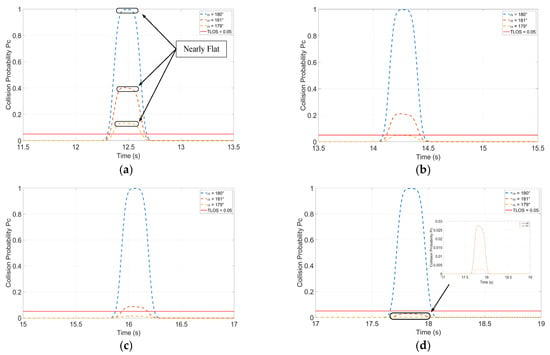
Figure 7.
Instantaneous probability graphs for encounter scenarios with UAV a and UAV c flying on reciprocal tracks at the same altitude: (a) Detection range R = 350 (m). (b) Detection range R = 400 (m). (c) Detection range R = 450 (m). (d) Detection range R = 500 (m).
Figure 8, Figure 9 and Figure 10 show the horizontal and vertical well clear thresholds for the intruder approaching the host from omni-azimuths at the headings and climb angles of the intruder with maximum collision risks not satisfying the specified TLOS determined with Equation (26). Note that Figure 8 covers the scenario where the fast intruder UAV c approaches the slow host UAV a, while Figure 9 and Figure 10 represent the slow intruder UAV a approaching the fast host UAV b and c. The findings of the results are listed below:
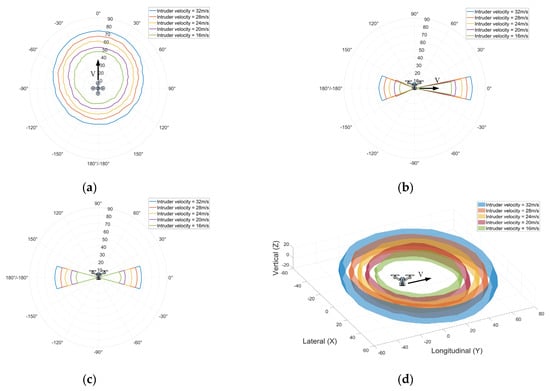
Figure 8.
Well clear thresholds for fast UAV c approaching slow UAV a: (a) Well clear thresholds (in meters) for the horizontal profile at the same altitude. (b) Well clear thresholds (in meters) for the vertical profile (YOZ). (c) Well clear thresholds (in meters) for the vertical profile (XOZ). (d) 3D well clear thresholds (in meters).
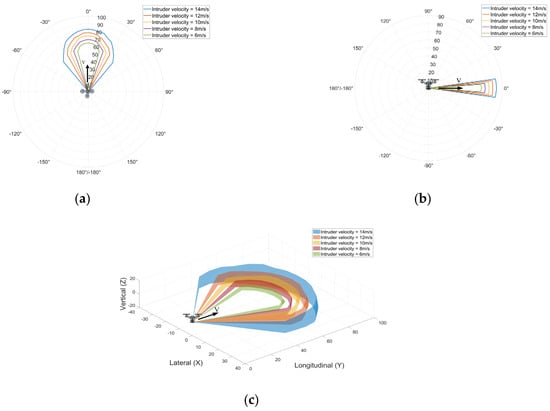
Figure 9.
Well clear thresholds for slow UAV a approach fast UAV c: (a) Well clear thresholds (in meters) for the horizontal profile. (b) Well clear thresholds (in meters) for the vertical profile (YOZ). (c) 3D well clear thresholds (in meters).
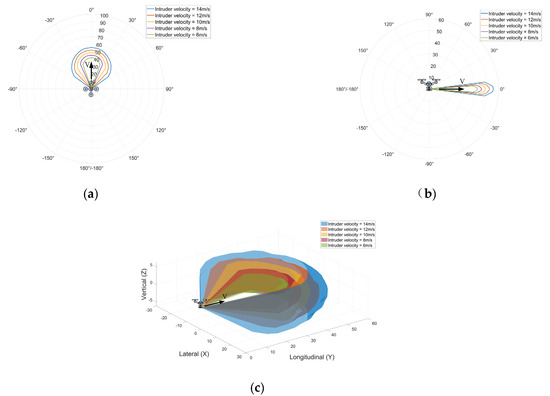
Figure 10.
Well clear thresholds for slow UAV a approach fast UAV b: (a) Well clear thresholds (in meters) for the horizontal profile. (b) Well clear thresholds (in meters) for the vertical profile (YOZ). (c) 3D well clear thresholds (in meters).
- (i)
- As the fast intruder approaches the slow host, the omni-azimuths of the intruder at the heading of intruder pose collision risks to the host; therefore, the host must maneuver to avoid the intruder before reaching the well clear thresholds. However, when the slow intruder approaches the fast host, only those intruders roughly in reciprocal azimuths pose collision risks to the host.
- (ii)
- As the fast intruder approaches the slow host and the intruder flies reciprocal to the host, the elevation range becomes progressively larger as the velocity of the intruder increases. In contrast, when two UAVs are flying on the same track, the elevation range becomes smaller as the velocity of the intruder increases.
- (iii)
- As the slow intruder approaches the fast host and the intruder flies reciprocal to the host, the elevation range becomes progressively larger as the velocity of the intruder increases.
- (iv)
- A larger intruder’s velocity yields a greater well clear threshold.
- (v)
- Reciprocally approaching azimuths (along the same track) yield larger well clear thresholds than other azimuths.
- (vi)
- A larger vertical altitude difference between two UAVs yields lower well clear thresholds.
- (vii)
- When the slow UAV approaches the fast UAV, the range of intruding azimuths that do not satisfy the TLOS increases as the host UAV’s velocity decreases.
6. Concluding Remarks
This study introduced the notion of trajectory conformity to address a variety of challenges in supervising and monitoring UAV operations, given their varied flight dynamics and performance metrics. Trajectory conformity comprehensively takes into account the complexity of UAV operating environments and the UAV’s inherent performance, determining the overall error of position uncertainty. Drawing from this concept, a comprehensive UAV collision risk model was developed and verified using real-world operational data to showcase its efficacy across different scenarios. Furthermore, this paper conducted hypothesis testing on the mean and variance of the trajectory deviation data to obtain the UAV’s trajectory conformity. Additionally, we developed a collision risk model based on the UAV’s relative state to determine the well clear thresholds for collision avoidance. This model holds considerable promise in enhancing UAV safety through mechanisms like detect and avoid (DAA) or unmanned aircraft system traffic management (UTM), offering real-time collision alerts within defined safety thresholds to bolster proactive risk management strategies. To showcase the effectiveness of the model, this study chose three UAVs with varying trajectory agreements for mutual intrusion simulations. It then determined the three-dimensional well clear thresholds for different intrusion directions at various speeds. Moreover, the model can be employed in different facets of UAV operations, including route planning, flight procedure formulation, airspace capacity evaluation, and determination of separation minima.
In future works, we will extend our model to the integrative operational scenario by incorporating manned and unmanned aircraft. Furthermore, we will consider the operational mechanisms and safety requirements of both UAVs and manned aircraft (such as collision avoidance systems and air traffic control (ATC) methods) to further improve the model for assessing the safety separation between UAVs and manned aircraft in typical fusion operational scenarios, such as terminal areas and air routes.
Author Contributions
Conceptualization, L.M., H.Z. and K.H.L.; methodology, L.M., H.Z. and K.H.L.; software, H.Z.; validation, L.M. and H.Z.; resources, Y.Z.; data curation, L.M.; writing—original draft preparation, H.Z.; writing—review and editing, L.M. and K.H.L.; supervision, Y.Z. and K.H.L.; funding acquisition, L.M. and Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work were supported by the National Key Research and Development Program Project of China (NO. 2022YFB4300904) and National Natural Science Foundation of China (NO. 52102409).
Data Availability Statement
The original data in the study are not easy to provide because they involve the privacy of the provider.
Conflicts of Interest
The authors declare no conflicts of interest. The funders have no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
| ANOVA | Analysis of variance |
| ATC | Air traffic control |
| DAA | Detect and avoid |
| FTE | Flight technical error |
| NMAC | Near mid-air collision |
| NSE | Navigation system error |
| PBN | Performance-based navigation |
| PDE | Path definition error |
| RTK | Real-time kinematic |
| TLOS | Target level of safety |
| TSE | Total system error |
| UAV | Unmanned air vehicle |
| UTM | Unmanned aircraft system traffic management |
| Symbols | |
| Well clear spatial distance | |
| DAA detect range | |
| Actual position vector of host UAV | |
| Actual position vector of intruder UAV | |
| Relative actual position vector | |
| Desired position vector of host UAV | |
| Desired position vector of intruder UAV | |
| Relative desired position vector | |
| Rotation matrix of host UAV | |
| Rotation matrix of intruder UAV | |
| Time at | |
| Maneuvering delay time | |
| Trajectory conformity of host UAV | |
| Trajectory conformity of intruder UAV | |
| Velocity vector of host UAV | |
| Velocity vector of intruder UAV | |
| Relative velocity vector | |
| Heading angle | |
| Climb angle | |
| Maneuvering time threshold | |
| The horizontal azimuth of the intruder from the host | |
| the elevation of the intruder from the horizontal profile | |
Appendix A
- (a)
- Normality Test
Normality tests assess whether the data follow a normal distribution, represented by a bell-shaped curve. Since many statistical methods, such as ANOVA, assume normal distribution, it is essential to verify this assumption before performing these tests [52]. The mean and variance of the 3D deviation for the 12-day datasets are shown in Table A1 and Table A2. We conducted a K-S test on each dataset to verify the normality of the data. We checked the p-value for each dataset. The p-value (probability value) [53] is a measure used in statistical hypothesis testing to help determine the significance of the results. It indicates the probability of observing the data (or something more extreme) assuming that the null hypothesis is true. If p > 0.05, the dataset is considered to be within normality (as shown in Table A1, Table A2 and Table A3 and Figure A1). The datasets that do not exhibit normality were removed from the sample space.

Table A1.
p-value for each dataset (H703-NG).
Table A1.
p-value for each dataset (H703-NG).
| Test Days (i) | Lateral (m) Equation (1) | Longitudinal (m) Equation (2) | Vertical (m) Equation (3) |
|---|---|---|---|
| Day 1 | 0.50000 | 0.13086 | 0.50000 |
| Day 2 | 0.15469 | 0.45561 | 0.14105 |
| Day 3 | 0.06741 | 0.33017 | 0.39374 |
| Day 4 | 0.17346 | 0.39796 | 0.30990 |
| Day 5 | 0.10891 | 0.50000 | 0.41185 |
| Day 6 | 0.50000 | 0.50000 | 0.50000 |
| Day 7 | 0.06700 | 0.50000 | 0.21887 |
| Day 8 | 0.50000 | 0.23459 | 0.50000 |
| Day 9 | 0.50000 | 0.19121 | 0.11343 |
| Day 10 | 0.44522 | 0.44478 | 0.50000 |
| Day 11 | 0.50000 | 0.24395 | 0.43476 |
| Day 12 | 0.50000 | 0.50000 | 0.29910 |

Table A2.
p-value for each dataset (H723-200).
Table A2.
p-value for each dataset (H723-200).
| Test Days (i) | Lateral (m) Equation (1) | Longitudinal (m) Equation (2) | Vertical (m) Equation (3) |
|---|---|---|---|
| Day 1 | 0.50000 | 0.50000 | 0.46930 |
| Day 2 | 0.41560 | 0.49634 | 0.50000 |
| Day 3 | 0.50000 | 0.15743 | 0.50000 |
| Day 4 | 0.50000 | 0.42746 | 0.29661 |
| Day 5 | 0.46523 | 0.50000 | 0.11429 |
| Day 6 | 0.20951 | 0.50000 | 0.39196 |
| Day 7 | 0.50000 | 0.19556 | 0.50000 |
| Day 8 | 0.50000 | 0.50000 | 0.50000 |
| Day 9 | 0.46339 | 0.12305 | 0.24851 |
| Day 10 | 0.34975 | 0.50000 | 0.50000 |
| Day 11 | 0.50000 | 0.50000 | 0.34832 |
| Day 12 | 0.50000 | 0.14986 | 0.46893 |

Table A3.
p-value for each dataset (H713-400).
Table A3.
p-value for each dataset (H713-400).
| Test Days (i) | Lateral (m) Equation (1) | Longitudinal (m) Equation (2) | Vertical (m) Equation (3) |
|---|---|---|---|
| Day 1 | 0.43565 | 0.25334 | 0.50000 |
| Day 2 | 0.50000 | 0.34600 | 0.50000 |
| Day 3 | 0.50000 | 0.45299 | 0.50000 |
| Day 4 | 0.50000 | 0.50000 | 0.37140 |
| Day 5 | 0.26004 | 0.50000 | 0.39384 |
| Day 6 | 0.27960 | 0.40441 | 0.38868 |
| Day 7 | 0.50000 | 0.50000 | 0.50000 |
| Day 8 | 0.10518 | 0.50000 | 0.50000 |
| Day 9 | 0.50000 | 0.26932 | 0.50000 |
| Day 10 | 0.50000 | 0.06105 | 0.50000 |
| Day 11 | 0.15414 | 0.25313 | 0.50000 |
| Day 12 | 0.31150 | 0.41983 | 0.44073 |
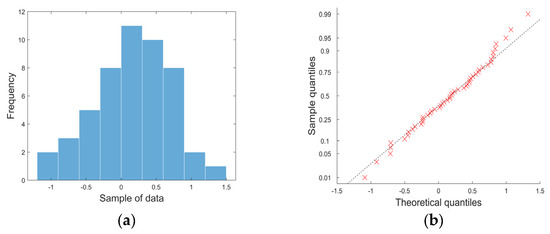
Figure A1.
A lateral deviation example of a histogram and P-P plot for the normal distribution: (a) Deviation frequency plot. (b) P-P plot.
- (b)
- Homogeneity test of the variance
ANOVA is used to compare the means of three or more groups to determine if at least one group’s mean differs from the others. It evaluates whether there is a statistically significant difference among the group means [54]. The normality of the deviation data in 3D tests are shown in the above section. This section shows the ANOVA (analysis of variance) test on each dataset to assess whether they have the same variance in 3D. Let be the variance of the dataset on day , and testing days be the independent variable.
The hypotheses () for all sample variances are the following:
We then calculated the p-value for each dataset. If p > 0.05, we accept H0 and reject H1; if p < 0.05, we reject H0 and accept H1. The 3D p-values for H703-NG were 0.6535, 0.6836, and 0.1841, those for H723-200 were 0.2261, 0.6915, and 0.3416, and those for H713-400 were 0.9371, 0.0784, and 0.1923. They are all greater than 0.05, as shown in Figure A2, Figure A3 and Figure A4. In the test for homogeneity of variance, we found that the p-value for the longitudinal deviation dataset of the H713-400 was 0.0784. Although this is greater than 0.05, it is close to 0.05, which does not provide sufficient evidence for the homogeneity of variance. Therefore, the Brown–Forsythe test was performed, resulting in a p-value of 0.3754, which is greater than 0.05. Therefore, we conclude that the trajectory conformities in the three dimensions have no significant difference at a 5% significance level in their variances.
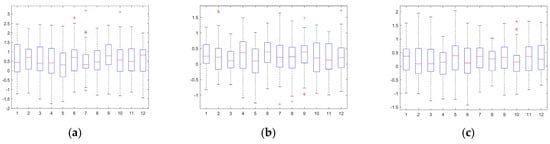
Figure A2.
Results of the homogeneity test for lateral, longitudinal, and vertical trajectory conformity (H703-NG): (a) Lateral. (b) Longitudinal. (c) Vertical.
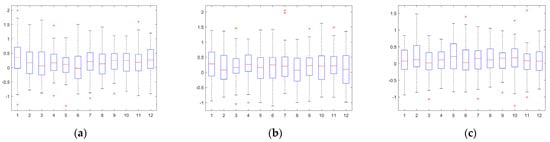
Figure A3.
Results of the homogeneity test for lateral, longitudinal, and vertical trajectory conformity (H723-200): (a) Lateral. (b) Longitudinal. (c) Vertical.
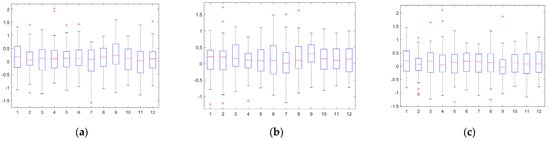
Figure A4.
Results of the homogeneity test for lateral, longitudinal, and vertical trajectory conformity (H713-400): (a) Lateral. (b) Longitudinal. (c) Vertical.
- (c)
- Hypothesis test of the mean
Similarly, we performed a one-way ANOVA to test whether the trajectory conformity means in three dimensions significantly differ between different testing days. Let be the mean of the day dataset. The hypotheses () for all sample means are as follows:
The 3D p-values for H703-NG were 0.4604, 0.7224, and 0.5009, those for H723-200 were 0.4404, 0.8719, and 0.7913, and those for H713-400 were 0.4252, 0.4451, and 0.9670. They are all greater than 0.05, as shown in Figure A5, Figure A6 and Figure A7. Therefore, we accept H0 and reject H1.
Figure A5.
Results of the homogeneity test of lateral, longitudinal, and vertical trajectory conformity means (H703-NG): (a) Lateral. (b) Longitudinal. (c) Vertical.
Figure A6.
Results of the homogeneity test of lateral, longitudinal, and vertical trajectory conformity means (H723-200): (a) Lateral. (b) Longitudinal. (c) Vertical.
Figure A7.
Results of the homogeneity test of lateral, longitudinal, and vertical trajectory conformity means (H713-400): (a) Lateral. (b) Longitudinal. (c) Vertical.
References
- FAA and NASA. FAA UTM Concept of Operations—v1.0. 2018. Available online: https://utm.arc.nasa.gov/docs/2018-UTM-ConOps-v1.0.pdf (accessed on 5 June 2024).
- FAA and NASA. FAA UTM Concept of Operations—v2.0. 2022. Available online: https://www.faa.gov/sites/faa.gov/files/2022-08/UTM_ConOps_v2.pdf (accessed on 5 June 2024).
- Davies, L.; Bolamm, R.C.; Vagapov, Y.; Anuchin, A. Review of Unmanned Aircraft System Technologies to Enable Beyond Visual Line of Sight (BVLOS) Operations. In Proceedings of the 2018 X International Conference on Electrical Power Drive Systems (ICEPDS), Novocherkassk, Russia, 3–6 October 2018; pp. 1–6. [Google Scholar]
- Sorbelli, F.B.; Chatterjee, P.; Das, P.; Pinotti, C.M. Risk Assessment in BVLoS Operations for UAVs: Challenges and Solutions. In Proceedings of the 2024 20th International Conference on Distributed Computing in Smart Systems and the Internet of Things (DCOSS-IoT), Abu Dhabi, United Arab Emirates, 29 April–1 May 2024; pp. 300–307. [Google Scholar]
- Usach, H.; Vila, J.A.; Gallego, Á. Trajectory-Based, Probabilistic Risk Model for UAS Operations; IntechOpen: London, UK, 2020. [Google Scholar]
- Bauranov, A.; Rakas, J. Designing airspace for urban air mobility: A review of concepts and approaches. Prog. Aerosp. Sci. 2021, 125, 100726. [Google Scholar] [CrossRef]
- Pang, B.; Hu, X.; Dai, W.; Low, K.H. UAV path optimization with an integrated cost assessment model considering third-party risks in metropolitan environments. Reliab. Eng. Syst. Saf. 2022, 222, 108399. [Google Scholar] [CrossRef]
- Blom, H.A.P.; Jiang, C.; Grimme, W.B.A.; Cheung, Y.S. Third-party risk modelling of Unmanned Aircraft System operations, with application to parcel delivery service. Reliab. Eng. Syst. Saf. 2021, 214, 107788. [Google Scholar] [CrossRef]
- Jang, D.S.; Ippolito, C.A.; Sankararaman, S.; Stepanyan, V. Concepts of airspace structures and system analysis for uas traffic flows for urban areas. In Proceedings of the AIAA Information Systems-AIAA Infotech@Aerospace, Grapevine, TX, USA, 9–13 January 2017; p. 0449. [Google Scholar]
- Sunil, E.; Hoekstra, J.; Ellerbroek, J.; Bussink, F.; Nieuwenhuisen, D. Metropolis: Relating airspace structure and capacity for extreme traffic densities. In Proceedings of the ATM Seminar 2015, 11th USA/EUROPE Air Traffic Management R&D Seminar, Lisbon, Portugal, 23–26 June 2015. [Google Scholar]
- Yang, J.; Wang, Y.; Hang, X.; Delahaye, D. A review on airspace design and risk assessment for urban air mobility. IEEE Access 2024, 11, 3481148. [Google Scholar] [CrossRef]
- Pang, B.; Dai, W.; Ra, T.; Low, K.H. A Concept of Airspace Configuration and Operational Rules for UAS in Current Airspace. In Proceedings of the 2020 AIAA/IEEE 39th Digital Avionics Systems Conference (DASC), San Antonio, TX, USA, 11–15 October 2020; pp. 1–9. [Google Scholar]
- Zhu, D.; Chen, Z.; Xie, X.; Chen, J. Discretization Method to Improve the Efficiency of Complex Airspace Operation. Aerospace 2023, 10, 780. [Google Scholar] [CrossRef]
- Zhang, Z.; Liang, Y. Bayesian network-based study on collision risk in free flight. China Saf. Sci. J. 2014, 24, 40–45. [Google Scholar]
- Zhang, Z.N.; Yu, S. On the collision risk in rectification of the aircraft positioning error under the free flight condition. Saf. Environ. Eng. 2017, 17, 16331636. [Google Scholar]
- International Civil Aviation Organization (ICAO). Doc 9613: Performance Based Navigation (PBN) Manual; ICAO: Montréal, QC, Canada, 2013. [Google Scholar]
- Wang, C.H.J.; Ng, E.M.; Low, K.H. Investigation and modeling of flight technical error (FTE) associated with UAS operating with and without pilot guidance. IEEE Trans. Veh. Technol. 2021, 70, 12389–12401. [Google Scholar] [CrossRef]
- Pang, B.; Zhang, M.; Deng, C.; Low, K.H. Investigation of Flight Technical Error for UAV Separation Requirement Based on Flight Trajectory Data. In Proceedings of the AIAA Aviation 2022 Forum, Chicago, IL, USA, 27 June–1 July 2022; p. 3763. [Google Scholar]
- Zhang, N.; Liu, H.; Ng, B.F.; Low, K.H. Collision probability between intruding drone and commercial aircraft in airport restricted area based on collision-course trajectory planning. Transp. Res. Part C Emerg. Technol. 2020, 120, 102736. [Google Scholar] [CrossRef]
- Lee, H.T.; Meyn, L.A.; Kim, S.Y. Probabilistic safety assessment of unmanned aerial system operations. J. Guid. Control. Dyn. 2013, 36, 610–617. [Google Scholar] [CrossRef]
- Bijjahalli, S.; Gardi, A.; Pongsakornsathien, N.; Sabatini, R. A Unified Collision Risk Model for Unmanned Aircraft Systems. In Proceedings of the 2021 IEEE/AIAA 40th Digital Avionics Systems Conference (DASC), San Antonio, TX, USA, 3–7 October 2021; pp. 1–10. [Google Scholar]
- Johnson, M.; Santiago, C.; Mueller, E. Characteristics of a well clear definition and alerting criteria for encounters between uas and manned aircraft in class e airspace. In Proceedings of the Air Traffic Management (ATM) Research and Development Seminar, Lisbon, Portugal, 23–26 June 2015. No. ARC-E-DAA-TN22684. [Google Scholar]
- Park, J.W.; Oh, H.D.; Tahk, M.J. UAV collision avoidance based on geometric approach. In Proceedings of the 2008 SICE Annual Conference, Tokyo, Japan, 20–22 August 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 2122–2126. [Google Scholar]
- McFadyen, A.; Martin, T. Understanding vertical collision risk and navigation performance for unmanned aircraft. In Proceedings of the AIAA 37th Digital Avionics Systems Conference (DASC), London, UK, 23–27 September 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–10. [Google Scholar]
- la Cour-Harbo, A.; Schiøler, H. Probability of Low-Altitude Midair Collision Between General Aviation and Unmanned Aircraft. Risk Anal. 2019, 39, 2499–2513. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Li, B.; Liu, H.; Zhong, G.; Fei, Y. Demarcation method of safety separation for multi-rotor UAV in free airspace. Syst. Eng. Electron. 2023, 45, 3149–3156. [Google Scholar]
- Weibel, R.; Edwards, M.; Fernandes, C. Establishing a risk-based separation standard for unmanned aircraft self separation. In Proceedings of the 11th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference, including the AIAA Balloon Systems Conference and 19th AIAA Lighter-Than, Virginia Beach, VA, USA, 20–22 September 2011; p. 6291. [Google Scholar]
- Weinert, A.; Campbell, S.; Vela, A.; Schuldt, D.; Kurucar, J. Well-clear recommendation for small unmanned aircraft systems based on unmitigated collision risk. J. Air Transp. 2018, 26, 113–122. [Google Scholar] [CrossRef]
- Munoz, C.; Narkawicz, A.; Chamberlain, J.; Consiglio, M.C.; Upchurch, J.M. A Family of Well-Clear Boundary Models for the Integration of UAS in the NAS. In Proceedings of the 14th AIAA Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 16–20 June 2014; p. 2412. [Google Scholar]
- Mullins, M.; Holman, M.W.; Foerster, K.M.; Kaabouch, N.; Semke, W. Dynamic separation thresholds for a small airborne sense and avoid system. In Proceedings of the AIAA Infotech@ Aerospace (I@A) Conference, Boston, MA, USA, 19–22 August 2013; p. 5148. [Google Scholar]
- Fellner, A.; Konieczka, R. Rotorcraft in the performance-based navigation international civil aviation organization implementation. Trans. Aerosp. Res. 2019, 2019, 53–64. [Google Scholar] [CrossRef]
- Dai, W.; Deng, C. Urban Performance-Based Navigation (uPBN): Addressing the CNS Variation Problem in the Urban Airspace in the Context of UAS Traffic Management. In Proceedings of the 2023 IEEE 26th International Conference on Intelligent Transportation Systems (ITSC), Bizkaia, Spain, 24–28 September 2023; pp. 5524–5529. [Google Scholar]
- Pang, B.; Ng, E.M.; Low, K.H. UAV trajectory estimation and deviation analysis for contingency management in urban environments. In Proceedings of the AIAA Aviation 2020 Forum, Online, 15–19 June 2020; p. 2919. [Google Scholar]
- Deng, C.; Wang, C.H.J.; Low, K.H. Preliminary UAS navigation performance analysis in urban-like environments. In Proceedings of the AIAA Aviation 2021 Forum, Online, 2–6 August 2021; p. 2385. [Google Scholar]
- Kallinen, V.; Martin, T.; McFadyen, A. Required navigation performance specifications for unmanned aircraft based on UTM flight trials. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 196–203. [Google Scholar]
- Bernard, J.; Lacher, A.R. Flight Trajectory Options to Mitigate the Impact of Unmanned Aircraft Systems (UAS) Contingency Trajectories—A Concept of Operations. In Center for Advanced Aviation System Development; MITRE Corporation: McLean, VA, USA, 2013. [Google Scholar]
- Zou, Y.; Zhang, H.; Feng, D.; Liu, H.; Zhong, G. Fast collision detection for small unmanned aircraft systems in urban airspace. IEEE Access 2021, 9, 16630–16641. [Google Scholar] [CrossRef]
- Mohamed Salleh, M.F.B.; Wanchao, C.; Wang, Z.; Huang, S.; Tan, D.Y.; Huang, T.; Low, K.H. Preliminary concept of adaptive urban airspace management for unmanned aircraft operations. In Proceedings of the 2018 AIAA Information Systems-AIAA Infotech@Aerospace, Kissimmee, FL, USA, 8–12 January 2018; p. 2260. [Google Scholar]
- Guan, X.; Lyu, R.; Shi, H.; Chen, J. A survey of safety separation management and collision avoidance approaches of civil UAS operating in integration national airspace system. Chin. J. Aeronaut. 2020, 33, 2851–2863. [Google Scholar] [CrossRef]
- Lin, L. Application of GPS RTK and total station system on dynamic monitoring land use. In Proceedings of the ISPRS Congress, Istanbul, Turkey, 12–23 July 2004; pp. 1–6. [Google Scholar]
- Federal Aviation Administration. Federal Aviation Regulations/Aeronautical Information Manual 2014; Simon and Schuster: New York, NY, USA, 2013.
- International Civil Aviation Organization. Thirteenth Air Navigation Conference: Report of the Conference. In Proceedings of the AN-Conf/13, ICAO, Montreal, QC, Canada, 9–19 October 2018. [Google Scholar]
- Lin, X.; Fulton, N.; Westcott, M. Target level of safety measures in air transportation-Review, validation and recommendations. In Proceedings of the IASTED International Conference, Beijing, China, 12–14 October 2009. [Google Scholar]
- Li, D.B.; Xu, X.H.; Li, X. Target level of safety for Chinese airspace. Saf. Sci. 2009, 47, 421–424. [Google Scholar] [CrossRef]
- Brooker, P. P-RNAV, safety targets, blunders and parallel route spacing. J. Navig. 2004, 57, 371–384. [Google Scholar] [CrossRef]
- Zhong, G.; Du, S.; Zhang, H.; Zhou, J.; Liu, H. Demarcation method of safety separations for sUAV based on collision risk estimation. Reliab. Eng. Syst. Saf. 2024, 242, 109738. [Google Scholar] [CrossRef]
- Paielli, R.A.; Erzberger, H. Conflict probability estimation for free flight. J. Guid. Control Dyn. 1997, 20, 588–596. [Google Scholar] [CrossRef]
- Fasano, G.; Accado, D.; Moccia, A.; Moroney, D. Sense and avoid for unmanned aircraft systems. IEEE Aerosp. Electron. Syst. Mag. 2016, 31, 82–110. [Google Scholar] [CrossRef]
- Dai, W.; Quek, Z.H.; Low, K.H. Probabilistic modeling and reasoning of conflict detection effectiveness by tracking systems towards safe urban air mobility operations. Reliab. Eng. Syst. Saf. 2024, 244, 109908. [Google Scholar] [CrossRef]
- Cook, S.P.; Brooks, D.; Hackenberg, D.; Raska, V. Defining well clear for unmanned aircraft systems. In Proceedings of the AIAA Infotech@Aerospace, Kissimmee, FL, USA, 5–9 January 2015; p. 0481. [Google Scholar]
- Weibel, R.E.; Hansman, R.J. Safety Considerations for Operation of Unmanned Aerial Vehicles in the National Airspace System. Available online: http://hdl.handle.net/1721.1/34912 (accessed on 20 June 2024).
- Ghasemi, A.; Zahediasl, S. Normality tests for statistical analysis: A guide for non-statisticians. Int. J. Endocrinol. Metab. 2012, 10, 486. [Google Scholar] [CrossRef] [PubMed]
- Lever, J.; Krzywinski, M.; Altman, N. Points of significance: Principal component analysis. Nat. Methods 2017, 14, 641–643. [Google Scholar] [CrossRef]
- Pace, L. One-Way Analysis of Variance. In Statistics in Plain English; Routledge: London, UK, 2022. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).