Latency Analysis of Drone-Assisted C-V2X Communications for Basic Safety and Co-Operative Perception Messages
Abstract
1. Introduction
1.1. Contributions
- We calculate the average delay experienced by a packet when BSM inter-arrival time () is varied. In real-world scenarios where multiple vehicles compete to communicate with the drone in each TTI, the drone needs to make a time-bound decision on whether to accept a vehicle’s data or not.
- We investigate the interplay between the variation of average delay for CPMs with number of vehicles (V) for different transmission window length () and CPM inter-arrival time () pairs. We also study the variation of average delay with the inter-arrival time of CPMs for varying packet arrival rates ().
- For BSM and CPM transmissions, we analyze the variation of the drone’s average energy consumption (Joules/s) with number of vehicles (V) for varying vehicle speed and road length () in a single sub frame of C-V2X mode 4 [10].
- For varying , , , and values, we plot the variations in average packet delay for varying number of vehicles (V) and the vehicle velocity under different road length () segments.
1.2. Organization
2. Related Work
2.1. Message Generation Standards for Co-Operative and Intelligent Transportation Systems
2.2. Mixed Integer Non-Linear Programming Approaches in UAV-Assisted Wireless Communications
2.3. UAV Trajectory Optimization for Sum-Rate Maximization and Performance Enhancement
2.4. Task Offloading and UAV-Assisted Vehicular Edge Computing Approaches
3. System Model
4. Problem Formulation
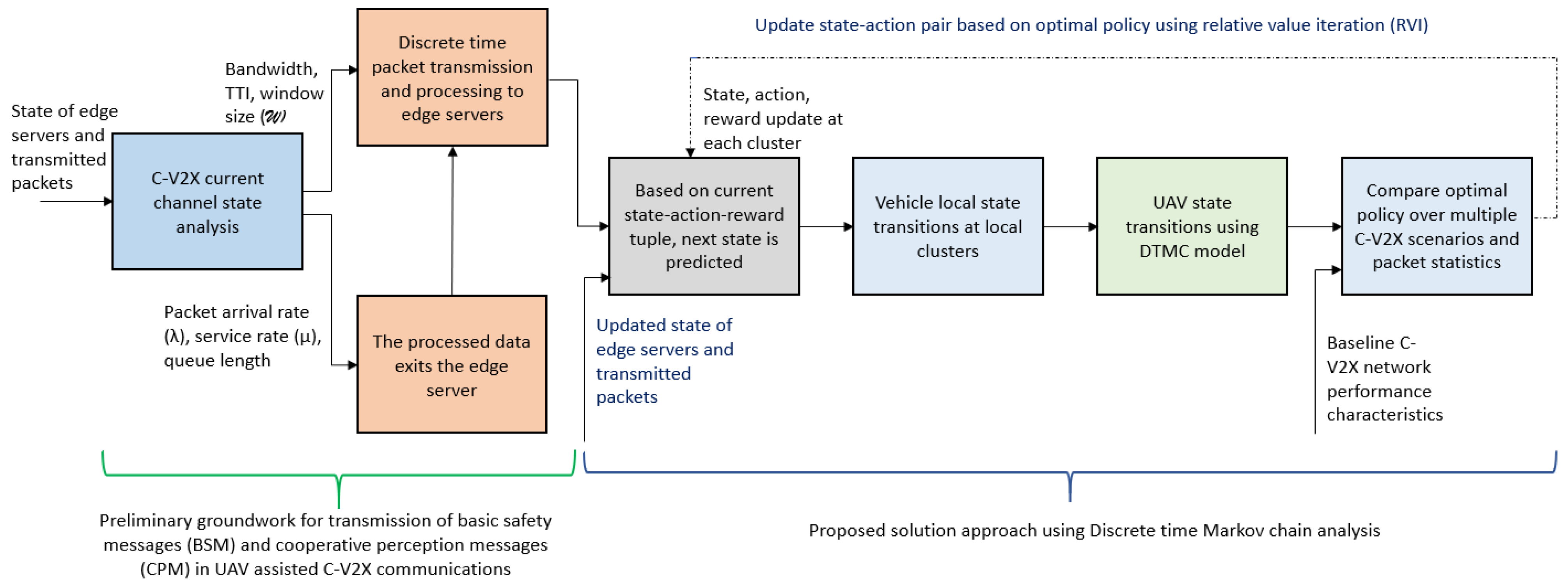
5. Proposed Solution Approach Based on DTMC Analysis
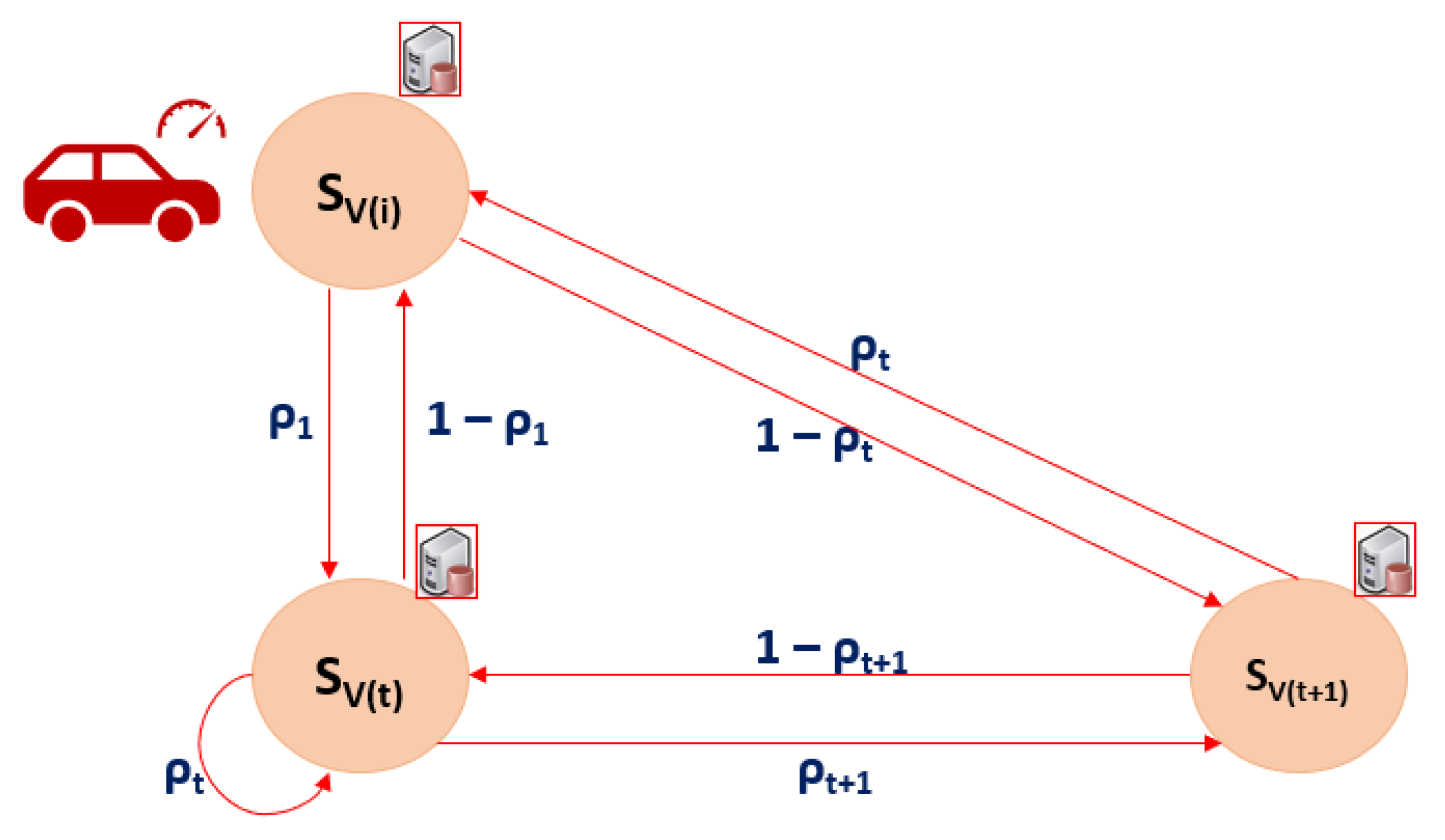
5.1. Intermittent States of Vehicles and State-Transitions During Communication with Drone
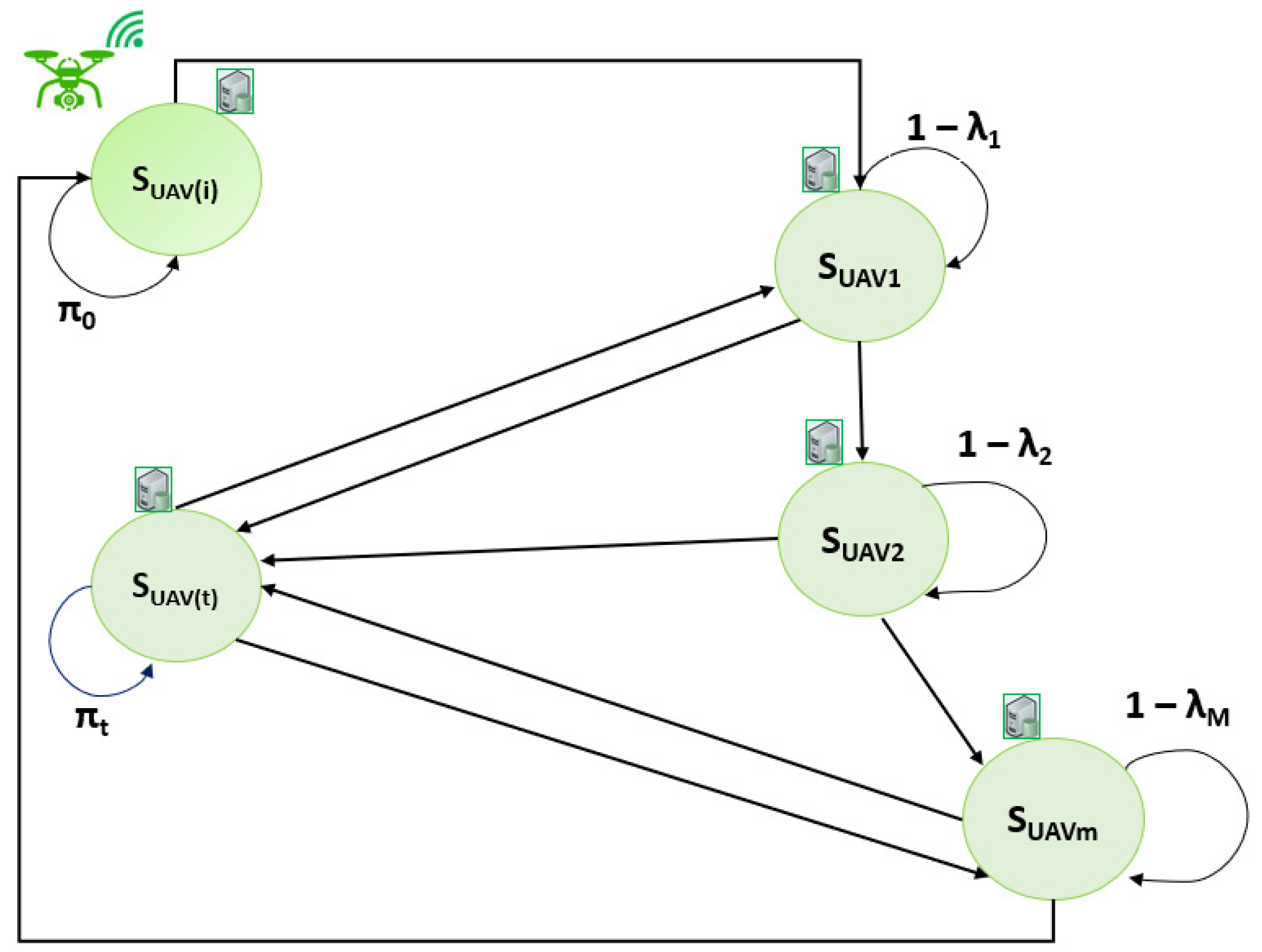
5.2. Impact of Drone Server Occupancy on State Transitions
5.3. State-Transitions and Transition Probability
- BSM in the next arrival and CPM in the subsequent arrival.
- CPM now and BSM in the next arrival.
- BSM now and BSM in the next arrival.
6. Simulation Results and Discussion
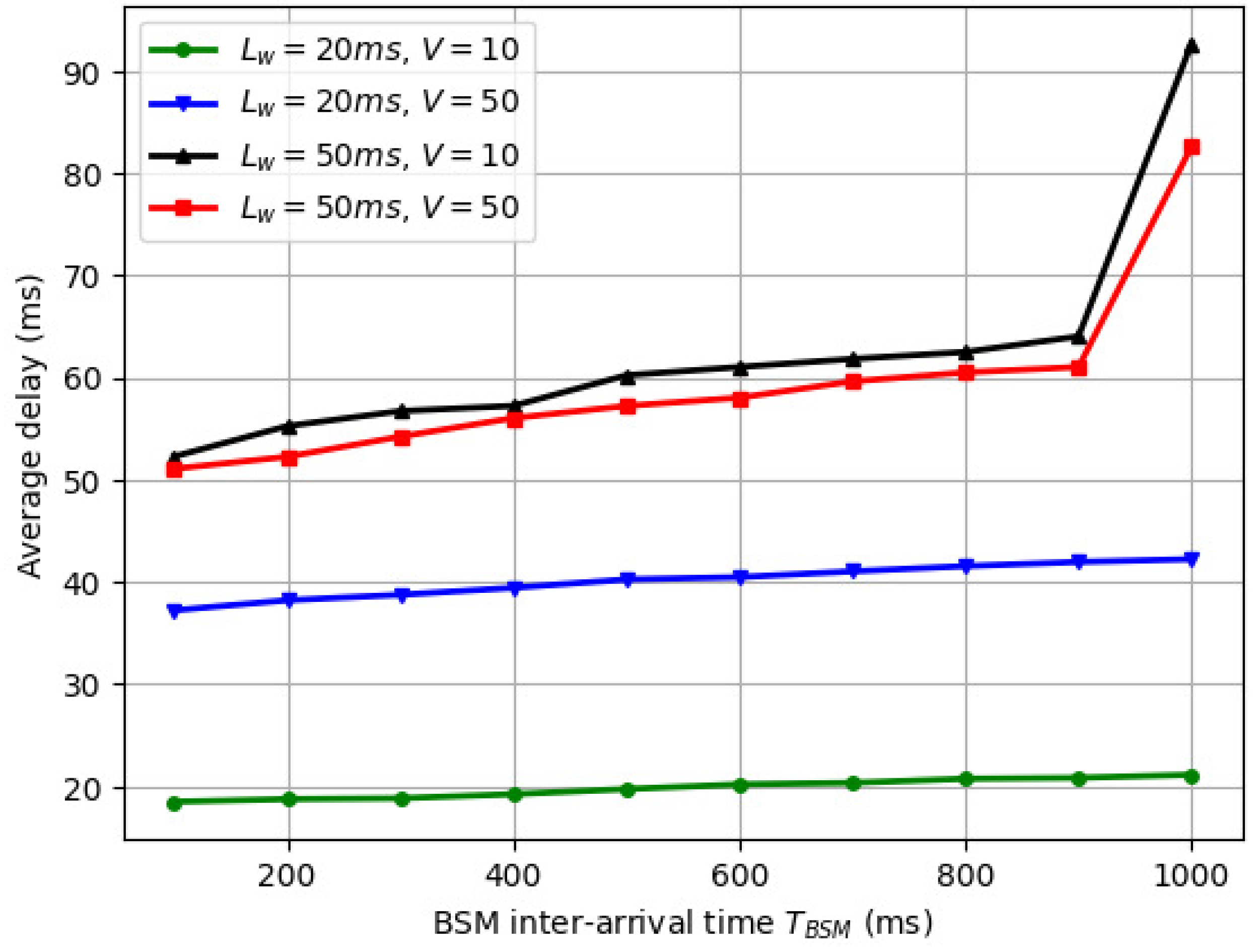
6.1. Variation of Average Delay with Inter-Arrival Time of BSM
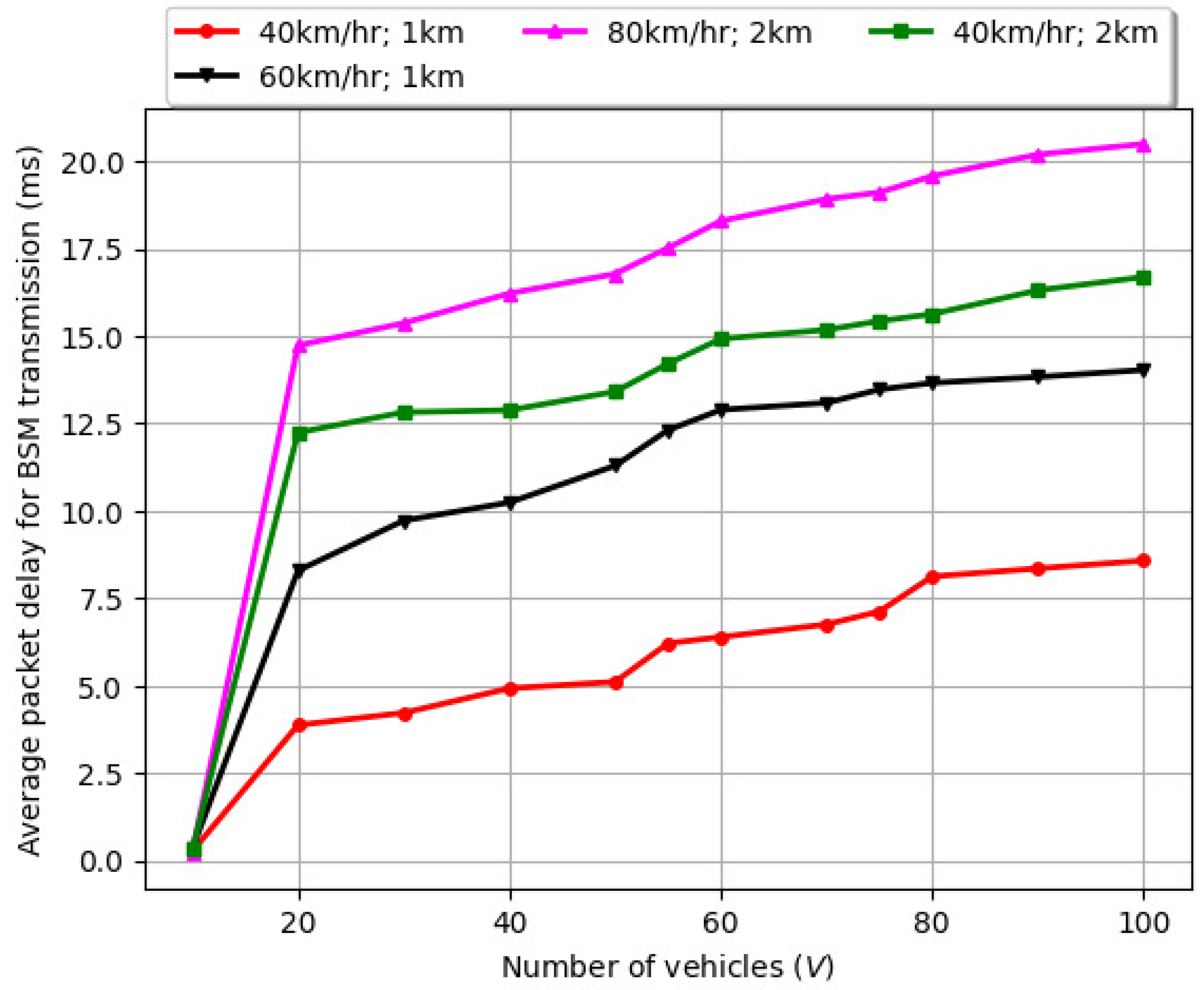
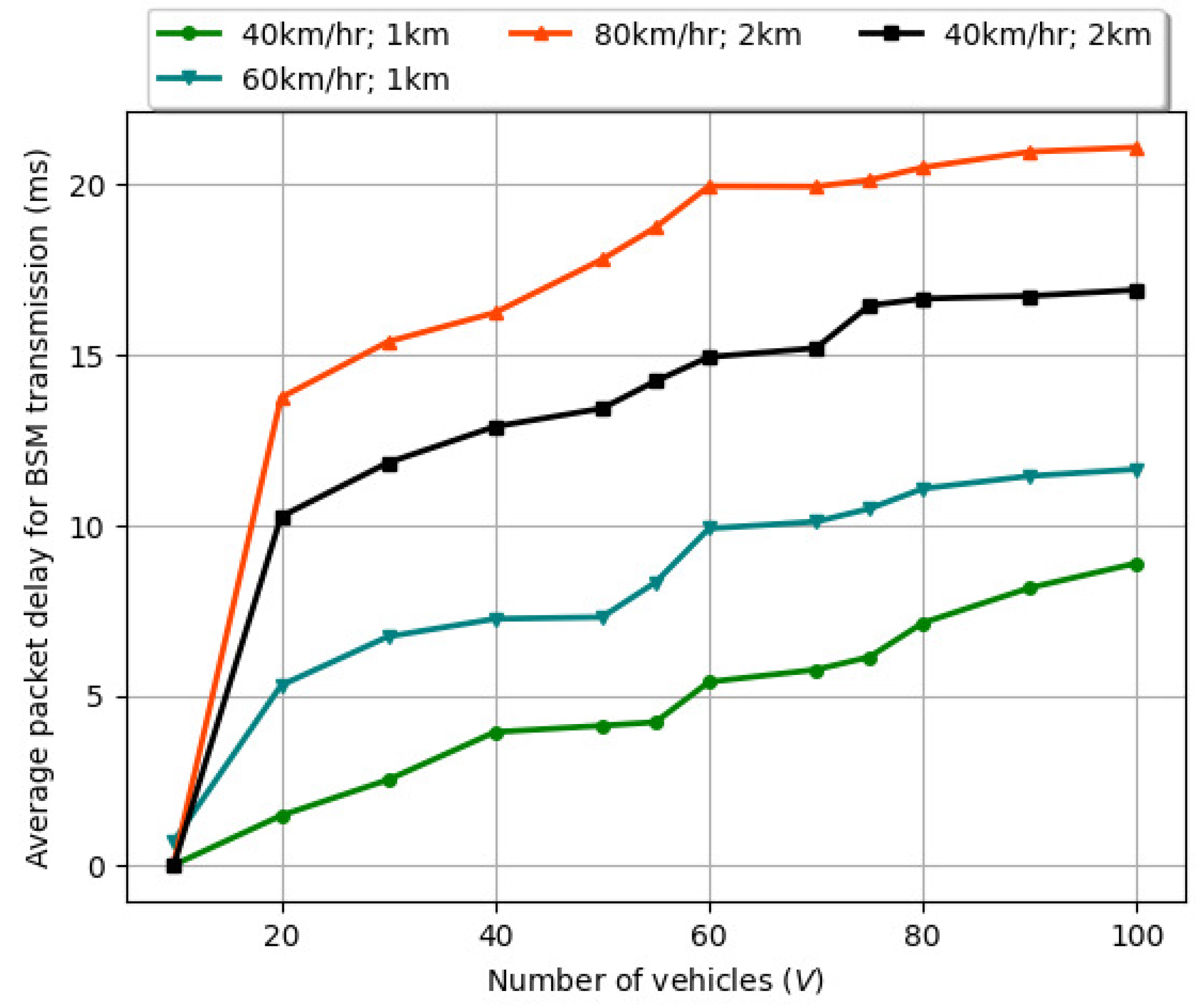
6.2. Variation of Average Packet Delay for BSMs with Number of Vehicles (V), Varying Vehicle Speed, and Road Length ()
6.3. Variation of Average Delay for CPMs with Number of Vehicles (V) for Different
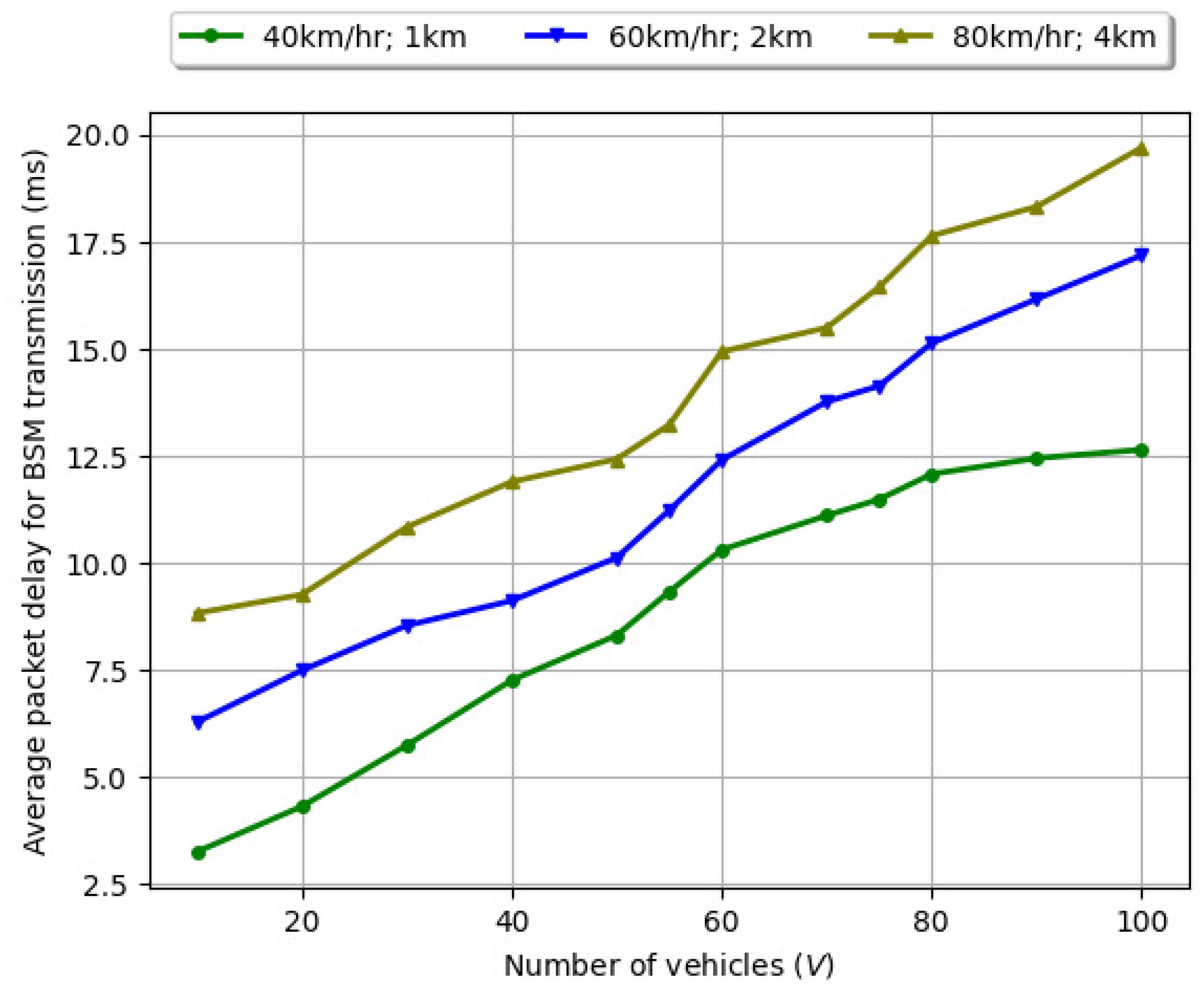
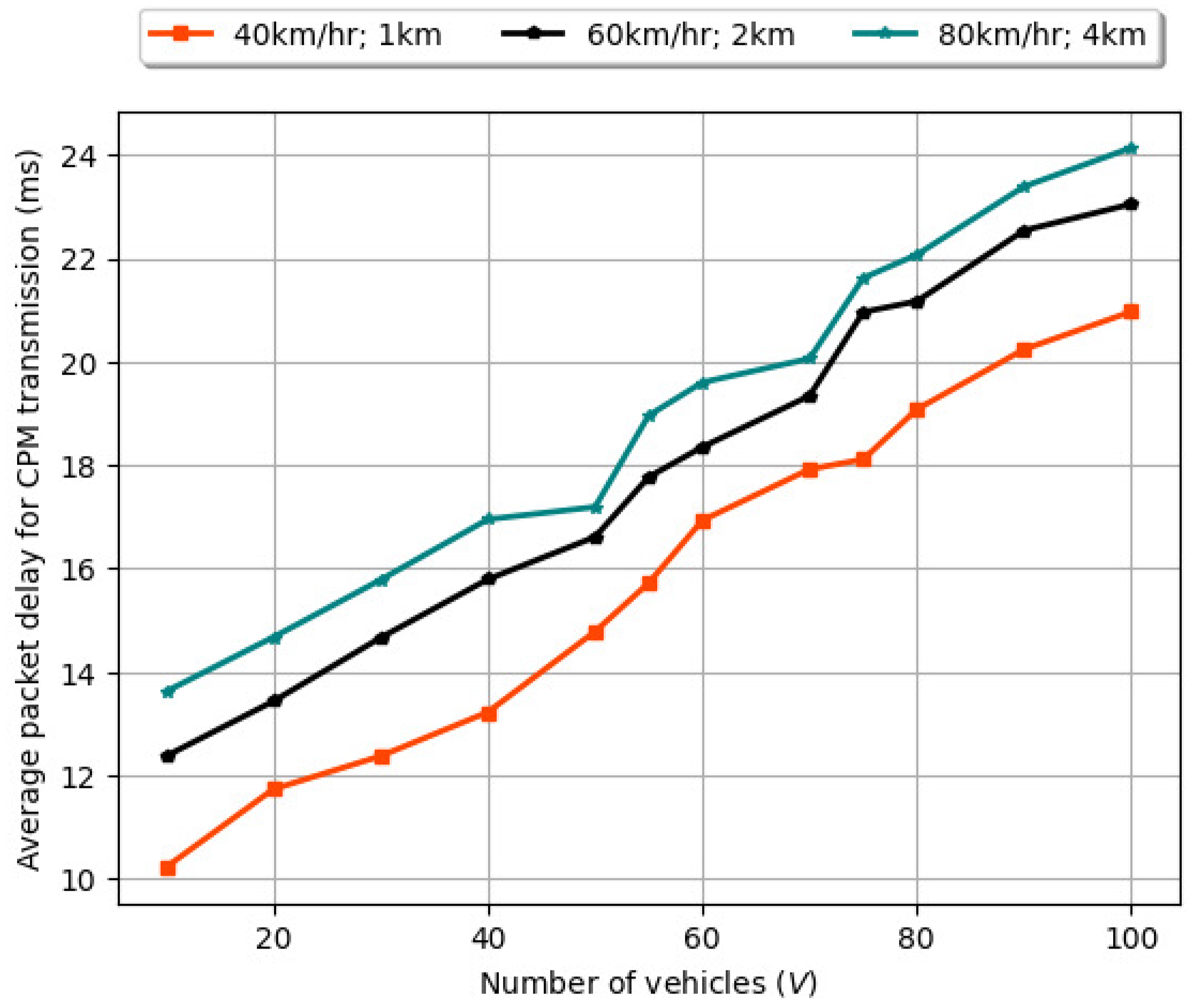
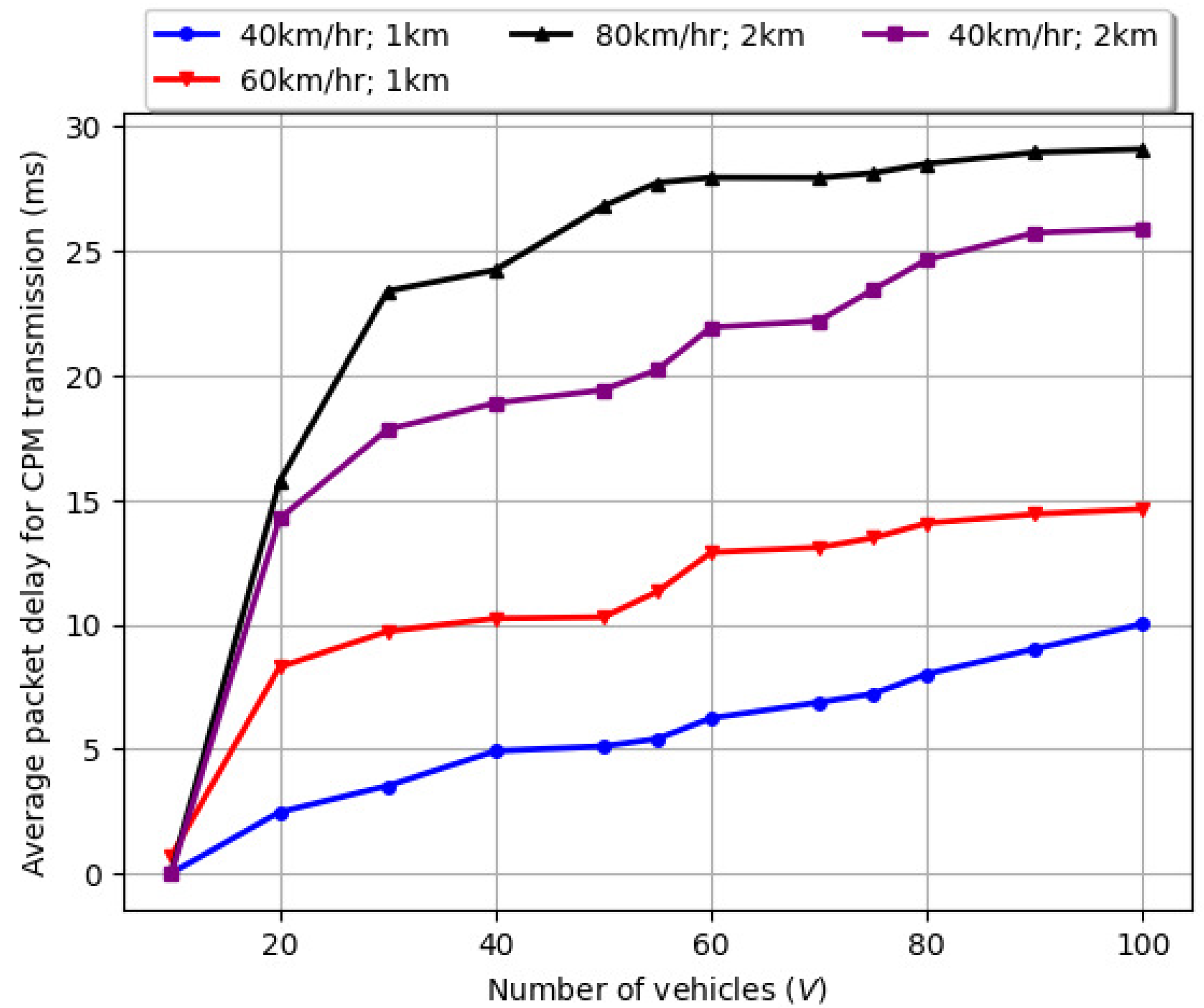
6.4. Variation of Average Packet Delay for CPMs with Number of Vehicles (V), Varying Vehicle Speed, and Road Length ()
6.5. Variation of Drone’s Average Energy Consumption (Joules/s) with Number of Vehicles (V)
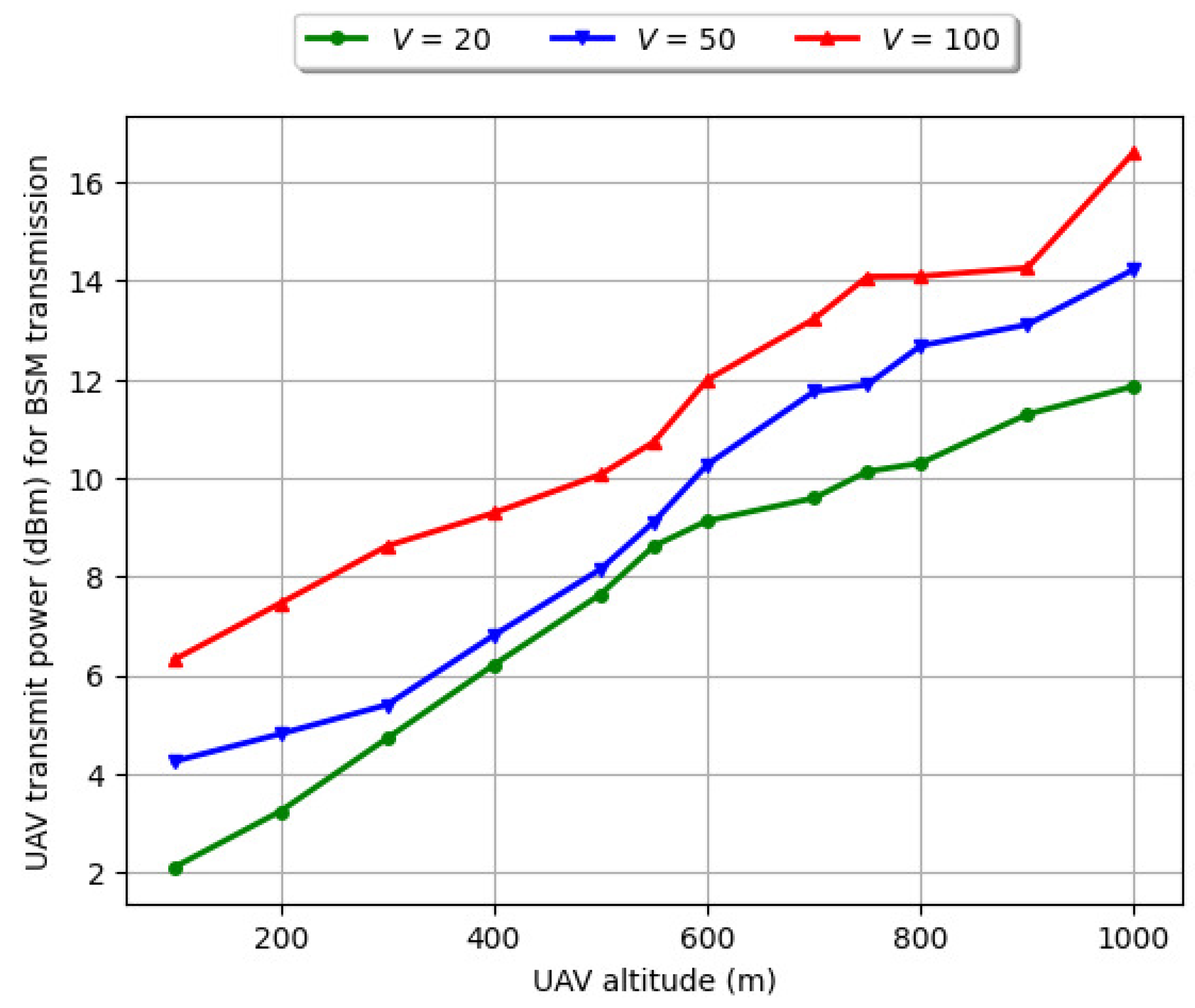
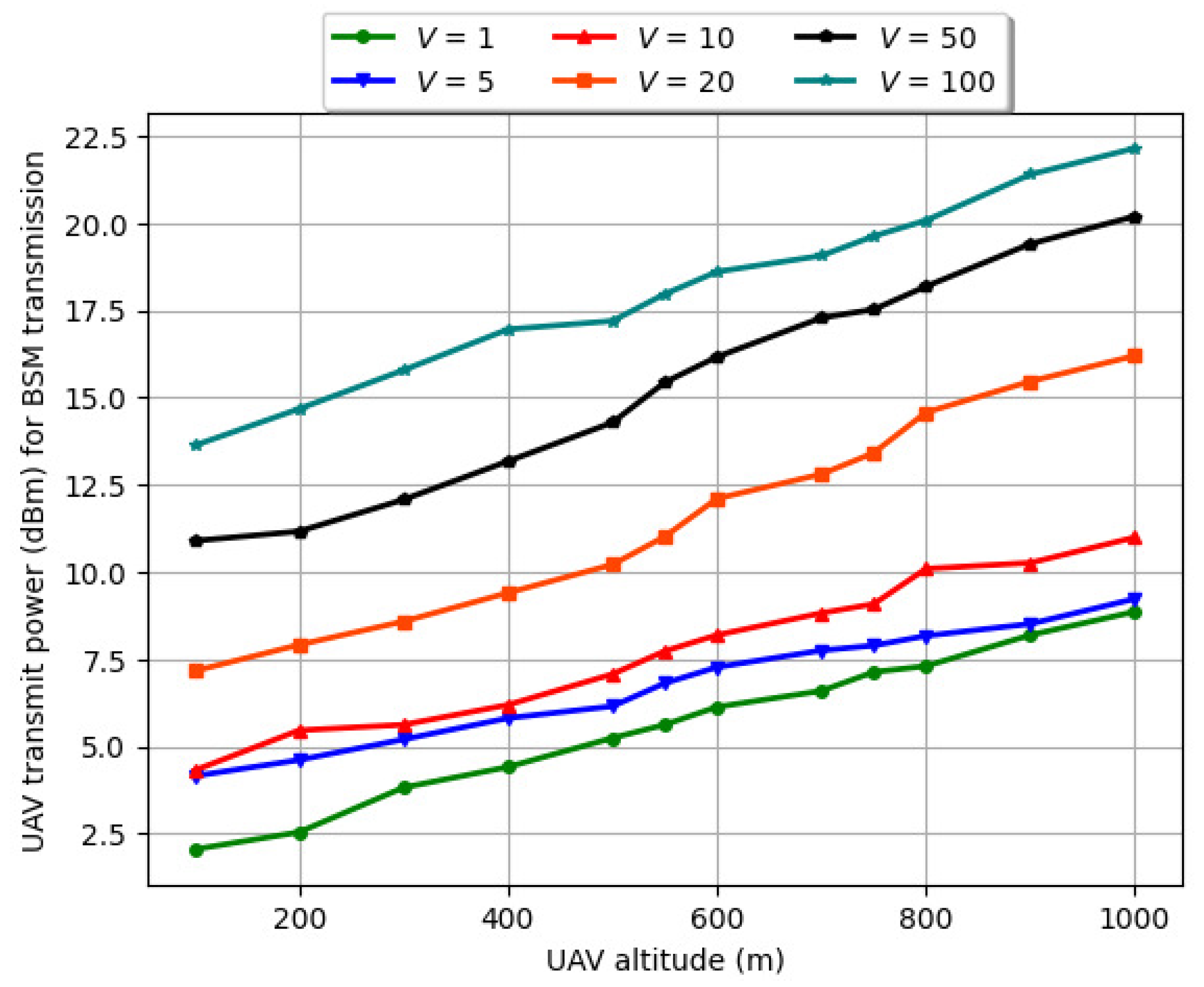
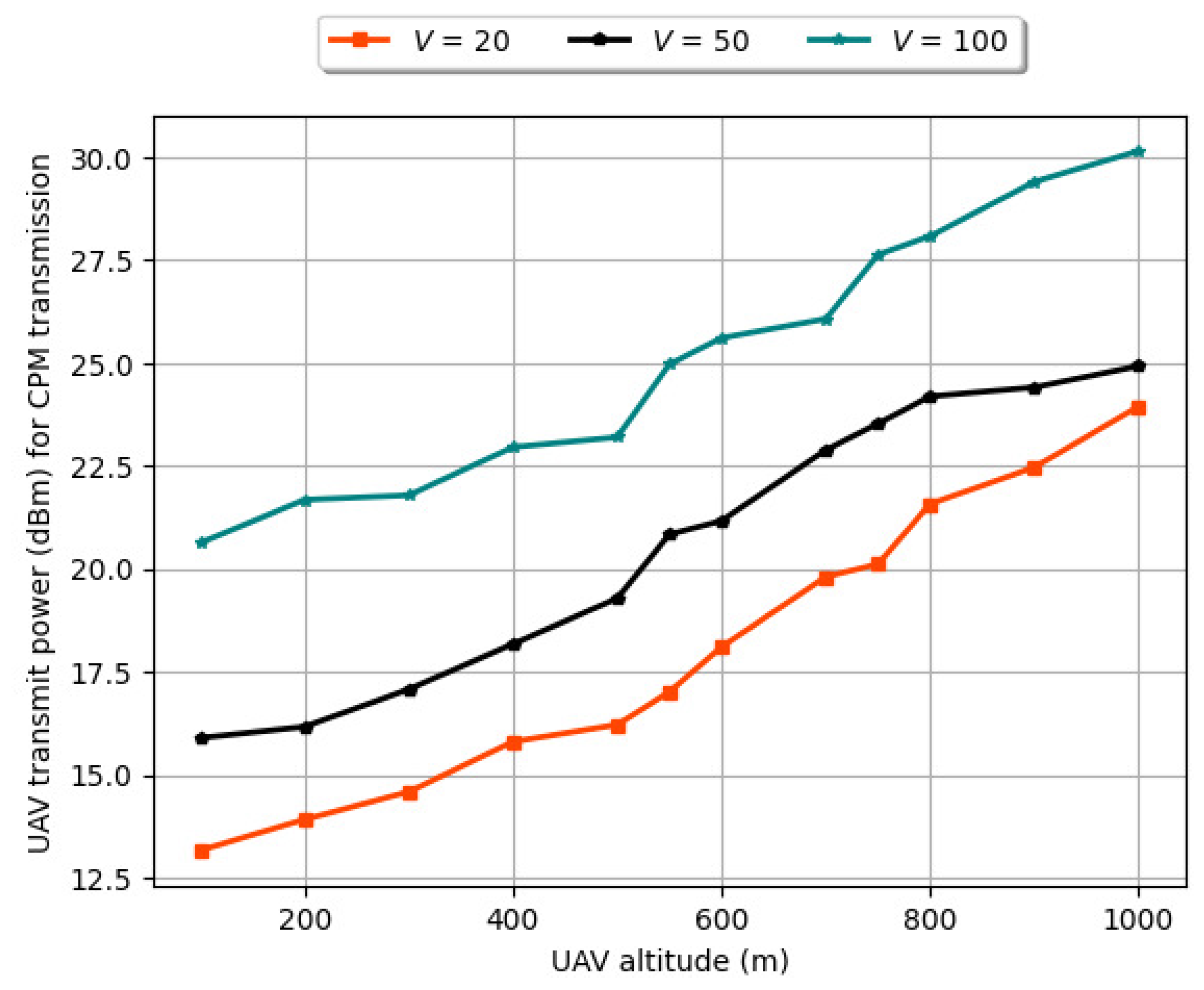
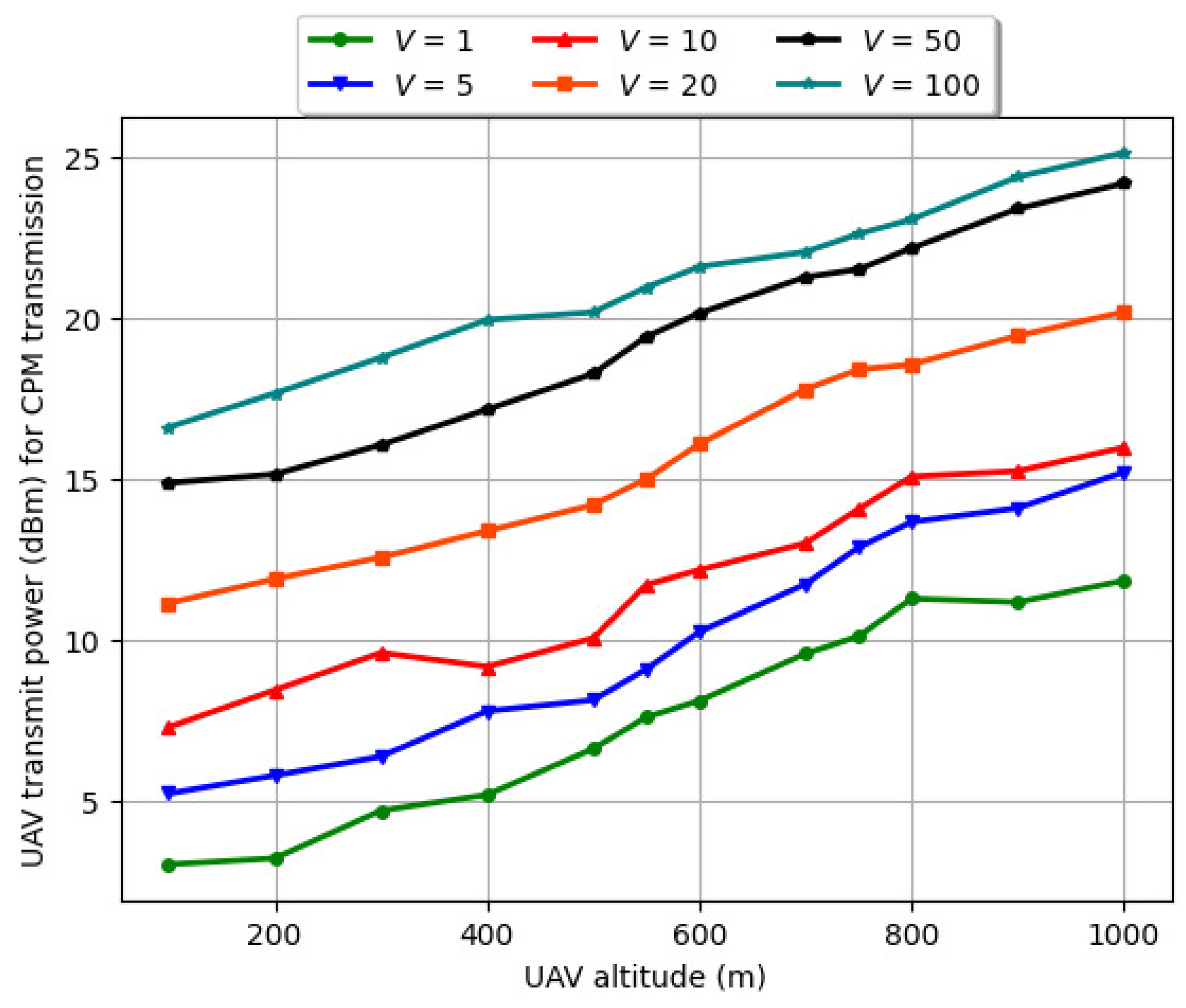
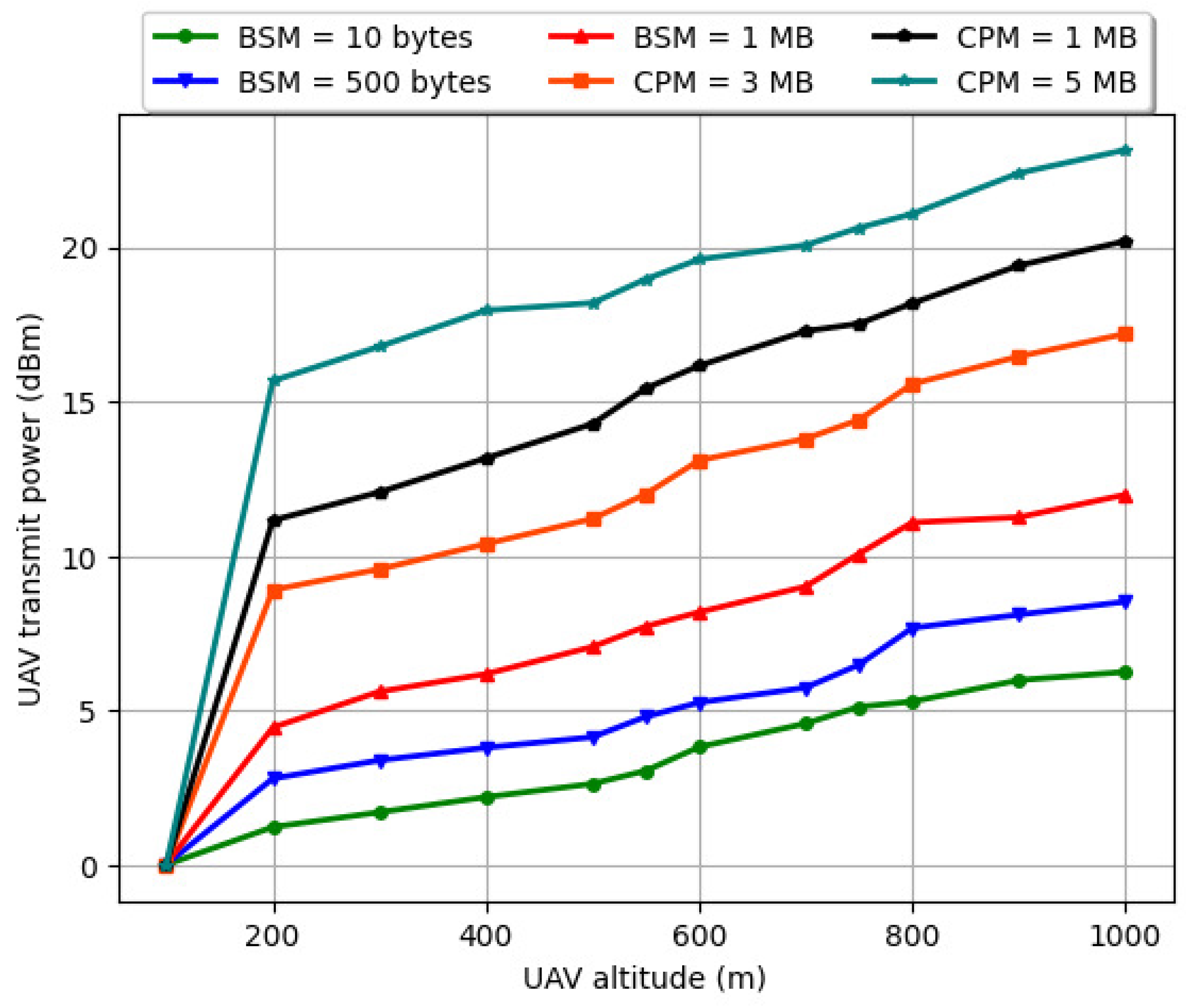
6.6. Variation of Drone’s Transmit Power (dBm) vs. Drone’s Altitude (m) with Number of Vehicles (V) for Varying Vehicle Velocity and
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 3GPP | Third-generation partnership project |
| 5GAA | Fifth-generation automotive association |
| 6G | Sixth-generation (Communication networks) |
| BCD | Block coordinate descent |
| BS | Base station |
| BSMs | Basic safety messages |
| CAV | Connected and automated vehicles |
| CBR | Channel busy ratio |
| CCCP | ConCave–convex procedure |
| C-ITS | Co-operative intelligent transport systems |
| CPMs | Cooperative perception messages |
| C-V2X | Cellular vehicle-to-everything |
| DNN | Deep neural network |
| DTMC | Discrete time Markov chain |
| DQN | Deep Q-network |
| DDQN | Double deep Q-network |
| E2E | End-to-end |
| ES | Edge Server |
| ETSI | European Telecommunications Standards Institute |
| FoI | Freshness of information |
| FL | Federated learning |
| FRL | Federated reinforcement learning |
| GHz | GigaHertz |
| ITS-G5 | Short-range vehicular communication, G5 implies 5.9 GHz frequency band |
| LoS | Line-of-sight |
| LTE | Long-term evolution |
| MAC | Medium access control |
| MDP | Markov Decision Process |
| MFC | Mobile fog computing |
| MINLP | Mixed integer non-linear programming |
| ML | Machine learning |
| MR-DC | Multi-radio access technology with dual connectivity |
| NR | New radio |
| PDR | Packet delivery ratio |
| QoS | Quality of service |
| RSU | Roadside unit |
| RTT | Round trip time |
| RVI | Relative value iteration |
| SAE | Society of automotive engineers |
| SAGIN | Space-air-ground integrated network |
| SATOA | Simulated annealing trajectory optimization algorithm |
| SCA | Successive convex approximation |
| SCAoI | Spatial correlation age of information |
| SPS | Sensing-based semi persistent scheduling |
| TFAM | Transmission frequency adjustment mechanism |
| THz | TeraHertz |
| TTI | Transmission time interval |
| UAV | Unmanned aerial vehicle |
| VEC | Vehicular edge computing |
| V2V | Vehicle to vehicle |
| VECNs | Vehicular edge computing networks |
| VSNs | Visual sensor networks |
| WSN | Wireless sensor networks |
References
- Manogaran, G.; Hsu, C.H.; Shakeel, P.M.; Alazab, M. Non-Recurrent Classification Learning Model for Drone Assisted Vehicular Ad-Hoc Network Communication in Smart Cities. IEEE Trans. Netw. Sci. Eng. 2021, 8, 2792–2800. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, G.; Zhong, Q.; Zheng, H.; Zhao, S. UAV-Aided Vehicular Communication Design with Vehicle Trajectory’s Prediction. IEEE Wirel. Commun. Lett. 2021, 10, 1212–1216. [Google Scholar] [CrossRef]
- Hosseini, M.; Ghazizadeh, R. Stackelberg Game-Based Deployment Design and Radio Resource Allocation in Coordinated UAVs-Assisted Vehicular Communication Networks. IEEE Trans. Veh. Technol. 2023, 72, 1196–1210. [Google Scholar] [CrossRef]
- Deng, D.; Wang, C.; Wang, W. Joint Air-to-Ground Scheduling in UAV-Aided Vehicular Communication: A DRL Approach with Partial Observations. IEEE Commun. Lett. 2022, 26, 1628–1632. [Google Scholar] [CrossRef]
- Shimizu, T.; Cheng, B.; Lu, H.; Kenney, J. Comparative Analysis of DSRC and LTE-V2X PC5 Mode 4 with SAE Congestion Control. In Proceedings of the 2020 IEEE Vehicular Networking Conference (VNC), New York, NY, USA, 16–18 December 2020; pp. 1–8. [Google Scholar]
- Chafii, M.; Bariah, L.; Muhaidat, S.; Debbah, M. Twelve Scientific Challenges for 6G: Rethinking the Foundations of Communications Theory. IEEE Commun. Surv. Tutor. 2023, 25, 868–904. [Google Scholar] [CrossRef]
- Bithas, P.S.; Nikolaidis, V.; Kanatas, A.G.; Karagiannidis, G.K. UAV-to-Ground Communications: Channel Modeling and UAV Selection. IEEE Trans. Commun. 2020, 68, 5135–5144. [Google Scholar] [CrossRef]
- Stefanovic, C.; Panic, S.; Bhatia, V.; Kumar, N. On Second-Order Statistics of the Composite Channel Models for UAV-to-Ground Communications with UAV Selection. IEEE Open J. Commun. Soc. 2021, 2, 534–544. [Google Scholar] [CrossRef]
- Gemici, O.F.; Hokelek, I.; Crpan, H.A. Modeling Queuing Delay of 5G NR with NOMA Under SINR Outage Constraint. IEEE Trans. Veh. Technol. 2021, 70, 2389–2403. [Google Scholar] [CrossRef]
- Sempere-García, D.; Sepulcre, M.; Gozalvez, J. LTE-V2X Mode 3 scheduling based on adaptive spatial reuse of radio resources. Ad Hoc Netw. 2021, 113, 102351. [Google Scholar] [CrossRef]
- Moreira, I.; Pimentel, C.; Barros, F.P.; Chaves, D.P.B. Modeling Fading Channels with Binary Erasure Finite-State Markov Channels. IEEE Trans. Veh. Technol. 2017, 66, 4429–4434. [Google Scholar] [CrossRef]
- NBA, G.P.W.; Haapola, J.; Samarasinghe, T. A Discrete-Time Markov Chain Based Comparison of the MAC Layer Performance of C-V2X Mode 4 and IEEE 802.11p. IEEE Trans. Commun. 2021, 69, 2505–2517. [Google Scholar] [CrossRef]
- Kang, B.; Yang, J.; Paek, J.; Bahk, S. ATOMIC: Adaptive Transmission Power and Message Interval Control for C-V2X Mode 4. IEEE Access 2021, 9, 12309–12321. [Google Scholar] [CrossRef]
- Molina-Masegosa, R.; Gozalvez, J.; Sepulcre, M. Comparison of IEEE 802.11p and LTE-V2X: An Evaluation with Periodic and Aperiodic Messages of Constant and Variable Size. IEEE Access 2020, 8, 121526–121548. [Google Scholar] [CrossRef]
- Wang, B.; Yuan, Z.; Zheng, S.; Liu, Y. Data-Driven Intelligent Receiver for OTFS Communication in Internet of Vehicles. IEEE Trans. Veh. Technol. 2023, 73, 6968–6979. [Google Scholar] [CrossRef]
- Gupta, A.; Fernando, X. Federated Reinforcement Learning for Collaborative Intelligence in UAV-assisted C-V2X Communications. Drones 2024, 8, 321. [Google Scholar] [CrossRef]
- Fernando, X.; Gupta, A. Analysis of Unmanned Aerial Vehicle-Assisted Cellular Vehicle-to-Everything Communication Using Markovian Game in a Federated Learning Environment. Drones 2024, 8, 238. [Google Scholar] [CrossRef]
- González, E.E.; Garcia-Roger, D.; Monserrat, J.F. LTE/NR V2X Communication Modes and Future Requirements of Intelligent Transportation Systems Based on MR-DC Architectures. Sustainability 2022, 14, 3879. [Google Scholar] [CrossRef]
- Petrov, T.; Pocta, P.; Kovacikova, T. Benchmarking 4G and 5G-Based Cellular-V2X for Vehicle-to-Infrastructure Communication and Urban Scenarios in Cooperative Intelligent Transportation Systems. Appl. Sci. 2022, 12, 9677. [Google Scholar] [CrossRef]
- Ghodhbane, C.; Kassab, M.; Maaloul, S.; Aniss, H.; Berbineau, M. A Study of LTE-V2X Mode 4 Performances in a Multiapplication Context. IEEE Access 2022, 10, 63579–63591. [Google Scholar] [CrossRef]
- Thandavarayan, G.; Sepulcre, M.; Gozalvez, J. Generation of Cooperative Perception Messages for Connected and Automated Vehicles. IEEE Trans. Veh. Technol. 2020, 69, 16336–16341. [Google Scholar] [CrossRef]
- Thandavarayan, G.; Sepulcre, M.; Gozalvez, J.; Coll-Perales, B. Scalable cooperative perception for connected and automated driving. J. Netw. Comput. Appl. 2023, 216, 103655. [Google Scholar] [CrossRef]
- Kunibe, M.; Yamazaki, R.; Murakawa, T.; Shigeno, H. Adaptive Message Prioritization for Vehicular Cooperative Perception at Target Intervals. J. Inf. Process. 2023, 31, 57–65. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, H.; Feng, W.; Lin, S. Vehicle Environment Awareness based Messages Transmission Frequency Optimization in C-V2X. IEEE Wirel. Commun. Lett. 2023, 12, 1116–1119. [Google Scholar] [CrossRef]
- Zhong, K.; Liu, S.; Fu, L. Throughput Maximization in Cellular Networks with Wireless Backhaul and Energy Harvesting. IEEE Trans. Veh. Technol. 2024, 73, 3551–3567. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, H.; Liu, Y.; Li, X.; Ji, H. An Intelligent UAV Deployment Scheme for Load Balance in Small Cell Networks Using Machine Learning. In Proceedings of the 2019 IEEE Wireless Communications and Networking Conference (WCNC), Marrakesh, Morocco, 15–18 April 2019; pp. 1–6. [Google Scholar]
- Huq, K.M.S.; Otung, I.E.; Rodriguez, J. A Study of Coverage Probability-Based Energy-Efficiency Analysis for UAV-Aided THz-Enabled 6G Networks. IEEE Trans. Intell. Transp. Syst. 2023, 24, 7404–7411. [Google Scholar] [CrossRef]
- Li, D.; Xu, S.; Li, Y. Massive heterogeneous data collecting in UAV-assisted wireless IoT networks. IET Commun. 2023, 17, 1706–1720. [Google Scholar] [CrossRef]
- Zhu, X.; Zhou, M. Maximal Weighted Coverage Deployment of UAV-Enabled Rechargeable Visual Sensor Networks. IEEE Trans. Intell. Transp. Syst. 2023, 24, 11293–11307. [Google Scholar] [CrossRef]
- Xie, Q.; Zhao, W.; Liu, C.; Peng, L. Task Assignment Optimization in Multi-UAV-Assisted WSNs Considering Energy Budget and Sensor Distribution Characteristics. Sensors 2023, 23, 7842. [Google Scholar] [CrossRef]
- Elnabty, I.A.; Fahmy, Y.; Kafafy, M. Framework for fast and low-complexity deployment of UAVs-assisted communication. Phys. Commun. 2023, 61, 102198. [Google Scholar] [CrossRef]
- Asim, M.; Junhong, C.; Muthanna, A.; Wenyin, L.; Khan, S.; El-Latif, A.A.A. A novel simulated annealing trajectory optimization algorithm in an autonomous UAVs-empowered MFC system for medical internet of things devices. Wirel. Netw. 2023, 29, 3163–3176. [Google Scholar] [CrossRef]
- Zhou, X.; Zhu, Q. Optimization Algorithm for AoI-Based UAV-Assisted Data Collection. Int. J. Distrib. Sens. Netw. 2024, 2024, 6691579. [Google Scholar] [CrossRef]
- Xue, T.; Ding, H.; Zhang, H.; Yuan, D. Two-timescale Vehicle Association and Resource Management for C-V2X Networks. IEEE Wirel. Commun. Lett. 2023, 12, 1259–1263. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, C.; Chen, X.; Wu, F. Joint Hybrid Caching and Replacement Scheme for UAV-Assisted Vehicular Edge Computing Networks. IEEE Trans. Intell. Veh. 2024, 9, 866–878. [Google Scholar] [CrossRef]
- Lin, N.; Fu, L.; Zhao, L.; Min, G.; Al-Dubai, A.; Gacanin, H. A Novel Multimodal Collaborative Drone-Assisted VANET Networking Model. IEEE Trans. Wirel. Commun. 2020, 19, 4919–4933. [Google Scholar] [CrossRef]
- Chai, J.; Meng, Y.; Wang, W.; Lyu, Y.; Yue, H.; Liu, X. Task scheduling of computation-intensive graph jobs in UAV-assisted hybrid vehicular networks. Veh. Commun. 2023, 42, 100630. [Google Scholar] [CrossRef]
- Yan, X.; Fang, X.; Deng, C.; Wang, X. Joint Optimization of Resource Allocation and Trajectory Control for Mobile Group Users in Fixed-Wing UAV-Enabled Wireless Network. IEEE Trans. Wirel. Commun. 2024, 23, 1608–1621. [Google Scholar] [CrossRef]
- Nguyen, M.D.; Le, L.B.; Girard, A. Integrated Computation Offloading, UAV Trajectory Control, Edge-Cloud and Radio Resource Allocation in SAGIN. IEEE Trans. Cloud Comput. 2024, 12, 100–115. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, W.; Ansari, N. Completion Time Minimization for Data Collection in a UAV-enabled IoT Network: A Deep Reinforcement Learning Approach. IEEE Trans. Veh. Technol. 2023, 72, 14734–14742. [Google Scholar] [CrossRef]
- Chetlur, V.V.; Dhillon, H.S. Coverage and Rate Analysis of Downlink Cellular Vehicle-to-Everything (C-V2X) Communication. IEEE Trans. Wirel. Commun. 2020, 19, 1738–1753. [Google Scholar] [CrossRef]
- Bedewy, A.M.; Sun, Y.; Kompella, S.; Shroff, N.B. Optimal Sampling and Scheduling for Timely Status Updates in Multi-Source Networks. IEEE Trans. Inf. Theory 2021, 67, 4019–4034. [Google Scholar] [CrossRef]
- Plaisted, D. Some Polynomial and Integer Divisibility Problems are NP-Hard. SIAM J. Comput. 1978, 7, 458–464. [Google Scholar] [CrossRef]





| Symbol | Definition |
|---|---|
| = | UAV trajectory at different time steps |
| Vehicle cluster | |
| Number of vehicles in a cluster | |
| Number of edge servers | |
| Packet arrival rate | |
| Packet departure rate | |
| Utilization of the edge server | |
| Queuing model considered in this paper | |
| Probability of a packet being queued at the ES | |
| Queuing delay of the ES | |
| Steady-state probability that the ES is available | |
| Steady-state probability that number of edge servers are occupied | |
| Size of the batch of packets arriving at the drone in a transmission window | |
| The number of packets that depart the queue in a TTI | |
| Capacity of the queue | |
| Queue length at the end of the previous window | |
| Drone utilization | |
| Size of the data transmitted from vehicle v, accumulated at the ES | |
| Average delay experienced by a batch of packets | |
| Size of packets arriving at the drone | |
| Number of packets arriving at the drone in a single transmission window | |
| Varying road lengths considered in this work | |
| Size of data transmitted from vehicle v, accumulated at the ES | |
| Number of packets transmitted to the drone | |
| The queuing probability at the () ES remains below this predefined value | |
| , | Steady-state probability distributions |
| Process where drone is busy when packet (m) arrives at the drone | |
| Successful arrival of packet (m) at the drone | |
| Drone state-space | |
| Time spent by packets in the queue waiting to arrive at the drone | |
| Occupancy indicator for the buffer queue | |
| Drone occupancy indicator | |
| Occupancy indicator for the transmission queue | |
| Cumulative occupancy indicator for the drone in a TTI | |
| Status update at the drone | |
| Duration for which packet is processed at the drone | |
| Cost of selecting an action when the drone is in the state | |
| State-transition probability of the agent | |
| An irrelevant delay when the drone is idle | |
| Real number between 0 and 1 | |
| Function that depends on packet arrival rate and service rate | |
| Processing delay experienced by a packet following the queuing delay | |
| An optimal policy for the state change with minimal delay | |
| Set of optimal values for all states () |
| Parameter | Value |
|---|---|
| Vehicle Mobility | Manhattan Mobility |
| Number of vehicles (V) | 1–100 |
| Number of drones | 1 |
| Drone deployment altitude | 100 m–2 km |
| Edge server location | In-vehicle |
| Communication frequency | 5.9 GHz |
| Distance between vehicles | 10–100 m |
| Modulation technique | 16-QAM |
| Road length | 1–5 km |
| Vehicle speed | 0–100 kmph |
| Payload size for BSM, CPM | 1 byte–3 Megabytes |
| 100 ms–1000 ms | |
| 100, 200, 300, 500 ms | |
| 1000, 2000 packets/s | |
| Mean speed of vehicles | 50 km/h |
| Drone transmission power | 30 dBm (1000 mW) |
| Drone receiving threshold | −80 dBm |
| Vehicle transmission power | 25 dBm (316.2 mW) |
| Standard deviation in speed | 10 km/h |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gupta, A.; Fernando, X.N. Latency Analysis of Drone-Assisted C-V2X Communications for Basic Safety and Co-Operative Perception Messages. Drones 2024, 8, 600. https://doi.org/10.3390/drones8100600
Gupta A, Fernando XN. Latency Analysis of Drone-Assisted C-V2X Communications for Basic Safety and Co-Operative Perception Messages. Drones. 2024; 8(10):600. https://doi.org/10.3390/drones8100600
Chicago/Turabian StyleGupta, Abhishek, and Xavier N. Fernando. 2024. "Latency Analysis of Drone-Assisted C-V2X Communications for Basic Safety and Co-Operative Perception Messages" Drones 8, no. 10: 600. https://doi.org/10.3390/drones8100600
APA StyleGupta, A., & Fernando, X. N. (2024). Latency Analysis of Drone-Assisted C-V2X Communications for Basic Safety and Co-Operative Perception Messages. Drones, 8(10), 600. https://doi.org/10.3390/drones8100600







