Probabilistic Risk Assessment for Data Rate Maximization in Unmanned Aerial Vehicle-Assisted Wireless Networks

Abstract

The evolution of beyond fifth generation (B5G) wireless networks poses significant technical and economic challenges across urban, suburban, and rural areas, demanding increased capacity for users whose positions continually change. This study investigated the dynamic positioning of an unmanned aerial vehicle (UAV), acting as a mobile base station (MoBS) to enhance network efficiency and meet ground terminals (GTs) expectations for data rates, particularly in emergency scenarios or temporary events. While UAVs show great promise, existing research often assumes certainty in network architecture, overlooking the complexities of unpredictable user movements. We introduce a decision-making framework utilizing the ordered weighted averaging (OWA) operator to address uncertainties in GT locations, enabling the optimization of UAV trajectories to maximize the overall network data rate. An optimization problem is formulated by modeling GT dynamics through a Markov process and discretizing UAV movements while accounting for communication thresholds and movement constraints. Extensive simulations reveal that our approach significantly improves expected data rates by up to 48% compared to traditional fixed base stations (BSs) and predefined UAV movement patterns. This research underscores the potential of UAV-assisted networks to bolster communication reliability while effectively managing dynamic user movements to maintain optimal quality of service (QoS).

1. Introduction

The development of beyond fifth generation (B5G) wireless networks poses technical and economic obstacles in urban, suburban, and rural areas. This transition to next-generation networks requires more capacity per user and better quality of service (QoS) [1]. The increase in users and progressive deployment of Internet of Things (IoT) devices, fostered by the smart city paradigm, contributes to the traffic growth [2]. The inherent dynamics of mobile users, such as their unpredictable movement, introduce considerable complexities in maintaining the desired QoS. These dynamics affect the stability and reliability of the network, particularly in scenarios where users frequently change locations, which can lead to fluctuating signal quality and bandwidth availability. The fundamental challenge is to develop an efficient method to serve a group of mobile users within a given area, ensuring that data rate thresholds are consistently met. This requires adapting the network’s resources in real time to account for different user densities, mobility patterns, and communication demands.

One viable strategy to tackle these challenges is to increase the number of base stations (BSs), which reduces the distance to users or ground terminals (GTs). This network densification can enhance capacity and energy efficiency [3]. However, the deployment of numerous BSs in small cells demands substantial financial investment, leading to increased capital expenditures (CAPEX) and operating expenditures (OPEX). Furthermore, densification may result in oversizing resources to meet the variable traffic demand [4].

The deployment of flying BSs promises to be crucial in optimizing network efficiency by reducing spatial redundancy with GTs. One solution is physically relocating drone-based BSs between residential and enterprise areas as needed [5]. This strategy, referred to as mobile base station (MoBS), has been successfully implemented in various scenarios providing temporary services at outdoor events or in disaster-affected areas [6]. As a result, the emergence of the moving network paradigm (MNP) has paved the way for using unmanned aerial vehicles (UAVs) or drones to support communication in a wide range of applications [7]. The commercial drone market has experienced significant growth and is projected to reach 58.4 million by 2026, which suggests that it could be a viable solution [8]. However, including dynamic elements like MoBS introduces new challenges regarding network architecture and resource allocation [9].

Most of the reported solutions lack an analysis of the deployment or trajectory of the UAV under risk or ignorance of the movement dynamics of GTs. Typically, authors assume a condition of certainty, wherein the network architecture is presumed to be known at each time instant [10,11]. However, decision-making under uncertainty provides a more realistic network model and allows quantifying the system performance by optimizing QoS. It is imperative to select the optimal decision alternative when the environment is uncertain and various payoff outcomes arise for different states of nature, such as the variety of GT positions. Following this direction, nonstationary environments have been addressed through reinforcement learning approaches, which often entail increased time complexity and require a preliminary training stage [12]. The high computational complexity and energy demand of machine learning algorithms render them unsuitable for execution on UAVs powered by batteries. In contrast, the ordered weighted averaging (OWA) operator brings a unifying framework to determine the action that yields the most significant reward, only analyzing the statistical features of GT mobility models [13].

This study was motivated by the growing interest in integrating MoBSs into existing networks to accommodate the expected surge in users and traffic demands in B5G networks. Additionally, UAV-assisted networks can deliver more reliable communication to users in areas with limited accessibility or those isolated by emergencies. In such scenarios, it is plausible that communication links may be unstable, leading to inaccurate or unknown positions of GTs within the network. Therefore, effectively managing the dynamics of GT motion patterns becomes essential to ensure the QoS.

The principal contributions can be summarized as follows:

• A comprehensive scenario is developed in alignment with the novel MNP, which captures the network dynamics of both GTs through a Markov process and a UAV performing discrete movement alternatives.
• An optimization problem is formulated to maximize the data rate during operation while imposing constraints on the movement perimeter and the communication threshold for each time slot.
• A decision-making framework is introduced, utilizing the OWA operator to account for certainty and uncertainty in GTs locations, thereby determining the optimal trajectory of the UAV and effectively maximizing the average data rate.
• Extensive simulations are conducted for single- and multi-user cases to validate our proposal compared to a traditional fixed base station and a predefined circular trajectory. Various mobility models are evaluated, including the equal probability of neighboring positions and hotspot movement patterns for GT, reflecting realistic emergencies.

The rest of the paper is organized as follows. Section 2 presents the related works in the state of the art. Section 3 presents the moving network model, including propagation, QoS metric, and GT and UAV motion patterns. Section 4 introduces the optimization problem and the decision-making framework based on the OWA operator. Section 5 explores various simulation scenarios consistent with disaster-affected areas to validate the proposal performance. Finally, Section 6 concludes the paper.

2. Related Work

The path planning for UAVs acting as flying BSs has been addressed from two perspectives: certainty and uncertainty. Typically, certainty-based solutions refer to the knowledge of the GT’s spatial coordinate within the network. One method to identify the GT location involves utilizing the control channel to transmit this information to the UAV at each time slot. In [10,11], the throughput and energy consumption were optimized by adequately planning the drone routes. A multi-agent deep reinforcement learning strategy has been proposed to jointly maximize throughput and energy efficiency by optimally determining the UAV’s altitude while operating under fully observable settings [14]. In [15], a centralized algorithm for UAV positioning is introduced to maximize throughput in a software-defined disaster area network, utilizing real-time information on network topology, data rate demands, and flow paths maintained by the software-defined networking controller. In practice, this approach has the shortcoming of incurring additional data traffic on the network. A second method focuses on detecting the presence or absence of users in the network. In [16], they applied a sweep and search algorithm to find the optimal deployment of a flying BS, while [17] reports on the use of a UAV equipped with an onboard radar transceiver to localize a GT at an unknown position. The latter method assumes that the evolution of the GT positions adheres to predefined patterns, such as the Random Waypoint or Gauss–Markov mobility models [18,19].

Uncertainty-based trajectory planning has been explored from different points of view, including handling unknown environmental boundaries and dynamic obstacles [20,21], addressing uncertainties in communication and computation [22], and managing scenarios where GTs positions are disregarded [12,23,24,25,26,27,28]. From the uncertain GT location perspective, future user trajectories have been predicted by extracting temporal and spatial regularity data from real-world trajectories [23]. In [24], the authors devise a UAV route to minimize total power consumption in a scenario where GTs are equipped with global positioning system (GPS) modules that offer imperfect position accuracy. A reinforcement learning formulation is proposed in [25] that maximizes the cumulative collected data of the UAV by optimizing its flight trajectory without knowledge of static sensors’ location. For dynamic users, reinforcement learning approaches have been explored to guide UAV flights for fair communication coverage [26], coordinate UAVs’ sensing tasks using a sense-and-send protocol [27], and maximize network throughput despite limited access to user-side information [12,28].

Our proposed UAV path planning approach requires neither capturing real-time user mobility patterns nor prior training time to converge efficiently, which could be computationally expensive. Instead, we leverage the OWA operator for decision-making under uncertainty, focusing solely on the statistical features of GT motion patterns.

3. Moving Network Model

The wireless network comprises a UAV acting as a MoBS, which flies over a square area of side s and serves a set of K GTs randomly distributed within the simulation area, as illustrated in Figure 1. The GTs are depicted as black dots, representing mobile entities that simulate random movements across the UAV’s coverage area. This design emulates real-world scenarios where users change positions unpredictably, enabling a thorough evaluation of the UAV’s communication capabilities and optimizing throughput in dynamic environments. For simplicity, both the UAV and the GTs are permitted to change their respective positions within each time slot. This may entail relocating to one of the eight surrounding positions within the grid or remaining at the current position, as illustrated with arrows in Figure 1. Furthermore, the UAV is deployed at a predefined height H, enabling movement in a two-dimensional (2D) Cartesian coordinate system, which can be extrapolated to three-dimensional (3D) scenarios. The time is discretized to facilitate the description of movement patterns and derive closed-form expressions for the evolution of the dynamic system. The vector ${\mathit{p}}_{\mathbf{uav}}\left(t\right)=[x_{\mathrm{uav}}\left(t\right),y_{\mathrm{uav}}\left(t\right),H]$ describes the UAV position on each time slot t, and ${\mathit{p}}_{\mathbf{gt}}\left(t\right)=[x_{\mathrm{gt}}\left(t\right),y_{\mathrm{gt}}\left(t\right),0]$ denotes the GT trajectory. The distance $d_j\left(t\right)$ between the UAV and j-th GT is defined over the entire simulation time T based on the Euclidean norm $\parallel ·\parallel$ as follows:

$$d_j\left(t\right)=\parallel {\mathit{p}}_{\mathbf{uav}}\left(t\right)-{\mathit{p}}_{{\mathbf{gt}}_{\mathit{j}}}\left(t\right)\parallel .$$

(1)

The mobility of both devices leads to a dynamic network where devices, UAV and GTs, are continuously moving, i.e., Euclidean distance $d_j\left(t\right)$ becomes a time-varying parameter. The UAV needs to appropriately reduce the distance to devices it serves to improve the quality of communication links. We leverage drone driving facilities to accomplish the above requirements.

In general, this model points in two directions: (i) it replicates a scenario where a UAV serves isolated ground users as a consequence of a natural disaster or any other undesirable phenomenon that prevents them from communicating with the ground base station; (ii) it simulates wireless communication links from various devices to a given fusion terminal (UAV), which is relevant to the Internet of Mobile Things (IoMT) paradigm [29]. The aim is to reduce the distance from the UAV to the GTs to improve the expected network data rate.

3.1. Propagation and Network Metrics

The wireless communication channel between the UAV and the j-th GT is modeled by the general complex-valued channel coefficient expressed as [30]

$$h_j\left(t\right)=\sqrt{{\beta }_j\left(t\right)}{\tilde{h}}_j\left(t\right),j\in [1,K],\mathrm{and}t\in [1,T],$$

(2)

where ${\beta }_j\left(t\right)$ represents the large-scale fading such as path loss and shadowing. It depends on the random distance ${\tilde{d}}_j$, which denotes the distance between the UAV and the j-th GT as a result of the random mobility of GTs per time slot. The parameter ${\tilde{h}}_j\left(t\right)$ is a complex Gaussian random variable with $\mathbb{E}\left[\right|{\tilde{h}}_j\left(t\right){|}^2]=1$ that describes the small-scale fading due to multi-path propagation.

We adopt the elevation angle-dependent probabilistic line-of-sight (LoS) model to simulate large-scale fading as fully developed for aerial-to-ground communication links [31]. This model is suitable for urban environments, utilizing statistical data on building height and distribution. Although further experimental validation is needed, it offers valuable insights for theoretical analysis and simplified shadowing effects. Specifically, the channel coefficient is determined based on LoS and non-line-of-sight (NLoS) propagation environments. The large-scale parameter ${\beta }_j\left(t\right)$ is defined as follows [11]:

$${\beta }_j\left(t\right)=\left\{\begin{array}{cc}{\beta }_0{d}_j^{-\gamma }\left(t\right)\hfill & \mathrm{LoS}\mathrm{link}\hfill \\ k{\beta }_0{d}_j^{-\gamma }\left(t\right)\hfill & \mathrm{NLoS}\mathrm{link}\hfill \end{array}\right.,$$

(3)

where ${\beta }_0$ is the free-space path loss at the reference distance $d_0=1 \mathrm{m}$, the parameter k describes the additional attenuation due to the NLoS condition, $\gamma$ represents the path loss exponent that typically varies from 2 to 6, and we also assume isotropic transmitter and receiver antennas.

To address the impact of link blockage caused by obstacles such as surrounding buildings, we define the probabilities of LoS and NLoS links between the UAV and the j-th GT at time interval t. These probabilities can be represented as functions of the elevation angle ${\theta }_j\left(t\right)$ [31]:

$$P_{j,\mathrm{LoS}}\left(t\right)={\displaystyle \frac{1}{1+aexp(-b[{\theta }_j\left(t\right)-a])}},$$

(4)

and

$$P_{j,\mathrm{NLoS}}\left(t\right)=1-P_{j,\mathrm{LoS}}\left(t\right),$$

(5)

where parameters a and b are related to propagation conditions, and ${\theta }_j\left(t\right)={\displaystyle \frac{180}{\pi }}{sin}^{-1}\left({\displaystyle \frac{H}{d_j\left(t\right)}}\right)$ in degree, as shown in Figure 1. Then, the channel coefficient depends on two random variables: the probabilities of occurrence of LoS and NLoS, and the small-scale fading. One approximation to predict the channel state or propagation loss can be stated if we analyze the expected value of the channel $h_j\left(t\right)$ as follows:

$$\mathbb{E}\left[\right|h_j\left(t\right){|}^2]=P_{j,\mathrm{LoS}}\left(t\right){\beta }_0{d}_j^{-\gamma }\left(t\right)+P_{j,\mathrm{NLoS}}\left(t\right)k{\beta }_0{d}_j^{-\gamma }\left(t\right).$$

(6)

In emergency or disaster management, efficient communication between the MoBS and GTs requires a reliable, high-speed, and uninterrupted link to support maximum data throughput. This requirement is critical for delivering vital information to users, such as an updated route to a rescue point, a map of the affected area, or notifications of collateral events. Then, we must optimize the instantaneous channel capacity, which represents the total number of transmitted bits per second (bps) for a specific bandwidth B in Hertz (Hz) at each time slot t.

The maximum amount of information that can be transmitted over the channel from the UAV to the j-th GT, known as the data rate, is determined by the Shannon capacity theorem [32]. However, the channel coefficient $h_j\left(t\right)$ is a time-varying parameter due to the dynamics of mobile GTs and the UAV. This characteristic establishes an alternative deterministic metric to quantify the expected data rate. The first-order statistical moment of the channel can be upper-bounded based on the concavity of the logarithmic function and using Jensen’s inequality as follows:

$$\mathbb{E}\left[R_j\left(t\right)\right]\le B{log}_2\left(1+{\displaystyle \frac{P_t\mathbb{E}\left[\right|h_j\left(t\right){|}^2]}{{\sigma }^2}}\right),$$

(7)

where $P_t$ is the transmission power by the UAV, and ${\sigma }^2$ is the noise power defined by the variance of an Additive White Gaussian Noise (AWGN) random process of zero mean. The target is to maneuver the UAV by changing its spatial position at each time slot t to maximize the total number of bits transmitted over the entire simulation time T while only considering short-term network performance.

3.2. GT Motion Pattern

Here, we present the motion characteristics of users according to the extensively explored mobility models suitable for dynamic networks. Currently, there are two principal categories: entity models and group models. The former is associated with individual movements for each user, and the latter is focused on situations in which user decisions on movement depend upon other users’ positions in the group [33]. In this work, we choose an entity mobility pattern for GT based on the model discussed in [34] provided we do not have any assumptions on group mobility models.

The GT motion is modeled by a stochastic process $X\left(t\right)$ that fully complies with the Markovian property. The time is discretized by $t=1,2,...,T$, and each GT may perform one movement per time slot towards the nine potential positions as indicated with arrows in Figure 1. The total number of states $l^2={\lfloor s/r\rfloor }^2$ in the Markov chain depends on the size of the rectangular area s and the grid resolution r. The next state is determined based only on the current state and is independent of time.

Let $X\left(t\right)=i$ represent the current process in state i during time slot t. We suppose whenever the process is in state i, there is a fixed probability $p_{ik}$ to be in the next state k as presented in [35]:

$$P\{X(t+1)=k|X\left(t\right)=i\}=p_{ik},$$

(8)

where $p_{ik}>0$ and ${\sum }_{k=0}^{l^2}{p}_{ik}=1$, $i=0,1,2,...,l^2$. The one-step transition probability matrix $\mathbf{P}$ is composed of $p_{ik}$ values. Additionally, it can be expressed in terms of ${\mathbf{P}}_{\mathbf{h}}$ and ${\mathbf{P}}_{\mathbf{v}}$, accounting for the matrix of transition probabilities for the horizontal and vertical movements, respectively. Then, assuming that both motion patterns are statistically independent, the general one-step transition probability matrix can be defined as follows [36]:

$$\mathbf{P}=\left[p_{ik}\right]={\mathbf{P}}_{\mathbf{h}}\otimes {\mathbf{P}}_{\mathbf{v}},$$

(9)

where $\mathbf{P}\in {\mathbb{R}}^{l^2\times l^2}$, $({\mathbf{P}}_{\mathbf{h}},{\mathbf{P}}_{\mathbf{v}})\in {\mathbb{R}}^{l\times l}$ are provided below, and ⊗ represent the Kronecker product. For simplicity, we establish the probabilities of moving to the left, remaining in the current position, or going to the right as $(q,r,p)$. Similarly, we define the probabilities of moving up, staying at the current position, or going down. The matrices are defined as follows:

$${\mathbf{P}}_{\mathbf{h}}={\mathbf{P}}_{\mathbf{v}}=\left[\begin{array}{cccccc}{r}_0& p_0& 0& 0& \dots & 0\\ q_1& r_1& p_1& 0& \dots & 0\\ 0& q_2& r_2& p_2& \dots & 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& \dots & q_i& r_i& p_i& 0\\ 0& \dots & 0& q_{l-1}& r_{l-1}& p_{l-1}\\ 0& \dots & 0& 0& q_l& r_l\end{array}\right],$$

(10)

where these probability values for a given GT must satisfy $r_0+p_0=1$, $q_l+r_l=1$, $q_i+r_i+p_i=1$ and $i=0,1,2,...,l$ in both cases: horizontal and vertical displacements.

In accordance with the established rules, a given GT (denoted by black circles in Figure 1) has the potential to move to any of nine positions during each time slot by either following arrow directions or remaining in the current position. The probability of reaching state k after t discrete steps, represented by vector ${\mathbf{p}}^{\left(t\right)}$, is calculated based on the initial probability distribution ${\mathbf{p}}^{\left(0\right)}=(p_1^{\left(0\right)},\cdots ,p_{l^2}^{\left(0\right)})$ as follows:

$${\mathbf{p}}^{\left(t\right)}={\mathbf{p}}^{\left(0\right)}{\mathbf{P}}^t.$$

(11)

The previous relation enables modeling the dynamic behavior of GTs and facilitates informed decision-making regarding UAV path planning to optimize channel capacity.

3.3. UAV Flight Operation

The UAV flight parameters are analyzed and updated at the beginning of each time slot. This task involves selecting one of nine potential surrounding positions, similar to the GT motion pattern. This pattern implies an angular resolution of 45° on the horizontal plane. The only distinction is that the drone flies at a specified height H, as depicted in Figure 1. Furthermore, the UAV possesses aerodynamic properties, enabling it to hover as necessary. As a first approximation, we assume that the drone maintains a constant speed and zero acceleration throughout the flight time T. The battery capacity is also sufficient to complete the entire trip without depletion.

The flight trajectory of the UAV should remain within the operational area and maximize the expected data rate. This type of flight operation is crucial in applications such as wide-area monitoring for emergency management, where stability and consistency are paramount. The UAV must determine the best destination for the next step to serve dispersed users in a particular area. The same model can be applied in adjacent fields to handle larger-scale scenarios. The following section introduces the problem of optimizing the trajectory for the UAV as a flying BS to maximize the expected network data rate.

4. Data Rate Optimization

The QoS metric to be optimized is the total expected data rate $R_T$. In this regard, we must adequately plan the UAV trajectory during the execution time to be closer to the GTs. However, this is challenging because of the communication channel dynamics associated with the mobility of users. For instance, in a single-user network, the objective is typically to monitor or track a specific target. In a network that comprises multiple GTs, determining the next movement of a UAV can be accomplished based on traffic priority or bandwidth requirements of individual users. The MoBS must build its route considering a global consensus about the minimum network throughput required.

Assuming the decision-making strategy is based solely on the expected data rate, the following optimization problem can be formulated to maximize the total expected data rate $R_T$ for K GTs over the entire simulation time T:

$$\begin{array}{cc}\underset{x_{\mathrm{uav}},y_{\mathrm{uav}}}{argmax}\hfill & R_T={\displaystyle \sum _{t=1}^T}\left({\displaystyle \frac{1}{K}}{\displaystyle \sum _{j=1}^K}\mathbb{E}\left[R_j\left(t\right)\right]\right)\hfill \\ \mathrm{s}.\mathrm{t}.\hfill & {\displaystyle \sum _{j=1}^K}\mathbb{E}\left[R_j\left(t\right)\right]\ge R_{\tau }\hfill \\ & 0\le \left(x_{\mathrm{uav}},y_{\mathrm{uav}}\right)\le l\hfill \end{array}$$

(12)

where the expected throughput for the j-th GT is calculated according to (7). The first constraint sets a threshold $R_{\tau }$ that must be met in each time slot to ensure a satisfactory level of service for network users. The final constraint limits UAVs movement to a designated area to prevent collisions with other drones in adjacent cells.

The optimization problem posed in (12) requires obtaining the optimal UAV coordinates along the execution time. The primary challenge is managing the user movement uncertainty, which causes changes in their positions within the network. To address this, we simplified the strategy by partitioning the problem into smaller pieces, deriving a short-term outcome. This approach entails solving a static version of the optimization problem for each time instant, focusing on the current setup and disregarding the influence on future states.

4.1. Decision-Making Framework

To tackle the optimal solution when facing uncertainty regarding the position of GTs, we propose a general approach to determine the appropriate movements of the UAV per time slot. The method is based on the OWA operator, which involves three terms in decision-making strategy: the states of nature $S_n$, the actions or alternatives available $A_m$, and the rewards or payoffs $C_{mn}$ obtained by applying action $A_m$ when state $S_n$ occurs [13]. The matrix below illustrates the interaction among the three parameters,

$$\begin{array}{cc}\hfill & \begin{array}{ccccc} S_1& \cdots & S_n& \cdots & S_N\end{array}\hfill \\ \hfill \begin{array}{c}{A}_1\\ ⋮\\ A_m\\ ⋮\\ A_M\end{array}& \left[\begin{array}{ccccc}{C}_{11}& \cdots & C_{1n}& \cdots & C_{1N}\\ ⋮& & ⋮& & ⋮\\ C_{m1}& \cdots & C_{mn}& \cdots & C_{mN}\\ ⋮& & ⋮& & ⋮\\ C_{M1}& \cdots & C_{Mn}& \cdots & C_{MN}\end{array}\right]\hfill \end{array},$$

(13)

where the set of states $S=\{{\mathit{p}}_{{\mathbf{gt}}_{\mathit{j}}}^{\mathbf{1}},{\mathit{p}}_{{\mathbf{gt}}_{\mathit{j}}}^{\mathbf{2}},\dots ,{\mathit{p}}_{{\mathbf{gt}}_{\mathit{j}}}^{\mathit{N}}\}$ denotes the total possible GT positions in the network, which are equal to the number of states $N=l^2$ in the Markov chain. The set of actions $A=\{{\mathit{p}}_{\mathbf{uav}}^{\mathbf{1}},{\mathit{p}}_{\mathbf{uav}}^{\mathbf{2}},\dots ,{\mathit{p}}_{\mathbf{uav}}^{\mathit{M}}\}$ distinguishes the motion options available to the UAV in a given grid location. In this context, the grid employed in Figure 1 provides $M=9$ movement alternatives. The rewards or payoffs C represent the expected data rate for links between the UAV and the j-th GT, as previously defined as $\mathbb{E}\left[R_j\left(t\right)\right]$ in (7). Following the nomenclature of the OWA operator, rewards are expressed in terms of the expected data rate as $C_{mn}={\overline{R}}_j^{mn}$. This relation refers to the GT position, denoted by $S_n={\mathit{p}}_{{\mathbf{gt}}_{\mathit{j}}}^{\mathit{n}}$, within the set of states, and the selected next position for the UAV, denoted by $A_m={\mathit{p}}_{\mathbf{uav}}^{\mathit{m}}$, within the set of actions.

The decision-making strategy based on the OWA operator involves selecting the UAV displacement that yields the maximum data rate. However, this approach relies on the state per time slot, which depends on the UAV knowledge about the current GTs positions. Here, we focus on two perspectives for decision-making, namely under certainty or uncertainty, if an exact or probabilistic knowledge of GTs position is provided to the UAV. The certainty approach implies a reliable communication link between the UAV and the GTs, where users report their positions via the control channel. In contrast, the uncertainty approach is suitable for chaotic situations frequently encountered in emergency scenarios, where communication interruptions may occur.

4.1.1. Uncertainty Case

Uncertainty scenario relates to a UAV that only has access to information regarding the user’s initial or last reported position. In this context, the GT tends to exhibit motion patterns whose statistics are known by the UAV, which is acting as a flying BS. It is sufficient to be aware of the probability of users being in a particular coordinate, which enables the UAV to ascertain the prevailing network state. This assumption aligns with an emergency scenario where a UAV must serve a group of isolated users exhibiting predetermined motion patterns. In addition, this approach has the advantage of not requiring any extra information to be transmitted between UAV and GTs beyond essential data, thereby avoiding communication overhead.

A typical procedure to manage uncertainty is computing the expected rewards given a probability distribution over the states of nature $S_n={\mathit{p}}_{{\mathbf{gt}}_{\mathit{j}}}^{\mathit{n}}$. The UAV initiates the process by evaluating the total expected data rate for each of its potential movements (actions $A_m={\mathit{p}}_{\mathbf{uav}}^{\mathit{m}}$) as follows:

$$R_{T_j}^m=\sum _n{\overline{R}}_j^{mn}·p_n^{\left(t\right)},\forall t,\mathrm{and}n\in [1,N],$$

(14)

where $p_n^{\left(t\right)}$ is the probability that a j-th GT reaches one of N positions after t discrete steps. Equation (14) provides potential rewards for each network user, which must be aggregated to achieve a global consensus on the optimal next location for the UAV. One possible solution is to identify this location based on the average data rate across all K GTs as follows:

$$R_T^m={\displaystyle \frac{1}{K}}{\displaystyle \sum _{j=1}^K}{R}_{T_j}^m,\forall t,\mathrm{and}m\in [1,M].$$

(15)

This information can be used by the UAV to guide the decision-making via the selection of the optimal next displacement, referred to as $A^{*}={\mathit{p}}_{\mathbf{uav}}^{\mathbf{*}}$. This action provides the largest total expected data rate $C^{*}=R_T^{*}$ for each time instant t:

$$R_T^{*}=\underset{m}{max}{R}_T^m,\forall t,\mathrm{and}m\in [1,M].$$

(16)

Note that this approach requires knowledge or at least an estimation of the transition probability matrix associated with GTs positions, denoted as $\mathbf{P}$ in (9). The values of the matrix $\mathbf{P}$ can be determined by considering emergency scenarios where users may adopt one of two postures due to multiple factors. The first scenario involves chaos, with random movement in any direction, resulting in equal transition probabilities between possible states. The second scenario involves orderly movement toward a specific location on the map, increasing the likelihood of reaching the desired point.

4.1.2. Certainty Case

The certainty scenario considers that the UAV can identify all GT positions, which is reasonable if the control channel is utilized to report their spatial coordinates. This situation constitutes a specific case of uncertainty when there is a probability $p_n^{\left(t\right)}=1$ that state $S_n={\mathit{p}}_{{\mathbf{gt}}_{\mathit{j}}}^{\mathit{n}}$ occurs, and the remaining probabilities equals zero. From this perspective, if the current network state is known, then the optimal course of action for the UAV is clear: (i) it merges the local reward $R_{T_j}^m$ from all K GTs as shown in (15); (ii) it must choose its motion alternative $A_m={\mathit{p}}_{\mathbf{uav}}^{\mathit{m}}$ with the highest payoff (total expected data rate $R_T^{*}$), following (16).

Decision-making strategies that incorporate both certainty and uncertainty using the OWA operator enable the dynamic adjustment of the UAV trajectory to maximize the expected data rate, thereby enhancing the QoS for network participants. This framework provides a foundational basis for developing more complex scenarios by incorporating additional variables, allowing for a more accurate representation of real-world applications.

4.2. Algorithm Implementation

Algorithm 1 outlines the main steps of the proposed solution leveraging the OWA operator. The goal is to identify the optimal action that maximizes the expected payoff across all time slots t. Initially, the UAV acquires network parameters, aligning them with the input variables through bidirectional communication with the GTs via the control channel. If communication is inefficient, the UAV can only make decisions based on statistical information about the GTs. Then, the procedure requires updating the set of UAV locations within the field that are reachable, as exposed in line 2. The primary stage, spanning from line 3 to 12, delineates the decision-making process of the UAV (certainty or uncertainty) to select its next position within a 2D plane, maintaining a fixed altitude H.

Notice that the OWA operator is applied to each user individually to obtain local payoff denoted by $R_{T_j}^m$ as shown in line 9. The results are then merged into $R_T^m$ at the end of the actions loop in line 10. Ultimately, the UAV guides its movement based on the optimal action $A^{*}$, which yields the greatest total expected reward $R_T^{*}$ per time slot.

The time complexity of Algorithm 1 is dependent on the total number of actions M, states N, and users K per time slot t. The actions loop assesses potential alternatives for the UAV routes concerning the motion’s angular resolution, which we previously designated as $M=9$. The number of states $N=l^2={\lfloor s/r\rfloor }^2$ is determined based on the Markov process providing the available grid location for both UAV and GTs. Consequently, each tentative action must evaluate N communication links for K GTs and obtain local rewards regarding the probabilities of occupying a given location. Next, the UAV aggregates local payoffs to derive a decision matrix of expected data rates for all GTs. Finally, selecting the optimal alternative (UAV coordinate) returns the maximum expected data rate. Hence, the computational complexity of the proposed algorithm is $O\left(M·K·N\right)$ for each time instant $t\in [1,T]$. This analysis reveals that the proposed solution becomes progressively more time-consuming as the network size expands and is also affected by an increase in the number of users.

Algorithm 1: DM-OWA-R (under risk)

5. Performance Analysis

This section presents the simulation environment to validate our theoretical analysis for decision-making over a square area 200 m on a side. The selected scenario is appropriate for a limited area affected by an emergency such as a forest fire. We assume that the UAV serves one or multiple GTs located within its coverage area, consistent with the concept of a small-cell UAV-based network as outlined in [37]. Initially, GTs are randomly located, and afterward, they start moving according to the rules explained above. Users can perform random movements with equal probabilities to reach all possible positions per time slot. Alternatively, users can move towards a specific location by accurately replicating a hotspot scenario in the network. The UAV is deployed at the center of the field on the coordinate $p_{\mathrm{uav}}\left(t\right)=[100,100,100]$. Then, it must decide proper trajectories in a 2D plane to maximize the expected data rate according to Algorithm 1.

The network parameters are typically specified as follows: the UAV transmission power is $P_t=10 \mathrm{dBm}$; the noise power is ${\sigma }^2=N_{0}B=-110 \mathrm{dBm}$, where the noise power spectrum density at each GT is $N_0=-170 \mathrm{dBm}/\mathrm{Hz}$; and the communication bandwidth is $B=1 \mathrm{MHz}$. The operating frequency is set to $28 \mathrm{GHz}$ according to the $K_a$ band available for new millimeter wave links in 5G networks [38]. The modeling parameters for the probabilistic LoS channel in (4) are established as $a=10$, $b=0.6$, $k=0.2$, and $\gamma =2.3$ as indicated in [11].

The numerical results showcase the robustness of data transmission quality throughout the UAV flight trajectory, particularly in scenarios where communication loss occurs. Such instances are addressed through two distinct approaches: one where the UAV1 possesses knowledge of GT positions, referred to as certainty, and another where UAV2 must make decisions relying on the probability of position changes for each GT, referred to as uncertainty. For comparison, we include UAV3 hovering at the center of the area to provide the best service on average and UAV4 performing simple circular trajectories as presented in [10]. All numerical simulations were conducted using MATLAB, which streamlined the programming and validation of the proposed methodology, thereby simplifying its reproducibility. The results were derived from Monte Carlo simulations, generating 100 individual trajectories for each GT. This method provides a broad spectrum of outcomes, which are averaged to estimate the expected throughput for each scenario analyzed.

5.1. Random Movement Scenario

The scenario discussed in this section assumes that each GT has an equal probability $q_i=r_i=p_i=1/3$ of changing state for both matrix ${\mathbf{P}}_{\mathbf{h}}$ and ${\mathbf{P}}_{\mathbf{v}}$. This strategy allows for reaching any of the nine tentative positions in the square area with equal probability. The expected data rate is evaluated for the simplest case with only one GT and a more complex case with multiple GTs.

5.1.1. Single User

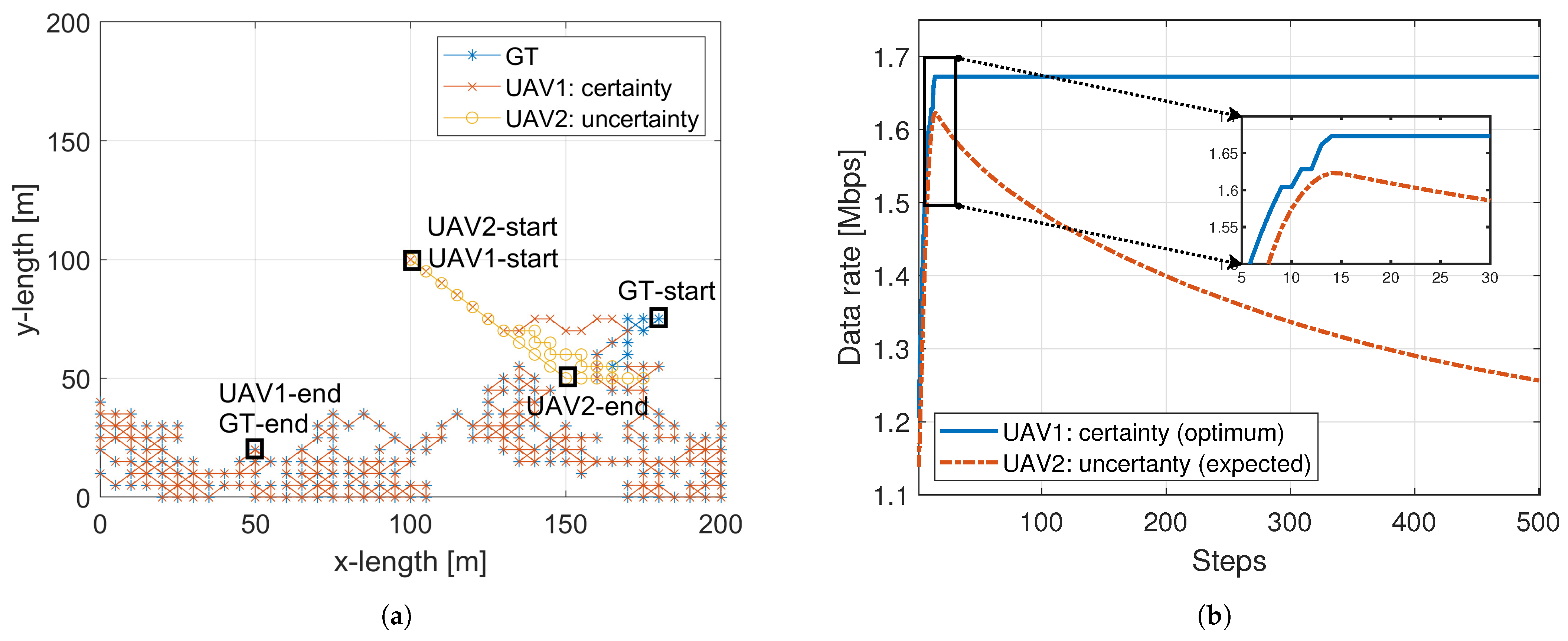
The single-user scenario is essentially a tracking problem where a UAV aims to reduce the distance to the GT by choosing the best possible route, as depicted in Figure 2. In this scenario, we simulate the optimal trajectory for UAV1 and an approximate solution for UAV2, either by knowing the user’s position with certainty or relying on statistical features in cases of uncertainty, respectively.

Figure 2a illustrates such cases, representing UAV1 by red tails, UAV2 by yellow circles, and the GT as blue asterisks. It is evident that in the case of certainty, UAV1 is able to reach the GT after approximately 15 steps and continue flying over it until the end of the simulation. In the case of uncertainty, UAV2 also endeavors to approach the GT. However, it fails because the transition probability matrix for the single user converges towards a stationary state, posing a challenge in determining the UAV’s subsequent movement. In such a state, the GT has nearly the same probability of being in any position when the number of steps is sufficiently large.

The achievable communication data rate for the downlink increases for the first 15 steps as both UAVs approach their target, as shown in the zoomed-in graph in Figure 2b. Once UAV1 is above the GT, the maximum signal to noise ratio (SNR) value of 3.4 dB can be obtained, which, in turn, results in a data rate $R_{\max }=1.67 \mathrm{Mbps}$ for the minimum distance of 100 m. This value remains constant throughout the simulation time. On the contrary, UAV2 eventually cannot move closer to the GT, leading to a progressive decrease in the expected data rate due to a nearly uniform probability distribution of GT locations in the grid. Therefore, the uncertainty approach should only be employed for a limited period, during which communication disruptions prevent the GTs from reporting their positions to the UAV.

5.1.2. Multiple Users

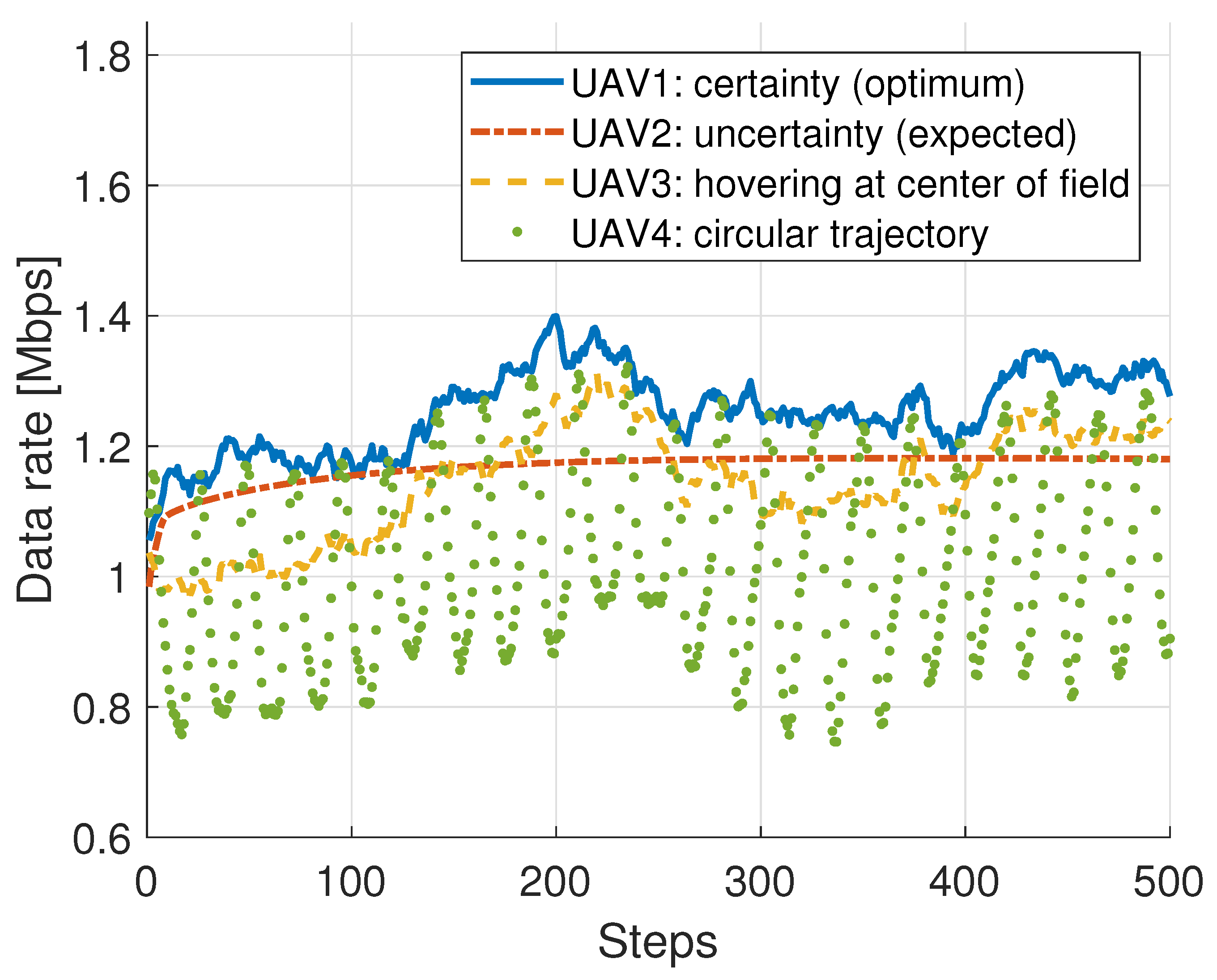
Advancing to a more intricate and realistic scenario, we introduce a model where a UAV serves multiple GTs within its coverage area, complicating the decision-making process required to maximize the data rate. To illustrate, 10 GTs are randomly placed in the square area, and two UAVs execute Algorithm 1: DM-OWA-R to plan their trajectory. Figure 3 shows the achievable communication data rate for the certainty (UAV1) and uncertainty (UAV2) approaches. For comparison, we introduce UAV3, which is either hovering or deployed at the center of the field, alongside an additional UAV4 flying in circular trajectories around this central point.

Under certainty, our proposed decision-making strategy outperforms the other solutions regarding the expected data rate. This result is possible because exchanging information through the control channel increases awareness of the GTs position in each time slot. Under uncertainty, UAV2 is able to make accurate decisions only in the early stages, as indicated before for the single-user scenario. Nevertheless, UAV2 displays data rate values that align with the anticipated outcomes for a scenario of certainty, a consequence of the successful initial tracking. On the contrary, UAV3 remains stationary at the center of the network, which leads to a decline in data transmission rates for the nodes. UAV4, which follows circular paths, exhibits oscillatory tendencies as it moves closer to or further away from GTs.

5.2. Hotspot Scenario

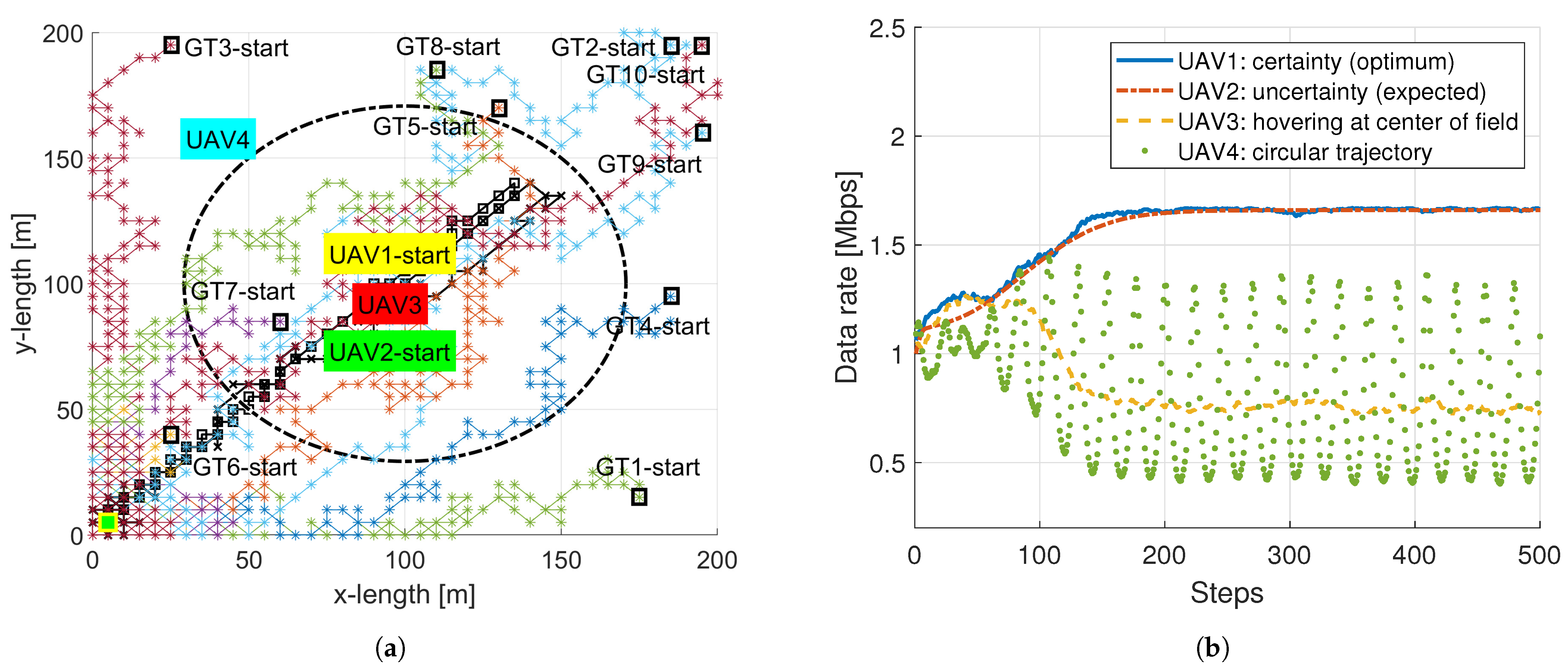
Next, we consider a different scenario with multiple GTs randomly moving within the given area with a higher probability of going left or down for the stochastic processes $X\left(t\right)$ and $Y\left(t\right)$, respectively. Figure 4 shows an illustrative example for probability values $q_i=1/2$ and $r_i=p_i=1/4$. Additionally, Figure 4a showcases the network dynamics of 4 UAVs and 10 GTs whose displacements converge at the origin of the coordinates. In this situation, we observe that both the certainty and uncertainty approaches bring UAV1 and UAV2 closer to GTs to enhance the QoS. The black lines represent the routes of all UAVs, with UAV1 and UAV2 terminating at a green box with yellow edges.

As indicated in Figure 4b, the proposed solutions present higher data rates by leveraging UAV mobility towards users. The uncertainty approach is highly effective because the transition probability matrix governing users’ mobility tends towards a stationary state where the most significant weights are concentrated around the position $[0,0,0]$. Additionally, GTs do not need to report their positions to UAV2, which results in negligible communication overhead. In contrast, the fixed UAV3 hovering or deployed at the center of the field results in lower data rates as the GTs move further away. The circular trajectory also demonstrates oscillatory behavior for reasons similar to those mentioned in the previous section.

5.3. Statistical Analysis

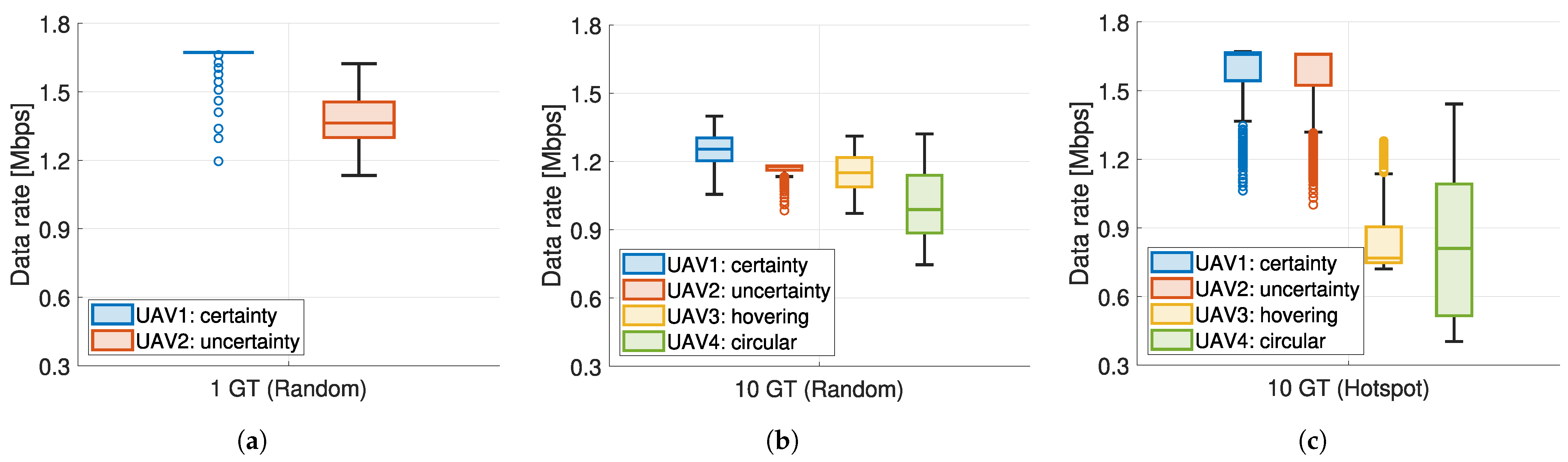
A visual representation of the summary statistics for throughput samples in each step is provided as box charts, as shown in Figure 5. Each box chart displays the following information: the median, the lower (25th) and upper (75th) quartiles, any outliers, and the minimum and maximum values that are not outliers. To facilitate analysis, the boxes are divided into three groups according to the total number of GTs and their mobility patterns, including random motion with equal probabilities and tendency to the coordinate origin.

The first group, labeled “1 GT (Random)” in Figure 5a, presents the outcomes for both proposed solutions under certainty and uncertainty conditions in the single-user scenario. The certainty approach proves more effective, achieving a higher mean data rate of 1.67 Mbps. The uncertainty approach has a root mean square error (RMSE) of 302 kbps, representing a 18% discrepancy in comparison to the certainty approach. The interquartile range for the uncertainty solution, representing the difference between upper and lower quartiles, is 156 kbps. However, this value may increase with a longer simulation time. This statement restricts the applicability of the uncertainty approach to brief time intervals where GTs are unable to report their positions to the UAV.

The second group, labeled “10 GT (Random)” in Figure 5b, describes the statistical behavior of data rate values in a scenario of 10 GTs performing random movements with equal probabilities. The certainty approach outperforms the remaining solutions, as evidenced by a higher mean data rate of 1.25 Mbps. However, the uncertainty approach demonstrates a narrower spread of data. The performance of the hovering strategy at the center of the field is comparable to the uncertainty approach, as indicated by similar RMSE values relative to the optimum case (certainty) of 100 kbps and 117 kbps, respectively. This scenario validates that decision-making under certainty maximizes the network QoS in each time step. Conversely, decision-making under uncertainty is not a viable solution for nodes governed by random movement with equal probabilities in all directions.

The final group, designated “10 GT (Hotspot)” in Figure 5c, is concerned with the statistical outcomes associated with the movement of GTs towards the coordinate origin. The proposed solutions for certainty and uncertainty are demonstrably superior, with significantly higher mean data rates of 1.57 Mbps and 1.55 Mbps. In comparison, the hovering and circular trajectory methods are inferior by 45% and 48%, respectively. Moreover, the interquartile range for certainty and uncertainty approaches differs by 14 kbps, which only represents 11%. The RMSE for the uncertainty case is 29 kbps, using the certainty case as the reference. In contrast, the hovering and circular trajectory scenarios exhibit RMSE values that are 27 and 29 times higher, respectively. These statistical data validate the proposed approaches for the hotspot scenario.

5.4. Challenges and Future Scope

One significant challenge associated with the implementation of Algorithm 1 in real-world scenarios is its adaptability to the unpredictable movements of GTs. Conventional methodologies frequently presume a state of certainty concerning network conditions, disregarding the inherently dynamic nature of GT locations and movement patterns. The proposed solution based on the OWA operator requires prior knowledge or at least an estimation of the probability of the GT being in a given position within the network. Another challenge is the computational complexity, which depends on the number of users, the network area, and the possible motion alternatives of the UAV. One potential alternative to overcome this issue is modifying the sample time to adjust the dot resolution in the entire simulation area. Furthermore, more extensive networks could be addressed by partitioning them into smaller parts served by other UAVs working in tandem.

The subsequent development phase will entail the incorporation of more energy-efficient decision-making algorithms designed explicitly for battery-powered UAV platforms. Additionally, further research is needed to develop GT mobility models that accurately reflect human behavior and the movement patterns of IoT devices. While the potential improvements in data rates are significant, ongoing experimentation and refinement are essential. This includes exploring additional performance metrics such as energy efficiency and latency, analyzing more complex UAV movement patterns, and adapting the proposed framework to diverse operational scenarios.

6. Conclusions

This paper addresses the decision-making problem of UAV path planning to maximize QoS in B5G wireless networks. We propose a framework based on the OWA operator to effectively manage the conditions of certainty and uncertainty associated with GT motion dynamics. The certainty approach, which relies on a stable communication link between the UAV and GTs, emerges as the optimal strategy for maximizing data rates. In contrast, the uncertainty approach operates without prior communication for localization, resulting in a slight reduction in data rates during trajectory planning. Despite this difference, both approaches yield comparable performance, with only a 1.3% disparity in mean data rate when users follow a predetermined path toward a designated coordinate, such as a rescue point during emergencies. Furthermore, our proposed solutions significantly outperform traditional network configurations, such as a UAV hovering centrally, (akin to a fixed base station) and predefined circular flight patterns, achieving up to an 8% increase in mean data rate. Future work will focus on developing innovative reward mechanisms, exploring more intricate UAV motion alternatives, and adapting the framework for various network types.