Efficient Ensemble Adversarial Attack for a Deep Neural Network (DNN)-Based Unmanned Aerial Vehicle (UAV) Vision System
Abstract
1. Introduction
- (1)
- We propose a novel frequency decomposition-based perturbation generator that first decomposes the image into different frequency bands using wavelet decomposition. Then, it refines the weight updates within these frequency bands based on historical query information to generate adversarial perturbations that more effectively mislead the model. Furthermore, in addition to using the model’s gradient information when adding perturbations, we also introduce randomly generated squared Gaussian noise perturbations in high-gradient areas to enhance the attack’s success rate.
- (2)
- We propose an efficient integrated black-box adversarial attack method that combines query-based and transfer-based attack strategies. This method effectively performs the attack by minimizing a weighted loss function on a set of fixed surrogate models. Additionally, adversarial images generated by the perturbation generator are used to query and update the weights in the loss function. Experimental results demonstrate that, compared to the latest methods on various image classifiers trained on ImageNet (such as VGG-19, DenseNet-121, and ResNext-50), our approach achieves a success rate over 98% for targeted attacks and a nearly 100% success rate for non-targeted attacks with only 1–2 queries per image.
2. Related Work
2.1. Adversarial Example
2.2. Transfer-Based Black Box Attacks
2.3. Query-Based Black Box Attacks
2.4. Transfer-Query-Based Black Box Attacks
3. Attack Scenario
4. The Proposed Attacks
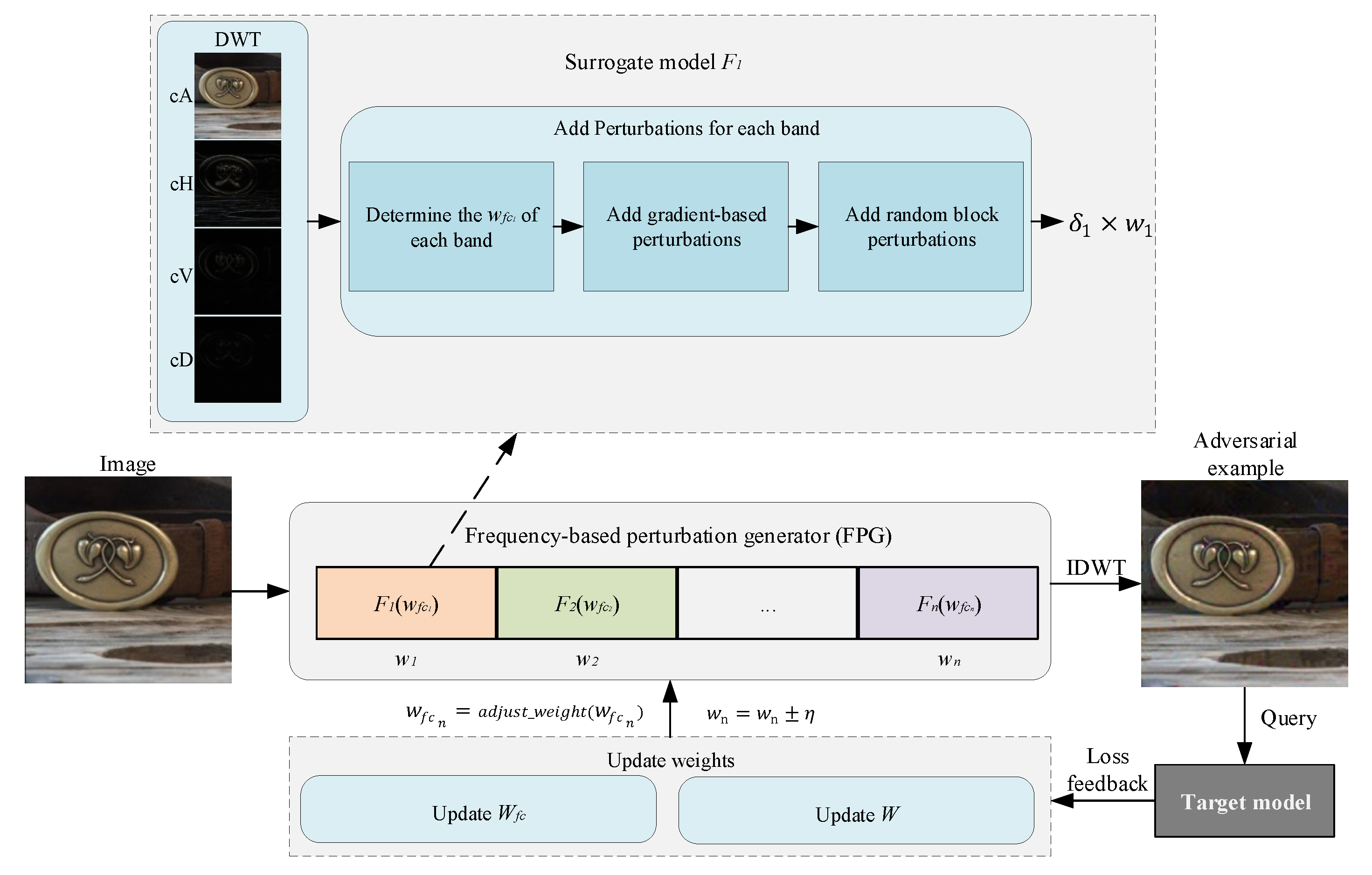
4.1. Overall Architecture
4.2. Construction of Frequency-Based Perturbation Generator for Surrogate Ensemble Models
4.2.1. Frequency Decomposition
4.2.2. Weighted Ensemble Loss Function Optimization
4.2.3. Frequency Band Weights Optimization
4.2.4. Perturbation Addition
4.3. Frequency-Based Surrogate Ensemble Black-Box Attack
4.3.1. Model Weight Optimization
4.3.2. Frequency-Based Surrogate Ensemble Black-Box Attack (FSEBA)
| Algorithm 1 Frequency-Based Perturbation Generator (FPG) |
|
| Algorithm 2 Frequency-Based Surrogate Ensemble Black-Box Attack (FSEBA) |
|
5. Experiments
5.1. Dataset and Target Model
5.2. Ensemble of Surrogate Models
5.3. Experimental Environment
5.4. Evaluation Indicators
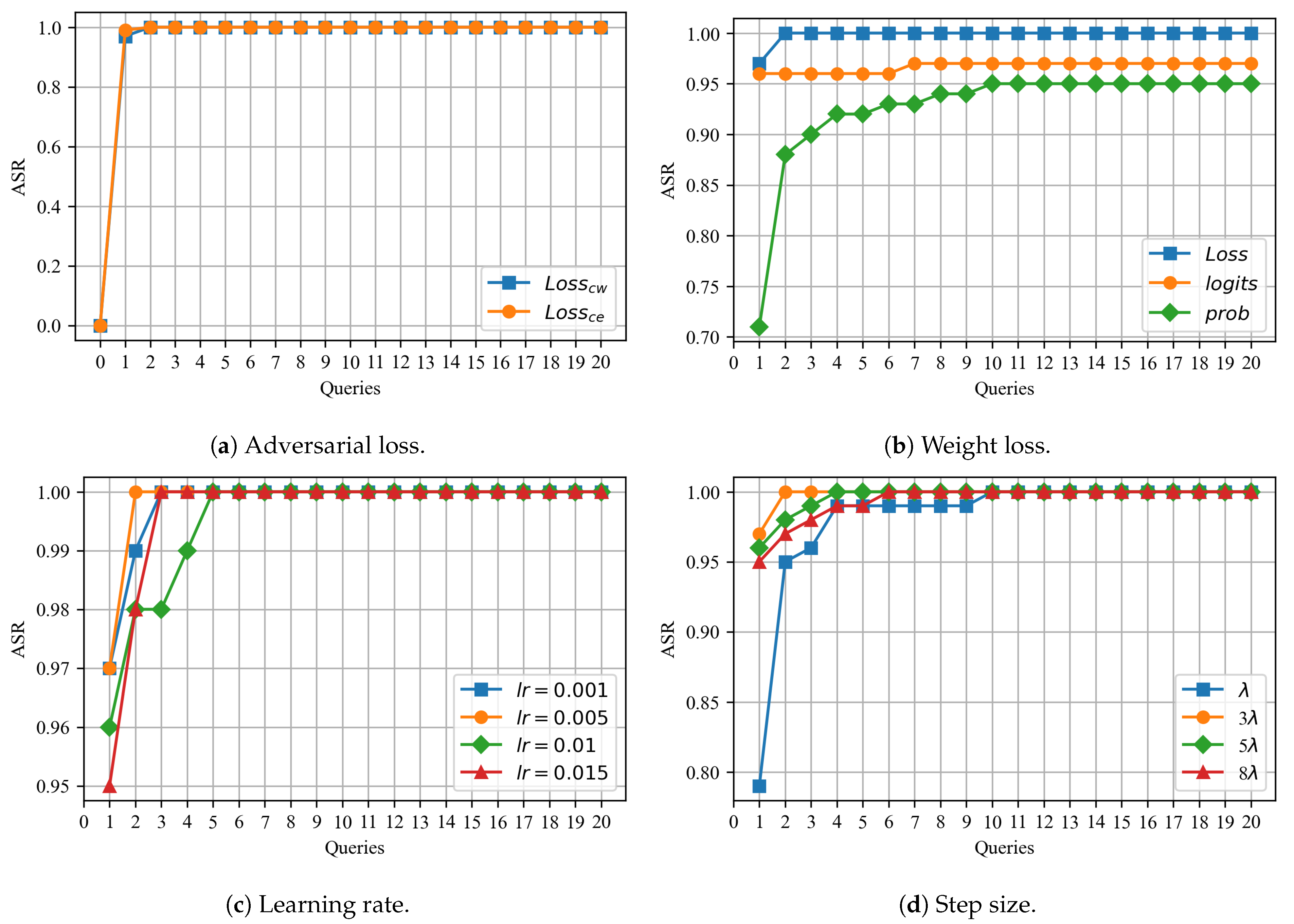
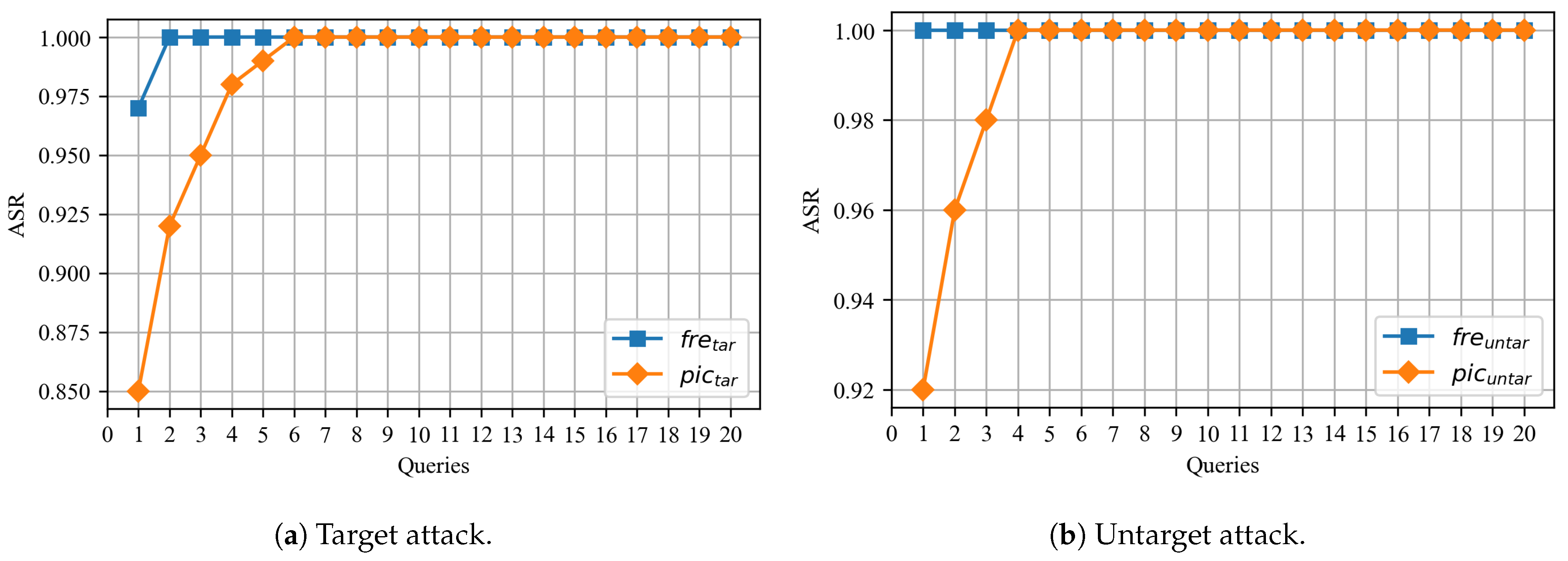
5.5. Ablation Experiment
5.6. Comparison Experiment
5.7. Effect of Attacking Robust Models
5.8. Visualization of Adversarial Examples
6. Limitations
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
DURC Statement
Conflicts of Interest
Correction Statement
References
- Istiak, M.A.; Syeed, M.M.; Hossain, M.S.; Uddin, M.F.; Hasan, M.; Khan, R.H.; Azad, N.S. Adoption of Unmanned Aerial Vehicle (UAV) imagery in agricultural management: A systematic literature review. Ecol. Inform. 2023, 78, 102305. [Google Scholar] [CrossRef]
- Engesser, V.; Rombaut, E.; Vanhaverbeke, L.; Lebeau, P. Autonomous delivery solutions for last-mile logistics operations: A literature review and research agenda. Sustainability 2023, 15, 2774. [Google Scholar] [CrossRef]
- Roberts, N.B.; Ager, E.; Leith, T.; Lott, I.; Mason-Maready, M.; Nix, T.; Gottula, A.; Hunt, N.; Brent, C. Current summary of the evidence in drone-based emergency medical services care. Resusc. Plus 2023, 13, 100347. [Google Scholar] [CrossRef]
- Li, Y.; Fan, Q.; Huang, H.; Han, Z.; Gu, Q. A modified YOLOv8 detection network for UAV aerial image recognition. Drones 2023, 7, 304. [Google Scholar] [CrossRef]
- Chen, K.; Chen, B.; Liu, C.; Li, W.; Zou, Z.; Shi, Z. Rsmamba: Remote sensing image classification with state space model. IEEE Geosci. Remote Sens. Lett. 2024, 21, 8002605. [Google Scholar] [CrossRef]
- Zeng, L.; Chen, H.; Feng, D.; Zhang, X.; Chen, X. A3D: Adaptive, Accurate, and Autonomous Navigation for Edge-Assisted Drones. IEEE/Acm Trans. Netw. 2023, 32, 713–728. [Google Scholar] [CrossRef]
- Hadi, H.J.; Cao, Y.; Li, S.; Xu, L.; Hu, Y.; Li, M. Real-time fusion multi-tier DNN-based collaborative IDPS with complementary features for secure UAV-enabled 6G networks. Expert Syst. Appl. 2024, 252, 124215. [Google Scholar] [CrossRef]
- Akshya, J.; Neelamegam, G.; Sureshkumar, C.; Nithya, V.; Kadry, S. Enhancing UAV Path Planning Efficiency through Adam-Optimized Deep Neural Networks for Area Coverage Missions. Procedia Comput. Sci. 2024, 235, 2–11. [Google Scholar]
- Dutta, A.; Das, S.; Nielsen, J.; Chakraborty, R.; Shah, M. Multiview Aerial Visual Recognition (MAVREC): Can Multi-view Improve Aerial Visual Perception? In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 22678–22690. [Google Scholar]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv 2014, arXiv:1412.6572. [Google Scholar]
- Chakraborty, A.; Alam, M.; Dey, V.; Chattopadhyay, A.; Mukhopadhyay, D. A survey on adversarial attacks and defences. CAAI Trans. Intell. Technol. 2021, 6, 25–45. [Google Scholar] [CrossRef]
- Long, T.; Gao, Q.; Xu, L.; Zhou, Z. A survey on adversarial attacks in computer vision: Taxonomy, visualization and future directions. Comput. Secur. 2022, 121, 102847. [Google Scholar] [CrossRef]
- Baniecki, H.; Biecek, P. Adversarial attacks and defenses in explainable artificial intelligence: A survey. Inf. Fusion 2024, 107, 102303. [Google Scholar] [CrossRef]
- Brendel, W.; Rauber, J.; Bethge, M. Decision-Based Adversarial Attacks: Reliable Attacks Against Black-Box Machine Learning Models. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Zhou, M.; Wu, J.; Liu, Y.; Liu, S.; Zhu, C. Dast: Data-free substitute training for adversarial attacks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 234–243. [Google Scholar]
- Guo, Y.; Yan, Z.; Zhang, C. Subspace attack: Exploiting promising subspaces for query-efficient black-box attacks. Adv. Neural Inf. Process. Syst. 2019, 32, 3820–3829. [Google Scholar]
- Cheng, S.; Dong, Y.; Pang, T.; Su, H.; Zhu, J. Improving black-box adversarial attacks with a transfer-based prior. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, T. Black-Box Adversarial Attack with Transferable Model-based Embedding. In Proceedings of the 8th International Conference on Learning Representations, ICLR 2020, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Xiang, S.; Liang, Q. Remote sensing image compression based on high-frequency and low-frequency components. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5604715. [Google Scholar] [CrossRef]
- Lin, Y.; Xie, Z.; Chen, T.; Cheng, X.; Wen, H. Image privacy protection scheme based on high-quality reconstruction DCT compression and nonlinear dynamics. Expert Syst. Appl. 2024, 257, 124891. [Google Scholar] [CrossRef]
- Sharma, Y.; Ding, G.W.; Brubaker, M.A. On the effectiveness of low frequency perturbations. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 3389–3396. [Google Scholar]
- Guo, C.; Gardner, J.; You, Y.; Wilson, A.G.; Weinberger, K. Simple black-box adversarial attacks. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 2484–2493. [Google Scholar]
- Wang, H.; Wu, X.; Huang, Z.; Xing, E.P. High-frequency component helps explain the generalization of convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 8684–8694. [Google Scholar]
- Yin, D.; Gontijo Lopes, R.; Shlens, J.; Cubuk, E.D.; Gilmer, J. A fourier perspective on model robustness in computer vision. Adv. Neural Inf. Process. Syst. 2019, 32, 13276–13286. [Google Scholar]
- Dong, Y.; Liao, F.; Pang, T.; Su, H.; Zhu, J.; Hu, X.; Li, J. Boosting adversarial attacks with momentum. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 9185–9193. [Google Scholar]
- Xie, C.; Zhang, Z.; Zhou, Y.; Bai, S.; Wang, J.; Ren, Z.; Yuille, A.L. Improving transferability of adversarial examples with input diversity. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 2730–2739. [Google Scholar]
- Liu, Y.; Chen, X.; Liu, C.; Song, D. Delving into Transferable Adversarial Examples and Black-box Attacks. In Proceedings of the International Conference on Learning Representations, Online, 25–29 April 2022. [Google Scholar]
- Yuan, Z.; Zhang, J.; Jia, Y.; Tan, C.; Xue, T.; Shan, S. Meta gradient adversarial attack. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 7748–7757. [Google Scholar]
- Ma, C.; Chen, L.; Yong, J.H. Simulating unknown target models for query-efficient black-box attacks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 11835–11844. [Google Scholar]
- Brunner, T.; Diehl, F.; Le, M.T.; Knoll, A. Guessing smart: Biased sampling for efficient black-box adversarial attacks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 4958–4966. [Google Scholar]
- Chen, P.Y.; Zhang, H.; Sharma, Y.; Yi, J.; Hsieh, C.J. Zoo: Zeroth order optimization based black-box attacks to deep neural networks without training substitute models. In Proceedings of the 10th ACM Workshop on Artificial Intelligence and Security, Dallas, TX, USA, 3 November 2017; pp. 15–26. [Google Scholar]
- Tu, C.C.; Ting, P.; Chen, P.Y.; Liu, S.; Zhang, H.; Yi, J.; Hsieh, C.J.; Cheng, S.M. Autozoom: Autoencoder-based zeroth order optimization method for attacking black-box neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 742–749. [Google Scholar]
- Ilyas, A.; Engstrom, L.; Madry, A. Prior Convictions: Black-box Adversarial Attacks with Bandits and Priors. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Tashiro, Y.; Song, Y.; Ermon, S. Diversity can be transferred: Output diversification for white-and black-box attacks. Adv. Neural Inf. Process. Syst. 2020, 33, 4536–4548. [Google Scholar]
- Lord, N.A.; Mueller, R.; Bertinetto, L. Attacking deep networks with surrogate-based adversarial black-box methods is easy. arXiv 2022, arXiv:2203.08725. [Google Scholar]
- Cai, Z.; Song, C.; Krishnamurthy, S.; Roy-Chowdhury, A.; Asif, S. Blackbox attacks via surrogate ensemble search. Adv. Neural Inf. Process. Syst. 2022, 35, 5348–5362. [Google Scholar]
- Feng, Y.; Wu, B.; Fan, Y.; Liu, L.; Li, Z.; Xia, S.T. Boosting black-box attack with partially transferred conditional adversarial distribution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 15095–15104. [Google Scholar]
- Mohaghegh Dolatabadi, H.; Erfani, S.; Leckie, C. Advflow: Inconspicuous black-box adversarial attacks using normalizing flows. Adv. Neural Inf. Process. Syst. 2020, 33, 15871–15884. [Google Scholar]
- Al-Dujaili, A.; O’Reilly, U.M. Sign bits are all you need for black-box attacks. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Yin, F.; Zhang, Y.; Wu, B.; Feng, Y.; Zhang, J.; Fan, Y.; Yang, Y. Generalizable black-box adversarial attack with meta learning. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 46, 1804–1818. [Google Scholar] [CrossRef]
- Antonini, M.; Barlaud, M.; Mathieu, P.; Daubechies, I. Image coding using wavelet transform. IEEE Trans. Image Process. 1992, 1, 205–220. [Google Scholar] [CrossRef]
- Wu, Z.; Lim, S.N.; Davis, L.S.; Goldstein, T. Making an invisibility cloak: Real world adversarial attacks on object detectors. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part IV 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–17. [Google Scholar]
- Kingma, D.P. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Croce, F.; Hein, M. Reliable evaluation of adversarial robustness with an ensemble of diverse parameter-free attacks. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 13–18 July 2020; pp. 2206–2216. [Google Scholar]
- Google Brain. Neurips 2017: Targeted Adversarial Attack. 2017. Available online: https://www.kaggle.com/competitions/nips-2017-targeted-adversarial-attack/data (accessed on 15 October 2024).
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated residual transformations for deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1492–1500. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32, 8026–8037. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Kyoto, Japan, 29 September–2 October 2009; IEEE: New York, NY, USA, 2009; pp. 248–255. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Tan, M. Efficientnet: Rethinking model scaling for convolutional neural networks. arXiv 2019, arXiv:1905.11946. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Salman, H.; Ilyas, A.; Engstrom, L.; Kapoor, A.; Madry, A. Do adversarially robust imagenet models transfer better? Adv. Neural Inf. Process. Syst. 2020, 33, 3533–3545. [Google Scholar]
- Peng, S.; Xu, W.; Cornelius, C.; Hull, M.; Li, K.; Duggal, R.; Phute, M.; Martin, J.; Chau, D.H. Robust principles: Architectural design principles for adversarially robust cnns. arXiv 2023, arXiv:2308.16258. [Google Scholar]
- Croce, F.; Andriushchenko, M.; Sehwag, V.; Debenedetti, E.; Flammarion, N.; Chiang, M.; Mittal, P.; Hein, M. RobustBench: A standardized adversarial robustness benchmark. arXiv 2020, arXiv:2010.09670. [Google Scholar]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning deep features for discriminative localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2921–2929. [Google Scholar]



| Models | Top-1 | Top-5 | Parameters |
|---|---|---|---|
| VGG19 | 72.37% | 90.87% | 143.7 M |
| DenseNet-121 | 74.43% | 91.97% | 8.0 M |
| ResNeXt-50 | 81.19% | 95.34% | 25.0 M |
| Method | VGG-19 | DenseNet-121 | ResNeXt-50 | |||||
|---|---|---|---|---|---|---|---|---|
| AQC | ASR | AQC | ASR | AQC | ASR | |||
| P-RGF [17] | 156 | 93.5% | 164 | 92.9% | 166 | 92.5% | ||
| ODS [34] | 38 | 99.9% | 52 | 99.0% | 54 | 98.4% | ||
| GFCS [35] | 14 | 100.0% | 16 | 99.9% | 15 | 99.7% | ||
| TREMBA [18] | 2.4 | 99.7% | 5.9 | 99.5% | 7.5 | 98.9% | ||
| BASES [36] | 1.2 | 99.8% | 1.2 | 99.9% | 1.2 | 100.0% | ||
| Ours | 1.0 | 99.9% | 1.0 | 100.0% | 1.0 | 100.0% | ||
| Methods | VGG-19 | DenseNet-121 | ResNeXt-50 | |||||
|---|---|---|---|---|---|---|---|---|
| AQC | ASR | AQC | ASR | AQC | ASR | |||
| P-RGF * [17] | - | - | - | - | - | - | ||
| ODS [34] | 261 | 49.0% | 266 | 49.7% | 270 | 42.7% | ||
| GFCS [35] | 101 | 89.1% | 76 | 95.2% | 86 | 92.9% | ||
| TREMBA [18] | 92 | 89.2% | 70 | 90.5% | 100 | 85.1% | ||
| BASES [36] | 3.0 | 95.9% | 1.8 | 99.4% | 1.8 | 99.7% | ||
| Ours | 1.2 | 98.7% | 1.1 | 99.7% | 1.0 | 99.9% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Liu, Q.; Zhou, S.; Deng, W.; Wu, Z.; Qiu, S. Efficient Ensemble Adversarial Attack for a Deep Neural Network (DNN)-Based Unmanned Aerial Vehicle (UAV) Vision System. Drones 2024, 8, 591. https://doi.org/10.3390/drones8100591
Zhang Z, Liu Q, Zhou S, Deng W, Wu Z, Qiu S. Efficient Ensemble Adversarial Attack for a Deep Neural Network (DNN)-Based Unmanned Aerial Vehicle (UAV) Vision System. Drones. 2024; 8(10):591. https://doi.org/10.3390/drones8100591
Chicago/Turabian StyleZhang, Zhun, Qihe Liu, Shijie Zhou, Wenqi Deng, Zhewei Wu, and Shilin Qiu. 2024. "Efficient Ensemble Adversarial Attack for a Deep Neural Network (DNN)-Based Unmanned Aerial Vehicle (UAV) Vision System" Drones 8, no. 10: 591. https://doi.org/10.3390/drones8100591
APA StyleZhang, Z., Liu, Q., Zhou, S., Deng, W., Wu, Z., & Qiu, S. (2024). Efficient Ensemble Adversarial Attack for a Deep Neural Network (DNN)-Based Unmanned Aerial Vehicle (UAV) Vision System. Drones, 8(10), 591. https://doi.org/10.3390/drones8100591





