Abstract
This paper introduces a swift method for intercepting the state trajectory of large-scale invading drone swarms using quadrotor drones. The research primarily concentrates on the design and computation of multi-target interception trajectories, with an analysis of the trajectory state constraints inherent to multi-target interception tasks. Utilizing Pontryagin’s principle of motion, we have designed computationally efficient motion primitives for multi-target interception scenarios. These motion primitives’ durations have informed the design of cost matrices for multi-target interception tasks. In contrast to static planar scenarios, the cost matrix in dynamic scenarios displays significant asymmetry, correlating with the speed and spatial distribution of the targets. We have proposed an algorithmic framework based on three genetic operators for solving multi-target interception trajectories, offering certain advantages in terms of solution accuracy and speed compared to other optimization algorithms. Simulation results from large-scale dynamic target interception scenarios indicate that for an interception task involving 50 targets, the average solution time for trajectories is a mere 3.7 s. Using the methods proposed in this paper, we conducted a comparative analysis of factors affecting the performance of interception trajectories in various target interception scenarios. This study represents the first instance in existing public research where precise evaluations have been made on the trajectories of drone interceptions against large-scale flying targets. This research lays the groundwork for further exploration into game-theoretic adversarial cluster interception methods.
1. Introduction
Recent years have witnessed significant advancements in drone technology, with applications extending to target surveillance [1], disaster prevention [2], and agricultural measurement [3], among others. However, the burgeoning drone market has also introduced serious safety concerns. Inappropriate use or malicious activities can compromise social security and result in substantial economic losses. For instance, in 2018, hundreds of flights were disrupted at London Gatwick Airport due to drone interference [4]. In the UK, 62% of close encounters between small drones and aircrafts in 2019 were deemed high-risk [5]. To mitigate these issues, it is crucial to develop new technologies capable of detecting, identifying, and responding to malevolent drones. Consequently, the development of countermeasure systems that can effectively identify and counteract single or multiple threatening drones has become an urgent priority [4].
Multi-rotor drones, exemplified by quadrotors, are renowned for their superior maneuverability. Their high thrust-to-weight ratio facilitates excellent linear and angular acceleration performance, making them an ideal platform for testing advanced algorithms. In recent years, quadrotor drones have achieved notable success in areas such as autonomous flight [6] and obstacle avoidance during flight [7]. Successful application cases, including agile ball catching [8] and rapid aircraft capture [9], underscore the immense potential of quadrotors in the realm of malicious drone prevention and control [10].
The interception of multiple moving targets can be approached from two perspectives. The first perspective focuses on the individual interception efficacy of drones against a single target. For optimal results, drones must possess precise target tracking abilities, necessitating alignment with the target across various dimensions—position, speed, and acceleration in state space. To ensure precision in spatial approach, control algorithms must account for drone dynamics such as thrust constraints, maneuverability, and air resistance. Furthermore, the effectiveness of drone-borne interception mechanisms like net guns and electronic jammers is paramount when approaching targets accurately. This underscores the need for a synergistic design between interception methods and mechanisms to ensure effective interception. The second perspective emphasizes the efficiency of task coordination among drones targeting multiple moving entities. Drones must make swift decisions in dynamic scenarios, factoring in their inherent dynamics, target motion characteristics, and spatial distribution. They must devise logical task sequences to efficiently accomplish the interception of multiple targets within constrained time and space.
In the realm of academic research concerning single-target interception problems, a variety of classic strategy methods have been extensively utilized. These include path planning [11,12], optimal control [13], and reinforcement learning [14]. The primary objective of these methods is to furnish precise pursuit guidance for drones, enabling them to successfully intercept predefined targets. (1) Path planning technology concentrates on the application of geometric principles or numerical optimization methods to meticulously compute and determine an optimal flight path from the drone’s current position to the anticipated position of the target. In this domain, heuristic algorithms [15,16] are highly favored due to their superior computational efficiency and practicality, which can yield satisfactory solutions in a brief period. (2) Optimal control technology, on the other hand, shifts the research emphasis towards the design and optimization of control laws. The principal goal is to maximize or minimize certain specific performance indicators during the drone’s pursuit of the target. These indicators may encompass but are not limited to interception time [17], energy consumption [18], and other crucial factors. By fine-tuning control parameters, optimal control methods can significantly enhance the interception efficiency and operational performance of drones. (3) Reinforcement learning, an emerging data-driven method, facilitates autonomous target interception by continuously training and adjusting the drone’s interception strategy in a simulated environment [19]. The crux of this method lies in drones learning how to make optimal decisions in complex and dynamic situations through interaction with the environment.
In the realm of multi-target interception problems, scholars predominantly conceptualize it as a variant of the Traveling Salesman Problem or Routing Problem. In this paradigm, each target for interception is represented as a distinct node, subject to specific arrival and sequencing constraints [20]. Within this framework, researchers have devised an intricate evaluation system centered on pivotal metrics such as the distance and velocity between drones and their targets [21]. They have also endeavored to determine optimal or near-optimal sequences for task execution by employing dynamic task allocation algorithms. These encompass heuristic search techniques like Genetic Algorithms (GA) [22], Ant Colony Optimization (ACO) [23], Particle Swarm Optimization (PSO) [24], and sophisticated mathematical optimization methods grounded in Integer Linear Programming (ILP) [25]. Such approaches adeptly harmonize the importance of task execution with resource distribution in addressing multi-target interception challenges. Furthermore, some scholars interpret multi-target interception issues as sequence decision tasks endowed with Markov properties [26], leveraging reinforcement learning algorithms within multi-agent systems for resolution [27]. This line of inquiry has marked notable advancements in augmenting the intelligence of drone swarms and facilitating collaborative interception, offering fresh insights and methodologies for tackling multi-target interception challenges.
Given the dynamic constraints drones encounter, some research methodologies have incorporated the concept of Dubins paths during the path planning stage. This approach consistently considers the turning radius constraints imposed by the overload capacity limitations of drones, thereby ensuring the feasibility of the planned path [28]. Conversely, other studies employ spline curves to characterize the flight path of drones, generating continuous and smooth trajectories in space [29]. However, these trajectory planning methods do not strictly incorporate time information at the initial stage. Instead, they rely on feedback from the speed and acceleration of controllers in later stages to track the predetermined trajectory [30]. This phased approach may introduce additional errors because the actual tracking effect of drones on the planned path has not been effectively predicted and guaranteed during the planning stage. This makes precise control of the final actual flight trajectory complex and difficult to achieve, posing a significant challenge for practical engineering applications. Under certain conditions, onboard payloads may not function as expected, and higher terminal relative speeds could even pose serious collision risks to the drone itself.
An effective approach is to leverage the differential flatness properties of quadrotor drones [31] to generate time-differentiable trajectories. These trajectories inherently encapsulate state information, such as position changes over time and their multi-order derivatives during flight. This information can precisely describe the aircraft’s state during the planning phase, thereby enabling precise control in high-speed dynamic scenarios.
The paper [8] introduced a method for the swift generation and detection of motion primitives, enabling the rapid evaluation of numerous flight trajectories within seconds. This facilitated precise control over the terminal state of quadrotor flight. Our subsequent research [32] enhanced this method by applying it to drone swarm interception scenarios. We recognized the significant influence of air resistance on quadrotors during high-speed flight interception. By linearizing the aerodynamic drag term in the quadrotor dynamics model, we derived a method for the expedited solution and evaluation of modified motion primitives. This advancement allowed for precise control over the terminal state of quadrotor flight trajectories in high-speed flight conditions.
This article seeks to augment our prior research by addressing the issue of large-scale target interception. The primary contributions are as follows:
- A comprehensive analysis and modeling of multi-target interception challenges were undertaken, establishing trajectory state constraints essential for accomplishing multi-target interception objectives. Consequently, a theoretical framework for addressing multi-target interception issues was formulated.
- This study juxtaposed the multi-objective interception problem with the routing problem. A cost matrix for dynamic multi-objective interception was meticulously designed, utilizing motion primitives as a foundational element. Furthermore, an in-depth analysis was conducted to elucidate the impact of target movement on the aforementioned cost matrix.
- We designed an interception path optimization algorithm, leveraging the cost matrix of motion primitives. Additionally, we developed three optimization operators tailored for multi-objective interception challenges, yielding efficient solutions for interception trajectories.
- The simulation experiments conducted validate the substantial benefits of the method proposed in this paper, particularly in terms of result rationality and solution efficiency. A comprehensive series of tests were executed using this method across various scenarios. The influences of drone performance parameters, initial drone positions, and target cluster structures on interception tasks were subsequently analyzed based on the test results.
This paper is structured as follows: Section 2 offers a foundational overview of the quadrotor dynamics model and the multi-objective interception problem. Section 3 introduces a method for swiftly generating and evaluating motion primitives. Section 4 delves into the rapid planning approach for multi-objective interception paths. Section 5 confirms the logic and computational efficiency of the trajectory planning algorithm proposed herein. Section 6 examines the influence of performance parameters and changes in positional structure on both parties involved in multi-objective interception tasks, using the methods detailed in this paper. Section 7 concludes the paper.
2. System Dynamics and Problem Statement
This section commences with an introduction to the quadrotor dynamics model employed in this study, encompassing factors such as gravity, thrust, and external disturbance forces encountered during flight. Subsequently, an analysis of the control input constraints of the quadrotor is presented, followed by a clear articulation of the problem that this paper aims to address.
2.1. Quadrotor Dynamics Model and Input Constraints
The quadrotor is conceptualized as a six degree of freedom rigid body, represented by two three-dimensional column vectors: the linear translation along the orthogonal inertial axis, and the rotation about the three degrees of freedom that describe the frame attached to the fuselage in relation to the inertial frame.
Figure 1 illustrates the system’s control input, which is considered as a scalar that signifies the total thrust generated by the quadrotor and a column vector that denotes the body rate in the body coordinate system. Given the relatively low moment of inertia and substantial torque generation capacity of the quadrotor, this study disregards angular dynamics and assumes perfect tracking of the angular rate command. As a result, the state of the quadrotor aircraft is conceptualized as a nine-dimensional column vector, encompassing position, velocity, and attitude angle.
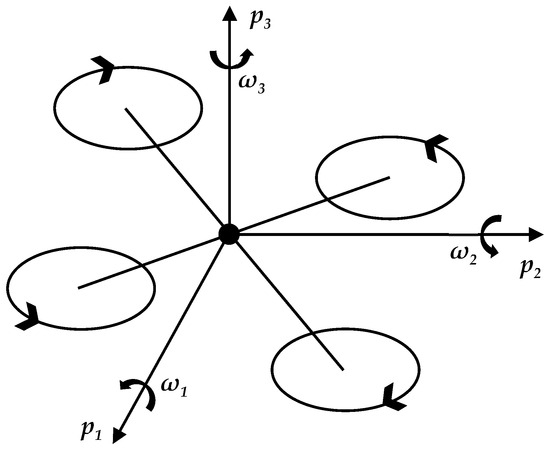
Figure 1.
Quadcopter dynamic model.
This study employs the differential equations of rigid bodies [33] as a foundational framework for controlling quadrotor aircraft flight. Additionally, external disturbances are modeled using the methodology delineated in [34]:
In the equations above, p denotes position, v represents velocity, at signifies the acceleration component generated by the drone’s thrust, and ae indicates the acceleration component resulting from external disturbance forces. The term g refers to the gravitational acceleration as depicted in the inertial coordinate system, while R is an orthogonal matrix that describes rotation. The symbol represents a constant vector in the fixed object coordinate system. The term denotes the drag force experienced by the body structure during the quadrotor flight process [35], and signifies the drag force generated by propeller and rotor rotation [36]. Finally, represents the matrix form of the vector cross-product.
The quadrotor’s capacity to generate actual thrust, denoted as ft, is constrained within a specific range:
where fmin is a non-negative value, typically restricted to the minimum operational speed of the rotor motor. The angular velocity command’s magnitude is confined within a three-dimensional sphere:
Herein, denotes the Euclidean norm, which ensures rotational invariance and offers computational convenience. This constraint typically arises from the saturation rate of the flight control gyroscope components or the operational conditions of certain loads mounted on the quadrotor.
2.2. Problem Statement
This study assumes that the invasive swarm of UAVs consists of low-cost, small-scale aircraft exhibiting uniform performance characteristics and adhering to consistent mission objectives, maintaining a stable flight speed and direction. The objective of this research is to precisely intercept n invasive targets through a series of pre-determined defensive maneuvers by the UAVs, which will sequentially engage these targets. The specific problem is elaborated as follows.
Let and denote the state translation variables for the defensive drone and the m-th invading target, respectively. These variables encompass their position, velocity, and acceleration.
Let Ti denote the terminal moment at which the trajectory of the i-th target is intercepted. Consequently, for an interception task encompassing n targets, the cumulative duration required is Tn. Throughout this operation, the state translation variable of the defending drone must adhere to the following constraints:
wherein, denotes the process translation variable constraint.
The objective of this paper is to propose a highly versatile trajectory generation method for a variety of potential interception scenarios. Readers are afforded the flexibility to define the trajectory translational variable constraints , encompassing aspects such as position, velocity, and acceleration, based on the characteristics of different interception mechanisms. Subsequently, these trajectories with flexibly defined constraints are optimized for multiple objectives efficiently using the method introduced in Section 4.
This work does not delve into specific interception schemes but rather presents an intuitive approach as a demonstration. As illustrated in Figure 2, it is assumed that the sensors and interception mechanisms are mounted on the centroid of the UAV and adhere to the UAV’s body coordinate system. Upon reaching the target position, the defensive UAV is required to match the velocity of the target, i.e., the quadcopter arrives at the target position with zero relative velocity. This is beneficial for the operation of the on-board sensors and interception mechanisms, which may fail when there is a significant velocity disparity between the two parties. Additionally, intersecting at a relatively stationary velocity can effectively reduce the risk of high-speed collisions, which could lead to mission failure.
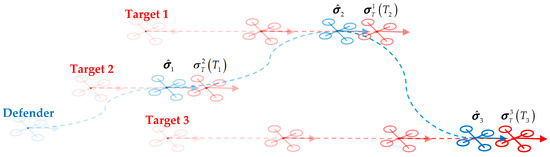
Figure 2.
A schematic diagram of a defense drone intercepting three invading targets, where the drone intercepts the second, first, and third targets at moments T1, T2, and T3 respectively.
Therefore, in this paper’s scenario, we define the process translation variable constraint as:
This suggests that our task can be conceptualized as the effective concatenation of multiple trajectory segments, where the end of one trajectory is rigidly attached to the state transition variable of the intercepted target and serves as the starting point for the subsequent segment. The advantages of this approach will be further discussed in Section 4.1.
Note that the index m is for n targets, while i is the interception order of n targets. The solution method will be described in Section 4.2.
In summary, for a quadrotor drone, it is imperative to establish suitable input trajectories ft(t) and ω(t) within the time interval [T0, Tn] from the initial state set T0, which encompasses position, velocity, and acceleration. These trajectories must adhere to specific conditions:
- The drone adheres to the quadrotor dynamics Equations (1), (2) and (5), as well as the input constraints (7) and (8) throughout its entire flight trajectory.
- The drone is constrained to Equation (10) at each endpoint time .
- Identify an optimal time series, denoted as , which minimizes the task completion time, represented as .
3. Generation and Evaluation of Motion Primitives
The objective of motion primitives is to compute a quadratic, differentiable trajectory using jerk as the input parameter. This trajectory directs the quadrotor from an initial state to either a fully or partially defined terminal state within a timeframe of T, while simultaneously minimizing a cost function:
3.1. Single-Axis Trajectory Generation
The three axes of the quadrotor exhibit formal symmetry. For ease of comprehension, subsequent analysis will disregard the subscript k for a singular axis.
The state is defined, encompassing scalar position, velocity, and acceleration thrust components. The jerk j serves as the input, in accordance with the modeling delineated in Section 2.1:
By incorporating the co-state variable, , and formulating the Hamiltonian function, , the optimal state trajectory can be determined directly through Pontryagin’s minimum principle [37]:
In the equation, and denote the optimal input and state trajectory of a single axis respectively, while C signifies an unspecified constant. By applying Equation (13) in conjunction with the initial value condition , we can deduce:
The residual unknown constant C is determined as a function of the anticipated process translation variable constraint , as depicted in Equation (10).
The Equation (17) is restructured to isolate the unknown constant C, based on the anticipated terminal state as defined by variable :
wherein
The generation of motion primitives necessitates only the aforementioned matrix multiplication for each axis, succeeded by the identification of the optimal state trajectory that corresponds to the motion primitive via Equation (17). A comprehensive derivation process can be referenced in our prior research [32].
3.2. Trajectory Feasibility Assessment
Given a specific time interval, , and an optimal state trajectory, , represented in the form of (17), along with its corresponding jerk input, , the objective is to ascertain whether the system inputs, ft and ω, present in the quadrotor dynamics model (3) and (5) from Section 2.1, fulfill the feasibility conditions of (7) and (8) respectively.
3.2.1. Thrust
The thrust fk for each axis can be represented as a function of the acceleration component ak of the thrust acceleration at on axis k and the gravitational component gk on the same axis:
By integrating the extremum of each axis, denoted as , we can determine the thrust boundary of a trajectory with a duration of :
By determining the roots of the differential jk of ak and juxtaposing them with the endpoint values at the left and right boundaries of , we can ascertain the maximum and minimum values (represented as and , respectively) of the thrust fk in Equation (21). These values can be obtained in a closed form:
In these equations, , , and are two distinct branches of the Lambert W function. The extremum of is denoted as:
Consequently, the sufficient condition for the interval input thrust to be infeasible is:
In accordance with (22), the necessary condition for ensuring input thrust feasibility is as follows:
In the absence of both conditions (26) and (27), the thrust feasibility of the segment remains undetermined.
3.2.2. Body Rate
The literature [8] suggests that the magnitude of body rate can be perceived as a function of acceleration and thrust, with its upper limit defined by as follows:
Under the assumption , as per the aforementioned equation, if , then the body rate input for time period is deemed feasible; otherwise, it is classified as uncertain.
As illustrated in Figure 3, the viability of a specified time interval, , is assessed by conducting the aforementioned thrust and body rate tests on . The algorithm will be recursively applied to and , respectively. If both tests yield feasible results, then is designated as input feasible, and the algorithm concludes; if one test yields an infeasible result, the algorithm concludes with being marked as input infeasible. In any other instance, is bisected. When the time interval falls below a predefined minimum, , the algorithm designates the motion primitive as uncertain and concludes.
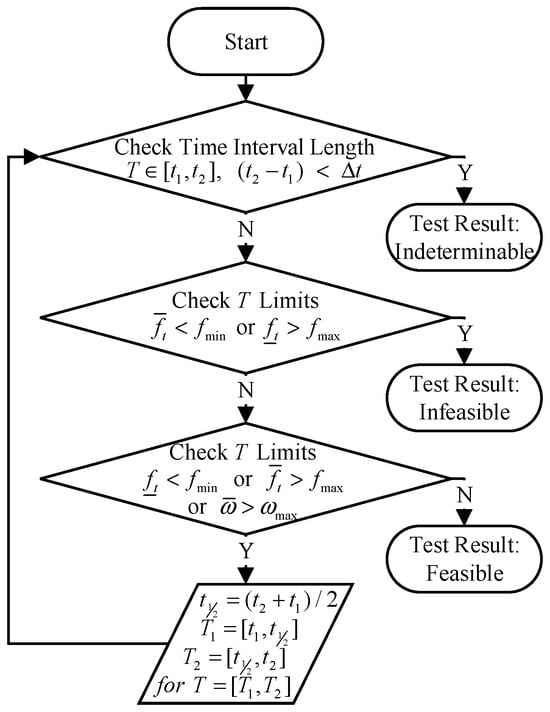
Figure 3.
Flowchart for efficient recursive testing of trajectory feasibility.
As the interval narrows, both the upper and lower bounds of Equation (25) progressively converge. Consequently, Equation (22) also tends to converge, thereby enhancing the precision of the thrust feasibility test.
4. Multi-Target Trajectory Planning for Interception
This scenario parallels a routing problem, where the drone must traverse each target in sequence without repetition, but does not necessitate a return to the starting point. This is considered as task completion. The subsequent section will elucidate the process of determining the optimal trajectory for multi-objective interception. Furthermore, the rationality of the trajectory will be validated in Section 5.
4.1. The Cost Matrix of Motion Primitives
As delineated in Section 2.2, an interception trajectory with a duration of from target i to target j, can be re-expressed using the Formula (20) from Section 3.1 as follows:
In this context, pi, vi, ai, pj, vj, and aj, respectively denote the position, velocity, and acceleration of target i and target j on a singular axis.
In addressing the interception problem involving n targets, we define a cost matrix G with n × n elements. Each element, gij, denotes the minimum movement time required to travel from target i to target j. The term signifies the shortest duration of feasible motion primitives, which is determined using the rapid testing method discussed in Section 3.2:
Given a cluster with fixed internal structure, the speeds of all individuals can be assumed to be consistent, accelerations are zero, and relative distances between individuals remain constant. This suggests that for any intercept trajectory, ‖pj − pi‖, vi, vj, ai, and aj in Equation (29) will not vary over time. As a result, each element gij in the cost matrix is independent and can be determined initially, thereby facilitating our solution process.
Figure 4 illustrates the motion primitive cost matrices for five targets, each flying at varying speeds, as generated by the aforementioned method. In this figure, numbers denote trajectory time. It is evident that the characteristics of the cost matrix vary depending on both the target’s speed and spatial distribution. The cost matrix maintains symmetry only when the target remains stationary and is distributed on an identical horizontal plane. Deviation from these conditions results in a reduction in the symmetry of the cost matrix.
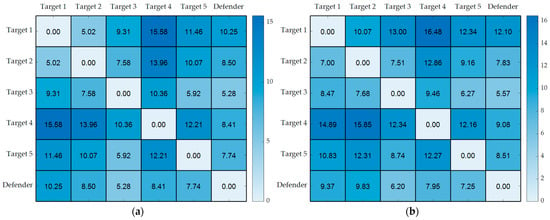
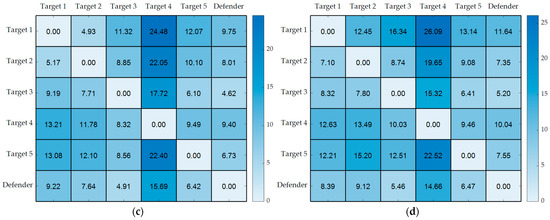
Figure 4.
The cost matrix of motion primitives for planar and spatial targets under different flight speeds, where numbers represent trajectory time: (a) stationary planar target, the matrix is symmetric; (b) stationary spatial target; (c) moving planar target; (d) moving spatial target.
To assess the influence of target dynamics and spatial distribution characteristics on the cost matrix, we employ established mathematical techniques to formulate an index that quantifies the asymmetry of the cost matrix [38]:
where denotes the Frobenius norm of matrix A, computed as . The indicator’s value oscillates between 0 and 1, with 0 signifying total symmetry and 1 indicating total asymmetry.
Table 1 and Figure 5 illustrate the asymmetry of the cost matrix for the five objectives under varying speed conditions. It is evident that when the planar target (height range = 0) remains stationary, the asymmetry is null. In this instance, the multi-target interception issue parallels a routing problem, wherein the round-trip cost between two targets remains constant. The elements within the matrix accurately represent the distance disparities between the targets.

Table 1.
Asymmetric index of cost matrix in scenarios with different target speeds and altitude ranges.
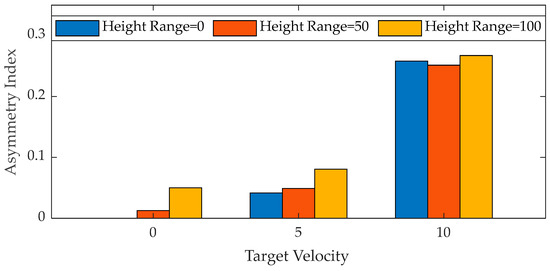
Figure 5.
Histogram of asymmetric index of cost matrix in different scenarios.
When the spatial target, defined by an altitude range greater than zero, remains stationary, we observe that the cost matrix is not symmetrical. Furthermore, the round-trip time between the two targets becomes inconsistent, with the outbound time from the higher to the lower target being less than the return time. The dynamic characteristics of the drone impose constraints, leading to the emergence of the target’s spatial distribution impact on path cost.
When a planar target is in motion, the cost matrix exhibits an asymmetric distribution. Notably, the index of this asymmetry changes more significantly than the impact of variations in the height range. This suggests that the dynamic characteristics of the target exert a greater influence on the interception trajectory solution than the spatial distribution attributes of the target.
It is important to note that the cost matrix is concurrently influenced by a space target’s dynamic characteristics and spatial distribution when it moves. A closer examination of the data underscored in bold within the table reveals that planar moving targets exhibit greater asymmetry than their spatial counterparts. This suggests that the influence of a target’s dynamic characteristics and spatial distribution on interception trajectories is not merely additive. Instead, these two factors are interwoven, thereby complicating the analysis of optimal interception trajectories.
In Section 5.1, we will examine the logic and benefits of utilizing the cost matrix of motion primitives within the context of dynamic target interception tasks.
4.2. Intercept Trajectory Planning
As delineated in Section 2.2, the multi-target interception trajectory of a UAV is constructed by applying a series of start and end state constraints to multiple single-target interception trajectories. Consequently, we represent the path as a distinct single chain comprising 1 + n units, as illustrated in Figure 6.
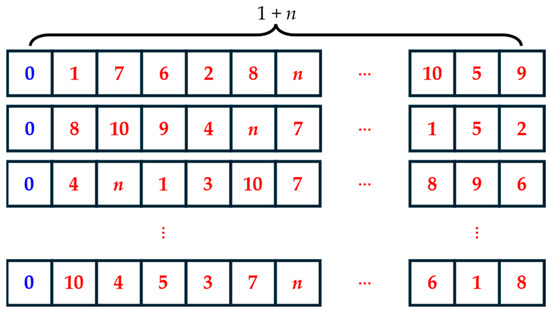
Figure 6.
The schematic diagram of path encoding, where blue represents the defense drone and is the starting point of the path, and red represents the sequence numbers of n targets.
In the optimization process of the path, we draw inspiration from genetic algorithms and have designed three distinct operation operators for the previously mentioned encoded paths, as depicted in Figure 7. By generating a substantial number of individuals concurrently, we can fully leverage the parallel computing capabilities of computers to expediently yield satisfactory results within a brief timeframe.
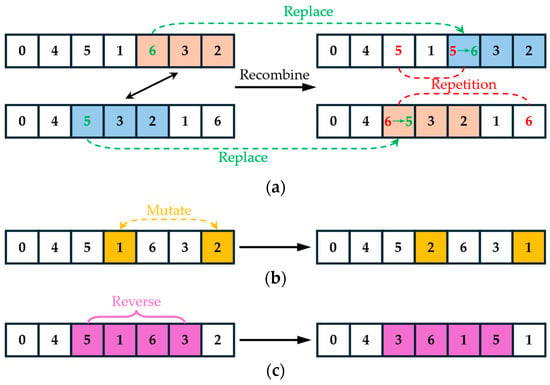
Figure 7.
Schematic diagram of operator genetic evolution: (a) crossover; (b) variation; (c) reverse.
In Section 5.2, we will validate the optimization prowess and computational efficiency of our proposed method, benchmarking it against a range of prevalent optimization algorithms within the same multi-objective interception task scenario.
5. Validation of Trajectory Planning Results
This section substantiates the efficacy of our method for large-scale target interception tasks, examining aspects such as trajectory quality, time required for interception tasks, and computational efficiency. All simulations were conducted on a personal portable laptop equipped with an Ryzen™ 9 7945HX CPU manufactured by AMD in Santa Clara, CA, USA, boasting 16 cores and a base clock frequency of 2.5 GHz. Given that the trajectory calculations in practical applications can be entirely executed with the robust computing support at the ground end, before being uploaded to the aircraft for execution, these results are deemed reliable.
5.1. Comparison of Cost Functions
Our approach utilizes the motion primitive cost matrix, as generated in Section 4.1, which takes into account dynamic characteristics and constraints during the planning phase. Subsequently, by employing the multi-objective interception trajectory planning method delineated in Section 4.2, we can derive multi-objective interception trajectories that adhere to complex state constraints in near real time.
We will employ the widely recognized distance cost matrix solution typically utilized in routing problems as a benchmark. Upon obtaining the sequence for the planning task, we will then solve for the interception trajectory using the motion primitives and Formula (29) as outlined in Section 3.1.
Figure 8 shows the comparison of the two methods in multi-target interception scenarios, where the difference in interception trajectories is mainly reflected in the use of altitude. The trajectory time obtained from motion primitives is optimized by our method, which first intercepts the target at its highest point through continuous ascent and then gradually dives downward with greater potential energy. The task time of our method is 82 s. The comparative method optimizes based on Euclidean distance, first intercepting targets that are closer. When the target is stationary, this method can achieve the shortest path, but in interception problems, the task time is not only related to the path length, but also to its geometric features and the dynamic characteristics of the drone. When the target is moving, paths that are poorly coupled with the dynamic characteristics of the drone require longer tracking times, and the final task time of the comparative method is 89 s. Our method has achieved better results.
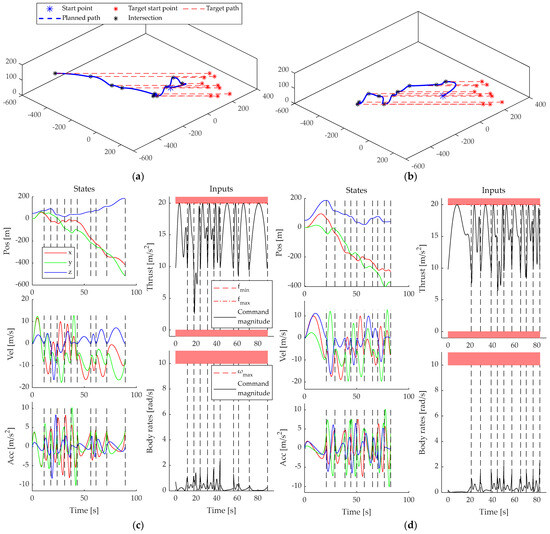
Figure 8.
Comparison display of optimization results based on distance and motion primitives: (a) 3D view of the flight path of the comparison method; (b) our method provides a three-dimensional view of the flight path; (c) compare the flight state trajectory of the method; (d) our method’s flight state trajectory.
To further assess the benefits of our approach, we conducted additional experiments based on the parameter groups outlined in Table 2. Each group was subjected to a random simulation of 1000 iterations, adhering to their respective parameters. The statistical data pertaining to task time consumption are presented in Figure 9.

Table 2.
The simulation parameters for various scenarios are as follows: the drone’s initial position is [0, 0, 50] m, the desired velocity is [−6, −6, 0] m/s, the drone’s maximum thrust capacity is 20, and there are five targets in total.
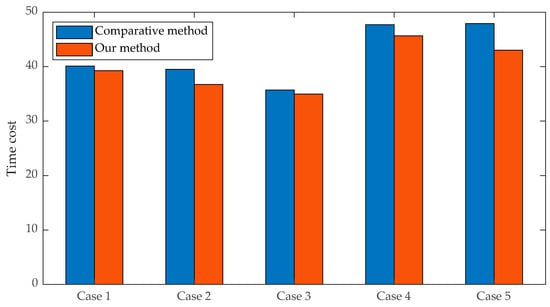
Figure 9.
Histogram of the statistical results of the comparison method and our method on 1000 sets of data.
As illustrated, the average time consumption of our method outperforms that of the comparative methods in all six cases. Specifically, comparing Case 1 and Case 2, when the target distribution range contracts horizontally and expands vertically, the overall spatial range of the target distribution is reduced to half its original size. The average time consumption of the comparative method remains relatively stable, while the time consumption of our method decreases as the spatial range diminishes. Furthermore, as the longitudinal distribution range of the target increases, the gap between the two methods widens, exacerbating the impact of drone dynamics on planning outcomes. This supports our analysis in Section 4.1, indicating that our method can effectively account for the dynamic characteristics of drones and make more judicious use of their performance. This trend is also evident in the comparison between Case 4 and Case 5.
Upon comparing Case 2 and Case 3, it becomes evident that when the range of the target distribution space remains constant, yet the longitudinal distribution range contracts, there is a reduction in the average time consumption for both methods. Furthermore, as the longitudinal distribution range of the target decreases, indicating a more horizontally distributed overall situation, the disparity between the two methods diminishes. Consequently, the interception problem reconfigures into a routing problem.
5.2. Comparison of Algorithm Efficiency
This section aims to validate the performance of the trajectory planning method proposed in Section 4.2. Intercepting invasive targets constitutes an urgent task where an excessive pursuit of solution quality might not offset the negative impact of computational time on mission delays. Consequently, this paper does not employ exact solution methods such as dynamic programming but rather compares it with other typical optimization algorithms including Simulated Annealing, ACO, and PSO. The computational efficiency of our method is examined across scenarios with varying numbers of targets.
The parameter configurations for both the comparative and our proposed algorithms are detailed in Table 2, Table 3, Table 4, Table 5 and Table 6. Within a bounding box of dimensions 200 m × 200 m × 200 m, centered at the coordinate origin, we generated 20 targets moving at a consistent velocity of 8 m/s. The defensive drone initiates its movement from a position 250 m distant from the target’s center, aligned with the direction of the target’s trajectory. Each simulation was executed 100 times, and the resulting statistical data concerning task time consumption are presented in Figure 10.

Table 3.
Parameters of simulated annealing method.

Table 4.
Parameters of Ant Colony Algorithm.

Table 5.
Parameters of Particle Swarm Optimization Algorithm.

Table 6.
The parameters of our method.
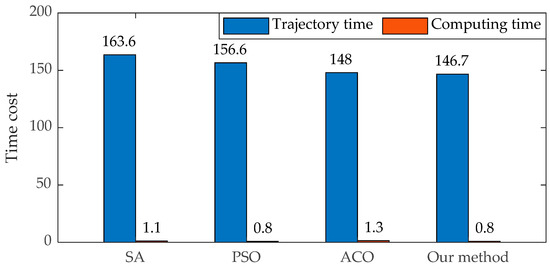
Figure 10.
Histogram of average planning results and computational efficiency of different optimization algorithms on 20 target scenarios.
The comparative test results presented in Figure 10 indicate that simulated annealing and particle swarm optimization are primarily suited for continuous multi-variable problem solving. While their solution efficiency surpasses that of the Ant Colony Algorithm, they are more prone to local solutions. The Ant Colony Algorithm, which is derived from ant foraging where the destination is typically stationary, performs well in static routing problems. However, experimental results suggest a decrease in its applicability to dynamic issues such as target interception trajectory planning.
Subsequently, in accordance with the aforementioned scenarios, we established target interception tasks of varying scales and conducted each set of experiments 100 times in simulation to ascertain the computational efficiency of our method in large-scale target interception scenarios.
The results depicted in Figure 11 indicate that as the number of targets increases, the optimal interception trajectory time for the mission increases approximately linearly with the number of targets. Additionally, there is a slight increase in the computation time for trajectory solution; however, even for interception missions involving 50 targets, the average solution time is only around 3.7 s, which constitutes approximately 1.2% of the mission time. Although this may exceed the capability limits of some UAVs, in practical applications, the number of mission targets should be set according to the actual performance capabilities of the quadrotor.
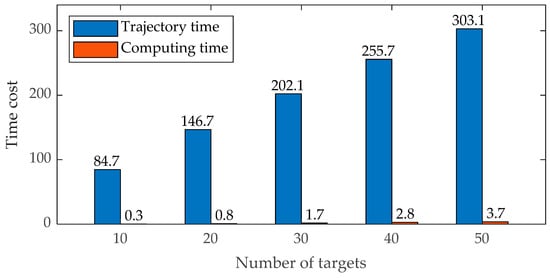
Figure 11.
Histogram of computational efficiency and error of the proposed method on tasks with different target quantities.
The method presented in this study demonstrates favorable computational efficiency, which is of paramount importance for large-scale target interception missions. This further validates the rationality of our approach and its robustness in dealing with large-scale target interception tasks.
5.3. Validation of Trajectory Replanning
In real-world scenarios, the configuration of a target group is not static; continued reliance on task planning outcomes from the initial phase may no longer guarantee the efficacy of an interception scheme over time. This section delineates instances wherein the structure of a target group experiences temporal alterations. The computational efficiency of our proposed method is leveraged to facilitate rapid replanning in response to significant changes in the target group’s structure. Figure 12 illustrates the modifications to the interception trajectory and mission duration subsequent to replanning.
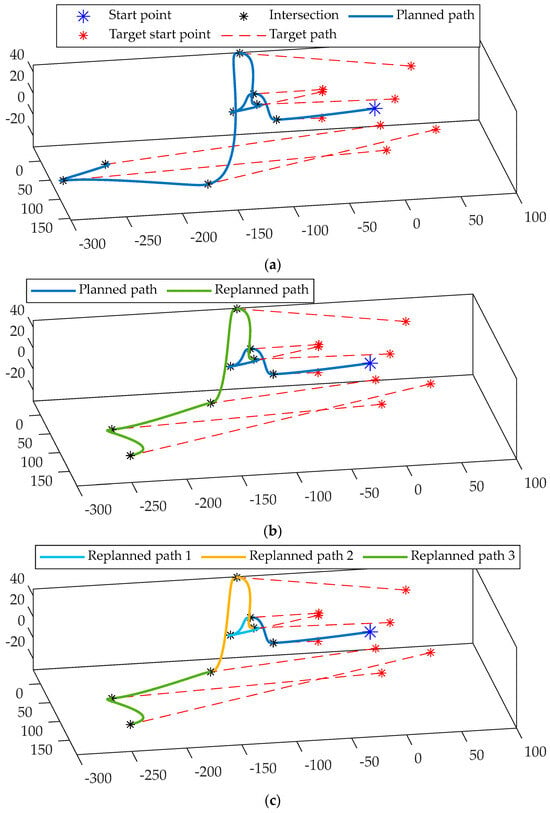
Figure 12.
Simulation results for different numbers of replanning on 10 different targets: (a) No replanning, taking 63.6 s; (b) replanning once, taking 60.1 s; (c) replanning three times, taking 60.1 s.
As previously outlined, the comparative simulation outcomes of replanning indicate that this process can mitigate the effects associated with the incessant alterations in the internal structure of the target group, thereby enhancing task efficiency. However, the extent of improvement is contingent upon the degree of variation in the internal structure of the target group. This is evidenced by the comparison between Figure 12a,b, wherein the quadrotor executed replanning at the midpoint of the mission, yielding an interception trajectory that deviated from the initial planning. This trajectory effectively accounted for the impact of changes in target position, thereby further augmenting task efficiency.
As illustrated in Figure 12c, increasing the number of replanning iterations does not yield the anticipated improvement in interception task efficiency. This is primarily due to the fact that the internal structural changes within the target group over a brief period are insufficient to significantly influence interception efficiency. Consequently, while the implementation of replanning technology can enhance the interception efficiency of moving targets to a certain degree, it is crucial to ensure that the extent and frequency of replanning align with the dynamic characteristics of the target group. This approach will prevent unnecessary consumption of computational resources.
6. Efficiency Analysis of Swarms Interception
The validation results detailed in Section 4 substantiate the efficacy of our method in intercepting large-scale targets and adapting to evolving target group structures, as gauged by metrics such as trajectory quality, duration of interception missions, and computational efficiency. This section offers an exhaustive analysis of the determinants of drone interception mission efficiency using our method, scrutinizing factors such as drone performance, initial drone position, and target group structure. The aim of this chapter is to furnish generalizable insights into enhancing the efficiency of large-scale target interception missions through iterative simulations across multiple scenarios and subsequent statistical analysis of the outcomes.
6.1. Analysis of UAV Performance
In this study, we examine the interception tasks of 10 targets as outlined in Section 4.2. We conduct 100 repetitive experiments across different control group scenarios, each with varying UAV performance as shown in Table 7. The aim is to investigate the optimal configuration of UAV performance in multi-target interception situations.

Table 7.
Performance configuration of UAV in different scenarios and corresponding simulation results.
Figure 13 presents the efficacy of our method across varying drone performance metrics, namely thrust and body rate. The data reveal that, in comparison to three distinct datasets under different thrusts, an increase in the drone’s thrust from 20 to 25 results in a reduction of approximately 17% in average task time. Similarly, when the drone’s thrust escalates from 25 to 30, there is a decrease of approximately 10% in average task time. This suggests that an enhancement in the drone’s thrust can markedly reduce the overall task duration. However, as the thrust progressively increases, the efficiency improvement yielded by equivalent magnitudes of thrust augmentation will correspondingly diminish.
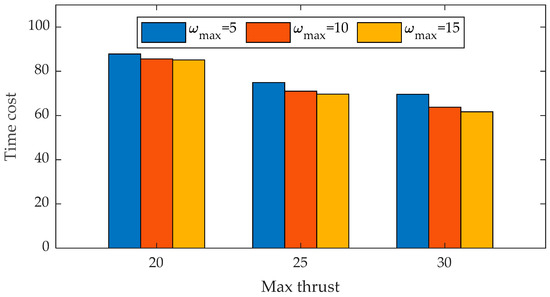
Figure 13.
The histogram of the optimal interception trajectory time of our method in different drone performance scenarios.
When comparing the results of three groups under identical thrust, it was observed that an increase in body velocity from 5 to 15 resulted in a decrease in task time by 3%, 7%, and 11%, respectively. This suggests that an increase in body velocity can effectively reduce the average task time, with the impact becoming more pronounced as the upper limit of drone thrust increases. However, it was also noted that the impact of increasing body velocity from 10 to 15 was generally less than that of increasing it from 5 to 10. This implies that, similar to thrust performance, as the performance of body velocity improves, the efficiency improvement impact brought about by the same magnitude increase in body velocity will gradually diminish.
We also observe that the efficiency gain (3%) from body rate performance improvement at lower thrusts (Scenario 1 and 2) is much smaller than the efficiency gain (8%) from body rate performance improvement at higher thrusts (Scenario 7 and 8), while the efficiency gain (15%) from thrust performance improvement at lower thrusts (Scenario 1 and 4) is much larger.
In conclusion, the efficacy of multi-target interception tasks is contingent upon a myriad of performance parameters inherent to the drone. A singular parameter is inadequate for an accurate representation of the drone’s task capability. The dominant factors influencing the interception efficiency vary among drones with distinct performance characteristics. Optimal results in multi-target interception necessitate harmonious coordination across multiple drone performance indicators.
It is noteworthy that our method can yield satisfactory planning outcomes with exceptional computational efficiency across various performance characteristics of UAV scenarios. This underscores the robustness of our approach in dynamic environments and its potential for application in a broader range of scenarios.
6.2. Analysis of the UAV Initial Position Impact
We examine separately the influence of alterations in the interception position on interception efficacy when the target cluster exhibits a uniform movement speed. As depicted in Figure 14, targets are randomly distributed within a cubic area with a side length of 200 m. The defender’s initial position is established on the vertical extension line between the center of the target distribution and the boundary surfaces of six distinct target distributions, situated at a distance of 250 m from the center of the target.
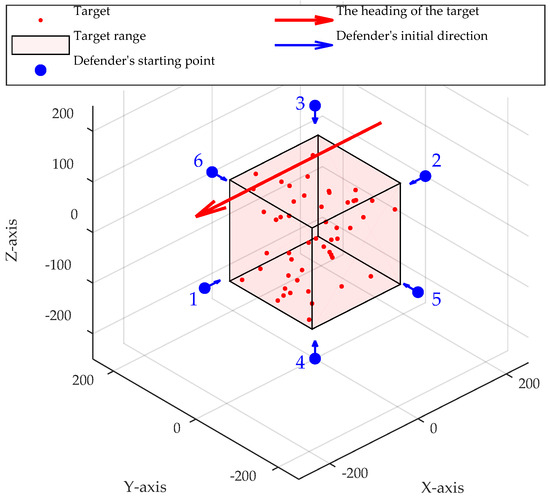
Figure 14.
Schematic diagram of simulation scenarios with different initial positions of initial defenders.
Figure 15 provides a schematic representation of the simulation scenario, showcasing various initial positions for the defender. Figure 15c presents the results of these simulations, demonstrating that different initial positions yield markedly inconsistent optimal interception trajectories. Notably, initiating from the apex of the target cluster can significantly diminish the task duration. As indicated by the circled section in Figure 15c, when the defending drone descends from an elevated position, it intercepts a substantial number of targets at the outset due to its advantage in potential energy. This substantially enhances the interception efficiency, thereby enabling the drone to complete the entire task more rapidly. Table 8 shows the simulation results of different control groups.
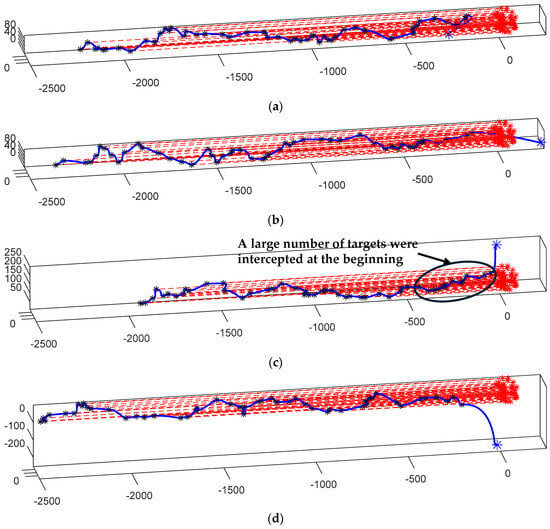
Figure 15.
Simulation results of initial positions of different initial defenders: (a) The initial position of the drone is located at position 1 (front), taking 287.3 s; (b) the initial position of the drone is at position 2 (behind), taking 296.4 s; (c) the initial position of the drone is at position 3 (above), which takes 250.2 s; (d) the initial position of the drone is at position 4 (below) and takes 320.1 s.

Table 8.
The simulation results of 50 target scenarios with 100 different initial defender positions, with the target’s forward direction as the forward direction.
We contend that, due to the inherent power limitations of UAVs, a greater proportion of available power can be allocated to pursuit and target approach rather than sustaining its fundamental flight. This is particularly true when the UAV initiates the task from an elevated position, thereby affording more flexibility for interception trajectory planning of the target.
6.3. Analysis of Target Group Structure Impact
This section examines the interception effects of varying target distribution configurations. Figure 16 presents a three-dimensional trajectory view of intercepting targets with different formations, alongside an initial distribution schematic diagram of the target group. Our findings indicate that the square distribution of targets results in the longest interception time, whereas the circular distribution of targets necessitates the shortest interception time. It is evident that, when the number of targets is comparable, the interception task time is primarily associated with the range of spatial distribution of the target group, as compared to the optimal interception time of four formations.
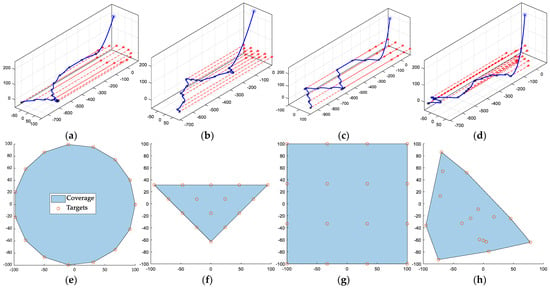
Figure 16.
The performance of our method in different target structure scenarios: (a) circular distribution, taking 93.6 s; (b) triangular distribution, takes 82 s; (c) square distribution, takes 119.9 s; (d) random distribution, taking 87.9 s; (e–h) is the convex hull of the corresponding target group distribution structure.
While it is noteworthy that the optimal interception trajectories of square and circular matrices display a pronounced regularity, which offers advantages in terms of trajectory planning and aircraft execution, paths with random distribution present significant challenges in their planning. Nevertheless, our method consistently delivers plausible outcomes within a brief timeframe.
7. Conclusions
This paper introduces a novel method for rapidly determining the state trajectory of quadrotor UAVs to intercept large-scale invading UAV swarms. The proposed approach has been extensively validated through simulation, demonstrating its efficiency and effectiveness in real-time trajectory planning for multiple target interception. The average task time and solution time of this method significantly reduce the interception duration for multiple targets. Notably, the solution time for 50 targets is an average of only 3.7 s, meeting the requirements for real-time solutions in large-scale target interception tasks.
We have executed a multitude of simulation experiments across various scenarios, grounded in the rationality and computational efficiency of the method proposed in this paper. The results from these experiments offer an exhaustive analysis of the potential influences that factors such as drone performance, initial position, and target distribution structure may exert on task efficiency within multi-objective dynamic interception mission scenarios.
This study presents a real-time methodology for generating high-quality, precise target interception trajectories. The resultant trajectories offer comprehensive detailing of the drone’s state transitions, accurately mirroring the actual flight task process and facilitating a swift and accurate estimation of task completion time. This advancement will contribute significantly to the judicious allocation of drone equipment and the rational design of drone performance.
It is important to note that this study has certain limitations which could be addressed in future research:
- Existing models fail to account for environmental and energy variables that could influence drone performance, including wind speed [39], air pressure, obstacles [40], and endurance. Future studies should explore how drone performance may vary with altitude, refine the logic of trajectory planning, and establish task plans that align with the drone’s endurance.
- The current study operates under the assumption that the performance and task objectives of the target drone are congruent. However, in real-world scenarios, it is possible to encounter individuals within the target group who exhibit varying performances or have distinct task objectives. Future research will explore more dynamic scenarios, taking into account the computational efficiency of the method proposed in this paper.
- The current research discusses only the computational efficiency of the proposed algorithm on hardware; however, it is equally important to address the deployment of the algorithm on actual UAV hardware. This encompasses the integration of the algorithmic code with the physical system, the refinement of physical models, and the establishment of a safe and robust testing environment. In future work, we intend to consider the validation of the algorithm’s performance in real-world settings.
Author Contributions
Y.Z.: Conceptualization, methodology, software, validation, formal analysis, investigation, resources, data curation, writing—original draft preparation, writing—review and editing, visualization, supervision, and project administration. X.G.: Conceptualization, methodology, software, validation, investigation, data curation, writing—original draft preparation, writing—review and editing, and visualization. J.Z.: Conceptualization, methodology, software, investigation, data curation, writing—original draft preparation, writing—review and editing, and visualization. Z.L.: Software, writing—review and editing. Z.H.: Validation, resources, writing—review and editing, supervision, and project administration. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
Z.L. declares no conflicts of interest related to this study. He has not received any research grants from any company, nor has he received any speaker honoraria associated with this study. Furthermore, he does not hold stocks in any company connected to this research and has not served as a consultant or expert witness for any such entity. Finally, he is not the inventor of any patents related to this research. The other authors declare no conflicts of interest.
References
- Vujasinović, S.; Becker, S.; Breuer, T.; Bullinger, S.; Scherer-Negenborn, N.; Arens, M. Integration of the 3D Environment for UAV Onboard Visual Object Tracking. Appl. Sci. 2020, 10, 7622. [Google Scholar] [CrossRef]
- Sudhakar, S.; Vijayakumar, V.; Sathiya Kumar, C.; Priya, V.; Ravi, L.; Subramaniyaswamy, V. Unmanned Aerial Vehicle (UAV) based Forest Fire Detection and monitoring for reducing false alarms in forest-fires. Comput. Commun. 2020, 149, 1–16. [Google Scholar] [CrossRef]
- Onishi, M.; Ise, T. Explainable identification and mapping of trees using UAV RGB image and deep learning. Sci. Rep. 2021, 11, 903. [Google Scholar] [CrossRef]
- Castrillo, V.U.; Manco, A.; Pascarella, D.; Gigante, G. A Review of Counter-UAS Technologies for Cooperative Defensive Teams of Drones. Drones 2022, 6, 65. [Google Scholar] [CrossRef]
- Swinney, C.J.; Woods, J.C. A Review of Security Incidents and Defence Techniques Relating to the Malicious Use of Small Unmanned Aerial Systems. IEEE Aerosp. Electron. Syst. Mag. 2022, 37, 14–28. [Google Scholar] [CrossRef]
- Zhou, B.; Gao, F.; Wang, L.; Liu, C.; Shen, S. Robust and Efficient Quadrotor Trajectory Generation for Fast Autonomous Flight. IEEE Robot. Autom. Let. 2019, 4, 3529–3536. [Google Scholar] [CrossRef]
- Zhou, X.; Wen, X.; Wang, Z.; Gao, Y.; Li, H.; Wang, Q.; Yang, T.; Lu, H.; Cao, Y.; Xu, C.; et al. Swarm of micro flying robots in the wild. Sci. Robot. 2022, 7, eabm5954. [Google Scholar] [CrossRef]
- Mueller, M.W.; Hehn, M.; D’Andrea, R. A Computationally Efficient Motion Primitive for Quadrocopter Trajectory Generation. IEEE Trans. Robot. 2015, 31, 1294–1310. [Google Scholar] [CrossRef]
- Vrba, M.; Stasinchuk, Y.; Báča, T.; Spurný, V.; Petrlík, M.; Heřt, D.; Žaitlík, D.; Saska, M. Autonomous capture of agile flying objects using UAVs: The MBZIRC 2020 challenge. Robot. Auton. Syst. 2022, 149, 103970. [Google Scholar] [CrossRef]
- Chamola, V.; Kotesh, P.; Agarwal, A.; Naren; Gupta, N.; Guizani, M. A Comprehensive Review of Unmanned Aerial Vehicle Attacks and Neutralization Techniques. Ad Hoc Netw. 2021, 111, 102324. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, Z.; Yang, Q.; Deng, C.; Wei, Y. Robot trajectory planning for autonomous 3D reconstruction of cockpit in aircraft final assembly testing. Chin. J. Aeronaut. 2024, 37, 332–350. [Google Scholar] [CrossRef]
- Chai, R.; Tsourdos, A.; Savvaris, A.; Chai, S.; Xia, Y. High-fidelity trajectory optimization for aeroassisted vehicles using variable order pseudospectral method. Chin. J. Aeronaut. 2021, 34, 237–251. [Google Scholar] [CrossRef]
- Tao, H.; Lin, D.; He, S.; Song, T.; Jin, R. Optimal terminal-velocity-control guidance for intercepting non-cooperative maneuvering quadcopter. J. Field Robot. 2022, 39, 457–472. [Google Scholar] [CrossRef]
- Valianti, P.; Papaioannou, S.; Kolios, P.; Ellinas, G. Multi-Agent Coordinated Close-in Jamming for Disabling a Rogue Drone. IEEE Trans. Mobile Comput. 2022, 21, 3700–3717. [Google Scholar] [CrossRef]
- Phung, M.D.; Ha, Q.P. Safety-enhanced UAV path planning with spherical vector-based particle swarm optimization. Appl. Soft Comput. 2021, 107, 107376. [Google Scholar] [CrossRef]
- Liu, X.; Su, Y.; Wu, Y.; Guo, Y. Multi-Conflict-Based Optimal Algorithm for Multi-UAV Cooperative Path Planning. Drones 2023, 7, 217. [Google Scholar] [CrossRef]
- Foehn, P.; Romero, A.; Scaramuzza, D. Time-optimal planning for quadrotor waypoint flight. Sci. Robot. 2021, 6, eabh1221. [Google Scholar] [CrossRef]
- Bianchi, D.; Borri, A.; Cappuzzo, F.; Di Gennaro, S. Quadrotor Trajectory Control Based on Energy-Optimal Reference Generator. Drones 2024, 8, 29. [Google Scholar] [CrossRef]
- Gao, X.; Zhang, Y.; Wang, B.; Leng, Z.; Hou, Z. The Optimal Strategies of Maneuver Decision in Air Combat of UCAV Based on the Improved TD3 Algorithm. Drones 2024, 8, 501. [Google Scholar] [CrossRef]
- Salii, Y.V.; Sheka, A.S. Improving dynamic programming for travelling salesman with precedence constraints: Parallel Morin-Marsten bounding. Optim. Method Softw. 2021, 36, 1128–1154. [Google Scholar] [CrossRef]
- Zhao, D.; Yu, X.; Wen, G.; Hu, Y.; Huang, T. Dynamic Task Allocation Algorithm for Moving Targets Interception. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 776–788. [Google Scholar] [CrossRef]
- Wu, Y.; Song, W.; Cao, Z.; Zhang, J.; Lim, A. Learning Improvement Heuristics for Solving Routing Problems. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 5057–5069. [Google Scholar] [CrossRef]
- Mavrovouniotis, M.; Yang, S.; Van, M.; Li, C.; Polycarpou, M. Ant Colony Optimization Algorithms for Dynamic Optimization: A Case Study of the Dynamic Travelling Salesperson Problem [Research Frontier]. IEEE Comput. Intell. Mag. 2020, 15, 52–63. [Google Scholar] [CrossRef]
- Phung, M.D.; Ha, Q.P. Motion-encoded particle swarm optimization for moving target search using UAVs. Appl. Soft Comput. 2020, 97, 106705. [Google Scholar] [CrossRef]
- Asadi, M.M.; Gianoli, L.G.; Saussie, D. Optimal Vehicle-Target Assignment: A Swarm of Pursuers to Intercept Maneuvering Evaders Based on Ideal Proportional Navigation. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 1316–1332. [Google Scholar] [CrossRef]
- Jiang, W.; Lyu, Y.; Li, Y.; Guo, Y.; Zhang, W. UAV path planning and collision avoidance in 3D environments based on POMPD and improved grey wolf optimizer. Aerosp. Sci. Technol. 2022, 121, 107314. [Google Scholar] [CrossRef]
- Puente-Castro, A.; Rivero, D.; Pazos, A.; Fernandez-Blanco, E. UAV swarm path planning with reinforcement learning for field prospecting. Appl. Intell. 2022, 52, 14101–14118. [Google Scholar] [CrossRef]
- Buzikov, M.E.; Galyaev, A.A. Minimum-time lateral interception of a moving target by a Dubins car. Automatica 2022, 135, 109968. [Google Scholar] [CrossRef]
- Huang, G.; Hu, M.; Yang, X.; Lin, P. Multi-UAV Cooperative Trajectory Planning Based on FDS-ADEA in Complex Environments. Drones 2023, 7, 55. [Google Scholar] [CrossRef]
- Duan, H.; Zhao, J.; Deng, Y.; Shi, Y.; Ding, X. Dynamic Discrete Pigeon-Inspired Optimization for Multi-UAV Cooperative Search-Attack Mission Planning. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 706–720. [Google Scholar] [CrossRef]
- Faessler, M.; Franchi, A.; Scaramuzza, D. Differential Flatness of Quadrotor Dynamics Subject to Rotor Drag for Accurate Tracking of High-Speed Trajectories. IEEE Robot. Autom. Let. 2018, 3, 620–626. [Google Scholar] [CrossRef]
- Zhang, Y.; Zong, J.A.; Gao, X.; Hou, Z. An Efficient Trajectory Planning Method for High-Speed Interception of Invasive Drones. Appl. Sci. 2024, 14, 7030. [Google Scholar] [CrossRef]
- Zipfel, P.H. Modeling and Simulation of Aerospace Vehicle Dynamics, 3rd ed.; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 2014. [Google Scholar]
- Tal, E.; Karaman, S. Accurate Tracking of Aggressive Quadrotor Trajectories Using Incremental Nonlinear Dynamic Inversion and Differential Flatness. IEEE Trans. Control Syst. Technol. 2018, 29, 1203–1218. [Google Scholar] [CrossRef]
- Martin, P.; Salaun, E. The true role of accelerometer feedback in quadrotor control, 2010-1-1. In Proceedings of the IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 1623–1629. [Google Scholar]
- Mahony, R.; Kumar, V.; Corke, P. Multirotor Aerial Vehicles: Modeling, Estimation, and Control of Quadrotor. IEEE Robot. Autom. Mag. 2012, 19, 20–32. [Google Scholar] [CrossRef]
- Weber, R. Dynamic Programming and Optimal Control; Athena Scientific: Nashua, NH, USA, 2014. [Google Scholar]
- Olszewski, D. Asymmetry index for data and its verification in dimensionality reduction and data visualization. Inf. Sci. 2025, 689, 121405. [Google Scholar] [CrossRef]
- Phadke, A.; Medrano, F.A.; Chu, T.; Sekharan, C.N.; Starek, M.J. Modeling Wind and Obstacle Disturbances for Effective Performance Observations and Analysis of Resilience in UAV Swarms. Aerospace 2024, 11, 237. [Google Scholar] [CrossRef]
- Du, H.; Wang, Z.; Zhang, X. EF-TTOA: Development of a UAV Path Planner and Obstacle Avoidance Control Framework for Static and Moving Obstacles. Drones 2023, 7, 359. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).