A Nonlinear Adaptive Control and Robustness Analysis for Autonomous Landing of UAVs
Abstract
1. Introduction
2. Overview
2.1. Dynamical Model
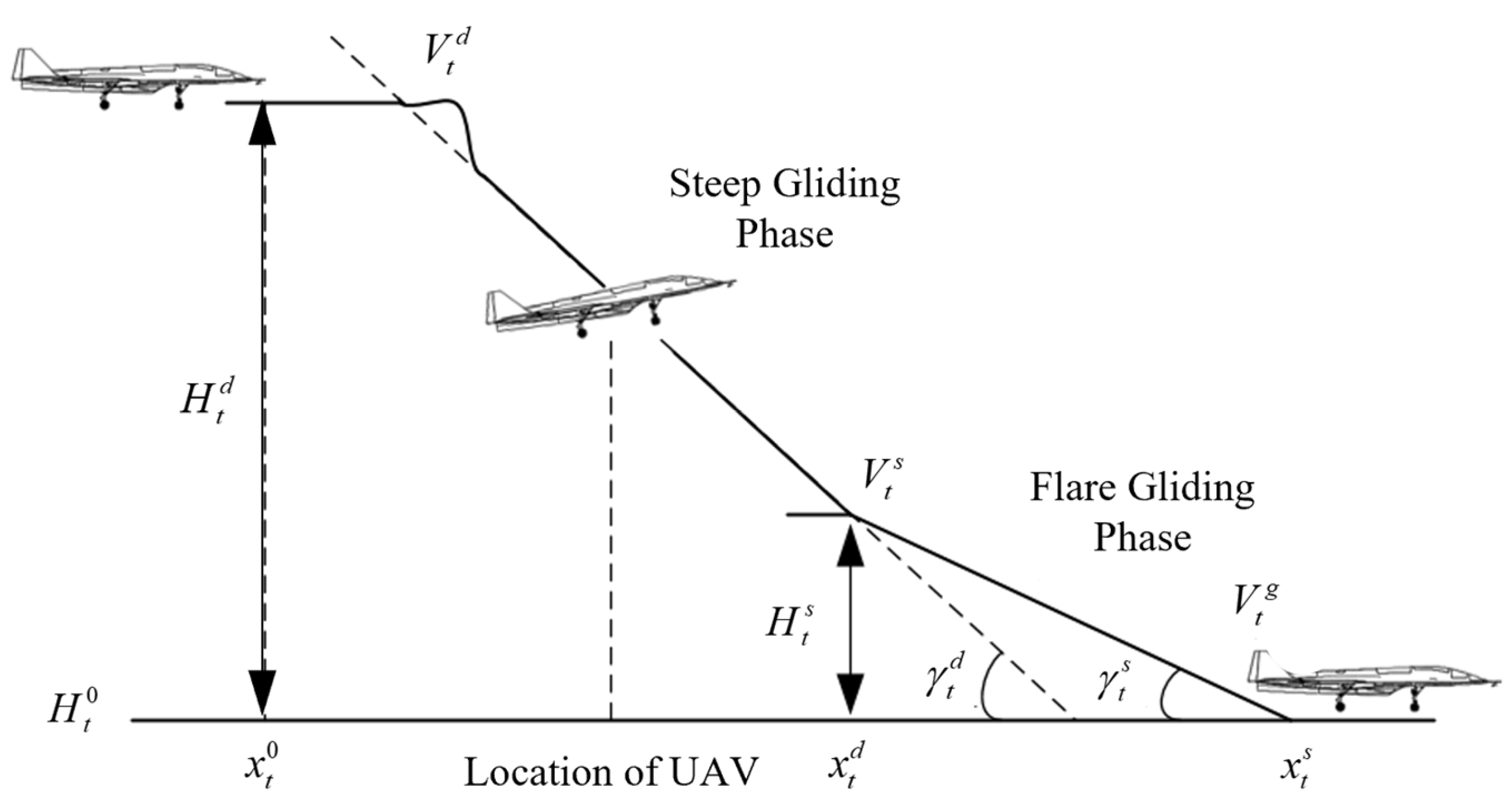
2.2. Landing Trajectory
2.3. Problem Description
3. Design of the Autonomous Landing Control
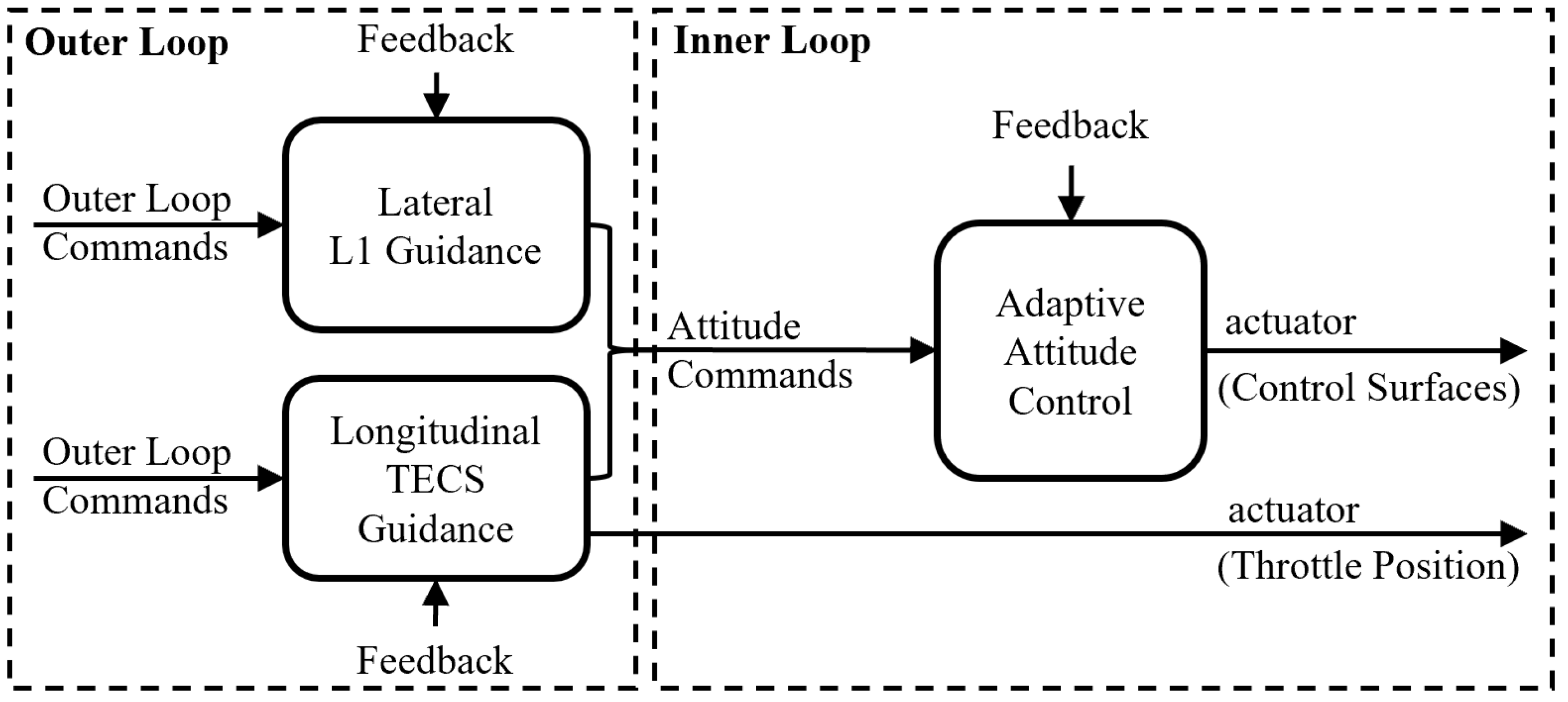
3.1. Control Structure
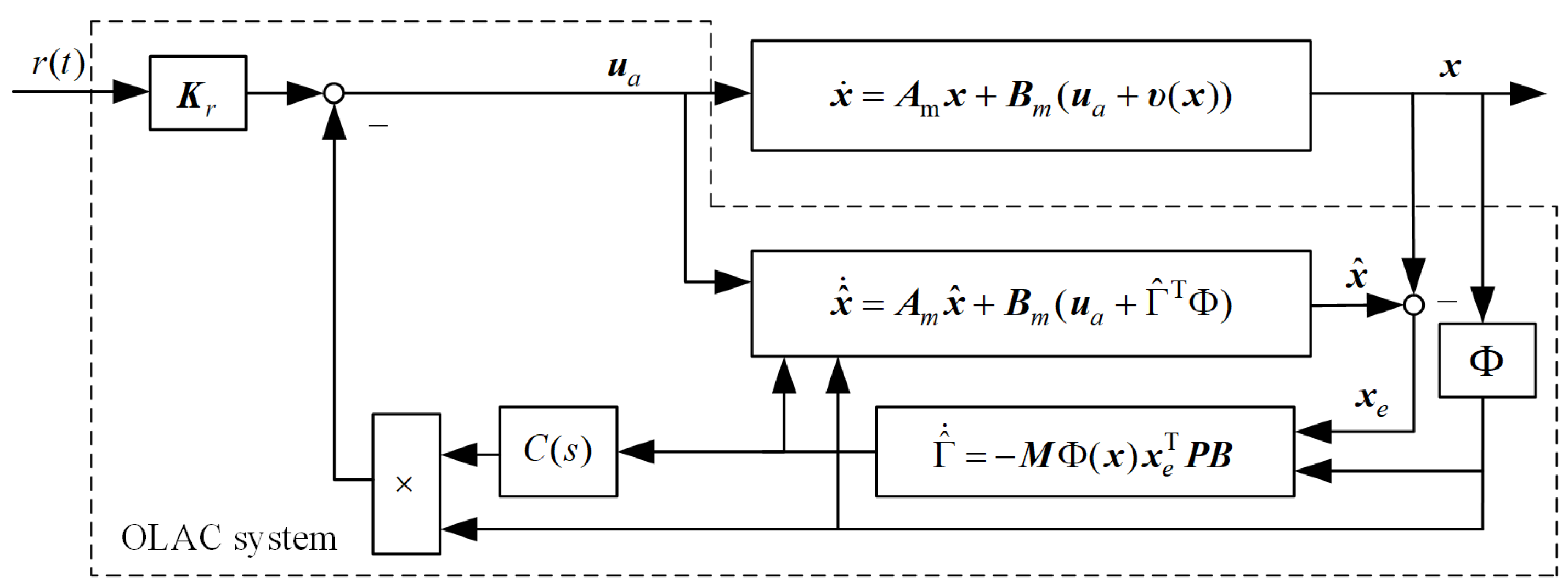
3.2. OLAC for Attitude Control
3.3. Outer Loop Control
3.3.1. Longitudinal TECS Guidance
3.3.2. Lateral L1 Guidance
4. Results
4.1. Configure for Simulation
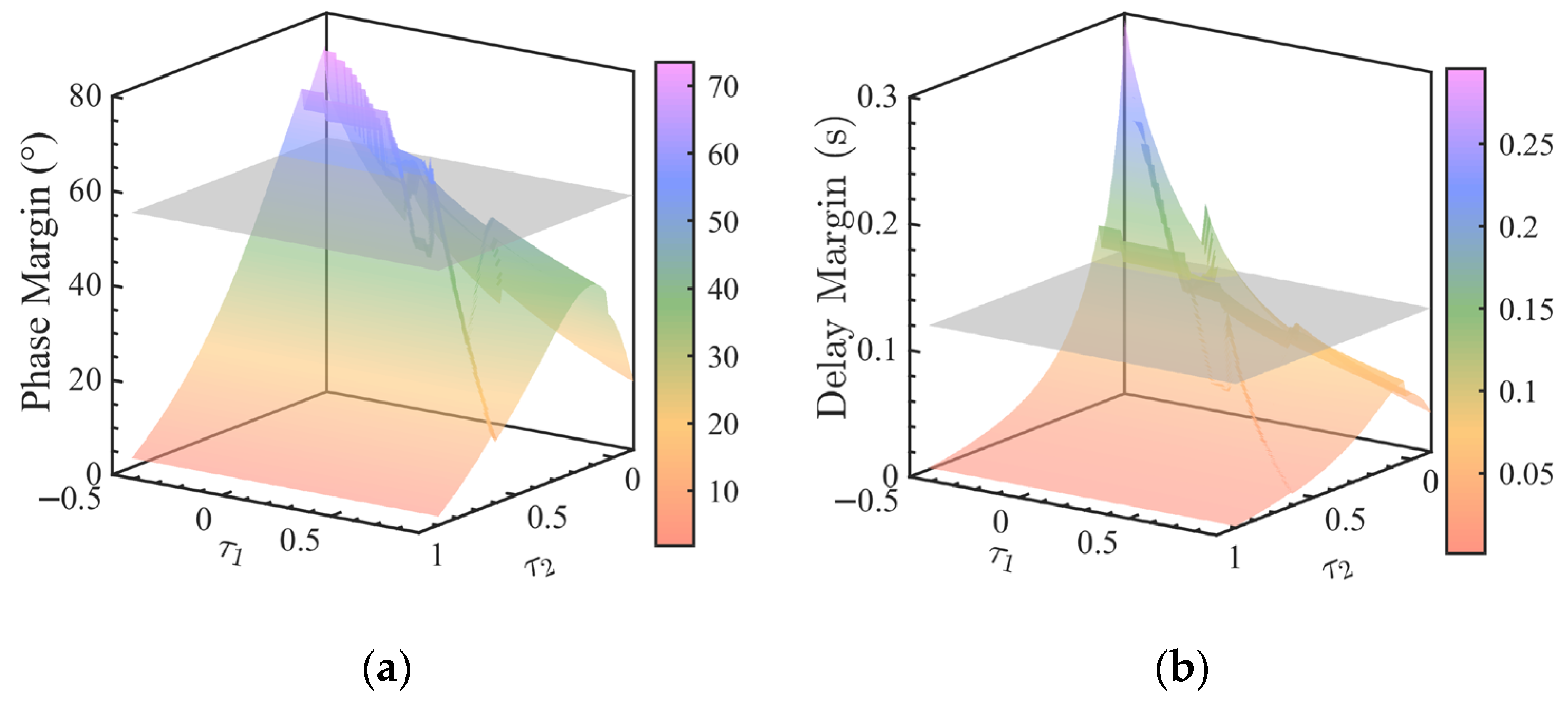
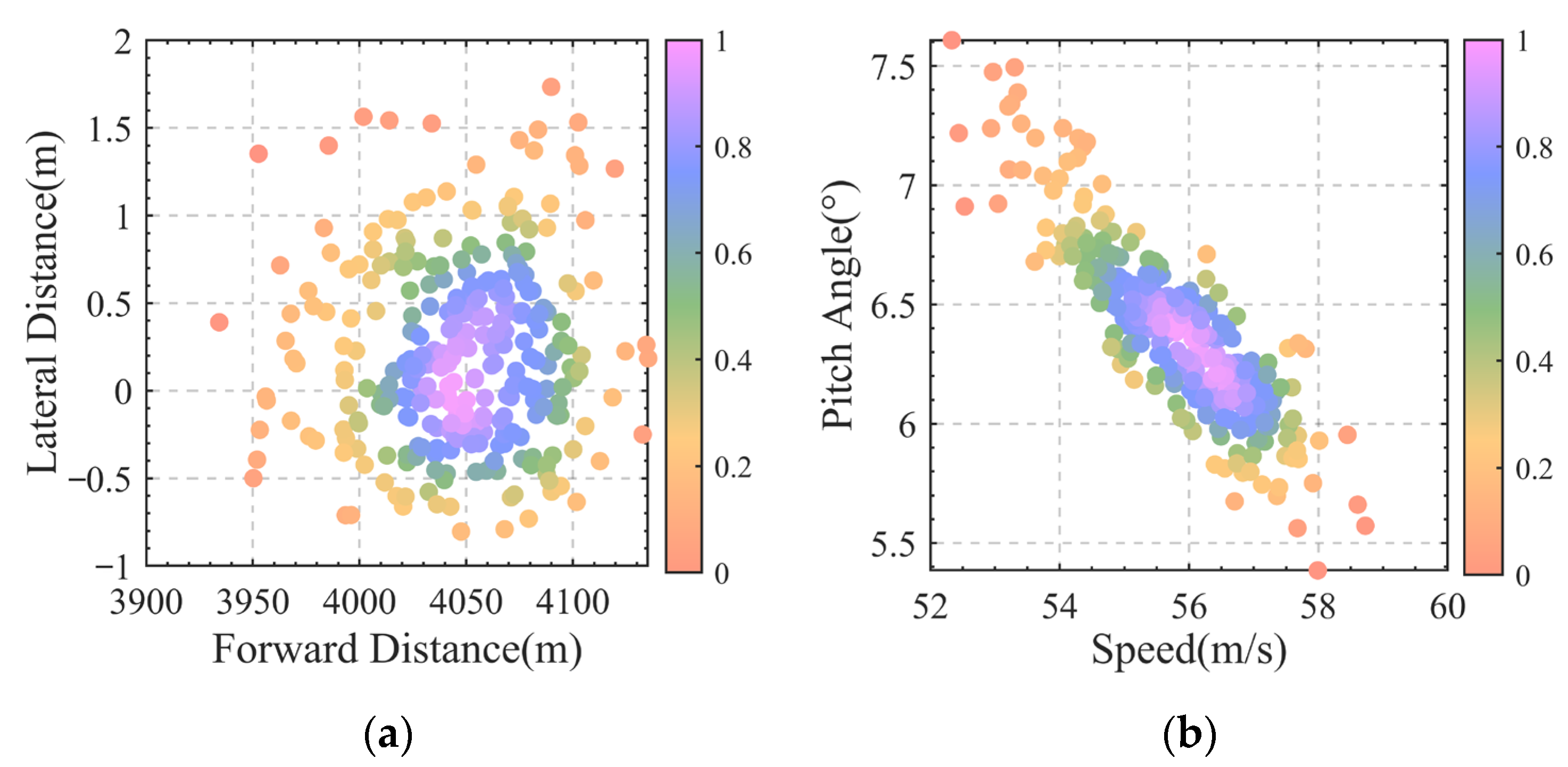
4.2. Robustness Analysis
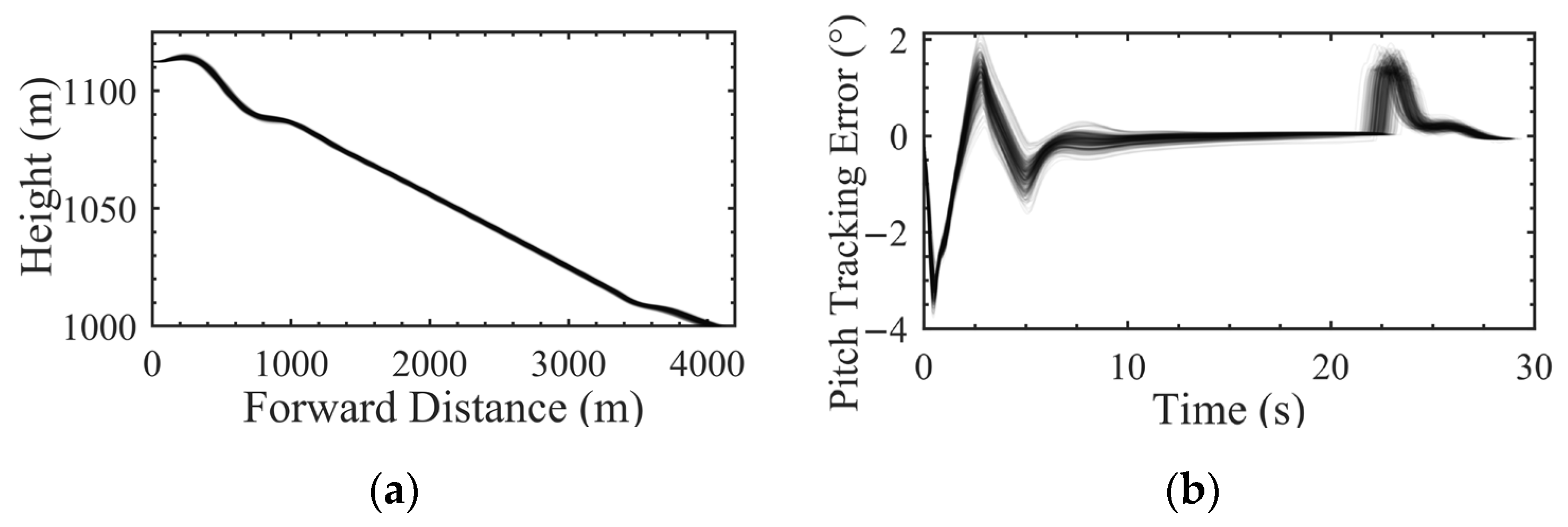
4.3. Time–Domain Simulation Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Z.T.; Gao, C.S.; Jing, W.X. Dynamic analysis and coupling control of underactuated flight vehicles with single moving mass. Aerosp. Sci. Technol. 2021, 116, 106854. [Google Scholar] [CrossRef]
- Efremov, A.V.; Efremov, E.V.; Tiaglik, M.S.; Irgaleev, I.K.; Shcherbakov, A.I.; Mbikayi, Z. Adaptive flight control system for flight safety improvement in reentry and other high-velocity vehicles. Acta Astronaut. 2023, 204, 900–911. [Google Scholar] [CrossRef]
- Barber, H.; Wall, A.; Larose, G.L.; Schajnoha, S. RPAS operations in urban airflow: Efficient modelling of representative wind speed variations along a flight path through a flow field with changing turbulence characteristics. J. Wind Eng. Ind. Aerodyn. 2024, 247, 105702. [Google Scholar] [CrossRef]
- Wang, L.; Liang, Y. Statistical analysis on global civil aviation accident investigation data. China Transp. Rev. 2021, 43, 7–12. [Google Scholar]
- Wang, L.; Ren, Y.; Wu, C.X. Effects of flare operation on landing safety: A study based on ANOVA of real flight data. Saf. Sci. 2018, 102, 14–25. [Google Scholar] [CrossRef]
- Meng, S.; Xiang, J.; Luo, Z.; Ren, Y.; Zhuang, N. A novel trajectory planning strategy for aircraft emergency landing using Gauss pseudospectral method. Control Theory Technol. 2014, 12, 393–401. [Google Scholar] [CrossRef]
- Zhang, H.; Guo, Z.; Sun, Z. Vertical control technology of autonomous landing of high-speed UAVs. J. Nanjing Univ. Aeronaut. Astronaut. 2020, 52, 881–888. [Google Scholar] [CrossRef]
- Lambregts, A. Avoiding the pitfalls in automatic landing control system design. In Proceedings of the Guidance and Control Conference, San Diego, CA, USA, 9–11 August 1982; p. 1599. [Google Scholar]
- Åström, K.J. Adaptive control. In Mathematical System Theory: The Influence of RE Kalman; Springer: Berlin/Heidelberg, Germany, 1995; pp. 437–450. [Google Scholar]
- Whitaker, H.; Kezer, A. Model reference adaptive systems to improve reliability. In Guidance and Control; Elsevier: Amsterdam, The Netherlands, 1962; pp. 499–522. [Google Scholar]
- Chen, Y.; Pérez-Arancibia, N.O. Adaptive control of a VTOL uncrewed aerial vehicle for high-performance aerobatic flight. Automatica 2024, 159, 109922. [Google Scholar] [CrossRef]
- Hovakimyan, N.; Cao, C. L1 Adaptive Control Theory: Guaranteed Robustness with Fast Adaptation; SIAM: Philadelphia, PA, USA, 2010. [Google Scholar]
- Ackerman, K.; Puig-Navarro, J.; Hovakimyan, N.; Cotting, M.C.; Duke, D.J.; Carrera, M.J.; McCaskey, N.C.; Esposito, D.; Peterson, J.M.; Tellefsen, J.R. Recovery of desired flying characteristics with an L1 adaptive control law: Flight test results on Calspan’s VSS Learjet. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 1084. [Google Scholar]
- Calise, A.J.; Yucelen, T. Adaptive loop transfer recovery. J. Guid. Control Dyn. 2012, 35, 807–815. [Google Scholar] [CrossRef]
- Singh, L.; Miotto, P.; Breger, L.S. L1 adaptive control design for improved handling of the F/A-18 class of aircraft. In Proceedings of the AIAA Guidance, Navigation and Control (GNC) Conference, Boston, MA, USA, 19–22 August 2013; p. 5236. [Google Scholar]
- Nguyen, N.; Krishnakumar, K.; Kaneshige, J.; Nespeca, P. Flight dynamics and hybrid adaptive control of damaged aircraft. J. Guid. Control Dyn. 2008, 31, 751–764. [Google Scholar] [CrossRef]
- Snyder, S.; Zhao, P.; Hovakimyan, N. Adaptive control for linear parameter-varying systems with application to a VTOL aircraft. Aerosp. Sci. Technol. 2021, 112, 106621. [Google Scholar] [CrossRef]
- Feng, Y.; Sun, Z.H.; Wu, L.N.; Wang, Y.S.; Xi, B.; Ho, W.K.; You, Y.C. Nonlinear adaptive flight control system: Performance enhancement and validation. Chin. J. Aeronaut. 2023, 36, 354–365. [Google Scholar] [CrossRef]
- He, X.K.; Wu, J.D.; Huang, Z.Y.; Hu, Z.X.; Wang, J.; Sangiovanni-Vincentelli, A.; Lv, C. Fear-Neuro-Inspired Reinforcement Learning for Safe Autonomous Driving. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 267–279. [Google Scholar] [CrossRef]
- Niu, C.; Yan, X.T.; Chen, B.Y. Control-oriented modeling of a high-aspect-ratio flying wing with coupled flight dynamics. Chin. J. Aeronaut. 2023, 36, 409–422. [Google Scholar] [CrossRef]
- Duan, X.B.; Cong, J.Q.; Dai, Z.Z.; Cheng, J.H.; Zhang, X.; Jing, J.P. Influence mechanism and quantificational evaluation of key factors affecting flutter stability of a transonic fan. Aerosp. Sci. Technol. 2023, 138, 108312. [Google Scholar] [CrossRef]
- He, X.K.; Huang, W.H.; Lv, C. Toward Trustworthy Decision-Making for Autonomous Vehicles: A Robust Reinforcement Learning Approach with Safety Guarantees. Engineering 2024, 33, 77–89. [Google Scholar] [CrossRef]
- He, X.K.; Huang, W.H.; Lv, C. Trustworthy autonomous driving via defense-aware robust reinforcement learning against worst-case observational perturbations. Transp. Res. Part C-Emerg. Technol. 2024, 163, 104632. [Google Scholar] [CrossRef]
- Das, S.S.; Shtessel, Y.; Zhang, C.; Plestan, F. Definition and analysis of stability margins for a class of nonlinear systems. Int. J. Robust Nonlinear Control 2022, 32, 1055–1074. [Google Scholar] [CrossRef]
- Das, S.S.; Shtessel, Y.; Plestan, F. Phase and gain stability margins for a class of nonlinear systems. IFAC-PapersOnLine 2018, 51, 263–268. [Google Scholar] [CrossRef]
- Beard, R.W.; McLain, T.W. Small Unmanned Aircraft: Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Stevens, B.L.; Lewis, F.L.; Johnson, E.N. Aircraft Control and Simulation: Dynamics, Controls Design, and Autonomous Systems; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Chen, B.Y.; Chen, J.B.; Liu, Y.B.; Lei, H.; Jia, S. Guardian maps based robust stability analysis with applications in flight control of hypersonic vehicles. Aerosp. Sci. Technol. 2020, 106, 106208. [Google Scholar] [CrossRef]
- Zhang, Q.-Z.; An, T.-W. A new method for designing decoupling controller of flight speed/flight path based on total energy control. Acta Aeronaut. Astronaut. Sin. 2004, 25, 389–392. [Google Scholar]
- Park, S.; Deyst, J.; How, J. A new nonlinear guidance logic for trajectory tracking. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Providence, RI, USA, 16–19 August 2004; p. 4900. [Google Scholar]
- Van Drongelen, W. Signal Processing for Neuroscientists; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]


| Modal | Eigenvalue | Damping | Period (s) |
|---|---|---|---|
| Phugoid mode | −0.0112 ± 0.106 i | 0.104 | 58.7 |
| Short-period mode | −1.26 ± 2.36 i | 0.470 | 2.35 |
| Spiral-Divergence Time Constant (s) | Roll Time Constant (s) | Dutch-Roll Mode | ||
|---|---|---|---|---|
| Eigenvalue | Damping | Period (s) | ||
| −48.5 | 0.535 | −0.738 ± 7.70 i | 0.103 | 1.26 |
| Parameters | Number | Range |
|---|---|---|
| Lift coefficient | 1 | ±10% |
| Drag coefficient | 2 | ±10% |
| Pitch moment | 3 | ±10% |
| Control surface efficiency | 4 | ±10% |
| Dynamic derivative | 5 | ±50% |
| Moment of inertia | 6 | ±20% |
| Wind speed | 7 | ±5 m/s |
| Thrust angle | 8 | ±1° |
| Distance from thrust to the gravity center | 9 | ±0.05 m |
| Center of gravity | 10 | ±0.01 m |
| Weight | 11 | ±30 kg |
| Indicators | Speed (m/s) | Pitch Angle (°) | Sink Rate (m/s) | Distance (m) |
|---|---|---|---|---|
| Range | 52.3~58.7 | 5.4~10.2 | −2.1~−1.9 | 3934~4135 |
| Mean | 55.8 | 7.8 | −2.0 | 4047 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Hu, Q.; Wu, W.; Wu, L.; Guo, Q.; Zhang, H. A Nonlinear Adaptive Control and Robustness Analysis for Autonomous Landing of UAVs. Drones 2024, 8, 587. https://doi.org/10.3390/drones8100587
Feng Y, Hu Q, Wu W, Wu L, Guo Q, Zhang H. A Nonlinear Adaptive Control and Robustness Analysis for Autonomous Landing of UAVs. Drones. 2024; 8(10):587. https://doi.org/10.3390/drones8100587
Chicago/Turabian StyleFeng, Yue, Quanwen Hu, Weihan Wu, Liaoni Wu, Qiuquan Guo, and Haitao Zhang. 2024. "A Nonlinear Adaptive Control and Robustness Analysis for Autonomous Landing of UAVs" Drones 8, no. 10: 587. https://doi.org/10.3390/drones8100587
APA StyleFeng, Y., Hu, Q., Wu, W., Wu, L., Guo, Q., & Zhang, H. (2024). A Nonlinear Adaptive Control and Robustness Analysis for Autonomous Landing of UAVs. Drones, 8(10), 587. https://doi.org/10.3390/drones8100587






