Abstract
This article presents the development of the AZTLI-NN network and the evaluation of this network as a set of evolutionary algorithms in airfoil optimization tasks. AZTLI-NN has the characteristic of predicting the aerodynamic coefficients of the airfoils in the form of images (graphs of the aerodynamic coefficients as a function of the angle of attack) from parameter vectors corresponding to the parameterization method CST. This feature allows the network to achieve good performance when generalizing the predictions of the aerodynamic coefficients, being on par with neural networks that have the aerodynamic coefficients encoded in the form of structured data, and has the ability to handle a wide range of usage airfoils in general aviation. In addition, a case of how AZTLI-NN together with an adaptive evolutionary algorithm and population size reduction methods achieve good performance in finding the airfoil that provides the highest possible endurance value is shown, so this work is considered as an option in the early stages of the design for the selection of airfoils in the design of large-endurance UAVs.
1. Introduction
Currently, in the design of unmanned aerial vehicles (UAV), great attention is still paid to aerodynamic design, in order to reduce fuel consumption (therefore reducing pollutant emissions) and increase the performance of the aircraft [1,2,3]. In medium-altitude long-endurance (MALE) and high-altitude long-endurance (HALE) UAVs mainly, high aspect ratio wing configurations are opted for to achieve better aerodynamic performance. In subsonic flight regimes, a UAV with a high aspect ratio provides high values of the endurance parameter (CL1.5/CD, CL—lift coefficient of the aircraft, CD—drag coefficient of the aircraft), which provides high flight times, ideal for tracking missions, target tracking, or as pseudo satellites [4]. To further improve the endurance of the UAV, in addition to having a wing with a high aspect ratio, it is recommended that the shape of the airfoils along the wingspan provide a high value of cl1.5/cd (cl—lift coefficient of the airfoil, cd—drag coefficient of the airfoil) [4,5,6,7].
The design of airfoils that provide a long endurance parameter is obtained through shape optimization processes, where the objective is to produce a high value of the endurance parameter with respect to a design lift coefficient. There are several approaches for the design or optimization of airfoils, among which computational fluid dynamics (CFD), wind tunnel testing, and analytical analysis stand out. From the previous approaches, CFD is currently the principal method for aerodynamic analysis because wind tunnel tests have a high cost and analytical analyses are limited to not very complex cases [8].
In the process of aerodynamic optimization of an airfoil, four aspects are taken into account: the geometric configuration of the airfoil (as a design object), the aerodynamic characteristics of the airfoil to be improved (as a design objective), the design constraints, and the optimization method [8].
Optimization methods can be generally classified into gradient-based and gradient-free optimization methods. Gradient-based approaches make use of discrete adjunct sensitivity analysis, scale approximately linearly with the number of design variables, are capable of operating with large numbers of variables and design constraints, and the computational costs they require are low over large design spaces. Meanwhile, the disadvantages are the tendency to converge on local optima, high sensitivity to the starting point, poor efficiency for nonlinear cost functions, and the need for continuous forms. Furthermore, conventional adjoint-based optimization has been shown to diverge for Large Eddy Simulations (LES) and Direct Numerical Simulation (DNS), due to the chaotic nature of the Navier–Stokes equations at high Reynolds numbers [9]. Due to its characteristics and limitations, the gradient-based approach is more appropriate at stages of detailed aerodynamic design in non-chaotic cases [8]. Gradient-free methods can be more complex to implement than gradient-based methods, but these methods have the advantage that they do not require continuity or predictability in the design space and usually have a higher probability of finding a global optimum. The most used methods with the gradient-free approach are the metaheuristic methods. It is known that these methods are able to address numerically noisy optimization problems that are difficult for gradient-based methods. Additionally, unlike gradient methods, derivatives of cost functions are not necessary. In addition, these methods do not require a predefined baseline design, nor knowledge of the design space, and usually have the ability to optimize several solutions in parallel. However, the convergence speeds are usually too slow to be able to cooperate with CFD analysis [8]. In order to improve the performance of metaheuristic algorithms in convergence, in the first instance, the use of more robust computer equipment is opted for (which implies raising the economic cost of the optimization process), or making use of methods based on surrogate models [10,11,12].
Traditional methods for training surrogate models (polynomial response surface method, the support vector regression method, the Kriging method, etc.) work with adjustable parameters, but have the limitation of not being able to operate with a large number of training data. These methods generally operate with a small amount of data in a relatively limited space [8,13]. For example, the Kriging method, which is one of the most widely used methods for the prediction of aerodynamic coefficients, in works such as the one presented in [14] has shown low performance when training to adapt in cases of big data.
Recent advances in deep learning (artificial neural networks) have provided a new option for generating surrogate models. Like the traditional surrogate methods, neural networks are not based on aerodynamic theories or physical models, and they have the advantage that they can be used for solving high-dimensional, multiscale, and nonlinear problems [15].
Currently, there are several proposals in which neural networks are used as a substitute model for obtaining aerodynamic coefficients in airfoil optimization processes using metaheuristic algorithms (mainly evolutionary algorithms). One of the main characteristics that these proposals show is that the neural networks use structured data to represent the aerodynamic coefficients. Additionally, the most used evolutionary algorithms are the standard Genetic Algorithm (GA) and the Particle Swarm Optimization (PSO) [15,16,17,18,19]. In this work, an optimization methodology based on deep learning models and evolutionary algorithms is proposed, having as its main differences: the use of a neural network that predicts the aerodynamic coefficients in the form of unstructured data (using images that represent the graphs of the aerodynamic coefficients depending on the angle of attack) and the use of a variant of the Differential Evolution (DE) algorithm, which makes use of adaptive methods of evolutionary operators and methods of Population Size Reduction (PSR). The idea of providing the predictions of the aerodynamic coefficients in the form of an image lies in the better performance that convolutional neural networks have demonstrated when predicting the distribution of the pressure coefficient of an airfoil compared to neural network architectures that use structured data [20]. The methodology that is proposed to develop neural network architecture (AZTLI-NN) is based on the methodology used by J. Wang, in which the use of a Multi-Layer Perceptron (MLP) and Variational Autoencoder (VAE) is proposed to predict images that represent the physical fields of an airfoil, from airfoil design parameters [21]. Additionally, to resolve the optimization tasks, we opted to use the Success-History based Adaptive Differential Evolution (SHADE) algorithm [22]. This variant of the DE algorithm has the advantage that it adapts its evolutionary operators as it finds better values of the mutation and crossover factors; that is, it evolves as it searches for the optimal solution to the ongoing problem. Another advantage of the SHADE algorithm is that it can be adapted to the use of PSR methods [22,23,24]. These methods help to solve part of the disadvantage of evolutionary algorithms, which is to reduce the number of objective functions to be evaluated in each generation, without having to lose performance in the search for an optimal global value. To evaluate the performance of the proposed methodology, a case study is proposed based on the need exposed at the beginning, which is to provide an airfoil with the best performance to be used in the design of MALE or HALE type UAVs, taking subsonic flight conditions as limitations and considering the airflow as viscous, turbulent, steady, and incompressible.
The present work is structured as follows: Section 2 shows the mathematical formulation of the problem, the airfoil parameterization method to be used, the methodology to create the AZTLI-NN neural network, and how to create the database to train it, and the optimization algorithm used is shown; Section 3 shows how the final configuration of the AZTLI-NN architecture was reached, and the performance of the network together with the optimization algorithm at the time of solving the case study is provided; finally, the conclusions of the work are provided.
2. Materials and Methods
2.1. Mathematical Formulation of the Case Study
Mathematically, the optimization problem of the proposed case study is the determination of the shape of an aerodynamic airfoil that produces a long endurance parameter (cl1.5/cd) with respect to a specified lift coefficient and other design constraints.
where ξ is the vector of design parameters; h(ξ) are constraint functions (equalities); g(ξ) are constraint functions (inequalities); Ω is the decision space of the design parameters.
max f1(ξ) = cl1.5/cd,
such that ha(ξ) = 0, a = 1, 2, …, A,
gb(ξ) ≤ 0, b = 1, 2, …, B,
ξ ∊ Ω.
such that ha(ξ) = 0, a = 1, 2, …, A,
gb(ξ) ≤ 0, b = 1, 2, …, B,
ξ ∊ Ω.
To provide a solution to the above optimization tasks, the following methodology is proposed:
- Selecting a method of parameterization of the airfoil; the method should allow modeling airfoils used for the design of UAVs with long-span wings;
- Selecting a robust method that allows the aerodynamic coefficients of the airfoils to be calculated. The method should take into account the viscosity and turbulence effects of the flow;
- Proposing a model based on deep learning models to predict the values of the objective functions; this is in order to speed up the process of calculating the objective functions;
- Finally, selecting the appropriate optimization algorithms for each task.
2.2. Selection of the Method of Airfoil Parameterization
For an airfoil parameterization method to be considered effective, it must possess at least 2 of the following 3 characteristics: intuition, flexibility, and representative accuracy. Intuition takes into account whether the method correlates with the physical design values of the parameters, which in turn facilitates the selection of input limits or the evaluation of the design. Flexibility is the ability of a method to adapt to complex design requirements. Finally, the representative accuracy indicates the possibility that few design variables can represent a sufficiently large aerodynamically shaped design space [25].
In works such as [26,27,28], comparisons have been made in the performance offered by various parameterization methods (for example: PARSEC, B-Splines, Bezier-PARSEC, CST, etc.), of which one of the best evaluated is the CST method, mainly due to the great flexibility offered by this method.
The CST (Class-Shape function Transformation) method was proposed by Kulfan in 2006 [29]. The upper and lower curves of the airfoil are represented as the product of the class C function(x) and a shape function S(x) plus a component indicating the thickness of the trailing edge of the airfoil Δyte (in case the trailing edge of the airfoil has no thickness this term is omitted):
The class function for defining the airfoil geometries is expressed as:
To generate an arbitrary aerodynamic shape, the Bernstein polynomial is chosen as the shape function. The definition of the Bernstein polynomial (BPn) of order n is:
where Kr,n are binomial coefficients defined as:
Then, S(x) is defined as:
The extended equations for the upper and lower curves are:
where u subscript indicates the upper curve of the airfoil; l subscript indicates the lower curve of the airfoil; Au,r and Al,r are the coefficients of the components of the Bernstein polynomial, and in turn are the design variables for numerical design optimization; x is a succession of values between 0 and 1.
The following equations are used to determine the thickness line and the sag line of the airfoil:
To be able the reconstruction of most of the existing airfoils, it is recommended to use Bernstein polynomials of order 6, which implies having a total of 14 design variables [21].
2.3. Creation of a Database of Airfoils and Their Aerodynamic Coefficients
2.3.1. Airfoils Database
To carry out the training of neural networks, airfoils used for the design of wings in general aviation (aircraft operating at subsonic and transonic speeds) were collected [30]. We considered carrying out the training of the neural network with databases of different sizes (500, 1000, and 1500 airfoils) to evaluate the performance of the network.
Since there were not enough general aviation airfoils to generate the aforementioned databases, airfoils with geometries similar to the original ones were generated using a Generative Adversarial Network (GAN). The GANs make use of a learning scheme that allows for coding of the defining features of the probability distribution, which allows for the generation of new instances similar to the original probability distribution [31,32]. The architecture of the GAN that was used for the generation of new airfoils is shown in Figure 1 and its specifications are shown in Table 1 and Table 2. Because the airfoils to be generated can be encoded as ξreal vectors (each vector consisting of the airfoil parameters CST), the generator and the discriminator can be MLP.
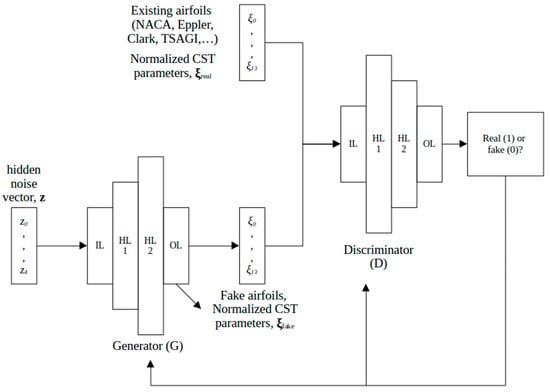
Figure 1.
Architecture of the GAN used to create new airfoils.

Table 1.
Generator (G).

Table 2.
Discriminator (D).
2.3.2. Obtaining the Aerodynamic Coefficients
As mentioned above, the methodology presented will be limited to viscous, turbulent, steady, and incompressible flow conditions. To obtain the aerodynamic coefficients of the airfoils based on the established flow conditions, it was determined that we should make use of a CFD package, specifically the OpenFOAM 11 [33] package and the GMSH mesh generator [34].
For the selection of the turbulence model, the k-ω SST model was considered since, in other works, it has demonstrated good performance when modeling published experimental data from other researchers in a wide range of angles of attack [35]. This is a two-equation turbulence model that is widely used to calculate the aerodynamic coefficients in subsonic and transonic flows. This model has the operating characteristics of the k-ω model at low Reynolds number conditions and the operating characteristics of the k-ε model at high Reynolds numbers, which allows the k-omega SST model to obtain accurate results over a wide range of flow conditions. The k-ω SST model is computationally more expensive than other two-equation models but can provide more accurate results for more complex flows [35,36,37]. OpenFOAM uses the version of the k-ω SST model exposed by Menter in [38]. The model equations and the default values that are used in OpenFOAM 11 are shown in detail in [38].
The k-ω SST model allows for the use of wall functions, which allows for the use of meshes that are not so thin next to the wall (y+ values between 10 and 100) without losing as much precision [38]. By having this tolerance in the y+ values, greater flexibility is possible when developing the mesh.
For the creation of the mesh, a control volume with a type C configuration [39] (see Figure 2a) and the use of hexahedral elements is considered (OpenFOAM does not work with two-dimensional meshes). Each mesh has 21360 hexahedral elements, which allows y+ values close to 10 when using turbulent flows with Re values between 1 million and 6 million (see Figure 2b). Figure 2c shows how the surfaces that make up the control volume are grouped so that the respective boundary conditions can then be assigned to them. The surfaces that define the airfoil are assigned the name “airfoil”. The vertical surface of the control volume located on the right is assigned the name “outlet”. The surfaces defining the arc and the lower and upper horizontal surfaces of the control volume are assigned the name “inlet”. The front and back surfaces of the control volume are assigned the name “frontBack”. Finally, the internal volume of the control volume is assigned the name “internalField”.
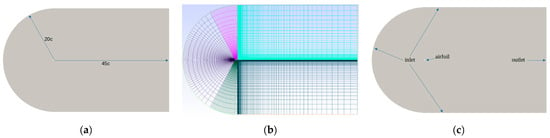
Figure 2.
(a) Dimensions of the control volume, c is the chord length of the airfoil; (b) general view of the mesh; (c) grouping of surfaces.
In the simulations, five physical fields are mainly evaluated: pressure (p) (in incompressible flow simulations, OpenFOAM uses a specific pressure, p/ρ [33]), velocity (U), turbulent kinematic viscosity (νt), turbulent kinetic energy (k), and specific turbulence dispersion velocity (ω)). Table 3 shows the boundary conditions for each physical field at each grouping and for the internalField.

Table 3.
Boundary conditions.
As the name of the fixedValue and zeroGradient boundary conditions indicates, these conditions apply fixed values and zero gradient conditions, respectively. The empty boundary condition applies to patches whose normal is aligned with geometric directions that do not constitute solution directions (this condition indicates whether the case is reduced to the analysis of one-dimensional or two-dimensional geometries). The noSlip boundary condition is used to set velocities equal to zero on solid faces [33].
For the case of “airfoil” representing solid surfaces, three wall functions were applied as boundary conditions: kqRWallFunction (for the k), omegaWallFunction (for the ω), and nutUWallFunction (for the νt), which are recommended in [3] for the calculation of the respective physical fields at flow conditions with high Reynolds numbers.
The value of ω0 at the inlet, outlet, and internalField is specified by default to work together with the wall function implemented on the airfoil wall [33,40]. The initial value of k0 is determined by the following equation [33]:
where I is the intensity of the turbulence and U∞ is the velocity of the free flow.
The indicated solver for this type of simulation is the Semi-Implicit Method for Pressure Linked Equations (SIMPLE) [41], in the version 11 of OpenFOAM this solver is called incompressibleFluid [33]. The recommended schemes for working with the SIMPLE solver and the k-ω SST turbulence model are as shown in Table 4.

Table 4.
List of schemes used [33,36].
where, φ—flux of velocity on the cell faces for constant-density flows; for example, Divergence(φ, U) indicates the advection of velocity.
To support the configuration of the simulation in OpenFOAM 11 and the mesh generated in GMSH, the aerodynamic coefficients of the NACA 0012 airfoil with different Reynolds and Mach numbers were obtained, comparing them with the coefficients obtained experimentally in the laboratories of the National Aeronautics and Space Administration of the United States [42]. At the suggestion of OpenFOAM, the comparison between the experimental results, and those obtained by CFD, the data obtained in the tests with fixed transition of the boundary layer should be used, and tests with grain sizes of 80, 120, and/or 180 are suggested [43]. The characteristics of the tests and the coefficients obtained at different Re and M are shown in detail in Table 5 and Figure 3.

Table 5.
Characteristics of the simulated flows in the NACA 0012 airfoil.
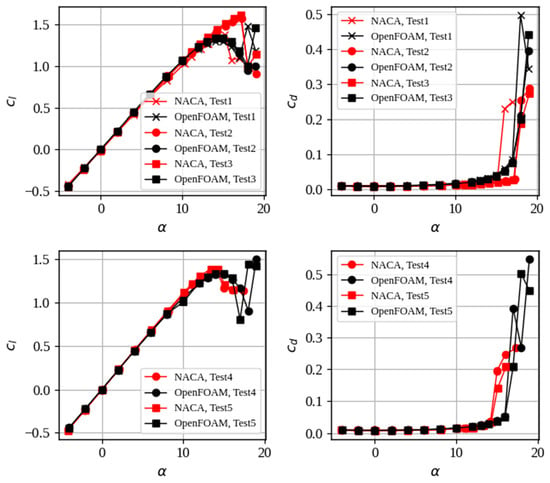
Figure 3.
Aerodynamic coefficients of the NACA 0012 airfoil.
The results obtained using OpenFOAM are suitable for generating the aerodynamic coefficient database of the airfoils. It is important to mention that in this work the CFD simulations will be limited until the maximum value of the endurance parameter is found; this because, for the moment, the evaluation of the airfoil loss region will be avoided due to its complexity.
2.3.3. Encoding of the Data
When training neural networks, it is often useful to make sure that the data are normalized at all stages of the network. Normalization helps to stabilize and accelerate the training of the network by means of a downward gradient. If the data have been scaled badly, the loss function value may become an undefined value (NaN) and the network parameters may diverge during training. Common ways to normalize data include rescaling data so that their interval is [0, 1] or that they have a mean of zero and a standard deviation of one [44,45].
For normalization of the input vectors, which are the design parameters of the airfoils, the MinMax scaler is used [46], where the transformation is given by:
where ξj,min and ξj,max are the lower and upper limits of the calculated interval of the parameter ξj and dmin and dmax are new design intervals, 0 and 1, respectively.
For the case of the output data, the aerodynamic coefficients are represented in graphs, that is, images, which can be represented in matrices (three matrices representing the RGB layers), and whose components (pixels) have values between 0 and 1 (the original ranges are between 0 and 255, but the Python (version 3.12.4) graphers also detect the range between 0 and 1 as valid) [47]. The graphs of interest are: cl vs. α, cd vs. α, and cl1.5/cd vs. α. Each graph was normalized in images of 256 × 256 pixels, the axes and labels were eliminated, and only the curve representing the values was left; the pixels that make up the curve have values of 1 (white color), while the pixels that make up the background have values of 0 (black color). Finally, the three images become layers of an RGB-encoded image (see Figure 4).
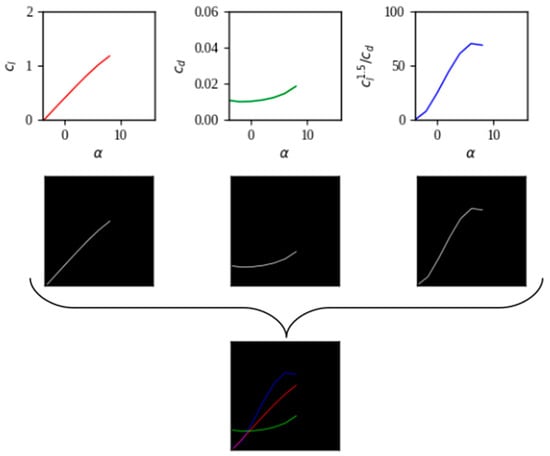
Figure 4.
Creation of the output data (output images) representing the aerodynamic coefficients of the airfoils (red for cl vs. α, green for cd vs. α and blue for cl1.5/cd vs. α).
At this stage of the research, it is only considered that the neural network is capable of identifying the maximum value of the autonomy parameter. For this reason, all the graphs show information on the aerodynamic coefficients from −4° to a value of 2° higher than the α value where the maximum value of cl1.5/cd is found.
2.4. Design of the Neural Network for the Prediction of Aerodynamic Coefficients of Airfoils
To develop a neural network that will perform prediction of the graphs of the aerodynamic coefficients of the airfoils, making use of the Wang methodology exposed in [21] was proposed. This methodology involves the development of an architectural neural network composed of an MLP and the decoder of a VAE in order to carry out image prediction with a given vector. The MLP is responsible for performing a non-linear mapping of the vector that indicates the characteristics associated with the images derived from the VAE and the normalized parameters of the airfoil parameterization method. In [21], the purpose is to obtain images that describe the velocity (Ux, and Uy) and pressure fields as a function of the vector of airfoil design parameters (the parameters of the CST method). In our case, the images do not contain information on physical fields, they contain information on the plot of the curves of the graphs of the aerodynamic coefficients of the airfoil as a function of the angle of attack.
The methodology to design this neural network consists of four steps (see Figure 5):
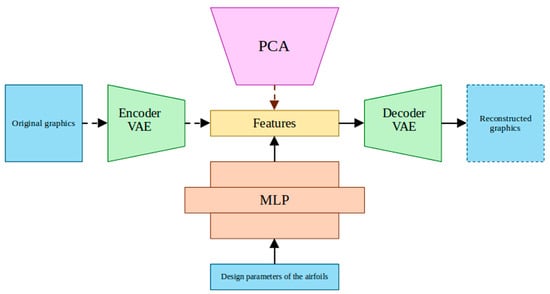
Figure 5.
Methodology of design of a neural network to predict aerodynamic coefficients [21].
- Make use of Principal Component Analysis (PCA) [46,48] to obtain a first approximation of the representative characteristics of the output images, which will allow a first estimation of the hidden vector dimension of a VAE;
- Make use of a VAE to extract representative characteristics of the output images by unsupervised reconstruction-based learning [21,49];
- An MLP is developed to construct a non-linear mapping between the parameters representing the geometry of the airfoils and the characteristics extracted by the VAE [21];
- Finally, once the MLP architecture is defined, it is connected to the VAE decoder to obtain a neural network that is capable of predicting the graphs of the aerodynamic coefficients of an aerodynamic airfoil from a vector of design parameters (see Figure 6).
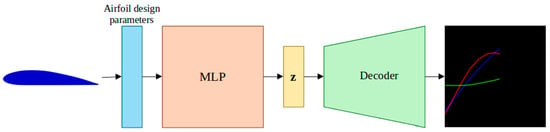 Figure 6. Final architecture of the neural network AZTLI-NN used to predict aerodynamic coefficients of the airfoils.
Figure 6. Final architecture of the neural network AZTLI-NN used to predict aerodynamic coefficients of the airfoils.
2.4.1. VAE Configuration
A VAE is a model consisting of an encoder and a decoder (see Figure 7). The encoder, also known as the output model or the recognition model, approximates the posterior distribution of the hidden variables of the decoder. The decoder is a deep hidden variable model and is a variation of the generative model. Both components, the encoder and the decoder, are directional graphic models that are totally or partially parameterized by deep neural networks [49].
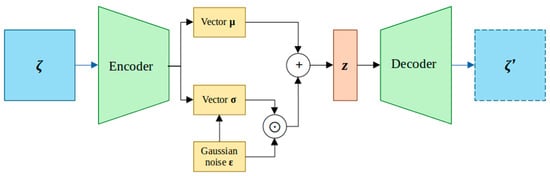
Figure 7.
General architecture of a VAE.
The proposed configuration for the encoder is composed of 6 convolutional layers and 6 MaxPooling layers (see Figure 8). After several blocks of convolutional residuals, the mean and standard deviation are extracted for each input image and the z vector is determined. The first 5 convolutional layers use the rectified linear unit (ReLU) activation function and the sixth layer uses the sigmoid activation function.
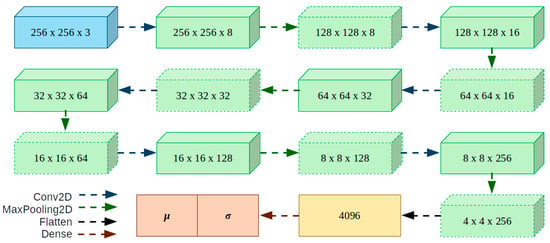
Figure 8.
Architecture of the encoder.
The architecture of the decoder is similar to that of the encoder, as shown in Figure 9, with the only difference being that the convolutional layers are replaced by deconvolutive layers (or transposed convolution layer) and the layers of the MaxPooling operation are replaced by UpSamplin layers. The first five deconvolutive layers use the ReLU activation function and the last layer uses the sigmoid activation function.
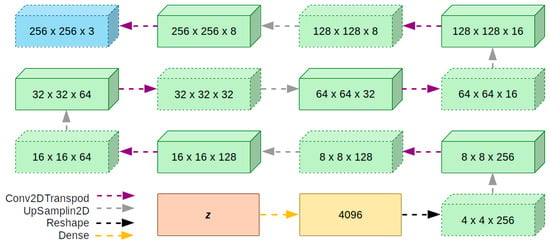
Figure 9.
Architecture of the decoder.
The loss function to be minimized has the form of:
where BCE—binary cross entropy recovery loss function is used to minimize the differences between the generated image and the original image, and is expressed as follows [47]:
and KL—Kullback–Leiber divergence. KL is used to reduce the gap between the prior and posterior distributions, i.e.,
where: ζ—input information; ζ′—reconstructed form of ζ; z—latent vector (z = μ + σ ε); q(z|ζ) and p(ζ|z)—learned distributions. We assume that the posterior q(z|ζ) of the m latent variables is a diagonal Gaussian with mean μ and standard deviation σ, and the prior p(ζ|z) is a normal Gaussian with μ = 0 and σ = 1 [21,49].
To determine the performance in image reconstruction by the VAE, the mean absolute error (MAE) metric is used. The MAE describes the difference between the output data and the original input data [21]:
where nP is the number of pixels of the images; ζ′p is the value of the pixel p of the reconstructed image; ζp is the value of the pixel p of the real image.
Having the reconstructed images of the graphs of the aerodynamic coefficients, it is necessary to evaluate how efficient these images are to perform the readings of each coefficient in comparison to the original graphs. For this case, the use of the determination factor (R2) as a metric is proposed. R2 measures the fraction of variance of a dependent variable explained by independent variables. The values of R2 vary between 0 and 1; the closer the values of R2 are to 1, the better the fit of the model [19,50,51].
2.4.2. MLP Configuration
The MLP is in charge of performing a non-linear mapping of the vector that indicates the characteristics associated with the graphs derived from the VAE and the normalized parameters of the airfoil parameterization method. The loss function to be minimized is the mean square error (MSE) between the difference between the z vectors provided by the encoder and the z′ vectors predicted by the MLP [21]:
The proposed MLP architecture has an input layer with j neurons (corresponding to the number of parameters of the airfoil parameterization method), an output layer with m neurons (corresponding to the size of the z vector), and three hidden layers. To determine the number of neurons and the activation function of each hidden layer, an optimization algorithm is used, where the optimization task is defined as:
In this case, η represents the vector formed by the parameters n1, n2, and n3, representing the number of neurons in each of the hidden layers, respectively, and by a1, a2, and a3, representing the activation function in each hidden layer. The optimization algorithm chosen to solve this optimization task is the Integer Encoding Differential Evolution (IEDE) [50]. IEDE is a version of the standard DE algorithm where only the mutation operator is modified so that it can operate with integer type values [52].
min f1(η) = MSE(z’, z),
such that η ∊ Ω.
such that η ∊ Ω.
2.5. Optimization Algorithms
The variant of the SHADE algorithm that was used in this work incorporates the Continuous Adaptive Population Reduction (CAPR) [53] method. The performance of the CAPR-SHADE algorithm has been tested in aerodynamic optimization tasks [54,55].
The CAPR-SHADE algorithm as well as the standard DE algorithm are created to be used in unconstrained optimization tasks. A penalty function is used to convert a constrained optimization task to an unconstrained one. The penalty function is expressed as [56]:
where
where U* is the minimum value of the values of the objective functions of those vectors that satisfied the constraints. This parameter is not updated until a feasible solution has been found. R is a penalty parameter that allows us to regularize the obtained values of ψ(ξ) and U*. The constraints expressed as equalities (h(ξ)) have to be reformulated as inequalities (g(ξ)).
Using the penalty function, optimization tasks as expressed in (1) are expressed as:
min L(ξ),
such that ξ ∊ Ω.
such that ξ ∊ Ω.
3. Results and Discussion
The calculations that were performed in each of the stages were performed with a computer with the following characteristics:
- Motherboard model—Gigabyte B760 GAMING X;
- Processor—13th Gen Intel® CoreTM i5-13400f x 12;
- RAM—64 GB;
- GPU—NVIDIA GeForce RTX 4090;
- OS—Ubuntu 22.04.4 LTS.
3.1. Creation of the Databases
In the first instance, the search of general aviation airfoils was carried out in [30], collecting 322 airfoils, corresponding to airfoil families such as NACA, Eppler, TSAGI, etc. The coordinates of these airfoils were obtained from the airfoil database of the University of Illinois at Urbana-Champaign (UIUC) [57].
The next step was to reconstruct these airfoils making use of the CST method. To determine the value of each of the parameters of the method, an optimization algorithm was used. The objective is to find the values of the parameters that provide the smallest geometric deviation, comparing the reconstructed and the real aerodynamic airfoils [26]. The value of the geometric deviation is obtained by the L2 error norm:
where ytar is the set of heights of the original points of the target airfoil; y is the set of heights of the reconstructed points; P is the number of points that make up the geometry of the airfoil.
At this stage it, was considered that each of the 14 parameters has a design range of −0.5 to 0.5. Some examples of airfoil reconstructions using the CST method are shown in Figure 10. The graphs show the local deviations in the upper curve and in the lower curve of the airfoil. The values of the parameters of the CST method for each of the airfoils are shown in Table 6.
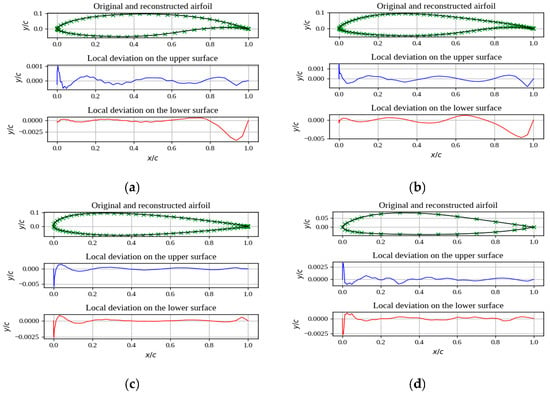
Figure 10.
Airfoils reconstructed using the CST method (black), original coordinates are shown in green. The blue graph indicates the local deviations on the upper surface, while the red one indicates the local deviations on the lower surface. (a) Eppler 407 airfoil, (b) FX 61140 airfoil, (c) NACA 23016 airfoil, and (d) TSAGI 12 airfoil.

Table 6.
CST parameters for Eppler 407, FX 61140, NACA 23106, and TSAGI 12 airfoils.
By obtaining the parameters of each of the reconstructed airfoils, the design space could be redefined. The 14 parameters of the CST method with their respective design intervals are shown in Table 7; these intervals are the ones that will be used in the optimization processes and creation of new geometries with the help of a GAN.

Table 7.
Design intervals of the parameters of the CST method.
From the reconstructions of the 322 real airfoils with the CST method, this information is used for the creation of new geometries and to be able to have the previously established quantities (500, 1000, and 1500 airfoils). Figure 11 shows examples of airfoils created with the proposed GAN making use of the information of the 322 airfoils extracted from [30].

Figure 11.
Sample of airfoils obtained with a GAN using information from real airfoils.
3.2. Development of AZTLI-NN
3.2.1. Approximation of the Representative Features of the Output Images
Figure 12, Figure 13 and Figure 14 show four tests with different numbers of PC (5, 10, 15, 20) applied to the three layers of one of the output images. From 10 PC, the shape of the curves can be recreated, only having variation in the color saturation in the pixels, which is not of great importance for reading values.
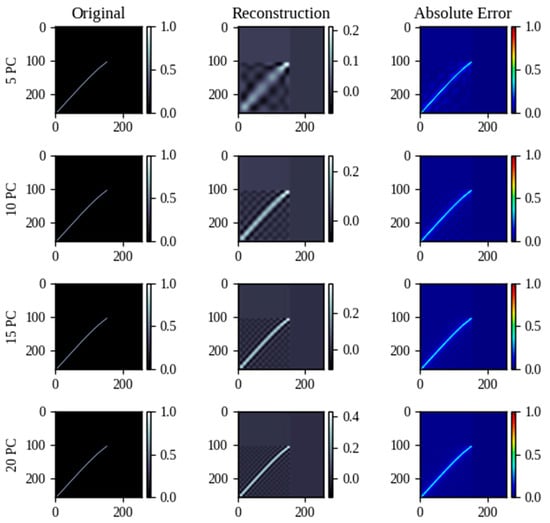
Figure 12.
Reconstruction of the graph of cl vs. α by PCA using different numbers of PCs.
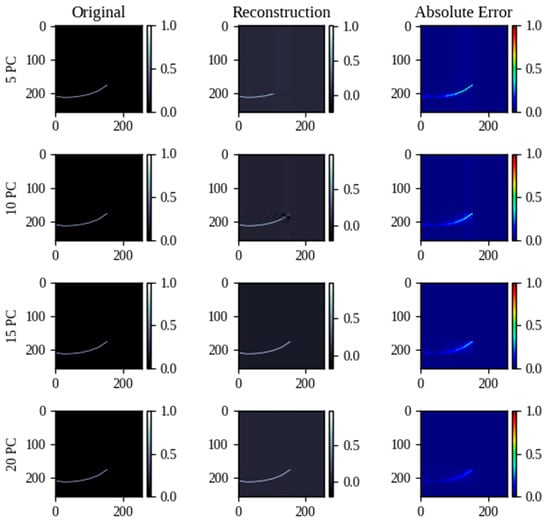
Figure 13.
Reconstruction of the graph of cd vs. α by PCA using different numbers of PCs.
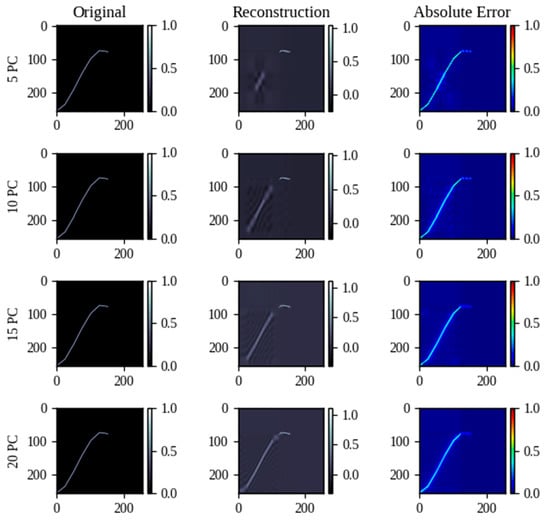
Figure 14.
Reconstruction of the graph of cl1.5/cd vs. α by PCA using different numbers of PCs.
3.2.2. Evaluation of the VAE
In the PCA tests it was determined that at least 10 main components are required to be able to reconstruct the images. A VEA being a more robust model requires fewer components; for this reason, five different sizes of the z vector will be tested, 5, 6, 7, 8, and 9. Considering a database of 500 airfoils, 90% of the data were selected for the VAE training and the remaining 10% were used for testing. For the training of the VAE, 300 epochs were used, with a batch size of 20, and the optimizer used was ADAM, making use of a learning rate schedule (with an exponential decay). The results of the reconstruction of the images in both stages are shown in Figure 15 and Figure 16.
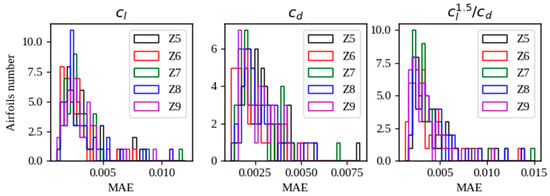
Figure 15.
Statistical distribution of MAE in the reconstruction of graphs with a VAE. Stage of training.
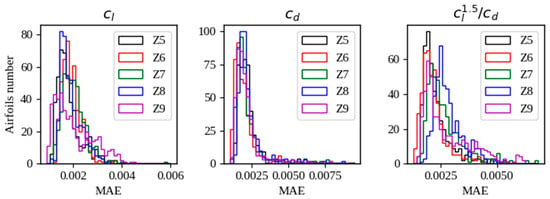
Figure 16.
Statistical distribution of MAE in the reconstruction of graphs with a VAE. Stage of testing.
In the testing stage, the generalization capacity of a neural network is defined. The average MAE values of the test data for each z size are shown in Table 8. The best values are highlighted in green. The z vectors of size 6 and 9 come to generalize in a similar way; in this case, the vector of smaller size is chosen.

Table 8.
Average values of MAE in the reconstruction of graphs in the VAE testing stage. Best results highlighted in green.
An example of graph reconstruction using the VAE with a 6-component z vector is shown in Figure 17. Figure 18 shows a linear fit analysis between the read values of the aerodynamic coefficients obtained from the real graphs (those obtained from the CFD simulations) and the graphs reconstructed by the VAE. The values of R2 are indicated for each case, the ideal fit line is indicated (when the predicted values (P) are equal to the target values (T)), as well as the line of the best linear fit (BLF) of the model.
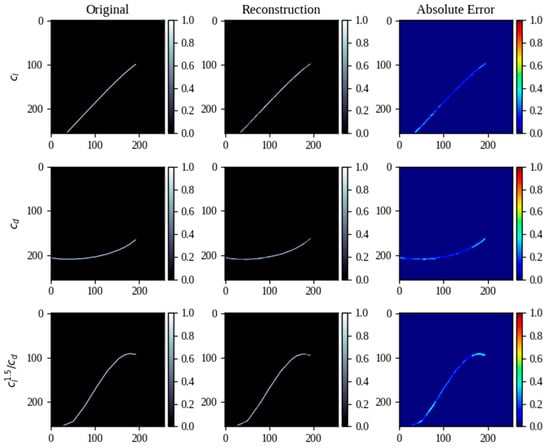
Figure 17.
Example of graph reconstruction of the aerodynamic coefficients of an airfoil by using a VAE.
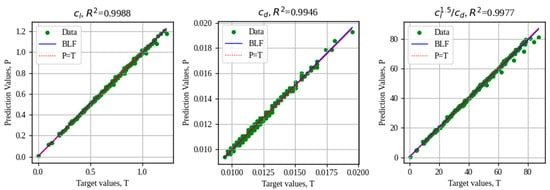
Figure 18.
Analysis of the performance in the reading of aerodynamic coefficients in the graphs reconstructed by the VAE.
3.2.3. MLP Architecture and Performance Evaluation of AZTLI-NN
To solve the optimization task shown in (18), the decision space Ω shown in Table 9 is considered.

Table 9.
Parameters and their design ranges to optimize MLP hyperparameters.
In the optimization task, the output layer has a sigmoidal activation function, the optimizer is ADAM, out of 90% of the data assigned for training, 10% is assigned for validation during training, and 500 epochs were considered. The IEDE algorithm has a F = 0.85, a population size of 30, and 30 generations were evaluated. The optimal architecture is shown in Figure 19. In the input layer, there are 14 neurons, corresponding to the parameters of the CST method, the first hidden layer has 512 neurons, the second has 256, and the third layer has 128; finally, the output layer has six neurons corresponding to the size of the z vector of the VAE.
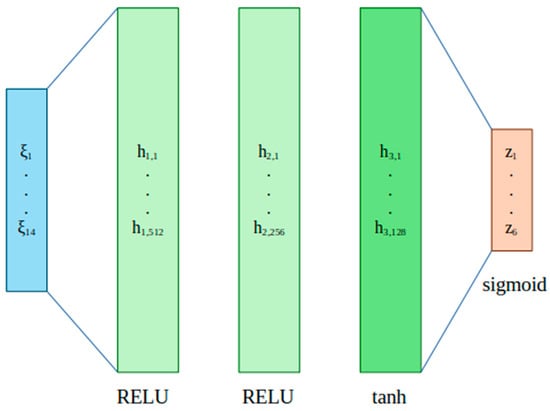
Figure 19.
The Architecture of MLP.
The MLP architecture is assembled with the VAE decoder, and this composite architecture is called AZTLI-NN. The results of R2 of the coefficient reading with the graphs predicted by the AZTLI-NN assembled network are shown in Figure 20.
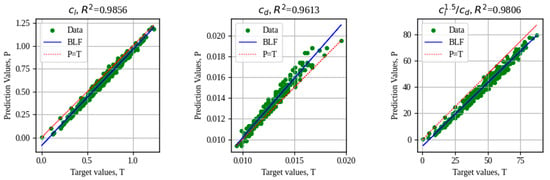
Figure 20.
Performance analysis of prediction of aerodynamic coefficients using AZTLI-NN (database size = 500).
Currently, it can be considered that the neural network achieves a good generalization, but at present, many of the neural networks dedicated to the prediction of aerodynamic coefficients achieve values of R2 ~ 0.99. To analyze whether it is possible to increase the accuracy of the neural network, the network is cross-linked with larger databases. Network performance analysis using databases of sizes 1000 and 1500 are shown in Figure 21 and Figure 22, respectively.
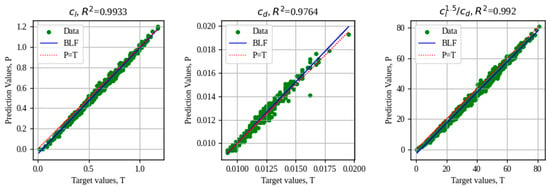
Figure 21.
Performance analysis of prediction of aerodynamic coefficients using AZTLI-NN (database size = 1000).
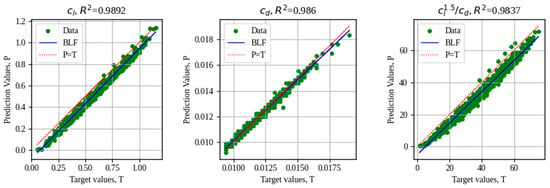
Figure 22.
Performance analysis of prediction of aerodynamic coefficients using AZTLI-NN (database size = 1500).
As can be seen in Figure 21 and Figure 22, there was an improvement with increasing the number of data. Using 1000 data, it is observed that the network performance improves by predicting the values of all the coefficients, especially with the R2 values of cl and cl1.5/cd. When using 1500 data, the R2 values in each analysis are similar, but this slightly decreases the accuracy in the predictions of cl and cl1.5/cd. Because in the case study analyzed in this article, obtaining the value of cl1.5/cd is given great importance, it was determined that the neural network trained with 1000 data is suitable to be used in the optimization process.
A comparison between AZTLI-NN and two other neural networks using structured data to represent the aerodynamic coefficients is shown in Table 10. An MLP capable of predicting three aerodynamic coefficients at the same time is shown in [51]. To train the network, 1680 data corresponding only to airfoils of the 4- and 5-digit NACA series were required. Meanwhile, in [58], a Deep Feedforward Neural Network (DFNN) is shown that only predicts one aerodynamic coefficient at a time; that is, you have a configuration of the DFNN to predict the cl and another for the cd of the airfoils. Airfoils based on the geometry of the FX63-137 airfoil were used for their training.

Table 10.
Performance analysis of the prediction of aerodynamic coefficients of different neural networks (values of R2).
Based on the results shown in Table 10, it can be said that the proposed neural network resembles the performance of other current neural networks, with the advantage that our network provides semi-complete graphs and that it covers a greater diversity of types of airfoils.
From the airfoils used for testing, information was sought about experimental tests with similar characteristics to which the neural network was trained. Information on experimental tests of the FX 66-S-161 airfoil was found in [59]. The experimental tests were developed in a laminar wind tunnel with Re = 1.5 × 106 and M = 0.25. The aerodynamic coefficients corresponding to the FX 66-S-161 airfoil are shown in Figure 23.
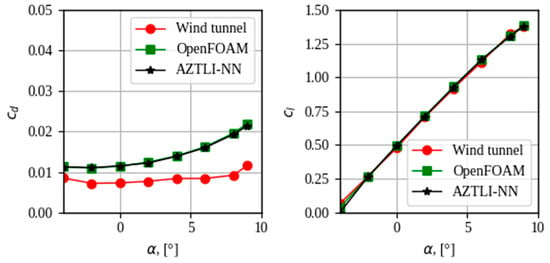
Figure 23.
Aerodynamic coefficients of the FX 66-S-161 airfoil obtained with a laminar wind tunnel, with OpenFOAM, and with AZTLI-NN.
3.3. Case Study
The optimization case that is proposed is the following: during the conceptual design process of a UAV, it is necessary to find an aerodynamic airfoil that has the following characteristics: design lift coefficient, cl,d = 0.59; minimum maximum thickness of the airfoil, yt,min = 11%; maximum permissible angle of attack, αmax = 4°. The flow conditions are: Re = 1.5 × 106 and M = 0.15. To solve the optimization task, the use of AZTLI-NN in conjunction with different evolutionary algorithms was tested. Three variants of the DE algorithm were evaluated, the standard DE/current-to-best version, the SHADE version proposed by Tanabe in [23], and the modified version of SHADE proposed by us (see Appendix A). All algorithms were evaluated with different initial population sizes (10|ξ|, 20|ξ|, and 50|ξ|) considering 200 generations. In the case of L-SHADE and CARP-SHADE, a minimum population (NPmin) of four was considered. Each test was evaluated five times to analyze the repeatability of the algorithm. The results of this series of tests are shown in Table 11, Table 12 and Table 13.

Table 11.
Repeatability analysis of the values obtained by the standard DE algorithm. Best result highlighted in green.

Table 12.
Repeatability analysis of the values obtained by the L-SHADE algorithm. Best result highlighted in green.

Table 13.
Repeatability analysis of the values obtained by the CAPR-SHADE algorithm. Best result highlighted in green.
The results presented in the tables showed that the standard DE version showed the lowest performance, both in computing time and in the ability to find the global maximum. The L-SHADE algorithm showed great performance in computing time, especially when working with large population sizes. However, the results did not show good repeatability when finding the global optimum. The proposed algorithm, CAPR-SHADE, maintained a similar performance to the standard version at computation time, but it was the one that best maintained repeatability by finding the best global optimum of all the tested cases, the initial population size of 50|ξ| being the best option for there to be the global optimum. In the previous tables, those cases that provided the airfoil with the best endurance parameter and with the lowest maximum thickness were highlighted in green. The geometries of these airfoils are shown in Figure 24 and their respective CST parameters are indicated in Table 14.

Figure 24.
Better airfoils obtained in the optimization tests. Red—standard DE, green—L-SHADE, blue—CAPR-SHADE.

Table 14.
CST parameters of the optimal airfoils obtained by different evolutionary algorithms.
Finally, the previous airfoils were simulated with OpenFOAM using the angle of attack with which the airfoil offers the best endurance, depending on the restrictions provided. The aerodynamic coefficients obtained using AZTLI-NN and OpenFOAM are shown in Table 15.

Table 15.
Comparison of the aerodynamic coefficients of optimal airfoils obtained using OpenFOAM and AZTLI-NN.
As can be seen, the aerodynamic coefficients obtained with the proposed neural network offer similar results to those provided by a simulation performed in CFD. In the case of the lift coefficient, there is an error of approximately 3.4%, in the drag coefficient, of 2.9%, and for the endurance parameter, of 4.1%.
4. Conclusions
In the present work, an alternative was provided to carry out the resolution of airfoil optimization tasks. A neural network architecture, AZTLI-NN, was presented, which is composed of a multilayer perceptron and the decoder of a variational autoencoder. The main feature of this network is that it presents the predictions of the aerodynamic coefficients in the form of images (graphs of the aerodynamic coefficients as a function of the angle of attack). AZTLI-NN showed good generalization when making predictions of the aerodynamic coefficients, similar to that shown by current neural networks that use structured data to describe the aerodynamic coefficients, but having the advantage that AZTLI-NN handles a greater diversity of airfoil geometries and that, with a prediction, provides the user with information on the aerodynamic coefficients of the airfoil at various angles of attack.
One of the objectives of having developed AZTLI-NN is that this network can be used as a surrogate model for CFD in optimization processes, where evolutionary algorithms are used. To evaluate the performance of AZTLI-NN together with evolutionary algorithms in optimization processes, a case study was proposed in which it was necessary to obtain airfoils that provide a high endurance parameter depending on the design conditions. Three evolutionary algorithms were evaluated, the standard version of Differential Evolution, the SHADE version with a linear population reduction method, and a variant proposed by us of SHADE changing the linear population reduction method by the CAPR method. The results of the tests showed that AZTLI-NN works well together with the CAPR-SHADE algorithm, providing repeatability in the results, regardless of the initial population size.
At this point of our research, it is considered that AZTLI-NN is in the early stages of development since the neural network is trained to be used in a very specific optimization task. At the moment, AZTLI-NN can only provide predictions of graphs of cl, cd, and cl1.5/cd vs. α, which in turn are conditioned to viscous, turbulent, steady, and incompressible flows. Additionally, the range of angles of attack is limited to finding the maximum value of cl1.5/cd of the airfoil; the database still needs to be developed so that AZTLI-NN can predict areas close to the airfoil stall. It is necessary to carry out further studies to analyze the reliability of the resolution of the images used for the description of the graphs. Another point to improve in the future is that AZTLI-NN will have the ability to predict graphs that describe the behavior of the airfoil under transonic flow conditions. However, at the moment, as well as AZTLI-NN is configured and with the use of the CAPR-SHADE algorithm, they are a good tool for the selection of airfoils for the design of large-endurance UAVs, specifically in the early stages of design.
Author Contributions
Conceptualization, J.G.Q.P.; methodology, J.G.Q.P.; software, J.G.Q.P.; validation, J.G.Q.P.; formal analysis, J.G.Q.P.; investigation, J.G.Q.P.; resources, E.K. and O.L.; data curation, J.G.Q.P.; writing—original draft preparation, J.G.Q.P.; writing—review and editing, V.S., E.M., E.K., and O.L.; visualization, V.S. and E.K.; supervision, V.S., E.M., E.K., and O.L.; project administration, J.G.Q.P.; funding acquisition, E.M. and E.K. All authors have read and agreed to the published version of the manuscript.
Funding
Analytical Center for the Government of the Russian Federation (agreement identifier 000000D730324P540002, grant No 70-2023-001317 dated 28 December 2023).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author/s, J.G.Q.P.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analysis, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A
Selection of mutation (F) and crossover (CR) operators:
where randni(M, 0.1) and randci(M, 0.1) are randomly selected values of normal and Cauchy distributions, respectively, with mean of historical memory M (MCR or MF) and variance of 0.1; the index ri from [1, H].
The mutation operator (current-to-pbest/1):
the individual ξpbest,g is randomly selected from the upper p·NP members in the g-th generation (p ∊ [0, 1]). Fi is the parameter F used by individual ξi. In case any component j of the mutated vectors vi is out of the decision range, the value will be adjusted to the nearest extreme value.
The crossover operator:
where ui is a trial vector.
The selection operator:
| Algorithm A1. Memory update algorithm in SHADE [2] | |
| Input: SCR, SF, MCR,k,g, MF,k,g, k, H | |
| Output: MCR,k,g+1, MF,k,g+1, k | |
| 1 | if SCR ≠ ∅ and SF ≠ ∅ then |
| 2 | if MCR,k,g = −1 or max(SCR) = 0 then |
| 3 | MCR,k,g+1 = −1; |
| 4 | else |
| 5 | MCR,k,g+1 = meanWL(SCR); |
| 6 | MF,k,g+1 = meanWL(SF); |
| 7 | k++; |
| 8 | if k > H then |
| 9 | k = 1; |
| 10 | else |
| 11 | MCR,k,g+1 = MCR,k,g; |
| 12 | MF,k,g+1 = MF,k,g; |
| 13 | return Output |
The index k determines the position in the memory to be updated. The weighted mean of Lehmer mean WL(S) is calculated as follows:
The amount of improvement ∆fm is used to influence the adaptation parameter S.
CAPR method:
where
where favg indicates the averaging of the values of the objective functions of all individuals in each generation.
| Algorithm A2. CAPR-SHADE + GAN + AZTLI-NN algorithm [60] | |
| Inputs: Ω, cy,d, αmax, yt,min M, Re, G, NP, NPmin, U*, γ, H, p | |
| Outputs: L(ξopt), ξopt | |
| 1 | Download the parameter normalization model; |
| 2 | Download AZTLI-NN architecture and Weights; |
| 3 | g = 1; |
| 4 | Initialize the Pg aggregate using GAN; |
| 5 | Normalize the parameters of the CST vectors of the initial population;; |
| 6 | Create images of graphs of aerodynamic coefficients using AZTLI-NN; |
| 7 | for i = 1 to NP do |
| 8 | Divide the images into three layers; |
| 9 | Get αi(cl,d) with the graph (cl vs. α)i; |
| 10 | Get (αi(cl,d)) with the graph (cl1.5/cd vs. α)i; |
| 11 | Apply (A7), to obtain max(yt(x))i; |
| 12 | Get ψ(ξg) with (20); |
| 13 | Get L(ξg) with (19); |
| 14 | Update U*; |
| 15 | mean(L(ξg))→ Lavg; |
| 16 | Assign values of 0,5 in memories MCR and MF; |
| 17 | Create A = ∅, |A| = round(2,6NP); |
| 18 | k = 1; |
| 19 | for g = 2 to G do |
| 20 | SCR = ∅, SF = ∅, Δf = ∅; |
| 21 | for i = 1 to NP do |
| 22 | ri = choose randomly from [1, H]; |
| 23 | Get CRi,g with (A1); |
| 24 | Get Fi,g with (A2); |
| 25 | Get the mutated vector vi,g with(A3); |
| 26 | for j = 1 to |ξ| do |
| 27 | Get the component of the trial vector uj,i,g with (A4); |
| 28 | Create images of graphs of aerodynamic coefficients of P(ug) using AZTLI-NN; |
| 29 | for i = 1 to NP do |
| 30 | Divide the images into three layers (from ug); |
| 31 | Get αi(cl,d) with the graph (cl vs. α)i; |
| 32 | Get (αi(cl,d)) with the graph (cl1.5/cd vs. α)i; |
| 33 | Apply (A7), to obtain max(yt(x))i; |
| 34 | Get ψ(ug) with (20); |
| 35 | Get L(ug) with (19); |
| 36 | Update U*; |
| 37 | for i = 1 to NP do |
| 38 | if L(ui,g) ≤ L(ξi,g) then |
| 39 | ξi,g+1 = ui,g; |
| 40 | ξi,g→ A; |
| 41 | CRi,g→ SCR, Fi,g→ SF; |
| 42 | |L(ui,g) − L(ξi,g)|→ Δf; |
| 43 | else |
| 44 | ξi,g+1 = ξi,g; |
| 45 | Update the memories MCR and MF with Algorithm C1; |
| 46 | mean(L(ξg+1))→ Lavg; |
| 47 | if g ≥ 3 then |
| 48 | Get Δg and Δg−1 with (A11); |
| 49 | Get NPg+1 with (A9); |
| 50 | if NPg+1 < NPmin then |
| 51 | Apply (A10); |
| 52 | (NPg − NPg+1) worst elements → A; |
| 53 | if |A| > round(2,6NP) then |
| 54 | Delete (|A|-round(2,6NP)) elements randomly; |
| 55 | k++; |
| 56 | return Output |
References
- Ma, Y.; Elham, A. Designing high aspect ratio wings: A review of concepts and approaches. Prog. Aerosp. 2024, 145, 100983. [Google Scholar] [CrossRef]
- Martins, J.R.; Kennedy, G.; Kenway, G.K. High aspect ratio wing design: Optimal aero structural trade offs for the next generation of materials. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar]
- Vassberg, J.C.; Jameson, A. Industrial applications of aerodynamic shape optimization. In Proceedings of the VKI Lecture-II, Brussels, Belgium, 11 September 2018. [Google Scholar]
- Nikolaev, N.V. Optimization of airfoils along high-aspect-ratio wing of long-endurance aircraft in trimmed flight. J. Aerosp. Eng. 2019, 32, 04019090. [Google Scholar] [CrossRef]
- Anderson, J.D.; Bowden, M.L. Introduction to Flight, 9th ed.; McGraw-Hill Higher Education: New York, NY, USA, 2021; pp. 508–513. [Google Scholar]
- Steinbuch, M.; Marcus, B.; Shepshelovich, M. Development of UAV wings-subsonic designs. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003. [Google Scholar]
- Park, K.; Kim, B.S. Optimal design of an airfoil plataform shapes with high aspect ratio using genetic algorithms. Int. J. Aerosp. Mech. Eng. 2013, 7, 584–590. [Google Scholar]
- Wang, L.; Zhang, H.; Wang, C.; Tao, J.; Lan, X.; Sun, G.; Feng, J. A review of intelligent airfoil aerodynamic optimization methods based on data-driven advanced models. Mathematics 2024, 12, 1417. [Google Scholar] [CrossRef]
- Karbasian, H.R.; Vermeire, B.C. Gradient-free aerodynamics shape optimization using large eddy simulation. Comput. Fluids 2022, 232, 105185. [Google Scholar] [CrossRef]
- Dussage, T.P.; Sung, W.J.; Pinon Fischer, O.J.; Mavris, D.N. A reinforcement learning approach to airfoil shape optimization. Sci. Rep. 2023, 13, 9753. [Google Scholar] [CrossRef]
- Yan, X.; Zhu, J.; Kuang, M.; Wang, X. Aerodynamic shape optimization using a novel optimizer based on machine learning techniques. Aerosp. Sci. Technol. 2019, 86, 826–835. [Google Scholar] [CrossRef]
- Skinner, S.N.; Zare-Behtash, H. State-of-the-art in aerodynamic shape optimization methods. Appl. Soft Comput. 2018, 62, 933–962. [Google Scholar] [CrossRef]
- Li, J.; Du, X.; Martins, J.R. Machine learning in aerodynamic shape optimization. Prog. Aerosp. Sci. 2022, 134, 100849. [Google Scholar] [CrossRef]
- Chen, K.; Quian, W.; Wang, S. Multiple aerodynamic coefficient prediction of airfoils using a convolutional neural network. Symmetry 2020, 12, 544. [Google Scholar] [CrossRef]
- Hu, L.; Zhang, J.; Xiang, Y.; Wnag, W. Neural networks-based aerodynamic data modeling: A comprehensive review. IEEE Access 2020, 8, 90805–90823. [Google Scholar] [CrossRef]
- Hacioglu, A. Fast evolutionary algorithm for airfoil design via neural network. AIAA J. 2007, 45, 2196–2203. [Google Scholar] [CrossRef]
- Kharal, A.; Saleem, A. Neural networks based airfoil generation for a given cp using Bezier-PARSEC parameterization. Aerosp. Sci. Technol. 2012, 23, 330–344. [Google Scholar] [CrossRef]
- Khurana, M.; Winarto, H.; Sinha, A. Application of swarm approach and artificial neural networks for airfoil shape optimization. In Proceedings of the 12th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Victoria, BC, Canada, 10–12 September 2008. [Google Scholar]
- Sun, G.; Sun, Y.; Wang, S. Artificial neural network based inverse design: Airfoils and wings. Aerosp. Sci. Technol. 2015, 42, 415–428. [Google Scholar] [CrossRef]
- Hui, X.; Bai, J.; Wang, H.; Zhang, Y. Fast pressure distribution prediction of airfoils using deep learning. Aerosp. Sci. Technol. 2020, 105, 105949. [Google Scholar] [CrossRef]
- Wang, J.; He, C.; Li, R.; Chen, H.; Zhai, C.; Zhang, M. Flow field predictions of supercritical airfoils via variational autoencoder based deep learning framework. Phys. Fluids 2021, 33, 086108. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunuga, A. Success-history based parameter adaptation for differential evolution. In Proceedings of the IEEE Congress on Evolution Computation (CEC), Cancun, Mexico, 20–23 June 2013. [Google Scholar]
- Tanabe, R.; Fukunuga, A.S. Improving the search performance of SHADE using linear population size reduction. In Proceedings of the 2014 IEEE Congress on Evolution Computation (CEC), Beijing, China, 6–11 July 2014. [Google Scholar]
- Renkavieski, C.; Parpinelli, R.S. L-SHADE with alternative population size reduction for unconstrained continuous optimization. An. Do Comput. Beach 2020, 11, 351–358. [Google Scholar]
- Xie, H.; Wang, J.; Zhang, M. Parametric generative schemes with geometric constrains for encoding and synthesizing airfoils. Eng. Appl. Artif. Intell. 2024, 128, 107505. [Google Scholar] [CrossRef]
- Derksen, R.W.; Rogalsky, T. Bezier-PARSEC: An optimized aerofoil parameterization for design. Adv. Eng. Softw. 2010, 41, 923–930. [Google Scholar] [CrossRef]
- Liao, Y.; Liu, L.; Long, T. Investigation of various parametric geometry representation methods for airfoils. Appl. Mech. Mater. 2012, 110, 3040–3046. [Google Scholar] [CrossRef]
- Sripawadkul, V.; Padulo, M.; Guenov, M. A comparison of airfoil shape parameterization techniques for early design optimization. In Proceedings of the 13th AIAA/ISSMO Multidisciplinary Analysis Optimization Conference, Fort Worth, TX, USA, 13–15 September 2010. [Google Scholar]
- Kulfan, B.M.; Bussoletti, J.E. “Fundamental” parametric geometry representations for aircraft component shapes. In Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Portsmouth, VA, USA, 6–8 September 2006. [Google Scholar]
- The Incomplete Guide to Airfoil Usage. Available online: https://m-selig.ae.illinois.edu/ads/aircraft.html#conventional (accessed on 19 February 2024).
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumuran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE Signal Process. 2018, 35, 53–68. [Google Scholar] [CrossRef]
- OpenFOAM v11 User Guide. Available online: https://doc.cfd.direct/openfoam/user-guide-v11/index (accessed on 20 March 2024).
- Welcome to Pygmsh’ Documentation! Available online: https://pygmsh.readthedocs.io/en/latest (accessed on 10 March 2024).
- Eleni, D.C.; Athanasios, T.I.; Dionissios, M.P. Evaluation of the turbulence models for the simulation of the flow over a National Advisory Committe for Aeronautics (NACA) 0012 airfoil. J. Mech. Eng. Res. 2012, 4, 100–111. [Google Scholar]
- Suvanjumrat, C. Comparison of turbulence models for flow past NACA0015 airfoil using OpenFOAM. Eng. J. 2017, 21, 207–221. [Google Scholar] [CrossRef]
- Khan, S.A.; Bashir, M.; Baig, M.A.A.; Ali, F.A.G.M. Comparing the effect of different turbulence models on the CFD predictions of NACA0018 airfoil aerodynamics. CFD Lett. 2020, 3, 1–10. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Lagtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Lu, S.; Liu, J.; Hekkenberg, R. Mesh properties for RANS simulations of airfoil-shaped airfoils: A case study of ruder hydrodynamics. J. Mar. Sci. Eng. 2021, 9, 1062. [Google Scholar] [CrossRef]
- A thorough Description of How Wall Functions Are Implemented in OpenFOAM. Available online: https://www.tfd.chalmers.se/~hani/kurser/OS_CFD_2016/FangqingLiu/openfoamFinal.pdf (accessed on 8 October 2024).
- Caretto, L.S.; Gosman, A.D.; Patankar, S.V.; Spalding, D.B. Two calculation procedures for steady, three-dimensional flows with recirculation. In Proceedings of the Third International Conference on Numerical Methods in Fluid Mechanics, Paris, France, 3–7 July 1972; Springer: Berlin/Heidelberg, Germany, 1973; Volume 2, pp. 60–68. [Google Scholar]
- Ladson, C.L. Effects of Independent Variation of Mach and Reynolds Numbers on the Low-Speed Aerodynamic Characteristics of the NACA 0012 Airfoil Section (Vol 4074); National Aeronautics and Space Administration, Scientific and Technical Information Division: NASA Langley Research Center: Hamton, VA, USA, 1988; pp. 3–20.
- Turbulent Flow over NACA0012 Airfoil (2D). Available online: https://www.openfoam.com/documentation/guides/latest/doc/verification-validation-naca0012-airfoil-2d.html (accessed on 20 March 2024).
- Sola, J.; Sevilla, J. Importance of input data normalization for the application of neural networks to complex industrial problems. IEEE Trans. Nucl. Sci. 1997, 44, 1464–1468. [Google Scholar] [CrossRef]
- Gokhan, A.K.S.U.; Guzeller, C.O.; Eser, M.T. The effect of the normalization method used in different sample sizes on the success of artificial neural network model. Int. J. Assess. Tools Educ. 2019, 6, 170–192. [Google Scholar]
- Pedregosa, F.; Varoquax, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Research. 2011, 12, 2825–2830. [Google Scholar]
- Keras. Available online: https://keras.io (accessed on 15 April 2024).
- Tharwat, A. Principal component analysis—A tutorial. Int. J. Appl. Pattern Recognit. 2016, 3, 197–240. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. An introduction to variational autoencoders. Found. Trends Mach. Learn. 2019, 12, 307–392. [Google Scholar] [CrossRef]
- Espinosa Barcenas, O.U.; Quijada Pioquinto, J.G.; Kurkina, E.; Lukyanov, O. Surrogate aerodynamic wing modeling based on a multilayer perceptron. Aerospace 2023, 10, 149. [Google Scholar] [CrossRef]
- Moin, H.; Khan, H.Z.I.; Mobeen, S.; Riaz, J. Airfoil’s aerodynamic coefficients prediction using artificial neural network. In Proceedings of the 2022 19th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 16–20 August 2022. [Google Scholar]
- Deng, C.; Zhao, B.; Yang, Y.; Deng, A. Integer encoding differential evolution algorithm for integer programming. In Proceedings of the 2010 2nd International Conference on Information Engineering and Computer Science, Hangzhou, China, 4–6 December 2010. [Google Scholar]
- Wong, I.; Liu, W.; Ho, C.M.; Ding, X. Continuous adaptive population reduction (CAPR) for differential evolution optimization. SLAS Technol. 2017, 22, 289–305. [Google Scholar] [CrossRef] [PubMed]
- Pioquinto, J.G.Q.; Moreno, R.A.F. Methods for increasing the efficiency of the differential evolution algorithm for aerodynamic shape optimization applications. In Proceedings of the XXVI All-Russian Seminar on Motion Control and Navigation of Aircraft, Kazan, Russia, 14–16 June 2023. [Google Scholar]
- Sedelnikov, A.; Kurkin, E.; Quijada Pioquinto, J.G.; Lukyanov, O.; Nazarov, D.; Chertykovtseva, V.; Kurkina, E.; Hoang, V.H. Algorithm for propeller optimization based on differential evolution. Computation 2024, 12, 52. [Google Scholar] [CrossRef]
- Ali, M.M.; Zhu, W.X. A penalty function-based differential evolution algorithm for constrained global optimization. Comput. Optim. Appl. 2013, 54, 707–739. [Google Scholar] [CrossRef]
- UIUC Airfoil Coordinates Database. Available online: https://m-selig.ae.illinois.edu/ads/coord_database.html (accessed on 20 February 2024).
- Shirvani, A.; Nili-Ahmadabadi, M.; Ha, M.Y. A deep learning-genetic algorithm approach for aerodynamic inverse design via optimization of pressure distribution. Comput. Methods Appl. Mech. Eng. 2024, 429, 117187. [Google Scholar] [CrossRef]
- Althaus, D.; Wortmann, F.X. Experimental Results from Laminar Wind Tunnel of the Institut fur Aero- und Gasdynamic der Universitat Stuttgart; Fried, Vieweg & Sohn: Born, Germany, 1981; pp. 1–20. [Google Scholar]
- OpenVozduj/AZTLI-NN. Available online: https://github.com/OpenVozduj/AZTLI-NN (accessed on 22 July 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).