Evolution of Unmanned Surface Vehicle Path Planning: A Comprehensive Review of Basic, Responsive, and Advanced Strategic Pathfinders

Abstract

Unmanned Surface Vehicles (USVs) are rapidly becoming mission-indispensable for a variety of naval operations, from search and rescue to environmental monitoring and surveillance. Path planning lies at the heart of the operational effectiveness of USVs, since it represents the key technology required to enable the vehicle to transit the unpredictable dynamics of the marine environment in an efficient and safe way. The paper develops a critical review of the most recent advances in USV path planning and a novel classification of algorithms according to operational complexity: Basic Pathfinders, Responsive Pathfinders, and Advanced Strategic Pathfinders. Each category can adapt to different requirements, from environmental predictability to the desired degree of human intervention, and from stable and controlled environments to highly dynamic and unpredictable conditions. The review includes current methodologies and points out the state-of-the-art algorithmic approaches in their experimental validations and real-time applications. Particular attention is paid to the description of experimental setups and navigational scenarios showing the realistic impact of these technologies. Moreover, this paper goes through the key, open challenges in the field and hints at the research direction to leverage in order to enhance the robustness and adaptability of path planning algorithms. This paper, by offering a critical analysis of the current state-of-the-art, lays down the foundation of future USV path planning algorithms.

1. Introduction

The advancement of artificial intelligence and machine learning has significantly propelled the study of unmanned vehicles. Unmanned Ground Vehicles (UGVs) and Unmanned Aerial Vehicles (UAVs) have been adopted in various fields, from industrial automation to military operations, demonstrating their versatility and growing importance [1,2,3]. UAVs, initially used primarily for military purposes, have expanded into civilian applications, undertaking tasks such as agricultural spraying and disaster response [4,5,6].

In the midst of the increasing applications of UGVs and UAVs, Unmanned Surface Vehicles (USVs) have emerged as important players in maritime and utilization. Although USVs may not yet have as many applications as their land and air counterparts, their potential is vast and largely untapped [7,8]. USVs are essential for ocean sampling, seabed mapping, and cooperative network monitoring alongside UAVs and UGVs. Their roles also include search and rescue operations and harbor patrolling, offering promising solutions for reducing congestion in crowded city waterways [9,10,11,12].

Autonomy in the context of USVs involves the ability to independently devise and execute a navigational plan based on predefined rules, without human intervention. A key component of this autonomy is path planning, which involves creating a safe and efficient route for the vehicle to follow [13]. The complexity of path planning for USVs is heightened by the dynamic and often unpredictable maritime environment, where factors such as wind, waves, and currents present unique challenges that are more severe than those faced by UGVs and UAVs [14]. Table 1 summarizes some comparisons between UGVs, UAVs, and USVs.

To address the complexities of USV path planning, researchers must go beyond the traditional questions of “Where am I?”, “Where am I going?”, and “How do I get there?” proposed by Durrant-Whyte (1994). The multifaceted nature of the maritime environment requires a more detailed inquiry, leading to a new set of questions that better capture the needs for USV navigation: “What is my current situation?”, “Where are the possible destinations?”, “Which destination should I prioritize?”, and “What is the best way to reach my destination?”. These questions reflect a deeper understanding of the USV’s operational context and the need for an advanced approach to path planning.

USVs represent a rapidly evolving technological area, finding applications in marine research, military operations, and commercial shipping [15,16]. Operated remotely or through autonomous systems, USVs can perform complex tasks without a human crew. Advances in sensor technology, communication systems, and artificial intelligence algorithms have greatly benefited the development of USVs, enabling more precise navigation and task execution [17,18,19]. Key challenges in USV development include environmental perception, autonomous decision-making, path planning, and interaction with human operators.

Table 1. Contrast and analysis of UGVs, UAVs, and USVs.

Elements	UAVs [20]	UGVs [21]	USVs [22]
Motion Speed and Inertia	Fast, Low Inertia	Moderate, High Inertia	Moderate, High Inertia
Significant Disturbance	Wind	Traffic, Pavement	Waves, Wind
Operating Environments	Expansive Airspace	Road Networks	Aquatic Environments
Response Time	Short	Short	Extended
Application Scenarios	Remote Sensing, Communications, Surveillance	Automation, Logistics, Rescue	Oceanography, Environmental Monitoring

Table 1. Contrast and analysis of UGVs, UAVs, and USVs.

Elements	UAVs [20]	UGVs [21]	USVs [22]
Motion Speed and Inertia	Fast, Low Inertia	Moderate, High Inertia	Moderate, High Inertia
Significant Disturbance	Wind	Traffic, Pavement	Waves, Wind
Operating Environments	Expansive Airspace	Road Networks	Aquatic Environments
Response Time	Short	Short	Extended
Application Scenarios	Remote Sensing, Communications, Surveillance	Automation, Logistics, Rescue	Oceanography, Environmental Monitoring

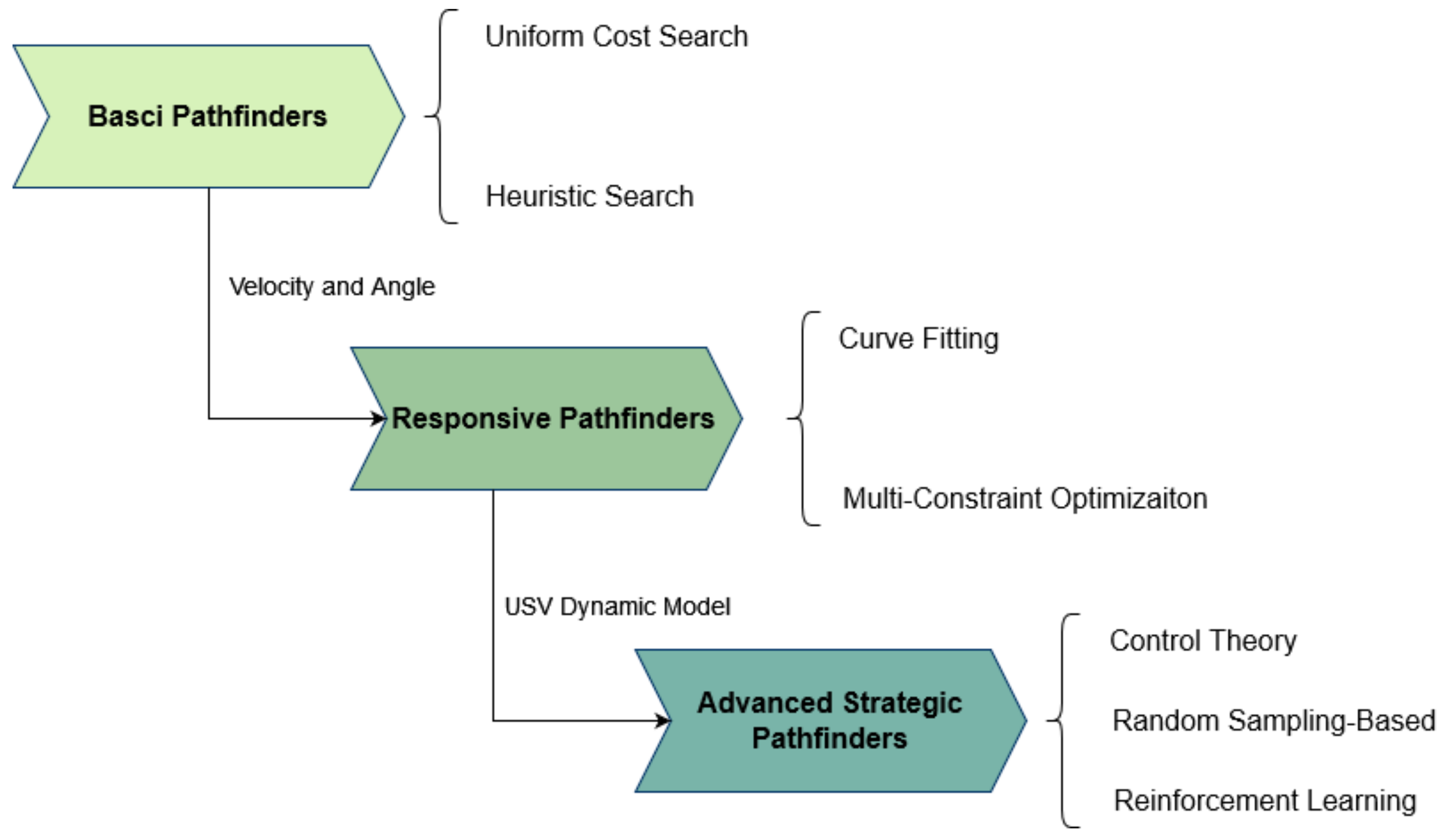
2. USV Path Planning Algorithms Progress

The development of path planning algorithms for USVs has seen a remarkable transformation over the years, closely aligned with the rapid advancements in computational algorithms and sensor technologies. As depicted in

Table 2. Capabilities of path planning algorithms.

Feature	Basic Pathfinders	Responsive Pathfinders	Advanced Strategic Pathfinders
Basic Static Map Path Planning	✓	✓	✓
Dynamic Obstacle Avoidance		✓	✓
Temporal Dynamics Path Planning		✓	✓
Consideration of Motion Constraints			✓
Real-Time Environmental Sensing and Response			✓
Path Optimization in Complex Environments			✓

, these developments can be categorized into distinct stages, each representing a significant leap in the complexity and sophistication of the algorithms. This progression has empowered USVs to tackle increasingly challenging navigation scenarios with greater autonomy and efficiency.

The evolution of these algorithms can be broadly categorized into three main stages: Basic Pathfinders, Responsive Pathfinders, and Advanced Strategic Pathfinders. Each stage marks a pivotal moment in the advancement of USV navigation, addressing the growing demands for more complex and adaptive path planning capabilities. Figure 1 illustrates this evolutionary process and the key methods associated with each stage. The following subsections delve into these categories, outlining their respective characteristics, strengths, and applications.

2.1. Basic Pathfinders

Initially, the focus in USV path planning was on basic navigational algorithms, which are primarily concerned with charting a path from the start point to the goal point in controlled or well-known environments. These Basic Pathfinders operate on the premise that the environment is static and fully known, optimizing routes based on geometric considerations on pre-defined, static maps. The primary goal of these algorithms is to minimize path length or travel time, assuming that environmental conditions remain stable and predictable throughout the journey. Such methods include classical approaches like Dijkstra’s algorithm or the A* algorithm, which effectively compute the shortest path in a graph. However, because these algorithms do not consider dynamic factors such as changes in the environment or the physical constraints of the USV, they are best suited for applications where real-time adaptability is not required. Their simplicity and efficiency make them ideal for situations where the operational environment is predictable and free of significant disturbances or obstacles.

2.2. Responsive Pathfinders

As USVs began to be deployed in more dynamic and less predictable environments, the limitations of Basic Pathfinders became apparent, leading to the development of Responsive Pathfinders. These algorithms extend the basic pathfinding principles by incorporating the temporal dynamics of the USV into the path planning process. Unlike their static counterparts, Responsive Pathfinders create schedules for the USV’s position over time, taking into account the vehicle’s velocity, acceleration, and sometimes even its maneuvering capabilities. This is particularly important in environments where conditions can change, such as the presence of moving obstacles or variable weather patterns. Responsive Pathfinders are designed to handle semi-dynamic environments where occasional changes in conditions or moving obstacles occur. They leverage kinematic constraints to ensure that the planned path is not only feasible, but also safe and efficient, given the USV’s physical capabilities. By dynamically adjusting the path in response to real-time data, these algorithms offer a more robust solution for environments that are not entirely predictable but do not require the most advanced levels of adaptability.

2.3. Advanced Strategic Pathfinders

The most sophisticated stage in USV path planning is represented by Advanced Strategic Pathfinders. These algorithms integrate the concepts of both route planning and responsive pathfinding with real-time environmental interaction. Designed for highly dynamic and complex marine environments, Advanced Strategic Pathfinders are capable of making dynamic decisions based on current and anticipated conditions. They leverage advanced sensor arrays, such as LiDAR, sonar, and GPS, along with predictive models that can forecast environmental changes, such as water waves, weather variations, or the movement of other vessels. These pathfinders are tasked with not only responding to immediate obstacles, but also anticipating future challenges, enabling the USV to modify its path proactively. This is critical in scenarios like high-traffic maritime zones or under severe weather conditions, where rapid adjustments and high-level decision-making are essential for safe and efficient navigation. Advanced Strategic Pathfinders are designed to ensure that the USV can operate autonomously with minimal human intervention, even in the most challenging conditions.

2.4. Summary

In summary, the development of path planning algorithms for USVs shows a clear progression from basic, static methods to more adaptive and strategic approaches. This evolution reflects technological advancements that have enhanced the operational capabilities of USVs, enabling them to become more autonomous, resilient, and effective in navigating complex maritime environments. Basic Pathfinders provide a foundational approach, but are limited by their failure to consider USV dynamics, turning constraints, and real-time environmental changes. As more responsive solutions were needed, Responsive Pathfinders were introduced, incorporating kinematic constraints. However, they still do not fully address the USV’s dynamic model or the challenges of highly dynamic environments. The most advanced stage in this evolution is represented by Advanced Strategic Pathfinders, which integrate both kinematic and dynamic models with real-time environmental data. Despite their sophistication, these systems can still encounter difficulties in extremely complex or rapidly changing conditions, where the demands on computational resources and decision-making processes are particularly high.

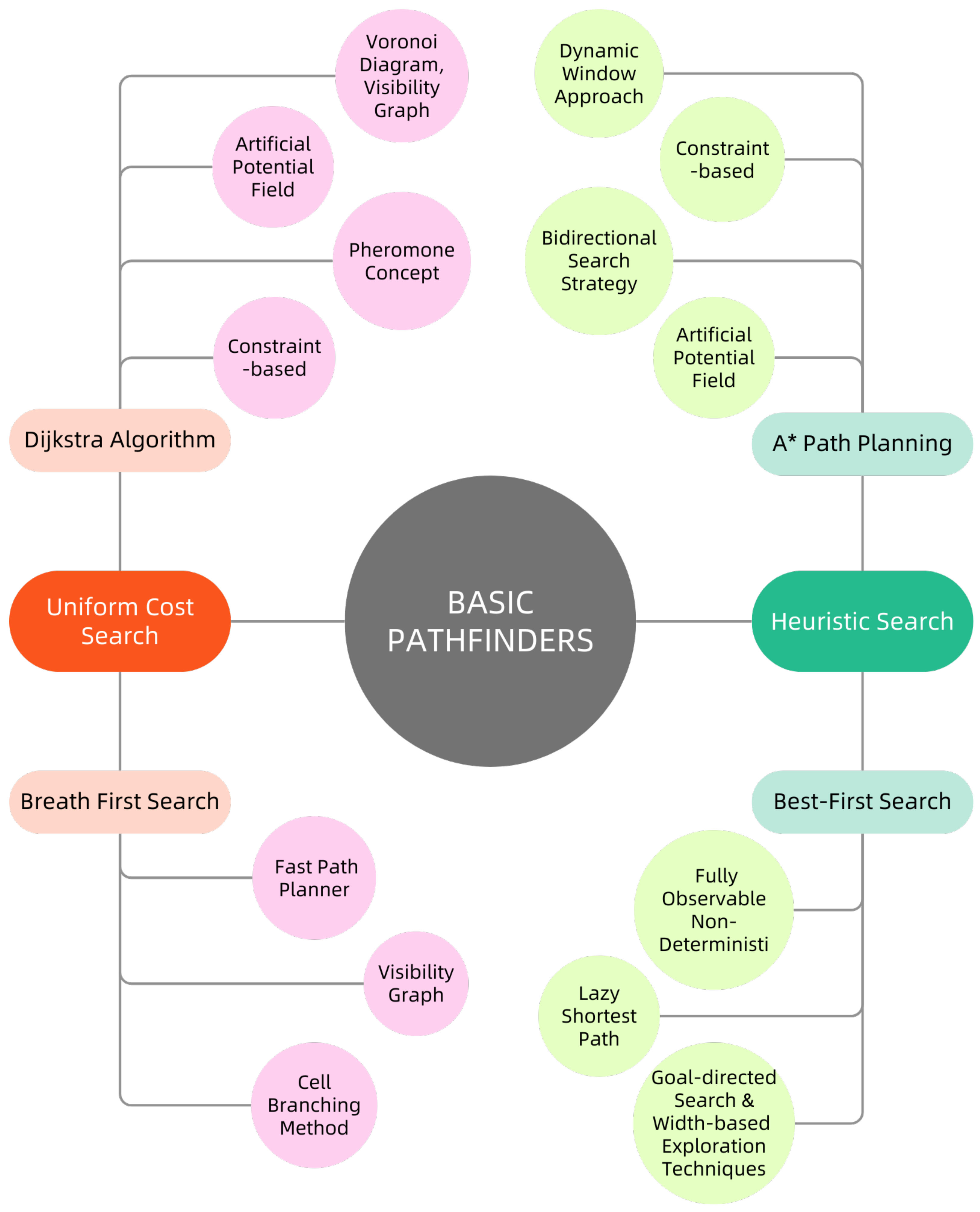
3. Basic Pathfinders

Basic Pathfinders represent the foundational stage in the evolution of path planning algorithms for USVs. These global path planning algorithms are essential for directing USVs from a start point to a goal point within well-defined and predictable maritime environments [23]. Utilizing detailed marine charts, Basic Pathfinders identify navigable waters and locate static obstacles like buoys and barriers, providing a framework for USVs to determine an optimal or feasible path. The primary focus at this level is on minimizing basic navigational challenges such as reducing travel distance, time, or computational demands, setting the stage for more complex pathfinding capabilities that respond to dynamic environmental changes and higher operational complexities. Figure 2 provides an overview of the algorithms reviewed. The basic pathfinders are categorized into two main types: uniform cost-based search and heuristic search. Each category includes classic algorithms and their application-based improvements, illustrating the various enhanced techniques discussed in the review.

3.1. Uniform Cost Search

Uniform Cost Search (UCS) is an essential algorithm in graph theory, designed to find the most cost-effective path from a start node to a target node in graphs with non-negative edge weights [24]. UCS consistently expands the least costly node at the search frontier. This approach guarantees that when a node is first reached, it is via the shortest possible path. The algorithm employs a priority queue to keep nodes organized by their cumulative path costs from the source, facilitating an efficient exploration of paths.

3.1.1. Dijkstra Algorithm

Dijkstra’s algorithm, conceived by computer scientist Edsger W. Dijkstra in 1956 [25], is a method for finding the shortest paths between nodes in a graph, which can represent road networks. Initially developed to find the shortest path between two nodes, the algorithm is more commonly used in a variant that establishes a single node as the “source”. From this source node, it determines the shortest paths to all other nodes in the graph, effectively creating a shortest-path tree. Additionally, it can be adapted to find the shortest path from the source to a specific destination node by terminating the algorithm once the shortest route to the destination is found. Dijkstra is a general-purpose algorithm that does not require any heuristic knowledge of the graph, making it broadly applicable across different domains. However, Dijkstra’s algorithm can be inefficient for very large graphs or in cases where only the shortest path to a single destination is needed, as it explores a large portion of the graph unnecessarily. The steps of Dijkstra’s algorithm can be mathematically represented as follows:

• Initialization:

  $$\mathrm{dist}\left(s\right)=0,\mathrm{dist}\left(v\right)=\infty \forall v\ne s$$

  (1)
• Iteration:
  Select the node u with the minimum distance:

  $$u=arg\underset{v\in Q}{min}\mathrm{dist}\left(v\right)$$

  (2)
  For each neighbor v of u:

  $$\mathrm{dist}\left(v\right)=min\left(\mathrm{dist}\left(v\right),\mathrm{dist}\left(u\right)+w(u,v)\right)$$

  (3)
• Update:
  Mark u as visited.
• Termination:
  Continue the process until all nodes have been visited.

$\mathrm{dist}\left(s\right)$ is the distance from the source node s to itself, initialized as 0. $\mathrm{dist}\left(v\right)$ is the current known shortest distance from the source node s to node v, initialized as ∞ for all $v\ne s$. u is the node currently being processed, selected based on the smallest known distance, and Q is the set of unvisited nodes in the graph. $min\left(\mathrm{dist}\left(v\right),\mathrm{dist}\left(u\right)+w(u,v)\right)$ updates the distance to node v to the smaller value between the current known distance and the distance through node u.

In the field of autonomous maritime navigation, Singh et al. [26] advanced the traditional Dijkstra algorithm by incorporating a constraint-based approach that takes into account moving obstacles and varying sea currents. Their modification introduces a safety margin within the algorithm, effectively mapping out optimal paths while considering USV speed and the need for collision avoidance. This adaptation is particularly useful in confined maritime areas like harbors, where path planning must also factor in environmental disturbances.

Further refining path planning strategies, Zhu et al. [27] integrated the pheromone concept from ant colony optimization with the Dijkstra algorithm. This hybrid approach reduces redundant waypoints, resulting in smoother and more practical navigation routes. The enhanced algorithm contributes to more efficient and cost-effective USV operations by optimizing basic pathfinders.

Building on these integrations, Niu et al. [28] introduced a novel combination of the Voronoi diagram, Visibility graph, and Dijkstra’s algorithm. Their method focuses on energy efficiency, optimizing path planning to potentially offer significant energy savings while maintaining safety in dynamic maritime contexts. This approach adapts well to various sea conditions, highlighting the importance of environmental responsiveness in path planning.

Xie et al. [29] merged global and local path planning techniques by coupling a modified Dijkstra algorithm with an Artificial Potential Field (APF) approach. This composite strategy enables real-time obstacle avoidance, enhancing the USV’s capability to navigate efficiently during mission-critical operations like environmental monitoring.

While these innovative approaches mark substantial progress in USV path planning, challenges remain, especially concerning simulation-based discrepancies and computational complexity. These issues may hinder real-time decision-making, underscoring the need for ongoing refinement and adaptation of path planning algorithms to better suit real-world conditions.

3.1.2. Breath-First Search (BFS)

Breadth-First Search is an algorithmic approach for searching a graph in a breadthward motion. This algorithm commences from a selected node, systematically exploring its adjacent nodes before progressing to the next level of adjacent nodes. As a path planning technique, BFS is adept at determining the shortest path in an unweighted graph due to its inherent nature of level-wise exploration. The implementation of BFS for path planning involves the initialization of a queue to facilitate the orderly examination of nodes, marking each visited node to prevent redundant inspections. The iterative process continues until the queue is depleted, ensuring that all accessible nodes are explored, thereby ascertaining the shortest path from the origin to the destination node, contingent upon the absence of weights on the edges. One of the key strengths of BFS is its guarantee to find the shortest path in an unweighted graph. Additionally, its simplicity and ease of implementation make it a versatile choice for various graph search problems. However, BFS can be inefficient in terms of memory usage, as it requires storing all nodes at the current level in the queue. Moreover, it is not suitable for weighted graphs, where algorithms like Dijkstra’s are more appropriate for finding the shortest path.

Building on this foundation, Li et al. [30] introduced the Fast Path Planner (FPP), a sophisticated algorithm utilizing a sparse visibility graph and bidirectional search to optimize path planning in complex environments. This method accelerates the construction of visibility graphs and decreases update costs through obstacle contour filtering, showcasing a 40% improvement in speed and a 25% reduction in path length compared to the Fast, Attemptable Route (FAR) Planner. Although FPP relies on simplified models, its substantial enhancements in speed and path efficiency demonstrate its potential utility across various autonomous navigation systems, albeit further refinements are required to increase its environmental adaptability.

Additionally, Yan Zhou et al. [31] developed a pathfinding algorithm that minimizes both turns and distance using BFS. By integrating a visibility graph with bidirectional search, this approach simplifies navigation by creating intuitive and less redundant paths. Performance tests reveal that it surpasses traditional methods by offering simpler, shorter routes. Despite its effectiveness, current limitations include a dependency on predefined settings, with future improvements aimed at boosting adaptability and lowering computational demands.

Further enhancing BFS, Subramanian et al. [32] investigated the use of the BFS algorithm for path planning in dynamic environments for autonomous mobile robots (AMRs). It employs a cell branching method in a grid-based map, where the BFS algorithm systematically explores all neighboring nodes at the current depth before moving on to nodes at the next depth level. This makes it suitable for environments where the structure is not known in advance. Its main advantages are simplicity, ease of implementation, and the guarantee of finding the shortest path if all edges have the same cost. However, it has significant drawbacks, including high computational complexity and slower expansion speed, particularly in complex environments. Experimental results demonstrate that BFS explores paths more quickly in unknown environments compared to other algorithms like A*.

3.2. Heuristic Search

Heuristic search is an effective strategy used in pathfinding and graph traversal, leveraging informed estimates to predict promising paths from start to target nodes [33]. This approach is widely used in artificial intelligence and navigation systems, where it optimizes searches by prioritizing paths likely to lead directly to the goal.

3.2.1. Best-First Search

Best-First Search (BFS) is an informed search strategy that employs a heuristic function to prioritize nodes in the pathfinding process. The heuristic function estimates the cost from a node to the goal, guiding the search direction towards the most promising paths. Unlike uninformed search strategies that explore the search space without direction, BFS leverages domain-specific knowledge encapsulated in the heuristic to make informed decisions about which nodes to explore next.

The algorithm maintains a priority queue, often implemented as a min-heap, where nodes are ordered based on their heuristic values. At each step, the node with the lowest heuristic value is dequeued and expanded. The children of this node are then evaluated by the heuristic function and added to the priority queue. This process continues until the goal node is reached or the search space is exhausted.

The efficiency and performance of Best-First Search are highly dependent on the accuracy of the heuristic function. An ideal heuristic is one that accurately reflects the actual cost to reach the goal from any node in the graph. The more accurate the heuristic, the fewer nodes the algorithm will have to explore, resulting in faster search times.

Best-First Search is the foundation for more sophisticated search algorithms like A* and Greedy Best-First Search, which refine the basic BFS approach by incorporating additional information or optimization strategies to improve search efficiency.

Dellin et al. [34] introduced the Lazy Shortest Path (LazySP) approach, a significant innovation in shortest path algorithms designed for scenarios where the computational cost is dominated by edge weight evaluations. By integrating a lazy evaluation mechanism into traditional pathfinding methods, this approach reduces the number of expensive edge evaluations, proving highly beneficial in robotic Advanced Strategic Pathfinders where interactions between robots and their environments are complex and computationally demanding. A key aspect of their contribution is the development of various novel edge selector strategies, which have demonstrated substantial improvements over traditional algorithms in specific test scenarios. However, the authors acknowledge that the primary applicability of LazySP is in domains with detail edge evaluations, and it may not be as effective in broader contexts where different algorithmic efficiencies are more crucial.

Building on the theme of specialized search algorithms, Messa et al. [35] introduced AND*, a Best-First heuristic search algorithm that optimizes policy-space search within the context of Fully Observable Non-Deterministic (FOND) planning. Extending traditional concepts of optimality and admissibility to FOND scenarios, they developed heuristic functions aimed at minimizing the number of mapped states in solution policies. This methodology streamlines the search process and enhances the efficiency of the resulting policies, with AND* showing superior performance in theoretical and empirical evaluations compared to traditional FOND planners. Despite its theoretical advancements, the practical application of AND* could benefit from incorporating dynamic environmental factors to enhance its relevance in real-world scenarios.

Lipovetzky et al. [36] introduced the Best-First Width Search (BFW) algorithm, which combines goal-directed search with width-based exploration techniques to tackle complex search spaces. Notably effective in classical planning, BFW has shown significant improvements in problem-solving efficiency over conventional planners such as Fast Forward (FF), Fast Downward (FD), and Landmark-Adaptive A* Heuristic (LAMA). By balancing exploitation with exploration, BFW excels particularly in game-like scenarios found in competitions like Atari and GVG-AI. Despite its success, challenges remain in managing the complexity and computational demands of integrating width-based search techniques. This pioneering work lays essential groundwork for future enhancements in planning algorithms that effectively merge heuristic and exploratory search methods, aiming to optimize both performance and applicability in diverse planning environments.

3.2.2. A* Path Planning

The A* algorithm stands as a cornerstone in the domain of pathfinding and graph traversal algorithms. It epitomizes an informed search strategy that ingeniously blends the virtues of the heuristic-driven Best-First Search with the practical thoroughness of Dijkstra’s algorithm [37,38]. A* is highly efficient in terms of both time and space when the heuristic function is well-chosen, as it can often find the shortest path faster than Dijkstra’s algorithm. It also guarantees the optimal path, provided the heuristic is admissible and consistent. However, A* can be memory-intensive, particularly in large or complex graphs, as it stores all explored nodes. Its performance also heavily depends on the quality of the heuristic function; a poor heuristic can degrade its efficiency significantly.

The algorithm operates by maintaining a priority queue of paths based on the cost function

$$f\left(n\right)=g\left(n\right)+h\left(n\right)$$

(4)

where $f\left(n\right)$ represents the estimated total cost of the cheapest solution path going through node n, $g\left(n\right)$ denotes the cost of the path from the start node to n, and $h\left(n\right)$ is a heuristic function that estimates the cost of the cheapest path from n to the goal.

The heuristic function is pivotal to the A* algorithm’s performance; it influences both the efficiency and completeness of the search. An admissible heuristic, one that never overestimates the cost to reach the goal, guarantees that A* always finds a solution if one exists, and that the solution will be optimal.

The A* algorithm iteratively explores the graph by expanding the most promising node n, chosen from a priority queue known as the open set. For each neighbor m of n, the algorithm evaluates the path from the start node to m through n and updates $f\left(m\right)$ accordingly.

Expanding on the A* algorithm, Song et al. [39] integrated it with an Artificial Potential Field (APF) method to optimize path planning in complex maritime contexts. This integration incorporates boundary detection and secondary target setting within the APF, enabling smoother navigation and effective local obstacle avoidance, which is pivotal in overcoming the issue of local minima often encountered in autonomous navigation.

Further, Wang et al. [40] developed a hybrid navigation approach that combines a post-smoothed A* algorithm with a Dynamic Window approach. This adaptation enhances both global path planning and local maneuvering capabilities of USVs, streamlining path planning to yield routes with fewer and shorter waypoints through post-processing smoothing.

Singh et al. [14] introduced a constrained A* approach tailored for maritime navigation’s dynamic challenges by incorporating a safety distance around the USV. This adjustment takes into account the unpredictability of ocean currents and moving obstacles, enhancing path planning across diverse environmental conditions.

Moreover, Zhang et al. [41] optimized the traditional A* algorithm with a bidirectional search strategy and an improved evaluation function. This enhancement effectively smooths the USV’s navigational paths and reduces the computational burden, addressing the conventional A* algorithm’s inefficiencies and better meeting the practical navigation demands of USVs.

These developments represent significant strides in enhancing the path planning capabilities of autonomous maritime navigation using the A* algorithm. Despite these advancements, several challenges persist, including high computational demand and simplification of dynamic maritime scenarios.

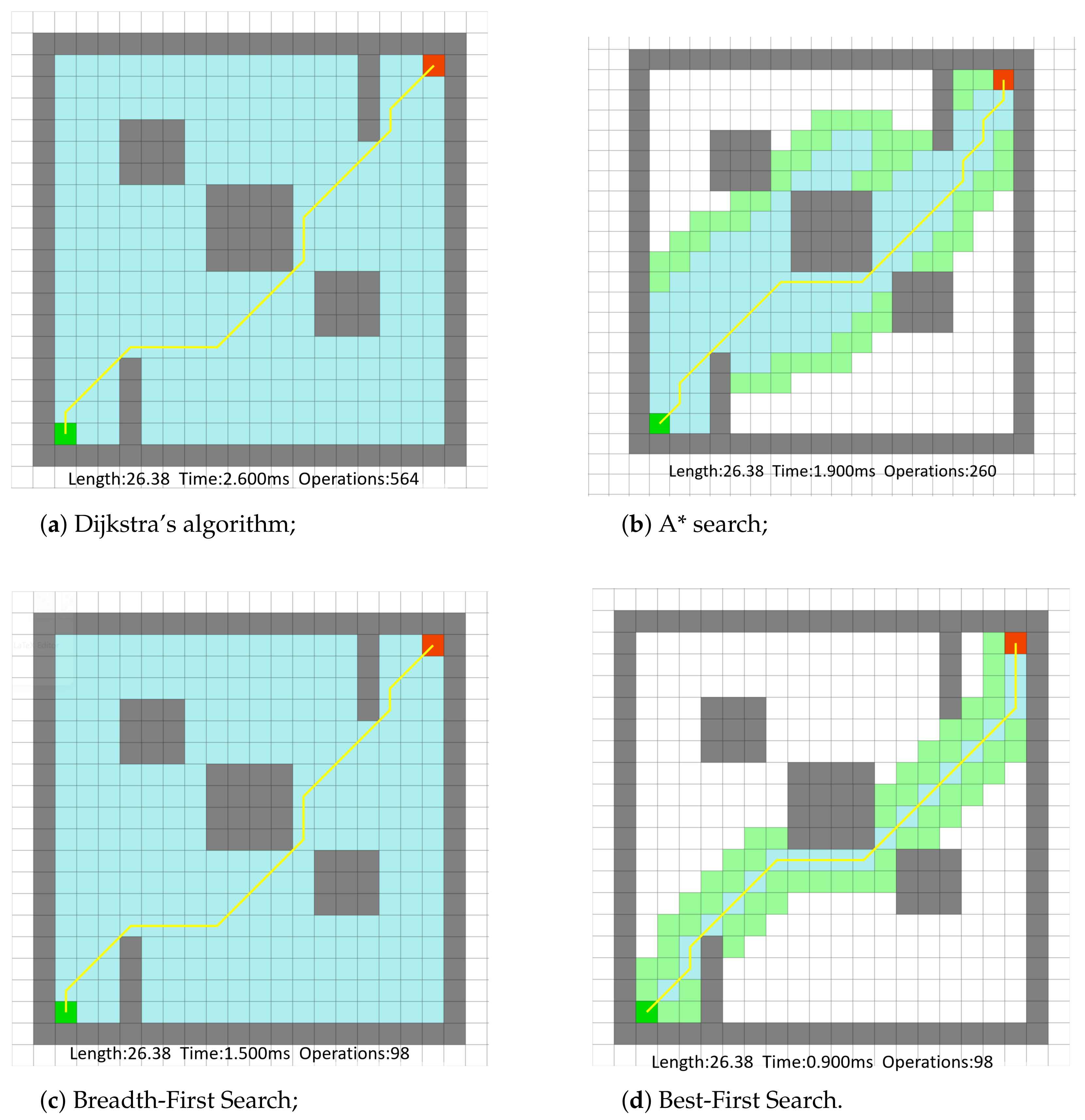
3.3. Summary

In Figure 3, where the starting point is denoted in deep green and the destination in red, a comparative analysis of four basic pathfinding algorithms—A*, Dijkstra’s, Best-First Search, and Breadth-First Search—reveals that each algorithm consistently identifies the shortest path of 26.38 units. The tests were conducted using a comprehensive path-finding library written in a JavaScript environment, executed within the PathFinding.js library. The simulations were performed on a Windows 10 system equipped with an Intel(R) Core(TM) i9-8950HK CPU.

Each algorithm was tested over 10 independent trials to account for OS interrupts and variations in processing. The average results of these trials are reported to ensure that transient system factors, such as background processes, did not skew the outcome. The average planning times (in milliseconds) for each algorithm are as follows:

• A*: 1.7 ms (average).
• Dijkstra’s: 2.31 ms (average).
• Best-First Search: 1.05 ms (average).
• Breadth-First Search: 1.92 ms (average).

These averages were computed to provide a clearer picture of each algorithm’s performance. Dijkstra’s algorithm consistently showed the longest planning time at an average of 2.31 ms, reflecting its exhaustive search strategy, which evaluates every possible path to ensure optimality. Breadth-First Search also demonstrated relatively long planning times, with an average of 1.92 ms, largely due to its indiscriminate exploration of nodes.

On the other hand, A* and Best-First Search exhibited significantly lower planning times, averaging 1.7 ms and 1.05 ms, respectively. These lower times can be attributed to their heuristic-driven strategies, which prioritize specific nodes based on expected path costs, thus reducing the number of unnecessary node expansions.

The benchmark of operations was based on the number of node expansions, with the values recorded for each algorithm across the trials as follows:

• A*: 260 nodes.
• Dijkstra’s: 564 nodes.
• Best-First Search: 98 nodes.
• Breadth-First Search: 564 nodes.

The values “564”, “260”, and “98” represent the total number of nodes expanded by each algorithm during a single trial. These numbers directly correlate with the computational effort required by each algorithm, with higher values indicating more extensive exploration of the search space. As expected, both Dijkstra’s and Breadth-First Search expanded the most nodes (564 of each), as they explored the entire graph or grid indiscriminately, leading to higher computational overhead.

Conversely, Best-First Search, by leveraging its heuristic function, expanded the fewest nodes (only 98 per trial), demonstrating its operational efficiency. A* falls between the two extremes, with 260 node expansions, balancing heuristic efficiency and thorough exploration.

Furthermore, while Dijkstra’s and Breadth-First Search algorithms each expanded 564 nodes, they showed little distinction in path selection. A* and Best-First Search, in contrast, executed significantly fewer operations due to their heuristic-driven nature. Despite this, the reliance on heuristics in A* and Best-First Search means their effectiveness heavily depends on the quality of the heuristic function used.

In conclusion, although all algorithms found the shortest path, they varied significantly in terms of planning efficiency, operational depth, and computational overhead. Dijkstra’s algorithm, while guaranteeing optimality, was the most computationally expensive in terms of both time and node expansions. Breadth-First Search, though simpler, was similarly inefficient due to its exhaustive search approach. In contrast, A* and Best-First Search offered a more balanced trade-off between computational efficiency and search precision, but their performance is highly dependent on the quality of the heuristics used.

These tests underscore the necessity of balancing precision, efficiency, and scalability when applying these algorithms in real-world dynamic scenarios. Future work could explore adaptive heuristics or hybrid models that optimize performance across various operational contexts.

4. Responsive Pathfinders

Responsive Pathfinders mark a critical advancement in the development of path planning algorithms for USVs, building upon the foundational capabilities of Basic Pathfinders [42]. These algorithms are specially designed to manage dynamic environmental challenges and ensure that USVs adhere to their predefined paths despite such disturbances. Unlike basic pathfinding that establishes a static route, Responsive Pathfinders employ advanced trajectory tracking to dynamically adjust to both the vessel’s operational constraints and external environmental variations. This capability is pivotal for maintaining robust performance under varied and unpredictable conditions.

The methodologies underpinning Responsive Pathfinders can be categorized into two main approaches: curve fitting and multi-constraint optimization. Each approach offers unique strategies to enhance the adaptability and efficiency of USV navigation by addressing different aspects of the path planning challenges.

4.1. Curve Fitting

Curve fitting is a technique used to construct a smooth curve that closely aligns with a specific polyline, optimizing the fit for a planned path. This method is particularly beneficial for USVs as it considers environmental conditions and dynamic constraints, such as the minimum turning radius, resulting in a smoother and more continuous path in moderately constrained environments.

A widely used curve-fitting method in path planning is the Dubins path [43], which seeks the shortest path that a particle moving at constant speed can take while adhering to a minimum curvature constraint. The total path length L of a Dubins path is composed of up to three segments:

$$L=L_1+L_2+L_3,$$

(5)

where $L_1$, $L_2$, and $L_3$ represent the lengths of the segments, each being either a straight line (denoted by “L”) or a circular arc (denoted by “C”). These segments can be configured in types such as $CSC$ (e.g., “LSL”, “RSR”) or $CCC$ (e.g., “LRL”, “RLR”) [44].

The curvature k of the path, which dictates the turning radius, is inversely related to the minimum turning radius $R_{min}$:

$$k={\displaystyle \frac{1}{R_{min}}}.$$

(6)

This approach is particularly advantageous for ensuring that the path remains feasible and efficient while meeting the physical constraints of the USV.

An example of applying curve fitting in USV path planning is illustrated in Figure 4, emphasizing their adaptation to different operational constraints. The ETSP represents the simplest form, where only the shortest Euclidean distance between points is considered, ignoring vehicle orientation and turning constraints. In contrast, the blue lines show more complex models: DTSP considers the minimum turning radius applicable for vehicles with steering limitations, and DDTSP extends this to differential drive vehicles, which require different rotational capabilities at each waypoint.

Originally applied in UAVs [45], the Dubins path has also found applications in USV responsive pathfinders in recent years [46,47]. For instance, Yi Chen et al. [46] addressed the turning process in USV navigation by integrating the “CLC” Dubins path with a genetic algorithm to optimize the transition of poses—positions and heading angles—from start to end. However, the Dubins path introduces discontinuities in curvature as the curvature of a straight line is zero, but transitions to a defined curvature at circular arcs, leading to a sudden change.

Figure 4. Curve fitting [48].

Figure 4. Curve fitting [48].

To mitigate these discontinuities, some researchers have substituted circular arcs with specialized curves that better handle curvature transitions, such as Fermat’s spiral (FS) [49], B-splines [50], and Bessel curves [51]. These curves smoothly connect successive straight lines by maintaining zero curvature at the origin, thereby avoiding abrupt changes in curvature. Xiaojie Sun [52] utilized floating-point numbers and the turning radius defined by KT equations to shape the curvature of Bessel curves, achieving a smooth and continuous trajectory for USVs.

Additionally, Wang, N. et al. [53] developed a multilayer path planning algorithm that uses the B-spline method to minimize yaw-cost in complex marine environments, further refining the path planning process for USVs. Building upon the existing methodologies in mobile robot path planning, Jiang et al. [54] proposed an advanced adaptive genetic algorithm inspired by the ordered clustered Traveling Salesman Problem (TSP). The algorithm employs innovative mutation and crossover strategies specifically designed to optimize pathfinding in complex environments, thereby improving path efficiency and enhancing obstacle avoidance capabilities. Although simulation results validate the algorithm’s effectiveness, further tests in real-world conditions are necessary to fully assess its robustness and practical applicability.

4.2. Multi-Constraint Optimization

Multi-constraint optimization addresses the challenges of path planning in constrained environments by incorporating dynamic and environmental constraints into the standard algorithm [55]. This approach ensures that the planned paths are not only optimized, but also feasible in practical applications, particularly for USVs.

The optimization problem considers several key constraints:

• Dynamic constraints:

  $$\parallel \mathbf{v}\left(t\right)\parallel \le v_{\max },\parallel \mathbf{a}\left(t\right)\parallel \le a_{\max },R\left(t\right)\ge R_{min}$$

  (7)

  where $\mathbf{v}\left(t\right)$ and $\mathbf{a}\left(t\right)$ are the velocity and acceleration, and $R\left(t\right)$ is the turning radius at time t.
• Environmental constraints:

  $$\parallel \mathbf{p}\left(t\right)-{\mathbf{p}}_{\mathrm{obs}}\left(t\right)\parallel \ge d_{\mathrm{safe}}$$

  (8)

  where $\mathbf{p}\left(t\right)$ is the position of the vehicle and ${\mathbf{p}}_{\mathrm{obs}}\left(t\right)$ is the position of obstacles at time t, with $d_{\mathrm{safe}}$ being the minimum safe distance.
• Energy constraint:

  $$E_{\mathrm{total}}=\sum _{t=0}^{T}P\left(t\right)\Delta t$$

  (9)

  $$E_{\mathrm{total}}\le E_{\max }$$

  (10)

  where $P\left(t\right)$ is the power consumption, T is the total time, and $E_{\max }$ is the maximum allowable energy consumption.

The objective of multi-constraint optimization is to minimize a cost function $J\left(\mathbf{p}\right(t\left)\right)$ that might include terms for path length, time, and energy, subject to the above constraints:

$$\underset{\mathbf{p}\left(t\right)}{min}J\left(\mathbf{p}\left(t\right)\right)=\sum _{t=0}^T\left[\alpha L\left(\mathbf{p}\right(t\left)\right)+\beta T\left(\mathbf{p}\right(t\left)\right)+\gamma E\left(\mathbf{p}\right(t\left)\right)\right]\Delta t$$

(11)

By integrating these constraints, multi-constraint optimization ensures that the generated paths are not only optimal, but also realistic and implementable in dynamic and constrained environments.

Kim, M. et al. [56] proposed ARC-Theta*, an innovative path planning method combining multi-constraint optimization and curve fitting techniques. This algorithm primarily addresses the path planning problem for USVs under various constraints using a weighted occupancy grid map and Theta* search. ARC-Theta* not only considers the heading angle and angular rate constraints of the vehicle, but also integrates Dubins curves for smooth path fitting at the start and end points. Although the algorithm involves curve fitting, its core feature and main contribution lie in efficiently solving the multi-constraint path planning problem. Figure 5 illustrates the operation of the ARC-Theta* algorithm in comparison to the basic Theta* algorithm. The figure demonstrates how ARC-Theta* optimizes pathfinding by adhering to multiple constraints, such as maintaining a feasible heading angle, considering angular rate limits, and ensuring smooth navigation around obstacles. The basic Theta* algorithm, represented by the solid line, generates a path that disregards these constraints, often resulting in sharp turns and unrealistic paths that may not be feasible for real-world vehicles. In contrast, the dashed line representing the ARC-Theta* path shows how the algorithm adjusts the trajectory to respect the vehicle’s physical constraints, such as turning radius and smooth heading transitions. This results in a more practical and executable path, especially for systems where sudden changes in direction are not possible due to mechanical or dynamic limitations. Additionally, the ARC-Theta* algorithm ensures obstacle avoidance and continuous heading adjustments, making it more suitable for real-time applications in constrained environments.

Liang Hu et al. [57] introduced an innovative online path planning method for USVs that generates collision-free and COLREGs-compliant paths through a multi-objective optimization strategy using particle swarm optimization. This method assesses the type of maritime encounter and compliance with COLREGs, thereby prioritizing the adequacy of planning behavior, including specific motion restrictions such as velocity and heading.

Yang J. M. et al. [58] presented a multi-constraint optimization approach using the Finite Angle A* (FAA*) algorithm for the path planning of USVs. This approach addresses the limitations of traditional A* algorithms by incorporating constraints related to the vehicle’s dimensions and its initial heading, which are critical for practical navigation in real-world environments. The FAA* algorithm enhances the path planning process by allowing for smoother and more feasible paths that account for the turning capabilities of the USV and avoid collisions. The implementation on satellite thermal images further demonstrates the practical applicability of this method, ensuring that the calculated paths are not only optimal in terms of distance, but also safe and executable by the USV. The study concludes that the FAA* algorithm, with its ability to handle complex environments and constraints, provides a robust solution for collision-free path planning in autonomous maritime navigation. At the same time, Zuquan et al. [59] emphasized speed constraints to navigate around dynamic obstacles, initially using the Particle Swarm Optimization algorithm to plan paths in static environments, then adjusting for the relative speed between the USV and dynamic obstacles to maintain navigability.

4.3. Summary

In responsive pathfinders, the planning space, environmental conditions, and select dynamic constraints are taken into account. Methods such as the Dubins approach consider factors like environmental accessibility and the shape of objects. The planning process unfolds over time as a sequence of decisions. However, only certain limitations on the actions of the research objects are factored in, such as curve fitting and multi-constraint optimization which account for an object’s speed and turning radius. Moreover, the objective of planning is to determine an optimal trajectory, aiming to align the planned path closely with the actual trajectory.

However, the approach to incorporating dynamic constraints typically treats them as independent variables. This method often involves linearly integrating one or two constraints into the algorithm without considering the interplay between them. As a result, trajectory planning, while enhancing the path’s adherence to projected movements, does not fully address the complex dynamics at play.

Moreover, responsive pathfinders does not entirely fulfill the ultimate objective of path planning for USVs, which is to effectively reach a designated goal point.

5. Advanced Strategic Pathfinders

Advanced Strategic Pathfinders represent the pinnacle in the development of path planning algorithms for USVs, especially designed to tackle the most challenging and dynamic maritime environments. These pathfinders are particularly critical for underactuated USVs, which cannot independently control movement in all directions and thus require sophisticated strategies to navigate effectively. Unlike simpler pathfinding methods, Advanced Strategic Pathfinders integrate complex models of the vehicle’s kinetics and dynamics, along with environmental data, to optimize navigation in real time [60,61]. They are capable of making rapid adjustments in response to unexpected changes in the environment, such as sudden weather shifts or unanticipated obstacles. Figure 6 illustrates the paths generated by these pathfinders, demonstrating how they adapt preplanned trajectories to actual conditions, ensuring accuracy and safety under high-complexity scenarios.

Environmental factors are crucial in this process. Advanced Strategic Pathfinders must effectively adapt to and utilize natural forces like wind and water currents. Strong control systems are crucial for maintaining the USV’s trajectory stability amidst the unpredictability of marine environments. Advanced control strategies enable the USV to dynamically adjust to immediate changes, such as unexpected weather conditions and obstacles, ensuring the USV remains on path to meet objectives like data collection or surveillance.

Generally, three primary methods are employed to address the challenges of Advanced Strategic Pathfinders for underactuated systems like USVs. The first method relies on Control Theory, the second utilizes random sampling techniques, and the third leverages reinforcement learning.

5.1. Control Theory for USV Advanced Strategic Pathfinders

Control Theory plays a pivotal role in the Advanced Strategic Pathfinders for underactuated USVs, particularly within environments constrained by dynamic factors. Initially, this approach leverages a fundamental pathfinding algorithm, typically a references from the Basic Pathfinders class, to establish a preliminary collision-free trajectory from the origin to the destination. The primary focus then shifts to the second phase, which involves the development of a sophisticated control system. This system, predicated on a robust mathematical model of the USV, meticulously integrates both kinematic and dynamic constraints. The designed controller is essential for refining the trajectory in real time, ensuring that the USVs can dynamically adjust their path in response to both predictable and unpredictable environmental stimuli. This dual-phase approach not only enhances the navigational precision, but also significantly boosts the operational resilience of the USVs under complex maritime conditions.

This control system, based on a robust mathematical model of the USV, meticulously integrates both kinematic and dynamic constraints. The kinematic model describes the motion of the USV without considering forces. The kinematic equations might be

$$\dot{x}=vcos\left(\theta \right),\dot{y}=vsin\left(\theta \right),\dot{\theta }=\omega$$

(12)

where $(x,y)$ are the coordinates of the USV, v is the linear speed, $\theta$ is the heading angle and $\omega$ is the angular velocity.

The dynamic model includes the forces and torques acting on the USV [62], leading to equations such as

$$m\dot{v}=F_x-d\left(v\right),I\dot{\omega }=M-r\left(\omega \right)$$

(13)

where m is the mass of the USV, $F_x$ is the force along the x-axis, $d\left(v\right)$ is the drag force, I is the moment of inertia, $\omega$ is the angular velocity, M is the torque, and $r\left(\omega \right)$ is the rotational drag.

The designed controller, such as a PID controller [63], is essential for refining the trajectory in real time, ensuring that the USVs can dynamically adjust their path in response to both predictable and unpredictable environmental simulations:

$$u\left(t\right)=K_{p}e\left(t\right)+K_d\dot{e}\left(t\right)+K_i\int e\left(t\right)dt$$

(14)

where $u\left(t\right)$ is the control input (e.g., thrust or rudder angle), subject to physical constraints such as saturation limits, $e\left(t\right)$ is the error between the desired trajectory and the actual trajectory, with units matching the output $u\left(t\right)$ (e.g., position error or heading angle error) and $K_p$, $K_d$, and $K_i$ are the proportional, derivative, and integral gains, respectively, and their units are chosen to ensure consistent dimensions in the control equation.

This dual-phase approach not only enhances the navigational precision, but also improves operational ability of the USVs under complex maritime conditions.

At the heart of this method is the concept of motion control, which involves applying a control strategy to either reconstruct or approximate the initially formulated “ideal path” [64]. Depending on the specific objectives, motion control can be categorized into three types: point stabilization, path tracking, and path following [64]. While this approach is effective within its domain, it leans more towards control techniques than planning strategies.

Moreover, Zhe Du et al. [60] developed trajectory units based on ship mathematics, specifically using the Maneuvering Mathematical Group (MMG) model [65]. They considered the dynamic requirements of a USV and introduced a advanced strategic path solver algorithm tailored for such vehicles. Building on their previous work, Zhe Du et al. [66] went on to propose 32 directional USV trajectory units and a novel path search algorithm for USV Advanced Strategic Pathfinders.

Similarly, Bitar, G. et al. [67] explored an optimized Advanced Strategic Pathfinders algorithm that starts with the A* algorithm to determine the shortest piecewise linear path. However, since such paths are not directly applicable to USV Advanced Strategic Pathfinders due to their practical limitations, they refined the approach by connecting the waypoints generated by the A* algorithm with circles and introduced artificial dynamics to make the path more feasible and practical. However, this modification may compromise the path’s optimality by altering the shortest waypoints.

Furthermore, expanding on these advancements, Feng et al. [68] introduced innovative control strategies based on the Serret–Frenet coordinate system and Lyapunov stability theory, which enhance the precision of path following and motion control in USVs. Particularly, it details solutions for adjusting USV’s velocity dynamically in scenarios like derailment correction and dynamic obstacle avoidance. These methods enable USVs to adapt their maneuvering strategies effectively in real-time, ensuring both accurate path following and efficient obstacle avoidance without deviating from their intended paths. However, the paper notes the need for real-world testing to confirm these advancements’ applicability across diverse operational environments, pointing out a potential limitation in their current experimental validation. Li et al. [69] introduced a novel control algorithm designed for USVs. The key contributions of this work include the development of a dynamic event-triggered mechanism (DETM) combined with a prescribed performance control (PPC) technique to ensure that the path-following error remains within a predetermined boundary. This approach reduces the need for continuous computation of the guidance reference signal, optimizing communication efficiency between the controller and the actuator systems. The effectiveness of the proposed algorithm is demonstrated through numerical simulations, showing its ability to maintain stable and accurate path following while minimizing communication loads.

5.2. Random Sampling-Based Approach

The Random Sampling-Based Approach in Advanced Strategic Pathfinders offers a stark contrast to the deterministic methodologies typically employed in basic pathfinders [70]. This approach is particularly relevant in high-dimensional planning spaces, like those encountered with USVs [71]. It introduces unpredictability and versatility, effectively handling the rapid increase in complexity faced by advanced path planners in constrained environments.

First, the Probabilistic Roadmap Method (PRM) is a strategic algorithm originally developed for spatial planning, involving the generation of random nodes throughout the planning space to mark feasible regions or ’free spaces’. These nodes create a network of potential paths, forming a ’random roadmap’ that conceptualizes all possible routes within the planning space [72,73]. Chowdhury introduced PRM-A*, which combines PRM with the A* algorithm to balance safety and optimality, initially running both algorithms and then refining the path using PRM [74]. Further, Chowdhury developed a recursive variant called Recursive Probabilistic Roadmap (r-PRM) for both local and global USV path planning. This method enhances real-time obstacle avoidance by routing the USV behind moving obstacles to minimize collision risks [75].

Second, the Rapidly exploring Random Tree (RRT) algorithm is particularly suited for optimal control and navigating nonholonomic systems, expanding dynamically until it connects with the target region. Ma’s method based on RRT focuses on integrating rule-template sets for traffic scenes to improve planning speed and accuracy [70]. Wen enhanced traditional RRT with a heuristic dual sampling domain reduction to plan efficient, safe paths with considerations for the USV’s motion states and environmental factors [76]. Additionally, Ouyang modified the RRT algorithm to improve formation shape stability in unmanned boats by using non-strictly conformal correction vectors during the expansion phase [77]. Lastly, Ding introduced the Expanding Path RRT* (EP-RRT*) to quickly identify feasible paths and expand these using a heuristic sampling area, which enhances node utilization and accelerates convergence in complex environments like narrow corridors [78].

These methods demonstrate significant advancements in USV Advanced Strategic Pathfinders, combining robust control with innovative algorithms to optimize path safety, efficiency, and adaptability in complex maritime environments.

5.3. Reinforcement Learning Approach

Reinforcement Learning (RL) is a type of machine learning where an agent learns to make decisions by interacting with an environment [79]. In RL, the agent takes actions in the environment, observes the outcomes, and receives feedback in the form of rewards or penalties. Over time, the agent learns to maximize cumulative rewards by identifying the most effective actions to take in different situations. This learning process makes RL particularly suitable for dynamic and complex environments, where traditional rule-based or static approaches may struggle to adapt. In the context of USVs, RL provides a powerful framework for path planning by enabling the USV to continuously learn from its experiences and improve its decision-making process over time, even in the face of unpredictable marine conditions [80,81].

Unlike traditional path planning methods that often rely on pre-defined models and static algorithms, RL introduces a level of adaptability and flexibility that is critical for effective USV navigation in real-world scenarios [82]. Traditional approaches may be limited by their inability to cope with new or unforeseen challenges, such as sudden changes in weather or unexpected obstacles. RL, on the other hand, allows USVs to dynamically adjust their paths by learning from real-time data and past experiences, ensuring that they can navigate safely and efficiently even in the most challenging environments [83]. This continuous learning capability positions RL as a highly relevant and advanced method for enhancing the robustness and autonomy of USV path planning. The basic principle is as follows.

The Markov Decision Process (MDP) is defined as:

$$(S,A,P,R,\gamma )$$

(15)

where S is set of states (e.g., USV positions), A is set of actions (e.g., navigational commands), $P(s^{\prime }\mid s,a)$ is transition probability from state s to state $s^{\prime }$ given action a, $R(s,a)$ is reward function for taking action a in state s and $\gamma$ is discount factor, $0\le \gamma \le 1$.

The MDP framework models the decision-making environment for the USV, where the goal is to choose actions that maximize cumulative rewards over time.

The policy is defined as:

$$\pi (a\mid s)$$

(16)

where $\pi (a\mid s)$ is the probability of taking action a when in state s. The policy defines the strategy the USV uses to select actions based on its current state.

The value function under policy $\pi$ is given by:

$$V^{\pi }\left(s\right)={\mathbb{E}}_{\pi }\left[\sum _{t=0}^{\infty }{\gamma }^{t}R(s_t,a_t)\right]$$

(17)

where $V^{\pi }\left(s\right)$ is expected cumulative reward starting from state s following policy $\pi$, $R(s_t,a_t)$ is reward at time t for state $s_t$ and action $a_t$ and ${\gamma }^t$ is discount factor raised to the power of time t. The value function estimates the total expected reward for the USV starting from a given state s and following a specific policy $\pi$.

The action-value function under policy $\pi$ is defined as:

$$Q^{\pi }(s,a)={\mathbb{E}}_{\pi }\left[\sum _{t=0}^{\infty }{\gamma }^{t}R(s_t,a_t)\mid s_0=s,a_0=a\right]$$

(18)

where $Q^{\pi }(s,a)$ is expected cumulative reward starting from state s, taking action a, and then following policy $\pi$, $s_0$ is the initial state and $a_0$ is the initial action. The action-value function estimates the total expected reward for taking a specific action a in state s and then following policy $\pi$.

In path following scenarios, Zhao et al. [81] included the development of a Smoothly Convergent Deep Reinforcement Learning (SCDRL) approach based on Deep Q Networks (DQN), which is designed to reduce the complexity of control laws for USV path following. The authors introduced an improved DQN structure, an exploring function based on adaptive gradient descent for efficient training, and a new reward function to enhance decision-making capabilities. The effectiveness of the proposed method was validated through numerical simulations, demonstrating smoother convergence and competitive path-following performance compared to traditional methods. At same time, in search goal path scenarios, Hao et al. [84] proposed a Dynamic and Fast Q-learning (DFQL) algorithm for the path planning problem of underactuated Unmanned Surface Vehicles (USVs). The authors optimized the initialization of the Q-table by combining the Artificial Potential Field (APF) method with the Q-learning algorithm and designed a reward function that incorporates both static and dynamic rewards to accelerate the convergence of the algorithm and reduce computation time. The main contributions of this paper include the introduction of a novel algorithm capable of addressing both online and offline path planning for USVs, the validation of the algorithm’s effectiveness and superiority in various environments, and the demonstration of its advantages in terms of path length, turning angle, and computation time. However, both studies lack simulation or real-world testing, leaving the effectiveness of their path planning algorithms under disturbances in practical environments unverified.

To bring the testing environment closer to real-world conditions, Zhou et al. [85] developed a novel real-time navigation algorithm for USVs using Deep Reinforcement Learning (DRL). The key contributions of their work include the creation of a DRL-based approach that allows USVs to autonomously navigate through complex environments in real time, adapting effectively to dynamic obstacles and varying conditions. The algorithm is specifically designed to optimize the path from a starting point to a target destination, demonstrating its effectiveness through simulations that account for the actual movement of the vehicle rather than simple point motion. Wang et al. [86] developed an improved Q-Learning algorithm, specifically the Neural Network Smoothing and Fast Q-Learning (NSFQ) algorithm, for the path planning of USVs. The algorithm is tested both in simplified point-mass simulations and more realistic marine simulation environments. The NSFQ algorithm is designed to handle global path planning and obstacle avoidance for USVs by integrating a radial basis function (RBF) neural network to approximate the Q-function, thereby enhancing the convergence speed and computational efficiency. The algorithm also considers the dynamic characteristics of USVs, including heading angle, motion characteristics, and safety measures, to ensure the planned paths are both safe and efficient. The testing results indicate that the NSFQ algorithm outperforms traditional methods like A* and RRT in terms of path length, sailing time, heading stability, and path smoothness in both types of simulation environments. However, the study acknowledges that the computation time for the NSFQ algorithm is longer than that of traditional methods.

RL has rapidly evolved as a key approach in USV path planning, driven by its ability to adapt to dynamic and complex environments. Unlike traditional methods, which often rely on static models, RL enables USVs to continuously learn and improve their decision-making processes by interacting with the environment in real time. However, despite the progress, there remains a need for further research in applying RL to real-world scenarios, ensuring that these algorithms can robustly handle the complexities of actual marine environments.

5.4. Summary

Advanced Strategic Pathfinders represent the apex in USV path planning technologies, addressing not only the geometric and kinetic challenges, but also integrating complex environmental interactions and dynamic constraints. This section outlines the comprehensive decision-making framework employed by these pathfinders, which is depicted in Figure 7, illustrating the multi-faceted approach necessary for effective navigation in unpredictable maritime environments.

The Advanced Strategic Pathfinders process incorporates several key considerations:

• Reachability (R) = 1 or 0: indicates whether a destination is reachable (R = 1) or not (R = 0), influencing subsequent planning stages.
• Import USV model and environment factors: starts by integrating a detailed model of the USV along with critical environmental factors such as wave height, wind speed, and water currents that significantly affect navigational decisions.
• Planning space: considers the spatial constraints imposed by the environment and the USV’s own dynamic capabilities.
• Planning time: time is discretized, with each interval representing a decision point in the navigation process.
• Planning behavior: focuses on operational decisions such as power and rudder adjustments needed to navigate effectively.
• Planning criterion: aims to devise a navigational path that not only maintains environmental and spatial connectivity, but also adheres to the USV’s operational constraints and objectives.

This structured approach allows for precise and adaptive navigation strategies that can dynamically respond to changing conditions, ensuring both the safety and efficiency of USV operations in complex maritime settings.

6. Advancements and Challenges in USV Path Planning

6.1. Advancements in Path Planning

The field of USV path planning has advanced significantly, driven by the need for autonomous navigation in increasingly complex water environments. This review categorized USV path planning algorithms into three levels: Basic Pathfinders, Responsive Pathfinders, and Advanced Strategic Pathfinders, each offering unique benefits and facing distinct challenges.

Basic Pathfinders focus on geometric considerations and static maps, which are suitable for stable and predictable environments. These algorithms optimize distance or time, and provide a solid foundation for USV navigation in environments with minimal dynamic changes. However, their main limitation lies in their inability to adapt to real-time environmental changes, making them less suitable for dynamic or unpredictable conditions.

Responsive Pathfinders improve upon Basic Pathfinders by incorporating temporal dynamics and kinematic constraints. These algorithms enable USVs to adapt to changing conditions and moving obstacles, improving navigation efficiency in semi-dynamic settings. While these algorithms can handle more complexity than Basic Pathfinders, they may struggle with highly unpredictable environments where real-time decision-making and predictive capabilities are essential.

Advanced Strategic Pathfinders excel in real-time interaction with complex and unpredictable environments by utilizing advanced sensors and predictive models. These algorithms allow USVs to make informed decisions, modify courses in real time, and anticipate future changes, which is particularly crucial in severe weather conditions or congested waterways. The main advantage of these algorithms is their adaptability and foresight; however, they can be computationally expensive and require sophisticated hardware.

Looking ahead, one promising research direction involves the integration of multi-modal sensor fusion into USV path planning algorithms. By leveraging diverse data sources from multiple types of sensors, such as LiDAR, radar, sonar, 4D mmWave radar, near-infrared cameras, and visual cameras, path planning systems can achieve a more comprehensive understanding of the marine environment. This integration can enhance the USV’s ability to accurately interpret and react to complex and dynamic maritime scenarios. Future studies could focus on developing robust algorithms that effectively merge these sensor inputs to improve decision-making processes, ensuring safer and more efficient navigational outcomes. Such advancements could revolutionize USV operations, particularly in adverse weather conditions, by providing a richer situational awareness and more reliable path planning capabilities.

6.2. Challenges in USV Path Planning

Despite these advancements, significant challenges remain in USV path planning. One of the main challenges is handling environmental uncertainty. USVs operate in environments where conditions can change rapidly, such as shifting weather patterns, tides, and the presence of dynamic obstacles like other vessels. This makes it difficult for any single algorithm to perform optimally across all scenarios. The ability to predict and adapt to these changes in real time remains an ongoing challenge for developers of path planning algorithms.

Another challenge is sensor reliability and data integration. While multi-modal sensor fusion holds promise for improving situational awareness, integrating data from different sensors in real time can be computationally intensive and prone to errors due to inconsistencies or inaccuracies in sensor data. Additionally, communication constraints in maritime environments can impact the ability of USVs to process external data or receive updates from control centers, especially in remote areas.

6.3. Conclusions

In summary, while significant progress has been made in the development of USV path planning algorithms, further refinement is necessary to address the challenges posed by real-world conditions. Basic Pathfinders, Responsive Pathfinders, and Advanced Strategic Pathfinders each offer distinct benefits, but none can fully address the complexities of all maritime environments without some limitations. To move forward, the development of more adaptive, sensor-integrated, and computationally efficient algorithms is critical. Future research should focus not only on improving the capabilities of individual algorithms, but also on addressing the practical challenges faced during implementation, such as energy constraints, sensor integration, and real-time adaptability.

By overcoming these challenges, USV technology will be better positioned to meet the increasing demands of autonomous maritime navigation, enabling safer, more efficient, and more reliable operations in even the most complex and dynamic environments.