Thermal Monitoring of an Internal Combustion Engine for Lightweight Fixed-Wing UAV Integrating PSO-Based Modelling with Condition-Based Extended Kalman Filter
Abstract
1. Introduction
- Development and experimental validation of a novel 0D SZ dynamic model for predicting the cylinder head temperature of ICE engines.
- Development of a revised EKF capable of diagnosing thermal flow degradations in the ICE based on CHT measurements and its dynamic model.
- As a relevant case study, the performance of the proposed method is assessed by simulating degradation transients related to thermal degradation in an ICE used for the propulsion of a modern lightweight fixed-wing UAV. However, the approach can be applied to any ICE.
2. Materials and Methods
2.1. UAV Basic Characteristics
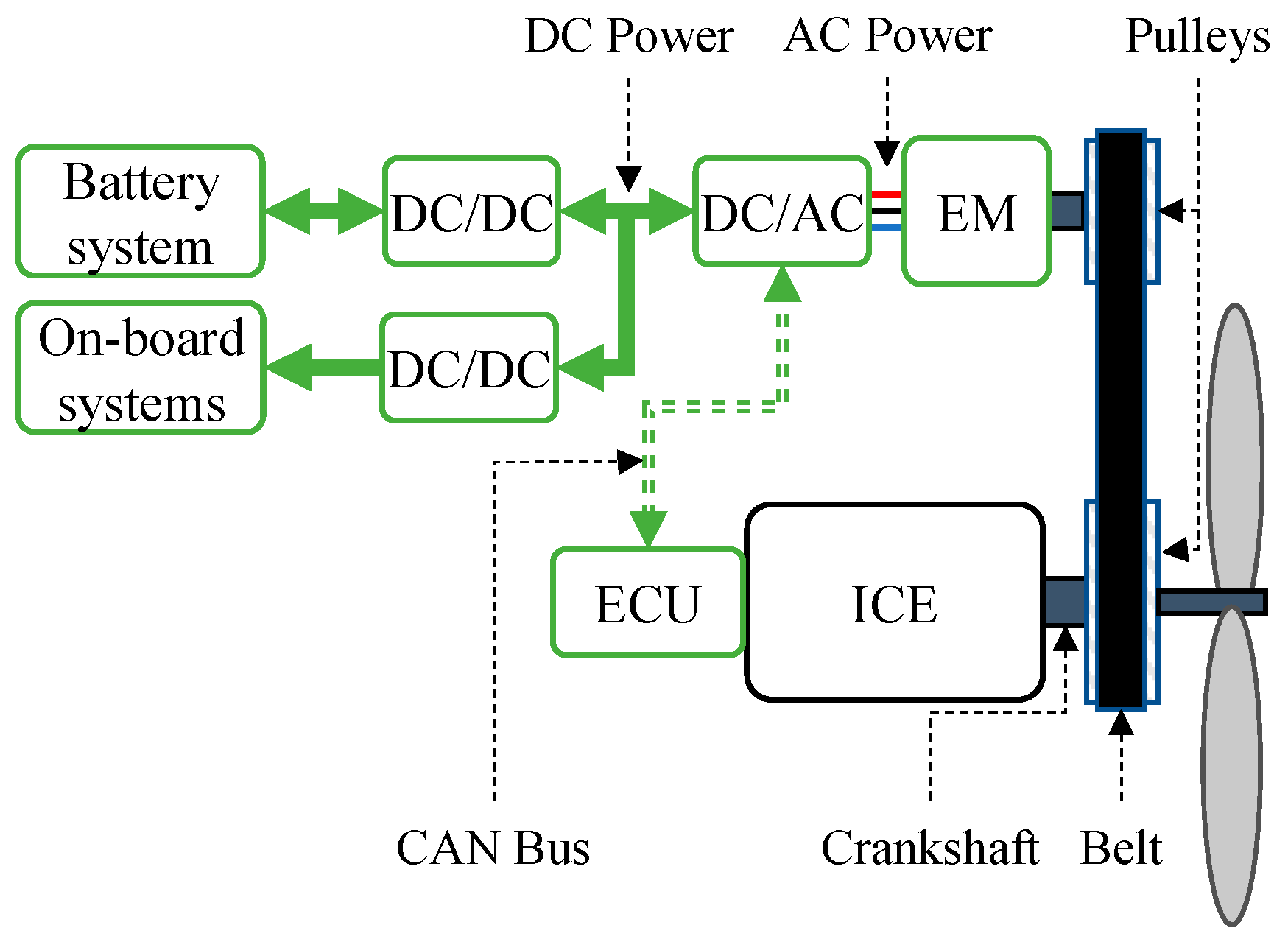
2.2. Propulsion System Description
- A twin-blade fixed-pitch propeller [19];
- A three-phase brushless DC Electric Machine (EM), used as ICE starter and generator for conventional operation [20];
- A belt-pulley mechanical transmission, connecting in parallel arrangement the ICE and the EM;
- A Li-Po battery pack for emergency operations [21];
- On-board systems, including flight controls and payload.
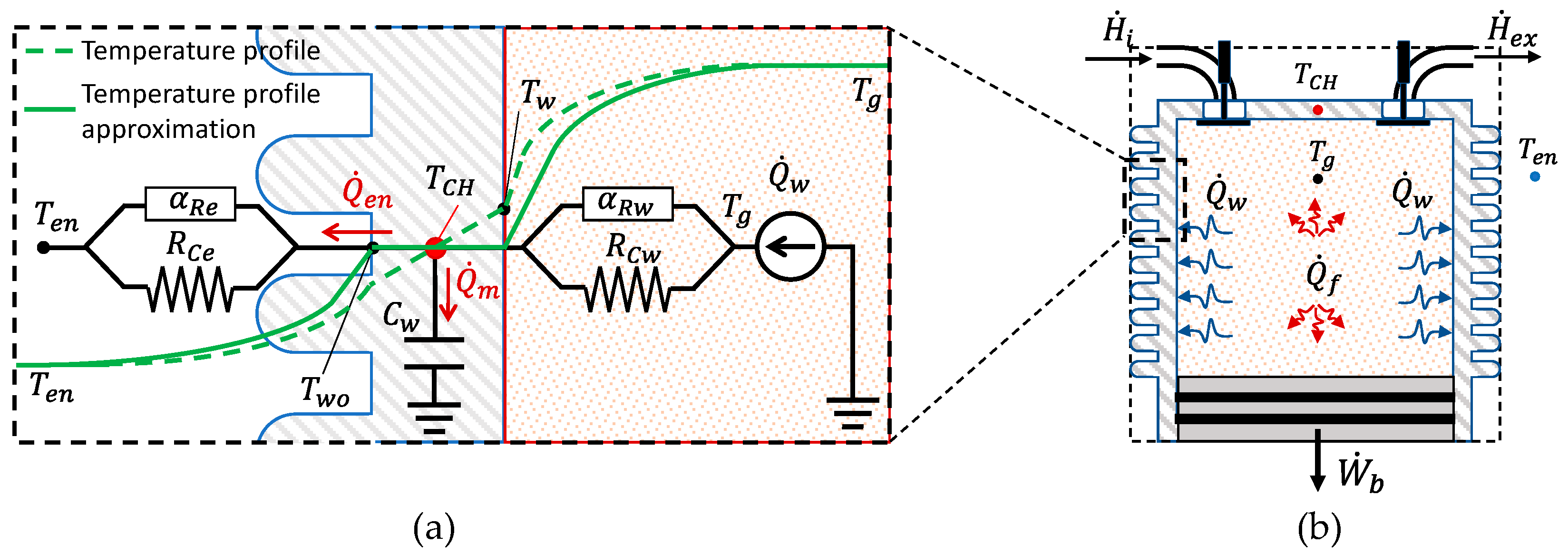
2.3. 0D-SZ Model of the CHT Dynamics
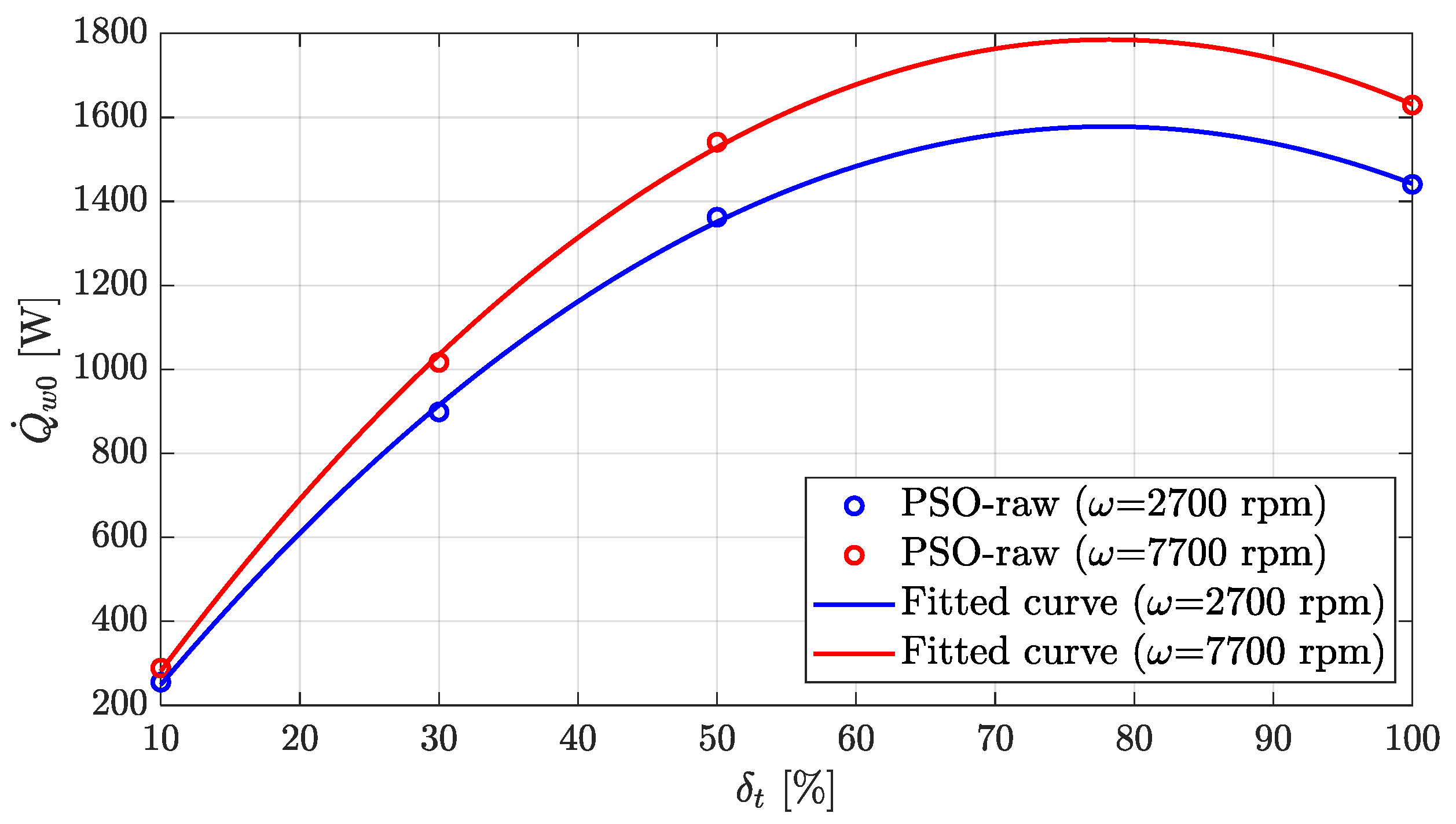
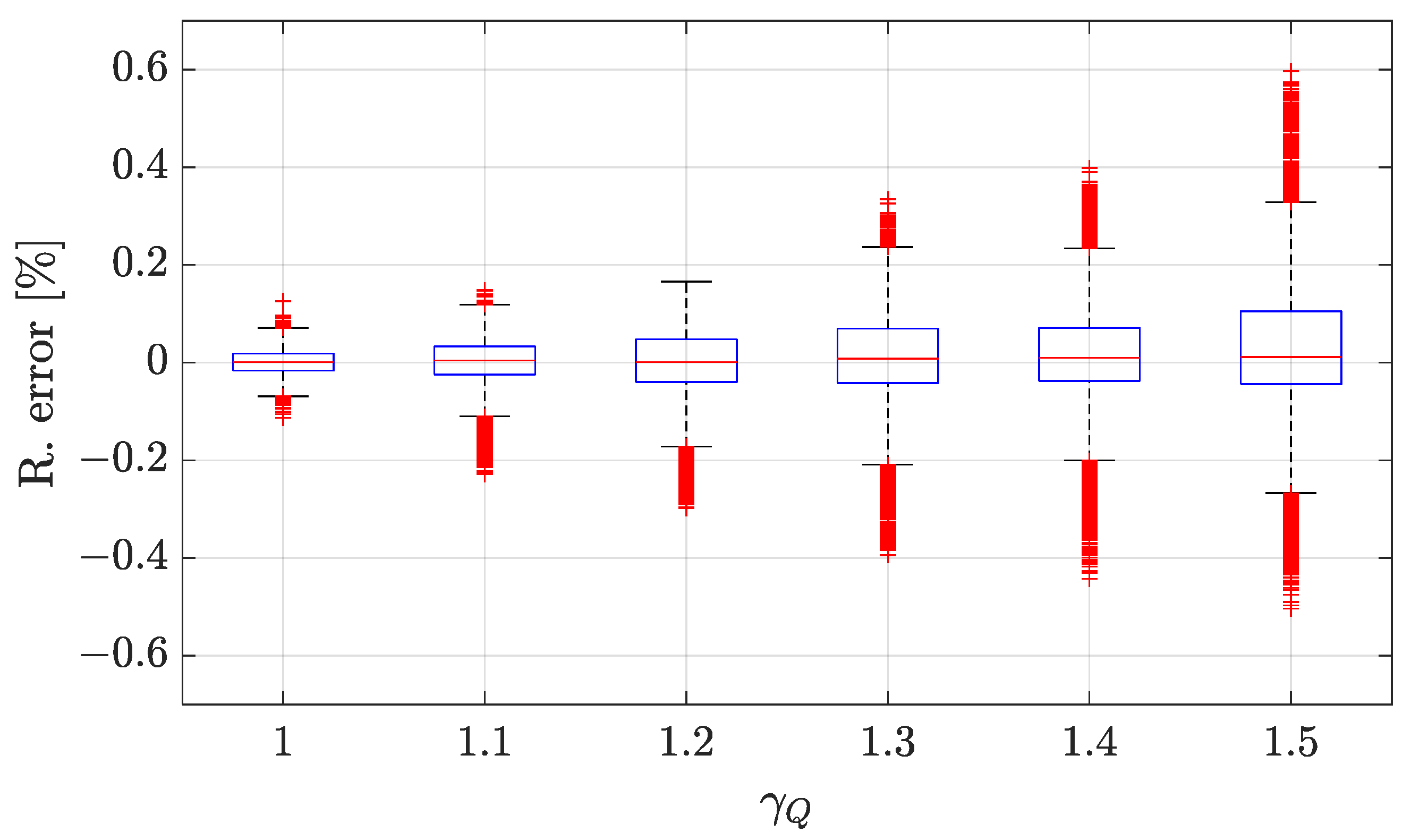
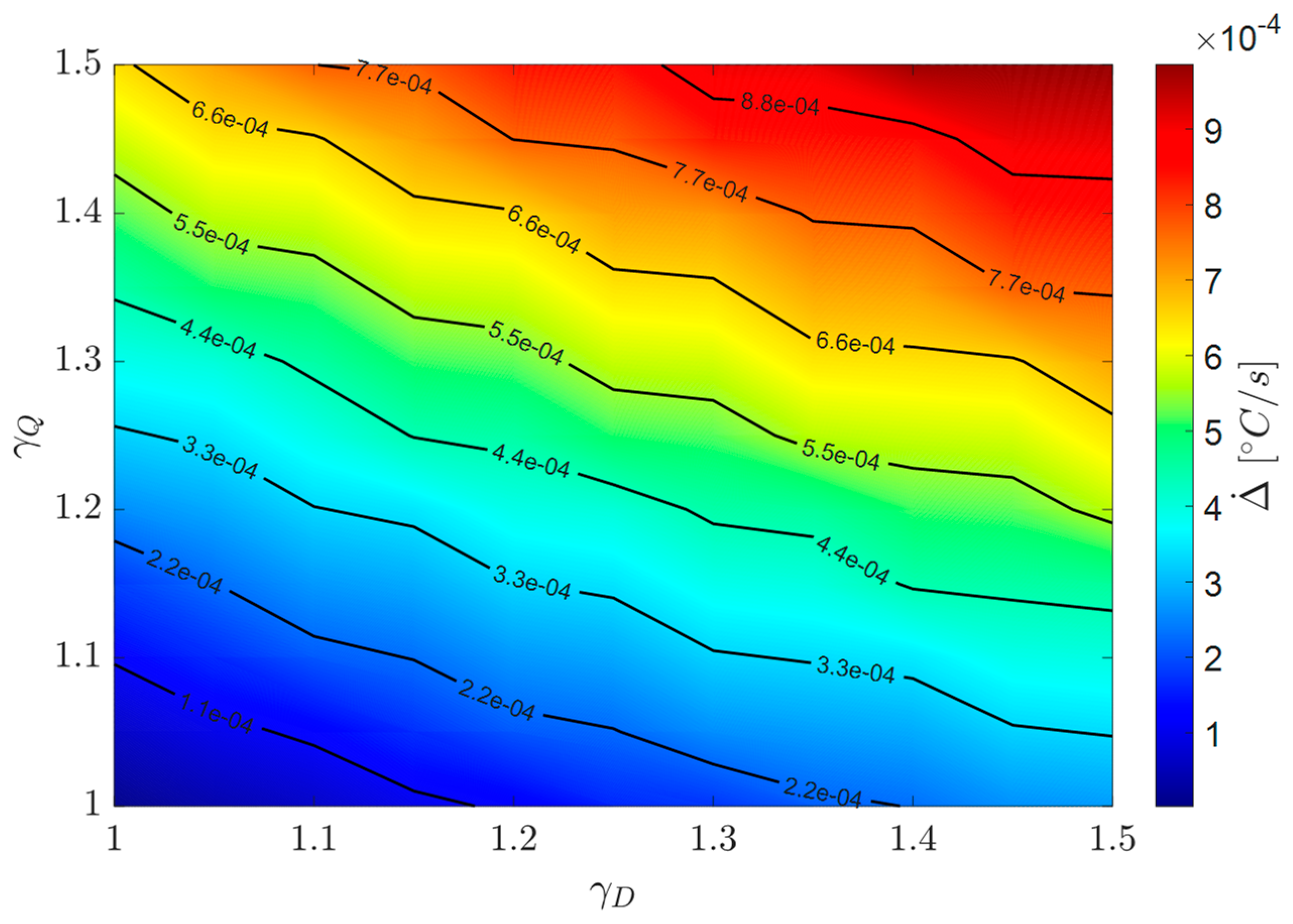
2.4. Particle-Swarm Optimization for Model Identification in Normal Conditions
2.5. CHT Modelling in Degraded Conditions
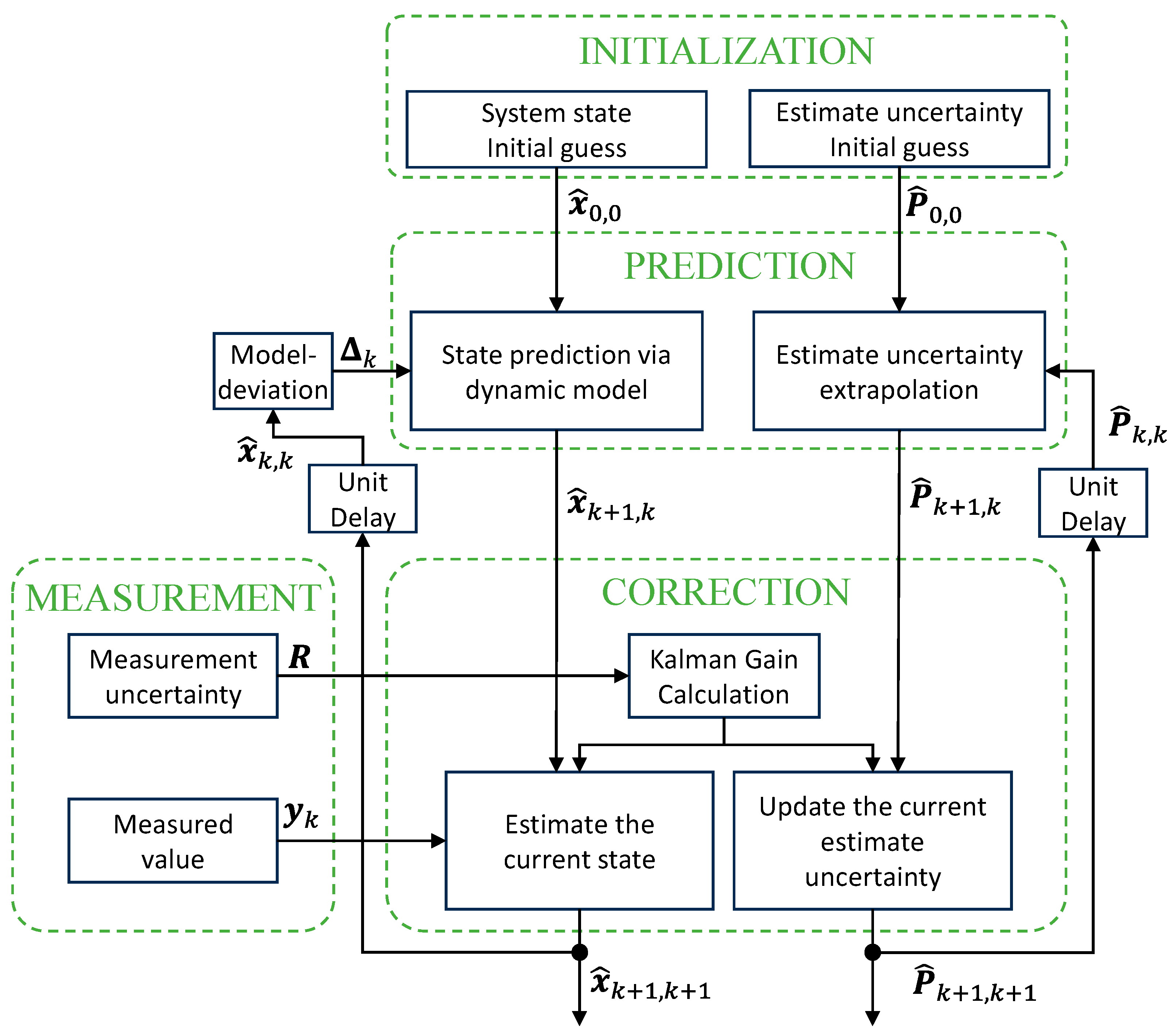
2.6. Condition-Based Extended Kalman Filter for CHT Estimation in Degraded Conditions
- Initialization: set a state estimate () and a state estimation error covariance matrix () at time step 0.
- Prediction: predict the state () and the state error covariance matrix () ahead (a priori) at time step conditioned by measurements at time step :where is the model-deviation term that, estimating the state derivative variation due to degradation, corrects the standard EKF formulation, and is the Jacobian matrix of the dynamic model with respect to the state evaluated at time step :
- Correction: compute the Kalman gain (), update the state estimate () with the measurement (a posteriori), and update the state error covariance matrix , as in Equation (22) [13]:where is the identity matrix, and is the Jacobian matrix of the measurement model with respect to the state variables evaluated at time step :
2.7. CHT Estimation in Degraded Conditions via CBEKF
3. Results and Discussion
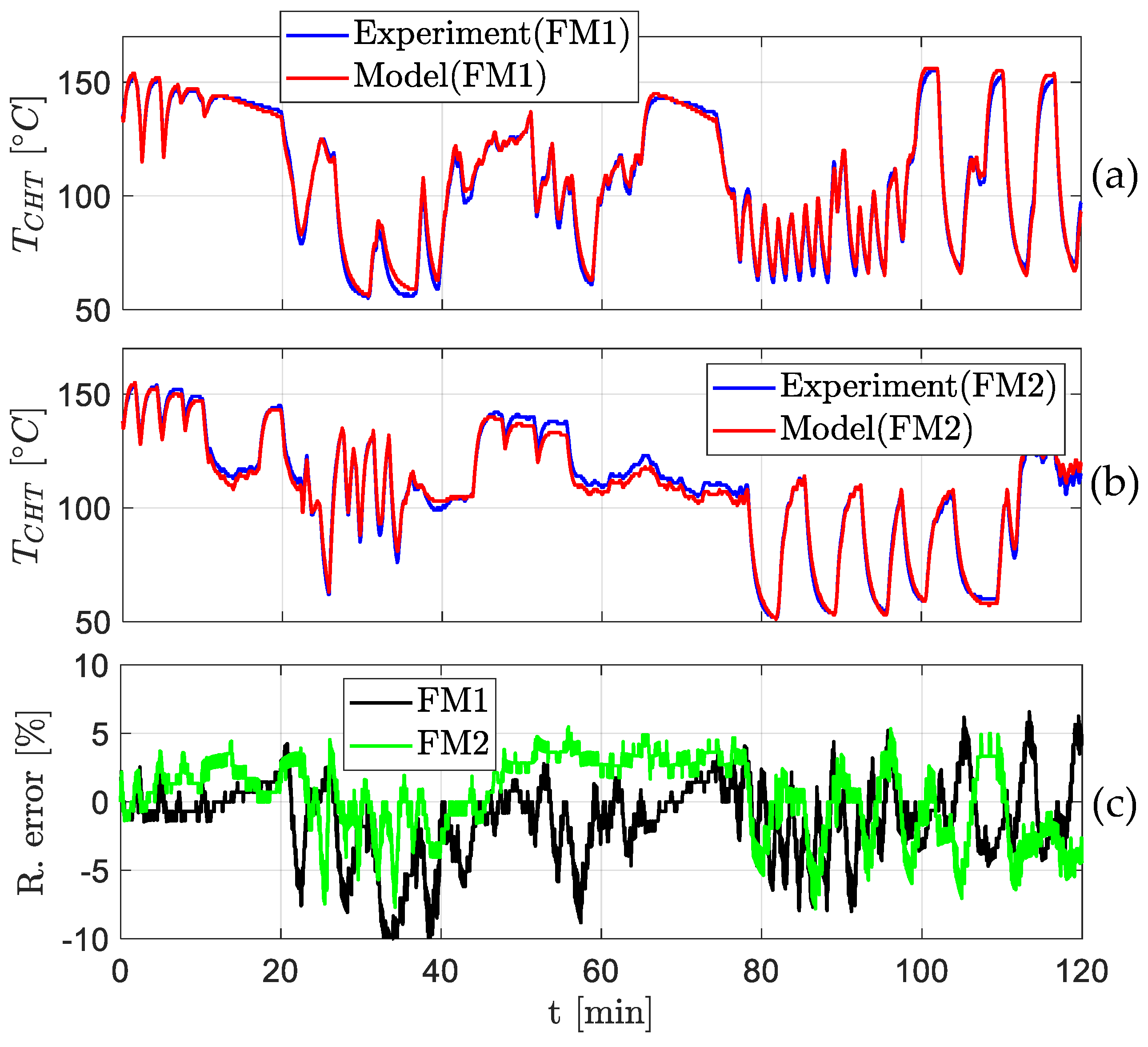
3.1. Model Validation in Nominal Conditions with Experimental Flight Data
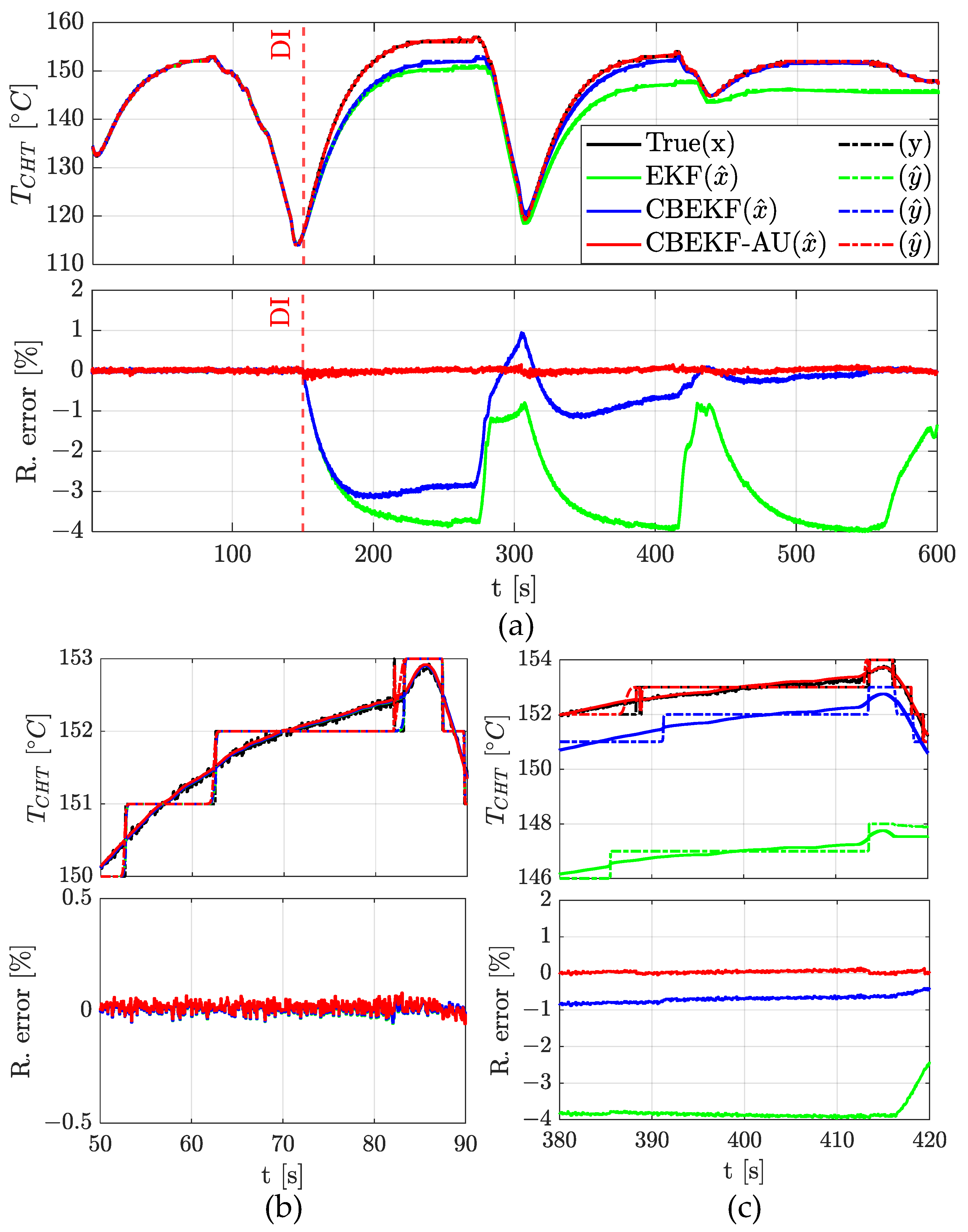
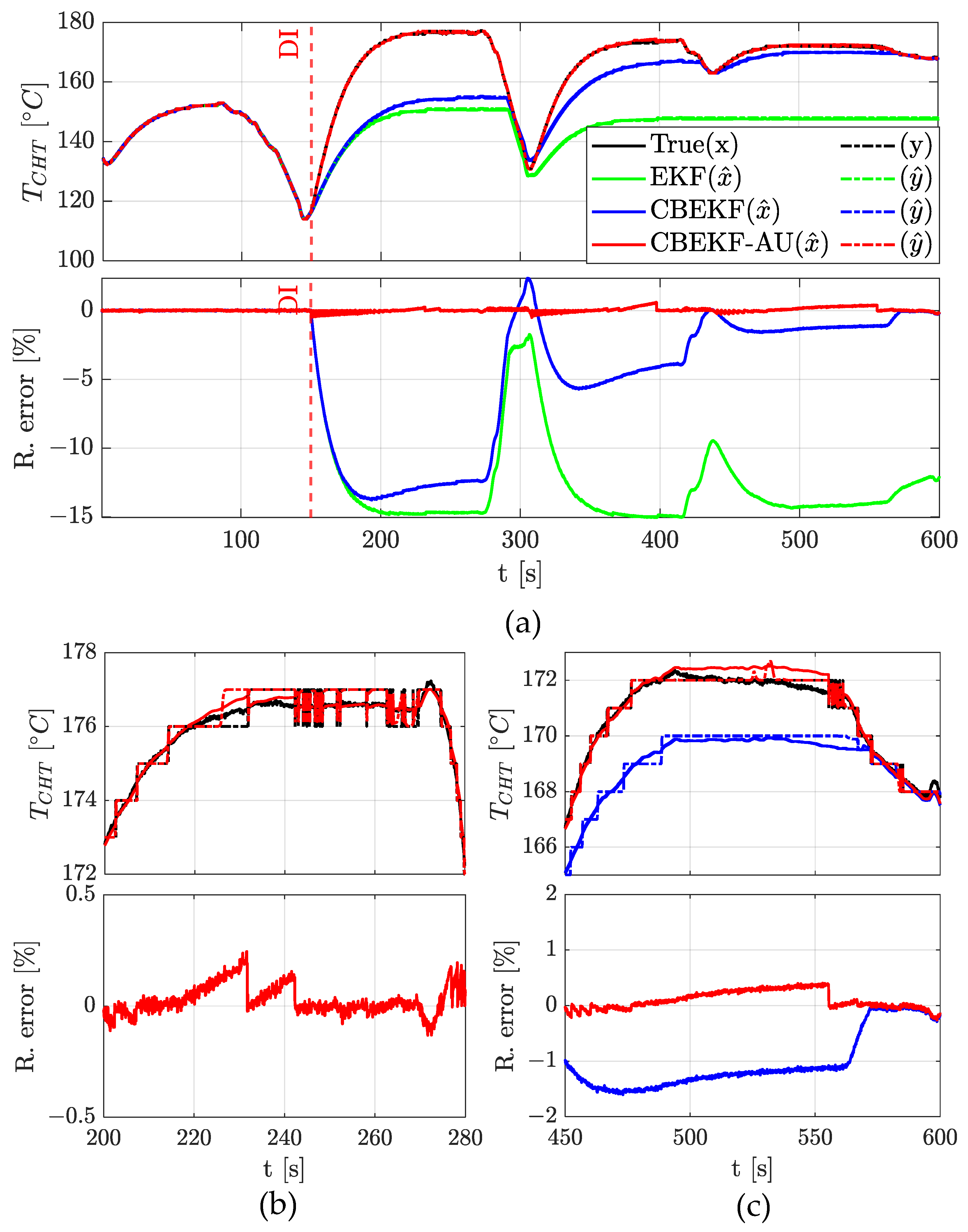
3.2. CHT Estimation via EKF Strategies and Thermal Flow Monitoring
4. Conclusions and Future Developments
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
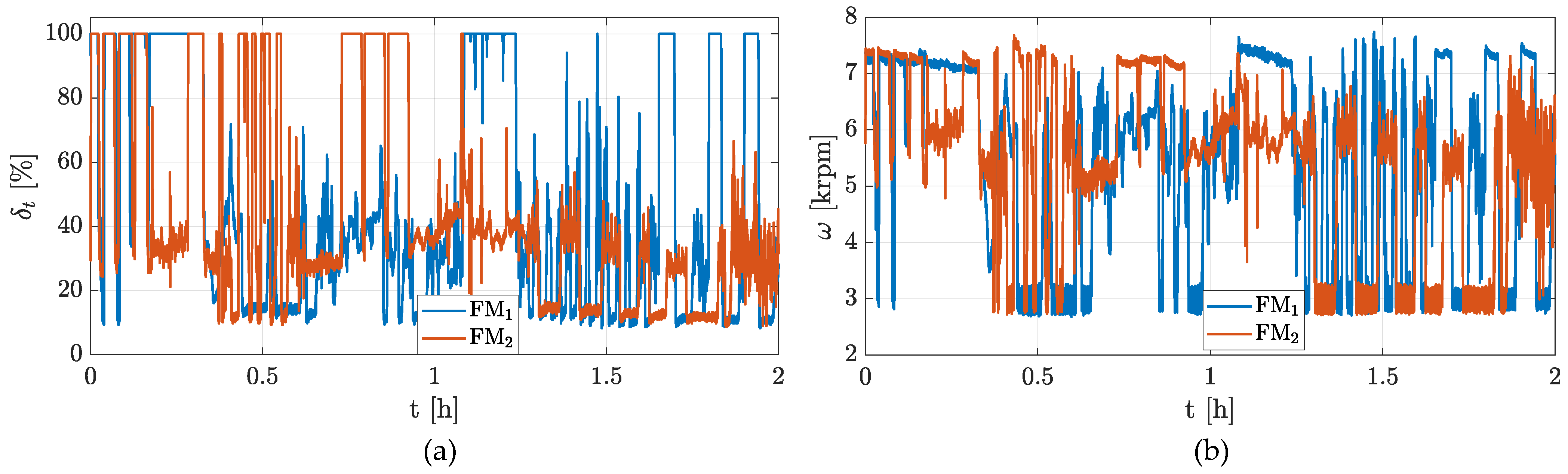
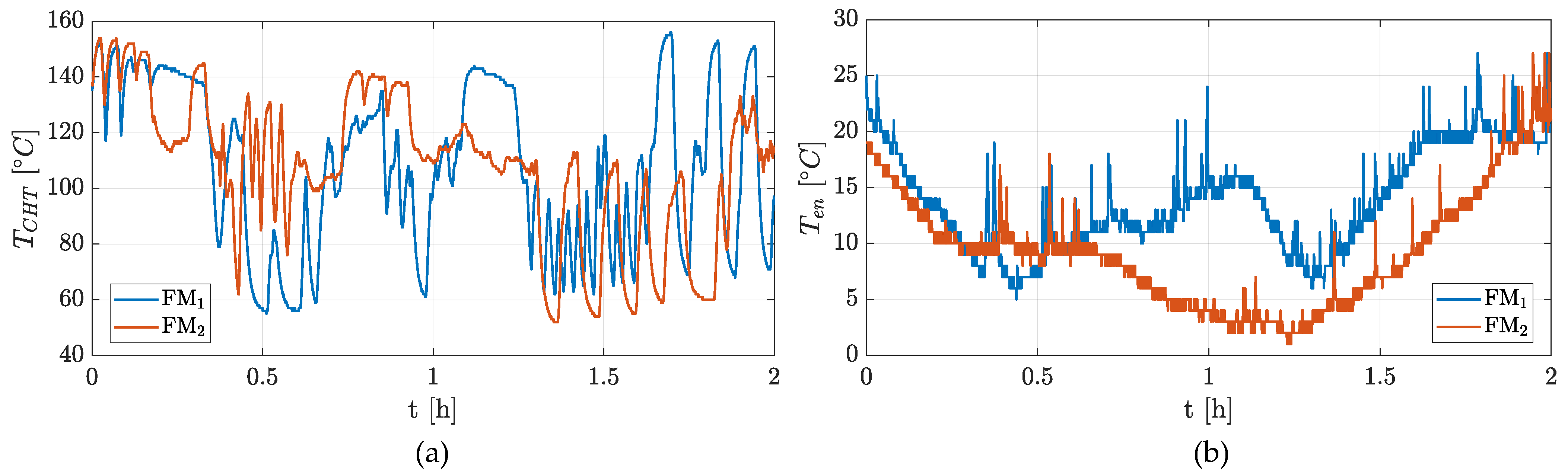
- The experimental data used in this work (The experimental data, which are proprietary to the company, can only be shared in graphical form. Readers interested in obtaining the numerical data file should contact the company Sky Eye Systems s.r.l. (Foligno, Italy) directly) are provided as time histories. The Rapier X-25 system integrates a ground control station that, via the datalink, allows both mission execution and real-time monitoring of key system data. These data are provided below: Figure A1 reports the throttle position () and crankshaft angular speed (); Figure A2 reports the altitude () and calibrated air speed of the UAV (); Figure A3 reports the CHT () and the outside air temperature ().
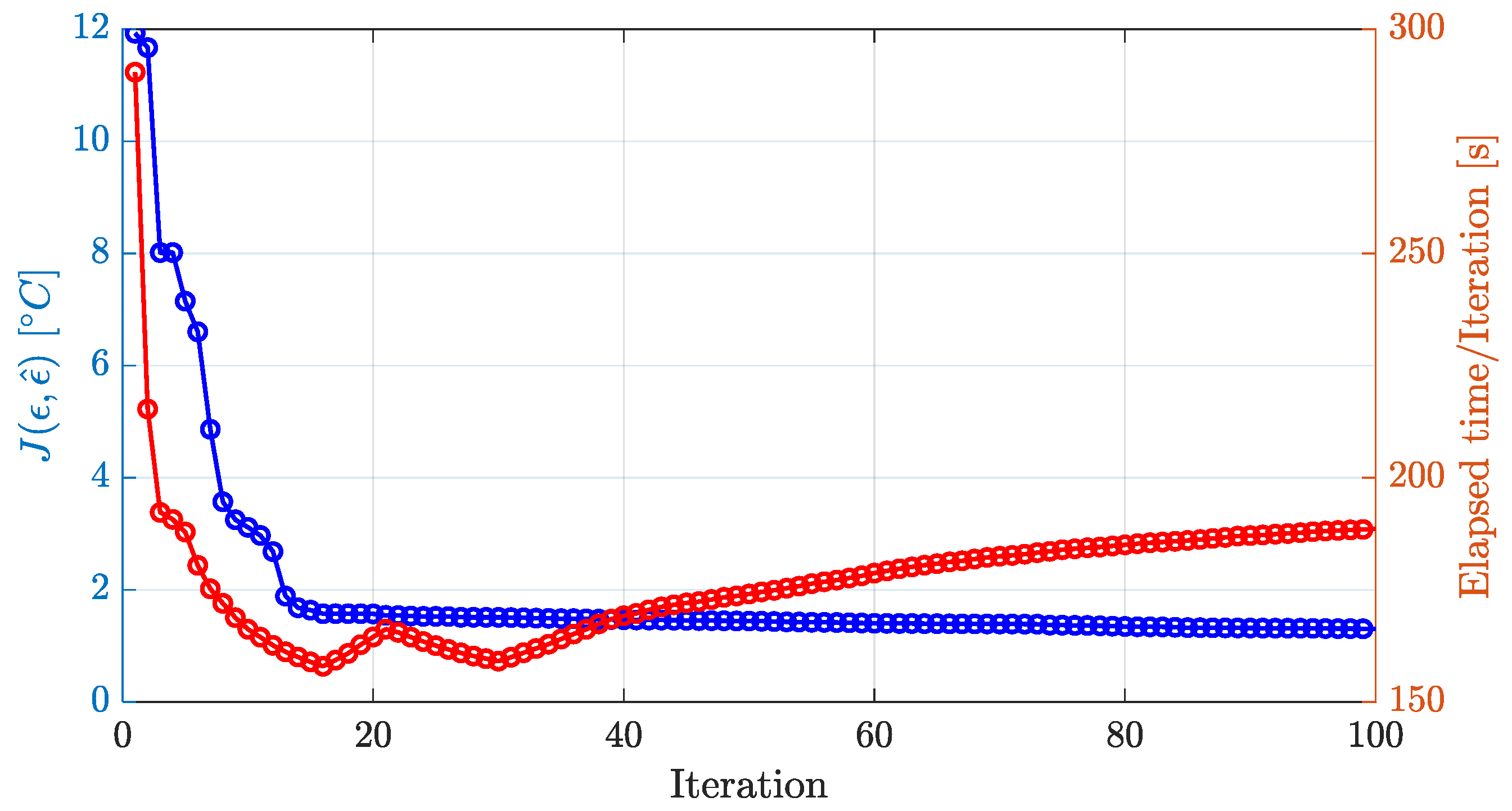
- The PSO cost function and elapsed time over 100 iteration, Figure A5.

| Parameter | Value | Unit |
|---|---|---|
| 570 | J/°C | |
| 0.15 | W/°C | |
| 8.1 × 105 | W/°C4 | |
| 6 | s | |
| 1.55 | - | |
| 2 | - |
References
- Suti, A.; Di Rito, G.; Galatolo, R. Climbing Performance Enhancement of Small Fixed-Wing UAVs via Hybrid Electric Propulsion. In Proceedings of the 2021 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Modena, Italy, 8–9 April 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 305–310. [Google Scholar]
- Silva, F.S. Fatigue on Engine Pistons—A Compendium of Case Studies. Eng. Fail. Anal. 2006, 13, 480–492. [Google Scholar] [CrossRef]
- Thomaz, F.; Teixeira Malaquias, A.C.; Resende de Paula, G.A.; Baêta, J.G.C. Thermal Management of an Internal Combustion Engine Focused on Vehicle Performance Maximization: A Numerical Assessment. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 2296–2310. [Google Scholar] [CrossRef]
- Fonseca, L.; Olmeda, P.; Novella, R.; Valle, R.M. Internal Combustion Engine Heat Transfer and Wall Temperature Modeling: An Overview. Arch. Comput. Methods Eng. 2020, 27, 1661–1679. [Google Scholar] [CrossRef]
- Broatch, A.; Olmeda, P.; Margot, X.; Escalona, J. New Approach to Study the Heat Transfer in Internal Combustion Engines by 3D Modelling. Int. J. Therm. Sci. 2019, 138, 405–415. [Google Scholar] [CrossRef]
- Marinoni, A.; Tamborski, M.; Cerri, T.; Montenegro, G.; D’Errico, G.; Onorati, A.; Piatti, E.; Pisoni, E.E. 0D/1D Thermo-Fluid Dynamic Modeling Tools for the Simulation of Driving Cycles and the Optimization of IC Engine Performances and Emissions. Appl. Sci. 2021, 11, 8125. [Google Scholar] [CrossRef]
- Mauro, S.; Şener, R.; Gül, M.Z.; Lanzafame, R.; Messina, M.; Brusca, S. Internal Combustion Engine Heat Release Calculation Using Single-Zone and CFD 3D Numerical Models. Int. J. Energy Environ. Eng. 2018, 9, 215–226. [Google Scholar] [CrossRef]
- Sjeric, M.; Kozarac, D.; Bogensperger, M. Implementation of a Single Zone K-ε Turbulence Model in a Multi Zone Combustion Model. In Proceedings of the SAE 2012 World Congress & Exhibition, Detroit, MI, USA, 24–26 April 2012. [Google Scholar]
- Giglio, V.; di Gaeta, A. Novel Regression Models for Wiebe Parameters Aimed at 0D Combustion Simulation in Spark Ignition Engines. Energy 2020, 210, 118442. [Google Scholar] [CrossRef]
- Boiarciuc, A.; Floch, A. Evaluation of a 0D Phenomenological SI Combustion Model. In Proceedings of the SAE International Powertrains, Fuels and Lubricants Meeting, Kyoto, Japan, 30 August–2 September 2011. [Google Scholar]
- Payri, F.; Olmeda, P.; Martín, J.; García, A. A Complete 0D Thermodynamic Predictive Model for Direct Injection Diesel Engines. Appl. Energy 2011, 88, 4632–4641. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J. Investigation of the Effect of Simulated Atmospheric Conditions at Different Altitudes on the Combustion Process in a Heavy-Duty Diesel Engine Based on Zero-Dimensional Modeling. J. Eng. Gas. Turbine Power 2022, 144, 061013. [Google Scholar] [CrossRef]
- Grewal, M.S.; Andrews, A.P. Kalman Filtering; Wiley: Hoboken, NJ, USA, 2008; ISBN 9780470173664. [Google Scholar]
- Lu, F.; Lv, Y.; Huang, J.; Qiu, X. A Model-Based Approach for Gas Turbine Engine Performance Optimal Estimation. Asian J. Control 2013, 15, 1794–1808. [Google Scholar] [CrossRef]
- Simon, D. A Comparison of Filtering Approaches for Aircraft Engine Health Estimation. Aerosp. Sci. Technol. 2008, 12, 276–284. [Google Scholar] [CrossRef]
- Lu, F.; Ju, H.; Huang, J. An Improved Extended Kalman Filter with Inequality Constraints for Gas Turbine Engine Health Monitoring. Aerosp. Sci. Technol. 2016, 58, 36–47. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, J.; Luo, C.; Xiong, L.; Pan, Q. Aero-Engine Health Degradation Estimation Based on an Underdetermined Extended Kalman Filter and Convergence Proof. ISA Trans. 2022, 125, 528–538. [Google Scholar] [CrossRef] [PubMed]
- Currawong Engineering. CORVID-29. Available online: https://www.currawongeng.com/corvid-29/ (accessed on 12 August 2024).
- APC—INTERNAL COMBUSTION ENGINES/SPORT/18 × 8. Available online: https://www.apcprop.com/product/18x8/ (accessed on 12 August 2024).
- Maxon. View Product, Motor. Available online: https://www.maxongroup.it/maxon/view/product/motor/ecmotor/ec4pole/305015 (accessed on 15 October 2023).
- Maxamps Lithium Batteries. LiPo 1850 6S 22.2v Battery Pack. Available online: https://maxamps.com (accessed on 15 October 2023).
- Memon, Z.K.; Sundararajan, T.; Lakshminarasimhan, V.; Babu, Y.R.; Harne, V. Parametric Study on Fin Heat Transfer for Air Cooled Motorcycle Engine. In Proceedings of the International Mobility Engineering Congress & Exposition 2005—SAE India Technology for Emerging Markets, Chennai, India, 23 October 2005. [Google Scholar]
- Sachar, S.; Parvez, Y.; Khurana, T.; Chaubey, H. Heat Transfer Enhancement of the Air-Cooled Engine Fins through Geometrical and Material Analysis: A Review. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Reddy Kummitha, O.; Reddy, B.V.R. Thermal Analysis of Cylinder Block with Fins for Different Materials Using ANSYS. Mater. Today Proc. 2017, 4, 8142–8148. [Google Scholar] [CrossRef]
- Suti, A.; Di Rito, G.; Mattei, G. Model-Based Temperature Monitoring of the Internal Combustion Engine of a Lightweight Long-Endurance Fixed-Wing UAV. In Proceedings of the 2024 11th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Lublin, Poland, 3–5 June 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 254–259. [Google Scholar]
- Zhang, C.; Chen, F.; Li, L.; Xu, Z.; Liu, L.; Yang, G.; Lian, H.; Tian, Y. A Free-Piston Linear Generator Control Strategy for Improving Output Power. Energies 2018, 11, 135. [Google Scholar] [CrossRef]
- Abedin, M.J.; Masjuki, H.H.; Kalam, M.A.; Sanjid, A.; Rahman, S.M.A.; Masum, B.M. Energy Balance of Internal Combustion Engines Using Alternative Fuels. Renew. Sustain. Energy Rev. 2013, 26, 20–33. [Google Scholar] [CrossRef]
- Ashok, B.; Denis Ashok, S.; Ramesh Kumar, C. Trends and Future Perspectives of Electronic Throttle Control System in a Spark Ignition Engine. Annu. Rev. Control 2017, 44, 97–115. [Google Scholar] [CrossRef]
- Le Solliec, G.; Le Berr, F.; Colin, G.; Corde, G.; Chamaillard, Y. Engine Control of a Downsized Spark Ignited Engine: From Simulation to Vehicle. Oil Gas Sci. Technol.—Rev. L’IFP 2007, 62, 555–572. [Google Scholar] [CrossRef][Green Version]
- Payri, F.; Olmeda, P.; Martín, J.; Carreño, R. Experimental Analysis of the Global Energy Balance in a DI Diesel Engine. Appl. Therm. Eng. 2015, 89, 545–557. [Google Scholar] [CrossRef]
- Heywood, J.B. Internal Combustion Engine Fundamentals, 2nd ed.; McGraw-Hill Education: New York, NY, USA, 2018. [Google Scholar]
- Kalantzis, N.; Pezouvanis, A.; Ebrahimi, K.M. Internal Combustion Engine Model for Combined Heat and Power (CHP) Systems Design. Energies 2017, 10, 1948. [Google Scholar] [CrossRef]
- Hassantabar, A.; Najjaran, A.; Farzaneh-Gord, M. Investigating the Effect of Engine Speed and Flight Altitude on the Performance of Throttle Body Injection (TBI) System of a Two-Stroke Air-Powered Engine. Aerosp. Sci. Technol. 2019, 86, 375–386. [Google Scholar] [CrossRef]
- Lee, G.; Myung, C.-L.; Park, S.; Cho, Y. Sensitivity of Hot Film Flow Meter in Four Stroke Gasoline Engine. KSME Int. J. 2004, 18, 286–293. [Google Scholar] [CrossRef]
- Lapuerta, M.; Armas, O.; Agudelo, J.R.; Sánchez, C.A. Estudio Del Efecto de La Altitud Sobre El Comportamiento de Motores de Combustión Interna. Parte 1: Funcionamiento. Inf. Tecnol. 2006, 17, 21–30. [Google Scholar] [CrossRef]
- Ceballos, J.J.; Melgar, A.; Tinaut, F.V. Influence of Environmental Changes Due to Altitude on Performance, Fuel Consumption and Emissions of a Naturally Aspirated Diesel Engine. Energies 2021, 14, 5346. [Google Scholar] [CrossRef]
- Wu, Y.; Gou, J.; Ji, H.; Deng, J. Hierarchical Mission Replanning for Multiple UAV Formations Performing Tasks in Dynamic Situation. Comput. Commun. 2023, 200, 132–148. [Google Scholar] [CrossRef]
- Suti, A.; Di Rito, G.; Mattei, G. Heuristic Estimation of Temperature-Dependant Model Parameters of Li-Po Batteries for UAV Applications. In Proceedings of the 2023 IEEE 10th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Milan, Italy, 19–21 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 269–274. [Google Scholar]
- Speight, J.G. Handbook of Industrial Hydrocarbon Processes, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2019; ISBN 9780128099230. [Google Scholar]
- Koksal, H.; Ceviz, M.A.; Yakut, K.; Kaltakkiran, G.; Özakin, A.N. A Novel Ignition Timing Strategy to Regulate the Energy Balance during the Warm up Phase of an SI Engine. Case Stud. Therm. Eng. 2023, 41, 102602. [Google Scholar] [CrossRef]



| Characteristic | Value | Unit |
|---|---|---|
| Maximum take-off weight | 25 | kg |
| Wingspan | 3.5 | m |
| Total length | 2.3 | m |
| Height | 0.7 | m |
| Endurance | 16 | h |
| Rate of climb | 3 | m/s |
| Cruise speed | 23 | m/s |
| Maximum operational altitude | 4000 | m |
| Datalink range | 100 | km |
| Characteristic | Value | Unit |
|---|---|---|
| Engine type | 2-stroke single cylinder | - |
| Total weight | 3.17 | kg |
| Speed operating range | [2000, 9000] | rpm |
| Power operating range | [0.4, 1.9] | kW |
| Speed at cruise | 6000 | rpm |
| Power at cruise | 0.8 | kW |
| Fuel consumption at cruise | 500 | g/kW-h |
| Generator continuous power | 250 | W |
| Displacement | 29 | cc |
| Approximated cylinder boar range | [36, 38] | mm |
| Approximated cylinder stroke range | [26, 28] | mm |
| Time Between Overhaul | 350 | h |
| Cooling | air-cooled | - |
| Ability to be started from cold | [−20, 50] | °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suti, A.; Di Rito, G.; Mattei, G. Thermal Monitoring of an Internal Combustion Engine for Lightweight Fixed-Wing UAV Integrating PSO-Based Modelling with Condition-Based Extended Kalman Filter. Drones 2024, 8, 531. https://doi.org/10.3390/drones8100531
Suti A, Di Rito G, Mattei G. Thermal Monitoring of an Internal Combustion Engine for Lightweight Fixed-Wing UAV Integrating PSO-Based Modelling with Condition-Based Extended Kalman Filter. Drones. 2024; 8(10):531. https://doi.org/10.3390/drones8100531
Chicago/Turabian StyleSuti, Aleksander, Gianpietro Di Rito, and Giuseppe Mattei. 2024. "Thermal Monitoring of an Internal Combustion Engine for Lightweight Fixed-Wing UAV Integrating PSO-Based Modelling with Condition-Based Extended Kalman Filter" Drones 8, no. 10: 531. https://doi.org/10.3390/drones8100531
APA StyleSuti, A., Di Rito, G., & Mattei, G. (2024). Thermal Monitoring of an Internal Combustion Engine for Lightweight Fixed-Wing UAV Integrating PSO-Based Modelling with Condition-Based Extended Kalman Filter. Drones, 8(10), 531. https://doi.org/10.3390/drones8100531







