Delivery Route Scheduling of Heterogeneous Robotic System with Customers Satisfaction by Using Multi-Objective Artificial Bee Colony Algorithm
Abstract
1. Introduction
2. Route Scheduling of the Multi-Objective Heterogeneous Robotic Delivery System
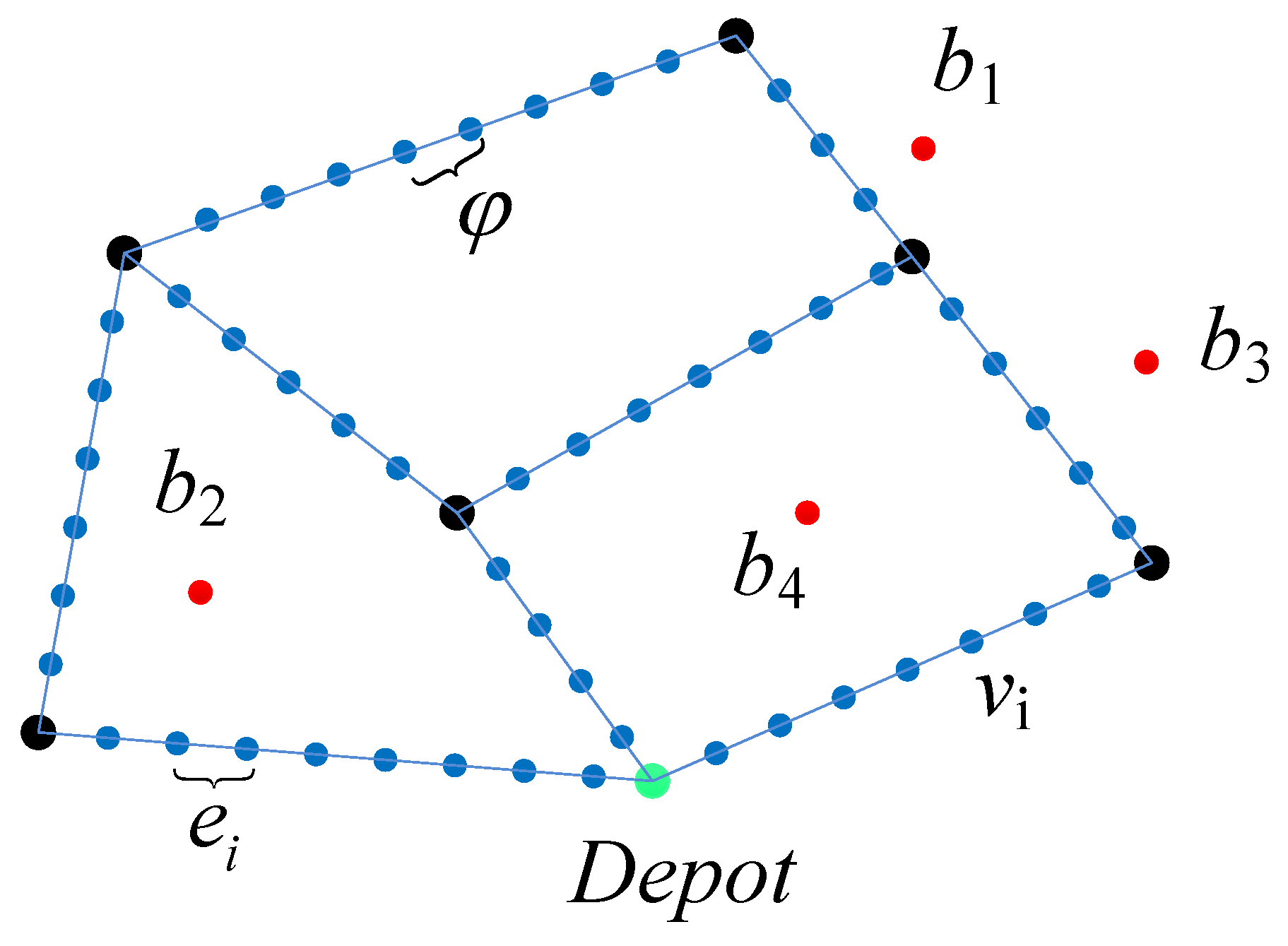
2.1. Problem Description
2.2. Definition of a New Delivery Customers Satisfaction
2.3. Route Scheduling Model for MOHRDS
3. Modified Artificial Bee Colony Algorithm for the Problem
3.1. Overview of the ABC
3.2. Discretization of the ABC
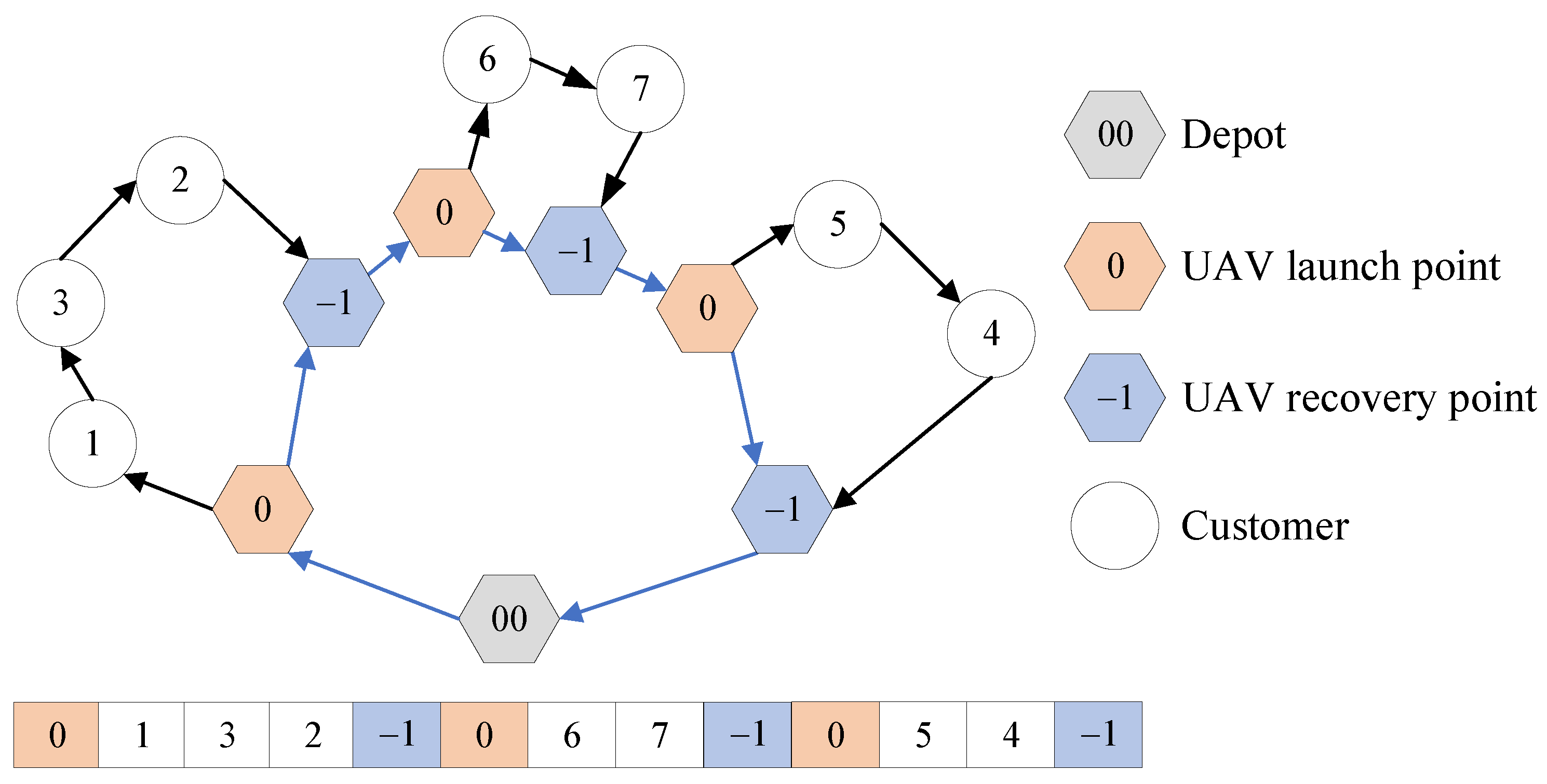
3.2.1. Encoding and Decoding
- The UGV departs from depot S, carrying the UAV, and selects the temporary stopping point closest to the first customer in the decoded individual as the launch point for the UAV. It then checks if the constraints are satisfied. If the conditions are not met, a penalty is applied.
- Iterate through the remaining customers until the current customer does not meet the endurance or payload constraints. Then, return to the previous customer and find the closest temporary stopping point to it as the recovery point for the UAV. It checks if the constraints are satisfied. If the conditions are not met, a penalty is applied.
- Remove the customers before from the solution individual. If there are still unvisited customers remaining in the solution individual, go back to Step 1. Otherwise, proceed to Step 4.
- At this point, all customers have been visited, indicating that all the missions of the UAV have been determined. The UGV, carrying the UAV, returns to depot S. As shown in Figure 5, both UGV and UAV paths are recorded. The total distance traveled by UGV and UAV is calculated based on Equations (8) and (9), and the overall customer satisfaction is evaluated.
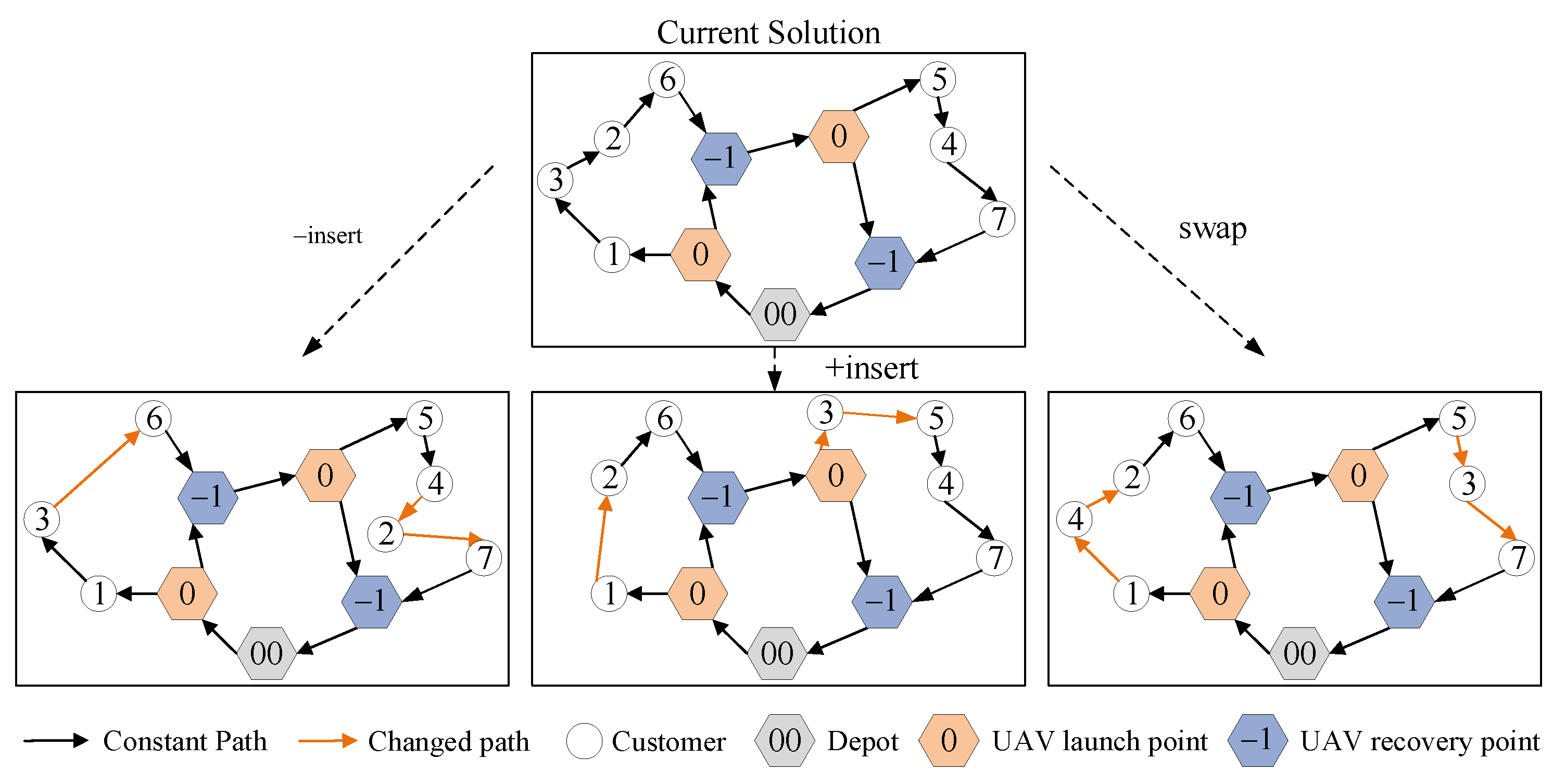
3.2.2. Position Updating Strategy
- The Partial-Mapped Crossover (PMX) operator is an efficient and widely used crossover operator, especially for permutation optimization problems. The PMX operator cross-combines the gene information of the two parent individuals during the crossover process to generate a new offspring individual, which retains the chromosome structure of the parent individual and ensures that no gene will be lost in the offspring. PMX is introduced to avoid premature convergence to local optimal solutions in this section.
- Random Customer Exchange Mutation (RCEM) is a mutation operator with strong local search capability. RCEM can effectively explore the local solution space by exchanging elements within the neighborhood of the solution, thus helping to find the locally optimal solution. Due to the lack of convergence of the initial position update strategy, RCEM is introduced in this section to improve the local search capability of the algorithm.
- Random Customer Reversal Mutation (RCRM) is a mutation operator with strong disturbance. By inverting a part of the current solution, this operator is able to break the local structure of the original solution and thus explore new solutions in the search space. Due to the poor perturbation of the initial location update strategy, RCRM is introduced in this section to improve the diversity of the population.
- Random Customer Transfer Mutation (RCTM) is a mutation operator with simple strategy and good exploration ability. By inserting elements, RCTM can change the structure of the solution and increase the diversity of solutions to avoid falling into a local optimal solution. RCTM is introduced in this section to improve the possibility of finding the global optimal solution.
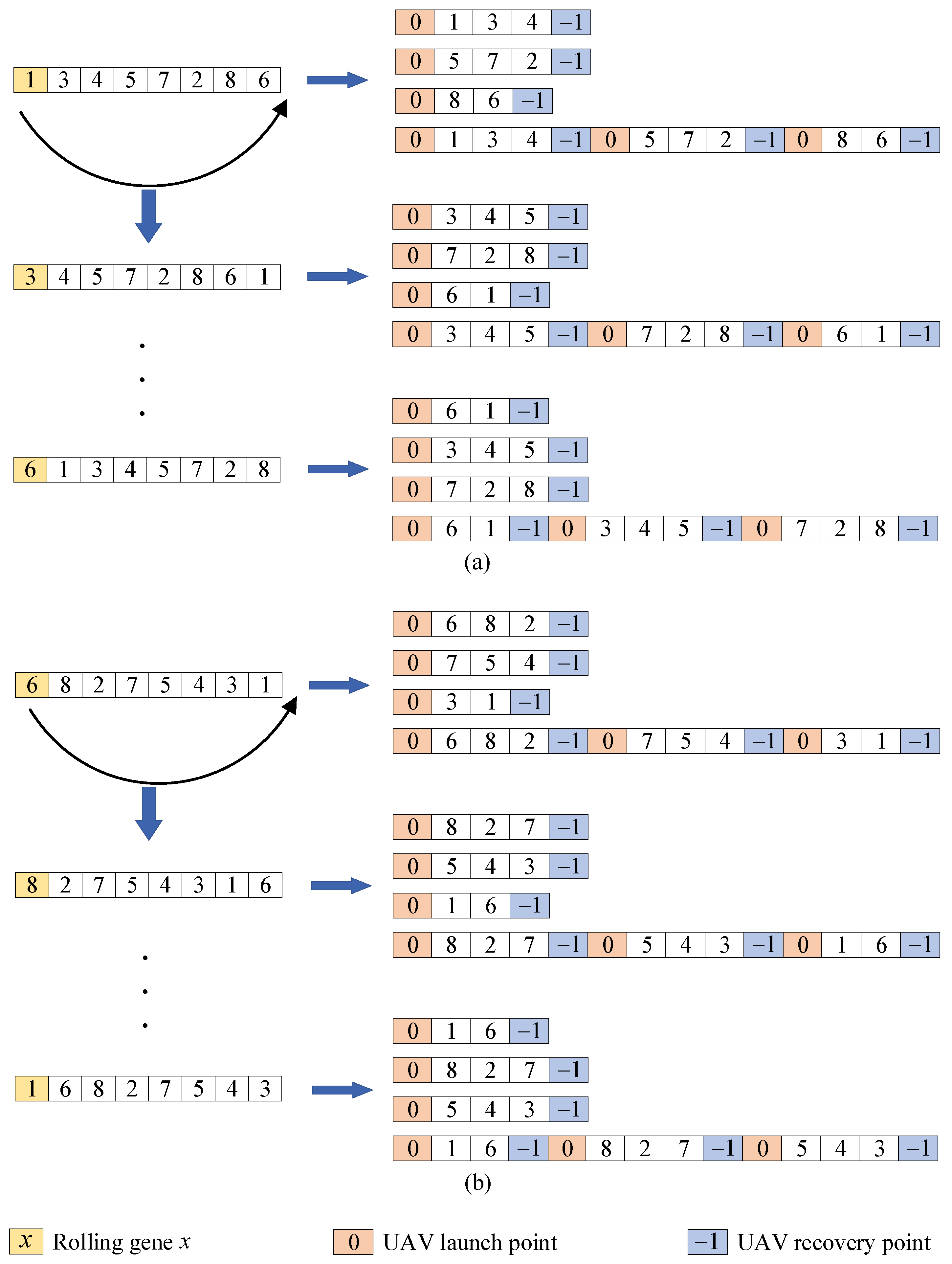
3.2.3. Local Search Strategy
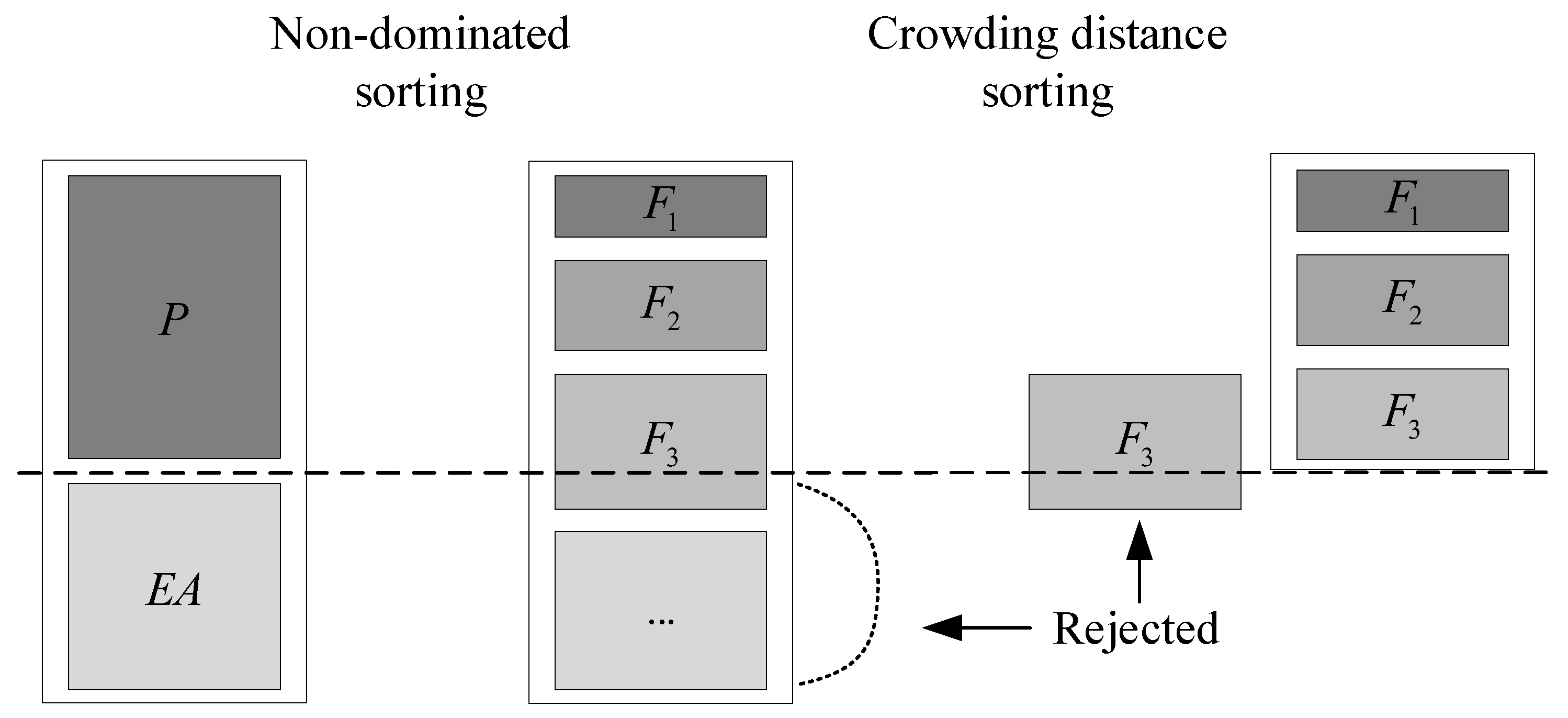
3.3. Multi-Objective Improvement of the ABC
3.3.1. Acceptance Criteria
3.3.2. Food Source Evaluation Strategy
4. Simulations Validation
4.1. Prerequisite Knowledge
4.1.1. Algorithms for Comparison
4.1.2. Algorithm Performance Metrics
4.2. Simulation Analysis
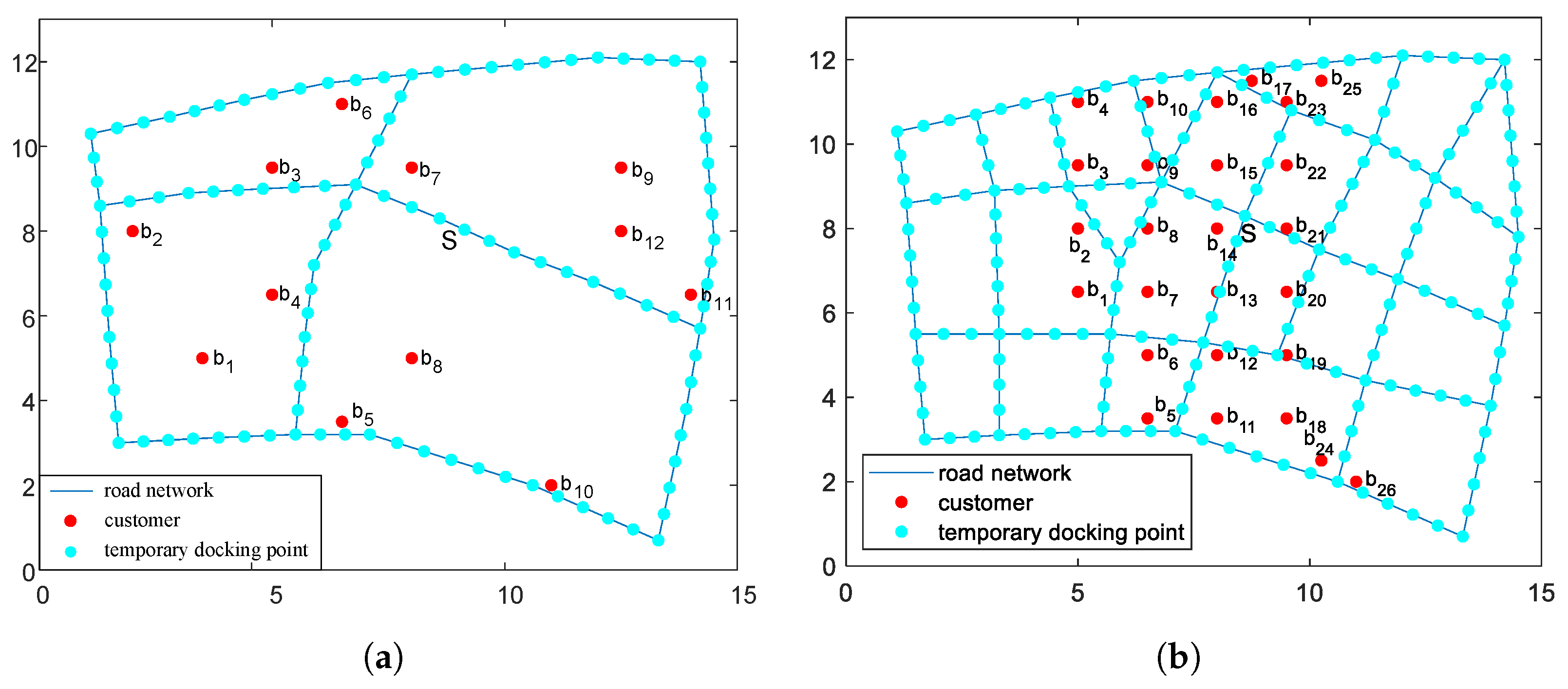
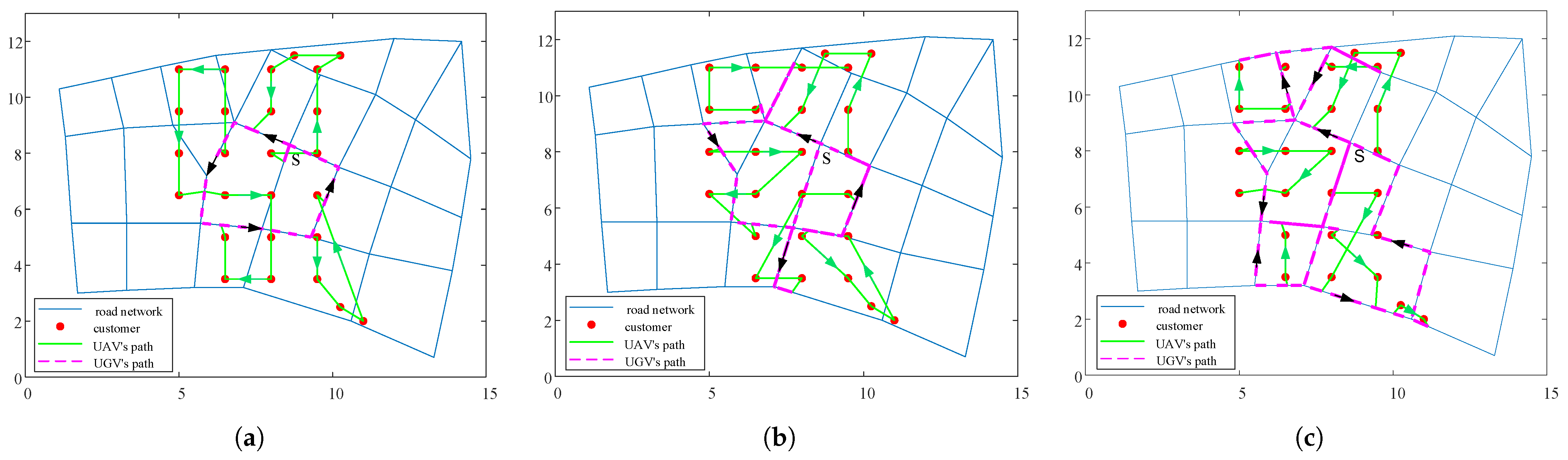
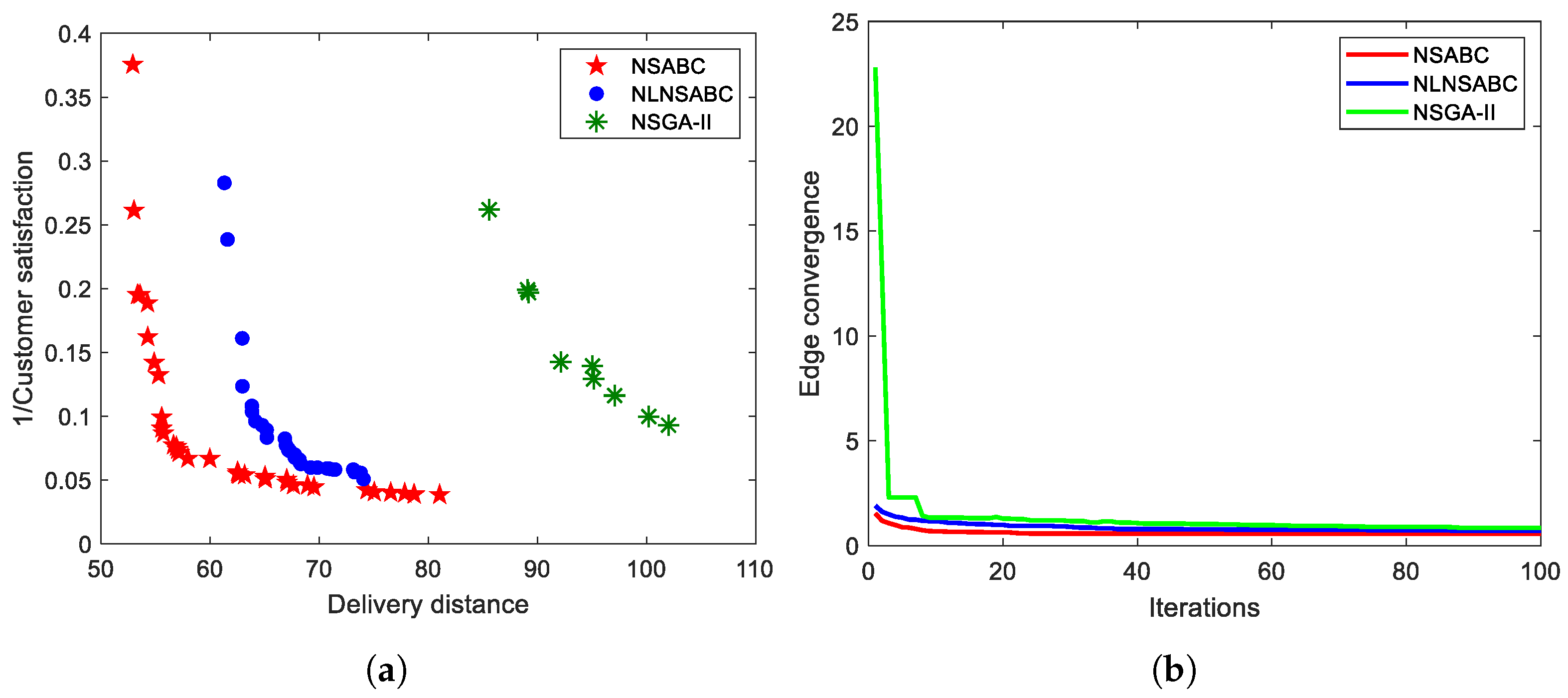
4.2.1. Simple Road Network
4.2.2. Complex Road Network
4.2.3. Tight Time Windows
4.3. The Computational Complexity of NSABC
5. Physical Experiments to Prove the Concept of the Model
5.1. Setup of the Physical Experiment
5.2. Experimental Results and Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rodrigues, G.; Caldas, R.; Araujo, G.; de Moraes, V.; Rodrigues, G.; Pelliccione, P. An architecture for mission coordination of heterogeneous robots. J. Syst. Softw. 2022, 191, 111363. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, M.; Chen, Z.; Cheng, L.; Yang, Y.; Li, H. Delivery path planning of heterogeneous robot system under road network constraints. Comput. Electr. Eng. 2021, 92, 107197. [Google Scholar] [CrossRef]
- Kumar, S.P.; Jat, D.; Sahni, R.K.; Jyoti, B.; Kumar, M.; Subeesh, A.; Parmar, B.S.; Mehta, C. Measurement of droplets characteristics of UAV based spraying system using imaging techniques and prediction by GWO-ANN model. Measurement 2024, 234, 114759. [Google Scholar] [CrossRef]
- Farrag, T.A.; Askr, H.; Elhosseini, M.A.; Hassanien, A.E.; Farag, M.A. Intelligent Parcel Delivery Scheduling Using Truck-Drones to Cut down Time and Cost. Drones 2024, 8, 477. [Google Scholar] [CrossRef]
- Mourelo Ferrandez, S.; Harbison, T.; Webwer, T.; Sturges, R.; Rich, R. Optimization of a truck-drone in tandem delivery network using k-means and genetic algorithm. J. Ind. Eng. Manag. 2016, 9, 374–388. [Google Scholar] [CrossRef]
- He, Y.; Wang, D.; Huang, F.; Zhang, R.; Min, L. Aerial-Ground Integrated Vehicular Networks: A UAV-Vehicle Collaboration Perspective. IEEE Trans. Intell. Transp. Syst. 2023, 25, 5154–5169. [Google Scholar] [CrossRef]
- Niu, G.; Wu, L.; Gao, Y.; Pun, M.O. Unmanned aerial vehicle (UAV)-assisted path planning for unmanned ground vehicles (UGVs) via disciplined convex-concave programming. IEEE Trans. Veh. Technol. 2022, 71, 6996–7007. [Google Scholar] [CrossRef]
- Bacheti, V.P.; Brandão, A.S.; Sarcinelli-Filho, M. A path-following controller for a uav-ugv formation performing the final step of last-mile-delivery. IEEE Access 2021, 9, 142218–142231. [Google Scholar] [CrossRef]
- Murray, C.C.; Chu, A.G. The flying sidekick traveling salesman problem: Optimization of drone-assisted parcel delivery. Transp. Res. Part Emerg. Technol. 2015, 54, 86–109. [Google Scholar] [CrossRef]
- Agatz, N.; Bouman, P.; Schmidt, M. Optimization approaches for the traveling salesman problem with drone. Transp. Sci. 2018, 52, 965–981. [Google Scholar] [CrossRef]
- Kitjacharoenchai, P.; Min, B.C.; Lee, S. Two echelon vehicle routing problem with drones in last mile delivery. Int. J. Prod. Econ. 2020, 225, 107598. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, H.; Qiao, L.; Tian, J.; Su, Y. Path planning for UAV/UGV collaborative systems in intelligent manufacturing. IET Intell. Transp. Syst. 2020, 14, 1475–1483. [Google Scholar] [CrossRef]
- Rajesh, S.; Abd Algani, Y.M.; Al Ansari, M.S.; Balachander, B.; Raj, R.; Muda, I.; Bala, B.K.; Balaji, S. Detection of features from the internet of things customer attitudes in the hotel industry using a deep neural network model. Meas. Sens. 2022, 22, 100384. [Google Scholar] [CrossRef]
- Omar Ali, S.R.; Abd Hakim Amir, S.N. Service quality and customer satisfaction: Experience of customers in postal service. J. Intelek 2020, 15, 67–75. [Google Scholar] [CrossRef]
- Xu, Z.; Elomri, A.; Pokharel, S.; Mutlu, F. A model for capacitated green vehicle routing problem with the time-varying vehicle speed and soft time windows. Comput. Ind. Eng. 2019, 137, 106011. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, W.; Zhao, Y.; Cattani, C. Multiobjective quantum evolutionary algorithm for the vehicle routing problem with customer satisfaction. Math. Probl. Eng. 2012, 2012. [Google Scholar] [CrossRef]
- Yan, X.; Xiao, B.; Zhao, Z. Multi-objective vehicle routing problem with simultaneous pick-up and delivery considering customer satisfaction. In Proceedings of the 2019 IEEE International Conference on Smart Manufacturing, Industrial & Logistics Engineering (SMILE), Hangzhou, China, 20–21 April 2019; pp. 93–97. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, C.; Wu, J. Vehicle routing optimization of instant distribution routing based on customer satisfaction. Information 2020, 11, 36. [Google Scholar] [CrossRef]
- Ghannadpour, S.F.; Noori, S.; Tavakkoli-Moghaddam, R. Multiobjective dynamic vehicle routing problem with fuzzy travel times and customers’ satisfaction in supply chain management. IEEE Trans. Eng. Manag. 2013, 60, 777–790. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Q.; Ma, L.; Zhang, Z.; Liu, Y. A hybrid ant colony optimization algorithm for a multi-objective vehicle routing problem with flexible time windows. Inf. Sci. 2019, 490, 166–190. [Google Scholar] [CrossRef]
- Hong, C.; Choi, E.K.C.; Joung, H.W.D. Determinants of customer purchase intention toward online food delivery services: The moderating role of usage frequency. J. Hosp. Tour. Manag. 2023, 54, 76–87. [Google Scholar] [CrossRef]
- Lebedev, D.; Goulart, P.; Margellos, K. A dynamic programming framework for optimal delivery time slot pricing. Eur. J. Oper. Res. 2021, 292, 456–468. [Google Scholar] [CrossRef]
- Afshar-Bakeshloo, M.; Mehrabi, A.; Safari, H.; Maleki, M.; Jolai, F. A green vehicle routing problem with customer satisfaction criteria. J. Ind. Eng. Int. 2016, 12, 529–544. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. Artificial bee colony (ABC) optimization algorithm for solving constrained optimization problems. In Proceedings of the International Fuzzy Systems Association World Congress, Cancun, Mexico, 18–21 June 2007; pp. 789–798. [Google Scholar] [CrossRef]
- Choong, S.S.; Wong, L.P.; Lim, C.P. An artificial bee colony algorithm with a modified choice function for the traveling salesman problem. Swarm Evol. Comput. 2019, 44, 622–635. [Google Scholar] [CrossRef]
- Öztürk, Ş.; Ahmad, R.; Akhtar, N. Variants of Artificial Bee Colony algorithm and its applications in medical image processing. Appl. Soft Comput. 2020, 97, 106799. [Google Scholar] [CrossRef]
- Xu, F.; Li, H.; Pun, C.M.; Hu, H.; Li, Y.; Song, Y.; Gao, H. A new global best guided artificial bee colony algorithm with application in robot path planning. Appl. Soft Comput. 2020, 88, 106037. [Google Scholar] [CrossRef]
- Jiang, Y.; Qian, H.; Chu, Y.; Liu, J.; Jiang, Z.; Dong, F.; Jia, L. Convergence analysis of ABC algorithm based on difference model. Appl. Soft Comput. 2023, 146, 110627. [Google Scholar] [CrossRef]
- Xiao, S.; Wang, H.; Wang, W.; Huang, Z.; Zhou, X.; Xu, M. Artificial bee colony algorithm based on adaptive neighborhood search and Gaussian perturbation. Appl. Soft Comput. 2021, 100, 106955. [Google Scholar] [CrossRef]
- Wang, H.; Wang, W.; Xiao, S.; Cui, Z.; Xu, M.; Zhou, X. Improving artificial bee colony algorithm using a new neighborhood selection mechanism. Inf. Sci. 2020, 527, 227–240. [Google Scholar] [CrossRef]
- Ye, T.; Wang, W.; Wang, H.; Cui, Z.; Wang, Y.; Zhao, J.; Hu, M. Artificial bee colony algorithm with efficient search strategy based on random neighborhood structure. Knowl.-Based Syst. 2022, 241, 108306. [Google Scholar] [CrossRef]
- Xiao, W.S.; Li, G.X.; Liu, C.; Tan, L.P. A novel chaotic and neighborhood search-based artificial bee colony algorithm for solving optimization problems. Sci. Rep. 2023, 13, 20496. [Google Scholar] [CrossRef]
- Zhou, X.; Tan, G.; Wang, H.; Ma, Y.; Wu, S. Artificial bee colony algorithm based on multi-neighbor guidance. Expert Syst. Appl. 2024, 259, 125283. [Google Scholar] [CrossRef]
- Hakli, H.; Kiran, M.S. An improved artificial bee colony algorithm for balancing local and global search behaviors in continuous optimization. Int. J. Mach. Learn. Cybern. 2020, 11, 2051–2076. [Google Scholar] [CrossRef]
- Dumez, D.; Lehuédé, F.; Péton, O. A large neighborhood search approach to the vehicle routing problem with delivery options. Transp. Res. Part Methodol. 2021, 144, 103–132. [Google Scholar] [CrossRef]
- Masmoudi, M.A.; Mancini, S.; Baldacci, R.; Kuo, Y.H. Vehicle routing problems with drones equipped with multi-package payload compartments. Transp. Res. Part Logist. Transp. Rev. 2022, 164, 102757. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the strength Pareto evolutionary algorithm. Tik Rep. 2001, 103. [Google Scholar] [CrossRef]
- Srivastava, G.; Singh, A.; Mallipeddi, R. NSGA-II with objective-specific variation operators for multiobjective vehicle routing problem with time windows. Expert Syst. Appl. 2021, 176, 114779. [Google Scholar] [CrossRef]
- Shuai, Y.; Yunfeng, S.; Kai, Z. An effective method for solving multiple travelling salesman problem based on NSGA-II. Syst. Sci. Control. Eng. 2019, 7, 108–116. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, H.; Chen, Y.; Cheng, L.; Zhang, B. Patrol robot path planning in nuclear power plant using an interval multi-objective particle swarm optimization algorithm. Appl. Soft Comput. 2022, 116, 108192. [Google Scholar] [CrossRef]
- Elgharably, N.; Easa, S.; Nassef, A.; El Damatty, A. Stochastic multi-objective vehicle routing model in green environment with customer satisfaction. IEEE Trans. Intell. Transp. Syst. 2022, 24, 1337–1355. [Google Scholar] [CrossRef]
- Sheng, B.; Chen, L.; Cheng, J.; Zhang, Y.; Hua, Z.; Tao, J. A markless 3D human motion data acquisition method based on the binocular stereo vision and lightweight open pose algorithm. Measurement 2024, 225, 113908. [Google Scholar] [CrossRef]
- Saponi, M.; Borboni, A.; Adamini, R.; Faglia, R.; Amici, C. Embedded payload solutions in UAVs for medium and small package delivery. Machines 2022, 10, 737. [Google Scholar] [CrossRef]



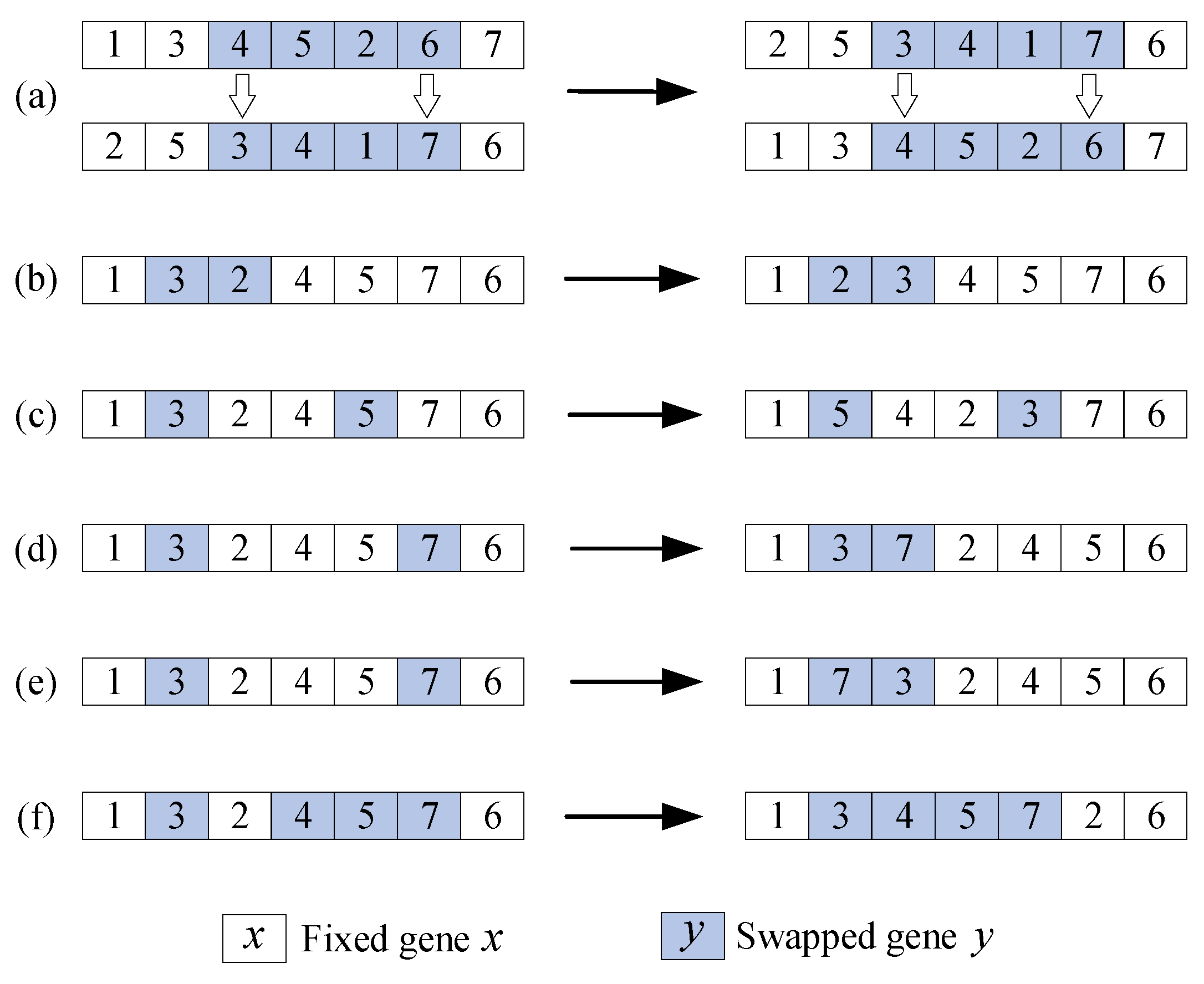















| Symbols | Description |
|---|---|
| E 1 | UAV endurance |
| Q | Maximum payload of the UAV |
| Flight speed of the UAV | |
| Drive speed of the UGV | |
| M | Number of customers |
| N | Number of temporary docking points |
| B | Set of customers |
| A | The set A, consisting of customers B and temporary docking points V, in the undirected graph G. |
| P | The sequence P of UAV delivering services to customers. |
| The i-th customer in the delivery sequence set P. | |
| The weight of the i-th customer’s demand . | |
| The flying distance between the customer point and the temporary docking point for the UAV. | |
| The flying distance between the customer points and for the unmanned aerial vehicle (UAV) . | |
| The driving distance between the vehicle’s temporary stopping points is and . |
| Equations | Meanings |
|---|---|
| Equation (8) | Minimizing the total distance traveled by UGV and UAV |
| Equation (9) | Maximizing the customer satisfaction |
| Equation (10) | Indicate that each temporary docking point allows at most one takeoff for the UAV |
| Equation (11) | Indicate that each temporary docking point allows at most one landing for the UAV |
| Equation (12) | States that the UAV can only visit one customer at a time |
| Equation (13) | Ensures that each customer is visited only once |
| Equation (14) | Allows the UAV to serve multiple customers within one flight |
| Equation (15) | Stipulates that the UAV starts the delivery immediately after takeoff |
| Equation (16) | Requires the UAV to return to the UGV for replenishment immediately after completing the delivery task |
| Equation (17) | Ensures that the takeoff point for each flight of the UAV is before the landing point |
| Equation (18) | Indicates that the UAV can only take off for the next flight after completing replenishment from the previous flight |
| Equation (19) | Restricts the UAV’s distance traveled within its endurance limit during the delivery task |
| Equation (20) | Limits the weight of packages carried by the UAV to its capacity |
| Equation (21) | Ensures that the UGV does not arrive at the landing point later than the UAV to facilitate timely recovery and replenishment |
| Equation (22) | States that each UGV is dispatched at most once |
| Equation (23) | Represents the movement of UGV carrying UAV from the depot, and they return to the depot after completing their tasks |
| Equation (24) | Defines the calculation of the UAV’s arrival time at each customer |
| Description | Value | Description | Value |
|---|---|---|---|
| Iteration count | The speed of the UAV | ||
| Population size | The speed of the UGV | ||
| Number of employed bees | The endurance of the UAV | ||
| Number of onlooker bees | The payload capacity of the UAV | ||
| Number of stagnation iterations |
| No. | Location | Demand (kg) | Time Windows | No. | Location | Demand (kg) | Time Windows |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 7 | 2 | ||||
| 2 | 8 | 1 | |||||
| 3 | 1 | 9 | |||||
| 4 | 1 | 10 | 1 | ||||
| 5 | 2 | 11 | |||||
| 6 | 12 |
| Solution | Route | Delivery Distance | Customer Satisfaction |
|---|---|---|---|
| the shortest delivery distance solution | UGV route: UAV route: | km | |
| the maximum customer satisfaction solution | UGV route: UAV route: | km | |
| the optimal compromise solution | UGV route: UAV route: | km |
| (a) Comparison of Pareto solutions obtained using three algorithms under simple road network restriction | |||||||||||
| Trials | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| QM | NSABC | 73.077 | 92.308 | 72.000 | 72.000 | 69.231 | 96.154 | 68.000 | 100 | 70.370 | 96.296 |
| NLNSABC | 50.000 | 61.379 | 44.000 | 44.000 | 42.308 | 65.385 | 48.000 | 73.077 | 48.148 | 66.667 | |
| NSGAII | 65.385 | 19.231 | 48.000 | 48.000 | 50.000 | 3.8462 | 48.000 | 0 | 14.815 | 3.7037 | |
| SM | NSABC | 1.1139 | 1.1139 | 1.1139 | 1.1139 | 1.1139 | 1.1139 | 1.0821 | 1.1139 | 1.1139 | 1.1139 |
| NLNSABC | 1.2640 | 1.2198 | 1.1610 | 1.0710 | 1.1141 | 1.5484 | 0.9714 | 1.3183 | 1.2944 | 1.1733 | |
| NSGAII | 1.6137 | 0.6254 | 1.4464 | 1.3882 | 1.6709 | 1.8512 | 1.9879 | 1.3452 | 1.2942 | 1.5175 | |
| (b) Comparison of Pareto solutions obtained using three algorithms under complex road network restriction | |||||||||||
| Trials | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| QM | NSABC | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| NLNSABC | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| NSGAII | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| SM | NSABC | 0.1724 | 0.3456 | 0.2075 | 0.3492 | 0.1585 | 0.2984 | 0.3563 | 0.3353 | 0.2209 | 0.2979 |
| NLNSABC | 0.4985 | 1.0222 | 0.5119 | 0.5677 | 0.6818 | 0.2849 | 0.6529 | 0.4092 | 0.2107 | 1.5201 | |
| NSGAII | 4.3103 | 2.1266 | 0.2478 | 1.0276 | 1.8850 | 1.6967 | 0.8098 | 2.2704 | 1.1836 | 2.2978 | |
| (c) Comparison of Pareto solutions obtained using three algorithms under tight time windows restriction | |||||||||||
| Trials | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| QM | NSABC | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| NLNSABC | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| NSGAII | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| SM | NSABC | 0.9292 | 0.7881 | 0.7652 | 0.8047 | 1.0028 | 0.8733 | 0.7128 | 0.9702 | 0.9994 | 0.8728 |
| NLNSABC | 0.2448 | 0.2881 | 0.3538 | 1.3584 | 0.9174 | 0.7730 | 0.9271 | 0.6960 | 0.7450 | 0.8794 | |
| NSGAII | 1.2276 | 0.5357 | 0.5901 | 0.6555 | 0.6481 | 0.9137 | 0.5154 | 1.0406 | 0.6354 | 0.6296 | |
| No. | Location | Demand (kg) | Time Windows | No. | Location | Demand (kg) | Time Windows |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 14 | |||||
| 2 | 15 | ||||||
| 3 | 1 | 16 | |||||
| 4 | 1 | 17 | 1 | ||||
| 5 | 2 | 18 | 1 | ||||
| 6 | 19 | 2 | |||||
| 7 | 1 | 20 | 2 | ||||
| 8 | 21 | ||||||
| 9 | 2 | 22 | |||||
| 10 | 1 | 23 | 1 | ||||
| 11 | 1 | 24 | 1 | ||||
| 12 | 1 | 25 | 2 | ||||
| 13 | 2 | 26 |
| Solution | Route | Delivery Distance | Customer Satisfaction |
|---|---|---|---|
| the shortest delivery distance solution | UGV route: UAV route: | km | |
| the maximum customer satisfaction solution | UGV route: UAV route: | km | |
| the optimal compromise solution | UGV route: UAV route: | km |
| No. | Location | Demand (kg) | Time Windows | No. | Location | Demand (kg) | Time Windows |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 14 | |||||
| 2 | 15 | ||||||
| 3 | 1 | 16 | |||||
| 4 | 1 | 17 | 1 | ||||
| 5 | 2 | 18 | 1 | ||||
| 6 | 19 | 2 | |||||
| 7 | 1 | 20 | 2 | ||||
| 8 | 21 | ||||||
| 9 | 2 | 22 | |||||
| 10 | 1 | 23 | 1 | ||||
| 11 | 1 | 24 | 1 | ||||
| 12 | 1 | 25 | 2 | ||||
| 13 | 2 | 26 |
| Solution | Route | Delivery Distance | Customer Satisfaction |
|---|---|---|---|
| the shortest delivery distance solution | UGV route: UAV route: | km | |
| the maximum customer satisfaction solution | UGV route: UAV route: | km | |
| the optimal compromise solution | UGV route: UAV route: | km |
| Simple Road Network | Complex Road Network | Increased Running Time | |
|---|---|---|---|
| Average running time (s) | |||
| Shortest running time (s) | |||
| Longest running time (s) |
| Experimental Data | Simulation Experiment (Equal Scaling) | Physical Experiment | Error |
|---|---|---|---|
| The first flight distance of UAV (m) | |||
| The second flight distance of UAV (m) | |||
| The third flight distance of UAV (m) | |||
| The fourth flight distance of UAV (m) | |||
| The distance of UGV (m) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Hou, S.; Wang, Z.; Chen, Y.; Hu, M.; Ikram, R.M.A. Delivery Route Scheduling of Heterogeneous Robotic System with Customers Satisfaction by Using Multi-Objective Artificial Bee Colony Algorithm. Drones 2024, 8, 519. https://doi.org/10.3390/drones8100519
Chen Z, Hou S, Wang Z, Chen Y, Hu M, Ikram RMA. Delivery Route Scheduling of Heterogeneous Robotic System with Customers Satisfaction by Using Multi-Objective Artificial Bee Colony Algorithm. Drones. 2024; 8(10):519. https://doi.org/10.3390/drones8100519
Chicago/Turabian StyleChen, Zhihuan, Shangxuan Hou, Zuao Wang, Yang Chen, Mian Hu, and Rana Muhammad Adnan Ikram. 2024. "Delivery Route Scheduling of Heterogeneous Robotic System with Customers Satisfaction by Using Multi-Objective Artificial Bee Colony Algorithm" Drones 8, no. 10: 519. https://doi.org/10.3390/drones8100519
APA StyleChen, Z., Hou, S., Wang, Z., Chen, Y., Hu, M., & Ikram, R. M. A. (2024). Delivery Route Scheduling of Heterogeneous Robotic System with Customers Satisfaction by Using Multi-Objective Artificial Bee Colony Algorithm. Drones, 8(10), 519. https://doi.org/10.3390/drones8100519







