Quadrotor Trajectory Control Based on Energy-Optimal Reference Generator
Abstract
1. Introduction
1.1. Context
1.2. Relevant and Related Work
1.3. Original Contributions and Organization
- Section 2: Introduction to the dynamical model of the quadrotor and the electrical model of a brushless DC motor.
- Section 3: Details on the identification of parameters for the chosen model. This identification is done with respect to the commercial physical model based on Simcenter Amesim and provided by Siemens.
- Section 4: Presentation and solution of the optimal control problem, using the identified model. This section includes an analysis of optimal control results and the derivation of rules for generating near-optimal time-mission and state-variable references.
- Section 5: Design and implementation of the hierarchical controller.
- Section 6: Assessment of the hierarchical controller’s performance, particularly in terms of trajectory tracking and energy/battery consumption.
- Section 7: Conclusions drawn from the research findings, and a discussion of potential future research developments.
2. Modeling the Energetics of UAV Operations
2.1. Characterizing Brushless-DC-Motor Dynamics in UAVs
2.2. Quadrotor Dynamic Model
- g is the acceleration due to gravity;
- m is the mass of the quadrotor;
- J is the total inertia of a motor;
- is the diagonal rotational inertia matrix of the rotorcraft;
- and are the thrust and aerodynamic drag factors of the propellers (see [40]), respectively;
- ℓ is the distance between each motor and the center of mass of the quadrotor.
2.3. Energy and Motor Efficiency
3. Parameter Identification of Quadrotor Model
4. Energetic Rule–Based Reference Generation Based on Optimal Control
4.1. Optimal Control Problem
- : Final time of the process;
- : The costate at the final time is a vector of zeros. The costate is a concept in optimal-control theory that represents the sensitivity of the cost function to changes in the state variables;
- : Optimal state trajectory;
- : Optimal control function;
- and : Jacobian matrices of functions f and L, with respect to the state variable x.
4.2. Rule–Based Energetic Reference Generation
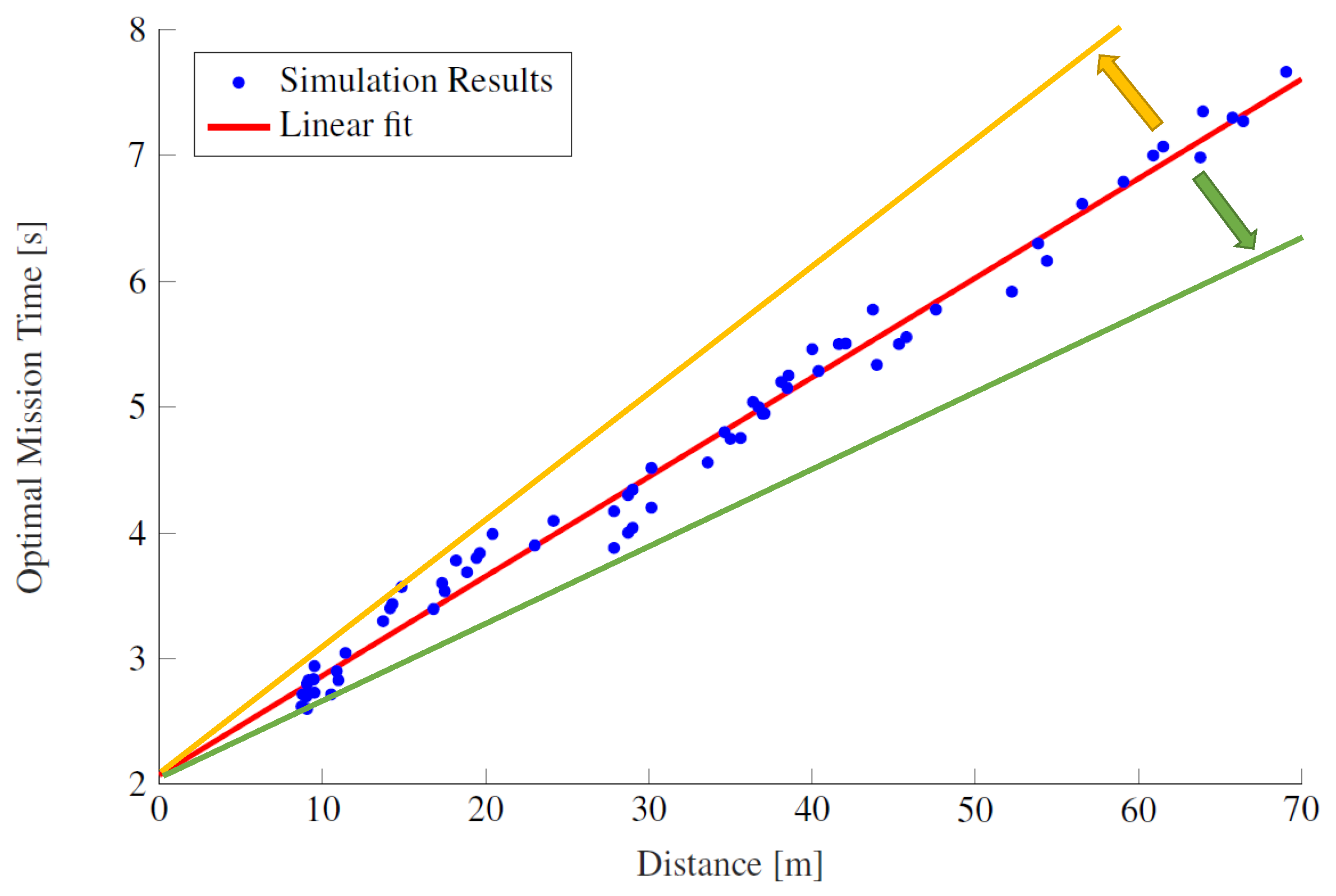
4.2.1. Optimal Mission-Time Setting
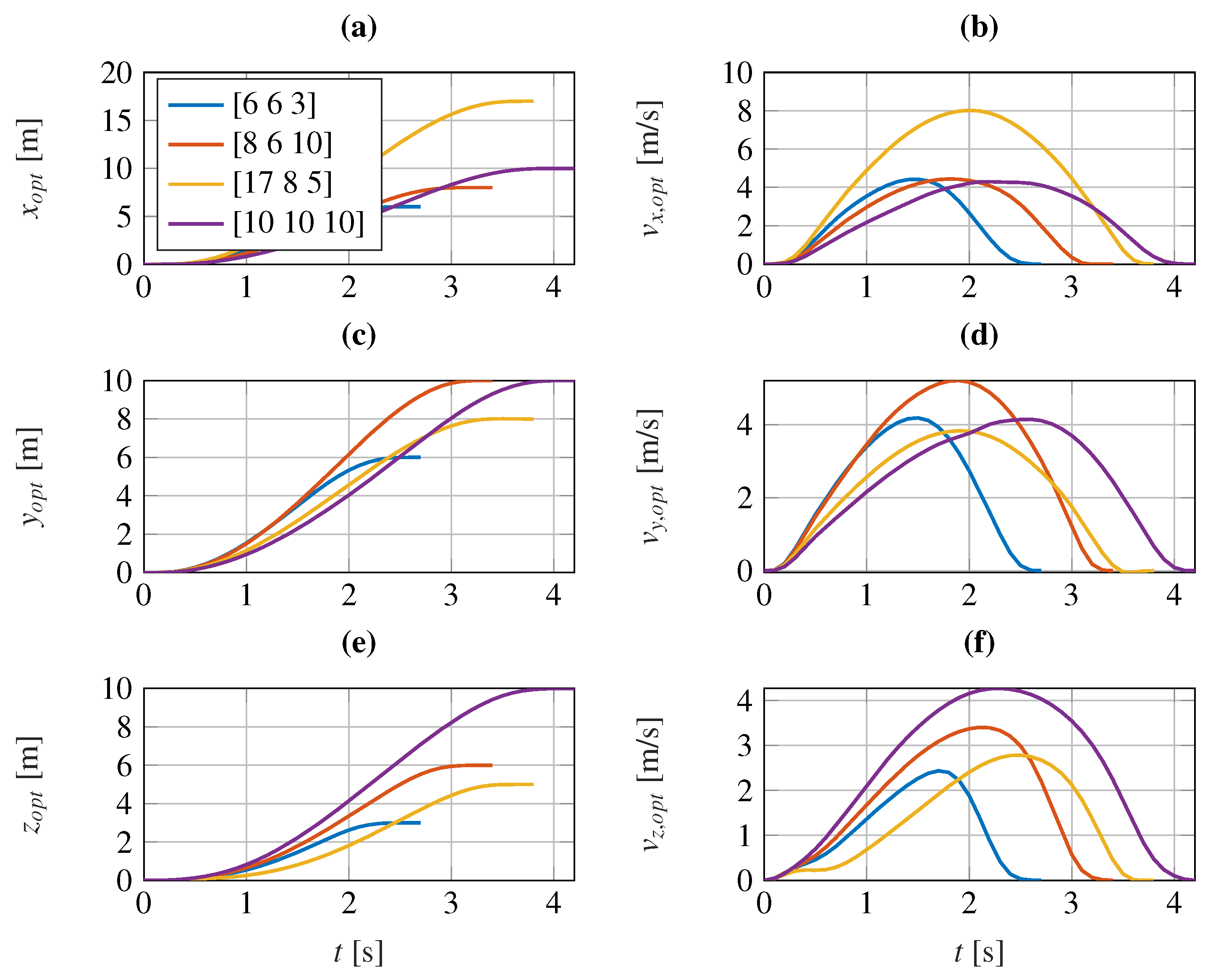
4.2.2. Optimal Trajectory References
5. Hierarchical Real–Time Control
6. Simulation Results
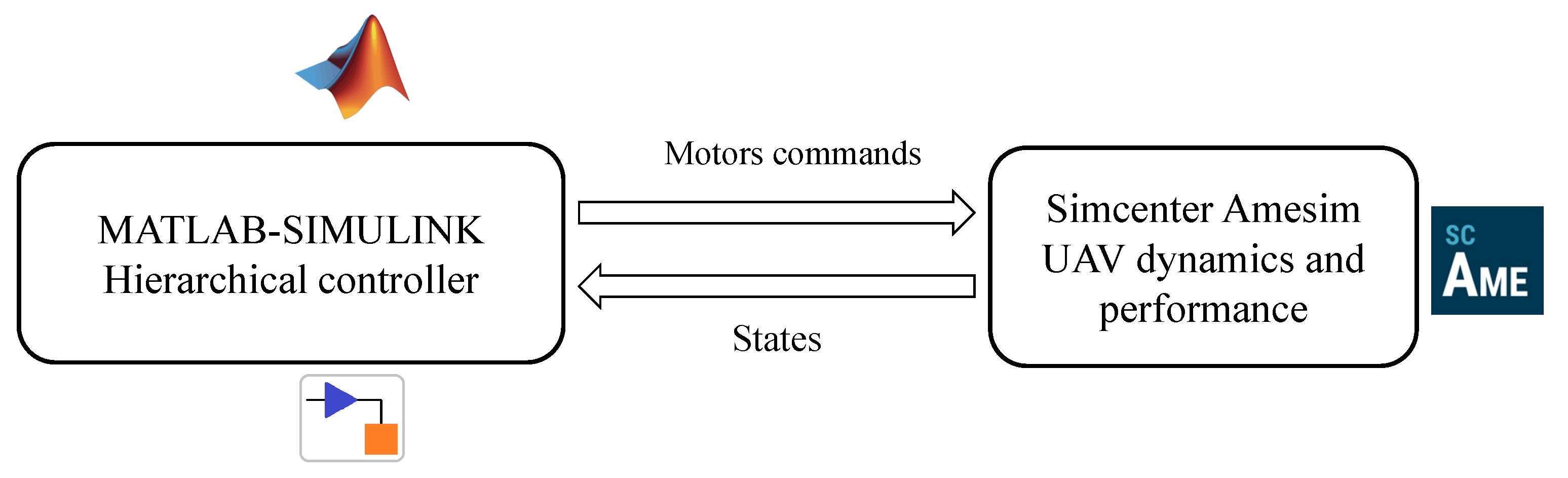
6.1. Co-Simulation Environment with Matlab and Simcenter Amesim
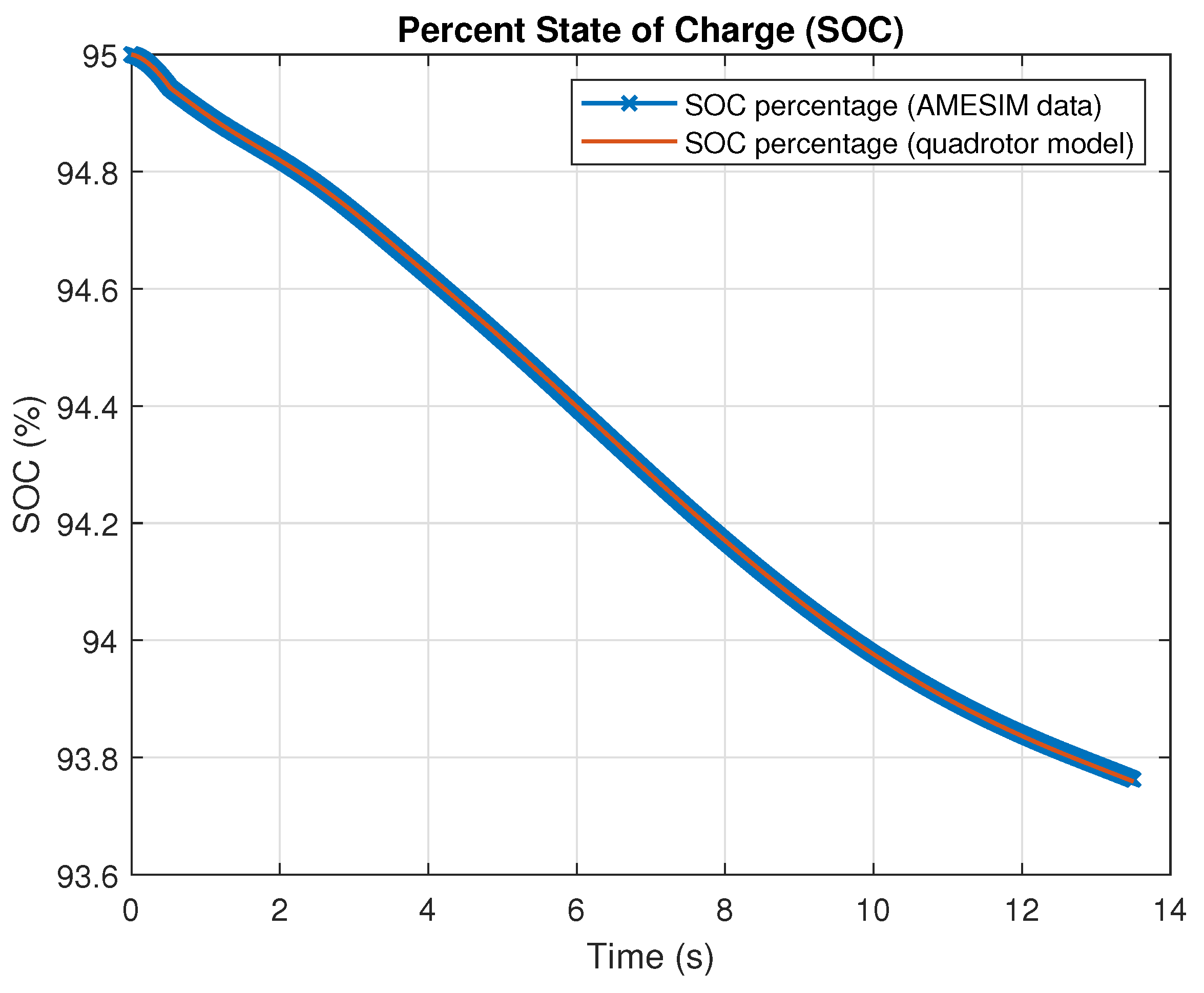
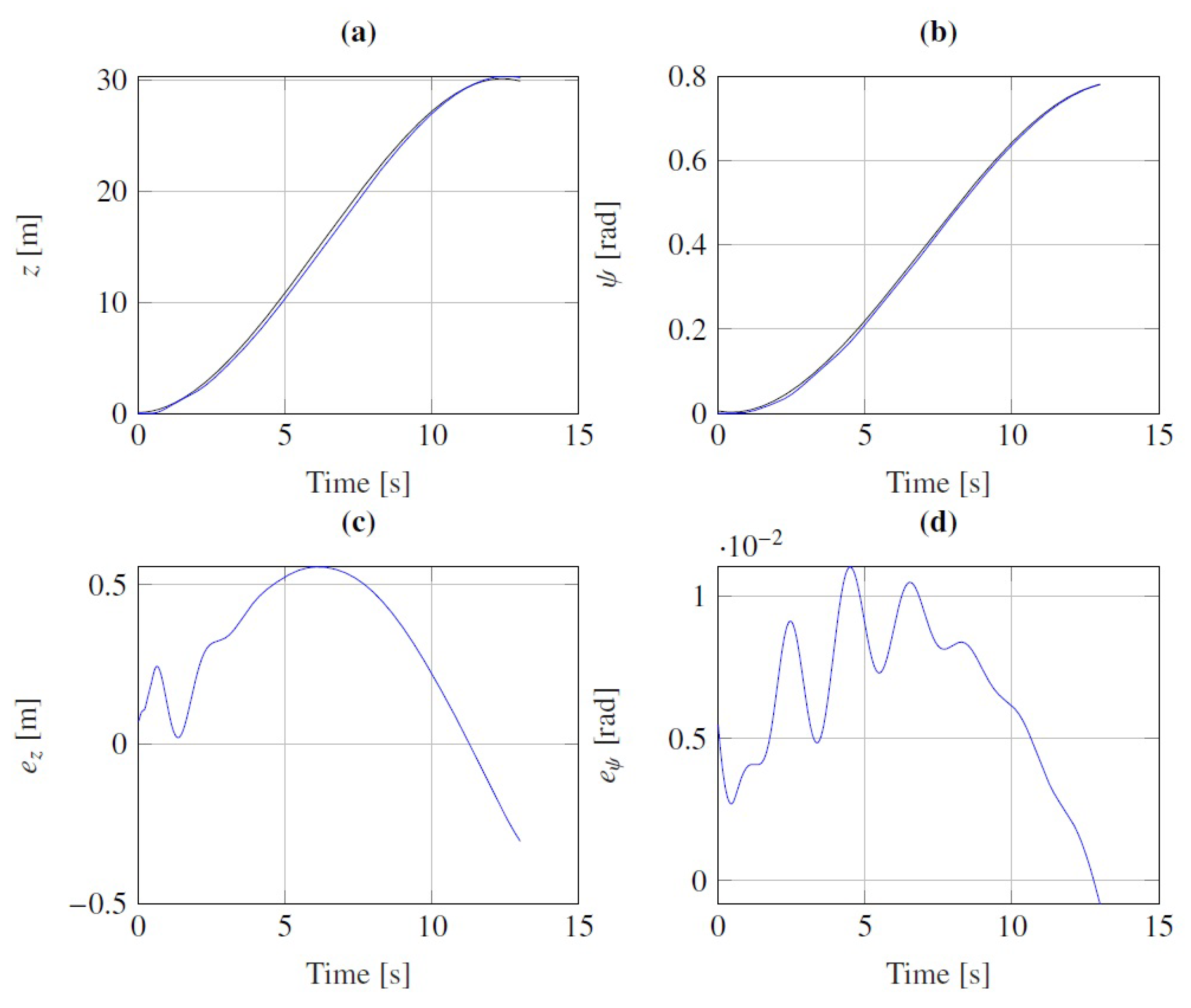
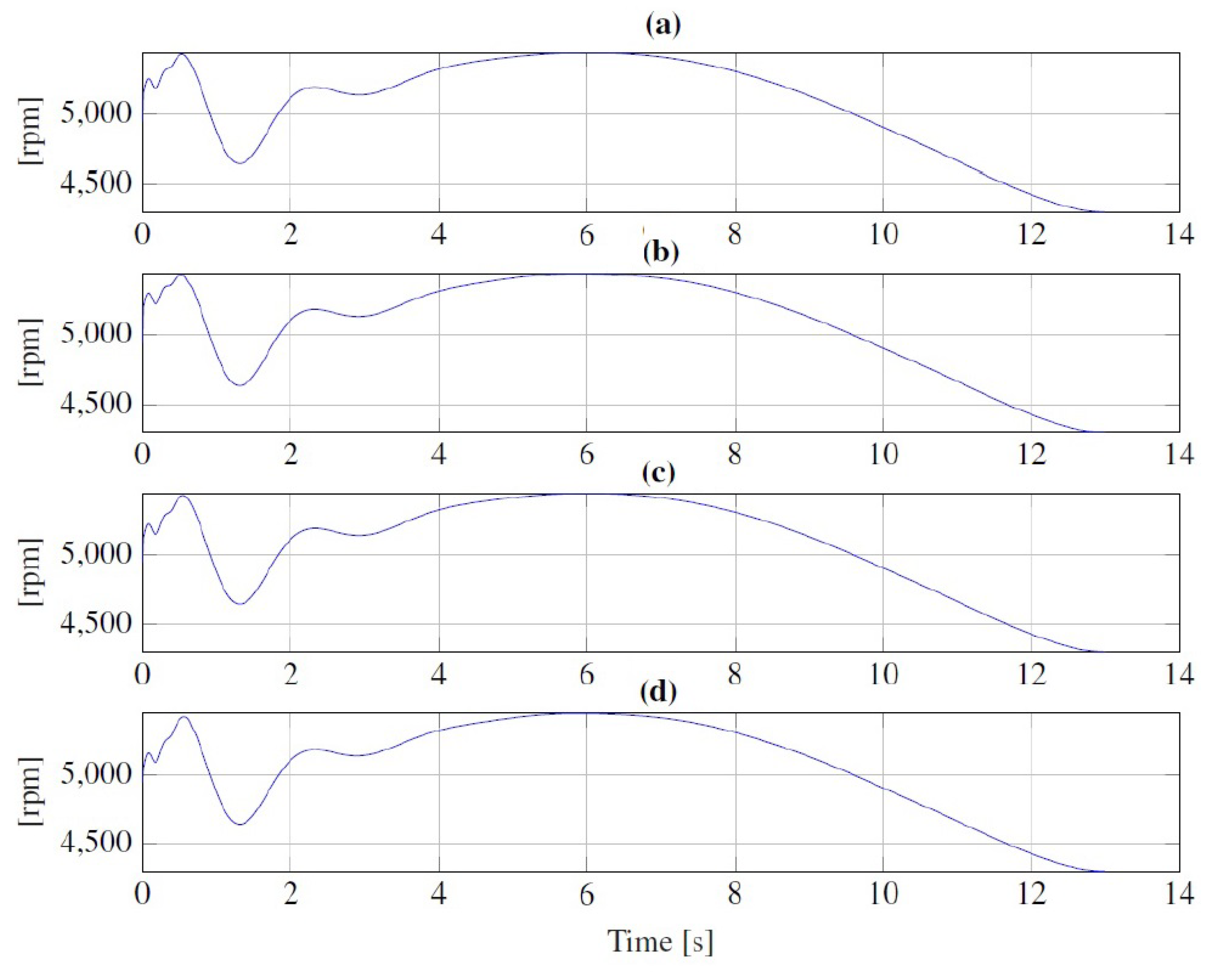
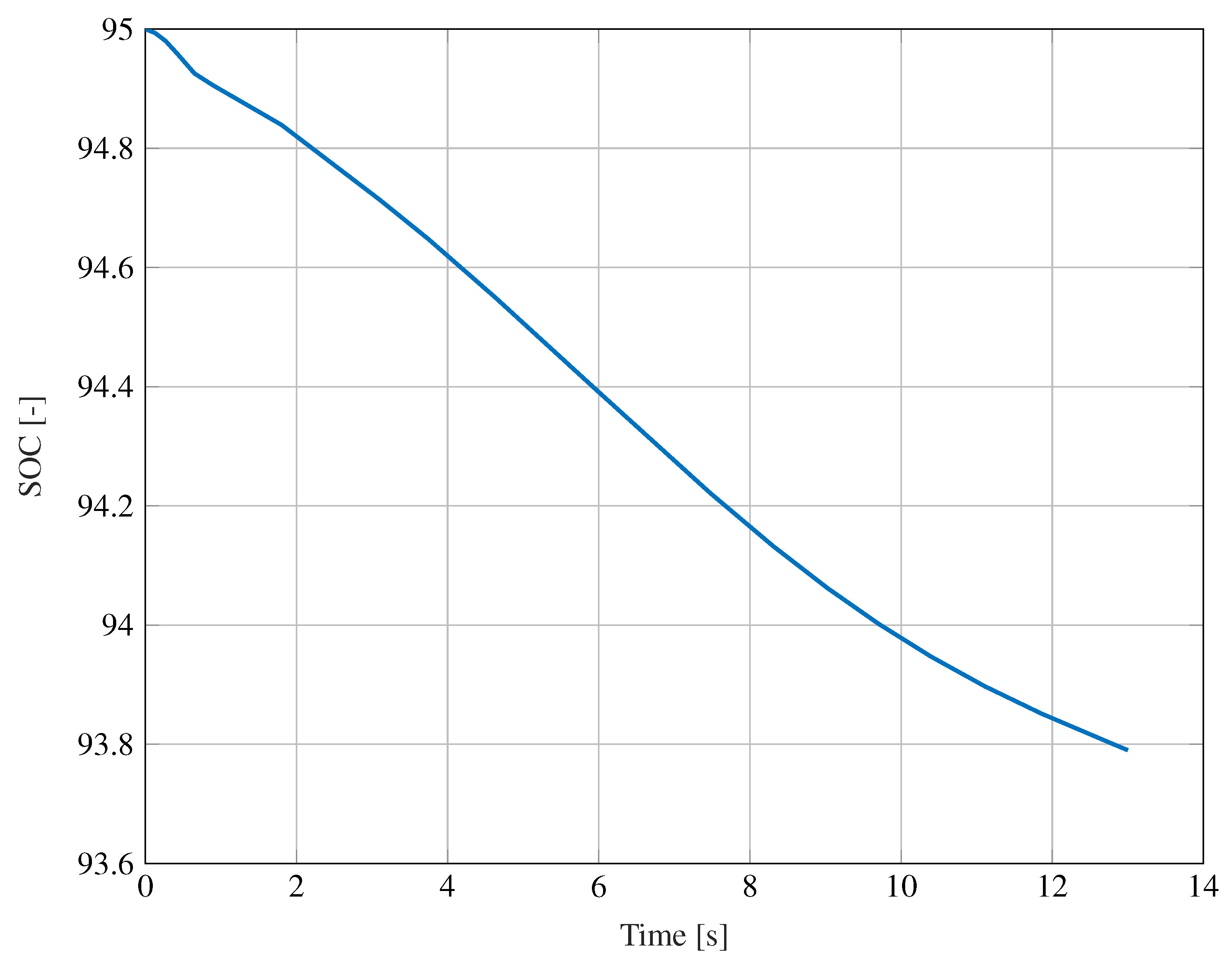
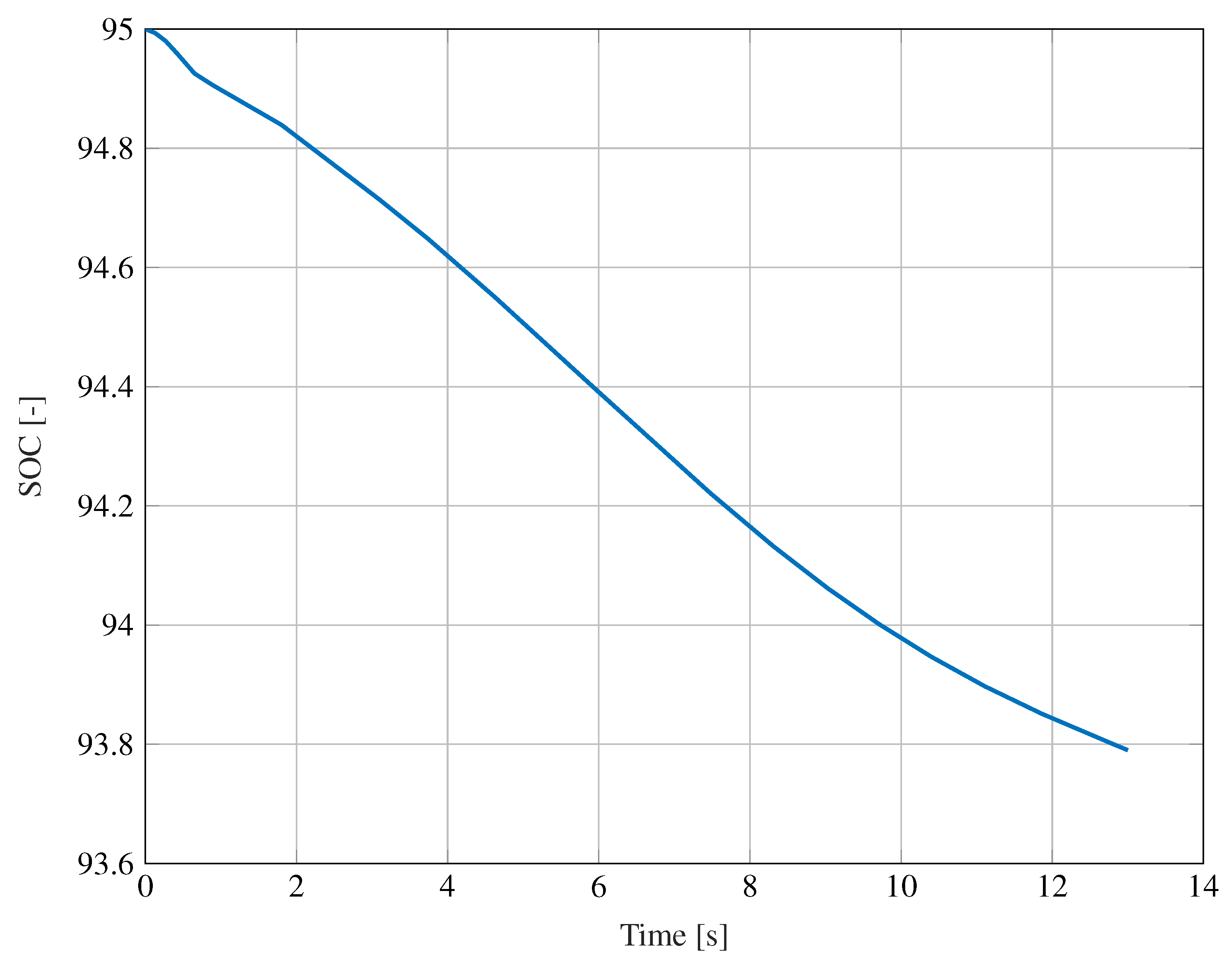
6.2. Simulation Results in Simulink and Simcenter Amesim Co-Simulation Platform
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mathews, A.J.; Singh, K.; Cummings, A.R.; Rogers, S.R. Fundamental practices for drone remote sensing research across disciplines. Drone Syst. Appl. 2023, 11, 1–22. [Google Scholar] [CrossRef]
- Santoso, F.; Garratt, M.A.; Anavatti, S.G. State-of-the-art intelligent flight control systems in unmanned aerial vehicles. IEEE Trans. Autom. Sci. Eng. 2018, 15, 613–627. [Google Scholar] [CrossRef]
- DDC: Drone Delivery Canada. Available online: https://dronedeliverycanada.com/ (accessed on 17 August 2023).
- Wall Street Journal, Google Drones Can Already Deliver You Coffee In Australia. Available online: www.youtube.com/watch?v=prhDrfUgpB0 (accessed on 6 April 2019).
- Zraick, K. Like ‘Uber for Organs’: Drone Delivers Kidney to Maryland Woman. The New York Times. Available online: www.nytimes.com/2019/04/30/health/drone-delivers-kidney.html (accessed on 17 August 2023).
- Estevez, J.; Lopez-Guede, J.M.; Grana, M. Quasi-stationary state transportation of a hose with quadrotors. Robot. Auton. Syst. 2015, 63, 187–194. [Google Scholar] [CrossRef]
- Post, S. Drones: A Vision Has Become Reality. Available online: http://www.swisspost.ch/drones (accessed on 17 August 2023).
- Stolaroff, J.K.; Samaras, C.; O’Neill, E.R.; Lubers, A.; Mitchell, A.S.; Ceperley, D. Energy use and life cycle greenhouse gas emissions of drones for commercial package delivery. Nat. Commun. 2018, 9, 409. [Google Scholar] [CrossRef] [PubMed]
- Jensen-Nau, K.R.; Hermans, T.; Leang, K.K. Near-optimal area-coverage path planning of energy-constrained aerial robots with application in autonomous environmental monitoring. IEEE Trans. Autom. Sci. Eng. 2021, 18, 1453–1468. [Google Scholar] [CrossRef]
- Lin, J.; Wang, Y.; Miao, Z.; Wang, H.; Fierro, R. Robust image-based landing control of a quadrotor on an unpredictable moving vehicle using circle features. IEEE Trans. Autom. Sci. Eng. 2023, 20, 1429–1440. [Google Scholar] [CrossRef]
- Bresciani, T. Modelling, Identification and Control of a Quadrotor Helicopter. Master’s Thesis, Department of Automatic Control, Lund University, Lund, Sweden, 2008. [Google Scholar]
- Swieringa, K.A.; Hanson, C.B.; Richardson, J.R.; White, J.D.; Hasan, Z.; Qian, E.; Girard, A. Autonomous battery swapping system for small–Scale helicopters. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AL, USA, 3–8 May 2010; pp. 3335–3340. [Google Scholar] [CrossRef]
- Leonard, J.; Savvaris, A.; Tsourdos, A. Energy management in swarm of unmanned aerial vehicles. J. Intell. Robot. Syst. 2014, 74, 233–250. [Google Scholar] [CrossRef]
- Junaid, A.B.; Konoiko, A.; Zweiri, Y.; Sahinkaya, M.; Seneviratne, L. Autonomous wireless selfcharging for multi-rotor unmanned aerial vehicles. Energies 2017, 10, 803. [Google Scholar] [CrossRef]
- Campi, T.; Cruciani, S.; Feliziani, M. Wireless power transfer technology applied to an autonomous electric uav with a small secondary coil. Energies 2018, 11, 352. [Google Scholar] [CrossRef]
- Kumar, V.; Michael, N. Opportunities and challenges with autonomous micro aerial vehicles. Int. J. Robot. Res. 2012, 31, 1279–1291. [Google Scholar] [CrossRef]
- Abdilla, A.; Richards, A.; Burrow, S. Power and endurance modelling of battery-powered rotorcraft. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–2 October 2015; pp. 675–680. [Google Scholar] [CrossRef]
- Morton, S.; Papanikolopoulos, N. A small hybrid ground-air vehicle concept. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 1–5 October 2017; pp. 5149–5154. [Google Scholar] [CrossRef]
- Economou, J.; Kladis, G.; Tsourdos, A.; White, B. UAV optimum energy assignment using Dijkstra’s algorithm. In Proceedings of the European Control Conference (ECC), Kos, Greece, 2–5 July 2007; pp. 287–292. [Google Scholar] [CrossRef]
- Carvajal, C.P.; Andaluz, V.H.; Roberti, F.; Carelli, R. Path-following control for aerial manipulators robots with priority on energy saving. Control. Eng. Pract. 2023, 131, 105401. [Google Scholar] [CrossRef]
- Mohiuddin, A.; Taha, T.; Zweiri, Y.; Gan, D. Dual-uav payload transportation using optimized velocity profiles via real-time dynamic programming. Drones 2023, 7, 171. [Google Scholar] [CrossRef]
- Levermore, T.; Sahinkaya, M.N.; Zweiri, Y.; Neaves, B. Real-time velocity optimization to minimize energy use in passenger vehicles. Energies 2017, 10, 30. [Google Scholar] [CrossRef]
- Rossi, R.; Santamaria-Navarro, A.; Andrade-Cetto, J.; Rocco, P. Trajectory generation for unmanned aerial manipulators through quadratic programming. IEEE Robot. Autom. Lett. 2017, 2, 389–396. [Google Scholar] [CrossRef]
- Kreciglowa, N.; Karydis, K.; Kumar, V. Energy efficiency of trajectory generation methods for stop-and-go aerial robot navigation. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 656–662. [Google Scholar] [CrossRef]
- Jacewicz, M.; Zugaj, M.; Glebocki, R.; Bibik, P. Quadrotor model for energy consumption analysis. Energies 2022, 15, 7136. [Google Scholar] [CrossRef]
- Chodnicki, M.; Siemiatkowska, B.; Stecz, W.; Stepien, S. Energy efficient uav flight control method in an environment with obstacles and gusts of wind. Energies 2022, 15, 3730. [Google Scholar] [CrossRef]
- Morbidi, F.; Cano, R.; Lara, D. Minimum-energy path generation for a quadrotor UAV. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1492–1498. [Google Scholar] [CrossRef]
- Zhou, H.; Xiong, H.L.; Liu, Y.; Tan, N.D.; Chen, L. Trajectory planning algorithm of uav based on system positioning accuracy constraints. Electronics 2020, 9, 250. [Google Scholar] [CrossRef]
- Yu, G.; Cabecinhas, D.; Cunha, R.; Silvestre, C. Quadrotor trajectory generation and tracking for aggressive maneuvers with attitude constraints. IFAC-PapersOnLine. 2019, 52, 55–60. [Google Scholar] [CrossRef]
- Schacht-Rodriguez, R.; Ponsart, J.C.; Garcia-Beltran, C.D.; Astorga-Zaragoza, C.M.; Theilliol, D.; Zhang, Y. Path planning generation algorithm for a class of uav multirotor based on state of health of lithium polymer battery. J. Intell. Robot. Syst. 2018, 91, 115–131. [Google Scholar] [CrossRef]
- Wu, M.; Chen, W.; Tian, X. Optimal Energy Consumption Path Planning for Quadrotor UAV Transmission Tower Inspection Based on Simulated Annealing Algorithm. Energies 2022, 15, 8036. [Google Scholar] [CrossRef]
- Jiang, B.; Li, B.; Zhou, W.; Lo, L.-Y.; Chen, C.-K.; Wen, C.-Y. Neural Network Based Model Predictive Control for a Quadrotor UAV. Aerospace 2022, 9, 460. [Google Scholar] [CrossRef]
- Giernacki, W. Minimum Energy Control of Quadrotor UAV: Synthesis and Performance Analysis of Control System with Neurobiologically Inspired Intelligent Controller (BELBIC). Energies 2022, 15, 7566. [Google Scholar] [CrossRef]
- Bianchi, D.; Rolando, L.; Serrao, L.; Onori, S.; Rizzoni, G.; Al-Khayat, N.; Hsieh, T.; Kang, P.T. Layered control strategies for hybrid electric vehicles based on optimal control. Int. J. Electr. Hybrid Veh. (IJEHV) 2011, 3, 191–217. [Google Scholar] [CrossRef]
- Gieras, J.F. Permanent Magnet Motor Technology: Design and Applications; CRC Press, Taylor and Francis Group: Boca Raton, FL, USA, 2009. [Google Scholar]
- Bouabdallah, S.; Murrieri, P.; Siegwart, R. Towards autonomous indoor micro vtol. Auton. Robot. 2005, 18, 171–183. [Google Scholar] [CrossRef]
- Carrillo, L.R.; Lopez, A.E.; Lozano, R.; Pegard, C. Quad Rotorcraft Control: Vision-Based Hovering and Navigation; Springer: London, UK, 2013. [Google Scholar]
- Lua, C.A.; Garcia, C.C.V.; Di Gennaro, S.; Castillo–Toledo, B.; Morales, M.E.S. Real–time hovering control of unmanned aerial vehicles. Math. Probl. Eng. 2020, 2020, 2314356. [Google Scholar] [CrossRef]
- Mendoza, L.F.M.; Bonilla, J.T.G.; Garcia-Torales, G.; Lua, C.A.; Di Gennaro, S. Visual Sensor System Applied to Trajectory Generation for UAVs. In Proceedings of the IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 9–11 November 2022. [Google Scholar] [CrossRef]
- Li, Y.R.; Peng, C.C. Development of a full orientation flight robotics: Dynamics modeling, analysis, and control design. IEEE Access 2023, 11, 110234–110244. [Google Scholar] [CrossRef]
- Jongerden, M.R.; Haverkort, B.R. Which battery model to use? IET Softw. 2012, 3, 445–457. [Google Scholar] [CrossRef]
- Cappuzzo, F.; Dezobry, V.; Bianchi, D.; Di Gennaro, S. A Novel Co-simulation framework for Verification and Validation of GNC Algorithms for Autonomous UAV. In Proceedings of the Vertical Flight Society’s 78th Annual Forum & Technology Display, Fort Worth, TX, USA, 10–12 May 2022. [Google Scholar]
- Siemens: Simcenter Amesim 2021.1 Reference Guide 2021. Available online: https://docs.plm.automation.siemens.com/content/amesim/17/help/en_US/quick_start_guide/references.html (accessed on 19 January 2024).
- Nguyen, D.H.; Liu, Y.; Mori, K. Experimental study for aerodynamic performance of quadrotor helicopter. Trans. Jpn. Soc. Aeronaut. Space Sci. 2018, 61, 29–39. [Google Scholar] [CrossRef]
- Six, D.; Briot, S.; Erskine, J.; Chriette, A. Identification of the propeller coefficients and dynamic parameters of a hovering quadrotor from flight data. IEEE Robot. Autom. Lett. 2020, 5, 1063–1070. [Google Scholar] [CrossRef]
- Bianchi, D.; Di Gennaro, S.; Di Ferdinando, M.D.; Lua, C.A. Robust control of uav with disturbances and uncertainty estimation. Machines 2023, 11, 352. [Google Scholar] [CrossRef]


| m | Mass of the Airframe | 5 kg |
|---|---|---|
| l | Distance of the center of mass to the rotor shaft | 0.3 m |
| Inertia in the x-axis | 0.011521 kg | |
| Inertia in the y-axis | 0.0362132 kg | |
| Inertia in the z-axis | 0.029142 kg | |
| Inertia of the propellers | 0.0003 kg | |
| g | Gravity acceleration | 9.81 m |
| b | Trust factor | N |
| c | Drag factor | N m |
| EC J | BC | |||||
|---|---|---|---|---|---|---|
| Final Point | OC | SMC | SAC | OC | SMC | SAC |
| [10,20,30] | 100 | 101.52 | 101.43 | 100 | 101.31 | 101.27 |
| [12,10,−40] | 100 | 102.23 | 102.3 | 100 | 102.09 | 102.14 |
| [8,10,6] | 100 | 101.1 | 100.71 | 100 | 100.92 | 100.54 |
| [−30,40,50] | 100 | 102.3 | 101.9 | 100 | 102.11 | 101.78 |
| [20,−20,−40] | 100 | 102.17 | 102.02 | 102 | 102.21 | 101.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bianchi, D.; Borri, A.; Cappuzzo, F.; Di Gennaro, S. Quadrotor Trajectory Control Based on Energy-Optimal Reference Generator. Drones 2024, 8, 29. https://doi.org/10.3390/drones8010029
Bianchi D, Borri A, Cappuzzo F, Di Gennaro S. Quadrotor Trajectory Control Based on Energy-Optimal Reference Generator. Drones. 2024; 8(1):29. https://doi.org/10.3390/drones8010029
Chicago/Turabian StyleBianchi, Domenico, Alessandro Borri, Federico Cappuzzo, and Stefano Di Gennaro. 2024. "Quadrotor Trajectory Control Based on Energy-Optimal Reference Generator" Drones 8, no. 1: 29. https://doi.org/10.3390/drones8010029
APA StyleBianchi, D., Borri, A., Cappuzzo, F., & Di Gennaro, S. (2024). Quadrotor Trajectory Control Based on Energy-Optimal Reference Generator. Drones, 8(1), 29. https://doi.org/10.3390/drones8010029








