Disturbance Observer-Enhanced Adaptive Fault-Tolerant Control of a Quadrotor UAV against Actuator Faults and Disturbances
Abstract
:1. Introduction
- The existing ASMC methods usually adaptively modify the gain of the discontinuous control part while ignoring the continuous part, which may result in system control chattering due to parameter overestimation.
- In addition, the existing adaptive schemes are commonly constructed with a sliding variable, if the system tracking error is not zero in practical applications, the adaptation does not cease, which also causes parameter overestimation.
- The majority of the existing fault-tolerant control techniques depend on the robustness of the designed controller to accommodate the adverse effects of the external disturbances. However, when the encountered disturbances are significantly large, it may cause instability in the system.
- The proposed control approach does not merely rely on the robustness of SMC, and it can also adaptively create control signals to compensate for actuator faults and disturbances. The proposed method can alter the gain of both the continuous and discontinuous control sections while decreasing the system control chattering caused by the overuse of the discontinuous control gain.
- The proposed adaptive control approach is formulated with the sliding variable and the boundary layer thickness, which can avoid overestimation of the control parameters, compared to the existing adaptive control schemes in the literature, where the adaptive control is commonly constructed merely with a sliding variable. The adaptation can be stopped using the proposed approach as long as the sliding variable is contained inside the boundary layer.
- A sliding mode observer is proposed and integrated with the designed ASMC scheme to actively compensate both actuator faults and disturbances. It can further contribute to decreasing the value of the discontinuous control gain and suppress the unexpected control chattering.
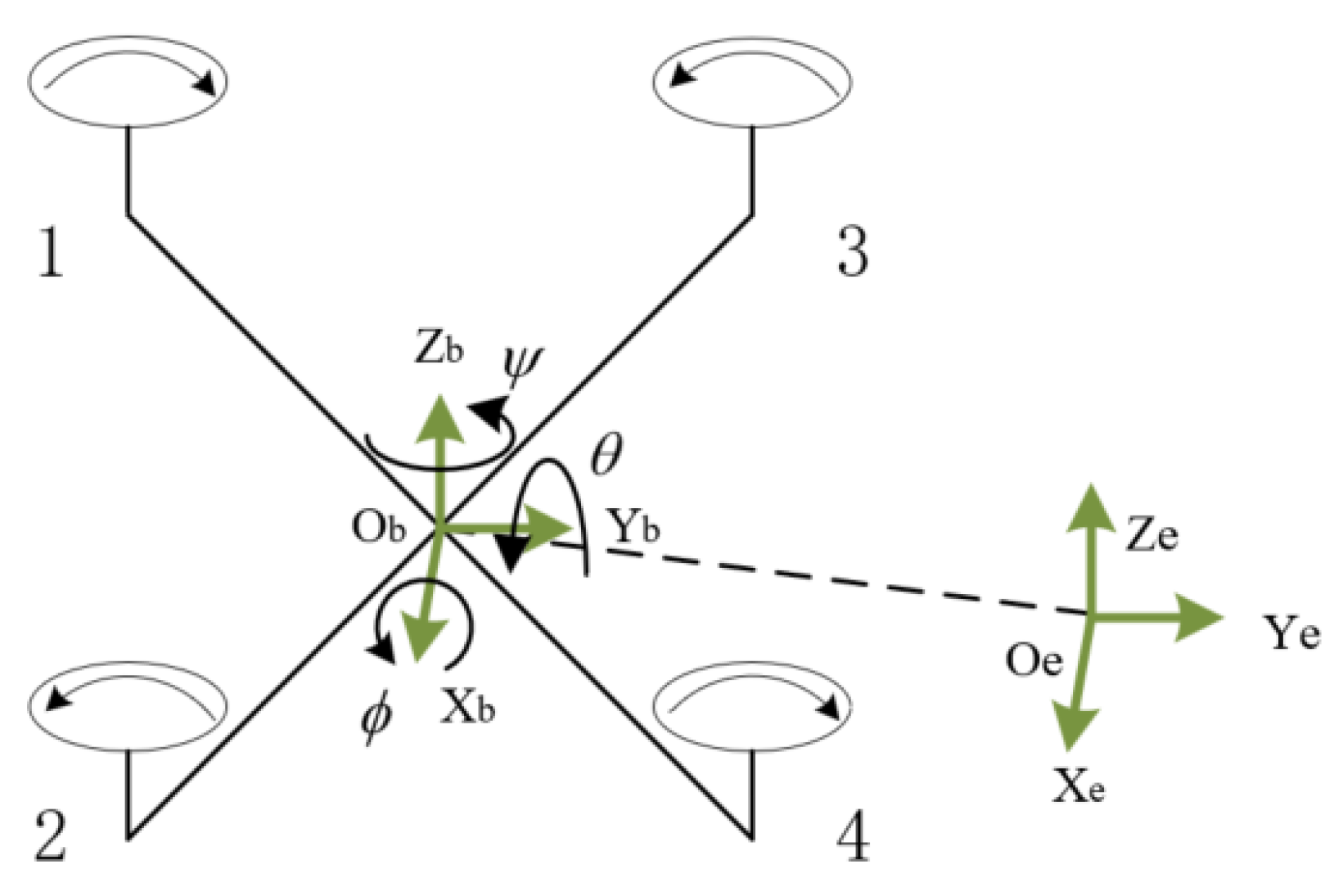
2. Modeling of the Quadrotor UAV
3. Design of Adaptive Fault-Tolerant Control Strategy
3.1. Design of Attitude Control Strategy
3.1.1. Baseline Sliding Mode Control
3.1.2. Adaptive Sliding Mode Control
3.2. Design of the Position Control Strategy
3.2.1. Baseline Sliding Mode Control
3.2.2. Adaptive Sliding Mode Control
3.3. Disturbance Observer-Based Adaptive Sliding Mode Control
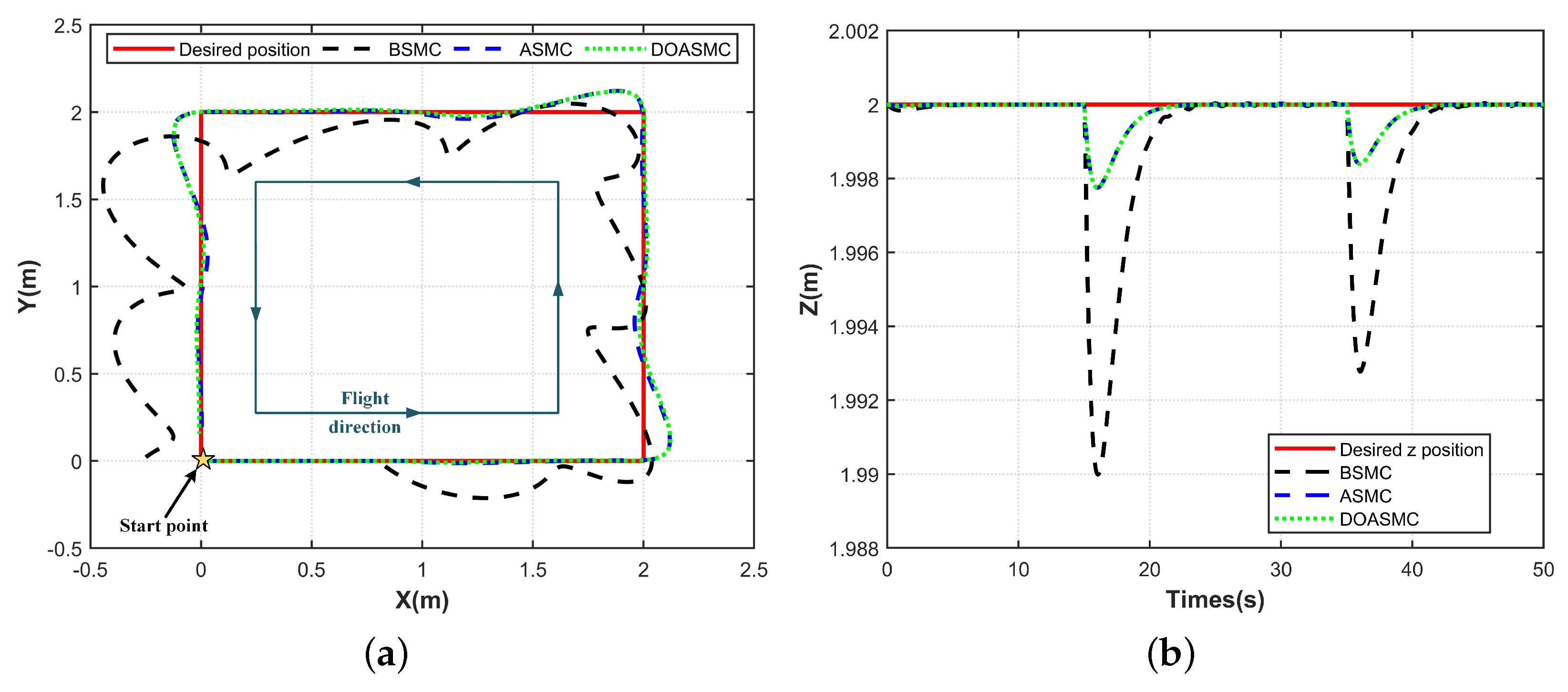
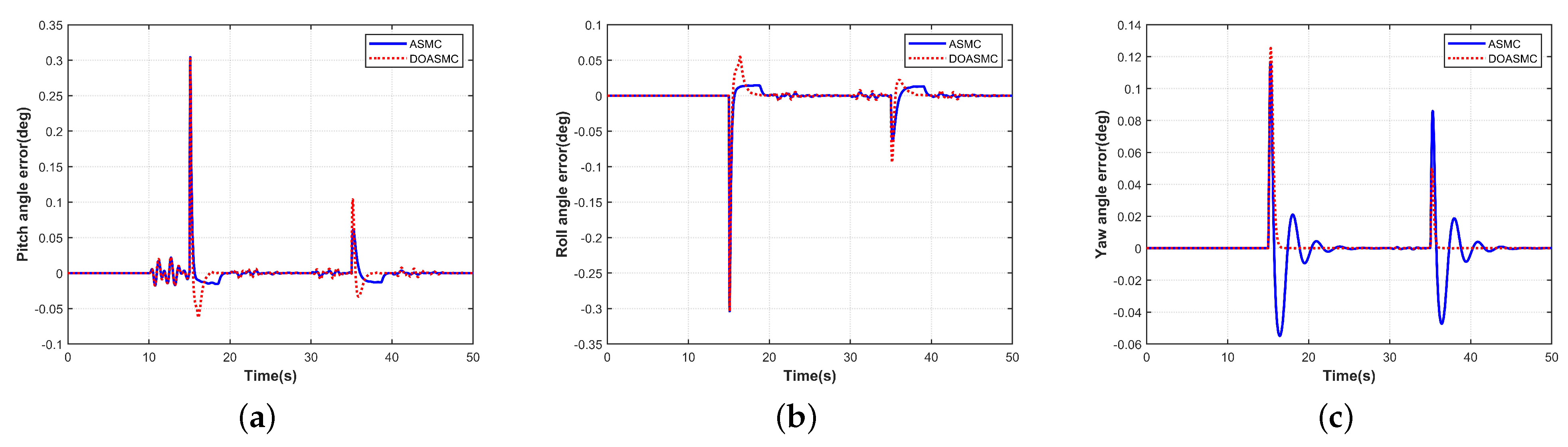
4. Simulation Results and Discussions
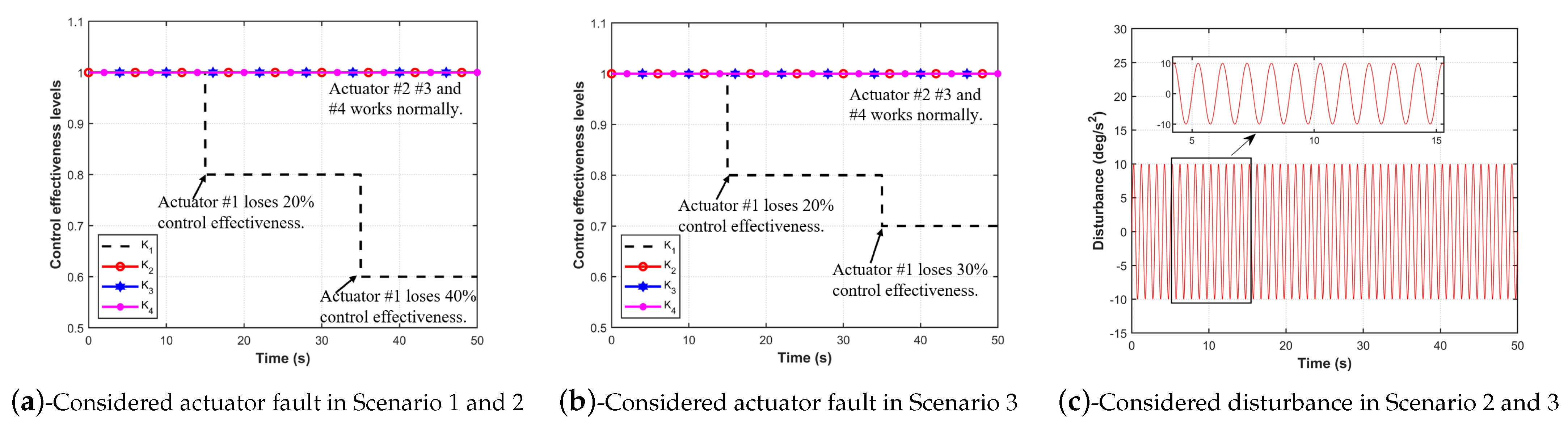
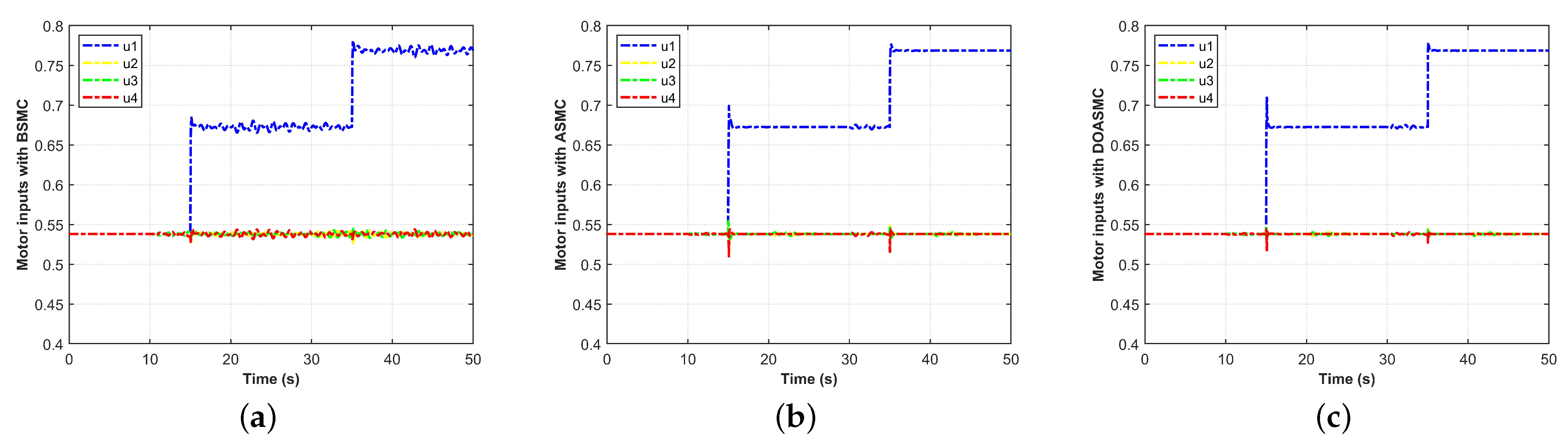
4.1. Scenario 1
4.2. Scenario 2
4.3. Scenario 3
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Griffin, B.; Fierro, R.; Palunko, I. An autonomous communications relay in GPS-denied environments via antenna diversity. J. Def. Model. Simul. 2012, 9, 33–44. [Google Scholar] [CrossRef]
- Ji, S.; Tang, H.; Ming, Y.; Zhao, C. Design of high automatic target recognition unmanned reconnaissance system based on YOLOv5. In Proceedings of the 2022 IEEE 4th International Conference on Civil Aviation Safety and Information Technology (ICCASIT), Dali, China, 12–14 October 2022; pp. 1446–1449. [Google Scholar]
- Cruz, P.J.; Fierro, R. Cable-suspended load lifting by a quadrotor UAV: Hybrid model, trajectory generation, and Control. Auton. Robot. 2017, 41, 1629–1643. [Google Scholar] [CrossRef]
- Ghamry, K.A.; Zhang, Y.M. Cooperative control of multiple UAVs for forest fire monitoring and detection. In Proceedings of the 2016 12th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Auckland, New Zealand, 29–31 August 2016; pp. 1–6. [Google Scholar]
- Duggal, V.; Sukhwani, M.; Bipin, K.; Reddy, G.S.; Krishna, K.M. Plantation monitoring and yield estimation using autonomous quadcopter for precision agriculture. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation, Stockholm, Sweden, 16–21 May 2016; pp. 5121–5127. [Google Scholar]
- Araar, O.; Aouf, N. Visual servoing of a quadrotor uav for autonomous power lines inspection. In Proceedings of the 22nd Mediterranean Conference on Control and Automation, Palermo, Italy, 16–19 June 2014; pp. 1418–1424. [Google Scholar]
- Budiharto, W.; Irwansyah, E.; Suroso, J.S.; Chowanda, A.; Ngarianto, H.; Gunawan, A.A.S. Mapping and 3D modelling using quadrotor drone and GIS software. J. Big Data 2021, 8, 48. [Google Scholar] [CrossRef]
- Martins, L.; Cardeira, C.; Oliveira, P. Inner-outer feedback linearization for quadrotor control: Two-step design and validation. Nonlinear Dyn. 2022, 110, 479–495. [Google Scholar] [CrossRef]
- Pan, J.; Shao, B.; Xiong, J.; Zhang, Q. Attitude control of quadrotor UAVs based on adaptive sliding mode. Int. J. Control Autom. Syst. 2023, 21, 2698–2707. [Google Scholar] [CrossRef]
- Liu, K.; Wang, R. Antisaturation command filtered backstepping control-based disturbance rejection for a quadrotor UAV. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 3577–3581. [Google Scholar]
- Amin, R.; Aijun, L.; Shamshirband, S. A review of quadrotor UAV: Control methodologies and performance evaluation. Int. J. Autom. Control 2016, 10, 87–103. [Google Scholar] [CrossRef]
- Maaruf, M.; Mahmoud, M.S.; Ma’arif, A. A survey of control methods for quadrotor UAV. Int. J. Robot. Control Syst. 2022, 2, 652–665. [Google Scholar] [CrossRef]
- Mo, H.; Farid, G. Nonlinear and adaptive intelligent control techniques for quadrotor UAV—A survey. Asian J. Control 2019, 21, 989–1008. [Google Scholar] [CrossRef]
- Rahmat, M.F.; Eltayeb, A.; Basri, M.A.M. Adaptive feedback linearization controller for stabilization of quadrotor UAV. Int. J. Integr. Eng. 2020, 12, 1–17. [Google Scholar]
- Wu, X.; Xiao, B.; Qu, Y. Modeling and sliding mode-based attitude tracking control of a quadrotor UAV with time-varying mass. ISA Trans. 2022, 124, 436–443. [Google Scholar] [CrossRef]
- Liu, W.; Cheng, X.; Zhang, J. Command filter-based adaptive fuzzy integral backstepping control for quadrotor UAV with input saturation. J. Frankl. Inst. 2023, 360, 484–507. [Google Scholar] [CrossRef]
- Fourlas, G.K.; Karras, G.C. A survey on fault diagnosis and fault-tolerant control methods for unmanned aerial vehicles. Machines 2021, 9, 197. [Google Scholar] [CrossRef]
- Chamseddine, A.; Theilliol, D.; Zhang, Y.M.; Rabbath, C.A. Active fault-tolerant control system design with trajectory replanning against actuator faults and saturation: Application to a quadrotor unmanned aerial vehicle. Int. J. Adapt. Control Signal Process. 2015, 29, 1–23. [Google Scholar] [CrossRef]
- Merheb, A.R.; Noura, H.; Bateman, F. Passive fault tolerant control of quadrotor uav using regular and cascaded sliding mode Control. In Proceedings of the 2013 Conference on Control and Fault-Tolerant Systems, Nice, France, 9–11 October 2013; pp. 330–335. [Google Scholar]
- Wang, T.; Xie, W.; Zhang, Y.M. Sliding mode fault tolerant control dealing with modeling uncertainties and actuator faults. ISA Trans. 2012, 51, 386–392. [Google Scholar] [CrossRef] [PubMed]
- Zeghlache, S.; Mekki, H.; Bouguerra, A.; Djerioui, A. Actuator fault tolerant control using adaptive RBFNN fuzzy sliding mode controller for coaxial octorotor UAV. ISA Trans. 2018, 80, 267–278. [Google Scholar] [CrossRef]
- Eliker, K.; Zhang, W. Finite-time adaptive integral backstepping fast terminal sliding mode control application on quadrotor UAV. Int. J. Control Autom. Syst. 2020, 18, 415–430. [Google Scholar]
- Ha, L.N.N.T.; Hong, S.K. Robust dynamic sliding mode control-based PID–super twisting algorithm and disturbance observer for second-order nonlinear systems: Application to UAVs. Electronics 2019, 8, 760. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, G.; Dong, Q. Multi-variable finite-time observer-based adaptive-gain sliding mode control for fixed-wing UAV. IET Control Theory Appl. 2021, 15, 223–247. [Google Scholar] [CrossRef]
- Zheng, E.H.; Xiong, J.J.; Luo, J.L. Second order sliding mode control for a quadrotor UAV. ISA Trans. 2014, 53, 1350–1356. [Google Scholar] [CrossRef]
- Nguyen, L.V.; Phung, M.D.; Ha, Q.P. Iterative Learning Sliding Mode Control for UAV Trajectory Tracking. Electronics 2021, 10, 2474. [Google Scholar] [CrossRef]
- Zheng, B.; Wu, Y.; Li, H.; Chen, Z. Adaptive sliding mode attitude control of quadrotor uavs based on the delta operator framework. Symmetry 2022, 14, 498. [Google Scholar] [CrossRef]
- Hassani, H.; Mansouri, A.; Ahaitouf, A. A new robust adaptive sliding mode controller for quadrotor UAV flight. In Proceedings of the 2020 IEEE 2nd International Conference on Electronics, Control, Optimization and Computer Science (ICECOCS), Kenitra, Morocco, 2–3 December 2020; pp. 1–6. [Google Scholar]
- Islam, S.; Faraz, M.; Ashour, R.; Cai, G.; Dias, J.; Seneviratne, L. Adaptive sliding mode control design for quadrotor unmanned aerial vehicle. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 34–39. [Google Scholar]
- Mofid, O.; Mobayen, S. Adaptive sliding mode control for finite-time stability of quad-rotor UAVs with parametric uncertainties. ISA Trans. 2018, 72, 1–14. [Google Scholar] [CrossRef]
- Bouadi, H.; Cunha, S.S.; Drouin, A.; Mora-Camino, F. Adaptive sliding mode control for quadrotor attitude stabilization and altitude tracking. In Proceedings of the 2011 IEEE 12th International Symposium on Computational Intelligence and Informatics (CINTI), Budapest, Hungary, 21–22 November 2011; pp. 449–455. [Google Scholar]
- Wang, B.; Shen, Y.Y.; Li, N.; Zhang, Y.M.; Gao, Z.H. An adaptive sliding mode fault-tolerant control of a quadrotor unmanned aerial vehicle with actuator faults and model uncertainties. Int. J. Robust Nonlinear Control 2023, 1–17. [Google Scholar] [CrossRef]
- Wang, B.; Zhu, D.; Han, L.; Gao, H.; Gao, Z.; Zhang, Y.M. Adaptive fault-tolerant control of a hybrid canard rotor/wing UAV under transition flight subject to actuator faults and model uncertainties. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4559–4574. [Google Scholar] [CrossRef]
- Chaoraingern, J.; Tipsuwanporn, V.; Numsomran, A. Modified adaptive sliding mode control for trajectory tracking of mini-drone quadcopter unmanned aerial vehicle. Int. J. Intell. Eng. Syst. 2020, 13, 145–158. [Google Scholar] [CrossRef]
- Oh, H.; Kim, S.; Tsourdos, A.; White, B.A. Decentralised standoff tracking of moving targets using adaptive sliding mode control for UAVs. J. Intell. Robot. Syst. 2014, 76, 169–183. [Google Scholar] [CrossRef]
- Eltayeb, A.; Rahmat, M.F.; Basri, M.A.M.; Eltoum, M.M.; El-Ferik, S. An improved design of an adaptive sliding mode controller for chattering attenuation and trajectory tracking of the quadcopter UAV. IEEE Access 2020, 8, 205968–205979. [Google Scholar] [CrossRef]
- Huang, T.; Huang, D.; Wang, Z.; Dai, X.; Shah, A. Generic adaptive sliding mode control for a quadrotor UAV system subject to severe parametric uncertainties and fully unknown external disturbance. Int. J. Control Autom. Syst. 2021, 19, 698–711. [Google Scholar] [CrossRef]
- Huang, T.; Huang, D.; Wang, Z.; Shah, A. Robust tracking control of a quadrotor UAV based on adaptive sliding mode controller. Complexity 2019, 2019, 7931632. [Google Scholar] [CrossRef]
- Hassani, H.; Mansouri, A.; Ahaitouf, A. Robust autonomous flight for quadrotor UAV based on adaptive nonsingular fast terminal sliding mode Control. Int. J. Dyn. Control 2021, 9, 619–635. [Google Scholar] [CrossRef]
- Lin, X.; Yu, Y.; Sun, C.Y. A decoupling control for quadrotor UAV using dynamic surface control and sliding mode disturbance observer. Nonlinear Dyn. 2019, 97, 781–795. [Google Scholar] [CrossRef]
- Ahmed, N.; Chen, M.; Shao, S. Disturbance observer based tracking control of quadrotor with high-order disturbances. IEEE Access 2020, 8, 8300–8313. [Google Scholar] [CrossRef]
- Kang, B.; Miao, Y.; Liu, F.; Duan, J.; Wang, K.; Jiang, S. A second-order sliding mode controller of quad-rotor UAV based on PID sliding mode surface with unbalanced load. J. Syst. Sci. Complex. 2021, 34, 520–536. [Google Scholar] [CrossRef]
- Li, B.; Gong, W.; Yang, Y.; Xiao, B.; Ran, D. Appointed fixed time observer-based sliding mode control for a quadrotor UAV under external disturbances. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 290–303. [Google Scholar] [CrossRef]
- Ahmed, N.; Chen, M. Sliding mode control for quadrotor with disturbance observer. Adv. Mech. Eng. 2018, 10, 1–16. [Google Scholar] [CrossRef]
- Fethalla, N.; Saad, M.; Michalska, H.; Ghommam, J. Robust observer-based dynamic sliding mode controller for a quadrotor UAV. IEEE Access 2018, 6, 45846–45859. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, Y.M.; Zhang, W. A Composite Adaptive Fault-Tolerant Attitude Control for a Quadrotor UAV with Multiple Uncertainties. J. Syst. Sci. Complex. 2022, 35, 81–104. [Google Scholar] [CrossRef]
- Chen, M.; Shi, P.; Lim, C.C. Robust constrained control for MIMO nonlinear systems based on disturbance observer. IEEE Trans. Autom. Control 2015, 60, 3281–3286. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, F.; Guo, Y.; Hua, C. Multivariable sliding mode backstepping controller design for quadrotor UAV based on disturbance observer. Sci. China Inf. Sci. 2018, 61, 112207. [Google Scholar] [CrossRef]
- Besnard, L.; Shtessel, Y.B.; Landrum, B. Quadrotor vehicle control via sliding mode controller driven by sliding mode disturbance observer. J. Frankl. Inst. 2012, 349, 658–684. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Mung, N.X.; Thanh, H.L.N.N.; Huynh, T.T.; Lam, N.T.; Hong, S.K. Adaptive sliding mode control for attitude and altitude system of a quadcopter UAV via neural network. IEEE Access 2021, 9, 40076–40085. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Hong, S.K. Fault-tolerant control of quadcopter UAVs using robust adaptive sliding mode approach. Energies 2018, 12, 95. [Google Scholar] [CrossRef]
- Hadi, R.; Sima, A. Neural network-based adaptive sliding mode control design for position and attitude control of a quadrotor UAV. Aerosp. Sci. Technol. 2019, 91, 12–27. [Google Scholar]
- Wang, B.; Yu, X.; Mu, L.X.; Zhang, Y.M. Disturbance observer-based adaptive fault-tolerant control for a quadrotor helicopter subject to parametric uncertainties and external disturbances. Mech. Syst. Signal Process. 2019, 120, 727–743. [Google Scholar] [CrossRef]






| Parameter | Explanation | Value |
|---|---|---|
| m | total mass | 1.121 kg |
| distance between motor #1 and motor #2 | 0.2136 m | |
| distance between motor #3 and motor #4 | 0.1758 m | |
| rolling moment of inertia | 0.01 kgm | |
| pitching moment of inertia | 0.0082 kgm | |
| yawing moment of inertia | 0.0148 kgm |
| Control Loop | Controller | |||
|---|---|---|---|---|
| attitude | 40 | 400 | 1 | |
| 40 | 400 | 1 | ||
| 40 | 400 | 1 | ||
| position | X | 0.2 | 0.01 | 0.1 |
| Y | 0.2 | 0.01 | 0.1 | |
| Z | 2 | 1 | 10 |
| Scenario 1 | Scenario 2 | Scenario 3 | |
|---|---|---|---|
| 20% loss of effectiveness fault in actuators #1 at 15 s | ✓ | ✓ | ✓ |
| 40% loss of effectiveness fault to actuators #1 at 35 s | ✓ | ✓ | |
| 30% loss of effectiveness fault to actuators #1 at 35 s | ✓ | ||
| Disturbances cover the entire simulation. | ✓ | ✓ | |
| Parametric uncertainties cover the entire simulation. | ✓ |
| Simulation Scenario | Attitude-Angle | BSMC (deg) | ASMC (deg) | DOASMC (deg) |
|---|---|---|---|---|
| 1 | 1.2229 | 0.0209 | 0.0190 | |
| 1.2177 | 0.0214 | 0.0197 | ||
| 0.0573 | 0.0082 | 0.0000 | ||
| 2 | 1.5668 | 0.0418 | 0.0238 | |
| 1.5614 | 0.0418 | 0.0238 | ||
| 0.0777 | 0.0235 | 0.0035 | ||
| 3 | 1.0324 | 0.0189 | 0.0178 | |
| 1.0284 | 0.0186 | 0.0179 | ||
| 0.0443 | 0.0042 | 0.0032 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, X.; Wang, B.; Shen, Y.; Fu, Y.; Li, N. Disturbance Observer-Enhanced Adaptive Fault-Tolerant Control of a Quadrotor UAV against Actuator Faults and Disturbances. Drones 2023, 7, 541. https://doi.org/10.3390/drones7080541
Hu X, Wang B, Shen Y, Fu Y, Li N. Disturbance Observer-Enhanced Adaptive Fault-Tolerant Control of a Quadrotor UAV against Actuator Faults and Disturbances. Drones. 2023; 7(8):541. https://doi.org/10.3390/drones7080541
Chicago/Turabian StyleHu, Xinyue, Ban Wang, Yanyan Shen, Yifang Fu, and Ni Li. 2023. "Disturbance Observer-Enhanced Adaptive Fault-Tolerant Control of a Quadrotor UAV against Actuator Faults and Disturbances" Drones 7, no. 8: 541. https://doi.org/10.3390/drones7080541
APA StyleHu, X., Wang, B., Shen, Y., Fu, Y., & Li, N. (2023). Disturbance Observer-Enhanced Adaptive Fault-Tolerant Control of a Quadrotor UAV against Actuator Faults and Disturbances. Drones, 7(8), 541. https://doi.org/10.3390/drones7080541








