Auto-Landing of Moving-Mass Actuated Unmanned Aerial Vehicles Based on Linear Active Disturbance Rejection Control

Abstract

Unlike the roll motion of the unmanned aerial vehicle (UAV) controlled by the ailerons, the moving-mass actuated unmanned aerial vehicle (MAUAV) uses the motion of the mass block inside the wing to generate the roll moment. The light weight and severe coupling of lateral and longitudinal motion of this type of small UAV make its landing control a challenging task. Considering the above problems, the dynamic models of MAUAV are first established. Then, forward velocity, altitude, attitude, and moving-mass position controllers are designed separately to make the MAUAV track a given path during the landing process. Linear active disturbance rejection control (LADRC) is introduced in the design process of all four controllers, compensating for unknown disturbances in the system. Simulation results show that the proposed control scheme can achieve fast and accurate tracking of forward velocity and flight trajectory commands with good robustness to model uncertainties.

1. Introduction

In recent years, thanks to the advantages of low cost, simple structure, strong stealth, and high mobility, unmanned aerial vehicles (UAVs) have been widely used in civil and military fields, such as meteorological monitoring, aerial surveying and mapping, unmanned cargo system, and battlefield surveillance [1,2,3,4,5]. The application of UAVs in these fields can reduce the consumption of human resources, improve work efficiency, and at the same time, ensure the safety of personnel to reduce the casualty rate. According to the classification of wing structure, UAVs are mainly divided into two types: fixed-wing and rotary-wing. They each have their advantages and disadvantages, but in general, fixed-wing UAVs are more widely used than rotary-wing UAVs and capable of long-distance flight missions. Traditionally, fixed-wing UAVs realize their attitude movement through the control of ailerons, rudders, and elevators. With the development of moving-mass control techniques in many different fields (including satellites [6,7], re-entry vehicles [8,9,10], and underwater vehicles [11], etc.), researchers have also started to focus on applying this control scheme to the flight control of UAVs. As a reliable alternative to the traditional scheme, the moving-mass control scheme allows the controlled mass blocks to be mounted inside the aircraft, and the attitude motion of UAVs can be controlled by driving the movement of the mass blocks. Therefore, this control scheme can optimize the aerodynamic shape, simplify the wing structure to reduce the manufacturing difficulty of the wing shape, and improve the integrity of the shape to further enhance the stealthiness of the UAVs.

The landing phase is one of the most critical and accident-prone phases of the entire mission execution process for fixed-wing UAVs. A typical UAV landing consists of three phases: approach, glide slope, and flare. In order to reduce accidents during the landing process of UAVs, it is necessary to design an auto-landing control strategy with good control performance and high precision in order that UAVs can closely track the desired path in the three landing stages and finally land safely. The application of superior auto-landing control strategies will also greatly improve the recovery rate of UAVs, and thus save costs. The more common methods used for UAV control include PID control, H_∞, sliding mode control, model predictive control, backstepping, adaptive control, linear-quadratic Gaussian approach, robust adaptive control, etc. [12,13,14,15,16,17,18]. They are applied in all phases of UAV flight (including the landing phase, which has the highest accident rate) to improve flight stability and safety. In particular, an attitude controller based on the PID method was designed to overcome the loss of stability in the flying aircraft [12]. Rao and Go [13] proposed an automatic landing controller for UAVs using sliding mode technology, and avoided the problems of chatter and high feedback gain by selecting suitable reaching laws. Mihai [19] designed backstepping and dynamic inversion-based control strategies to assist the automatic landing of UAVs under the superposition of various wind disturbances, which are measured by the estimator and compensated in the design process of the controller. With the development of intelligent systems, more and more intelligent control algorithms are being applied to the flight control of UAVs. A convolutional neural network is trained to predict the heading angle of the aircraft by using image inputs in the case of beacon failure [20]. Authors in [21] proposed a deep learning-based vision transformer particle region-based convolutional neural network for navigation when the fixed-wing UAV was autonomous landing.

It is not difficult to find that the above control methods are all applied to fixed-wing UAVs driven by ailerons. For moving-mass actuated fixed-wing UAVs, many related studies [22,23,24,25] have been carried out by Erturk et al. Based on dynamics analysis and simulation tests of MAUAVs under different flight conditions, they pointed out that the moving-mass scheme can reduce fuel consumption to some extent since this method is able to eliminate the drag generated by aerodynamic surface deflection. In [16], authors concluded that the controllability of moving-mass control is similar or higher than that with aerodynamic surface solutions when the UAV is flying at low speeds. As mentioned earlier, the development of artificial intelligence in recent years has led to its increasingly widespread use in fixed-wing UAVs. At the same time, researchers have also used AI technology to control MAUAVs. Qiu et al. [26] proposed a fixed-wing UAV structure with a combination of rudder, elevator, and movable slider to control the attitude. The offset of the internal slider is able to generate a rolling moment to control the roll motion of the UAV, thus the parameters of the slider are important factors affecting the dynamic performance of the vehicle. The maximum rolling moment provided by this solution depends to a large extent on the mass and displacement of the slider. In addition, this moment is related to the attitude of the UAV, which decreases with the increasing roll (and pitch) angle within a certain range when the mass and displacement of the slider remain unchanged. Based on this structure, they analyzed its dynamic characteristics and designed an adaptive sliding mode attitude controller incorporating the fuzzy system and RBF neural network for it. Based on deep reinforcement learning, an end-to-end attitude controller of MAUAVs was designed and the robustness of this controller was verified by random initialization and parameter perturbation during simulation [27]. However, these studies related to MAUAVs did not design detailed and complete automatic landing control strategies for the landing phase. Both the coupling of different channels and model uncertainties in MAUAV systems bring difficulties to the design of auto-landing control strategies.

The linear active disturbances rejection controller (LADRC) was first proposed in the literature [28]. This control method works by expanding the unknown disturbances into additional states of the system, and then estimating the values of all states using a linear state estimator. Finally, the control input of the system is designed based on PI control and the estimated values. Compared with the above-mentioned control methods, this control method not only has a simple design form, the selection of control parameters follows certain rules (reducing the possibility of artificial blind selection of parameter values), but also can obtain excellent tracking performance. The simplicity of the structure, the regularity of the parameters, and the accuracy of the control results are more conducive to the practical application in the system with unknown disturbance. A practical application of LADRC to the sensorless control of internal permanent-magnet synchronous motor was carried out by authors in [29]. They used linear extended state observers (LESO) to achieve high-performance position estimation and good robustness of the system over full-speed range. The LADRC has also been extensively studied for use in the field of aerial vehicles [30,31,32]. In [31], a fuzzy controller and LADRC are combined to simultaneously obtain their adaptive and anti-interference capabilities, and subsequently increase the response speed of a quadrotor UAV and improve the dynamic performance of the system. Similarly, Wang et al. [32] designed a mass adaptive control method combined with sliding mode control (SMC) and LADRC for a quadrotor load UAV. This is due to the fact that the bandwidth limitation of LADRC can be overcome by enhancing the robustness of the system through SMC. And the LESO is able to estimate the unmodelled dynamics caused by SMC chattering and external unknown disturbances. In this paper, in the view of achievements of the LADRC method in the field of control, four controllers are designed with the help of this method and work together to realize the autonomous landing of MAUAV. The main contributions of this paper are summarized in the following four aspects:

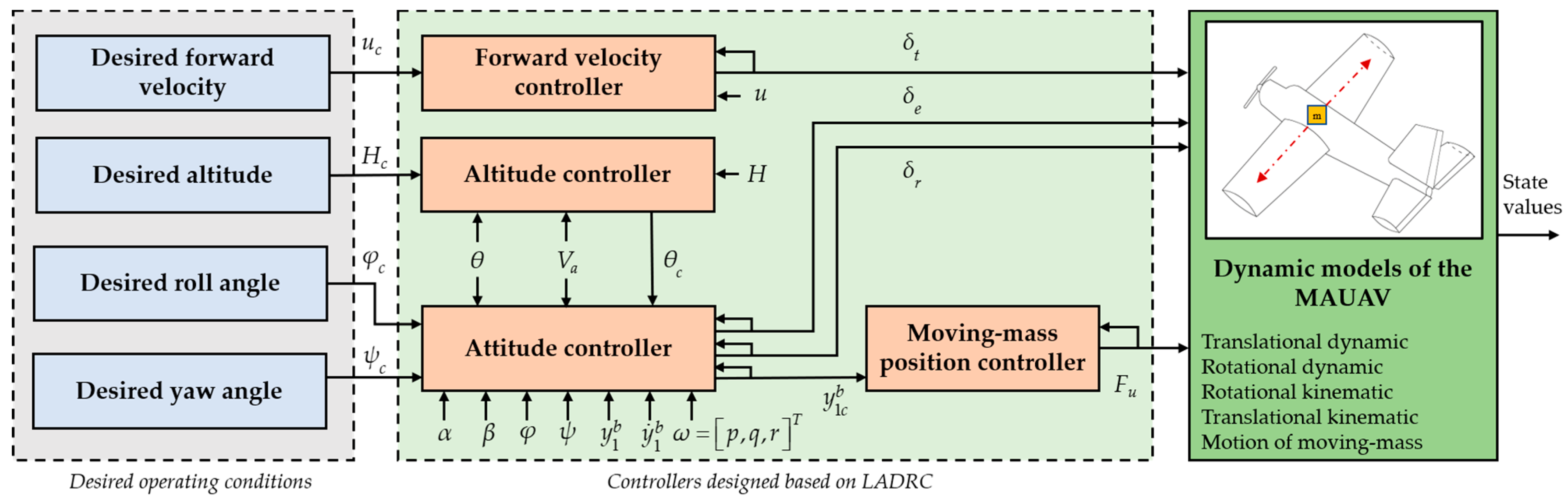
• The characteristics and dynamic models of the moving-mass actuated unmanned aerial vehicle are presented and an automatic landing control strategy is designed, which has not been studied yet for this type of UAV. Both lateral and longitudinal movements of the UAV are taken into account during landing and the tracking error in both planes is kept within a small range. This is in contrast to many papers [33,34] where only separate lateral and longitudinal dynamics are studied in auto-landings.
• The control strategy of the MAUAV is divided into an altitude-attitude slider system and a forward velocity tracking system. The former includes three controllers of altitude, attitude, and slider to provide the expected driving force for slider and expected deflections for rudder and elevator; the latter establishes a throttle command to maintain a steady forward velocity, due to the fact that accurate control of forward velocity is essential for an efficient and safe landing. In addition, compared with the attitude control of the same type of UAV [26], this paper considers the influence of wind disturbance during the whole landing process, which is more in line with the actual situation.
• The design of all four controllers in this paper is based on the LADRC, which simplifies the difficulty of the controller design and the complexity of the algorithm. The designed controllers are not based on accurate dynamic models and are able to estimate and compensate for external disturbances, offering better applicability than existing controllers used in the field of mass-actuated UAVs [24,35].
• The LuGre friction model has been introduced into the moving-mass position model to provide a more detailed description of the friction behavior of the slider and to make the simulation environment more realistic.

The remainder of this paper is arranged as follows: In Section 2, by analyzing the motion characteristics of the MAUAV, its dynamic models, such as attitude, position, and slider displacement models, are established. Based on these dynamic models, the controller design models of forward velocity, altitude, attitude, and moving-mass position are sorted out in Section 3, and four corresponding controllers with disturbance compensation functions are designed. In addition, by drawing the actual flight trajectory of the MAUAV and comparing it with the expected trajectory in the simulation test, the specific landing process of the MAUAV is demonstrated, and the effectiveness of the auto-landing method composed of four controllers is verified in Section 4. Finally, Section 5 includes some conclusions of the paper.

2. Problem Formulation and Dynamic Models

2.1. Configuration of the MAUAV

The schematic diagram of the studied moving-mass actuated UAV is shown in Figure 1. Unlike conventional fixed-wing UAVs fitted with ailerons, the roll motion of the MAUAV is achieved by mounting a movable slider in the lateral direction. The longitudinal movement and forward power mode remain unchanged and are still controlled by the elevator and propeller, respectively. Compared to the dual-slider scheme in literature [24], the rudder was retained in the single-slide scheme. This kind of scheme not only reduces the manufacturing difficulty of the airframe, but also alleviates the space constraint problem, which in turn improves the control capability of the vehicle by installing a larger slider [26]. Considering the special characteristics of the MAUAV, the definition of the body frame is given first. The origin O is the center of mass when the airframe is not fitted with the slider. The x_b-axis points out the nose along the airframe’s longitudinal axis; the y_b-axis points out the right wing; the z_b-axis points out the belly and completes a right-handed rectangular coordinate.

2.2. Wind Description

The wind acts as a disturbance by altering the attitude and velocity of the UAV. Define ${\mathit{V}}_g$ as the velocity of the airframe relative to the ground, ${\mathit{V}}_a$ as the velocity of the airframe relative to the surrounding air mass, and ${\mathit{V}}_w$ as the velocity of the air mass relative to the ground. These velocities can be expressed in the body frame in terms of components along the x_b, y_b, and z_b axes as ${\mathit{V}}_g^b={\left[u,v,w\right]}^T$, ${\mathit{V}}_a^b={\left[u_r,v_r,w_r\right]}^T$, and ${\mathit{V}}_w^b={\left[u_w,v_w,w_w\right]}^T$. The relationship between ground velocity, air velocity, and wind velocity is given by

$${\mathit{V}}_g={\mathit{V}}_a+{\mathit{V}}_w.$$

(1)

For the purposes of simulation, we will assume that the total wind vector consists of the steady ambient wind ${\mathit{V}}_{w_s}$ and random winds ${\mathit{V}}_{w_g}$ (including wind gusts and atmospheric disturbances), i.e., ${\mathit{V}}_w={\mathit{V}}_{{\mathit{w}}_s}+{\mathit{V}}_{w_g}.$ The steady wind can be represented in the inertial frame as ${\mathit{V}}_{w_s}^i={\left[w_{n_s},w_{e_s},w_{d_s}\right]}^T$, where $w_{n_s},w_{e_s},w_{d_s}$ are the speeds of the steady wind in the north, east, and down directions, respectively. The stochastic component of the wind is typically expressed in the aircraft body frame as ${\mathit{V}}_{w_g}^b={\left[u_{w_g},v_{w_g},w_{w_g}\right]}^T$. The two most widely used models of continuous gusts are the Dryden and von Karman models [36]. The Dryden turbulence model is mathematically simpler and the forming filters in this model are derived from the spectral square roots of the spectrum equations. The definitions of the longitudinal, lateral, and vertical component spectra functions are described as

$$\begin{array}{l}{H}_u\left(s\right)={\sigma }_u\sqrt{\frac{2V_a}{L_u}}\frac{1}{s+\frac{V_a}{L_u}};H_v\left(s\right)={\sigma }_v\sqrt{\frac{3V_a}{L_v}}\frac{\left(s+\frac{V_a}{\sqrt{3}{L}_v}\right)}{{\left(s+\frac{V_a}{L_v}\right)}^2};\\ H_w\left(s\right)={\sigma }_w\sqrt{\frac{3V_a}{L_w}}\frac{\left(s+\frac{V_a}{\sqrt{3}{L}_w}\right)}{{\left(s+\frac{V_a}{L_w}\right)}^2},\end{array}$$

(2)

where σ_u, σ_v, and σ_w are the intensities of the turbulence; L_u, L_v, and L_w are spatial wavelengths; $V_a=\sqrt{u_r^2+v_r^2+w_r^2}$ is the airspeed of the vehicle. Then, the total winds in the body frame can be expressed as

$${\mathit{V}}_w^b={\left[u_w,v_w,w_w\right]}^T={\mathit{R}}_i^b{\mathit{V}}_{w_s}^i+{\mathit{V}}_{w_g}^b,$$

(3)

where ${\mathit{R}}_i^b$ is the rotation matrix from inertial frame to body frame given as

$${\mathit{R}}_i^b=\left[\begin{array}{ccc}\cos \theta \cos \psi & \cos \theta sin\psi & -sin\theta \\ \sin \phi \sin \theta \cos \psi -\cos \phi \sin \psi & \sin \phi \sin \theta \cos \psi +\cos \phi \cos \psi & sin\phi \cos \theta \\ \cos \phi \sin \theta \cos \psi +\sin \phi \sin \psi & \cos \phi \sin \theta \sin \psi -\sin \phi \cos \psi & \cos \phi \cos \theta \end{array}\right],$$

(4)

where φ, θ, ψ are roll, pitch, and yaw angles of the MAUAV, and their units are radians in the following dynamic models.

The derivative of the wind is ${\dot{\mathit{V}}}_w^b={\left[{\dot{u}}_w,{\dot{v}}_w,{\dot{w}}_w\right]}^T,$ which is calculated as [19]

$$\begin{array}{l}{\dot{u}}_w={\left(\frac{\partial u_w}{\partial x}\right)}_{b}u+{\left(\frac{\partial u_w}{\partial y}\right)}_{b}v+{\left(\frac{\partial u_w}{\partial z}\right)}_{b}w+{\left(\frac{\partial u_w}{\partial t}\right)}_b;\\ {\dot{v}}_w={\left(\frac{\partial v_w}{\partial x}\right)}_{b}u+{\left(\frac{\partial v_w}{\partial y}\right)}_{b}v+{\left(\frac{\partial v_w}{\partial z}\right)}_{b}w+{\left(\frac{\partial v_w}{\partial t}\right)}_b;\\ {\dot{w}}_w={\left(\frac{\partial w_w}{\partial x}\right)}_{b}u+{\left(\frac{\partial w_w}{\partial y}\right)}_{b}v+{\left(\frac{\partial w_w}{\partial z}\right)}_{b}w+{\left(\frac{\partial w_w}{\partial t}\right)}_b.\end{array}$$

(5)

2.3. Dynamic Model of the MAUAV

The translational dynamic equations describing the components of the velocity relative to the ground are shown in body frame as follows [26]:

$$\begin{array}{l}\dot{u}=rv-qw+\frac{\overline{q}S}{m_S}{C}_X-g\sin \theta +\frac{F_P}{m_S}-{\mu }_1\left(-\dot{r}{y}_1^b-2r{\dot{y}}_1^b+pq{y}_1^b\right);\\ \dot{v}=pw-ru+\frac{\overline{q}S}{m_S}{C}_Y+g\sin \phi \cos \theta -{\mu }_1\left({\ddot{y}}_1^b-y_1^b\left(r^2+p^2\right)\right);\\ \dot{w}=qu-pv+\frac{\overline{q}S}{m_S}{C}_Z+g\cos \phi \cos \theta -{\mu }_1\left(\dot{p}{y}_1^b+2p{\dot{y}}_1^b+qr{y}_1^b\right),\end{array}$$

(6)

where p, q, r are the angular rates of roll, pitch, and yaw angles, respectively; $\overline{q}=\rho V_a^2/2$ is the UAV dynamic pressure depending on the nominal flight velocity ($V_a=\sqrt{u_r^2+v_r^2+w_r^2}$) and ρ is the atmospheric density; S is the wing area of the MAUAV; m_S is the total mass of the whole system, which is the sum of the slider mass m₁ and airframe mass m_B, i.e., m_S = m₁ + m_B; μ₁ = m₁/m_S is the mass ratio of the slider; g is the gravitational acceleration; ${\mathit{r}}_1^b={\left[x_1^b, y_1^b, z_1^b\right]}^T$ is slider’s position vector in the body frame (since the slide is fixedly mounted on the airframe and is placed along the y_b-axis of the body frame, it is possible to conclude that $x_1^b={\dot{x}}_1^b=z_1^b={\dot{z}}_1^b=0$). F_P is the thrust force, which can be expressed as [26]

$$F_P=\frac{1}{2}\rho S_{prop}{C}_{prop}\left[{\left(k_{motor}{\delta }_t\right)}^2-V_a^2\right],$$

(7)

where S_prop is the area swept by the propeller; C_prop is the propeller’s efficiency factor; k_motor is a constant depending on the properties of the selected engine; δ_t is the throttle control size of the engine, which varies from 0 to 1; the expressions of the dimensionless coefficients C_X, C_Y, C_Z are described as [1]

$$\begin{array}{l}{C}_X=C_L\sin \alpha -C_D\cos \alpha ;\\ C_Y=C_{Y_0}+C_{Y_{\beta }}\beta +C_{Y_p}\frac{b}{2V_a}p+C_{Y_r}\frac{b}{2V_a}r+C_{Y_{{\delta }_r}}{\delta }_r;\\ C_Z=-C_D\sin \alpha -C_L\cos \alpha ,\end{array}$$

(8)

where δ_r is the rudder deflection, which is measured in radian in this model; b is the wing span; $C_{Y_0}, C_{Y_{\beta }}, C_{Y_p}, C_{Y_r}, C_{Y_{{\delta }_r}}$ are coefficients of the lateral force; α and β represent the attack and the sideslip angles, their expressions are [1]

$$\alpha =arctan\left(\frac{w_r}{u_r}\right);\beta =arcsin\left(\frac{v_r}{\sqrt{u_r{}^2+v_r{}^2+w_r{}^2}}\right),$$

(9)

the lift and the drag coefficients C_L and C_D are described as [1]

$$\begin{array}{l}{C}_L=C_{L_0}+C_{L_{\alpha }}\alpha +C_{L_q}\frac{c}{2V_a}q+C_{L_{{\delta }_e}}{\delta }_e;\\ C_D=C_{D_p}+\frac{{\left(C_{L_0}+C_{L_{\alpha }}\alpha \right)}^2}{\pi \cdot e\cdot AR}+C_{D_q}\frac{c}{2V_a}q+C_{D_{{\delta }_e}}{\delta }_e,\end{array}$$

(10)

where c is the average aerodynamic chord length of the wing; δ_e is the elevator deflection, and its unit is radian in the dynamic models; e is the Oswald efficiency factor, which ranges between 0.8 and 1.0; AR is the wing aspect ratio, which is equal to b²/S; $C_{L_0},C_{L_{\alpha }},C_{L_q},C_{L_{{\delta }_e}},C_{D_p},C_{D_q},C_{D_{{\delta }_e}}$ are coefficients of the lift force and drag force.

Define $\omega ={\left[p,q,r\right]}^T$ as the angular rates vector of MAUAV, then the roll, pitch, and yaw angular rates relative to the body frame can be described in the rotational dynamic equations as follows [26]:

$$\mathit{J}\dot{\mathit{\omega }}=\mathit{M}-\mathit{\omega }\times \left(\mathit{J}\cdot \mathit{\omega }\right)-\dot{\mathit{J}}\cdot \mathit{\omega },$$

(11)

where M is the external moment in the body frame, which is described as [26]

$$\mathit{M}={\mu }_{1}G\left[\begin{array}{c}{y}_1^b\cos \phi \cos \theta \\ 0\\ y_1^{b}sin\theta \end{array}\right]+\left[\begin{array}{c}-k_{T_p}{\left(k_{\Omega }{\delta }_t\right)}^2\\ 0\\ 0\end{array}\right]+\overline{q}S\left[\begin{array}{c}b{C}_l\\ c{C}_m\\ b{C}_n\end{array}\right],$$

(12)

where $\Omega =k_{\Omega }{\delta }_t$ is the propeller speed (rotation angular velocity) and $k_{T_p}$ is a constant coefficient depending on the selected propeller; C_l, C_m, C_n are the aerodynamic coefficients with the expressions [26]

$$\begin{array}{l}{C}_l=C_{l_0}+C_{l_{{}_{\beta }}}\beta +\frac{b}{2V_a}\left(C_{l_{{}_p}}p+C_{l_{{}_r}}r\right)+C_{l_{{}_{{\delta }_r}}}{\delta }_r;\\ C_m=C_{m_0}+C_{m_{\alpha }}\alpha +\frac{c}{2V_a}{C}_{m_{{}_q}}q+C_{m_{{}_{{\delta }_e}}}{\delta }_e;\\ C_n=C_{n_0}+C_{n_{{}_{\beta }}}\beta +\frac{b}{2V_a}\left(C_{n_{{}_p}}p+C_{n_{{}_r}}r\right)+C_{n_{{}_{{\delta }_r}}}{\delta }_r,\end{array}$$

(13)

where $C_{l_{(·)}},C_{m_{(·)}},C_{n_{(·)}}$ denote related aerodynamic coefficients. And J is the inertia moment, which is described as [26]

$$\mathit{J}=\left[\begin{array}{ccc}{J}_x& -J_{xy}& -J_{xz}\\ -J_{xy}& J_y& -J_{yz}\\ -J_{xz}& -J_{yz}& J_z\end{array}\right],$$

(14)

where

$$\{\begin{array}{l}{J}_x=J_{x_B}+m_1{\left(y_1^b\right)}^2\\ J_y=J_{y_B}\\ J_z=J_{z_B}+m_1{\left(y_1^b\right)}^2\end{array}; \{\begin{array}{l}{J}_{xy}=J_{x{y}_B}\\ J_{yz}=J_{y{z}_B}\\ J_{xz}=J_{x{z}_B}\end{array}; \{\begin{array}{l}{\dot{J}}_x=2m_1{y}_1^b{\dot{y}}_1^b\\ {\dot{J}}_z=2m_1{y}_1^b{\dot{y}}_1^b\\ {\dot{J}}_y={\dot{J}}_{xy}={\dot{J}}_{xz}={\dot{J}}_{yz}=0\end{array},$$

(15)

where $J_{x_B},J_{y_B},J_{z_B},J_{x{y}_B},J_{y{z}_B},J_{x{z}_B}$ represent the inertia moments of the airframe when it is not fitted with the slider.

Define $\mathbf{\Phi }={\left[\phi ,\theta ,\psi \right]}^T$ as an angular vector, then the rotational kinematic equations of the MAUAV can be obtained as [26]

$$\dot{\mathbf{\Phi }}=\mathit{A}\mathit{\omega },$$

(16)

where A is a transformation matrix described as

$$\mathit{A}=\left[\begin{array}{ccc}1& \sin \phi \tan \theta & \cos \phi \tan \theta \\ 0& \cos \phi & -\sin \phi \\ 0& \sin \phi \sec \theta & \cos \phi \sec \theta \end{array}\right].$$

(17)

Newton’s second law applied to the moving mass can be stated as

$$m_1\frac{d{\mathit{V}}_1}{d{t}_i}={\mathit{F}}_1,$$

(18)

where $\frac{d}{d{t}_i}$ is the time derivative in the inertial frame, ${\mathit{V}}_1$ is the velocity vector of the moving mass with respect to the inertial frame, and ${\mathit{F}}_1$ is the sum of all external forces acting on the moving mass.

The derivative of velocity taken in the inertial frame can be written in terms of the derivative in the body frame and the angular velocity as

$$\frac{d{\mathit{V}}_1}{d{t}_i}=\frac{d{\mathit{V}}_1}{d{t}_b}+{\mathit{\omega }}_{b/i}\times {\mathit{V}}_1,$$

(19)

where $\frac{d}{d{t}_b}$ is the time derivative in the body frame and ${\mathit{\omega }}_{b/i}$ is the angular velocity of the MAUAV with respect to the inertial frame.

Combining (18) and (19), we can easily apply Newton’s second law by expressing the forces and velocities in the body frame as

$$m_1\left(\frac{d{\mathit{V}}_1^b}{d{t}_b}+{\mathit{\omega }}_{b/i}^b\times {\mathit{V}}_1^b\right)={\mathit{F}}_1^b,$$

(20)

where ${\mathit{V}}_1^b={\mathit{V}}_g^b+{\dot{\mathit{r}}}_1^b+{\mathit{\omega }}_{b/i}^b\times {\mathit{r}}_1^b$, ${\mathit{\omega }}_{b/i}^b={\left[p,q,r\right]}^T$ and ${\mathit{F}}_1^b={\left[F_{1x}^b,F_{1y}^b,F_{1z}^b\right]}^T$.

Expanding Equation (20) to take the component representation along the y_b-direction of the body frame, then the dynamic motion of the moving mass in the body frame can be expressed as

$$m_1\left( {\ddot{y}}_1^b+\dot{v}-y_1^b\left(r^2+p^2\right)+ru-pw\right)= F_{1y}^b,$$

(21)

where $F_{1y}^b=F_u+m_{1}g\sin \phi \cos \theta -F_f$, F_u represents the active control force exerted by the servo mechanism on the movable mass and F_f is the friction that hinders the motion of the mass block. To precisely model the nonlinear friction, the LuGre model [37] is extensively utilized, which can be described by

$$F_f={\sigma }_{0}z+{\sigma }_1\dot{z}+{\sigma }_2{\dot{y}}_1^b,$$

(22)

where ${\sigma }_0,{\sigma }_1,{\sigma }_2$ are friction force parameters, which can be physically interpreted as the stiffness of the bristles between two contact surfaces, damping coefficient of the bristles, and viscous coefficient, respectively; the unmeasurable internal friction state z physically stands for the average deflection of the bristles between two contact surfaces, and its characteristic is governed by

$$\dot{z}={\dot{y}}_1^b-\frac{{\dot{y}}_1^b}{g\left({\dot{y}}_1^b\right)}z,$$

(23)

in which the nonlinear static function is used to describe different friction effects and can be parameterized to characterize the Stribeck effect. Typically, the function is modeled by

$$g\left({\dot{y}}_1^b\right)=\left[\frac{f_c+\left(f_s-f_c\right)e^{-{\left({\dot{y}}_1^b/{\dot{y}}_{}^b{}_{1s}\right)}^2}}{{\sigma }_0}\right]\mathrm{sgn}\left({\dot{y}}_1^b\right),$$

(24)

where ${\dot{y}}_{1s}^b$ is the Stribeck velocity; f_c and f_s are the levels of the normalized Coulomb friction and stiction force, respectively; and sgn is a standard signum function.

We assume that the inertial coordinates are defined as being aligned with the runway. The origin of the inertial system is the desired touchdown point of MAUAV and X-axis of inertial coordinates coincides with the runway centerline, which is directed north. Then, the translational kinematic equations can be obtained as [19,38]

$$\begin{array}{l}\dot{X}=u\cos \theta \cos \psi +v\left(\sin \phi \sin \theta \cos \psi -\cos \phi \sin \psi \right)\\ +w\left(\cos \phi \sin \theta \cos \psi +\sin \phi \sin \psi \right);\\ \dot{Y}=u\cos \theta \sin \psi +v\left(\sin \phi \sin \theta \sin \psi +\cos \phi \cos \psi \right)\\ +w\left(\cos \phi \sin \theta \sin \psi -\sin \phi \cos \psi \right);\\ \dot{H}=u\sin \theta -v\sin \phi \cos \theta -w\cos \phi \cos \theta ,\end{array}$$

(25)

where X is the horizontal displacement; Y is the lateral deviation relative to the runway; and H is the flight altitude.

3. Design of the Controllers

This section describes the specific design process of the four controllers in the automatic landing system (Figure 2). These controllers enable the automatic landing of the MAUAV by providing the desired values of the four controls: the driving force of the slider—F_u, elevator deflection—δ_e, rudder deflection—δ_r, and throttle command—δ_t. According to the functional classification, the control strategy of this UAV is divided into two main parts: an altitude-attitude slider system and a forward velocity tracking system. The former consists of three controllers: an altitude controller, an attitude controller, and a moving-mass position controller. The altitude controller generates the desired pitch angle signal based on the desired altitude trajectory. The attitude controller generates the desired slider displacement, elevator deflection, and rudder deflection based on the desired pitch, roll, and yaw signals. The moving-mass position controller generates the desired driving force of the slider based on the desired slider displacement. The latter develops a throttle input to ensure that the MAUAV tracks desired forward velocity throughout the landing process. All controllers are designed using LADRC, with the help of which unknown disturbances are compensated and the form of controllers is not complicated. The controller design results are slightly different depending on the system order. Figure 3 illustrates the process of LADRC-based controller design for first-order and second-order systems.

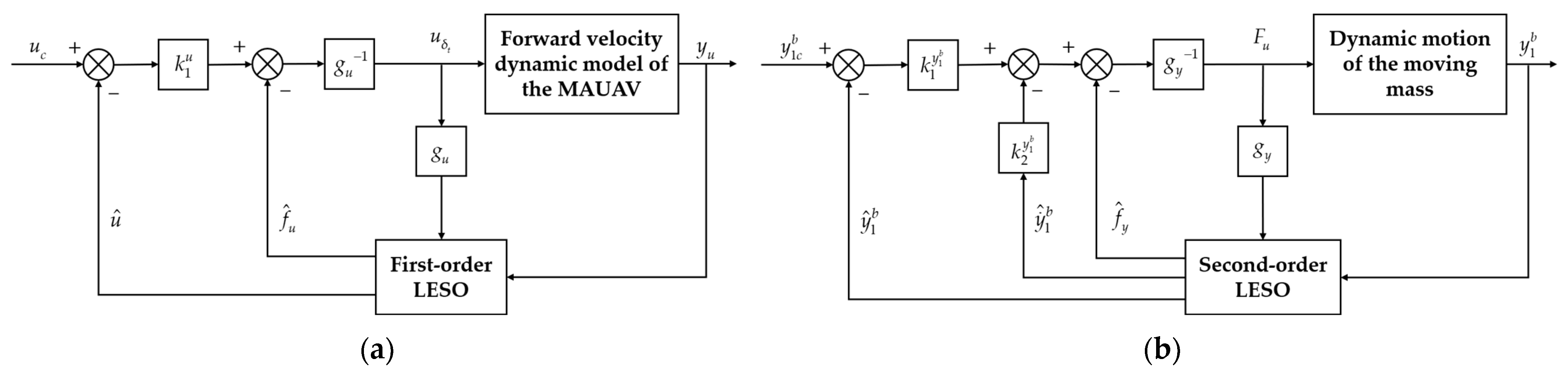
3.1. Forward Velocity Controller

Equation (25) shows that the position of the MAUAV relative to the ground runway during the approach, glide slope, and flare is affected by the speed of vehicle. Considering that the ground speed of the MAUAV during landing with low wind disturbances mainly depends on the forward velocity u, it is necessary to control the forward velocity to make the MAUAV land efficiently and safely. Based on Equation (6), we can derive the forward velocity dynamic model as

$$\dot{u}=rv-qw+\frac{\overline{q}S}{m_S}{C}_X-g\sin \theta +\frac{F_P}{m_S}-{\mu }_1\left(-\dot{r}{y}_1^b-2r{\dot{y}}_1^b+pq{y}_1^b\right).$$

(26)

From Equations (7), (8), (10) and (26), the design model can be written as

$$\dot{u}=f_u+g_u{u}_{{\delta }_t},$$

(27)

where

$$\begin{array}{l}{f}_u=rv-qw+\frac{\overline{q}S}{m_S}{C}_X-g\sin \theta -\frac{1}{2m_S}\rho S_{prop}{C}_{prop}{V}_a^2-{\mu }_1\left(-\dot{r}{y}_1^b-2r{\dot{y}}_1^b+pq{y}_1^b\right);\\ g_u=\frac{1}{2m_S}\rho S_{prop}{C}_{prop}{k}_{motor}^2{\delta }_t; u_{{\delta }_t}={\delta }_t^2.\end{array}$$

(28)

According to the design model (27), the expansion state space can be expressed as

$$\begin{array}{l}\dot{u}=f_u+g_u{u}_{{\delta }_t};\\ {\dot{f}}_u={\dot{f}}_u;\\ y_u=u,\end{array}$$

(29)

where $f_u$ is designed as an extended state.

To estimate the two states of the new system, we construct the LESO as

$$\begin{array}{l}\dot{\widehat{u}}={\beta }_1^u\left(y_u-\widehat{u}\right)+{\widehat{f}}_u+g_u{u}_{{\delta }_t};\\ {\dot{\widehat{f}}}_u={\beta }_2^u\left(y_u-\widehat{u}\right),\end{array}$$

(30)

where $\widehat{u}$ and ${\widehat{f}}_u$ represent the estimate of u and $f_u$; ${\beta }_1^u$ and ${\beta }_2^u$ are the tuning parameters and are determined by the value of the bandwidth of the LESO, which is denoted as ${\omega }_0^u$. Perfect estimations of the true value of the states in the system can be achieved when adjusting these two gains by the following relationships [39]:

$${\beta }_1^u=2{\omega }_0^u;{\beta }_2^u={\omega }_0^u\cdot {\omega }_0^u,$$

(31)

Based on the accurate estimation of the system state, the final throttle command has the following form:

$$u_{{\delta }_t}=g_u{}^{-1}\left(k_1^u\left(u_c-\widehat{u}\right)-{\widehat{f}}_u+{\dot{u}}_c\right),$$

(32)

where $k_1^u={\omega }_c^u$ represents a positive feedback gain, ${\omega }_c^u$ is the desired closed-loop natural frequencies of the controller; u_c is the desired forward velocity. The specific design idea of the forward velocity controller can be referred to Figure 3a.

3.2. Altitude Controller

A combination of lateral and longitudinal motion control is required during the landing of the MAUAV. In the longitudinal plane, the pitch angle is controlled to ensure that the MAUAV can track the altitude trajectory for the three processes of approach, glide slope, and flare. From Equation (25), we can know that the altitude of the MAUAV relative to the ground can be expressed as

$$\begin{array}{ll}\dot{H}& =u\sin \theta -v\sin \phi \cos \theta -w\cos \phi \cos \theta \\ & =V_a\theta -V_a\theta +u\sin \theta -v\sin \phi \cos \theta -w\cos \phi \cos \theta \\ & =V_a\theta +f_H,\end{array}$$

(33)

where $f_H=-V_a\theta +u\sin \theta -v\sin \phi \cos \theta -w\cos \phi \cos \theta$.

Based on the altitude design model (33), the expansion state space can be expressed as

$$\begin{array}{l}\dot{H}=f_H+V_a\theta ;\\ {\dot{f}}_H={\dot{f}}_H;\\ y_H=H.\end{array}$$

(34)

In a similar way to the design of the forward velocity control, the LESO and the desired pitch angle are designed as follows:

$$\begin{array}{l}\dot{\widehat{H}}={\beta }_1^H\left(y_H-\widehat{H}\right)+{\widehat{f}}_H+V_a\theta ;\\ {\dot{\widehat{f}}}_H={\beta }_2^H\left(y_H-\widehat{H}\right);\\ {\theta }_c=V_a{}^{-1}\left(k_1^H\left(H_c-\widehat{H}\right)-{\widehat{f}}_H+{\dot{H}}_c\right),\end{array}$$

(35)

where H_c is the desired altitude; the values of the adjustment parameters ${\beta }_1^H$, ${\beta }_2^H$, and $k_1^H$ are taken according to the following rules [39]:

$$k_1^H={\omega }_c^H;{\beta }_1^H=2{\omega }_0^H;{\beta }_2^H={\omega }_0^H\cdot {\omega }_0^H.$$

(36)

3.3. Attitude Controller

In the previous section on the design of the altitude controller, we have obtained the control command for the pitch angle, making it as one of the desired output commands in the attitude controller. In addition, the goal of lateral motion control is to minimize the lateral error between the command trajectory and the position of the MAUAV. The lateral motion guidance method in this paper is derived from [1], which constructs a commanded course angle ${\chi }_c$ at every spatial point relative to the desired straight-line path that results in the MAUAV moving toward the path. The commanded course angle is described by the following equation [1]:

$$\begin{array}{l}{\chi }_c\left(t\right)={\chi }_a-{\chi }^{\infty }\frac{2}{\pi }{\tan }^{-1}\left(k_{path}{e}_{ay}\right); {\chi }_a=\mathrm{atan}2\left(a_e,a_n\right);\\ e_{ay}=-\sin \left({\chi }_a\right)\left(X-r_x\right)+\cos \left({\chi }_a\right)\left(Y-r_y\right),\end{array}$$

(37)

where ${\mathit{r}}_0=\left[r_x,r_y,r_z\right]$ is the origin of the desired path; $\mathit{a}=\left[a_n,a_e,a_d\right]$ is a unit vector whose direction indicates the desired direction of travel, where $a_n,$ $a_e$, $a_d$ expresses the north, east, and down components of the unit direction vector. The straight-line path in this paper coincides with the centerline of the runway, and it is assumed that its origin ${\mathit{r}}_0=\left[-3016,0,0\right]$ and its direction along the inertial north direction, i.e., $\mathit{a}=\left[1,0,0\right]$; ${\chi }^{\infty }\in \left(0,\pi /2\right]$ is an approach angle for large distance from straight-line path, k_path is a positive constant that influences the rate of the transition from ${\chi }^{\infty }$ to zero,$e_{ay}$ is the cross-track error.

From [1], we know the course angle $\chi =\mathrm{atan}2\left(\dot{Y},\dot{X}\right)$ and the coordinated turn condition is described by

$$\dot{\chi }=\frac{g}{V_g}\tan \phi \cos \left(\chi -\psi \right),$$

(38)

where $V_g=\sqrt{u^2+v^2+w^2}$ is the velocity of the airframe relative to the inertial frame.

Then, the desired tracking control of course angle is achieved by having first-order error dynamics in $\chi$ as shown

$${\dot{e}}_{\chi }+k_{\chi }{e}_{\chi }=0,$$

(39)

where error $e_{\chi }=\chi -{\chi }_c$, $k_{\chi }$ is positive constant and an expression for desired φ_c is obtained as

$${\phi }_c=\arctan \left(\frac{\left(-k_{\chi }{e}_{\chi }+{\dot{\chi }}_c\right)V_g}{g\cos \zeta }\right),$$

(40)

where $\zeta =\chi -\psi$ is the crab angle. The crab angle is small when the MAUAV is flying in low wind condition, we can assume $\cos \zeta \approx 1$ and (40) can be simplified as [40]

$${\phi }_c=\arctan \left(\frac{\left(-k_{\chi }{e}_{\chi }+{\dot{\chi }}_c\right)V_g}{g}\right).$$

(41)

Then, we have the desired change rate of yaw angle ψ_c as [1]

$${\dot{\psi }}_c=g\tan \left({\phi }_c\right)/V_a.$$

(42)

According to the rotational kinematic equations of the MAUAV above (16), the desired tracking control of attitude angles is achieved by having first-order error dynamics in $\mathbf{\Phi }$ as shown

$${\dot{\mathit{e}}}_{\mathsf{\Phi }}+{\mathit{k}}_{\mathsf{\Phi }}{\mathit{e}}_{\mathsf{\Phi }}=0,$$

(43)

where error ${\mathit{e}}_{\mathsf{\Phi }}=\mathbf{\Phi }-{\mathbf{\Phi }}_c,$ ${\mathbf{\Phi }}_c={\left[{\phi }_c,{\theta }_c,{\psi }_c\right]}^T$ and ${\mathit{k}}_{\mathsf{\Phi }}=\mathrm{diag}\left\{k_{\phi },k_{\theta },k_{\psi }\right\}$ is an adjustable matrix of positive parameters.

Rearranging the above equations and substituting equation, desired rotation rates ${\mathit{\omega }}_c={\left[p_c,q_c,r_c\right]}^T$ are designed as follows:

$${\mathit{\omega }}_c={\mathit{A}}^{-1}\left({\dot{\mathsf{\Phi }}}_c-{\mathit{k}}_{\mathsf{\Phi }}{\mathit{e}}_{\mathsf{\Phi }}\right).$$

(44)

According to the rotational dynamic equations of the MAUAV above (11), we get

$$\begin{array}{l}\dot{\mathit{\omega }}={\mathit{f}}_{\omega }+{\mathit{g}}_{\omega }{\mathit{u}}_{\omega };\\ {\dot{\mathit{f}}}_{\omega }={\dot{\mathit{f}}}_{\omega };\\ {\mathit{y}}_{\omega }=\mathit{\omega },\end{array}$$

(45)

where ${\mathit{u}}_{\omega }={\left[y_{1c}^b,{\delta }_e,{\delta }_r\right]}^T$, ${\mathit{f}}_{\omega }$ and ${\mathit{g}}_{\omega }$ are given by

$${\mathit{f}}_{\omega }={\mathit{J}}^{-1}\left[{\mathit{M}}_1-\mathit{\omega }\times \left(\mathit{J}\cdot \mathit{\omega }\right)-\dot{\mathit{J}}\cdot \mathit{\omega }\right];{\mathit{g}}_{\omega }={\mathit{J}}^{-1}{\mathit{B}}_M,$$

(46)

where

$$\begin{array}{l}{\mathit{M}}_1=\left[\begin{array}{c}-k_{T_p}{\left(k_{\Omega }{\delta }_t\right)}^2+\overline{q}Sb\left(C_{l_0}+C_{l_{{}_{\beta }}}\beta +\frac{b}{2V_a}\left(C_{l_{{}_p}}p+C_{l_{{}_r}}r\right)\right)\\ \overline{q}Sc\left(C_{m_0}+C_{m_{\alpha }}\alpha +\frac{c}{2V_a}{C}_{m_{{}_q}}q\right)\\ \overline{q}Sb\left(C_{n_0}+C_{n_{{}_{\beta }}}\beta +\frac{b}{2V_a}\left(C_{n_{{}_p}}p+C_{n_{{}_r}}r\right)\right)\end{array}\right];\\ {\mathit{B}}_M=\left[\begin{array}{ccc}{\mu }_{1}G\cos \phi \cos \theta & 0& \overline{q}b{C}_{l_{{}_{{\delta }_r}}}\\ 0& \overline{q}c{C}_{m_{{}_{{\delta }_e}}}& 0\\ {\mu }_{1}G\sin \theta & 0& \overline{q}b{C}_{n_{{}_{{\delta }_r}}}\end{array}\right].\end{array}$$

(47)

Then, the LESO and control input ${\mathit{u}}_{\omega }$ are designed as follows:

$$\begin{array}{l}\dot{\widehat{\mathit{\omega }}}={\mathit{\beta }}_1^{\omega }\left({\mathit{y}}_{\omega }-\widehat{\mathit{\omega }}\right)+{\widehat{\mathit{f}}}_{\omega }+{\mathit{g}}_{\omega }{\mathit{u}}_{\omega };\\ {\dot{\widehat{\mathit{f}}}}_{\omega }={\mathit{\beta }}_2^{\omega }\left({\mathit{y}}_{\omega }-\widehat{\mathit{\omega }}\right);\\ {\mathit{u}}_{\omega }={\mathit{g}}_{\omega }{}^{-1}\left({\mathit{k}}_1^{\omega }\left({\mathit{\omega }}_c-\widehat{\mathit{\omega }}\right)-{\widehat{\mathit{f}}}_{\omega }+{\dot{\mathit{\omega }}}_c\right),\end{array}$$

(48)

where the values of the adjustment parameters ${\mathit{\beta }}_1^{\omega }$, ${\mathit{\beta }}_2^{\omega }$, and ${\mathit{k}}_1^{\omega }$ are taken according to the following rules [39]:

$${\mathit{k}}_1^{\omega }={\mathit{\omega }}_c^{\omega };{\mathit{\beta }}_1^{\omega }=2{\mathit{\omega }}_0^{\omega };{\mathit{\beta }}_2^{\omega }={\mathit{\omega }}_0^{\omega }\cdot {\mathit{\omega }}_0^{\omega }.$$

(49)

3.4. Moving-Mass Position Controller

In the previous section on the design of the attitude controller, we have obtained the control command for the slider displacement, making it the desired output command in the moving-mass position controller. According to the dynamic motion of the moving mass above (21), the expression of expansion state space can be obtained as

$$\begin{array}{l}{\dot{y}}_1^b={\dot{y}}_1^b;\\ {\ddot{y}}_1^b=f_y+g_y{F}_u;\\ {\dot{f}}_y={\dot{f}}_y,\end{array}$$

(50)

where f_y and g_y are given by

$$f_y=g\sin \phi \cos \theta -\frac{F_f}{m_1}+y_1^b\left(r^2+p^2\right)-\dot{v}-ru+pw;\hspace{1em}\hspace{1em}{g}_y=\frac{1}{m_1}.$$

(51)

Unlike the previously designed controllers based on the first-order system, the moving-mass position controller is based on the second-order system, the design idea of which is shown in Figure 3b. Therefore, the LESO and the final desired position of the slider are designed differently and have the following form:

$$\begin{array}{l}{\dot{\widehat{y}}}_1^b={\beta }_1^{y_1^b}\left(y_1^b-{\widehat{y}}_1^b\right)+{\widehat{\dot{y}}}_1^b;\\ {\dot{\widehat{\dot{y}}}}_1^b={\beta }_2^{y_1^b}\left(y_1^b-{\widehat{y}}_1^b\right)+{\widehat{f}}_y+g_y{F}_u;\\ {\dot{\widehat{f}}}_y={\beta }_3^{y_1^b}\left(y_1^b-{\widehat{y}}_1^b\right);\\ F_u=g_y{}^{-1}\left(k_1^{y_1^b}\left(y_{1c}^b-{\widehat{y}}_1^b\right)+k_2^{y_1^b}\left({\dot{y}}_{1c}^b-{\widehat{\dot{y}}}_1^b\right)-{\widehat{f}}_y+{\ddot{y}}_{1c}^b\right),\end{array}$$

(52)

where ${\beta }_1^{y_1^b},{\beta }_2^{y_1^b}$, and ${\beta }_3^{y_1^b}$ represent observer gains; $k_1^{y_1^b}$ and $k_2^{y_1^b}$ represent positive feedback gains. In order to obtain good state estimation and position tracking effect, their values are given according to the following relationships [28]:

$$\begin{array}{l}{\beta }_1^{y_1^b}=3{\omega }_0^{y_1^b};{\beta }_2^{y_1^b}=3{\omega }_0^{y_1^b}\cdot {\omega }_0^{y_1^b};{\beta }_3^{y_1^b}={\omega }_0^{y_1^b}\cdot {\omega }_0^{y_1^b}\cdot {\omega }_0^{y_1^b};\\ k_1^{y_1^b}=2{\omega }_c^{y_1^b};k_2^{y_1^b}={\omega }_c^{y_1^b}\cdot {\omega }_c^{y_1^b}.\end{array}$$

(53)

To facilitate the handling of the control problem of MAUAV system, an assumption is described as follows:

Assumption 1.

The disturbances ${\mathit{V}}_w^b$, ${\dot{\mathit{V}}}_w^b$, ${\dot{f}}_u,$ ${\dot{f}}_H,$ ${\dot{\mathit{f}}}_w$ and ${\dot{f}}_y$ are bounded, i.e., $\Vert {\mathit{V}}_w^b\Vert \le d_1$, $\Vert {\dot{\mathit{V}}}_w^b\Vert \le d_2$, $\left|{\dot{f}}_u\right|\le d_3,$ $\left|{\dot{f}}_H\right|\le d_4$, $\Vert {\dot{f}}_w\Vert \le d_5$, and $\left|{\dot{f}}_y\right|\le d_6$, where $d_1,d_2,d_3,d_4,d_5$, and $d_6$ are positive constants.

3.5. Convergence Analysis of LESO

The four controllers designed above all employ LESO to estimate the states and disturbances of the system. Considering the similarity of the principles, an example analysis of the convergence of the LESO in the moving-mass position controller is given below, the convergence of the other three observers can be argued by the same method [41].

Define $\mathit{x}={\left[x_1,x_2,x_3\right]}^T={\left[y_1^b,{\dot{y}}_1^b,f_y\right]}^T$ and i = 1, 2, 3. From (50) and (52), the observer estimation error can be shown as

$$\begin{array}{l}{\dot{\tilde{x}}}_1={\tilde{x}}_2-3{\omega }_0^{y_1^b}{\tilde{x}}_1;\\ {\dot{\tilde{x}}}_2={\tilde{x}}_3-3{\omega }_0^{y_1^b}\cdot {\omega }_0^{y_1^b}{\tilde{x}}_1;\\ {\dot{\tilde{x}}}_3={\dot{f}}_y-{\omega }_0^{y_1^b}\cdot {\omega }_0^{y_1^b}\cdot {\omega }_0^{y_1^b}{\tilde{x}}_1.\end{array}$$

(54)

Now, let ${\epsilon }_i={\tilde{x}}_i/{\left({\omega }_0^{y_1^b}\right)}^{i-1},$ i = 1, 2, 3. And (54) can be rewritten as

$$\dot{\mathit{\epsilon }}={\omega }_0^{y_1^b}{\mathit{A}}_1\mathit{\epsilon }+{\mathit{B}}_1{\dot{f}}_y/{\left({\omega }_0^{y_1^b}\right)}^2,$$

(55)

where ${\mathit{A}}_1=\left[\begin{array}{ccc}-3& 1& 0\\ -3& 0& 1\\ -1& 0& 0\end{array}\right],$ ${\mathit{B}}_1=\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$.

Theorem 1.

Assuming ${\dot{f}}_y$is bounded, there exists a constant ${\sigma }_i>$0 and a finite T₁ > 0 in order that $\left|{\tilde{x}}_i\left(t\right)\right|\le {\sigma }_i,$i = 1, 2, 3, $\forall t\ge T_1>$0, and ${\omega }_0^{y_1^b}>$0. Furthermore, ${\sigma }_i=O\left(1/{\left({\omega }_0^{y_1^b}\right)}^k\right),$for some positive integer k.

Proof of Theorem 1.

Solving (55), it follows that

$$\mathit{\epsilon }\left(t\right)=e^{{\omega }_0^{y_1^b}{\mathit{A}}_{1}t}\mathit{\epsilon }\left(0\right)+{\displaystyle \underset{0}{\overset{t}{\int }}{e}^{{\omega }_0^{y_1^b}{\mathit{A}}_1\left(t-\tau \right)}}{\mathit{B}}_1{\dot{f}}_y/{\left({\omega }_0^{y_1^b}\right)}^{2}d\tau .$$

(56)

Let

$$\mathit{p}\left(t\right)={\displaystyle \underset{0}{\overset{t}{\int }}{e}^{{\omega }_0^{y_1^b}{\mathit{A}}_1\left(t-\tau \right)}}{\mathit{B}}_1{\dot{f}}_y/{\left({\omega }_0^{y_1^b}\right)}^{2}d\tau ,$$

(57)

since ${\dot{f}}_y$ is bounded, namely, $\left|{\dot{f}}_y\right|\le d_6,$ for i = 1, 2, 3, we have

$$\left|p_i\left(t\right)\right|\le d_6\left[\left|{\left({\mathit{A}}_1^{-1}{\mathit{B}}_1\right)}_i\right|+\left|{\left({\mathit{A}}_1^{-1}{e}^{{\omega }_0^{y_1^b}{\mathit{A}}_{1}t}{\mathit{B}}_1\right)}_i\right|\right]/{\left({\omega }_0^{y_1^b}\right)}^3.$$

(58)

According to the definitions of ${\mathit{A}}_1$ and ${\mathit{B}}_1$, we have

$$\left|{\left({\mathit{A}}_1^{-1}{\mathit{B}}_1\right)}_i\right|\le 3.$$

(59)

Since ${\mathit{A}}_1$ is Hurwitz, there exists a finite time T₁ > 0, in order that

$$\left|{\left[e^{{\omega }_0^{y_1^b}{\mathit{A}}_{1}t}\right]}_{ij}\right|\le 1/{\left({\omega }_0^{y_1^b}\right)}^3$$

(60)

for all t $\ge$ T₁, i, j = 1, 2, 3. And then we have

$$\left|{\left({\mathit{A}}_1^{-1}{e}^{{\omega }_0^{y_1^b}{\mathit{A}}_{1}t}{\mathit{B}}_1\right)}_i\right|\le 4/{\left({\omega }_0^{y_1^b}\right)}^3.$$

(61)

From (58), (59), and (61), we obtain

$$\left|p_i\left(t\right)\right|\le 3d_6/{\left({\omega }_0^{y_1^b}\right)}^3+4d_6/{\left({\omega }_0^{y_1^b}\right)}^6$$

(62)

for all t $\ge$ T₁, i = 1, 2, 3. Let ${\epsilon }_{sum}\left(0\right)=\left|{\epsilon }_1\left(0\right)\right|+\left|{\epsilon }_2\left(0\right)\right|+\left|{\epsilon }_3\left(0\right)\right|.$ It follows that

$$\left|{\left[e^{{\omega }_0^{y_1^b}{\mathit{A}}_{1}t}\epsilon \left(0\right)\right]}_i\right|\le {\epsilon }_{sum}\left(0\right)/{\left({\omega }_0^{y_1^b}\right)}^3$$

(63)

for all t $\ge$ T₁, i = 1, 2, 3. From (56), one has

$$\left|{\epsilon }_i\left(t\right)\right|\le \left|{\left[e^{{\omega }_0^{y_1^b}{\mathit{A}}_{1}t}\epsilon \left(0\right)\right]}_i\right|+\left|p_i\left(t\right)\right|.$$

(64)

Let ${\tilde{x}}_{sum}\left(0\right)=\left|{\tilde{x}}_1\left(0\right)\right|+\left|{\tilde{x}}_2\left(0\right)\right|+\left|{\tilde{x}}_3\left(0\right)\right|.$ According to ${\epsilon }_i={\tilde{x}}_i/{\left({\omega }_0^{y_1^b}\right)}^{i-1}$ and Equations (62)–(64), we have

$$\left|{\tilde{x}}_i\left(t\right)\right|\le \left|{\tilde{x}}_{sum}\left(0\right)/{\left({\omega }_0^{y_1^b}\right)}^3\right|+3d_6/{\left({\omega }_0^{y_1^b}\right)}^{4-i}+4d_6/{\left({\omega }_0^{y_1^b}\right)}^{7-i}={\sigma }_i$$

(65)

for all t $\ge$ T₁, i = 1, 2, 3. Q.E.D. □

3.6. Stabitily Analysis of LADRC

Let ${\left[r_1,r_2,r_3\right]}^T={\left[y_{1c}^b,{\dot{y}}_{1c}^b,{\ddot{y}}_{1c}^b\right]}^T$. Define $e_i=r_i-x_i,$ i = 1, 2.

Theorem 2.

Assuming ${\dot{f}}_y$ is bounded, there exists a constant ${\rho }_i>$ 0 and a finite T₃ > 0 in order that $\left|e_i\left(t\right)\right|\le {\rho }_i,$ i = 1, 2, $\forall t\ge T_3>$ 0 and ${\omega }_0^{y_1^b},{\omega }_c^{y_1^b}>$ 0. Furthermore, ${\rho }_i=O\left(1/{\left({\omega }_c^{y_1^b}\right)}^j\right),$ for some positive integer j.

Proof of Theorem 2.

From (52) one has

$$F_u=g_y{}^{-1}\left(k_1^{y_1^b}\left(e_1+{\tilde{x}}_1\right)+k_2^{y_1^b}\left(e_2+{\tilde{x}}_2\right)-\left(x_3-{\tilde{x}}_3\right)+r_3\right).$$

(66)

It follows that

$$\begin{array}{l}{\dot{e}}_1={\dot{r}}_1-{\dot{x}}_1=r_2-x_2=e_2,\\ {\dot{e}}_2={\dot{r}}_2-{\dot{x}}_2=r_3-\left(x_3+g_y{F}_u\right)=-k_1^{y_1^b}\left(e_1+{\tilde{x}}_1\right)-k_2^{y_1^b}\left(e_2+{\tilde{x}}_2\right)-{\tilde{x}}_3.\end{array}$$

(67)

Let $\mathit{e}={\left[e_1,e_2\right]}^T$, then we have

$$\dot{\mathit{e}}\left(t\right)={\mathit{A}}_e\mathit{e}\left(t\right)+{\mathit{A}}_{\tilde{x}}\tilde{\mathit{x}}\left(t\right),$$

(68)

where ${\mathit{A}}_e=\left[\begin{array}{cc}0& 1\\ -k_1^{y_1^b}& -k_2^{y_1^b}\end{array}\right]$ and ${\mathit{A}}_{\tilde{x}}=\left[\begin{array}{ccc}0& 0& 0\\ -k_1^{y_1^b}& -k_2^{y_1^b}& -1\end{array}\right]$.

Solving (68), we have

$$\mathit{e}\left(t\right)=e^{{\mathit{A}}_{e}t}\mathit{e}\left(0\right)+{\displaystyle \underset{0}{\overset{t}{\int }}{e}^{{\mathit{A}}_e\left(t-\tau \right)}}{\mathit{A}}_{\tilde{x}}\tilde{\mathit{x}}\left(\tau \right)\mathrm{d}\tau .$$

(69)

According to (68) and Theorem 1, one has

$${\left[{\mathit{A}}_{\tilde{x}}\tilde{\mathit{x}}\left(\tau \right)\right]}_1=0;\hspace{1em}\hspace{1em}{\left[{\mathit{A}}_{\tilde{x}}\tilde{\mathit{x}}\left(\tau \right)\right]}_2\le k_s{\sigma }_i=\gamma ,\forall t\ge T_1,$$

(70)

where $k_s=1+k_1^{y_1^b}+k_2^{y_1^b}$. Define $\mathbf{\Psi }={\left[0,\gamma \right]}^T$. Let $\mathit{\phi }\left(t\right)={\displaystyle \underset{0}{\overset{t}{\int }}{e}^{{\mathit{A}}_e\left(t-\tau \right)}}{\mathit{A}}_{\tilde{x}}\tilde{\mathit{x}}\left(\tau \right)d\tau$. It follows that

$$\left|{\phi }_i\left(t\right)\right|\le \left|{\left({\mathit{A}}_e^{-1}\mathbf{\Psi }\right)}_i\right|+\left|{\left({\mathit{A}}_e^{-1}{e}^{{\mathit{A}}_{e}t}\mathbf{\Psi }\right)}_i\right|$$

(71)

and

$$\left|{\left({\mathit{A}}_e^{-1}\mathbf{\Psi }\right)}_1\right|=\gamma /{\left({\omega }_c^{y_1^b}\right)}^2;\hspace{1em}\hspace{1em}\left|{\left({\mathit{A}}_e^{-1}\mathbf{\Psi }\right)}_2\right|=0.$$

(72)

Since ${\mathit{A}}_e$ is Hurwitz, there exists a finite time T₂ > 0 in order that

$$\left|{\left[e^{{\mathit{A}}_{e}t}\right]}_{ij}\right|\le 1/{\left({\omega }_0^{y_1^b}\right)}^3$$

(73)

for all t $\ge$ T₂, i, j = 1, 2. Note that T₂ depends on ${\mathit{A}}_e$. Let $T_3=\max \left\{T_1,T_2\right\}$. It follows that

$$\left|{\left[e^{{\mathit{A}}_{e}t}\mathbf{\Psi }\right]}_i\right|\le \gamma /{\left({\omega }_0^{y_1^b}\right)}^3$$

(74)

for all t $\ge$ T₃, i = 1, 2, and

$$\left|{\left[{\mathit{A}}_e^{-1}{e}^{{\mathit{A}}_{e}t}\mathbf{\Psi }\right]}_i\right|\le \{\begin{array}{c}\gamma \left(1+k_2^{y_1^b}\right)/{\left({\omega }_c^{y_1^b}\right)}^5|{}_{i=1}\\ \gamma /{\left({\omega }_c^{y_1^b}\right)}^3|{}_{i=2}\end{array}$$

(75)

for all t $\ge$ T₃. From (71), (72), and (75), we obtain

$$\left|{\phi }_i\left(t\right)\right|\le \{\begin{array}{c}\gamma /{\left({\omega }_c^{y_1^b}\right)}^2+\gamma \left(1+k_2^{y_1^b}\right)/{\left({\omega }_c^{y_1^b}\right)}^5|{}_{i=1}\\ \gamma /{\left({\omega }_c^{y_1^b}\right)}^3|{}_{i=2}\end{array}$$

(76)

for all t $\ge$ T₃. Let $e_s\left(0\right)=\left|e_1\left(0\right)\right|+\left|e_2\left(0\right)\right|$. It follows that

$$\left|{\left[e^{{\mathit{A}}_{e}t}\mathit{e}\left(0\right)\right]}_i\right|\le e_s\left(0\right)/{\left({\omega }_c^{y_1^b}\right)}^3$$

(77)

for all t $\ge$ T₃, i = 1, 2. From (69), one has

$$\left|e_i\left(t\right)\right|\le \left|{\left[e^{A_{e}t}e\left(0\right)\right]}_i\right|+\left|{\phi }_i\left(t\right)\right|.$$

(78)

According to (70), (76)–(78), we have

$$\begin{array}{l}\left|e_i\left(t\right)\right|\le \{\begin{array}{c}{e}_s\left(0\right)/{\left({\omega }_c^{y_1^b}\right)}^3+\gamma /{\left({\omega }_c^{y_1^b}\right)}^2+\gamma \left(1+k_2^{y_1^b}\right)/{\left({\omega }_c^{y_1^b}\right)}^5|{}_{i=1}\\ \left(e_s\left(0\right)+\gamma \right)/{\left({\omega }_c^{y_1^b}\right)}^3|{}_{i=2}\end{array}\le {\rho }_i,\\ {\rho }_i=\max \left\{e_s\left(0\right)/{\left({\omega }_c^{y_1^b}\right)}^3+\gamma /{\left({\omega }_c^{y_1^b}\right)}^2+\gamma \left(1+k_2^{y_1^b}\right)/{\left({\omega }_c^{y_1^b}\right)}^5,\left(e_s\left(0\right)+\gamma \right)/{\left({\omega }_c^{y_1^b}\right)}^3\right\}\end{array}$$

(79)

for all t $\ge$ T₃, i = 1, 2. Q.E.D. □

It can be derived by the same method that the tracking errors between desired and actual outputs in subsystems (29), (34), and (45) are also bounded after a period of time.

4. Numerical Simulation Results

4.1. Numerical Simulation Setup

The task of this section is to verify the effectiveness of the proposed control scheme for the MAUAV landing process using numerical simulations. A sampling period of 0.2 ms is used in the simulation. The simulation parameters of MAUAV are given as: total mass of the system m_S = 20 kg, mass of the slider m₁ = 4 kg, wing area S = 0.55 m², wing span b = 2.8956 m, mean aerodynamic chord c = 0.1899 m. The inertia moments of the airframe without a slider are presented as: $J_{x_B}$ = 0.8244, $J_{y_B}$ = 1.135, $J_{z_B}$ = 1.759, $J_{x{y}_B}$ = 0, $J_{y{z}_B}$ = 0, $J_{x{z}_B}$ = 0.1204. The parameters of the propeller are selected as: S_prop = 0.2027, C_prop = 1, k_motor = 80. The parameters of the friction LuGre model are given as: σ₀ = 0.03, σ₁ = 0.8, σ₂ = 0.65, f_s = 2.19, f_c = 16.69, ${\dot{y}}_{1s}^b$ = 0.01. The simulation parameters for wind disturbance are selected as: $w_{n_s}$ = 4 m/s, $w_{e_s}$ = 2 m/s, $w_{d_s}$ = 1 m/s, σ_u = 1.06 m/s, σ_v = 1.06 m/s, σ_w = 0.7 m/s, L_u = 200 m, L_v = 200 m, and L_w = 50 m. The data for aerodynamic coefficients are obtained from literature [1], which is also used in literature [26]. The initial values of MAUAV system are set as: X = −3016 m, Y = 100 m, H = 100 m, u = 38 m/s, v = 1 m/s, w = 2 m/s, ϕ = −1 deg, θ = 0 deg, ψ = 1 deg, p = q = r = 0 deg/s.

Our control target is to enable the MAUAV to fly along the designed path and eventually land on the designated location on the ground runway (inertial coordinates of the touchdown point are [X_td, Y_td, H_td] = [0, 0, 0]) under the coordinated work of forward velocity, attitude, altitude, and moving-mass position controllers. In order to achieve this goal, it is necessary to give a reasonable expected path, expected forward velocity, and to select the appropriate controller parameters. Clearly, the desired lateral displacement command is Y_c = 0, and the desired height trajectory is designed as follows:

$$H_c=\{\begin{array}{ll}100,& 0\le t\le 10; \\ 100-1.832\left(t-10\right),& 10<t<56.4;\\ 16.64\times e^{-0.122\left(t-56.4\right)}-1.64,& 56.4\le t\le 75.4;\\ 0,& t>75.4.\end{array}$$

(80)

Specifically, in the approach stage, the height of the MAUAV is kept constant at 100 m; in the glide slope stage, the MAUAV declines along a straight line with an inclination angle of about −2.6°; in the flare stage, the MAUAV declines along an exponential curve, and the leveling decision height is about 15 m. To improve the tracking accuracy in the inertial X-axis direction of the MAUAV when landing on the runway, the commanded value of forward velocity is designed as u_c = −X(t)/(75.4 − t) when t < 75.4 s. When t = 75.4 s, the commanded forward velocity is kept the same as the value taken at 75.38 s to avoid singularity. In addition, the desired three attitude angles are determined based on the desired flight trajectory. The desired roll angle φ_c is obtained based on Equation (40), and the desired yaw angle ψ_c is updated by Equation (41). The desired pitch angle θ_c is determined by the height trajectory and its value is selected according to Equation (34).

In order to obtain an excellent control effect, it is necessary to select the appropriate regulation parameters for the designed controllers. The bandwidth and the desired closed-loop natural frequencies for the forward velocity, altitude, attitude, and moving-mass position controllers are chosen as: ${\omega }_0^u$ = 40, ${\omega }_c^u$ = 10, ${\omega }_0^H$ = 40, ${\omega }_c^H$ = 1.5, ${\mathit{\omega }}_0^{\omega }$ = diag{40, 40, 40}, ${\mathit{\omega }}_c^{\omega }$ = diag{10, 10, 10}, ${\omega }_c^{y_1^b}$ = 60, ${\omega }_0^{y_1^b}$ = 10. The adjustable parameter matrix ${\mathit{k}}_{\mathrm{\Phi }}$ = diag{0.1, 0.1, 0.1}. And the parameters for the lateral motion guidance are selected as: ${\chi }^{\infty }$ = π/3, k_path = 0.05, $k_{\chi }$ = 0.25.

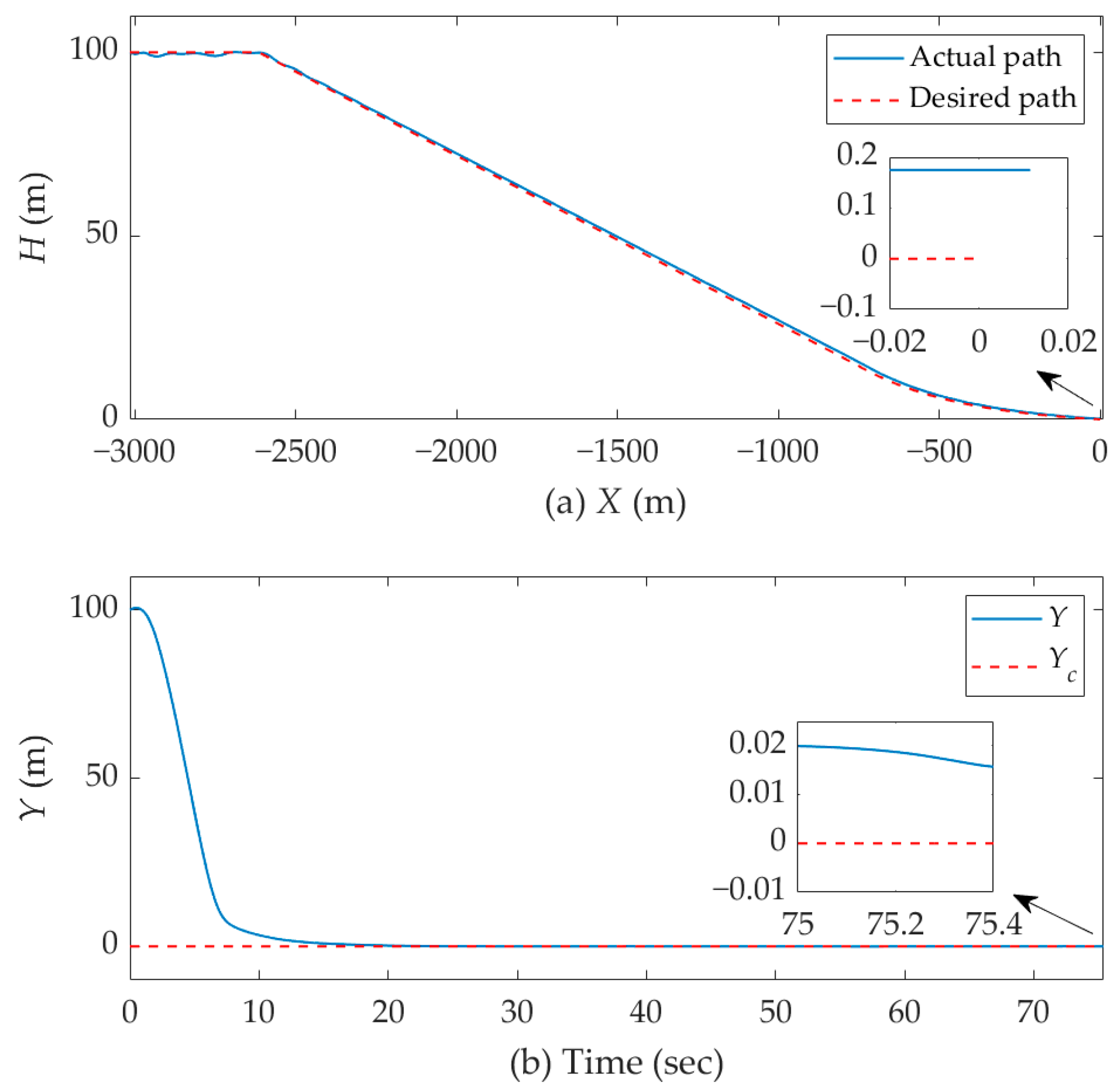
4.2. Simulation Results

Simulations were performed using the physical and control parameters described above, and the final simulation results are shown in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9. Figure 4 shows the forward velocity of the MAUAV and the throttle control size of the engine. The propeller throttle opening size is adjusted according to the designed forward velocity controller (31) to quickly control the forward velocity to the desired value. In Figure 5, we can find the slider offset, elevator offset, and rudder offset designed by the attitude controller. As can be seen from the figure, the signals are relatively smooth and continuous, except for some slight oscillations in the local area. The driving force designed by the moving-mass position controller can be found in Figure 6. As shown, the driving force is mainly activated in the first 10 s, since the lateral deflection of MAUAV is eliminated by adjusting the roll angle and a certain amount of force is needed to quickly move the slider, and thus change the roll angle. After the lateral deflection is close to 0 m, the drive maintains the wing level through a small range of outputs under the influence of wind disturbance. Figure 7a–c represent the roll angle, pitch angle, and yaw angle, respectively. During the whole landing process, the three attitude angles are smooth and continuous. The three-dimensional trajectory of the MAUAV during landing is shown in Figure 8. In order to demonstrate the accuracy of the landing process more intuitively, we show the path of MAUAV in X–H planes and lateral deviation in Figure 9. It is not difficult to find that the actual path is consistent with the desired path throughout the landing process except for the approach phase, which is due to the relatively large airspeed fluctuations in this phase. In addition, the tracking accuracy in the X and H directions of the MAUAV eventually reach errors of about 0.01 m and 0.2 m, respectively. In addition, the lateral deviation is rapidly reduced during the approach stage and finally converged to the runway centerline at about 15 s. When the MAUAV lands on the runway, the lateral deviation of it reaches about 0.02 m. Overall, the effectiveness of the proposed four controllers can be demonstrated by the above simulation results. These controllers work together to assist the MAUAV to perform landing tasks according to the desired path and ultimately land on the runway precisely.

5. Conclusions

In this paper, the automatic landing control of a fixed-wing UAV with moving mass rather than ailerons has been studied. Considering the specificity of the structure of the studied UAV, its control design models were established based on the analysis of dynamic models, and then four controllers were designed based on these design models using LADRC. Among them, the forward velocity controller is designed to make the MAUAV reach the desired speed quickly from the initial speed by controlling the engine oil port opening. The designed altitude controller is able to generate the corresponding pitch angle signal based on the desired altitude trajectory and serve as the pitch angle tracking command in the attitude controller. The designed attitude controller can ensure that the MAUAV moves at the desired attitude angles, and its generated mass block movement signal serves as a tracking command for the moving-mass position controller. Then, the movement of the slider is achieved by controlling the magnitude of the driving force, which is taken by the designed moving-mass position controller. The simulation results demonstrate the accuracy and effectiveness of the proposed control strategy. Specifically, the synergy of the four controllers allows the MAUAV to land on the runway according to a given trajectory. Not only the actual longitudinal trajectory matches the desired altitude, but also the lateral deviation of the MAUAV when landing on the runway is small. The design of the controllers in this paper is based on LADRC, and thus the control algorithm itself lacks novelty. In view of this shortcoming, we will endeavor to design new algorithms, which takes into account the characteristics of MAUAVs, to improve the safety and accuracy of the landing process in our future researches.