Joint Task Allocation and Resource Optimization Based on an Integrated Radar and Communication Multi-UAV System
Abstract
1. Introduction
- We consider a joint task allocation and resource optimization problem in the IRCU system under the resource, priority and timing constraints by jointly optimizing task allocation, power as well as channel bandwidth, and formulate the considered problem.
- Considering the mentioned complex non-convex problem, we propose an LIO algorithm, which obtains the optimal solution in a loop iterative manner.
- The considered problem is actually decomposed into three sub-problems, such as task allocation, power optimization and channel bandwidth optimization. At the same time, these three problems are solved by the divide-and-conquer algorithm, the SCA algorithm and the improved PSO algorithm, respectively.
- Simulation results demonstrate that the LIO algorithm consumes fewer iterations or gains higher maximum joint performance than other baseline schemes for solving the considered problem.
2. System Model and Problem Formulation
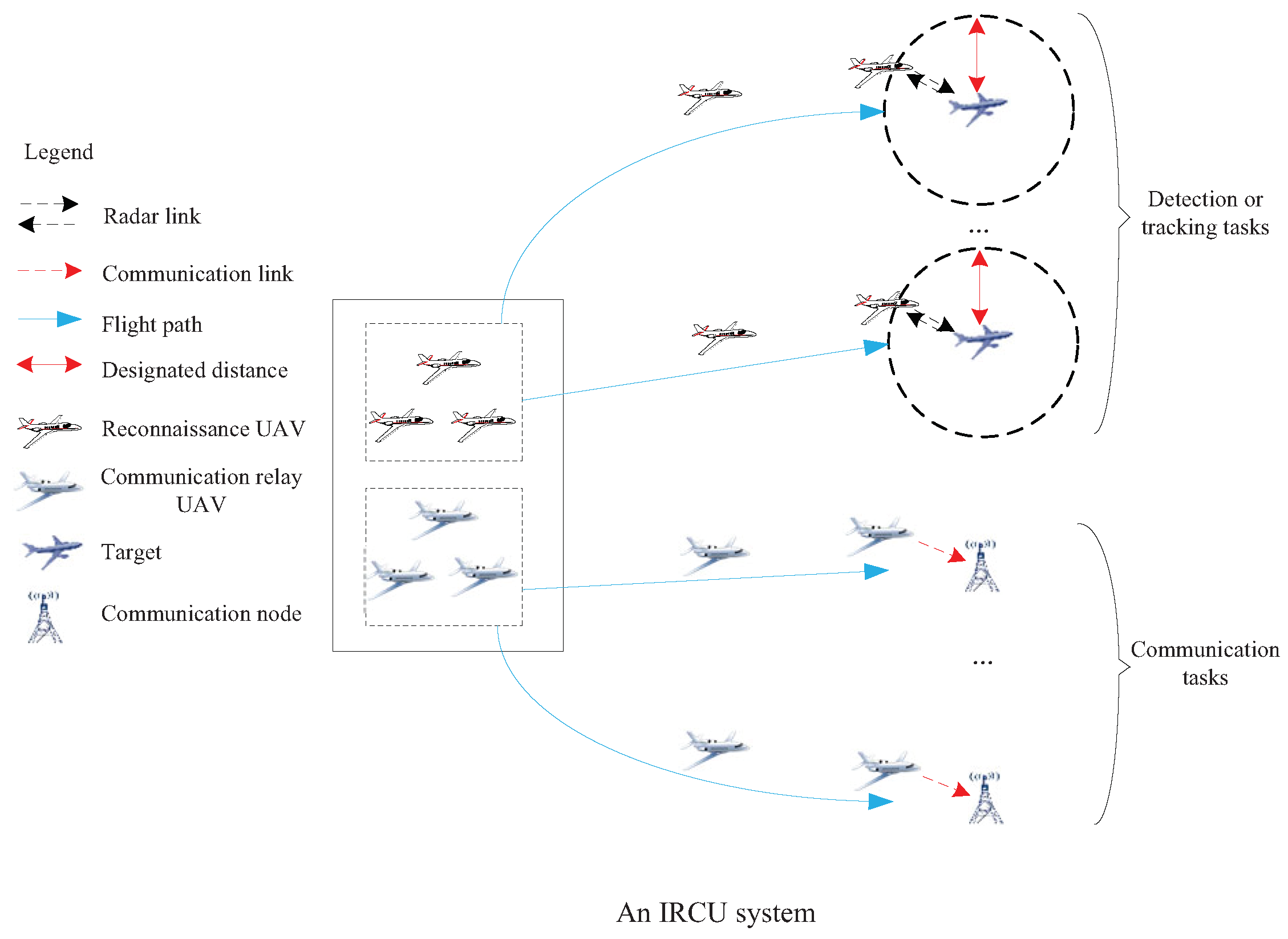
2.1. System Model
2.2. Task Model
2.2.1. Detection
2.2.2. Tracking
2.2.3. Communication
2.3. Constraints
2.3.1. Task Constraint
2.3.2. Time Constraint
2.3.3. Return Time Constraint
2.3.4. Power Constraint
2.3.5. Bandwidth Constraint
2.4. Problem Formation
3. Algorithm Analysis
3.1. Task Allocation
3.2. Power
3.3. Channel Bandwidth
| Algorithm 1 Improved PSO Algorithm |
Input: Maximum number of iterations , , Output:
|
| Algorithm 2 Loop Iterative Optimization Algorithm |
Input: , , . Output: or .
|
3.4. Analysis on Convergence and Computational Complexity
4. Simulation Analysis
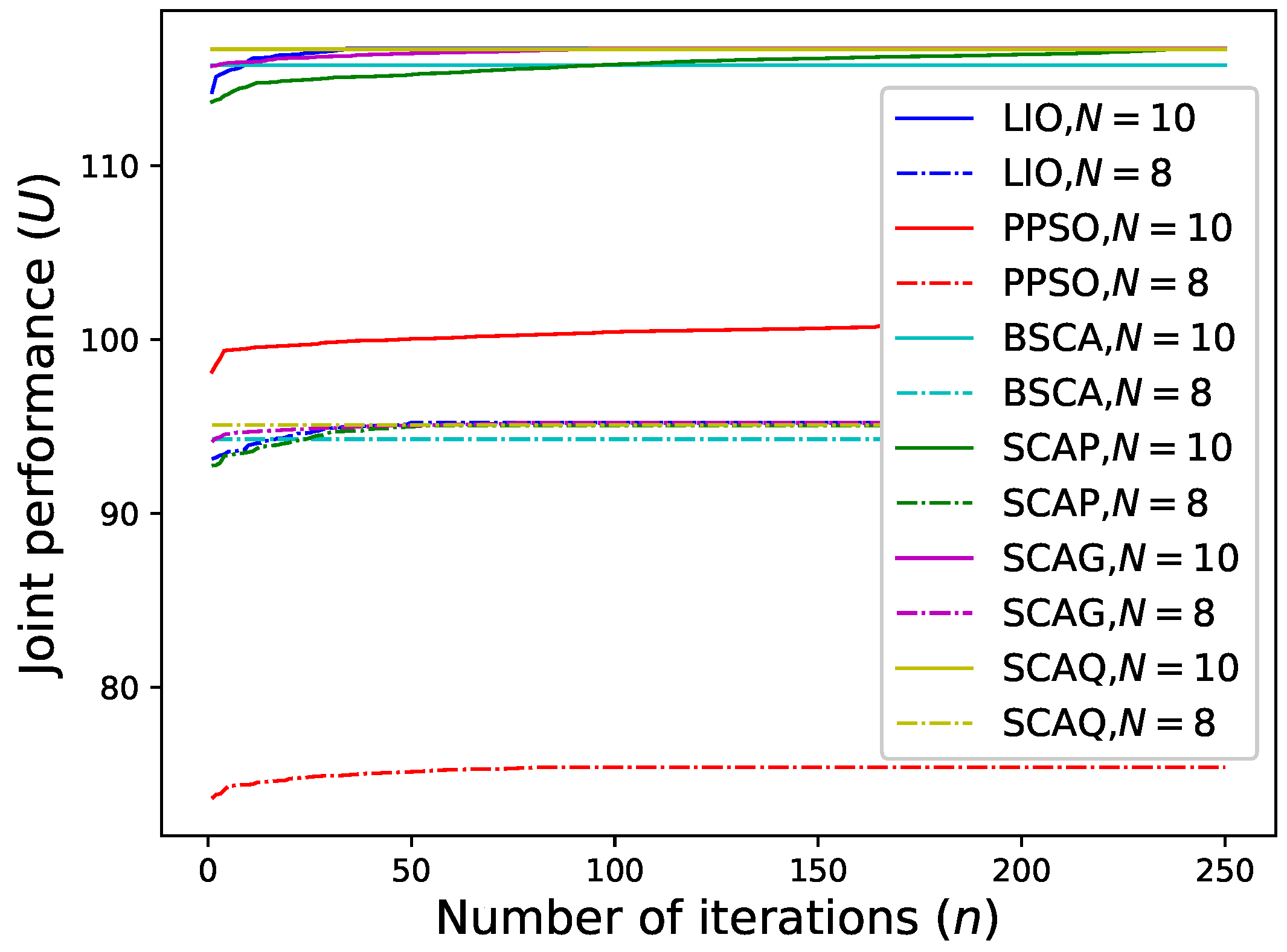
- Equal power and Improved PSO (PPSO): Powers of all tasks are equal, then other algorithms are the same for solving the remaining sub-problems.
- Equal channel bandwidth and SCA (BSCA): Channel bandwidths of all communication tasks are equal, then similar to the first scheme, other algorithms are also the same for solving the remaining sub-problems.
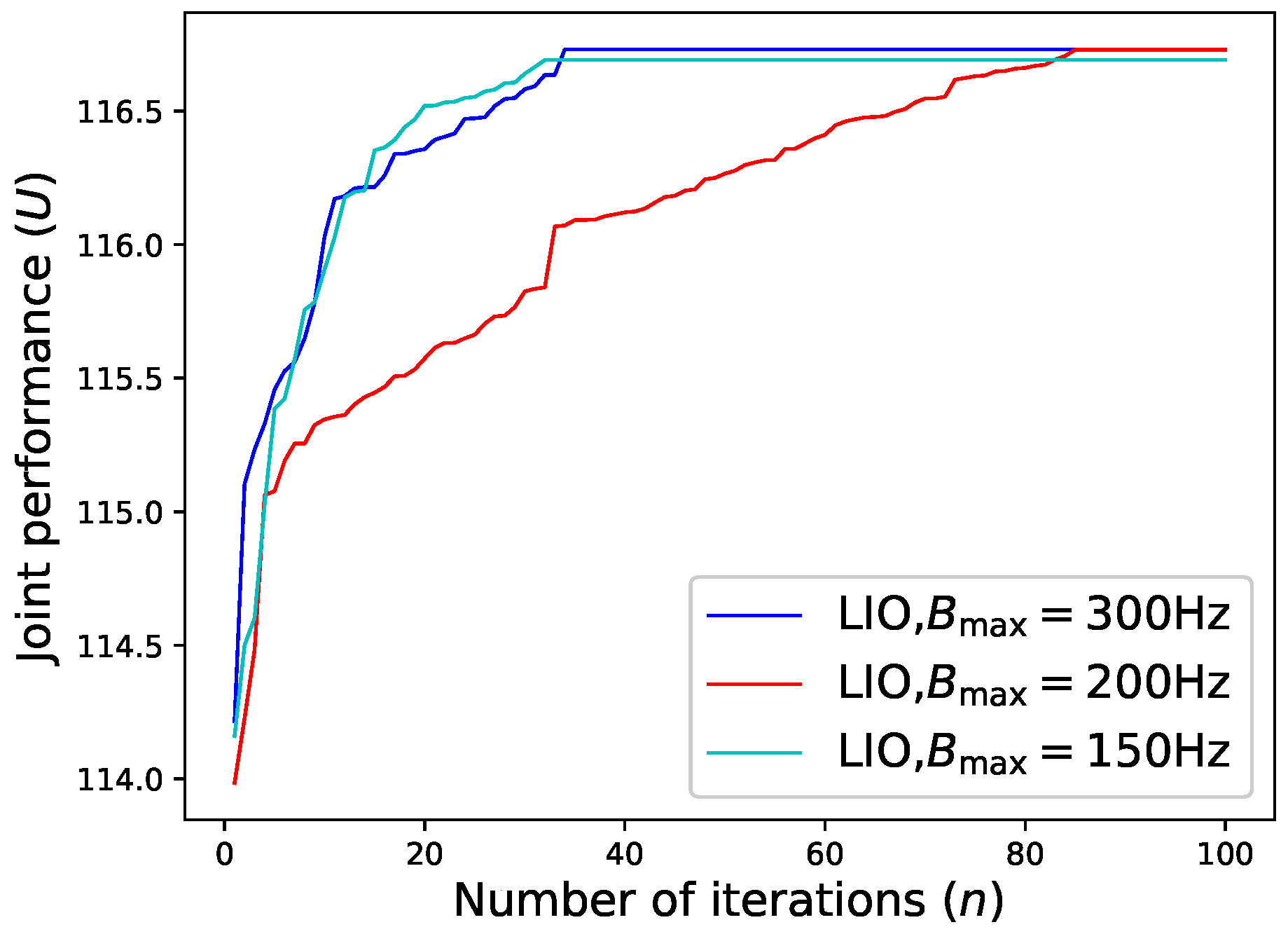
4.1. Case
4.2. Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Zeng, Y.; Lyu, J.; Zhang, R. Cellular-connected UAV: Potential, challenges, and Promising technologies. IEEE Wirel. Commun. 2019, 26, 120–127. [Google Scholar] [CrossRef]
- Fotouhi, A.; Qiang, H.; Ding, M.; Hassan, M.; Giordano, L.G.; Garcia-Rodriguez, A.; Yuan, J. Survey on UAV cellular communications: Practical aspects, standardization advancements, regulation, and security challenges. IEEE Commun. Surv. Tuts. 2019, 21, 3417–3442. [Google Scholar] [CrossRef]
- Li, B.; Fei, Z.; Zhang, Y. UAV communications for 5G and beyond: Recent advances and future trends. IEEE Internet Things J. 2019, 6, 2241–2263. [Google Scholar] [CrossRef]
- Ryan, A.; Zennaro, M.; Howell, A.; Sengupta, R.; Hedrick, J.K. An overview of emerging results in cooperative UAV control. In Proceedings of the 2004 43rd IEEE Conference on Decision and Control (CDC), Nassau, Bahamas, 14–17 December 2004; pp. 602–607. [Google Scholar]
- Li, B.; Fei, Z.; Dai, Y.; Zhang, Y. Secrecy-optimized resource allocation for UAV-assisted relaying networks. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Xiao, Z.; Liu, D.; Fei, B.; Men, T.; Zhou, Z.; Zhang, X.; Zhou, Y. Moving Target Tracking for Single UAV In Open Outdoor Environment. In Proceedings of the 2020 6th International Conference on Big Data and Information Analytics (BigDIA), Shenzhen, China, 4–6 December 2020; pp. 317–324. [Google Scholar]
- Wu, H.-H.; Zhou, Z.; Feng, M.; Yan, Y.; Xu, H.; Qian, L. Real-Time Single Object Detection on The UAV. In Proceedings of the 2019 International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 11–14 June 2019; pp. 1013–1022. [Google Scholar]
- Wu, Q.; Zeng, Y.; Zhang, R. Joint trajectory and communication design for multi-UAV enabled wireless networks. IEEE Trans. Commun. 2018, 17, 2109–2121. [Google Scholar] [CrossRef]
- Ji, Y.; Dong, C.; Zhu, X.; Wu, Q. Fair-energy trajectory planning for cooperative UAVs to locate multiple targets. In Proceedings of the ICC 2019—2019 IEEE International Conference on Communications (ICC), Shanghai, China, 21–23 May 2019; pp. 1–7. [Google Scholar]
- Do, D.T.; Le, C.B.; Vahid, A.; Mumtaz, S. Antenna selection and device grouping for spectrum-efficient UAV-assisted IoT systems. IEEE Internet Things J. 2023, 10, 8014–8030. [Google Scholar] [CrossRef]
- Kumaravelu, V.B.; Jadhav, H.K.; Bs, A.; Gudla, V.V.; Murugadass, A.; Imoize, A.L. Unmanned Aerial Vehicle-Assisted Reconfigurable Intelligent Surface for Energy Efficient and Reliable Communication. In Unmanned Aerial Vehicle Cellular Communications; Springer International Publishing: Cham, Switzerland, 2023; pp. 173–201. [Google Scholar]
- Van Nguyen, M.S.; Do, D.T.; Phan, V.D.; Ullah Khan, W.; Imoize, A.L.; Fouda, M.M. Ergodic performance analysis of double intelligent reflecting surfaces-aided NOMA–UAV systems with hardware impairment. Drones 2022, 6, 408. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.; Cong, M.; Wang, Z.; Wang, J. A Novel Method for Multi-UAV Cooperative Reconnaissance Mission Planning in Denied Environment. In Proceedings of the 2021 International Symposium on Computer Science and Intelligent Controls (ISCSIC), Rome, Italy, 12–24 November 2021; pp. 1–5. [Google Scholar]
- Wang, X.; Chen, H.; Liu, T.; He, K.; Ding, D.; Yong, E. Application of Improved K-means Clustering Algorithm in UAV Reconnaissance Mission Planning. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021; pp. 2744–2748. [Google Scholar]
- Wu, Y.; Low, K.H.; Lv, C. Cooperative Path Planning for Heterogeneous Unmanned Vehicles in a Search-and-Track Mission Aiming at an Underwater Target. IEEE Trans. Veh. Technol. 2020, 69, 6782–6787. [Google Scholar] [CrossRef]
- Zhang, K.; Li, Z.; Zhao, X.; Zhao, B. Dynamic Multi-UAV Cooperative Reconnaissance Task Assignment Based on ICNP. In Proceedings of the 2020 5th International Conference on Mechanical, Control and Computer Engineering (ICMCCE), Harbin, China, 25–27 December 2020; pp. 773–779. [Google Scholar]
- Xia, Z.; Du, J.; Jiang, C.; Wang, J.; Ren, Y.; Li, G. Multi-UAV Cooperative Target Tracking Based on Swarm Intelligence. In Proceedings of the ICC 2021—IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar]
- Gao, S.; Zuo, L.; Bao, S.X. UAV Reconnaissance Task Allocation with Reinforcement Learning and Genetic Algorithm. In Proceedings of the 2022 International Conference on Automation, Robotics and Computer Engineering (ICARCE), Wuhan, China, 14–16 December 2022; pp. 1–3. [Google Scholar]
- Pitre, R.R.; Li, X.R.; Delbalzo, R. UAV Route Planning for Joint Search and Track Missions—An Information-Value Approach. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2551–2565. [Google Scholar] [CrossRef]
- Hassanien, A.; Amin, M.G.; Zhang, Y.D.; Ahmad, F. Dual-function radar-communications: Information embedding using sidelobe control and waveform diversity. IEEE Trans. Signal Process. 2016, 64, 2168–2181. [Google Scholar] [CrossRef]
- Liu, F.; Zhou, L.; Masouros, C.; Li, A.; Luo, W.; Petropulu, A. Toward dual-functional radar-communication systems: Optimal waveform design. IEEE Trans. Signal Process. 2018, 66, 4264–4279. [Google Scholar] [CrossRef]
- Liu, F.; Zhou, L.; Masouros, C.; Li, A.; Luo, W.; Petropulu, A. Dual-functional cellular and radar transmission: Beyond coexistence. In Proceedings of the 2018 IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Kalamata, Greece, 25–28 June 2018; pp. 1–5. [Google Scholar]
- Liu, F.; Masouros, C.; Li, A.; Sun, H.; Hanzo, L. MU-MIMO communications with MIMO radar: From co-existence to joint transmission. IEEE Trans. Wirel. Commun. 2018, 17, 2755–2770. [Google Scholar] [CrossRef]
- Sturm, C.; Zwick, T.; Wiesbeck, W. An OFDM system concept for joint radar and communications operations. In Proceedings of the VTC Spring 2009—IEEE 69th Vehicular Technology Conference, Barcelona, Spain, 26–29 April 2009; pp. 1–5. [Google Scholar]
- Zhang, J.A.; Huang, X.; Guo, Y.J.; Yuan, J.; Heath, R.W. Multibeam for joint communication and radar sensing using steerable analog antenna arrays. IEEE Trans. Veh. Technol. 2019, 68, 671–685. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, J.A.; Ni, W.; Pan, J.; Huang, X. Constrained multibeam optimization for joint communication and radio sensing. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar]
- Xu, X.; Tao, R.; Li, S.; Chen, Y. Collaborative UAV Deployment and Task Allocation for Environment Sensing in Multi-UAV Networks. In Proceedings of the 2022 IEEE International Conference on Unmanned Systems (ICUS), Guangzhou, China, 28–30 October 2022; pp. 738–743. [Google Scholar]
- Zhou, L.; Leng, S.; Wang, Q.; Liu, Q. Integrated Sensing and Communication in UAV Swarms for Cooperative Multiple Targets Tracking. IEEE Trans. Mob. Comput. 2022; in press. [Google Scholar] [CrossRef]
- Meng, K.; He, X.; Wu, Q.; Li, D. Multi-UAV Collaborative Sensing and Communication: Joint Task Allocation and Power Optimization. IEEE Trans. Wirel. Commun. 2023, 22, 4232–4246. [Google Scholar] [CrossRef]
- Meng, K.; He, X.; Wu, Q.; Li, D. Multi-UAV Cooperative Sensing and Communication with Replicated Task Allocation. In Proceedings of the 2022 IEEE Globecom Workshops (GC Wkshps), Rio de Janeiro, Brazil, 4–8 December 2022; pp. 910–915. [Google Scholar]
- Hou, D.; Qi, F.; Dai, J.; Yang, Z. Models for Radar Detection Probability Based on Operation Simulation. Electron. Inf. Warf. Technol. 2016, 31, 61–64. [Google Scholar]
- Yan, J.; Pu, W.; Dai, J.; Liu, H.; Bao, Z. Resource Allocation for Search and Track Application in Phased Array Radar Based on Pareto Bi-Objective Optimization. IEEE Trans. Veh. Technol. 2019, 68, 3487–3499. [Google Scholar] [CrossRef]
- Mynar, Z.; Vaclavek, P.; Blaha, P. Synchronous Reluctance Motor Parameter and State Estimation Using Extended Kalman Filter and Current Derivative Measurement. IEEE Trans. Ind. Electron. 2021, 68, 1972–1981. [Google Scholar] [CrossRef]
- Li, X.; Yao, H.; Wang, J.; Xu, X.; Jiang, C.; Hanzo, L. A Near-Optimal UAV-Aided Radio Coverage Strategy for Dense Urban Areas. IEEE Trans. Veh. Technol. 2019, 68, 9098–9109. [Google Scholar] [CrossRef]
- Chen, J.; Wu, Q.; Xu, Y.; Qi, N.; Guan, X.; Zhang, Y.; Xue, Z. Joint Task Assignment and Spectrum Allocation in Heterogeneous UAV Communication Networks: A Coalition Formation Game-Theoretic Approach. IEEE Trans. Wirel. Commun. 2021, 20, 440–452. [Google Scholar] [CrossRef]
- Smith, E.; Trefftz, C.; DeVries, B. A Divide-and-Conquer Algorithm for Computing Voronoi Diagrams. In Proceedings of the 2020 IEEE International Conference on Electro Information Technology (EIT), Chicago, IL, USA, 31 July–1 August 2020; pp. 495–499. [Google Scholar]
- Razaviyayn, M.; Hong, M.; Luo, Z.-Q.; Pang, J.-S. Parallel successive convex approximation for nonsmooth nonconvex optimization. In Proceedings of the 27th International Conference on Neural Information Processing Systems—Volume 1 (NIPS’14), Montreal, QC, Canada, 8–13 December 2014; MIT Press: Cambridge, MA, USA, 2014; pp. 1440–1448. [Google Scholar]
- Grant, M.; Boyd, S.; Ye, Y. CVX: Matlab Software for Disciplined Convex Programming; CVX Research. Inc.: Austin, TX, USA, 2008. [Google Scholar]
- Li, Y.; Long, X.; Liu, X. Mission Arrangement Optimization with Improved PSO for Multiple Plant Protecion UAVs in Heterogeneous Farmlands. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021; pp. 7772–7776. [Google Scholar]
- Fan, S.; Wang, Y.; Tian, H.; Jie, Z.; Shi, J. Joint Task optimization of trajectory and resource allocation for UAV integrated radar and communication system. IEEE J. Commun. 2021, 42, 182–192. [Google Scholar]
- Sarfo, K.; Wang, K.; Rakotomandimby F., M.; Ntiamoah-Sarpong, K. Large-scale UAV-Network using the Hata—Okumura model with PSO algorithm for Open Area Communication. In Proceedings of the 2021 International Conference on Computer Engineering and Artificial Intelligence (ICCEAI), Shanghai, China, 27–29 August 2021; pp. 138–142. [Google Scholar]
- Wu, X.; Yin, Y.; Xu, L.; Wu, X.; Meng, F.; Zhen, R. Multi-UAV Task Allocation Based on Improved Genetic Algorithm. IEEE Access 2021, 9, 100369–100379. [Google Scholar] [CrossRef]
- Jones, M.R.; Djahel, S.; Welsh, K. MQTPP—Towards Multiple Q-Table based Path Planning in UAV Environments. In Proceedings of the 2022 IEEE 19th Annual Consumer Communications and Networking Conference (CCNC), Las Vegas, NV, USA, 8–11 January 2022; pp. 457–460. [Google Scholar]




| Variables | Explanation |
|---|---|
| N | The number of tasks |
| The number of communication tasks | |
| The number of task types | |
| M | The number of UAVs |
| The task set | |
| The UAV set | |
| H | The hovering altitude of the large flying platform |
| The total time | |
| The total power | |
| The total channel bandwidth | |
| i | The task index |
| j | The task type |
| The task type to which the i-th task belongs | |
| The importance level of task i | |
| The deadline time of task i | |
| The dwell time of task i | |
| The return time of task i | |
| The designated distance of task i | |
| The consumption power of task i | |
| The channel bandwidth of task i | |
| a 0–1 decision function | |
| The task type matrix | |
| The task consumption power vector | |
| The channel bandwidth vector | |
| The task allocation matrix | |
| The observation noise covariance | |
| The scheduling interval | |
| The task performance of task i that belongs to task type j | |
| The minimum task performance of task type j | |
| The mainimum power | |
| The maximum power | |
| The mainimum channel bandwidth | |
| The maximum channel bandwidth | |
| The false alarm probability of the receiver | |
| The channel gain of the line-of-sight channel | |
| The power spectral density of noise | |
| The power consumed by each UAV while hovering | |
| The minimum task scheduling success rate | |
| The weight coefficient of the j-th task type |
| Parameter | Value |
|---|---|
| Total time | |
| Total power | |
| Total channel bandwidth | |
| Number of tasks | |
| Number of UAVs | |
| Hovering altitude of the platform in the IRCU system | |
| False alarm probability | |
| Effective receiving antenna area for phased-array radars | = 0.0173 dB · m |
| Detecting target cross area | = 1 m |
| Tracking target cross area | =1 m |
| Radar constant | |
| Channel gain of LOS | |
| Noise power spectral density | |
| The minimum power | |
| The maximum power | |
| UAV hovering power | |
| The minimum bandwidth | |
| The maximum bandwidth | |
| The minimum task scheduling success rate | |
| Weight coefficients | , , |
| Error accuracy of LIO algorithm | |
| Learing factors of LIO algorithm |
| Task | Task Priority | Dwell Time (s) | Task Distance (km) |
|---|---|---|---|
| Detection task | 1.1 | 3 | 10 |
| Communication task | 1.9 | 4 | - |
| Tracking task | 2.3 | 8 | 2.5 |
| Communication task | 2.5 | 5 | - |
| Detection task | 2.9 | 2 | 19 |
| Tracking task | 3.2 | 7 | 3.5 |
| Tracking task | 3.8 | 6 | 4.5 |
| Communication task | 4.6 | 4 | - |
| Detection task | 5.2 | 5 | 11 |
| Communication task | 6.0 | 3 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wang, K.; Li, X.; Liu, K.; Cong, Y. Joint Task Allocation and Resource Optimization Based on an Integrated Radar and Communication Multi-UAV System. Drones 2023, 7, 523. https://doi.org/10.3390/drones7080523
Zhang X, Wang K, Li X, Liu K, Cong Y. Joint Task Allocation and Resource Optimization Based on an Integrated Radar and Communication Multi-UAV System. Drones. 2023; 7(8):523. https://doi.org/10.3390/drones7080523
Chicago/Turabian StyleZhang, Xun, Kehao Wang, Xiaobai Li, Kezhong Liu, and Yirui Cong. 2023. "Joint Task Allocation and Resource Optimization Based on an Integrated Radar and Communication Multi-UAV System" Drones 7, no. 8: 523. https://doi.org/10.3390/drones7080523
APA StyleZhang, X., Wang, K., Li, X., Liu, K., & Cong, Y. (2023). Joint Task Allocation and Resource Optimization Based on an Integrated Radar and Communication Multi-UAV System. Drones, 7(8), 523. https://doi.org/10.3390/drones7080523








