Sliding-Mode Control for Flight Stability of Quadrotor Drone Using Adaptive Super-Twisting Reaching Law

Abstract

In this study, a sliding-mode controller is designed using an adaptive reaching law with a super-twisting algorithm. A dynamic model of a drone is designed with a quadrotor that has four motors and considers disturbances and model uncertainties. Given that the drone operates as an under-actuated system, its flight stability and maneuverability are influenced by the discontinuous signal produced by the reaching law of the sliding-mode control. Therefore, this study aims to improve the sliding-mode control and stability of drone flight using the proposed adaptive law, which is based on exponential properties. The discontinuous signal of a conventional strategy is overcome using the super-twisting algorithm, and the drone rapidly reaches equilibrium using the proposed adaptive law that utilizes the sliding surface value. The proposed control strategy covers a higher dimension than the conventional sliding-mode control strategy; the system stability is proven using the strict Lyapunov function. The reaching time estimation results are introduced and used to compare the respective reaching times of the control strategies. To verify the superior performance of the proposed control method, multiple experiments are conducted under various situations and realizations. The simulation results prove that the proposed control method achieved a superior rapid response, stable maneuvering, and robustness with shorter reaching time.

1. Introduction

A quadrotor is an unmanned aerial vehicle actuated by four motors, called drones. quadcopters, and so on. Quadrotors manifest simplicity, controllability, and vertical takeoff and landing ability compared with other aircraft. By controlling the rotation direction of the four actuators, there is no requirement for an additional motor design to manipulate forward directional movement, such as a helicopter. Furthermore, because the motor is oriented perpendicularly to the ground, the quadrotor drone can navigate tight spaces without the need for an airstrip like traditional airplanes and can hover by maintaining a fixed 3-axis coordinate position. Unmanned aircraft vehicles are anticipated to take the place of manned aircraft and submarines in a variety of functions, including remote sensing, border patrol, aerial and underwater photography, environmental surveillance, package delivery, imaging, inspection of various underwater structures, and military operation [1]. Therefore, drones are used in various industrial applications and have promising prospects [2,3,4,5].

In several studies, proportional–integral–derivative (PID) and sliding-mode control (SMC) techniques were used to control quadrotor stabilization and movement [6,7,8,9]. The PID method is widely used as a basic control technique due to its simplicity and ease of design, not only for quadrotors but also for other control objects. However, several control techniques have been proposed to substitute for the PID method because of its restricted response to disturbances, model uncertainty, and precision control. SMC has been identified as an efficient nonlinear control strategy that shows robustness to external disturbances and delays, which are included in most mechanical systems. Due to these advantages, SMC overcomes the limitations of PID and is proposed as a control method with robust performance [10,11].

The conventional SMC (CSMC) guarantees system stability based on a weak Lyapunov function (WLF) with a sliding surface for finite-time convergence and robustness [12]. The sliding surface was designed in a second-order sliding plane based on the error between the current and target states. The operating characteristics of the sliding plane are divided into two phases. The first phase is the reaching phase, which indicates a process wherein the initial state of the control target is settled on the sliding surface. The second phase is the sliding phase, in which the state of the control target reaches the equilibrium origin of the state space after reaching the phase. According to WLF, discontinuous control inputs are generated in the sliding phase due to the derived sign function. This discontinuous control input causes a chattering effect, and hence brings about unstable results on discrete signal processing and control performance of the system when implementing hardware and simulation. In order to improve the chattering effect, several studies were presented. Labbadi [13] proposed an advanced sliding mode controller for a quadrotor drone’s position and attitude. The exponential reaching law was suggested, with modifying of the sign term as hyperbolic tangent function to overcome the discontinuous signal. Nekoukar [14] proposed the adaptive fuzzy terminal sliding mode strategy to control the attitude of a quadrotor. The position controller was designed with a PD controller for providing continuous desired signal. Moreover, many studies have been conducted to overcome this chattering effect [15,16,17].

In this study, the chattering effect was overcome and the flight performance of the quadrotor was improved. Therefore, we applied the super-twisting algorithm (STA) in the design of CSMC for a quadrotor to overcome the chattering effect. As STA is a continuous design technique that integrates the discontinuous signal generated in the sliding phase, it transforms the conventional single-dimensional control input of CSMC into a second-order control input. Although the single-dimensional control law proves the stability of the system through the conventional Lyapunov function, that is, WLF, the secondary control input should be guaranteed by other stability conditions. Therefore, it is necessary to evaluate the stability of the high-order control inputs. In this study, the stability of the secondary control input was proven using a strict Lyapunov function (SLF). The condition required for the sliding surface to converge to zero is referred to as the attractiveness condition [18,19]. To satisfy the attractiveness condition in the higher dimension of the control law, the evaluation in linear algebra is performed using the algebraic Lyapunov equation (ALE).

The primary issues for SMC are the stability of the system and finiteness of the reaching time. As STA is applied to the CSMC method, stability evaluation is performed through SLF with ALE, and the reaching time in STA can be derived from SLF conventionally proven as ALE [20]. In this study, an adaptive law is proposed and proven through the reaching time, which is faster than the reaching time of the traditional STA (TSTA). As the proposed adaptive law cannot be verified using the traditional reaching time estimation method, a novel estimation method is required for a specific comparison. Therefore, in this study, the proposed reaching time estimation method is adopted [21].

Various methods have been used in several studies on SMC strategies for quadrotors. Huang [22] proposed a control method that guaranteed the stability of the system in uncertainty and extremely strong disturbances through an adaptive method. Huang proved the error convergence of the control method mathematically and demonstrated its performance through simulations. Eliker [23] proposed an adaptive terminal SMC controller that focused on the finiteness of the reaching time. The robustness of the system was secured by proposing an adaptive method to estimate disturbances within a finite time. Luo [24] presented a gain-adaptation mechanism for the STA for adaptive sliding-mode controller design. Derafa [25] implemented the hardware using STA to the quadrotor and mathematically proved the system stability and reaching time. Labbadi [26] proposed a PID sliding surface by adding the integral equation of the error to a conventional sliding surface and applied it to STA. This study improved the robustness of the system by adding an adjustment factor.

Thus, the aforementioned studies [22,23,24,25,26] improved the performance of the conventional control method using additional terms or adaptive laws without mathematical comparison. Based on this research, STA with the adaptive law and/or an additional mathematical term improved not only the chattering effect of CSMC but also the rapid response and robustness of the system. We propose the exponential function based adaptive law with STA that induces inertial controllability for the stability of quadrotor flight. Moreover, in this study, the reduction in reaching time is mathematically proven compared to the conventional and traditional control methods. Therefore, we propose the adaptive super-twisting reaching law (ASTRL) for effective performance of quadrotor flight.

In several studies, the performance of the controller was improved using the characteristics of the exponential function [27,28]. The adaptive law proposed in this study is an activation function based on the exponential term and sliding surface. In the sliding plane, when the initial state of the system is far from the target state, the control input is applied with a higher gain instead of a fixed control gain using a relatively large value of the sliding surface value. In addition, when the system state is close to the target state, the control input is applied with an adaptively reduced gain, considering the inertia affected by the proposed adaptive control input. Therefore, the proposed adaptation scheme has a faster response and robustness than other control schemes. In this study, the improvement in rapid response and robustness using the proposed adaptive law is mathematically proven through simulations and experiments.

The quadrotor is an under-actuated system with six degrees of freedom and four control outputs. Therefore, the error signals of the quadrotor were generated by designing four objective states, and the simulation was conducted under the assumption that the position and attitude of the quadrotor were measured by a gyroscope sensor, an accelerometer sensor, and an ultrasonic sensor, and the noise generated by each sensor was considered. The control input was designed in four types, and only the first control input was used for the position control of the quadrotor. The position control input generated the reference angles of roll and pitch, which are required for quadrotor flight to satisfy the two degrees of freedom. The simulation was performed considering the disturbance and model uncertainty occurring in the tracking trajectory of the quadrotor.

The remainder of this paper is organized as follows. In Section 2, the modeling of the quadrotor is derived and the principle of operation of the quadrotor is introduced. In Section 3, the flight control system is designed, and an adaptive law is proposed. In Section 4, we demonstrate the stability of the system using the designed controller and estimate its reaching time. In Section 5 and Section 6, the simulation results and conclusions are presented, respectively.

2. Dynamic Modeling of Quadrotor Drone

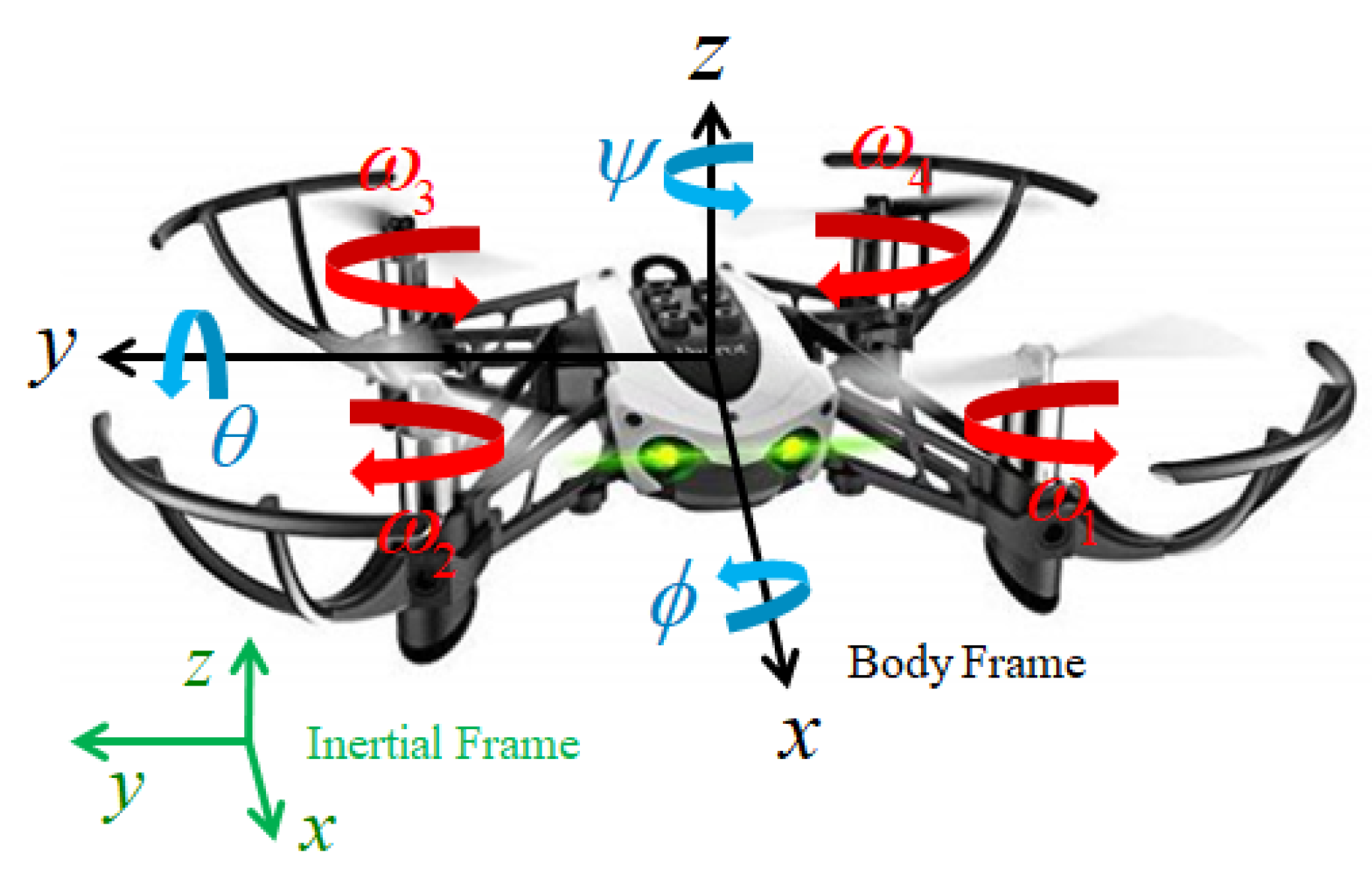
Quadrotor drones are typically designed with four actuators oriented perpendicular to the ground. In this study, structural definition and dynamic modeling were adopted for the Parrot Mambo mini drone. Figure 1 shows a structural diagram of a quadrotor. The quadrotor can hover when the counter-clockwise rotational direction of the actuator $\left({\omega }_1,{\omega }_3\right)$ and the clockwise rotational direction of the actuator $\left({\omega }_2,{\omega }_4\right)$ are designed to be equal.

Quadrotor hovering is possible with symmetrically different rotational directions, and the parameters of the quadrotor used in this study are defined as shown in Figure 1. Figure 1 also specifies the definition of the position $\left(x,y,z\right)$ and attitude $\left(\varphi ,\theta ,\psi \right)$ of the quadrotor regarding the body frame. The quadrotor is an under-actuated system because it must control six degrees of freedom $\left(x,y,z,\varphi ,\theta ,\psi \right)$ with four actuators. For the quadrotor system in this study, $\varphi$ and $\theta$ are limited to be between −90 and +90 degrees, and yaw is limited to be between -180 and +180 degrees for practical quadrotor flight. Based on the limited attitude angles, the state-space form is obtained as follows [29,30]:

$$\begin{array}{cc}\hfill \ddot{x}& =-\frac{r_4}{m}\dot{x}+\left(cos\varphi sin\theta cos\psi +sin\varphi sin\psi \right)\frac{U_1}{m},\hfill \\ \hfill \ddot{y}& =-\frac{r_5}{m}\dot{y}+\left(cos\varphi sin\theta sin\psi -sin\varphi sin\psi \right)\frac{U_1}{m},\hfill \\ \hfill \ddot{z}& =-\frac{r_6}{m}\dot{z}+g+cos\varphi cos\theta \frac{U_1}{m},\hfill \\ \hfill \ddot{\varphi }& =\dot{\theta }\dot{\psi }\frac{I_y-I_z}{I_x}-\frac{J_r}{I_x}\omega \dot{\theta }-\frac{r_1}{I_x}{\dot{\varphi }}^2+\frac{l}{I_x}{U}_2,\hfill \\ \hfill \ddot{\theta }& =\dot{\varphi }\dot{\psi }\frac{I_z-I_x}{I_y}+\frac{J_r}{I_y}\omega \dot{\varphi }-\frac{r_2}{I_y}{\dot{\theta }}^2+\frac{l}{I_y}{U}_3,\hfill \\ \hfill \ddot{\psi }& =\dot{\varphi }\dot{\theta }\frac{I_x-I_y}{I_z}-\frac{r_3}{I_z}{\dot{\psi }}^2+\frac{U_4}{I_z},\hfill \end{array}$$

(1)

where $r_{1,2,\cdots ,6}$ denotes the aerodynamic resistance for each state, m denotes the mass of the quadrotor, l denotes the distance from the center of the quadrotor to the actuator, g denotes the gravitational acceleration, $I_{x,y,z}$ denotes the coefficient of inertia corresponding to each axis of the quadrotor, $\omega =-{\omega }_1+{\omega }_2-{\omega }_3+{\omega }_4$ denotes the overall speed of the actuators, $J_r$ denotes the inertia coefficient of the actuator, and $U_1,U_2,U_3,U_4$ denote the control inputs.

In this paper, we consider $\mathbf{X}={\left[\begin{array}{cccc}{x}_1& x_2& \cdots & x_6\end{array}\right]}^{\mathbf{T}}={\left[\begin{array}{cccccc}x& y& z& \varphi & \theta & \psi \end{array}\right]}^{\mathbf{T}}$ as the state vector. The control inputs and velocity of the respective actuators are related as follows:

$$\begin{array}{cc}\hfill U_1& ={\rho }_1\left({\omega }_1^2+{\omega }_2^2+{\omega }_3^2+{\omega }_4^2\right),\hfill \\ \hfill U_2& ={\rho }_1\left({\omega }_1^2-{\omega }_2^2-{\omega }_3^2+{\omega }_4^2\right),\hfill \\ \hfill U_3& ={\rho }_1\left({\omega }_1^2+{\omega }_2^2-{\omega }_3^2-{\omega }_4^2\right),\hfill \\ \hfill U_4& ={\rho }_2\left(-{\omega }_1^2+{\omega }_2^2-{\omega }_3^2+{\omega }_4^2\right),\hfill \end{array}$$

(2)

where ${\rho }_1$ and ${\rho }_2$ represent the thrust and drag coefficient, respectively. For position control of the quadrotor, the auxiliary control input is considered as $\left(cos\varphi sin\theta cos\psi +sin\varphi sin\psi \right)·U_1/\phantom{U_{1}m}m$ and $\left(cos\varphi sin\theta sin\psi -sin\varphi sin\psi \right)·U_1/\phantom{U_{1}m}m$ in Equation (1). The auxiliary control input is used to calculate the desired roll and pitch $\left({\varphi }_d,{\theta }_d\right)$, which are controlled by $U_2$ and $U_3$, respectively. With small angle approximation, the translational dynamic of Equation (1) can be calculated as the desired roll and pitch angles to obtain the virtual controller as follows [31,32]:

$$\begin{array}{c}\hfill {\varphi }_d=\frac{m}{U_1}\left(-{\ddot{x}}_{d}sin{\psi }_d+{\ddot{y}}_{d}cos{\psi }_d\right),\\ \hfill {\theta }_d=\frac{m}{U_1}\left(-{\ddot{x}}_{d}cos{\psi }_d-{\ddot{y}}_{d}sin{\psi }_d\right).\end{array}$$

(3)

The values of ${\varphi }_d$ and ${\theta }_d$ are equally limited to be between −90 and +90 as $\varphi$ and $\theta$, respectively.

3. Problem Formulation and Controller Design

From Equation (1), the conventional structure of the second-order state-space equation can be obtained as follows [32]:

$$\begin{array}{c}\hfill \ddot{\mathbf{X}}=\mathbf{F}\left(\mathbf{X}\right)+\mathbf{G}\left(\mathbf{X}\right)\mathbf{U}+\mathbf{D}\left(t\right),\end{array}$$

(4)

where

$$\begin{array}{cc}\hfill \mathbf{U}& ={\left[\begin{array}{cccc}{U}_1& U_2& U_3& U_4\end{array}\right]}^T,\hfill \\ \hfill \mathbf{F}\left(\mathbf{X}\right)& ={\left[\begin{array}{cccccc}{f}_1& f_2& f_3& f_4& f_5& f_6\end{array}\right]}^T,\hfill \\ \hfill \mathbf{G}\left(\mathbf{X}\right)& =\left[\begin{array}{cccc}{g}_1& 0& 0& 0\\ g_2& 0& 0& 0\\ g_3& 0& 0& 0\\ 0& g_4& 0& 0\\ 0& 0& g_5& 0\\ 0& 0& 0& g_6\end{array}\right],\hfill \end{array}$$

(5)

with

$$\begin{array}{cc}\hfill f_1& =-\frac{r_4}{m},\hfill \\ \hfill f_2& =-\frac{r_5}{m},\hfill \\ \hfill f_3& =-\frac{r_6}{m}+g,\hfill \\ \hfill f_4& =\dot{\theta }\dot{\psi }\frac{I_y-I_z}{I_x}-\frac{J_r}{I_x}\omega \dot{\theta }-\frac{r_1}{I_x}{\dot{\varphi }}^2,\hfill \\ \hfill f_5& =\dot{\varphi }\dot{\psi }\frac{I_z-I_x}{I_y}+\frac{J_r}{I_y}\omega \dot{\varphi }-\frac{r_2}{I_y}{\dot{\theta }}^2,\hfill \\ \hfill f_6& =\dot{\varphi }\dot{\theta }\frac{I_x-I_y}{I_z}-\frac{r_3}{I_z}{\dot{\psi }}^2,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill g_1& =\frac{\left(cos\varphi sin\theta cos\psi +sin\varphi sin\psi \right)}{m},\hfill \\ \hfill g_2& =\frac{\left(cos\varphi sin\theta sin\psi -sin\varphi sin\psi \right)}{m},\hfill \\ \hfill g_3& =\frac{cos\varphi cos\theta }{m},\hfill \\ \hfill g_4& =\frac{l}{I_x},\hfill \\ \hfill g_5& =\frac{l}{I_y},\hfill \\ \hfill g_6& =\frac{1}{I_z}.\hfill \end{array}$$

Here, $\mathbf{D}\left(t\right)$ is a system disturbance that includes unknown external disturbances and nonlinear dynamic uncertainties assumed to be bounded. The objective of this study is to build a robust tracking control strategy that guarantees convergence of the output tracking error for quadrotor flight.

Assumption A1. 

$\left|\mathbf{D}\left(t\right)\right|$ is supposed to be bounded by a positive constant considering the issue of parametric uncertainties.

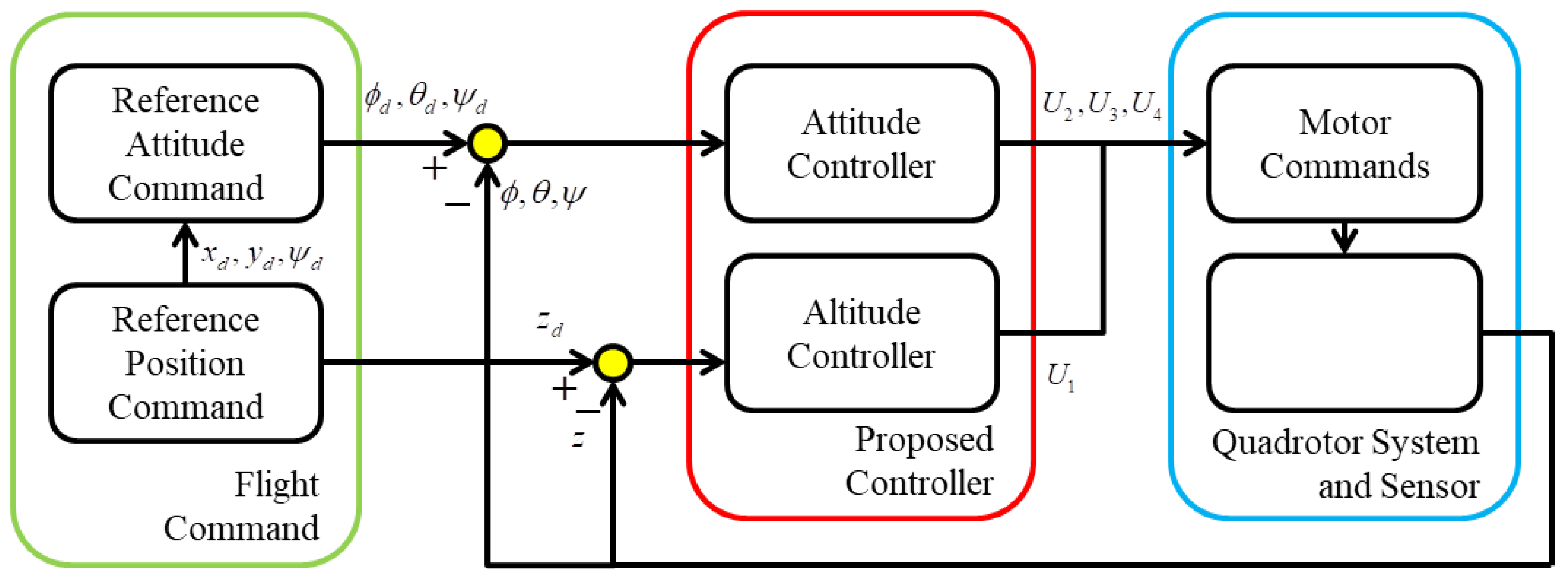
The diagram for the flight control scheme in this study is shown in Figure 2. The flight command generated the reference trajectory and yaw angle for the desired attitude of the quadrotor. The objective of this system was to derive a control law using the proposed method. The designed control inputs were transformed into motor commands for the actuators of the Parrot mini drone. The state of the quadrotor was measured using a mounted sensor on the quadrotor. The system errors for the SMC design are defined as follows:

$$\begin{array}{c}\hfill \mathbf{E}=\mathbf{X}-{\mathbf{X}}_{\mathbf{d}},\end{array}$$

(6)

where ${\mathbf{X}}_{\mathbf{d}}$ denotes the desired state vector. The definition of a sliding surface by positional error is as follows:

$$\begin{array}{c}\hfill \mathbf{S}=\mathbf{CE}+\dot{\mathbf{E}},\end{array}$$

(7)

where

$$\begin{array}{c}\hfill \begin{array}{c}\mathbf{S}={\left[\begin{array}{cccccc}{\sigma }_1& {\sigma }_2& {\sigma }_3& {\sigma }_4& {\sigma }_5& {\sigma }_6\end{array}\right]}^T,\hfill \\ \mathbf{C}=diag\left(c_i\right),\left(c_i>0,i=1,2,\cdots ,6\right)\hfill \end{array}\end{array}$$

is the slope of the sliding surface, which is a positive definite constant matrix. To satisfy the attractiveness condition, the value of this sliding surface converges to zero for the equilibrium of the position control system. The derivative of the sliding surface can be expressed as follows:

$$\begin{array}{c}\hfill \begin{array}{c}\dot{\mathbf{S}}=\mathbf{C}\dot{\mathbf{E}}+\ddot{\mathbf{X}}-{\ddot{\mathbf{X}}}_{\mathbf{d}},\hfill \\ =\mathbf{C}\dot{\mathbf{E}}+\mathbf{F}+\mathbf{GU}+\mathbf{D}-{\ddot{\mathbf{X}}}_{\mathbf{d}}.\hfill \end{array}\end{array}$$

(8)

Without any consideration of disturbance estimation method, the SMC law is obtained as follows [33,34]:

$$\begin{array}{c}\hfill \begin{array}{c}\mathbf{U}={\mathbf{G}}^{-\mathbf{1}}\left(\mathbf{C}\dot{\mathbf{E}}+\mathbf{F}-{\ddot{\mathbf{X}}}_{\mathbf{d}}-\dot{\mathbf{S}}\right),\hfill \\ ={\mathbf{U}}_{\mathbf{eq}}+{\mathbf{U}}_{\mathbf{rl}},\hfill \end{array}\end{array}$$

(9)

where ${\mathbf{U}}_{\mathbf{eq}}$ and ${\mathbf{U}}_{\mathbf{rl}}$ are equivalent controller and reaching law, respectively, and are expressed as follows:

$$\begin{array}{c}\hfill \begin{array}{c}{\mathbf{U}}_{\mathbf{eq}}={\mathbf{G}}^{-\mathbf{1}}\left(\mathbf{C}\dot{\mathbf{E}}+\mathbf{F}-{\ddot{\mathbf{X}}}_{\mathbf{d}}\right),\hfill \\ {\mathbf{U}}_{\mathbf{rl}}=-{\mathbf{G}}^{-\mathbf{1}}\dot{\mathbf{S}}.\hfill \end{array}\end{array}$$

(10)

The reaching law (${\mathbf{U}}_{\mathbf{rl}}$) of CSMC is outlined as follows:

$$\begin{array}{c}\hfill \begin{array}{c}{\mathbf{U}}_{\mathbf{SMC}}=-{\mathbf{G}}^{-\mathbf{1}}\dot{\mathbf{S}},\hfill \\ =-{\mathbf{G}}^{-\mathbf{1}}\mathbf{K}\mathrm{sgn}\left(\mathbf{S}\right),\hfill \end{array}\end{array}$$

(11)

where $\mathbf{K}=diag\left(k_i\right)$, $i=1,2,\cdots 6$, denotes the CSMC control gain with $k_{1,2,\cdots ,6}>0$. $\mathrm{sgn}\left(·\right)$ refers to the sign of a variable and induces a discontinuous chattering effect. To eliminate chattering, many studies have proposed TSTA to design the reaching law of the controller with a continuous input as follows [35,36]:

$$\begin{array}{c}\hfill \begin{array}{c}{\mathbf{U}}_{\mathbf{STA}}=-{\mathbf{G}}^{-\mathbf{1}}\dot{\mathbf{S}},\hfill \\ =-{\mathbf{G}}^{-\mathbf{1}}\left({\mathbf{K}}_{\mathbf{1}}{\left|\mathbf{S}\right|}^{1/2}\mathrm{sgn}\left(\mathbf{S}\right)+{\mathbf{U}}_{\mathbf{disc}}\right),\hfill \\ {\dot{\mathbf{U}}}_{\mathbf{disc}}={\mathbf{K}}_{\mathbf{2}}\mathrm{sgn}\left(\mathbf{S}\right),\hfill \end{array}\end{array}$$

(12)

where

$$\begin{array}{c}\hfill \begin{array}{c}{\mathbf{K}}_{\mathbf{1}}=diag\left(k_{1,i}\right),\left(k_{1,i}>0,i=1,2,\cdots ,6\right),\hfill \\ {\mathbf{K}}_{\mathbf{2}}=diag\left(k_{2,i}\right),\left(k_{2,i}>0,i=1,2,\cdots ,6\right).\hfill \end{array}\end{array}$$

In this study, using the exponential property along with the sliding surfaces, the adaptive method is proposed as follows:

$$\begin{array}{c}\hfill L\left({\sigma }_i\right)=\alpha +(1-\alpha ){\epsilon }^{-{\left|{\sigma }_i\right|}^{\beta }},\end{array}$$

(13)

where $0<\alpha <1$ and $\beta >0$ denote adjustable coefficients of the adaptive law, and $\epsilon$ denotes a natural exponential constant. Therefore, the adaptive law is designed to satisfy $0<L(·)\le 1$. The singular case in which the function closes to zero was solved by setting the minimum value of the function $L\left({\sigma }_i\right)$ considering specification of the actuators.

Figure 3 shows the case in which the adaptive law is applied through a typical control gain $K_{gain}=10$ and a sliding surface $\sigma$. As shown in Figure 3, the relationship between the sliding surface and the adaptive law shows that the adaptive gain has symmetric results based on the absolute value of the sliding surface. The proposed control scheme has a higher gain than the conventional control gain ($K_{gain}=10$) because the absolute value of the sliding surface is larger than 0. Therefore, the initial state quickly converges to a zero error. The results of the adaptive law function values based on $\alpha$ and $\beta$ are represented in Figure 3A and B, respectively. Using Equations (12) and (13), the reaching law ${\mathbf{U}}_{\mathbf{rl}}$ of ASTRL is designed as follows:

$$\begin{array}{c}\hfill \begin{array}{c}{\mathbf{U}}_{\mathbf{rl}}=-{\mathbf{G}}^{-\mathbf{1}}\dot{\mathbf{S}},\hfill \\ =-{\mathbf{G}}^{-\mathbf{1}}\left({\mathbf{K}}_{\mathbf{1}}\mathbf{L}{\left|\mathbf{S}\right|}^{1/\phantom{12}2}\mathrm{sgn}\left(\mathbf{S}\right)+{\mathbf{U}}_{\mathbf{disc}}\right),\hfill \\ {\dot{\mathbf{U}}}_{\mathbf{disc}}={\mathbf{K}}_{\mathbf{2}}\mathbf{L}\mathrm{sgn}\left(\mathbf{S}\right),\hfill \end{array}\end{array}$$

(14)

where

$$\begin{array}{c}\hfill \mathbf{L}=diag\left(L^{-1}\left({\sigma }_i\right)\right),\left(i=1,2,\cdots ,6\right).\end{array}$$

The adaptive law was designed as the denominator of the TSTA control gain. To confirm the performance of the adaptation scheme, the control gain of ASTRL in this study was designed with the same value as the control gain of the TSTA. In this study, using Equations (9) and (14), the proposed SMC law is expressed as follows:

$$\begin{array}{c}\hfill \begin{array}{c}\mathbf{U}={\mathbf{G}}^{-\mathbf{1}}\left(\mathbf{C}\dot{\mathbf{E}}+\mathbf{F}-{\ddot{\mathbf{X}}}_{\mathbf{d}}\right.\hfill \\ \left.-{\mathbf{K}}_{\mathbf{1}}\mathbf{L}{\left|\mathbf{S}\right|}^{1/\phantom{12}2}\mathrm{sgn}\left(\mathbf{S}\right)+{\mathbf{U}}_{\mathbf{disc}}\right),\hfill \\ {\dot{\mathbf{U}}}_{\mathbf{disc}}={\mathbf{K}}_{\mathbf{2}}\mathbf{L}\mathrm{sgn}\left(\mathbf{S}\right).\hfill \end{array}\end{array}$$

(15)

Finally, the under-actuated system of the quadrotor is controlled by the proposed Equation (15).

4. System Stability Analysis and Reaching Time Estimation

In this study, the proposed control method is evaluated using the SLF to ensure the stability of the quadrotor system. As STA has a higher control dimension than CSMC, there is a limit for verifying the stability of the system using WLF, which was used to evaluate SMC. Therefore, STA stability is determined by the ALE in the unperturbed case.

As a conventional methodology, the stability of the SMC and STA strategies is guaranteed using the Lyapunov stability. However, considering the finiteness of the reaching time, the state error of the system must converge within a finite time. Therefore, in this study, we attempted to derive the exact reaching time of the proposed reaching law through a new estimation method for the reaching time of STA [21] with specific gain conditions. The specific gain condition is identified in [21], covering the eigenvalue condition. In addition, the TSTA reaching time has the same process as that of the reaching time comparison. This section proves that ASTRL exhibits a mathematically rapid response compared with TSTA.

Theorem 1. 

If the proposed SMC method provided in Equation (15) with ASTRL of Equation (11) is applied to the dynamic system in Equation (4), the stability of the closed-loop system and tracking error convergence are ensured.

Proof. 

To prove the proposed Equation (15) and Theorem 1, an integrated reaching law form is needed for individual elements of Equation (15). Therefore, the reaching law of ASTA based on STA in references [25,37] is redefined as follows:

$$\begin{array}{c}\hfill \begin{array}{c}{\dot{\sigma }}_{i1}=-\frac{K_1}{L\left({\sigma }_{i1}\right)}{\left|{\sigma }_{i1}\right|}^{\frac{1}{2}}sign\left({\sigma }_{i1}\right)+{\sigma }_{i2},\hfill \\ {\dot{\sigma }}_{i2}=-\frac{K_2}{L\left({\sigma }_{i1}\right)}sign\left({\sigma }_{i1}\right),\hfill \end{array}\end{array}$$

(16)

where ${\sigma }_{i1}=e+c\dot{e}$ is a typical sliding-mode surface, and $K_{1,2}$ is a positive gain to be designed. As the reaching law has two dimensions, the sliding surface can be defined in a quadratic form. Accordingly, the Lyapunov function in [20] can be written in quadratic form as follows:

$$\begin{array}{c}\hfill \mathbf{V}={\xi }^T\mathbf{P}\xi ,\end{array}$$

(17)

where $\mathbf{P}$ represents a symmetric positive definite matrix, and $\xi$ represents a Lyapunov vector in this study and can be expressed through a quadratic relationship in ASTRL. This vector can be expressed mathematically using Equation (16) as follows:

$$\begin{array}{c}\hfill {\xi }^T=\left[\begin{array}{cc}{\xi }_1& {\xi }_2\end{array}\right]=\left[\begin{array}{cc}{\left|{\sigma }_{i1}\right|}^{1/2}sign\left({\sigma }_{i1}\right)& {\sigma }_{i2}\end{array}\right].\end{array}$$

(18)

Differentiation of the Lyapunov vector is required for system stability determination and time estimation. Considering Equations (16) and (18), the relation between the reaching law and Lyapunov vector can be represented as follows [38]:

$$\begin{array}{c}\hfill \dot{\xi }=\frac{1}{\left|{\xi }_1\right|}\mathbf{A}\xi ,\end{array}$$

(19)

where

$$\begin{array}{c}\hfill \mathbf{A}=\left[\begin{array}{cc}-\frac{K_1}{2L\left({\sigma }_{i1}\right)}& \frac{1}{2}\\ -\frac{K{}_2}{L\left({\sigma }_{i1}\right)}& 0\end{array}\right].\end{array}$$

The $\mathbf{A}$ matrix is a Hurwitz matrix, because its determinant is greater than zero. The final solution of ALE is derived by differentiating the second-order Lyapunov function through the $\mathbf{A}$ and $\mathbf{P}$ matrices as follows:

$$\begin{array}{c}\hfill {\mathbf{A}}^T\mathbf{P}+\mathbf{AP}=-\mathbf{Q}.\end{array}$$

(20)

According to the final solution of Equation (20), ALE is satisfied when $\mathbf{Q}$ is a symmetric positive definite matrix. To determine the stability of the system, Equation (17) can be expressed as follows:

$$\begin{array}{c}\hfill {\lambda }_{min}\left\{\mathbf{P}\right\}{∥\xi ∥}_2^2\le {\xi }^T\mathbf{P}\xi \le {\lambda }_{max}\left\{\mathbf{P}\right\}{∥\xi ∥}_2^2,\end{array}$$

(21)

where ${\lambda }_{min}\left\{·\right\}$ and ${\lambda }_{max}\left\{·\right\}$ denote the minimum and maximum eigenvalues, respectively. Considering the left term, Equation (22) can be derived as ${∥\xi ∥}_2^2={\xi }_1^2+{\xi }_2^2=\left|{\sigma }_{i1}\right|+{\sigma }_{i2}^2$.

$$\begin{array}{c}\hfill \left|{\xi }_1\right|\le {∥\xi ∥}_2\le {\lambda }_{min}^{-1/2}\left\{\mathbf{P}\right\}{\mathbf{V}}^{1/2}.\end{array}$$

(22)

To prove the stability of the system using the ALE, the relationship between the Lyapunov vector and $\mathbf{Q}$ is expressed as follows:

$$\begin{array}{c}\hfill {\lambda }_{min}\left\{\mathbf{Q}\right\}{∥\xi ∥}_2^2\le {\xi }^T\mathbf{Q}\xi \le {\lambda }_{max}\left\{\mathbf{Q}\right\}{∥\xi ∥}_2^2.\end{array}$$

(23)

Considering the term on the left in Equation (23), $-{\left|{\xi }_1\right|}^{-1/2}{\xi }^T\mathbf{Q}\xi \le -{\left|{\xi }_1\right|}^{-1/2}{\lambda }_{min}$$\left\{\mathbf{Q}\right\}{∥\xi ∥}_2^2$. Therefore, by multiplying the right side of Equation (21) by $-{\left|{\xi }_1\right|}^{-1/2}{\lambda }_{min}\left\{\mathbf{Q}\right\}$ on both sides, the following expression can be obtained:

$$\begin{array}{c}\hfill -{\left|{\xi }_1\right|}^{-1/2}{\lambda }_{min}\left\{\mathbf{Q}\right\}{∥\xi ∥}_2^2\le -{\left|{\xi }_1\right|}^{-1/2}{\lambda }_{min}\left\{\mathbf{Q}\right\}·{\lambda }_{max}^{-1}\left\{\mathbf{P}\right\}·\mathbf{V}.\end{array}$$

(24)

According to Equation (22), Equation (25) is as follows:

$$\begin{array}{c}\hfill -{\left|{\xi }_1\right|}^{-1/2}\le -{\lambda }_{min}^{1/2}\left\{\mathbf{P}\right\}{\mathbf{V}}^{-1/2}.\end{array}$$

(25)

Using Equations (24) and (25), we obtain the following:

$$\begin{array}{c}\hfill -{\left|{\xi }_1\right|}^{-1/2}{\xi }^T\mathbf{Q}\xi \le -{\left|{\xi }_1\right|}^{-1/2}{\lambda }_{min}\left\{\mathbf{Q}\right\}{∥\xi ∥}_2^2\\ \hfill \le -\frac{{\lambda }_{min}^{1/2}\left\{\mathbf{P}\right\}{\lambda }_{min}\left\{\mathbf{Q}\right\}}{{\lambda }_{max}^{}\left\{\mathbf{P}\right\}}{\mathbf{V}}^{1/2}.\end{array}$$

(26)

With the result of Equation (26), the derivative of Lyapunov function is expressed as follows:

$$\begin{array}{cc}\hfill \dot{\mathbf{V}}& =-{\left|{\xi }_1\right|}^{-1/2}{\xi }^T\mathbf{Q}\xi \le -\gamma \left(\mathbf{Q}\right){\mathbf{V}}^{1/2},\hfill \\ \hfill \gamma \left(\mathbf{Q}\right)& =\frac{{\lambda }_{min}^{1/2}\left\{\mathbf{P}\right\}{\lambda }_{min}\left\{\mathbf{Q}\right\}}{{\lambda }_{max}^{}\left\{\mathbf{P}\right\}}.\hfill \end{array}$$

(27)

According to Equation (27), because $\gamma \left(\mathbf{Q}\right)$ is positive, SLF is satisfied with tracking error convergence within a finite reaching time derived as follows [12]:

$$\begin{array}{c}\hfill T_c=\frac{2}{\gamma \left(\mathbf{Q}\right)}{\mathbf{V}}^{1/2}.\end{array}$$

(28)

However, the conventionally derived reaching time in Equation (28) is not suitable for comparing the accurate reaching time of TSTA with the proposed method because $\gamma \left(\mathbf{Q}\right)$ is determined by an arbitrary symmetric positive definite matrix $\mathbf{P}$. Therefore, a novel estimation method is proposed to demonstrate that the reaching time of ASTRL is shorter than that of TSTA. □

Assumption A2. 

TSTA and ASTRL expressed in Equations (12) and (14) are considered to be unperturbed cases with the gain condition $k_1^2\ge 8k_2$ [21]. The sliding surface becomes ${\sigma }_{i1}=0$ when the state error of the system converges to zero within a finite time.

Theorem 2. 

ASTRL expressed in Equation (15) has a rapid response due to the fast estimated reaching time compared to TSTA in Equation (12).

Proof. 

As the dimension of the STA control input increases, the differential value of a typical sliding surface ${\sigma }_{i1}$ includes perturbations. However, in this study, the finiteness of the reaching time, that is, ${\sigma }_{i1}=0$, is demonstrated under the specific gain condition and the assumption that there is no perturbation. The following equation is presented as a solution for a continuous function $\xi \left(t\right)$ satisfying Equation (19) [21]:

$$\begin{array}{c}\hfill \xi \left(t\right)={\epsilon }^{\mathbf{A}\eta \left(t\right)}\xi \left(0\right).\end{array}$$

(29)

In this equation, $\epsilon$ means the Euler’s constant, the function $\eta \left(t\right)$ denotes the to-be-determined function, and $\eta \left(0\right)$ is 0 because of the initial condition $\xi \left(0\right)=0$ when $t=0$. The derivative of the function $\eta \left(t\right)$ is obtained by substituting Equation (29) into (19) as follows:

$$\begin{array}{c}\hfill \dot{\eta }\left(t\right)=\frac{1}{\left|{\xi }_1\right|}=\frac{1}{\left|{\mathbf{e}}_{\mathbf{1}}^T{\epsilon }^{\mathbf{A}\eta }\xi \left(0\right)\right|}.\end{array}$$

(30)

In this equation, ${\mathbf{e}}_{\mathbf{1}}$ refers to ${\mathbf{e}}_{\mathbf{1}}={\left[10\right]}^T$. By multiplying $dt$ and integrating both sides of Equation (30), the relation can be obtained as follows:

$$\begin{array}{c}\hfill {\int }_0^{\eta \left(t\right)}\left|{\mathrm{e}}_1^T{\epsilon }^{\mathbf{A}\tau }\xi \left(0\right)\right|d\tau =t.\end{array}$$

(31)

Considering that $\xi \left(t\right)$ converges to zero as the system is stable, the function $\eta \left(t\right)$ should diverge to infinity. The following equation is supposed to be guaranteed:

$$\begin{array}{c}\hfill \underset{t\to T}{lim}\eta \left(t\right)=\infty ,\end{array}$$

(32)

where T denotes the reaching time. By applying Equation (32) to both sides of Equation (31), an expression for the reaching time can be obtained. Therefore, an explicit infinite solution for ASTRL without perturbation is expressed as follows:

$$\begin{array}{c}\hfill T={\int }_0^{\infty }\left|{\mathrm{e}}_1^T{\epsilon }^{\mathbf{A}\eta }\xi \left(0\right)\right|d\eta .\end{array}$$

(33)

For comparison with TSTA, the reaching time of TSTA is also obtained as follows:

$$\begin{array}{c}\hfill T_{TSTA}={\int }_0^{\infty }\left|{\mathrm{e}}_1^T{\epsilon }^{\tilde{\mathbf{A}}\eta }\xi \left(0\right)\right|d\eta .\end{array}$$

(34)

Here, $T_{TSTA}$ is the reaching time of TSTA.

$$\begin{array}{c}\hfill \tilde{\mathbf{A}}=\left[\begin{array}{cc}-\frac{{\mathit{K}}_1}{2}& \frac{1}{2}\\ -{\mathit{K}}_2& 0\end{array}\right].\end{array}$$

Equations (33) and (34) can be calculated as follows, respectively [21]:

$$\begin{array}{c}\hfill \begin{array}{c}T=\frac{L\left({\sigma }_{i1}\right)}{K_2}\left|{\xi }_2\left({\sigma }_{i1}\right)-2{\xi }_1\left({\sigma }_{i1}\right)\right|,\hfill \\ T_{TSTA}=\frac{1}{K_2}\left|{\xi }_2\left({\sigma }_{i1}\right)-2{\xi }_1\left({\sigma }_{i1}\right)\right|.\hfill \end{array}\end{array}$$

(35)

Finally, because $0<L\left({\sigma }_{i1}\right)\le 1,$ and $L\left({\sigma }_{i1}\right)/\phantom{L\left({\sigma }_{i1}\right)K_1}{K}_1\le 1/\phantom{1K_1}{K}_1$, $T\le T_{TSTA}$ has become clear. Thus, it is mathematically proven that the reaching time of ASTRL is smaller than that of TSTA. □

5. Simulation and Experiment

In this study, simulations and experiments were conducted using MATLAB and Simulink for the quadrotor drone flight. The solver of the simulation was chosen as ODE3, and a fixed step size was defined as 0.01 s. All experiments were performed for three simulations. The first scenario (Simulation I) was an x-axis fixed-roll angle step response experiment. First, assuming that the axis was fixed, the attitude-control flight stability of the drone was tested. The response between the roll angle and reference angle was confirmed through the first simulation. The second scenario (Simulation II) was a comparison of the 3D trajectory tracking performance using Simulink. We used the Parrot Mambo platform as the Simulink application, which is a support package for Parrot mini drones.

Considering the sensor noise and wind disturbance, the simulation was verified using a virtual machine for a realistic environment. The platform comprises tools for realizing a drone in a 3D environment before the hardware is actuated. In this experiment, the position, attitude, and control input response of the virtual Parrot drone were confirmed using a predefined reference trajectory. The third scenario (Experiment I) was developed using a Parrot Mambo mini drone. The hovering performance of the proposed controller was evaluated by directly checking the flight log.

Table 1. Parameters for drone modeling [39].

Specification	Parameter	Value	Unit
Quadrotor mass	m	$0.0630$	$\mathrm{kg}$
Gravity acceleration	g	$9.8066$	$\mathrm{m}/{\mathrm{s}}^2$
Lateral moment arm	l	$0.0624$	$\mathrm{m}$
Rolling moment of inertia	$Ix$	0.0583 $\times {10}^{-3}$	$\mathrm{kg}·{\mathrm{m}}^2$
Pitching moment of inertia	$Iy$	$0.0717\times {10}^{-3}$	$\mathrm{kg}·{\mathrm{m}}^2$
Yawing moment of inertia	$Iz$	$0.1000\times {10}^{-3}$	$\mathrm{kg}·{\mathrm{m}}^2$
Air resistance	$r_{1,2,3,4,5,6}$	$0.0100$	$\mathrm{Ns}/\mathrm{m}$
Thrust coefficient	${\rho }_1$	$0.0107$	${\mathrm{Ns}}^2$
Drag coefficient	${\rho }_2$	$0.7826\times {10}^{-3}$	$\mathrm{N}·{\mathrm{ms}}^2$
Rotor moment of inertia	$Jr$	$0.1021\times {10}^{-6}$	$\mathrm{kg}·{\mathrm{m}}^2$

presents the parameters for the Parrot drone modeling for the overall simulation [39].

Simulation I was conducted to stabilize the attitude of the drone. The proposed controller was compared with the CSMC and TSTA strategies based on the roll angle response of the drone by commanding a reference angle. As the quadrotor drone is an under-actuated system, its state has a complex effect on the other states. To confirm the monotonic performance of the proposed controller, only the roll response of the quadrotor was checked after fixing its position in the x-direction.

Table 2. Control parameters for Simulation I.

Parameter	Value
$c_4$	5
$k_4$	60
$k_{1,4}$	30
$k_{2,4}$	30
$\alpha$	0.5
$\beta$	0.9

lists the control parameters for Simulation I. The gain of each controller was tuned to achieve optimal performance, and the slope of the sliding surface was set to the same value for each controller to confirm the accuracy of the performance. In the case of TSTA and ASTRL, the control gains were set to the same values, but only ASTRL had more control parameters for the adaptive law.

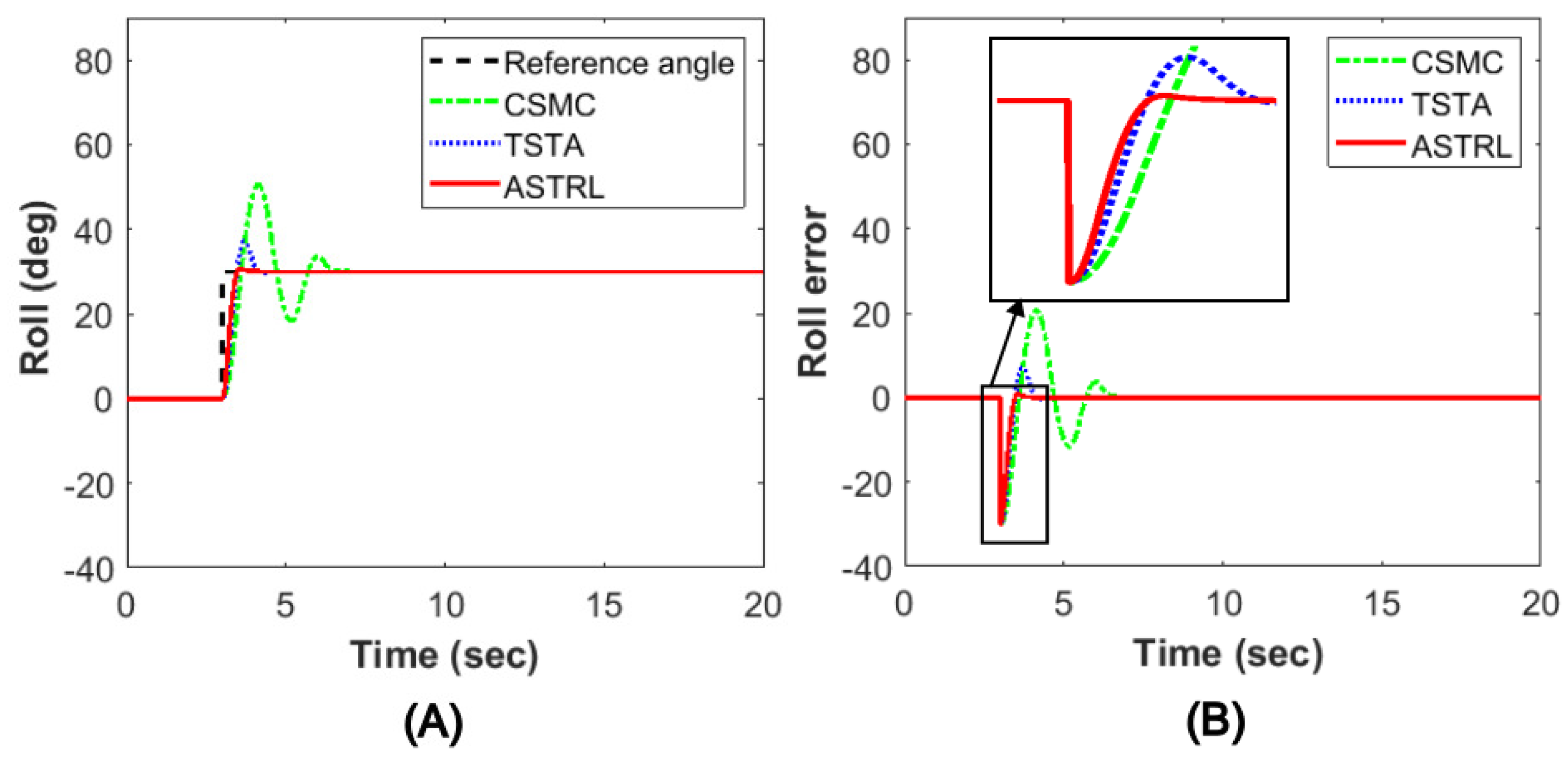
Figure 4 shows the roll angle response of the quadrotor in Simulation I. The simulation was conducted for 20 s. In Figure 4A, the roll response of the fixed quadrotor is shown, and the reference angle is the dashed black line, which consists of a step signal set to 30${}^{\circ }$ in 4 s. The initial roll state of the fixed quadrotor was set to 0${}^{\circ }$. The green dashed-dotted line is the response by CSMC, the blue dotted line is the response by TSTA, and red solid line is the response by ASTRL. Figure 4B shows the roll error corresponding to Figure 4A. According to Figure 4B, ASTRL overcomes the error the fastest, and the roll error converges to 0. The exact arrival times, overshoots, and settling times of the controllers are listed in

Table 3. Controller performance for Simulation I.

Strategy	Arrival Time	Overshoot	Settling Time
SMC	3.60 s	50.57 (deg)	7.05 s
STA	3.47 s	37.17 (deg)	5.11 s
ASTA	3.47 s	30.82 (deg)	4.41 s

. In the case of arrival time, STA and ASTA have similar performances; however, the proposed controller has the best performance when considering overshoot and settling time.

Figure 5 shows the control input and sliding plane actions of the controllers according to Figure 4. In Figure 5A, the chattering band of CSMC input occurs after CSMC settling time of 7.05 s. On the other hand, TSTA and ASTRL have continuous control inputs even after their respective settling times. Figure 5B shows the operating characteristics of each controller in the sliding plane. The black dashed line represents the sliding surface, and the slope was set to five. To reach the equilibrium point, the initial state of all the controllers reached the origin in a clockwise direction. As shown in Figure 5B, the proposed controller arrived at the origin with the shortest trajectory in the sliding plane.

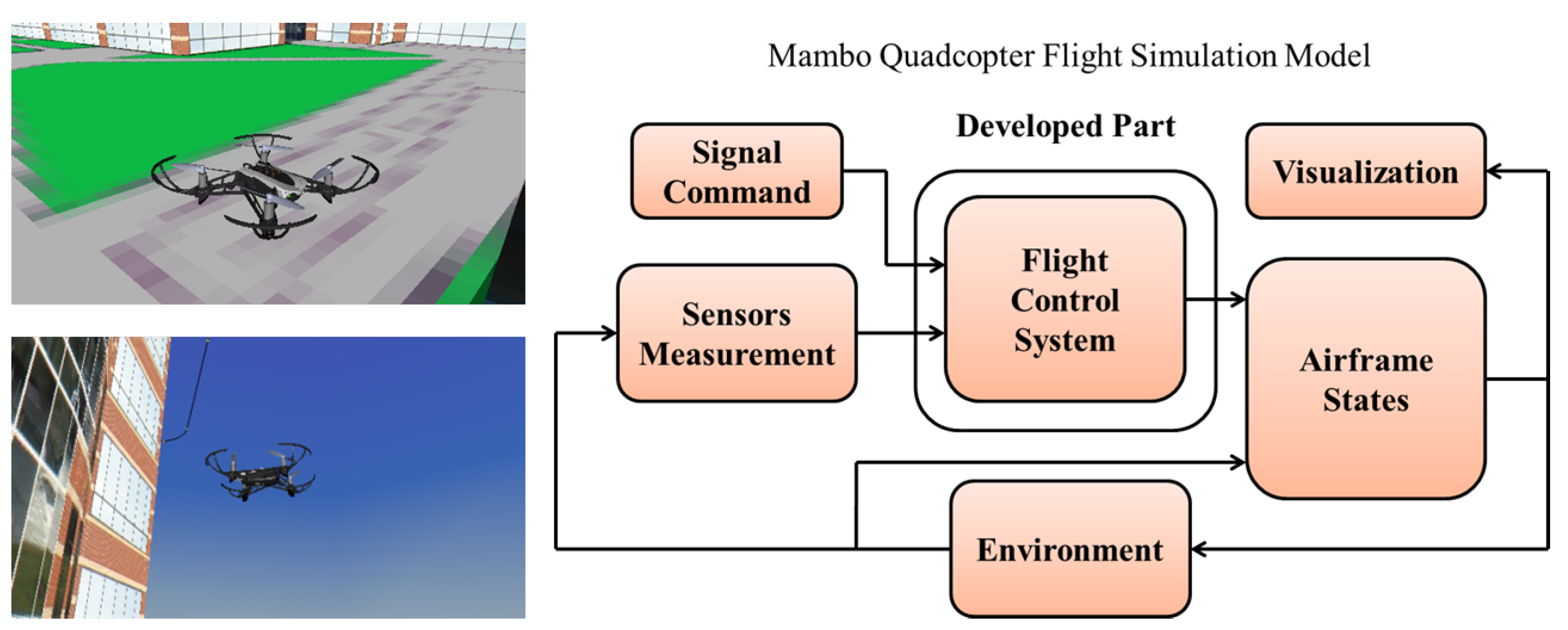
Simulation II was designed to control the flight path of the quadrotor drone. In this simulation, the Simulink support package for Parrot mini drones, which is an application of Simulink provided by Parrot, was used to construct a realistic environment. This application provides firmware built for the virtual hardware controller. Based on the data output from a realistic environment, the drone was 3D visualized in Simulink. The drone flew following the reference trajectory for 100 s in this environment.

Figure 6 shows the 3D visualization results and simulation scheme that represents the quadrotor drone of the Parrot Mambo mini drone under experimental conditions. In a 3D environment, a flat ground surface was implemented for the ground assertion flag, sensor noise, and wind disturbance. Figure 6 shows the preparation of the quadrotor with all propellers pointing up on the flat ground surface before the takeoff. Figure 6 also shows the quadrotor flight following the reference trajectory. The proposed simulation model consists of a flight command, flight control system, measurement sensor, environment, and airframe of the quadrotor model. In this study, we developed a flight control system and designed the proposed controller by replacing the existing the flight control system represented in Figure 6 with CSMC, TSTA, and ASTARL for comparative study.

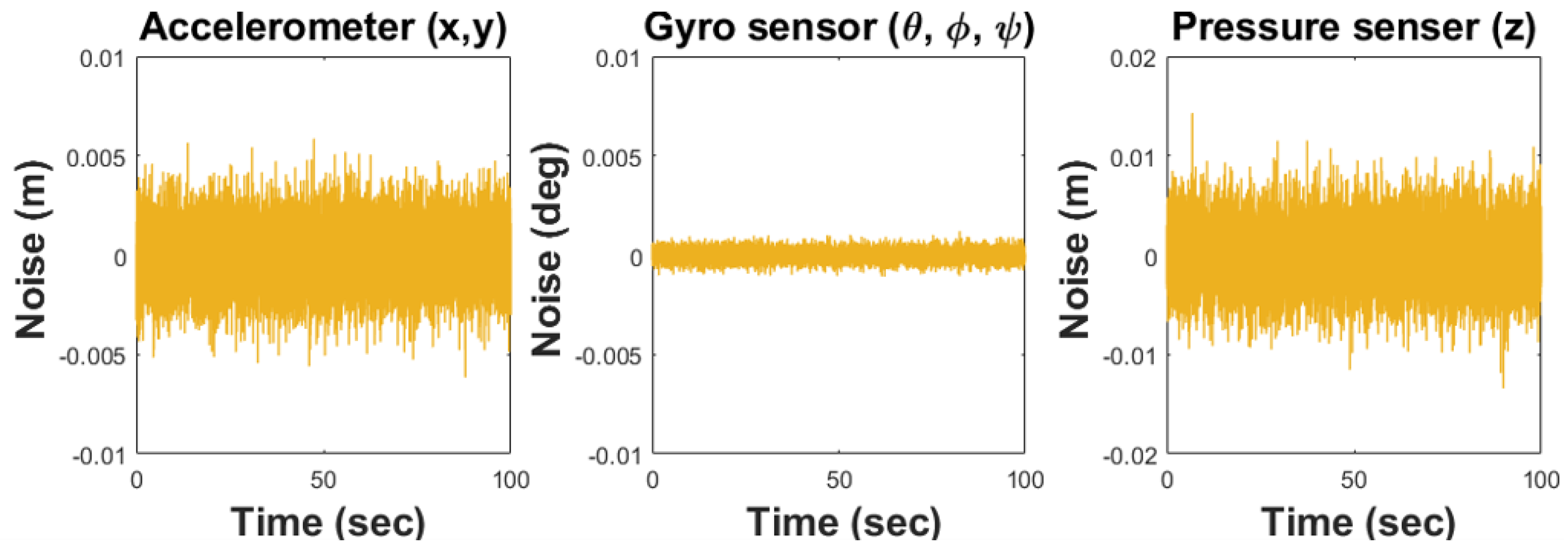
As shown in Figure 7 and Figure 8, the sensor noise and wind disturbance of Simulation II were implemented as white Gaussian noise. In the case of sensor noise, the noise from the accelerometer, gyro, and pressure sensors was implemented, and the noise was added to the data corresponding to x, y, $\varphi$, $\theta$, $\psi$, and z, respectively. 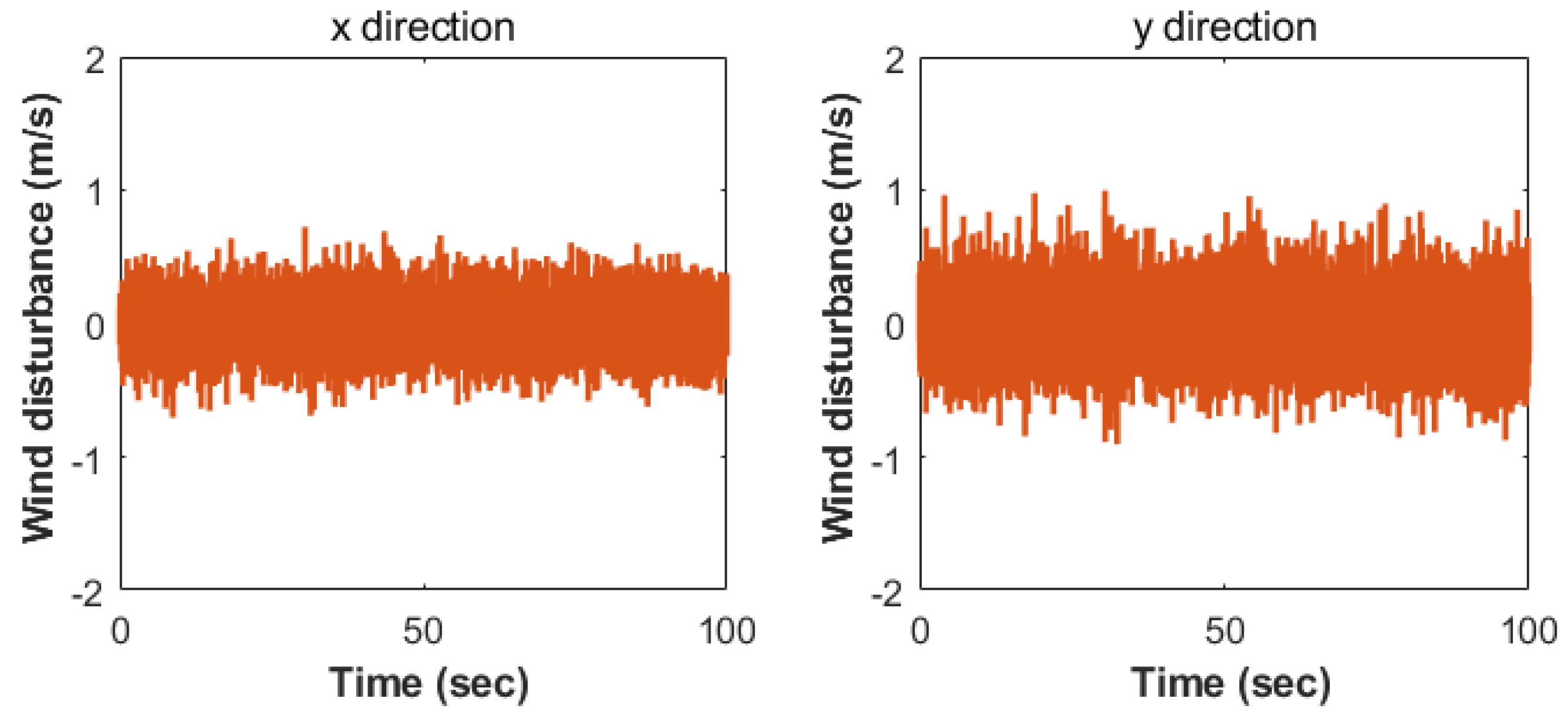These sensor noises can cause model uncertainty and parametric errors, and they can affect the drone system modeling by the disturbance term in Equation (4). For wind disturbance, the wind speed was set to within approximately ±0.5 m/s, and the disturbance in the y-direction was set a little stronger, that is, ±0.8 m/s.

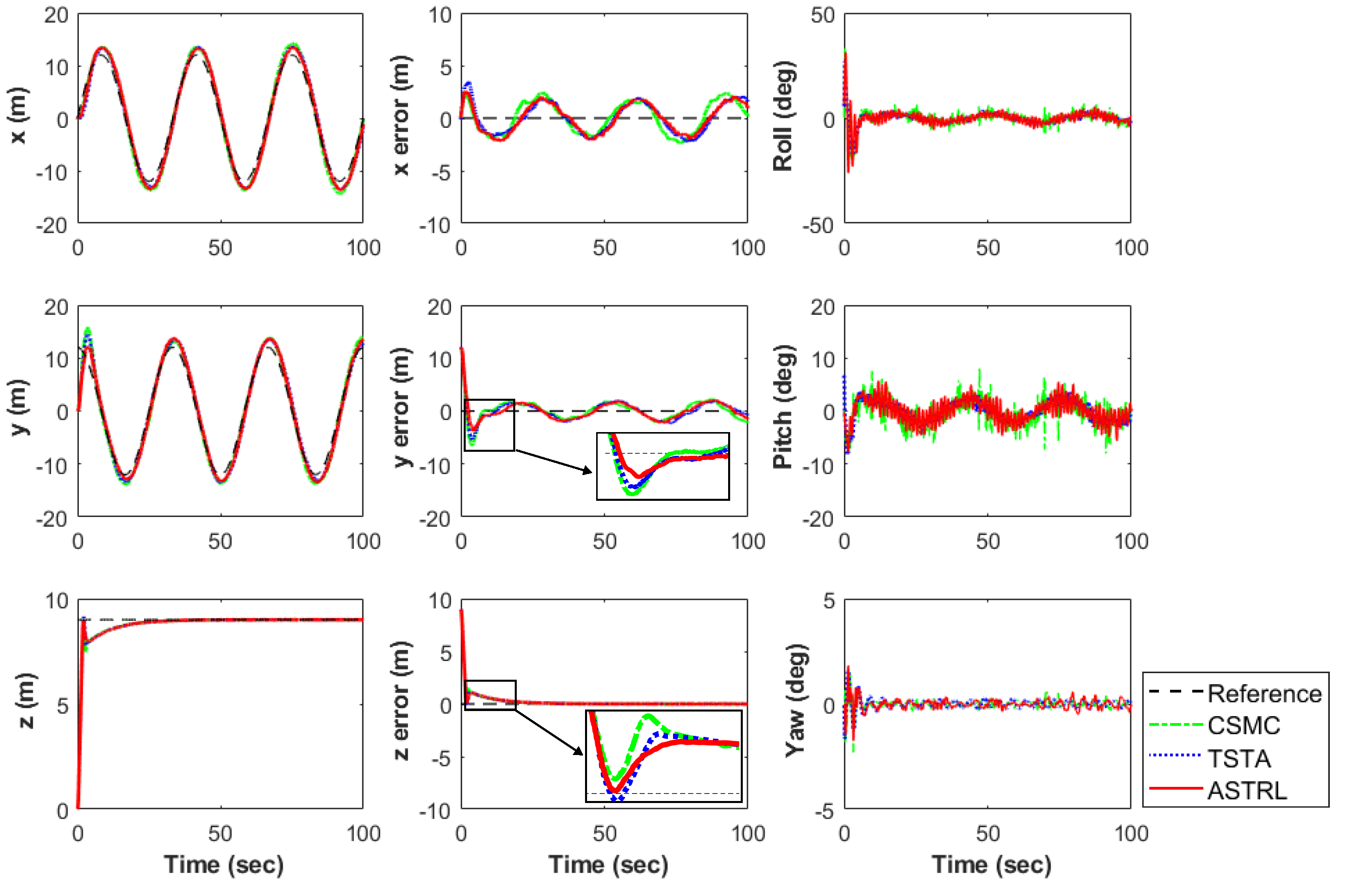
Figure 9 shows the position and attitude-control performance of the proposed controller based on the reference trajectory. To compare the proposed strategies, the controllers compared in Simulation I for the roll angle step response (CSMC and TSTA) were implemented identically in Simulation II for trajectory tracking. Starting at the initial position $\left(x_0,y_0,z_0\right)=\left(0,0,0\right)$, the quadrotor implemented with the proposed controller followed a trajectory based on the reference Equation (36) for 100 s:

$$\begin{array}{c}\hfill \begin{array}{c}{x}_d=12·sin\left(0.06·\pi t\right),\hfill \\ y_d=12·cos\left(0.06·\pi t\right),\hfill \\ z_d=9,\hfill \\ {\psi }_d=0.\hfill \end{array}\end{array}$$

(36)

We used the control parameter for Simulation II represented in

Table 4. Control parameters for Simulation II.

Specification	Parameter	Value
Slope of sliding surface	$c_{1,2,\cdots ,6}$	2.5
CSMC gain	K = $diag\left(k_i\right)$	$diag$ (0.50, 0.50, 0.50, 0.01, 0.01, 0.01)
ASTRL and TSTA gain 1	${\mathbf{K}}_1=diag\left(k_{1,i}\right)$	$diag$ (1.00, 1.00, 1.00, 0.02, 0.02, 0.02)
ASTRL and TSTA gain 2	${\mathbf{K}}_2=diag\left(k_{2,i}\right)$	$diag$ (0.01, 0.01, 0.01, 0.03, 0.03, 0.03)
ASTRL parameter 1	$\alpha$	0.9
ASTRL parameter 2	$\beta$	0.4

. The plots in the first column of Figure 9 correspond to the position response, the second column represents the position response error, and the third column represents the attitude response. In all the cases of position response, the proposed controller shows the best performance, overcoming the entire disturbances represented in Figure 7 and Figure 8. For tracking errors based on the x- and y-position response, ASTRL converges to zero error the fastest. In the case of the z-position response, to move the quadrotor to the reference position, the tracking error in the z-direction decreases as the propeller is directed to the initial reference trajectory. However, when the target z-value is reached, the quadrotor is supposed to change the direction of the propeller to be in the opposite direction. Due to this operation, the z-position response has a single shudder. In the error based on the z-position response, the proposed controller handles the wave most stably, as shown in Figure 9. In the attitude response, under the same sensor noise and wind disturbance environment that induce model uncertainty, parametric error, and physical obstruction, TSTA and ASTRL effectively outperformed the CSMC. According to the third column of Figure 9, TSTA and ASTRL are less affected than CSMC in roll and pitch responses to entire disturbances.

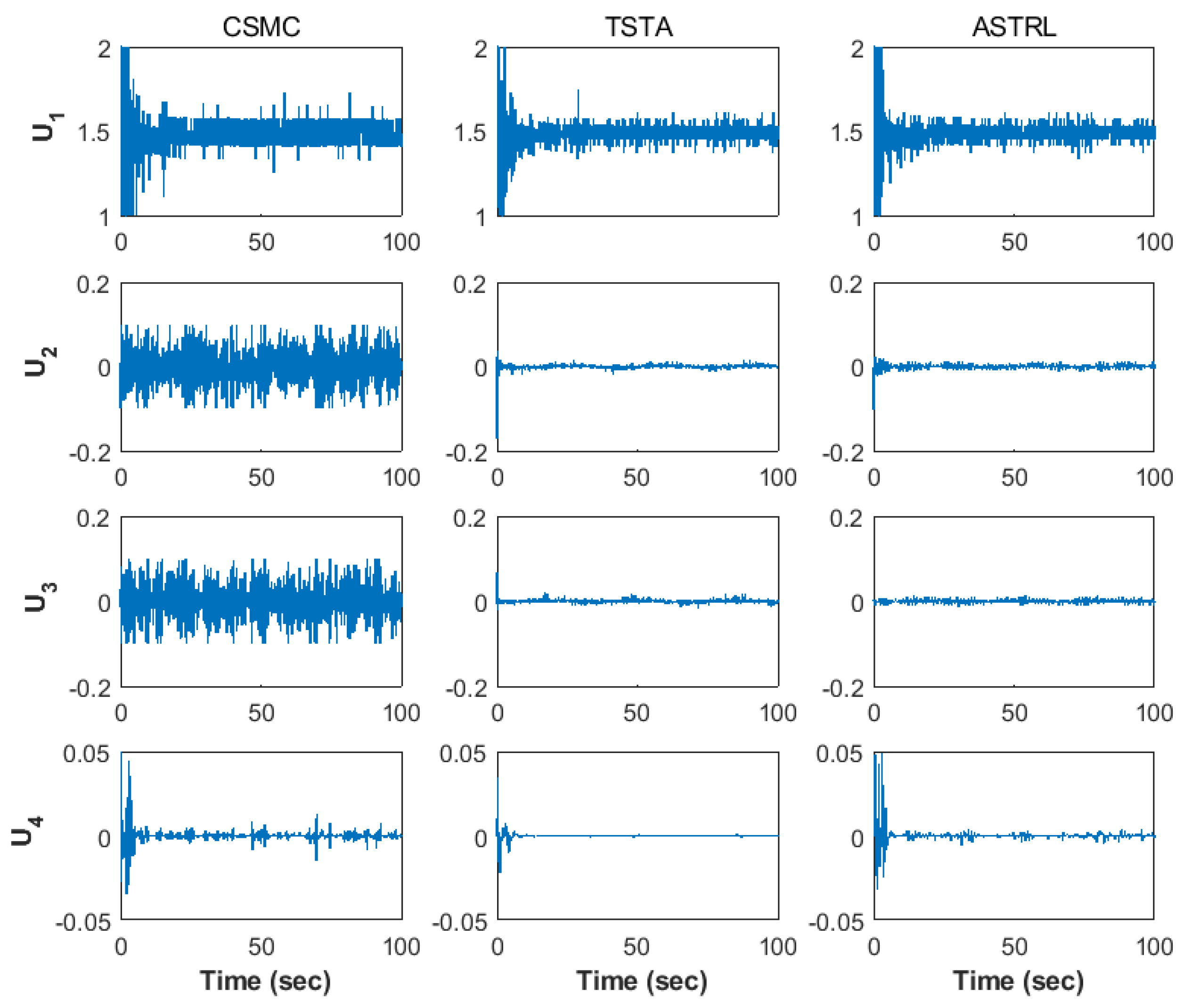
Figure 10 shows the control inputs of the compared controllers. Each row represents the control input of the quadrotor to its respective controller. Compared to Simulation I, the reference angle for quadrotor flight was calculated in radians; therefore, the control inputs in Figure 10 were induced to be smaller than the result values in Figure 5. Considering stable hovering and reasonable actuator operation, $U_1$ was limited to be within $\left(1,2\right)$, $U_2$ and $U_3$ were limited to be within $\left(-0.2,0.2\right)$, and $U_4$ was limited to be within $\left(-0.05,0.05\right)$. In all control inputs, TSTA and ASTRL significantly reduced the chattering effect that occurred in the control inputs of CSMC. Continuous control inputs of TSTA and ASTRL overcome chattering caused by discontinuous control inputs of CSMC. As ASTRL has better performance in position and attitude of the quadrotor, ASTRL has a dynamic control input compared to TSTA by adaptive law, overcoming the chattering effect.

Experiment I was conducted using the Parrot Mambo mini drone platform, MATLAB, and Simulink. As the quadrotor drone endured single designated waypoint, a response with six degrees of freedom was observed. The proposed controller ASTRL strategy was updated to quadrotor firmware using the Simulink support package for the Parrot mini drone application. In this application, the firmware built into Simulink was updated to the quadrotor through the CRS 4.0 dongle Bluetooth module without a remote controller. The 3D visualization was configured by receiving the flight data of the quadrotor in real time from Simulink via Bluetooth communication. This support package was designed with additional controls for takeoff and landing.

Figure 11 shows the experimental scheme for the Parrot Mambo platform. Figure 11A,B show the experimental scheme and the experimental environment, respectively. The Parrot Mambo mini drone platform was equipped with an acceleration sensor, gyro sensor, and ultrasonic sensor, and the position and attitude were measured using these sensors. The accelerometer and gyro sensor were built into the vehicle, and an ultrasonic sensor was installed at the bottom of the vehicle to face the ground. After the firmware was updated, the quadrotor received flight commands through the developed Simulink and maneuvers. As shown in Figure 11B, this experiment used wind gusts to overcome the external flight impediments. The numerical value of wind disturbance corresponded to a wind speed of 3–5 m/s in the positive x- and y-direction and was implemented using a fan. The experiment was conducted for 25 s for each controller.

Table 5. Control parameter for Experiment I.

Specification	Parameter	Value
Slope of sliding surface	$c_{1,2,\cdots ,6}$	1
CSMC gain	K = $diag\left(k_i\right)$	$diag$(10, 10, 10, 0.3, 0.3, 0.001)
ASTRL and TSTA gain 1	${\mathbf{K}}_1=diag\left(k_{1,i}\right)$	$diag$(15, 15, 15, 0.4, 0.4, 0.01)
ASTRL and TSTA gain 2	${\mathbf{K}}_2=diag\left(k_{2,i}\right)$	$diag$(0.5, 0.5, 0.5, 0.0001, 0.0001, 0.0001)
ASTRL parameter 1	$\alpha$	0.5
ASTRL parameter 2	$\beta$	0.3

and Figure 12 show the control parameters for Experiment I, 3D visualization, and the $x-y$ plane for the experimental results. The specifications of all lines illustrated in the figure are the same as those in Simulation II. As shown in Figure 12A, the experiment moved from the initial point to the objective point with wind disturbance and continued hovering. As shown in Figure 12, the proposed controller in the same experimental environment shows the closest position response to the objective point.

Figure 13 shows the results of Figure 12 with respect to time. The reference line represents the objective point in continuous time. ASTRL is closest to the reference line compared with CSMC and TSTA in the x- and y-direction responses. In the z-direction response, CSMC has an inevitable steady-state error, but TSTA and ASTRL reduce the z-position error over time. In the attitude response, ASTRL shows a flight attitude that allows the quadrotor to pursue stable flight compared with CSMC and TSTA. The results of the platform experiment indicate that the proposed controller is effective. The following link represents the real-time Experiment I for comparison of the respective controller: https://youtu.be/vNh4nQqz8Fs (accessed on 1 August 2023).

6. Conclusions

In this study, to improve the performance of quadrotor drone control through CSMC, TSTA was used to effectively reduce the chattering effect, which is a critical disadvantage of the SMC. For the control of the under-actuated quadrotor drone, the six-degrees-of-freedom challenge was addressed using four actuators by introducing additional target degrees of freedom. To improve TSTA, ASTRL was introduced by proposing an exponential function based adaptive law for a rapid response and flight stability. To apply this technique, the stability of the proposed controller was strictly verified through SLF and ALE. The superiority of ASTRL was mathematically verified through a novel reaching time estimation. Simulation results and platform experiments support the demonstration of ASTRL outperformance, which induces more stable maneuvering of drone. In the future, a better performance can be achieved with stable flight in the application of cutting-edge technology fields, such as object detection technology using drones, load-bearing flight, and adaptation technology to respond to strong disturbances such as natural wind.