Adaptive Collision Avoidance for Multiple UAVs in Urban Environments
Abstract
1. Introduction
1.1. Related Prior Work
- (1)
- Heuristic optimization methods
- (2)
- Optimal control theory methods
- (3)
- Artificial intelligence methods
1.2. Our Contributions
- (1)
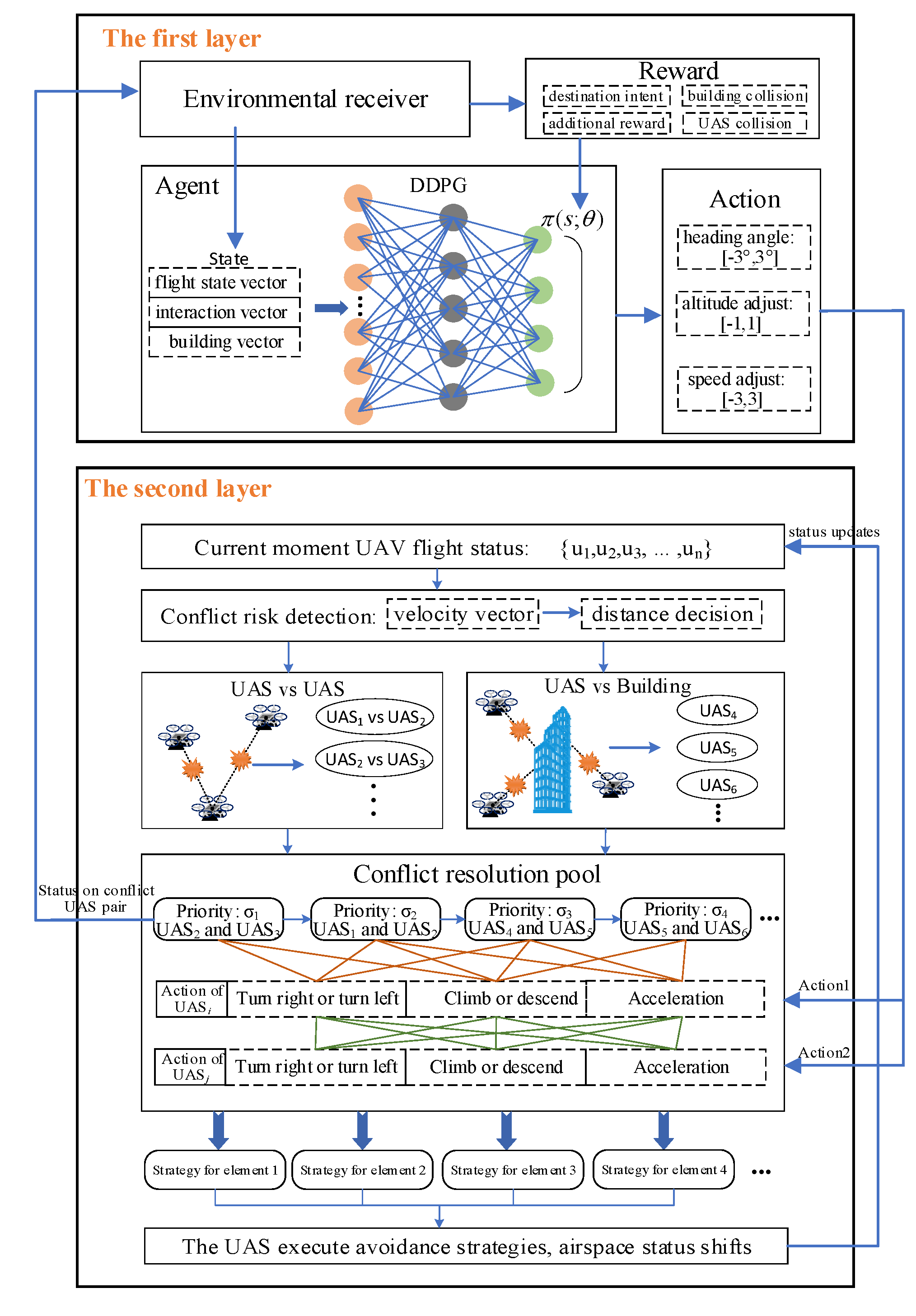
- In this paper, an adaptive decision-making framework for mUAV collision avoidance is proposed. The adaptive framework enables UAVs to autonomously determine the avoidance action to be taken in 3D space, providing the UAVs with more options for extrication strategies when faced with static or dynamic obstacles. This framework combines the conflict resolution pool in order to transform mUAV conflicts into UAV pairs for avoidance, controlling the computational complexity at the polynomial level, thereby providing a new idea for mUAV collision avoidance.
- (2)
- A DRL model for UAV pairs is designed based on a continuous action space and state space, reflecting the maneuverability of UAVs and avoiding wastage of urban airspace resources. The model endows each UAV with decision-making ability, and utilizes a fixed sector format to explore conflicting obstacles, thus simplifying the state of the agent and making it more adaptable to dense urban building environments.
- (3)
- The DDPG algorithm is introduced to train the agent, and its convergence speed is enhanced by proposing the mechanism of destination area dynamic adjustment.
2. Problem Formulation
2.1. First Layer: DRL-Based Method for Collision Avoidance between UAVs in a UAV Pair
2.1.1. Continuous State Space
- (1)
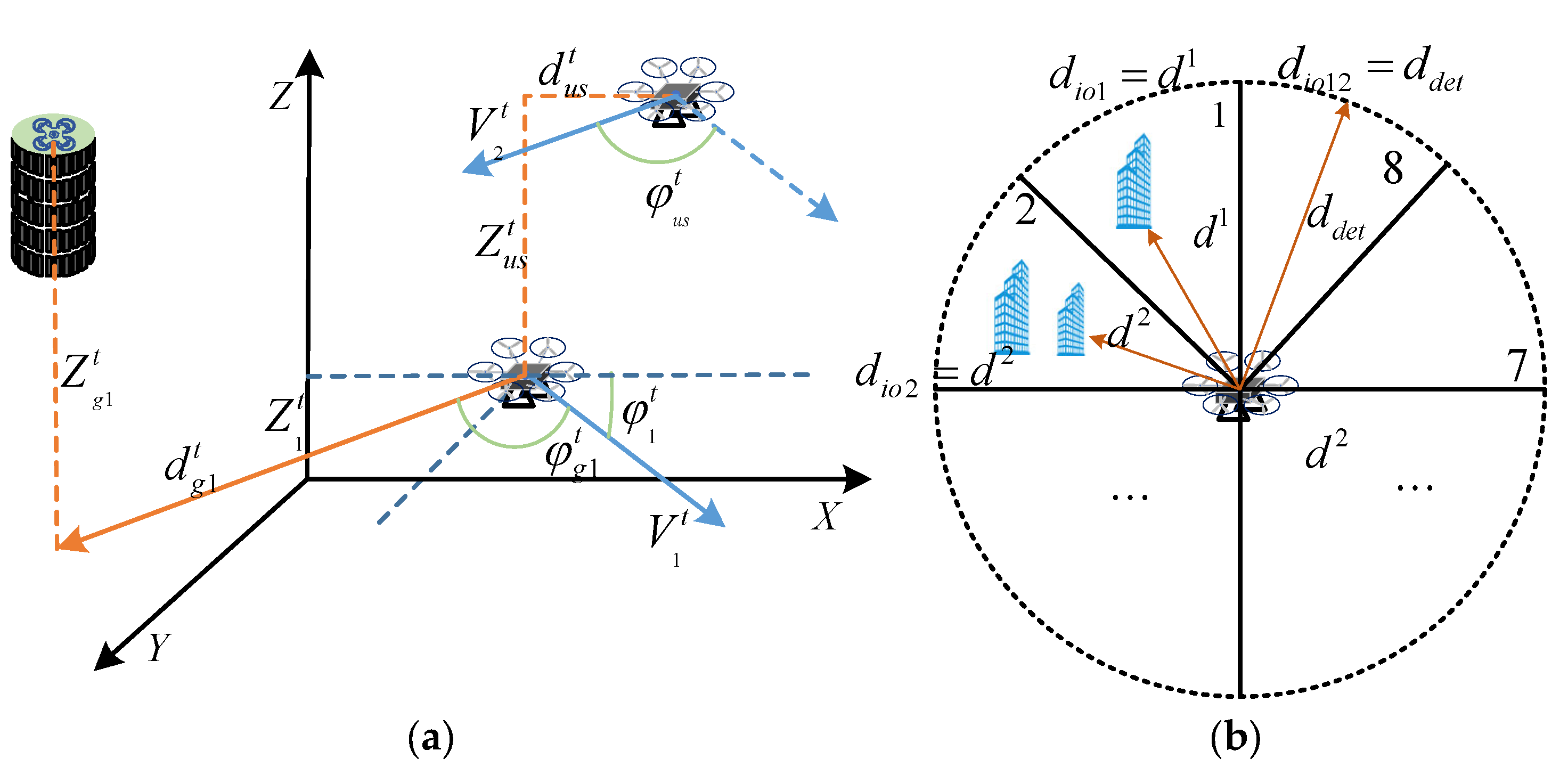
- The flight state vector of the UAV, including six attributes (φ: heading angle; V: horizontal speed; Z: the altitude of UAV; φg: relative heading angle of the destination to UAV; dg: the horizontal distance of the destination to UAV), as shown in Figure 2. These attributes are able to accurately reflect the current flight status of the UAV, and the agent guides the UAV to its destination based on the flight status vector.
- (2)
- Interaction vectors between UAV pairs (φus: the difference in heading angle; Zus: the difference in altitude; dus: the horizontal distance between two UAVs). These attributes reflect the position and heading relationships between the UAVs in a UAV pair, and the agent avoids collision between UAVs in a UAV pair based on the interaction vectors.
- (3)
- Building vectors. There are lots of buildings in the urban airspace, and if all building information is put into the agent, this will result in high state vector dimensionality and affect the speed of convergence. In this paper, considering the detection range of the UAV in the horizontal direction, a flight sector is used to map obstacles affecting flight into a fixed-length vector, and these are regarded as the obstacle vectors, as shown in Figure 2.
2.1.2. Continuous Action Space
2.1.3. Reward Function Design
- (1)
- Destination intent reward: when there are no obstacles in the sector of the UAV pair, the destination intent reward is used to ensure that the UAV takes the shortest path to the destination. The entire movement of the UAV is divided into multiple “intensive” actions, and the reward function is set for them to ensure that each action of the UAV affects the final reward value, thus contributing to the improvement of the overall strategy, as shown in Equation (6):
- (2)
- Building collision avoidance reward: when there are obstacles in the sector of the UAV pair, it is necessary to ensure that the UAVs avoid colliding with buildings while flying to their destinations; therefore, we need to balance the two tasks, and the reward function at this time is shown in Equation (7).
- (3)
- UAV collision avoidance reward: the UAV collision avoidance reward is used to avoid collisions between the UAV and other UAVs. A UAV alert area is set up, and UAV collision avoidance is made the main task when there are other UAVs within the alert area, as shown in Equation (8).where is the direction vector of the velocity of the UAV at moment t.
- (4)
- Additional reward: There are four final states of the UAV: reaching the destination, flying out of the control area, colliding with obstacles, and colliding with other drones. This additional reward is used to provide a relatively large reward or penalty value when the UAV reaches its final state, which can be used to guide the UAV to its destination and avoid bad events such as collisions or loss of control, as shown in Equation (9).
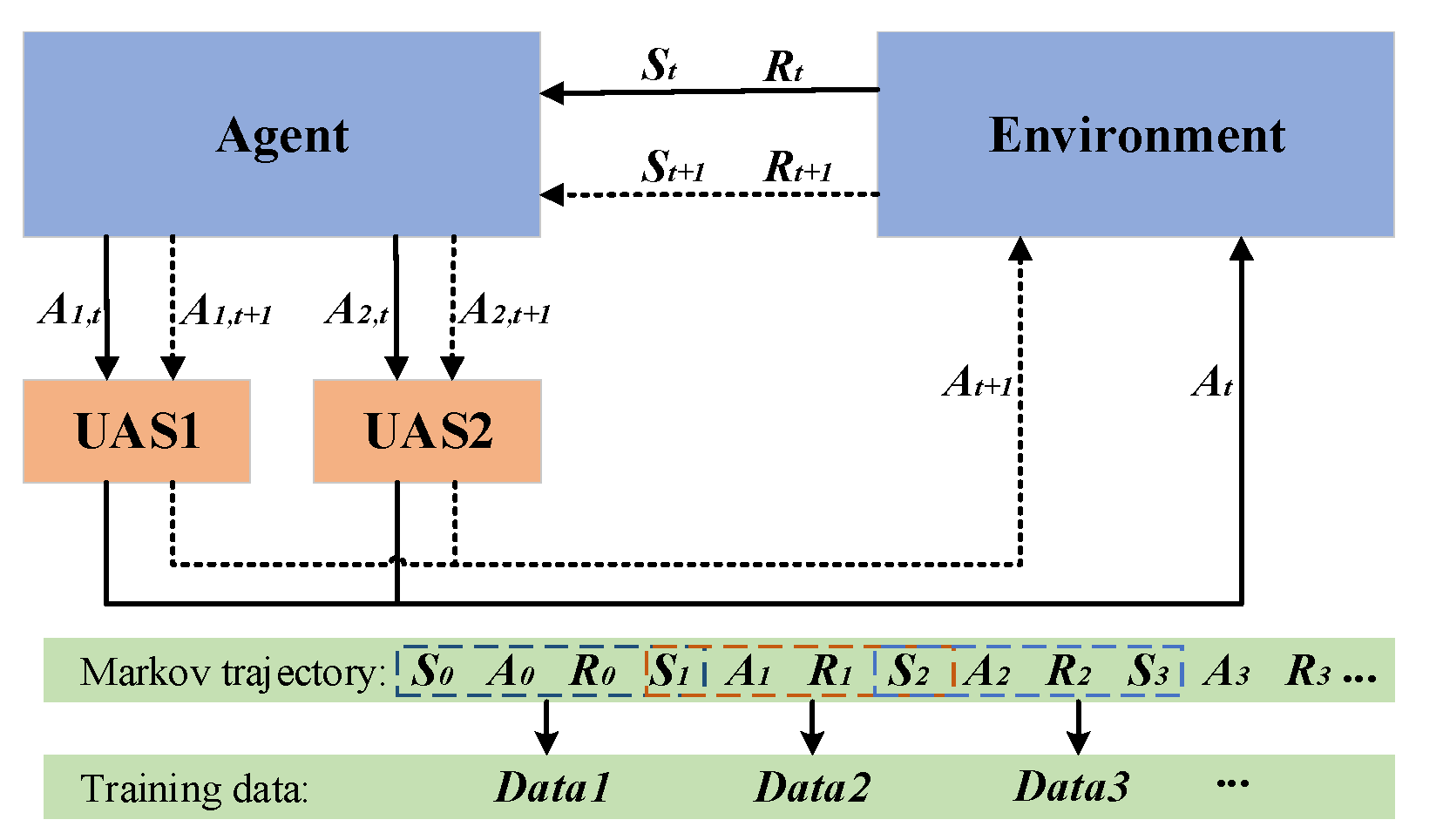
2.1.4. The Interaction between the Agent and the Environment
2.2. Second Layer: Collaborative Collision Avoidance for mUAVs
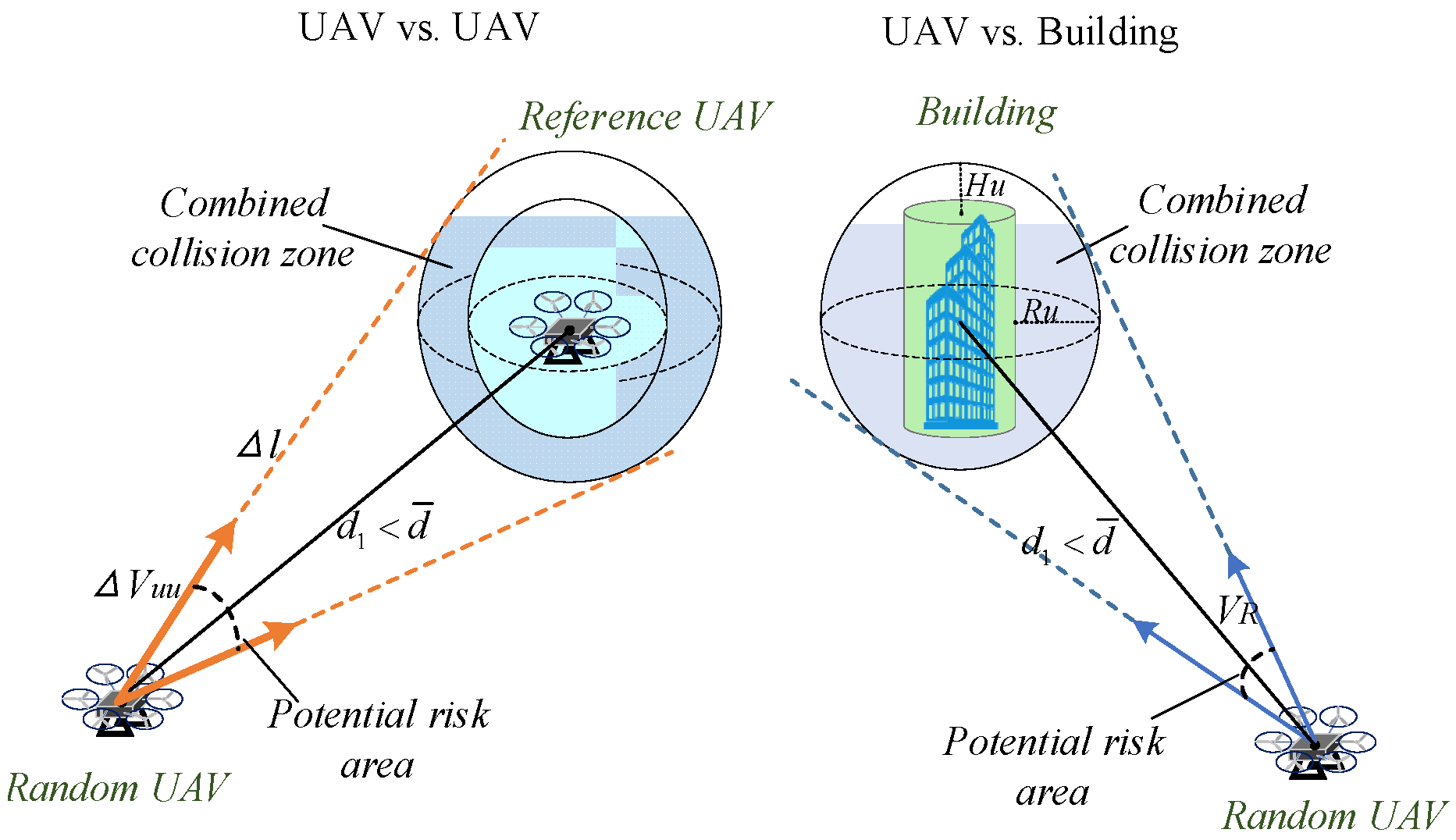
2.2.1. Three-Dimensional Conflict Detection
2.2.2. Conflict Resolution Pool
2.2.3. Collaborative Resolution Process for mUAVs
3. Improved Algorithm for Agent Training
3.1. Deep Deterministic Policy Gradient
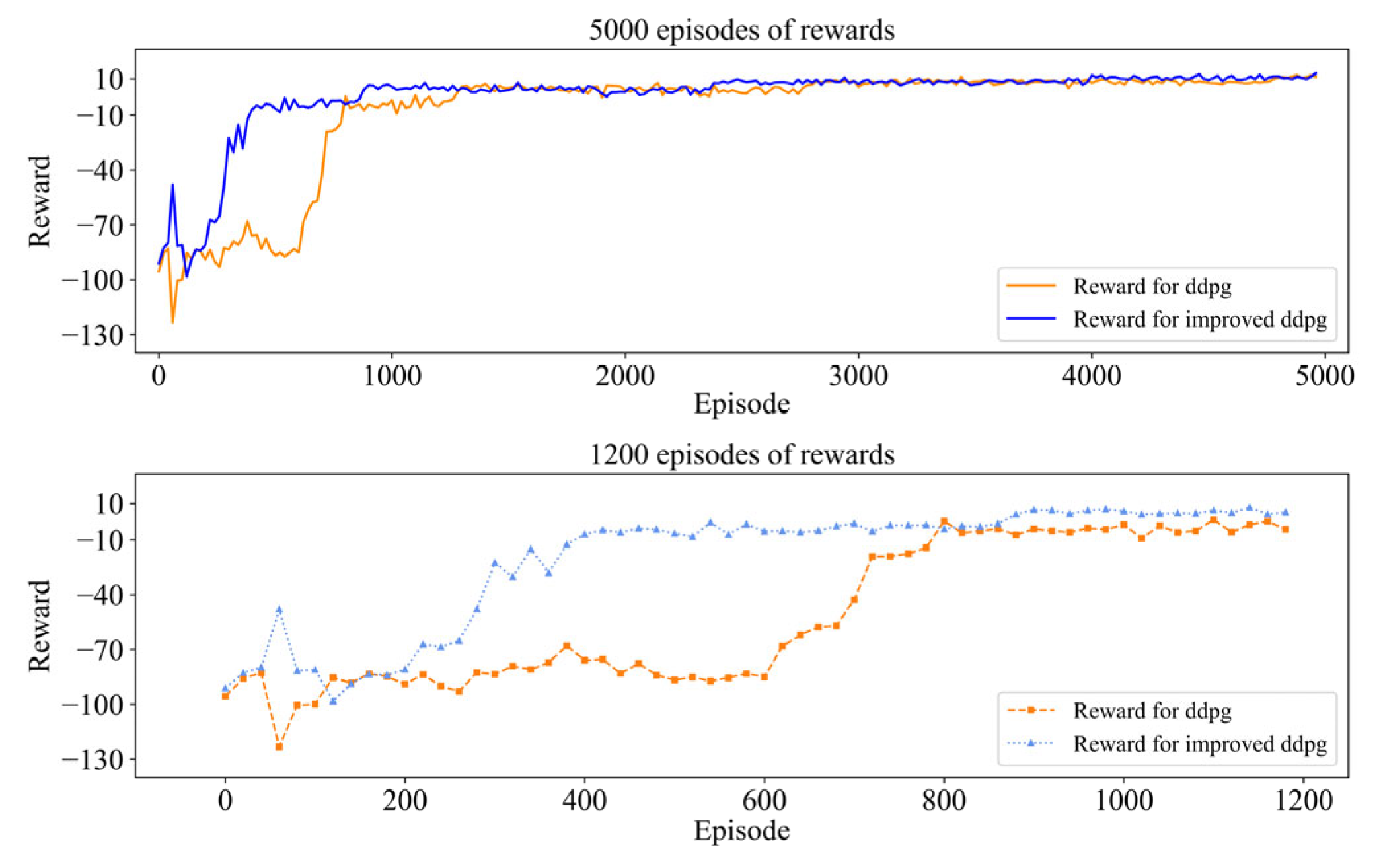
3.2. An Improved Measure for DDPG
4. Results and Discussion
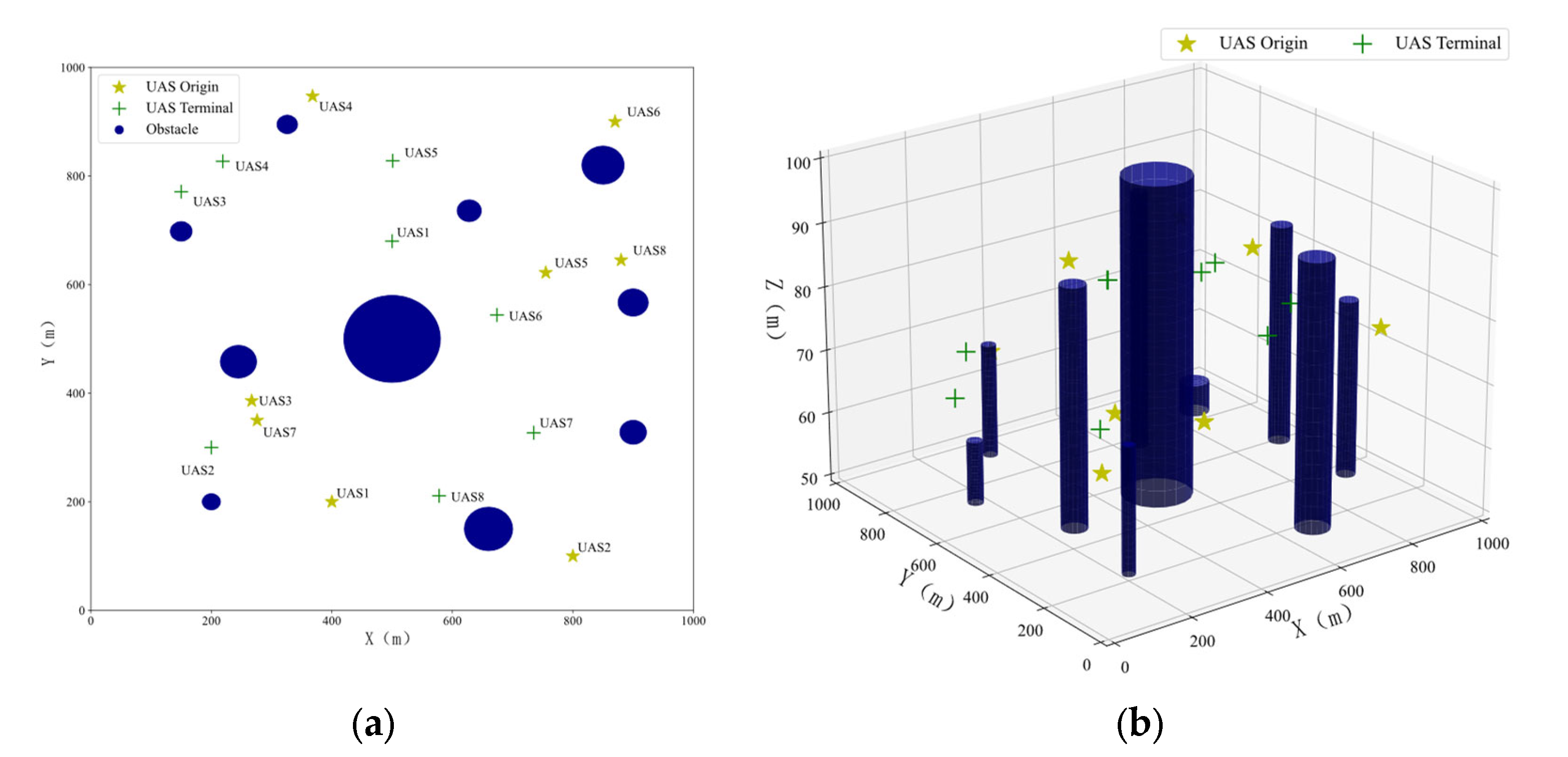
4.1. Environment Setting and Hyperparameters
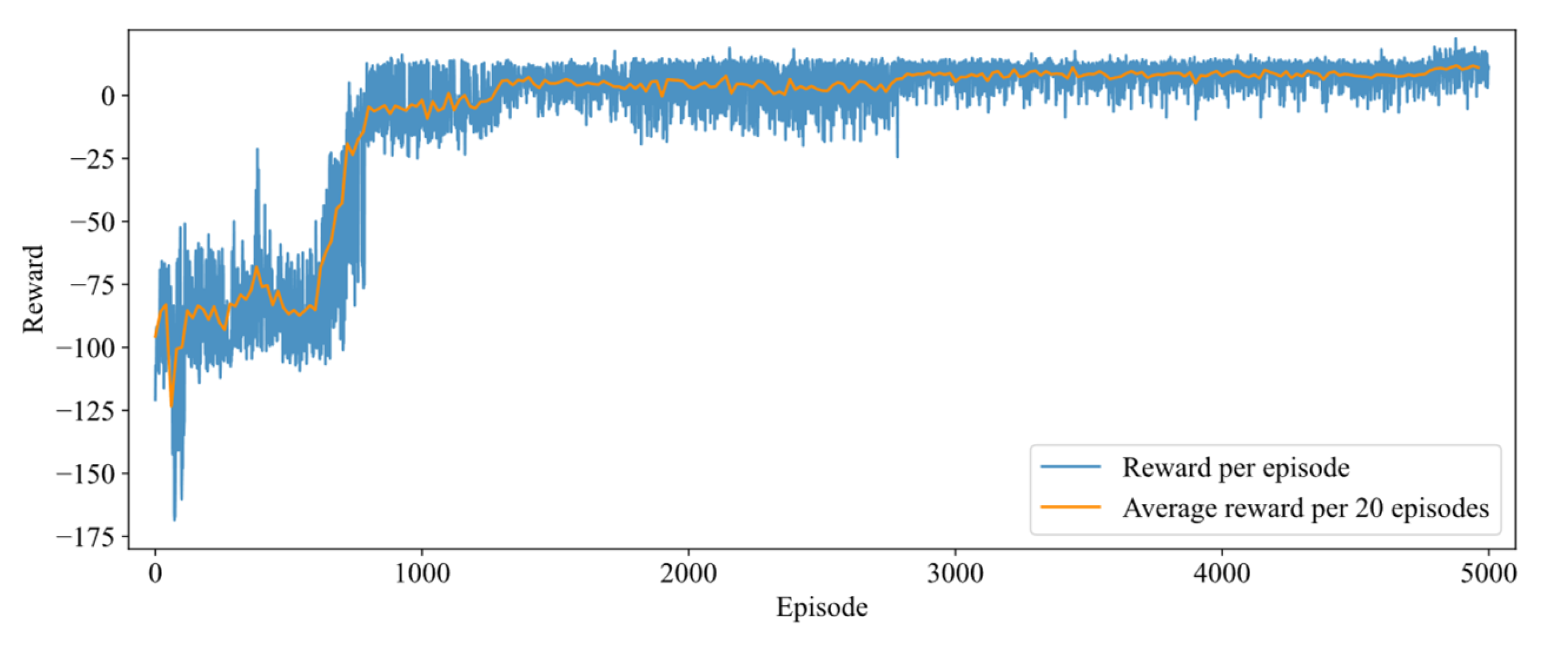
4.2. Collision Avoidance Agent Training
4.3. Numerical Results Analysis
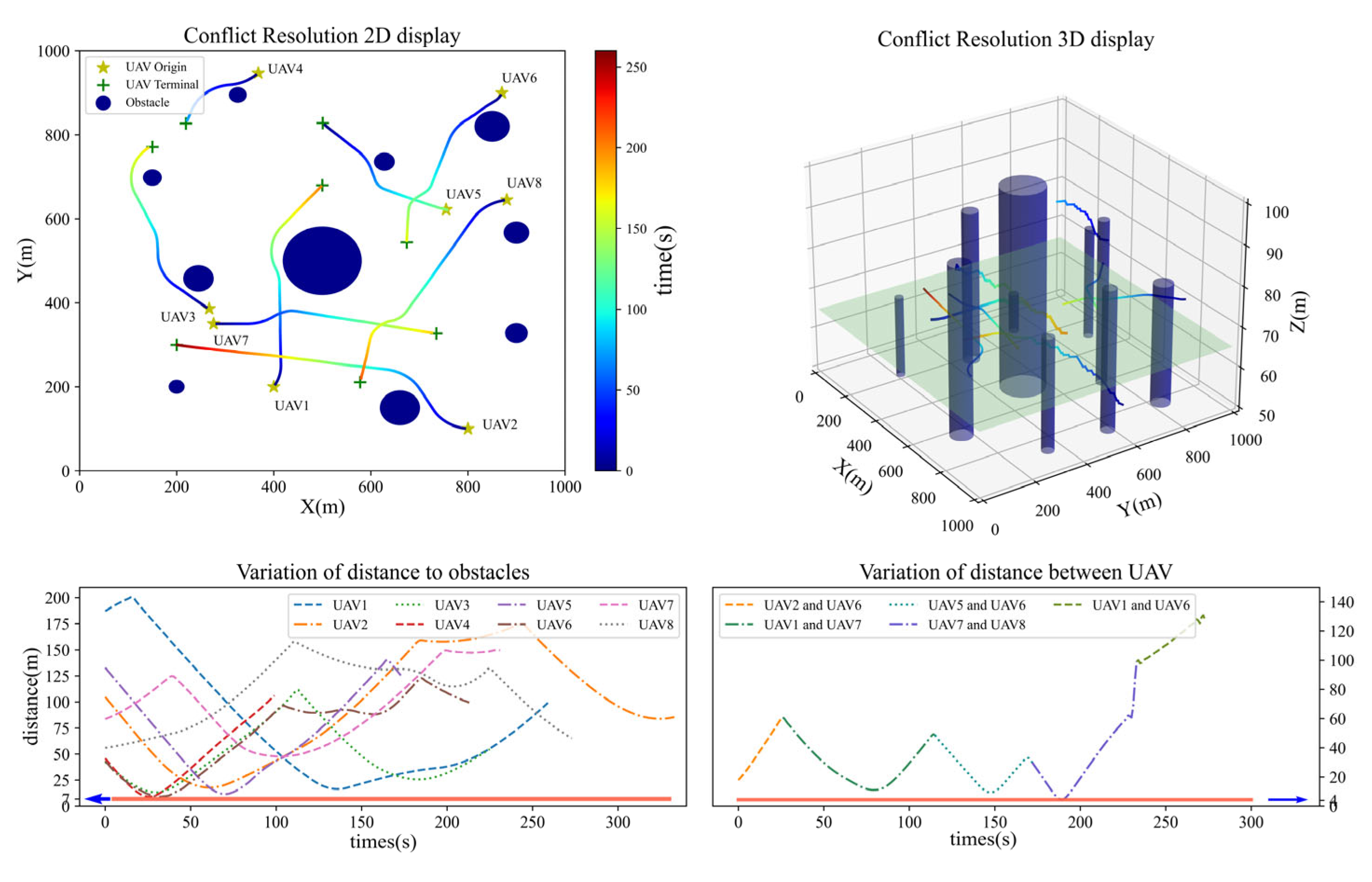
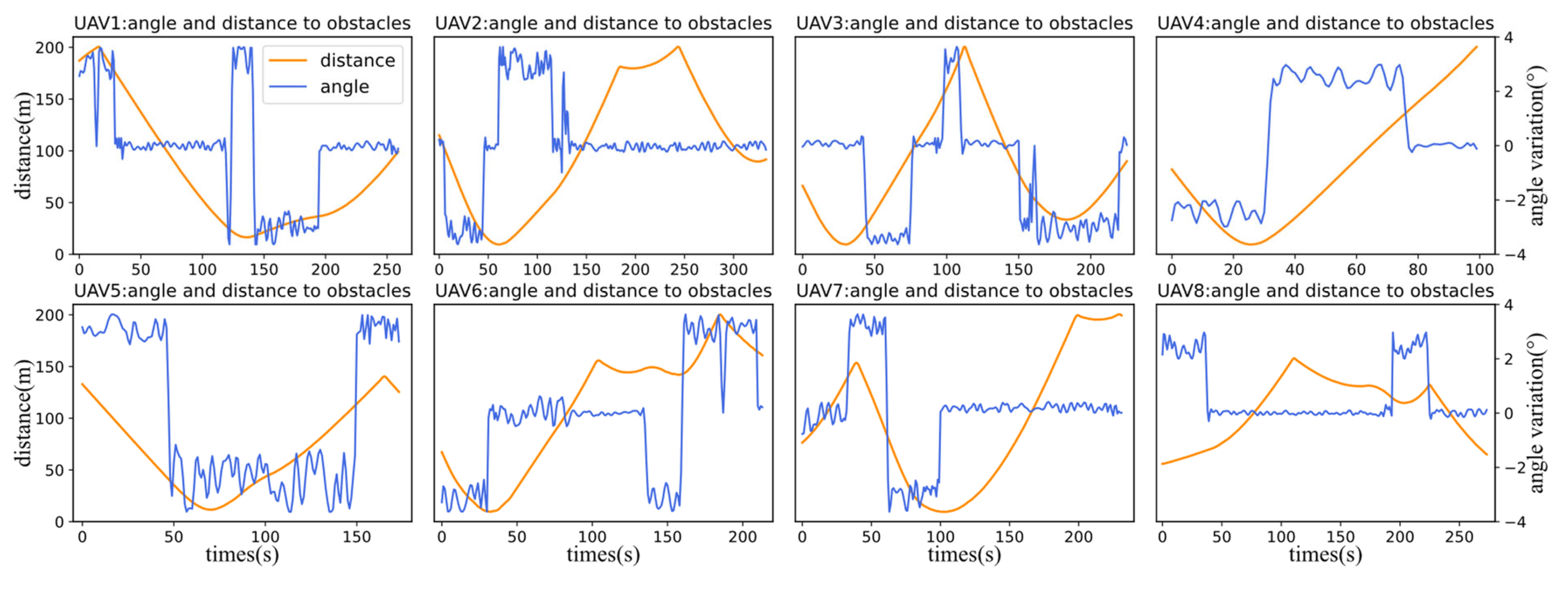
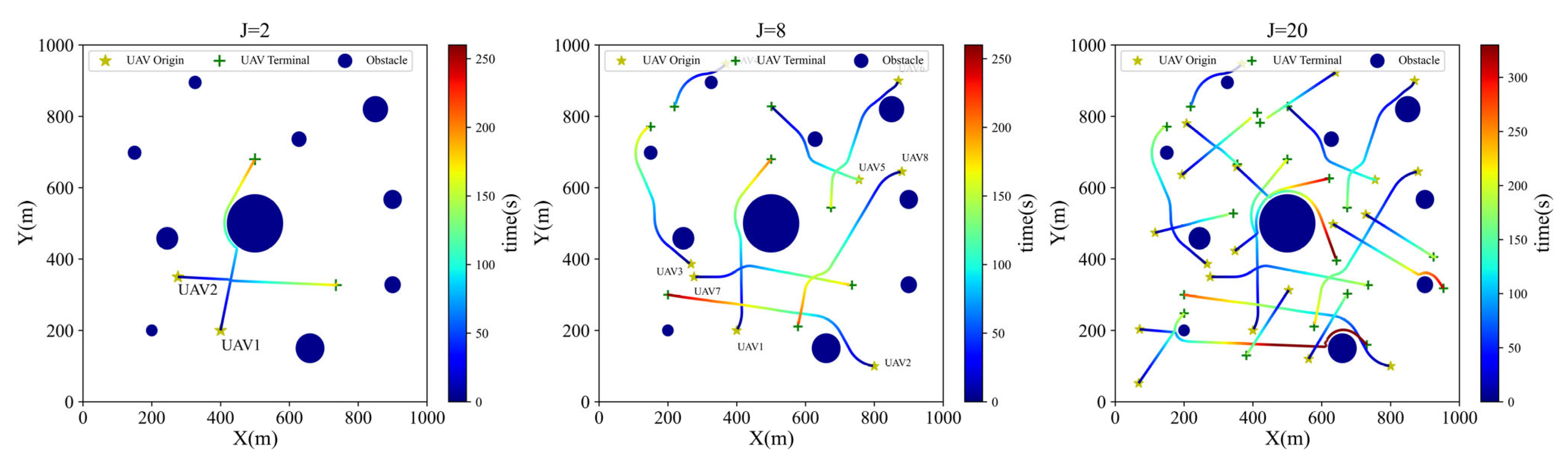
4.3.1. Collision Avoidance Results
4.3.2. Avoidance Strategy Analysis
4.4. Performance Analysis
4.4.1. Performance Testing of the Method
- (1)
- Collision avoidance success rate
- (2)
- Computational efficiency
- (3)
- Extra flight distance
4.4.2. Impact of Noisy States
4.4.3. Different Numbers of UAVs
4.4.4. Comparison with Other Algorithms
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Du, Do | The collision zone of UAV and building |
| φ | The heading angle, horizontal speed and latitude |
| V | The horizontal speed of UAV |
| Z | The latitude of UAV |
| φg | The relative heading angle of the destination to UAV |
| dg | The horizontal distance of the destination to UAV |
| φus | The difference in heading angle between two UAV |
| Zus | The difference in altitude between two UAV |
| dus | The horizontal distance between two UAV |
| ddet | The UAV detection distance |
| Policy network | |
| Target policy network | |
| The learned policy function | |
| i, j | Superscript or subscript, denote the specific UAV |
| Δφ | Alteration in direction |
| ΔZ | Alteration in altitude |
| ΔV | Alteration in horizontal speed |
| dom | The distance attribute of obstacle in sector m |
| Rd | Destination intent or collision avoidance reward |
| Ruu | The UAV collision avoidance reward |
| Rex | The additional reward |
| S | The state space of agent |
| A | The action space of agent |
| P | The collision resolution pool |
| Q network | |
| Target Q network | |
| The learned value function | |
| t | Subscript, denote the specific moment |
References
- Garrow, L.A.; German, B.J.; Leonard, C.E. Urban air mobility: A comprehensive review and comparative analysis with autonomous and electric ground transportation for informing future research. Transp. Res. Part C Emerg. Technol. 2021, 132, 103377. [Google Scholar] [CrossRef]
- Barrado, C.; Boyero, M.; Brucculeri, L.; Ferrara, G.; Hately, A.; Hullah, P.; Martin-Marrero, D.; Pastor, E.; Rushton, A.P.; Volkert, A. U-Space Concept of Operations: A Key Enabler for Opening Airspace to Emerging Low-Altitude Operations. Aerospace 2020, 7, 24. [Google Scholar] [CrossRef]
- 2022 Civil Aviation Development Statistical Bulletin. 2023. Available online: https://file.veryzhun.com/buckets/carnoc/keys/7390295f32633128e6e5cee44fc9fe4e.pdf (accessed on 1 May 2023).
- Kiran, B.R.; Sobh, I.; Talpaert, V.; Mannion, P.; Sallab, A.A.A.; Yogamani, S.; Pérez, P. Deep Reinforcement Learning for Autonomous Driving: A Survey. IEEE Trans. Intell. Transp. Syst. 2022, 23, 4909–4926. [Google Scholar] [CrossRef]
- Wu, Y. A survey on population-based meta-heuristic algorithms for motion planning of aircraft. Swarm Evol. Comput. 2021, 62, 100844. [Google Scholar] [CrossRef]
- Zeng, D.; Chen, H.; Yu, Y.; Hu, Y.; Deng, Z.; Leng, B.; Xiong, L.; Sun, Z. UGV Parking Planning Based on Swarm Optimization and Improved CBS in High-Density Scenarios for Innovative Urban Mobility. Drones 2023, 7, 295. [Google Scholar] [CrossRef]
- Zhao, P.; Erzberger, H.; Liu, Y. Multiple-Aircraft-Conflict Resolution Under Uncertainties. J. Guid. Control Dyn. 2021, 44, 2031–2049. [Google Scholar] [CrossRef]
- Yun, S.C.; Ganapathy, V.; Chien, T.W. Enhanced D* Lite Algorithm for mobile robot navigation. In Proceedings of the 2010 IEEE Symposium on Industrial Electronics and Applications (ISIEA), Penang, Malaysia, 3–5 October 2010; pp. 545–550. [Google Scholar]
- Wu, Y.; Low, K.H.; Pang, B.; Tan, Q. Swarm-Based 4D Path Planning For Drone Operations in Urban Environments. IEEE Trans. Veh. Technol. 2021, 70, 7464–7479. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Z.; Zhang, H.; Jiang, C.; Hu, M. SMILO-VTAC Model Based Multi-Aircraft Conflict Resolution Method in Complex Low-Altitude Airspace. J. Traffic Transp. Eng. 2019, 19, 125–136. [Google Scholar]
- Radmanesh, M.; Kumar, M. Flight formation of UAVs in presence of moving obstacles using fast-dynamic mixed integer linear programming. Aerosp. Sci. Technol. 2016, 50, 149–160. [Google Scholar] [CrossRef]
- Waen, J.D.; Dinh, H.T.; Torres, M.H.C.; Holvoet, T. Scalable multirotor UAV trajectory planning using mixed integer linear programming. In Proceedings of the 2017 European Conference on Mobile Robots (ECMR), Paris, France, 6–8 September 2017; pp. 1–6. [Google Scholar]
- Alonso-Ayuso, A.; Escudero, L.F.; Martín-Campo, F.J. An exact multi-objective mixed integer nonlinear optimization approach for aircraft conflict resolution. TOP 2016, 24, 381–408. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; van den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef]
- Pham, H.X.; La, H.M.; Feil-Seifer, D.; Nguyen, L.V. Autonomous uav navigation using reinforcement learning. arXiv 2018, arXiv:1801.05086. [Google Scholar]
- Liu, X.; Liu, Y.; Chen, Y. Reinforcement Learning in Multiple-UAV Networks: Deployment and Movement Design. IEEE Trans. Veh. Technol. 2019, 68, 8036–8049. [Google Scholar] [CrossRef]
- Singla, A.; Padakandla, S.; Bhatnagar, S. Memory-Based Deep Reinforcement Learning for Obstacle Avoidance in UAV with Limited Environment Knowledge. IEEE Trans. Intell. Transp. Syst. 2021, 22, 107–118. [Google Scholar] [CrossRef]
- Zhai, P.; Zhang, Y.; Shaobo, W. Intelligent Ship Collision Avoidance Algorithm Based on DDQN with Prioritized Experience Replay under COLREGs. J. Mar. Sci. Eng. 2022, 10, 585. [Google Scholar] [CrossRef]
- Li, C.; Gu, W.; Zheng, Y.; Huang, L.; Zhang, X. An ETA-Based Tactical Conflict Resolution Method for Air Logistics Transportation. Drones 2023, 7, 334. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Ribeiro, M.; Ellerbroek, J.; Hoekstra, J. Improvement of conflict detection and resolution at high densities through reinforcement learning. In Proceedings of the ICRAT2020: International Conference on Research in Air Transportation 2020, Tampa, FL, USA, 23–26 June 2020. [Google Scholar]
- Rubí, B.; Morcego, B.; Pérez, R. Deep reinforcement learning for quadrotor path following with adaptive velocity. Auton. Robot. 2021, 45, 119–134. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Yu, Z. Path Following Control for UAV Using Deep Reinforcement Learning Approach. Guid. Navig. Control 2021, 1, 18. [Google Scholar] [CrossRef]
- Wen, H.; Li, H.; Wang, Z.; Hou, X.; He, K. Application of DDPG-based Collision Avoidance Algorithm in Air Traffic Control. In Proceedings of the 2019 12th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 14–15 December 2019; pp. 130–133. [Google Scholar]
- Hu, J.; Yang, X.; Wang, W.; Wei, P.; Ying, L.; Liu, Y. Obstacle Avoidance for UAS in Continuous Action Space Using Deep Reinforcement Learning. IEEE Access 2022, 10, 90623–90634. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, J.; Zhong, G.; Liu, H.; Liu, W. Multivariate Combined Collision Detection for Multi-Unmanned Aircraft Systems. IEEE Access 2022, 10, 103827–103839. [Google Scholar] [CrossRef]
- Qiu, C.; Hu, Y.; Chen, Y.; Zeng, B. Deep Deterministic Policy Gradient (DDPG)-Based Energy Harvesting Wireless Communications. IEEE Internet Things J. 2019, 6, 8577–8588. [Google Scholar] [CrossRef]
- Bagdi, Z.; Csámer, L.; Bakó, G. The green light for air transport: Sustainable aviation at present. Cogn. Sustain. 2023, 2. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, X.; Jiang, W.; Zhang, W. Collision-Free 4D Dynamic Path Planning for Multiple UAVs Based on Dynamic Priority RRT* and Artificial Potential Field. Drones 2023, 7, 180. [Google Scholar] [CrossRef]
- Sun, J.; Tang, J.; Lao, S. Collision Avoidance for Cooperative UAVs with Optimized Artificial Potential Field Algorithm. IEEE Access 2017, 5, 18382–18390. [Google Scholar] [CrossRef]
- Song, J.; Hu, Y.; Su, J.; Zhao, M.; Ai, S. Fractional-Order Linear Active Disturbance Rejection Control Design and Optimization Based Improved Sparrow Search Algorithm for Quadrotor UAV with System Uncertainties and External Disturbance. Drones 2022, 6, 229. [Google Scholar] [CrossRef]
- Bauer, P.; Ritzinger, G.; Soumelidis, A.; Bokor, J. LQ servo control design with Kalman filter for a quadrotor UAV. Period. Polytech. Transp. Eng. 2008, 36, 9–14. [Google Scholar] [CrossRef]




| Ref. | Methods | Type | State and Action Space | Action | Multi-UAV | Environment |
|---|---|---|---|---|---|---|
| [16] | Q-leaning | Value-based | Discrete/Discrete | choosing from 4 possible directions | NO | 2D |
| [17] | Q-leaning | Value-based | Discrete/Discrete | choosing from 7 possible directions | YES | 3D |
| [18] | DDQN | Value-based | Continuous/Discrete | choosing from 3 possible directions | NO | 2D |
| [20] | D3QN | Value-based | Continuous/Discrete | choosing acceleration; choosing yaw angular velocity | YES | 2D |
| [22] | DDPG | police-based | Discrete/Continuous | choosing heading angle(max:15/s); choosing acceleration (1.0 kts/s) | NO | 2D |
| [23] | DDPG | police-based | Continuous/Continuous | choosing altitude, heading angle | NO | 3D |
| [24] | DDPG | police-based | Continuous/Continuous | choosing heading angle (−30°, 30°) | NO | 2D |
| [26] | PPO | police-based | Continuous/Continuous | choosing heading angle (−30°, 30°),and speed [0 m/s, 40 m/s] | NO | 2D |
| This paper | Improved DDPG | police-based | Continuous/Continuous | choosing velocity, heading angle, and altitude | YES | 3D |
| Obstacle Number | X (m) | Y (m) | R (m) | Z (m) | Obstacle Number | X (m) | Y (m) | R (m) | Z (m) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 500 | 500 | 80 | 100 | 6 | 245 | 458 | 30 | 89 |
| 2 | 200 | 200 | 15 | 70 | 7 | 660 | 150 | 40 | 56 |
| 3 | 900 | 567 | 25 | 85 | 8 | 900 | 328 | 22 | 78 |
| 4 | 850 | 820 | 35 | 80 | 9 | 326 | 895 | 17 | 78 |
| 5 | 150 | 698 | 18 | 60 | 10 | 628 | 736 | 20 | 91 |
| Parameter | Value |
|---|---|
| Total number of training episodes | 5000 |
| Discount factor | 0.99 |
| Target network update rate | 0.001 |
| Buffer size | 10,000 |
| Batch size | 100 |
| The initial destination area radius: | 10 |
| Attenuation coefficient: C | 0.8 |
| With Buildings | With Other UAVs | Total | |
|---|---|---|---|
| Number of conflicts | 3656 | 867 | 4523 |
| Number of resolutions | 3502 | 796 | 4298 |
| Success rate | 95.79% | 91.81% | 95.03% |
| mx, mx, mx ≠ 0 vx = 0, | mx, mx, mx ≠ 0 vx = 0, | mx, mx, mx ≠ 0 vx = 0, | No Noise | |
| SR | 94.32% | 93.98% | 92.90% | 95.03% |
| ED | 27.2 m | 30.3 m | 35.6 m | 26.8 m |
| mx, mx, mx = 0 vx ≠ 0, | mx, mx, mx = 0 vx ≠ 0, | mx, mx, mx = 0 vx ≠ 0, | ||
| SR | 94.54% | 93.52% | 93.3% | |
| ED | 27.5 m | 29.6 m | 34.3 m | |
| mx, mx, mx ≠ 0 vx ≠ 0, | mx, mx, mx ≠ 0 vx ≠ 0, | mx, mx, mx ≠ 0 vx ≠ 0, | ||
| SR | 94.01% | 92.83% | 91.61% | |
| ED | 27.6 m | 33.3 m | 36.2 m |
| J = 2 | J = 4 | J = 8 | J = 10 | J = 12 | J = 20 | |
|---|---|---|---|---|---|---|
| SR | 100% | 99.1% | 95.03% | 95.62% | 92.10% | 90.56% |
| CE | 0.0832 s | 0.0721 s | 0.0963 s | 0.1861 s | 0.0910 s | 0.216 s |
| ED | 20.3 m | 25.2 m | 26.8 m | 27.6 m | 39.1 m | 38.2 m |
| SR | CE | ED | |
|---|---|---|---|
| APF without two−layer framework | 89.32% | 1.8329 s | 41.2 m |
| APF with two−layer framework | 91.65% | 0.0821 s | 34.3 m |
| DDQN | 93.83% | 0.1839 s | 56.3 m |
| Improved DDPG | 95.03% | 0.0963 s | 26.8 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Zhang, H.; Zhou, J.; Hua, M.; Zhong, G.; Liu, H. Adaptive Collision Avoidance for Multiple UAVs in Urban Environments. Drones 2023, 7, 491. https://doi.org/10.3390/drones7080491
Zhang J, Zhang H, Zhou J, Hua M, Zhong G, Liu H. Adaptive Collision Avoidance for Multiple UAVs in Urban Environments. Drones. 2023; 7(8):491. https://doi.org/10.3390/drones7080491
Chicago/Turabian StyleZhang, Jinpeng, Honghai Zhang, Jinlun Zhou, Mingzhuang Hua, Gang Zhong, and Hao Liu. 2023. "Adaptive Collision Avoidance for Multiple UAVs in Urban Environments" Drones 7, no. 8: 491. https://doi.org/10.3390/drones7080491
APA StyleZhang, J., Zhang, H., Zhou, J., Hua, M., Zhong, G., & Liu, H. (2023). Adaptive Collision Avoidance for Multiple UAVs in Urban Environments. Drones, 7(8), 491. https://doi.org/10.3390/drones7080491









