Comparative Analysis of Nonlinear Programming Solvers: Performance Evaluation, Benchmarking, and Multi-UAV Optimal Path Planning
Abstract
1. Introduction
2. Nonlinear Programming Problem Statements
2.1. Unconstrained Optimization Problem
2.1.1. Statement
2.1.2. Optimality Conditions
2.2. Constrained Optimization Problem
2.2.1. Statement
2.2.2. Optimality Conditions
- Stationarity:
- Primal feasibility:
- Dual feasibility:
- Complementary slackness:
3. NLP Solvers and Convergence Metrics
3.1. NLP Solvers Selection
- Accelerated Particle Swarm Optimization (APSO): an algorithm developed by Yang at Cambridge University in 2007, and based on swarm-intelligent search of the optimum [39]. Due to the nature of the algorithm, only constrained nonlinear programming problems can be solved.
- Branch and Reduced Optimization Navigator (BARON): a commercial global optimization software that solves both NLP and mixed-integer nonlinear programs (MINLP) by using deterministic global optimization algorithms of the branch and bound search type [40,41,42]. It comes with embedded linear programming (LP) and NLP solvers, such as CLP/CBC [43], IPOPT [44,45], FilterSD [46] and FilterSQP [47]. BARON selects the NLP solver by default and may switch between other NLP solvers during the search based on problem characteristics and solver performance. To refer to the default option, the name BARON (auto) is chosen. For this study, we have acquired the monthly license of the software to be used in conjunction with the MATLAB interface. Such choice reflects the fact that the free demo version is characterized by some limitations, namely, it can only handle problems with up to ten variables, ten constraints, and it does not support trigonometric functions.
- FMINCON: a MATLAB optimization toolbox used to solve constrained NLP problems [37]. FMINCON provides the user the option to select amongst five different algorithms to solve nonlinear problems: Active-set, Interior-point, Sequential Quadratic Programming (SQP), Sequential Quadratic Programming legacy (SQP-legacy), and Trust region reflective. Four out of the five algorithms are implemented in our analysis as one of them, the Trust Region Reflective algorithm, does not support most of the constraints considered in our benchmark cases.
- Nonlinear Interior point Trust Region Optimization (ARTELYS KNITRO): a commercially available nonlinear optimization software package developed by Zienna Optimization since 2001 [53] for finding local solutions to both continuous and discrete optimization problems with integer or binary variables, with or without constraints [53,54]. In this work, the software free trial license is used, in conjunction with the MATLAB interface. Several algorithms are included in the software, such as Interior-point/Direct, Interior-point/CG, Active-set, and Sequential Quadratic Programming. Interior-point/CG mainly differs from the Interior-point/Direct algorithm because of the primal-dual KKT system solved using a projected conjugate gradient iteration [54].
- Mixed Integer Distributed Ant Colony Optimization (MIDACO): a global optimization solver that combines an extended evolutionary probabilistic technique, called the Ant Colony Optimization algorithm, with the Oracle Penalty method for constrained handling [55,56]. In this work, we have obtained a license; otherwise, it must be noted that the free trial version has a limitation, namely, that it does not support more than four variables per problem.
- Modified Quasilinearization Algorithm (MQA): the modified version of the Standard Quasilinearization Algorithm (SQA) [58,59]. The goal is the progressive reduction of the performance index. Convergence to the desired solution is achieved when the performance index or , with and small preselected positive constants, for the unconstrained and constrained case, respectively [60,61]. Regarding NLP problems, it must be noted that the MQA can only handle equality constraints. As a result, slack variables are introduced to convert the inequality constraints into equality constraints.
- Sequential Gradient-Restoration Algorithm (SGRA): a first-order NLP solver, characterized by a restoration phase, followed by a gradient phase [66,67]. The goal is the progressive reduction of the performance index. The performance index is expressed by , which includes both the feasibility index , and the optimality index . Convergence is achieved when the constraint error and the optimality condition error are , respectively, with , small preselected positive constants. It must be noted that only equality constraints can be handled by the SGRA. As a result, slack variables are introduced to convert the inequality constraints into equality constraints.
- Standard Quasilinearization Algorithm (SQA): the standard version of the QA, and it uses QA techniques for solving nonlinear problems by generating a sequence of linear problems solutions [58,59]. As the MQA, SQA can only handle equality constraints. As a result, slack variables are introduced to convert the inequality constraints into equality constraints.
3.2. Convergence Metrics
- Mean error [%]:with the benchmark test function evaluated at the numerical solution provided by the solver, the benchmark test function evaluated at the optimal solution , the error associated to the run from the k-th randomly generated initial guess, the mean error associated to the n-th benchmark test function, and the mean error delivered by the m-th solver. The biunivocal choice of the denominator of is based on the fact that some benchmark test functions at the optimal solution have zero value; in this case, a value of is chosen instead as reference value.
- Mean variance [%]:where is the variance correspondent to the n-th benchmark test function, and the mean variance delivered by the m-th solver.
- Mean convergence rate [%]:with the number of runs (from a pool of K distinct initial guesses) which successfully reach convergence for the n-th function, the convergence rate for the n-th function, and the mean convergence rate delivered by the m-th solver. The convergence rate is computed considering successful a run that satisfies the converging threshold conditions , and s, with the CPU time required to the run starting from the k-th initial guess.
- Mean CPU time [s]:where is the mean CPU time per z-th repetition, is the mean CPU time related to the n-th benchmark test function, and is the mean CPU time delivered by the m-th solver.
3.3. Solvers Implementation
3.3.1. APSO
3.3.2. BARON
3.3.3. FMINCON/FMINUNC
3.3.4. GCMMA/MMA
3.3.5. KNITRO
3.3.6. MIDACO
3.3.7. MQA
3.3.8. PENLAB
3.3.9. SGRA
3.3.10. SNOPT
3.3.11. SOLNP
3.3.12. SQA
4. Benchmark Test Functions Analysis
4.1. Results for Unconstrained Optimization Problems
4.2. Results for Constrained Optimization Problems
5. UAV Path Planning: Real-World Application Benchmark
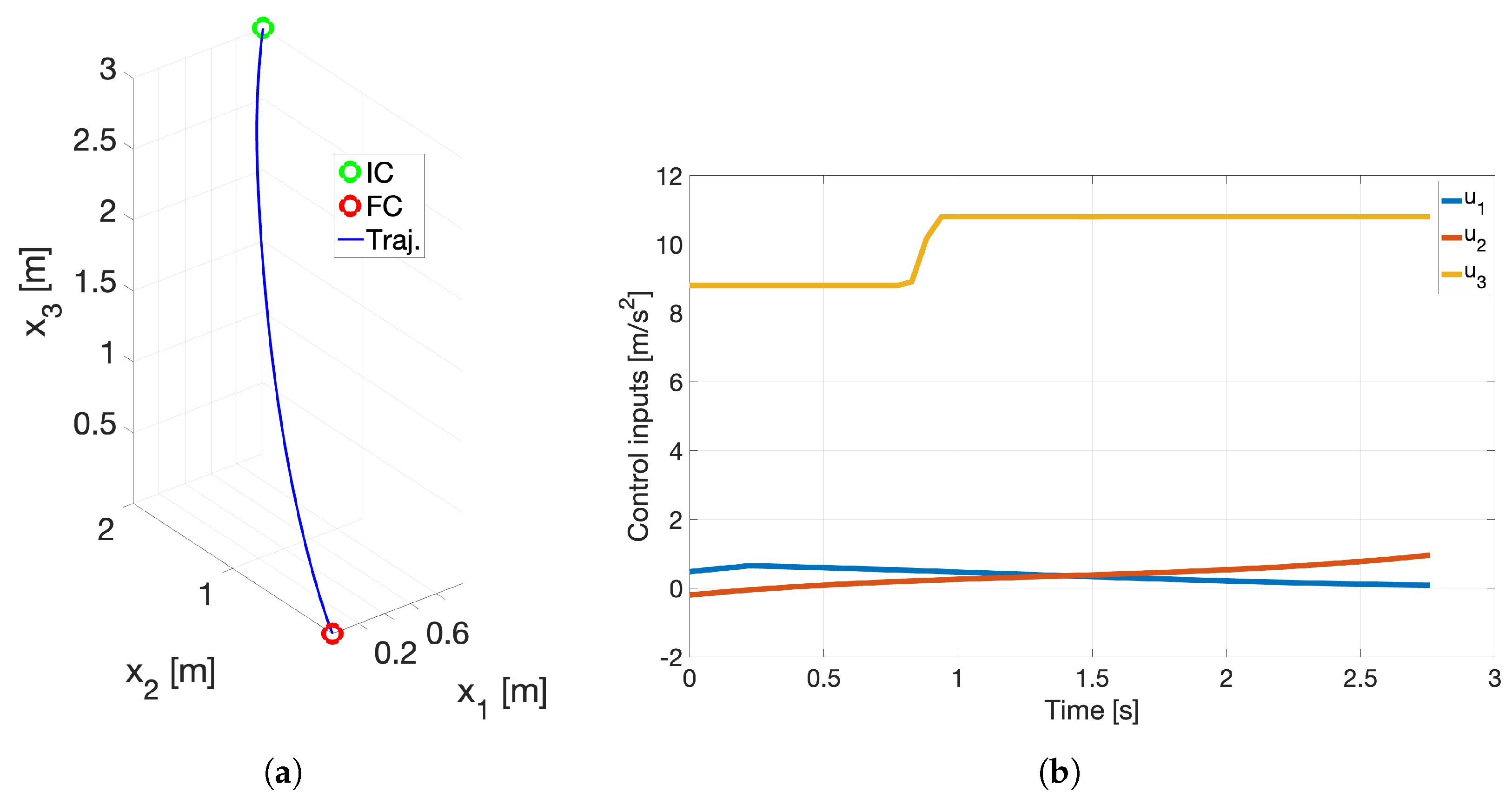
5.1. The 3D Minimum Time Problem: UAV Landing
5.2. The 3D Minimum Time Problem: UAV Formation Flying
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lasdon, L.A.; Warren, A.D. Survey of Nonlinear Programming Applications. J. Oper. Res. Soc. Am. 1980, 28, 1029–1073. [Google Scholar] [CrossRef]
- Grossmann, I.E. Global Optimization in Engineering Design; Springer-Science+Business, B.V.: Berlin/Heidelberg, Germany, 1996. [Google Scholar] [CrossRef]
- Charalambous, C. Acceleration of the Least pth Algorithm for MiniMax Optimization with Engineering Applications. Math. Program. 1979, 17, 270–297. [Google Scholar] [CrossRef]
- Grossmann, I.E.; Kravanja, Z. Mixed-Integer Nonlinear Programming: A Survey of Algorithms and Applications. In Large-Scale Optimization with Applications; Biegler, L.T., Coleman, T.F., Conn, A.R., Santosa, F.N., Eds.; Springer: New York, NY, USA, 1997; Volume 93, pp. 73–100. [Google Scholar] [CrossRef]
- Wu, X.; William, S.L. Assimilation of ERBE Data with a Nonlinear Programming Technique to Improve Cloud-Cover Diagnosis. Am. Meteorol. Soc. 1992, 120, 2009–2024. [Google Scholar] [CrossRef]
- Wansuo, D.; Haiying, L. A New Strategy for Solving a Class of Constrained Nonlinear Optimization Problems Related to Weather and Climate Predictability. Adv. Atmos. Sci. 2010, 27, 741–749. [Google Scholar] [CrossRef]
- Rustagi, J. Optimization Techniques in Statistics; Academic Press Limited: Cambridge, MA, USA, 1994. [Google Scholar] [CrossRef]
- Ziemba, W.T.; Vickson, R.G. Stochastic Optimization Models in Finance; Academic Press INC.: Cambridge, MA, USA, 1975. [Google Scholar] [CrossRef]
- MathWorks. Fmincon. 2020. Available online: https://www.mathworks.com/help/optim/ug/fmincon.html#busp5fq-6 (accessed on 1 September 2021).
- MATLAB. The MathWorks Inc. 2020. Available online: https://www.mathworks.com/products/matlab.html (accessed on 1 September 2021).
- Box, M.J. A comparison of several current optimization methods, and the use of transformations in constrained problems. Comput. J. 1966, 9, 67–77. [Google Scholar] [CrossRef]
- Levy, A.V.; Guerra, V. On the Optimization of Constrained Functions: Comparison of Sequential Gradient-Restoration Algorithm and Gradient-Projection Algorithm; American Elsevier Publishing Company: Amsterdam, The Netherlands, 1976. [Google Scholar] [CrossRef]
- Schittkowski, K.; Zillober, C.; Zotemantel, R. Numerical Comparison of Nonlinear Programming Algorithms for Structural Optimization. Struct. Optim. 1994, 7, 1–19. [Google Scholar] [CrossRef]
- George, G.; Raimond, K. A Survey on Optimization Algorithms for Optimizing the Numerical Functions. Int. J. Comput. Appl. 2013, 61, 41–46. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.303.5096&rep=rep1&type=pdf (accessed on 1 September 2021). [CrossRef]
- Gearhart, J.L.; Adair, K.L.; Detry, R.J.; Durfee, J.D.; Jones, K.A.; Martin, N. Comparison of Open-Source Linear Programming Solvers; Technical Report; Sandia National Laboratory: Albuquerque, NM, USA, 2013. [Google Scholar] [CrossRef]
- Kronqvist, J.; Bernal, D.E.; Lundell, A.; Grossmann, I.E. A Review and Comparison of Solvers for Convex MINLP. Optim. Eng. 2018, 20, 397–455. [Google Scholar] [CrossRef]
- Saxena, P. Comparison of Linear and Nonlinear Programming Techniques for Animal Diet. Appl. Math. 2012, 1, 106–108. [Google Scholar] [CrossRef]
- Pucher, H.; Stix, V. Comparison of Nonlinear Optimization Methods on a Multinomial Logit-Model in R. Int. Multi-Conf. Eng. Technol. Innov. 2008. Available online: https://www.iiis.org/cds2009/cd2009sci/imeti2009/PapersPdf/F216BU.pdf (accessed on 1 September 2021).
- Yuan, G.; Chang, K.; Hsieh, C.; Lin, C. A Comparison of Optimization Methods and Software for Large-scale L1-regularized Linear Classification. J. Mach. Learn. Res. 2010, 11, 3183–3234. Available online: https://www.jmlr.org/papers/volume11/yuan10c/yuan10c.pdf (accessed on 1 September 2021).
- Neumaier, A.; Shcherbina, O.; Huyer, W.; Vinko, T. A Comparison of Complete Global Optimization Solvers. Math. Program. 2005, 103, 335–356. [Google Scholar] [CrossRef]
- Obayash, S.; Tsukahara, T. Comparison of Optimization Algorithms for Aerodynamic Shape Design. AIAA J. 1997, 35, 1413–1415. [Google Scholar] [CrossRef]
- McIlhagga, M.; Husbands, P.; Ives, R. A Comparison of Optimization Techniques for Integrated Manufacturing Planning and Scheduling. In Parallel Problem Solving from Nature; Voigt, H.M., Ebeling, W., Rechenberg, I., Schwefel, H.P., Eds.; Springer: Berlin/Heidelberg, Germany, 1996; Volume 1141, pp. 604–613. [Google Scholar] [CrossRef]
- Haupt, R. Comparison Between Genetic and Gradient-Based Optimization Algorithms for Solving Electromagnetics Problems. IEEE Trans. Magn. 1995, 31, 1932–1935. [Google Scholar] [CrossRef]
- Hamdy, M.; Nguyen, A.; Hensen, J.L. A Performance Comparison of Multi-objective Optimization Algorithms for Solving Nearly-zero-energy-building Design Problems. Energy Build. 2016, 121, 57–71. [Google Scholar] [CrossRef]
- Frank, P.D.; Shubin, G.R. A Comparison of Optimization-Based Approaches for a Model Computational Aerodynamics Design Problem. J. Comput. Phys. 1992, 98, 74–89. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. On the Performance of Artificial Bee Colony (ABC) Algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Hedar, A.R. Global Optimization Test Problems. 2020. Available online: http://www-optima.amp.i.kyoto-u.ac.jp/member/student/hedar/Hedar_files/TestGO.htm (accessed on 1 September 2021).
- Schittkowski, K. Test Examples for Nonlinear Programming Codes; Technical Report; University of Bayreuth: Bayreuth, Germany, 2009; Available online: http://www.apmath.spbu.ru/cnsa/pdf/obzor/Schittkowski_Test_problem.pdf (accessed on 1 September 2021).
- Floudas, C.; Pardalos, P.M.; Adjiman, C.; Esposito, W.R.; Gümüs, Z.H.; Harding, S.T.; Klepeis, J.L.; Meyer, C.A.; Schweiger, C.A. Handbook of Test Problems in Local and Global Optimization. In Nonconvex Optimization and Its Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999; Volume 33. [Google Scholar] [CrossRef]
- Kielas-Jensen, C.; Cichella, V.; Berry, T.; Kaminer, I.; Walton, C.; Pascoal, A. Bernstein Polynomial-Based Method for Solving Optimal Trajectory Generation Problems. Sensors 2022, 22, 1869. [Google Scholar] [CrossRef]
- Bellman, R.E. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Clarke, F.H.; Ledyaev, Y.S.; Stern, R.J.; Wolenski, P.R. Nonsmooth Analysis and Control Theory; Springer Science & Business Media: New York, NY, USA, 2008; Volume 178. [Google Scholar]
- Bryson, A.E.; Ho, Y.C. Applied Optimal Control; Hemisphere: New York, NY, USA, 1975. [Google Scholar]
- Cichella, V.; Kaminer, I.; Walton, C.; Hovakimyan, N. Optimal motion planning for differentially flat systems using Bernstein approximation. IEEE Control. Syst. Lett. 2017, 2, 181–186. [Google Scholar] [CrossRef]
- Cichella, V.; Kaminer, I.; Walton, C.; Hovakimyan, N.; Pascoal, A. Consistency of Approximation of Bernstein Polynomial-Based Direct Methods for Optimal Control. Machines 2022, 10, 1132. [Google Scholar] [CrossRef]
- Cichella, V.; Kaminer, I.; Walton, C.; Hovakimyan, N.; Pascoal, A.M. Optimal multivehicle motion planning using bernstein approximants. IEEE Trans. Autom. Control 2020, 66, 1453–1467. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer Science+Business Media, LLC.: Berlin/Heidelberg, Germany, 2006; Available online: https://link.springer.com/book/10.1007/978-0-387-40065-5 (accessed on 1 September 2021).
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004; Available online: https://web.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf (accessed on 1 September 2021).
- Yang, X. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Bristol, UK, 2014. [Google Scholar] [CrossRef]
- Firm, T.O. Analytics and Optimization Software. 2021. Available online: https://minlp.com/baron-downloads (accessed on 1 September 2021).
- Tawarmalani, M.; Sahinidis, N.V. Global Optimization of Mixed-integer Nonlinear Programs: A Theoretical and Computational Study. Math. Program. 2004, 99, 563–591. [Google Scholar] [CrossRef]
- Sahinidis, N. BARON User Manual; The Optimization Firm LLC. Available online: http://www.minlp.com/ (accessed on 1 September 2021).
- COIN-OR. Computational Optimization Infrastructure for Operations Research. 2016. Available online: https://www.coin-or.org/ (accessed on 1 September 2021).
- Wächter, A.; Biegler, L. On the Implementation of an Interior-Point Filter Line-Search Algorithm for Large-Scale Nonlinear Programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- COIN-OR. IPOPT. 2021. Available online: https://coin-or.github.io/Ipopt/ (accessed on 1 September 2021).
- FilterSD. Computational Infrastructure for Operations Research, COIN-OR Project. 2020. Available online: https://projects.coin-or.org/filterSD/export/19/trunk/filterSD.pdf (accessed on 1 September 2021).
- Fletcher, R.; Leyffer, S. User Manual for Filter SQP; Technical Report, University of Dundee, Department of Mathematics: Dundee, UK, 1999; Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.139.7769&rep=rep1&type=pdf (accessed on 1 September 2021).
- MathWorks. Fminunc. 2020. Available online: https://www.mathworks.com/help/optim/ug/fminunc.html#but9q82-2_head (accessed on 1 September 2021).
- MathWorks. Quasi-Newton Algorithm. 2020. Available online: https://www.mathworks.com/help/optim/ug/unconstrained-nonlinear-optimization-algorithms.html#brnpcye (accessed on 1 September 2021).
- Svanberg, K. A Class of Globally Convergent Optimization Methods Based on Conservative Convex Separable Approximations. SIAM J. Optim. 2002, 12, 555–573. [Google Scholar] [CrossRef]
- Svanberg, K. MMA and GCMMA—Two Methods for Nonlinear Optimization. 2014. Available online: https://people.kth.se/~krille/mmagcmma.pdf (accessed on 1 September 2021).
- Svanberg, K. MMA and GCMMA Matlab Code. 2020. Available online: http://www.smoptit.se/ (accessed on 1 September 2021).
- Artelys Knitro. Artelys Optimization Solutions. 2021. Available online: https://www.artelys.com/solvers/knitro/ (accessed on 1 September 2021).
- Artelys Knitro. Artelys Knitro User’s Manual. 2021. Available online: https://www.artelys.com/docs/knitro//index.html (accessed on 1 September 2021).
- MIDACO-Solver, User Manual. MIDACO-SOLVER: Numerical High-Performance Optimization Software. 2021. Available online: http://www.midaco-solver.com/index.php/download (accessed on 1 September 2021).
- Schlueter, M.; Erb, S.O.; Gerdts, M.; Kemble, S.; Rückmann, J. MIDACO on MINLP space applications. Adv. Space Res. 2013, 51, 1116–1131. [Google Scholar] [CrossRef]
- Svanberg, K. The method of moving asymptotes—A new method for structural optimization. Int. J. Numer. Methods Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]
- Eloe, P.W.; Jonnalagadda, J. Quasilinearization and boundary value problems for Riemann-Liouville fractional differential equations. Electron. J. Differ. Equations 2019, 2019, 1–15. Available online: https://ejde.math.txstate.edu/Volumes/2019/58/eloe.pdf (accessed on 1 September 2021). [CrossRef]
- Yeo, B.P. A quasilinearization algorithm and its application to a manipulator problem. Int. J. Control 1974, 20, 623–640. [Google Scholar] [CrossRef]
- Miele, A.; Iyer, R.R. Modified quasilinearization method for solving nonlinear, two-point boundary-value problems. J. Math. Anal. Appl. 1971, 36, 674–692. [Google Scholar] [CrossRef]
- Miele, A.; Mangiavacchi, A.; Aggarwal, A.K. Modified quasilinearization algorithm for optimal control problems with nondifferential constraints. J. Optim. Theory Appl. 1974, 14, 529–556. [Google Scholar] [CrossRef]
- Fiala, J.; Kočvara, M.; Stingl, M. PENLAB: A MATLAB solver for nonlinear semidefinite optimization. arXiv 2013, arXiv:1311.5240. [Google Scholar] [CrossRef]
- Kocvara, M.; Stingl, M. PENNON—A generalized augmented Lagrangian method for semidefinite programming. In High Performance Algorithms and Software for Nonlinear Optimization; Applied, Optimization; Gianni Di Pillo, A.M., Ed.; Springer: Boston, MA, USA, 2003; Volume 82, pp. 303–321. [Google Scholar] [CrossRef]
- Polyak, R. Modified barrier functions (theory and methods). Math. Program. Ser. B 1992, 54, 177–222. [Google Scholar] [CrossRef]
- Kocvara, M. PENLAB. 2017. Available online: http://web.mat.bham.ac.uk/kocvara/penlab/ (accessed on 1 September 2021).
- COKER, E.M. Sequential Gradient-Restoration Algorithm for Optimal Control Problems with Control Inequality Constraints and General Boundary Conditions. Ph.D. Thesis, Rice University, Houston, TX, USA, 1985. Available online: https://www.proquest.com/dissertations-theses/sequential-gradient-restoration-algorithm-optimal/docview/303398376/se-2?accountid=15159 (accessed on 1 September 2021).
- Miele, A.; Huang, H.Y.; Heideman, J.C. Sequential gradient-restoration algorithm for the minimization of constrained functions—Ordinary and conjugate gradient versions. J. Optim. Theory Appl. 1969, 4, 213–243. [Google Scholar] [CrossRef]
- Gill, P.; Murray, W.; Saunders, M.; Drud, A.; Kalvelagen, E. SNOPT: An SQP algorithm for large-scale constrained optimization. SIAM Rev. 2001, 47, 99–131. [Google Scholar] [CrossRef]
- Gill, P.E.; Murray, W.; Saunders, M.A.; Wong, E. User’s Guide for SNOPT 7.7: Software for Large-Scale Nonlinear Programming; Center for Computational Mathematics Report CCoM 18-1, Department of Mathematics, University of California: San Diego, CA, USA, 2018. [Google Scholar]
- Ye, Y. SOLNP USERS’ GUIDE—A Nonlinear Optimization Program in MATLAB. 1989. Available online: https://web.stanford.edu/~yyye/matlab/manual.ps (accessed on 1 September 2021).
- Ye, Y. SOLNP. 2020. Available online: https://web.stanford.edu/~yyye/matlab.html (accessed on 1 September 2021).
- Lavezzi, G.; Guye, K.; Ciarcià, M. Nonlinear Programming Solvers for Unconstrained and Constrained Optimization Problems: A Benchmark Analysis. arXiv 2022, arXiv:2204.05297. [Google Scholar] [CrossRef]
- Kielas-Jensen, C.; Cichella, V. BeBOT: Bernstein polynomial toolkit for trajectory generation. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 3288–3293. [Google Scholar]
- Cichella, V.; Kaminer, I.; Walton, C.; Hovakimyan, N.; Pascoal, A. Bernstein approximation of optimal control problems. arXiv 2018, arXiv:1812.06132. [Google Scholar]
- Farouki, R.T. The Bernstein polynomial basis: A centennial retrospective. Comput. Aided Geom. Des. 2012, 29, 379–419. [Google Scholar] [CrossRef]
- Kalczynski, P.; Drezner, Z. Extremely non-convex optimization problems: The case of the multiple obnoxious facilities location. Optim. Lett. 2022, 16, 1153–1166. [Google Scholar] [CrossRef]

| Settings | P&P | HA | QS |
|---|---|---|---|
| no. particles | 15 | 50 | 10 |
| no. iterations | 300 | 500 | 100 |
| 0.9 | 0.95 | 0.95 |
| Settings | P&P | HA | QS |
|---|---|---|---|
| Settings | P&P | HA | QS |
|---|---|---|---|
| FMINCON | |||
| FMINUNC (quasi-newton) | |||
| FMINUNC (trust-region) | |||
| Settings | P&P | HA | QS |
|---|---|---|---|
| 80 | 150 | 30 |
| Settings | P&P | HA | QS |
|---|---|---|---|
| Settings | P&P | HA | QS |
|---|---|---|---|
| 50,000 | 150,000 | 10,000 |
| Settings | P&P | HA | QS |
|---|---|---|---|
| Settings | P&P | HA | QS |
|---|---|---|---|
| 100 | 1000 | 25 | |
| 100 | 1000 | 25 | |
| Settings | P&P | HA | QS |
|---|---|---|---|
| Settings | P&P | HA | QS |
|---|---|---|---|
| 1000 | 10,000 | 100 | |
| 500 | 5000 | 100 | |
| Settings | P&P | HA | QS |
|---|---|---|---|
| 1 | 1 | 1 | |
| 10 | 500∣10 | 10 | |
| 10 | 500∣10 | 10 | |
| Settings | P&P | HA | QS |
|---|---|---|---|
| Ranking | Solver | [%] | [%] | [%] | [s] | Free |
|---|---|---|---|---|---|---|
| 1 | BARON (auto) | 2.766 | 1.448 | 94.7 | 0.208 | No |
| 2 | BARON (ipopt) | 2.766 | 1.443 | 94.7 | 0.205 | No |
| 3 | BARON (sd) | 8.469 | 1.743 | 94.7 | 0.216 | No |
| 4 | BARON (sqp) | 1.690 | 2.821 | 94.7 | 0.195 | No |
| 5 | PENLAB | 1.016 | 5.340 | 88.5 | 0.0125 | Yes |
| 6 | MIDACO | 1.435 | 1.445 | 88.4 | 0.349 | No |
| 7 | SNOPT | 7.008 | 2.444 | 73.8 | 0.0071 | No |
| 8 | FMINUNC (trust-region) | 7.836 | 2.068 | 68.8 | 0.0153 | No |
| 9 | KNITRO (sqp) | 8.139 | 9.254 | 60.8 | 0.049 | No |
| 10 | KNITRO (interior-point/D) | 1.045 | 1.279 | 60.3 | 0.019 | No |
| 11 | KNITRO (interior-point/CG) | 1.045 | 1.066 | 59.9 | 0.017 | No |
| 12 | KNITRO (active-set) | 1.163 | 1.409 | 59.8 | 0.017 | No |
| 13 | FMINUNC (quasi-newton) | 8.643 | 1.669 | 52.8 | 0.0045 | No |
| 14 | SQA | 2.362 | 1.383 | 52.5 | 0.0005 | Yes |
| 15 | MQA | 2.031 | 8.748 | 51.7 | 0.1345 | Yes |
| 16 | SOLNP | 4.648 | 1.908 | 48.2 | 0.0097 | Yes |
| 17 | SGRA | 5.921 | 8.627 | 40.8 | 0.2227 | Yes |
| Ranking | Solver | [%] | [%] | [%] | [s] | Free |
|---|---|---|---|---|---|---|
| 1 | BARON (sqp) | 1.690 | 2.821 | 94.7 | 0.194 | No |
| 2 | BARON (auto) | 2.107 | 1.448 | 94.7 | 0.208 | No |
| 3 | BARON (ipopt) | 2.107 | 1.443 | 94.7 | 0.206 | No |
| 4 | BARON (sd) | 1.433 | 2.408 | 94.7 | 0.301 | No |
| 5 | PENLAB | 4.042 | 8.944 | 88.5 | 0.0121 | Yes |
| 6 | SOLNP | 9.420 | 7.900 | 69.1 | 0.0095 | Yes |
| 7 | SNOPT | 1.260 | 1.298 | 74.2 | 0.0099 | No |
| 8 | MQA | 3.160 | 5.835 | 52.1 | 0.1520 | Yes |
| 9 | FMINUNC (quasi-newton) | 3.526 | 8.852 | 59.2 | 0.0062 | No |
| 10 | SQA | 3.984 | 9.000 | 53.2 | 0.0003 | Yes |
| 11 | FMINUNC (trust-region) | 1.860 | 1.423 | 68.8 | 0.0238 | No |
| 12 | KNITRO (interior-point/D) | 7.130 | 1.921 | 67.8 | 0.021 | No |
| 13 | KNITRO (active-set) | 7.200 | 1.883 | 67.8 | 0.022 | No |
| 14 | KNITRO (interior-point/CG) | 7.467 | 1.381 | 68.0 | 0.022 | No |
| 15 | MIDACO | 7.754 | 7.188 | 92.0 | 1.035 | No |
| 16 | KNITRO (sqp) | 1.034 | 1.785 | 68.9 | 0.074 | No |
| 17 | SGRA | 2.709 | 1.335 | 44.9 | 0.2555 | Yes |
| Ranking | Solver | [%] | [%] | [%] | [s] | Free |
|---|---|---|---|---|---|---|
| 1 | SQA | 1.964 | 1.609 | 43.3 | 0.0002 | Yes |
| 2 | FMINUNC (quasi-newton) | 6.076 | 8.157 | 33.8 | 0.0024 | No |
| 3 | SNOPT | 1.581 | 1.367 | 66.4 | 0.0040 | No |
| 4 | SOLNP | 5.357 | 3.847 | 41.2 | 0.0093 | Yes |
| 5 | FMINUNC (trust-region) | 1.924 | 1.997 | 49.3 | 0.0108 | No |
| 6 | PENLAB | 5.452 | 5.623 | 84.6 | 0.0118 | Yes |
| 7 | KNITRO (interior-point/D) | 4.555 | 4.975 | 45.5 | 0.014 | No |
| 8 | KNITRO (interior-point/CG) | 4.851 | 3.918 | 44.2 | 0.014 | No |
| 9 | KNITRO (active-set) | 4.927 | 4.737 | 44.1 | 0.014 | No |
| 10 | KNITRO (sqp) | 5.821 | 5.660 | 46.9 | 0.022 | No |
| 11 | MIDACO | 2.455 | 2.985 | 74.6 | 0.070 | No |
| 12 | MQA | 2.405 | 2.930 | 42.2 | 0.1819 | Yes |
| 13 | BARON (sqp) | 1.690 | 2.821 | 94.7 | 0.198 | No |
| 14 | BARON (ipopt) | 2.602 | 1.443 | 94.7 | 0.204 | No |
| 15 | BARON (auto) | 2.602 | 1.448 | 94.7 | 0.205 | No |
| 16 | BARON (sd) | 3.929 | 1.846 | 89.5 | 0.206 | No |
| 17 | SGRA | 8.640 | 2.211 | 23.8 | 0.3033 | Yes |
| Ranking | Solver | [%] | [%] | [%] | [s] | Free |
|---|---|---|---|---|---|---|
| 1 | BARON (auto) | 1.299 | 2.141 | 92.0 | 1.497 | No |
| 2 | BARON (ipopt) | 1.298 | 2.894 | 92.0 | 1.767 | No |
| 3 | BARON (sd) | 1.296 | 5.178 | 92.0 | 1.379 | No |
| 4 | BARON (sqp) | 1.298 | 2.332 | 92.0 | 1.412 | No |
| 5 | KNITRO (interior-point/D) | 1.782 | 2.035 | 77.7 | 0.034 | No |
| 6 | KNITRO (interior-point/CG) | 1.756 | 2.085 | 77.5 | 0.033 | No |
| 7 | FMINCON (interior-point) | 1.985 | 2.413 | 75.9 | 0.0271 | No |
| 8 | KNITRO (sqp) | 1.851 | 2.102 | 75.7 | 0.160 | No |
| 9 | SNOPT | 1.689 | 2.010 | 72.1 | 0.0040 | No |
| 10 | FMINCON (active-set) | 1.795 | 2.123 | 71.9 | 0.0204 | No |
| 11 | FMINCON (sqp-legacy) | 1.893 | 2.429 | 69.4 | 0.0111 | No |
| 12 | KNITRO (active-set) | 1.994 | 2.702 | 72.2 | 0.070 | No |
| 13 | FMINCON (sqp) | 1.908 | 2.446 | 69.3 | 0.0093 | No |
| 14 | MIDACO | 7.348 | 3.500 | 66.9 | 0.353 | No |
| 15 | SOLNP | 3.243 | 3.211 | 48.1 | 0.0095 | Yes |
| 16 | GCMMA | 4.490 | 3.742 | 45.7 | 0.9681 | Yes |
| 17 | MMA | 7.188 | 5.743 | 44.1 | 0.5856 | Yes |
| 18 | APSO | 1.512 | 1.025 | 39.2 | 0.1772 | Yes |
| 19 | PENLAB | 1.127 | 3.258 | 31.0 | 0.0379 | Yes |
| 20 | SGRA | 6.360 | 7.011 | 30.3 | 0.9815 | Yes |
| 21 | MQA | 5.125 | 3.460 | 20.8 | 3.1559 | Yes |
| 22 | SQA | 3.990 | 5.778 | 20.2 | 3.1822 | Yes |
| Ranking | Solver | [%] | [%] | [%] | [s] | Free |
|---|---|---|---|---|---|---|
| 1 | PENLAB | 1.502 | 6.711 | 31.0 | 0.0488 | Yes |
| 2 | BARON (auto) | 1.943 | 5.777 | 92.0 | 2.056 | No |
| 3 | BARON (sd) | 1.943 | 1.405 | 92.0 | 2.469 | No |
| 4 | BARON (sqp) | 1.943 | 4.745 | 92.0 | 2.041 | No |
| 5 | BARON (ipopt) | 8.074 | 9.457 | 90.8 | 3.568 | No |
| 6 | SNOPT | 1.689 | 2.010 | 72.4 | 0.0069 | No |
| 7 | KNITRO (interior-point/CG) | 1.754 | 2.085 | 77.7 | 0.040 | No |
| 8 | FMINCON (active-set) | 1.770 | 2.082 | 72.3 | 0.0214 | No |
| 9 | KNITRO (interior-point/D) | 1.782 | 2.035 | 78.0 | 0.039 | No |
| 10 | FMINCON (sqp-legacy) | 1.857 | 2.365 | 69.7 | 0.0110 | No |
| 11 | KNITRO (sqp) | 1.872 | 2.120 | 75.6 | 0.209 | No |
| 12 | FMINCON (sqp) | 1.881 | 2.388 | 69.4 | 0.0082 | No |
| 13 | KNITRO (active-set) | 1.951 | 2.791 | 73.4 | 0.078 | No |
| 14 | FMINCON (interior-point) | 1.985 | 2.413 | 75.9 | 0.0326 | No |
| 15 | SQA | 2.754 | 2.838 | 20.1 | 3.1838 | Yes |
| 16 | SOLNP | 2.949 | 3.106 | 44.8 | 0.0112 | Yes |
| 17 | MIDACO | 3.662 | 2.938 | 87.0 | 1.053 | No |
| 18 | GCMMA | 5.112 | 5.668 | 45.2 | 1.0599 | Yes |
| 19 | MQA | 5.358 | 4.601 | 20.8 | 3.2012 | Yes |
| 20 | SGRA | 6.248 | 7.673 | 30.0 | 0.9632 | Yes |
| 21 | MMA | 9.786 | 5.748 | 42.1 | 0.7101 | Yes |
| 22 | APSO | 1.173 | 1.014 | 45.9 | 1.0168 | Yes |
| Ranking | Solver | [%] | [%] | [%] | [s] | Free |
|---|---|---|---|---|---|---|
| 1 | SNOPT | 1.767 | 2.045 | 70.2 | 0.0027 | No |
| 2 | FMINCON (sqp) | 1.916 | 2.448 | 69.0 | 0.0071 | No |
| 3 | SOLNP | 4.790 | 6.452 | 46.6 | 0.0087 | Yes |
| 4 | FMINCON (sqp-legacy) | 1.902 | 2.431 | 69.1 | 0.0092 | No |
| 5 | FMINCON (active-set) | 2.850 | 3.484 | 68.9 | 0.0165 | No |
| 6 | KNITRO (interior-point/D) | 2.221 | 2.700 | 72.7 | 0.024 | No |
| 7 | FMINCON (interior-point) | 2.166 | 2.554 | 72.3 | 0.0262 | No |
| 8 | KNITRO (interior-point/CG) | 3.082 | 3.585 | 72.2 | 0.028 | No |
| 9 | KNITRO (active-set) | 2.212 | 2.975 | 69.3 | 0.030 | No |
| 10 | PENLAB | 1.896 | 1.454 | 31.0 | 0.0323 | Yes |
| 11 | APSO | 1.531 | 5.677 | 35.2 | 0.0538 | Yes |
| 12 | KNITRO (sqp) | 2.458 | 3.221 | 72.5 | 0.063 | No |
| 13 | MIDACO | 9.737 | 8.263 | 53.0 | 0.070 | No |
| 14 | SGRA | 8.774 | 1.198 | 27.5 | 0.9369 | Yes |
| 15 | MMA | 1.161 | 1.189 | 41.0 | 0.1324 | Yes |
| 16 | GCMMA | 6.967 | 4.256 | 45.5 | 0.5574 | Yes |
| 17 | BARON (sqp) | 1.395 | 8.212 | 92.0 | 0.869 | No |
| 18 | BARON (auto) | 1.374 | 4.647 | 92.0 | 0.874 | No |
| 19 | BARON (ipopt) | 1.369 | 2.163 | 92.0 | 0.880 | No |
| 20 | BARON (sd) | 1.370 | 1.291 | 92.0 | 0.999 | No |
| 21 | MQA | 5.844 | 4.193 | 20.8 | 3.1174 | Yes |
| 22 | SQA | 3.316 | 3.131 | 20.1 | 3.1361 | Yes |
| Settings | Ad hoc |
|---|---|
| 1 | |
| 3,000,000 | |
| 100,000 | |
| 5 | 50 | 150 | |
|---|---|---|---|
| Variables | 48 | 460 | 1360 |
| Equality constr. | 36 | 318 | 918 |
| Inequality const. | 55 | 306 | 906 |
| [s] | 20 | 75 | 500 |
| Ranking | Solver | [%] | [%] | [%] | [s] |
|---|---|---|---|---|---|
| 1 | BARON (auto) | 4.076 | 7.082 | 100.0 | 0.499 |
| 2 | BARON (ipopt) | 4.076 | 7.084 | 100.0 | 0.475 |
| 3 | BARON (sqp) | 4.084 | 7.084 | 100.0 | 0.359 |
| 4 | FMINCON (sqp) | 4.084 | 7.084 | 100.0 | 0.061 |
| 5 | FMINCON (active-set) | 3.957 | 7.372 | 100.0 | 0.059 |
| 6 | SNOPT | 4.101 | 7.348 | 100.0 | 0.023 |
| 7 | KNITRO (active-set) | 4.084 | 7.084 | 100.0 | 0.072 |
| 8 | KNITRO (sqp) | 4.084 | 7.083 | 100.0 | 0.178 |
| 9 | KNITRO (interior-point/CG) | 2.144 | 2.125 | 98.0 | 0.145 |
| 10 | FMINCON (sqp-legacy) | 3.900 | 6.299 | 96.0 | 0.082 |
| 11 | BARON (sd) | 4.076 | 1.144 | 78.0 | 0.920 |
| 12 | SOLNP | 4.015 | 8.380 | 76.0 | 0.073 |
| 13 | SGRA | 1.908 | 5.960 | 46.0 | 0.804 |
| 14 | KNITRO (interior-point/D) | 4.573 | 9.251 | 42.0 | 0.234 |
| 15 | FMINCON (interior-point) | 6.862 | 1.392 | 26.0 | 0.142 |
| - | APSO | - | - | - | |
| - | GCMMA | - | - | - | |
| - | MIDACO | - | - | - | |
| - | MMA | - | - | - | |
| - | MQA | - | - | - | |
| - | PENLAB | 3.863 | 8.382 | 100.0 | |
| - | SQA | - | - | - |
| Ranking | Solver | [%] | [%] | [%] | [s] |
|---|---|---|---|---|---|
| 1 | BARON (auto) | 4.148 | 9.990 | 100.0 | 5.802 |
| 2 | BARON (ipopt) | 4.148 | 9.990 | 100.0 | 5.647 |
| 3 | BARON (sqp) | 4.141 | 9.977 | 100.0 | 5.115 |
| 4 | KNITRO (active-set) | 4.141 | 9.977 | 100.0 | 5.763 |
| 5 | SNOPT | 4.101 | 1.000 | 100.0 | 1.001 |
| 6 | KNITRO (sqp) | 4.125 | 1.017 | 98.0 | 16.402 |
| 7 | FMINCON (active-set) | 3.155 | 3.774 | 92.0 | 26.765 |
| 8 | KNITRO (interior-point/CG) | 9.074 | 1.511 | 84.0 | 46.202 |
| 9 | KNITRO (interior-point/D) | 1.351 | 6.208 | 68.0 | 23.080 |
| 10 | BARON (sd) | 6.585 | 2.221 | 32.0 | 48.799 |
| 11 | FMINCON (sqp-legacy) | 4.991 | 1.371 | 58.0 | 24.868 |
| 12 | FMINCON (sqp) | 4.973 | 1.325 | 60.0 | 19.498 |
| 13 | SOLNP | 1.424 | 4.673 | 44.0 | 4.863 |
| - | APSO | - | - | - | |
| - | FMINCON (interior-point) | - | - | - | |
| - | GCMMA | - | - | - | |
| - | MIDACO | - | - | - | |
| - | MMA | - | - | - | |
| - | SGRA | - | - | - |
| Ranking | Solver | [%] | [%] | [%] | [s] |
|---|---|---|---|---|---|
| 1 | BARON (auto) | 3.679 | 7.324 | 100.0 | 70.685 |
| 2 | BARON (ipopt) | 3.678 | 7.352 | 100.0 | 70.194 |
| 3 | SNOPT | 3.766 | 6.505 | 100.0 | 7.396 |
| 4 | KNITRO (sqp) | 8.930 | 2.950 | 74.0 | 211.029 |
| 5 | KNITRO (active-set) | 6.241 | 1.285 | 66.0 | 186.258 |
| 6 | KNITRO (interior-point/D) | 4.840 | 1.237 | 62.0 | 352.009 |
| 7 | SOLNP | 1.141 | 1.665 | 18.0 | 178.791 |
| 8 | BARON (sd) | 1.558 | 3.421 | 12.0 | 424.121 |
| 9 | FMINCON (sqp) | 3.041 | 2.228 | 12.0 | 411.148 |
| 10 | BARON (sqp) | 1.870 | 3.548 | 10.0 | 430.064 |
| 11 | FMINCON (active-set) | 1.196 | 3.600 | 8.0 | 386.340 |
| 12 | KNITRO (interior-point/CG) | 4.848 | 4.374 | 6.0 | 371.203 |
| - | APSO | - | - | - | |
| - | FMINCON (interior-point) | - | - | - | |
| - | FMINCON (sqp-legacy) | - | - | - | |
| - | GCMMA | - | - | - | |
| - | MIDACO | - | - | - | |
| - | MMA | - | - | - |
| 5 | 10 | 25 | |
|---|---|---|---|
| Variables | 271 | 541 | 1351 |
| Equality constr. | 240 | 480 | 1200 |
| Inequality const. | 240 | 630 | 2700 |
| [s] | 20 | 75 | 200 |
| Ranking | Solver | [%] | [%] | [%] | [s] |
|---|---|---|---|---|---|
| 1 | BARON (auto) | 3.681 | 7.563 | 100.0 | 0.755 |
| 2 | BARON (ipopt) | 3.681 | 7.563 | 100.0 | 0.795 |
| 3 | BARON (sd) | 3.681 | 7.563 | 100.0 | 0.727 |
| 4 | BARON (sqp) | 3.681 | 7.560 | 100.0 | 0.734 |
| 5 | FMINCON (sqp) | 3.681 | 7.563 | 100.0 | 0.397 |
| 6 | FMINCON (sqp-legacy) | 3.681 | 7.563 | 100.0 | 0.446 |
| 7 | KNITRO (active-set) | 3.681 | 7.563 | 100.0 | 0.761 |
| 8 | KNITRO (interior-point/D) | 3.681 | 7.564 | 100.0 | 0.498 |
| 9 | KNITRO (sqp) | 3.681 | 7.563 | 100.0 | 0.680 |
| 10 | KNITRO (interior-point/CG) | 3.678 | 7.963 | 98.0 | 0.862 |
| 11 | SNOPT | 3.632 | 7.401 | 96.0 | 0.071 |
| 12 | FMINCON (interior-point) | 1.400 | 2.390 | 76.0 | 0.594 |
| 13 | FMINCON (active-set) | 2.811 | 3.926 | 30.0 | 0.535 |
| 14 | SOLNP | 1.125 | 8.907 | 34.0 | 2.846 |
| - | APSO | - | - | - | |
| - | GCMMA | - | - | - | |
| - | MIDACO | - | - | - | |
| - | MMA | - | - | - | |
| - | SGRA | - | - | - |
| Ranking | Solver | [%] | [%] | [%] | [s] |
|---|---|---|---|---|---|
| 1 | BARON (auto) | 3.492 | 6.299 | 100.0 | 1.481 |
| 2 | BARON (ipopt) | 3.492 | 6.299 | 100.0 | 1.530 |
| 3 | BARON (sd) | 3.492 | 6.299 | 100.0 | 1.415 |
| 4 | BARON (sqp) | 3.492 | 6.299 | 100.0 | 1.432 |
| 5 | FMINCON (sqp) | 3.492 | 6.299 | 100.0 | 1.785 |
| 6 | FMINCON (sqp-legacy) | 3.492 | 6.299 | 100.0 | 2.047 |
| 7 | KNITRO (interior-point/D) | 3.492 | 6.299 | 100.0 | 3.172 |
| 8 | KNITRO (sqp) | 3.492 | 6.299 | 100.0 | 9.651 |
| 9 | KNITRO (interior-point/CG) | 3.400 | 6.397 | 96.0 | 6.333 |
| 10 | KNITRO (active-set) | 3.233 | 4.785 | 96.0 | 10.044 |
| 11 | SNOPT | 8.069 | 1.035 | 96.0 | 2.811 |
| 12 | FMINCON (active-set) | 3.803 | 4.417 | 36.0 | 1.963 |
| 13 | SOLNP | 1.064 | 8.218 | 12.0 | 16.013 |
| - | APSO | - | - | - | |
| - | FMINCON (interior-point) | - | - | - | |
| - | GCMMA | - | - | - | |
| - | MIDACO | - | - | - | |
| - | MMA | - | - | - |
| Ranking | Solver | [%] | [%] | [%] | [s] |
|---|---|---|---|---|---|
| 1 | BARON (auto) | 1.953 | 6.562 | 96.0 | 5.782 |
| 2 | BARON (ipopt) | 1.953 | 6.562 | 96.0 | 13.923 |
| 3 | BARON (sd) | 1.953 | 6.563 | 96.0 | 5.052 |
| 4 | BARON (sqp) | 1.953 | 6.562 | 96.0 | 5.299 |
| 5 | KNITRO (interior-point/D) | 3.117 | 3.899 | 90.0 | 119.081 |
| 6 | FMINCON (sqp) | 2.506 | 2.302 | 74.0 | 48.901 |
| 7 | FMINCON (sqp-legacy) | 2.506 | 2.302 | 74.0 | 54.861 |
| 8 | SNOPT | 2.083 | 7.497 | 44.0 | 45.408 |
| 9 | KNITRO (sqp) | 2.025 | 7.837 | 22.0 | 133.070 |
| 10 | FMINCON (active-set) | 4.678 | 2.198 | 10.0 | 21.308 |
| 11 | KNITRO (active-set) | 3.933 | 4.017 | 6.0 | 65.720 |
| 12 | KNITRO (interior-point/CG) | 1.484 | 0.000 | 2.0 | 165.145 |
| - | APSO | - | - | - | |
| - | FMINCON (interior-point) | - | - | - | |
| - | GCMMA | - | - | - | |
| - | MIDACO | - | - | - | |
| - | MMA | - | - | - | |
| - | SOLNP | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lavezzi, G.; Guye, K.; Cichella, V.; Ciarcià, M. Comparative Analysis of Nonlinear Programming Solvers: Performance Evaluation, Benchmarking, and Multi-UAV Optimal Path Planning. Drones 2023, 7, 487. https://doi.org/10.3390/drones7080487
Lavezzi G, Guye K, Cichella V, Ciarcià M. Comparative Analysis of Nonlinear Programming Solvers: Performance Evaluation, Benchmarking, and Multi-UAV Optimal Path Planning. Drones. 2023; 7(8):487. https://doi.org/10.3390/drones7080487
Chicago/Turabian StyleLavezzi, Giovanni, Kidus Guye, Venanzio Cichella, and Marco Ciarcià. 2023. "Comparative Analysis of Nonlinear Programming Solvers: Performance Evaluation, Benchmarking, and Multi-UAV Optimal Path Planning" Drones 7, no. 8: 487. https://doi.org/10.3390/drones7080487
APA StyleLavezzi, G., Guye, K., Cichella, V., & Ciarcià, M. (2023). Comparative Analysis of Nonlinear Programming Solvers: Performance Evaluation, Benchmarking, and Multi-UAV Optimal Path Planning. Drones, 7(8), 487. https://doi.org/10.3390/drones7080487






