On IRS-Assisted Covert Communication with a Friendly UAV

Abstract

Driven by the rapidly growing demand for information security, covert wireless communication has become an essential technology and attracted tremendous attention. However, traditional wireless covert communication is continuously exposing the inherent limitations, creating challenges around deployment in environments with a large number of obstacles, such as cities with high-rise buildings. In this paper, we propose an intelligent reflecting surface (IRS)-assisted covert communication system (CCS) for communicating with a friendly unmanned aerial vehicle (UAV) in which the UAV generates artificial noise (AN) to interfere with monitoring. Furthermore, we model the power of AN emitted by the UAV using an uncertainty model, through which the closed-form detection error probability (DEP) of the covert wireless communication for monitoring is derived. Under the derived DEP, we formulate the optimization problem to maximize the covert rate, then design an iterative algorithm to solve the optimization problem and obtain the optimal covert rate using Dinkelbach method. Simulation results show that the proposed system achieves the maximum covert rate when the phase of the IRS units and the trajectory and transmit power of the UAV are optimized jointly.

1. Introduction

Traditional cryptography mechanisms protect sensitive data by the encryption of messages into cipher text, thereby preventing access by unauthenticated users. However, cipher texts generated with cryptography mechanisms exhibit a high degree of randomization, which can easily arouse the suspicion of adversaries (e.g., eavesdroppers, hackers, crackers, etc.) [1]. In this case, more powerful decryption methods and mechanisms may be employed to crack randomized data streams, which can severely threaten the security of the information protected by the cryptography regime [2]. In this scenario, covert communication which can be used to transmit sensitive information without being perceived attracts tremendous attention [3].

In general, a transmitter can use covert communication to transmit sensitive data to legal receivers without the communication process being detected by malicious adversaries, which can provide a higher level of security to transmitters [4]. In covert communication systems, covert information can be carried by normal messages and transmitted together with these normal messages to avoid being perceived by adversaries [5]. Recently, covert communications have been intensively investigated in different scenarios. As an example, a covert communication system has been developed to conceal covert information in sound documents by utilizing sound information concealing systems [6]. However, the covert rate of this system is significantly limited by the implementing software. Furthermore, a large amount of public data are required to carry a very small amount of covert information. To cope with this problem, the authors of [7] proposed a system in which covert communication and secure transmission are jointly implemented in untrusted relaying networks by adopting a power allocation strategy. In this approach, there is a tradeoff between covertness and covert rate for covert communication systems. To increase the covert rate, multiple jammers have been introduced to the covert communication system [8], where friendly relaying nodes operate as jammers to cooperatively interfere with the adversary in order to aid in the receipt of private information. However, the small capacity and high bit error rate (BER) limits the application of traditional covert communication systems (CCS).

Intelligent reflecting surfaces (IRS) have been introduced into CCS to improve the efficiency and reliability of systems [9]. IRS, sometimes known as reconfigurable intelligent surfaces, is a low-cost technology that integrates a large number of passive reflecting units to intelligently adjust the reflected phase shift of signals in the environment [10]. Recently, IRS has been gradually applied to wireless CCS to improve its performance. Initially, an IRS-based method was proposed to take advantage of the smart controlled surfaces to modify unforeseen propagation conditions that could reveal messages [11]. The authors of [12] proposed an IRS-aided CCS system and jointly optimized the data rate, transmitting power, and reflection matrix of the IRS. To reduce computational complexity, a low-complexity penalty-based successive convex approximation (SCA) algorithm was proposed in [13] to jointly optimize the communication schedule and IRS reflection matrix. In [14,15], an IRS-aided CCS with multiple-input multiple-output (MIMO) was proposed; high coupling was exploited for alternative optimization to find the optimal solution. Similarly, non-orthogonal multiple access methods were adopted in [16,17] to design an IRS-assisted CCS, exploiting the phase shift uncertainty of the IRS as a cover medium to hide the existence of covert transmission. A passive IRS-assisted CCS was proposed in [18] to adjust the phase shifts of the IRS to align the phases of the received reflected signals while adjusting the reflection amplitude to satisfy the covert constraint. However, the covert information in IRS-assisted wireless CCS is vulnerable to adversaries.

To improve the security of wireless CCS, friendly nodes can be utilized to jam adversaries, as in [19,20]. Due to their fast deployment with flexible configurations and the presence of short-range line-of-sight links, unmanned aerial vehicles (UAVs) are frequently utilized as friendly nodes. A UAV equipped with a base station operates as a moving base station to provide comprehensive communication services. However, the exposure of the transmitted wireless signals to open space threatens the information security of communication systems that rely on UAVs [21]. To reduce this security threat, a communication protocol was proposed in [22] to ensure secure communication between UAVs and other UAVs as well as between UAV and ground users. For CCS, when the locations of legal users and monitors cannot be determined, the UAV can operate as a relaying node to deliver messages between the legal users covertly in order to avoid detection by monitors. In a pioneering work, a UAV-aided CCS was designed in [23], where the UAV trajectory and transmit power for the UAV were alternately optimized to maximize the average covert rate. Based on this, Xu proposed a model for UAV-assisted CCS with multiple users [24]. Similarly, the authors of [25] developed a multi-user mmWave covert communication system wherein proper covert beam training and data transmission between legitimate parties was designed. In order to cope with the complex communication environment, in [26] a UAV with multiple antennas was designed to jam the monitor in the CCS; this approach can account for multiple monitors colluding to listen to adjacent users. Similarly, Du proposed a multi-antenna UAV to assist a covert communication system, along with a power allocation algorithm that can be used to avoid detection from a monitor with multiple antennas [27]. Owing to the substantial enhancements in performance obtained by combining UAVs and IRS, numerous frameworks incorporating these technologies have been proposed [28,29,30]. However, the effective use of UAVs with IRS to design an efficient wireless covert communication system remains a challenging problem.

In this paper, we propose an IRS-assisted covert communication system with a friendly UAV, where the UAV can be utilized to reinforce message security and the IRS can be employed to improve the covert rate. Moreover, thanks to the high mobility of UAVs, the proposed CCS can be deployed in complex communication environments with various communication barriers, resulting in improved reliability. The contributions of this paper are listed as follows:

• We propose an IRS-assisted covert communication system in which a UAV operates as a jammer to interfere with the monitor and reduce the detection rate.
• We derive the minimum detection error probability (DEP) for the monitor by modeling the artificial noise (AN) power of the UAV as an uncertainty model, under the assumption that the coordinates of both the UAV and the transmitter are available.
• We formulate the optimization problem to maximize the covert rate for a covert communication system by optimizing the trajectory and transmitting power of the UAV. Furthermore, we develop an iterative algorithm that uses the SCA and Dinkelbach methods to solve the optimization problem.

The rest of this paper is organized as follows: Section 2 describes the system model; Section 3 formulates the optimization method, considering the goal of maximizing the covert rate for Bob; Section 4 presents the optimal algorithm designed to solve the problem described in Section 3; and Section 5 presents the simulation results of the algorithm. Finally, Section 6 concludes the paper.

2. System Model

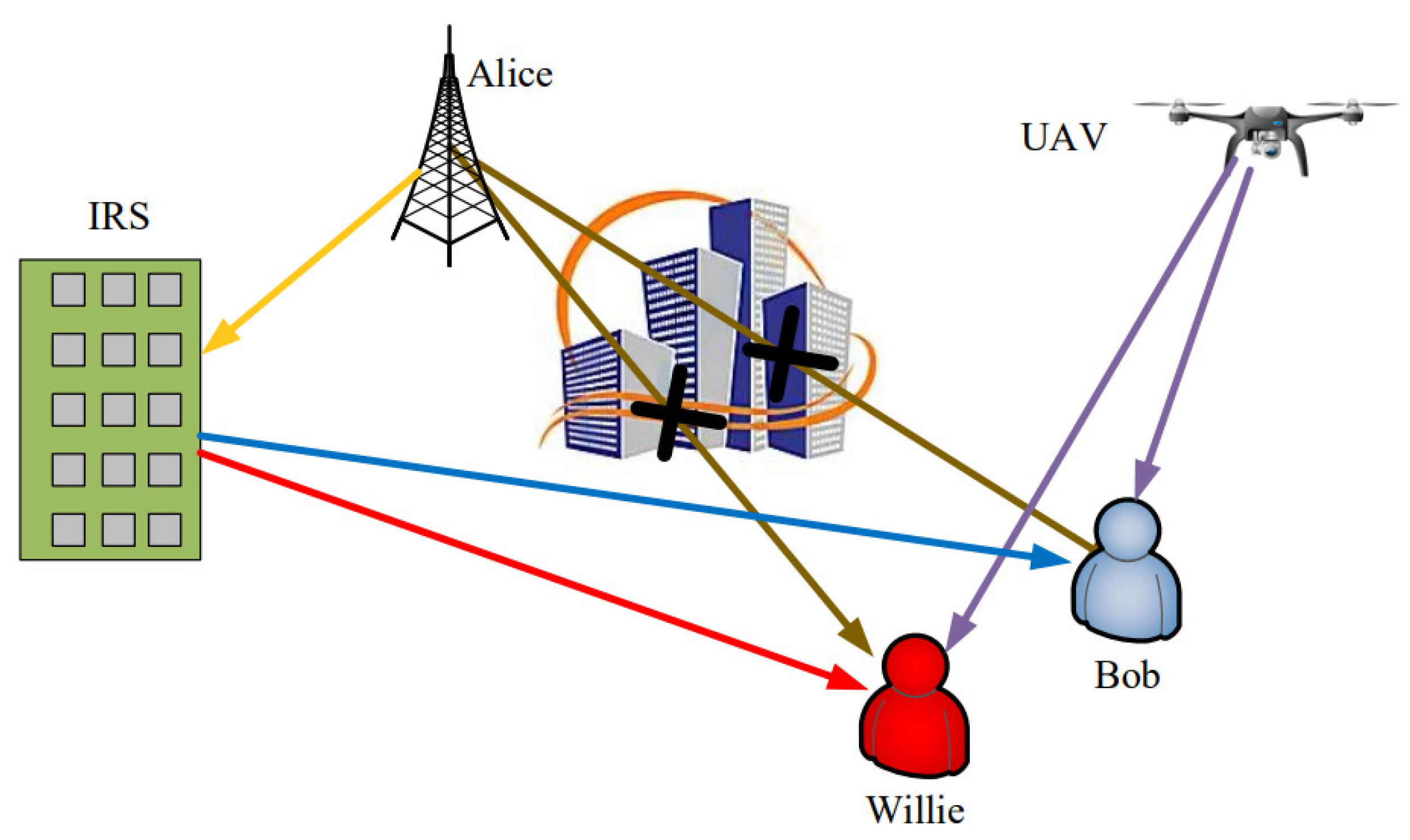
Figure 1 demonstrates an IRS-assisted CCS with a transmitter and receiver for covert messages and a monitor. The transmitter of covert messages, which generally is a base station, is denoted as Alice in a typical CCS, while the receiver is denoted as Bob. The monitor, denoted as Willie, observes communications between Alice and Bob to determine whether there is a covert communication channel between them. Because a large volume of barriers exists in the surroundings, such as in a city with large buildings, the links between Alice and Bob and between Alice and Willie are not line-of-sight (LoS). In this case, we propose deploying IRS on the surfaces of buildings to relay messages from Alice to Bob. However, if Willie is located close to Bob, the received signal power of Willie increases with that of Bob when adopting the IRS, which enlarges the probability of Willie detecting covert communication between Alice and Bob. Thus, we adopt a UAV as a friendly node used by Alice to interfere with Willie’s attempts to detect covert communication between Alice and Bob. In the proposed system, Alice acts as the coordinator who controls the UAV and IRS by delivering the control command and collecting the running parameters. The covert communication system works as both a hacking tool and as an important mechanism for transmitting secret information such as private keys. Therefore, such covert communication systems have become a novel solution for network authentication, copyright protection, and cybercrime evidence-gathering.

The fades of the channels are respectively denoted as $h_{AI}$ (Alice and IRS), $h_{IB}$ (IRS and Bob), and $h_{IW}$ (IRS and Willie). Let all nodes be in a three-dimensional Cartesian coordinate system, and let Alice, the IRS, Bob, and Willie be in the ground plane with a height of 0. Thus, their coordinates can be expressed as ${\omega }_A={\left[x_A,y_A\right]}^T$, ${\omega }_I={\left[x_I,y_I\right]}^T$, ${\omega }_B={\left[x_B,y_B\right]}^T$, and ${\omega }_W={\left[x_W,y_W\right]}^T$, respectively. Moreover, we assume here that the respective positions of Alice, the IRS, the UAV, Bob, and Willie are all known to each other. Because Willie knows the location of Bob, Willie’s location close to Bob leads to a significant increase in the detection rate of covert communication. Let the start and end coordinates of the UAV be $c_A$ and $c_F$, respectively; the UAV flies from the start coordinate to the coordinate in finite time N, where $N=TL$ and L is the length of a single time slot, allowing N to be divided into T intervals. Let H be the altitude of the UAV and M the number of IRS units. Changes in the flying altitude of the UAV change the power of the received jamming signals at Willie’s location, leading to different detection rates of covert communication. Here, $V_{max}$ denotes the maximum speed of the UAV, which may influence the covert rate of the system, and P denotes the transmission power of the base station.

We define $C={\left[c\right[1],c[2],\dots ,c[T\left]\right]}^T$ as the set of UAV coordinates; thus, letting $c\left[T\right]=c_F$$,c\left[1\right]=c_A$, we have

$${∥c[t+1]-c\left[t\right]∥}^2\le D^2,$$

(1)

where $c\left[t\right]={\left[x\right[t],y[t\left]\right]}^T$ represents the position of the UAV in the t-th time slot, $V_{max}$ is the maximum speed of the UAV, and $D=V_{max}L$.

In addition, the IRS consists of M reflecting elements. The phase shift and amplitude of the IRS in the t-th time slot are defined as a matrix $\mathrm{\Theta }\left[t\right]=diag\{{\alpha }_1{e}^{j{\alpha }_1\left[t\right]},\dots ,{\alpha }_M{e}^{j{\theta }_M\left[t\right]}\}$, where ${\alpha }_m\left[t\right]\in [0,1]$. When the optimal amplitude is obtained, $\alpha$ can be set as 1, allowing the diagonal matrix to be rewritten as $\mathrm{\Theta }\left[t\right]=diag\{e^{j{\theta }_1\left[\mathrm{t}\right]},\dots ,e^{j{\theta }_M\left[t\right]}\}$.

2.1. Channel Model

In a practical system, due to the high altitude of the UAV the UAV-to-ground communications can be treated as line-of-sight (LOS) links. Therefore, we model the UAV-to-ground communication channel as a free-space path loss model, where the signal can propagate along a straight line without obstacles between the transmitter and the receiver. In this scenario, the gain of the channel between the UAV and Bob can be described as

$$h_{UB}\left[t\right]=\sqrt{{\beta }_0{d}_{UB}^{-2}\left[t\right]}=\sqrt{\frac{{\beta }_0}{H^2+∥c\left[t\right]-{\omega }_B∥}}.$$

(2)

Similarly, the channel gain between the UAV and Willie is

$$h_{UW}\left[t\right]=\sqrt{{\beta }_0{d}_{UW}^{-2}\left[t\right]}=\sqrt{\frac{{\beta }_0}{H^2+∥c\left[t\right]-{\omega }_W∥}},$$

(3)

where ${\beta }_0$ is the channel power gain over the channel at distance $D_0=$ 1 m. The channel between Alice, Bob, and Willie is considered a non-line-of-sight (NLOS) channel due to the blockage caused by obstacles. Consider the IRS as a uniform linear array (ULA) antenna, i.e., a system of antennas arranged in a plane according to a linear law, called an antenna array. Then, the gain of the channel from Alice and IRS is

$$h_{AI}\left[t\right]=\sqrt{{\beta }_0{d}_{AI}^{-\alpha }\left[t\right]}{\left[1,e^{-j\frac{2\pi }{\lambda }d{\varphi }_{AI}\left[t\right]},\dots ,e^{-j\frac{2\pi }{\lambda }d(M-1){\varphi }_{AI}\left[t\right]}\right]}^T,$$

(4)

where $\alpha$ denotes the path loss, $d_{AI}\left[t\right]=\sqrt{{∥w_A-w_I∥}^2}$ is the distance between Alice and IRS, ${\varphi }_{AI}\left[n\right]$ is the cosine of the AoA of the signal from the UAV to the IRS in the t-th time slot, d is the antenna distance, and $\lambda$ is the carrier wavelength.

Similarly, the channels from the IRS to Bob and Willie are considered LOS channels; thus, the fading of the channels between IRS and Bob and Willie can be respectively expressed as

$$h_{IB}\left[t\right]=\sqrt{{\beta }_0{d}_{IB}^{-\alpha }\left[t\right]}{\left[1,e^{-j\frac{2\pi }{\lambda }d{\varphi }_{IB}\left[t\right]},\dots ,e^{-j\frac{2\pi }{\lambda }d(M-1){\varphi }_{IB}\left[t\right]}\right]}^T,$$

(5)

and

$$h_{IW}\left[t\right]=\sqrt{{\beta }_0{d}_{IW}^{-\alpha }\left[t\right]}{\left[1,e^{-j\frac{2\pi }{\lambda }d{\varphi }_{IW}\left[t\right]},\dots ,e^{-j\frac{2\pi }{\lambda }d(M-1){\varphi }_{IW}\left[t\right]}\right]}^T,$$

(6)

where $d_{IB}\left[t\right]=\sqrt{{∥w_I-w_B∥}^2}$ is the distance between the IRS and Bob, $d_{IW}\left[t\right]=\sqrt{{∥w_I-w_W∥}^2}$ is the distance between the IRS and Willie, and ${\varphi }_{IB}\left[t\right]$ and ${\varphi }_{IW}\left[t\right]$ are the cosines of the angles of departure (AoD) of the signals that Bob and Willie receive from the IRS, respectively.

Assuming that the channel utilization tends to be maximized in each time slot according to (3)–(5), the signal received by Bob is

$$y_B\left[t\right]=\sqrt{P_a\left[t\right]}\left(h_{IB}^H\left[t\right]\mathrm{\Theta }\left[t\right]h_{AI}\left[t\right]\right)x_a\left[t\right]+\sqrt{P_u\left[t\right]}{h}_{UB}\left[t\right]x_u\left[t\right]+n_B\left[t\right],$$

(7)

where $P_a\left[t\right]$ is the transmitting power of Alice and $x_a\left[t\right]$ is the signal sent by Alice in the t-th time slot, which follows a complex Gaussian distribution with mean 0 and variance 1, i.e., $x_a\left[t\right]\sim CN(0,1)$. Moreover, $x_u\left[t\right]$ is the AN signal transmitted by the UAV, which satisfies $\mathbb{E}\left[{\left|x_u\left[t\right]\right|}^2\right]=1$; $n_B\left[t\right]$ is the AWGN, with mean 0 and variance ${\sigma }_b^2$ at Bob, i.e., $n_B\left[t\right]\sim CN(0,{\sigma }_b^2)$; and $P_u\left[t\right]$ is the AN transmit power of the UAV, which follows a uniform distribution over the interval $\left[0,{\hat{P}}_u\left[t\right]\right]$, where ${\hat{P}}_u\left[t\right]$ is the maximum AN transmit power of the UAV and takes values in the range $\left[0,{\hat{P}}_{u,max}\left[t\right]\right]$.

Accordingly, the Probability Density Function (PDF) is expressed as

$$f_{P_u\left[t\right]}\left(x\right)=\left\{\begin{array}{cc}\frac{1}{{\hat{P}}_u\left[t\right]},& 0\le x\le {\hat{P}}_u\left[t\right]\\ 0,& otherwise.\end{array}\right.$$

(8)

According to (7), the receiving rate of Bob is

$$C\left[t\right]={log}_2\left(1+\frac{P_a\left[t\right]{\left|h_{IB}^H\left[t\right]\mathrm{\Theta }\left[t\right]h_{AI}\left[t\right]\right|}^2}{P_u\left[t\right]{\left|h_{UB}\left[t\right]\right|}^2+{\sigma }_b^2}\right).$$

(9)

2.2. Detection on CCS by Willie

In this subsection, Willie determines the presence of covert communications by analyzing the received signals. To detect covert communications, Willie employs the hypothesis testing method. Willie first perceives the location of Alice, the UAV, and the IRS; then, according to (3), (4), and (6), the received signal at Willie’s location can be obtained as follows:

$$y_W\left[t\right]=\left\{\begin{array}{cc}\sqrt{P_u\left[t\right]}{h}_{UW}\left[t\right]x_u\left[t\right]+n_W\left[t\right],& H_0\\ \sqrt{P_a\left[t\right]}\left(h_{IW}^H\left[t\right]\mathrm{\Theta }\left[t\right]h_{AI}\left[t\right]\right)x_a\left[t\right]+\sqrt{P_u\left[t\right]}{h}_{UW}\left[t\right]x_u\left[t\right]+n_W\left[t\right],& H_1,\end{array}\right.$$

(10)

where $H_0$ indicates that there is no covert message transmitted between the UAV and Bob, $H_1$ indicates the opposite, and $n_W\left[t\right]$ is the additive white Gaussian noise (AWGN) with mean 0 and variance ${\sigma }_w^2$ at Willie’s location, i.e., $n_W\left[t\right]\sim CN(0,{\sigma }_w^2)$. Because the data rate tends to be the same in each time slot, the received power at Willie’s location can be expressed as

$$\mathbb{R}\left[t\right]=\left\{\begin{array}{cc}{P}_u\left[t\right]{\left|h_{UW}\left[t\right]\right|}^2+{\sigma }_w^2,& H_0\\ P_a\left[t\right]{\left|h_{IW}^H\left[t\right]\mathrm{\Theta }\left[t\right]h_{AI}\left[t\right]\right|}^2+P_u\left[t\right]{\left|h_{UW}\left[t\right]\right|}^2+{\sigma }_w^2,& H_1.\end{array}\right.$$

(11)

Assuming that Willie employs a radiometer detector in each time slot to detect transmissions from Alice to Bob, we can consider $\tau \left[t\right]$ to be Willie’s detection threshold. If $\mathbb{R}\left[t\right]>\tau \left[t\right]$, then the decision state is $D_1$, indicating that Willie determines that covert communication exists between the UAV and Bob. Otherwise, the decision state is $D_0$, indicating that Willie determines that no covert message is being transmitted. Thus, Willie’s decision rule can be denoted as

$$D\left[t\right]=\left\{\begin{array}{c}\hfill D_1,\mathbb{R}\left[t\right]>\tau \left[t\right]\hfill \\ \hfill D_0,\mathbb{R}\left[t\right]<\tau \left[t\right].\hfill \end{array}\right.$$

(12)

3. System Optimization

In this section, we first derive the false alarm probability (FAP) and the missed detection probability (MDP) for Willie, then derive the closed-form detection error probability (DEP). Under the constraint that the derived DEP of Willie is optimal, we formulate the optimization problem to maximize the covert rate.

3.1. Optimal DEP for Willie

To optimize the DEP for Willie, we first present the definition of FAP and MDP. On the one hand, the FAP is the probability of Willie determining that there is covert communication between Alice and Bob when no such communication exists, denoted as $P_{FA}\left[t\right]$. According to (11), we have

$$P_{FA}\left[t\right]=Pr\left(D_1|H_0\right)=Pr\left(P_u\left[t\right]{\left|h_{UW}\left[t\right]\right|}^2+{\sigma }_w^2>\tau \left[t\right]|H_0\right).$$

(13)

On the other hand, the MDP is the probability of Willie determining that there is no covert message transmitted from Alice to Bob when in fact there is covert communication, denoted as $P_{MD}\left[t\right]$. According to (12), we have

$$\begin{array}{cc}\hfill P_{MD}\left[t\right]& =Pr\left(D_0|H_1\right)\hfill \\ \hfill & =Pr\left(P_a\left[t\right]{\left|h_{IW}^H\left[t\right]\mathrm{\Theta }\left[t\right]h_{AI}\left[t\right]\right|}^2+P_u\left[t\right]{\left|h_{UW}\left[t\right]\right|}^2\right.\left.+{\sigma }_w^2<\tau \left[t\right]|H_1\right).\hfill \end{array}$$

(14)

According to (13) and (14), the DEP for Willie to detect covert communication between Alice and Bob is

$$\xi \left[t\right]=P_{FA}\left[t\right]+P_{MD}\left[t\right],$$

(15)

where $\xi \left[t\right]\ge 1-\epsilon$ and $\epsilon$ is the specific value for determining the required covertness.

According to (8) and (13), the FAP for Willie is expressed as

$$P_{FA}\left[t\right]=\left\{\begin{array}{cc}1,\hfill & \tau \left[t\right]<{\sigma }_w^2\hfill \\ 1-\frac{\tau \left[t\right]-{\sigma }_w^2}{{\zeta }_1\left[t\right]},\hfill & {\sigma }_w^2\le \tau \left[t\right]\le {\zeta }_1\left[t\right]+{\sigma }_w^2\hfill \\ 0,\hfill & \tau \left[t\right]>{\zeta }_1\left[t\right]+{\sigma }_w^2,\hfill \end{array}\right.$$

(16)

where ${\zeta }_1\left[t\right]={\hat{P}}_u\left[t\right]{\left|h_{UW}\left[t\right]\right|}^2$.

Equally, according to (8) and (14), Willie’s MDP in the t-th time slot is

$$P_{MD}\left[t\right]=\left\{\begin{array}{cc}0,\hfill & \tau \left[t\right]<{\zeta }_2\left[t\right]+{\sigma }_w^2\hfill \\ \frac{\tau \left[t\right]-{\zeta }_2\left[t\right]-{\sigma }_w^2}{{\zeta }_1\left[t\right]},\hfill & {\zeta }_2\left[t\right]+{\sigma }_w^2\le \tau \left[t\right]\le {\zeta }_1\left[t\right]+{\zeta }_2\left[t\right]+{\sigma }_w^2\hfill \\ 1,\hfill & \tau \left[t\right]>{\zeta }_1\left[t\right]+{\zeta }_2\left[t\right]+{\sigma }_w^2,\hfill \end{array}\right.$$

(17)

where ${\zeta }_2\left[t\right]=P_a\left[t\right]{\left|h_{IW}^H\left[t\right]\mathrm{\Theta }\left[t\right]h_{AI}\left[t\right]\right|}^2$.

To optimize DEP, we can define a detection threshold ${\tau }^{*}\left[t\right]$ that corresponds to an optimal detection error rate ${\xi }^{*}\left[t\right]$. Then, the DEP for Willie can be expressed as

$$\xi \left[t\right]=\left\{\begin{array}{cc}1,\hfill & \tau \left[t\right]<{\sigma }_w^2\hfill \\ 1-\frac{\tau \left[t\right]-{\sigma }_w^2}{{\zeta }_1\left[t\right]},\hfill & {\sigma }_w^2\le \tau \left[t\right]<{\zeta }_2\left[t\right]+{\sigma }_w^2\hfill \\ \frac{{\zeta }_1\left[t\right]-{\zeta }_2\left[t\right]}{{\zeta }_1\left[t\right]},\hfill & {\zeta }_2\left[t\right]+{\sigma }_w^2\le \tau \left[t\right]<{\zeta }_1\left[t\right]+{\sigma }_w^2\hfill \\ \frac{\tau \left[t\right]-{\zeta }_2\left[t\right]-{\sigma }_w^2}{{\zeta }_1\left[t\right]},\hfill & {\zeta }_1\left[t\right]+{\sigma }_w^2\le \tau \left[t\right]<{\zeta }_1\left[t\right]+{\zeta }_2\left[t\right]+{\sigma }_w^2\hfill \\ 1,\hfill & \tau \left[t\right]\ge {\zeta }_1\left[t\right]+{\zeta }_2\left[t\right]+{\sigma }_w^2.\hfill \end{array}\right.$$

(18)

Note that ${\zeta }_1\left[t\right]>{\zeta }_2\left[t\right]$, as the UAV is used to interfere with Willie. According to (18), when $\tau \left[t\right]<{\sigma }_w^2$ and $\tau \left[t\right]\ge {\zeta }_1\left[t\right]+{\zeta }_2\left[t\right]+{\sigma }_w^2$, an error is detected for $\xi \left[t\right]=1$. Therefore, these two cases are not considered by Willie. When ${\sigma }_w^2\le \tau \left[t\right]<{\zeta }_2\left[t\right]+{\sigma }_w^2$, we have

$$\frac{\partial \xi \left[t\right]}{\partial \tau \left[t\right]}=-\frac{1}{{\zeta }_1\left[t\right]}<0.$$

(19)

Similarly, When ${\zeta }_1\left[t\right]+{\sigma }_w^2\le \tau \left[t\right]<{\zeta }_1\left[t\right]+{\zeta }_2\left[t\right]+{\sigma }_w^2$, we have

$$\frac{\partial \xi \left[t\right]}{\partial \tau \left[t\right]}=\frac{1}{{\zeta }_1\left[t\right]}>0.$$

(20)

According to (18)–(20), when ${\sigma }_w^2\le \tau \left[t\right]<{\zeta }_2\left[t\right]+{\sigma }_w^2$, then ${\xi }_t$ is monotone declining with regard to ${\tau }_t$. When ${\zeta }_2\left[t\right]+{\sigma }_w^2\le \tau \left[t\right]<{\zeta }_1\left[t\right]+{\sigma }_w^2$, c is a constant.

If ${\zeta }_1\left[t\right]+{\sigma }_w^2\le \tau \left[t\right]<{\zeta }_1\left[t\right]+{\zeta }_2\left[t\right]+{\sigma }_w^2$, then $\xi \left[t\right]$ is monotone increasing with regard to $\tau \left[t\right]$. As a result, $\xi \left[t\right]$ is first decreasing and then increasing for $\tau \left[t\right]$. If the detection threshold ${\tau }^{*}\left[t\right]$ is in the range ${\zeta }_2\left[t\right]+{\sigma }_w^2\le {\tau }^{*}\left[t\right]<{\zeta }_1\left[t\right]+{\sigma }_w^2$, then the corresponding best detection error rate is expressed as follows:

$${\xi }^{*}\left[t\right]=\frac{{\zeta }_1\left[t\right]-{\zeta }_2\left[t\right]}{{\zeta }_1\left[t\right]}=\frac{{\hat{P}}_u\left[t\right]{\left|h_{UW}\left[t\right]\right|}^2-P_a\left[t\right]{\left|h_{IW}^H\left[t\right]\mathrm{\Theta }\left[t\right]h_{AI}\left[t\right]\right|}^2}{{\hat{P}}_u\left[t\right]{\left|h_{UW}\left[t\right]\right|}^2}.$$

(21)

3.2. Reliability of CCS

When the UAV interferes with Willie in receiving signals, Bob is interfered with as well, which may reduce the covert rate and exert an influence on the reliability of the CCS. According to (9), the outage probability of the covert channel between Alice and Bob is provided by

$$\begin{array}{cc}\hfill P_{out}\left[t\right]& =Pr\left(C\left[t\right]<R_b\left[t\right]\right)\hfill \\ \hfill & =Pr\left(\frac{P_a\left[t\right]{\left|h_{IB}^H\left[t\right]\mathrm{\Theta }\left[t\right]h_{AI}\left[t\right]\right|}^2}{P_u\left[t\right]{\left|h_{UB}\left[t\right]\right|}^2+{\sigma }_b^2}<2^{R_b\left[t\right]}-1\right)\hfill \\ \hfill & =Pr\left(\frac{z}{\left(2^{R_b\left[t\right]}-1\right){\left|h_{UB}\left[t\right]\right|}^2}-\frac{{\sigma }_b^2}{{\left|h_{UB}\left[t\right]\right|}^2}<P_u\left[t\right]\right)\hfill \\ \hfill & ={\int }_{\frac{z}{\left(2^{R_b\left[t\right]}-1\right){\left|h_{UB}\left[t\right]\right|}^2}-\frac{{\sigma }_b^2}{{\left|h_{UB}\left[t\right]\right|}^2}}^{{\hat{P}}_u\left[t\right]}{f}_{P_u\left[t\right]}\left(x\right)dx\hfill \\ \hfill & =1-\frac{z}{\left(2^{R_b\left[t\right]}-1\right){\hat{P}}_u\left[t\right]{\left|h_{UB}\left[t\right]\right|}^2}+\frac{{\sigma }_b^2}{{\hat{P}}_u\left[t\right]{\left|h_{UB}\left[t\right]\right|}^2},\hfill \end{array}$$

(22)

where $R_b\left[t\right]$ is the transmission rate of Bob.

Considering the upper bound on the outage probability as $P_{out}^{*}\left[t\right]$, i.e., when the outage probability satisfies $P_{out}\left[t\right]\le P_{out}^{*}\left[t\right]$, the reliability of the covert channel between Bob and Alice can be guaranteed. From (22), we know that $P_{out}\left[t\right]$ is monotone increasing with regard to $R_b\left[t\right]$. Thus, as the covert rate $R_b\left[t\right]$ achieves its maximum value, the outage probability reaches its upper limit $P_{out}^{*}\left[t\right]$. Then, the maximum covert rate is provided by

$$R_b\left[t\right]={log}_2\left(1+\frac{P_a\left[t\right]{\left|h_{IB}^H\left[t\right]\mathrm{\Theta }\left[t\right]h_{AI}\left[t\right]\right|}^2}{\left(1-P_{out}^{*}\left[t\right]\right){\hat{P}}_u\left[t\right]{\left|h_{UB}\left[t\right]\right|}^2+{\sigma }_b^2}\right).$$

(23)

To ensure covertness, the UAV is used to jam Willie while maximizing the average received rate of Bob. Therefore, the maximization of the covert rate can be formulated as a joint optimization problem of the UAV trajectory, the IRS phase shift, the transmitting power at Alice’s location, and the transmitting power of the UAV. According to (21) and (22), this optimization problem can be expressed as

$$\begin{array}{cc}\hfill & \hfill \underset{C,\mathrm{\Theta },P,{\hat{P}}_u}{max}\frac{1}{T}{\sum }_{t=1}^T{R}_b\left[t\right],\hfill \\ \hfill s.t.\end{array}$$

(24)

$$\begin{array}{c}\hfill {\xi }^{*}\left[t\right]\ge 1-\epsilon ,\hfill \end{array}$$

(25)

$$\begin{array}{c}\hfill 0\le {\theta }_m\left[t\right]\le 2\pi ,\hfill \end{array}$$

(26)

$$\begin{array}{c}\hfill 0\le {\hat{P}}_u\left[t\right]\le {\hat{P}}_{u,max}\left[t\right],\hfill \end{array}$$

(27)

$$\begin{array}{c}\hfill 0\le P\left[t\right]\le P_{max}\left[t\right],\hfill \end{array}$$

(28)

$$\begin{array}{c}\hfill {∥c[t+1]-c\left[t\right]∥}^2\le D^2,\hfill \end{array}$$

(29)

$$\begin{array}{c}\hfill c\left[T\right]=c_F,c\left[1\right]=c_A,\hfill \end{array}$$

(30)

where $C\stackrel{\mathsf{\Delta }}{=}\left\{c\right[t],\forall t\}$ and $\mathrm{\Theta }\stackrel{\mathsf{\Delta }}{=}\{{\theta }_m\left[t\right],\forall m,t\}$; here, (24) is a linear objective function and (29) and (30) are mobility constraints of the UAV with convexity. However, (25) is non-convex about C and $\mathrm{\Theta }$, which results in this optimization problem not being solved efficiently.

4. Optimization Algorithm

To solve (24), we can decompose it into two separate problems: optimization of the Alice’s transmitting power and the AN power of the UAV, and optimization of the UAV’s trajectory. For this purpose, the phase of the received signal is first used to obtain the maximum transmission rate, allowing the optimal pahase shift of the IRS to be obtained. Then, (24) is transformed into a trajectory optimization problem for the UAV. Finally, we formulate the optimal trajectory optimization problem with the SCA method.

4.1. Phase Shift Optimization for IRS

To optimize the phase shift of the IRS, $h_{IB}^H\left[t\right]\mathrm{\Theta }\left[t\right]h_{AI}\left[t\right]$ in (23) can be expressed as

$$h_{IB}^H\left[t\right]\mathrm{\Theta }\left[t\right]h_{AI}\left[t\right]=\frac{{\beta }_0{\displaystyle \sum _{m=1}^M}{e}^{j\left({\theta }_m\left[t\right]+\frac{2\pi }{\lambda }d\left(m-1\right)\left({\varphi }_{IB}\left[t\right]-{\varphi }_{AI}\left[t\right]\right)\right)}}{\sqrt{d_{IB}^{\alpha }\left[t\right]d_{AI}^{\alpha }\left[t\right]}}.$$

(31)

Then, Bob can combine the signals transmitted from different paths via the IRS and the received power of the combined signals can be increased in order to improve the covert rate. The phase shift of the IRS can now be expressed as

$$\begin{array}{cc}\hfill {\theta }_1\left[t\right]& ={\theta }_2\left[t\right]+\frac{2\pi }{\lambda }d\left({\varphi }_{IB}\left[t\right]-{\varphi }_{AI}\left[t\right]\right)\hfill \\ \hfill & ={\theta }_M\left[t\right]+\frac{2\pi }{\lambda }d\left(M-1\right)\left({\varphi }_{IB}\left[t\right]-{\varphi }_{AI}\left[t\right]\right)\hfill \\ \hfill & =\omega ,\hfill \end{array}$$

(32)

where $\omega =[0,2\pi ]$ is the direction to be aligned. Thus, the cell phase shift of the m-th IRS can be expressed as

$${\theta }_m\left[t\right]=\frac{2\pi }{\lambda }d\left(m-1\right)\left({\varphi }_{AI}\left[t\right]-{\varphi }_{IB}\left[t\right]\right)+\omega .$$

(33)

For simplicity, we substitute (33) into (31); the maximum value can be approximated by deriving the upper bound on ${\left|h_{IB}^H\left[t\right]\mathrm{\Theta }\left[t\right]h_{AI}\left[t\right]\right|}^2$ with

$$\begin{array}{c}{\left|h_{IB}^H\left[t\right]\mathrm{\Theta }\left[t\right]h_{AI}\left[t\right]\right|}^2={\left|\frac{{\beta }_0{\displaystyle \sum _{m=1}^M}{e}^{j\left({\theta }_m\left[t\right]+\frac{2\pi }{\lambda }d\left(m-1\right)\left({\varphi }_{IB}\left[t\right]-{\varphi }_{AI}\left[t\right]\right)\right)}}{\sqrt{d_{IB}^{\alpha }\left[t\right]d_{AI}^{\alpha }\left[t\right]}}\right|}^2={\left|\frac{{\beta }_{0}M{e}^{j\omega }}{\sqrt{d_{IB}^{\alpha }\left[t\right]d_{AI}^{\alpha }\left[t\right]}}\right|}^2\le \frac{{\beta }_0^2{M}^2}{d_{IB}^{\alpha }\left[t\right]d_{AI}^{\alpha }\left[t\right]}.\end{array}$$

(34)

Then, through phase alignment, we can obtain the best $\mathrm{\Theta }$.

4.2. Power Optimization

For a given C, the optimization problem formulated in (24) can be rewritten as

$$\begin{array}{cc}\hfill & \hfill \underset{P,{\hat{P}}_u}{max}\frac{1}{T}{\sum }_{t=1}^T{R}_b\left[t\right],\hfill \\ \hfill s.t.\end{array}$$

(35)

$$\begin{array}{c}\hfill {\xi }^{*}\left[t\right]\ge 1-\epsilon ,\end{array}$$

(36)

$$\begin{array}{cc}\hfill & \hfill 0\le {\hat{P}}_u\left[t\right]\le {\hat{P}}_{u,max}\left[t\right],\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill & \hfill 0\le P\left[t\right]\le P_{max}\left[t\right],\hfill \end{array}$$

(38)

where (35) and (36) are non-convex functions and are not easily solvable. To solve the problem, $R_b$ in (35) can be re-expressed as

$${\gamma }_b=\frac{P_a\left[t\right]{\left|h_{IB}^H\left[t\right]\mathrm{\Theta }\left[t\right]h_{AI}\left[t\right]\right|}^2}{\left(1-P_{out}^{*}\left[t\right]\right){\hat{P}}_u\left[t\right]{\left|h_{UB}\left[t\right]\right|}^2+{\sigma }_b^2}.$$

(39)

According to Dinkelbach’s theory, (39) can be transformed into a linear function with an equation factor $\eta$ as follows:

$$\frac{P_a\left[t\right]{\left|h_{IB}^H\left[t\right]\mathrm{\Theta }\left[t\right]h_{AI}\left[t\right]\right|}^2}{\left(1-P_{out}^{*}\left[t\right]\right){\hat{P}}_u\left[t\right]{\left|h_{UB}\left[t\right]\right|}^2+{\sigma }_b^2}=\eta ,$$

(40)

where the initial value of $\eta$ is obtained by choosing the small maximum values for $P_a\left[t\right]$ and ${\hat{P}}_u\left[t\right]$.

According to (21) and (37), this can be equivalently expressed as

$$P_a\left[t\right]{\left|h_{IW}^H\left[t\right]\mathrm{\Theta }\left[t\right]h_{AI}\left[t\right]\right|}^2-\epsilon {\hat{P}}_u\left[t\right]{\left|h_{UW}\left[t\right]\right|}^2\le 0.$$

(41)

According to (40) and (41), (35) can be rewritten as

$$\begin{array}{cc}\hfill & \hfill \underset{P,{\hat{P}}_u}{max}\frac{1}{T}{\sum }_{t=1}^T\left(P_a\left[t\right]{\left|h_{IB}^H\left[t\right]\mathrm{\Theta }\left[t\right]h_{AI}\left[t\right]\right|}^2-\eta {\hat{P}}_u\left[t\right]\left(1-P_{out}^{*}\left[t\right]\right){\left|h_{UB}\left[t\right]\right|}^2-\eta {\sigma }_b^2\right),\hfill \\ \hfill s.t.\end{array}$$

(42)

$$\begin{array}{c}\hfill P_a\left[t\right]{\left|h_{IW}^H\left[t\right]\mathrm{\Theta }\left[t\right]h_{AI}\left[t\right]\right|}^2-\epsilon {\hat{P}}_u\left[t\right]{\left|h_{UW}\left[t\right]\right|}^2\le 0,\end{array}$$

(43)

$$\begin{array}{cc}\hfill & \hfill 0\le {\hat{P}}_u\left[t\right]\le {\hat{P}}_{u,max}\left[t\right],\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill & \hfill 0\le {\hat{P}}_u\left[t\right]\le {\hat{P}}_{u,max}\left[t\right],\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill & \hfill 0\le P\left[t\right]\le P_{max}\left[t\right].\hfill \end{array}$$

(46)

Because (42) and (43) are convex functions, the optimal $P,{\hat{P}}_u$ can be obtained by using the CVX solver, where the values of $\eta$ can be updated with (40).

4.3. Optimization of UAV Trajectory

For a given P and ${\hat{P}}_u$, the alternative to (24) is

$$\begin{array}{cc}\hfill & \hfill \underset{Q}{max}\frac{1}{T}{\sum }_{t=1}^T{log}_2\left(1+\frac{A\left[t\right]}{\frac{\left(1-P_{out}^{*}\left[t\right]\right){\beta }_0{\hat{P}}_u\left[t\right]}{H^2+{∥c\left[t\right]-w_B∥}^2}+{\sigma }_b^2}\right),\hfill \\ \hfill s.t.\end{array}$$

(47)

$$\begin{array}{c}\hfill {\xi }^{*}\left[t\right]\ge 1-\epsilon ,\end{array}$$

(48)

$$\begin{array}{cc}\hfill & \hfill 0{∥c[t+1]-c\left[t\right]∥}^2\le D^2,\hfill \end{array}$$

(49)

$$\begin{array}{cc}\hfill & \hfill c\left[T\right]=c_F,c\left[1\right]=c_A,\hfill \end{array}$$

(50)

where $A\left[t\right]=P_a\left[t\right]{\beta }_0^2{M}^2/\phantom{P_a\left[t\right]{\beta }_0^2{M}^2{d}_{IB}^{\alpha }\left[t\right]d_{AI}^{\alpha }\left[t\right]}{d}_{IB}^{\alpha }\left[t\right]d_{AI}^{\alpha }\left[t\right]$ and (47) and (48) are non convex. According to (21), (36) can be rewritten as

$$H^2+{∥c\left[t\right]-w_W∥}^2\le \frac{\epsilon {\hat{P}}_u\left[t\right]{\beta }_0}{P_a\left[t\right]{\left|h_{IW}^H\left[t\right]\mathrm{\Theta }\left[t\right]h_{AI}\left[t\right]\right|}^2}.$$

(51)

The right side of (51) is a constant with all known variables, and the left side of (51) includes the variables to be optimized. The distance between the UAV and Bob or Willie can be expressed as $d_l\left[t\right]=\sqrt{H^2+{∥c\left[t\right]-w_j∥}^2}$, where $l=\{UB,UW\}$ and $j=\{B,W\}$. For $d_l^2\left[t\right]$, we have

$$d_l^2\left[t\right]=H^2+∥c\left[t\right]-w_j∥={\left(x\left[t\right]-x_j\right)}^2+{\left(y\left[t\right]-y_j\right)}^2+H^2.$$

(52)

The first-order partial derivatives of $d_l^2\left[t\right]$ with respect to $x\left[t\right]$ and $y\left[t\right]$ are respectively expressed as

$$\frac{\partial d_l^2\left[t\right]}{\partial x\left[t\right]}=2\left(x\left[t\right]-x_j\right)$$

(53)

and

$$\frac{\partial d_l^2\left[t\right]}{\partial y\left[t\right]}=2\left(y\left[t\right]-y_j\right).$$

(54)

According to (53) and (54), we have

$$\frac{{\partial }^2{d}_l^2\left[t\right]}{\partial x^2\left[t\right]}=\frac{{\partial }^2{d}_l^2\left[t\right]}{\partial y^2\left[t\right]}=2$$

(55)

and

$$\frac{{\partial }^2{d}_l^2\left[t\right]}{\partial x\left[t\right]y\left[t\right]}=\frac{{\partial }^2{d}_l^2\left[t\right]}{\partial y\left[t\right]x\left[t\right]}=0.$$

(56)

Therefore, the Hessian matrix ${\nabla }^2{d}_l^2\left[t\right]$ can be obtained with (53)–(56), provided by

$${\nabla }^2{d}_l^2\left[t\right]=\left(\begin{array}{cc}\begin{array}{c}\frac{{\partial }^2{d}_l^2\left[t\right]}{\partial x^2\left[t\right]}\\ \frac{{\partial }^2{d}_l^2\left[t\right]}{\partial y\left[t\right]x\left[t\right]}\end{array}& \begin{array}{c}\frac{{\partial }^2{d}_l^2\left[t\right]}{\partial x\left[t\right]y\left[t\right]}\\ \frac{{\partial }^2{d}_l^2\left[t\right]}{\partial y^2\left[t\right]}\end{array}\end{array}\right)=\left(\begin{array}{cc}\begin{array}{c}2\\ 0\end{array}& \begin{array}{c}0\\ 2\end{array}\end{array}\right).$$

(57)

Due to $\frac{{\partial }^2{d}_l^2\left[t\right]}{\partial x^2\left[t\right]}>0$ and $\frac{{\partial }^2{d}_l^2\left[t\right]}{\partial y^2\left[t\right]}>0$, the Hessian matrix ${\nabla }^2{d}_l^2\left[t\right]$ is a positive definite matrix, which means that $d_l^2\left[t\right]$ is a convex function. The left side of the inequality in (51) is consequently a convex function; thus, (48) can be replaced by a convex function. For (47), we can relax the objective function by introducing relaxation variables $u\stackrel{\mathsf{\Delta }}{=}\{u[t],\forall t\}$ and $v\stackrel{\mathsf{\Delta }}{=}\{v[t],\forall t\}$. Therefore, (47) can be rewritten as

$$\begin{array}{cc}\hfill & \hfill \underset{Q,u,v}{max}\frac{1}{T}{\sum }_{t=1}^{T}u\left[t\right],\hfill \\ \hfill s.t.\end{array}$$

(58)

$$\begin{array}{c}\hfill H^2+{∥c\left[t\right]-w_W∥}^2\le B\left[t\right],\end{array}$$

(59)

$$\begin{array}{cc}\hfill & \hfill u\left[t\right]\le {log}_2\left(1+\frac{A\left[t\right]}{\frac{\left(1-P_{out}^{*}\left[t\right]\right){\beta }_0{\hat{P}}_u\left[t\right]}{v\left[t\right]}+{\sigma }_b^2}\right),\hfill \end{array}$$

(60)

$$\begin{array}{cc}\hfill & \hfill H^2+{∥c\left[t\right]-w_W∥}^2\ge v\left[t\right],\hfill \end{array}$$

(61)

$$\begin{array}{cc}\hfill & \hfill {∥c[t+1]-c\left[t\right]∥}^2\le D^2,\hfill \end{array}$$

(62)

$$\begin{array}{cc}\hfill & \hfill c\left[T\right]=c_F,c\left[1\right]=c_A,\hfill \end{array}$$

(63)

where $B\left[t\right]=\epsilon {\hat{P}}_u\left[t\right]{\beta }_0/\phantom{\epsilon {\hat{P}}_u\left[t\right]{\beta }_0{P}_a\left[t\right]{\left|h_{IW}^H\left[t\right]\mathrm{\Theta }\left[t\right]h_{AI}\left[t\right]\right|}^2}{P}_a\left[t\right]{\left|h_{IW}^H\left[t\right]\mathrm{\Theta }\left[t\right]h_{AI}\left[t\right]\right|}^2$. Here, (61) is a non-convex function, while the left side of (61) is convex; thus, we can obtain a global lower bound estimate for the original function using first-order Taylor expansion of the convex function. After conducting Taylor expansion of $H^2+{∥c\left[t\right]-w_W∥}^2$ at $c_0\stackrel{\mathsf{\Delta }}{=}\{c_0\left[t\right],\forall t\}$, we have

$$\begin{array}{c}{∥c\left[t\right]-w_W∥}^2+H^2\ge {∥c_0\left[t\right]-w_W∥}^2+H^2+2{\left(c_0\left[t\right]-w_W\right)}^T\left(c\left[t\right]-c_0\left[t\right]\right)\stackrel{\mathsf{\Delta }}{=}F\left(c\left[t\right]\right).\end{array}$$

(64)

According to (58), (64) can be rephrased as

$$\begin{array}{cc}\hfill & \hfill \underset{C,u,v}{max}\frac{1}{T}{\sum }_{t=1}^{T}u\left[t\right],\hfill \\ \hfill s.t.\end{array}$$

(65)

$$\begin{array}{c}\hfill H^2+{∥c\left[t\right]-w_W∥}^2\le B\left[t\right],\end{array}$$

(66)

$$\begin{array}{cc}\hfill & \hfill u\left[t\right]\le {log}_2\left(1+\frac{A\left[t\right]}{\frac{\left(1-P_{out}^{*}\left[t\right]\right){\beta }_0{\hat{P}}_u\left[t\right]}{v\left[t\right]}+{\sigma }_b^2}\right),\hfill \end{array}$$

(67)

$$\begin{array}{cc}\hfill & \hfill F\left(c\left[t\right]\right)\ge v\left[t\right],\hfill \end{array}$$

(68)

$$\begin{array}{cc}\hfill & \hfill {∥c[t+1]-c\left[t\right]∥}^2\le D^2,\hfill \end{array}$$

(69)

$$\begin{array}{cc}\hfill & \hfill c\left[T\right]=c_F,c\left[1\right]=c_A.\hfill \end{array}$$

(70)

When expressed in this manner, the objective function and constraints of problem (65) are both convex; thus, (65) is convex, and can be solved using the CVX solver to obtain the optimal flight trajectory of the UAV.

4.4. Optimization Algorithm

In this subsection, we develop an iterative optimization algorithm based on SCA and Dinkelbach to solve problem (24), which is presented in Algorithm 1.

Algorithm 1 Iterative Optimization Algorithm

1: Initialization:$Q_0$, $c_0$, $R_b$, $\eta$, and index parameter $j=1$ 2: obtain optimal $\mathrm{\Theta }$ according to (32) 3: repeat 4:   Update $\left(P_k,{\hat{P}}_{u,k}\right)$ based on (42) with obtained $\left(C_{k-1},\mathrm{\Theta }\right)$. 5:   Update $\eta$ based on (40) with $\left(P_k,{\hat{P}}_{u,k}\right)$. 6:   Update $Q_k$ based on (65) with $\mathrm{\Theta }$ and $\left(P_k,{\hat{P}}_{u,k}\right)$. 7:   Update $R_{b,k}$ based on (24) with $\left(C_k,\mathrm{\Theta },P_k,{\hat{P}}_{u,k}\right)$. 8:   $j\leftarrow j+1$ 9: until  $\left|R_{b,j}-R_{b,j-1}\right|\le J$ Output: maximum average transmission rate received at Bob $R_b$, optimal UAV AN power $P_u$, optimal UAV transmission power P, and optimal trajectory of UAV Q.

As shown in Algorithm 1, the initial trajectory set $C_0$ and coordinate set $c_0$ of the UAV are set up first, then $R_0$ is calculated and the iteration parameter k is set. The optimal $\mathrm{\Theta }$ is calculated with (32). In lines 3 to 9, an iterative loop design is used. First, $\left(P_k,{\hat{P}}_{u,k}\right)$ is updated by solving problem (42) with the CVX solver. Second, the $\eta$ factor is updated via (40) and $Q_k$ is updated by solving (65). Finally, $R_{b,k}$ is updated through (24). The loop terminates when the condition $\left|R_{b,k}-R_{b,k-1}\right|\le K$ is satisfied. The algorithm returns the optimal UAV AN power $P_u$, optimal transmission power P, optimal trajectory of the UAV Q, and maximum average covert rate received by Bob $R_b$.

In Algorithm 1, we first derive the upper bound of a variable, then adopt Dinkelbach method to transform the formulated problem into a convex one. Thus, the complexity of the solution algorithm is determined by the SCA. The complexity of the proposed algorithm is $\mathrm{O}\left({\mathrm{I}}_{\max }{(T\times M)}^3\log {\kappa }^{-1}\right)$, where T is the number of time slots, M is the number of IRS units, $I_{max}$ is the iterative function, and K is the accuracy required for the approximations. Accordingly, the complexity of the proposed algorithm significantly increases with the increase of M and T, which can become computationally intensive.

5. Numerical Results

In this section, we present the numerical results for the IRS-assisted CCS with UAV. We use Algorithm 1, designed based on SCA and Dinkelbach, to solve the formulated optimization problem. The parameters are listed in

Table 1. Simulation parameters.

Parameter	Meaning	Value
N	UAV flying time	30 s
T	Number of time slots	30
L	Duration of time slot	1 s
H	Altitude of UAV	50 m
M	Number of IRS units	30
$V_{max}$	Maximum speed of UAV	50 m/s
D	Maximum moving distance of UAV per time slot	50 m
${\beta }_0$	Channel gain at a channel distance of 1m	−50 dB
$\alpha$	Path loss parameter	2.2
d	Antenna spacing	$\frac{\lambda }{2}$
P	Transmission power of BS	1 W
${\rho }_{w,dB}$	Parameters for quantifying noise uncertainty at Willie	6 dB
${\hat{\sigma }}_{w,dB}^2$	Standard noise power variance at Willie	−120 dBm
${\sigma }_b^2$	Noise power variance at Bob	−120 dBm
$\epsilon$	Values for the covertness required at Willie	0.01
J	Loop threshold	${10}^{-5}$
${\omega }_B$	Coordinates of Bob	${[0,150]}^T$
${\omega }_W$	Coordinates of Willie	${[0,100]}^T$
${\omega }_{BS}$	Coordinates of base station	${[0,0]}^T$
$c_A$	Initial coordinates of UAV	${[-300,0]}^T$
$c_F$	End coordinates of UAV	${[300,0]}^T$

.

Figure 2 shows the trajectory comparison of the UAV that works as a jammer to assist the CCS. The initial trajectory, denoted as $C_0$, represents the UAV moving with uniform speed from the initial point to the endpoint without optimization. For the trajectory optimized using the proposed algorithm, it can be observed that the UAV starts from the initial point, then flies at its maximum speed to Willie following the shortest path. When approaching Willie, the UAV hovers closer to Willie than to Bob. Finally, the UAV travels to the endpoint at the maximum speed using the shortest distance. It can be observed that the transmitting power of Alice and the AN power of the UAV are adjusted simultaneously to guarantee the maximum covert rate. In addition, due to the limit on its AN power, the UAV achieves a higher covert rate by approaching Willie more closely, which can ensure covertness for the CCS. Furthermore, if the UAV is close to the initial point, Alice can reduce her transmitting power and the UAV can enlarge its AN power to guarantee covertness, which leads to a small covert rate. In this case, the UAV flies close to Willie at its maximum speed, and the UAV must expend a large amount of energy in order to jam the communications between Alice and Willie. Thus, to save energy, the UAV is launched only when covert messages are being transmitted.

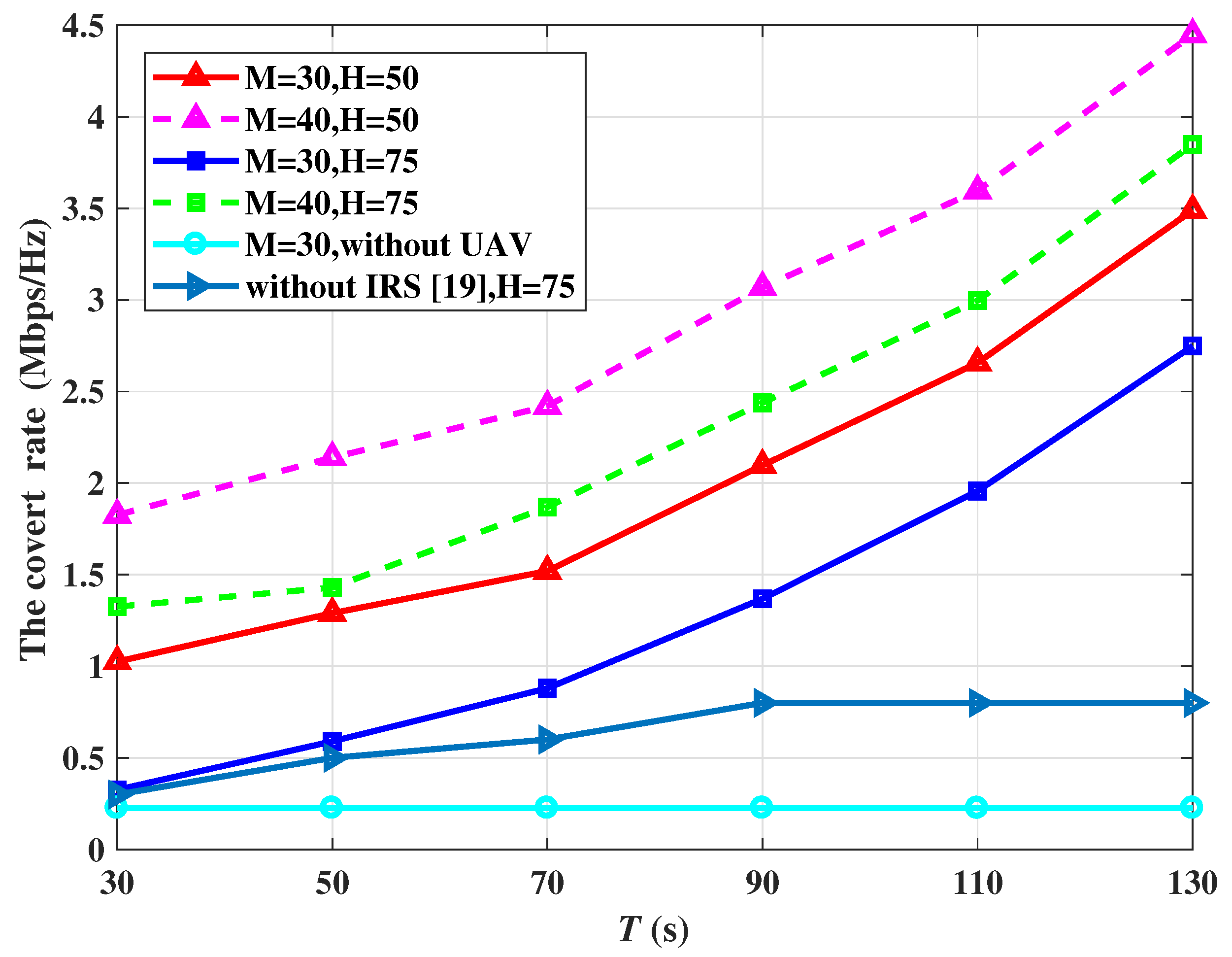
Figure 3 displays the covert rate versus the flying time with different UAV altitudes and different numbers of IRS units. The IRS is used with 30 and 40 units, the UAV flying times are 30 s, 50 s, 70 s, 90 s, 110 s, and 130 s, and the UAV altitudes are 50 m and 75 m.

From Figure 3, it can first be observed that the average covert rate increases with the flying time. As the flying time increases, the UAV spends a longer percentage of its time jamming Willie’s received signals. Therefore, increasing the flying time improves transmission efficiency. Second, as the number of IRS units increases, the corresponding average transmission rate increases as well. The reason for this is that the IRS can intelligently adjust the reflection of the signals in the best direction to achieve a higher covert rate. Third, it can be observed that the covert rate of the covert communication system without any IRS [19] is much lower than that with IRS, demonstrating that IRS can significantly improve the covert rate. Third, the average covert rate decreases with the height of the UAV. The reason for this is that increasing the altitude results in a larger distance between the UAV and Willie, which in turn results in higher path loss for the interfering signal. In this case, Alice must reduce her transmitting power in order to ensure the covertness of the communication, leading to a lower covert rate.

To evaluate the convergence of the proposed algorithm, Figure 4 plots the average covert rate versus iterations for different outage probabilities and the maximum speed of the UAV. The outage probability $P_{out}^{*}$ is set as 0.05, 0.1, and 0.3, and the maximum speed of the UAV $V_{max}$ is set as 50 m/s and 70 m/s. It can be observed that a high average transmission rate can be obtained with an increase in outage probability. In addition, when the speed of the UAV increases, the average transmission rate increases accordingly. This is because as the speed of the UAV increases, the time required for UAV to arrive at the optimal jamming coordinate is reduced. Thus, the UAV can jam Willie’s communications for a longer time at the optimal jamming coordinate, which results in an improvement in the covert rate. In this way, increasing both the upper limit of the outage probability and the speed of the UAV elevates the covert rate of the proposed CCS.

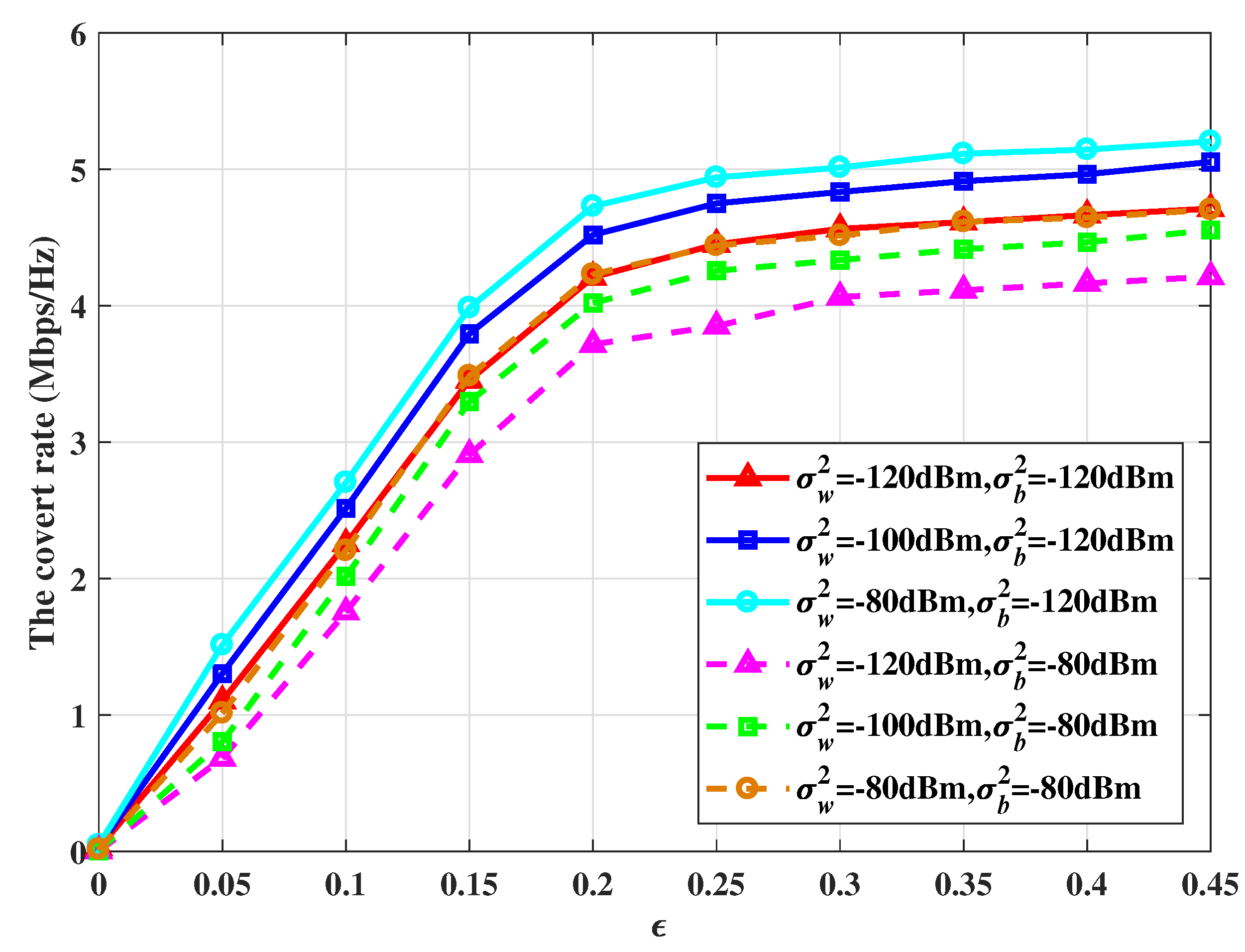
Figure 5 illustrates the covert rate versus $\epsilon$ for different noise variances at Willie’s location and Bob location. The noise variance at Willie’s location is set as −120 dBm, −100 dBm, and −80 dBm, while the noise variance at Bob’s location is set as −120 dBm and −80 dBm. First, it can be observed that as $\epsilon$ grows, the average covert rate increases; this is because $1-\epsilon$ is comparatively smaller, which means that the covertness constraint is relatively loose, leading to a higher average covert rate. In the $\epsilon$ range of 0 to 0.2 the average covert rate is significantly influenced by $\epsilon$, while when $\epsilon$ is larger than 0.2 the change in the average covert rate is negligible. This is because when the value of $\epsilon$ is large the covertness constraint is relatively loose, and the average rate can reach its maximum value. Moreover, there is an increase in the covert rate as the noise variance at Willie’s location becomes larger. This is because the increased interference imposed on Willie can help Alice to increase her transmitting power, improving the covert rate. However, when the noise at Bob’s location increases, the signal received by Bob is influenced as well, reducing the outage probability. Therefore, artificial noise generated by Willie or noise signals used to interfere with Willie influence covert communications between Alice and Bob, decreasing the covert rate.

Figure 6 plots the average covert rate versus Alice’s transmitting power with different flying times of 30 s, 70 s, and 110 s. The maximum AN power is set to 1 W and 2 W. It can be observed that the average covert rate increases with the flying time of the UAV; thus, the transmitting power is determined by the flying time of the UAV as well. Therefore, higher transmitting power results in a significant improvement in the covert rate, and higher AN power can ensure better covertness, though resulting in correspondingly higher energy consumption. In addition, the covert rate was maintained almost unchanged as the transmission power increased from 1 W to 2 W when a UAV was not included in the system [31]. This is due to the fact that, while the increase in AN transmitting power decreases Willie’s detection performance, it also introduces extra interference with Bob’s attempts to receive covert messages.

6. Conclusions

In this paper, we have proposed an IRS-assisted covert communication system including a friendly UAV deployed in complex environments with communication barriers. The closed form of the DEP of covert communication for Willie is derived by considering Willie’s uncertainty about the transmitting power. To maximize the covert rate, we formulate the joint optimization problem by adjusting the jamming power of the UAV and the transmitting power of the transmitter, where the optimal DEP for Willie, the transmitting power of the transmitter, and the transmitting power of the AN are established as the constraints. An iterative algorithm based on Dinkelbach is designed to solve the established optimization problem. Our simulation results demonstrate that the covertness and covert rate of the system can be improved by increasing the number of IRS, the UAV flying time, and the interference power.

This work serves as a first foray into the design of a covert communication system assisted by IRS and UAVs. Many interesting directions follow from this work and are deserving of further investigation. First, covert wireless communication aided by UAVs can serve multiple users. How to extend the traditional covert wireless communication model to one with more receivers of covert messages and more monitors remains an open issue. Second, because the base station is equipped with multiple antennas, different ways of selecting more than one antenna to transmit covert messages from among all antennas is a matter that requires further investigation. Third, in order to be deployed in complex environments, the proposed covert communication system with IRS and UAVs could be extended to include scenarios in which, in addition to interfering with Willie’s attempts to detect covert communication, the UAV is able to forward covert messages from Alice to Bob as well.