Deployment Method with Connectivity for Drone Communication Networks

Abstract

In this paper, we consider a drone deployment problem in situations where the number of drones to be deployed is small compared to the number of users on the ground. In this problem, drones are deployed in the air to collect information, but they cannot collect information from all ground users at once due to the limitations of their communication range. Therefore, the drones need to continue to move until they collect the information for the all ground users. To efficiently realize such drone deployment, we propose two deployment methods. One is an integer linear programming (ILP)-based deployment method and the other is an adjacent deployment method. In the ILP-based deployment method, the positions of the drones at each point in time are determined by solving an ILP problem in which the objective function is the total number of users from whom data can be collected. In contrast, in the adjacent deployment method, drones are sequentially deployed in areas with probabilities determined according to the number of user nodes in adjacent areas at which other drones are already deployed. Through numerical experiments, we show that these deployment methods can be used to efficiently collect data from user nodes on the ground.

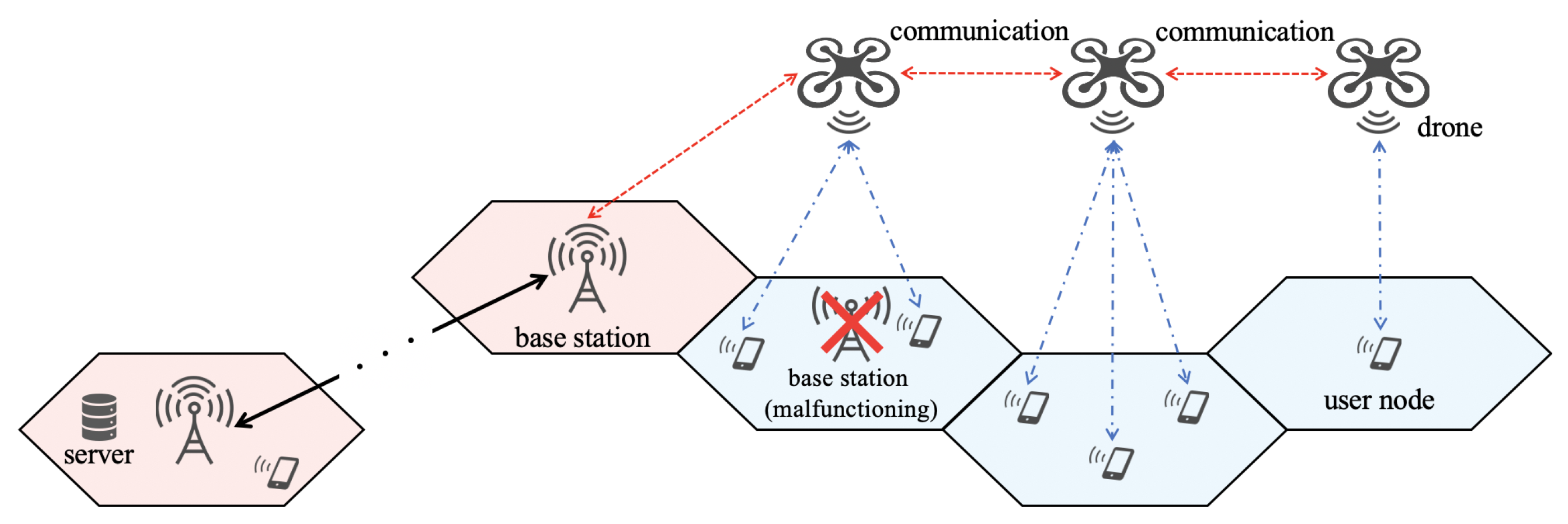
1. Introduction

In recent years, drone technologies have attracted much attention [1,2,3] for object tracking [4], the transportation of goods [5,6], traffic surveillance [7], and remote sensing [8]. Moreover, drone technologies are expected to be useful in responding to natural disasters [9,10,11,12]. In the communication field, drone communication networks that comprise multiple drones are expected to be used in disaster situations. Base stations can be destroyed in a natural disaster, and thus victims on the ground will not be connected to the Internet. After the disaster, multiple drones can be flown to recover from disconnections, and the victims can use these drones as access points (Figure 1). Such drone communication networks can monitor the situation in disaster areas and help many victims.

To date, many drone communication networks have been considered [13,14,15,16,17,18,19,20]. Drone communication networks can be considered as a new form of mobile ad hoc network (MANET) where the drones can move more freely than mobile devices in conventional MANETs. Therefore, early studies considered improvements to the routing schemes used in conventional MANETs. In [13], based on optimized link state routing (OLSR), directional OLSR was proposed, assuming that each drone was equipped with a directional antenna. In [14], ad hoc on-demand distance vector (AODV) routing was applied to a drone communication network. These early studies did not fully consider the characteristics of drone communication networks. In particular, unlike the case for conventional MANETs, they did not consider that drone movements can be managed by ground control systems. In [15], a ground control system-based routing method was proposed. The effectiveness of the routing method was demonstrated in experiments using real drones implementing the routing method and simulation experiments.

In [18,19,20,21,22,23,24,25,26,27,28], the drone deployment problem was studied. In the drone deployment problem, the placement of drones was considered in order to efficiently collect data from user nodes on the ground. In [23], the placement of a single drone was considered, and the optimum altitude in terms of the maximum allowed path loss was analyzed. The placement of multiple drones was considered in [24,25,26]. In [24,25], without considering the direct connectivity between drones, drone placement could be determined because the drones were connected via satellite links. Since drones are not always equipped with satellite communication devices, direct connectivity between drones needs to be considered. In [26], the authors considered an optimization problem involving minimizing the number of drones to accommodate the traffic of users on the ground under the condition of the drones being connected with each other. Numerical experiments showed that the connected drone networks could be efficiently constructed. In [26], although it was assumed that a minimum number of drones is generally available, in practice, the number of users on the ground may be so large that the available drones may not cover all users at once.

In this paper, we consider a connected drone deployment problem; that is, which areas to place drones in to connect them to each other. By connecting drones, the coverage area can be extended and services can be provided to users in locations where the signals from the base station cannot directly reach. As shown in Figure 1, the drones can communicate with each other if they are placed in adjacent areas, and users in areas far from the base station can communicate with servers on the Internet using connections established by drones located in adjacent areas. For this problem, it was assumed that the number of drones to be deployed is much smaller than the number of users on the ground. The drones cannot collect information from all ground users at once due to the limitations of their communication range. The drones need to continue to move until they collect the information from all the ground users. Therefore, in our problem, it was necessary to consider the placement of the drones at each point in time, maintaining connectivity between them. In addition, it was judged to be desirable for the information from all ground users to be collected as quickly as possible. Therefore, in summary, the solution to the problem must satisfy the following conditions: the connection between the drones should be maintained in every time slot, and the connection requests of the users should be satisfied as quickly as possible.

To obtain such a solution, we considered two deployment methods: the integer linear programming (ILP)-based deployment method and the adjacent deployment method. In the ILP-based deployment method, at each point in time, the ground control system must solve the ILP problem, the objective function of which is to maximize the total number of users that can communicate with the drone at each time, and determine the positions of the drones that are connected with each other. As time elapses, the ground control system repeatedly solves the ILP problem. With this process, the drones can collect the information from all ground users. In contrast, the adjacent deployment method is a heuristic algorithm and, at each point in time, the ground control system deploys drones to an area adjacent to the areas in which drones are already placed. More specifically, there is a high probability that a drone will be deployed to the area with the largest number of user nodes and a low probability that it will be deployed to other areas. Through numerical experiments, we show that ILP-based deployment is the fastest way to collect information from all users. Furthermore, we show that the performance of the adjacent deployment method is comparable to that of the ILP-based deployment method.

The contributions of this paper can be summarized as follows:

• We consider the connected drone placement problem; i.e., in which areas should drones be placed in order to connect drones to each other. By solving this problem, the coverage area can be extended and communications can be established even in areas beyond the range of the base station’s signal. This is useful for the collection of information after a disaster;
• To solve the connected drone placement problem, we formalized the ILP optimization problem and propose an ILP-based deployment method. As shown in Section 4, the ILP-based deployment method can realize efficient drone deployment;
• We propose a heuristic algorithm named the adjacent deployment method for large-scale networks. The computation time for our ILP optimization problem is generally huge because it is NP-hard. Therefore, the adjacent deployment method can be used to obtain the solution for large-scale networks for which it would be difficult for the ILP-based deployment method to obtain the solution.

The rest of this paper proceeds as follows. In Section 2, the problem addressed in this paper is described. In Section 3, we describe the ILP-based deployment method and the adjacent deployment method. In Section 4, we evaluate the proposed methods through simulation experiments. Finally, in Section 5, we conclude this paper.

2. Problem Formulation

There are $N_U$ users and $N_D$ drones in area A. Let $\mathcal{U}$ and $\mathcal{D}$ denote the sets of users and drones, respectively. $\mathcal{U}=\{1,2,\dots ,N_U\}$ and $\mathcal{D}=\{1,2,\dots ,N_D\}$. The area A is divided into L disjoint subareas $A_l$ ($l\in \mathcal{L}$), where $\mathcal{L}=\{1,2,\dots ,L\}$. By definition, ${\bigcup }_{l\in \mathcal{L}}{A}_l=A$ and $A_i\cap A_j=\varphi$ ($i,j\in \mathcal{L},i\ne j$). The set of subareas is defined as $\mathcal{A}=\{A_l\mid l\in \mathcal{L}\}$.

In this paper, we assume that each user has a connection request destined for the sink node, as shown in Figure 1, where a base station is regarded as the sink node. Through the sink node, requests for connection to the Internet can be fulfilled; i.e., to the servers outside of area A. We aim to establish connections for all the requests, but it is hard to simultaneously cover all the requests because the number of drones is supposed to be much smaller than the number of users (i.e., the number of connection requests). Therefore, we can achieve this by iteratively establishing connections. Specifically, we first establish connections for some users by deploying drones to ensure the connectivity to the sink node. Then, we reposition the drones to a different set of subareas to cover the connection requests of other users. Until we have covered all the connection requests, we repeat this procedure.

To do so, time is divided into time slots with the same duration. In the problem, for each time slot, to maintain the connectivity to the base station, the deployment subareas for the drones are selected in such a way that a connected graph can be constructed with the drones as nodes (Figure 2). Then, the drones stay in the selected areas until the end of the time slot. Here, let $P_d\left(t\right)$ denote the subarea of drone d$(d\in \mathcal{D})$ at time slot t ($t=1,2,\dots$). Note that $P_d\left(t\right)\in \mathcal{A}$. Drone d is equipped with an omnidirectional antenna and can communicate with ground users in area $P_d\left(t\right)$ at time t. The size of a subarea depends on the communication radius of the drones’ antennas, and we thus assume that the subarea size is fixed to fit within the communication radius of an antenna.

At time 0, there are $N_U$ connection requests in the network. In each connection request, an application-layer message is sent, and thus its data size is supposed to be relatively large. Moreover, in each time slot, each drone is supposed to accommodate at most M connection requests. The number M of served connection requests depends on the length of the time slot. As the length of a time slot increases, the value of M increases. However, for a long time slot, even if all users in the area have sent all the data that they want to send, the drone cannot move to another area until the end of the time slot, and this waiting is wasteful.

Note that the value of M depends on not only the length of the time slot but also several other factors, such as radio interference. For example, when the impact of the radio interference is strong, the value of M decreases. This is because the throughput of each connection decreases due to the radio interference, and thus the number of connection requests that the drone can complete for the data transmission during the time slot decreases. We can indirectly consider such situations by appropriately setting the value of M. In this paper, the value of M is given as a parameter without discussing how the length of the time slot is determined and how much radio interference there is because we aim to discuss a common way to construct connected drone networks that can accommodate all the connection requests for various situations.

We also assume that the drones have directional antennas. The transmission distance of a directional antenna is long compared to the transmission distance of an omnidirectional antenna [29]. Therefore, when the drones are deployed in the neighboring areas (Figure 1), they can communicate with each other.

Under the above assumptions, we consider the connected drone placement problem of minimizing the completion time T required to respond to the connection requests from all users by moving drones. Formally, the completion time T is defined as

$$T=\underset{t\in \mathbb{N}}{inf}\{t\mid \mathcal{R}\left(t\right)=\varphi \},$$

where $\mathcal{R}\left(t\right)$ denotes the unsatisfied connection requests at time t. Note that $\mathcal{R}\left(0\right)=\mathcal{U}$. The completion time T depends on the drone deployment, and we consider good drone deployment as having a short completion time T in this paper. Moreover, for the communication with the cloud servers via a base station, for each time t, we consider only the drone deployment where all drones are connected at each time slot. The desirable solution for the connected drone placement problem can be summarized as follows:

• The completion time T is short;
• For each time slot, a connected graph is constructed with drones as nodes.

In the problem formulation, we assume that users $\mathcal{U}$ and their positions are known in advance. In practice, the information needs to be collected before our proposed methods are applied. One way of doing this is to fly drones over areas and investigate the number of users in each area. If there are user devices in each area that have been able to communicate with the drone, the drone counts the number of these devices. Our proposed methods are supposed to be used in situations some time after a disaster. Immediately after a disaster, drones fly around to find and rescue victims, but after some time has passed, users with devices remain in fixed positions, allowing their locations to be collected by drones.

Moreover, although solving the problem allows us to obtain the solution regarding which area to place the drones in to maintain connectivity to the base station, it does not indicate where the best place to collect information from the ground user is. The best drone placements for collecting information from ground users have been studied [24,25,27,28], and these methods can be applied. Although our proposed method can combine these methods, we leave the combination problem for future work.

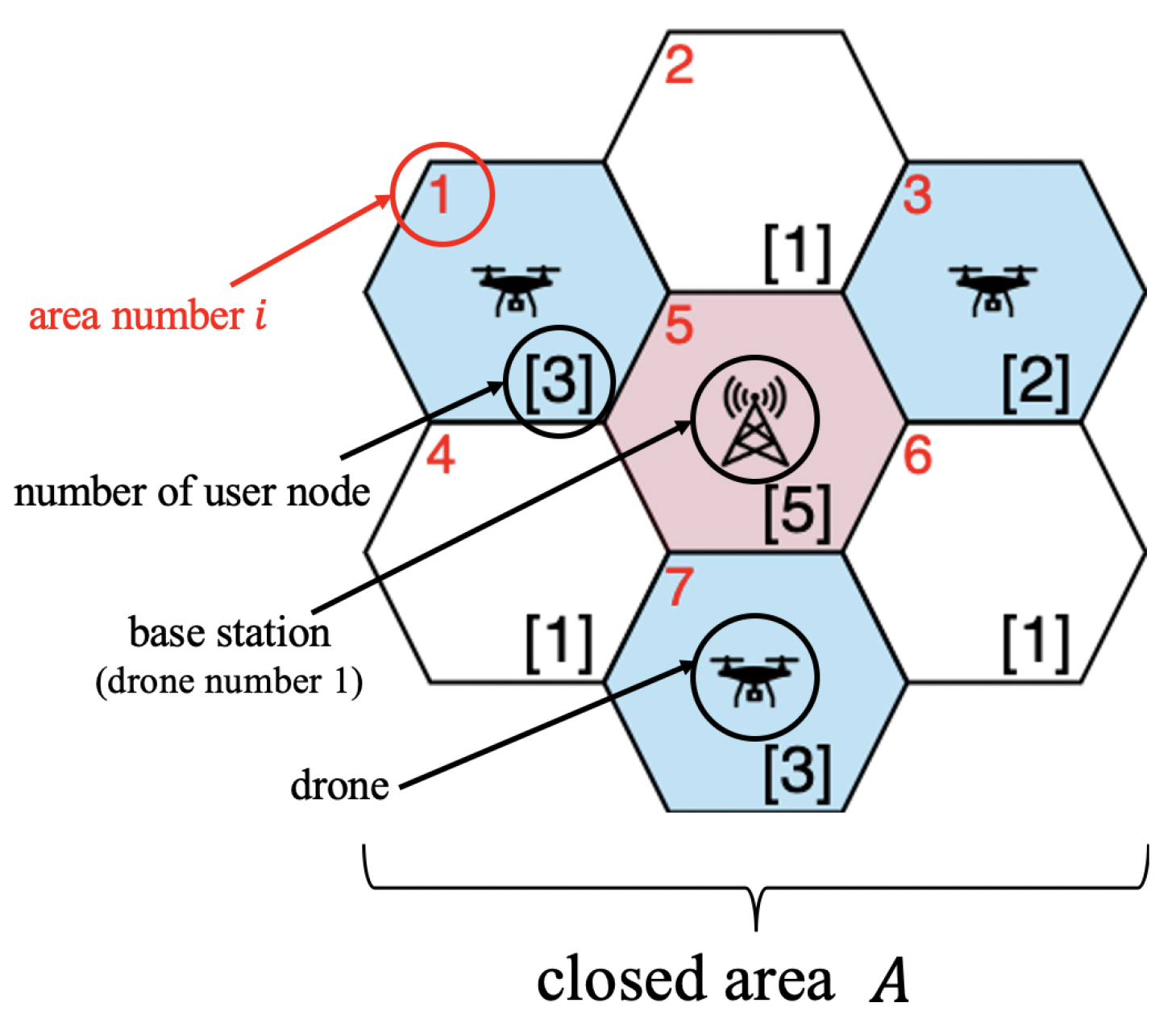
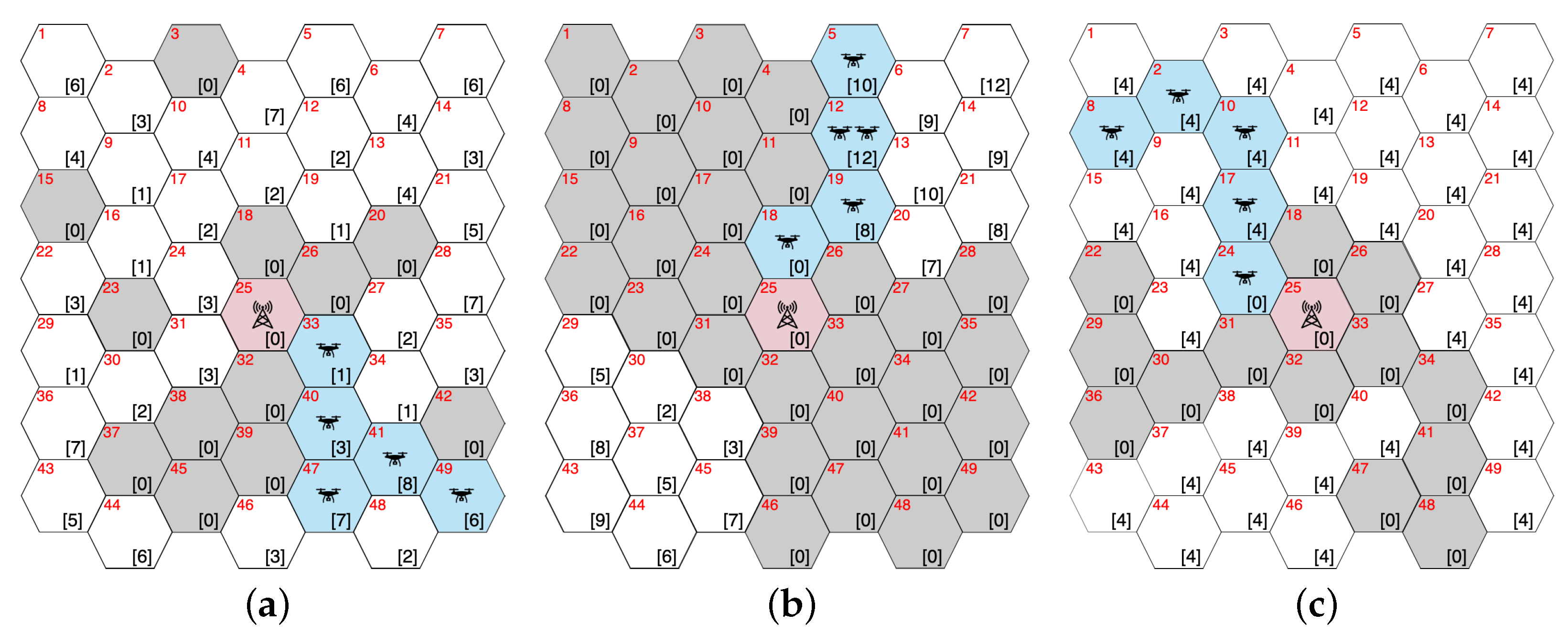
3. Proposed Method

We explain the ILP-based method and adjacent placement method in Section 3.1 and Section 3.2, respectively.

3.1. ILP-Based Deployment

In the ILP-based method, until all connection requests are satisfied, the placements $P_d\left(t\right)$ ($d\in \mathcal{D}$) are determined for each time t. The placements $P_d\left(t\right)$ at time t are determined by solving the ILP problem explained later. Table 1 summarizes the symbols used in the ILP-based method. The procedure of the ILP-based method is as follows:

Step 1. 

$t:=1$ and $\mathcal{R}\left(1\right):=\mathcal{U}$;

Step 2. 

$k:=1$, $n:=1$, and $\mathcal{W}\left(t\right):=\varphi$;

Step 3. 

The maximum number $N_G$ of drones in each group is set to $N_G:=n$ and the number of groups K is set to $K:=\lceil \left|\mathcal{D}\right|/N_G\rceil$. Therefore, the drones are divided into K groups ${\mathcal{G}}_{\ell }$ ($\ell =1,2,\dots ,K$) as follows:

$${\mathcal{G}}_{\ell }=\left\{\begin{array}{cc}\{(\ell -1)N_G+1,(\ell -1)N_G+2,\dots ,\ell N_G\}\hfill & (\ell =1,2,\dots ,K-1),\hfill \\ \{(\ell -1)N_G+1,(\ell -1)N_G+2,\dots ,|\mathcal{D}\left|\right\}\hfill & (\ell =K);\hfill \end{array}\right.$$

Step 4. 

By solving the ILP problem, the placements $P_d\left(t\right)$ ($d\in {\mathcal{G}}_k$) can be determined;

Step 5. 

If $k=K$, the procedure goes to step 6. Otherwise, k is updated to $k:=k+1$ and the procedure returns to step 4;

Step 6. 

${\mathcal{W}}_n\left(t\right)$, which is the set of users with satisfied connection requests according to the placements ${\mathcal{P}}_d\left(t\right)$ ($d\in \mathcal{D}$) when $N_G=n$, is calculated. If $|{\mathcal{W}}_n\left(t\right)|>|\mathcal{W}\left(t\right)|$, $\mathcal{W}\left(t\right)$ is updated to $\mathcal{W}\left(t\right):={\mathcal{W}}_n\left(t\right)$;

Step 7. 

If $n=\left|\mathcal{D}\right|$, the procedure goes to step 8. Otherwise, $k:=1$, $n:=n+1$, and the procedure returns to step 3;

Step 8. 

t is updated to $t:=t+1$. $\mathcal{R}\left(t\right)$ is updated to $\mathcal{R}\left(t\right):=\mathcal{R}(t-1)\setminus \mathcal{W}(t-1)$. If $\mathcal{R}\left(t\right)=\varphi ,$ the algorithm is stopped. Otherwise, the procedure returns to step 2.

Table 1. List of symbols.

Symbol	Meaning
$\mathcal{A}$	Set of subareas
${\overline{\mathcal{D}}}_k$	Set of drones in groups ${\mathcal{G}}_i$ ($i=1,2,\dots ,k-1$); i.e., ${\cup }_{i=1}^{k-1}{\mathcal{G}}_i$
${\mathcal{G}}_k$	Set of drones in group k
$\mathcal{R}\left(t\right)$	Set of users for which no data have been collected by time t
$l_k$	Minimum identification number of the drone included in ${\mathcal{G}}_k$
$m\left(d\right)$	Placement of drone d ($d\in {\overline{\mathcal{D}}}_k$)
$v_{u,d}$	Binary variable that is equal to 1 if user u is communicating with drone d; otherwise, 0
$a_{i,j}$	Variable that is equal to 1 if areas i and j are adjacent; otherwise, 0
$x_{d,i}$	Binary variable that is equal to 1 if drone d is deployed in area i; otherwise, 0
$y_{i,d}^{j,e}$	Binary variable that is equal to 1 if drones d and e deployed in areas i and j are communicating; otherwise, 0
$z_{d,e}$	Binary variable that is equal to 1 if drones d and e are communicating; otherwise, 0
$c_{u,i}$	Binary variable that is equal to 1 if user u is in area i; otherwise, 0
$w_{u,d,i}$	Binary variable that is equal to 1 if user u communicates with drone d and is in area i; otherwise, 0
${\gamma }_i$	${\sum }_{u\in \mathcal{R}\left(t\right)}{c}_{u,i}$
M	Maximum number of users that a drone can communicate with
$N_G$	Maximum number of drones in group
B	Area number of the base station

Table 1. List of symbols.

Symbol	Meaning
$\mathcal{A}$	Set of subareas
${\overline{\mathcal{D}}}_k$	Set of drones in groups ${\mathcal{G}}_i$ ($i=1,2,\dots ,k-1$); i.e., ${\cup }_{i=1}^{k-1}{\mathcal{G}}_i$
${\mathcal{G}}_k$	Set of drones in group k
$\mathcal{R}\left(t\right)$	Set of users for which no data have been collected by time t
$l_k$	Minimum identification number of the drone included in ${\mathcal{G}}_k$
$m\left(d\right)$	Placement of drone d ($d\in {\overline{\mathcal{D}}}_k$)
$v_{u,d}$	Binary variable that is equal to 1 if user u is communicating with drone d; otherwise, 0
$a_{i,j}$	Variable that is equal to 1 if areas i and j are adjacent; otherwise, 0
$x_{d,i}$	Binary variable that is equal to 1 if drone d is deployed in area i; otherwise, 0
$y_{i,d}^{j,e}$	Binary variable that is equal to 1 if drones d and e deployed in areas i and j are communicating; otherwise, 0
$z_{d,e}$	Binary variable that is equal to 1 if drones d and e are communicating; otherwise, 0
$c_{u,i}$	Binary variable that is equal to 1 if user u is in area i; otherwise, 0
$w_{u,d,i}$	Binary variable that is equal to 1 if user u communicates with drone d and is in area i; otherwise, 0
${\gamma }_i$	${\sum }_{u\in \mathcal{R}\left(t\right)}{c}_{u,i}$
M	Maximum number of users that a drone can communicate with
$N_G$	Maximum number of drones in group
B	Area number of the base station

In step 3, the drones in the kth group ${\mathcal{G}}_k$ are deployed through the ILP. To obtain the connected drone deployment for each time t, instead of determining the deployment of all drones at once, the drones are divided into K groups. The formulation of the ILP is difficult when all drones are assigned at once, as a topology with branches cannot be obtained. We overcome this problem by dividing the drones into groups.

In the ILP, the placement of the kth group ${\mathcal{G}}_k$ is considered under the assumption that the drones in ${\mathcal{G}}_{\ell }$ ($\ell =1,2,\dots ,k-1$) have already been placed. Let ${\overline{\mathcal{D}}}_k$ denote the set of the drones already deployed when the deployment of drones in ${\mathcal{G}}_k$ is considered: ${\overline{\mathcal{D}}}_k={\cup }_{\ell =1}^{k-1}{\mathcal{G}}_{\ell }$. Furthermore, ${\overline{\mathcal{L}}}_k$ denotes the set of the areas where drones have already been deployed: ${\overline{\mathcal{L}}}_k={\cup }_{\ell =1}^{k-1}{\cup }_{d\in {\mathcal{G}}_{\ell }}\left\{P_d\left(t\right)\right\}$. The drones in ${\mathcal{G}}_k$ can be placed in subareas $\mathcal{L}\setminus \overline{{\mathcal{L}}_k}$. For these subareas, we determine the placement of the drones in ${\mathcal{G}}_k$ by solving the following optimization problem.

$$\begin{array}{cc}\hfill \mathrm{Maximize}& \sum _{u\in \mathcal{R}\left(t\right)}\sum _{d\in {\mathcal{G}}_k}{v}_{u,d}\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \mathrm{Subject}\mathrm{to}& \forall d,e\in {\overline{\mathcal{D}}}_k\cup {\mathcal{G}}_k,\forall i,j\in \mathcal{L},\hfill \end{array}$$

$$\begin{array}{cc}\hfill & a_{i,j}+x_{d,i}+x_{e,j}-2\le y_{i,d}^{j,e}\hfill \\ \hfill & a_{i,j}\ge y_{i,d}^{j,e}\hfill \\ \hfill & x_{d,i}\ge y_{i,d}^{j,e}\hfill \\ \hfill & x_{e,j}\ge y_{i,d}^{j,e}\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & \forall d,e\in {\overline{\mathcal{D}}}_k\cup {\mathcal{G}}_k,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \sum _{i\in \mathcal{L}}\sum _{j\in \mathcal{L}}{y}_{i,d}^{j,e}=z_{d,e}\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill & d=l_k,l_k+1,\dots ,l_k+\left|{\mathcal{G}}_k\right|-2,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & z_{d,d+1}=z_{d+1,d}=1\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & \sum _{\overline{d}\in {\overline{\mathcal{D}}}_k}{z}_{l_k,\overline{d}}\ge 1\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & \forall d\in {\mathcal{G}}_k,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \sum _{i\in \mathcal{L}}{x}_{d,i}=1\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & \forall d\in {\overline{\mathcal{D}}}_k,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & x_{d,m\left(d\right)}=1,\sum _{i\in \mathcal{L}}{x}_{d,i}=1\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & \forall d\in {\overline{\mathcal{D}}}_k\cup {\mathcal{G}}_k,\forall i\in \mathcal{L},\forall u\in \mathcal{R}\left(t\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill & x_{d,i}+c_{u,i}-1\le w_{u,d,i}\hfill \\ \hfill & x_{d,i}\ge w_{u,d,i}\hfill \\ \hfill & c_{u,i}\ge w_{u,d,i}\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & \forall d\in {\overline{\mathcal{D}}}_k\cup {\mathcal{G}}_k,\forall u\in \mathcal{R}\left(t\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \sum _{i\in \mathcal{L}}{w}_{u,d,i}=v_{u,d}\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & \forall i\in \mathcal{L},\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \left\{\begin{array}{cc}\sum _{d\in {\overline{\mathcal{D}}}_k\cup {\mathcal{G}}_k}{x}_{d,i}\le \lceil \frac{{\gamma }_i}{M}\rceil \hfill & ({\gamma }_i\ge 1)\hfill \\ \sum _{d\in {\overline{\mathcal{D}}}_k\cup {\mathcal{G}}_k}{x}_{d,i}\le 1\hfill & ({\gamma }_i=0)\hfill \end{array}\right.\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & d=1,\hfill \end{array}$$

$$\begin{array}{c}{x}_{d,B}=1\hfill \end{array}$$

(11)

Equation (1) is the objective function that represents the number of users that can communicate with the drones in ${\mathcal{G}}_k$. Equation (2) is the constraint that the drones are placed in subareas adjacent to each other. Equation (3) eliminates the area information $i,j$ from $y_{i,d}^{j,e}$, and $z_{d,e}$ represents whether drones d and e can communicate with each other. Equation (4) is the constraint that the drones with successive IDs are placed in adjacent subareas and can communicate with each other. Equation (5) is the constraint that the drone with the smallest index $l_k$ in ${\mathcal{G}}_k$ is able to communicate with and be adjacent to one of the drones in ${\overline{\mathcal{D}}}_k$. Equation (6) is the constraint that each drone is deployed in only one subarea among all subareas. Equation (7) is the constraint that the already deployed drone $d\in {\overline{\mathcal{D}}}_k$ is deployed in subarea $m\left(d\right)$ and is not deployed in other subareas $\mathcal{A}\setminus \left\{m\right(d\left)\right\}$. In Equation (8), $w_{u,d,i}$ represents whether user u stays in area $A_i$ and communicates with drone d. In Equation (9), $v_{u,d}$ is the transformation of $w_{u,d,i}$ through the elimination of the information in area i and represents whether user u can communicate with drone d. Equation (10) is the constraint for the maximum number of drones in each area $A_i$. Note that ${\gamma }_i$ is constant when solving the ILP. Equation (11) is the constraint that drone one is deployed in the area containing the base station.

Figure 3 shows an example of the drone deployment using the ILP-based deployment method. In the example, the number of drones $\left|\mathcal{D}\right|=6$ and the number of subareas $L=7$. We set the number of groups K to 3. Therefore, $N_G=2$, ${\mathcal{G}}_1=\{1,2\},{\mathcal{G}}_2=\{3,4\}$, and ${\mathcal{G}}_3=\{5,6\}$. The drones in each group are connected (e.g., for ${\mathcal{G}}_1$, drones one and two are connected). First, the deployment of the drones in ${\mathcal{G}}_1$ is determined through the ILP. Drones one and two are deployed in subareas five and one, respectively. The drones in ${\mathcal{G}}_2$ and drones three and four are then deployed to subareas seven and four, respectively. By connecting drone three to drone one, the drones in ${\mathcal{G}}_1$ and ${\mathcal{G}}_2$ are connected with each other. In the same way, the drones in ${\mathcal{G}}_3$ are deployed to subareas two and three. Although the deployment of drones at $t=1$ is determined, no connection request is satisfied (e.g., the connection request in subarea six is not satisfied). Therefore, t is updated to $t:=2$, and then the drones are deployed again using the ILP.

Note that, even though our system model described in Section 2 simplifies the radio interference, the computation time of our ILP optimization problem is generally huge because it is NP-hard. Therefore, our system model is suitable for solving the connected drone placement problem, as the computation time for solving the ILP optimization problem is reduced compared to a system model with a complex radio propagation model.

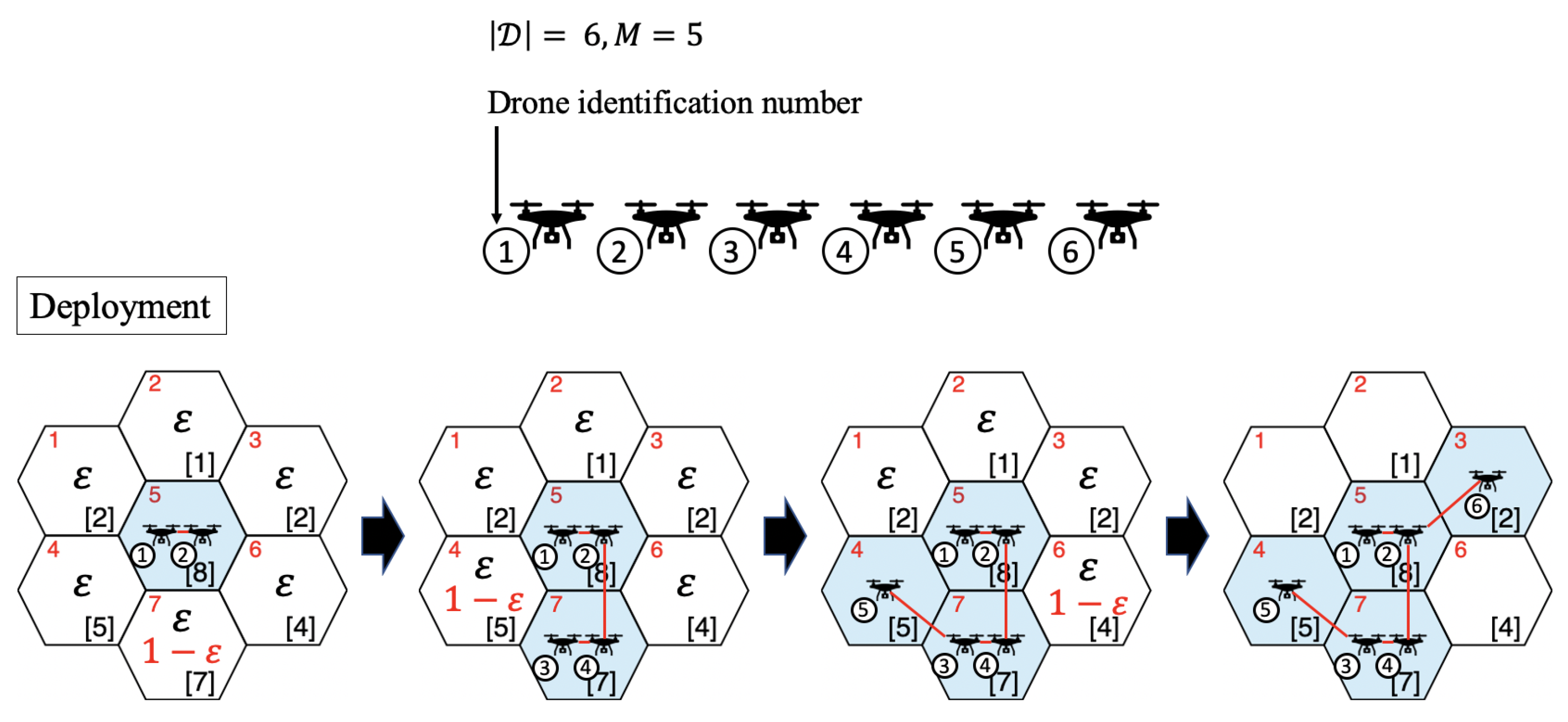
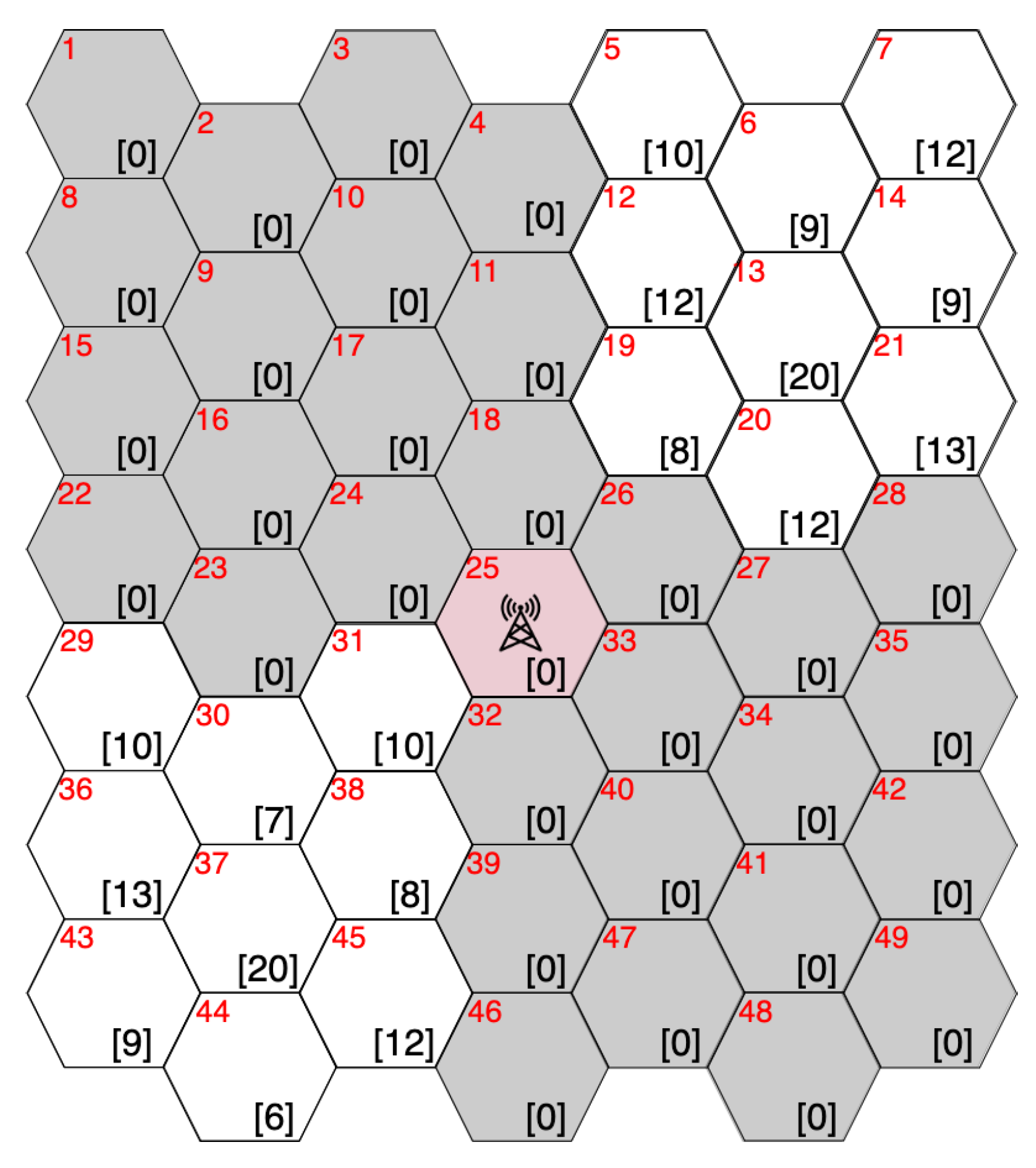
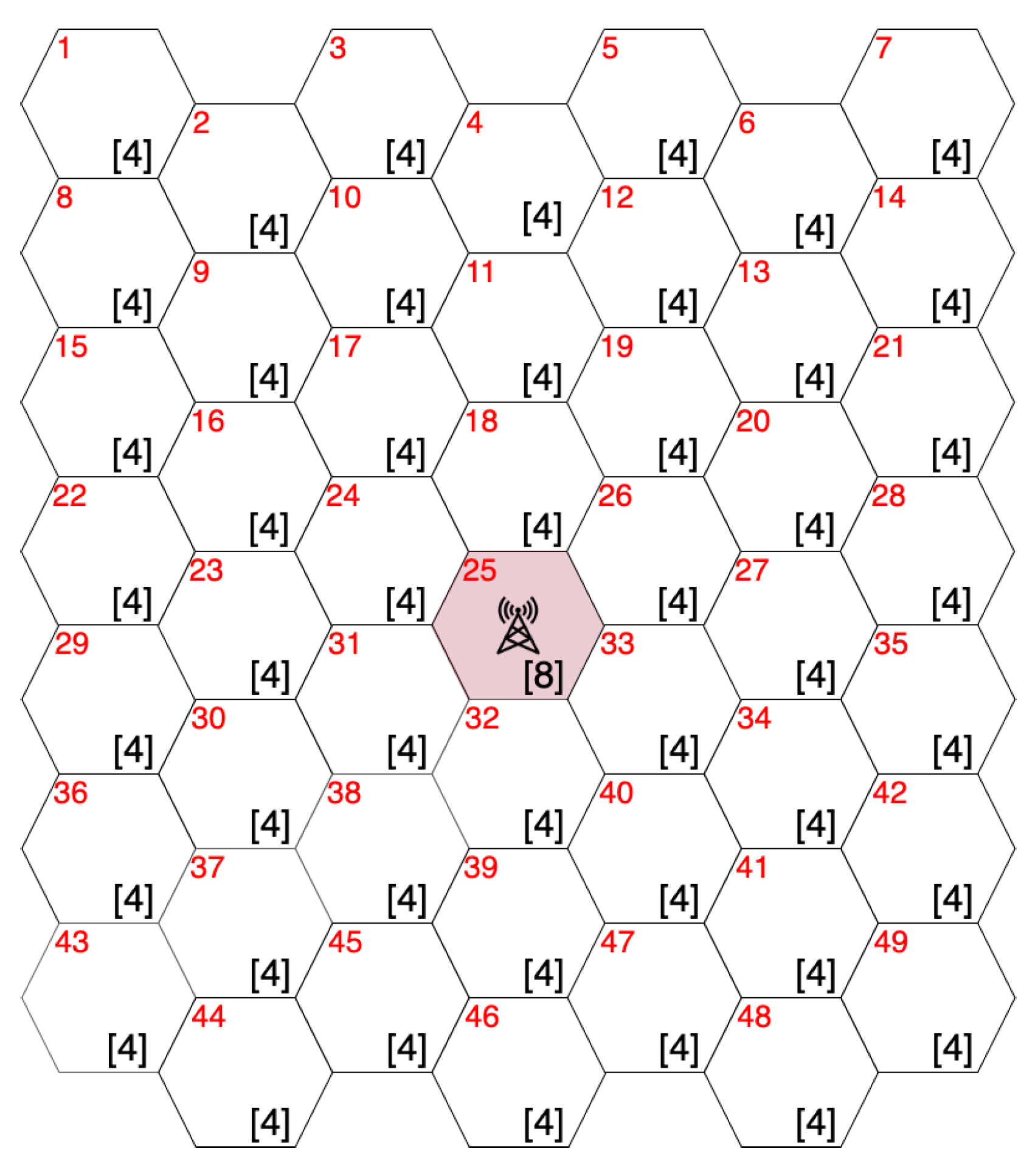
3.2. Adjacent Placement Method

In the adjacent placement method, to obtain a connected network, the deployment of drone d is chosen from the subareas $f_{\mathrm{NA}}\left(\mathcal{P}\left(t\right)\right)$ that are adjacent to the subareas where the drones are deployed already in $\mathcal{P}\left(t\right)$. Note that $f_{\mathrm{NA}}\left(\mathcal{P}\left(t\right)\right)\subset \mathcal{A}$. When there are no users in the neighboring subareas $f_{\mathrm{NA}}\left(\mathcal{P}\left(t\right)\right)$, the neighboring subarea in $f_{\mathrm{NA}}\left(\mathcal{P}\left(t\right)\right)$ is expanded outward to find a subarea with a user. If such a subarea is found, it is connected to the subarea in $\mathcal{P}\left(t\right)$ to make the connected deployment. The detailed procedure for the adjacent placement method is as follows:

Step 1. 

$t:=1$. For $A\in \mathcal{A}$, ${\mathcal{R}}_A\left(1\right):={\mathcal{U}}_A$, where ${\mathcal{U}}_A$ denotes the initial set of users with unsatisfied connection requests in subarea A;

Step 2. 

$d:=2$, $P_1\left(t\right)=A_B$, and $\mathcal{P}\left(t\right)=\left\{P_1\left(t\right)\right\}$;

Step 3. 

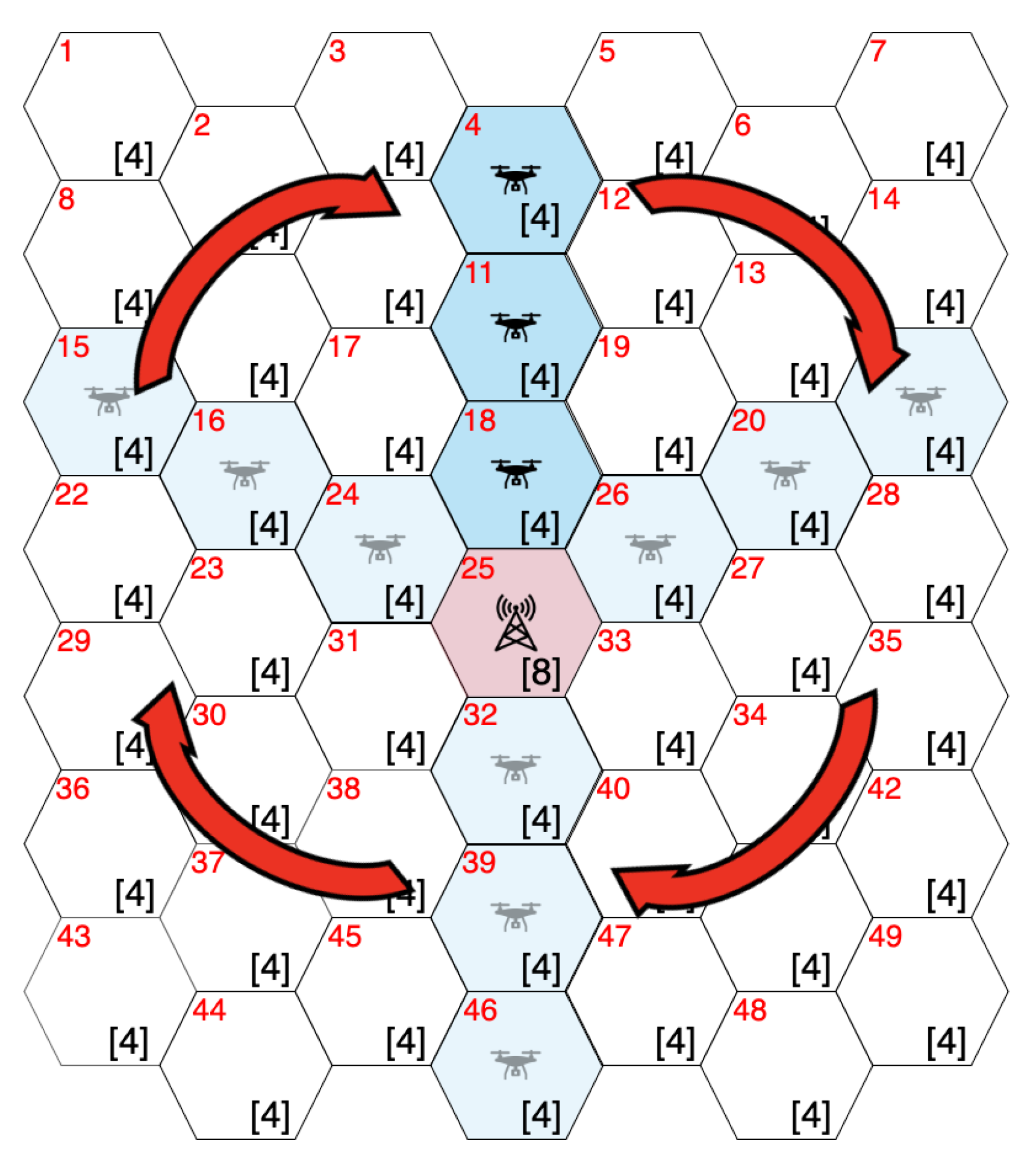
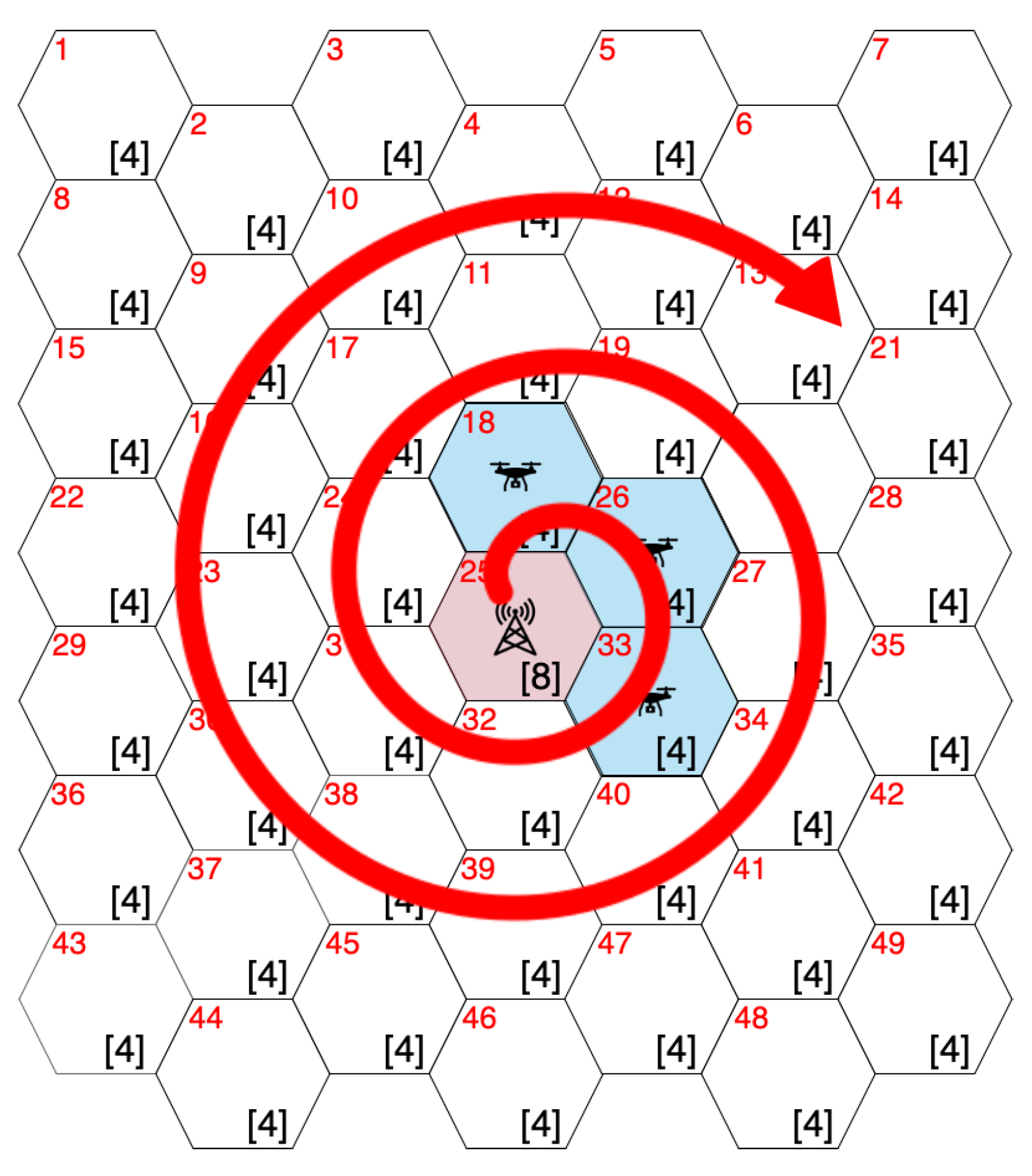
The set ${\mathcal{A}}_{\mathrm{UC}}$ of adjacent subareas with users with unsatisfied connection requests is updated to ${\mathcal{A}}_{\mathrm{UC}}:=\{A\mid |{\mathcal{R}}_A\left(t\right)|>0,A\in f_{\mathrm{NA}}\left(\mathcal{P}\left(t\right)\right)\}$. If $|{\mathcal{A}}_{\mathrm{UC}}|>0$, subarea A is randomly chosen from ${\mathcal{A}}_{\mathrm{UC}}$ with probability $ϵ$. In contrast, A is set to area $A_{\mathrm{large}}$ with the largest number of users in ${\mathcal{A}}_{\mathrm{UC}}$ with probability $1-ϵ$. When there are multiple subareas with the maximum number of users in ${\mathcal{A}}_{\mathrm{UC}}$, A is randomly chosen from among those areas. After the setting of A, drone d is assigned to $P_d\left(t\right)=A$ and $\mathcal{P}\left(t\right)$ is updated to $\mathcal{P}\left(t\right):=\mathcal{P}\left(t\right)\cup \left\{A\right\}$. Otherwise, the following steps are undertaken:

Step 3.1. 

$l=1$. ${\mathcal{A}}^{\left(0\right)}:=\mathcal{P}\left(t\right)\cup f_{\mathrm{NA}}\left(\mathcal{P}\left(t\right)\right)$ and ${\mathcal{A}}^{\left(1\right)}:=f_{\mathrm{NA}}\left({\mathcal{A}}^{\left(0\right)}\right)$;

Step 3.2. 

${\mathcal{A}}_{\mathrm{UC}}^{\left(l\right)}=\{A\mid |{\mathcal{R}}_A\left(t\right)|>0,A\in {\mathcal{A}}^{\left(l\right)}\}$ is calculated;

Step 3.3. 

If $|A_{\mathrm{UC}}^{\left(l\right)}|>0$, the procedure goes to step 3.4. Otherwise, $l:=l+1$, ${\mathcal{A}}^{\left(l\right)}$ is set to $f_{\mathrm{NA}}\left({\mathcal{A}}^{(l-1)}\right)\setminus {\bigcup }_{k=0}^{l-1}{\mathcal{A}}^{\left(k\right)}$, and the procedure returns to step 3.2;

Step 3.4. 

If $\left|\mathcal{D}\right|<d+l+1$, subarea A is randomly chosen from $A_{\mathrm{UC}}^{\left(l\right)}$. We select the set of subareas ${\mathcal{A}}_{\mathrm{short}}$, where subarea A is connected to one of the subareas in $\mathcal{P}\left(t\right)$ with the smallest number of hops. $d:=d+|{\mathcal{A}}_{\mathrm{short}}|$, and $\mathcal{P}\left(t\right):=\mathcal{P}\left(t\right)\cup {\mathcal{A}}_{\mathrm{short}}\cup \left\{A\right\}$. Otherwise, subarea A is randomly chosen from $f_{\mathrm{NA}}\left(\mathcal{P}\left(t\right)\right)$. Drone d is assigned to $P_d\left(t\right)=A$ and $\mathcal{P}\left(t\right)$ is updated to $\mathcal{P}\left(t\right):=\mathcal{P}\left(t\right)\cup \left\{A\right\}$;

Step 4. 

If the number $|{\mathcal{R}}_A\left(t\right)|$ of users in subarea A is greater than M, multiple drones are deployed in subarea A. Specifically, if $\lceil \left|{\mathcal{R}}_A\left(t\right)\right|/M\rceil \le \left|\mathcal{D}\right|-d+1$, $\lceil \left|{\mathcal{R}}_A\left(t\right)\right|/M\rceil$ drones are deployed to subarea A. In other words, drones $d,d+1,\dots ,d-1+\lceil \left|{\mathcal{R}}_A\left(t\right)\right|/M\rceil$ are deployed to subarea A. Otherwise, $\left|\mathcal{D}\right|-d+1$ drones are deployed to subarea A. d is updated to $d:=\left|\mathcal{D}\right|$;

Step 5. 

If $d=\left|\mathcal{D}\right|$, the procedure goes to step 6. Otherwise, $d:=d+1$, and then the procedure returns to step 3;

Step 6. 

Based on $P_d\left(t\right)$ ($d\in \mathcal{D}$), ${\mathcal{R}}_A(t+1)$ ($A\in \mathcal{A}$) is calculated, and $\mathcal{R}(t+1)$ is set to ${\cup }_{A\in \mathcal{A}}{\mathcal{R}}_A(t+1)$. If $\mathcal{R}(t+1)=\varphi$, the algorithm is stopped. Moreover, if $\mathcal{R}\left(t\right)=\mathcal{R}(t+1)$, $d:=2$, and then the procedure returns to step 3. Otherwise, t is updated to $t:=t+1$, and then the procedure returns to step 2.

Steps 3.1–3.4 are the process of finding the subarea where users exist and connecting that subarea to the subarea where the drones are already deployed. Step 4 is the process of deploying multiple drones in a subarea.

Figure 4 shows an example of drone placement using the adjacent placement method. In Figure 4, $\left|\mathcal{D}\right|$ is 6 and M is 5. First, drone one is deployed in subarea five. Drone two is placed in subarea five because the number of users in subarea five is larger than M. Next, drone three is placed in subarea seven with probability $1-ϵ$. Drone four is deployed in subarea seven because the number of users in subarea seven is greater than $M=5$. Drones three and four are placed in the small area adjacent to the small area where drones one and two are placed. Similarly, drones five and six are deployed in subareas four and three, respectively.

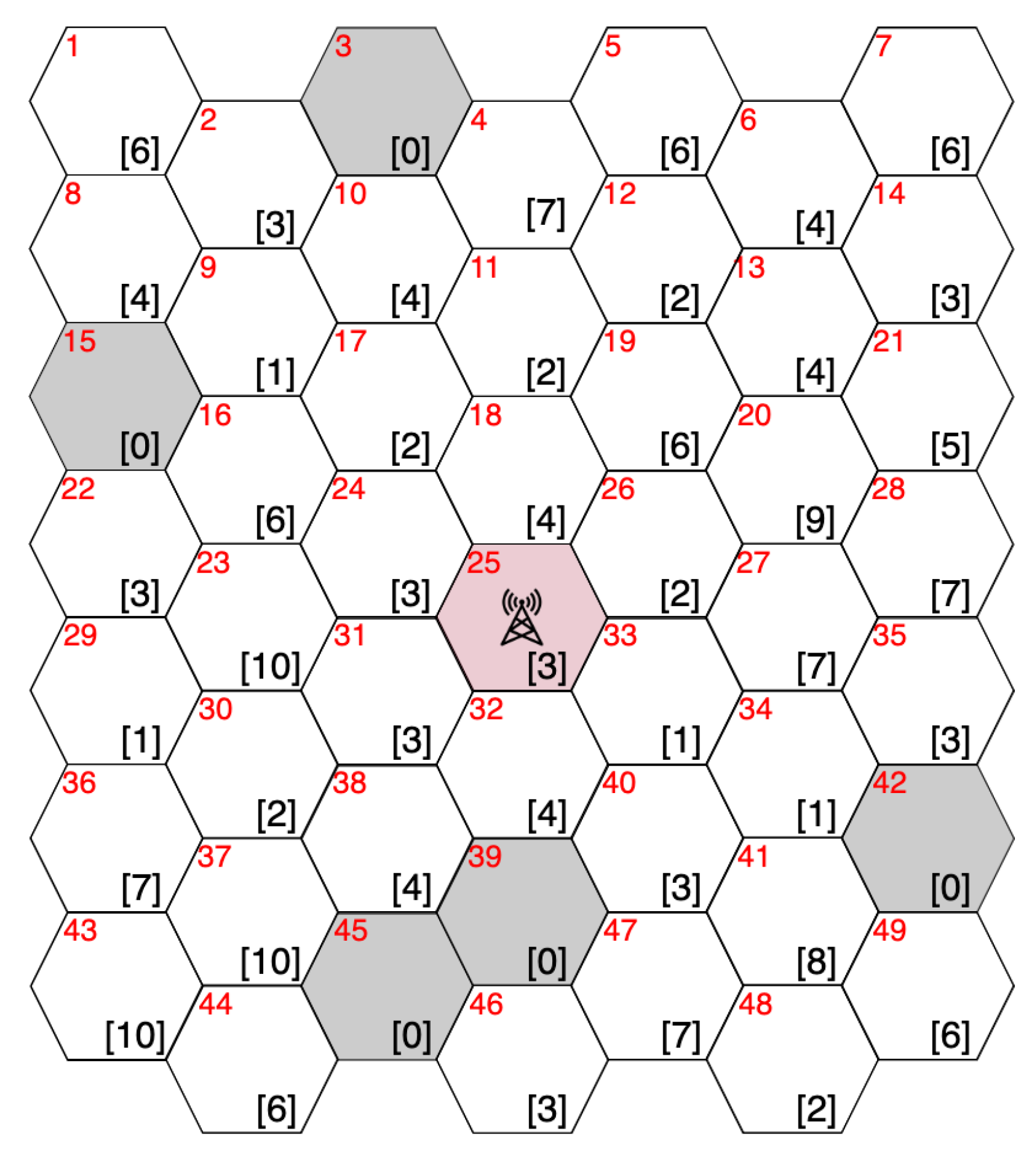
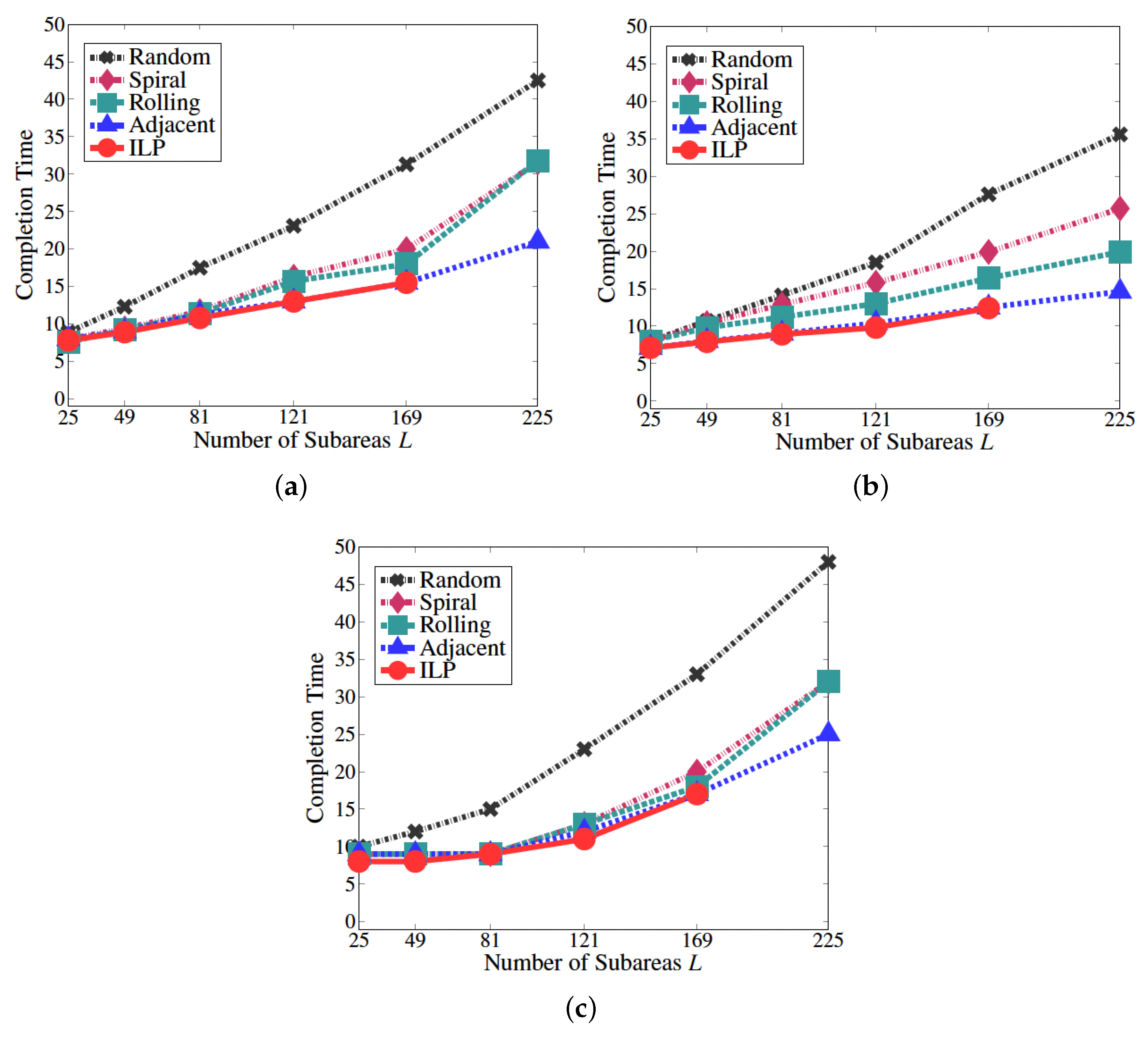
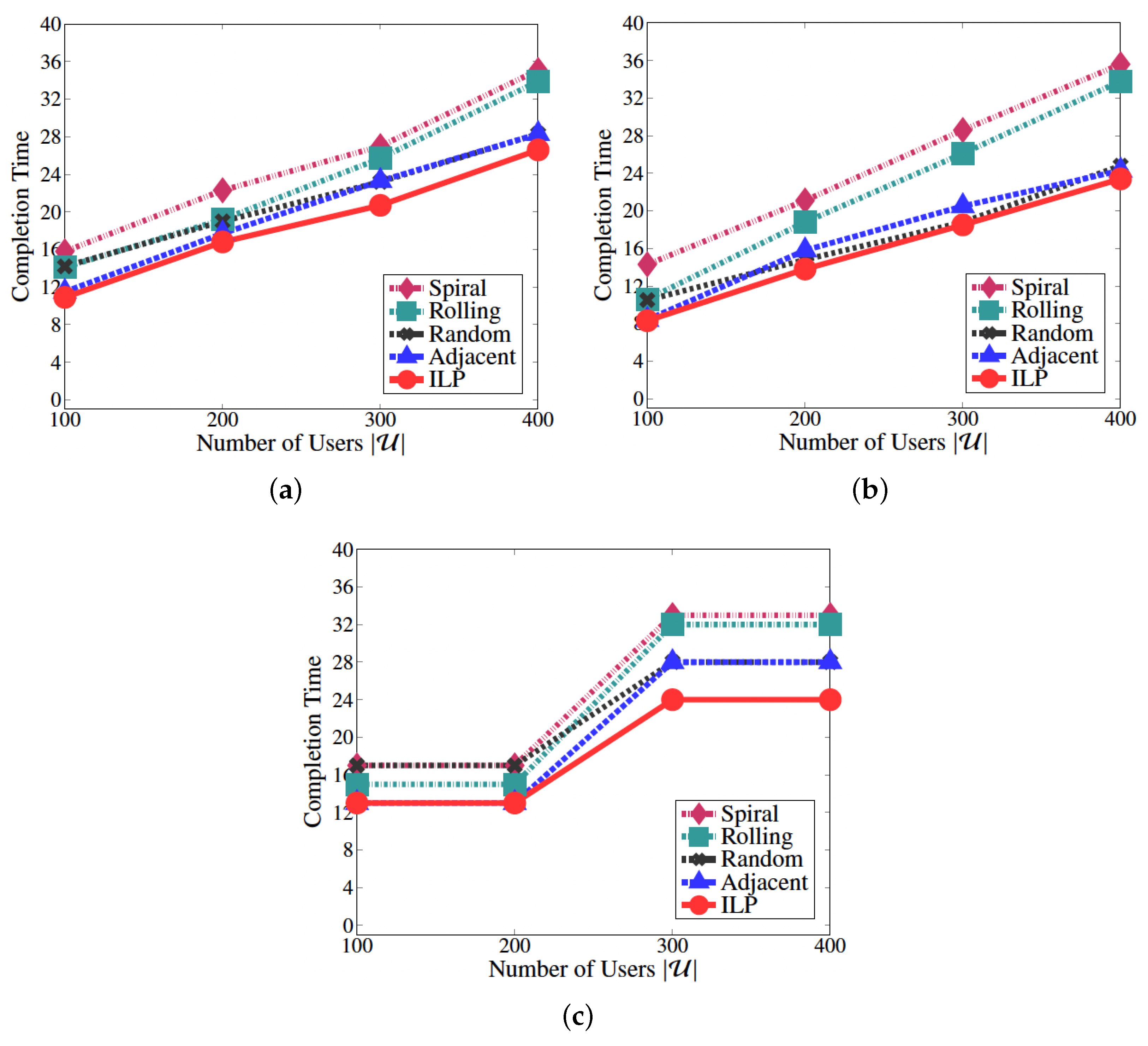
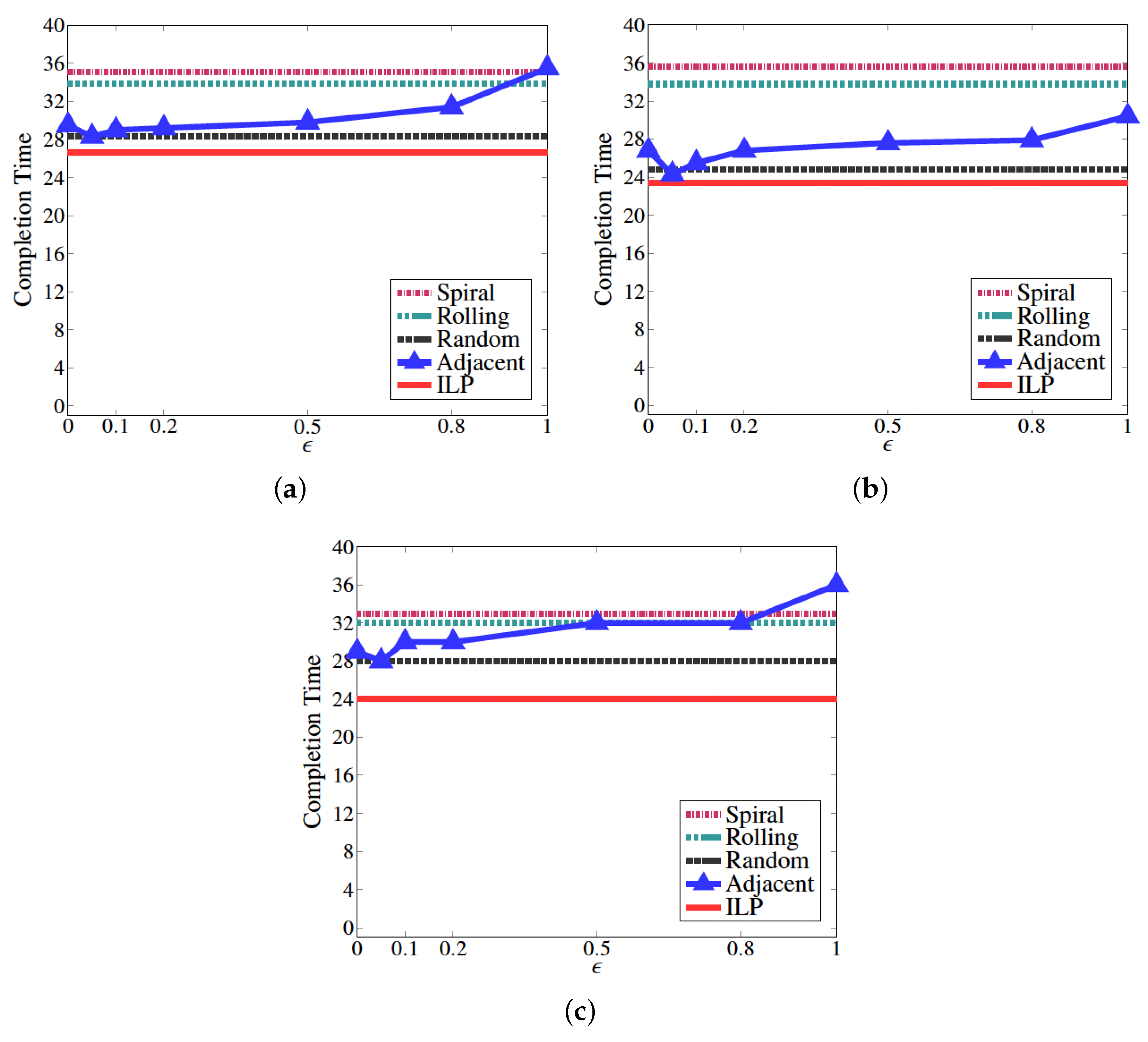
4. Performance Evaluation

4.1. Evaluation Model

Numerical experiments were conducted to verify the effectiveness of the proposed methods.

Table 2. Parameter settings.

Parameter	Value
Number of users $\left|\mathcal{U}\right|$	400
Number of subareas L	25, 49, 81, 121, 169, 225
Base station deployment area B	$\lceil L/2\rceil$
Number of drones $\left|\mathcal{D}\right|$	14
Maximum number of users from which one	5
drone can collect data M

shows the parameter values used in the numerical experiments. There are 400 users ($\left|\mathcal{U}\right|=400$) in a closed area A. The area A is divided into $L\in \{25,49,81,121,$$169,225\}$ subareas, and users are deployed in these subareas. The base station is located in subarea $B=\lceil L/2\rceil$. The number of drones $\left|\mathcal{D}\right|$ is set to 14, and each drone can communicate with $M=5$ users at each time. In this paper, we consider three scenarios with different user arrangements: random, uneven, and all-equal scenarios. In the random scenario, the number of users in each subarea is randomly chosen according to a uniform distribution on [0, 10]. Figure 5 shows an example of the deployment in the random scenario. In the uneven scenario, users only exist in some areas. Figure 6 shows an example of the deployment in the uneven scenario. Users exist only in the upper-right and lower-left subareas. The number of users in the upper-right and lower-left subareas is chosen according to a uniform distribution on [20, 30].

In the all-equal scenario, as shown in Figure 7, the number of users is the same for all subareas; i.e., $\left|\mathcal{U}\right|/L$.

In the ILP-based deployment method, to solve the ILP problem described in Section 3.1, we use the optimization solver CPLEX [30]. In the adjacent deployment method, the probability $ϵ$ is set to 0.05, unless otherwise stated.

The completion time T was used as the performance metric. For the random and uneven scenarios, 10 trials were conducted with different user arrangements, and the average over these trials was taken as the completion time.

Results for three other methods (random, rolling, and spiral methods) are presented for performance comparison. These are straightforward methods and thus regarded as the baseline methods. The random method is consistent with the adjacent placement method when $ϵ=1$ and determines the drone deployment area randomly from among the neighboring areas. The random method was run $1.0\times {10}^3$ times, and the results are shown for the most efficient data collection among the runs. In the rolling method, drones are repeatedly deployed so that they rotate to the right, as shown in Figure 8. The drones are deployed in a circular pattern until they have completed a full circle. In the spiral method, the drones are repeatedly deployed in a spiral pattern around the base station, as shown in Figure 9.

4.2. Results

Figure 10 shows the completion time T as a function of the number L of subareas. From Figure 10, we can observe that the proposed methods outperformed the comparison methods in all scenarios. As L increased, the difference between the proposed methods and the other methods increased. These results indicate that our proposed method performs well compared with the comparison methods. In particular, for a large L, the use of our proposed method is effective. Moreover, for a small L, the completion time T of the adjacent placement method is comparable with that of the ILP-based deployment method. For $L=225$, the computation complexity of the ILP-based deployment is high, and we cannot obtain the solution in a reasonable time. The adjacent placement method performs best and is useful for a large number of subareas.

Figure 11 shows the completion time T as a function of the number $\left|\mathcal{U}\right|$ of users. For any $\left|\mathcal{U}\right|$, the ILP-based deployment achieved the best performance. For a large $\left|\mathcal{U}\right|$, compared with the spiral and rolling deployments, the adjacent placement method and random deployments demonstrated short completion times T, and their performances were comparable. Note that the computation time of the random deployment was longer than that of the adjacent placement method because the random deployment performs the drone placement many times and then selects the best placement.

We next confirmed the connections of the drones when using the proposed methods. Figure 12 and Figure 13 show the drone deployment at time $t=4$ for the ILP-based and the adjacent placement methods, respectively, where $L=49$, $\left|\mathcal{U}\right|=200$, and $\left|\mathcal{D}\right|=6$. In both proposed methods, the drones were assigned to the connected positions. These results indicate that our proposed method can establish a communication path to the base station. In the ILP-based deployment method, the drones are deployed to the subareas with the highest total numbers of users. Moreover, from Figure 12, we can observe that there were branches in the topology of the drones because of the drone grouping. For the adjacent placement method, although the drones were not assigned to the subareas with the largest total numbers of users, we observed that the drones were assigned to subareas with many users.

Finally, we evaluated the effects of the probability $ϵ$ in the adjacent placement method. Figure 14 shows the completion time T as a function of $ϵ$, where $L=49$, $\left|\mathcal{U}\right|=400$, and $\left|\mathcal{D}\right|=6$. In all scenarios, for $ϵ=0.05$, the completion time T was the minimum and comparable to that of the random method. For the uneven scenario, the completion time was comparable to that of the ILP deployment method. In contrast, for large $ϵ$, the completion time T was long and the performance of the proposed method was almost the same as that of the spiral or rolling methods. These results indicate that the proposed method works well when $ϵ$ is set as sufficiently small.

5. Conclusions

In this paper, we addressed the drone deployment problem considering the connectivity of drone networks and proposed a deployment method based on ILP and the adjacent placement method. In the ILP-based deployment method, the position of drones is determined by solving an ILP problem, the objective function of which is to maximize the total number of users from whom data can be collected at each point in time. In the adjacent placement method, the largest area is selected with a high probability from the areas adjacent to where the drone has already been deployed, and a random selection is made with a low probability. Through numerical experiments, we evaluated the performance of the proposed methods and showed that they can be used to efficiently collect data. In this paper, we adopted the simple system model because it was sufficient to determine which areas drones should be deployed to construct connected drone networks. However, the collection of data from users on the ground could be improved by positioning the drones in a more suitable location. To address this problem, we can first identify the areas where a connected drone network can be constructed with our proposed method and then consider more complex propagation models to identify the best locations to collect data from users on the ground. We leave this combination problem for future work.