Abstract
Visual servoing is a control method that utilizes image feedback to control robot motion, and it has been widely applied in unmanned aerial vehicle (UAV) motion control. However, due to field-of-view (FOV) constraints, visual servoing still faces challenges, such as easy target loss and low control efficiency. To address these issues, visual servoing control for UAVs based on the deep reinforcement learning (DRL) method is proposed, which dynamically adjusts the servo gain in real time to avoid target loss and improve control efficiency. Firstly, a Markov model of visual servoing control for a UAV under field-of-view constraints is established, which consists ofquintuplet and considers the improvement of the control efficiency. Secondly, an improved deep Q-network (DQN) algorithm with a target network and experience replay is designed to solve the Markov model. In addition, two independent agents are designed to adjust the linear and angular velocity servo gains in order to enhance the control performance, respectively. In the simulation environment, the effectiveness of the proposed method was verified using a monocular camera.
1. Introduction
An unmanned aerial vehicle (UAV) is an integrated agent capable of functions including environmental perception, motion planning, and servoing control among others [1]. Meanwhile, it also represents an integration of sensing technology, electronic engineering, communication engineering, computer engineering, automation control, and artificial intelligence [2,3]. Quadrotor UAVs can take off and land vertically, hover in the air, fly at low altitudes, cruise slowly, and so on. Hence, UAVs represent a focus of current research [4]. Quadrotors are widely used in daily life, e.g., in drones, small logistics transportation, pesticide spraying, and high-altitude auxiliary fire extinguishing [5].
Visual servoing adopts the image information of the target position obtained from airborne cameras to control the relative position and altitude of a quadrotor UAV [6]. Generally, visual servoing can be divided into position-based visual servoing (PBVS) and image-based visual servoing (IBVS) [7]. Errors in PBVS originate from the three-dimensional Cartesian space; thus, it is sensitive to noise, camera parameter errors, and the estimation accuracy of the target position [8]. IBVS uses the image feature error to calculate the input of the control robot directly, which enhances the robustness of the camera parameters. In contrast to PBVS, an accurate geometric model of the visual target is no longer required [9]. Thus, IBVS is widely applied in the control of mobile robots [10] and UAVs [11,12,13]. Servo gain is critical for IBVS because it affects the output and convergence speed of the whole system [14].
In various applications, such as cluster control based on vision [15,16], target tracking [17], and visual navigation [18], the target may be lost because of the limited FOV. Once the target is lost, these tasks cannot be performed properly. Therefore, it is important to consider the FOV constraint in the design stage of the servo controller.
To avoid feature loss, several methods have been proposed in recent decades. Hajiloo et al. [19] optimized the trajectory of features in image frames using the MPC method to address the FOV constraints. Chesi et al. [20] used the in-plane trajectory of a camera in three-dimensional Cartesian space but did not optimize the trajectory of features in the image frame [20]. Huang et al. [21] designed a constraint controller using the control obstacle function and quadratic programming to prevent the target on the ship exceeding the FOV of the camera. Zhang et al. [22] presented a new real-time optimal trajectory planning method for a rotorcraft with the constraint of speed and inputs of thrust and altitude. Their framework ensures the field-of-view constraints on the visual servoing control of the rotorcraft by transforming the FOV constraint into an altitude constraint. Zheng et al. [23] established a control barrier function to ensure the FOV constraint to maintain visibility. The barrier function is used to create a visible range that sets the maximum distance between the center of the image plane and the visual feature coordinates in the image plane. This visible range can be defined as the upper limit of the distance between these two points.
In recent years, with the rapid development of artificial intelligence, machine learning has been widely applied in various fields. Meanwhile, formal methods for the verification and validation of machine learning systems have been proposed in [24,25]. In the field of robot control, the reinforcement learning (RL) algorithm is used to complete the visual servoing task [26]. Wang et al. [27] introduced controllers to addresses the retention of visual features in the field of view of the camera for wheeled mobile robots (WMRs). When the feature is located in a dangerous area, a controller based on Q-learning is activated to avoid feature loss. This method uses Q-learning to directly control the motion of a WMR, but these controllable actions are rare and only applicable to some scenarios. In contrast to directly using the RL algorithm for the input of the control system, Shi et al. [28,29] used the Q-learning algorithm to choose the adaptive law to update the gain of IBVS, and the stability and convergence of the control system were improved. However, these methods did not consider the issue of field-of-view constraints. As we know, there is little research on learning-based FOV constraint control for UAVs. A comparison of our work with related works is provided in Table 1.

Table 1.
Comparison of current related work.
In order to solve the problem of feature loss and improve the efficiency of IBVS, we propose a method of IBVS control of UAVs with visibility constraints based on the deep reinforcement learning method, which dynamically adjusts the servo gain in real time to avoid target loss and improve control efficiency. The Markov model of visual servoing control for a UAV under field-of-view constraints is established, and an improved DQN algorithm with a target network and experience replay is designed to solve the Markov model. Then, to enhance the control performance of the control system, we designed two independent servo gains for linear and angular velocities to replace the single servo gain in the traditional method.
The remainder of this paper is organized as follows. In Section 2, the works related to the proposed method are presented, which include a model of a quadrotor UAV and the method of classical IBVS. Section 3 describes the proposed algorithm for adjusting the adaptive servo gain using a DQN. To demonstrate the effectiveness of the proposed method, simulations are presented in Section 4. Finally, Section 5 summarizes the conclusions of the study.
2. Preliminaries
2.1. Quadrotor Model Description
The coordinate frames of a quadrotor are shown in Figure 1, where the body coordinate frame and world coordinate frame are denoted as and , respectively. The coordinate of the quadrotor’s centroid :
where represents the cross multiplication operation; is the rotation matrix from the body coordinate to world coordinate; is the UAVs constant inertia matrix around the centroid; is a skew-symmetric matrix with ; is the total lift force along the axis of the coordinate system; and are the moment of rotation for the x, y, and z axes of the body coordinate system. in the body coordinates can be calculated as follows:
where and are the lift coefficient and moment coefficient, respectively. The parameter is the arm of force, indicating the displacement of the motor relative to the center of mass of the aircraft. represents the rotational speed of each motor.
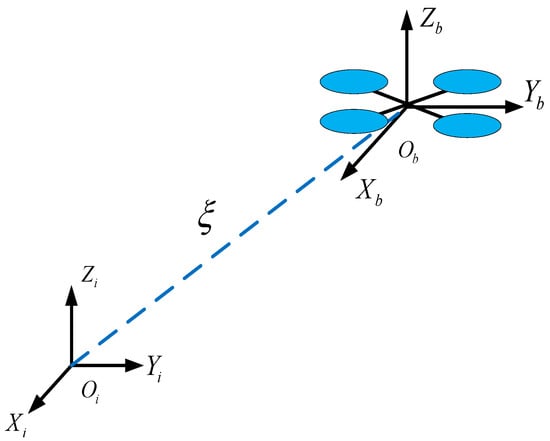
Figure 1.
The coordinate frames of a quadrotor.
2.2. The Classical IBVS Method
Assuming that is a point in the camera coordinate and is the observed target point in the image, the relationship between and is illustrated in Figure 2. The camera coordinate and image plane are represented by X-Y-Z and x-y, respectively. The principal point is the intersection of the Z-axis and image plane; its coordinates can be expressed as .
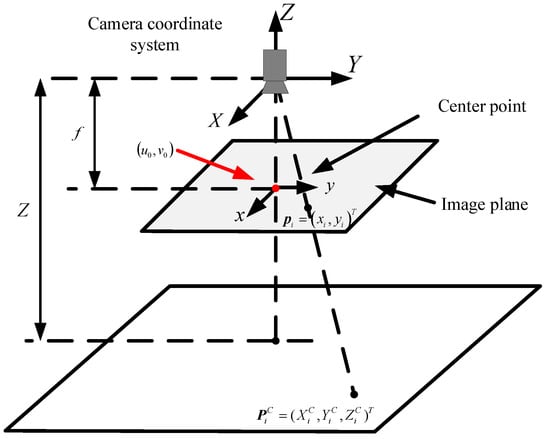
Figure 2.
The perspective imaging mode of the camera.
The conversion between a point in the camera coordinate system and the image coordinate system refers to the mapping of a 3D point in the world captured with a camera to a 2D point on the camera sensor. The conversion can be described as
The derivative of Equation (3) with respect to time is expressed as
Substituting Equation (3) into Equation (4) yields
The relationship between the velocity of the three-dimensional points and the spatial velocity of the camera is established using the spatial kinematic equation:
Substituting Equation (6) into Equation (5) yields
Equation (7) can be rewritten in matrix form:
where and . is the Jacobian matrix for each target point and it satisfies:
The crucial aspect of IBVS control is the discrepancy between the current coordinates of the feature target and the desired coordinates in the image. The feature error can be expressed as follows:
where are current positions of the target in the image and are the desired positions of the target in the image. Meanwhile, the motion of the target position in the image is directly related to the movement of the drone. The derivative of Equation (9) can be expressed as
where is the velocity vector of the UAV in the body frame and is the image Jacobian matrix.
To ensure the exponential decline in the characteristic error, the relationship between the UAV speed and the characteristic error vector can be obtained using the following method:
where is the pseudo-inverse matrix of and is the servo gain vector of IBVS.
3. IBVS with Deep Reinforcement Learning
This section presents an IBVS method based on a DQN. As shown in Figure 3, the MDP model is first established. Next, the error and state are fed into two different agents, respectively. Then, the DQN is applied to solve the MDP problems and automatic servo gain. The servo gains and depth Z are input into IBVS controller. Finally, the speed control quantity is obtained.
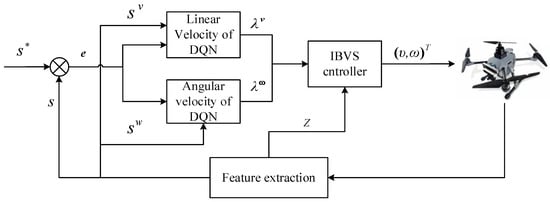
Figure 3.
The scheme of IBVS based on the DQN method.
3.1. The Markov Decision Process Model
To design an adaptive law based on the DQN algorithm, this task needs to be formulated as an MDP model consisting of quintuplet . The model of state transition is determined by the environment, and is generally set according to experience. Thus, this paper focuses on the design of , , and r.
- State Space
The image plane is divided into by pixel. A coordinate system is established in the current image plane, and the coordinates of the desired position in the image plane can be set as the origin. In the process of discretizing the image plane space, it is necessary to divide the pixel plane into a certain number of grids. The image plane can be divided into segments along the x-axis and segments along the y-axis, and it needs to meet the complete division, i.e.,
From the above formula, it can be deduced that the size of the divided state space is:
where K is the size of the state space.
If the pixel coordinate of the current position of the UAV in the image plane is , and the expected position is , then the formula can be obtained:
where is the pixel distance of the image plane coordinates and is the sign function.
Figure 4 shows that the pixel coordinates are divided into state spaces. When the agent is positioned in the black circle shown in Figure 4, it can be expressed as state 1; when the agent is in the blue circle, it is state 3; and when the agent is in the gray circle, it is state 5. Using this division method, a state space of size can be obtained, which is expressed as
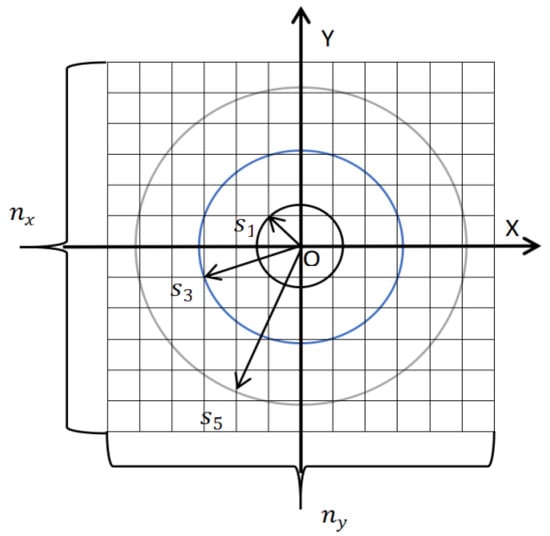
Figure 4.
The state spaces in the discrete gird coordinate system.
- Action Selection
The servo gain is the key factor affecting the control efficiency of the visual servo control system. It is directly related to the control input; thus, this paper selects two different gains for angular and linear velocities, respectively. If the servo gain is directly used as the action of the agent, the action space will be too large and the phenomenon of dimension disaster will arise. Therefore, it is necessary to perform an initial assignment to the two servo gains, respectively, and then further design a limited regulation range for this initial assignment, i.e., the action range. The action interval is also discrete; thus, we can better carry out the learning process.
First, we design the action set according to the above idea: set an initial value as the initial servo gain and then set the size of the action set. The angular and linear velocity servo gains have the same size.
The action space can be expressed as
The update rules of the servo gain satisfy
- Reward Function
The reward function is the agent’s feedback with respect to the environment, which is crucial to the convergence and stability of the whole learning algorithm. Indeed, it determines the effectiveness of the reinforcement learning algorithm to some extent. The reward function is the standard used to evaluate whether agents can learn the optimal strategy in the process of continuous interaction with the environment. If we choose to give only a reward value to the final goal or expected position of reinforcement learning in the design of the reward function, the convergence time of the algorithm will be greatly increased in the environment because the agent will obtain the reward only upon achieving the final goal. In the state action value function, the reward feedback of other positions in the state space is zero, and the amount of reinforcement learning will also be greatly increased. If a positive value smaller than the reward value fed back by the final goal is randomly designed in the reward function of a certain area in the state space, it is likely that a phenomenon similar to the repeated movement of the agent in this area will occur because the agent constantly swipes the reward value in this area without choosing to move to other areas in order to find a better reward or the final reward by using the influence of strategy.
In the design of the abovementioned state space and action set, we can understand that the UAV is controlled by the image visual servo controller, and deep reinforcement learning is responsible for regulating the servo gain. Therefore, in reinforcement learning, the agent can also represent the motion of the target in the image plane, which has a good mapping relationship with the three-dimensional inertial space. On this basis, the feedback of agents in the environment can be divided into three situations.
When the distance between all the feature points of the target and the coordinates of the desired position feature points in the image plane is less than a fixed value, it can be considered that the rotor UAV has reached the desired position and the one-time learning algorithm of reinforcement learning is completed. In these circumstances, the agent can obtain a maximum reward value.
When the UAV cannot obtain the total number of feature points of the desired target in the state space, it means that the UAV has exceeded the observation range of the target position by the visual servoing system. In this case, the target is lost and the minimum reward value should be given to the agent.
When the rotor UAV can detect all the feature points but has not reached the desired position, a function of feature error can be set:
where is the number of characteristic points, is the current location, and is the desired location.
The reward function can be set according to the above three situations as
where is the weight coefficient of the feature error vector and is the weight coefficient of penalized large actions.
3.2. DQN Algorithm
The Q function of Q-learning represents the value of each pair of state–action in a specific configuration environment. In order to represent the Q function that may have a large number of state actions, the deep Q-Network (DQN) uses the neural network approach to approximate the characteristics, and the Q function is expressed as a weight parameter as . and represent state and action, respectively. The next state is obtained after performing .
There are two major improvement measures for DQNs:
- Target Network: With only one network, updating the Q function in real time can result in a chaotic trajectory and poor training. To avoid instability caused by updating the Q function while simultaneously acquiring the Q value, a target network is used. The target network provides a stable Q value for the Q function to be updated. The target network is updated with the new Q function to improve performance.
- Experience Replays: Experience replays will build a replay buffer . The replay buffer is also called replay memory. Instead of using the samples in the standard sequence, small batches are randomly selected from the data set for training to diminish the relativity between training samples.
In each iteration, the state and action are sent to the DQN and the estimated Q value is generated.
The loss function expressed in the expected form is:
where denotes the target network parameters.
Including the experience replays in Equation (22),
The gradient of loss function is given by:
The optimization algorithm is gradient descent, which iteratively updates the model’s parameters to find the optimal set of values. The parameters of separate target networks are determined according to
The proposed iterative algorithm’s process is provided in Algorithm 1, where the max episode , denotes the MaxStep.
| Algorithm 1: DQN-based IBVS method |
| Initialization; For episode = 1: For = 1: If or (Termination condition); Break End Generate random number:; If < Random selection of action ; Else Select the corresponding strategic actions ; obtain the rewards , and servo gains and ; and are substituted to ; Observe the next State ; Store the experience replay with ; ; End If Experience replay full Randomly selected datasets of buffer ; Train the network by gradient descent method and updating network parameters according to (24); After training a certain number of times, update the target network according to (25); End End End |
4. Simulations and Experiments
This section describes various simulations that were carried out to prove the effectiveness and performance of IBVS based on a DQN. Due to the concise language and high programming efficiency of MATLAB, the proposed control system was simulated using MATLAB R2021b.
The parameters of the quadrotor used in the simulation are m = 1 kg, g = 9.81 m/s2, and J = diag{0.0081, 0.008, 0.0142} kg.m2/rad2. The focal length of the camera is 3.2 mm. The length and width of the camera pixels are m. The targets are four points on the horizontal plane. Their coordinates relative to the inertial system are (3,2,3), (2,2,3), (2,3,3), and (3,3,3). The parameters of the DQN are shown in Table 2, where is the error threshold, is the discount parameter, and is the learning rate, while and represent the initial servo gain values of angular velocity and linear velocity, respectively.

Table 2.
Intrinsic parameters of the DQN.
Figure 5 shows the two groups of servo gain obtained through deep reinforcement learning. In the beginning, small servo gains are selected to avoid target loss, because a large gain value will lead to an excessive control input and cause the UAV to move violently. In the later stage, a large gain is chosen to improve the efficiency of IBVS.
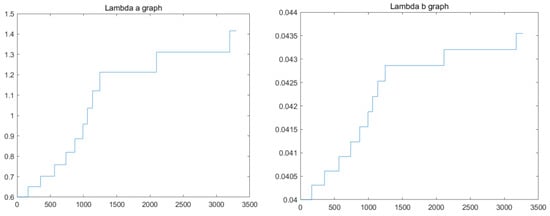
Figure 5.
The final servo gains obtained using the DQN algorithm.
To prove the effectiveness and practicability of the new method, we compare C-IBVS [28] under different servo gains in the simulation platform. Figure 6 shows the position path trajectory diagram of the quadrotor UAV under various conditions.
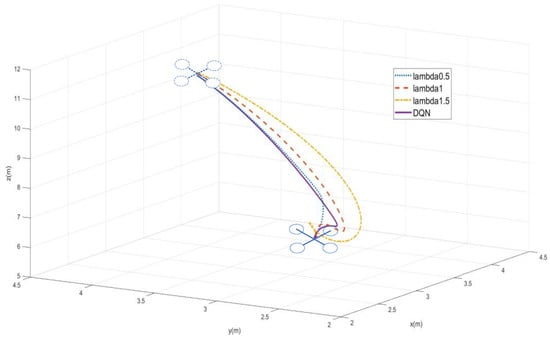
Figure 6.
Position trajectory of the UAV.
Figure 7 shows the feature trajectories of the image, and four colored lines represent the trajectories of different feature points in the image. It can be seen that when a gain of = 1.5 is adopted in the C-IBVS method, the trajectories vary drastically and there is a risk of losing the target because the feature points have reached the image border. When = 1, there is a safe distance between the image trajectory and the edge. When = 0.5, the image trajectory is the gentlest and the trajectory is shortest. The DQN method is also relatively gentle, and the image trajectory is a safe distance from the edge, which ensures that the target features are not lost.
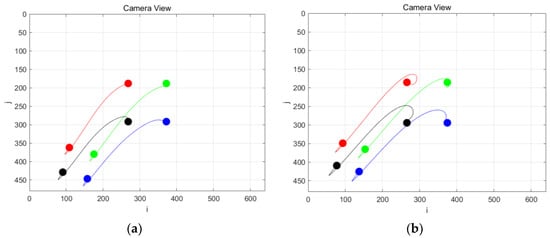
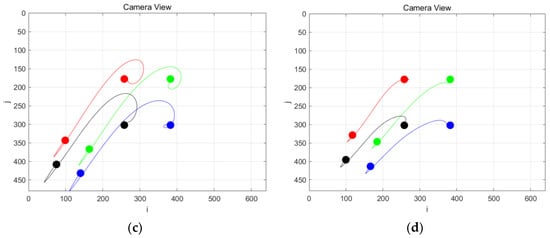
Figure 7.
Feature trajectories in the image plane under different conditions: (a) C-IBVS ( = 0.5); (b) C-IBVS ( = 1); (c) C-IBVS ( = 1.5); (d) IBVS based on a DQN.
Figure 8 shows the position movement trajectories of a UAV in four cases. It can be seen that when = 0.5, the convergence needs 25 time steps. When = 1, it needs 15 time steps, and when = 1.5, it is also needs 15 time steps because it involves overshoot and for other reasons. The convergence of the adopted DQN method takes 12 time steps, and the curve has fast convergence and no overshoot.
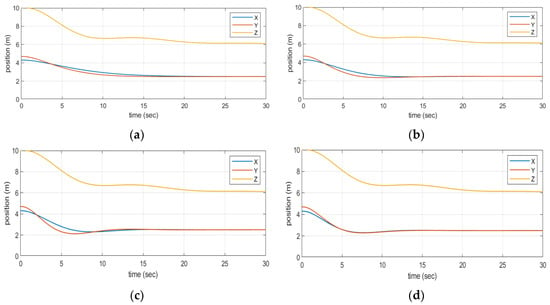
Figure 8.
Position movement trajectory of the UAV under different conditions: (a) C-IBVS ( = 0.5); (b) C-IBVS ( = 1); (c) C-IBVS ( = 1.5); (d) IBVS based on a DQN.
5. Conclusions
To address the problems of target loss and the low control efficiency in image-based visual servoing (IBVS), this paper proposes a DQN-based IBVS adaptive servo gain adjustment method. First, a Markov model of UAV visual servoing control under field-of-view constraints was established by designing the state space, action set, and reward function, which considers the improvement of the control efficiency. Second, an improved DQN algorithm with a target network and experience replay was designed to solve the Markov model. To enhance the control performance, two independent agents were designed, with each agent responsible for adjusting the linear and angular velocity servo gains, respectively. Through a simulation analysis of a quadrotor UAV equipped with a monocular camera, the proposed method can avoid target loss caused by FOV constraint and improve the efficiency of IBVS.
The process of action selection in this method is discrete and the number of actions is limited. In future work, a continuous action space will be designed to enhance the algorithm’s performance. Additionally, the algorithm will be further validated through real flight experiments.
Author Contributions
Conceptualization, G.F. and L.L.; methodology, G.F. and X.Z.; software, L.F.; validation, G.F. and L.F.; formal analysis, G.F.; writing—original draft preparation, G.F.; writing—review and editing, H.C. and G.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 61601382; Fund project for basic scientific research expenses of central universities, grant number J2022-024; Fund project for basic scientific research expenses of central universities, grant number J2022-07; and the Independent research project of the Key Laboratory of Flight Techniques and Flight Safety, grant number FZ2021ZZ04.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| UAV | unmanned aerial vehicle |
| FOV | field of view |
| DRL | deep reinforcement learning |
| DQN | deep Q-network |
| PBVS | position-based visual servoing |
| IBVS | image-based visual servoing |
| WMRs | wheeled mobile robots |
| MPC | model predictive control |
References
- Alzahrani, B.; Oubbati, O.S.; Barnawi, A.; Atiquzzaman, M.; Alghazzawi, D. UAV assistance paradigm: State-of-the-art in applications and challenges. J. Netw. Comput. Appl. 2020, 166, 102706. [Google Scholar] [CrossRef]
- Mahony, R.; Kumar, V.; Corke, P. Multirotor Aerial Vehicles: Modeling, Estimation, and Control of Quadrotor. IEEE Robot. Autom. Mag. 2012, 19, 20–32. [Google Scholar] [CrossRef]
- Zhen, Z.; Chen, Y.; Wen, L.; Han, B. An intelligent cooperative mission planning scheme of UAV swarm in uncertain dynamic environment. Aerosp. Sci. Technol. 2020, 100, 105826. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, H.; Tian, Y.; Sun, C. Reinforcement learning based two-level control framework of UAV swarm for cooperative persistent surveillance in an unknown urban area. Aerosp. Sci. Technol. 2020, 98, 105671. [Google Scholar] [CrossRef]
- Wu, Y.; Hu, X. An online route planning method for multi-rotor drone in urban environments. Control. Decis. 2021, 36, 2851–2860. [Google Scholar]
- Zheng, D.; Wang, H.; Wang, J.; Chen, S.; Chen, W.; Liang, X. Image-Based Visual servoing of a quadrotor using virtual camera approach. IEEE/ASME Trans. Mechatron. 2017, 22, 972–982. [Google Scholar] [CrossRef]
- Chaumette, F.; Hutchinson, S. Visual servo control. I. Basic approaches. IEEE Robot. Autom. Mag. 2006, 13, 82–90. [Google Scholar] [CrossRef]
- Chen, C.; Tian, Y.; Lin, L.; Chen, S.; Li, H.; Wang, Y.; Su, K. Obtaining World Coordinate Information of UAV in GNSS Denied Environments. Sensors 2020, 20, 2241. [Google Scholar] [CrossRef]
- Abdessameud, A.; Janabi-Sharifi, F. Image-based tracking control of VTOL unmanned aerial vehicles. Automatica 2015, 53, 111–119. [Google Scholar] [CrossRef]
- Zhang, X.; Fang, Y.; Li, B.; Wang, J. Visual servoing of nonholonomic mobile robots with uncalibrated Camera-to-Robot parameters. IEEE Trans. Ind. Electron. 2017, 64, 390–400. [Google Scholar] [CrossRef]
- Zhang, X.; Fang, Y.; Zhang, X.; Jiang, J.; Chen, X. Dynamic Image-Based Output Feedback Control for Visual Servoing of Multirotors. IEEE Trans. Ind. Inform. 2020, 16, 7624–7636. [Google Scholar] [CrossRef]
- Ceren, Z.; Altuğ, E. Image based and hybrid visual servo control of an unmanned aerial vehicle. J. Intell. Robot. Syst. 2012, 65, 325–344. [Google Scholar] [CrossRef]
- Liu, N.; Shao, X.; Yang, W. Desired compensation RISE-based IBVSS control of quadrotor for tracking a moving target. Nonlinear Dyn. 2019, 95, 2605–2624. [Google Scholar] [CrossRef]
- Santamaria-Navarro, À.; Andrade-Cetto, J. Uncalibrated image based visual servoing. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 5247–5252. [Google Scholar]
- Miao, Z.; Zhong, H.; Lin, J.; Wang, Y.; Chen, Y.; Fierro, R. Vision-Based Formation Control of Mobile Robots With FOV Constraints and Unknown Feature Depth. IEEE Trans. Control. Syst. Technol. 2021, 29, 2231–2238. [Google Scholar] [CrossRef]
- Lopez-Nicolas, G.; Aranda, M.; Mezouar, Y. Formation of differential-drive vehicles with field-of-view constraints for enclosing a moving target. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, Singapore, 29 May–3 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 261–266. [Google Scholar]
- Bhagat, S.; Pb, S. UAV Target Tracking in Urban Environments Using Deep Reinforcement Learning. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020. [Google Scholar]
- Bruno, H.M.S.; Colombini, E.L. LIFT-SLAM: A deep-learning feature-based monocular visual SLAM method. Neurocomputing 2021, 455, 97–110. [Google Scholar] [CrossRef]
- Hajiloo, A.; Keshmiri, M.; Xie, W.F.; Wang, T.T. Robust Online Model Predictive Control for a Constrained Image-Based Visual Servoing. IEEE Trans. Ind. Electron. 2016, 63, 2242–2250. [Google Scholar]
- Chesi, G. Visual Servoing Path Planning via Homogeneous Forms and LMI Optimizations. IEEE Trans. Robot. 2009, 25, 281–291. [Google Scholar] [CrossRef]
- Huang, Y.; Zhu, M.; Zheng, Z.; Low, K.H. Homography-based visual servoing for underactuated VTOL UAVs tracking a 6-DOF moving ship. IEEE Trans. Veh. Technol. 2022, 71, 2385–2398. [Google Scholar] [CrossRef]
- Zhang, X.; Fang, Y.; Zhang, X.; Shen, P.; Jiang, J.; Chen, X. Attitude-Constrained Time-Optimal Trajectory Planning for Rotorcrafts: Theory and Application to Visual Servoing. IEEE/ASME Trans. Mechatron. 2020, 25, 1912–1921. [Google Scholar] [CrossRef]
- Zheng, D.; Wang, H.; Wang, J.; Zhang, X.; Chen, W. Toward Visibility Guaranteed Visual Servoing Control of Quadrotor UAVs. IEEE/ASME Trans. Mechatron. 2019, 24, 1087–1095. [Google Scholar] [CrossRef]
- Krichen, M.; Mihoub, A.; Alzahrani, M.Y.; Adoni, W.Y.H.; Nahhal, T. Are Formal Methods Applicable To Machine Learning And Artificial Intelligence? In Proceedings of the 2022 2nd International Conference of Smart Systems and Emerging Technologies (SMARTTECH), Riyadh, Saudi Arabia, 9–11 May 2022; pp. 48–53. [Google Scholar]
- Seshia, S.A.; Sadigh, D.; Sastry, S.S. Toward Verified Artificial Intelligence. Commun. ACM 2022, 65, 46–55. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Wang, Y.; Lang, H.; De Silva, C.W. A Hybrid Visual Servo Controller for Robust Grasping by Wheeled Mobile Robots. IEEE/ASME Trans. Mechatron. 2010, 15, 757–769. [Google Scholar] [CrossRef]
- Shi, H.; Li, X.; Hwang, K.S.; Pan, W.; Xu, G. Decoupled visual servoing with fuzzy Q-learning. IEEE Trans. Ind. Inform. 2018, 14, 241–252. [Google Scholar] [CrossRef]
- Shi, H.; Shi, L.; Sun, G.; Hwang, K.S. Adaptive Image-Based Visual Servoing for Hovering Control of Quad-rotor. IEEE Trans. Cogn. Dev. Syst. 2020, 12, 417–426. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).