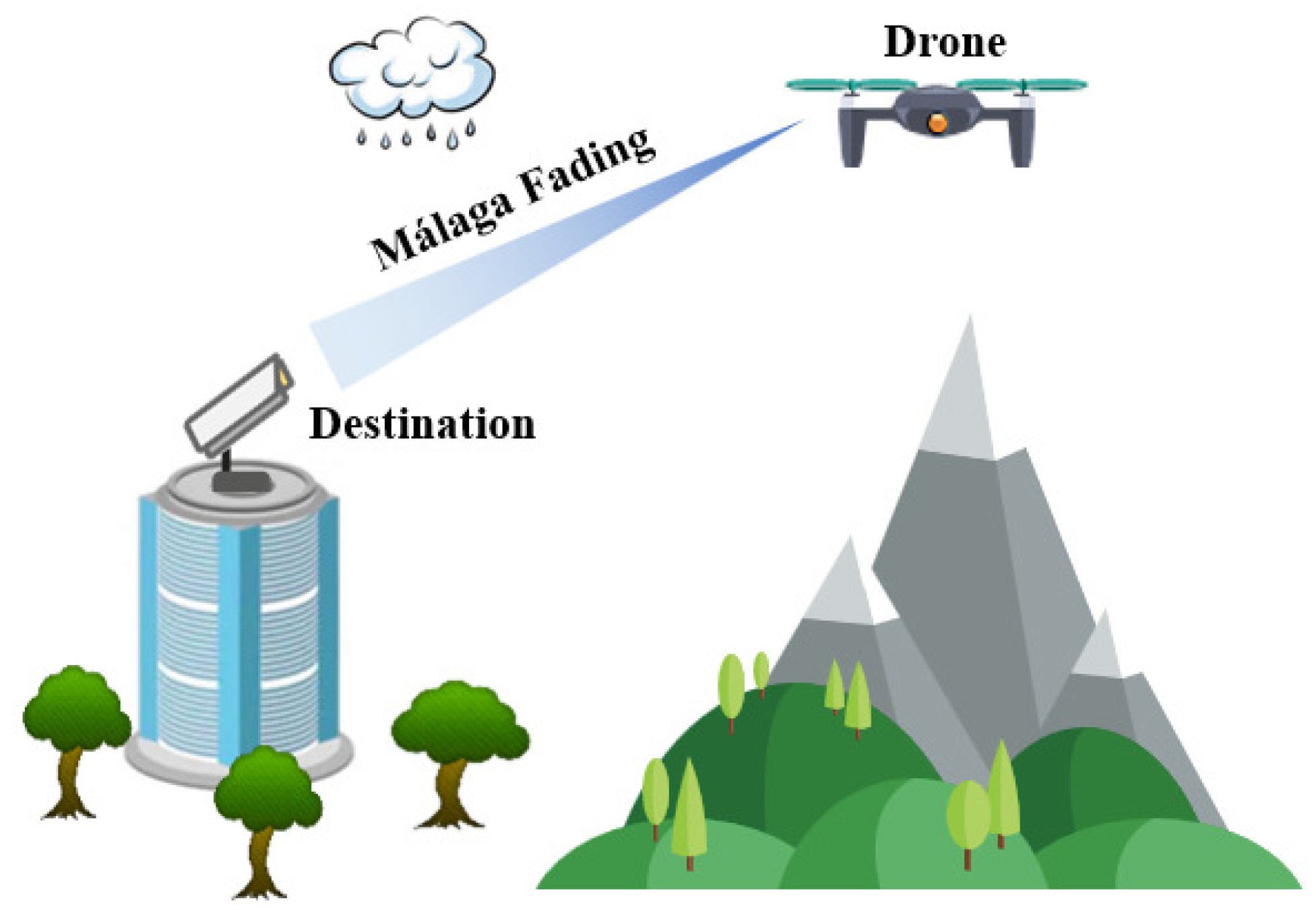
Performance Analysis of a Drone-Assisted FSO Communication System over Málaga Turbulence under AoA Fluctuations

Abstract

Future wireless communications have been envisaged to benefit from integrating drones and free space optical (FSO) communications, which would provide links with line-of-sight propagation and large communication capacity. The theoretical performance analysis for a drone-assisted downlink FSO system is investigated. Furthermore, this paper utilizes the Málaga distribution to characterize the effect of atmospheric turbulence on the optical signal for the drone–terrestrial user link, taking into account atmospheric attenuation, pointing errors, and angle-of-arrival fluctuations. The probability density function and cumulative distribution function are then expressed in closed-form using the heterodyne detection and indirect modulation/direct detection techniques, respectively. Thereafter, the analytical expressions including the average bit error rate (BER) and the ergodic capacity are given. Particularly, the asymptotic behavior of the average BER of the considered system is presented using heterodyne detection at high optical power. The Monte Carlo simulation results certify the theoretical analytical results. Correspondingly, the field-of-view of the receiver is analyzed for optimal communication performance.

1. Introduction

Future communications already benefit from free space optical (FSO) communication because of its large communication capacity, cost-effectiveness, ease of deployment, and high security [1]. FSO communication is often used to handle the “last mile” communication issue, especially in some dense areas [2]. Drones are already the preferred option as a relay or terminal due to their distinct mobility and line-of-sight (LOS) propagation [3,4]. Drone-assisted FSO communication is therefore frequently used in maritime rescue [5], post-disaster emergency communication [6], military reconnaissance [7], and other applications.

Pioneering work has been done on drone-assisted FSO communication systems [8]. The serial FSO decode-and-forward relay system based on hovering unmanned aerial vehicles (UAVs) was optimized by Wang et al. to achieve optimal communication performance [9]. A ground-to-UAV FSO link was built to demonstrate that increasing the total received optical area and field of view (FoV) can reduce the average bit error rate (BER) [10]. Additionally, Le et al. designed a satellite-to-UAV downlink FSO links and noted out that pointing errors can reduce the average fade duration [11]. Najafi et al. investigated the statistical behavior of the FSO link between the hovering UAV and terminal by considering random displacement of the UAV [12].

However, drone-assisted FSO communication is vulnerable to atmospheric turbulence and pointing errors. Changes in light intensity and phase are caused by atmospheric turbulence due to temperature, humidity, pressure, etc. Several fading distributions, including log-normal distribution [13], Gamma–Gamma distribution [14], Double-Weibull distribution [15], and others, have been proposed to characterize the influence of atmospheric turbulence on the FSO link. Although the above statistical models are highly accurate under specific conditions, log-normal distribution neglects the behavior in the tails [16]. Gamma–Gamma and Double-Weibull distributions are only accurate under the weak and moderate turbulence conditions. Recently, a universal statistical distribution called the Málaga distribution was proposed by [17], which could model weak-to-strong turbulence. Ansari et al. conducted an investigation of the FSO link over the Málaga channel model and indicated that the Málaga distribution has higher accuracy than other distributions [18]. Apart from atmospheric turbulence, pointing errors can also degrade communication quality, which refers to the misalignment of beams caused by the hovering of the drone and the thermal expansion of the building. Much effort was devoted to exploring the inevitable pointing errors in statistical models of FSO links [19,20]. Considering the pointing errors, the exact closed-form formulae for the average BER as well as the ergodic capacity for the relay-assisted FSO system were derived. The deterioration in communication performance was justified [19].

Thus, it is necessary to investigate the impacts of various factors, such as atmospheric turbulence and pointing errors, on the performance of drone-assisted FSO communication systems. Najafi et al. researched the UAV-assisted FSO communication system under atmospheric attenuation, atmospheric turbulence, and misalignment loss using the indirect modulation/direct detection (IM/DD) technique concerning the outage probability and the ergodic capacity [12]. Similarly, the FSO communication system subject to atmospheric attenuation, atmospheric turbulence, and pointing errors was developed by Vu et al. to evaluate the outage probability of the communication system with the IM/DD technique [21]. Considering path loss, atmospheric turbulence, pointing errors, and geometric expansion, the outage probability of a coherent FSO communication system with the IM/DD technique was evaluated in [22].

According to the previous discussions, the impact of atmospheric turbulence along with pointing errors on drone-aided FSO systems was investigated in detail. However, the influence of angle-of-arrival (AoA) fluctuations was rarely investigated. The AoA fluctuations because of orientation deviations of the receiver can cause fluctuations in the signal-to-noise ratio (SNR) and substantially reduce the communication performance of long-range FSO systems, such as drone-assisted FSO communication systems [8,23]. Therefore, the AoA fluctuations should be considered when assessing the performance of drone-assisted FSO communication systems. Dabiri et al. modeled a multi-rotor UAV-assisted FSO link considering the influence of AoA fluctuations [24]. However, the proposed model might need more flexibility due to its complexity. A simpler and easy-to-handle FSO system under AoA fluctuations was further proposed in [25]. However, only the outage probability was studied, which may be insufficient for constructing the drone-assisted FSO system. It is also important to note that the average BER and ergodic capacity of the FSO communication system under AoA fluctuations are also important metrics of the system’s performance and have hardly been investigated. Therefore, research on the effect of the AoA fluctuations on the system performance of the drone-assisted FSO system is still in the initial stage.

In this paper, a drone-assisted downlink FSO communication system is established in response to the abovementioned discussions. Comprehensive consideration is given to the impact of atmospheric attenuation, atmospheric turbulence, pointing errors, and AoA fluctuations on the communication system. Note that this is widely available in most practical communication scenarios, such as post-disaster rescue, emergency communication and mobile communication supplementation. Furthermore, the channel fading of the FSO link was also modeled using the Málaga distribution. To evaluate system performance, exact closed-form formulae are presented for the average BER and the ergodic capacity using the IM/DD and the heterodyne detection techniques, respectively. Hence, the main contributions are listed below:

•

A drone-assisted FSO communication system is established, considering the effects of atmospheric attenuation, atmospheric turbulence, pointing errors, and AoA fluctuations for the first time, where the FSO link undergoes the Málaga fading.

•

The statistical expressions for the probability density function (PDF) and the cumulative distribution function (CDF) of the drone-assisted FSO link are derived using the IM/DD and the heterodyne detection techniques, respectively. In addition, closed-form expressions for the average BER and the ergodic capacity are derived.

•

The asymptotic expression for the average BER under the heterodyne detection technique at high optical power is also proposed to offer enhanced insights into the system and gain useful engineering applications.

The rest of the paper is structured as follows. Section 2 proposes the system and channel models. The closed-form formulae for the average BER and the ergodic capacity are deduced in Section 3. Section 4 offers simulation results and discussions. Finally, the whole paper is summarized in Section 5.

2. System and Channel Models

This section will focus on a downlink FSO communication link, as depicted in Figure 1. The system includes a drone as the source and a receiver as the destination. The drone hovers in a fixed position and has a laser diode. The receiver has a photodiode (PD) that converts the optical signals into electrical signals. We have the assumption that the transmitter and the receiver are aimed at each other.

Mathematically, the received electrical signal can be written as

$$\begin{array}{c}\hfill y=\eta Ix+n\end{array},$$

(1)

where x is the optical signal emitted by drone, $\eta$ is the optoelectronic conversion efficiency of the PD, I is the channel coefficient, and n is an additive white Gaussian noise (AWGN) with zero mean and variance ${\sigma }_n^2$, i.e., $n\sim N\left(0,{\sigma }_n^2\right)$.

In this system, optical beams inevitably undergo attenuation and flicker as they propagate through the atmosphere. The building vibration, building sway, and thermal expansion also prevent the beam from reaching the receiver aperture accurately. Moreover, orientation deviations of the drone can affect the incidence angle of light and cause communication interruptions in severe cases. Thus, we consider the influence of atmospheric attenuation, atmospheric turbulence, pointing errors, as well as AoA fluctuations on the channel model, i.e.,

$$\begin{array}{c}\hfill I=I_{al} I_{at} I_{pe} I_{A\mathrm{o}A}\end{array},$$

(2)

where $I_{al}$, $I_{at}$, $I_{pe}$, and $I_{AoA}$ indicate atmospheric attenuation, atmospheric turbulence, geometric loss due to the pointing error impairments, and communication interruption because of AoA fluctuations, respectively.

2.1. Atmospheric Attenuation

Atmospheric attenuation refers to the absorption and scattering of light waves by gas molecules and aerosol particles in the atmosphere, which causes the attenuation of light energy. With the help of the Beers–Lambert law [26], we can express $I_{al}$ as

$$\begin{array}{c}\hfill I_{al}=exp\left(-L\psi \right)\end{array},$$

(3)

where L represents the communication distance, and $\psi$ is an attenuation coefficient that varies with visibility.

2.2. Atmospheric Turbulence

According to the discussion of atmospheric turbulence in the introduction, it is evident that it influences optical signal transmission. The Málaga model is universal in describing atmospheric turbulence because it can be converted to other common atmospheric turbulence models by adjusting its parameters [17], and it has higher accuracy than other distribution models. Meanwhile, the PDF of $I_{at}$ based on the Málaga fading model can be expressed as

$$\begin{array}{c}\hfill f_{I_{at}}\left(I_{at}\right)=\frac{A}{2}\sum _{i=1}^b{\mu }_i{I}_{at}^{\frac{a+i}{2}-1}{G}_{0,2}^{2,0}\left[\frac{ab}{\kappa b+\mathsf{𝚈}}{I}_{at}\left|{}_{\frac{a-i}{2},-\frac{a-i}{2}}^{}\right.\right]\end{array},$$

(4)

where

$$\begin{array}{cc}\hfill & A\triangleq \frac{2a^{\frac{a}{2}}}{{\kappa }^{1+\frac{\alpha }{2}}\Gamma \left(a\right)}{\left(\frac{\kappa b}{\kappa b+\mathsf{𝚈}}\right)}^{b+\frac{a}{2}},\hfill \end{array}$$

(5a)

$$\begin{array}{cc}\hfill & {\mu }_i\triangleq \left(\begin{array}{c}b-1\\ i-1\end{array}\right)\frac{{(\kappa b+\mathsf{𝚈})}^{1-\frac{i}{2}}}{(i-1)!}{\left(\frac{\mathsf{𝚈}}{\kappa }\right)}^{i-1}{\left(\frac{a}{b}\right)}^{\frac{i}{2}},\hfill \end{array}$$

(5b)

$$\begin{array}{cc}\hfill & \kappa =\varsigma \left(1-\rho \right),\hfill \end{array}$$

(5c)

$$\begin{array}{cc}\hfill & \mathsf{𝚈}=\chi +\varsigma \rho +2\sqrt{\varsigma \rho \chi }cos\Delta \varphi ,\hfill \end{array}$$

(5d)

where a and b denote two fading parameters associated with atmospheric turbulence, and higher values of a and b indicate weakened atmospheric turbulence. Note that b must be a natural number. $\kappa$ indicates the average power of the scattered components received by the off-axis eddies, $\rho$ indicates the ratio of the scattering components mixed into the LOS part to the total scattering components, subject to 0 $\le \rho \le$ 1, and $\varsigma$ denotes the average power of all scattered components. $\mathsf{𝚈}$ denotes the average power of the coherent parts, $\chi$ indicates the average power of the LOS part, and $\Delta \varphi$ denotes the difference of the definite phase between the LOS part and the scattered components that is combined with the LOS part. Additionally, $G_{p,q}^{m,n}[·]$ is the Meijer’s G function, defined in [27].

2.3. Pointing Error Impairments

Pointing error impairments occur due to the effects of wind, the thermal expansion of buildings, the undesirable fixing of the transmitter and the receiver, and so on, can lead to non-alignment of the transmitter beam and the receiver aperture. Mathematically, pointing error impairments can be expressed as [23]

$$\begin{array}{c}\hfill f_{I_{pe}|{\theta }_a}\left(I_{pe}\right)=B^{-{\xi }^2}{\xi }^2{I_{pe}}^{{\xi }^2-1}cos{\theta }_a,0\le I_{pe}\le B\end{array},$$

(6)

where $B=2{\left(r_r/\phantom{r_r{r}_L}{r}_L\right)}^2$, $\xi = r_L/\phantom{r_{L}2{\sigma }_c}2{\sigma }_c$, $r_r$ denotes the receiver aperture radius, and $r_L$ stands for the beam radius at a distance L. The variance ${\sigma }_c^2$ denotes the sum of the random displacements of the beam centroid and the receiver aperture, which are caused by the jitter of drone and the thermal expansion of buildings, respectively. The angle between the incident light and the normal to the receiver aperture ${\theta }_a$ can be expressed in terms of an approximate Rayleigh distribution as [23]

$$\begin{array}{c}\hfill f_{{\theta }_a}\left({\theta }_a\right)=\frac{{\theta }_a}{{\sigma }_a^2}exp\left(-\frac{{\theta }_a^2}{2{\sigma }_a^2}\right)\end{array},$$

(7)

where ${\sigma }_a^2$ represents variance.

2.4. Angle-of-Arrival Fluctuations

The hovering of the drone can cause the beam to deviate randomly in orientation due to wind and mechanical jitter and further reduces the energy of the optical beam reaching the receiver plane. Finally, the outage probability increases rapidly when the incident angle of the beam reaches a certain value [23]. The ${\theta }_{FoV}$ denotes the threshold of the FoV. Hence, AoA fluctuations can be expressed as [28]

$$\begin{array}{c}\hfill I_{AoA}\simeq \left\{\begin{array}{c}1,{\theta }_a\le {\theta }_{FoV}\\ 0,{\theta }_a>{\theta }_{FoV}\end{array}\right.\end{array}.$$

(8)

Theorem 1.

The analytical formulae for the PDF and CDF based on Meijer’s G function for the case of drone-assisted FSO communication, considering atmospheric attenuation, atmospheric turbulence, pointing errors, as well as AoA fluctuations, are displayed follows:

$$\begin{array}{c}\hfill f\left(\gamma \right)=\left(1-exp\left(-\frac{{\theta }_{{}_{FoV}}^2}{2{\sigma }_a^2}\right)\right)\frac{A{\xi }^{2}C{\sigma }_n^{\frac{2}{\tau }}}{2\eta P_t\tau }{\gamma }^{\frac{1}{\tau }-1}\sum _{i=1}^b{b}_i{G}_{3,5}^{3,2}\left[C\frac{{\left(\gamma {\sigma }_n^2\right)}^{\frac{1}{\tau }}}{\eta P_t}\left|\begin{array}{c}-1,0,{\xi }^2\\ {\xi }^2-1,a-1,i-1,0,-1\end{array}\right.\right]\end{array},$$

(9)

$$\begin{array}{c}\hfill F\left(\gamma \right)=\left(1-exp\left(-\frac{{\theta }_{{}_{FoV}}^2}{2{\sigma }_a^2}\right)\right)\frac{A{\xi }^2}{2}\sum _{i=1}^b{b}_i{G}_{2,4}^{3,1}\left[C\frac{{\left(\gamma {\sigma }_n^2\right)}^{\frac{1}{\tau }}}{\eta P_t}\left|\begin{array}{c}1,1+{\xi }^2\\ {\xi }^2,a,i,0\end{array}\right.\right]+exp\left(-\frac{{\theta }_{{}_{FoV}}^2}{2{\sigma }_a^2}\right)\end{array}.$$

(10)

Proof. 

See Appendix A. □

3. Performance Analysis

In this section, the analytic formulae are determined for the average BER and the ergodic capacity of the drone-assisted FSO downlink system using the derived statistical characteristics.

3.1. Average Bit Error Rate

The average BER refers to the ratio of the number of bits that are incorrectly received to the total number of bits that are transmitted. The average BER of the binary system depicts various detection techniques by adjusting two parameters, p and q, as [29]

$$\begin{array}{c}\hfill \overline{P_b}=\frac{q^p}{2\Gamma \left(p\right)}{\int }_0^{\infty }exp\left(-q\gamma \right){\gamma }_{}^{p-1}F\left(\gamma \right)d\gamma \end{array}.$$

(11)

Therefore, the average BER of the system under AoA fluctuations with the heterodyne detection and the IM/DD techniques, respectively, are stated as follows by substituting (10) into (11) and using Equation (2.24.3.1) in [30]

$$\begin{array}{c}\hfill \overline{P_b}=\frac{1}{4\Gamma \left(p\right)}\left(1-exp\left(-\frac{{\theta }_{{}_{FoV}}^2}{2{\sigma }_a^2}\right)\right)A{\xi }^2\sum _{i=1}^b{b}_i{G}_{3,4}^{3,2}\left[\frac{C{\sigma }_n^2}{\eta P_{t}q}\left|\begin{array}{c}1-p,1,1+{\xi }^2\\ {\xi }^2,a,i,0\end{array}\right.\right]+\frac{1}{2}exp\left(-\frac{{\theta }_{{}_{FoV}}^2}{2{\sigma }_a^2}\right)\end{array},$$

(12)

$$\begin{array}{c}\hfill \begin{array}{c}\overline{P_b}=\frac{2^{a-5}A{\xi }^2}{\pi \Gamma \left(p\right)}\left(1-exp\left(-\frac{{\theta }_{{}_{FoV}}^2}{2{\sigma }_a^2}\right)\right){\displaystyle \sum _{i=1}^b}{b}_i{2}^i\hfill \\ ·G_{5,8}^{6,3}\left[{\left(\frac{C}{\eta P_t}\right)}^2\frac{{\sigma }_n^2}{16q}\left|\begin{array}{c}1-p,\frac{1}{2},1,\frac{1+{\xi }^2}{2},\frac{2+{\xi }^2}{2}\\ \frac{{\xi }^2}{2},\frac{{\xi }^2+1}{2}\frac{a}{2}\frac{a+1}{2}\frac{i}{2},\frac{i+1}{2},0,\frac{1}{2}\end{array}\right.\right]+\frac{1}{2}exp\left(-\frac{{\theta }_{{}_{FoV}}^2}{2{\sigma }_a^2}\right)\hfill \end{array}\end{array}.$$

(13)

Remark 1.

For the particular situation, the average BER under the influence of atmospheric attenuation, atmospheric turbulence, and pointing errors may also be obtained according to (12) and (13), provided ${\sigma }_a\to 0$. The result is consistent with those in Equation (22) of [31].

Remark 2.

The average BER under the heterodyne detection technique can be computed asymptotically at high optical power using Equation (6.2.2) in [32] to transform the argument function in (12), followed by Equation (17) in [31], as shown below:

$$\begin{array}{c}\hfill \begin{array}{c}\overline{P_b}\underset{P_t>>1}{\approx }{\displaystyle \frac{1}{4\Gamma \left(p\right)}}\left(1-exp\left(-\frac{{\theta }_{{}_{FoV}}^2}{2{\sigma }_a^2}\right)\right)A{\xi }^2{\displaystyle \sum _{i=1}^b}{b}_i\left[{\displaystyle \sum _{k=1}^3}{\left(\frac{\eta P_{t}q}{C{\sigma }_n^2}\right)}^{-{\upsilon }_k}\right.\hfill \\ \left.·{\displaystyle \frac{{\prod }_{l=1,l\ne k}^3\Gamma \left({\upsilon }_l-{\upsilon }_k\right)\Gamma \left(p+{\upsilon }_k\right)}{{\upsilon }_k\Gamma \left(1+{\xi }^2-{\upsilon }_k\right)}}\right]+{\displaystyle \frac{1}{2}}exp\left(-\frac{{\theta }_{{}_{FoV}}^2}{2{\sigma }_a^2}\right)\hfill \end{array}\end{array},$$

(14)

where $\upsilon =\left({\xi }^2,\alpha ,i\right)$, ${\upsilon }_k$ represents the $k^{th}$-term of υ, and $\Gamma \left(·\right)$ is the Gamma function.

Then, the diversity order is achieved by expanding (14) in the following manner:

$$\begin{array}{c}\hfill \begin{array}{c}\overline{P_b}\underset{P_t>>1}{\approx }{\displaystyle \frac{1}{4\Gamma \left(p\right)}}\left(1-exp\left(-\frac{{\theta }_{{}_{FoV}}^2}{2{\sigma }_a^2}\right)\right)A{\xi }^2{\displaystyle \sum _{i=1}^b}{b}_i\left[{\left(\frac{\eta P_{t}q}{C{\sigma }_n^2}\right)}^{-{\xi }^2}\frac{\Gamma \left(a-{\xi }^2\right)\Gamma \left(i-{\xi }^2\right)\Gamma \left(p+{\xi }^2\right)}{{\xi }^2}\right.\hfill \\ \left.+{\left(\frac{\eta P_{t}q}{C{\sigma }_n^2}\right)}^{-a}\frac{\Gamma \left(i-a\right)\Gamma \left(p+a\right)}{a\left({\xi }^2-a\right)}+{\left(\frac{\eta P_{t}q}{C{\sigma }_n^2}\right)}^{-i}\frac{\Gamma \left(a-i\right)\Gamma \left(p+i\right)}{i\left({\xi }^2-i\right)}\right]+{\displaystyle \frac{1}{2}}exp\left(-\frac{{\theta }_{{}_{FoV}}^2}{2{\sigma }_a^2}\right)\hfill \end{array}\end{array}.$$

(15)

Therefore, the asymptotic formula for the average BER in (15) is mainly determined by the diversity order of min$\left({\xi }^2, a, 1\right)$. In other words, the atmospheric turbulence and pointing errors determine the average BER at high power. This is because the effects of atmospheric turbulence and pointing errors become more pronounced at high optical powers. The increased optical power amplifies the effects of amplitude and phase fluctuations caused by turbulence, and in addition, pointing errors cause misalignment between the transmitter and receiver, which leads to a degradation in signal quality and an increase in average BER.

3.2. Ergodic Capacity

The ergodic capacity, which represents the time average of the maximum information rate of the random signal in all fading states, is another important parameter of the communication system and is expressed as follows:

$$\begin{array}{c}\hfill \overline{C}\stackrel{\Delta }{=}\mathbb{E}\left[{log}_2\left(1+\tau \gamma \right)\right]\end{array},$$

(16)

where $\mathbb{E}\left[·\right]$ is expectation function.

Substituting (9) into (16) and using Equation (07.34.21.0013.01) in [33], while utilizing the identity of ln$\left(1+\epsilon \gamma \right)=G_{2,2}^{1,2}\left[\tau \gamma \left|{}_{1,0}^{1,1}\right.\right]$, the ergodic capacity of drone-aided downlink FSO system under AoA fluctuations with the heterodyne detection and the IM/DD techniques, respectively, as

$$\begin{array}{c}\hfill \overline{C}=\frac{A{\xi }^{2}C{\sigma }_n^2}{2ln2\eta P_t}\left(1-exp\left(-\frac{{\theta }_{{}_{FoV}}^2}{2{\sigma }_a^2}\right)\right)\sum _{i=1}^b{b}_i{G}_{5,7}^{5,3}\left[\frac{C{\sigma }_n^2}{\eta P_t}\left|\begin{array}{c}-1,0,-1,0,{\xi }^2\\ {\xi }^2-1,a-1,i-1,-1,-1,0,-1\end{array}\right.\right]\end{array},$$

(17)

$$\begin{array}{c}\hfill \begin{array}{c}\overline{C}={\displaystyle \frac{2^{a-\frac{13}{2}}A{\xi }^{2}C{\sigma }_n^{}}{\pi ln2\eta P_t}}\left(1-exp\left(-{\displaystyle \frac{{\theta }_{{}_{FoV}}^2}{2{\sigma }_a^2}}\right)\right){\displaystyle \sum _{i=1}^b}{b}_i{2}^i\hfill \\ ·G_{8,12}^{8,5}\left[{\left({\displaystyle \frac{C}{\eta P_t}}\right)}^2{\displaystyle \frac{{\sigma }_n^2}{32}}\left|\begin{array}{cc}-\frac{1}{2},0,0,\frac{1}{2},-\frac{1}{2},\frac{1}{2},\frac{{\xi }^2}{2},\frac{{\xi }^2+1}{2}& \\ \frac{{\xi }^2-1}{2},\frac{{\xi }^2}{2},\frac{a-1}{2},\frac{a}{2},\frac{i-1}{2},\frac{i}{2},-\frac{1}{2},-\frac{1}{2},0,\frac{1}{2},-\frac{1}{2},0\end{array}\right.\right]\hfill \end{array}\end{array}.$$

(18)

Remark 3.

Specifically, the ergodic capacity under the influence of atmospheric attenuation, atmospheric turbulence, and pointing errors also can be converted from (17) and (18) when ${\sigma }_a\to 0$, and the obtained expressions are consistent with the Equation (28) in [31].

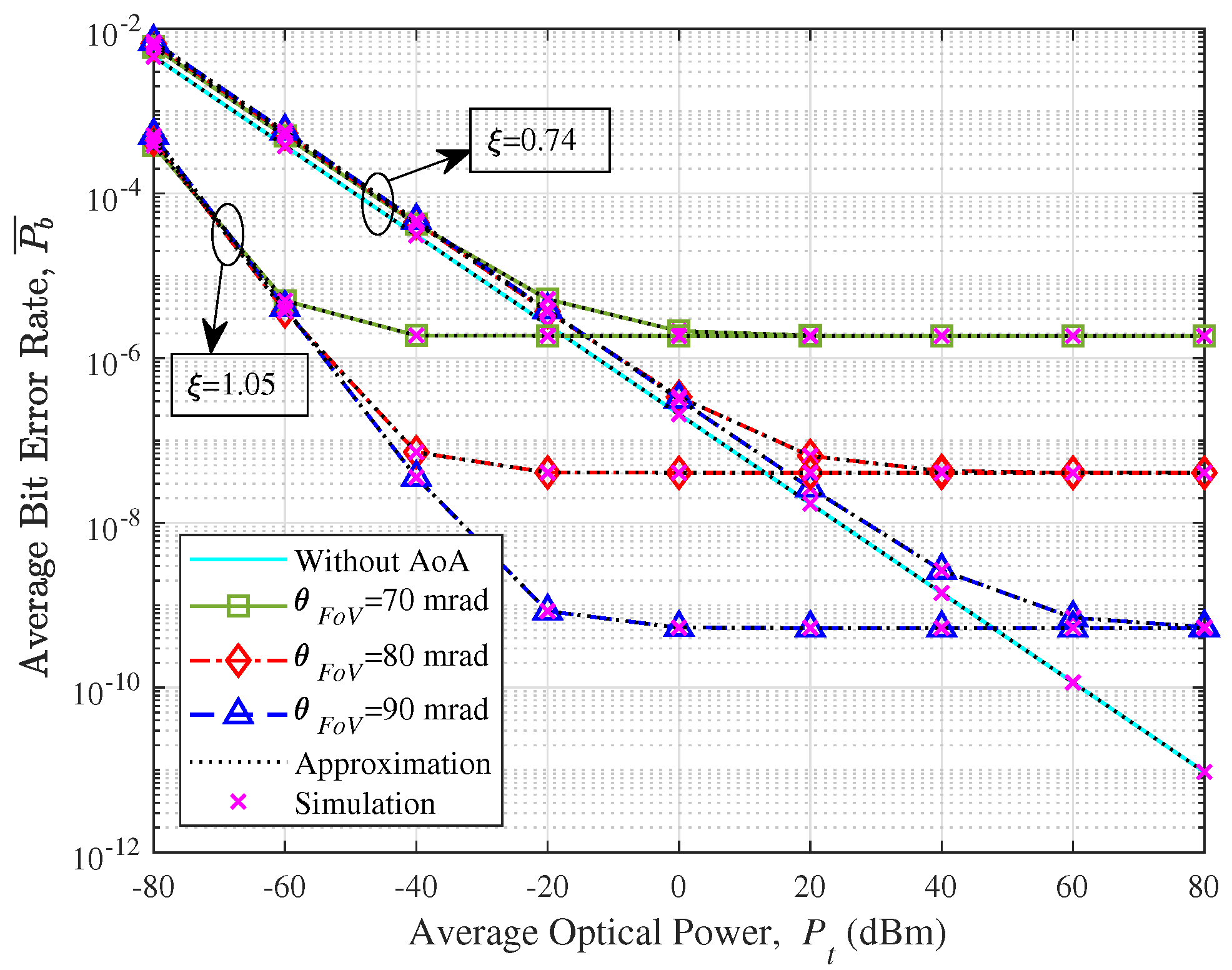
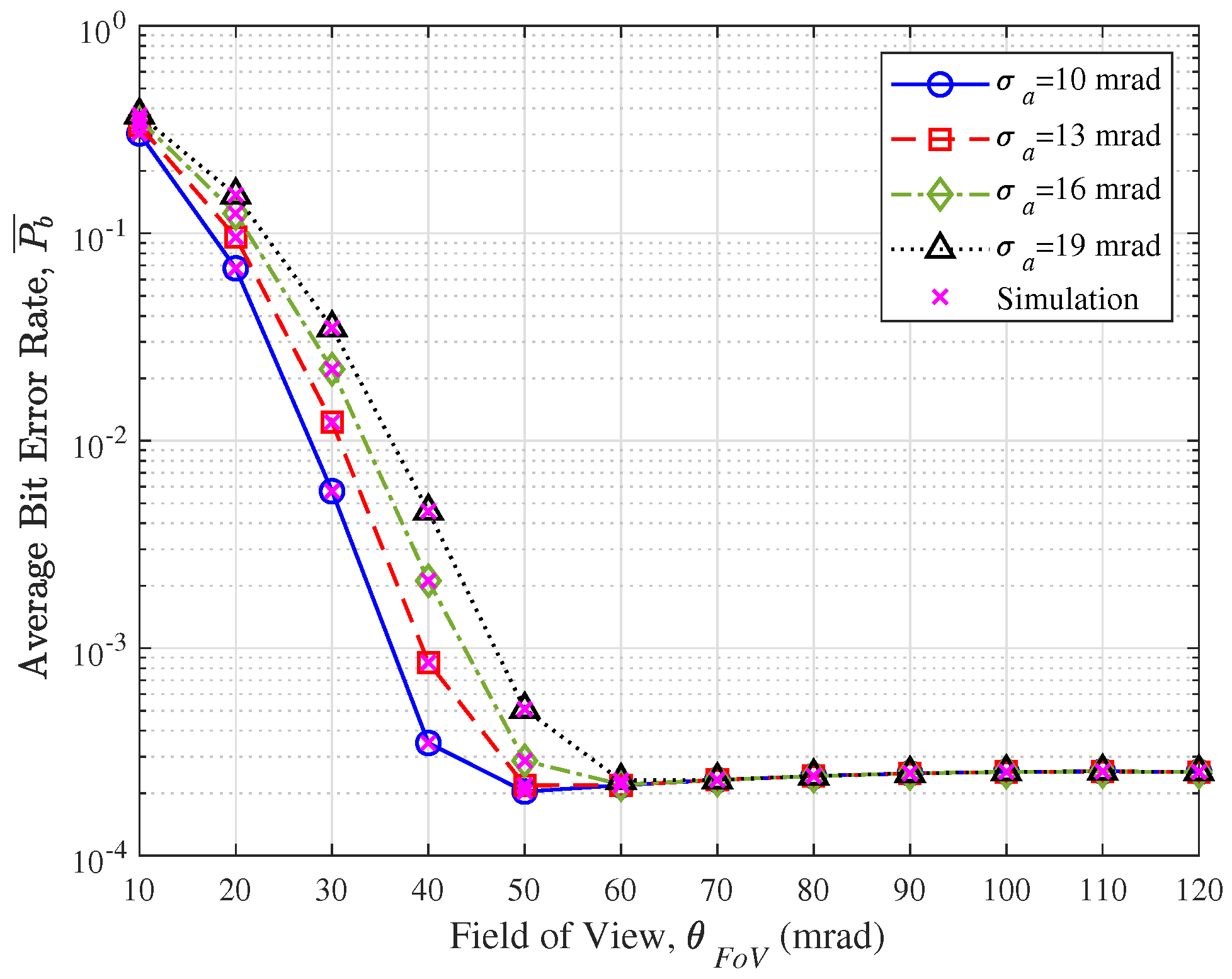
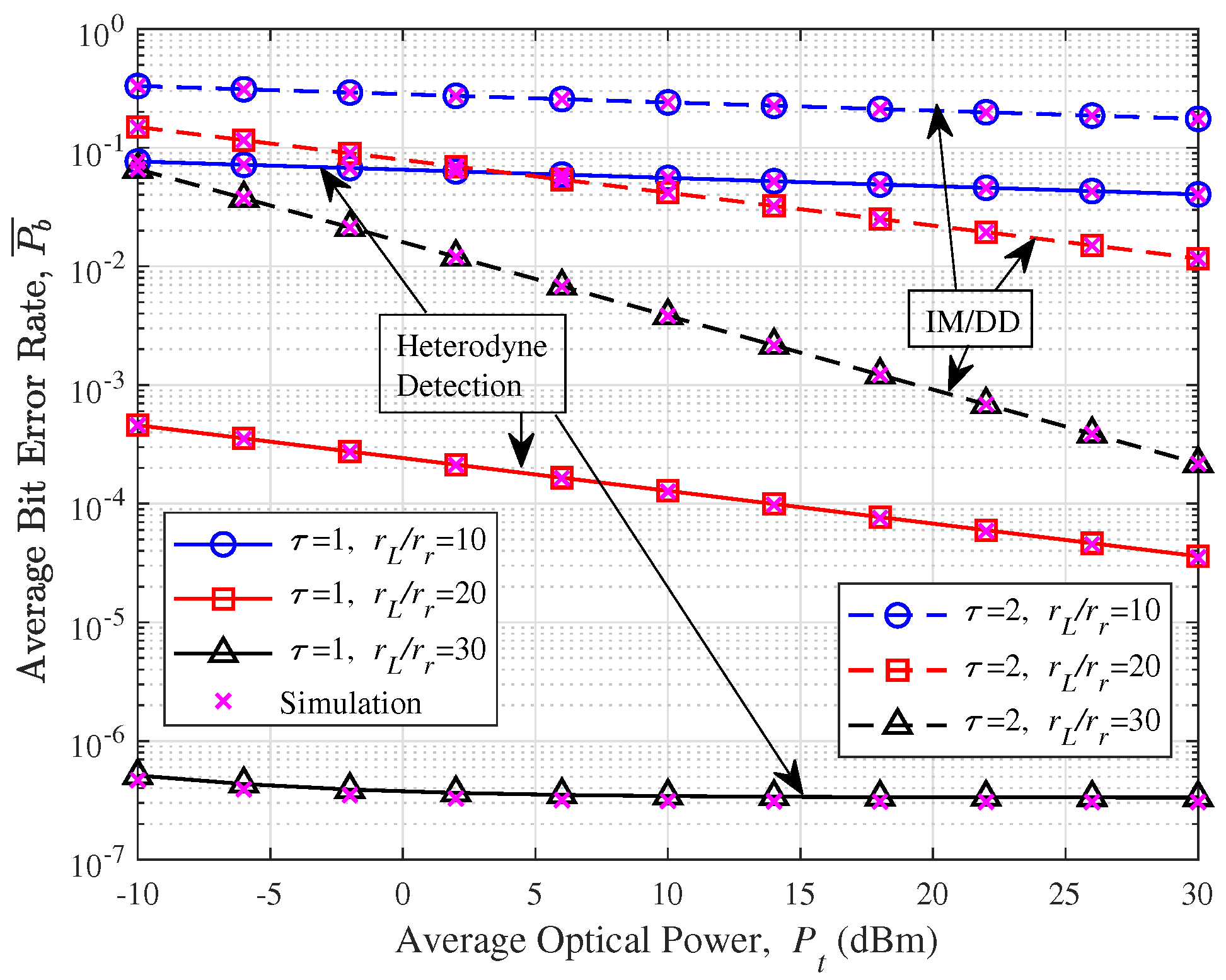
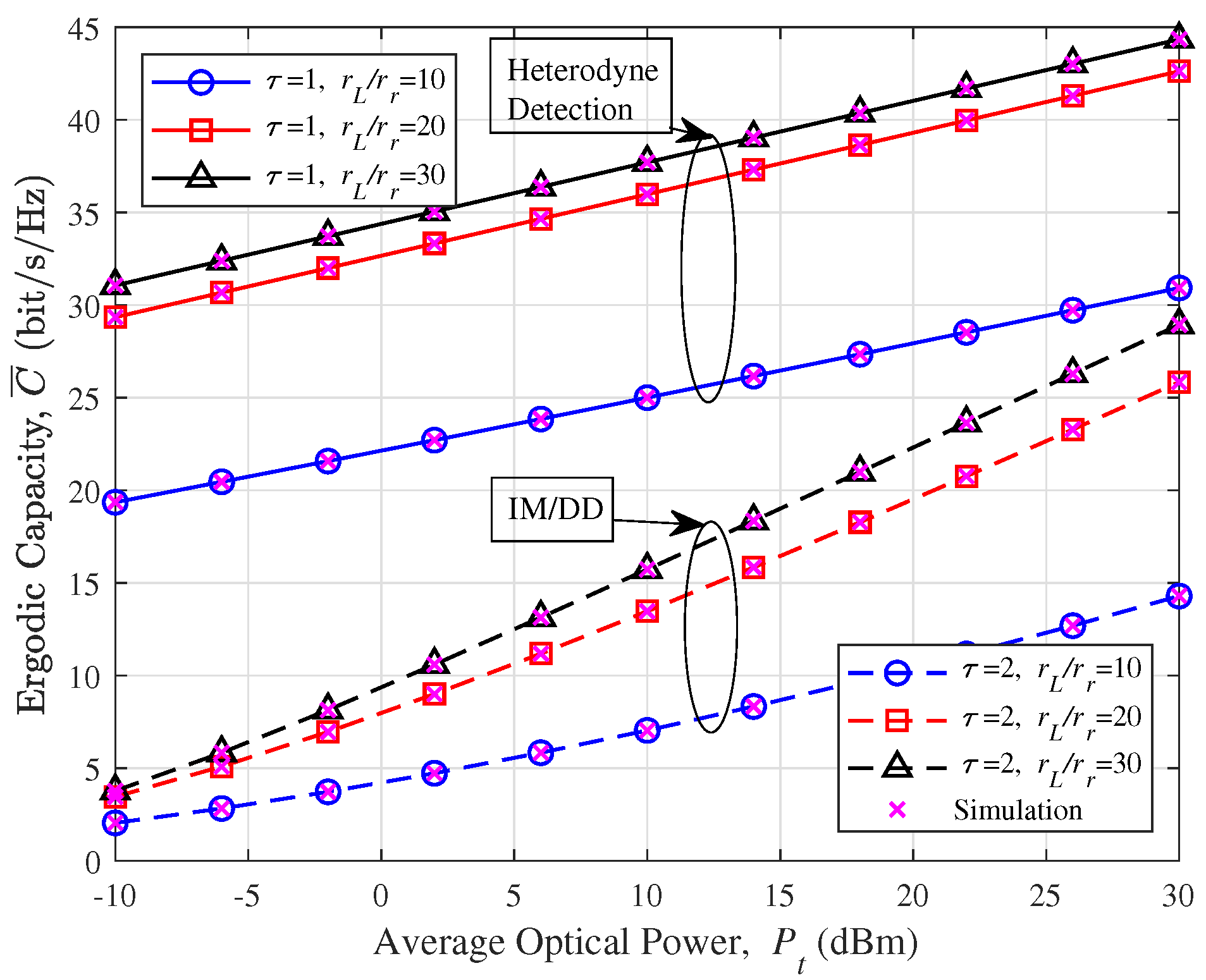
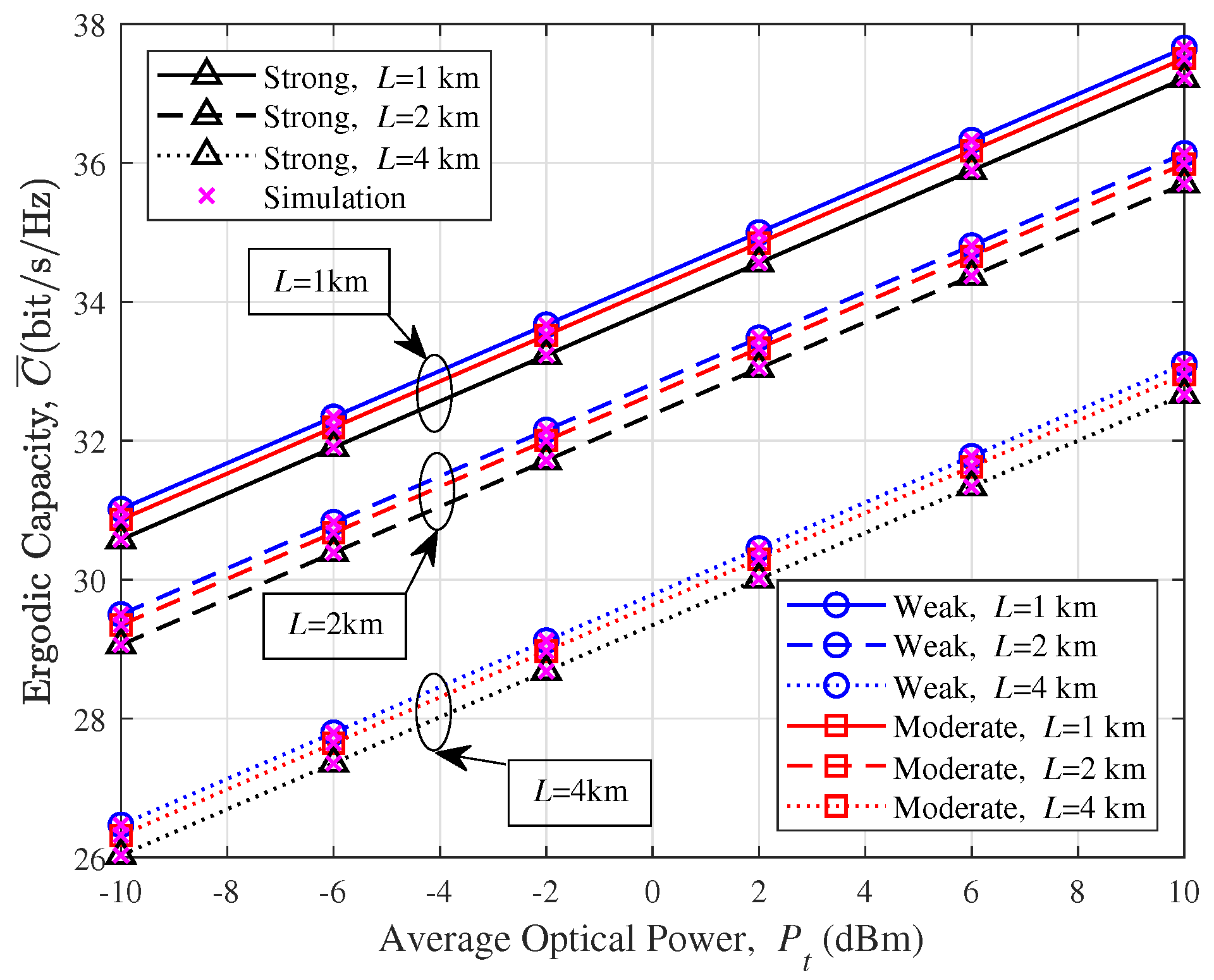
4. Simulations and Analysis

In this section, the Monte Carlo simulation method with ${10}^8$ independent runs is used to compare the theoretical results and numerical results. By adjusting some essential parameters, the communication performance of the downlink FSO communication system is assessed in terms of the average BER and the ergodic capacity. In the general case, some key parameters, from [9,19,28,34], are shown in

Table 1. Key parameters used in the simulation.

Parameters	Name	Value
${\sigma }_c$	Standard deviation of the random displacements of beam centroid and receiver aperture	0.95 mrad
$\psi$	Visibility-related attenuation coefficient	1.052
e	Electron charge	1.6 × 10−19 C
$\Delta f_e$	Receiver electrical bandwidth	1 GHz
$\Delta f_o$	Receiver optical bandwidth	10 nm
$N_o\left(\lambda \right)$	Spectral radiance of the background radiations	0.001 W/cm2-m-srad
$\lambda$	Optical wavelength	1500 nm
$\eta$	Optoelectronic conversion efficiency of the PD	0.9
$p,q$	Two parameters that determine the binary modulation method	0.5, 1

. Unless otherwise stated, the receiver FoV is ${\theta }_{FoV}=$ 80 mrad, the orientation deviation is ${\sigma }_a=$ 15 mrad, $r_L/r_r=$ 20, $L=$ 2 km, the average optical power is $P_t=$ 0 dBm, and the FSO link undergoes moderate turbulence. In addition, $\left(\alpha ,\beta \right)=\left\{\left(2.296, 2\right),\left(4.2, 3\right),\left(8, 4\right)\right\}$ denote strong turbulence, moderate turbulence, and weak turbulence, respectively [18].

The asymptotic results of the average BER under various receiver FoV and pointing errors against the average optical power are illustrated in Figure 2. Larger the impact of the pointing errors, namely, the smaller the $\xi$, the larger the average BER. Moreover, the average BER for the considered system without AoA fluctuations is lower than that of the system with AoA fluctuations for the same pointing errors. In addition, the average BER decreases as $P_t$ and ${\theta }_{FoV}$ increase. However, the system under AoA fluctuations with the same receiver FoV has the same average BER at a higher optical power regime. It is evident that the analytical and asymptotic results obtained from (15) at high optical power agree with the numerical results. The curves with different receiver FoVs have the same slope if the considered system is under the same pointing errors. As mentioned in the previous analysis, the diversity order depends on min$\left({\xi }^2, a, 1\right)$. For example, the diversity order for $\xi =$ 0.74 depends on ${\xi }^2$, but that for $\xi =$ 1.05 depends on 1.

To further investigate the correlation between ${\theta }_{FoV}$ and the average BER, we present the average BER versus ${\theta }_{FoV}$ in Figure 3 for various ${\sigma }_a$. The Monte Carlo results coincide with the theoretical results. From this figure, as ${\theta }_{FoV}$ increases, the average BER first decreases rapidly and then has a slight upward trend. It is because the influence of AWGN will be far more significant than that of the received light energy when ${\theta }_{FoV}$ increases to a particular value. Mainly, when ${\sigma }_a =$ 10 mrad, the average BER for ${\theta }_{FoV} =$ 50 mrad is 2.2 × 10⁻⁴, but the average BER for ${\theta }_{FoV} =$ 80 mrad is only 2.4 × 10⁻⁴. In addition, when ${\theta }_{FoV}$ is low, the average BER increases as ${\sigma }_a$ increases. Still, the degree of impact of orientation deviations on the average BER is nearly non-negligible when ${\theta }_{FoV}$ is high. For example, when ${\theta }_{FoV} =$ 40 mrad, the average BER for ${\sigma }_a=$ 10, 13, 16, 19 mrad are 3.5 × 10⁻⁴, 8.5 × 10⁻⁴, 2.1 × 10⁻³ and 4.6 × 10⁻³, respectively. At the same time, it is found that the slight upward trend is related to orientation deviations, i.e., the lower the orientation deviation, the more pronounced the increase is. The orientation deviation has been the dominant impactor for the performance of the average BER at this moment.

Figure 4 depicts the average BER for varying $r_L/r_r$ under different detection techniques. This figure shows that considered system with the heterodyne detection achieves lower average BER compared to the IM/DD, which is more favorable for drone-assisted FSO communication. Specifically, the average BER under the heterodyne detection and the IM/DD techniques for $r_L/r_r=$ 30 are 2.7 × 10⁻⁷ and 2.2 × 10⁻⁴ when $P_t =$ 30 dBm, respectively. Besides, when changing the ratio of beam radius to receiver aperture radius, the change in the performance of the considered system with the heterodyne detection technique is more evident than that with the IM/DD technique. This phenomenon is because the heterodyne detection has higher conversion gain and better filtering of background light compared to the IM/DD. Moreover, the energy of the received optical beam increases and the average BER decreases as the ratio of beam radius to receiver aperture radius increases. For the heterodyne detection technique, the average BERs are 4 × 10⁻², 3.6 × 10⁻⁵, and 2.7 × 10⁻⁷, respectively, when $r_L/r_r$ are 10, 20, and 30 at $P_t =$ 30 dBm. Finally, the Monte Carlo results fit the analytical results well.

The impact of link distance on the average BER as a function of atmospheric conditions is presented in Figure 5. It is apparent that the average BER increases with increasing link distances, e.g., for weak turbulence and $P_t =$ 2 dBm, the average BERs for $L =$ 1, 2, 4 km are 1.5 × 10⁻⁴, 2.1 × 10⁻⁴ and 3.7 × 10⁻⁴, respectively. Furthermore, when the degree of turbulence influence increases, the average BER also increases, i.e., at $P_t =$ 10 dBm and $L =$ 2 km, the average BERs from weak to strong turbulence are 1.2 × 10⁻⁴, 1.3 × 10⁻⁴, and 1.4 × 10⁻⁴, respectively.

Previously, the influence of different factors is already discussed on the average BER. Here, the influence of these factors on the ergodic capacity is further investigated. The influence of AoA fluctuations and the receiver FoV on the ergodic capacity are demonstrated in Figure 6. First, the ergodic capacity increases as $P_t$ increases, e.g., the ergodic capacity for $P_t =$ 10 dBm is 37.5 bit/s/Hz. The ergodic capacity for $P_t =$ 30 dBm is 44.1 bit/s/Hz, for the considered system without AoA fluctuations. Moreover, it is noticeable that the ergodic capacity is higher for the system without AoA fluctuations. Furthermore, the ergodic capacity increases and then decreases as ${\theta }_{FoV}$ increases when AoA fluctuations are considered. For example, the ergodic capacity for ${\theta }_{FoV} =$ 30, 80, and 40 mrad are 33.1, 35.9, and 36.4 bit/s/Hz when $P_t =$ 10 dBm, respectively. Finally, the Monte Carlo simulation results certify the theoretical results.

The ergodic capacity for versus ${\theta }_{FoV}$, under various orientation deviations, is presented in Figure 7. The analytical results match the Monte Carlo results, thus verifying that the closed-form formula for the ergodic capacity is highly accurate. This figure shows that as ${\theta }_{FoV}$ increases, the communication performance first improves rapidly and then has a slight downward trend. For instance, the ergodic capacity for ${\theta }_{FoV} =$ 20, 30, 40 mrad is 32.8, 36.4, and 36.1 bit/s/Hz when ${\sigma }_a =$ 10 mrad, respectively. This is because when ${\theta }_{FoV}$ is relatively low, the receiver can receive more optical signal energy, and the ergodic capacity increases rapidly as ${\theta }_{FoV}$ increases. However, when ${\theta }_{FoV}$ increases to the threshold, more background noise is introduced as ${\theta }_{FoV}$ increases and affects the communication quality. In addition, the slight downward trend is influenced by various orientation deviations, which becomes less pronounced when the orientation deviation is higher. At the same time, orientation deviations also affect the ergodic capacity when ${\theta }_{FoV}$ is low, i.e., the ergodic capacity decreases as the orientation deviation increases. When ${\theta }_{FoV} =$ 20 mrad, the ergodic capacity for ${\sigma }_a =$ 10, 15, 20, 25 mrad is 32.8, 22.3, 14.9, and 10.4 bit/s/Hz, respectively. This phenomenon is because that ${\sigma }_a$, which represents the variance of the beam center randomly deviated from the center of receiver lens, can reduce more received beam energy, resulting in lower ergodic capacity. It is worth noting that in engineering applications of drone-assisted FSO communications, a fast, high-precision stabilization and control system is required to obtain a better communication performance, i.e., to reduce the impact of random deviation on the received optical power.

Figure 8 depicts the influence of $r_L/r_r$ on the ergodic capacity for various detection techniques. Distinctly, the ergodic capacity under the heterodyne detection is higher than that under IM/DD due to the higher conversion gain and better noise-filtering performance of the heterodyne detection technique. Furthermore, for the same detection technique, the higher $r_L/r_r$, the higher ergodic capacity, and thus the better communication performance. For instance, for the heterodyne detection technique and $P_t =$ 10 dBm, the ergodic capacity for $r_L/r_r =$ 10, 20, 30 is 25, 36, and 37.7 bit/s/Hz, respectively. Finally, the Monte Carlo results are in excellent agreement with the numerical results.

In Figure 9, the ergodic capacity for varying link distances under various atmospheric conditions is depicted. Comprehensively, the higher the link distance, the worse the communication performance. For instance, for weak turbulence and $P_t =$ 2 dBm, the ergodic capacity for $L =$ 1, 2, 4 km is 35, 33.4, and 30.4 bit/s/Hz, respectively. Furthermore, the ergodic capacity declines as the deterioration of atmospheric turbulence. For instance, for $L =$ 1 km and $P_t =$ −2 dBm, the ergodic capacity under weak turbulence is 33.7 bit/s/Hz, but it drops to 33.5 bit/s/Hz and 33.2 bit/s/Hz for moderate and strong turbulence, respectively. Finally, the simulation results are consistent and correspond well to the analytical results.

5. Conclusions

This paper examined the performance of a drone-assisted downlink FSO system. Furthermore, the effect of AoA fluctuations due to the orientation deviation of the hovering drone on the FSO link was investigated in detail. The unified closed-form expressions for the PDF and the CDF were obtained using the IM/DD and the heterodyne detection techniques, respectively, where the FSO link followed Málaga fading distribution. After that, this paper derived closed-form expressions for the average BER and the ergodic capacity. In addition, the asymptotic formula for the average BER under heterodyne detection was obtained with convergence at high optical power. The derived analytical results were proved by Monte Carlo simulation results and demonstrated that the performance of such systems is dependent on the receiver FoV and the ratio of beam radius to receiver aperture radius. Moreover, the system with heterodyne detection performed better than that with IM/DD technique. Eventually, the results demonstrated that the performance of the drone-assisted communication system severely degraded when the turbulence conditions worsened and the link distance increased. All these fundamental investigations provide helpful guidance for the application of the drone-assisted FSO communication system.