Hybrid Data Augmentation and Dual-Stream Spatiotemporal Fusion Neural Network for Automatic Modulation Classification in Drone Communications
Abstract
1. Introduction
- We propose a hybrid data augmentation method based on phase shift and self-perturbation, which can effectively expand training samples without introducing additional information.
- We propose a DSSFNN structure for AMC, which can extract features from both the spatial and temporal dimensions of data. Compared to the single-dimensional feature extraction method, the features extracted by DSSFNN are more diverse and effective, which improve the accuracy of AMC.
2. Problem Formulation
2.1. Signal Model
2.2. Dual-Stream Data
2.3. Problem Description
3. Our Proposed Robust AMC Method
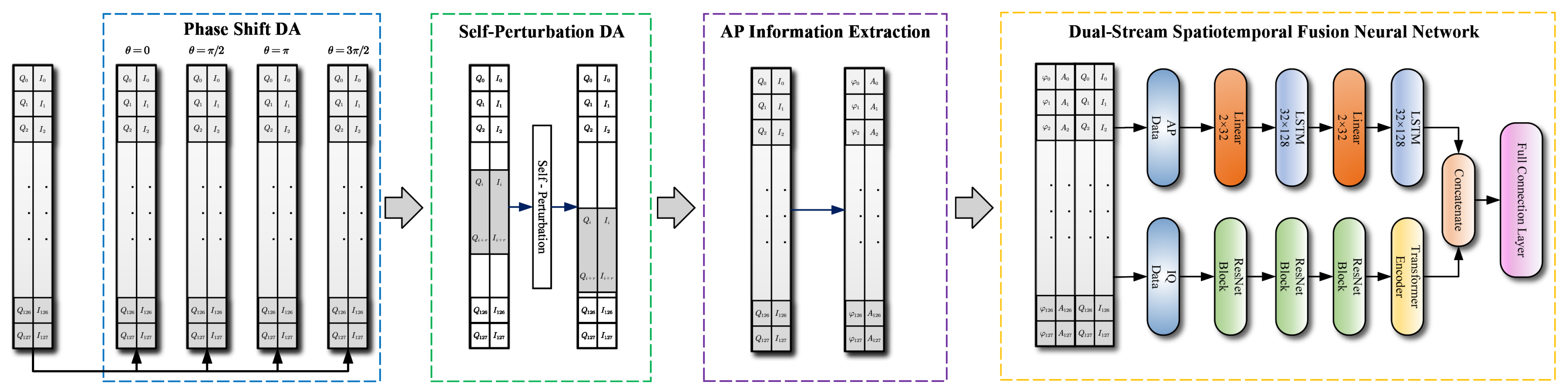
3.1. The Framework of the Proposed Method
3.2. Hybrid Data Augmentation
3.2.1. Phase-Shift Data Augmentation
3.2.2. Self Perturbation Data Augmentation
- Enhancing data diversity: The self-perturbation algorithm enhances the robustness and generalization ability of a model by adding new variations to the dataset. This augmentation of data diversity can enable the model to better capture the features of the dataset and improve its accuracy.
- Reducing overfitting: Overfitting is a common problem in machine learning, and the self-perturbation algorithm can reduce the risk of overfitting by increasing the size of the dataset. This is because training the model on more data can help to better learn the true distribution of the dataset.
- Simplicity and ease of implementation: The self-perturbation algorithm is relatively simple to implement, requiring only a small amount of manipulation on the original data. Compared to other complex data augmentation techniques, self-perturbation algorithm has lower implementation costs and higher practicality.
- No introduction of additional information: The self-perturbation algorithm achieves data augmentation by cropping parts of the original data and then splicing them together. This approach ensures that no additional information is introduced into the data. In contrast, adding noise as a form of data augmentation introduces additional information that may sometimes affect classification performance.
3.3. Dual-Stream Spatiotemporal Fusion Neural Network
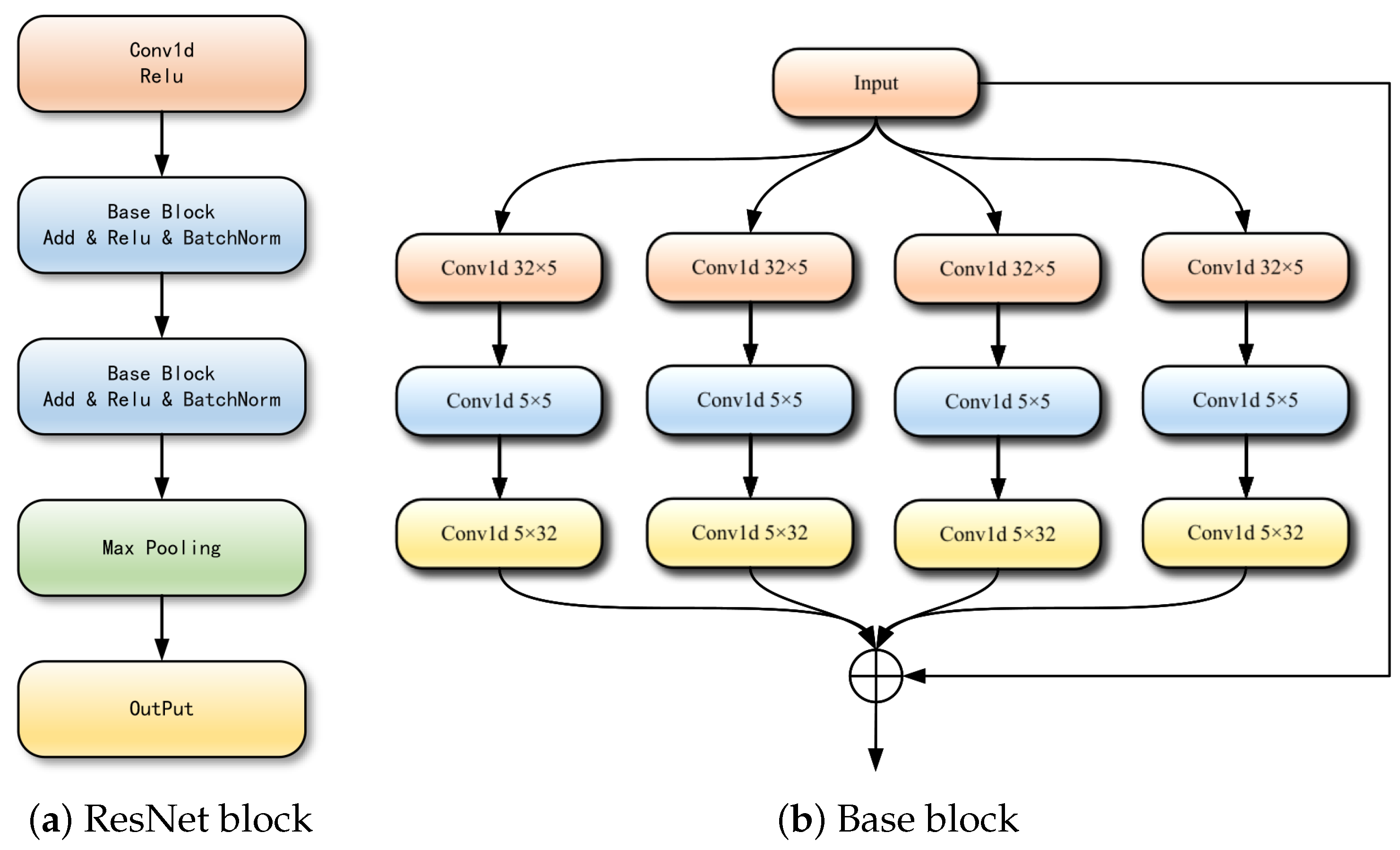
3.3.1. Spatial Feature Extraction Module for IQ Data
- Global information: the self-attention mechanism [35] can consider the entire sequence of information while processing the information at each position.
- Interpretability: the self-attention mechanism [35] can increase the interpretability of the model by assigning different weights to information from different positions.
- Addressing long-range dependencies: the self-attention mechanism can solve the problem of long-range dependencies, where the model is capable of correctly processing distantly related contextual information.
- Powerful feature representation capability: the self-attention mechanism can fuse information from different positions to obtain powerful feature representation capability.
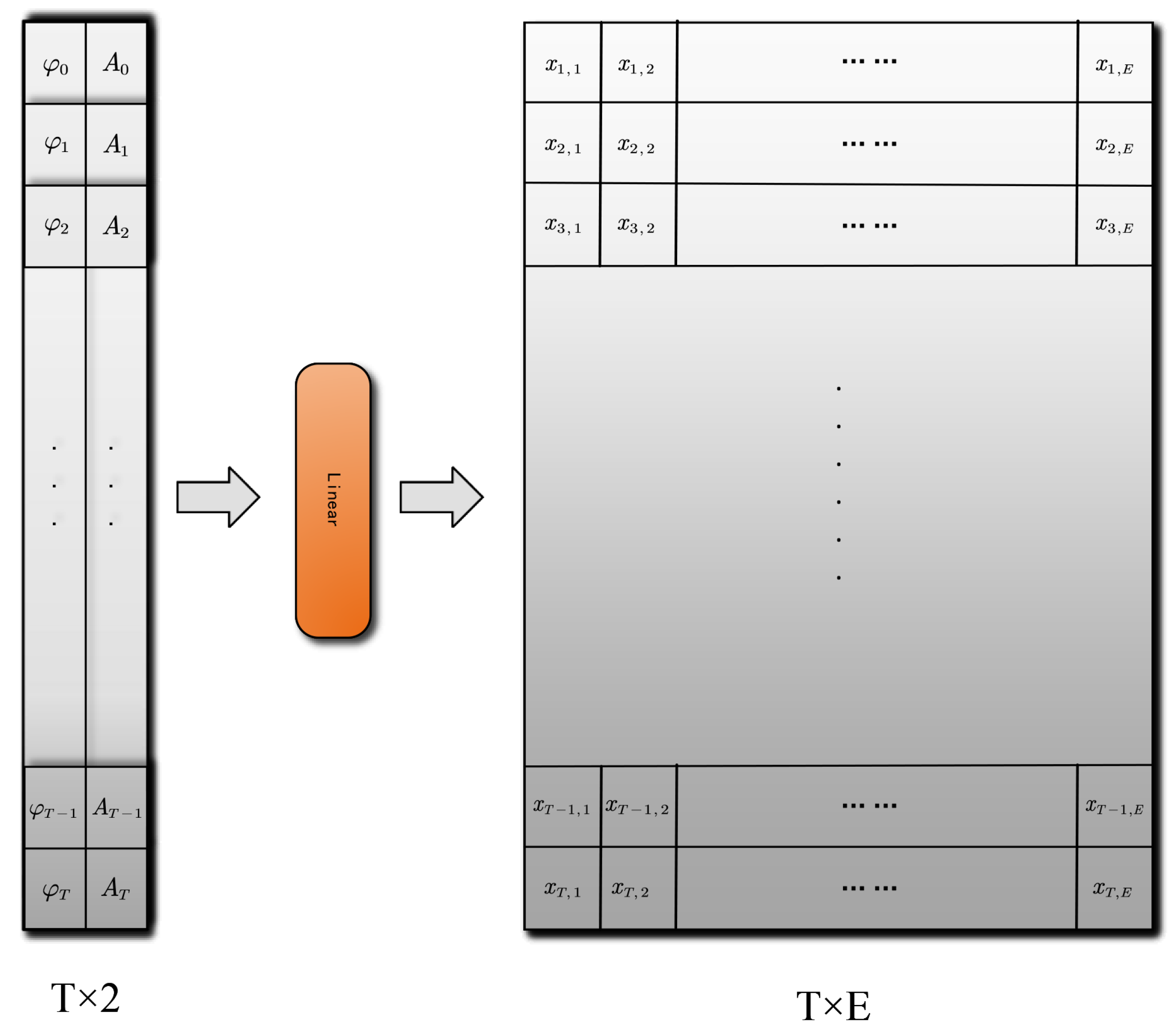
3.3.2. Time Feature Extraction Module for AP Data
3.3.3. Spatiotemporal Feature Fusion Mechanism
3.3.4. Loss Functions and Optimization Algorithms
4. Experimental Results
4.1. Simulation Environment, Parameters, and Performance Metrics
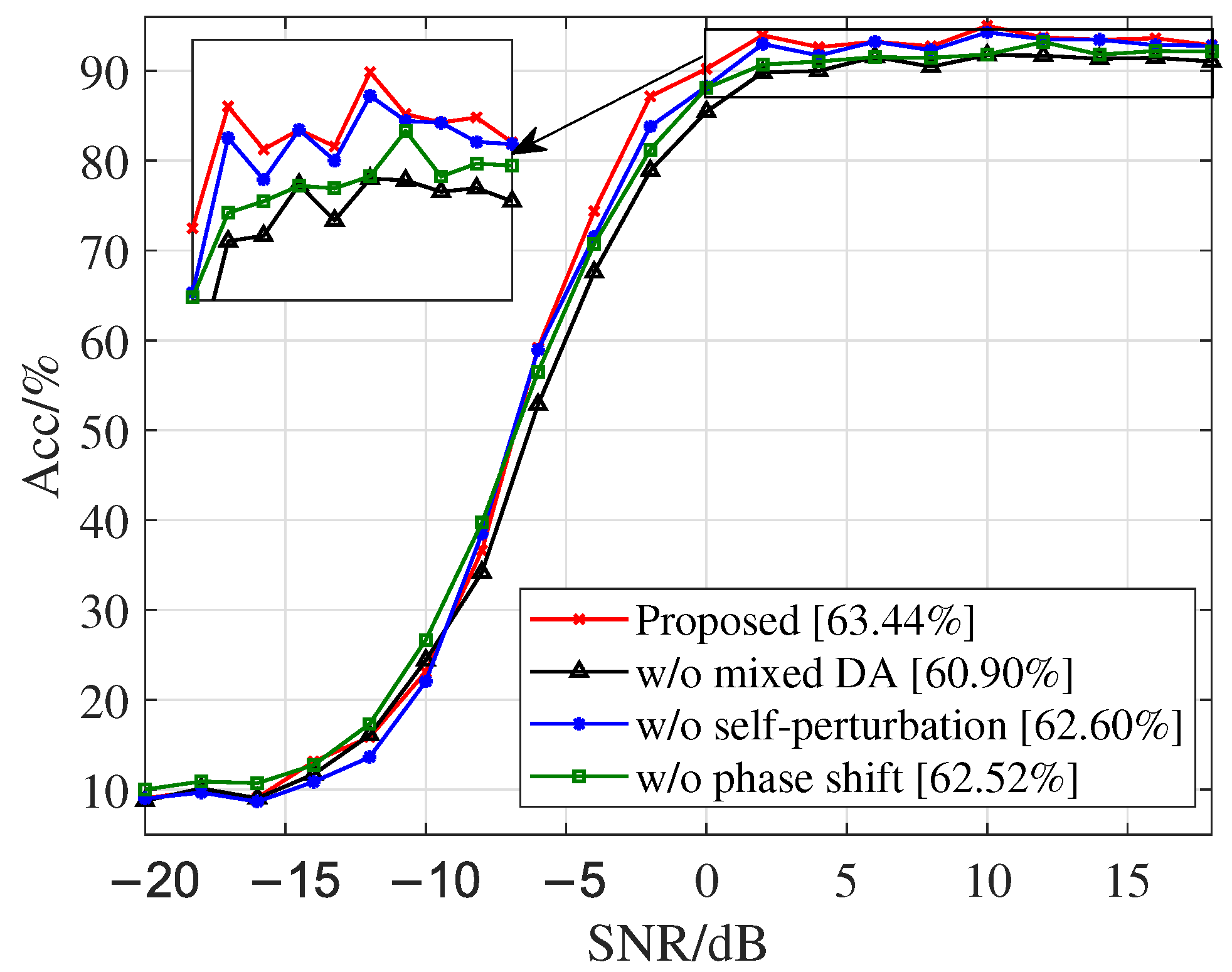
4.2. Ablation Experiment of Hybrid Data Augmentation Algorithm
4.3. Ablation Experiment of DSSFNN
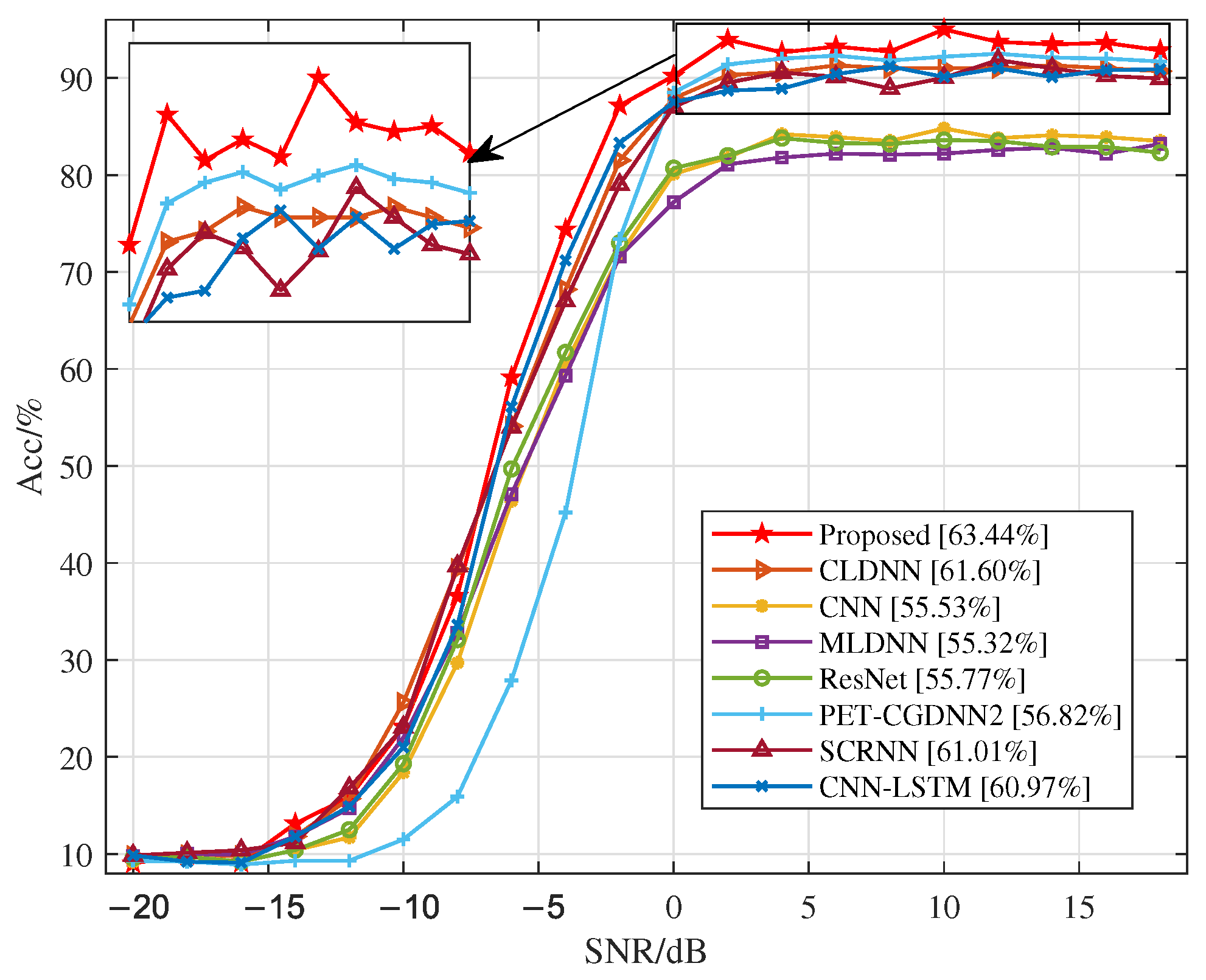
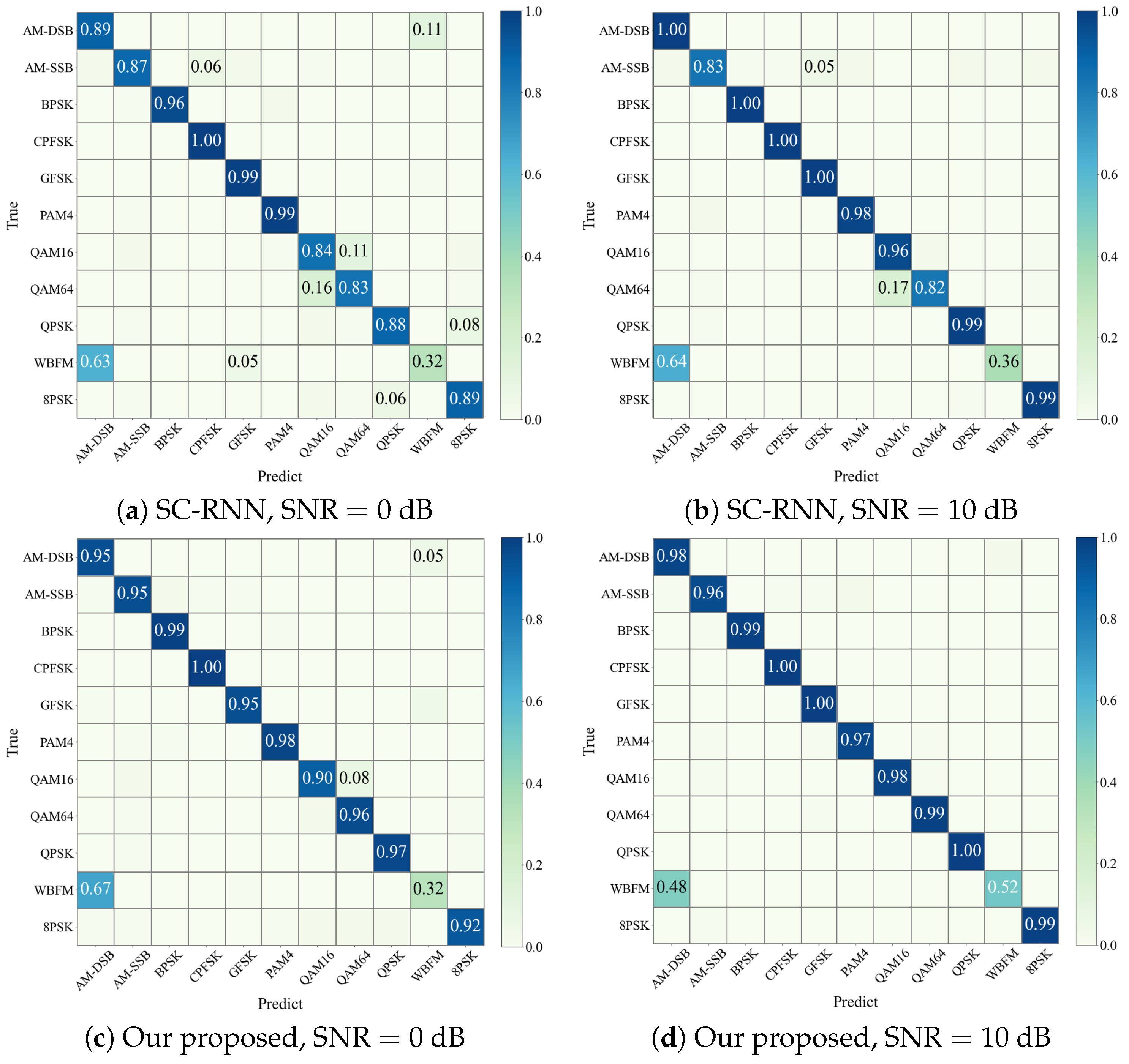
4.4. Our Proposed Method vs. Existing Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gui, G.; Liu, M.; Tang, F.; Kato, N.; Adachi, F. 6G: Opening New Horizons for Integration of Comfort, Security, and Intelligence. IEEE Wirel. Commun. 2020, 27, 126–132. [Google Scholar] [CrossRef]
- Huang, H.; Liu, M.; Gui, G.; Haris, G.; Adachi, F. Unsupervised learning-inspired power control methods for energy-efficient wireless networks over fading channels. IEEE Trans. Wirel. Commun. 2022, 21, 9892–9905. [Google Scholar] [CrossRef]
- Ohtsuki, T. Machine learning in 6G wireless communications. IEICE Trans. Commun. 2022, 106, 75–83. [Google Scholar] [CrossRef]
- Xu, Y.; Gui, G.; Gacanin, H.; Adachi, F. A Survey on Resource Allocation for 5G Heterogeneous Networks: Current Research, Future Trends, and Challenges. IEEE Commun. Surv. Tutor. 2021, 23, 668–695. [Google Scholar] [CrossRef]
- Yang, J.; Gu, H.; Hu, C.; Zhang, X.; Gui, G.; Gacanin, H. Deep complex-valued convolutional neural network for drone recognition based on RF fingerprinting. Drones 2022, 6, 374. [Google Scholar] [CrossRef]
- Azari, M.M.; Sallouha, H.; Chiumento, A.; Rajendran, S.; Vinogradov, E.; Pollin, S. Key technologies and system trade-offs for detection and localization of amateur drones. IEEE Commun. Mag. 2018, 56, 51–57. [Google Scholar] [CrossRef]
- Haring, L.; Chen, Y.; Czylwik, A. Automatic modulation classification methods for wireless OFDM systems in TDD mode. IEEE Trans. Commun. 2010, 58, 2480–2485. [Google Scholar] [CrossRef]
- Xu, J.L.; Su, W.; Zhou, M. Likelihood-ratio approaches to automatic modulation classification. IEEE Trans. Syst. Man Cybern. 2010, 41, 455–469. [Google Scholar] [CrossRef]
- Zhang, Z.; Luo, H.; Wang, C.; Gan, C.; Xiang, Y. Automatic modulation classification using CNN-LSTM based dual-stream structure. IEEE Trans. Veh. Technol. 2020, 69, 13521–13531. [Google Scholar] [CrossRef]
- Huang, S.; Lin, C.; Xu, W.; Gao, Y.; Feng, Z.; Zhu, F. Identification of active attacks in Internet of Things: Joint model-and data-driven automatic modulation classification approach. IEEE Internet Things J. 2020, 8, 2051–2065. [Google Scholar] [CrossRef]
- Dobre, O.A.; Abdi, A.; Bar-Ness, Y.; Su, W. Survey of automatic modulation classification techniques: Classical approaches and new trends. IET Commun. 2007, 1, 137–156. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, J.; Liu, M.; Gui, G. LightAMC: Lightweight Automatic Modulation Classification via Deep Learning and Compressive Sensing. IEEE Trans. Veh. Technol. 2020, 69, 3491–3495. [Google Scholar] [CrossRef]
- Sun, J.; Shi, W.; Yang, Z.; Yang, J.; Gui, G. Behavioral Modeling and Linearization of Wideband RF Power Amplifiers Using BiLSTM Networks for 5G Wireless Systems. IEEE Trans. Veh. Technol. 2019, 68, 10348–10356. [Google Scholar] [CrossRef]
- Krichen, M.; Mihoub, A.; Alzahrani, M.Y.; Adoni, W.Y.H.; Nahhal, T. Are Formal Methods Applicable To Machine Learning and Artificial Intelligence? In Proceedings of the 2022 2nd International Conference of Smart Systems and Emerging Technologies (SMARTTECH), Riyadh, Saudi Arabia, 9–11 May 2022; pp. 48–53. [Google Scholar]
- Raman, R.; Gupta, N.; Jeppu, Y. Framework for Formal Verification of Machine Learning Based Complex System-of-Systems. Insight 2023, 26, 91–102. [Google Scholar] [CrossRef]
- Tu, Y.; Lin, Y.; Zha, H.; Zhang, J.; Wang, Y.; Gui, G.; Mao, S. Large-scale real-world radio signal recognition with deep learning. Chin. J. Aeronaut. 2022, 35, 35–48. [Google Scholar] [CrossRef]
- Huang, H.; Peng, Y.; Yang, J.; Xia, W.; Gui, G. Fast beamforming design via deep learning. IEEE Trans. Veh. Technol. 2020, 69, 1065–1069. [Google Scholar] [CrossRef]
- Guan, G.; Zhou, Z.; Wang, J.; Liu, F.; Sun, J. Machine learning aided air traffic flow analysis based on aviation big data. IEEE Trans. Veh. Technol. 2020, 69, 4817–4826. [Google Scholar]
- Zhang, X.; Zhao, H.; Zhu, H.B.; Adebisi, B.; Gui, G.; Gacanin, H.; Adachi, F. NAS-AMR: Neural architecture search based automatic modulation recognition method for integrating sensing and communication system. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 1374–1386. [Google Scholar] [CrossRef]
- Fu, X.; Gui, G.; Wang, Y.; Gacanin, H.; Adachi, F. Automatic modulation classification based on decentralized learning and ensemble learning. IEEE Trans. Veh. Technol. 2022, 71, 7942–7946. [Google Scholar] [CrossRef]
- Fu, X.; Gui, G.; Wang, Y.; Ohtsuki, T.; Adebisi, B.; Gacanin, H.; Adachi, F. Lightweight automatic modulation classification based on decentralized learning. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 57–70. [Google Scholar] [CrossRef]
- Wang, Y.; Gui, G.; Gacanin, H.; Adebisi, B.; Sari, H.; Adachi, F. Federated learning for automatic modulation classification under class imbalance and varying noise condition. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 86–96. [Google Scholar] [CrossRef]
- Wang, Y.; Gui, G.; Ohtsuki, T.; Adachi, F. Multi-task learning for generalized automatic modulation classification under non-Gaussian noise with varying SNR conditions. IEEE Trans. Wirel. Commun. 2021, 20, 3587–3596. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhao, P.; Li, Y.; Wang, H.; Yang, Y. Spectrum interference-based two-level data augmentation method in deep learning for automatic modulation classification. Neural Comput. Appl. 2020, 33, 7723–7745. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhao, P.; Wang, H.; Elhanashi, A.; Saponara, S. Fine-grained modulation classification using multi-scale radio transformer with dual-channel representation. IEEE Commun. Lett. 2022, 26, 1298–1302. [Google Scholar] [CrossRef]
- Hou, C.B.; Liu, G.W.; Tian, Q.; Zhou, Z.C.; Hua, L.J.; Lin, Y. Multi-signal modulation classification using sliding window detection and complex convolutional network in frequency domain. IEEE Internet Things J. 2022, 9, 19438–19449. [Google Scholar] [CrossRef]
- Qi, P.; Zhou, X.; Ding, Y.; Zhang, Z.; Zheng, S.; Li, Z. FedBKD: Heterogenous federated learning via bidirectional knowledge distillation for modulation classification in IoT-edge system. IEEE J. Sel. Top. Signal Process. 2023, 17, 189–204. [Google Scholar] [CrossRef]
- O’Shea, T.J.O.; Corgan, J.; Clancy, T.C. Convolutional radio modulation recognition networks. In Proceedings of the Engineering Applications of Neural Networks: 17th International Conference, EANN 2016, Aberdeen, UK, 2–5 September 2016; pp. 213–226. [Google Scholar]
- Ramjee, S.; Ju, S.; Yang, D.; Liu, X.; Gamal, A.E.; Eldar, Y.C. Fast deep learning for automatic modulation classification. arXiv 2019, arXiv:1901.05850. [Google Scholar]
- Liao, K.; Zhao, Y.; Gu, J.; Zhang, Y.; Zhong, Y. Sequential convolutional recurrent neural networks for fast automatic modulation classification. IEEE Access 2021, 9, 27182–27188. [Google Scholar] [CrossRef]
- Chang, S.; Huang, S.; Zhang, R.; Feng, Z.; Liu, L. Multitask-learning-based deep neural network for automatic modulation classification. IEEE Internet Things J. 2021, 9, 2192–2206. [Google Scholar] [CrossRef]
- Guo, L.; Wang, Y.; Hou, C.; Lin, Y.; Zhao, H.; Gui, G. Ultra Lite Convolutional Neural Network for Automatic Modulation Classification. arXiv 2022, arXiv:2208.04659. [Google Scholar]
- Huang, L.; Pan, W.; Zhang, Y.; Qian, L.; Gao, N.; Wu, Y. Data augmentation for deep learning-based radio modulation classification. IEEE Access 2019, 8, 1498–1506. [Google Scholar] [CrossRef]
- Xie, S.; Girshick, R.; Dollar, P.; Tu, Z.; He, K. Aggregated residual transformations for deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1492–1500. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, A.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Graves, A. Long short-term memory. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 37–45. [Google Scholar]


| Related Works | DNN | Strength | Weakness |
|---|---|---|---|
| Shea et al. [28] | CNN | Innovative use of deep learning for modulation recognition achieved significant accuracy improvement compared to traditional methods. | Only explored the application of CNN for modulation recognition. |
| Ramjee et al. [29] | CLDNN | Both time and spatial features were extracted from IQ signals, resulting in a more diverse feature set. | Using only IQ data for feature extraction results in insufficiently diverse feature sets. |
| ResNet | Further exploration was conducted on top of CNN. | The time feature of IQ data was neglected. | |
| LSTM | RNNs were utilized to extract time information from IQ signals for modulation recognition. | The absence of convolutional neural networks (CNNs) for spatial feature extraction is a limitation. | |
| Zhang et al. [9] | CNN-LSTM | Features were extracted separately from IQ and AP data for modulation recognition. | Extracting temporal features from the spatial features extracted by CNN may have an impact on the accuracy of modulation recognition. |
| Liao et al. [30] | SCRNN | The accuracy of the model is ensured while reducing the required training time. | Extracting features solely from IQ data limits the diversity of the features. |
| Chang et al. [31] | MLDNN | Explored the interaction features and temporal information of both IQ and AP data, which resulted in a significantly improved accuracy rate. | The WBFM modulation scheme is highly susceptible to misclassification as AM-DSB. |
| CGDNN2 | The parameter estimator and the parameter transformer were introduced, resulting in a significant reduction in the model’s parameter count. | The design of the model architecture lacks significant innovation, impeding the extraction of improved features. |
| Models | Results under Different SNR Scenarios | Average ACC | Max ACC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | |||
| DSSFNN | 90.21 | 93.95 | 92.64 | 93.24 | 92.73 | 95.01 | 93.72 | 93.46 | 93.62 | 92.85 | 93.14 | 95.01 |
| DSSFNN w/o DA | 85.44 | 89.81 | 89.98 | 91.55 | 90.45 | 91.73 | 91.68 | 91.33 | 91.44 | 91.04 | 90.45 | 91.73 |
| DSSFNN w/ phase-shift DA | 88.24 | 92.98 | 91.70 | 93.24 | 92.28 | 94.28 | 93.50 | 93.45 | 92.86 | 92.80 | 92.54 | 94.28 |
| DSSFNN w/ self-perturbation DA | 88.08 | 90.68 | 91.04 | 91.51 | 91.43 | 91.81 | 93.20 | 91.80 | 92.20 | 92.13 | 91.39 | 93.20 |
| DSSFNN w/ 2 channels | 88.54 | 92.46 | 92.06 | 92.28 | 92.10 | 93.75 | 93.16 | 92.73 | 92.54 | 91.99 | 92.17 | 93.75 |
| DSSFNN w/ 6 channels | 89.21 | 93.01 | 91.82 | 92.48 | 92.38 | 93.81 | 93.09 | 93.07 | 92.84 | 92.24 | 92.40 | 93.81 |
| DSSFNN w/o grouped convolutions | 86.73 | 91.17 | 90.07 | 91.72 | 90.94 | 92.87 | 91.99 | 92.23 | 91.59 | 91.01 | 91.03 | 92.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, A.; Zhang, X.; Wang, Y.; Zhang, Y.; Li, M. Hybrid Data Augmentation and Dual-Stream Spatiotemporal Fusion Neural Network for Automatic Modulation Classification in Drone Communications. Drones 2023, 7, 346. https://doi.org/10.3390/drones7060346
Gong A, Zhang X, Wang Y, Zhang Y, Li M. Hybrid Data Augmentation and Dual-Stream Spatiotemporal Fusion Neural Network for Automatic Modulation Classification in Drone Communications. Drones. 2023; 7(6):346. https://doi.org/10.3390/drones7060346
Chicago/Turabian StyleGong, An, Xingyu Zhang, Yu Wang, Yongan Zhang, and Mengyan Li. 2023. "Hybrid Data Augmentation and Dual-Stream Spatiotemporal Fusion Neural Network for Automatic Modulation Classification in Drone Communications" Drones 7, no. 6: 346. https://doi.org/10.3390/drones7060346
APA StyleGong, A., Zhang, X., Wang, Y., Zhang, Y., & Li, M. (2023). Hybrid Data Augmentation and Dual-Stream Spatiotemporal Fusion Neural Network for Automatic Modulation Classification in Drone Communications. Drones, 7(6), 346. https://doi.org/10.3390/drones7060346






