1. Introduction
Unmanned aerial vehicles (UAVs) play an important role in wireless communication systems, providing stable and effective wireless connection in areas without extensive communication infrastructure coverage [
1,
2,
3,
4]. Due to their economical and flexible arrangement, UAVs are widely used in emergency rescue, traffic control, etc. [
5,
6]. For example, UAVs can provide emergency communication connection to ground rescue equipment when mountain fires occur. Compared with traditional ground-based communications, low-altitude UAVs have shorter line-of-sight (LoS) paths, which can effectively avoid interference and achieve better communication performance. However, their high mobility leads to rapid changes in channel state information (CSI) and ground equipment requires fast and accurate estimation of CSI to achieve high quality communication [
7].
Direction of arrival (DOA) is key information for channel estimation [
8,
9], which combined with multiple-input multiple-output (MIMO) technology [
10,
11,
12] can achieve secure and energy-efficient UAV information transmission by providing a highly accurate desired signal direction for directional modulation, beamforming, alignment and tracking [
13,
14]. In [
15], the authors proposed a novel 3D framework for UAV localization; the key is to measure the angle of arrival information.
However, due to the fact that the number of antennas tends to be massive in MIMO systems [
16,
17], the computational complexity and circuit cost are too high for commercial applications. A DOA-aided channel estimation method was proposed in [
18] for a hybrid millimeter-wave MIMO system based on a uniform planar array at the base stations, and the theoretical bounds of the mean squared errors (MSEs) and the Cramér–Rao Lower Bounds (CRLBs) of the joint DOA and channel gain estimation are derived. The simulation results show that the performances of the proposed methods are close to the theoretical MSE analysis, while the theoretical MSE is close to the CRLB. Therefore, hybrid analog and digital (HAD) beamforming structures using a parametric method to estimate DOA have emerged, which can achieve a good balance between beamforming computation, circuit cost and complexity, using a parametric method to estimate DOA.
Large antenna arrays using HAD architectures can provide large apertures at low cost and with hardware complexity, resulting in enhanced DOA estimation and reduced power consumption. The DOA estimation and power consumption tradeoff problem for large antenna arrays with HAD structures was presented in [
19], where the fully connected, sub-connected and switch-based hybrid architectures were formulated into a unified expression, with the compression matrix in a time-varying form. Based on this model, the authors derived dynamic maximum likelihood (D-ML) estimators for HAD and conventional fully digital (FD) structures and closed expressions for CRB to evaluate the performance limits of D-ML estimators for different HAD structures.
The authors of [
20] investigated the DOA estimation using HAD structure in the receiver part and proposed two phase alignment (PA) methods: HAD-PA and hybrid digital and analog PA (HDA-PA). Meanwhile, for this hybrid structure, a fast Root-MUSIC-HDAPA method was proposed to achieve an approximate analytical solution and reduce the computational complexity. In [
21], a new design of analog phase shifts was proposed to tackle the phase ambiguities. This enables the cross-correlations to be deterministically calibrated and constructively combined for noise-tolerant estimation of the propagation phase offset between adjacent subarrays. It is obvious from the simulation that the estimation accuracy of the method can be significantly improved by several orders of magnitude and asymptotically approaches the MSELB. For the DF ambiguity problem caused by HAD MIMO, a fast ambiguity phase elimination method was proposed in [
22], which uses only two data blocks to achieve DOA estimation. In [
23], the DOA estimation problem in the case of 1-bit ADC was considered. It demonstrated that the MUSIC method could be directly applied in cases without additional preprocessing, while system performance degradation was analyzed. The DOA estimation performance of the low-resolution ADC structure was investigated in [
24].
A generalized sparse Bayesian learning (Gr-SBL) method was considered in [
25] to solve the DOA estimation problem from one-bit quantized measurements in both single and multi-snapshot scenarios. By formulating the one-bit DOA estimation in single-fast-tempo, it is transformed into a generalized linear model inference problem and solved by applying the recently proposed Gr-SBL method. Then, Gr-SBL is extended to multi-fast-tempo scenarios by decoupling the multi-fast-tempo single-bit DOA estimation problem into a series of single-fast-tempo subproblems. Simulation results demonstrate the effectiveness of the Gr-SBL method. A DOA estimation method that is suitable for non-circular signals with a single snapshot was proposed in [
26]. By utilizing the waveform characteristics of the NC signal, the proposed algorithm can enlarge the virtual array aperture that is twice the length of the physical array and as a result enhance DOA estimation accuracy. Finally, the numerical simulation results are provided to demonstrate the effectiveness and superiority of the proposed method.
In order to avoid the high-complexity operation of eigenvalue decomposition (EVD) in DOA estimation, deep learning network (DNN) has been applied to DOA estimation in recent years. A DNN-based DOA and channel estimation schemes was proposed in [
27], which achieved better performance. In [
28], the authors introduced a low-complexity DNN-based method to a hybrid massive MIMO system with uniform circular array at the base station, which had similar or even better performance compared to the traditional ML method with lower complexity. An ESPRIT-based HAD method was proposed in [
29], which considered a machine learning framework to improve the estimation accuracy.
Aiming at rapidly estimating and tracking the main subspaces and major components of a vector sequence in [
30], a projection approximation and subspace tracking (PAST) method was proposed. Furthermore, the proposed PAST method in [
30] was improved in [
31]. It proved that the improved PAST method was better in both subspace estimation and computational complexity. In [
32], an improved power iteration (PI) method for modal analysis was proposed. The simulation results showed that the method significantly reduced the number of unnecessary iterations with a faster computational speed. An iterative method was also proposed in [
33] and good results were obtained.
Inspired by the idea of radar target detection, we considered a new SVD-based passive target detection model in [
34], which achieved better detection performance. The complexity of massive MIMO based on the covariance matrix decomposition method was extremely high, for example, when the number of antennas is closed to 10,000 and the computational complexity was tera (T) FLOPs. Therefore, how to significantly reduce the computational complexity of direction finding for UAV emitters is an extremely challenging problem, which is the key to its future applications. Therefore, in this paper, we propose a rapid convergent power iteration (RPI) structure to achieve high performance with low complexity. The main contributions in this paper are summarized as follows:
To significantly reduce the computational complexity of UAV direction finding, two PI-based DOA estimation methods are respectively proposed, which are called RPI-RI and RPI-PR. Here, the sampling covariance of the received signal vector is first computed. An initial vector subjected to power iteration is determined, which replaces the traditional EVD. Then the final DOA estimation is given by the corresponding signal and noise subspaces. The simulation results show that RPI-RI and RPI-PR can achieve better DOA accuracy and lower computational complexity than conventional algorithms; in particular, the RPI-PR can dramatically reduce the complexity while maintaining performance close to CRLB.
To reduce the number of unnecessary iterations and obtain a faster computation speed, the optional initial vectors are selected which can converge to the desired results. In each iteration, it must be ensured that the initial vector is not orthogonal to the incident wave and it is better to keep them away from orthogonality. Through computational analysis, we selected different initial vector values that satisfy the conditions and analyzed the performance of iterative convergence. Moreover, the computation result often has a great relationship with the relative error. When a good initial vector and relative error are determined, results with fast convergence and fewer iterations can be achieved.
The remainder of this paper is organized as follows.
Section 2 provides an in-depth discussion of related work.
Section 3 describes the structure of the rapid power iterative estimator for massive/ultra-massive MIMO receiver. In
Section 4, two low-complexity estimators are proposed and their performance is also analyzed. The simulation results are presented in
Section 5. Finally, we draw conclusions in
Section 6.
Notations: Throughout the paper, and in bold typeface are used to represent vectors and matrices, respectively, while scalars are presented in normal typeface, such as x. Signs and represent conjugate transpose and modulus, respectively. denotes the identity matrix. Furthermore, represents the expectation operator and denotes a circularly symmetric complex Gaussian stochastic vector with mean vector and covariance matrix . represents the estimated value of x.
Definitions of terms: DOA (direction of arrival) is the process of finding the angle or direction from which a signal is arriving at a receiver, with applications in various fields such as radar, sonar, wireless communication and audio signal processing.
HAD (hybrid analog and digital) is a special array structure. Analog components are used to process continuous signals, while digital components are used to process discrete signals. In the receiver array, it can be simply divided into fully connected, sub-connected and switch-based.
D-ML (dynamic maximum likelihood) is a generalized maximum likelihood algorithm for the three HAD structures as well as for the fully digital structure.
Root-MUSIC-HDAPA is a low-complexity DOA estimator. It firstly applies the conventional Root-MUSIC algorithm in the digital domain, followed by digital phase alignment. Finally, analog phase alignment is performed in the analog domain to eliminate pseudo-solutions.
PAST (projection approximation subspace tracking) is a robust and low-complexity signal subspace tracking method that solves the problem by making an appropriate projection approximation to the recursive least squares technique.
3. System Model
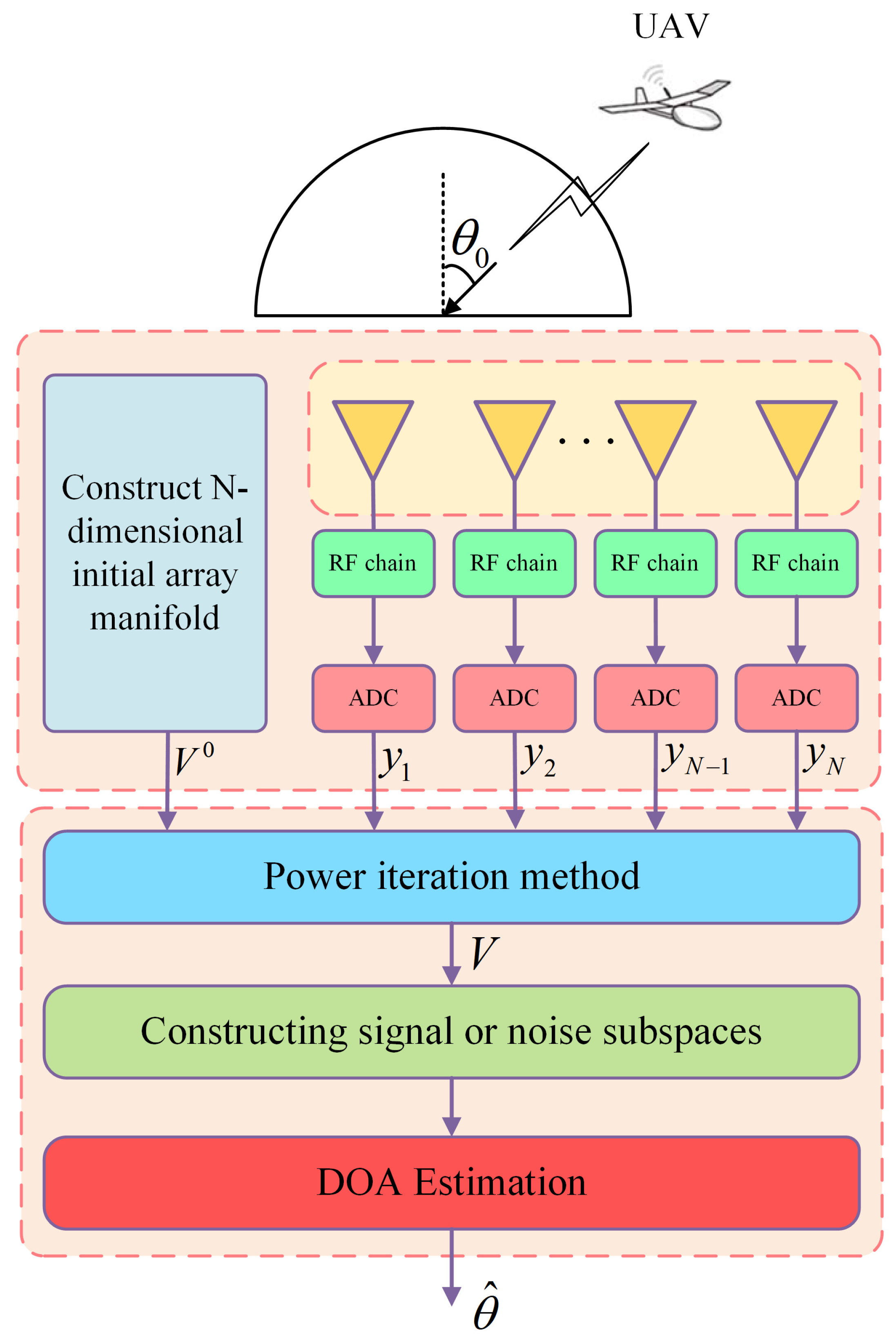
To rapidly achieve the direction finding of the UAV,
Figure 1 sketches a low-complexity massive MIMO RPI receiver structure for UAV direction estimation. In this structure, the PI method is considered for application in a uniformly spaced linear array (ULA) with
N antennas and an appropriate
N-dimensional initial array manifold is constructed as the input vector for it, which can effectively reduce the number of iterations. Then, the receive covariance matrix of all antennas is exploited as the object matrix to generate an eigenvector
V corresponding to the largest eigenvalue. Through constructing signal or noise subspaces, the optimal DOA estimation can be derived in different methods such as polynomial rooting [
38] and rotational invariance [
39].
In the proposed framework, it is assumed that the narrow band signals
transmitted via the UAV emitter will arrive at the array, where
is the baseband signal and
is the carrier frequency. Then the antennas will capture the signal with different time delays dependent on the DOAs. Therefore, the propagation delay of the
nth antenna element is expressed as
where
is the propagation delay from the UAV to a reference point on the receive array,
is the direction of the UAV relative to the line perpendicular to the array.
is the distance from the nth array element to the reference point and
c is the speed of light. Without loss of generality, we can assume that
. Thus,
The receive signal vector at the array can be expressed as
where
is the additive white Gaussian noise (AWGN) vector and
only composed by the phase difference of all antennas is called array manifold, defined as
In practice, although the ideal covariance matrix cannot be obtained directly, its estimated value is given by
where
K is the number of sampling points.
Make the eigenvalue decomposition of (
4)
where
is the diagonal matrix consisting of all non-zero eigenvalues of
and the matrices
and
stand for the signal and noise subspaces, respectively.
The CRLB is the minimum variance of DOA estimation errors. It can provide a useful characterization of the achievable accuracy of the systems. According to [
8], for an
N-element linear array the CRB can be given by
where
and SNR is the signal-to-noise ratio of the signal received at each antenna.
4. Proposed Two Rapid Power Iterative Estimators for Massive/Ultra-Massive MIMO Receiver
The subspace-based methods are widely used for direction finding of UAV emitters. However, their eigenvalue decomposition brings horrible complexity when the antenna tends to large-scale. Therefore, two low-complexity estimators are proposed in this section based on the RPI structure, the selection of the initial vector and the computational complexity.
4.1. Proposed RPI-RI Estimator
It is assumed that there exist two subarrays both with
antennas and overlapping with each other [
39]. The first subarray consists of the first
antennas of all antennas and the second subarray consists of the last
antennas of all antennas. Since the structures of the two subarrays are identical, the outputs of the two subarrays have only one phase difference
.
The following assumes that the received data of the first subarray is
and the received data of the second subarray is
, and by combining two subarrays, the
received data can be expressed as
where
is the additive white Gaussian noise (AWGN) vector and
is an
dimensional array manifold vector, which can be defined as
and
is a rotation-invariant value, which contains the direction of arrival information of the incoming wave signal and
.
The covariance matrix
can be given by
Let us define
and assume that the covariance matrix
has
M eigenvalues
with an associated collection of linearly independent eigenvectors
. Moreover, it is assumed that
has precisely one eigenvalue
, which is the largest in magnitude, i.e.,
There exists a random vector
that satisfies
where
are scalars.
Taking the vector
as the initial vector of the RPI-RI method and multiplying both sides of this equation by
,
, ...,
gives
can be rewritten as
where
Since
for all
, the above function can be further expressed as
therefore,
The eigenvector corresponding to the main eigenvalue
is
where
is expressed by the limit of the ratio of the
ith component of vector
to the
ith component of vector
, which has the following form
The estimated value of
is
In cases for which the power method generates a good approximation of a dominant eigenvector
, the Rayleigh quotient [
40] provides a correspondingly good approximation of the dominant eigenvalue
The key problem solved by the ESPRIT algorithm is the proper use of the translation-invariant property of the linear array, so that the eigenvalues of the rotation-invariant matrix can be found to estimate the signal incidence angle.
Based on (
13) and (
18), we perform the PI method on the covariance matrix
and obtain the signal subspace
. Since the shift invariance of the array implies that
can be decomposed as
where the two parts
and
correspond to the signal subspaces of the subarrays
and
. In accordance with the ESPRIT algorithm [
39], a matrix similar to
can be expressed as
Therefore, the corresponding eigenvalues of
, i.e., the diagonal elements, can be given by performing eigenvalue decomposition on
and the final DOA estimation can be calculated by
where
is the eigenvalues of
. The specific algorithm steps of the proposed RPI-RI estimator are described in Algorithm 1 as follows
| Algorithm 1 Proposed RPI-RI estimator |
| 1: Input subarray 1 and subarray 2 to receive and , forming the receive data model based on (8); |
| 2: Calculate the covariance matrix and use it as the object matrix of the power iteration to obtain the signal subspace corresponding to the two subarrays and further find the matrix similar to ; |
| 3: The corresponding eigenvalues are given by EVD on and the final DOA estimation is calculated based on (24). |
4.2. Proposed RPI-PR Estimator
The RPI-RI estimator can significantly reduce the computational complexity by using the power iteration and the rotational invariance of the signal subspace between subarrays, but it is difficult to achieve the desired performance and the complexity can be further optimized.
In order to further reduce the computational complexity and achieve better performance, the RPI-PR estimator is proposed in this subsection. From (
18), the signal subspace can be given by power iterating over
in (
4). Furthermore, we construct the noise subspace
where
is
unit matrix. The spatial spectral function can be defined as
The spectral peak corresponds to the desired DOA estimation. Furthermore, let us define
; the polynomial equation can be expressed as
The above polynomial Equation (
27) has
roots, i.e,
, which implies the existence of multiple emitter directions as follows
where
The angle corresponding to the root inside the unit circle and closest to it is chosen as the final DOA estimation .
The basic steps of the proposed RPI-PR method can be summarized as in Algorithm 2.
| Algorithm 2 Proposed RPI-PR method |
| 1: Input array receive signal y(t); |
| 2: Based on (4), calculate the covariance matrix ; |
| 3: Based on (25), estimate the noise subspace and use it to construct the spatial spectrum |
| 4: Multiple roots are given by the polynomial method for the spatial spectral function; the angle corresponding to the root inside the unit circle and closest to it is chosen as the final DOA estimation . |
4.3. Selecting Initial Vector and Relative Error
The initial vector has a direct effect on the speed of convergence and determines the number of iterations. A randomly generated vector is usually selected as the iterative initial vector, but not all the optional initial vectors can converge to obtain the desired results. Since orthogonality may cause the iterative process failures to converge, it is necessary to ensure that the initial vector is not orthogonal to the incident wave in each iteration.
From (
12) and (
14),
is formed as
where
is the sum of all elements in matrix
,
and
Based on the above discussion, the element distribution of initial vector
in (
30) is consistent with the distribution of matrix
, while the distribution is uniform, which can keep them far away from orthogonality and speed up the convergence of the iteration.
Therefore, let us define the array manifold as
where
and the initial vector
is assumed to be
The orthogonality equation can be expressed as
In order to make the incident wave direction not orthogonal to the initial vector, is constant. In the following, eight special initial vectors are discussed and their convergence performance is analyzed.
I. The initial vector is assumed to be
where all elements are 1. Based on (
37), the corresponding orthogonality equation is given by
where
and it can be discussed in three cases.
(1) When
and
,
can be calculated as
where
Z is an integer. It can be seen from (
40) that
holds when
and
is not an integer.
(2) When
,
is given by
Substituting
into (
39),
is verified to hold.
(3) When and , it is clear that holds. Through the above discussion, initial vector I is not guaranteed non-orthogonal always true.
II. The initial vector is assumed to be
where the odd element is 1 and the even elements is
. Depending on the value of
N, two cases can be discussed.
From the above discussion, it is clear that
holds when
satisfies the following form
If selects these cases, it may generate incorrect DOA estimation.
It can be seen that
holds when
satisfies the following conditions
where
is not an integer and orthogonality only can be avoided by selecting other
.
III. The initial vector is assumed to be
Assuming
N is even. The first half of the elements of vector
are 1 and the rest are
.
Therefore,
holds when
satisfies the following cases
The above value of will lead to orthogonality.
IV. Let us define
as the normalized DFT vector
with its elements given by [
41]
where
Therefore, (
37) can be calculated as
Solving the above equation yields
From the above discussion, when , where is not an integer, we have ; the orthogonality may lead to estimation failure.
V. The initial vector is assumed to be
where the
m-th element is 1, the
n-th is 1 and the rest of the elements are 0 (
).
When , .
VI. The initial vector is assumed to be
where
-th is 1 and the rest of the elements are 0 (
).
when
or
,
.
VII. The initial vector is assumed to be
where
-th is 1 and the rest of the elements are 0 (
).
when
or
or
,
.
So we can obtain the general rule, when is 1 and the rest of the elements are 0 (), when or or … or , .
VIII. The initial vector is assumed to be
where the
k-th element of
is 1 and the rest of the elements are 0.
is always true.
Among the above eight vector forms, the eighth vector form can be used as the initial vector of the power iteration due to its non-orthogonality, while the previous seven cannot guarantee the convergence of the power iteration.
In addition, the relative error
also influences the speed of convergence in the convergence process of power iteration, which can be expressed as
and
Therefore, (
61) can be further expressed as
Since
,
When the iteration approaches the final convergence, the convergence speed will be relatively slow and stable. In practice, the usefulness of the power method depends upon the ratio , since it dictates the rate of convergence.
The whole procedure is summarized in Algorithm 3.
| Algorithm 3 PI method on subspace |
| Input: matrix , tolerence |
| Output: , and n |
| Initialization: choose an initial vector , and n = 1. |
| repeat |
| 1. Calculate = ; |
| 2. Calculate = ; |
| 3. Calculate = ; |
| 4. Update = ; |
| 5. n = n + 1. |
| until |
|
. |
| Return , and n |
n is the number of iterations, is the dominant eigenvalue and is the dominant eigenvector corresponding to .
Notice that in each iteration we compute a single matrix–vector multiplication . We never perform matrix–matrix multiplication, which requires a greater number of operations . If the matrix R is sparse (only a small portion of the entries of A are non-zero), matrix–vector multiplication can be performed very efficiently. Therefore, the power method is practical even if N is very large, such as in Google’s Page Rank algorithm.
4.4. Complexity Analysis
We analyze the computational complexities of the proposed two estimators with traditional ESPRIT and Root-MUSIC algorithms as a complexity benchmark. Thus, the complexity of ESPRIT is as follows
FLOPs. The complexity of Root-MUSIC is
FLOPs. The complexity of RPI-RI is
FLOPs. The complexity of RPI-PR is
FLOPs, where is the iteration number of the power iteration. Assuming N is far larger than , compared with the conventional FD estimator, the complexity of the proposed two estimators is significantly reduced as the number of antennas tends to large-scale.
5. Simulation Results and Discussions
In this section, a simulation is presented to analyze the performance of the proposed massive MIMO DOA estimators for UAV and two conventional algorithms are used as a comparison. Furthermore, we consider the effect of SNR, the number of antennas and the number of snapshots on the proposed methods in the digital ADC architecture. In each simulation figure, the number of Monte Carlo simulations L is 1000. Without loss of generality, we assume that UAV emitter located in , the number of snapshots K is 1000, the antenna distance and the number of antenna elements N is 64 in the massive MIMO system.
Figure 2 plots the root mean square error (RMSE) curves using four different methods versus SNR with CRLB as the performance benchmark. Observing
Figure 2, it is clear that the proposed RPI-RI method can achieve a similar performance to ESPRIT but with some performance loss, while the proposed RPI-PR method can achieve the corresponding CRLB.
Figure 3 and
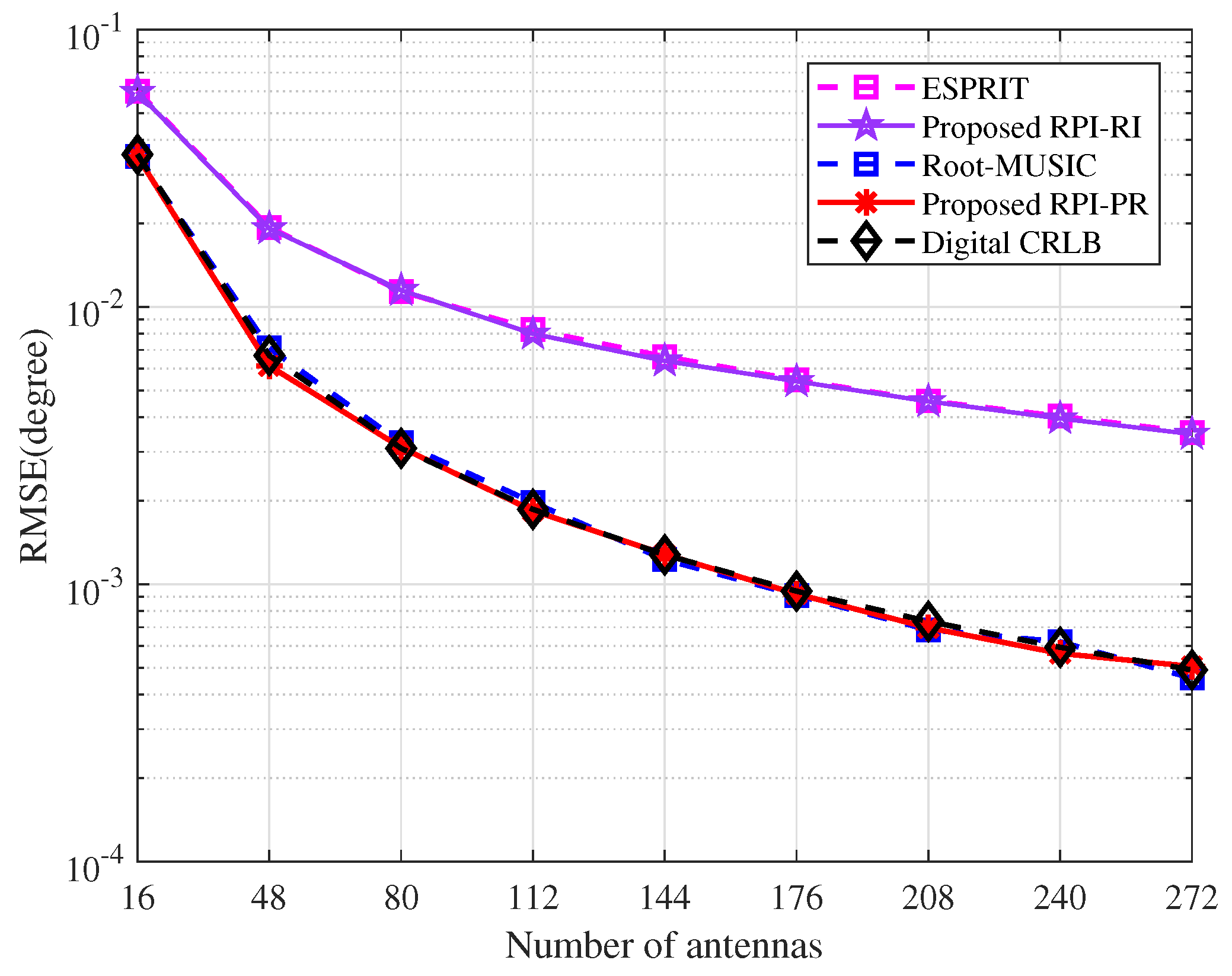
Figure 4 present the RMSE of four different methods versus the number of antennas
N and snapshots
K. Without loss of generality, we assume that
and
. From
Figure 3 and
Figure 4, it can be seen that the DOA estimators on the power iteration method achieve a performance close to the conventional algorithms for any number of antennas and snapshot scenarios; in particular, RPI-PR can reach the FD CRLB.
Figure 5 plots curves of complexity analysis versus the number of antennas
N with
, SNR = 0 dB. From this figure, it can be seen that the complexity of all methods gradually increases as the total number of antennas increases. However, the computational complexity of our proposed methods is two to three orders of magnitude lower when
N = 1024 compared to the conventional methods. In particular, the proposed RPI-PR method can achieve a performance close to CRLB.
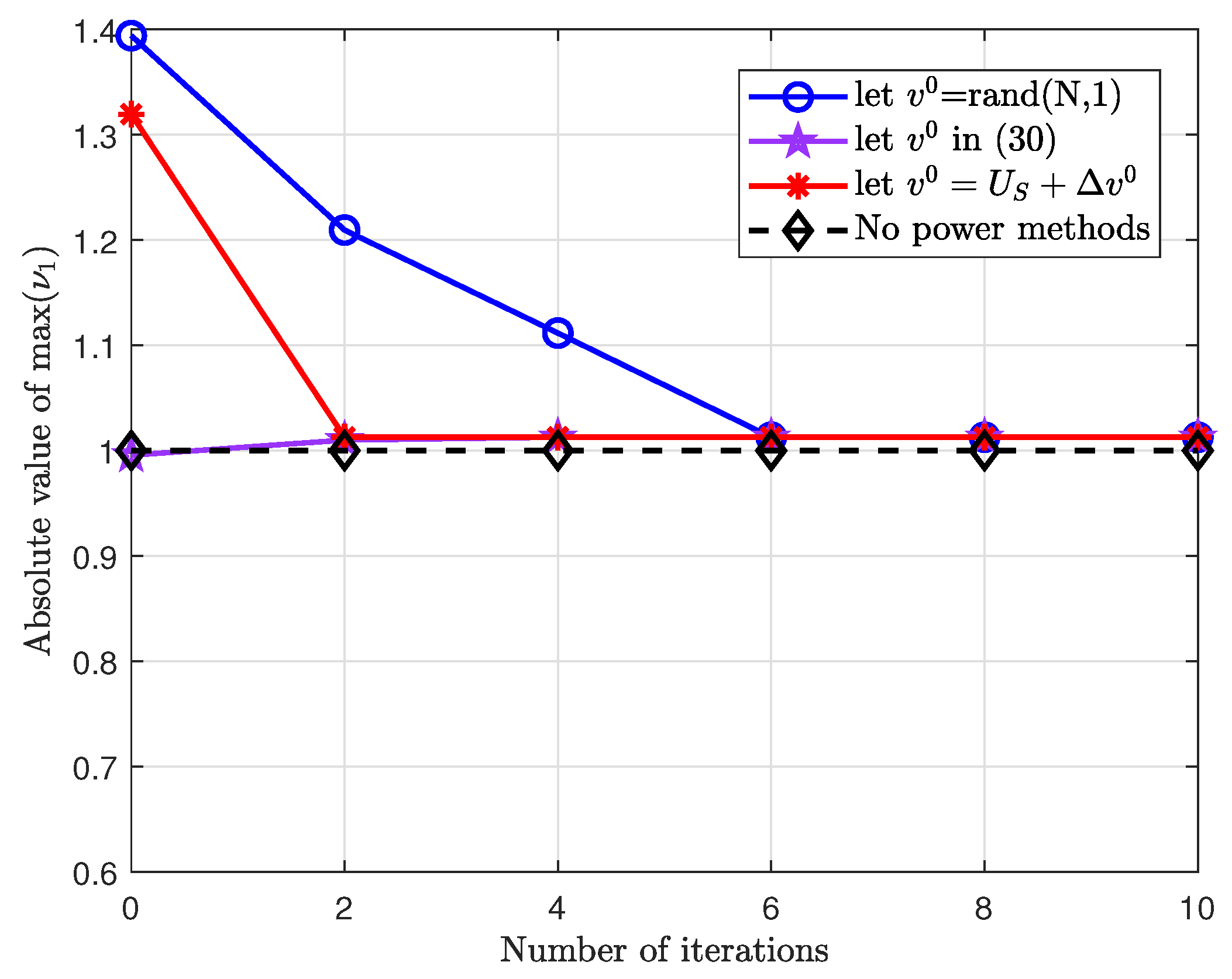
To explore the influence of the selection of the initial vector on the number of iterations and the convergence speed,
Figure 6 shows the relationship between the optimal eigenvector value
and the number of iterations
n, given three different initial vectors
. When the initial vector
is infinitely close to the signal subspace, only two iterations are needed to complete the convergence and the result is similar to that of the initial vector selected in (
30). In addition, when the
obeys a random vector distribution, the required number of iterations
n is increased, which requires an average of eight iterations to reach the convergence of the
.
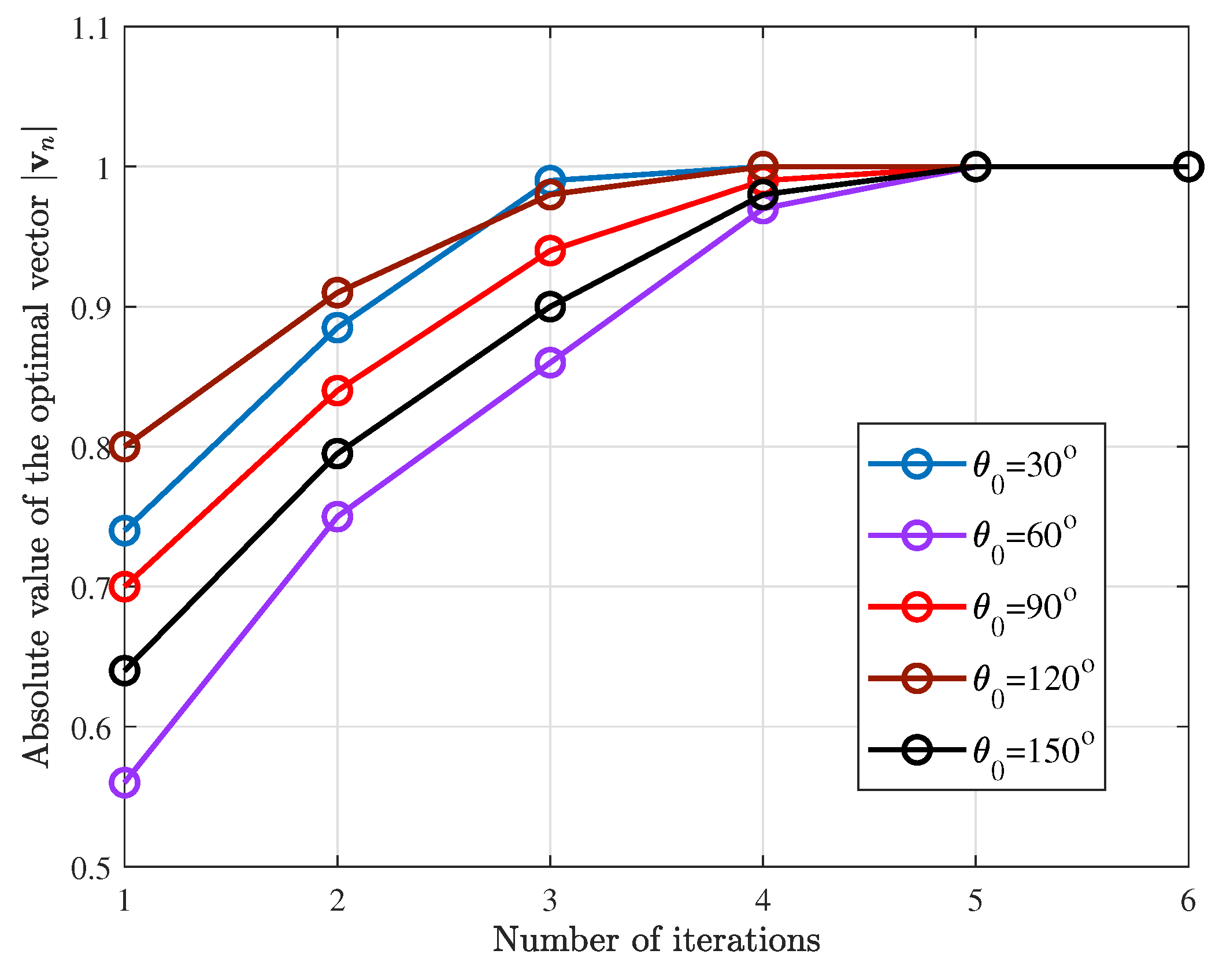
In order to verify the convergence performance of the initial vector
in (
60), five incident wave directions
,
are assumed in
Figure 7 and the number of iterations of RPI methods is given by numerical simulation when SNR = 0. As shown in
Figure 7, the proposed RPI methods require about five iterations to converge. The
in the figure indicates the absolute value of the vector at the
nth iteration.
To analyze the effect of SNR on the convergence speed of the proposed RPI methods,
Figure 8 plots the iteration error
of the RPI methods versus the number of iterations, where the iteration error
represents the absolute value of the difference between the result of the
nth iteration
and the result of the
th iteration
, i.e.,
. As shown in
Figure 8, it is assumed that the number of antennas
and the incident wave direction
. The number of iterations is 7, 5 and 4 for SNRs of −30 dB, 0 dB and 30 dB, respectively. the number of iterations of the proposed algorithm decreases sequentially as the SNR increases.