Online Motion Planning for Fixed-Wing Aircraft in Precise Automatic Landing on Mobile Platforms
Abstract
1. Introduction
- This study proposes an idea to solve the automatic landing problem by combining a motion planner with a controller. The planner focuses on the reasonability and feasibility of the landing trajectory, whereas the controller focuses on precising tracking of the glide path. To the best of our knowledge, this is the first time that a method is presented for consuming excess energy with a short deviation from the conventional glide path before reentering the path. The proposed method is radically different from the existing methods, which order the aircraft to abort and retry as soon as some strict constraints are violated due to the limited flexibility.
- An efficient algorithm for trajectory generation online is proposed for precise automatic landing on a fixed or moving platform with flexibility for adjustment. Based on the algorithm, the planner can guide the aircraft as an experienced pilot would based on their understanding of the aircraft’s performance.
2. Problem Statement
3. Theory and Algorithm
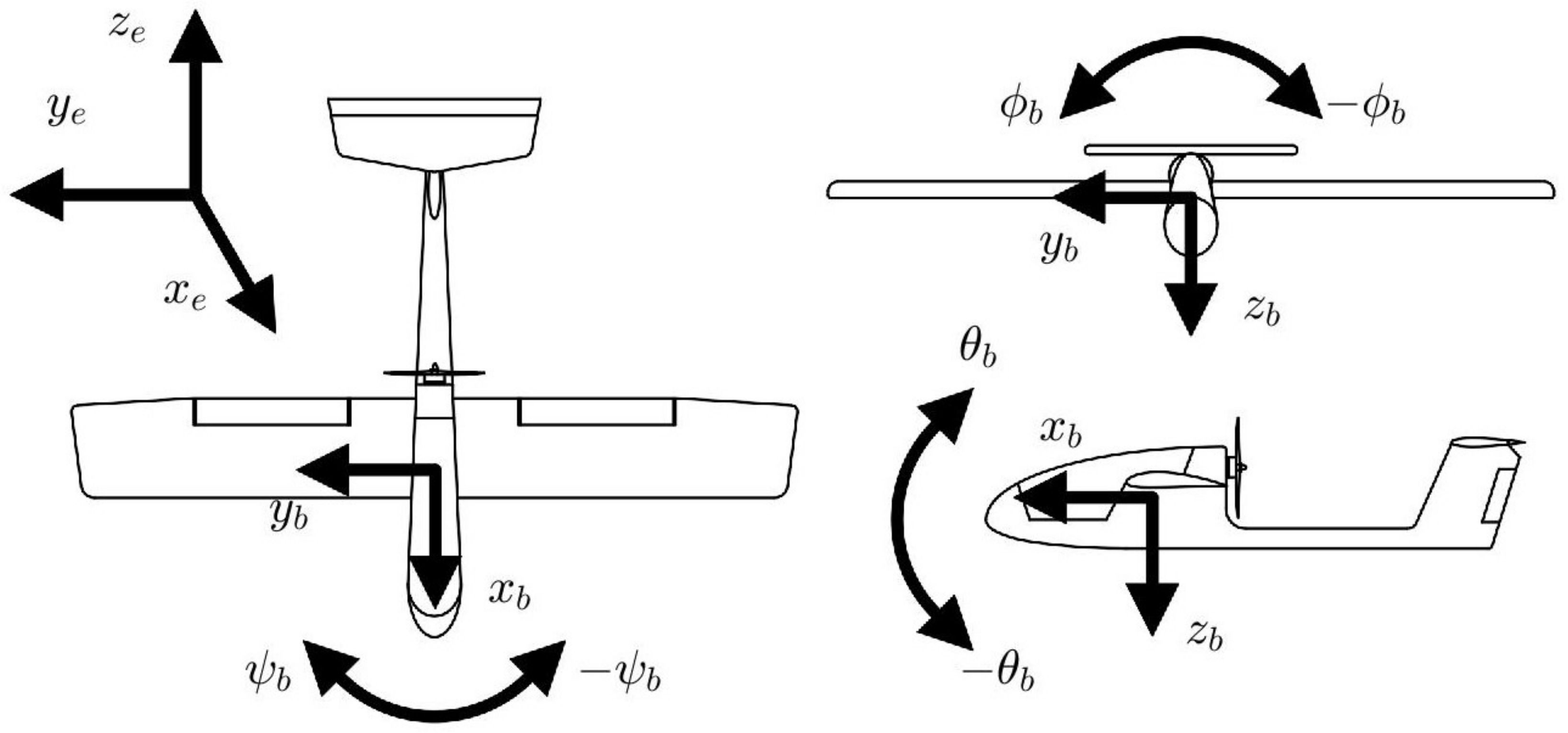
3.1. Coordinate Systems and Kinematic Model
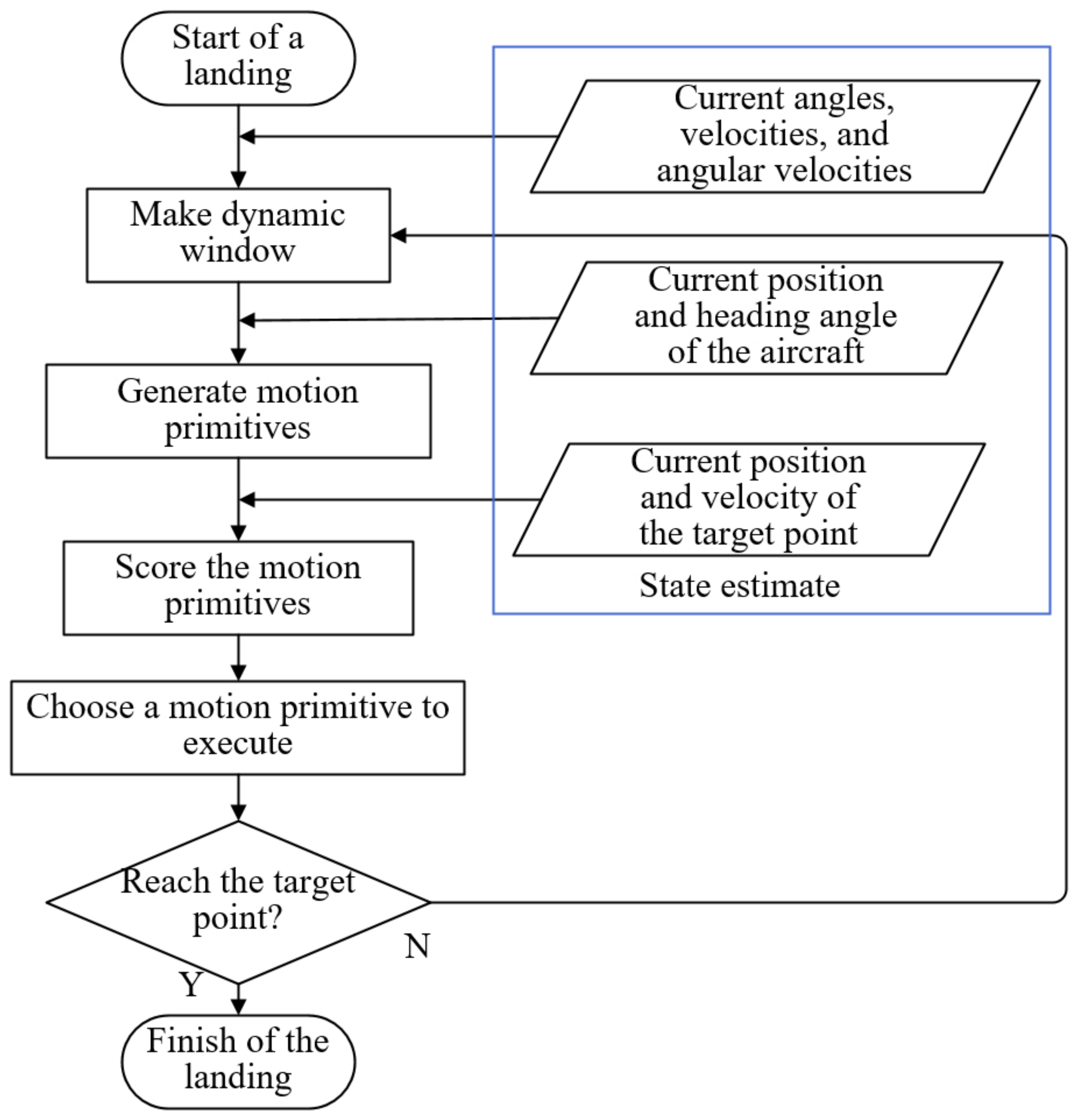
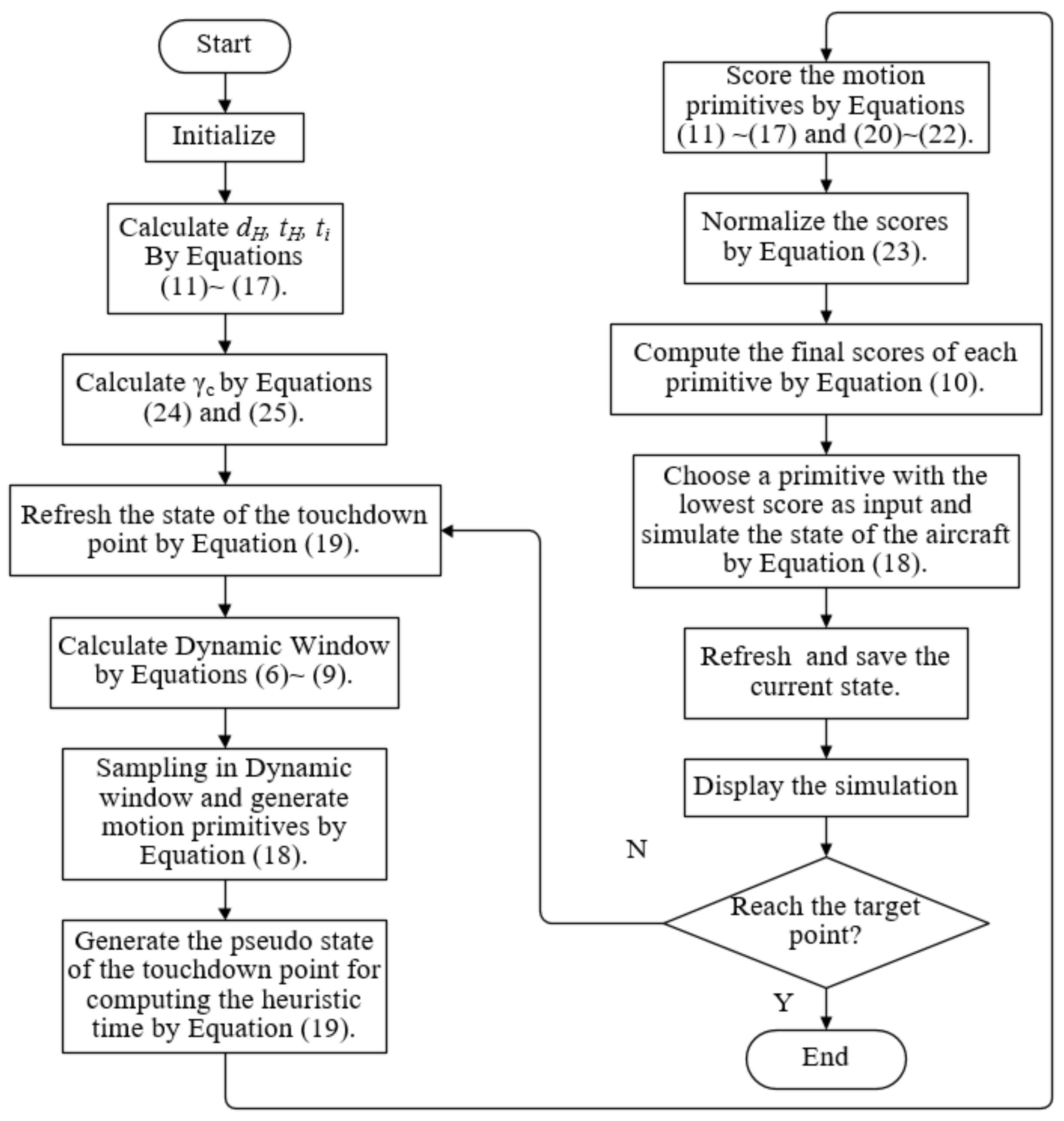
3.2. Algorithm Description
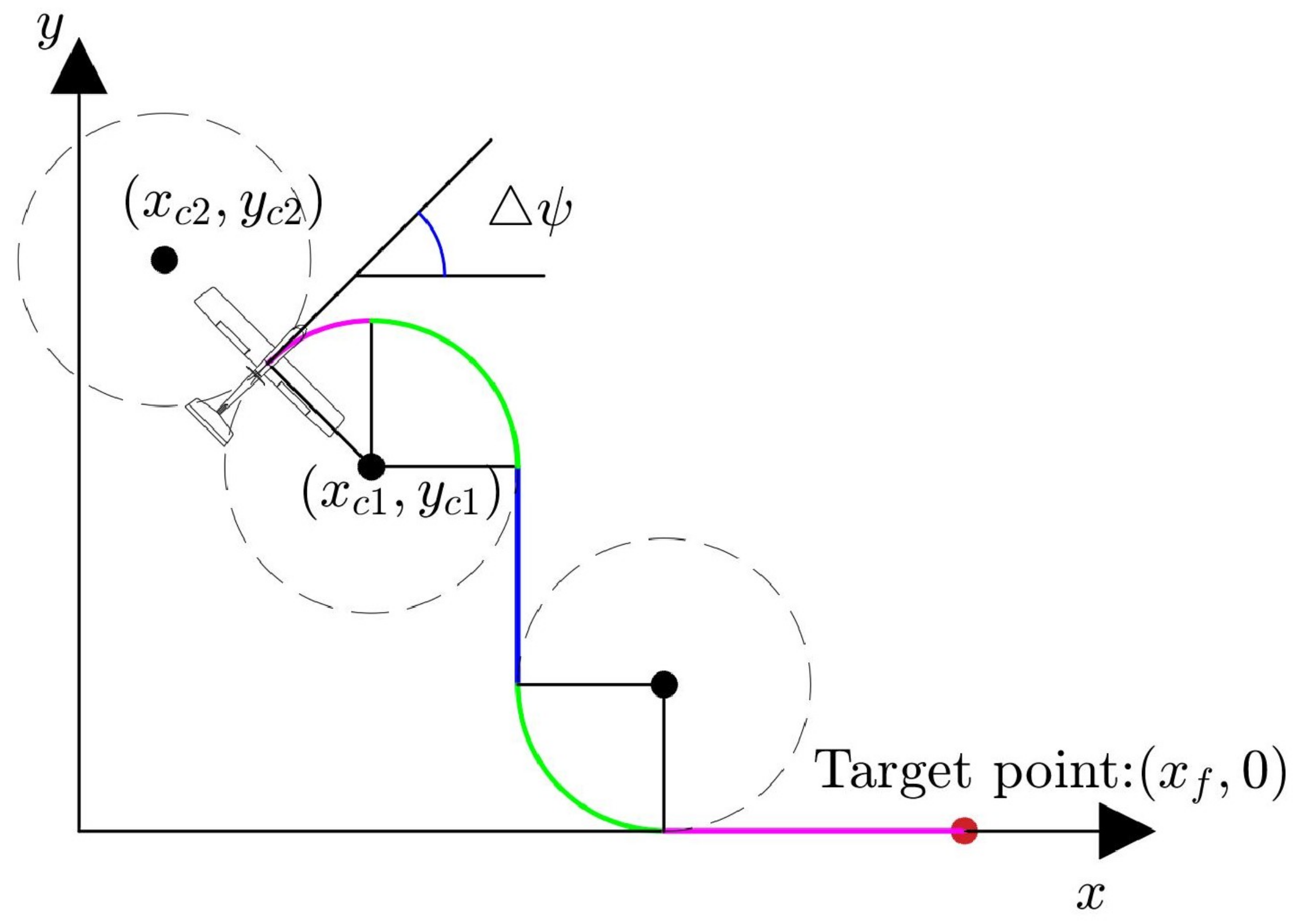
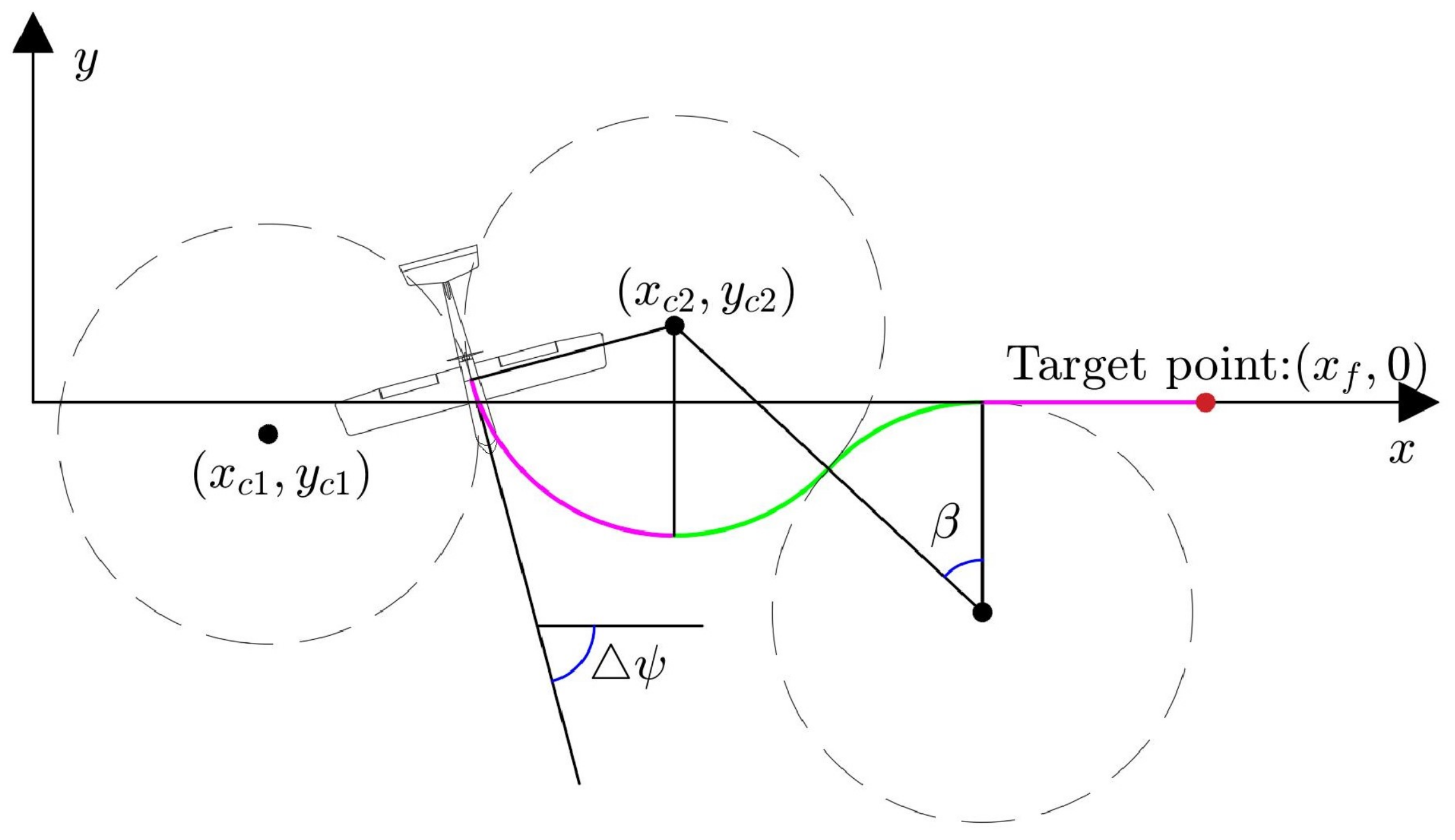
3.2.1. Motion Primitives
3.2.2. Evaluation Criteria
3.2.3. Algorithm Implementation
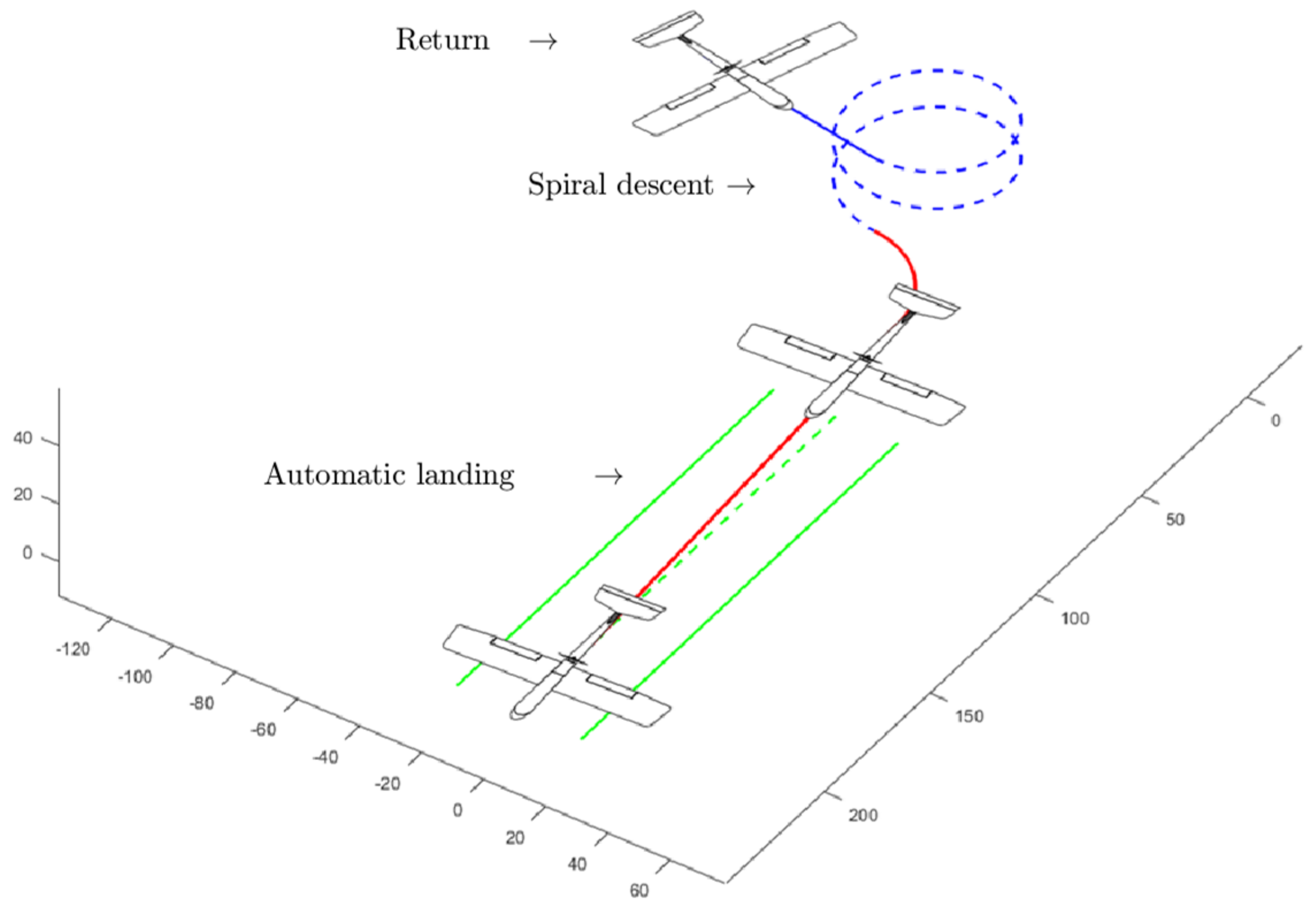
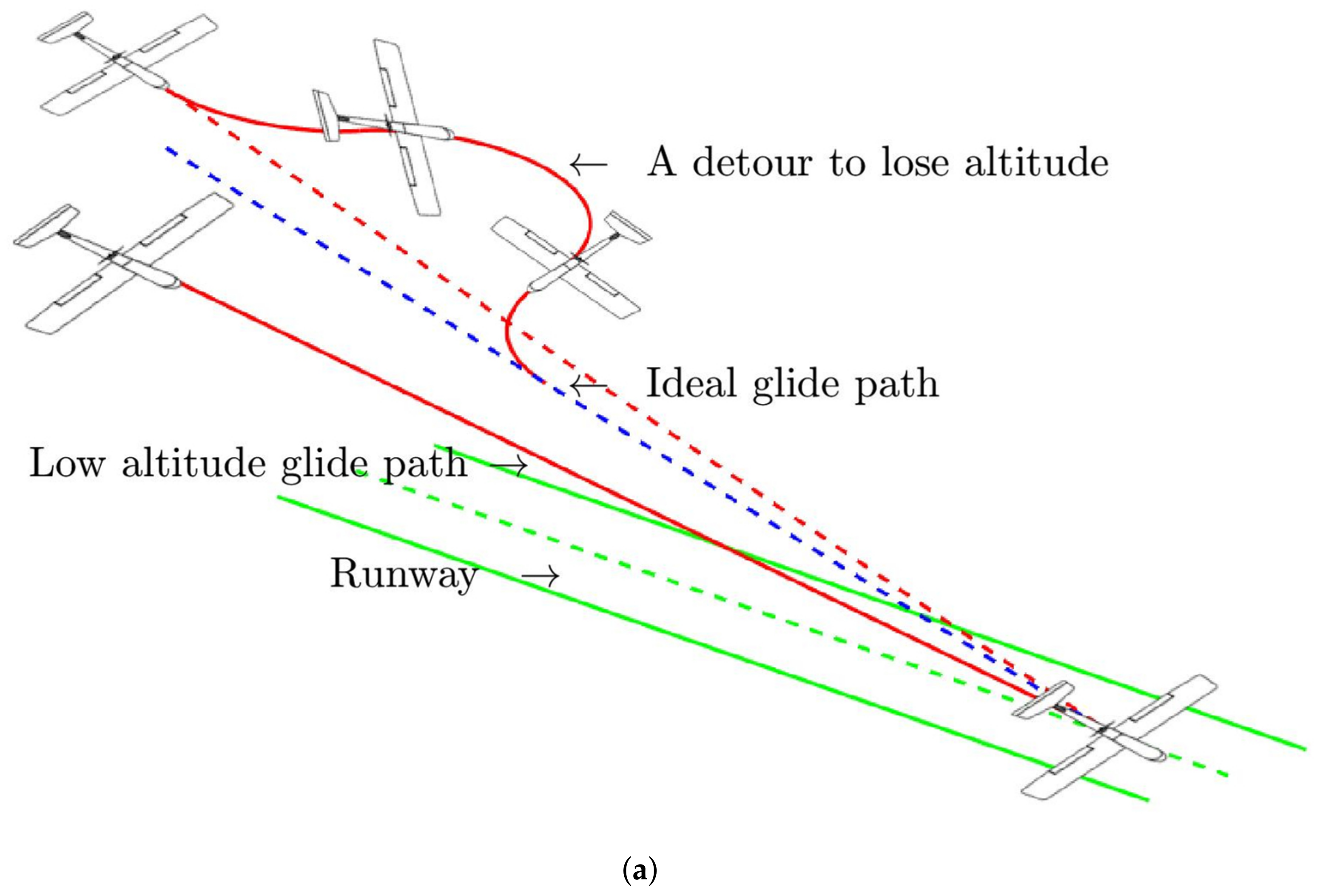
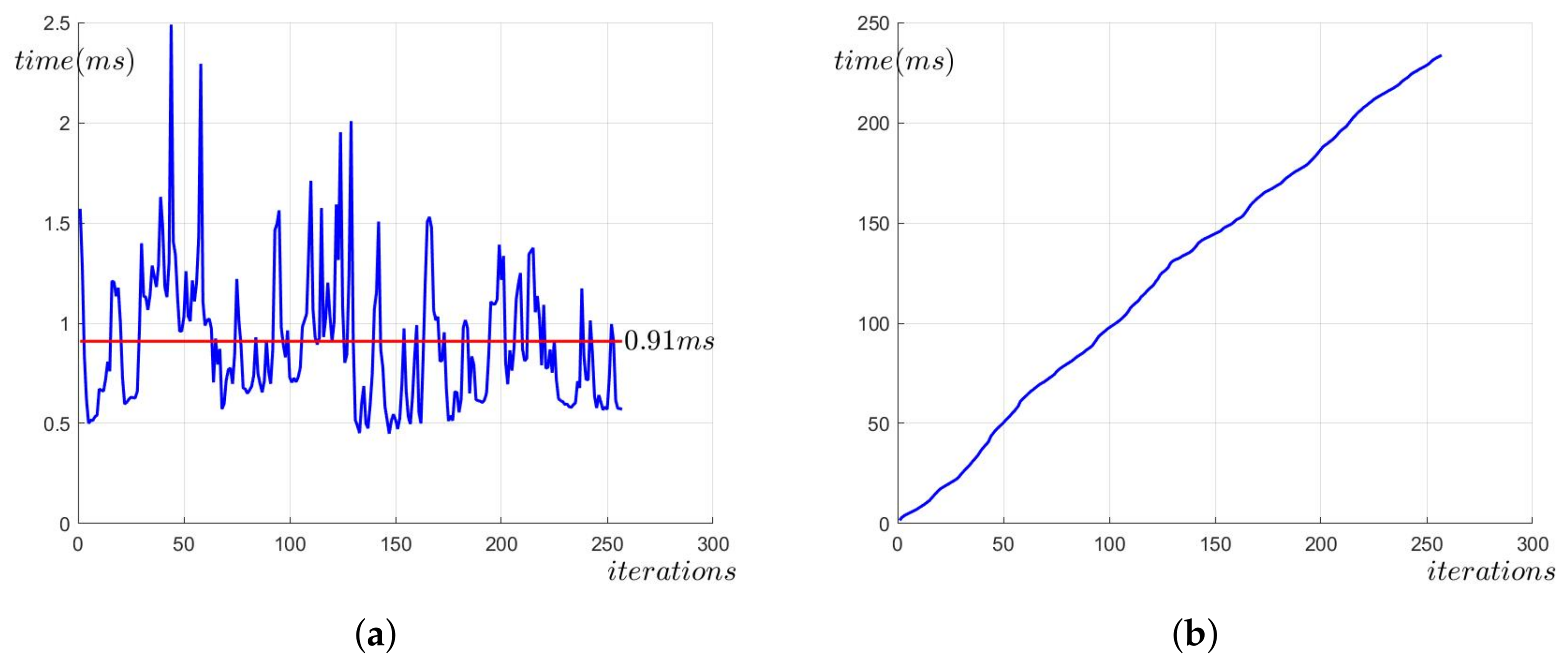
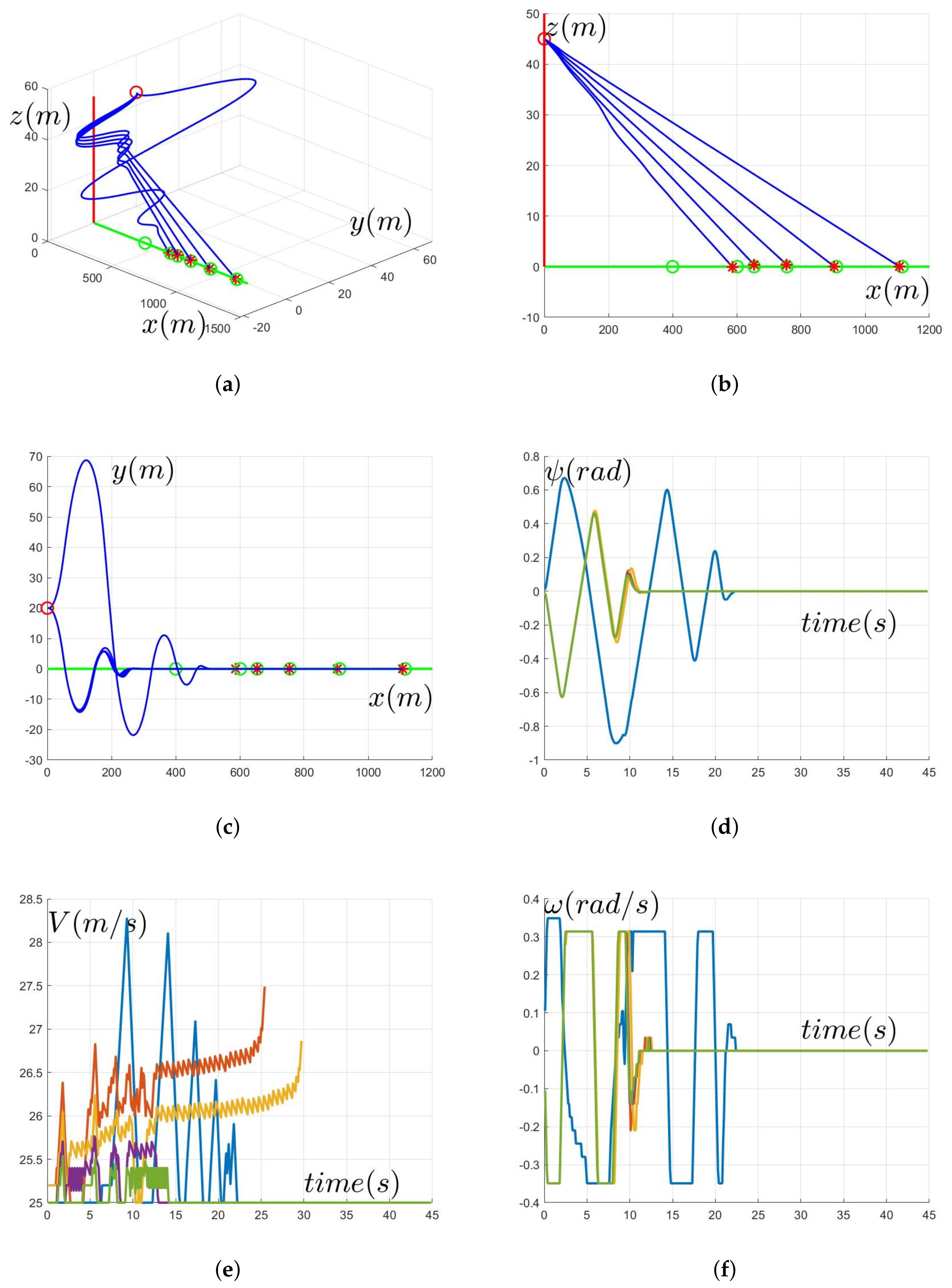
4. Numerical Simulation
5. Analysis and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| axes of body-fixed coordinate system | |
| axes of the inertial coordinate system | |
| position of the aircraft | |
| pitch, yaw (heading), and roll angle | |
| state vector, input vector | |
| speed, angular rate of the aircraft | |
| current velocity and angular rate | |
| altitude of start point of automatic landing | |
| minimum/maximum angular acceleration | |
| flight path angle | |
| ideal glide path angle, ideal touchdown speed of automatic landing | |
| path angle command | |
| roll angle command | |
| climb and sink rate | |
| m | mass of the aircraft |
| g | gravitational acceleration |
| a | linear acceleration |
| r | turning radius of the aircraft |
| R | radius of circular arcs of Dubins path |
| window restricting the velocity and angular rate | |
| window restricting the linear acceleration and the angular acceleration | |
| window restricting the heading angle | |
| intersection of , , and | |
| angle between the heading angle and the direction of runway | |
| integral time of motion primitives | |
| sampling period of state transition equation | |
| weight coefficients | |
| orthogonal distance to ideal glide path | |
| speed penalty function | |
| heuristic time penalty function | |
| D | integrated resistance of the aircraft |
| central angle of the arc of the tangent Dubins circle and the x-axis | |
| heuristic Dubins distance and time from the endpoints of primitives to the target point | |
| time threshold for determining the score function | |
| Subscripts | |
| min | minimum value |
| max | maximum value |
| f | states of target point (touchdown point) |
References
- Zhen, Z.; Jiang, J.; Wang, X.; Li, K. Modeling, control design, and influence analysis of catapult-assisted take-off process for carrier-based aircrafts. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 232, 2527–2540. [Google Scholar] [CrossRef]
- Wang, Z.; Gong, Z.; Zhang, C.; He, J.; Mao, S. Flight Test of L1 Adaptive Control on 120-kg-Class Electric Vertical Take-Off and Landing Vehicles. IEEE Access 2021, 9, 163906–163928. [Google Scholar] [CrossRef]
- Yoon, S.; Kim, H.J.; Kim, Y. Spiral landing trajectory and pursuit guidance law design for vision-based net-recovery UAV. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Chicago, IL, USA, 10–13 August 2009; pp. 1–25. [Google Scholar]
- Qiu, Z.; Lv, J.; Lin, D.; Yu, Y.; Sun, Z.; Zheng, Z. A Lidar-Inertial Navigation System for UAVs in GNSS-Denied Environment with Spatial Grid Structures. Appl. Sci. 2023, 13, 414. [Google Scholar] [CrossRef]
- Qiu, Z.; Lin, D.; Jin, R.; Lv, J.; Zheng, Z. A Global ArUco-Based Lidar Navigation System for UAV Navigation in GNSS-Denied Environments. Aerospace 2022, 9, 456. [Google Scholar] [CrossRef]
- Dubins, L.E. On curves of minimal length with a constraint on average curvature, and with prescribed initial and terminal positions and tangents. Am. J. Math. 1957, 79, 497–516. [Google Scholar] [CrossRef]
- Dolgov, D.; Thrun, S.; Montemerlo, M.; Diebel, J. Path planning for autonomous vehicles in unknown semi-structured environments. Int. J. Robot. Res. 2010, 29, 485–501. [Google Scholar] [CrossRef]
- Howard, T.M.; Green, C.J.; Kelly, A.; Ferguson, D. State space sampling of feasible motions for high-performance mobile robot navigation in complex environments. J. Field Robot. 2008, 25, 325–345. [Google Scholar] [CrossRef]
- Pivtoraiko, M.; Kelly, A. Generating near minimal spanning control sets for constrained motion planning in discrete state spaces. In Proceedings of the Intelligent Robots and Systems, IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 3231–3237. [Google Scholar]
- Howard, T.M.; Kelly, A. Optimal Rough Terrain Trajectory Generation for Wheeled Mobile Robots. Int. J. Robot. Res. 2007, 26, 141–166. [Google Scholar] [CrossRef]
- LaValle, S.M.; James, J.; Kuffner, J. Randomized Kinodynamic Planning. Int. J. Robot. Res. 2001, 20, 378–400. [Google Scholar] [CrossRef]
- Lavalle, S.M. Rapidly-Exploring Random Trees: A New Tool for Path Planning. 1998. Available online: http://lavalle.pl/papers/Lav98c.pdf (accessed on 29 March 2023).
- Owen, M.; Beard, R.W.; McLain, T.W. Handbook of Unmanned Aerial Vehicles: Implementing Dubins Airplane Paths on Fixed-Wing UAVs*; Springer: Dordrecht, The Netherlands, 2015; pp. 1677–1701. [Google Scholar]
- Askari, A.; Mortazavi, M.; Talebi, H.A.; Motamedi, A. A new approach in UAV path planning using Bezier-Dubins continuous curvature path. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2016, 230, 1103–1113. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, C.; Baek, S.; Rawashdeh, S.; Mohammadi, A. Autonomous Landing of a UAV on a Moving Platform Using Model Predictive Control. Drones 2018, 2, 34. [Google Scholar] [CrossRef]
- Wu, L.; Wang, C.; Zhang, P.; Wei, C. Deep Reinforcement Learning with Corrective Feedback for Autonomous UAV Landing on a Mobile Platform. Drones 2022, 6, 238. [Google Scholar] [CrossRef]
- Battiato, S.; Cantelli, L.; D’Urso, F.; Farinella, G.M.; Guarnera, L.; Guastella, D.; Melita, C.D.; Muscato, G.; Ortis, A.; Ragusa, F.; et al. A System for Autonomous Landing of a UAV on a Moving Vehicle. In Image Analysis and Processing—ICIAP 2017, Proceedings of the International Conference on Image Analysis and Processing, Catania, Italy, 11–15 September 2017; Battiato, S., Gallo, G., Schettini, R., Stanco, F., Eds.; Springer: Cham, Switzerland, 2017; pp. 129–139. [Google Scholar]
- Keller, A.; Ben-Moshe, B. A Robust and Accurate Landing Methodology for Drones on Moving Targets. Drones 2022, 6, 98. [Google Scholar] [CrossRef]
- Gautam, A.; Singh, M.; Sujit, P.B.; Saripalli, S. Autonomous Quadcopter Landing on a Moving Target. Sensors 2022, 22, 1116. [Google Scholar] [CrossRef] [PubMed]
- Muskardin, T.; Balmer, G.; Wlach, S.; Kondak, K.; Laiacker, M.; Ollero, A. Landing of a fixed-wing UAV on a mobile ground vehicle. In Proceedings of the International Conference on Robotics and Automation, Stockholm, Sweden, 16–21 May 2016; pp. 1237–1242.v. [Google Scholar]
- Fang, X.; Holzapfel, F.; Wan, N.; Jafarnejadsani, H.; Sun, D.; Hovakimyan, N. Emergency landing trajectory optimization for a fixed-wing UAV under engine failure. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; pp. 1–15. [Google Scholar]
- Stephan, J.; Fichter, W. Fast generation of landing paths for fixed-wing aircraft with thrust failure. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, San Diego, CA, USA, 4–6 January 2016; pp. 1–12. [Google Scholar]
- Warren, M.; Mejias, L.; Kok, J.; Yang, X.; Gonzalez, F.; Upcroft, B. An automated emergency landing system for fixed-wing aircraft: Planning and control. J. Field Robot. 2015, 32, 1114–1140. [Google Scholar] [CrossRef]
- De Lellis, E.; Di Vito, V.; Ruby, M.; Salbego, N. Adaptive algorithm for fixed wing UAV autolanding on aircraft carrier. In Proceedings of the AIAA Infotech at Aerospace (I at A) Conference, Boston, MA, USA, 19–22 August 2013; pp. 1–13. [Google Scholar]
- Beard, R.W.; McLain, T.W. Small Unmanned Aircraft: Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Cichella, V.; Xargay, E.; Dobrokhodov, V.; Kaminer, I.; Pascoal, A.M.; Hovakimyan, N. Geometric 3D path-following control for a fixed-wing UAV on SO(3). In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Portland, OR, USA, 8–11 August 2011; pp. 1–15. [Google Scholar]
- Park, S.; Deyst, J.; How, J.P. A new nonlinear guidance logic for trajectory tracking. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Providence, RI, USA, 16–19 August 2004; pp. 941–956. [Google Scholar]
- Sedlmair, N.; Theis, J.; Thielecke, F. Flight testing automatic landing control for unmanned aircraft including curved approaches. J. Guid. Control. Dyn. 2022, 45, 726–739. [Google Scholar] [CrossRef]
- Ishioka, S.; Uchiyama, K.; Masuda, K. Optimal landing guidance for a fixed-wing uav based on dynamic window approach. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; pp. 1–11. [Google Scholar]
- Fox, D.; Burgard, W.; Thrun, S. The dynamic window approach to collision avoidance. IEEE Robot. Autom. Mag. 1997, 4, 23–33. [Google Scholar] [CrossRef]
- Chitsaz, H.; Lavalle, S.M. Time-optimal paths for a Dubins airplane. In Proceedings of the 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2008; pp. 2379–2384. [Google Scholar]







| Characteristics | Range | Performance | Range |
|---|---|---|---|
| Length | 3.2 m | Max/Loiter Speed | 38/31 m/s |
| Wing Span | 6.4 m | Stall speed | 24 m/s |
| Gross weight | 90.0 kg | Min turning radius | 96 m |
| Max thrust | 35.0 kg |
| Parameters | Values | Parameters | Values | Parameters | Values |
|---|---|---|---|---|---|
| / | 25/34 m/s | rad/s | 0.1 s | ||
| / | −2.3/3.5 m/s2 | rad/s | 0.2 s | ||
| 25 m/s | Resolution of V | 0.2 m/s | 0.5 | ||
| −0.07 rad | Resolution of | rad/s | 0.02 | ||
| R | 100 m | 0.6 s | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, J.; Wang, S.; Wang, B. Online Motion Planning for Fixed-Wing Aircraft in Precise Automatic Landing on Mobile Platforms. Drones 2023, 7, 324. https://doi.org/10.3390/drones7050324
Liang J, Wang S, Wang B. Online Motion Planning for Fixed-Wing Aircraft in Precise Automatic Landing on Mobile Platforms. Drones. 2023; 7(5):324. https://doi.org/10.3390/drones7050324
Chicago/Turabian StyleLiang, Jianjian, Shoukun Wang, and Bo Wang. 2023. "Online Motion Planning for Fixed-Wing Aircraft in Precise Automatic Landing on Mobile Platforms" Drones 7, no. 5: 324. https://doi.org/10.3390/drones7050324
APA StyleLiang, J., Wang, S., & Wang, B. (2023). Online Motion Planning for Fixed-Wing Aircraft in Precise Automatic Landing on Mobile Platforms. Drones, 7(5), 324. https://doi.org/10.3390/drones7050324







