Robust Cooperative Control of UAV Swarms for Dual-Camp Divergent Tracking of a Heterogeneous Target

Abstract

Agents are used to exhibit swarm intelligence in the sense of convergence, while divergence is equivalently common in nature and useful in complex applications for multi-UAV systems. This paper proposes a robust target-tracking control algorithm, where UAV swarms are partitioned by a signed graph to perform opposite movements along or against the trajectory of the target. Uncertainties take place in both the fractional-order model of the target and the double-integrator dynamics of the UAVs. To tackle the challenge induced by the bipartite behavior and unknown components in the multi-UAV systems, the article comes up with a backstepping cascade controller and a new method for uncertainty estimation-compensation via a combined approach based on a neural network (NN) and an Uncertainty and Disturbance Estimator (UDE). Steered by the controller, UAVs in a structurally balanced network will display symmetry of their paths, pursuing or away from the target with respect to the origin. Theoretical derivation and numerical simulations have evidenced that the tracking errors converge to zero. Compared with the traditional NN method to solve such problems, this method is proposed for the first time, which can effectively improve the precision of cooperative target tracking and reduce the chattering phenomena of the controller.

1. Introduction

The swarm intelligence of the multi-agent system (MAS) is usually embodied in collective behavior, which takes many forms. Convergence is comparatively usual in collaboration and is supported by a large number of studies [1,2,3]. However, the phenomena of divergence are equally common in nature, for instance, the split of a school of fish when encountering an obstacle [4] and the division of an ant colony on their way to food sources [5,6]. In a similar way, when many practical multi-agent systems [7,8,9], especially UAV groups [10,11,12], perform complex behavior, such as coverage [13], formation [14], enclosing [15], surrounding [16] and containment [17], their states exhibit divergence in order to fulfill civil and military tasks related to searching and exploring by space expansion rather than convergence. Relevant studies show that the bipartition of a UAV network is an effective use of divergence behavior.

The bipartite consensus is behavior in a signed network based on its underlying structural balanced graph [18,19], and numerous state-of-the-art studies illustrate its popularity: the authors of [20] come up with the concept of bipartite consensus to present the relationship between collaboration and competition in swarm intelligence. With respect to the bipartite consensus problem, the order of the networked agents extends from first-order [21] to second-order [22] or even high-order [23], and its dynamics gradually change from linear [24] to nonlinear [25]. Specifically, the leader-follower collaborative structure has also extended to this symmetric divergence behavior, namely, the bipartite tracking problem [26,27,28], which has drawn much attention due to its potential application in scattered mobile target capturing and swarm confrontation.

On the other hand, swarm intelligence is not only performed among homogeneous UAVs. In the scenarios of air-ground cooperation, the UAVs and ground vehicles may display different dynamics, and the latter’s can be in the form of fractional-order differential equations when they move on the surface of viscoelastic materials (grass or muddy road) [29] or in special weather (dust rain, sand, snow, storm) [30]. It is difficult to model such moving bodies accurately and specify their exact system orders. Even worse, in practical tasks, UAVs are always subject to environmental disturbances. Such inevitable uncertainties lead to heterogeneity in a swarm, and these factors may affect the multi-UAV system stability, which is of extraordinary importance to the cooperation of networked UAVs. Multi-agent theory can be adopted as a framework to solve the above problems for multi-UAV systems.

In view of the above problems, this paper studies the robust dual-camp divergent tracking control problem of mixed-order heterogeneous systems in the presence of model uncertainties and unknown disturbances. Much of the existing literature [31,32,33] has attempted to focus on robust bipartite tracking control issues and innovatively come up with various approaches to reduce or impair the impact of undesirable conditions on system stability and control accuracy. In article [31], a distributed control method based on a neural network (NN) is proposed to solve the bipartite consensus problem of nonlinear MASs with time delays and an unknown nonlinear dynamics model. An adaptive disturbance rejection controller is presented in article [32] to ensure that bipartite consensus tracking can be accomplished if an agents’ dynamics is subjected to unknown time-varying disturbances on signed networks. Liu and Wang [33] investigated bipartite consensus and tracking control issues for MASs with nonidentical matching uncertainties and developed and constructed a discontinuous controller to deal with the influence of the matching uncertainties. However, the previous studies do not consider the robust bipartite tracking control of a mixed-order heterogeneous systems in a comprehensive way, while such research has significant application value in mobile target capturing.

Therefore, the neural network and cascade UDE (NNCUDE) method is put forward to tackle such problems. This paper makes efforts to guarantee the robustness of the bipartite tracking control among heterogeneous system that suffer from mixed-order dynamics in the presence of unmatched uncertainties and disturbances. Thus, with the help of a backstepping control technique, a hybrid estimation system is constructed to compensate for the unknown part in the models, which enjoys the complementary advantages of the NN- (for being applicable to uncontrollable fractional-order targets) and UDE (for being computational efficient)-based methods when they become compatible with each other through a careful Lyapunov-based design of update laws that empower the divergence control to robustness. The major contributions in this work include:

(I)

The paper designs a backstepping cascade robust controller for mixed-order (fractional- and integral-order) agents with unmatched uncertainties and disturbances, which solves the order-unmatched problems between the target’s and UAVs’ kinematics as well as the UAVs’ position dynamic loop and control input loop. Compared to the related article [34], the proposed method resolves the unmatched uncertainties and disturbances.

(II)

An NNCUDE-based method is a combination to guarantee the robustness of swarm systems by taking advantage of NN and UDE. NN is used to estimate the fractional-order targets, and UDE is applied to compensate for the UAVs’ unknown parts with low computing resources. Compared to the conventional NN-based method of [35], this proposed method can reduce the computational complexity and effectively reduce the occurrence of the chattering phenomenon.

The remainder of this paper is laid out as follows. In Section 2, the preliminaries of signed graph theory, fractional-order theory and problem formulation are provided. In Section 3, the bipartite tracking controller via NNCUDE is designed. After that, using the provided technique, it is demonstrated that multi-agent systems are capable of performing bipartite consensus tracking. Several numerical cases are presented in Section 4 as experimental demonstrations of the proposed method. Eventually, we summarize the main research achievements of this paper in Section 5.

2. Preliminary and Problem Formulation

In order to solve dual-camp divergent tracking of a heterogeneous target for a UAV swarm, we will introduce some required definitions, properties and lemmas of fractional calculus, as well as some related mathematical theories pertaining to signed graphs in this section. Some commonly used notations are presented in

Table 1. The explanation of symbols.

Symbols	Explanation
${\mathbb{R}}^n$	The set of real n-vectors
$\left|x\right|$	The absolute value for a scalar value of x
$∥x∥$	The 2-norm for a vector x
sgn()	The standard signum function
rec()	The reciprocal of a fraction
diag()	The diagonal matrix of the signum function
$\mathcal{G}\left(\mathcal{V},\mathcal{E},\mathcal{A}\right)$	The communication topology of multi-UAV systems
$\mathcal{A}$	The adjacency matrix of multi-UAV systems
L	The Laplacian matrix of $\mathcal{G}$
$\mathcal{D}$	The weighted degree matrix of signed graph
${\mathbf{D}}_t^{p}f\left(t\right)$	The three types of derivatives including GLDs, RLDs and CDs
$r_i\left(t\right),v_i\left(t\right),u_i\left(t\right)$	The position, velocity and control input of i-$\mathrm{t}\mathrm{h}$ UAV
$f_i(r_i,t)$	The unknown external disturbance imposed on position-loop
$g_i(r_i,v_i,t)$	The unknown external disturbance imposed on velocity-loop
$r_0\left(t\right)$	The position variable of target
$e_{ri}$,$e_{vi}$	The bipartite tracking errors of position-loop and velocity-loop
$\beta (r,t)$	The fractional-order dynamics model of target
${\varphi }_{\beta }^T(r,t)$	The Gaussian basis functions for estimation
${\epsilon }_{\beta }$	The approximation error based on neural network
$u_{i0}$	The nominal control input of system
${\widehat{g}}_i$	The estimates of unknown disturbance
${\mathcal{L}}^{-1}$	The inverse Laplace transformation
$G_d\left(s\right)$	A first-order filter
${\tau }_d$	The time scale parameter
${\alpha }_i(u_i,t)$	A virtual control input
${\widehat{f}}_i$	The estimate of uncertain part $f_i$
$F_i\left(s\right)$	The frequency domain expression of $f_i$
$\widetilde{f_i}$	The estimation error of $f_i$
$x_{i1}$,$x_{i2}$	The coordination transformations for constructing controller
$u_{i1}$,$u_{i2}$,$u_{i3}$	The three parts of controller
${\tilde{\theta }}_{\beta i}$	The parameter estimation error
${\tilde{e}}_{vi}$	The bipartite velocity tracking error
${\dot{\widehat{\theta }}}_{\beta i}^{}$,${\dot{\widehat{\delta }}}_{\beta i}^{}$	The adaptive law
$X_1$,$X_2$	The coordination transformations in a compact form
$k_r$, $k_v$	The control gains
$k_{\theta },k_{\delta }$	The adaptive law parameters
$V_1$	The Lyapunov function for proof
${\lambda }_{max}$, ${\lambda }_{min}$	The maximum and minimum eigenvalue of matrix $L+B$

. In addition, ${\mathbf{col}}_i^n\left[{\alpha }_i\right]\triangleq {[{\alpha }_1^T,{\alpha }_2^T,\dots ,{\alpha }_n^T]}^T$ or ${\mathbf{col}}^n\left[\alpha \right]\triangleq {[{\alpha }^T,{\alpha }^T,\dots ,{\alpha }^T]}_n^T$ generates a vector in the form of a column. The vector ${\mathbf{1}}_n$ is thus represented as ${\mathbf{1}}_n\triangleq {\mathbf{col}}^n\left[1\right]$.

2.1. Graph Theory

Graph theory is generally used as a mathematical method to explain a multi-UAV system communication network. The relationship between diverse agents is represented by a signed bipartite graph. Signed graph $\mathcal{G}\left(\mathcal{V},\mathcal{E},\mathcal{A}\right)$ can be capable of illustrating the communication topology of multi-agent systems, in which $\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}$ denotes edge sets, while $\mathcal{V}$ indicates node sets. For the expression of an n agents system, a finite index set $\mathcal{I}=\{1,\dots ,n\}$ is defined for it. $(s_i,s_j)$ signifies an edge-linked i and j in a signed graph, where $s_i$ and $s_j$ denote the nodes of agents i and j, respectively. Since this paper mainly studies undirected graphs, only undirected graphs are introduced here; therein, the relationship between $(i,j)\in \mathcal{E}$ and $(j,i)\in \mathcal{E}$ is equivalent, indicating that agent i and j are interconnected directly. Adjacent matrix $\mathcal{A}$ can represent the connection relationship between agents in terms of $\left[a_{ij}\right]\in {\mathbb{R}}^{n\times n}$, in which $a_{ii}=0$ for all $i\in \mathcal{I}$. In addition, $a_{ij}>0$ if $(s_i,s_j)\in \mathcal{E}$ and $j\ne i$ represent the convergence interaction between agents i and j, and that corresponds to $a_{ij}<0$ if $(s_i,s_j)\in \mathcal{E}$ and $j\ne i$, which indicates a divergence relationship for the linked agents. Generally, it is assumed that there exists at least a node, called the root, which can connect every other node in a signed graph; namely the signed graph is regarded as including a spanning tree.

Structurally balanced signed graphs are important for bipartite consensus, meaning that the node set $\mathcal{V}$ of a signed graph $\mathcal{G}\left(\mathcal{V},\mathcal{E},\mathcal{A}\right)$ can be separated into two distinct groups, ${\mathcal{V}}_a$ and ${\mathcal{V}}_b$, i.e., both of which satisfies ${\mathcal{V}}_a\cup {\mathcal{V}}_b=\mathcal{V}$, and ${\mathcal{V}}_a\cap {\mathcal{V}}_b=⌀$, that is $a_{ij}>0,\forall v_i,v_j\in {\mathcal{V}}_m$, or $\forall v_i,v_j\in {\mathcal{V}}_n$, and $a_{ij}<0$$\forall v_i\in {\mathcal{V}}_m,\forall v_j\in {\mathcal{V}}_n$ where $m\ne n$, and $m,n\in \{a,b\}$. $\mathcal{W}$, a signature matrix, is constructed in such a form that $\mathcal{W}=diag\left\{w_1,w_2,\dots ,w_n\right\}$, where $w_i=1,\forall v_i\in {\mathcal{V}}_m$ and $w_i=-1,\forall v_i\in {\mathcal{V}}_n$ where $m\ne n$. In addition, there exists an extra agent called "target" whose number index is 0, if the state of agent i and the target eventually achieves tracking convergence, then $w_i=1$; otherwise, if both eventually achieve divergence, $w_i=-1$. Additionally, the multi-UAV systems’ Laplacian matrix L is defined as follows

$$L=\mathcal{D}-\mathcal{A},$$

(1)

where $\mathcal{D}$ is a weighted degree matrix of a signed graph and specifically signifies $\mathcal{D}=\mathrm{diag}\{d_1,...,d_n\}$, therein $d_i={\sum }_{j=1}^n\left|a_{ij}\right|$.

2.2. Fractional Derivatives

First, we will provide two notable symbols related to the definition of fractional calculus in this section. One is the Euler’s Gamma function formulated by

$$\beta \left(p\right)={\int }_0^{\infty }{e}^{-t}{t}^{p-1}dt,$$

(2)

and the other is the generalized Newton’s binomial coefficient:

$${\mathcal{C}}_k^p=\frac{\beta (p+1)}{\beta (k+1)\beta (p-k+1)}.$$

(3)

Consequently, there are three definitions of arbitrary-order derivatives, including Grünwald–Letnikov Derivatives (GLDs), Riemann–Liouville Derivatives (RLDs) and Caputo Derivatives (CDs).

Definition 1 

(GLDs [36]). The fractional order $p\in \mathbb{R}$ of GLDs is taken as:

$${{}_a{}^{GL}\mathbf{D}}_t^{p}f\left(t\right)=\underset{\begin{array}{c}h\to 0\\ nh=t-a\end{array}}{lim}{h}^{-p}\sum _{r=0}^n{\mathcal{C}}_r^{-p}f(t-rh),$$

(4)

in which a is the GLDs’ base point.

Definition 2 

(RLDs [36]). The fractional order $p\in \mathbb{R}$ of RLDs is adopted as

$${{}_a{}^{RL}\mathbf{D}}_t^{p}f\left(t\right)=\left\{\begin{array}{ccc}\frac{1}{\beta (-p)}{\int }_a^t{(t-\tau )}^{-p-1}f\left(\tau \right)d\tau \hfill & \hfill while& p<0\hfill \\ f\left(t\right)\hfill & \hfill while& p=0\hfill \\ \frac{d^m}{d{t}^m}{{}_a{}^{RL}\mathbf{D}}_t^{p-m}f\left(t\right)\hfill & \hfill while& p>0\hfill \end{array}\right.,$$

(5)

where integer m confines the range of p such that $m-1<p\le m$, and similarly a is RLDs’ base point.

Definition 3 

(CDs [36]). Define the fractional order $p\in \mathbb{R}$ of CDs as

$${{}_a{}^C\mathbf{D}}_t^{p}f\left(t\right)=\frac{1}{\beta (m-p)}{\int }_a^t{(t-\tau )}^{m-p-1}{f}^{\left(m\right)}\left(\tau \right)d\tau ,$$

(6)

therein, correspondingly, integer m constrains the range of p such that $m-1<p\le m$, and a is the CDs’ base point.

For the simplification and standardization of the description, in this paper, the notation ${\mathbf{D}}_t^{p}f\left(t\right)$ is utilized to represent all three types of derivatives defined above, GLDs, RLDs and CDs, respectively. The fractional derivatives ${\mathbf{D}}_t^{p}f\left(t\right)$ have the following common properties.

Property 1. 

${\mathbf{D}}_t^{p}f\left(t\right)$ satisfies both homogeneity and additivity [36]:

$${\mathbf{D}}_t^p\left(\alpha f\left(t\right)+\beta g\left(t\right)\right)=\alpha {\mathbf{D}}_t^{p}f\left(t\right)+\beta {\mathbf{D}}_t^{p}g\left(t\right).$$

(7)

Property 2. 

${\mathbf{D}}_t^{p}f\left(t\right)$ follows the composition rule [36]:

$${\mathbf{D}}_t^p\left({\mathbf{D}}_t^{r}f\left(t\right)\right)={\mathbf{D}}_t^{p+r}f\left(t\right).$$

(8)

Property 3. 

${\mathbf{D}}_t^{p}f\left(t\right)$ can expand fractional derivatives into integer derivatives [37]:

$${\mathbf{D}}_t^{p}f\left(t\right)=\sum _{\lambda =0}^{\infty }{\mathcal{C}}_{\lambda }^p\frac{t^{\lambda -p}}{\beta (\lambda -p+1)}\frac{d^{\lambda }}{d{t}^{\lambda }}f\left(t\right).$$

(9)

2.3. Problem Description

As mentioned above, swarm intelligence can also be performed in heterogeneous systems. Thus multi-agent systems we study contain two kinds of heterogeneous agents, namely integer-order UAV and fractional-order targets. Among the mixed-order systems, partial UAVs are capable of sensing and knowing the position information of the target. The following uncertain nonlinear systems establish the dynamics of the i-$\mathrm{t}\mathrm{h}$ UAV from 1 to n.

$$\left\{\begin{array}{c}{\dot{r}}_i\left(t\right)=v_i\left(t\right)+f_i(r_i,t)\hfill \\ {\dot{v}}_i\left(t\right)=u_i\left(t\right)+g_i(r_i,v_i,t),i\in \mathcal{I},\hfill \end{array}\right.$$

(10)

where $r_i\left(t\right),v_i\left(t\right),u_i\left(t\right)\in {\mathbb{R}}^n$ denote the position, velocity and control input of i-$\mathrm{t}\mathrm{h}$ UAV, respectively, and index $\mathcal{I}$ satisfies $\mathcal{I}=(1,2,...,n)$. $f_i(r_i,t)\in {\mathbb{R}}^n$ and $g_i(r_i,v_i,t)\in {\mathbb{R}}^n$ are unknown smooth functions for UAVs. More concretely, $f_i(r_i,t)={\Delta }_1{r}_i\left(t\right)+{\kappa }_{i1}\left(t\right)$, where ${\Delta }_1{r}_i\left(t\right)\in {\mathbb{R}}^n$ denotes the model uncertainty and ${\kappa }_{i1}\left(t\right)\in {\mathbb{R}}^n$ is an unknown external disturbance input imposed on position-loop; $g_i(r_i,v_i,t)={\Delta }_2{r}_i\left(t\right)+{\Delta }_3{v}_i\left(t\right)+{\kappa }_{i2}\left(t\right)$, where ${\Delta }_2{r}_i\left(t\right)\in {\mathbb{R}}^n$ and ${\Delta }_3{v}_i\left(t\right)$ denote the model uncertainties and ${\kappa }_{i2}\left(t\right)\in {\mathbb{R}}^n$ is an unknown external disturbance input imposed on velocity-loop. Moreover, ${\Delta }_1{r}_i\left(t\right)\in {\mathbb{R}}^n$ and ${\Delta }_2{r}_i\left(t\right)\in {\mathbb{R}}^n$ also refer to the linearization of the function at time t.

Additionally, there is a target index 0 inside the mixed-order systems (10) since the dynamics of the target are inconsistent with other UAVs’ inside environment among multi-UAV systems, especially target could move in some special environments (often cannot be modeled in the form of integer order). Consequently, the fractional-order dynamics model of the target is described as follows:

$${\mathbf{D}}_t^q{r}_0\left(t\right)=f_0(r_0\left(t\right),t),$$

(11)

in which the fractional order q is confined so that $0<q\le 2$, and all other UAVs are not able to attain the smooth function $f_0(r_0\left(t\right),t)$. $r_0\left(t\right)$ is the target’s position variable.

Definition 4 

(Bipartite Tracking Consensus Error). In terms of the bipartite tracking consensus issue of the second-order nonlinear system, we define the position error $e_{ri}$ and velocity error $e_{vi}$ of the multi-agent system for subsequent controller design. All the bipartite tracking errors of position-loop and velocity-loop are satisfied using the following

$$e_{ri}=\sum _{j=1}^n\left|a_{ij}\right|(r_i-\mathrm{sgn}\left(a_{ij}\right)r_j)+b_i(r_i-w_i{r}_0),$$

(12)

$$e_{vi}=\sum _{j=1}^n\left|a_{ij}\right|({\dot{r}}_i-\mathrm{sgn}\left(a_{ij}\right){\dot{r}}_j)+b_i({\dot{r}}_i-w_i{\dot{r}}_0),$$

(13)

where $b_i>0$ means that i-$th$ UAV is able to receive information from the target directly; if not, $b_i=0$. A diagonal matrix $B=$$diag\left\{b_1,b_2,\dots ,b_n\right\}$. The bipartite tracking error of the position-loop defined above includes the sum of the position error between adjacent UAVs and the error between the target and UAVs, and the bipartite tracking errors of the velocity-loop have the same definition.

Remark 1. 

From the expression of the model dynamics, it is known that the i-$th$ UAVs suffer from the effect of disturbances caused by unknown smooth functions $f_i(r_i,t)$ and $g_i(r_i,v_i,t)$. The disturbances in the model can be regarded as the superposition of input disturbance and process disturbance. The input disturbance refers to the external input disturbance outside the nominal model, such as disturbance force and torque. Process disturbance refers to model uncertainty and process noise between the real and nominal models.

Involved in the dynamics model of UAVs, the smooth function $f_i(r_i,t)$ is the disturbance imposed on the system (10), which satisfies the following assumption:

Assumption 1. 

It is assumed that the uncertain parts imposed on each UAV are represented by a smooth function $f_i(r_i,t)$, which is bounded and unkown to all UAVs, i.e., $\exists \overline{f}>0$ and $\overline{f_d}>0$, satisfy conditions that $\left|f_i(r_i,t)\right|\le \overline{f}$ and $\left|{\dot{f}}_i(r_i,t)\right|\le \overline{f_d}$ with regard to $\forall i\in \mathcal{I}$. The upper bounds $\overline{f}$ and $\overline{f_d}$ are not required to be known. The unknown smooth function $g_i(r_i,v_i,t)$ has similar properties, which implies $\exists \overline{g}>0$ and ${\overline{g}}_d>0$, such that $\left|g_i(r_i,v_i,t)\right|\le \overline{g}$ and $\left|{\dot{g}}_i(r_i,v_i,t)\right|\le {\overline{g}}_d$ as for $\forall i\in \mathcal{I}$, $\overline{g}$ and $\overline{g_d}$ are also unknown upper bounds.

Then, this paper defines that $t=0$ indicates the initial start time; thus $r_i\left(0\right)$ and $v_i\left(0\right)$ represent the initial position and initial velocity, respectively. Based on this, the derivative ${\mathbf{D}}_t^q$’s base point is adopted as 0. It is worth noting that the primary aim of this paper is to design a robust controller for the UAVs with uncertainty and achieve bipartite tracking. Hence the relevant definitions of the distributed tracking control and graph weight coefficient with the target are expressed by the following:

Definition 5 

(Bipartite Tracking Control). The designed control input protocol $u_i\left(t\right)$ in (10) could achieve bipartite tracking control if all of the local bipartite tracking errors satisfy

$$\begin{array}{c}\underset{t\to \infty }{lim}\left|r_i\left(t\right)-w_i{r}_0\left(t\right)\right|=0,\hfill \end{array}$$

(14)

namely, all the UAVs are diverged into two subgroups based on the structurally balanced signed graphs, one subgroup tracks the trajectory of the target, and the other tracks the symmetrical trajectory with respect to the origin, i.e.

In respect to the bipartite tracking control issues, the critical challenges are summarized as:

(I)

In this heterogeneous system, both the target and the UAVs exist as uncertainties, including the target’s dynamics model and the UAV’s unknown parts, $f_i(r_i,t)$ and $g_i(r_i,v_i,t)$. Consequently, traditional methods based on known reference signals and standard feedback linearization methods have been unable to solve such synthesis problems.

(II)

The proposed system simultaneously has disturbance-unmatched and order-unmatched problems, namely, unknown disturbance exists in both the position-loop and velocity-loop; furthermore, integer-order and fractional-order agent (target and UAVs) models exist at the same time. Hence, the control protocol design should take into account both kinds of unmatched issues.

3. Bipartite Tracking Control via NNCUDE

In order to cope with the critical challenges of the bipartite tracking problem, we propose a new control scheme, NNCUDE, in which NN is adopted to estimate the uncertainties of the fractional target’s dynamics model. Since there are uncertain parts, $f_i$ and $g_i$, we innovatively propose cascade UDE to estimate the uncertain smooth functions. The state information of the model is fully used to obtain the estimates of the disturbance. Meanwhile, the virtual input imposed on the velocity loop is designed using the backstepping method, and the stability analysis of the closed-loop error system is explained by proper coordinate transformation.

3.1. The Approximation of Target’s Dynamics by Neural Network

Due to the uncertainty of the target’s nonlinear fractional-order model, the first stage is to eliminate the uncertainty by obtaining the estimates of the unknown smooth function in the target’s dynamics (11). Therefore, we make the following assumptions to utilize conventional linearly parameterized neural networks to approximate the true values of the unknown function:

Assumption 2. 

To simplify the fractional-order dynamics model, the following equivalent substitution is adopted such that $\beta (r,t)\triangleq {\mathbf{D}}_t^{1-q}{f}_0(r_0\left(t\right),t)$. Based on a linearly parameterized neural network, $\beta (r,t)$ could be represented on a prescribed compact set ${\mathsf{\Omega }}_{\beta }\subset {\mathbb{R}}^2$ as follows

$$\beta (r,t)={\varphi }_{\beta }^T(r,t){\theta }_{\beta }+{\epsilon }_{\beta },$$

(15)

where ${\varphi }_{\beta }^T(r,t)={\mathit{col}}_k^{h_{\beta }}\left[{\varphi }_{\beta ,k}(r,t)\right]\in {\mathbb{R}}^{h_{\beta }}$ is the known basis function, therein $h_{\beta }$ is the vector dimension; an unknown constant vector ${\theta }_{\beta }$ defines that ${\theta }_{\beta }={\mathit{col}}_k^{h_{\beta }}\left[{\theta }_{\beta ,k}\right]\in {\mathbb{R}}^{h_{\beta }}$; the approximation error based on the neural network is expressed as ${\epsilon }_{\beta }$.

Generally speaking, a RBF neural network with Gaussian basis functions is applied for the estimation of smooth function $\beta (r,t)$ as follows:

$${\varphi }_{\beta }^T(r,t)=e^{-\frac{{(r-{\mu }_{\beta r,k})}^2+{(t-{\mu }_{\beta t,k})}^2}{{\eta }_{\beta ,k}^2}},k\in \{1,2,\dots ,h_{\beta }\},$$

(16)

where r is the n-dimensional input vector; ${\eta }_{\beta ,k}$ is the smooth parameter, which determines the widths of the center point of the basis function; $({\mu }_{\beta r,k},{\mu }_{\beta t,k})$ is the center of the basis function, which evenly needs space in a specific range; and $h_{\beta }$ is the number of perception nodes.

Remark 2. 

To guarantee that the input of the RBF neural network stays in the effective range of the Gaussian basis function, the center coordinate vector $({\mu }_{\beta r,k},{\mu }_{\beta t,k})$ of the Gaussian basis function should be determined by the actual range of the input value. To ensure the effective mapping of the Gaussian basis function, the width ${\eta }_{\beta ,k}$ of the Gaussian basis function should be set to an appropriate value. Once the suitable parameters of the basis function are selected, the receptive fields would be able to approximate the unknown function $\beta (r,t)$. Additionally, in accordance with the chain rule [36] of fractional derivatives, the smoothness of $\beta (r,t)$ has been maintained by that of $f_0(r_0,t)$.

To facilitate the subsequent analysis, $\widehat{s}$ is defined as the estimate of s, and the difference between both indicates $\tilde{s}\triangleq \widehat{s}-s$, which is the estimation error. Correspondingly, by means of the RBF neural network, the estimate of smooth function ${\beta }_i(r,t)$ by i-th UAV would be obtained, expressed as ${\widehat{\beta }}_i(r,t)\triangleq {\varphi }_{\beta }^T(r,t){\widehat{\theta }}_{\beta i}$, and then the neural network approximation error by i-th UAV is ${\tilde{\beta }}_i(r,t)$. Moreover, it is noteworthy that the adjustment of parameter ${\widehat{\theta }}_{\beta i}$ is designed by the Lyapunov stability analysis.

The RBF network is capable of accomplishing the approximation of any nonlinear function with any accuracy [38]. Meanwhile, the approximation error will appear accordingly. The effect of it on the control precision will also be considered in the follow-up controller design. Here, we make the following assumption in terms of the common approximation result in [39] about the estimation error:

Assumption 3. 

The i-th UAV approximation error ${\epsilon }_{\beta i}$ of neural network estimation is bounded and satisfies $|{\epsilon }_{\beta i}|\le {\delta }_{\beta i}$ in the relevant compact set ${\mathsf{\Omega }}_{\beta i}$, where ${\delta }_{\beta i}$ is an unknown positive constant.

3.2. The Approximation of Unknown Disturbances by CUDE

The subsection will explain the working principle of cascade Uncertainty and Disturbance Estimator (CUDE) to achieve the approximation of unknown unmatched disturbances imposed on UAVs. We initially design the estimation ${\widehat{g}}_i$ of unknown function $g_i$ based on Zhong’s UDE method (2004) [40], such that the control protocol $u_i$ is divided into two parts:

$$u_i=u_{i0}-{\widehat{g}}_i,$$

(17)

where $u_{i0}$ is the nominal control input that helps the system achieve its goal.

By means of the designing process of UDE, the estimates of disturbance can be constructed as

$$\begin{array}{c}{\widehat{g}}_i={\mathcal{L}}^{-1}\left\{G_d\left(s\right)\right\}({\dot{v}}_i-u_i)\hfill \end{array},$$

(18)

where $G_d\left(s\right)$ is a filter to ensure the physical realizability of the system (18), and ${\mathcal{L}}^{-1}$ indicates the inverse Laplace transformation. Generally speaking, if the bandwidth can cover the bandwidth range of the disturbance signal by properly designed parameters about $G_d\left(s\right)$, the estimation of the unknown disturbance can be better realized. A first-order filter that can satisfy physical realizability is adopted, namely, to reduce the computational amount and the complexity of the controller. That is,

$$G_d\left(s\right)=\frac{1}{1+{\tau }_{d}s},$$

(19)

where ${\tau }_d$ is the time scale parameter of the above-mentioned first-order filter and a small positive value, which determines the approximation performance of the UDE by appropriate selection. The ultimate goal is to cover the spectrum of the unknown part $g_i$ with the bandwidth of the filter $G_d\left(s\right)$. Hence, the estimates of unknown smooth function ${\widehat{g}}_i$ can be written as

$$\begin{array}{c}\hfill {\widehat{g}}_i(r_i,v_i,t)={\mathcal{L}}^{-1}\left\{\frac{1}{1+{\tau }_{d}s}\right\}({\dot{v}}_i\left(t\right)-u_{i0}\left(t\right)+{\widehat{g}}_i(r_i,v_i,t)).\end{array}$$

(20)

Convert (20) to the frequency domain

$$\begin{array}{c}\hfill {\widehat{G}}_i\left(s\right)=\frac{1}{1+{\tau }_{d}s}(s{V}_i\left(s\right)-U_{i0}\left(s\right)+{\widehat{G}}_i\left(s\right)),\end{array}$$

(21)

then, simplify it to get

$$\begin{array}{c}\hfill {\widehat{G}}_i\left(s\right)=\frac{1}{{\tau }_{d}s}(s{V}_i\left(s\right)-U_{i0}\left(s\right)).\end{array}$$

(22)

if reconverted to the time domain, one gets

$$\begin{array}{c}\hfill {\widehat{g}}_i(r_i,v_i,t)=\frac{1}{{\tau }_d}(v_i\left(t\right)-v_i\left(0\right)-{\int }_0^t{u}_{i0}\left(\tau \right)d\tau ),\end{array}$$

(23)

where $v_i\left(0\right)$ is the initial velocity of the UAV, and the nominal control input $u_{i0}$ would be known, whose specific form of expression through the subsequent design.

From the above, one can conclude that the basic principle of UDE is to utilize the filtered information of the state variable and control input in the closed-loop (here it is Equation (17)) to construct an estimator that gradually approaches the actual value of the unknown part therein. Using a similar idea, we can design the estimation ${\widehat{f}}_i$ of $f_i$, where, according to the aspect of view of backstepping control, the state ${\alpha }_i\left(t\right)$ in (24) can be taken as a virtual control input ${\alpha }_i(u_i,t)$, which is determined by the actual controller $u_i$ from (17), and can be divided into two parts:

$${\alpha }_i\left(t\right)={\alpha }_{i0}\left(t\right)-{\widehat{f}}_i(r_i,t),$$

(24)

where ${\alpha }_{i0}$ is the nominal input of the virtual controller guaranteeing the convergence of state $r_i$ to its desired value. With the help of (19), the estimate of the uncertain part $f_i$ is similarly designed by

$$\begin{array}{cc}\hfill {\widehat{f}}_i(r_i,t)& ={\mathcal{L}}^{-1}\left\{\frac{1}{1+{\tau }_{d}s}\right\}({\dot{r}}_i\left(t\right)-{\alpha }_{i0}\left(t\right)+{\widehat{f}}_i(r_i,t)).\hfill \end{array}$$

(25)

Through the transformation between the time domain and the frequency domain, one gets

$$\begin{array}{c}\hfill {\widehat{f}}_i(r_i,t)=\frac{1}{{\tau }_d}(r_i\left(t\right)-r_i\left(0\right)-{\int }_0^t{\alpha }_{i0}\left(\tau \right)d\tau ),\end{array}$$

(26)

where $r_i\left(0\right)$ is the initial position of the UAV, and the nominal virtual control input ${\alpha }_{i0}$ would be known, which is designed later.

Remark 3. 

Since the information of the virtual input ${\alpha }_{i0}$ in (24) is determined by $u_i$, the two UDEs for uncertainties that appeared in the differential functions are cascades. Thus we call them the cascade UDEs.

Taking $f_i$ as an example, we analyze the properties of $\widehat{f_i}$ and put forward the subsequent analysis and proof of the corresponding Lemma. The unknown smooth function $f_i(r_i,t)={\Delta }_1{r}_i\left(t\right)+{\kappa }_{i1}\left(t\right)$ is given from the previous statement. The components of this function can be expressed as ${\Delta }_1{R}_i\left(s\right)$ and ${\mathrm{K}}_{i1}\left(s\right)$ in the frequency domain, so the function in the frequency domain $F_i\left(s\right)={\Delta }_1{R}_i\left(s\right)+{\mathrm{K}}_{i1}\left(s\right)$. Through this design, the uncertain parts $f_i$ and the corresponding estimates $\widehat{f_i}$ are represented in the frequency domain.

$${\widehat{F}}_i\left(s\right)=G_d\left(s\right)F_i\left(s\right).$$

(27)

The estimation error $\widetilde{f_i}$ is defined in the time domain as

$$\widetilde{f_i}=f_i-\widehat{f_i},$$

(28)

we then substitute (19) and (28) into (27),

$${\tau }_{d}s{\tilde{F}}_i\left(s\right)+{\tilde{F}}_i\left(s\right)={\tau }_{d}s{F}_i\left(s\right),$$

(29)

then transform (29) into the time domain and find the relationship between the estimation error $\widetilde{f_i}$ and $f_i$

$$\dot{\widetilde{f_i}}=-\frac{1}{{\tau }_d}\widetilde{f_i}+{\dot{f}}_i.$$

(30)

Lemma 1 

(Lemma 3 in [41]). Under Assumption 1, relationship (30) possesses the three properties shown below:

(1) $\widetilde{f_i}$ is uniformly bounded as t tends to infinity and satisfies

$$\underset{t\to \infty }{lim}\left|{\tilde{f}}_i(r_i,t)\right|\le {\tau }_d{\overline{f}}_d,$$

(31)

where ${\overline{f}}_d$ is a bounded positive value.

(2) For $\forall t\ge 0$, $\widetilde{f_i}$ is limited by $max(\left|{\tilde{f}}_{i0}\right|,{\tau }_d{\overline{f}}_d)$, which satisfies

$$\left|{\tilde{f}}_i(r_i,t)\right|\le max(\left|{\tilde{f}}_i\left(0\right)\right|,{\tau }_d{\overline{f}}_d),\forall t\ge 0,$$

(32)

where ${\tilde{f}}_i\left(0\right)$ is the initial estimation error while $t=0$.

(3) if the function $f_i$ is decaying, and ${\displaystyle \underset{t\to \infty }{lim}}{\dot{f}}_i(r_i,t)=0$, then

$$\underset{t\to \infty }{lim}{\tilde{f}}_i(r_i,t)=0.$$

(33)

Remark 4. 

Considering that unknown smooth functions $f_i$ and $g_i$ have similar properties, we use the same first-order inertial filter $G_d\left(s\right)$ based on UDE, and the derivative of the final estimate satisfies $\dot{\widetilde{g_i}}=-\frac{1}{{\tau }_g}\widetilde{g_i}+{\dot{g}}_i$. Moreover, Lemma 1 is also applied for $g_i$; that is, it satisfies ${\displaystyle \underset{t\to \infty }{lim}}\left|{\tilde{g}}_i(r_i,v_i,t)\right|\le {\tau }_d{\overline{g}}_d$, where $\widetilde{g_i}$ is uniformly bounded with ultimate bound ${\tau }_d{\overline{g}}_d$ while t tends to infinity; $\left|{\tilde{g}}_i(r_i,t)\right|\le max(\left|{\tilde{g}}_{i0}\right|,{\tau }_d{\overline{g}}_d),\forall t\ge 0$; and if ${\displaystyle \underset{t\to \infty }{lim}}{\dot{g}}_i(r_i,v_i,t)=0$, then ${\displaystyle \underset{t\to \infty }{lim}}{\tilde{g}}_i(r_i,v_i,t)=0.$

Lemma 1 and Remark 4 reveal the relationship between the time scale parameter ${\tau }_d$ and the estimation error $\widetilde{f_i}$. Simply speaking, a smaller time scale parameter can ensure a smaller estimation error, but at the same time, attention should be paid to the impact of accompanying noise.

3.3. Backstepping Controller Design

A robust adaptive control structure based on the backstepping scheme is given in this subsection for the mixed-order systems (10) and (11) under a signed graph. Then, the following coordination transformations are adopted for constructing the proposed controller,

$$\left\{\begin{array}{c}{x}_{i1}=r_i-w_i{r}_0\hfill \\ x_{i2}=v_i-{\alpha }_i\hfill \end{array},\right.$$

(34)

where $x_{i1}$ is the bipartite tracking error, and $x_{i2}$ represents the difference between virtual control and true velocity.

Combining (34) and (10), one takes the derivative of $x_{i1}$ and yields

$$\begin{array}{cc}\hfill {\dot{x}}_{i1}& ={\dot{r}}_i-w_i{\dot{r}}_0\hfill \\ \hfill & =v_i+f_i-w_i{\beta }_i\hfill \\ \hfill & =x_{i2}+{\alpha }_i+f_i-w_i{\beta }_i.\hfill \end{array}$$

(35)

Then, we construct a reference virtual control input ${\alpha }_i$ in position-loop:

$${\alpha }_i={\alpha }_{i0}-{\widehat{f}}_i=-k_r{e}_{ri}+w_i\widehat{{\beta }_i}-{\widehat{f}}_i,$$

(36)

where $k_r$ is the control gain and ${\widehat{f}}_i$ is the estimate of an unknown smooth function $f_i$. According to the universal approximation property of NN, $\widehat{{\beta }_i}\left(r_i,t\right)={\varphi }_{\beta }^T(r_i,t){\widehat{\theta }}_{\beta i}$, and define the derivative of $\widehat{{\beta }_i}$ to be $\dot{\widehat{{\beta }_i}}$, accordingly,

$$\dot{\widehat{{\beta }_i}}\left(r_i,t\right)={\varphi }_{\beta }^T(r_i,t){\dot{\widehat{\theta }}}_{\beta i}+\frac{\partial }{\partial r}{\varphi }_{\beta }^T(r_i,t){\widehat{\theta }}_{\beta i}+\frac{\partial }{\partial t}{\varphi }_{\beta }^T(r_i,t){\widehat{\theta }}_{\beta i},$$

(37)

Similarly, one has

$$\begin{array}{c}\hfill {\dot{x}}_{i2}={\dot{v}}_i-{\dot{\alpha }}_i=u_i+g_i-{\dot{\alpha }}_i,\end{array}$$

(38)

where $u_i$ is the true whole control input. In order to achieve ${lim}_{t\to \infty }\left|v_i-{\alpha }_i\right|=0$, the control input $u_i$ can be designed as

$$\begin{array}{c}{u}_i=\underset{u_{i1}}{\underbrace{-k_v{x}_{i2}-e_{ri}-k_r{\widehat{e}}_{vi}}}\underset{u_{i2}}{\underbrace{-{\widehat{g}}_i-{\zeta }_i}}+\underset{u_{i3}}{\underbrace{w_i\stackrel{.}{\widehat{{\beta }_i}}-rec\left({\mathsf{\Theta }}_i\right){\widehat{\delta }}_{\beta i}^{}}},\end{array}$$

(39)

The controller can be divided into three parts in terms of its function. The first part is the basis controller, which is able to achieve bipartite consensus tracking control without uncertainties and neural network approximation errors, where $k_r$ and $k_v$ are both the control gain and ${\widehat{e}}_{vi}$ is the estimate of velocity error $e_{vi}$ through replacing $\dot{r_i}$, ${\dot{r}}_0$ with ${\widehat{\dot{r}}}_i$, ${\widehat{\dot{r}}}_0$, respectively.

The second part is to compensate for the uncertainties imposed on the UAVs, where ${\widehat{g}}_i$ is the estimate of unknown smooth function $g_i$, and the derivative of ${\widehat{f}}_i$ holds ${\dot{\widehat{f}}}_i(r_i,t)=\frac{1}{{\tau }_d}(v_i+f_i)-{\alpha }_{i0}\left(t\right)$ under Equation (26), which is not completely known, thus its estimates are obtained as ${\zeta }_i(r_i,t)=\frac{1}{{\tau }_d}(v_i+{\widehat{f}}_i)-{\alpha }_{i0}\left(t\right)$.

The third part is target oriented, where the first item is the estimation of the second derivative of the target’s position state; the second item considers the effect of the neural network approximation errors, ${\mathsf{\Theta }}_i$ takes the form

$${\mathsf{\Theta }}_i=\frac{x_{i2}}{\left|e_{ri}+k_r{y}_i\right|}.$$

(40)

In addition, the elements of $y_i$ satisfy $y_i={\sum }_{j=1}^n\left(\left|a_{ij}\right|+\left|b_i\right|\right)(v_i-{\alpha }_{i0})-{\sum }_{j=1}^n{a}_{ij}(v_j-{\alpha }_{j0})$.

Substituting ${\alpha }_i$ and $u_i$ into the coordinate transformation (34), we get the closed-loop error system as follows,

$$\begin{array}{c}{\dot{x}}_{i1}=x_{i2}-k_r{e}_{ri}+{\tilde{f}}_i+w_i{\varphi }_{\beta }^T(r_i,t){\tilde{\theta }}_{\beta i}-w_i{\epsilon }_{\beta i},\hfill \\ {\dot{x}}_{i2}=-k_v{x}_{i2}-e_{ri}+{\tilde{g}}_i-\frac{1}{{\tau }_d}{\tilde{f}}_i+k_r{\tilde{e}}_{vi}-rec\left({\mathsf{\Theta }}_i\right){\widehat{\delta }}_{\beta i}^{}.\hfill \end{array}$$

(41)

where ${\tilde{\theta }}_{\beta i}={\widehat{\theta }}_{\beta i}-{\theta }_{\beta i}$ represents the parameter estimation error, ${\tilde{f}}_i$ and ${\tilde{g}}_i$ represent the disturbance estimation error and ${\tilde{e}}_{vi}=e_{vi}-{\widehat{e}}_{vi}$ is expressed as the bipartite velocity tracking error.

For achieving error approximation, the adaptive law is derived as follows:

$$\begin{array}{cc}\hfill {\dot{\widehat{\theta }}}_{\beta i}^{}& =-k_{\theta }{w}_i{\varphi }_{\beta }^T(r_i,t)(e_{ri}+k_r{y}_i),\hfill \\ \hfill {\dot{\widehat{\delta }}}_{\beta i}^{}& =k_{\delta }\left|e_{ri}+k_r{y}_i\right|,\hfill \end{array}$$

(42)

where $k_{\theta }$ and $k_{\delta }$ are adjustable adaptive gain.

To simplify the analysis, the following closed-loop error system is obtained for the entire multi-UAV systems in a compact form; accordingly, we define that,

$$\begin{array}{cc}\hfill X_1& ={\mathbf{col}}_i^n{[x_{11},x_{12},...,x_{1n}]}^T,\hfill \\ \hfill X_2& ={\mathbf{col}}_i^n{[x_{21},x_{22},...,x_{2n}]}^T,\hfill \\ \hfill E_r& ={\mathbf{col}}_i^n{[e_{r1},e_{r2},...,e_{rn}]}^T\hfill \\ \hfill {\mathsf{\Phi }}_{\beta }^T(r,t)& ={\mathbf{col}}_i^n{\left[w_i{\varphi }_{\beta }^T(r_i,t)\right]}^T,\hfill \\ \hfill {\tilde{\theta }}_{\beta }& ={\mathbf{col}}_i^n{\left[{\tilde{\theta }}_{\beta i}\right]}^T,\hfill \\ \hfill {\mathsf{\Xi }}_{\beta }& ={\mathbf{col}}_i^n{\left[w_i{\epsilon }_{\beta }\right]}^T,\hfill \\ \hfill \mathsf{\Gamma }& ={\mathbf{col}}_i^n{\left[rec\left(\frac{x_{i2}}{\left|e_{ri}+k_r{y}_i\right|}\right){\widehat{\delta }}_{\beta i}^{}\right]}^T,\hfill \\ \hfill \tilde{F}& ={\mathbf{col}}_i^n{\left[{\tilde{f}}_i\right]}^T,\hfill \end{array}$$

(43)

Apparently, $E_r=(L+B)X_1$, $E_v=(L+B){\dot{X}}_1$ and ${\widehat{E}}_v=(L+B){\widehat{\dot{X}}}_1$, where ${\widehat{\dot{X}}}_1={\mathbf{col}}_i^n{[{\widehat{\dot{r}}}_i-w_i{\widehat{\dot{r}}}_0]}^T$$={\mathbf{col}}_i^n{[v_i+{\widehat{f}}_i-w_i{\widehat{\dot{r}}}_0]}^T$, and note that ${\tilde{E}}_v={\mathbf{col}}_i^n\left[{\tilde{e}}_{vi}\right]$. One gets the compact form of (41) as

$$\begin{array}{cc}\hfill {\dot{X}}_1& =X_2-k_r{E}_r+{\mathsf{\Phi }}_{\beta }^T(r,t){\tilde{\theta }}_{\beta }+\tilde{F}-{\mathsf{\Xi }}_{\beta },\hfill \\ \hfill {\dot{X}}_2& =-k_v{E}_v-E_r+k_r{\tilde{E}}_v+\tilde{G}-\frac{1}{{\tau }_d}\tilde{F}-\mathsf{\Gamma }.\hfill \end{array}$$

(44)

3.4. The Theoretical Validation of the Proposed Controller

Theorem 1. 

Controller $u_i$ designed by (36) with the adaptive law shown in (42), resolves the distributed bipartite tracking control problem defined by Definition 5 under Assumption 2 if the control gains $k_r$, $k_v$ and the adaptive law parameters $k_{\theta },k_{\delta }$ satisfy:

$$k_r>0,k_v>0,k_{\theta }>0,k_{\delta }>0.$$

(45)

Proof. 

The Lyapunov function is considered as:

$$\begin{array}{cc}\hfill V_1& =\frac{1}{2}{X}_1^T(L+B)X_1+\frac{1}{2}{X}_2^T{X}_2+\frac{1}{2k_{\theta }}\sum _{i=1}^n{\tilde{\theta }}_{\beta i}^2+\frac{1}{2k_{\delta }}\sum _{i=1}^n{\tilde{\delta }}_{\beta i}^2.\hfill \end{array}$$

(46)

Apparently, $V_1$ is positive definite, its derivative is

$$\begin{array}{cc}\hfill {\dot{V}}_1& =X_1^T(L+B){\dot{X}}_1+X_2^T{\dot{X}}_2+\sum _{i=1}^n{\tilde{\theta }}_{\beta i}^{}{\dot{\widehat{\theta }}}_{\beta i}^{}+\sum _{i=1}^n{\tilde{\delta }}_{\beta i}^{}{\dot{\widehat{\delta }}}_{\beta i}^{}\hfill \\ \hfill & =X_1^T(L+B)\left\{X_2+{\mathsf{\Phi }}_{\beta 1}^T(r,t){\tilde{\theta }}_{\beta }+\tilde{F}-{\mathsf{\Xi }}_{\beta }-k_r{E}_r\right\}+X_2^T\{-k_v{X}_2^{}\hfill \\ \hfill & -E_r+k_r{\tilde{E}}_v+\tilde{G}-\frac{1}{{\tau }_d}\tilde{F}-\mathsf{\Gamma }\}+\frac{1}{k_{\theta }}\sum _{i=1}^n{\tilde{\theta }}_{\beta i}^{}{\dot{\widehat{\theta }}}_{\beta i}^{}+\frac{1}{k_{\delta }}\sum _{i=1}^n{\tilde{\delta }}_{\beta i}^{}{\dot{\widehat{\delta }}}_{\beta i}^{}\hfill \\ \hfill & =-k_r{\left((L+B)X_1^{}\right)}^T\left((L+B)X_1^{}\right)+X_1^T(L+B)\{{\mathsf{\Phi }}_{\beta }^T(r,t){\tilde{\theta }}_{\beta }\hfill \\ \hfill & +\tilde{F}-{\mathsf{\Xi }}_{\beta }\}-k_v{X}_2^T{X}_2^{}+X_2^T(k_r{\tilde{E}}_v+\tilde{G}-\frac{1}{{\tau }_d}\tilde{F}-\mathsf{\Gamma })\hfill \\ \hfill & +\frac{1}{k_{\theta }}\sum _{i=1}^n{\tilde{\theta }}_{\beta i}^{}{\dot{\widehat{\theta }}}_{\beta i}^{}+\frac{1}{k_{\delta }}\sum _{i=1}^n{\tilde{\delta }}_{\beta i}^{}{\dot{\widehat{\delta }}}_{\beta i}^{}.\hfill \end{array}.$$

(47)

Noting that the following inequality holds

$$\begin{array}{cc}\hfill & -k_r{\left((L+B)X_1^{}\right)}^T\left((L+B)X_1^{}\right)⩽0,\hfill \\ \hfill & -k_v{X}_2^T{X}_2^{}⩽0.\hfill \end{array}$$

(48)

In terms of (48), (47) can be rewritten as:

$$\begin{array}{cc}\hfill {\dot{V}}_1& ⩽X_1^T(L+B)\left\{{\mathsf{\Phi }}_{\beta }^T(r,t){\tilde{\theta }}_{\beta }+\tilde{F}-{\mathsf{\Xi }}_{\beta 1}\right\}+X_2^T(k_r{\tilde{E}}_v+\tilde{G}-\frac{1}{{\tau }_d}\tilde{F}-\mathsf{\Gamma })\hfill \\ \hfill & +\frac{1}{k_{\theta }}\sum _{i=1}^n{\tilde{\theta }}_{\beta i}^{}{\dot{\widehat{\theta }}}_{\beta i}^{}+\frac{1}{k_{\delta }}\sum _{i=1}^n{\tilde{\delta }}_{\beta i}^{}{\dot{\widehat{\delta }}}_{\beta i}^{}.\hfill \end{array}$$

(49)

Under the definition of the bipartite tracking consensus error, it is known that

$$\begin{array}{cc}\hfill {\tilde{E}}_v& =E_v-{\widehat{E}}_v\hfill \\ \hfill & =(L+B){\dot{X}}_1-(L+B){\widehat{\dot{X}}}_1\hfill \\ \hfill & =(L+B){\mathbf{col}}_i^n{\left[({\dot{r}}_i-w_i{\dot{r}}_0-{\widehat{\dot{r}}}_i+w_i{\widehat{\dot{r}}}_0)\right]}^T\hfill \\ \hfill & =(L+B){\mathbf{col}}_i^n{\left[(f_i-w_i{\dot{r}}_0-{\widehat{f}}_i+w_i{\widehat{\dot{r}}}_0)\right]}^T\hfill \\ \hfill & =(L+B){\mathbf{col}}_i^n{\left[\left\{{\tilde{f}}_i+w_i{\varphi }_{\beta }^T(r_i,t)-w_i{\epsilon }_{\beta }\right\}\right]}^T\hfill \\ \hfill & =(L+B)\left\{\tilde{F}+{\mathsf{\Phi }}_{\beta }^T(r,t){\tilde{\theta }}_{\beta }-{\mathsf{\Xi }}_{\beta }\right\}.\hfill \end{array}$$

(50)

Combining (49) and (50), it can be derived that

$$\begin{array}{cc}\hfill {\dot{V}}_1& ⩽X_1^T(L+B)\left\{{\mathsf{\Phi }}_{\beta }^T(r,t){\tilde{\theta }}_{\beta }+\tilde{F}-{\mathsf{\Xi }}_{\beta }\right\}+X_2^T\{k_r(L+B)(\tilde{F}+{\mathsf{\Phi }}_{\beta }^T(r,t){\tilde{\theta }}_{\beta }-{\mathsf{\Xi }}_{\beta })\hfill \\ \hfill & +\tilde{G}-\frac{1}{{\tau }_d}\tilde{F}-\mathsf{\Gamma }\}+\frac{1}{k_{\theta }}\sum _{i=1}^n{\tilde{\theta }}_{\beta i}^{}{\dot{\widehat{\theta }}}_{\beta i}^{}+\frac{1}{k_{\delta }}\sum _{i=1}^n{\tilde{\delta }}_{\beta i}^{}{\dot{\widehat{\delta }}}_{\beta i}^{}.\hfill \end{array}$$

To simplify the above inequality further, the following vectors’ form can be rewritten as a sum formula

$$\begin{array}{c}{X}_1^T(L+B){\mathsf{\Phi }}_{\beta }^T(r,t){\tilde{\theta }}_{\beta }={\displaystyle \sum _{i=1}^n}{w}_i{\varphi }_{\beta }^T(r_i,t){\tilde{\theta }}_{{\beta }_i}{e}_{ri},\hfill \\ X_1^T(L+B){\mathsf{\Xi }}_{\beta }={\displaystyle \sum _{i=1}^n}{w}_i{\epsilon }_{\beta }{e}_{ri},\hfill \\ X_2^T(L+B){\mathsf{\Phi }}_{\beta }^T(r,t){\tilde{\theta }}_{\beta }={\displaystyle \sum _{i=1}^n}{w}_i{\varphi }_{\beta }^T(r_i,t){\tilde{\theta }}_{{\beta }_i}{y}_i,\hfill \\ X_2^T(L+B){\mathsf{\Xi }}_{\beta }={\displaystyle \sum _{i=1}^n}{\epsilon }_{\beta }{y}_i,\hfill \\ X_2^T\mathsf{\Gamma }={\displaystyle \sum _{i=1}^n}{\widehat{\delta }}_{\beta i}^{}rec\left(\frac{x_{i2}}{\left|e_{ri}+k_r{y}_i\right|}\right)x_{i2},\hfill \end{array}$$

(51)

From the result in (51), we get that

$$\begin{array}{cc}\hfill {\dot{V}}_1& ⩽X_1^T(L+B)\tilde{F}+X_2^T(\tilde{G}-\frac{1}{{\tau }_d}\tilde{F})+k_r{X}_2^T(L+B)\tilde{F}\hfill \\ \hfill & +\sum _{i=1}^n{w}_i{\varphi }_{\beta }^T(r_i,t){\tilde{\theta }}_{{\beta }_i}{e}_{ri}-\sum _{i=1}^n{w}_i{\epsilon }_{\beta }{e}_{ri}+k_r\sum _{i=1}^n{w}_i{\varphi }_{\beta }^T(r_i,t){\tilde{\theta }}_{{\beta }_i}{y}_i\hfill \\ \hfill & -\sum _{i=1}^n{k}_r{w}_i{\epsilon }_{\beta }{y}_i-\sum _{i=1}^n{\widehat{\delta }}_{\beta i}^{}rec\left(\frac{x_{i2}}{\left|e_{ri}+k_r{y}_i\right|}\right)x_{i2}\hfill \\ \hfill & +\frac{1}{k_{\theta }}\sum _{i=1}^n{\tilde{\theta }}_{\beta i}^{}{\dot{\widehat{\theta }}}_{\beta i}^{}+\frac{1}{k_{\delta }}\sum _{i=1}^n{\tilde{\delta }}_{\beta i}^{}{\dot{\widehat{\delta }}}_{\beta i}^{}.\hfill \end{array}$$

Equivalently,

$$\begin{array}{cc}\hfill {\dot{V}}_1& ⩽X_1^T(L+B)\tilde{F}+X_2^T(\tilde{G}-\frac{1}{{\tau }_d}\tilde{F})+k_r{X}_2^T(L+B)\tilde{F}+D_v.\hfill \end{array}$$

Considering the adaptive law (42), one gets

$$\begin{array}{cc}\hfill D_v& =-\sum _{i=1}^n{w}_i{\epsilon }_{\beta }{e}_{ri}+\sum _{i=1}^n{w}_i{\varphi }_{\beta }^T(r_i,t){\tilde{\theta }}_{{\beta }_i}(e_{ri}+k_r{y}_i)\hfill \\ \hfill & -\sum _{i=1}^n{k}_r{w}_i{\epsilon }_{\beta }{y}_i+\sum _{i=1}^n{\tilde{\theta }}_{\beta i}^{}{w}_i(-{\varphi }_{\beta }^T(r_i,t)(e_{ri}+k_r{y}_i))\hfill \\ \hfill & -\sum _{i=1}^n{\widehat{\delta }}_{\beta i}^{}rec\left(\frac{x_{i2}}{\left|e_{ri}+k_r{y}_i\right|}\right)x_{i2}+\sum _{i=1}^n{\tilde{\delta }}_{\beta i}^{}\left|e_{ri}+k_r{y}_i\right|\hfill \\ \hfill & =-\sum _{i=1}^n{w}_i{\epsilon }_{\beta }(e_{ri}+k_r{y}_i)+\sum _{i=1}^n{\tilde{\delta }}_{\beta i}^{}\left|e_{ri}+k_r{y}_i\right|-\sum _{i=1}^n{\widehat{\delta }}_{\beta i}^{}\left|e_{ri}+k_r{y}_i\right|\hfill \\ \hfill & \le \sum _{i=1}^n\left|{\epsilon }_{\beta }\right|\left|e_{ri}+k_r{y}_i\right|+\sum _{i=1}^n{\tilde{\delta }}_{\beta i}^{}\left|e_{ri}+k_r{y}_i\right|-\sum _{i=1}^n{\widehat{\delta }}_{\beta i}^{}\left|e_{ri}+k_r{y}_i\right|\hfill \\ \hfill & \le \sum _{i=1}^n{\delta }_{\beta i}^{}\left|e_{ri}+k_r{y}_i\right|+\sum _{i=1}^n{\tilde{\delta }}_{\beta i}^{}\left|e_{ri}+k_r{y}_i\right|-\sum _{i=1}^n{\widehat{\delta }}_{\beta i}^{}\left|e_{ri}+k_r{y}_i\right|\hfill \\ \hfill & =\sum _{i=1}^n\left|e_{ri}+k_r{y}_i\right|({\delta }_{\beta i}^{}+{\tilde{\delta }}_{\beta i}^{}-{\widehat{\delta }}_{\beta i}^{})\hfill \\ \hfill & =0.\hfill \end{array}$$

Under condition $D_v\le 0$, we can deduce that

$${\dot{V}}_1⩽X_1^T(L+B)\tilde{F}+X_2^T(\tilde{G}-\frac{1}{{\tau }_d}\tilde{F})+k_r{X}_2^T(L+B)\tilde{F}.$$

(52)

From the previous description, it is known that matrix $L+B$ is positive definite and symmetric, on the basis of the Rayleigh–Ritz theorem, we obtain that ${\lambda }_{min}{X}_1^T{X}_1\le X_1^T(L+B)X_1\le {\lambda }_{max}{X}_1^T{X}_1$, so the following inequality exists

$$\begin{array}{c}{X}_1^T(L+B)(L+B)X_1\le {\lambda }_{max}^2{X}_1^T{X}_1\le \frac{{\lambda }_{max}^2}{{\lambda }_{min}}{X}_1^T(L+B)X_1,\hfill \\ X_2^T(L+B)(L+B)X_2\le {\lambda }_{max}^2{X}_2^T{X}_2,\hfill \end{array}$$

(53)

where ${\lambda }_{max}$ and ${\lambda }_{min}$ are the maximum and minimum eigenvalues of matrix $L+B$.

At the same time, the Lyapunov function $V_1$ can be written as $V_1=X_2^T{X}_2+{\Delta }_2$, where ${\Delta }_2⩾0$, so there is a norm $∥X_2∥⩽\sqrt{X_2^T{X}_2+{\Delta }_2}⩽\sqrt{2V_1}$. Therefore, ${\dot{V}}_1$ can be further written as

$$\begin{array}{cc}\hfill {\dot{V}}_1& ⩽X_1^T(L+B)\tilde{F}+X_2^T(\tilde{G}-\frac{1}{{\tau }_d}\tilde{F})+k_r{X}_2^T(L+B)\tilde{F}\hfill \\ \hfill & ⩽∥X_1^T(L+B)∥∥\tilde{F}∥+∥X_2^T∥∥\tilde{G}-\frac{1}{{\tau }_d}\tilde{F}∥\hfill \\ \hfill & +∥X_1^T(L+B)∥∥\tilde{F}∥.\hfill \end{array}$$

(54)

Under Lemma 1, by suitably lowering the value of ${\tau }_d$, the estimation error $\widetilde{f_i}$ and $\widetilde{g_i}$ of CUDE can be decreased to zero (or a negligibly tiny amount), noting that $\left|{\tilde{f}}_i\right|\le {\overline{f}}_h$, and ${\overline{f}}_h=max\left\{\left|{\tilde{f}}_{i0}\right|,{\tau }_d{\overline{f}}_d\right\}$, accordingly, one exists $\left|{\tilde{g}}_i-\frac{1}{t_d}{\tilde{f}}_i\right|\le {\kappa }_h$.

$$\begin{array}{cc}\hfill {\dot{V}}_1& ⩽\sqrt{2}n{\overline{f}}_h\sqrt{\frac{{\lambda }_{max}^2}{{\lambda }_{min}}{V}_1}+\sqrt{2}n{\kappa }_h\sqrt{V_1}+\sqrt{2}n{\overline{f}}_h{\lambda }_{max}\sqrt{V_1}\hfill \\ \hfill & ={\mathsf{\Omega }}_h\sqrt{V_1}.\hfill \end{array}$$

(55)

where ${\mathsf{\Omega }}_h=\sqrt{2\frac{{\lambda }_{{max}^2}}{{\lambda }_{min}}}n{\overline{f}}_h+\sqrt{2}n{\kappa }_h+\sqrt{2}n{\overline{f}}_h{\lambda }_{max}$.

Consequently,

$$\frac{d{V}_1}{\sqrt{V_1}}⩽{\mathsf{\Omega }}_{h}dt,$$

(56)

$$\sqrt{V_1\left(t\right)}-\sqrt{V_1\left(0\right)}⩽\frac{1}{2}{\mathsf{\Omega }}_h\left(t-t_0\right),$$

(57)

where it is obvious that ${\mathsf{\Omega }}_h$ is a bounded positive value, and inequality (57) is acquired by integrating inequality (56) over the interval $[0,t]$. Accordingly, $X_1$ and $X_2$ cannot diverge in finite time. Considering Lemma 1 in article [42], we can obtain that ${lim}_{t\to \infty }{X}_1=0$ and ${lim}_{t\to \infty }{X}_2=0$. Then according to Definition 5 and Equation (44), ${lim}_{t\to \infty }|r_i-w_i{r}_0|\to 0$ for all $i\in \mathcal{I}$. To sum up, Theorem 1 is proven. □

4. Simulations

In this section, to demonstrate the availability and effectiveness of the introduced control scheme, we will utilize numerical simulations for the robust bipartite tracking control to evaluate the theoretical results. Consider five connected UAVs and an additional target with the signed graph shown in Figure 1, the signed graph is structurally balanced, containing a spanning tree and only the 1-st UAV is able to obtain the position information of the target directly. In order to facilitate the observation of experimental results, this paper only shows the one-dimensional status information from the UAV.

From the signed graph, it is known that the UAV group is divided into two groups, ${\mathcal{V}}_1,{\mathcal{V}}_2$, where $\{v_0,v_1,v_2\}\in {\mathcal{V}}_1$ and $\{v_3,v_4,v_5\}\in {\mathcal{V}}_2$. The UAVs’ dynamics (10) with nonlinear components are set as in

Table 2. Five UAVs’ dynamics.

Index	UAVs’ Dynamics
UAV 1	${\dot{r}}_1=v_1+\frac{cos(-r_1)}{t^2+1},{\dot{v}}_1=u_1+0.1sin(r_1+v_1)$
UAV 2	${\dot{r}}_2=v_2+e^{-t^2}+sin{r}_2,{\dot{v}}_2=u_2-0.2r_2{e}^{-v_2^2}$
UAV 3	${\dot{r}}_3=v_3+e^{-\left|r_3\right|t}-1,{\dot{v}}_3=u_3-r_{3}sin\left(v_3\right)-cos(-r_3)$
UAV 4	${\dot{r}}_4=v_4+e^{-r_4}sin\left(r_{4}t\right),{\dot{v}}_4=u_4+e^{-r_4}cos\left(v_4\right)-1$
UAV 3	${\dot{r}}_5=v_5-5r_5+sin\left(r_{5}t\right),{\dot{v}}_5=u_5+sin\left(r_5{v}_5\right)$

.

To verify the effectiveness of the bipartite tracking control scheme proposed in (39) for mixed-order heterogeneous systems, we consider the different fractional-order models, which are described with different fractional-order q and dynamics model in

Table 3. Simulation results with different fractional orders q and dynamics.

Case	q	Target’s Dynamics ${\mathbf{D}}_{\mathit{t}}^{\mathit{q}}{\mathit{r}}_0$
Case 1	0.4	${\mathbf{D}}_t^q{r}_0=-0.45r_0+sin\left(t^{0.6}\right)+0.02t+2$
Case 2	0.4	${\mathbf{D}}_t^q{r}_0=-e^{{(-\left|r_0\right|)}^{0.5}}+sin\left(2r_0\right)+sin\left(t^{0.6}\right)+0.02t+2$
Case 3	0.8	${\mathbf{D}}_t^q{r}_0=-0.5r_0^3-e^{-r_0}+sin\left(t^{0.6}\right)+0.02t+2$
Case 4	1.1	${\mathbf{D}}_t^q{r}_0=sin\left(t^{0.6}\right)+0.02t+2$

. We chose Case 1 as the basic experiment to verify the proposed method. In this experiment, the fractional order q is equal to 0.4. The dynamics model of the target makes the state trajectory of the target change gradually over time. In Case 2, the same fractional order is selected as in Case 1, but the target’s dynamics model is different. In Case 2, the state trajectory of the target changes dramatically. The experimental comparison between Cases 1 and 2 can verify that the algorithm can adapt to tracking tasks under different target motion trajectories. In Cases 3 and 4, cases with fractional order greater than zero and less than zero are selected, respectively. These two supplementary experiments prove that the proposed method can cope with tracking tasks under different fractional orders of targets.

Only the first UAV obtains the target’s information with the weight $b_1=2.0$, the rest of the UAVs cannot receive it directly, hence $b_2=b_3=b_4=b_5=0$, and the signature matrix $\mathcal{W}$ denotes $\mathcal{W}={(1,1,-1,-1,-1)}^T$.

Here we rewrite the Gaussian basis functions (16) for the estimation of ${\beta }_i(r,t)$ by the i-th UAV:

$${\varphi }_{\beta i}^T(r,t)=e^{-\frac{{(r-{\mu }_{\beta ir,k})}^2+{(t-{\mu }_{\beta it,k})}^2}{{\eta }_{\beta i,k}^2}},k\in \{1,2,\dots ,h_{\beta i}\},$$

(58)

where the number of perception nodes is $h_{\beta i}=17\times 17$, the basis function’s widths are set as ${\eta }_{\beta i,k}=6$ and the centers $({\mu }_{\beta ir,k},{\mu }_{\beta it,k})$ are uniformly distributed in $[-25,25]\times [0,50]$.

Under the conditions in Theorem 1, the control gain is chosen as $k_r=0.5,k_v=0.5$, let UDE parameter ${\tau }_d=0.01$ and the parameter of the estimator’s update control law be defined as $k_{\beta }=2,k_{\delta }=0.001$. The initial value related to the position of the UAVs are:

$$\begin{array}{c}\hfill \left[\begin{array}{ccccc}{r}_1& r_2& r_3& r_4& r_5\\ v_1& v_2& v_3& v_4& v_5\end{array}\right]\left(0\right)=\left[\begin{array}{ccccc}1.6& -1& 1& 0.5& -1.5\\ 0& 0& 0& 0& 0\end{array}\right].\end{array}$$

and $r_0\left(0\right)=2,{\widehat{\theta }}_{\beta i}\left(0\right)=0,{\widehat{\delta }}_{\beta i}\left(0\right)=0$.

In the simulations, we first perform four cases with different fractional-order and target’s dynamics models. The relevant evaluation standards and specific evaluation indicators include (1) whether all the UAVs diverge into two subgroups, one subgroup tracks the trajectory of target, the other tracks the symmetrical trajectory with respect to the origin; (2) whether all the local bipartite tracking errors converge gradually to near zero; (3) whether the trajectories of neural network approximation error on the unknown smooth function of target converge gradually to near zero; (4) whether the trajectories of UDE estimation error on the unknown smooth function of UAV model converge gradually to near zero.

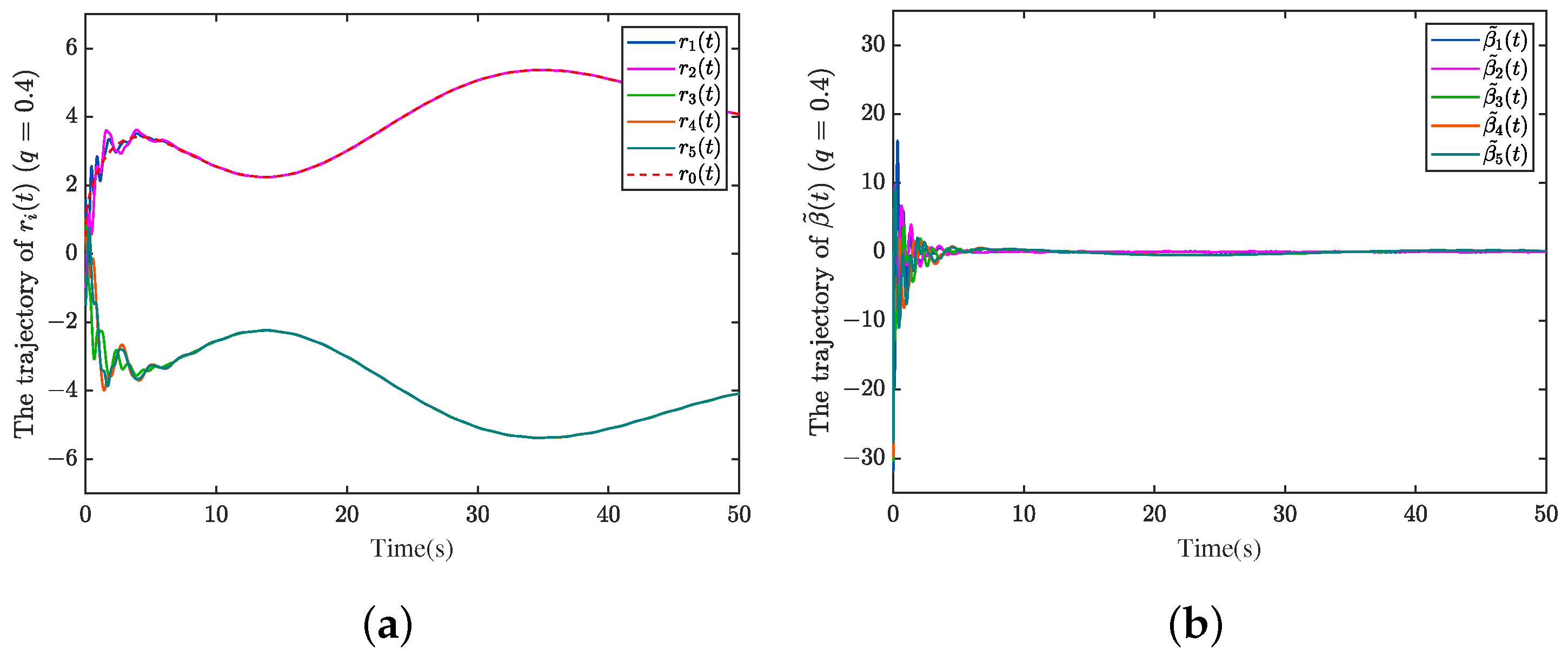
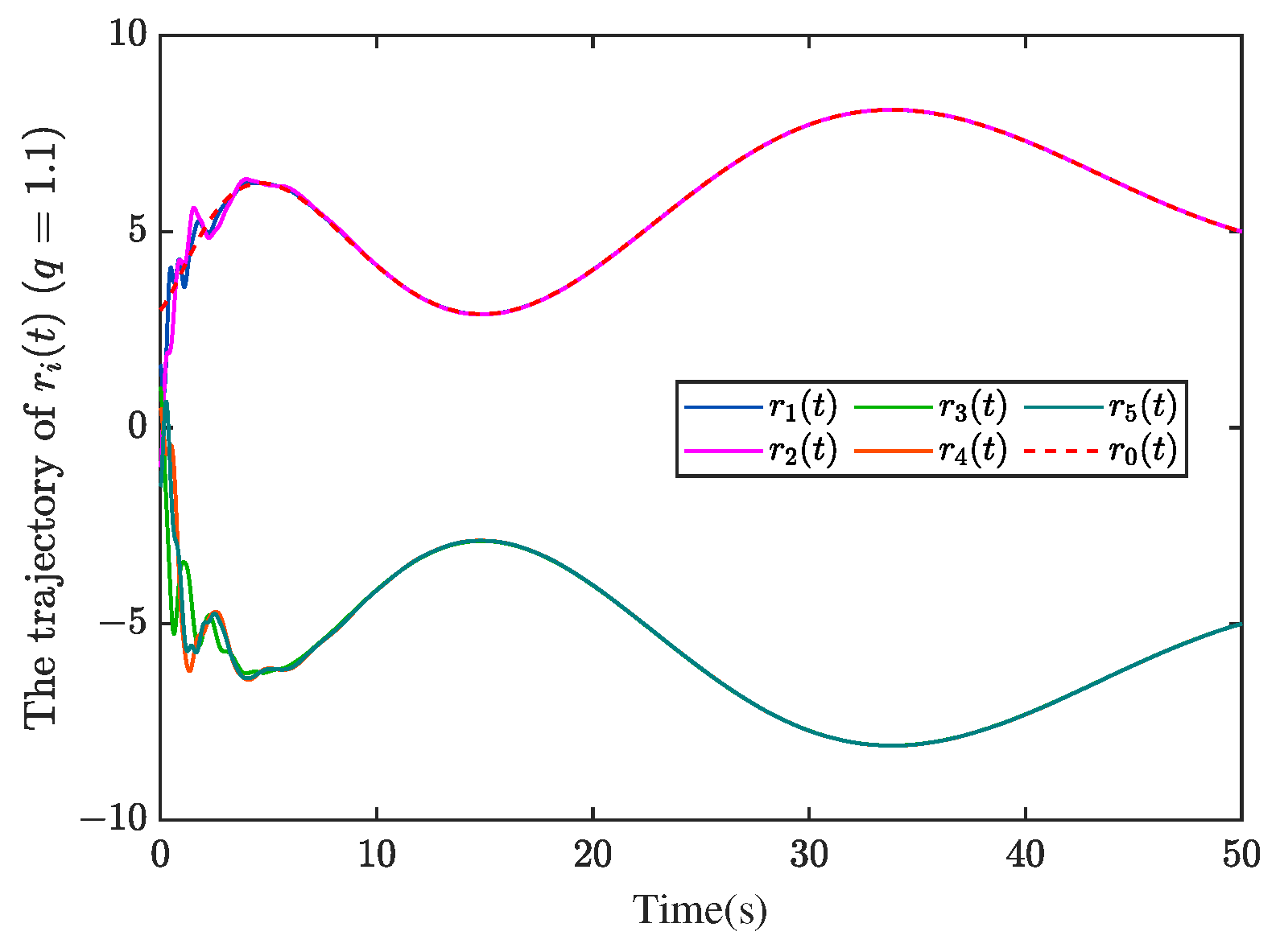
Case 1: Figure 2a–d are depicted to show the results of the bipartite tracking control with fractional-order $q=0.4$. From Figure 2a, it is apparent that the bipartite consensus tracking is well achieved and diverged into two sub-groups, steered by the designed controller, the UAVs in a structurally balanced network display symmetry of their paths pursuing or away from the target with respect to the origin. In the network, we can observe UAVs 1 and 2 follow the trajectory of the target’s path, and the subgroup comprised of UAVs 3, 4 and 5 follow a symmetric trajectory, which corresponds to the theoretical analysis on signed graph $\{v_0,v_1,v_2\}\in {\mathcal{V}}_1$ and $\{v_3,v_4,v_5\}\in {\mathcal{V}}_2$. The trajectory of NN estimate error ${\tilde{\beta }}_i(r_0,t)$ is shown in Figure 2b, which implies the estimation error eventually converges to a very small value approaching zero. The control input result is shown in Figure 2c, which ends up with regular continuous fluctuations within a certain range, and Figure 2d shows that the estimation error of CUDE tends to be zero, which demonstrates the validity and accuracy of the estimator. Due to the good estimation of the new scheme, NNCUDE, we achieve a better compensation performance for the existing uncertainties. Accordingly, the estimation error of the uncertain function finally converges to an almost negligibly small value.

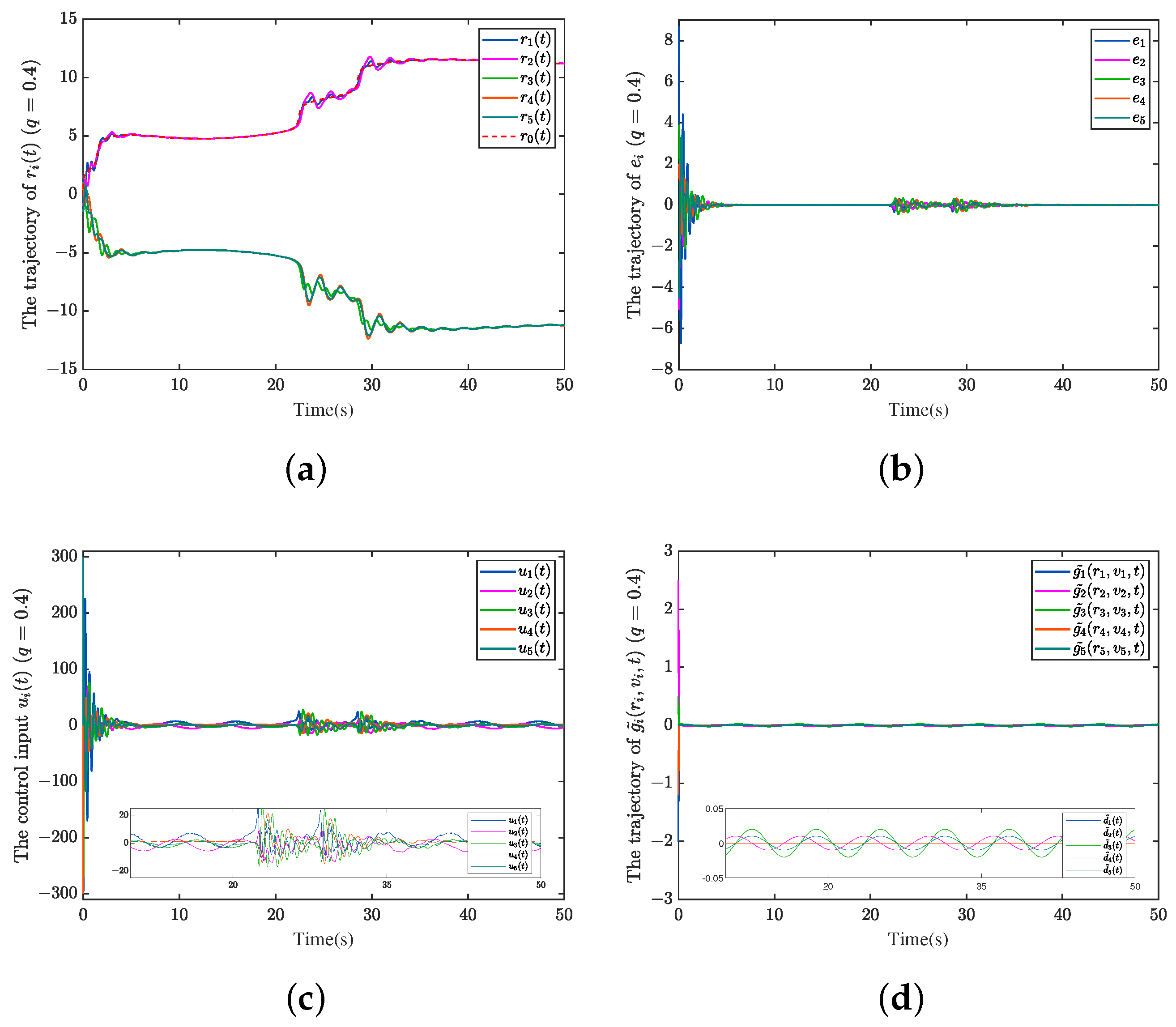
Case 2: Like Case 1, the same fractional-order size is given, but there are different target dynamics. It can be seen from the simulation results in Figure 3a that the bipartite tracking control is implemented, and the multiple UAVs and targets are diverged into two sub-groups $\{v_0,v_1,v_2\}\in {\mathcal{V}}_1$ and $\{v_3,v_4,v_5\}\in {\mathcal{V}}_2$, whereas the trajectory of targets changes more dramatically from $t=20$ to $t=30$. Furthermore, large fluctuations in target affect the stability of the UAVs’ tracking, and in this process, the trajectories of the UAVs also have certain fluctuations. Correspondingly, the control input, neural network estimation error and bipartite consensus error also arise at the corresponding time, respectively.

Remark 5. 

When the trajectory of the target changes dramatically, that is, the derivative is relatively large, there will be a temporary oscillation phenomenon. The reason is that the neural network estimation requires the trajectory of UAVs to be as smooth as possible.

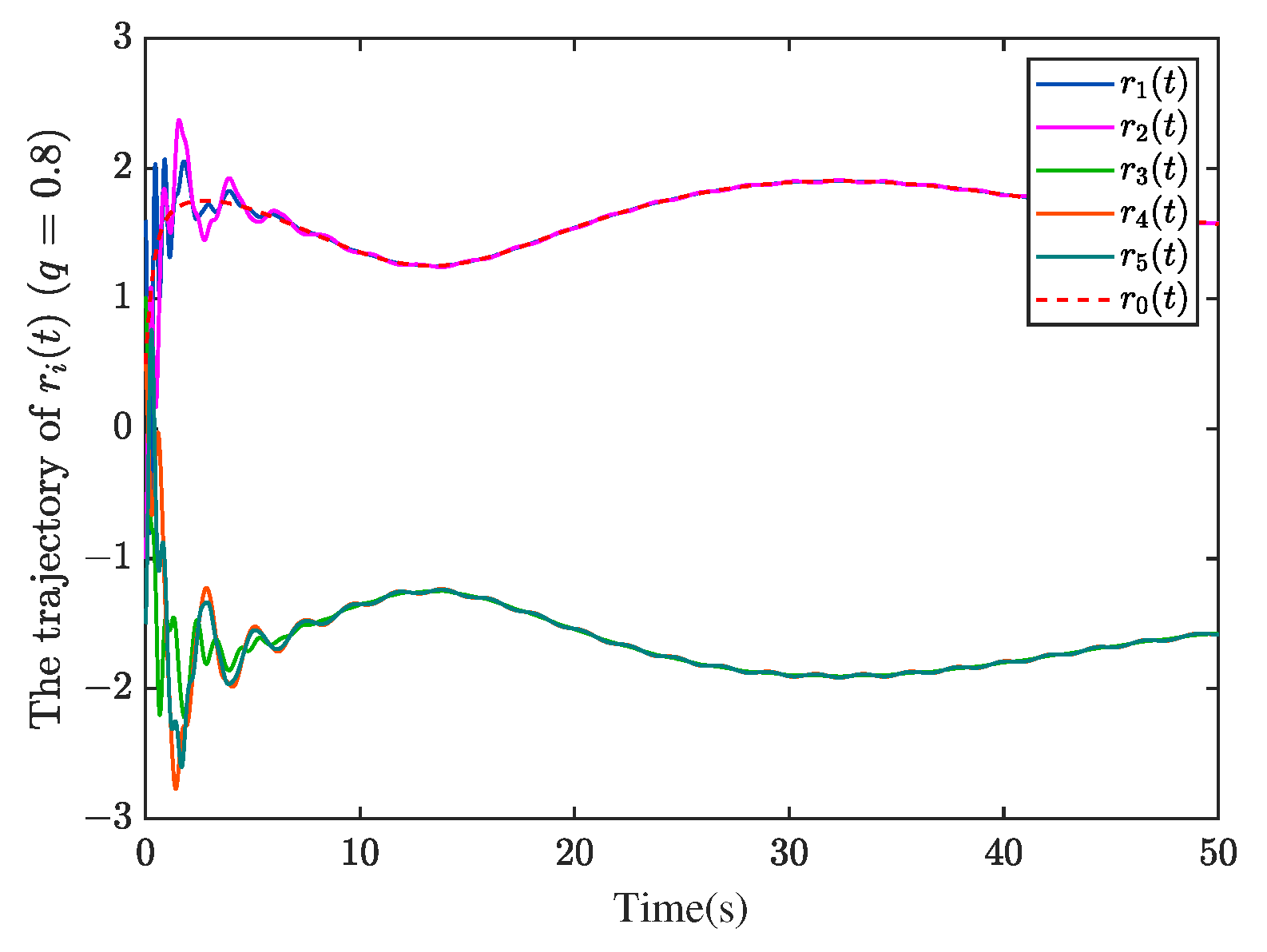
Case 3: As shown in Figure 4, this example considers the change in both fractional-order size and the target’s fractional-order dynamics at the same time. From the experimental results, it can be seen that all the UAVs achieve the bipartite consensus tracking, and the bipartite consensus error approximates to zero.

Case 4: Like Case 3, we change the targets in the fractional-order value and dynamics, where the change in the trajectory amplitude is bigger, but with no chattering phenomenon in Figure 5. Therefore, the chattering phenomenon will only appear in a certain range at the same time as the bipartite consensus error and estimation error achieve convergence.

To sum up, according to the simulation results and analysis, by applying the designed control protocol and selecting suitable control parameters, it is demonstrated that the bipartite consensus tracking can be achieved and the bipartite tracking errors converge to a small bounded set under different fractional-order target models and different UAV models.

In addition, in order to verify the superiority of the algorithm, we compared the proposed method (NNCUDE) with the conventional method. Considering the rationality of comparison, we take neural network (NN) as the comparison method in this paper. Specifically, the neural network is not only utilized to estimate the unknown model part of the target but also to deal with the disturbance existing in the UAV model, including $f_i(r_i,t)$ and $g_i(r_i,v_i,t)$. Since the application of the UDE method requires accurate modeling, we cannot solve the problems studied in this paper by only using UDE. The corresponding results are shown in Figure 6 and Figure 7. The superiority is mainly reflected in the position tracking accuracy and controller smoothness.

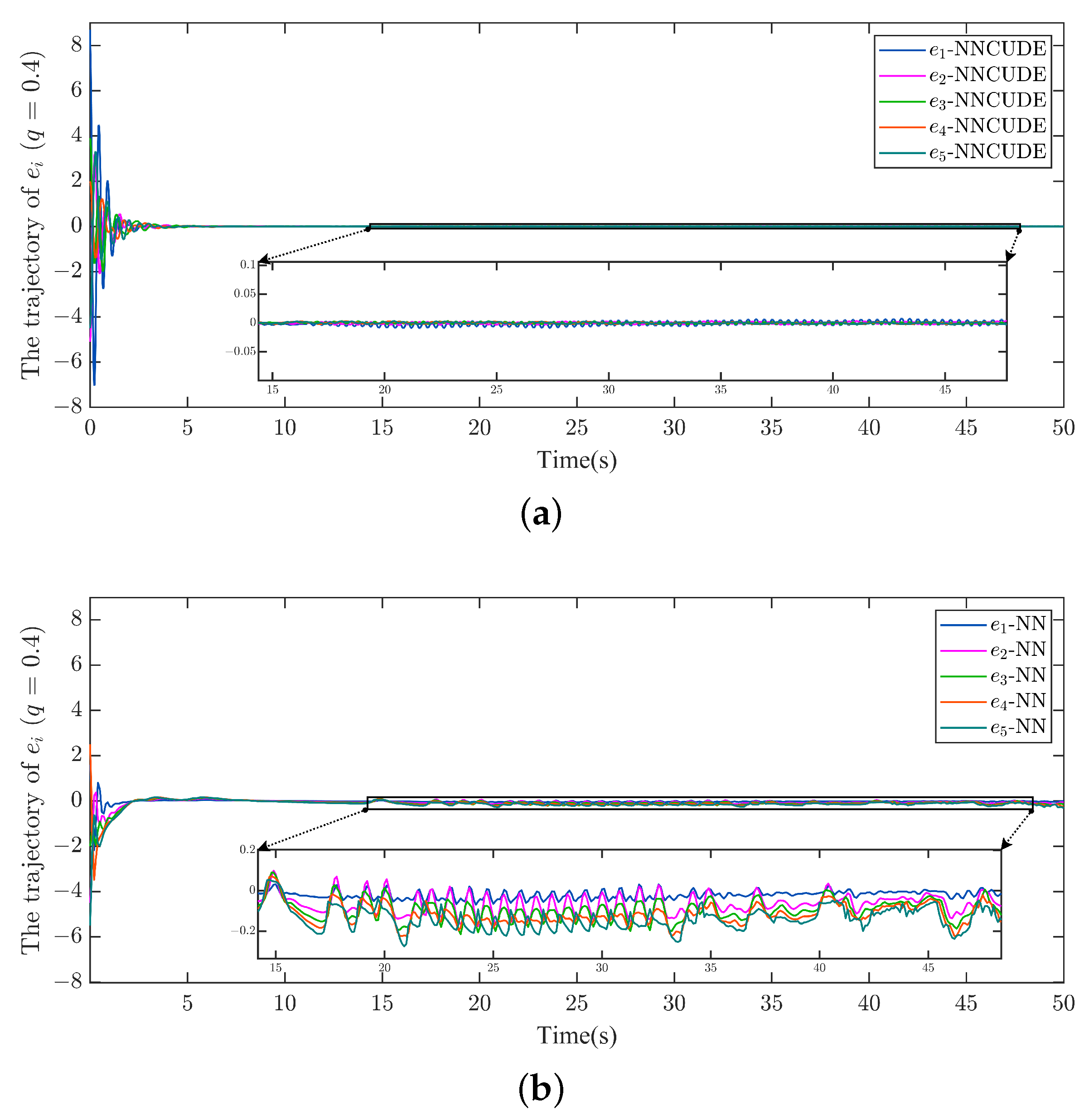
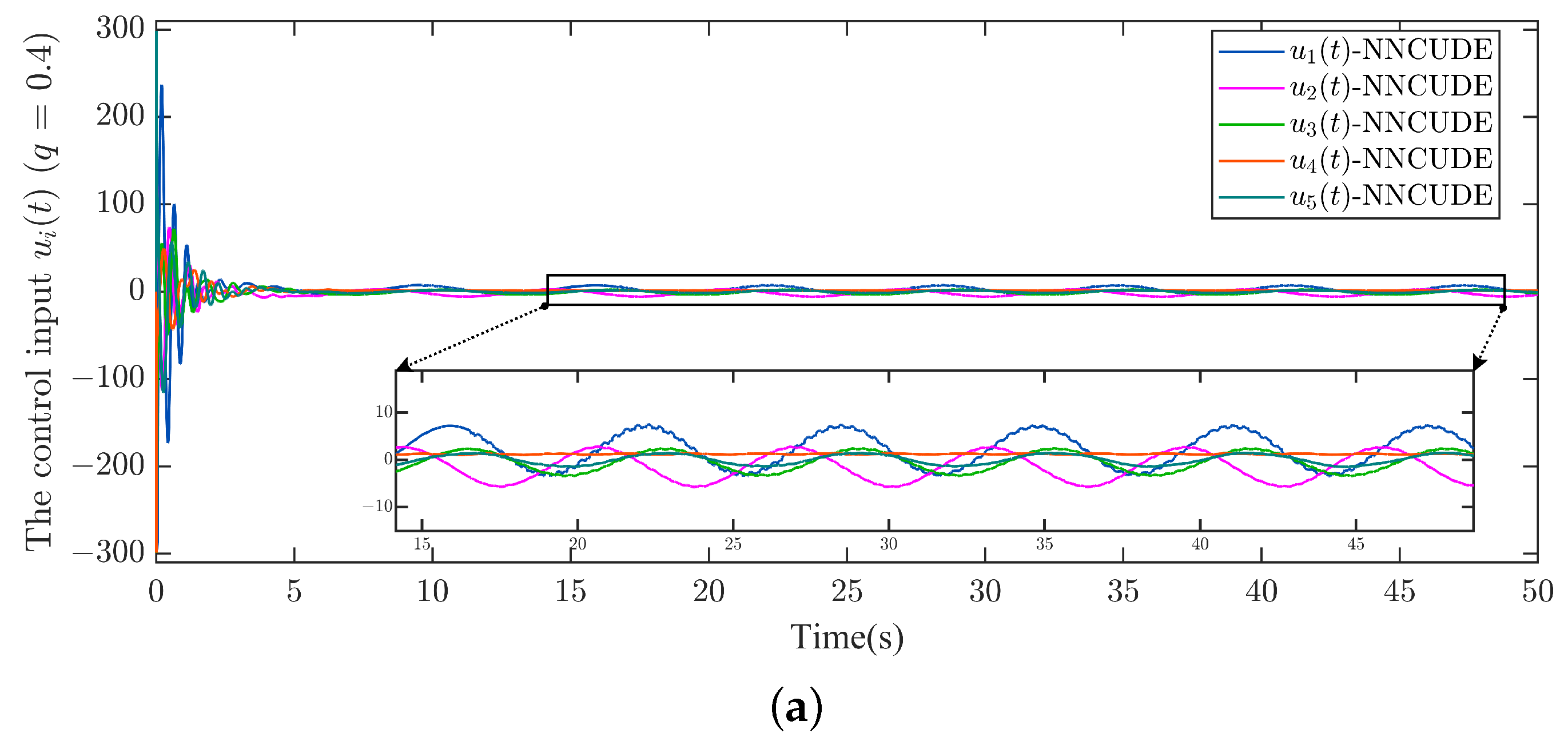
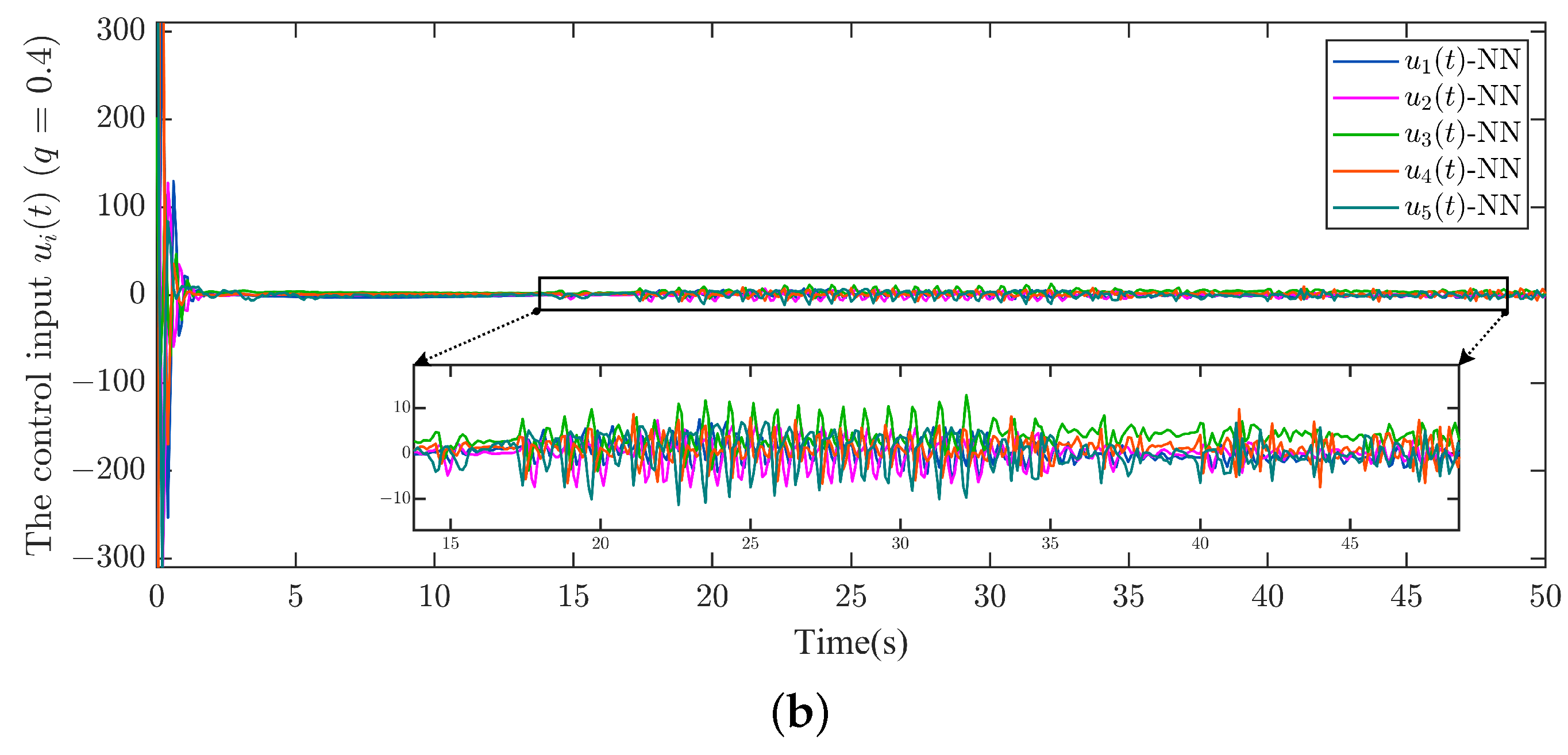
The experimental conditions are the same as Case 1, Figure 6 shows the trajectories of bipartite tracking error $e_i$ by the NNCUDE and NN methods, respectively. As can be seen from Figure 6, the NN-based method will cause some high-frequency chattering during target tracking, and the tracking error is obviously larger than the result obtained by NNCUDE. Figure 7 shows the trajectories of control input $u_i\left(t\right)$ obtained by the NNCUDE and NN methods, respectively. From the results, it indicates that the controller also appears to have the chattering phenomenon, which can lead to deviations and overshoots in the system results, and in severe cases, to instability. In addition, it may also cause damage to physical components such as mechanical structures. Comparatively, our proposed method effectively alleviates the chattering phenomenon.

5. Conclusions

In this paper, the robust cooperative control of UAV swarms problem is investigated for dual-camp divergent tracking of a heterogeneous target over a signed graph. A novel controller, NNCUDE, is designed for nonlinear systems subjected to unmatched uncertainties and disturbances. The target with unknown nonlinear fractional-order dynamics is considered, which is resolved using the neural network approximation approach in which fewer learning parameters need to be adjusted online. The influence of unmatched uncertainties related to the dynamics of UAVs is compensated by cascade UDE. By employing the Lyapunov function and some known theorems, proof of the proposed control scheme is derived. Finally, several numerical simulations are performed to testify to the innovative method’s availability in theory and practice, the bipartite consensus tracking based on multi-agent theory can be achieved and the bipartite tracking errors converge to a small bounded value by selecting suitable control gains and adaptive parameters.