UDE-Based Dynamic Surface Control for Quadrotor Drone Attitude Tracking under Non-Ideal Actuators
Abstract
1. Introduction
- (1)
- A cascade-structured, UDE-based dynamic surface controller is proposed to address the issues of mismatched disturbance and complexity explosion, which is characterized by its simple structure and easy implementation in a quadrotor drone system, thus increasing the robustness and accuracy of the attitude control system.
- (2)
- A rigorous proof of the ultimate boundedness of the closed-loop system is given by a mathematical analysis, especially based on the small gain theorem, while the stability conditions and constraints of the controller parameters are provided, indicating that the parameters of the different loops can be designed independently.
- (3)
- In the design process of the controller, the non-ideal actuator with the FOPTD dynamic model is fully considered to eliminate the parameter constraints of the outer-loop controller brought by the actuator dynamics and improve the attitude control accuracy.
2. Modeling
2.1. Quadrotor Drone Kinematics and Dynamics Model
2.2. Actuator Model
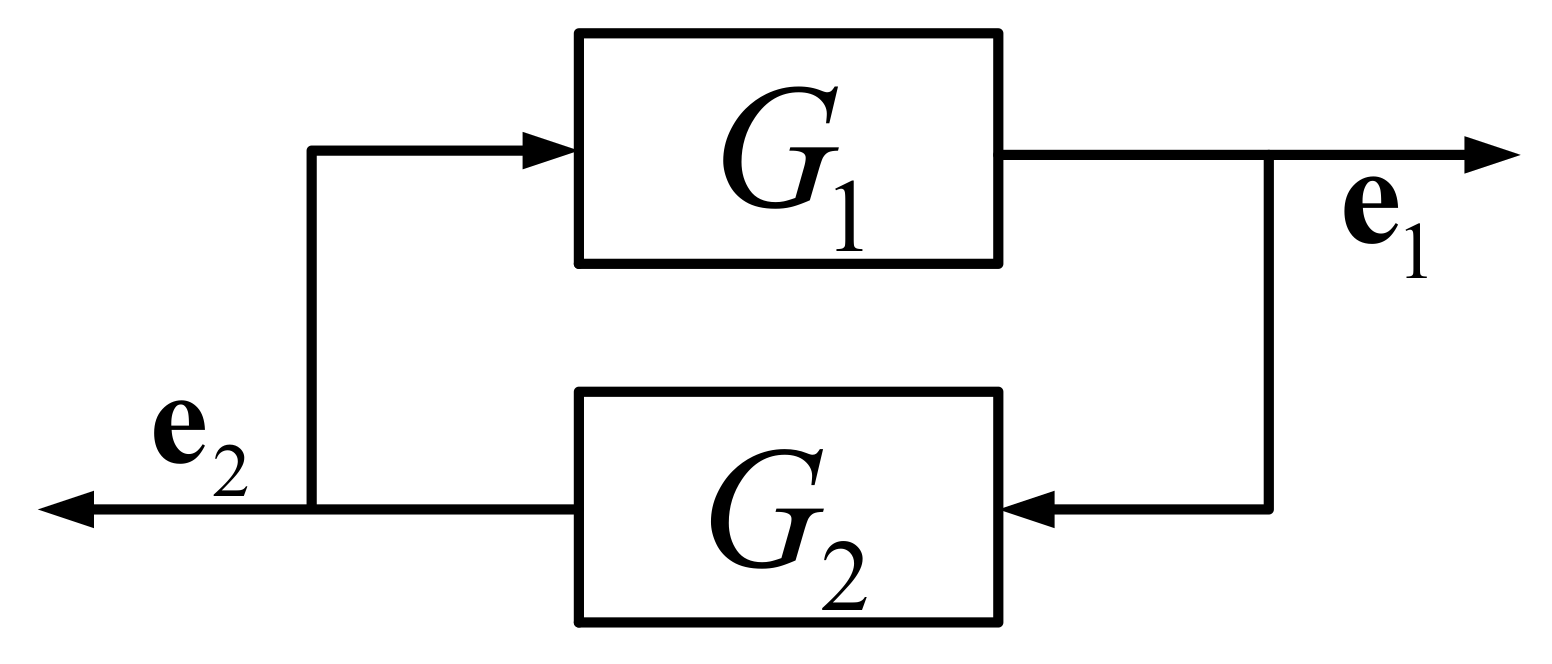
3. UDE-Based Dynamic Surface Controller Design
3.1. Step 1
3.2. Step 2
3.3. Step 3
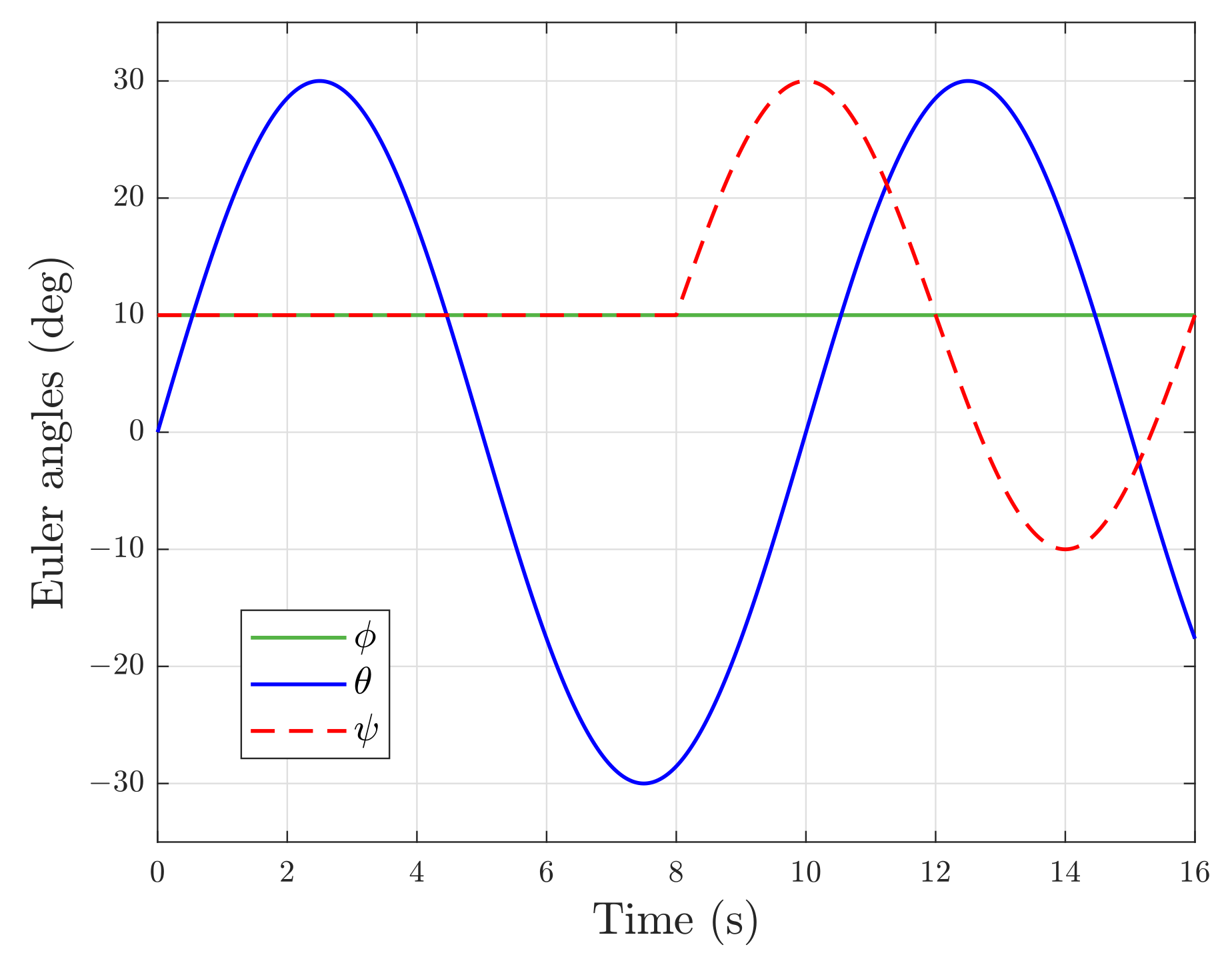
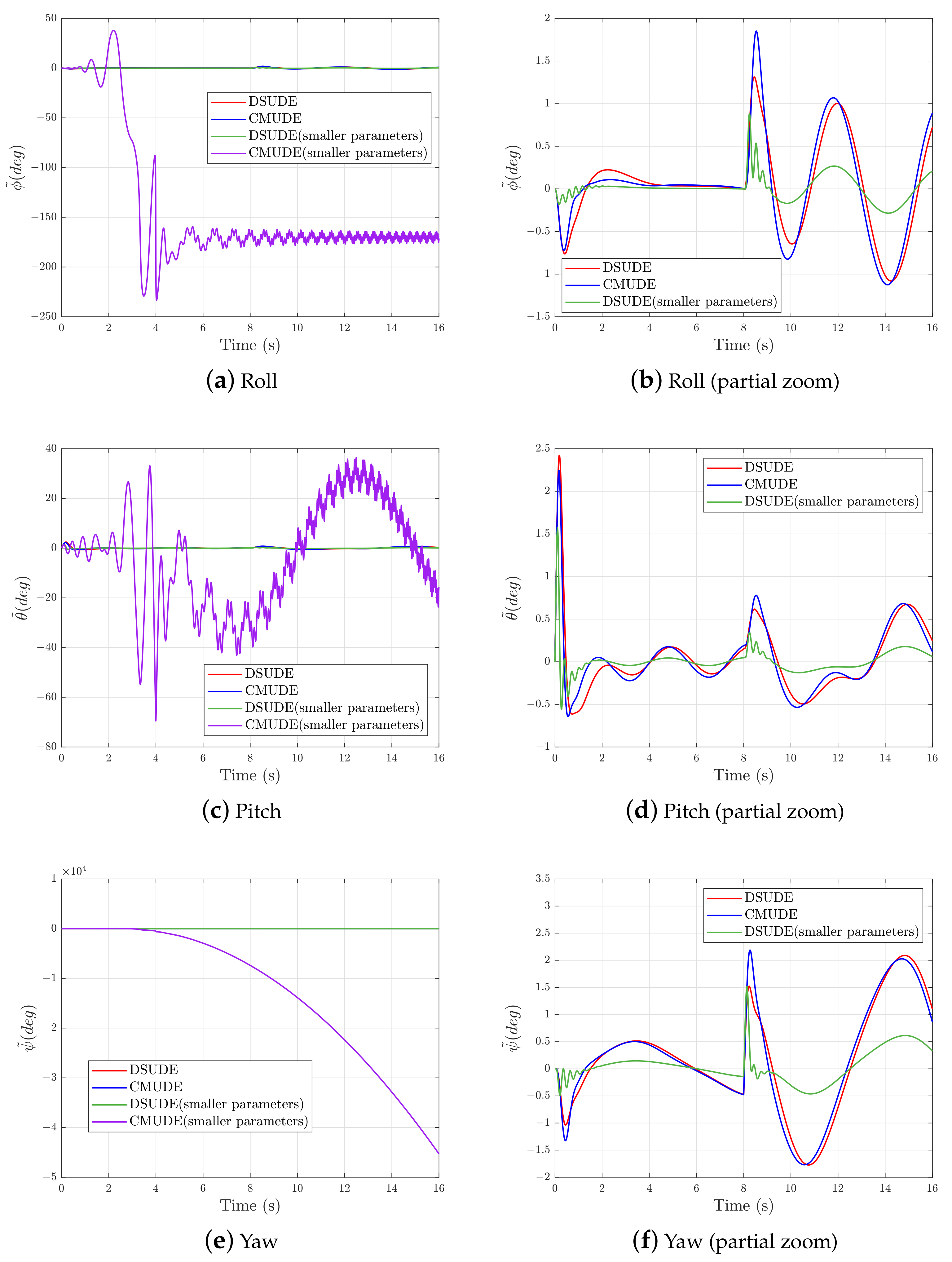
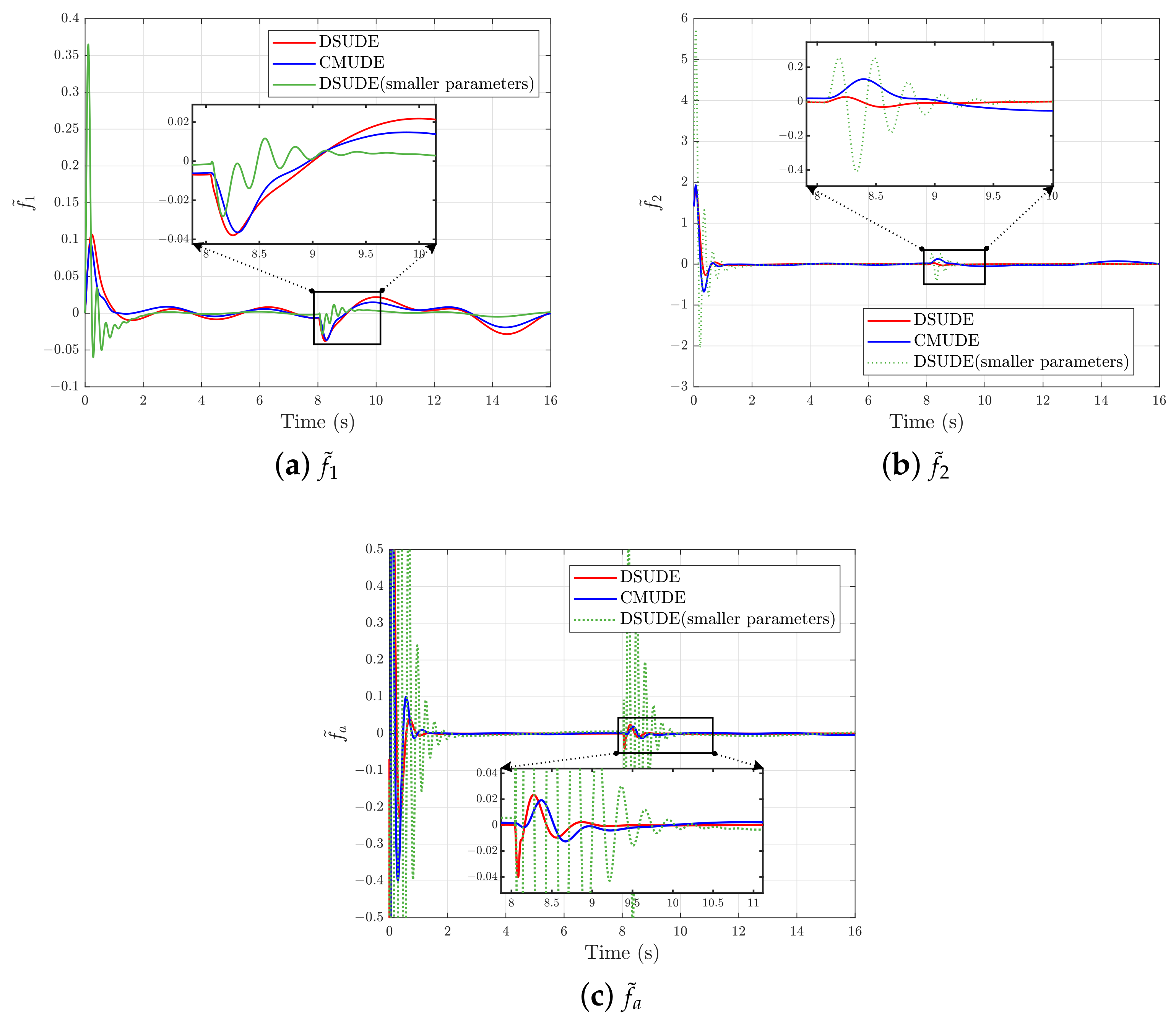
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gupte, S.; Mohandas, P.I.T.; Conrad, J.M. A survey of quadrotor unmanned aerial vehicles. In Proceedings of the 2012 IEEE Southeastcon, Orlando, FL, USA, 15–18 March 2012; pp. 1–6. [Google Scholar]
- Budiharto, W.; Irwansyah, E.; Suroso, J.S.; Chowanda, A.; Ngarianto, H.; Gunawan, A.A.S. Mapping and 3D modelling using quadrotor drone and GIS software. J. Big Data 2021, 8, 48. [Google Scholar] [CrossRef]
- Dalwadi, N.; Deb, D.; Muyeen, S. Adaptive backstepping controller design of quadrotor biplane for payload delivery. IET Intell. Transp. Syst. 2022, 16, 1738–1752. [Google Scholar] [CrossRef]
- Fernández-Guisuraga, J.M.; Sanz-Ablanedo, E.; Suárez-Seoane, S.; Calvo, L. Using unmanned aerial vehicles in postfire vegetation survey campaigns through large and heterogeneous areas: Opportunities and challenges. Sensors 2018, 18, 586. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.C.; AbouSleiman, R.; Sababha, B.; Gjioni, E.; Korff, D.; Rawashdeh, O. Implementation of an autonomous surveillance quadrotor system. In Proceedings of the AIAA Infotech@ Aerospace Conference and AIAA Unmanned… Unlimited Conference, Seattle, WA, USA, 6–9 April 2009; p. 2047. [Google Scholar]
- Zhang, X.; Zhuang, Y.; Zhang, X.; Fang, Y. A novel asymptotic robust tracking control strategy for rotorcraft UAVs. IEEE Trans. Autom. Sci. Eng. 2022, 1–12. [Google Scholar] [CrossRef]
- Duan, X.; Yue, C.; Liu, H.; Guo, H.; Zhang, F. Attitude tracking control of small-scale unmanned helicopters using quaternion-based adaptive dynamic surface control. IEEE Access 2020, 9, 10153–10165. [Google Scholar] [CrossRef]
- Razmi, H.; Afshinfar, S. Neural network-based adaptive sliding mode control design for position and attitude control of a quadrotor UAV. Aerosp. Sci. Technol. 2019, 91, 12–27. [Google Scholar] [CrossRef]
- Chen, Q.; Ye, Y.; Hu, Z.; Na, J.; Wang, S. Finite-time approximation-free attitude control of quadrotors: Theory and experiments. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1780–1792. [Google Scholar] [CrossRef]
- Wang, S.; Chen, J.; He, X. An adaptive composite disturbance rejection for attitude control of the agricultural quadrotor UAV. ISA Trans. 2022, 129, 564–579. [Google Scholar] [CrossRef]
- Noordin, A.; Mohd Basri, M.A.; Mohamed, Z. Position and Attitude Tracking of MAV Quadrotor Using SMC-Based Adaptive PID Controller. Drones 2022, 6, 263. [Google Scholar] [CrossRef]
- Lotufo, M.A.; Colangelo, L.; Perez-Montenegro, C.; Canuto, E.; Novara, C. UAV quadrotor attitude control: An ADRC-EMC combined approach. Control Eng. Pract. 2019, 84, 13–22. [Google Scholar] [CrossRef]
- Castillo, A.; Sanz, R.; Garcia, P.; Qiu, W.; Wang, H.; Xu, C. Disturbance observer-based quadrotor attitude tracking control for aggressive maneuvers. Control Eng. Pract. 2019, 82, 14–23. [Google Scholar] [CrossRef]
- Lu, Q.; Ren, B.; Parameswaran, S. Uncertainty and disturbance estimator-based global trajectory tracking control for a quadrotor. IEEE/ASME Trans. Mechatron. 2020, 25, 1519–1530. [Google Scholar] [CrossRef]
- Ren, B.; Zhong, Q.C.; Dai, J. Asymptotic reference tracking and disturbance rejection of UDE-based robust control. IEEE Trans. Ind. Electron. 2016, 64, 3166–3176. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Rees, D. Control of uncertain LTI systems based on an uncertainty and disturbance estimator. J. Dyn. Syst. Meas. Control 2004, 126, 905–910. [Google Scholar] [CrossRef]
- Sun, L.; Li, D.; Zhong, Q.C.; Lee, K.Y. Control of a class of industrial processes with time delay based on a modified uncertainty and disturbance estimator. IEEE Trans. Ind. Electron. 2016, 63, 7018–7028. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhu, B.; Liu, H.H.; Qin, K. Design and experimental verification of UDE-based robust control for Lagrangian systems without velocity measurements. IFAC-PapersOnLine 2017, 50, 9595–9600. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, Q.; Liu, H.H. Design and experimental evaluation of robust motion synchronization control for multivehicle system without velocity measurements. Int. J. Robust Nonlinear Control 2018, 28, 5437–5463. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.; Zhu, B.; Zhu, Y. Improved UDE and LSO for a class of uncertain second-order nonlinear systems without velocity measurements. IEEE Trans. Instrum. Meas. 2019, 69, 4076–4092. [Google Scholar] [CrossRef]
- Zhu, B.; Liu, H.H.T.; Li, Z. Robust distributed attitude synchronization of multiple three-DOF experimental helicopters. Control Eng. Pract. 2015, 36, 87–99. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhu, B.; Liu, H.H.; Qin, K. Rejecting the effects of both input disturbance and measurement noise: A second-order control system example. Int. J. Robust Nonlinear Control 2020, 30, 6813–6837. [Google Scholar] [CrossRef]
- Dai, J.; Ren, B.; Zhong, Q.C. Uncertainty and disturbance estimator-based backstepping control for nonlinear systems with mismatched uncertainties and disturbances. J. Dyn. Syst. Meas. Control 2018, 140, 121005. [Google Scholar] [CrossRef]
- Qin, Z.; Wang, H.; Liu, K.; Zhu, B.; Zhao, X.; Zheng, W.; Dang, Q. Cascade-modified uncertainty and disturbance estimator–based control of quadrotors for accurate attitude tracking under exogenous disturbance. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2023, 1–19. [Google Scholar] [CrossRef]
- Farrell, J.A.; Polycarpou, M.; Sharma, M.; Dong, W. Command filtered backstepping. IEEE Trans. Autom. Control 2009, 54, 1391–1395. [Google Scholar] [CrossRef]
- Swaroop, D.; Hedrick, J.K.; Yip, P.P.; Gerdes, J.C. Dynamic surface control for a class of nonlinear systems. IEEE Trans. Autom. Control 2000, 45, 1893–1899. [Google Scholar] [CrossRef]
- Wang, Y.; Ren, B.; Zhong, Q.C. Bounded UDE-based controller for input constrained systems with uncertainties and disturbances. IEEE Trans. Ind. Electron. 2020, 68, 1560–1570. [Google Scholar] [CrossRef]
- Falanga, D.; Kleber, K.; Mintchev, S.; Floreano, D.; Scaramuzza, D. The foldable drone: A morphing quadrotor that can squeeze and fly. IEEE Robot. Autom. Lett. 2018, 4, 209–216. [Google Scholar] [CrossRef]
- Mahony, R.; Kumar, V.; Corke, P. Multirotor aerial vehicles: Modeling, estimation, and control of quadrotor. IEEE Robot. Autom. Mag. 2012, 19, 20–32. [Google Scholar] [CrossRef]
- Xu, L.; Qin, K.; Zhu, Y.; Li, W.; Shi, M. Parameter Design Constraints of UDE-Based Control under Non-ideal Actuators. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Heifei, China, 25–27 July 2022; pp. 1078–1083. [Google Scholar]
- Aharon, I.; Shmilovitz, D.; Kuperman, A. Phase margin oriented design and analysis of UDE-based controllers under actuator constraints. IEEE Trans. Ind. Electron. 2018, 65, 8133–8141. [Google Scholar] [CrossRef]
- Ahmad, H.; Young, T.; Toal, D.; Omerdic, E. Control allocation with actuator dynamics for aircraft flight controls. In Proceedings of the 7th AIAA ATIO Conf, 2nd CEIAT Int’l Conf on Innov and Integr in Aero Sciences, 17th LTA Systems Tech Conf; followed by 2nd TEOS Forum, Belfast, UK, 18–20 September 2007; p. 7828. [Google Scholar]
- Kristiansen, R.; Hagen, D. Modelling of actuator dynamics for spacecraft attitude control. J. Guid. Control Dyn. 2009, 32, 1022–1025. [Google Scholar] [CrossRef]
- Mokhtari, K.; Abdelaziz, M. Passivity-based simple adaptive control for quadrotor helicopter in the presence of actuator dynamics. In Proceedings of the 2016 8th International Conference on Modelling, Identification and Control (ICMIC), Algiers, Algeria, 15–17 November 2016; pp. 800–805. [Google Scholar]
- Qi, Y.; Zhu, Y.; Wang, J.; Shan, J.; Liu, H.H. MUDE-based control of quadrotor for accurate attitude tracking. Control Eng. Pract. 2021, 108, 104721. [Google Scholar] [CrossRef]
- Kose, O.; Oktay, T. Simultaneous quadrotor autopilot system and collective morphing system design. Aircr. Eng. Aerosp. Technol. 2020, 92, 1093–1100. [Google Scholar] [CrossRef]
- Şahin, H.; Kose, O.; Oktay, T. Simultaneous autonomous system and powerplant design for morphing quadrotors. Aircr. Eng. Aerosp. Technol. 2022, 94, 1228–1241. [Google Scholar] [CrossRef]
- Kose, O.; Oktay, T. Quadrotor flight system design using collective and differential morphing with SPSA and ANN. Int. J. Intell. Syst. Appl. Eng. 2021, 9, 159–164. [Google Scholar] [CrossRef]
- Kose, O.; Oktay, T. Simultaneous design of morphing hexarotor and autopilot system by using deep neural network and SPSA. Aircr. Eng. Aerosp. Technol. 2023, 95, 939–949. [Google Scholar] [CrossRef]
- Çoban, S. Autonomous performance maximization of research-based hybrid unmanned aerial vehicle. Aircr. Eng. Aerosp. Technol. 2020, 92, 645–651. [Google Scholar] [CrossRef]
- Sal, F. Simultaneous swept anhedral helicopter blade tip shape and control-system design. Aircr. Eng. Aerosp. Technol. 2023, 95, 101–112. [Google Scholar] [CrossRef]
- Khalil, H.K.; Grizzle, J.W. Nonlinear Systems; Prentice-Hall: Upper Saddle River, NJ, USA, 2002; Volume 3, pp. 134–180. [Google Scholar]
- Zhou, K.; Doyle, J.; Glover, K. Robust and Optimal Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1996; p. 212. [Google Scholar]



| DSUDE/RDSUDE | CMUDE | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | 0.5 | 0.01 | 2 | 0.5 | |||||
| 1 | 0.2 | 0.01 | 1 | 0.2 | |||||
| 1 | 0.05 | 1 | 0.05 | ||||||
| 0.001 | 0.6434 | 0.3604 | 0.2545 |
| 0.01 | 0.6543 | 0.3729 | 0.3923 |
| 0.03 | 0.6571 | 0.3934 | 0.3953 |
| 0.05 | 0.6629 | 0.4131 | 0.4219 |
| DSUDE | CMUDE | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.08 | 0.001 | 1 | 0.08 | |||||
| 1 | 0.1 | 0.001 | 1 | 0.1 | |||||
| 1 | 0.05 | 1 | 0.05 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Qin, K.; Tang, F.; Shi, M.; Lin, B. UDE-Based Dynamic Surface Control for Quadrotor Drone Attitude Tracking under Non-Ideal Actuators. Drones 2023, 7, 305. https://doi.org/10.3390/drones7050305
Xu L, Qin K, Tang F, Shi M, Lin B. UDE-Based Dynamic Surface Control for Quadrotor Drone Attitude Tracking under Non-Ideal Actuators. Drones. 2023; 7(5):305. https://doi.org/10.3390/drones7050305
Chicago/Turabian StyleXu, Linxi, Kaiyu Qin, Fan Tang, Mengji Shi, and Boxian Lin. 2023. "UDE-Based Dynamic Surface Control for Quadrotor Drone Attitude Tracking under Non-Ideal Actuators" Drones 7, no. 5: 305. https://doi.org/10.3390/drones7050305
APA StyleXu, L., Qin, K., Tang, F., Shi, M., & Lin, B. (2023). UDE-Based Dynamic Surface Control for Quadrotor Drone Attitude Tracking under Non-Ideal Actuators. Drones, 7(5), 305. https://doi.org/10.3390/drones7050305






