Blade Twist Effects on Aerodynamic Performance and Noise Reduction in a Multirotor Propeller
Abstract
1. Introduction
2. Materials and Methods
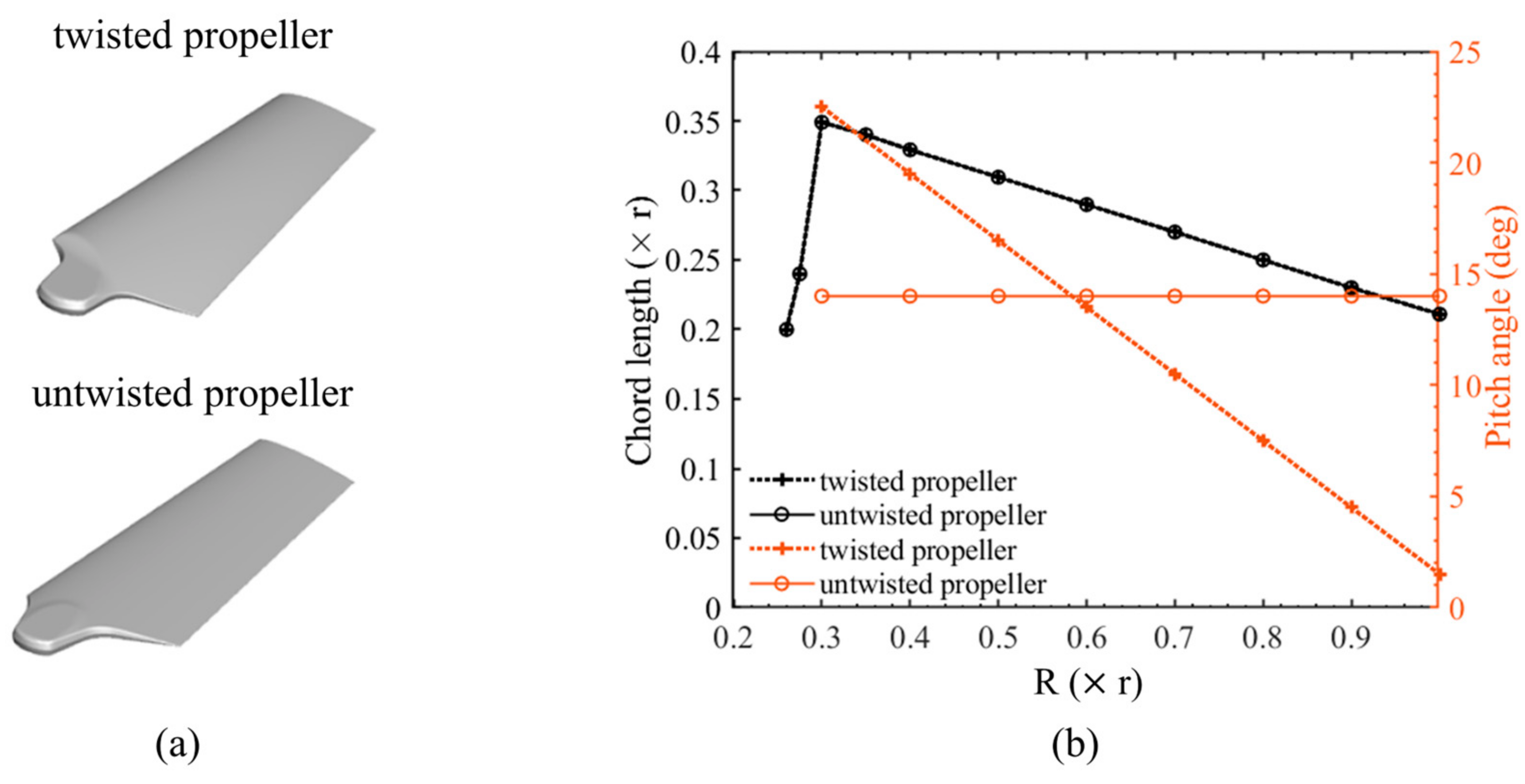
2.1. Propeller Models with Twisted and Untwisted Blades
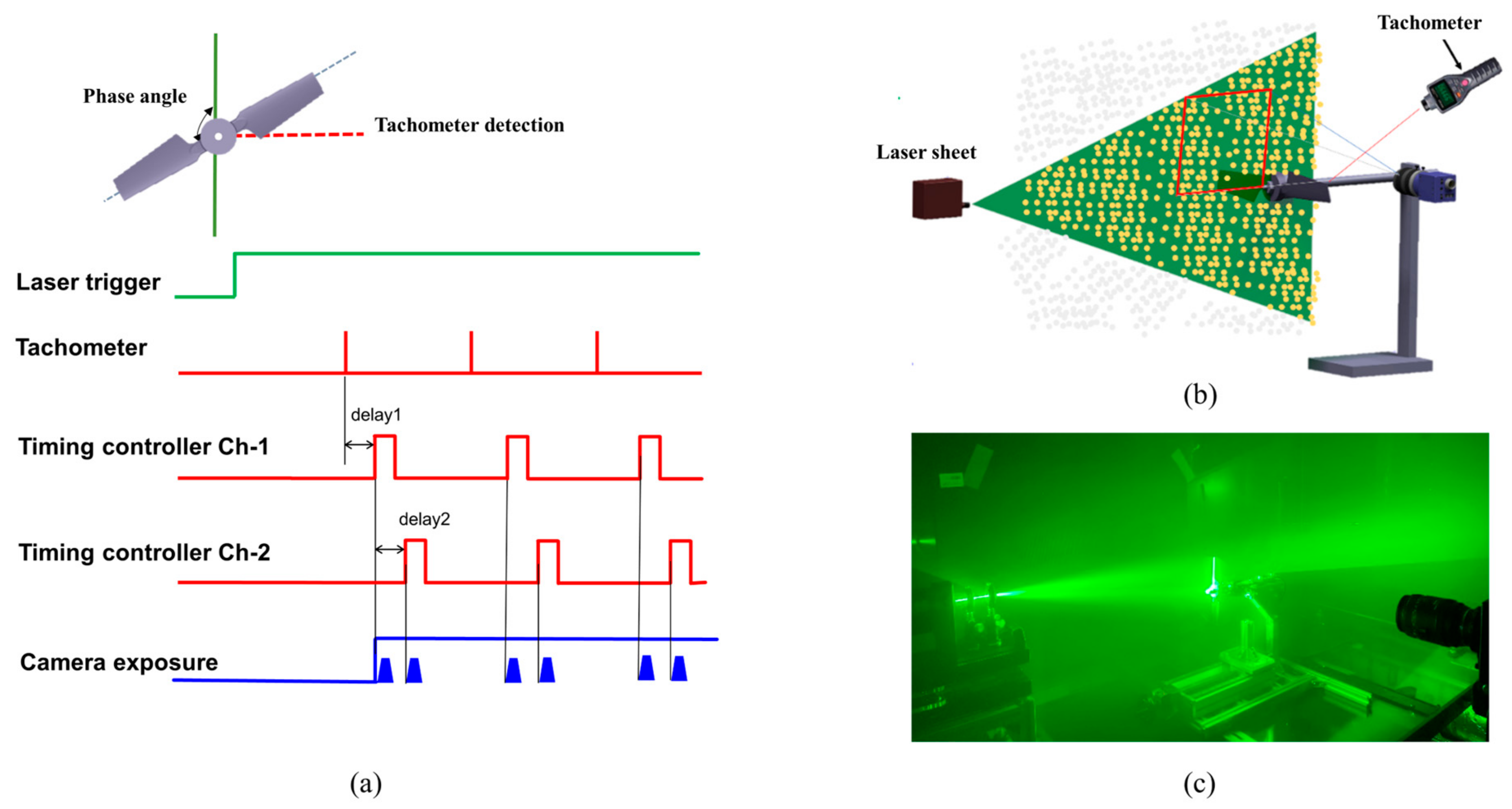
2.2. PIV Experiment
2.3. Measurements of Aerodynamic Force and Sound
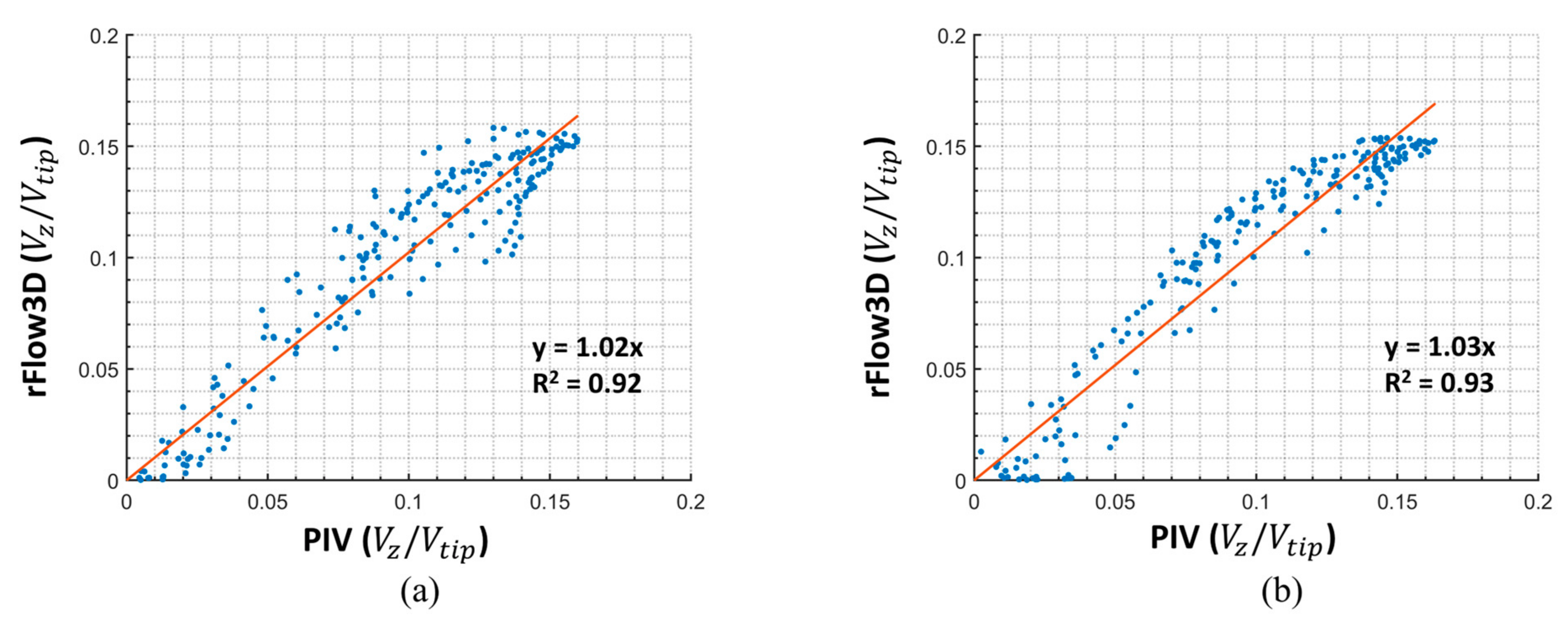
2.4. CFD Modeling
3. Results
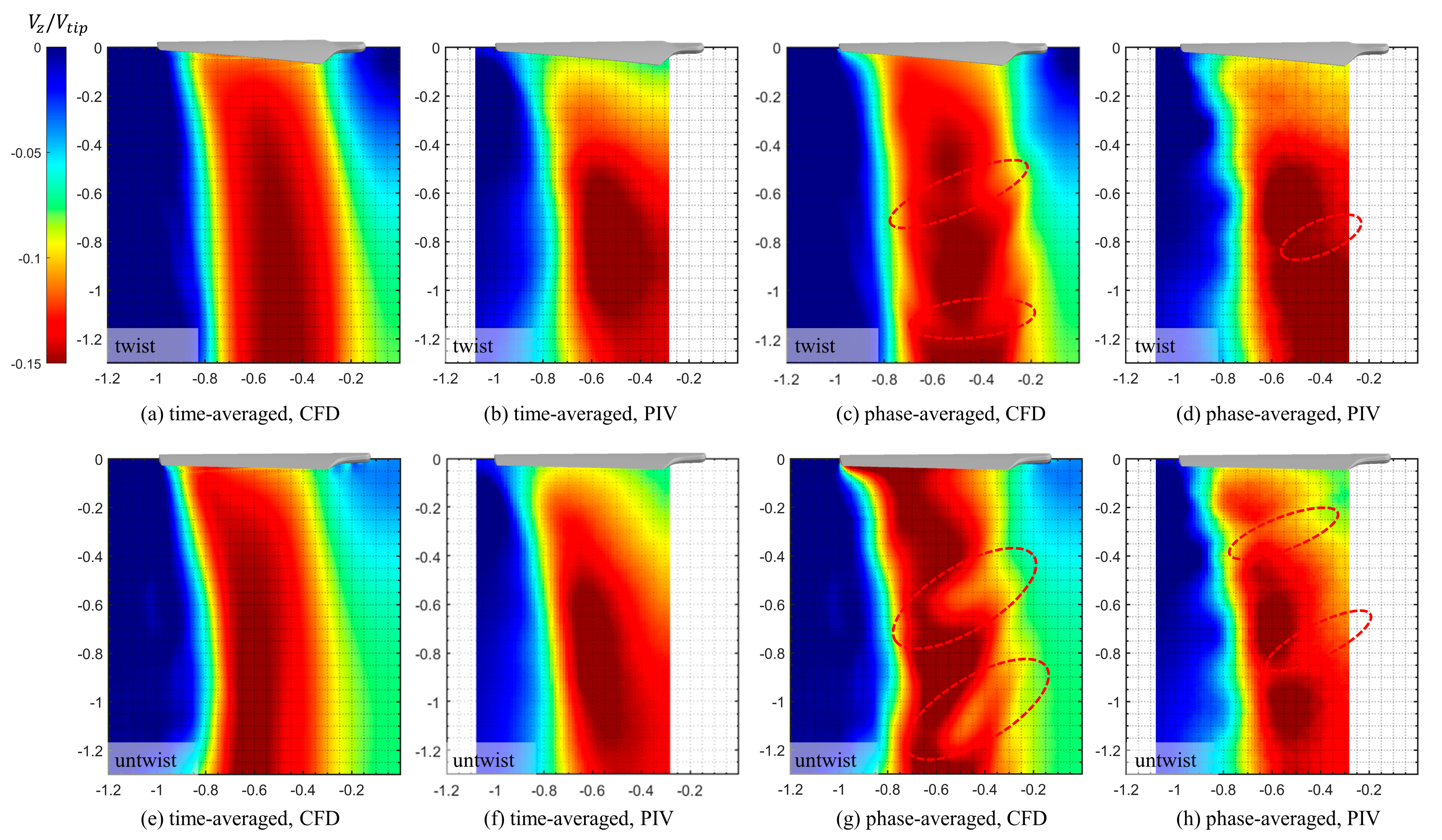
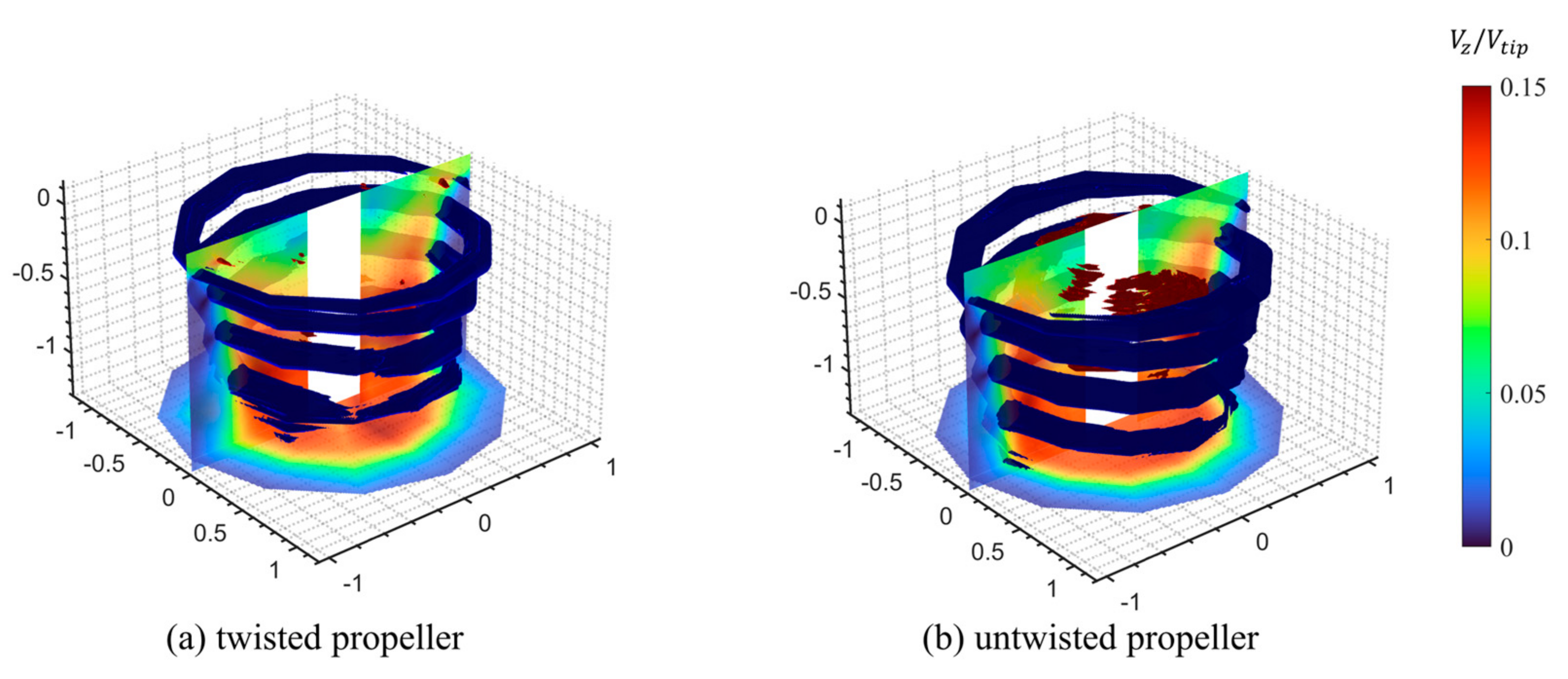
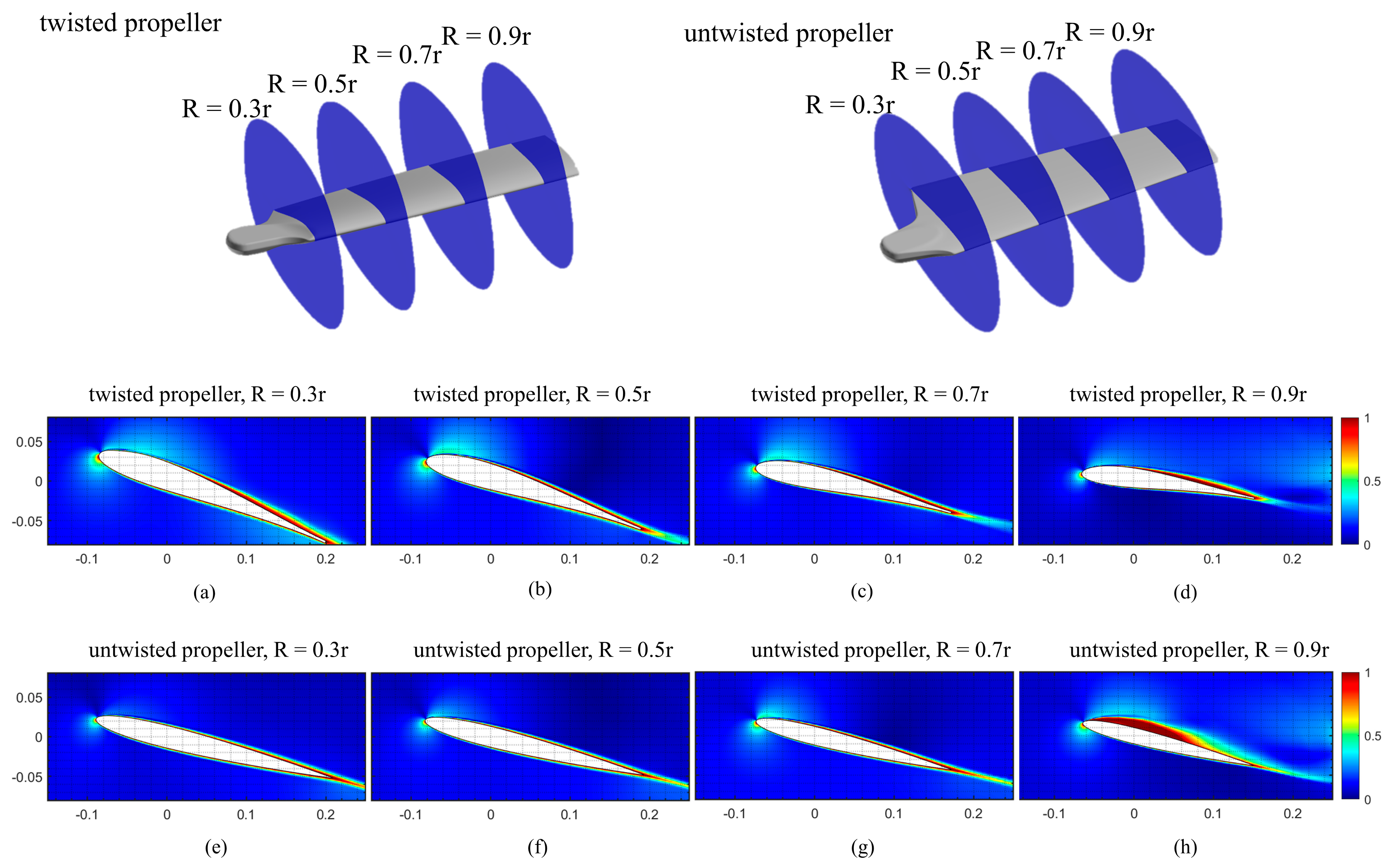
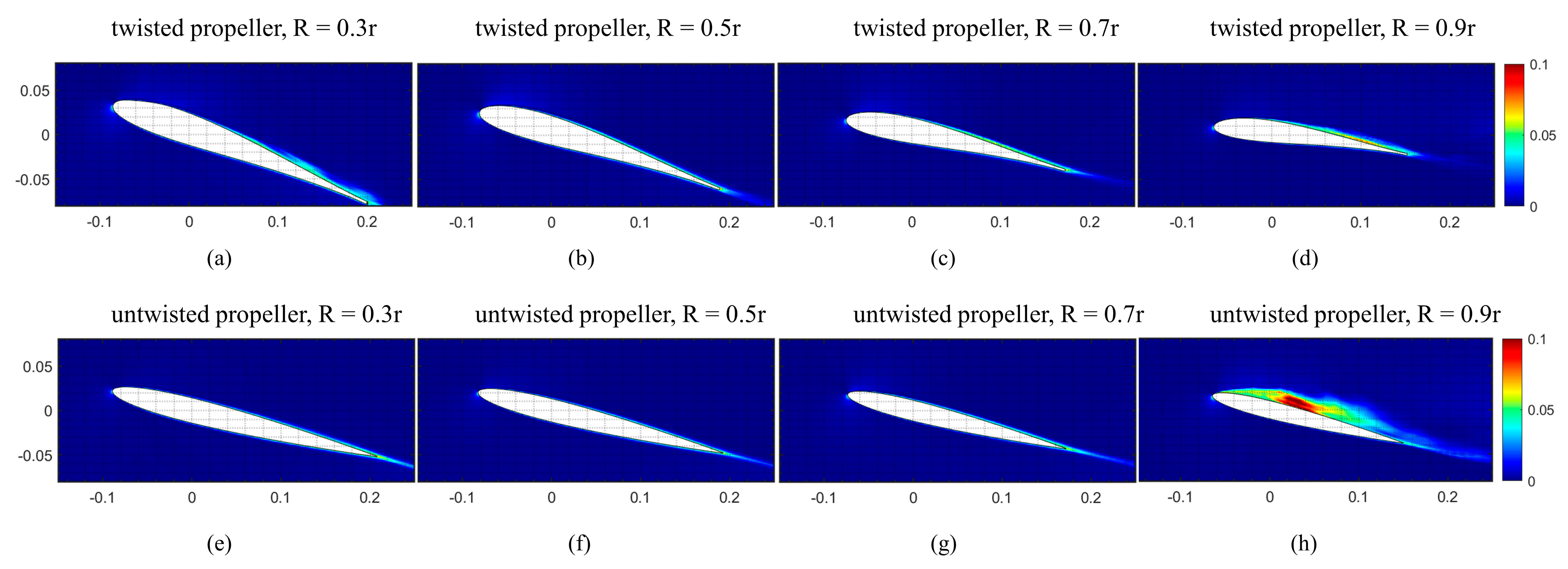
3.1. Flow Structure Visualization
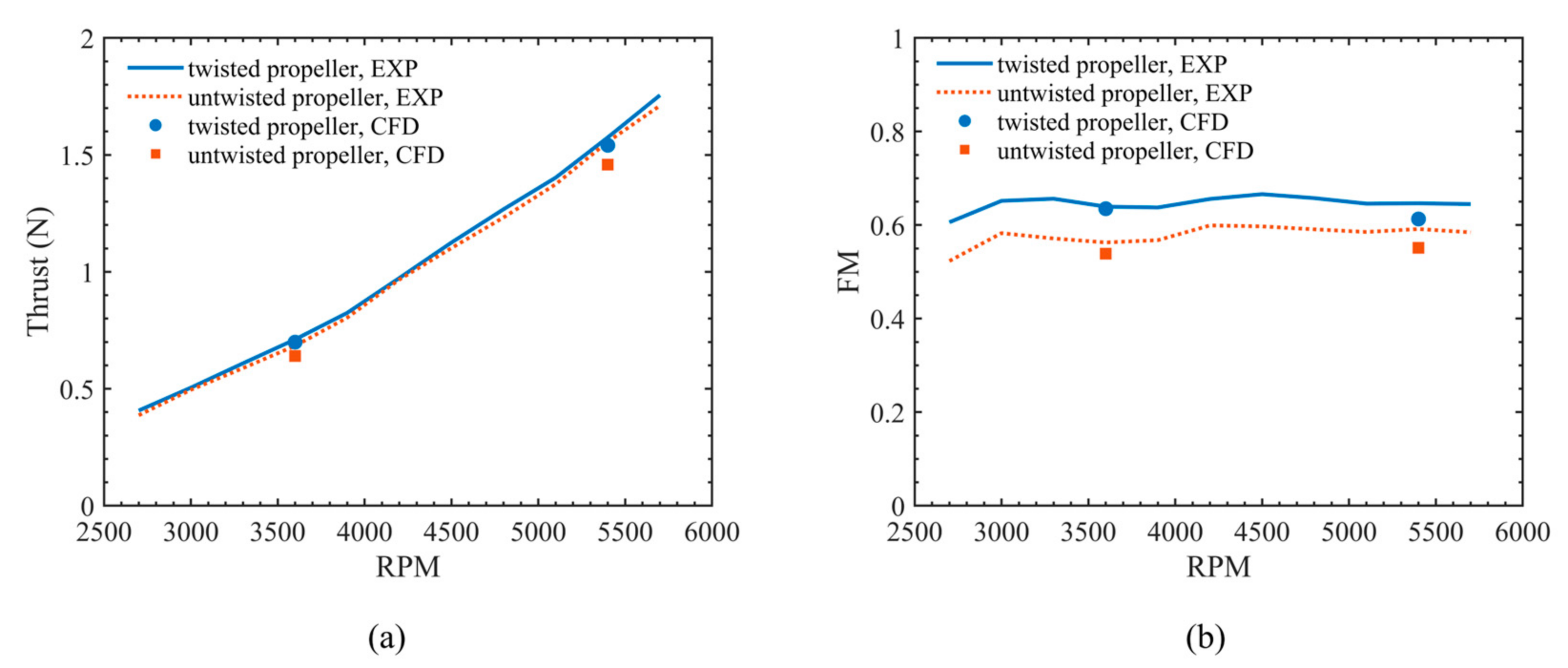
3.2. Aerodynamic Performance
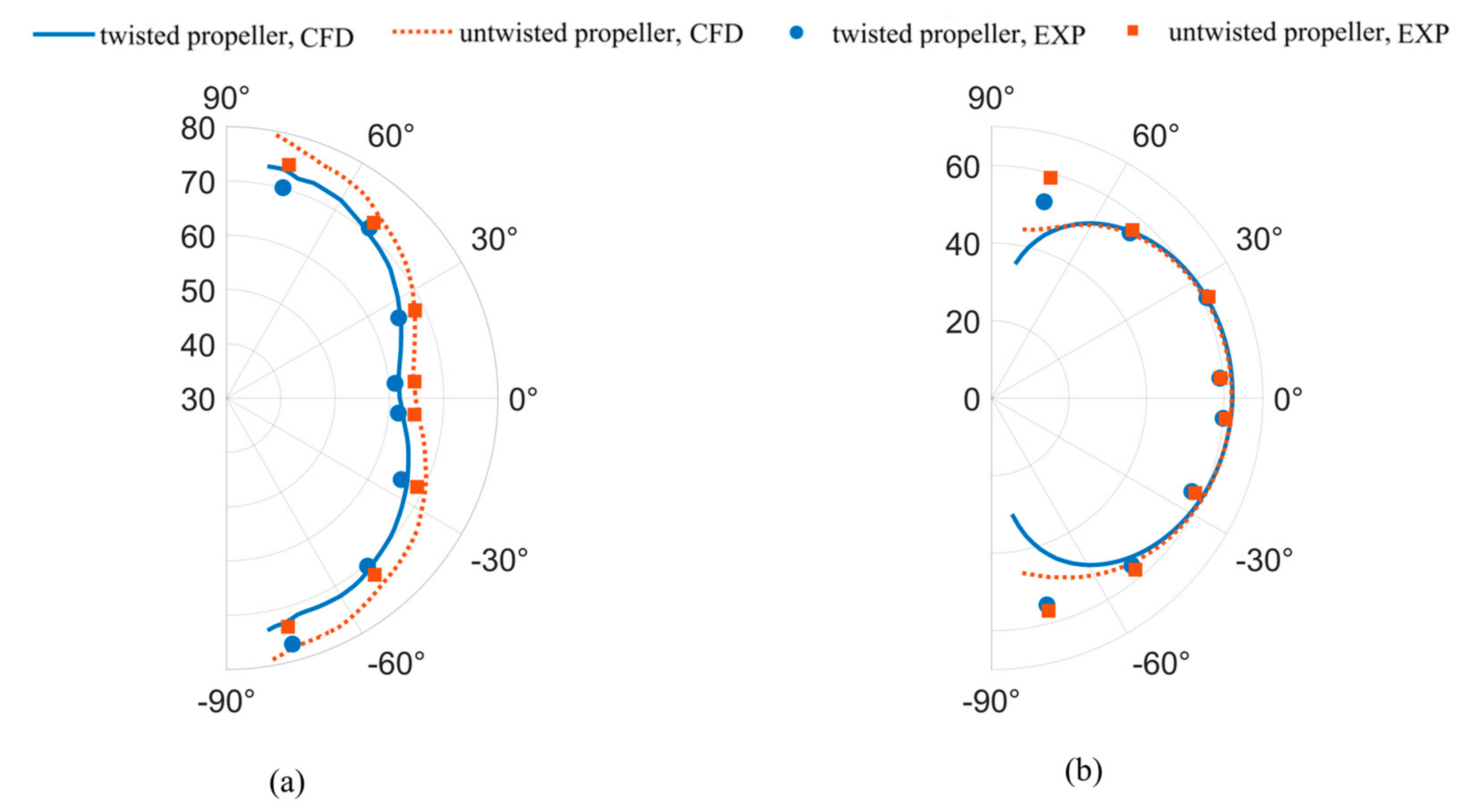
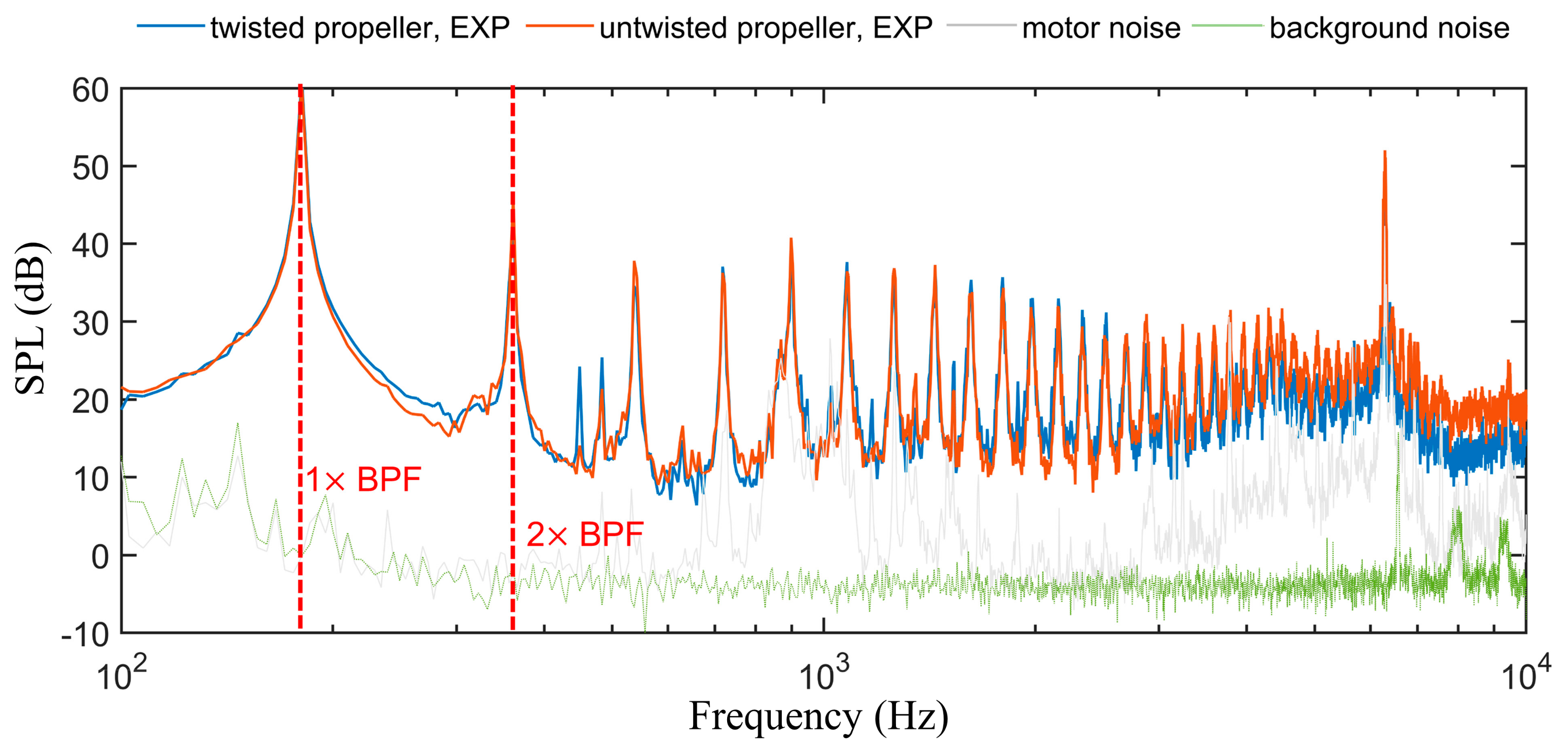
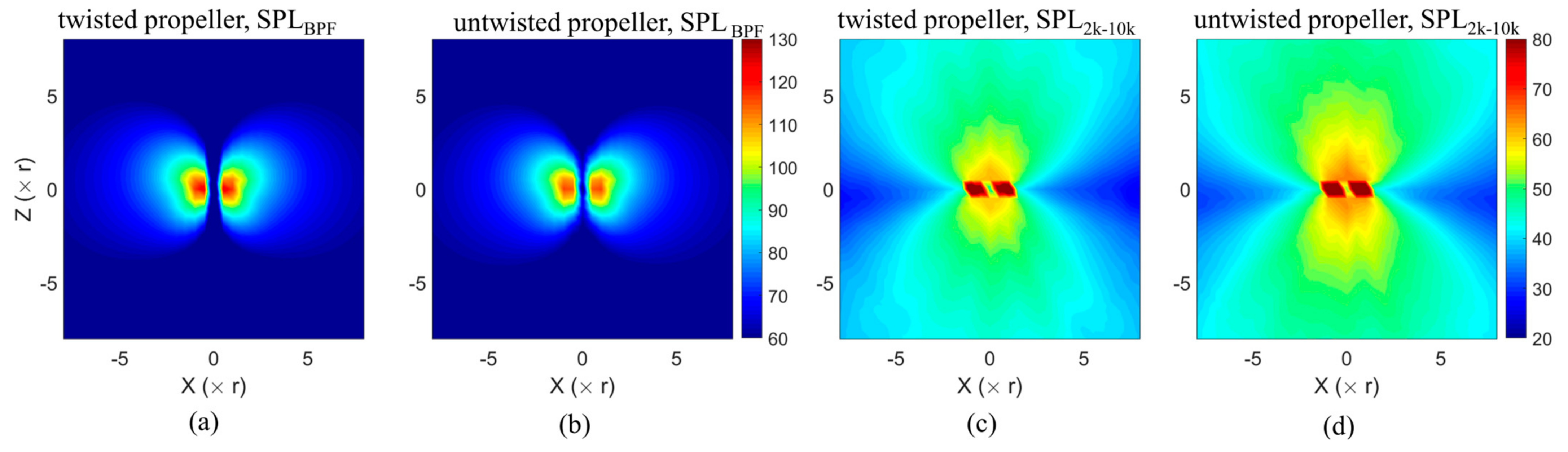
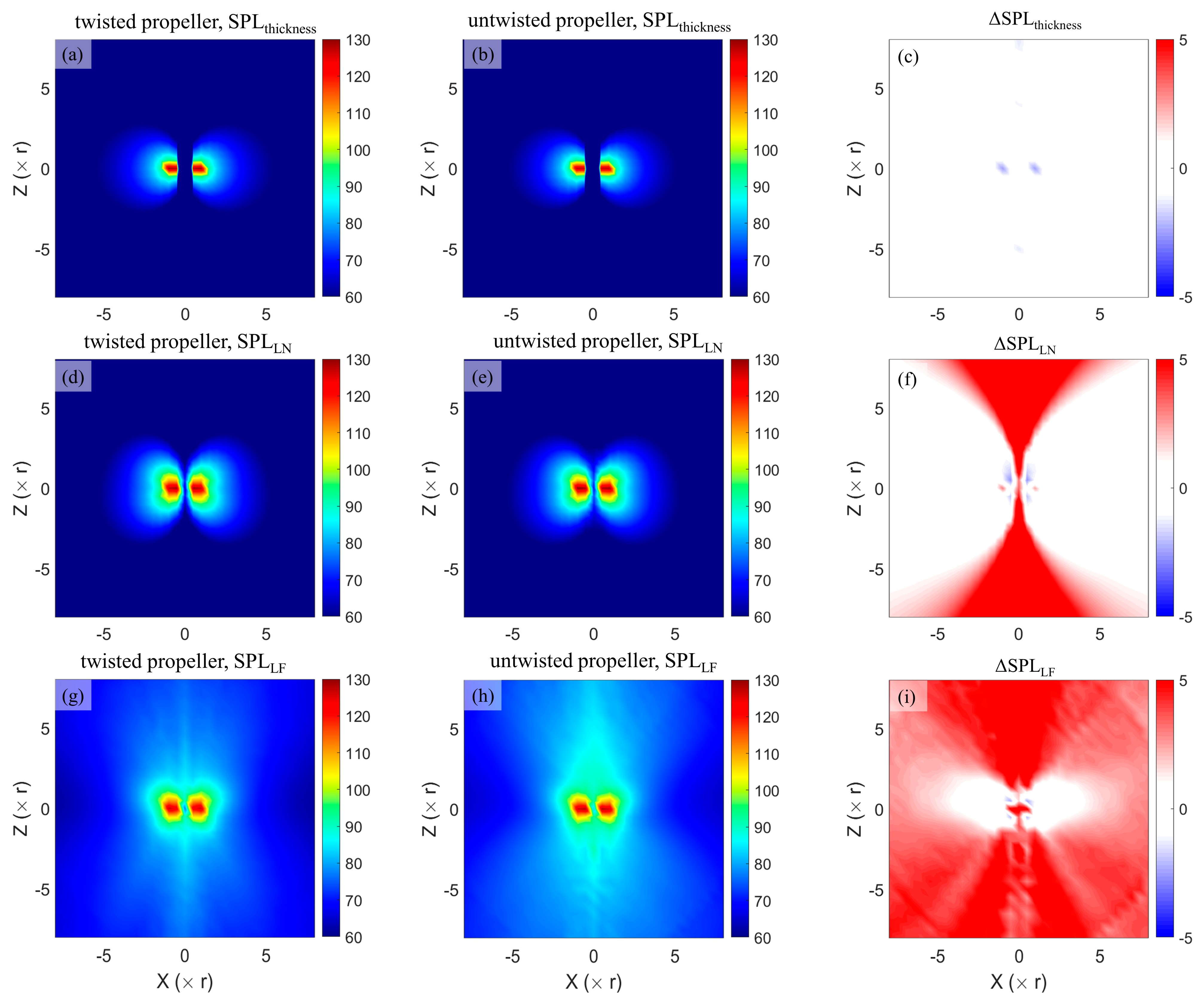
3.3. Acoustic Performance
4. Discussion
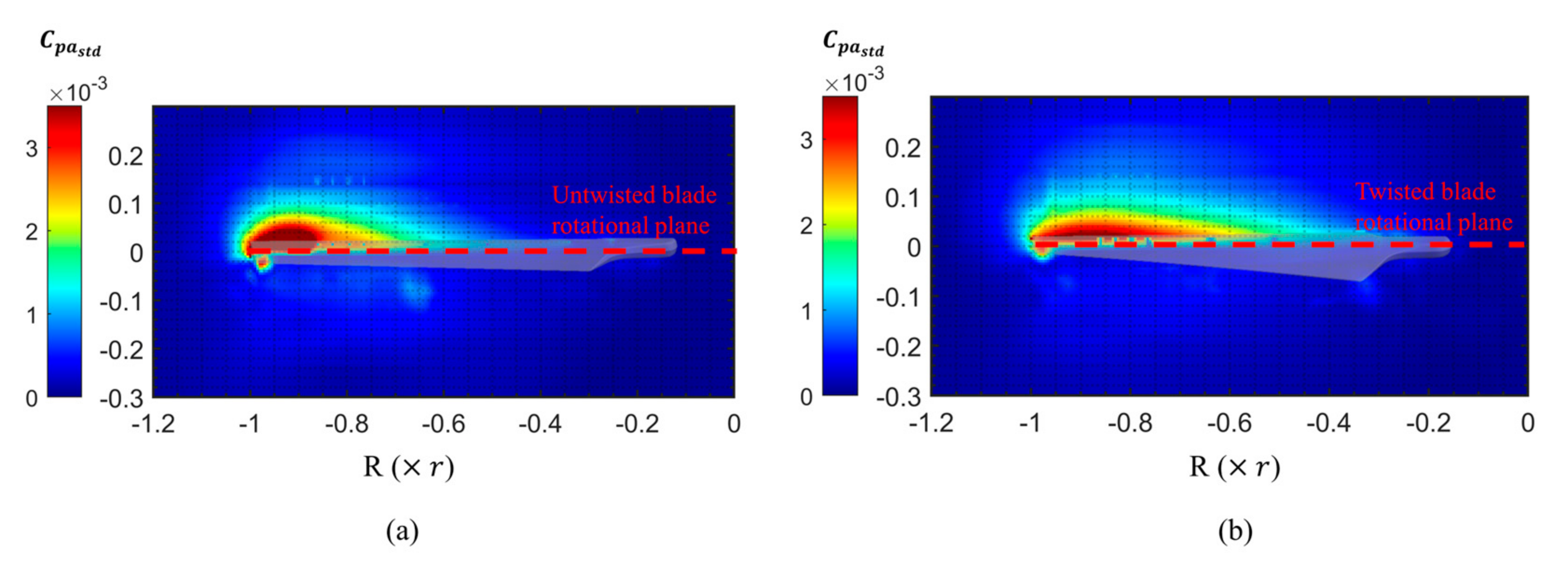
4.1. Near-Blade Flow Fields
4.2. Tip Vortex and Trailing Edge Vortex
5. Conclusions
- (1)
- The hover-stand experiments in an anechoic chamber show that the twisted blade enables achieving a remarked increase in figure of merit (FM) by 9.3% compared to the untwisted blade at the same thrust coefficient. In terms of acoustic performance, the twisted propeller blade is capable to reduce the overall sound pressure level (OASPL) by up to 4.3 dB at a polar angle of 75°. and by an average of 2.2 dB at a distance of 8 r apart from the rotational center.
- (2)
- The 2D phase-locked PIV method combined with the visualizations of both kinetic energy fluctuation (k) and pressure fluctuations reveal that the twisted propeller blade can mitigate kinetic energy fluctuations in the vicinity of the blade tip, suppressing the trailing edge vortices, hence reducing the OASPL in terms of broadband noise in the high-frequency range (2 kHz to 10 kHz).
- (3)
- Our results point to the possibility of optimal twisted blade design in significantly improving both aerodynamic and acoustic performance in multirotor propellers, which is of importance for the development of high-efficiency and low-noise drones.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviations | Definitions |
| CFD | computational fluid dynamic |
| PIV | particle image velocimetry |
| FM | figure of merit |
| OASPL | overall sound pressure level |
| fps | frames per second |
| SPL | sound pressure level |
| PSD | power spectral density |
| BPF | blade passing frequency |
| TV | tip vortices |
| TEV | trailing edge vortices |
References
- Floreano, D.; Wood, R.J. Science, technology and the future of small autonomous drones. Nature 2015, 521, 460–466. [Google Scholar] [CrossRef] [PubMed]
- Song, B.D.; Park, K.; Kim, J. Persistent UAV delivery logistics: MILP formulation and efficient heuristic. Comput. Ind. Eng. 2018, 120, 418–428. [Google Scholar] [CrossRef]
- Otto, A.; Agatz, N.; Campbell, J.; Golden, B.; Pesch, E. Optimization approaches for civil applications of unmanned aerial vehicles (UAVs) or aerial drones: A survey. Networks 2018, 72, 411–458. [Google Scholar] [CrossRef]
- Christian, A.W.; Cabell, R. Initial Investigation into the Psychoacoustic Properties of Small Unmanned Aerial System Noise. In Proceedings of the 23rd AIAA/CEAS Aeroacoustics Conference, AIAA AVIATION Forum, Denver, CO, USA, 5–9 June 2017; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2017. [Google Scholar]
- Sun, J.; Yonezawa, K.; Shima, E.; Liu, H. Integrated Evaluation of the Aeroacoustics and Psychoacoustics of a Single Propeller. Int. J. Environ. Res. Public Health 2023, 20, 1955. [Google Scholar] [CrossRef]
- Torija, A.J.; Li, Z.; Self, R.H. Effects of a hovering unmanned aerial vehicle on urban soundscapes perception. Transp. Res. D Transp. Environ. 2020, 78, 102195. [Google Scholar] [CrossRef]
- European Union Aviation Safety Agency. EASA Publishes First Guidelines on Noise Level Measurements for Drones below 600kg; European Union Aviation Safety Agency: Cologne, Germany, 2022. [Google Scholar]
- Jiang, H.; Wu, H.; Chen, W.; Zhou, P.; Zhong, S.; Zhang, X.; Zhou, G.; Chen, B. Toward high-efficiency low-noise propellers: A numerical and experimental study. Phys. Fluids 2022, 34, 076116. [Google Scholar] [CrossRef]
- Ning, Z.; Hu, H. An Experimental Study on the Aerodynamic and Aeroacoustic Performances of a Bio-Inspired UAV Propeller. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, Denver, CO, USA, 5–9 June 2017; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2017. [Google Scholar]
- Hu, H.; Yang, Y.; Liu, Y.; Liu, X.; Wang, Y. Aerodynamic and aeroacoustic investigations of multi-copter rotors with leading edge serrations during forward flight. Aerosp. Sci. Technol. 2021, 112, 106669. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Y.; Arcondoulis, E.; Wang, Y.; Li, Y. Aerodynamic and Aeroacoustic Performance of an Isolated Multicopter Rotor during Forward Flight. AIAA J. 2020, 58, 1171–1181. [Google Scholar] [CrossRef]
- Tinney, C.E.; Sirohi, J. Multirotor Drone Noise at Static Thrust. AIAA J. 2018, 56, 2816–2826. [Google Scholar] [CrossRef]
- Lee, H.; Ryu, J.; Ahn, S.; Kwon, O. Aerodynamic design optimization of uav rotor blades using a genetic algorithm and artificial neural networks. J. Comput. Fluids Eng. 2014, 19, 29–36. [Google Scholar] [CrossRef]
- Hoyos, J.D.; Jiménez, J.H.; Echavarría, C.; Alvarado, J.P.; Urrea, G. Aircraft Propeller Design through Constrained Aero-Structural Particle Swarm Optimization. Aerospace 2022, 9, 153. [Google Scholar] [CrossRef]
- Boutemedjet, A.; Samardžić, M.; Rebhi, L.; Rajić, Z.; Mouada, T. UAV aerodynamic design involving genetic algorithm and artificial neural network for wing preliminary computation. Aerosp. Sci. Technol. 2019, 84, 464–483. [Google Scholar] [CrossRef]
- Tang, D.; Tang, B.; Shen, W.; Zhu, K.; Quan, Q.; Deng, Z. On genetic algorithm and artificial neural network combined optimization for a Mars rotorcraft blade. Acta Astronaut. 2023, 203, 78–87. [Google Scholar] [CrossRef]
- Burger, C.; Hartfield, R.; Burkhalter, J. Performance and Noise Optimization of a Propeller Using the Vortex Lattice Method and a Genetic Algorithm. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2007; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2007. [Google Scholar]
- Liu, X.; Wang, L.; Tang, X. Optimized linearization of chord and twist angle profiles for fixed-pitch fixed-speed wind turbine blades. Renew. Energy 2013, 57, 111–119. [Google Scholar] [CrossRef]
- Shukla, D.; Komerath, N. Low Reynolds number multirotor aerodynamic wake interactions. Exp. Fluids 2019, 60, 77. [Google Scholar] [CrossRef]
- Lee, S.J.; Paik, B.G.; Yoon, J.H.; Lee, C.M. Three-component velocity field measurements of propeller wake using a stereoscopic PIV technique. Exp. Fluids 2004, 36, 575–585. [Google Scholar] [CrossRef]
- Shukla, D.; Komerath, N. Multirotor Drone Aerodynamic Interaction Investigation. Drones 2018, 2, 43. [Google Scholar] [CrossRef]
- Li, Y.; Yonezawa, K.; Liu, H. Effect of Ducted Multi-Propeller Configuration on Aerodynamic Performance in Quadrotor Drone. Drones 2021, 5, 101. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, H. Application of Phase-Locked PIV Technique to the Measurements of Flow Field in a Turbine Stage. J. Therm. Sci. 2020, 29, 784–792. [Google Scholar] [CrossRef]
- Ragni, D.; van Oudheusden, B.W.; Scarano, F. 3D pressure imaging of an aircraft propeller blade-tip flow by phase-locked stereoscopic PIV. Exp. Fluids 2011, 52, 463–477. [Google Scholar] [CrossRef]
- Ning, Z.; Wlezien, R.W.; Hu, H. An Experimental Study on Small UAV Propellers with Serrated Trailing Edges. In Proceedings of the 47th AIAA Fluid Dynamics Conference, Denver, CO, USA, 5–9 June 2017; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2017. [Google Scholar]
- Ffowcs-Williams, J.E.; Hawkings, D.L. Sound generation by turbulence and surfaces in arbitrary motion. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1969, 264, 321–342. [Google Scholar] [CrossRef]
- Iannace, G.; Ciaburro, G.; Trematerra, A. Acoustical unmanned aerial vehicle detection in indoor scenarios using logistic regression model. Build. Acoust. 2020, 28, 77–96. [Google Scholar] [CrossRef]
- Whelchel, J.; Alexander, W.N.; Intaratep, N. Propeller Noise in Confined Anechoic and Open Environments. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2020. [Google Scholar]
- Papa, U.; Iannace, G.; Del Core, G.; Giordano, G. Sound power level and sound pressure level characterization of a small unmanned aircraft system during flight operations. Noise Vib. Worldw. 2017, 48, 67–74. [Google Scholar] [CrossRef]
- Rong, J.; Liu, H. Effects of owl-inspired leading-edge serrations on tandem wing aeroacoustics. AIP Adv. 2022, 12, 115103. [Google Scholar] [CrossRef]
- Jiang, H.; Zhong, S.; Wu, H.; Zhang, X.; Huang, X.; Zhou, G.; Chen, B. Radiation Modes of Propeller Tonal Noise. J. Vib. Acoust. 2022, 144, 021009. [Google Scholar] [CrossRef]
- Tanabe, Y.; Sugawara, H.; Yonezawa, K.; Sunada, S.; Tokutake, H. Influence of Rotor Blade Twist on the Ducted Rotor Performance. In Proceedings of the 8th Asian/Australian Rotorcraft Forum 2019 (ARF), Ankara, Turkey, 30 October–2 November 2019. [Google Scholar]
- Tanabe, Y.; Sugawara, H.; Sunada, S.; Yonezawa, K.; Tokutake, H. Quadrotor Drone Hovering in Ground Effect. J. Robot. Mechatron. 2021, 33, 339–347. [Google Scholar] [CrossRef]
- Ikeda, T.; Ueda, T.; Nakata, T.; Noda, R.; Tanaka, H.; Fujii, T.; Liu, H. Morphology Effects of Leading-edge Serrations on Aerodynamic Force Production: An Integrated Study Using PIV and Force Measurements. J. Bionic Eng. 2018, 15, 661–672. [Google Scholar] [CrossRef]
- Thielicke, W.; Sonntag, R. Particle Image Velocimetry for MATLAB: Accuracy and enhanced algorithms in PIVlab. J. Open Res. Softw. 2021, 9, 12. [Google Scholar] [CrossRef]
- Bu, H.; Wu, H.; Bertin, C.; Fang, Y.; Zhong, S. Aerodynamic and acoustic measurements of dual small-scale propellers. J. Sound Vib. 2021, 511, 116330. [Google Scholar] [CrossRef]
- Sugiura, M.; Tanabe, Y.; Matayoshi, N.; Ishii, H.; Sugawara, H. Numerical Simulations and Measurements of the Helicopter Wake in Ground Effect. J. Aircr. 2017, 54, 209–219. [Google Scholar] [CrossRef]
- Tanabe, Y.; Sugiura, M.; Aoyama, T.; Sugawara, H.; Sunada, S.; Yonezawa, K.; Tokutake, H.; Systems, C.R. Multiple Rotors Hovering Near an Upper or a Side Wall. J. Robot. Mechatron. 2018, 30, 344–353. [Google Scholar] [CrossRef]
- Farassat, F. Derivation of Formulations 1 and 1A of Farassat; NASA: Hampton, VA, USA, 2007. [Google Scholar]
- Tanabe, Y.; Saito, S.; Sugawara, H. Evaluation of Rotor Noise Reduction by Active Devices Using a CFD/CSD Coupling Analysis Tool Chain. In Proceedings of the 1st Asian Australian Rotorcraft Forum and Exhibition, Busan, Republic of Korea, 12–15 February 2012; Volume 2012. [Google Scholar]
- Chatila, J.G.; Danageuzian, H.R. PIV and CFD investigation of paddle flocculation hydrodynamics at low rotational speeds. Sci. Rep. 2022, 12, 19742. [Google Scholar] [CrossRef] [PubMed]
- Leishman, G.J. Principles of Helicopter Aerodynamics; Cambridge University Press: Cambridge, UK, 2006; ISBN 0521858607. [Google Scholar]
- Kurtz, D.W.; Marte, J.E. A Review of Aerodynamic Noise from Propellers, Rotors, and Lift Fans; NASA: Pasadena, CA, USA, 1970. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Yonezawa, K.; Tanabe, Y.; Sugawara, H.; Liu, H. Blade Twist Effects on Aerodynamic Performance and Noise Reduction in a Multirotor Propeller. Drones 2023, 7, 252. https://doi.org/10.3390/drones7040252
Sun J, Yonezawa K, Tanabe Y, Sugawara H, Liu H. Blade Twist Effects on Aerodynamic Performance and Noise Reduction in a Multirotor Propeller. Drones. 2023; 7(4):252. https://doi.org/10.3390/drones7040252
Chicago/Turabian StyleSun, Jianwei, Koichi Yonezawa, Yasutada Tanabe, Hideaki Sugawara, and Hao Liu. 2023. "Blade Twist Effects on Aerodynamic Performance and Noise Reduction in a Multirotor Propeller" Drones 7, no. 4: 252. https://doi.org/10.3390/drones7040252
APA StyleSun, J., Yonezawa, K., Tanabe, Y., Sugawara, H., & Liu, H. (2023). Blade Twist Effects on Aerodynamic Performance and Noise Reduction in a Multirotor Propeller. Drones, 7(4), 252. https://doi.org/10.3390/drones7040252






