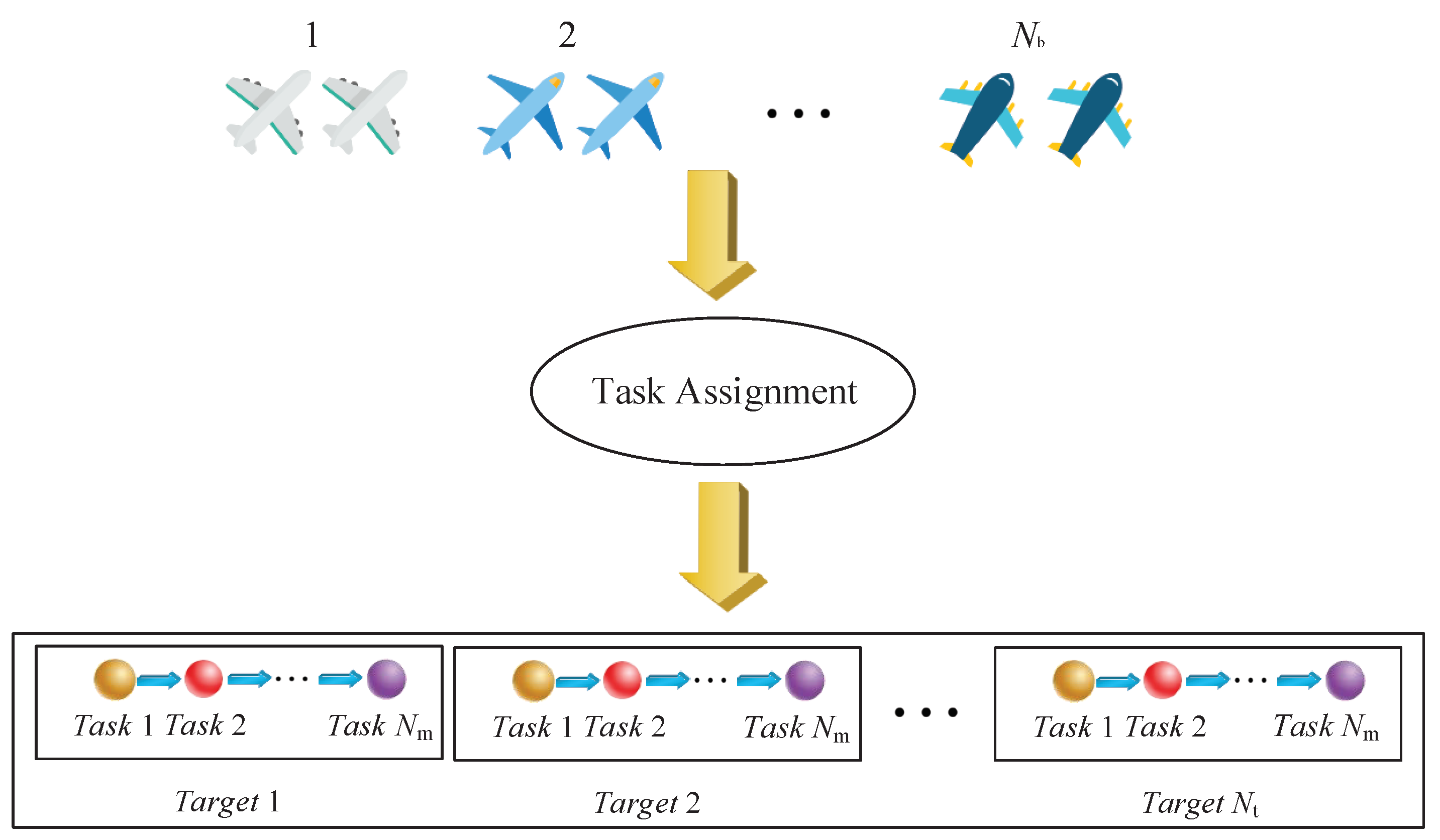
1. Introduction
Due to its rapid deployment and nearly unlimited mobility, an unmanned aerial vehicle (UAV) has great potential in both military and civilian applications, including modern warfare, disaster search and rescue, traffic control, celestial exploration, and a variety of other fields [
1,
2,
3,
4]. UAVs for these applications have limited capabilities and require sufficient resources to perform tasks autonomously. As a result, multi-UAVs can be regarded as a promising method by which to handle complex tasks. As more attention is focused on them, two problems in multi-UAV collaboration, such as multi-UAV cooperative path planning and cooperative task assignment, are becoming more widely recognized. The main consideration of this paper is the multi-UAV cooperative task assignment problem.
In recent years, many scholars have paid attention to the multi-UAV cooperative task assignment problem, while the related research of this problem is as follows. Chen et al. [
5] utilized mixed integer linear programming (MILP) to address the problem of multi-UAV cooperative task assignment and path planning for moving targets on the ground, but it had low scalability while maintaining global optimality. References [
6,
7] used a heuristic approach to produce near-optimal results in real time, which has been widely considered for large-scale problems and dynamic scenarios. For swarm intelligence algorithms, e.g., particle swarm optimization (PSO) [
8], ant colony optimization (ACO) [
9], and genetic algorithm (GA) [
10], when solving the task assignment problem, they had a fast convergence speed and could effectively obtain optimal assignment schemes, but there is a possibility of falling into local optimum. Moreover, the auction algorithm, game theory, and reinforcement learning have also been applied to the multi-UAV task assignment problem. Duan et al. [
11] presented a novel hybrid “two-stage” auction algorithm that combines the structural advantages of the centralized and distributed auction algorithms, which greatly facilitates the performance of UAVs in dynamic task assignments. Chen et al. [
12] studied the cooperative reconnaissance and spectrum access (CRSA) problem for task-driven heterogeneous coalition-based UAV networks, and proposed a joint bandwidth allocation and coalition formation (JBACF) algorithm to solve the task assignment and bandwidth allocation. Qie et al. [
13] proposed an artificial intelligence method called simultaneous target assignment and path planning (STAPP) to solve the multi-UAV target assignment and path planning problem, and the effectiveness of the algorithm was experimentally verified. In addition, references [
14,
15,
16,
17,
18,
19,
20,
21] provide a variety of alternative algorithms for the solution of analogous problems.
Similarly, some novel works on task assignment, e.g., UAV-assisted task assignment, have been presented. Liu et al. [
22] studied a UAV-assisted IoT system while presenting a nonconvex age-of-information (AoI) minimization problem, which was solved by jointly optimizing task assignment, interaction point selection (IPT), and UAV trajectories. Zhu et al. [
23] considered the problem of task loss rate (TLR) fairness among IoTs and equal energy consumption (EC) fairness among UAVs, and proposed a multiagent deep deterministic policy gradient (MA-DDPG) method by which to assign UAVs to accomplish tasks and guarantee the balance between IoT TLR and UAV EC. Seid et al. [
24] considered the assignment of UAVs to perform aerial base station tasks based on a multi-UAV-assisted IoT network framework, while presenting a joint optimization problem for computational offloading with energy harvesting (EH) and resource price, and the resource demands and pricing strategies between IoT devices and UAVs were continuously adjusted by the Stackelberg game. Hu et al. [
25] considered the aging of cache refreshing, computation offloading, and state updates in UAV-assisted vehicle task awareness, and formulated a task-assignment energy-minimization problem that was solved by a deep deterministic policy gradient (DDPG) method. Zhou et al. [
26] studied UAV-assisted mobile crowd sensing (MCS) scenarios and proposed a UAV-assisted multitasking assignment (UMA) method, while demonstrating the effectiveness of UMA. In addition, compared the UAV-assisted task assignment with the UAV task assignment, the difference is that UAVs play a secondary role in the former while serving as the primary reconnaissance and attack objects in the latter. Furthermore, the simulation scenarios in the paper are not consistent with the existing works (e.g., references [
22,
23,
24,
25,
26]).
In the complex stochastic network, the cross-entropy (CE) method [
27], a relatively new technique for dealing with combinatorial optimization problems, was initially utilized to estimate rare event probabilities. Then, references [
28,
29] discussed and analysed its convergence. Additionally, the cross-entropy (CE) method was proved by the authors in [
30] to be particularly meaningful for handling combinatorial optimization problems. Since then, it has also been proven by many scholars to be a simple and effective tool for different fields, e.g., vehicle routing [
31], buffer allocation [
31], and machine learning [
32]. In addition, researchers have also considered applying the cross-entropy (CE) method to the UAV task assignment [
33,
34,
35]. However, the authors of these papers did not consider the specific precedence and timing constraints among these tasks.
When it comes to task-assignment schemes in the field of UAVs, some researchers usually assume that each UAV is assigned to only one target, and they rarely consider the execution sequence and the time constraints among tasks. On the other hand, multi-UAVs are sometimes needed to perform some complex combinatorial tasks, such as classifying the target, attacking it, and then verifying the target’s damage level in a reasonable time on the battlefield. In addition, such deterministic approaches may not be able to find the optimal solution in a reasonable time for large-scale task assignment problems. Under these circumstances, we present an adjustable fully adaptive cross-entropy (AFACE) algorithm based on CE method.
Therefore, the purpose of this paper is to study the AFACE algorithm for the multi-UAV cooperative task assignment problem under resource, precedence, and timing constraints. The main contributions are summed up as follows.
We consider the multi-UAV cooperative task assignment problem in which different types of UAVs are assigned to perform classification, attack and verification tasks of targets under resource, and precedence and timing constraints. Considering complex coupling among these tasks, we decompose the considered problem into two subproblems: one with continuous and independent tasks and another with continuous and correlative tasks.
We propose an AFACE algorithm, which changes the random sample and the quantile at each iteration and adds a parameter to adjust the maximum sample based on the CE method. Meanwhile, the algorithm serves as a stepping stone for developing other algorithms.
To overcome task precedence and task coupling existing in these two problems, respectively, we present a mutually independent AFACE (MIAFACE) algorithm and a mutually correlative AFACE (MCAFACE) algorithm with polynomial time complexity. The former algorithm converges faster than the CE method, while the computational complexity of the latter algorithm is inferior to that of the former algorithm.
Simulation results demonstrate that both MIAFACE and MCAFACE algorithms consume less time than other existing optimization algorithms for solving the corresponding problem.
The rest of this paper is organized as follows. In
Section 2, we introduce the related works of the CE method and other algorithms for the UAV task assignment.
Section 3 depicts the multi-UAV cooperative task assignment problem with its mathematical formulation. In
Section 4, we decompose the considered problem into two subproblems, and propose an AFACE algorithm, a MIAFACE algorithm, and a MCAFACE algorithm, and apply the latter two algorithms to solving the corresponding problem.
Section 5 conducts several simulations and comparisons to verify the feasibility and effectiveness of the proposed algorithms. This paper is concluded in
Section 6.
4. Algorithm Analysis
In this section, an AFACE algorithm will be introduced for the considered problem, and the differences between the algorithm and cross-entropy (CE) method are that the former changes the random sample and the quantile at each iteration t, and adds a parameter to adjust the maximum sample . For details, please refer to the analysis of the algorithm below.
4.1. Adjustable Fully Adaptive Cross-Entropy Algorithm
Referring to the principle of CE method in references [
30,
35] and maximizing the subobjective function
of the considered problem, we have
where
is the maximum of
on
; that is, the optimal scheme vector is
.
After that, transform this problem into a probability estimator problem, which can be explained by the probability density function (PDF)
with respect to
u, and the problem can be written as
where
denotes a value close to
,
represents the probability measure under which the random vector
has the PDF
,
is the corresponding expectation operator, and
, i.e.,
, denotes the indicator function, which is
Then, at the
tth iteration of AFACE algorithm, we obtain
where
(
) denotes the
ith sample performance, and
and
are defined by
and
for convenience. Meanwhile, AFACE algorithm parameters
and
satisfy
where
denotes the random sample of the
tth iteration, varying between
and
(
) and
represents the quantile of the
tth iteration. The reason for presenting
h is that by adjusting the size of
, we can obtain the optimal
that matches the combat scenario, which can be conducted by the following simulations in
Section 5.
For the AFACE algorithm, the main idea is to update and based on the elite sample (), where and N are the elite sample influence coefficient of task m (usually ) and the fixed random sample, respectively. Therefore, the set of elite samples () are comprised of such samples in with the highest performances .
Next, referring to the formulas for solving
and
of CE method [
30], they are modified as
where
is generated from
,
denotes another PDF with respect to
v on
via minimizing the Kullback–Leibler distance,
is equal to the worst sample performance among the elite performances, while
is the best sample performance among the elite performances, and
converges to the probability density when
occurs.
Then, we devise a sampling scheme for each iteration
t, ensuring high probability that
Moreover, we simultaneously generate two sequences to validate the correctness of AFACE algorithm. One is the levels
, and the other is the parameters
. After that, the initialization process is set to
, and the quantile (
) is calculated at the
tth iteration according to Equation (
18), followed by the next two steps of Algorithm 1.
In addition, the main steps of AFACE algorithm applied to solving the subobjective function of the considered problem are given by Algorithm 2.
| Algorithm 1 Adaptive updating of and . |
Adaptive updating of :- 1:
Given a fixed at the tth iteration; - 2:
Let be a ()-quantile of under , then satisfies , where ; - 3:
Obtain a simple estimator of by drawing random samples from ; - 4:
Calculate and order all performances of from smallest to biggest: ; - 5:
Compute according to Equation ( 19);
Adaptive updating of :- 6:
Given a fixed and at the tth iteration, then derive according to Equation (20).
|
| Algorithm 2 AFACE algorithm. |
Input: , h, N.
Output: .- 1:
Set t = 1, and ; - 2:
while at the tth iteration () do - 3:
if then - 4:
Generate () random samples from ; - 5:
Calculate and according to Equations (19) and (20); - 6:
else - 7:
Draw () random samples from ; - 8:
end if - 9:
Update and according to Algorithm 1, then calculate ; - 10:
if Equation ( 21) occurs then - 11:
Set t = t + 1 and go to step 2; - 12:
else - 13:
Check whether or not for some , e.g., ; - 14:
if then - 15:
Stop, obtain and return; - 16:
else - 17:
Set , take random integer in and go to step 2; - 18:
end if - 19:
end if - 20:
end while
|
4.2. Adjustable Fully Adaptive Cross-Entropy Algorithm for Solving Problem
Considering complex coupling among the three tasks, we decompose the considered problem into two subproblems: the problem with continuous and independent tasks and the problem with continuous and correlative tasks.
Before discussing the algorithm for solving problem , we have to determine the number of the available schemes for each task. Please refer to Theorem 1 for the specific derivation process.
Theorem 1. Assume that and , the number of the available schemes for each task of targets is L. Then, according to the mathematical formulas of permutation and combination, we can obtain 4.2.1. Mutually Independent AFACE Algorithm for Solving Problem
In problem
, assume that there are
continuous and mutually independent tasks for each target. Time continuity among these tasks then needs to be considered. Assume that there are
L available schemes for each task, i.e., the scheme chosen by the previous task has no effect on the choice of the scheme for the next task, indicating that the available schemes among these tasks are independent. Thus, the problem
is rewritten as
where
is the available schemes when performing the
mth task.
Considering time sequence and independence of the available schemes among these tasks, we present a MIAFACE algorithm, which is a combination of
AFACE algorithms. For MIAFACE algorithm, we first introduce the probability matrix vector
and the performance vector
, where
and
are the probability matrix and the performance of task
m, respectively. Then,
is defined as
where
represents the probability of assigning the
kth UAV formation to accomplish task
m of target
j and
is subjected to
.
Then, for the mth task, we initialize with a uniform distribution. Let be the number of the feasible schemes of target j, and define as the element of . After that, we set .
At the tth iteration, we assume that the samples are drawn from . In addition, we calculate the performances , and order them from smallest to largest: . It is noted that is calculated by , and is updated by Equation (20). After that, we compare with , and obtain all eligible performances greater than and merge them into a set , where is the number of the element of , and is the maximum element of . Then, is calculated, and the specific derivation process can be seen in Theorem 2. Thus, is the probability matrix composed of , and is equal to .
Theorem 2. Assume that there are continuous and mutually independent tasks for each target. After that, tasks correspond to AFACE algorithms, which has an elite sample of . In the MIAFACE algorithm, is a combined vector of , e.g., . Thus, when performing the mth task, we can then obtain the updating formula of as follows: Through the iterative updating of
, the optimal probability matrix vector
and the maximum performance vector
are obtained. Then, the main steps of the MIAFACE algorithm applied to solving problem
are described in Algorithm 3, and the convergence of the MIAFACE algorithm is similar to that of the CE method in [
40].
| Algorithm 3 MIAFACE algorithm. |
Input: , , N, h.
Output: , .- 1:
Set and ; - 2:
for; ; do - 3:
Initialize with a uniform distribution and define , then set ; - 4:
while at the tth iteration () do - 5:
if then - 6:
Generate () random samples from ; - 7:
else - 8:
Draw () random samples from ; - 9:
end if - 10:
Update according to Equation ( 19) and calculate ; - 11:
- 12:
if and then - 13:
Stop, obtain and , then and ; - 14:
else - 15:
Calculate and update by ; - 16:
Set , take random integer in , then go to step 4; - 17:
end if - 18:
end while - 19:
end for - 20:
Return and .
|
4.2.2. Mutually Correlative AFACE Algorithm for Solving Problem
In problem
, assume that there are
continuous and mutually correlative tasks for each target. Then, time continuity among these tasks also needs to be considered. Assume that when performing the
mth task, there are only
available schemes since
schemes have been deleted before performing the
mth task. It means that the available schemes among these tasks are correlative. Thus, the problem
is rewritten as
where
is the remaining schemes when performing the
mth task.
Considering time sequence and relevance of the available schemes among these tasks, we present a MCAFACE algorithm, which is also combined by
AFACE algorithms. For the MCAFACE algorithm, we first introduce the probability matrix vector
and the performance vector
, where
and
are the probability matrix and the performance of task
m, respectively. Then,
is defined as
where
represents the probability of assigning the
kth UAV formation to accomplish task
m of target
j and
is subjected to
.
Then, for the mth task, we initialize with a uniform distribution. Let be the number of the feasible schemes of target j and define as the element of . After that, we set .
At the tth iteration, we assume that the samples are drawn from . In addition, we calculate the performances , and order them from smallest to largest: . It is noted that is calculated by , and is updated by (20). After that, we compare with , and obtain all eligible performances greater than and merge them into a set , where is the number of the element of and is the maximum element of . Then, is calculated and the specific derivation process can be found in Theorem 3. Thus, is the probability matrix composed of , and is equivalent to .
Theorem 3. Assume that there are continuous and mutually correlative tasks for each target. After that, the selected scheme is required to be deleted after each task is accomplished. The other settings are the same as Theorem 2. Thus, when performing the mth task, we can obtain the updating formula of , as follows: Through the iterative updating of
, the optimal probability matrix vector
and the maximum performance vector
are obtained. Then, the main steps of the MCAFACE algorithm for dealing with problem
are explained in Algorithm 4, and the convergence of the MCAFACE algorithm is also close to that of CE method in [
40].
| Algorithm 4 MCAFACE algorithm. |
Input: , , N, h.
Output:, .- 1:
Set and ; - 2:
for; ; do - 3:
Initialize with a uniform distribution and define , then set ; - 4:
while at the t-th iteration () do - 5:
if then - 6:
Generate () random samples from ; - 7:
else - 8:
Draw () random samples from ; - 9:
end if - 10:
Update according to Equation ( 19) and calculate ; - 11:
- 12:
if and then - 13:
Stop, obtain and , then and ; - 14:
else - 15:
Calculate and update by ; - 16:
Set , take random integer in , then go to step 4; - 17:
end if - 18:
end while - 19:
end for - 20:
Return and .
|
4.3. Complexity Analysis of the MIAFACE Algorithm and the MCAFACE Algorithm
Let
represent the number of tasks,
denote the random sample to perform each task,
represent the iteration number of AFACE algorithm to perform each task,
denote the elite sample,
represent the number of targets, and
L denote the number of all possible UAV deployment schemes. The computational complexity of AFACE algorithm is divided into four parts: initialization
, sample
, sort
, and update
. Meanwhile, these parts can be defined as
Specifically, the computational complexity of AFACE algorithm can be written as
Obviously,
increases with the increment of
, i.e.,
. Then, Equation (
31) is rewritten as
where
is greater than the other terms in the bracket on the right side of the equation. Thus, the time complexity of AFACE algorithm can be computed as
.
When the proposed algorithms are applied to accomplishing
tasks of targets in problems
and
, respectively, according to Algorithm 3 and Equation (
32), the computational complexity of MIAFACE algorithm is
Thus, its time complexity is written as
. However, based on Algorithm 4 and Equation (
32), the computational complexity of the MCAFACE algorithm is
Since , its time complexity is approximately equal to .
5. Simulation and Analysis
In order to verify the effectiveness of the proposed algorithms, we compared these proposed algorithms with the CE method and other intelligent algorithms by applying them to the multi-UAV cooperative task assignment problem. The simulations were implemented in Pycharm Community’s 2019.1.1 x64 version of the programming environment on an Intel Core PC with 8 GB memory. The total cumulative reward that the UAV formations earn by successfully completing three tasks from all targets are used to measure the system performance.
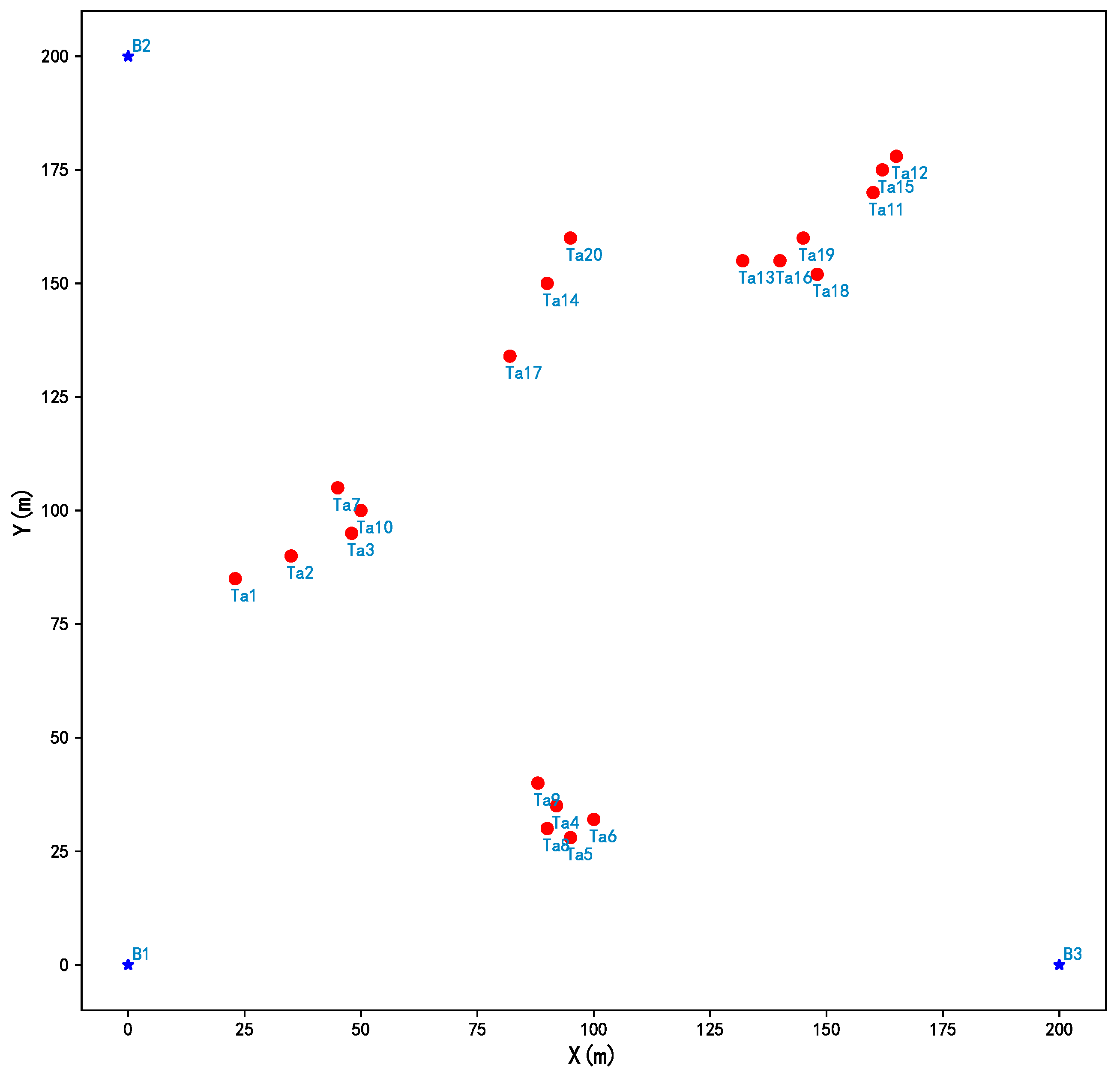
On the basis of the above algorithms, various simulations were performed by assigning three types of UAVs located in the corresponding bases to accomplish three tasks of 20 targets in a 200 m × 200 m combat scenario. The position of each base and these targets are shown in
Figure 2. Bases B1, B2, and B3 are located in (0,0), (0,200), and (200,0), respectively. The information of three types of UAVs and 20 target are given in
Table 2 and
Table 3, respectively, where a and b represent two types of resources, for example, the number of resources a and b needed for different types of UAVs or to accomplish different tasks, and also they have no units.
Referring to Theorem 1, we note that when z exceeds 3, these simulations are complicated. Thus, z is set to be 3, i.e., no more than 3 UAVs are needed to accomplish three tasks of targets in a specific order, and then the total number of each type of UAV is unrestricted. Then, each target in the following cases has 19 possible schemes, i.e., A, B, C, , , , , , , , , , , , , , , , and , respectively, and these schemes correspond to numbers from 1 to 19. After that, we can use a matching approach to quickly find the feasible schemes. The resources needed to accomplish three tasks of targets are randomly generated and satisfy the maximum cooperative number of UAVs.
In the following simulations, the notations used in the tables and the figures are displayed as
represents the initial resources consumed by three types of UAVs;
represents the resources consumed by three tasks; and
Time is CPU time in seconds for each case, and the time of each case is the average consumption time of running 100 times of each algorithm.
The parameters of the CE method, MIAFACE algorithm, MCAFACE algorithm, PSO algorithm, ACO algorithm, and GA algorithm are assumed to be set in
Table 4, where the settings of the speed and maximum flying distance of the UAV are referred to [
35] and they have no effect on the simulation results. For more detailed theory and parameter settings of CE, PSO, ACO, and GA (see [
8,
9,
10,
30,
35,
41]). For the targets in
Table 3, there are two scenarios in the multi-UAV cooperative task assignment problem.
- (1)
In scenario 1, we consider the first 10 targets or more similar targets. When performing the three tasks of each target, we obtain the identical optimal scheme vector of each task. Therefore, the situation in which each target has different tasks but each task has the same optimal scheme is called the problem with continuous and independent tasks.
- (2)
In scenario 2, the last 10 targets or more similar targets are considered. When performing the three tasks of each target, we obtain the different optimal scheme vector of each task. Thus, the situation in which each target has different tasks and each task does not have the same optimal scheme is called the problem with continuous and correlative tasks.
5.1. Scenario 1
In case 1, we used the first 10 targets in
Table 3 to perform continuous and independent tasks of problem
, and the results are shown in
Table 5.
According to
Table 5, we note that the optimal scheme vector and the total result of CE and MIAFACE are identical, while that of MCAFACE is suboptimal to the other two algorithms. Moreover, we can obtain some observations. (i) For CE, the number of iterations and the optimal scheme vector are both 4 and [3,3,3,2,2,2,3,2,2,3], respectively, and the results of each task are −79.50, 274.90, and −79.50, and the sum of the results of each task is 115.9. The situations of MIAFACE are similar to CE, except that the number of iterations is 3. (ii) For MCAFACE, the numbers of iterations and the optimal scheme vectors are 3, 2, 1 and [3,3,3,2,2,2,3,2,2,3], [9,9,9,7,7,7,9,7,7,9], [18,18,18,15,15,15,18,15,15,18], respectively, and the results of each task are −79.50, 179.0, and −82.14, and the sum of the results of each task is 17.36. (iii) The total times of using CE, MIAFACE and MCAFACE are 3.36, 3.29, and 2.17, respectively.
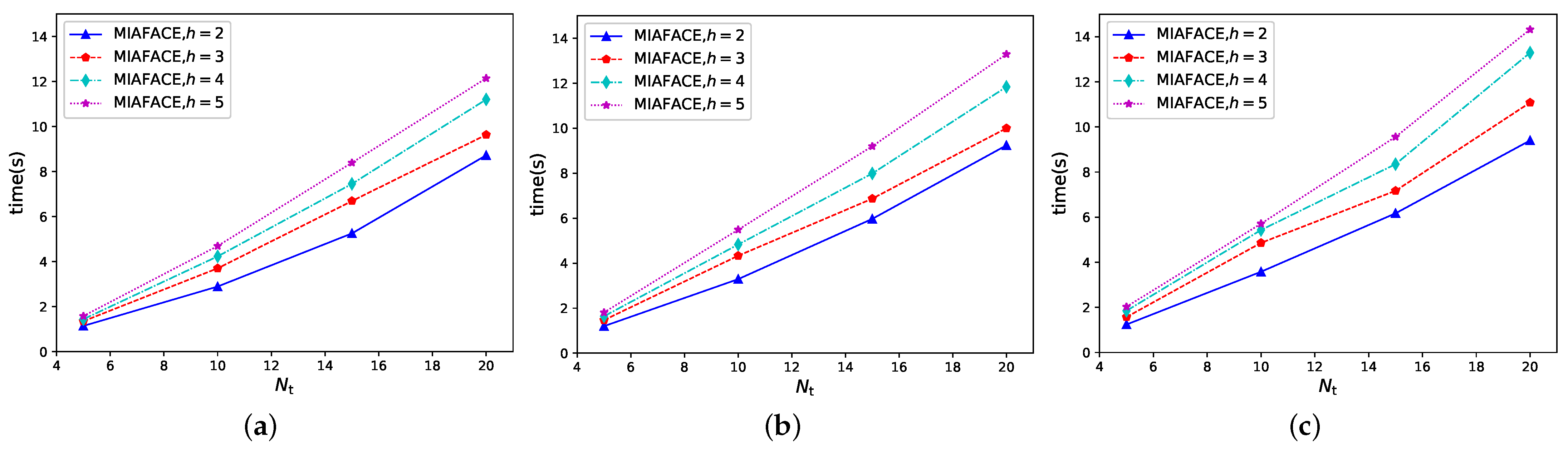
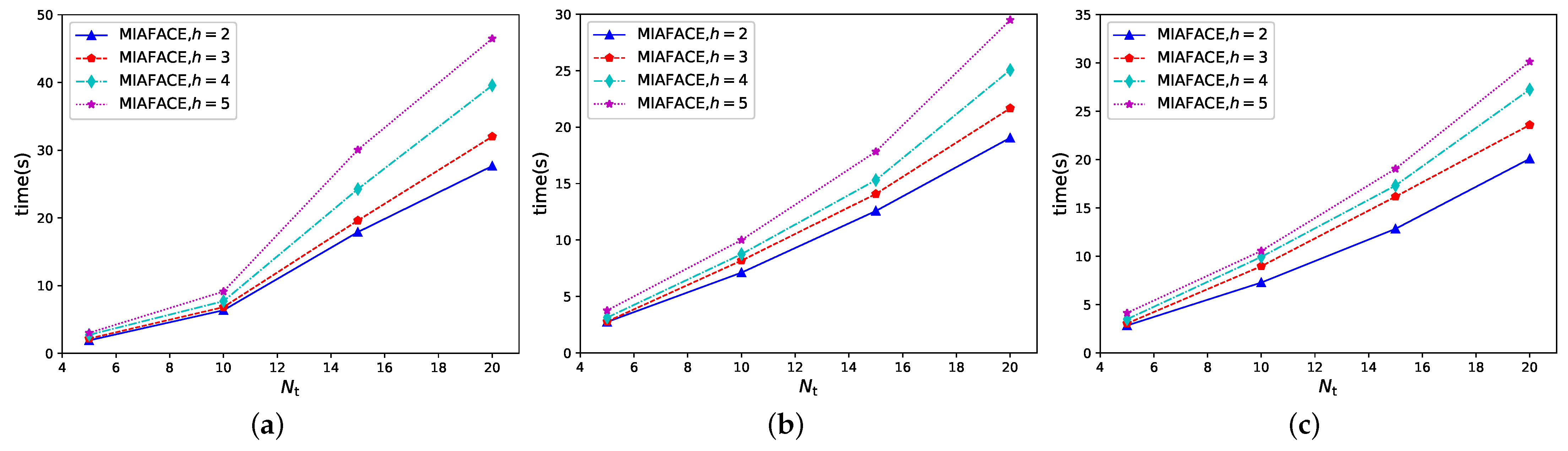
In case 2, we tested the MIAFACE algorithm and MCAFACE algorithm under
h and
, and their times change with
in
Figure 3a–c and
Figure 4a–c, respectively.
From
Figure 3 and
Figure 4, the curves of MIAFACE and MCAFACE both show an increasing trend as
grows, and their times increase with the increment of
and
h. Meanwhile, the time differences between the curves gradually increase with the growth of
in each figure. In
Figure 3a, the curve with
is at the lowest of the four curves, while the curve with
is at the highest of the four curves. The remaining two curves are in the middle, and the curve with
is at the top and the other one is at the bottom. Moreover, the time ranges of the four curves are both approximately in [1,12]. In
Figure 3b,c, their situations are described similarly to
Figure 3a, and their time ranges are in [1,14] and [1,15], respectively. From
Figure 4a, the order of the four curves is similar to
Figure 3a. Moreover, their time ranges are both roughly in [0.3,10]. In
Figure 4b,c, their situations are analogous to
Figure 4a, and their time ranges are in [0.3,10] and [0.3,12], respectively.
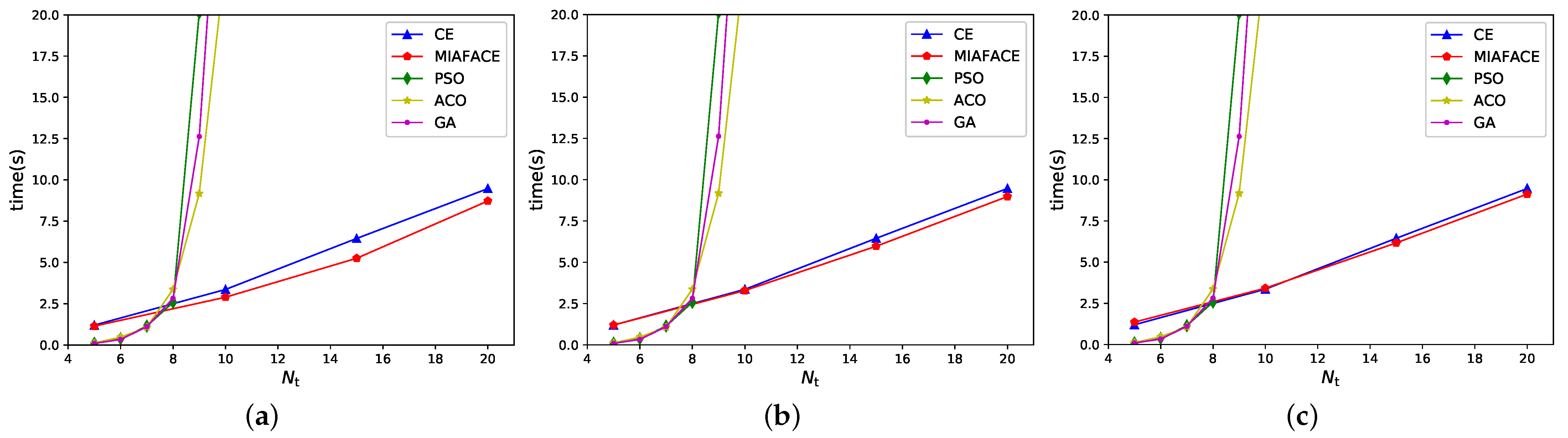
In case 3, the CE method, PSO algorithm, ACO algorithm, and GA algorithm are both used three times for three tasks continuously. We compared them with MIAFACE algorithm by obtaining the same optimal score under
and
, and their times change with
in
Figure 5a–c. Since MCAFACE algorithm obtains suboptimal results in scenario 1, it is not compared to other algorithms.
From
Figure 5, we note that the curves of CE and MIAFACE grow linearly, while the curves of PSO, ACO, and GA increase exponentially. In addition, their times increase gradually with the increment of
and
. In
Figure 5a, when
is in [5,20], the time of MIAFACE is less than that of CE, and the time difference between the two algorithms grows as
increases. Meanwhile, when
is below 8, the times of PSO, ACO, and GA are lower than that of CE and MIAFACE, but when
is more than 8, the situation is reversed. In addition, the time ranges of CE and MIAFACE are both approximately in [1,10], while the times of other algorithms are over 20 when
is larger than 10. From
Figure 5b,c, their situations are similar to
Figure 5a, except that the time difference between CE and MIAFACE in
Figure 5b is lower than that in
Figure 5a, and the time difference in
Figure 5c first decreases gradually to intersect at a point where
is 10, then increases slowly with the increment of
.
5.2. Scenario 2
In case 4, we utilized the last 10 targets in
Table 3 to perform continuous and correlative tasks of problem
, and the results are shown in
Table 6.
According to
Table 6, we note that the optimal scheme vectors and the total results of CE, MIAFACE, and MCAFACE are the same. The reason for this phenomenon is that for three tasks of the same 10 targets, the optimal scheme vectors are eventually obtained and identical by using the three algorithms, which leads to the same score of the total objective function; however, the consumption time by the different algorithms varies. Moreover, some observations are available. First, for CE, the number of iterations and the sum of each task’s result are 5 and 218.72, and the optimal solution vectors are [3,3,3,3,3,3,3,3,3,3], [9,9,9,7,7,7,9,7,7,9], [18,18,18,15,15,15,18,15,15,18], and the results of each task are −298.65, 819.85, and −302.48, respectively. Secondly, the situations using MIAFACE and MCAFACE are similar to that of CE, apart from the fact that the number of iterations in MIAFACE is 4 and the numbers of iterations in MCAFACE are 4, 4, and 3. Finally, the total times using CE, MIAFACE, and MCAFACE are 7.33, 7.11, and 6.9, respectively.
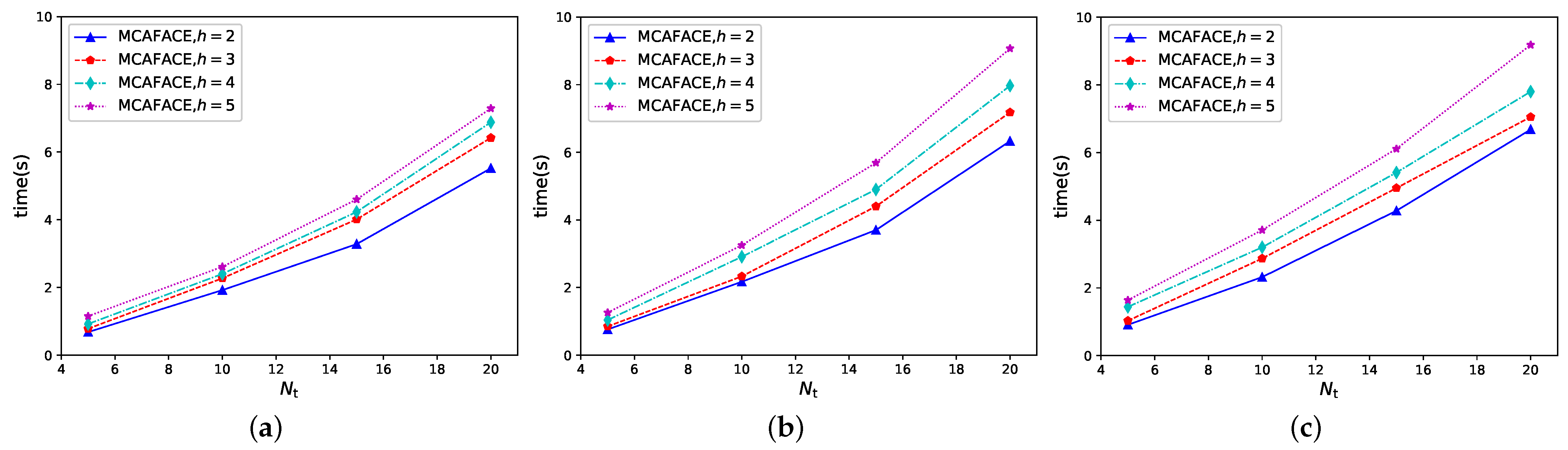
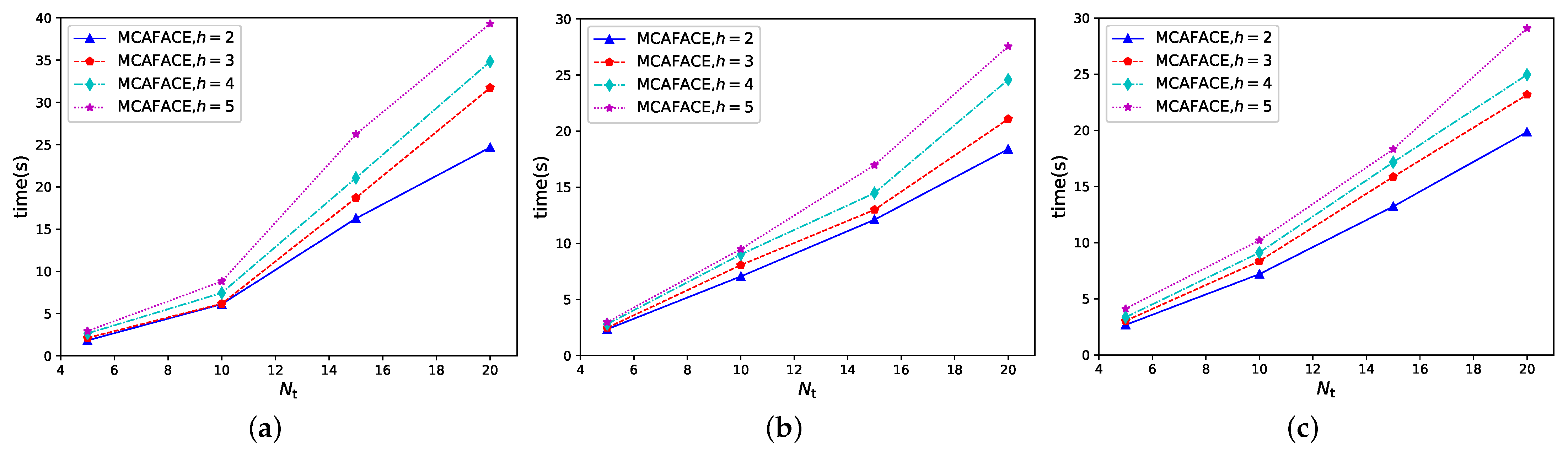
In case 5, we tested the MIAFACE algorithm and MCAFACE algorithm under
h and
, and their times change with
in
Figure 6a–c and
Figure 7a–c, respectively.
From
Figure 6 and
Figure 7, the variations of the curves, the times and the time differences are both similar to
Figure 3 and
Figure 4, while in
Figure 6a and
Figure 7a, the time grows rapidly when
is over 10. The reason is that the results of these two figures are suboptimal to others. In
Figure 6a, the order of the curves is the same as that of each figure in
Figure 3 and
Figure 4. In addition, the time ranges of these four curves are both approximately in [1,50]. From
Figure 6b,c, the situations are described similarly to that of
Figure 6a and their time ranges are in [2,30] and [2,32], except that their results are the optimal results. In
Figure 7, the situation of each figure is roughly similar to that of the corresponding figure in
Figure 6, apart from the fact that the time range is lower than that in
Figure 6.
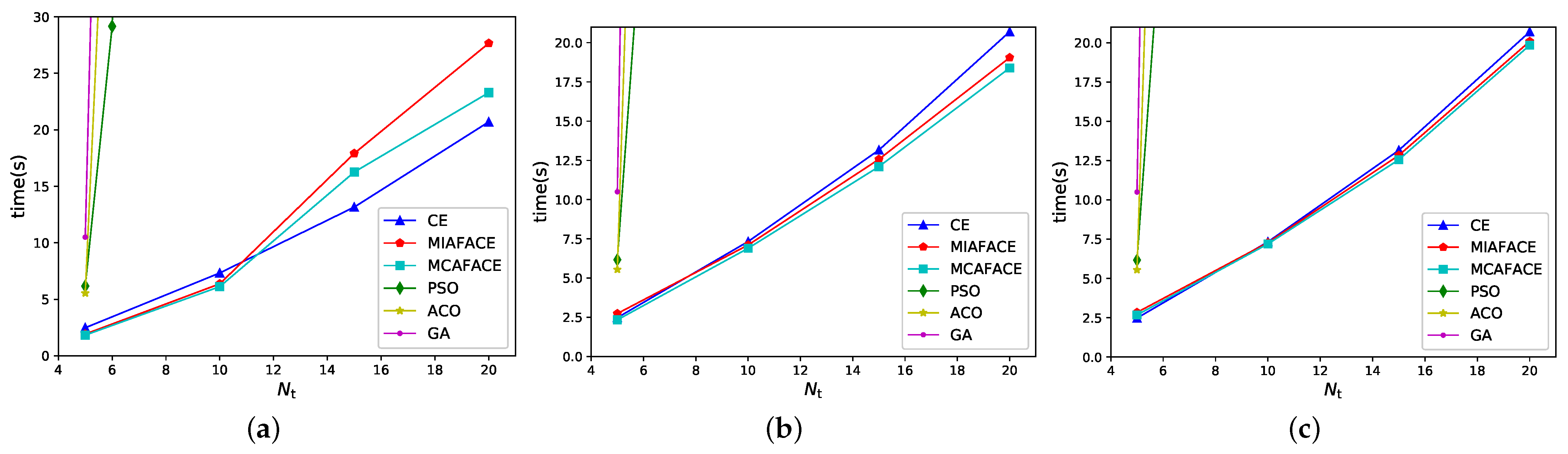
In case 6, we compared the CE method, MIAFACE algorithm, MCAFACE algorithm, PSO algorithm, ACO algorithm, and GA algorithm by obtaining the same optimal score under
and
, and their times change with
in
Figure 8a–c. The CE method, PSO algorithm, ACO algorithm, and GA algorithm are also used three times for three tasks continuously.
From
Figure 8, we note that for CE, MIAFACE, MCAFACE, PSO, ACO, and GA, the variations of the curves and the times are similar to the case in
Figure 5. In
Figure 8a, when
is below 11, the times of MIAFACE and MCAFACE are relatively close and less than that of CE; however, when
is over 11, the times of MIAFACE and MCAFACE grow quickly and more than that of CE due to obtaining the suboptimal results. Moreover, the time ranges of CE, MIAFACE, and MCAFACE are both approximately in [1,30]. Meanwhile, the times of PSO, ACO, and GA are much higher than that of CE, MIAFACE, and MCAFACE, and their time ranges are over 30 when
is more than 6. From
Figure 8b,c, the situations of PSO, ACO, and GA are similar to
Figure 8a. In
Figure 8b, the time differences between CE, MIAFACE, and MCAFACE grow as
increases. In addition, the time of MCAFACE is lower than that of CE and MIAFACE, and the curves of CE and MIAFACE intersect at
and the time of CE is also lower than that of MIAFACE when
is below 8, then the situation is reversed after
exceeds 8. Moreover, the time ranges of CE, MIAFACE, and MCAFACE are both in [2,22]. In
Figure 8c, the time differences between CE, MIAFACE, and MCAFACE decrease, and then increase as
grows. Furthermore, the curves of CE, MIAFACE, and MCAFACE intersect at
and the time of CE is lower than that of MIAFACE and MCAFACE when
is below 9, then the situation is reversed after
exceeds 9.
5.3. Analysis
Analysing the results of case 1 and case 4, we note that the optimal scheme vectors of using MIAFACE and MCAFACE algorithms in problems
and
, respectively, are obtained by initializing and updating the probability matrices
and
, which conforms to Algorithms 3 and 4 described in
Section 4.2. In addition, the result of MCAFACE in case 1 is suboptimal to that of other algorithms due to deleting the corresponding optimal solution after the end of each task.
Comprehensively considering the situations of case 2 and case 5, we note that the times of CE, MIAFACE, and MCAFACE increase with the increment of
,
h, as well as
and the time complexity of MCAFACE is lower than that of MIAFACE, and these phenomena comply with the complexity analysis of MIAFACE and MCAFACE in
Section 4.3. In addition, the time of case 5 is superior to that of case 2 because there are more available solutions for each target in case 5 than in case 2 after each iteration. Meanwhile, in case 5, using MIAFACE and MCAFACE for solving this problem is easy to fall into local optimum when
is inferior to a certain vector, e.g.,
. The reason behind this phenomenon is that when all elements in
are small and more solutions exist after each iteration, the optimal scheme may not be selected during one of the iterations of MIAFACE and MCAFACE, leading to a suboptimal result.
Comparing the situations of case 3 and case 6, we note that the times of PSO, ACO, and GA are only related to the growth of
. Meanwhile, CE, MIAFACE, and MCAFACE are superior to PSO, ACO, and GA for large-scale allocation problems, e.g., more than 8 targets of case 3 and 5 targets of case 6. Moreover, CE is inferior to MIAFACE in scenario 1, e.g.,
Figure 5, when
is over 10. Moreover, e.g.,
Figure 8c in scenario 2, MCAFACE is superior to MIAFACE and CE when
is over 9.
6. Conclusions
In this paper, the multi-UAV cooperative task assignment problem was described and formulated, and three types of UAVs were considered, cooperatively accomplishing the classification, attack, and verification tasks of targets under resource, precedence, and timing constraints. After that, considering complex coupling among these three tasks, we decomposed the considered problem into two subproblems. In order to solve them, we proposed an AFACE algorithm, a MIAFACE algorithm, and a MCAFACE algorithm. Finally, simulation results verified that both MIAFACE and MCAFACE consume less time than other intelligent algorithms for solving the corresponding problem.
Nevertheless, there still exist challenges when applying the MIAFACE algorithm and MCAFACE algorithm to processing optimization problems, e.g., appropriate parameter settings, falling into local optimum when using lower elements in , etc. In future work, it will be meaningful to concentrate on promoting these two algorithms on problems where it is vulnerable to local optimum when the number of samples is limited and on task assignment problems in complex dynamic scenarios.