N-Cameras-Enabled Joint Pose Estimation for Auto-Landing Fixed-Wing UAVs
Abstract
:1. Introduction
- (1)
- Independence of the Number of Cameras: Our proposed pose estimation method is versatile and compatible with ground vision systems utilizing any number of cameras, whether it is a monocular vision system (N = 1) or a stereo vision system (N > 1). Generally, the inclusion of more cameras enhances the system’s resilience to measurement errors, such as anchor detection inaccuracies and pan-tilt unit (PTU) attitude errors.
- (2)
- Elimination of Excessive Outdoor Data Requirement: Traditional approaches often entail an extensive and labor-intensive process of outdoor fixed-wing landing experiments to collect essential data, incurring significant time and resource costs. Our method, however, achieves accurate and robust outdoor UAV anchor detection by utilizing just 730 frames of data from two outdoor landings. This approach provides a viable solution for scenarios characterized by high outdoor experimental costs.
- (3)
- Robust and Accurate Pose Estimation: Autonomous landing necessitates quick and dynamic movement of the UAV in a three-dimensional space, resulting in rapid changes in visual appearance, imaging backgrounds, and more. These spatial and temporal variations present formidable challenges to ground vision-based UAV pose estimation. Our method adeptly addresses these challenges, enabling more precise and robust anchor detection and pose estimation than state-of-the-art methods. This improvement has been validated through the replacement of the onboard GPS-INS positioning system with our method as the sole source of position and attitude data during the outdoor UAV auto-landing process.
- (4)
- Simulated and Real Auto-landing Dataset: We have constructed a comprehensive dataset comprising eight simulated and four real landing videos, complete with labels such as target bounding boxes, anchors, and ground truth UAV pose information. This dataset, encompassing diverse conditions including varying wind directions and landing paths, serves as an invaluable resource for UAV detection and pose estimation research.
2. Related Works
3. Problem Formulation
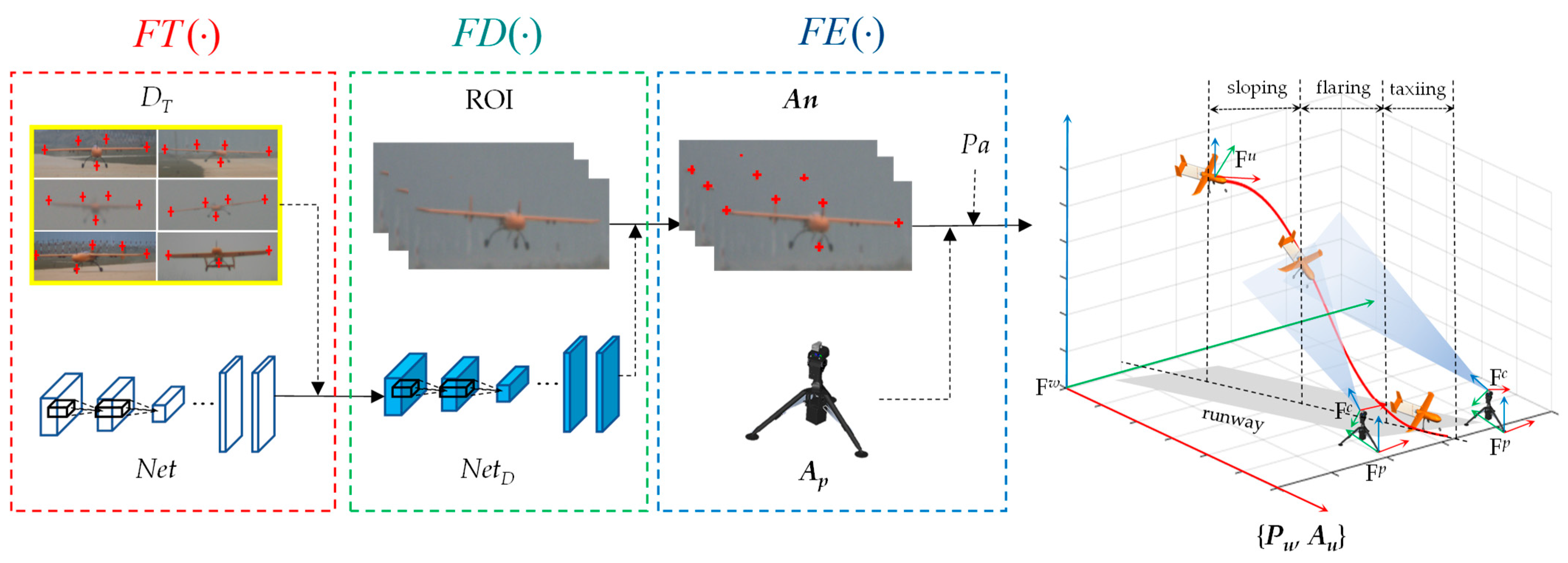
4. Methodology
4.1. Anchor Detection Operator
4.2. CNN Training Operator
4.3. 6D Pose Estimation Operator
5. Experiments
5.1. Anchor Detection
5.2. Pose Estimation
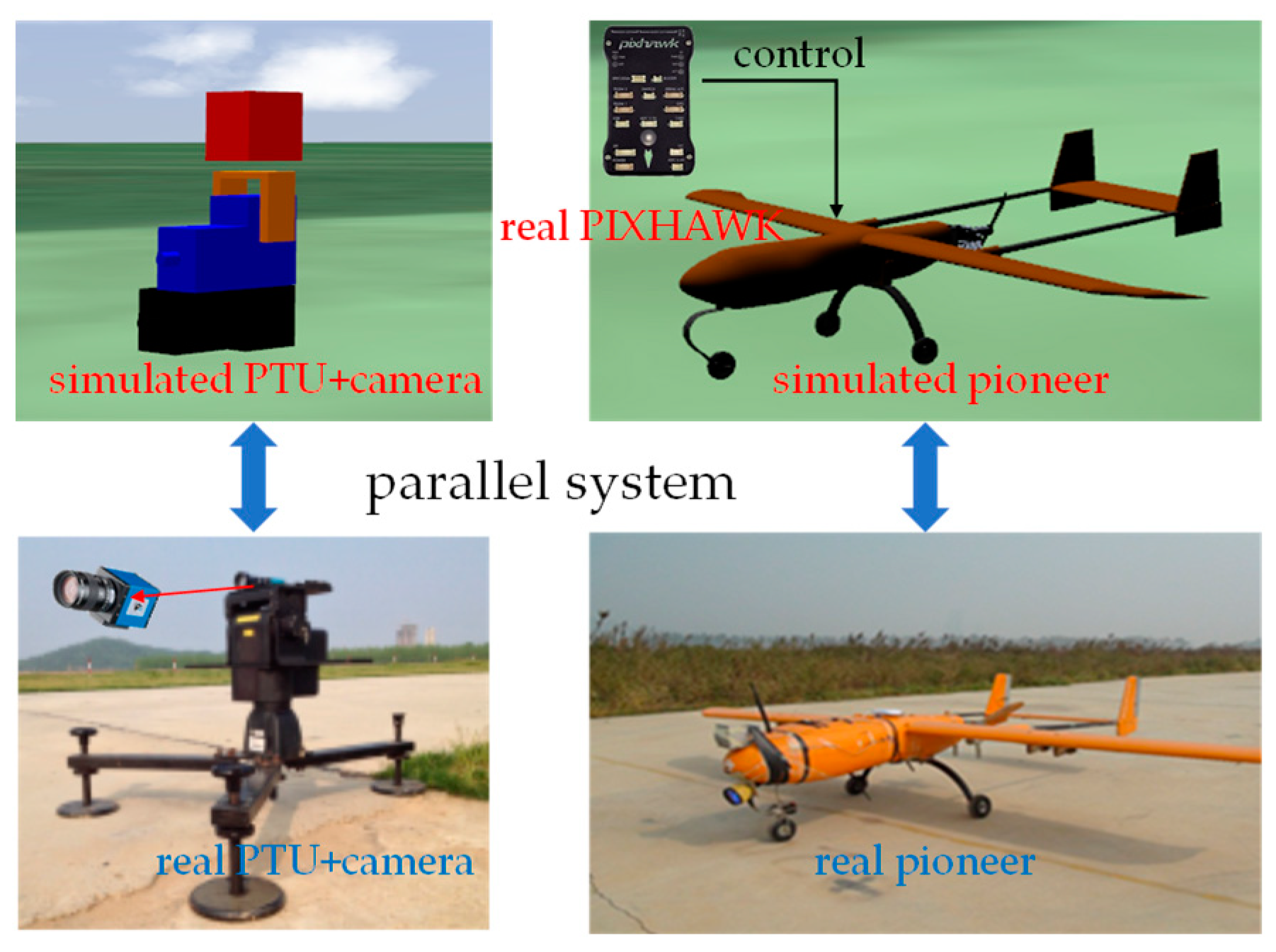
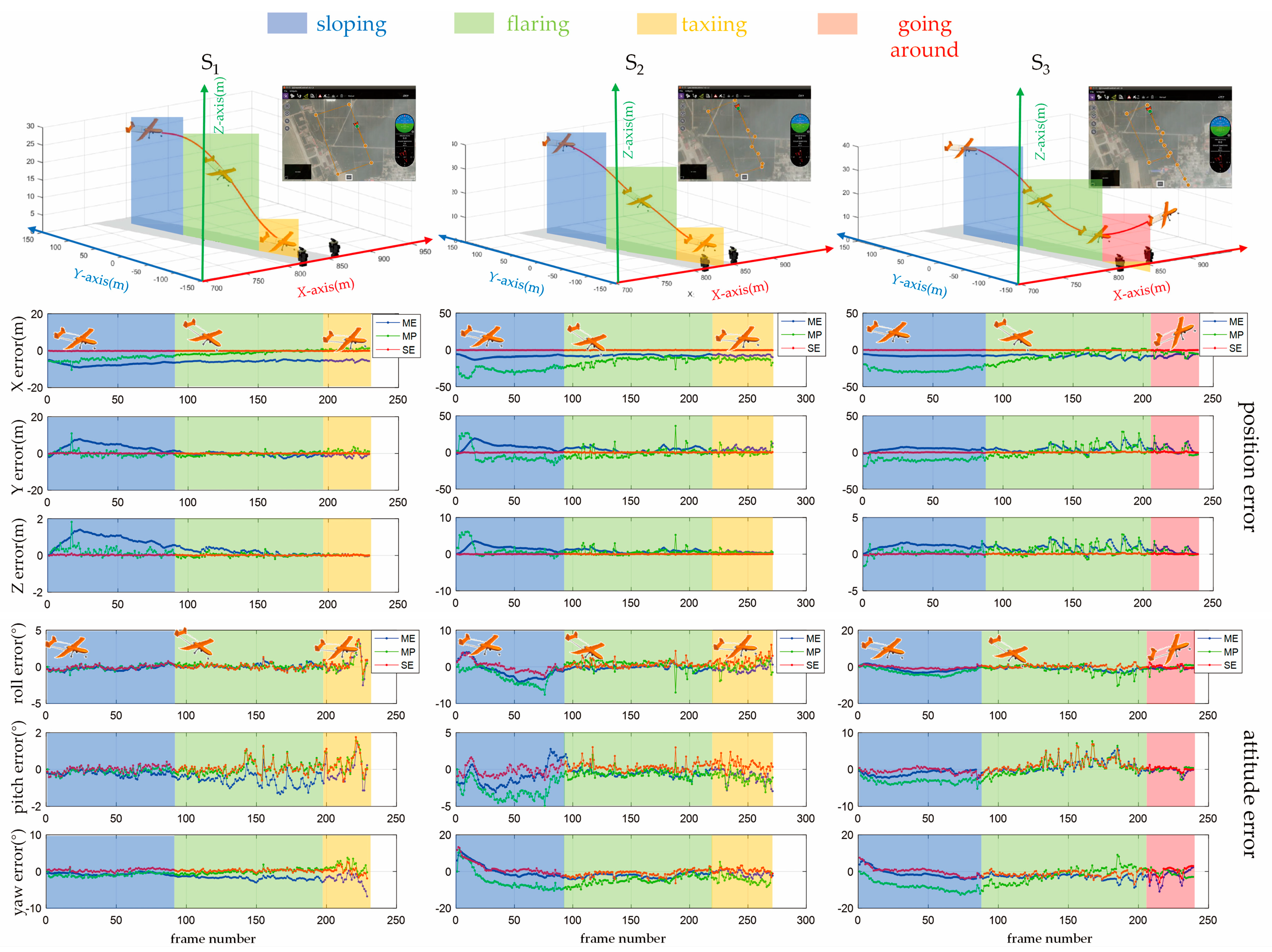
5.2.1. Simulations
5.2.2. Outdoor Evaluation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Quan, Q.; Fu, R.; Li, M.; Wei, D.; Gao, Y.; Cai, K.-Y. Practical Distributed Control for VTOL UAVs to Pass a Virtual Tube. IEEE Trans. Intell. Veh. 2021, 7, 342–353. [Google Scholar] [CrossRef]
- Shao, S.; Chen, M.; Hou, J.; Zhao, Q. Event-Triggered-Based Discrete-Time Neural Control for a Quadrotor UAV Using Disturbance Observer. IEEE/ASME Trans. Mechatron. 2021, 26, 689–699. [Google Scholar] [CrossRef]
- Souli, N.; Kolios, P.; Ellinas, G. Online Relative Positioning of Autonomous Vehicles using Signals of Opportunity. IEEE Trans. Intell. Veh. 2021, 7, 873–885. [Google Scholar] [CrossRef]
- Henawy, J.; Li, Z.; Yau, W.-Y.; Seet, G. Accurate IMU Factor Using Switched Linear Systems for VIO. IEEE Trans. Ind. Electron. 2021, 68, 7199–7208. [Google Scholar] [CrossRef]
- Herissé, B.; Hamel, T.; Mahony, R.; Russotto, F.-X. Landing a VTOL Unmanned Aerial Vehicle on a Moving Platform Using Optical Flow. IEEE Trans. Robot. 2012, 28, 77–89. [Google Scholar] [CrossRef]
- Tang, D.; Hu, T.; Shen, L.; Zhang, D.; Kong, W.; Low, K.H. Ground Stereo Vision-Based Navigation for Autonomous Take-Off and Landing of UAVs: A Chan-Vese Model Approach. Int. J. Adv. Robot. Syst. 2016, 13, 67. [Google Scholar] [CrossRef]
- Yang, B.; Yang, E. A Survey on Radio Frequency based Precise Localisation Technology for UAV in GPS-denied Environment. J. Intell. Robot. Syst. 2021, 103, 38. [Google Scholar] [CrossRef]
- Kim, J.; Woo, S.; Kim, J. Lidar-guided Autonomous Landing of an Aerial Vehicle on a Ground Vehicle. In Proceedings of the 14th International Conference on Ubiquitous Robots and Ambient Intelligence, Jeju, Republic of Korea, 28 June–1 July 2017; pp. 228–231. [Google Scholar]
- Pavlenko, T.; Schütz, M.; Vossiek, M.; Walter, T.; Montenegro, S. Wireless Local Positioning System for Controlled UAV Landing in GNSS-Denied Environmen. In Proceedings of the 5th International Workshop on Metrology for AeroSpace, Rome, Italy, 20–22 June 2019; pp. 171–175. [Google Scholar]
- Zhang, C.; Chen, L.; Yuan, S. ST-VIO: Visual Inertial Odometry Combined with Image Segmentation and Tracking. IEEE Trans. Instrum. Meas. 2020, 69, 8562–8570. [Google Scholar] [CrossRef]
- Garforth, J.; Webb, B. Visual Appearance Analysis of Forest Scenes for Monocular SLAM. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 1794–1800. [Google Scholar]
- Ho, H.; De Wagter, C.; Remes, B.; de Croon, G. Optical-Flow Based Self-Supervised Learning of Obstacle Appearance Applied to MAV Landing. Robot. Auton. Syst. 2018, 100, 78–94. [Google Scholar] [CrossRef]
- Yuan, H.; Xiao, C.; Xiu, S.; Zhan, W.; Ye, Z.; Zhang, F.; Zhou, C.; Wen, Y.; Li, Q. A Hierarchical Vision-Based UAV Localization for an Open Landing. Electronics 2018, 7, 68. [Google Scholar] [CrossRef]
- Wang, L.; Bai, X. Quadrotor Autonomous Approaching and Landing on a Vessel Deck. J. Intell. Robot. Syst. 2018, 92, 125–143. [Google Scholar] [CrossRef]
- Baca, T.; Stepan, P.; Spurny, V.; Hert, D.; Penicka, R.; Saska, M.; Thomas, J.; Loianno, G.; Kumar, V. Autonomous Landing on a Moving Vehicle with an Unmanned Aerial Vehicle. J. Field Robot. 2019, 36, 874–891. [Google Scholar] [CrossRef]
- Lim, J.; Lee, T.; Pyo, S.; Lee, J.; Kim, J.; Lee, J. Hemispherical InfraRed (IR) Marker for Reliable Detection for Autonomous Landing on a Moving Ground Vehicle from Various Altitude Angles. IEEE/ASME Trans. Mechatron. 2021, 27, 485–492. [Google Scholar] [CrossRef]
- Hu, B.; Mishra, S. Time-Optimal Trajectory Generation for Landing a Quadrotor Onto a Moving Platform. IEEE/ASME Trans. Mechatron. 2019, 24, 585–596. [Google Scholar] [CrossRef]
- Lungu, M. Auto-Landing of Fixed Wing Unmanned Aerial Vehicles Using the Backstepping Control. ISA Trans. 2019, 95, 194–210. [Google Scholar] [CrossRef]
- Abu-Jbara, K.; Sundaramorthi, G.; Claudel, C. Fusing Vision and Inertial Sensors for Robust Runway Detection and Tracking. J. Guid. Control Dyn. 2018, 41, 1929–1946. [Google Scholar] [CrossRef]
- Meng, Y.; Wang, W.; Han, H.; Zhang, M. A Vision/Radar/INS Integrated Guidance Method for Shipboard Landing. IEEE Trans. Ind. Electron. 2019, 66, 8803–8810. [Google Scholar] [CrossRef]
- Gui, Y. Research on Key Techniques of Airborne Vision-Based Navigation for Autonomous Landing of A UAV on A Ship Deck. Ph.D. Thesis, Aeronautical and Astronautical Science and Technology Graduate School of National University of Defense Technology, Changsha, China, 2013. [Google Scholar]
- Santos, N.P.; Lobo, V.; Bernardino, A. Autoland Project: Fixed-Wing UAV Landing on a Fast Patrol Boat Using Computer Vision. In OCEANS 2019 MTS/IEEE SEATTLE; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Ma, Z.; Hu, T.; Shen, L. Stereo Vision Guiding for the Autonomous Landing of Fixed-Wing UAVs: A Saliency-Inspired Approach. Int. J. Adv. Robot. Syst. 2016, 13, 43. [Google Scholar] [CrossRef]
- Li, M.; Hu, T. Deep Learning Enabled Localization for UAV Autolanding. Chin. J. Aeronaut. 2021, 34, 585–600. [Google Scholar] [CrossRef]
- Kong, W.; Zhou, D.; Zhang, Y.; Zhang, D.; Wang, X.; Zhao, B.; Yan, C.; Shen, L.; Zhang, J. A Ground-Based Optical System for Autonomous Landing of a Fixed Wing UAV. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2014), Chicago, IL, USA, 14–18 September 2014; pp. 4797–4804. [Google Scholar]
- Nguyen, T.H.; Cao, M.; Qiu, Z.; Xie, L. Integrated UWB-Vision Approach for Autonomous Docking of UAVs in GPS-denied Environments. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 9603–9609. [Google Scholar]
- Dong, X.; Gao, Y.; Guo, J.; Zuo, S.; Xiang, J.; Li, D.; Tu, Z. An Integrated UWB-IMU-Vision Framework for Autonomous Approaching and Landing of UAVs. Aerospace 2022, 9, 797. [Google Scholar] [CrossRef]
- Liu, F.; Wei, Z.; Zhang, G. An Off-Board Vision System for Relative Attitude Measurement of Aircraft. IEEE Trans. Ind. Electron. 2021, 69, 4225–4233. [Google Scholar] [CrossRef]
- Yang, J.; Du, T.; Liu, X.; Niu, B.; Guo, L. Method and Implementation of a Bioinspired Polarization-Based Attitude and Heading Reference System by Integration of Polarization Compass and Inertial Sensors. IEEE Trans. Ind. Electron. 2020, 67, 9802–9812. [Google Scholar] [CrossRef]
- Li, K.; Chang, L.; Chen, Y. Common Frame Based Unscented Quaternion Estimator for Inertial-Integrated Navigation. IEEE/ASME Trans. Mechatron. 2018, 23, 2413–2423. [Google Scholar] [CrossRef]
- Mammarella, M.; Campa, G.; Napolitano, M.R.; Fravolini, M.L.; Gu, Y.; Perhinschi, M.G. Machine Vision/GPS Integration Using EKF for the UAV Aerial Refueling Problem. IEEE Trans. Syst. Man Cybern. 2008, 38, 791–801. [Google Scholar] [CrossRef]
- Fu, Q.; Quan, Q.; Cai, K.-Y. Robust Pose Estimation for Multirotor UAVs Using Off-Board Monocular Vision. IEEE Trans. Ind. Electron. 2017, 64, 7942–7951. [Google Scholar] [CrossRef]
- Diogo, L.; David, P.; Hedi, T. Multi-Task Deep Learning for Real-Time 3D Human Pose Estimation and Action Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 2752–2764. [Google Scholar]
- Valle, R.; Buenaposada, J.; Baumela, L. Multi-Task Head Pose Estimation in-the-Wild. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 2874–2881. [Google Scholar] [CrossRef] [PubMed]
- Lin, W.; Anwar, A.; Li, Z.; Tong, M.; Qiu, J.; Gao, H. Recognition and Pose Estimation of Auto Parts for an Autonomous Spray Painting Robot. IEEE Trans. Ind. Inform. 2019, 15, 1709–1719. [Google Scholar] [CrossRef]
- Wu, H.; Zhou, J. Privacy Leakage of SIFT Features via Deep Generative Model Based Image Reconstruction. IEEE Trans. Inf. Forensics Secur. 2021, 16, 2973–2985. [Google Scholar] [CrossRef]
- Campos, C.; Elvira, R.; Rodriguez, J.; Montiel, J.; Tardos, J. ORB-SLAM3: An Accurate Open-Source Library for Visual, Visual–Inertial, and Multimap SLAM. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Nanni, L.; Ghidoni, S.; Brahnam, S. Handcrafted vs. Non-Handcrafted Features for Computer Vision Classification. Pattern Recognit. 2017, 71, 158–172. [Google Scholar] [CrossRef]
- Tang, D.; Fang, Q.; Shen, L.; Hu, T. Onboard Detection-Tracking-Localization. IEEE/ASME Trans. Mechatron. 2020, 25, 1555–1565. [Google Scholar] [CrossRef]
- Alexey, B.; Chien-Yao, W.; Hong-Yuan, M. Yolov4: Optimal Speed and Accuracy of Object Detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Liu, X.; Jonschkowski, R.; Angelova, A.; Konolige, K. Keypose: Multi-View 3D Labeling and Keypoint Estimation for Transparent Objects. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 11599–11607. [Google Scholar]


| Test Data | Networks | Conventional Network | KeyPose | Block-CNN | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Training Datasets | SD | RD | MD | SD | RD | MD | SD | RD | MD | |
| Simulation 1000 frames | LW (%) | 2.0 | 1.7 | 1.8 | 1.0 | 0.0 | 0.5 | |||
| LT (%) | 5.6 | 5.1 | 4.3 | 3.7 | 0.9 | 0.2 | ||||
| FT (%) | 2.3 | 0.2 | 1.4 | 0.6 | 0.0 | 0.2 | ||||
| RT (%) | 4.9 | 2.2 | 5.9 | 3.0 | 0.5 | 0.2 | ||||
| RW (%) | 5.2 | 1.2 | 2.0 | 1.0 | 1.1 | 0.2 | ||||
| Average | 4.0 | 2.1 | 3.1 | 1.9 | 0.5 | 0.3 | ||||
| Outdoor 1000 frames | LW (%) | 7.0 | 7.4 | 4.5 | 4.0 | 2.5 | 1.9 | |||
| LT (%) | 6.6 | 6.1 | 6.2 | 6.0 | 2.2 | 2.0 | ||||
| FT (%) | 5.2 | 5.2 | 3.9 | 4.0 | 2.2 | 1.5 | ||||
| RT (%) | 9.1 | 6.9 | 6.7 | 7.5 | 4.4 | 2.1 | ||||
| RW (%) | 8.0 | 7.7 | 6.0 | 5.8 | 3.3 | 3.9 | ||||
| Average | 7.2 | 6.7 | 5.5 | 5.5 | 2.9 | 2.3 | ||||
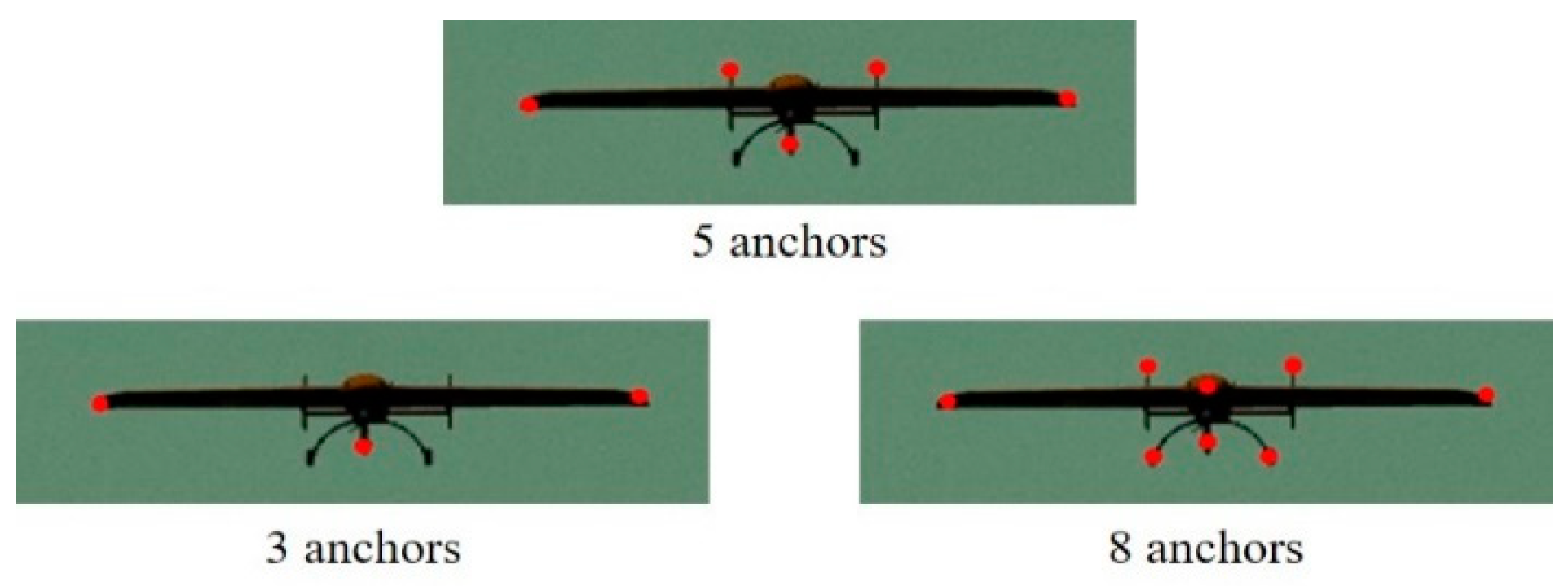
| Index | Anchor Number | Position RMSE (m) | Attitude RMSE (°) | ||||
|---|---|---|---|---|---|---|---|
| X | Y | Z | Roll | Pitch | Yaw | ||
| S2 | 3 | 3.54 | 16.99 | 5.03 | 2.16 | 15.58 | 2.11 |
| 5 | 0.14 | 0.64 | 0.09 | 0.84 | 0.79 | 2.01 | |
| 8 | 0.27 | 0.53 | 0.10 | 1.21 | 0.79 | 2.23 | |
| S3 | 3 | 5.83 | 20.15 | 3.38 | 1.92 | 18.62 | 2.66 |
| 5 | 0.19 | 0.71 | 0.08 | 0.69 | 1.57 | 1.64 | |
| 8 | 0.22 | 0.73 | 0.05 | 0.82 | 1.37 | 2.00 | |
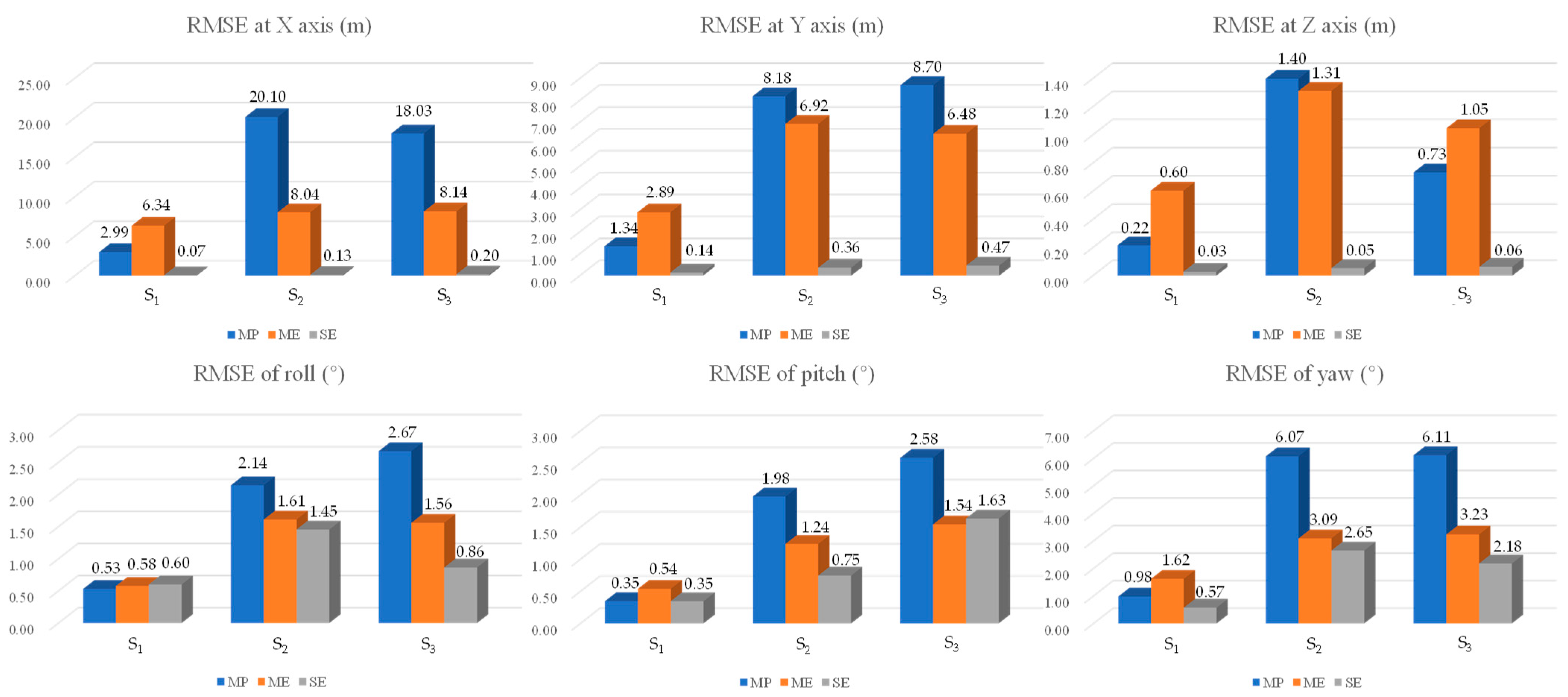
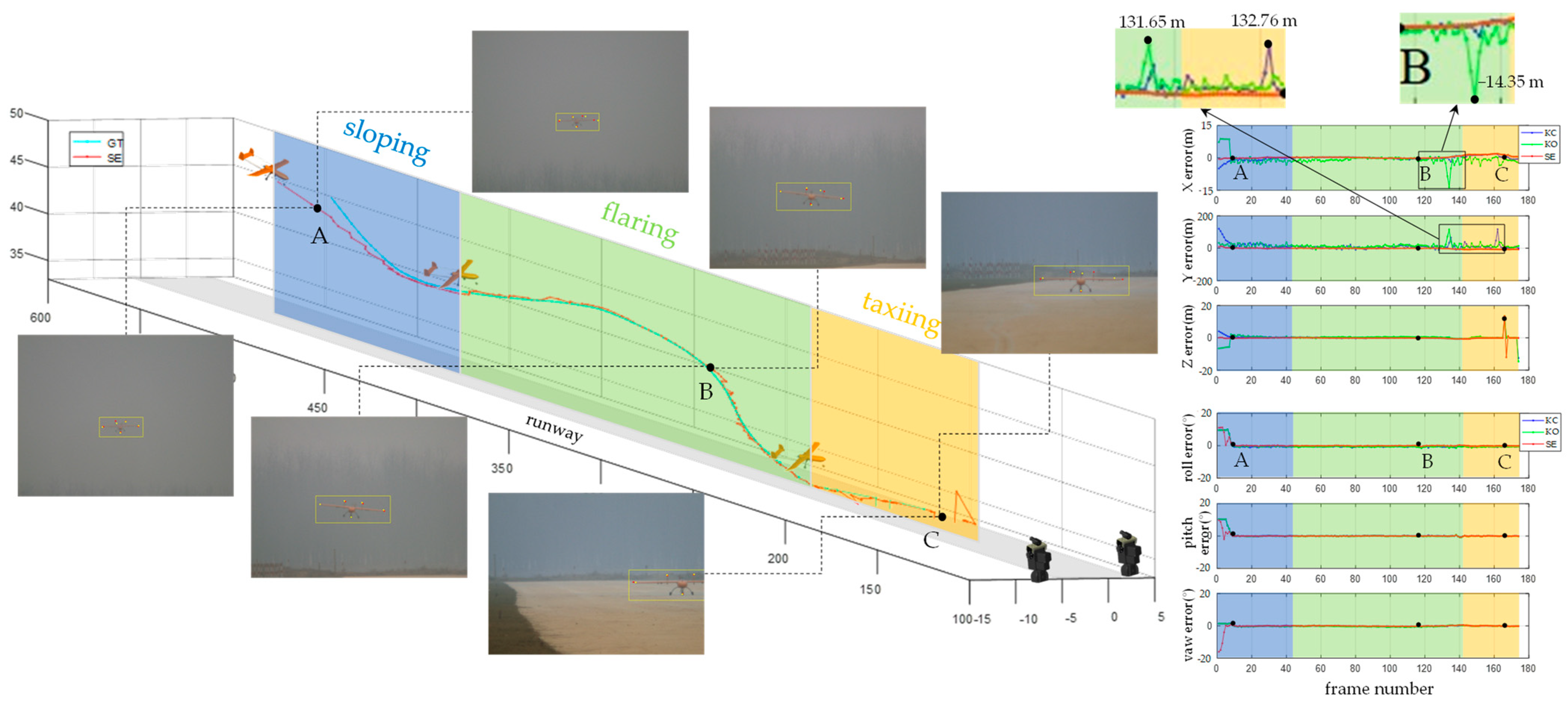
| RMSE | Solution | Sloping | Flaring | Taxiing | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Exp 1 | Exp 2 | Exp 3 | Exp 1 | Exp 2 | Exp 3 | Exp 1 | Exp 2 | Exp 3 | ||
| X axis (m) | SE | 3.2 | 2.8 | 3.8 | 0.3 | 0.5 | 0.6 | 1.9 | 1.9 | 2.8 |
| KC | 4.6 | 3.9 | 4.1 | 2.5 | 1.5 | 1.0 | 3.1 | 3.1 | 2.7 | |
| KO | 3.8 | 3.8 | 3.8 | 1.0 | 1.7 | 2.1 | 2.3 | 3.8 | 3.4 | |
| Y axis (m) | SE | 11.9 | 10.8 | 12.9 | 3.7 | 4.9 | 2.0 | 17.8 | 12.4 | 10.0 |
| KC | 23.4 | 24.6 | 18.5 | 22.9 | 19.4 | 15.8 | 34.9 | 30.6 | 20.1 | |
| KO | 24.1 | 29.2 | 21.0 | 20.1 | 22.5 | 17.6 | 30.4 | 30.8 | 26.4 | |
| Z axis (m) | SE | 5.4 | 2.9 | 1.8 | 0.4 | 0.3 | 0.5 | 7.5 | 5.9 | 5.4 |
| KC | 3.4 | 3.0 | 2.0 | 1.2 | 1.5 | 1.4 | 6.4 | 8.0 | 7.6 | |
| KO | 3.4 | 2.8 | 2.0 | 1.0 | 1.3 | 1.8 | 6.2 | 7.3 | 8.7 | |
| Roll (o) | SE | 21.0 | 19.3 | 17.8 | 0.7 | 1.5 | 0.9 | 0.8 | 1.5 | 1.1 |
| KC | 16.3 | 18.4 | 19.4 | 4.5 | 2.7 | 2.8 | 2.9 | 2.2 | 1.9 | |
| KO | 16.1 | 18.5 | 20.4 | 3.9 | 2.2 | 2.9 | 2.9 | 2.2 | 1.8 | |
| Pitch (o) | SE | 19.5 | 22.8 | 23.9 | 0.5 | 0.8 | 1.0 | 1.1 | 0.9 | 1.4 |
| KC | 21.5 | 23.5 | 23.9 | 1.2 | 1.4 | 1.8 | 1.6 | 2.5 | 3.1 | |
| KO | 22.3 | 23.4 | 31.0 | 0.9 | 1.9 | 0.9 | 1.3 | 2.2 | 2.4 | |
| Yaw (o) | SE | 11.5 | 10.3 | 11.8 | 1.8 | 2.2 | 1.9 | 2.2 | 1.4 | 2.0 |
| KC | 8.2 | 7.9 | 8.2 | 3.1 | 2.8 | 2.4 | 1.8 | 3.1 | 2.9 | |
| KO | 7.4 | 7.2 | 8.7 | 2.8 | 2.5 | 2.5 | 1.8 | 2.2 | 3.5 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, D.; Shen, L.; Xiang, X.; Zhou, H.; Lai, J. N-Cameras-Enabled Joint Pose Estimation for Auto-Landing Fixed-Wing UAVs. Drones 2023, 7, 693. https://doi.org/10.3390/drones7120693
Tang D, Shen L, Xiang X, Zhou H, Lai J. N-Cameras-Enabled Joint Pose Estimation for Auto-Landing Fixed-Wing UAVs. Drones. 2023; 7(12):693. https://doi.org/10.3390/drones7120693
Chicago/Turabian StyleTang, Dengqing, Lincheng Shen, Xiaojia Xiang, Han Zhou, and Jun Lai. 2023. "N-Cameras-Enabled Joint Pose Estimation for Auto-Landing Fixed-Wing UAVs" Drones 7, no. 12: 693. https://doi.org/10.3390/drones7120693
APA StyleTang, D., Shen, L., Xiang, X., Zhou, H., & Lai, J. (2023). N-Cameras-Enabled Joint Pose Estimation for Auto-Landing Fixed-Wing UAVs. Drones, 7(12), 693. https://doi.org/10.3390/drones7120693






