Meta-heuristic Algorithms in UAV Path Planning Optimization: A Systematic Review (2018–2022)

Abstract

Unmanned Aerial Vehicles (UAVs), a subset of aerial robots, play crucial roles in various domains, such as disaster management, agriculture, and healthcare. Their application proves invaluable in situations where human intervention poses risks or involves high costs. However, traditional approaches to UAV path planning struggle in efficiently navigating complex and dynamic environments, often resulting in suboptimal routes and extended mission durations. This study seeks to investigate and improve the utilization of meta-heuristic algorithms for optimizing UAV path planning. Toward this aim, we carried out a systematic review of five major databases focusing on the period from 2018 to 2022. Following a rigorous two-stage screening process and a thorough quality appraisal, we selected 68 papers out of the initial 1500 to answer our research questions. Our findings reveal that hybrid algorithms are the dominant choice, surpassing evolutionary, physics-based, and swarm-based algorithms, indicating their superior performance and adaptability. Notably, time optimization takes precedence in mathematical models, reflecting the emphasis on CPU time efficiency. The prevalence of dynamic environmental types underscores the importance of real-time considerations in UAV path planning, with three-dimensional (3D) models receiving the most attention for accuracy in complex trajectories. Additionally, we highlight the trends and focuses of the UAV path planning optimization research community and several challenges in using meta-heuristic algorithms for the optimization of UAV path planning. Finally, our analysis further highlights a dual focus in UAV research, with a significant interest in optimizing single-UAV operations and a growing recognition of the challenges and potential synergies in multi-UAV systems, alongside a prevalent emphasis on single-target mission scenarios, but with a notable subset exploring the complexities of multi-target missions.

1. Introduction

Unmanned Aerial Vehicles (UAVs), commonly known as drones, have revolutionized various industries and applications, leveraging their ability to fly without a human pilot onboard. This technological advancement has positioned UAVs as cost-effective, efficient, and safe solutions across various different sectors, fueling significant interest and innovation [1]. Initially designed for military purposes, UAVs have seamlessly transitioned into civilian domains [2,3]. Their applications range from military surveillance, reconnaissance, and combat operations, significantly contributing to reducing human casualties [4], to civilian applications such as forest-fire monitoring [5], rescue missions [6], agriculture [7], offshore platform operations [8], traffic management [9], drone delivery [10], medical emergencies [11], tracking operations [12], and tasks relating to smart cities [13,14]. UAVs play a crucial role in accessing remote or inaccessible areas and serve as pivotal tools in emergency scenarios, such as disaster rescue operations [15,16].

As UAVs are increasingly being regarded as autonomous vehicles, capable of making decisions in line with their programmed autonomy levels, path planning is emerging as a critical challenge in UAV navigation and control [3]. The expanded applications of UAVs underscore the importance of path planning optimization in enhancing overall performance and reducing costs [17,18,19]. UAVs operate in diverse workspaces, including urban, rural, and authorized areas, each adhering to specific regulations to prevent entry into prohibited or restricted flying zones [20,21,22].

Urban areas pose unique challenges, presenting obstacles like buildings, vehicles, and elevated structures, increasing collision risks during UAV rotations or maneuvers. In contrast, rural areas, characterized by lower obstacle density, present fewer collision risks and reduced potential for damage. High-altitude areas, while having fewer obstacles, demand greater energy consumption for UAVs flying in lower-collision-risk zones. Strategies for addressing energy consumption challenges include enhancing batteries with chemical substances or utilizing solar cells [23]. Obstacle and collision avoidance are integral aspects of UAV path planning, minimizing errors, and optimizing convergence speed, as a faster convergence speed leads to identifying the global optimum [24]. Achieving the global optimum allows UAVs to find a shorter path between start and end points, considering time and energy efficiency. Algorithms play a significant role in optimizing the mathematical models used for path planning [25].

Optimization, in the context of UAV path planning, involves seeking the most suitable combination of parameters and variables to meet specific goals related to efficiency, profit, cost reduction, and more [17,18,19]. This process entails minimizing or maximizing the objective function, allowing for the determination of the best possible solution [17,26]. Numerous research works have employed various approaches, such as machine learning, heuristics, classical techniques, and meta-heuristics, to solve and optimize the mathematical models for path planning.

Our research focuses on using meta-heuristic algorithms to optimize UAV path planning for several key reasons. Firstly, meta-heuristic algorithms are straightforward as they rely on basic concepts often inspired by natural processes like animal behaviors and evolution [17]. This simplicity makes them accessible to scientists for solving problems and innovating heuristic algorithms. Secondly, their flexibility enables their application to diverse problems without requiring extensive algorithm alterations [17,18]. Thirdly, most meta-heuristic algorithms operate without derivatives, optimizing problems stochastically from random starting points [17,19]. This feature enhances their suitability for real-world problems and allows for easy cross-domain application. Fourthly, compared to conventional optimization methods, meta-heuristic algorithms excel at avoiding local optima [17,18,19]. Their stochastic nature enables the extensive exploration of a search space, preventing stagnation in local solutions. These attributes make meta-heuristic algorithms a compelling choice for tackling complex and uncertain challenges, such as bushfire disaster assessment.

Based on these reasons, this paper aims to provide a systematic literature review to classify meta-heuristic algorithms and thus determine which types of meta-heuristic algorithms are efficient and effective for the optimization of UAV path planning.

Existing Systematic Literature Reviews and the Need for this Study

In examining the existing literature on UAV path planning optimization, three systematic review papers were identified, each with its strengths and weaknesses.

The first review [27] focused on autonomous path planning, classifying algorithms into heuristic and hybrid categories. While it identified common parameters, it failed to distinguish between heuristic and meta-heuristic algorithms, and its reliance on a single database, Web of Science, limited the scope of the review. Moreover, the omission of meta-heuristic algorithm details was a notable drawback.

The second review [28] addressed challenges and future directions but was not dedicated to optimization. Lacking systematic features like keywords and databases, it missed the opportunity to explore meta-heuristic algorithms’ nuances. The final review [18] investigated optimization path planning with meta-heuristic algorithms but overlooked objective functions and constraints. Its restricted sample size and failure to specify superior algorithms created gaps in understanding the broader applications of meta-heuristic approaches. Besides the already mentioned shortcomings, the above-mentioned review neither considered reviewing the grey literature along with mainstream scholar databases nor considered the quality appraisal step of systematic review, which is amongst the most crucial steps in conducting systematic reviews.

Recognizing these deficiencies, our systematic literature review aims to bridge the gaps left by previous reviews. By incorporating comprehensive categorization, keywords, and databases, we ensure a thorough exploration of meta-heuristic algorithms for UAV path planning optimization. Unlike previous reviews, we will dissect algorithm details, consider heuristic and meta-heuristic distinctions, and delve into the objectives and constraints of mathematical models. This approach guarantees a more nuanced understanding of the field, addressing the limitations of existing reviews and paving the way for a more robust analysis of UAV path planning optimization.

Eventually, we aim to promote systematic literature reviews for the optimization of UAV path planning using meta-heuristic algorithms in order to cover all the mentioned needs and deficiencies based on 68 articles spanning five years, from the beginning of 2018 to the end of 2022. Toward this aim, we set four research questions, as provided below:

• RQ1: What types of meta-heuristic algorithms were used the most for optimizing UAV path planning?
• RQ2: What characteristics are considered as objectives and constraints of mathematical models for optimizing path planning using meta-heuristic algorithms?
• RQ3: What type of mathematical model was used the most for the optimization of UAV path planning using meta-heuristic algorithms?
• RQ4: What are the environmental types and dimensions employed for the optimization of path planning?

2. Methods

Our research follows Kitchenham’s guidelines for designing and implementing a systematic literature review [29,30].

2.1. Database and Keywords

In our research, we endeavored to create a comprehensive and unbiased systematic literature review on the role of meta-heuristic algorithms in optimizing UAV path planning. To achieve this goal, we conducted searches on five reputable international databases, including ACM, IEEE, Scopus, ScienceDirect, and Web of Science. To avoid neglecting any relevant studies, we also considered the grey literature and reviewed the first ten pages of Google Scholar. Additionally, we performed backward and forward searches within the selected studies [31]. Importantly, we used various sets of keywords for each database as part of our search strategy. It should be emphasized that this approach is essential because each database follows its own guidelines and has its own limitations. For this reason,

Table 1. Databases and keyword grouping.

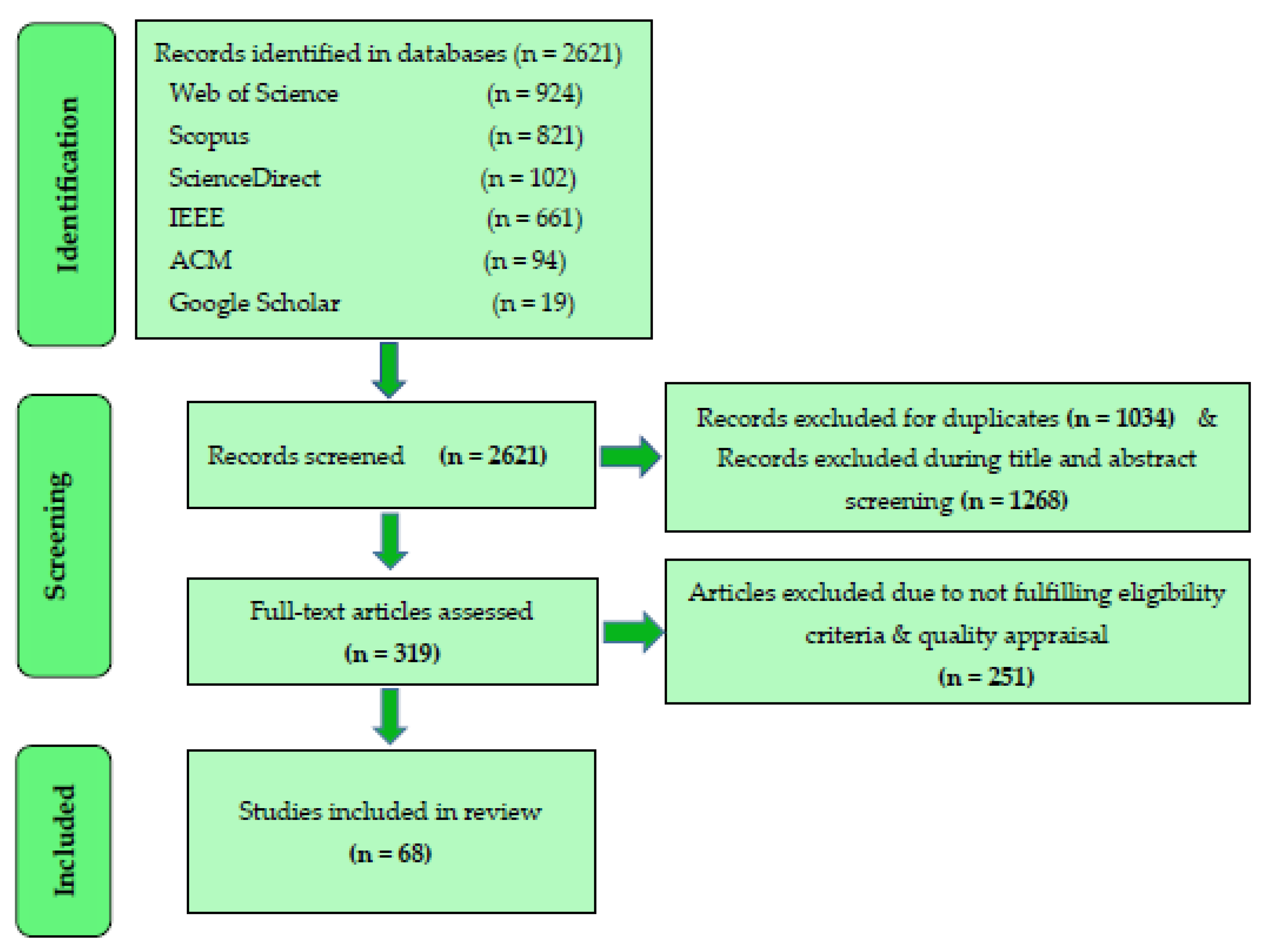
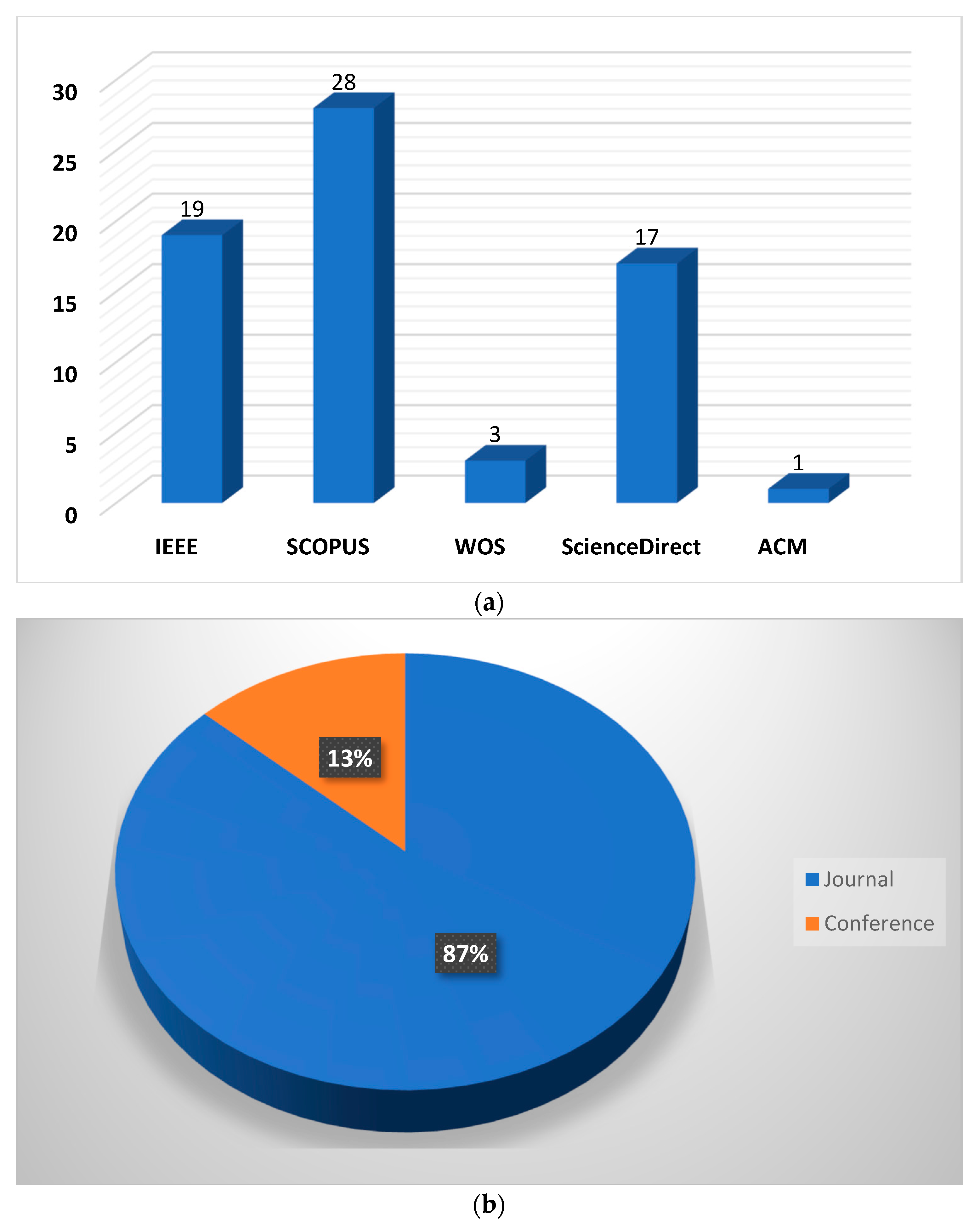
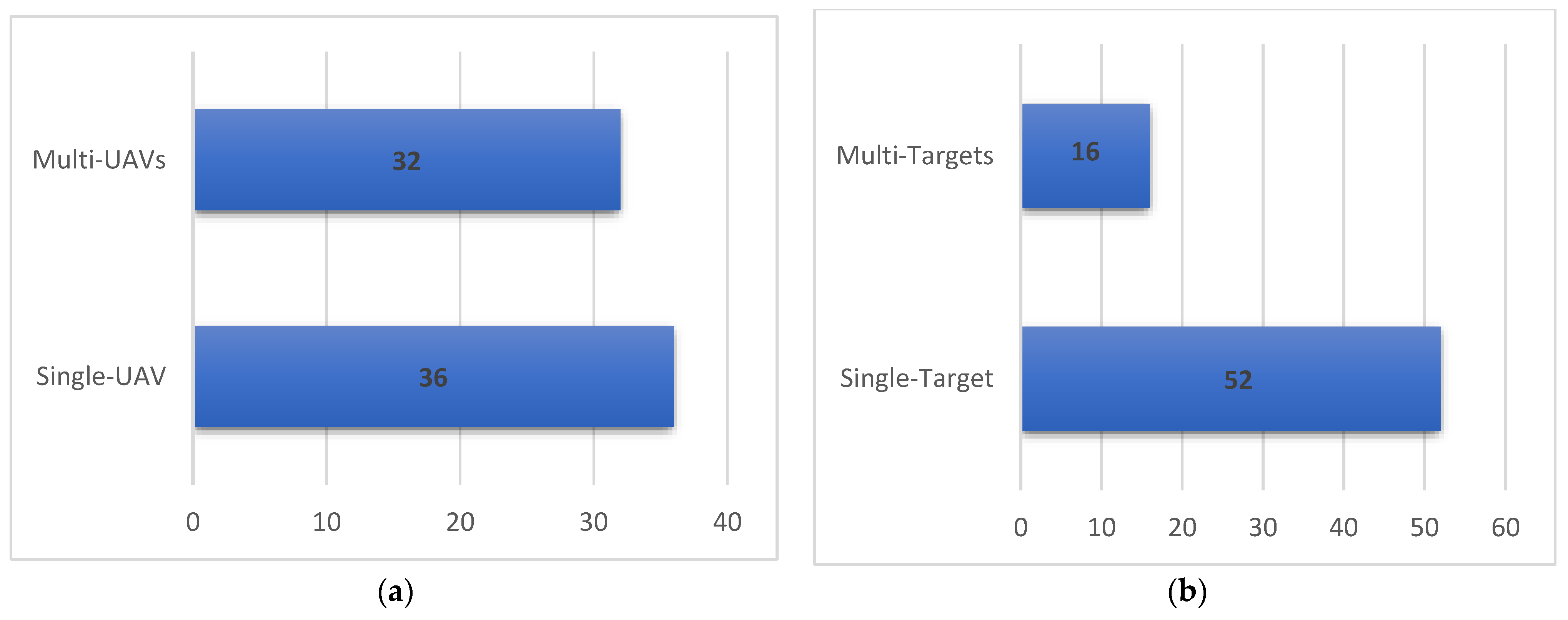
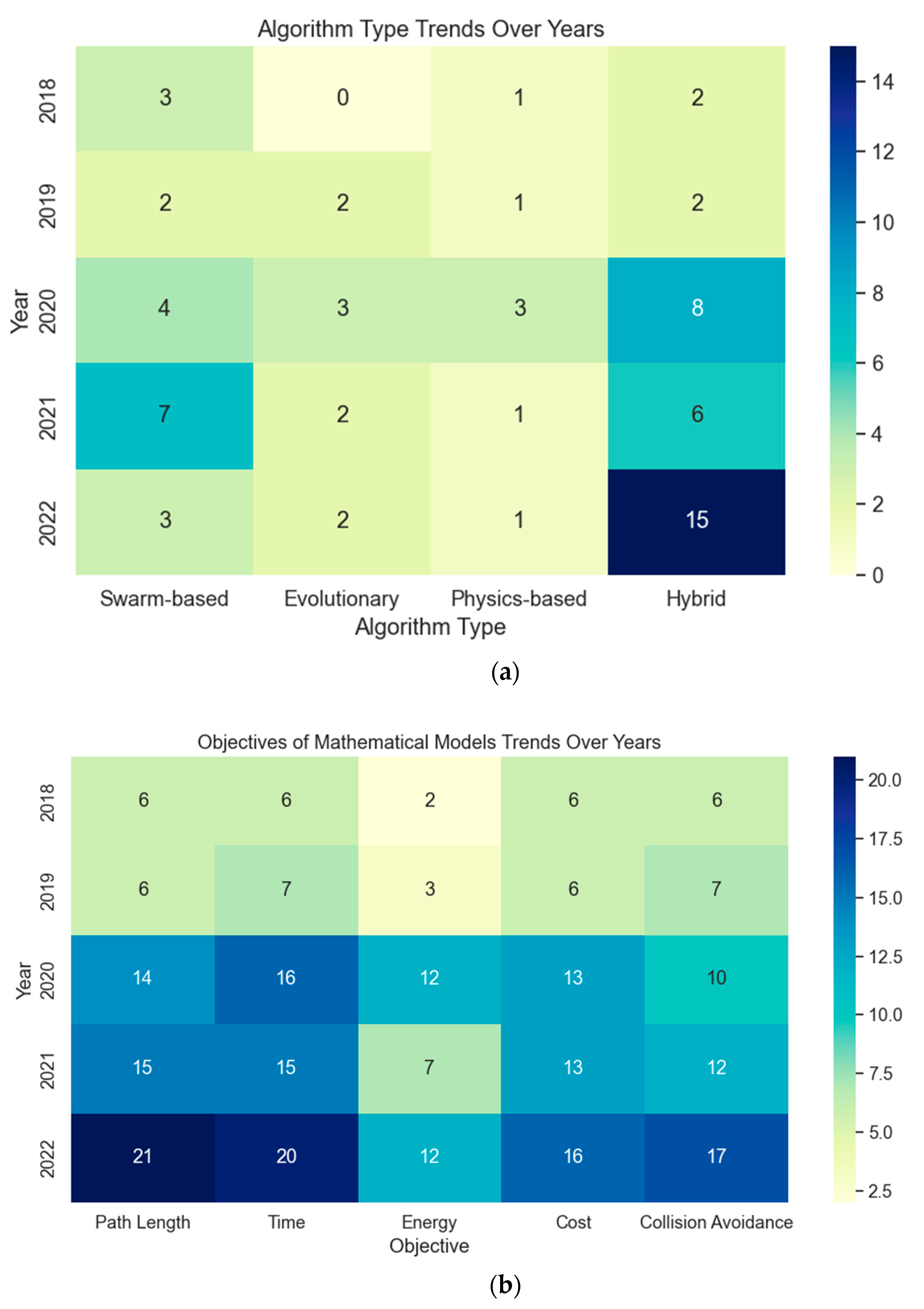
Database	Boolean/Phrase
ACM	(UAV OR “unmanned aerial vehicle” OR drone) AND (“path planning”) AND (“optimization”)
Web of Science	(UAV OR “unmanned aerial vehicle” OR drone) AND (“path plan *”) AND (“optim *”)
IEEE	(UAV OR “unmanned aerial vehicle” OR drone) AND (“path planning”) AND (“optimization”)
Scopus	TITLE-ABS-KEY((UAV OR “unmanned aerial vehicle” OR drone) AND (“path planning”) AND (“optimization”))
ScienceDirect	(UAV OR “unmanned aerial vehicle” OR drone) AND (“path planning”) AND (“optimization”)
Google Scholar	(UAV OR “unmanned aerial vehicle” OR drone) AND (“path planning”) AND (“optimization”)

presents the names of the databases along with the related keywords used to search for articles in the titles, abstracts, and keywords sections.

2.2. Eligibility Criteria

To ensure that we identified relevant articles for answering our research questions, we considered some criteria for inclusion and exclusion. The inclusion criteria were set and used during the search process, such as including material written in the English language, while the exclusion criteria were mostly defined and adjusted during the screening stages.

Table 2. Eligibility criteria.

Inclusion Criteria
IC1	Articles published between 2018 to 2023
IC2	Articles including conference publications or from peer-reviewed journals
IC3	In English and accessible
IC4	The study revolves around the use/development of optimization methods for UAV path planning
Exclusion criteria
EC1	Studies using other types of algorithms for path planning (e.g., machine learning)
EC2	Articles that do not propose a new method of path planning
EC3	Conference publications that were not part of the main conference (e.g., workshop papers), editorial reports, etc.
EC4	Articles for which more than one version of the study was published in different venues (reporting identical results)
EC5	Articles whose context was not properly in line with objectives and experiments
EC6	Articles suffering from issues in formulations or data collection

represents both inclusion and exclusion criteria for our research.

2.3. Study Selection

Our systematic literature review consists of three main stages for the article selection process: identification, screening, and eligibility evaluation. Figure 1 illustrates the entire process of collecting articles and highlights these three key stages. In the first stage, we used Zotero, a reference management software, to import identified papers and remove duplicates and similar searches from various databases. Subsequently, the first screening was conducted based on appropriate titles and abstracts, considering eligibility criteria. It is important to note that any articles we were uncertain about were moved to the second screening. In the second screening, we thoroughly studied and analyzed the full texts of articles, applying eligibility criteria. Our research was open to and ready to apply any new exclusion criteria that emerged during the screening process. Fortunately, constructive discussions between researchers led to unanimous decisions regarding the inclusion or exclusion of specific papers. To refine the results of the second screening, we adjusted and applied a quality appraisal step. Specifically, this step included the setting of six criteria to assess the quality of the studies, including the following examples: (i) Is the objective and context of research clear? (ii) Does the research adequately delineate the methodology? (iii) Does the research topic address development and validation of meta-heuristic methods in relation to path planning? We applied scores of 0, 0.5, and 1 if the quality criterion was not satisfied, partially satisfied, or fully satisfied, respectively. Accordingly, we categorized the studies into “low”, “medium”, and “high” quality and excluded “low”-quality studies from the final set of included articles. In total, 23 studies were excluded, and 68 proceeded to the information extraction stage.

2.4. Data Extraction

Following the completion of the primary three stages, a total of 68 papers were selected based on eligibility criteria and underwent quality assessment. Subsequently, our research proceeded to the fourth stage, which involved data extraction. This stage was instrumental in gathering diverse data points suitable for addressing our research questions and fulfilling our review criteria. Specifically, we sought to extract several items from each paper, such as title, year, country, publication venue, database, gap addressed, algorithm proposed or employed, meta-heuristic type, mathematical type, objective (e.g., cost function, time, energy, path lengths, and collision avoidance), constraints (e.g., angle, altitude, axes, obstacle, and thread), UAV dimensions (2D/3D/4D) and applications, challenges, and future directions.

3. Results and Analysis

3.1. Characteristics of the Studies

Table 3. Overview of the 68 included articles.

Article ID	Ref.	Title	Proposed Algorithm	Meta-Heuristic-Type
1	[32]	Three-dimensional UAV cooperative path planning based on the MP-CGWO algorithm	MP-CGWO	Hybrid
2	[33]	Adaptive path planning method for UAVs in complex environments	APP-PSO	Hybrid
3	[34]	Distributed 3-D path planning for multi-UAVs with full area surveillance based on particle swarm optimization	mPSO	Swarm-based algorithm
4	[35]	Threat-oriented collaborative path planning of unmanned reconnaissance mission for the target group	Improved NSGA-II	Evolutionary algorithm
5	[36]	An improved NSGA-II algorithm for UAV path planning problems	Improved NSGA-II	Evolutionary algorithm
6	[7]	A novel path planning optimization algorithm based on particle swarm optimization for UAVs for bird monitoring and repelling	PSO	Swarm-based algorithm
7	[37]	Meteorology-aware path planning for the UAV based on the improved intelligent water drops algorithm	IIWD	Swarm-based algorithm
8	[38]	Real time UAV path planning by parallel grey wolf optimization with align coefficient on CAN bus	IGWO	Swarm-based algorithm
9	[39]	Crossover recombination-based global-best brain storm optimization algorithm for UAV path planning	GBSO-CR	Hybrid
10	[17]	Autonomous UAV path planning optimization using meta-heuristic approach for pre-disaster assessment	DGBCO	Hybrid
11	[40]	Optimized multi-UAV cooperative path planning under the complex confrontation environment	IGWO	Swarm-based algorithm
12	[41]	Improved bat algorithm for UAV path planning in three-dimensional space	IBA	Hybrid
13	[42]	A novel hybrid chaotic aquila optimization algorithm with simulated annealing for unmanned aerial vehicles path planning	CAOSA	Hybrid
14	[43]	Analysis of parallel genetic algorithm and parallel particle swarm optimization algorithm UAV path planning on controller area network	Multi-master parallel GA	Evolutionary algorithm
15	[44]	Path planning of quadrotors in a dynamic environment using a multi-criteria multi-verse optimizer	MOMVO	Physics-based techniques
16	[45]	3D global path planning optimization for cellular-connected UAVs under link reliability constraint	PSO-GA	Hybrid
17	[46]	A new dynamic path planning approach for unmanned aerial vehicles	ACO-APF	Hybrid
18	[47]	Mission-oriented 3D path planning for high-altitude long-endurance solar-powered UAVs with optimal energy management	GPM-ACO	Hybrid
19	[48]	MVO-based 2-D path planning scheme for providing quality of service in UAV environment	MVO	Physics-based techniques
20	[49]	IHSSAO: An Improved Hybrid salp swarm algorithm and Aquila optimizer for UAV path planning in complex terrain	IHSSAO	Hybrid
21	[50]	A novel hybrid particle swarm optimization algorithm for path planning of UAVs	SDPSO	Hybrid
22	[51]	Safety-enhanced UAV path planning with spherical vector-based particle swarm optimization	Spherical vector- based with (PSO)	Hybrid
23	[52]	Meta-heuristic optimization-based path planning and tracking of quadcopter for payload hold-release mission	HHO-GWO	Hybrid
24	[53]	Social-class pigeon-inspired optimization and time stamp segmentation for multi-UAV cooperative path planning	SCPIO	Hybrid
25	[54]	Path planning for solar-powered UAV in urban environment	IWOA	Swarm-based algorithm
26	[55]	Multi-UAV optimal mission assignment and path planning for disaster rescue using adaptive genetic algorithm and improved artificial bee colony method	AGA-PSO and AGA-APFA and GA + APFA and GA + PSO	Hybrid
27	[56]	Path planning of UAV for oilfield inspections in a three- dimensional dynamic environment with moving obstacles based on an improved pigeon-inspired optimization algorithm	PIOFOA	Hybrid
28	[57]	Path planning of UAVs under dynamic environment based on a hierarchical recursive multi-agent genetic algorithm	HR-MAGA	Hybrid
29	[58]	Bypassing or flying above the obstacles? A novel multi- objective UAV path planning problem	NSGA-II	Evolutionary algorithm
30	[59]	Path planning of multiple UAVs with online changing tasks by an ORPFOA algorithm	ORPFOA	Swarm-based algorithm
31	[60]	Cost-effective placement of recharging stations in drone path planning for surveillance missions on large farms	BFKSA	Hybrid
32	[8]	An intelligent UAV path planning optimization method for monitoring the risk of unattended offshore oil platforms	NSGA-II	Evolutionary algorithm
33	[61]	Cooperative path planning of UAVs & UGVs for a persistent surveillance task in urban environments	EDA-GA	Hybrid
34	[62]	Collision free 4D path planning for multiple UAVs based on spatial refined voting mechanism and PSO approach	SRVM	Swarm-based algorithm
35	[63]	UAV path planning for data ferrying with communication constraints	GA	Evolutionary algorithm
36	[64]	Adaptive meta-heuristic-based methods for autonomous robot path planning: sustainable agricultural applications	I-GWO	Swarm-based algorithm
37	[11]	UAVs path planning architecture for effective medical emergency response in future networks	CVRP	Hybrid
38	[65]	Quantum behavior-based enhanced fruit fly optimization algorithm with application to UAV path planning	QFOA	Hybrid
39	[66]	A cooperative target search method based on intelligent water drops algorithm	LMIWD	Hybrid
40	[67]	Autonomous unmanned aerial vehicles in search and rescue missions using real-time cooperative model predictive control	PSO	Swarm-based algorithm
41	[12]	A grey wolf optimizer using gaussian estimation of distribution and its application in the multi-UAV multi-target urban tracking problem	GEDGWO	Hybrid
42	[68]	UAV trajectory planning based on PH curve improved by particle swarm optimization and quasi-newton method	PSO and Quasi–Newton Method	Hybrid
43	[69]	On-board real-time trajectory planning for fixed wing unmanned aerial vehicles in extreme environments	RTTP base GA	Evolutionary algorithm
44	[70]	Grey wolf optimization based sense and avoid algorithm in a bayesian framework for multiple UAV path planning in an uncertain environment	GWO	Swarm-based algorithm
45	[71]	Evolutionary collaborative human-UAV search for escaped criminals	HEA	Hybrid
46	[72]	A practical methodology for generating high-resolution 3D models of Open-Pit slopes using UAVs: flight path planning and optimization	GA	Evolutionary algorithm
47	[73]	A new method of solving UAV trajectory planning under obstacles and multi-constraint	PSO	Swarm-based algorithm
48	[74]	Synergistic path planning of multi-UAVs for air pollution detection of ships in ports	PSO	Swarm-based algorithm
49	[75]	Multi-UAV cooperative path planning with monitoring privacy preservation	OMACO	Hybrid
50	[76]	UCAV path planning for avoiding obstacles using cooperative co-evolution spider monkey optimization	CESMO	Hybrid
51	[77]	Parallel cooperative co-evolutionary grey wolf optimizer for path planning problem of unmanned aerial vehicles	PCCGWO	Hybrid
52	[78]	An accurate UAV 3-D path planning method for disaster emergency response based on an improved multi-objective swarm intelligence algorithm	APPMS	Swarm-based algorithm
53	[5]	UAV based spatiotemporal analysis of the 2019–2020 new South Wales bushfires	PSO	Swarm-based algorithm
54	[79]	Opposite and chaos searching genetic algorithm based for UAV path planning	OCGA	Hybrid
55	[80]	Multi-Verse algorithm based approach for multi-criteria path planning of unmanned aerial vehicles	MOMVO	Physics-based algorithm
56	[81]	Drone delivery multi-agent routing optimization	SA	Physics-based algorithm
57	[82]	Design and implementation of distributed path planning algorithm for a fleet of UAVs	PSO	Swarm-based algorithm
58	[83]	Adversarial swarm defence using multiple fixed-wing unmanned aerial vehicles	Adversarial swarm defense algorithm	Swarm-based algorithm
59	[84]	Hierarchical task assignment of multiple UAVs with improved firefly algorithm based on simulated annealing mechanism	SA-DFA	Hybrid
60	[85]	UAV path planning method based on modified white shark optimization	MWSO	Swarm-based algorithm
61	[86]	A novel simulated annealing based strategy for balanced UAV task assignment and path planning	SJSA	Physics-based algorithm
62	[87]	An improved equilibrium optimizer with application in unmanned aerial vehicle path planning	MHEO	Hybrid
63	[88]	Optimal energy consumption path planning for quadrotor UAV transmission tower inspection based on simulated annealing algorithm	SA	Physics-based algorithm
64	[89]	MVO-based path planning scheme with coordination of UAVs in 3-D environment	MVO	Physics-based algorithm
65	[90]	Pollution source localization based on multi-UAV cooperative communication	APF-PSO	Hybrid
66	[6]	A knee-guided differential evolution algorithm for unmanned aerial vehicle path planning in disaster management	DEAKP	evolutionary algorithm
67	[91]	UAV path planning algorithm based on improved Harris Hawks optimization	Improved HHO	Hybrid
68	[92]	Long-range path planning using an aircraft performance model for battery-powered sUAS equipped with icing protection system	PSO	Swarm-based algorithm

illustrates the list of the final included studies, along with their proposed algorithms and types meta-heuristics. Furthermore, Figure 2 shows the word cloud of the included articles’ keywords, highlighting the most frequently used terms, such as “Path”, “Planning”, “Optimization”, “UAV”, and “Algorithm”.

To specify the year and country with the highest number of contributions, we categorized the papers accordingly. As shown in Figure 3a,b, the year 2022 had the highest number of publications, and China had the highest number of articles.

Figure 4 shows the distribution of the papers based on their database and publication venue. As is apparent, Scopus led with 28 papers, followed by IEEE with 19, ScienceDirect with 17, Web of Science with 3, and ACM with only 1. When it comes to publication venues, we found that the majority of the publications were journal articles (n = 59) and only 9 were conference publications.

To highlight the applications of meta-heuristic algorithms in UAVs, we categorized them based on their application areas. As Figure 5 shows, 38 articles employed these techniques in general research in order to extend applications of UAVs with regard to different aspects. The other application areas include military, medicine, agriculture, etc.

Finally, we also investigated whether the focus of the reviewed articles leaned toward single or multiple Unmanned Aerial Vehicles (UAVs), as well as the scope of their mission objectives—single-target or multi-target scenarios. Figure 6 illustrates the distribution of research emphasis among the included 68 articles. Among these articles, 36 delved into the intricacies of single-UAV operations, underscoring a substantial interest in optimizing the performance of individual UAVs. Complementing this, 32 articles specifically targeted the domain of multi-UAV systems, reflecting a growing recognition of the potential synergies and challenges posed by collaborative UAV efforts.

Moreover, our investigation extended to discerning the prevailing research trends concerning mission objectives. The majority of the studies, precisely 52 out of 68, concentrated on single-target scenarios, highlighting a prevalent focus on refining UAV capabilities for singular mission objectives. In contrast, a noteworthy subset of 16 articles was dedicated to the complexities of and advancements in multi-target missions, shedding light on the evolving landscape, where UAVs are increasingly employed for diverse and simultaneous objectives. This nuanced exploration of UAV configurations and mission scopes provides a comprehensive overview of the diverse trajectories that contemporary research is taking in the realm of unmanned aerial systems. Figure 6 demonstrates a comparison of UAV type(s) and UAV destination(s).

3.2. Type of Meta-heuristic Algorithms

RQ1: What types of meta-heuristic algorithms were used the most for optimizing UAV path planning?

The predominance of hybrid-type methods in the optimization of UAV path planning, as observed in 33 out of the 68 reviewed articles, underscores the popularity and effectiveness of combining diverse algorithms to enhance performance. This inclination towards hybrid methods suggests a recognition among researchers of the need to harness the strengths of multiple algorithms and mitigate their individual limitations. Swarm-based algorithms emerge as the second most utilized category, with 19 articles adopting these nature-inspired approaches for UAV path planning optimization. The swarm-based paradigm, often drawing inspiration from collective behavior in nature, proves to be a compelling choice for addressing complex path planning scenarios. On the other hand, evolutionary algorithms and physics-based algorithms are less frequently employed, featuring in nine and seven articles, respectively. This relative underutilization may stem from the specialized nature of or computational demands associated with these algorithmic approaches. In Section 4, a comprehensive analysis of the reviewed articles delves deeper into the specific characteristics and outcomes for each meta-heuristic algorithm type, providing valuable insights into the nuanced landscape of UAV path planning optimization strategies.

Table 4. Classification of the 68 included articles based on meta-heuristic algorithms.

Algorithm-Type	Number of Articles	Article ID of Table 3
Swarm-based algorithm	19	3, 6, 7, 8, 11, 25, 30, 34, 36, 40, 44, 47, 48, 52, 53, 57, 58, 60, 68
Evolutionary algorithm	9	4, 5, 14, 29, 32, 35, 43, 46, 66
Physics-based algorithm	7	15, 19, 55, 56, 61, 63,64
Hybrid	33	1, 2, 9, 10, 12, 13, 16, 17, 18, 20, 21, 22, 23, 24, 26, 27,28, 31, 33, 37, 38, 39, 41, 42, 45, 49, 50, 51, 54, 59, 62, 65, 67

was prepared to demonstrate the classification of the 68 selected articles based on meta-heuristic algorithms.

3.3. Objectives and Constraints

RQ2: What characteristics are considered as objectives and constraints of mathematical models for optimizing path planning via meta-heuristic algorithms?

The second research question unveils a comprehensive understanding of the objectives and constraints governing mathematical models for optimizing UAV path planning through the use of meta-heuristic algorithms. The identified objectives, elucidated in

Table 5. Papers introducing the common objectives of mathematical models for optimizing path planning for UAV.

Objectives	Number of Articles	Article ID in Table 3
Path length/distance	62	1, 2, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 32, 33, 34, 35, 36, 37, 38, 40, 41, 42, 43, 44, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68
Time	65	1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 23, 24, 25, 26, 27, 28, 30, 31, 32, 33, 34, 35, 36, 37, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 67, 68
Energy	36	1, 3, 4, 6, 7, 8, 9, 10, 11, 12, 13, 14, 16, 17, 18, 23, 25, 26, 27, 29, 30, 31, 34, 35, 36, 42, 43, 46, 48, 50, 56, 58, 62, 63, 67, 68
Cost	54	1, 2, 3, 4, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 19, 20, 21, 22, 24, 25, 26, 27, 28, 30, 31, 34, 35, 36, 37, 38, 40, 41, 42, 43, 44, 47, 48, 49, 50, 51, 53, 54, 55, 56, 57, 58, 59, 62, 64, 65, 66, 67, 68
Collision avoidance	51	1, 2, 3, 5, 6, 7, 8, 9, 10, 13, 14, 15, 16, 17, 19, 20, 22, 23, 24, 25, 27, 28,29, 30, 32, 33, 34, 36, 39, 40, 41, 43, 44, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 60, 63, 64, 65, 66, 67, 68

, shed light on the multifaceted considerations researchers undertake in their quest for effective path planning solutions. Optimal path length or distance, a paramount concern, centers around minimizing the spatial gap between source and destination while ensuring collision-free navigation. Time optimization emerges as the most frequently pursued objective, with 65 instances prioritizing the efficient utilization of CPU time. Conversely, energy considerations, arising from the conflict between optimal path length and energy consumption, are relatively less prevalent, featuring in 36 instances among the 68 articles. The nuanced balance between optimal path length, shorter time, and faster velocity takes precedence in many instances, often relegating the optimization of cost to a secondary consideration.

Notably, the critical aspect of collision avoidance, integral for ensuring the safety of UAVs during path planning, is addressed in 51 out of the 68 articles. This emphasis reflects the acknowledgment of collision avoidance as a fundamental mechanism for enabling UAVs to detect and evade obstacles, thereby preventing damage and ensuring secure flight. However, it is noteworthy that 17 articles chose to bypass collision avoidance considerations, opting for theoretical or simplified models with fewer challenges and less complexity in terms of obstacles. This strategic decision in model creation underscores the varied approaches taken by researchers in balancing realism and computational simplicity in the realm of UAV path planning optimization.

Concerning the specific constraints of mathematical equations in the optimization of UAV path planning, seven prominent categories, detailed in

Table 6. The common constraints in the 68 included articles.

Constraint Items	Number of Articles	Article ID in Table 3
Angle	41	1, 2, 3, 6, 7, 8, 9, 12, 13, 14, 15, 16, 18, 20, 21, 22, 23, 24, 25, 28, 31, 32, 34, 38, 39, 40, 41, 43, 44, 46, 47, 50, 51, 52, 55, 58, 62, 63, 66, 67, 68
UAV’s axes	33	1, 6, 8, 9, 11, 12, 13, 14, 15, 16, 17, 18, 20, 21, 22, 23, 25, 30, 33, 34, 38, 41, 44, 47, 49, 50, 51, 53, 55, 61, 65, 66, 68
Altitude	40	1, 2, 5, 6, 7, 8, 9, 11, 12,13, 14, 15, 16, 18, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 38, 40, 41, 43, 46, 47, 52, 62, 66, 67, 68
Risk	11	3, 5, 7, 9, 29, 32, 34, 36, 38, 44, 66
Threat	34	1, 2, 3, 4, 5, 8, 9, 11, 12, 13, 14, 17, 19, 20, 21, 22, 24, 26, 32, 34, 38, 41, 42, 44, 47, 50, 51, 52, 54, 55, 60, 62, 66, 67
Obstacle	39	1, 2, 5, 9, 10, 12, 13, 15, 16, 17, 19, 21, 22, 23, 24, 25, 27, 29, 30, 33, 34, 36, 41, 42, 43, 44, 47, 50, 51, 53, 54, 55, 56, 60, 62, 64, 65, 66, 67
Velocity	42	1, 2, 3, 4, 6, 7, 8, 11, 12, 14, 15, 16, 18, 19, 21, 22, 23, 24, 25, 27, 29, 31, 34, 38, 39, 40, 41, 42, 43, 45, 46, 47, 48, 49, 50, 56, 57, 58, 59, 60, 65, 58

, delineate the crucial considerations guiding the development of these equations. Angle, the first constraint, encapsulates the degree of landing, takeoff, and flight at varying heights, with a direct impact on fuel consumption. UAV axes, denoted by the roll, pitch, and yaw axes, assume a pivotal role in imposing climbing and descending angle constraints during path planning. Altitude emerges as a significant constraint linked to drone safety, navigating the delicate balance between the risk of collision at low altitudes and increased energy consumption at higher altitudes. Risk, the fourth category, encompasses the safety of UAV flight, along with considerations of collision probability, mission completion, and timely arrival at a given destination. Threat, a crucial constraint in military scenarios, introduces the probability of missile attacks and dangers posed by obstacles or hazardous situations like bushfires.

Obstacle, a special category influencing collision avoidance, distinguishes between dynamic obstacles, such as moving vehicles, and static obstacles like trees or mountains. Velocity, the final constraint, directly correlates with the type of UAV application, affecting fuel consumption and playing a pivotal role in flight safety and collision prevention, particularly in military contexts. This comprehensive exploration of constraints enriches our understanding of the intricate considerations involved in formulating mathematical models for UAV path planning optimization using meta-heuristic algorithms.

3.4. Mathematical Types

RQ3: What type of mathematical model was used the most for the optimization UAV path planning using meta-heuristic algorithms?

The investigation into mathematical models for UAV path planning optimization via meta-heuristic algorithms sheds light on the dynamic interplay between linear and nonlinear approaches. Linear models, characterized by simplicity and direct relationships between variables, are preferred for tasks in straightforward environments, yielding shorter path lengths and reduced CPU time. These models, tailored for basic path planning scenarios, assume a linear approximation of UAV movement, suitable for relatively uncomplicated environments.

On the other hand, nonlinear models emerge as a more prevalent choice, with 43 articles opting for their utilization in the optimization of UAV path planning. The complexity inherent in UAV path planning tasks, involving factors such as wind speed, obstacles, and diverse landscapes, necessitates the sophistication offered by nonlinear models. The superior accuracy of nonlinear models becomes particularly evident when dealing with intricate maneuvers, curves, and complex trajectories.

The choice between linear and nonlinear models is intricately tied to the specific requirements of a UAV’s mission and the desired level of accuracy. The prevalence of nonlinear models in the literature attests to their efficacy in capturing the nuances and challenges associated with UAV path planning, providing a comprehensive understanding of the mathematical modeling landscape within the realm of meta-heuristic algorithms.

Table 7. Mathematical type.

Mathematical Type	Number of Articles	Article ID in Table 3
Linear	25	4, 10, 14, 28, 29, 30, 32, 33, 35, 36, 37, 39, 43, 44, 45, 46, 48, 50, 51, 53, 56, 61, 63, 64, 66
Nonlinear	43	1, 2, 3, 5, 6, 7, 8, 9, 11, 12, 13, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 31, 34, 38, 40, 41, 42, 47, 49, 52, 54, 55, 57, 58, 59, 60, 62, 65, 67, 68

classifies the 68 articles based on linear and nonlinear mathematical types.

3.5. Environmental Types

RQ4: What are the environmental types and dimensions employed for the optimization of path planning?

The exploration of environmental considerations in optimizing UAV path planning using meta-heuristic algorithms unveils a nuanced landscape characterized by diverse types and dimensions. According to

Table 8. Environment type.

Environment Type	Number of Articles	Article ID in Table 3
Dynamic	37	1, 2, 3, 5, 6, 8, 9, 14, 15, 18, 19, 21, 23, 24, 25, 27, 28, 34, 37, 40, 41, 42, 43, 44, 45, 46, 47, 48, 50, 53, 56, 57, 58, 60, 64, 65, 68
Static	26	4, 11,12, 13, 20, 22, 26, 29, 30, 31, 32, 33, 35, 36, 38, 39, 49, 51, 52, 54, 59, 61, 62, 63, 66, 67
Dynamic and Static	5	7, 10, 16, 17, 55

, three primary environmental types take center stage in the literature: dynamic (n = 37), static (n = 26), and both dynamic and static (n = 5). The prevalence of dynamic environments, accounting for the majority of cases, underscores the emphasis on real-time adaptability in UAV path planning scenarios. The integration of dynamic characteristics and parameters caters to the evolving nature of operational landscapes, enhancing the responsiveness of path planning algorithms to unforeseen changes.

Regarding the environmental dimension of mathematical models for UAV path planning, researchers have employed two-dimensional (2D), three-dimensional (3D), and, intriguingly, four-dimensional (4D) frameworks.

Table 9. Environment dimension.

Environment Dimension	Number of Articles	Article ID in Table 3
2D	19	4, 7, 10, 17, 19, 25, 31, 35, 37, 39, 40, 42, 48, 49, 50, 53, 56, 58, 59
3D	43	1, 2, 6, 8, 9, 11, 12, 13, 14, 15, 16, 18, 20, 21, 22, 23, 24, 26, 27, 28, 29, 30, 32, 33, 36, 38, 41, 43, 44, 45, 46, 47, 52, 55, 60, 61, 62, 63, 64, 65, 66, 67, 68
2D and 3D	5	3, 5, 51, 54, 57
4D	1	34

presents the distribution, revealing that 43 studies focus on 3D environments, 19 studies delve into 2D scenarios, and 5 studies simultaneously address the intricacies of both 2D and 3D environments. Remarkably, a singular study pioneered the exploration of 4D environments, pushing the boundaries of conventional spatial considerations.

The dominance of 3D environmental modeling aligns with the complexity inherent in UAV path planning tasks, where three-dimensional spatial awareness is crucial for maneuvering through dynamic landscapes. The inclusion of 2D environments, while less prevalent, suggests a focus on scenarios with simplified spatial constraints. The nascent exploration of 4D environments reflects an emerging trend, signaling a push toward incorporating time as a dynamic dimension in UAV path planning optimization.

In summary, these findings underscore the multifaceted nature of UAV path planning optimization, where adaptability to real-time changes and innovative modeling dimensions play pivotal roles in enhancing the effectiveness of meta-heuristic algorithms.

4. Discussion

Regarding the first research question, the majority of the articles investigated employed hybrid-type methods, with swarm-based algorithms and evolutionary algorithms also being widely applied for optimizing UAV path planning. Physics-based algorithms were also utilized but to a lesser extent.

In the realm of physics-based algorithms, the corresponding approaches draw inspiration from natural processes and physical laws to tackle complex problems [93]. They prove effective in handling high-dimensional models and nonlinear equations, generating multiple solutions, and minimizing fitness functions. However, a drawback is their longer running time compared to other algorithm types. Many studies expressed dissatisfaction with standalone physics-based algorithms due to their insufficient runtimes [27]. For instance, Jarray et al. [44] simulated three-dimensional cooperative path planning for quadrotors using Multi-Verse Optimization (MOMVO), which was compared with other algorithms. MOMVO proved superior in shortening the path length for multi-UAVs to multi targets but not with respect to the aspect of time. Similarly, Kumar et al. [48] proposed an MVO-based algorithm for two-dimensional dynamic environment UAV path planning, effectively minimizing collisions and threats. Wu et al. [88] focused on simulated annealing in order to optimize energy consumption for UAV transmission tower inspection, achieving a significant decrease in energy consumption. Jain et al. [89] compared MVO with GSO and BBO for optimizing UAV path planning with obstacle avoidance, finding MVO to be superior in optimizing path costs. These examples illustrate the versatility and effectiveness of physics-based algorithms, especially when employed for optimization approaches. It is notable that seven articles out of the sixty-eight selected papers embraced physics-based algorithms, making them the least popular type in our selection of the literature.

In the realm of evolutionary algorithms for UAV path planning, the focus is on generating optimal paths based on cost, travel distance, and reliability cost. These algorithms employ a process of randomly generating practical solutions in the first generation, followed by the selection of feasible solutions to determine their fitness. Evolutionary algorithms, while effective in generating optimal solutions through iteration processes [94,95], may face challenges such as long iterations leading to premature convergence and suboptimal results. Among the nine articles in this category, Chen et al. [35] utilized a fast search genetic algorithm (FSGA) and a non-dominated sorting genetic algorithm (NSGA-II) for military missions, demonstrating the efficiency of these algorithms in optimizing path planning models. Similarly, Wang et al. [36] employed an improved NSGA-II to optimize multi-objective UAV path planning in dynamic environments, showcasing its ability to overcome local optimum risks. In other studies, such as those conducted by Golabi et al. [58], Wang et al. [8], Jamshidi et al. [43], Joseph et al. [63], Schellenberg et al. [69], Battulwar et al. [72], and Yu et al. [6], evolutionary algorithms like NSGA-II and GA were utilized to optimize UAV path planning in various scenarios, ranging from collision avoidance and monitoring volcanic ash to disaster management. These examples highlight the versatility and effectiveness of evolutionary algorithms in addressing diverse challenges within UAV path planning. It is necessary to state that nine articles in our selected subset of the literature are of an evolutionary type.

Swarm-based algorithms, drawing inspiration from patterns observed in nature, such as those relating to ants, bird colonies, and schools of fish, demonstrate a unique problem-solving approach by combining the behaviors of simple individuals [96,97,98]. These algorithms, characterized by global modes and robust solutions, excel in solving complex problems, with a focus on optimizing path planning in three-dimensional environments regarding premature convergence and greater running time [99]. This research accounts for 19 articles out of the 68 included, showcasing the versatility of swarm-based algorithms. In the examined articles, Ahmed et al. [34] optimized PSO with the Bresenham algorithm for three-dimensional path planning, demonstrating mPSO’s superiority in terms of coverage speed, fitness, and runtime. Other studies, such as those conducted by Mesquita and Gaspar [7], Duan et al. [37], Jamshidi et al. [38], Xu et al. [40], Wu et al. [54], Li et al. [59], Yang et al. [62], Kiani et al. [64], Andrade et al. [67], Radmanesh et al. [70], Shao et al. [73], Shen et al. [74], Wan et al. [78], Ullah et al. [5], Belkadi et al. [82], Choi et al. [83], Zhang et al. [85], and Hovenburg et al. [92], applied various swarm-based algorithms like PSO, IIWD, IGWO, IWOA, ORPFOA, SRVM, I-GWO, EX-GWO, GWO, and MWSO in scenarios ranging from surveillance and monitoring to environmental optimization. These examples highlight the adaptability and effectiveness of swarm-based algorithms in addressing diverse challenges within the field of UAV path planning.

In the realm of UAV path planning, hybrid algorithms emerge as a dominant trend, surpassing the use of traditional single-meta-heuristic algorithms. A total of 33 articles out of the 68 selected papers embraced hybrid algorithms, making them the most popular type of study in our selection of the literature. The essence of hybridization lies in combining two or more algorithms to address the weaknesses inherent in using a single algorithm. Notably, our research defines one rule for a hybrid algorithm: at least one of the algorithms in the hybrid approach must be of the meta-heuristic type. Examining specific examples, Yang et al. [32] developed Multi-population chaotic Grey Wolf Optimization (MP-CGWO) as a hybrid algorithm for cooperative UAV path planning, showcasing its superiority over GWO, PSO, and DE in terms of efficiency and search accuracy. Ma and Chen [33] applied the Adaptive Path Planning Particle Swarm Optimization (APP-PSO) for collision avoidance in complex environments, outperforming several other PSO variants. Zhou et al. [39] developed a hybrid algorithm, which they called Global-best Brainstorm Optimization and Crossover Recombination (GBSO-CR), in order to optimize paths in three-dimensional threat situations. The results showed that GBSO-CR outperformed its competitors due to faster convergence and safer economical solutions. The diversity of hybrid approaches is evident in studies such as those conducted by Qadir et al. [17], Zhou et al. [41], Wang et al. [47], FU et al. [90], Ait-Saadi et al. [42], Behjati et al. [45], and many others, each addressing unique challenges in UAV path planning through innovative combinations of algorithms.

These examples collectively demonstrate the effectiveness of hybrid algorithms in overcoming various challenges, from collision avoidance and threat situations to real-time dynamic environments. The hybridization approach allows researchers to harness the strengths of different algorithms, leading to improved optimization results and more robust solutions in the context of UAV path planning.

Regarding the second research question, our exploration of the mathematical models for UAV path planning identified five common objectives guiding researchers. The predominant focus lies in time optimization, evident in 65 instances where researchers aimed to enhance the efficiency of the utilization of CPU time. Conversely, energy considerations are relatively less frequent, with only 36 instances recognizing the complex relationship between achieving an optimal path length and fuel-consumption. For instance, Zhang et al. [91] stated that the maximum path length should be less than the required amount of fuel in order to overcome the challenge regarding the relationship between path length and fuel consumption. In other words, the fuel parameter had a fixed role, without any changes, in ameliorating the impact of fuel in UAV flight. Then, a hybrid algorithm (SSHHO) was employed to optimize the UAV model. Finally, the obtained results demonstrated that SSHHO outperformed other algorithms in terms of reducing cost, time, and shortening length by considering a fixed amount of fuel when compared with HHO, PSO, SCA, and WOA [91].

Concerning the specific constraints of mathematical equations in the optimization of UAV path planning, we found seven common categories. As outlined in Table 6, angle, UAV axes, altitude, risk, threat, obstacle, and velocity emerge as the main constraints considered during the development of mathematical equations for UAV path planning. These constraints play pivotal roles in shaping the trajectory and safety of UAV flights. For instance, angle constraints influence fuel consumption during takeoff, landing, and changes in altitude, while UAV axes dictate climbing and descending angles. Altitude constraints contribute to drone safety, balancing the risks of collision and energy consumption. For example, Wang et al. [47] focused on optimizing a nonlinear path planning model with regard to the complexity of the relationship between high-altitude flight and energy consumption. Their aim was to enhance the efficiency of UAV missions through solar-battery integration.

Velocity constraints, influenced by the type of UAV application, impact flight efficiency and fuel consumption, emphasizing the delicate balance between speed and energy optimization, especially in military contexts. These constraints collectively shape the corresponding mathematical models, ensuring the accuracy and safety of UAV path planning through the use of meta-heuristic algorithms. The consideration of risk in constraints is associated with the safety of a UAV’s flight, in which the probability of collision, mission completion, and timely arrival at the chosen destination are assessed. Obstacle constraints are integral to path planning, addressing collision avoidance with both dynamic and static obstacles. Threat constraints, particularly significant in military scenarios, encompass the likelihood of attacks and the need to navigate hazardous situations. For instance, Zheng et al. [68] optimized UAV trajectories through the PH Curve method to address the constraints of threats including obstacles and radars. They applied Particle Swarm Optimization and the Quasi-Newton Method to increase convergence speed and solution quality. Despite these efforts, it was determined that the rate of accuracy and safety would change, but no algorithms could guarantee UAV safety in the presence of obstacles.

With regard to the third research question, we investigated the nature of mathematical models employed in UAV path planning, discerning a clear dichotomy between linear and nonlinear formulations. The choice between these models hinges on the intricacies of the task and the specific demands of the application. Linear models, marked by their simplicity and assumption of a direct relationship between variables, are favored in less-complex environments, facilitating shorter path lengths and reduced CPU time. These models are typically deployed for basic path planning tasks, especially when a UAV’s movement can be linearly approximated. For example, Wang et al. [8] designed a UAV path model for monitoring the risk of unattended offshore oil platforms using NSGA-II. The obtained results demonstrated that the multi-objective linear mathematical model was successful in shortening path length and time.

On the other hand, nonlinear models step into the forefront when addressing the challenges posed by factors such as wind speed, obstacles, and complex environments. The complexity of UAV path planning originates from maneuvers, curves, angles, and the UAV’s axes. In tackling the mentioned complexities, nonlinear models outperform other models. Our exploration revealed 43 articles opting for nonlinear mathematical models compared to 25 articles employing linear counterparts. This inclination toward nonlinear formulations underscores the recognition of the complex and dynamic nature inherent in UAV path planning scenarios. For example, Wang et al. [47] optimized a nonlinear UAV path model by using a hybrid of ACO and GMP. Their research focused on enhancing the efficiency of UAVs by using solar energy at high-altitude and in long endurance missions. It is notable that flying at high altitude consumes more energy. This is why solar-battery integration offers a promising solution for managing energy requirements.

With regard to the fourth research question, our investigation into the environmental considerations in UAV path planning revealed three primary environmental types: dynamic, static, and a combination of dynamic and static. The prevalence of dynamic environments indicates a strong inclination towards incorporating real-time parameters in UAV path planning models. For instance, Jamshidi et al. [38] designed a multi-master structure in order to optimize UAV path planning in a real-time, dynamic environment for a CAN bus. To tackle the complexity of real time, the parallel GWO was employed to reduce computational time.

Furthermore, the environmental dimensions of mathematical models for UAV path planning vary, with most studies focusing on three-dimensional (3D) environments and fewer addressing two- (2D) and four-dimensional (4D) scenarios. For example, Joseph et al. [63] worked on energy-efficient data ferrying in relation to time-sensitive applications in a two-dimensional complex environment for the offline mode of UAV path planning. They utilized genetic algorithms to obtain near-optimal solutions, ensuring faster processing times. Also as an example regarding 3D scenarios, Yang et al. [32] developed a three-dimensional cooperative UAV path planning model employing MP-CGWO to optimize the model and enhance accuracy. As an example for 4D, Yang et al. [62] designed devised a four-dimensional dynamic collision-free path planning approach for UAVs by employing PSO to address local optima resulting from low convergence speeds. To this end, a Spatial Refined Voting Mechanism was utilized to handle local optima attributed to the low convergence speed. Unfortunately, five-dimensional research for UAV path planning based on meta-heuristic algorithms was not found, while five-dimensional UAV path planning was developed using a heuristic method [100].

These findings highlight the significance of dynamic characteristics in preparing UAV path planning models for real-world, real-time situations, and the predominant focus on 3D environments underlines the importance of capturing spatial intricacies for accurate and effective path planning.

4.1. Trends and Focuses of the UAV Path Planning Optimization Research Community

To highlight how the focus of the UAV path planning optimization research community has evolved over time, we developed a heatmap showing the relationship between the employed algorithm types and the objectives of mathematical models for optimizing path planning in relation to the publication year of the included articles.

As Figure 7a illustrates, swarm-based algorithms dominated initially, but a shift occurred towards a more diverse landscape. Evolutionary algorithms maintained a steady presence, while physics-based algorithms peaked in 2020 and subsequently declined. Hybrid algorithms, combining different approaches (e.g., machine learning), surged and became the predominant category by 2022. This suggests a dynamic shift in research focus, highlighting a growing interest in hybrid approaches that combine different algorithmic strategies to achieve enhanced performance.

Furthermore, as Figure 7b shows, in 2018 and 2019, a predominant focus on path length and time optimization was evident, with a gradual expansion into energy and cost considerations. By 2020, there was a substantial increase in attention to energy optimization, suggesting a growing awareness of efficiency in path planning algorithms. The trend continued in 2021 and 2022, with a notable rise in collision avoidance objectives, indicating an increased emphasis on safety in path planning. This evolution underscores a shift from the early concentration on basic metrics like path length and time towards a more comprehensive optimization strategy that integrates considerations of energy, cost, and collision avoidance to achieve enhanced performance and safety.

4.2. Challenges for Optimizing UAV Path Planning using Meta-Heuristic Algorithms

Through an extensive exploration of the optimization of UAV path planning using meta-heuristic algorithms, our literature review has unveiled several inherent challenges. Surprisingly, the most prevalent challenges, encountered in 21 out of the 68 articles, include the issues of being trapped in local optima and facing challenges regarding convergence speed. The entrapment in local optima, attributed to low convergence speed, emerges as a recurring obstacle when employing meta-heuristic algorithms for UAV path planning optimization. Our in-depth examination of the articles allows us to delineate these challenges and provide a concise overview, complemented by relevant studies for each challenge:

• Challenge of Longer Running Time—identified in articles [33,39,41,90], particularly when considering real-time applications [38,43,67].
• Challenge of Searching Collision-Free Paths—noted in studies [5,34], along with the challenge of reaching targets when obstacles obstruct the path [46,58], and addressing collisions resulting from path conflicts and overlaps [66].
• Challenges of Optimal Path Battery or Fuel Consumption—explored in articles [7,47,81,92], as well as challenges associated with achieving an optimal path with higher costs [17] and longer distances [5,17].
• Challenge of Reducing Accuracy, Safety, and Robustness—discussed in studies [62,89], emphasizing the importance of addressing accuracy, safety, and robustness concerns [45,56,68].
• Challenge of Generating the Best and Feasible Solutions—Acknowledged in articles [42,86], recognizing the need for both optimal and achievable solutions.
• Challenge of Tackling Complexity and Large Amounts of Computation—explored in research [50,68], highlighting the intricacies associated with handling complexity and substantial computational loads [57,84].
• Challenge of UAV Path Model Simulation in Dynamic Environments—identified as a distinct challenge in one article [67].
• Challenge of Coordinating and Constraining Manipulation—highlighted in a study [53], emphasizing the difficulty of manipulating coordination and constraints.
• Challenge of Applying Wireless Communication and Large Coverage Area on the Optimal Path—recognized in various articles [45,63], illustrating the complexity associated with integrating wireless communication and expansive coverage considerations into the optimization of a UAV’s path.

5. Conclusions and Future Direction

In conclusion, our comprehensive literature review on optimizing UAV path planning through meta-heuristic algorithms reveals significant insights into the current state of research and the challenges that persist within the field. Over the past five years, UAVs have garnered increased attention, particularly in military and civilian applications. Our systematic review, covering articles published from the beginning of 2018 until the end of 2022, focused on categorizing meta-heuristic algorithms into four types: evolutionary, physics-based, swarm-based, and hybrid.

Upon analyzing the selected 68 articles, we found that hybrid algorithms emerged as the dominant choice, surpassing other types, such as evolutionary, physics-based, and swarm-based algorithms. The preference for hybrid algorithms indicates their superior performance and adaptability in optimizing UAV path planning. The mathematical models employed in UAV path planning predominantly target five common objectives: optimal path length, time, energy, cost, and collision avoidance. Notably, time optimization takes precedence, reflecting the emphasis on CPU time efficiency. Energy considerations, however, are less frequent due to conflicts with optimal path length. Collision avoidance, a crucial safety mechanism, is sometimes neglected in theoretical or simplified models, presenting a challenge in ensuring realistic simulations. The choice between linear and nonlinear mathematical models depends on the complexity of the task and specific mission requirements. Nonlinear models, favored by researchers, prove essential for addressing factors like wind speed, obstacles, and varying landscapes. Linear models, while generating less complexity, are suitable for basic path planning tasks in simpler environments. Our findings indicate the prevalence of dynamic environmental types, emphasizing the importance of real-time considerations in UAV path planning. Three-dimensional (3D) models receive the most attention, aligning with the need for accuracy in complex trajectories. The diversity in environmental types and dimensions reflects the versatility required in optimizing UAV path planning.

Finally, our review exposes several challenges in applying meta-heuristic algorithms to UAV path planning. Becoming stuck in local optima and convergence speed emerged as the most frequent challenges, emphasizing the need for addressing algorithmic limitations. The challenges ranged from longer running times to collision-free path searching, optimal path battery or fuel consumption, and tackling complexity and large computation amounts. Additionally, the heatmap analysis with regard to publication year and employed algorithm types revealed a dynamic shift in the UAV path planning optimization research community, with hybrid algorithms becoming the predominant category by 2022, showcasing a growing interest in combining different algorithmic strategies for enhanced performance. Furthermore, regarding the objectives of mathematical models for optimizing path planning, we found that there has been a shift from early concentration on basic metrics like path length and time towards a more comprehensive optimization strategy that integrates considerations of energy, cost, and collision avoidance to facilitate enhanced performance and safety.

In terms of future directions, our literature review provides a comprehensive roadmap for advancing the optimization of UAV path planning through meta-heuristic algorithms. One pivotal avenue involves the enhancement of UAV path planning by incorporating Quality of Service (QoS) metrics to measure and optimize performance. By establishing specific criteria for path planning quality, researchers can tailor solutions to meet stringent performance standards, ensuring the efficiency and reliability of UAV operations.

Another critical focus is the exploration of cooperative UAV path planning strategies tailored for multi-target scenarios in dynamic environments with real-time requirements. This approach acknowledges the complexities of real-world applications and encourages the development of collaborative algorithms that enable UAVs to navigate seamlessly through dynamic landscapes, adapting in real time to varying targets and environmental conditions. Additionally, the integration of hybrid algorithms takes center stage, offering a promising solution with which to empower UAV path models, overcoming challenges related to time, cost, and battery optimization while facilitating real-time implementation. These future directions collectively aim to propel the field toward more sophisticated, adaptive, and efficient UAV path planning solutions that align with the demands of contemporary applications.