An Autonomous Soaring for Small Drones Using the Extended Kalman Filter Thermal Updraft Center Prediction Method Based on Ordinary Least Squares
Abstract
1. Introduction
2. Autonomous Soaring System
2.1. Constitution of the Autonomous Soaring System
2.2. Wind Field Perception System
- (1)
- Perception of updraft
- (2)
- Perception of horizontal wind
- (3)
- Accuracy of perception
2.3. The EKF Thermal Updraft Center Prediction Method Based on OLS
- (1)
- The intensity and radius of the thermal are fixed, and their distribution does not change with altitude.
- (2)
- The thermal’s hot center point, denoted as () in a north-east-down coordinate system, drifts within the horizontal plane due to the horizontal wind’s velocity.
3. Experiments and Results
3.1. Simulation Experiments
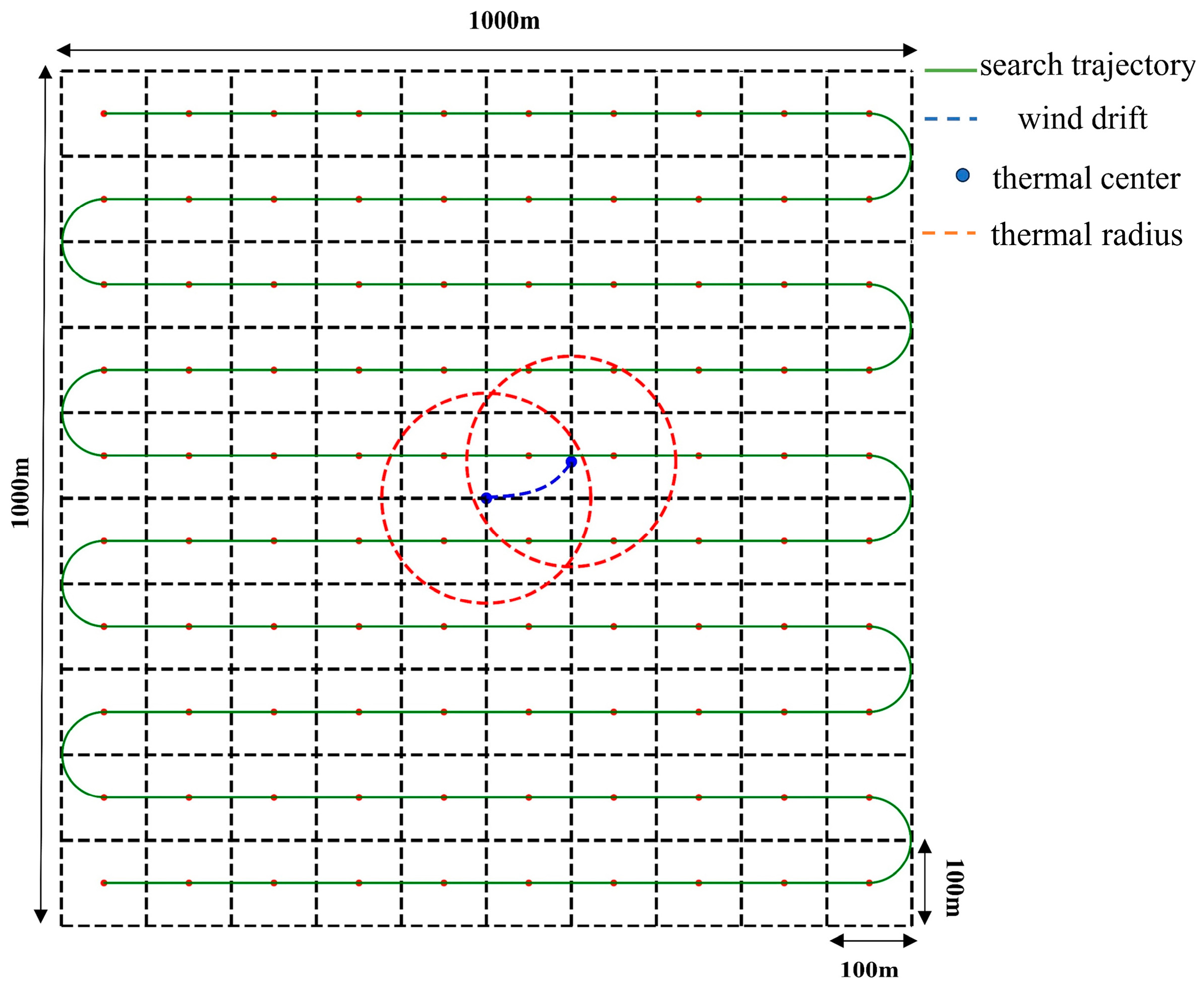
3.1.1. Simulation Environment
3.1.2. Case Settings
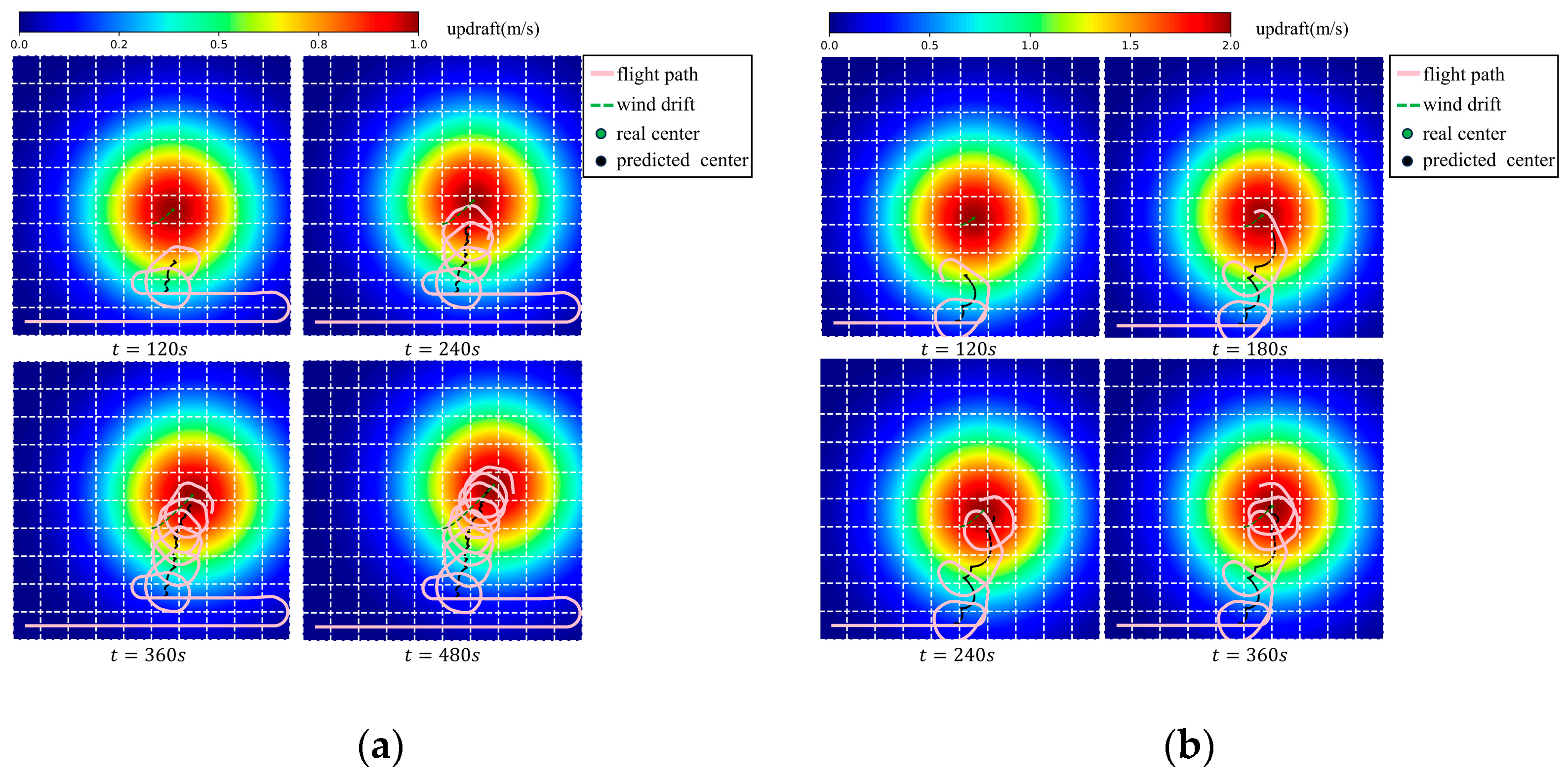
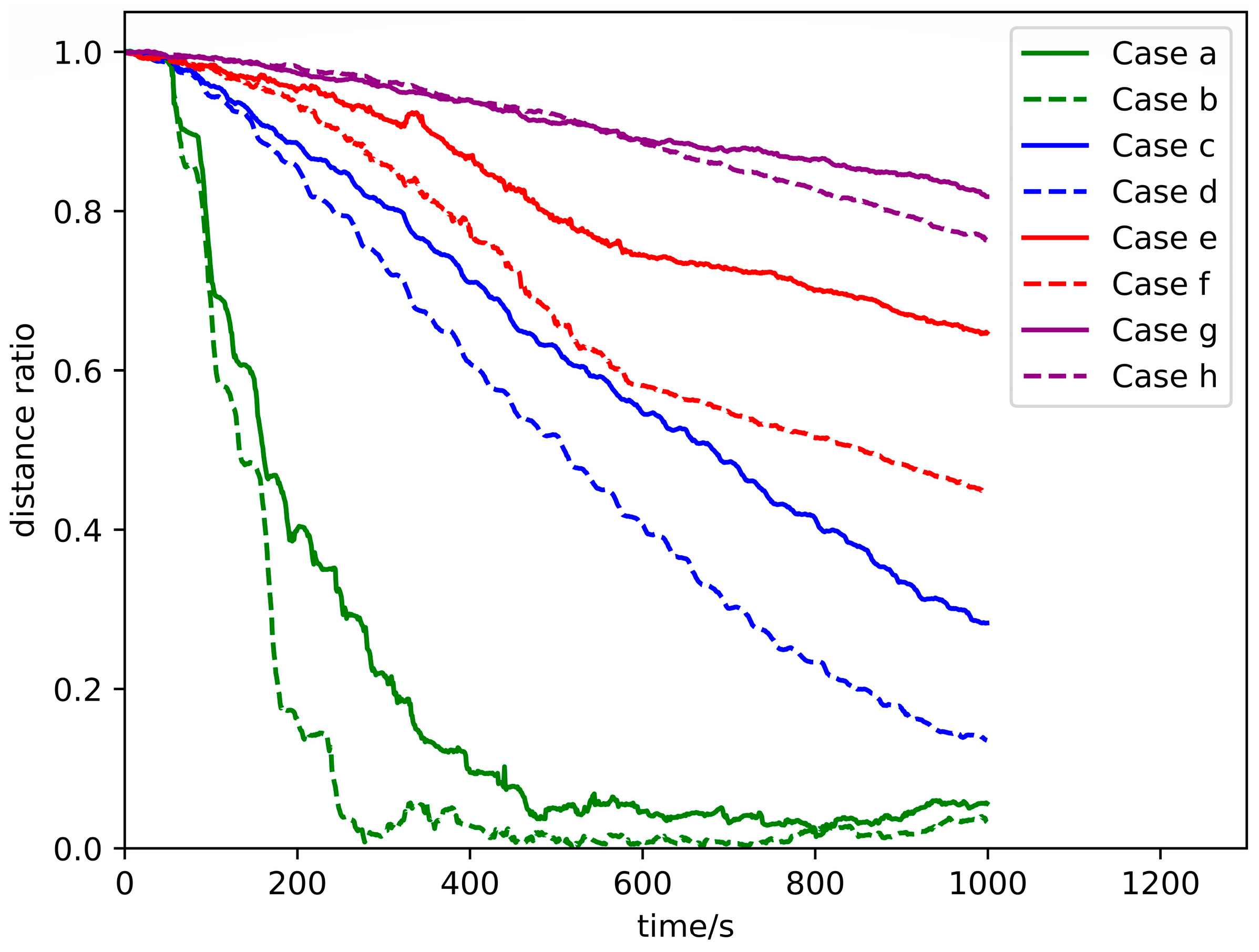
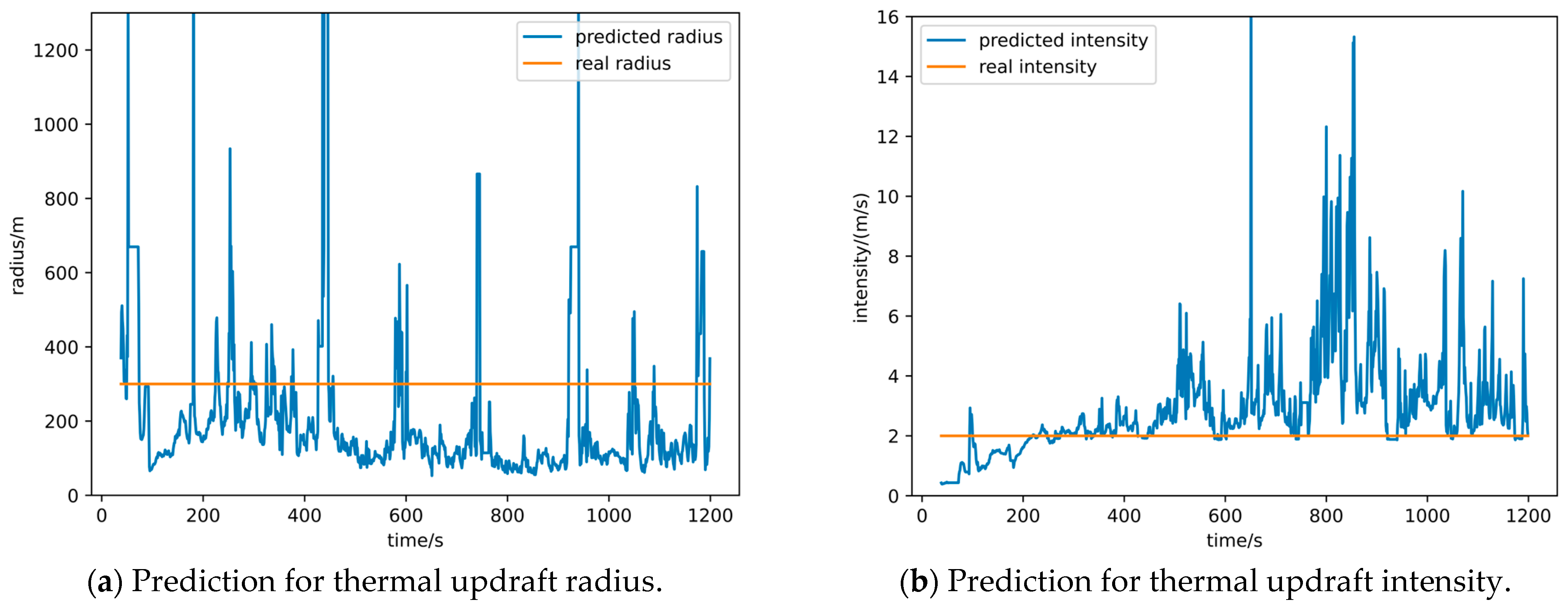
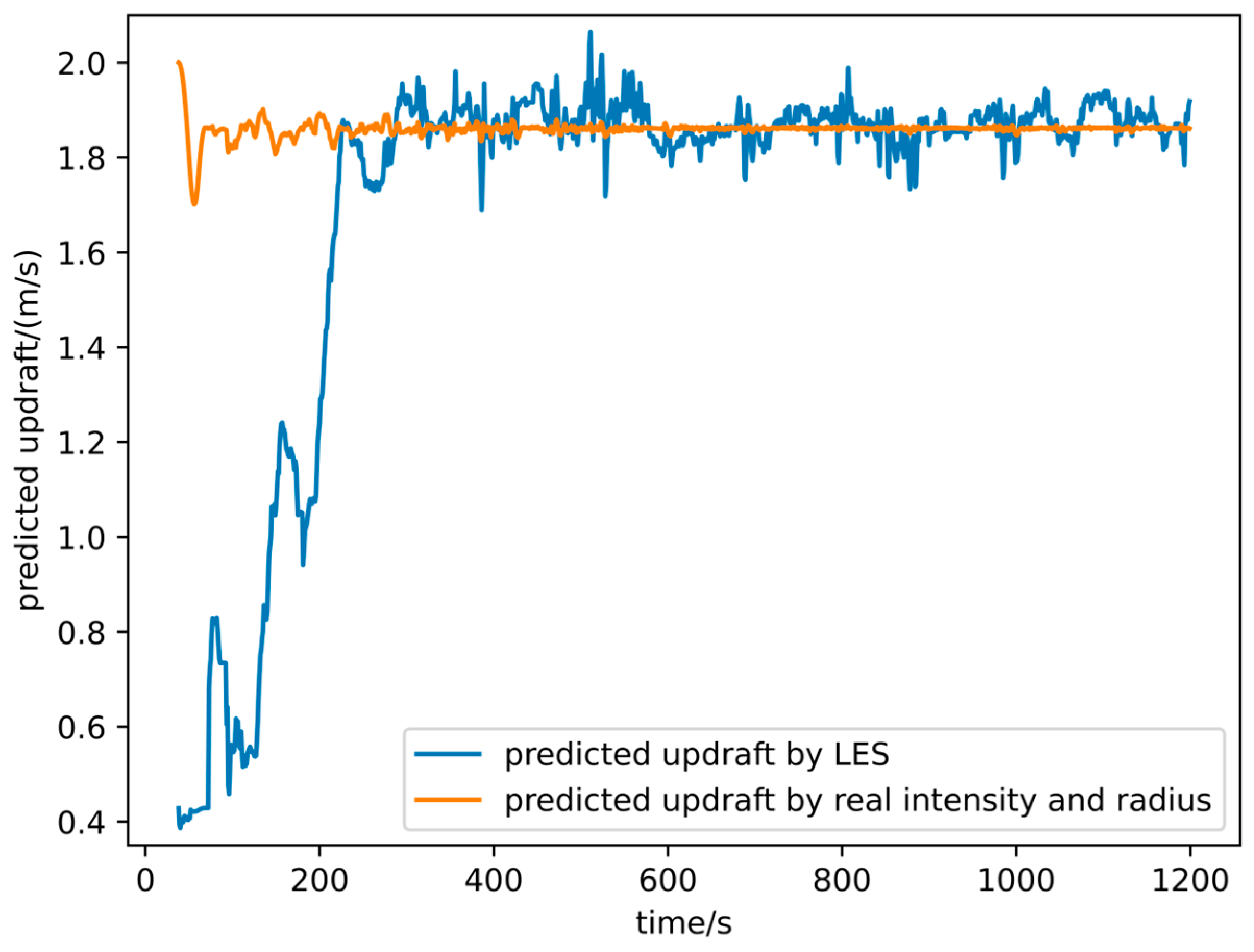
3.1.3. Simulation Results
3.1.4. Interpretation of the Results
3.2. Flight Experiments
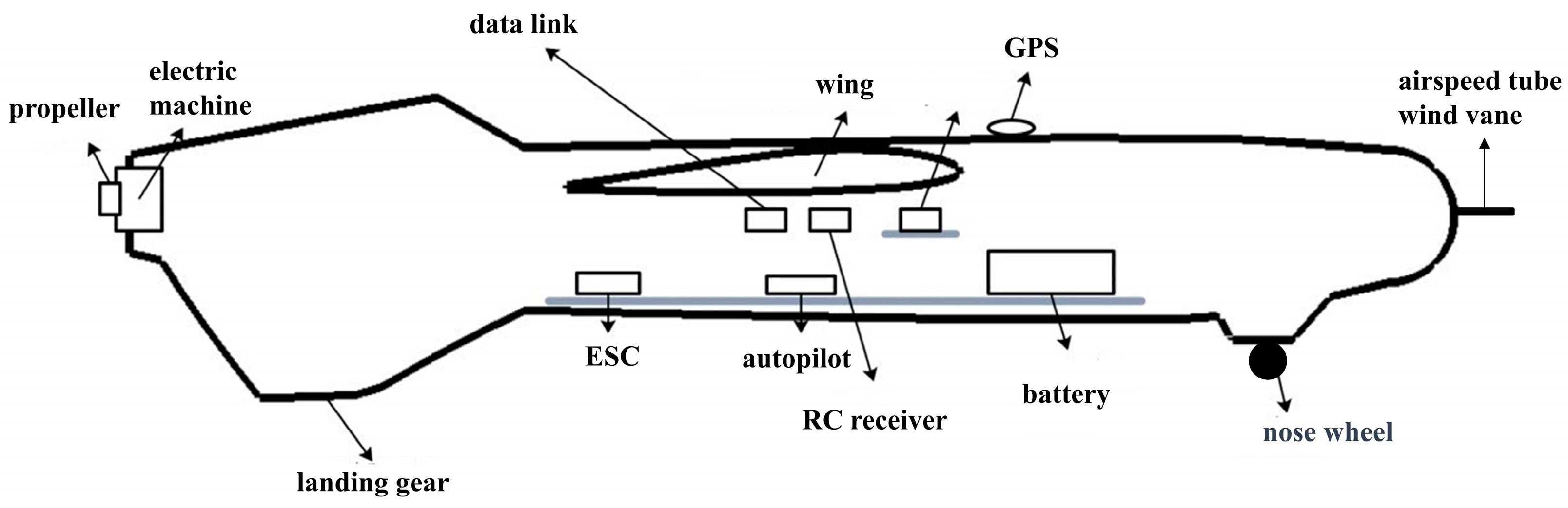
3.2.1. Configuration
- (1)
- Drone platform
- (2)
- Sensors
- (3)
- Flight controller
- (4)
- Experimental site
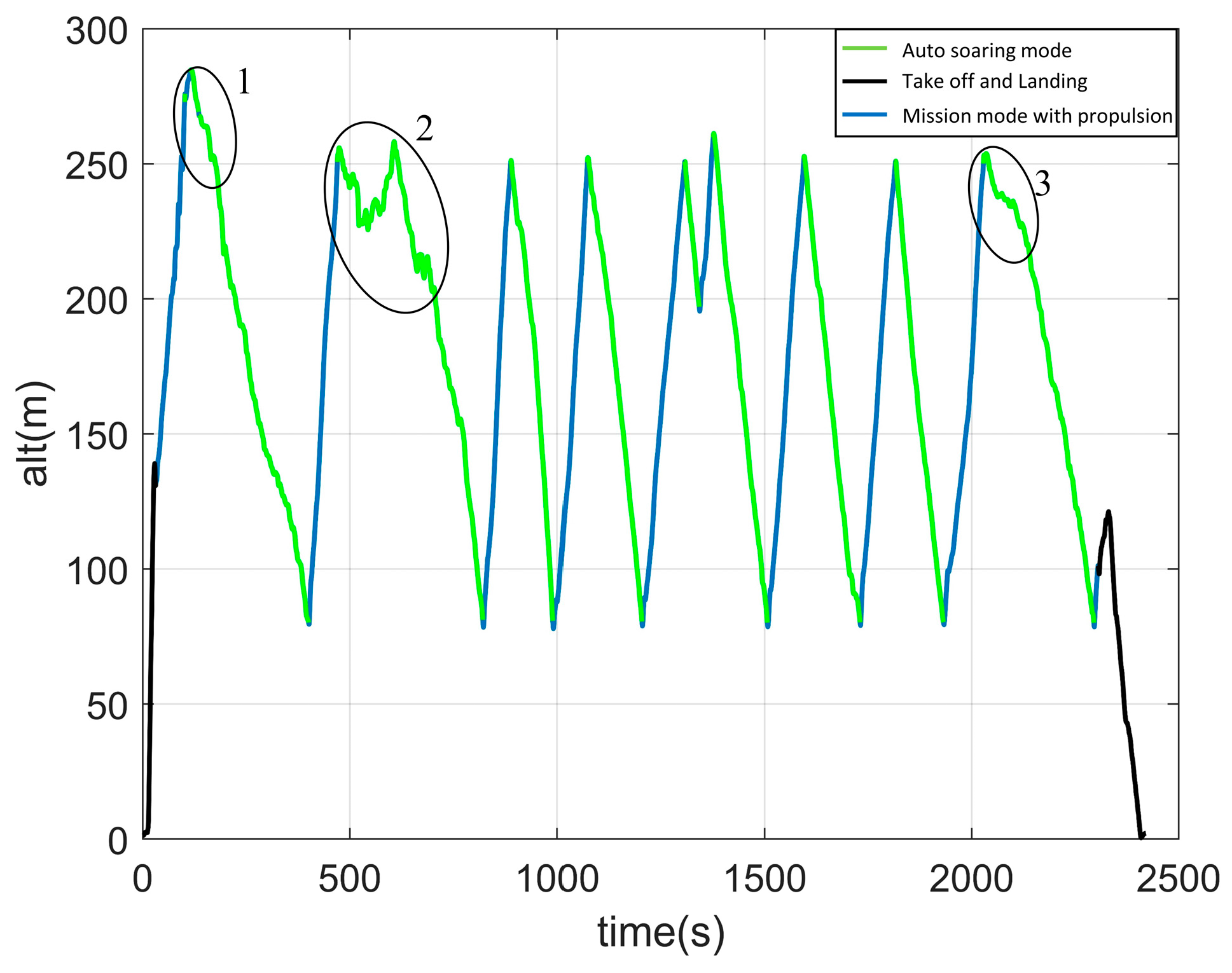
3.2.2. Results
4. Discussion
5. Conclusions
- (1)
- The thermal updraft intensity and radius obtained by the prediction method showed significant differences and large fluctuations compared with the true values. This was due to the overfitting phenomenon resulting from the OLS only using a small number of data points. However, the overfitting results of the least squares method were effective in localized areas, enabling the accurate prediction of updrafts around the drone. Thus, the OLS could significantly reduce the complexity of the EKF thermal center prediction, allowing for real-time and stable updates of the center with minimal computational load.
- (2)
- The adaptive step size update strategy significantly enhanced the convergence characteristics of the original EKF, leading to rapid convergence. This strategy enabled the prediction method to adapt to weak updrafts. Even if the initial predicted center point were at the edge of the thermal, the method could swiftly converge to the actual thermal updraft center.
- (3)
- The developed autonomous soaring system was tested in flight on the Talon fixed-wing drone platform. The thermal updraft center was updated at a frequency of 1 Hz. The L1 navigation algorithm guided the drone to circle in flight around the predicted thermal updraft center. In the flight test, the drone successfully engaged in static soaring within thermal updrafts, continuously hovering and gaining energy. Throughout the approximately 40 min flight duration, the drone only utilized its propulsion for about 8 min. This confirmed the effectiveness of the autonomous soaring system using the EKF thermal updraft center prediction method based on OLS on guiding small drones effectively in static soaring.
- (4)
- The current autonomous soaring system can only operate in an unpowered state. In future work, there is a plan to create an autonomous soaring system for small drones that considers propulsion. This system can maintain the drone’s altitude using minimal power in weaker thermal updrafts. This enhancement will significantly boost the drone’s mission capabilities and energy harvesting from wind fields, thereby expanding its application scope.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Watts, A.C.; Perry, J.H.; Smith, S.E.; Burgess, M.A.; Wilkinson, B.E.; Szantoi, Z.; Ifju, P.G.; Percival, H.F. Small unmanned aircraft systems for low-altitude aerial surveys. J. Wildl. Manag. 2010, 74, 1614–1619. [Google Scholar] [CrossRef]
- Pennycuick, C.J. Soaring behaviour and performance of some east African birds, observed from a motor-glider. Ibis 1972, 114, 178–218. [Google Scholar] [CrossRef]
- Pennycuick, C.J. Field Observations of Thermals and Thermal Streets, and the Theory of Cross-Country Soaring Flight. J. Avian Biol. 1998, 29, 33–43. [Google Scholar] [CrossRef]
- Pennycuick, C. The concept of energy height in animal locomotion: Separating mechanics from physiology. J. Theor. Biol. 2003, 224, 189–203. [Google Scholar] [CrossRef]
- Weimerskirch, H.; Bishop, C.; Jeanniard-du-Dot, T.; Prudor, A.; Sachs, G. Frigate birds track atmospheric conditions over months-long transoceanic flights. Science 2016, 353, 74–78. [Google Scholar] [CrossRef]
- De Monte, S.; Cotté, C.; d’Ovidio, F.; Lévy, M.; Le Corre, M.; Weimerskirch, H. Frigatebird behaviour at the ocean–atmosphere interface: Integrating animal behaviour with multi-satellite data. J. R. Soc. Interface 2012, 9, 3351–3358. [Google Scholar] [CrossRef][Green Version]
- Weimerskirch, H.; Chastel, O.; Barbraud, C.; Tostain, O. Frigatebirds ride high on thermals. Nature 2003, 421, 333–334. [Google Scholar] [CrossRef]
- Taylor, G.K.; Reynolds, K.V.; Thomas, A.L.R. Soaring energetics and glide performance in a moving atmosphere. Philos. Trans. R. Soc. B Biol. Sci. 2016, 371, 20150398. [Google Scholar] [CrossRef]
- Norberg, U.M.L.; Brooke, A.P.; Trewhella, W.J. Soaring and Non-Soaring Bats of the Family Pteropodidae (Flying Foxes, Pteropus spp.): Wing Morphology and Flight Performance. J. Exp. Biol. 2000, 203, 651–664. [Google Scholar] [CrossRef]
- Khosravifard, S.; Venus, V.; Skidmore, A.K.; Bouten, W.; Muñoz, A.R.; Toxopeus, A.G. Identification of Griffon Vulture’s Flight Types Using High-Resolution Tracking Data. Int. J. Environ. Res. 2018, 12, 313–325. [Google Scholar] [CrossRef]
- Palomaki, R.T.; Rose, N.T.; van den Bossche, M.; Sherman, T.J.; De Wekker, S.F. Wind estimation in the lower atmosphere using multirotor aircraft. J. Atmos. Ocean. Technol. 2017, 34, 1183–1191. [Google Scholar] [CrossRef]
- Van den Kroonenberg, A.; Martin, T.; Buschmann, M.; Bange, J.; Vörsmann, P. Measuring the wind vector using the autonomous mini aerial vehicle M2AV. J. Atmos. Ocean. Technol. 2008, 25, 1969–1982. [Google Scholar] [CrossRef]
- Edwards, D. Implementation Details and Flight Test Results of an Autonomous Soaring Controller. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, Hawaii, 18–24 August 2008; p. 7244. [Google Scholar]
- Edwards, D.J.; Kahn, A.D.; Kelly, M.; Heinzen, S.; Scheiman, D.A.; Jenkins, P.P.; Walters, R.; Hoheisel, R. Maximizing Net Power in Circular Turns for Solar and Autonomous Soaring Aircraft. J. Aircr. 2016, 53, 1237–1247. [Google Scholar] [CrossRef]
- Langelaan, J.W.; Alley, N.; Neidhoefer, J. Wind Field Estimation for Small Unmanned Aerial Vehicles. J. Guid. Control Dyn. 2011, 34, 1016–1030. [Google Scholar] [CrossRef]
- Pachter, M.; Ceccarelli, N.; Chandler, P.R. Estimating MAV’s heading and the wind speed and direction using GPS, inertial and airspeed measurements. In Proceedings of the AIAA Guidance Navigation and Control Conference, Honolulu, HI, USA, 18–21 August 2008; p. 6311. [Google Scholar]
- Ákos, Z.; Nagy, M.; Leven, S.; Vicsek, T. Thermal soaring flight of birds and unmanned aerial vehicles. Bioinspiration Biomim. 2010, 5, 045003. [Google Scholar] [CrossRef]
- Lawrance, N.R.J.; Sukkarieh, S. Autonomous Exploration of a Wind Field with a Gliding Aircraft. J. Guid. Control. Dyn. 2011, 34, 719–733. [Google Scholar] [CrossRef]
- Lawrance, N.R.; Sukkarieh, S. Path planning for autonomous soaring flight in dynamic wind fields. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2499–2505. [Google Scholar] [CrossRef]
- Singh, A.; Ramos, F.; Whyte, H.D.; Kaiser, W.J. Modeling and decision making in spatiotemporal processes for environmental surveillance. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 5490–5497. [Google Scholar]
- Lee, D.; Longo, S.; Kerrigan, E.C. Predictive Control for Soaring of Unpowered Autonomous UAVs. IFAC Proc. Vol. 2012, 45, 194–199. [Google Scholar] [CrossRef]
- Woodbury, T.; Dunn, C.; Valasek, J. Autonomous soaring using reinforcement learning for trajectory generation. In Proceedings of the 52nd AIAA Aerospace Sciences Meeting—AIAA Science and Technology Forum and Exposition, National Harbor, MD, USA, 13–17 January 2014; pp. 1–11. [Google Scholar]
- Li, W.; Shi, M.; Shi, L.; Lin, B.; Qin, K. Containment Tracking for Networked Agents Subject to Nonuniform Communication Delays. IEEE Trans. Netw. Sci. Eng. 2023, 1–12. [Google Scholar] [CrossRef]
- Li, W.; Qin, K.; Li, G.; Shi, M.; Zhang, X. Robust bipartite tracking consensus of multi-agent systems via neural network combined with extended high-gain observer. ISA Trans. 2023, 136, 31–45. [Google Scholar] [CrossRef]
- Allen, M. Updraft Model for Development of Autonomous Soaring Uninhabited Air Vehicles. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006; p. 1510. [Google Scholar] [CrossRef]
- Allen, M.J. Guidance and Control for an Autonomous Soaring UAV. U.S. Patent 7,431,243, 6 October 2008. pp. 58–61. [Google Scholar]
- Tabor, S.; Guilliard, I.; Kolobov, A. ArduSoar: An Open-Source Thermalling Controller for Resource-Constrained Autopilots. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 6255–6262. [Google Scholar]
- Bencatel, R. Thermal localization. In Proceedings of the 2010 International Conference on Autonomous and Intelligent Systems, AIS, Povoa de Varzim, Portugal, 21–23 June 2010; pp. 1–6. [Google Scholar]
- Hazard, M. Unscented Kalman Filtering for Real-Time Atmospheric Thermal Tracking; North Carolina State University: Raleigh, NC, USA, 2010. [Google Scholar]
- Depenbusch, N.T.; Bird, J.J.; Langelaan, J.W. The AutoSOAR autonomous soaring aircraft, part 1: Autonomy algorithms. J. Field Robot. 2018, 35, 868–889. [Google Scholar] [CrossRef]
- Notter, S.; Groß, P.; Schrapel, P.; Fichter, W. Multiple Thermal Updraft Estimation and Observability Analysis. J. Guid. Control. Dyn. 2020, 43, 490–503. [Google Scholar] [CrossRef]
- Liu, L.; Song, B.; An, W.; Yang, X.; Xuan, J. A UAV Wind Field Perception System Inspired by Biological Perception. Appl. Sci. 2023, 13, 6743. [Google Scholar] [CrossRef]


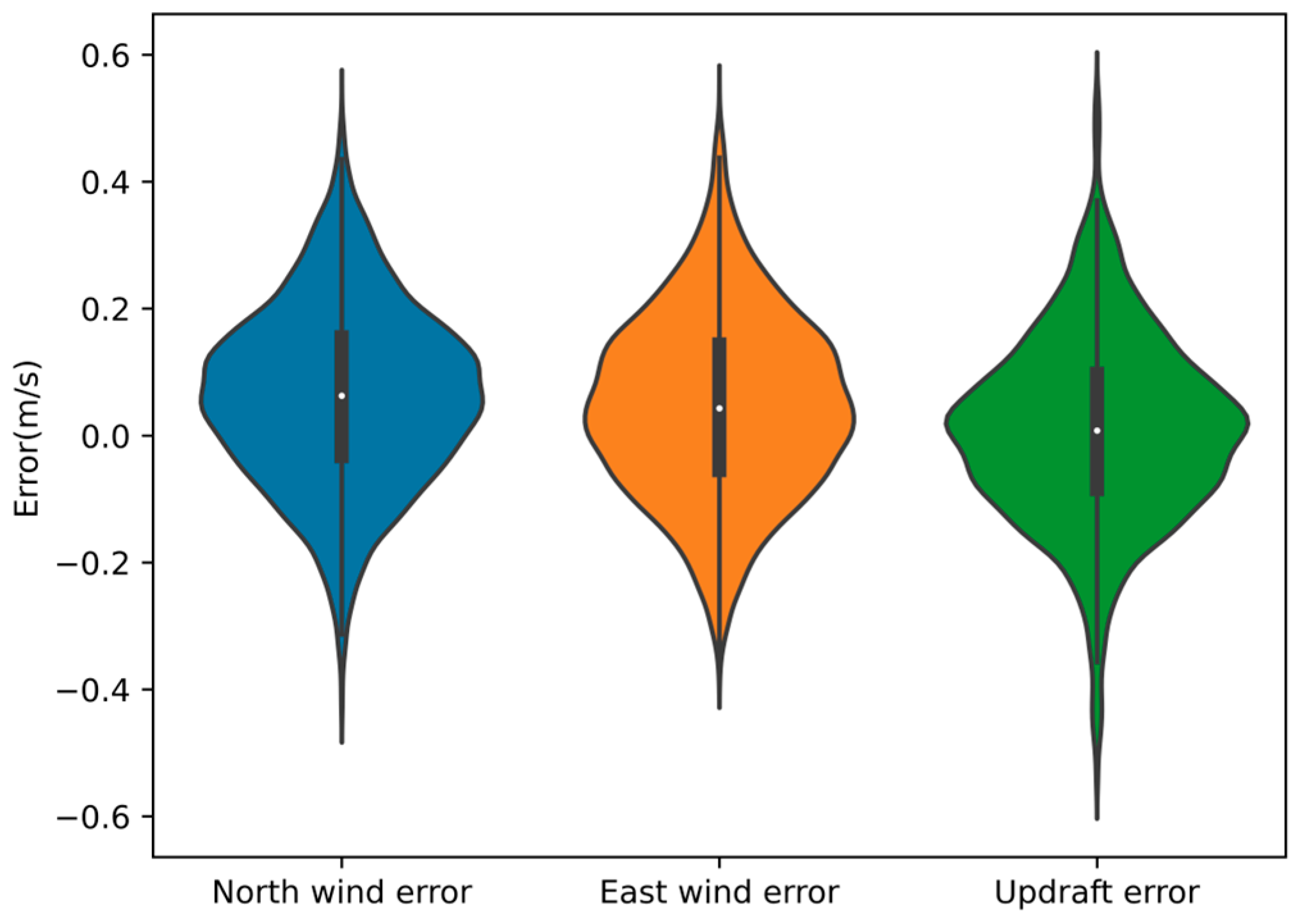








| Parameter | Mean Value | Standard Deviation |
|---|---|---|
| 0.0626 | 0.139 | |
| 0.0459 | 0.144 | |
| 0.0783 | 0.157 |
| Case Index | Updraft | OLS | Adaptive Update Step Size |
|---|---|---|---|
| (a) | W = 1 m/s, R = 300 m | Yes | Yes |
| (b) | W = 2 m/s, R = 300 m | Yes | Yes |
| (c) | W = 1 m/s, R = 300 m | Yes | No |
| (d) | W = 2 m/s, R = 300 m | Yes | No |
| (e) | W = 1 m/s, R = 300 m | No | Yes |
| (f) | W = 2 m/s, R = 300 m | No | Yes |
| (g) | W = 1 m/s, R = 300 m | No | No |
| (h) | W = 2 m/s, R = 300 m | No | No |
| Parameters | Value |
|---|---|
| Update frequency | 1.0 Hz |
| Queue length | 25 |
| ω0 | 10.0 |
| t0 | 300 s |
| Updraft threshold | 0.314 m/s |
| Circling radius | 80 m |
| Minimum circling radius | 50 m |
| Parameters | Value |
|---|---|
| Wing span | 1.718 m |
| Wing area | 0.545 m2 |
| Mean chord length | 0.185 m |
| Length | 1.100 m |
| Weight | 1.050 kg |
| Components | Model |
|---|---|
| Processor | STM32F765/STM32F100 |
| IMU | ICM-20689/BMI055 |
| Magnetometer | IST8310 |
| Barometer | MS5611×2 |
| Airspeed meter | MS5525 |
| GPS | NEO3-GNSS |
| Data link | P9-Radio |
| Electric machine | X4120/KV480 |
| Parameters | Value |
|---|---|
| Mission airspeed | 12 m/s |
| Mission altitude | 250 m |
| Safe altitude | 80 m |
| Safe airspeed | 6.5 m/s |
| Gliding airspeed | 11.0 or 8.5 m/s |
| Circling radius | 80 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, W.; Lin, T.; Zhang, P. An Autonomous Soaring for Small Drones Using the Extended Kalman Filter Thermal Updraft Center Prediction Method Based on Ordinary Least Squares. Drones 2023, 7, 603. https://doi.org/10.3390/drones7100603
An W, Lin T, Zhang P. An Autonomous Soaring for Small Drones Using the Extended Kalman Filter Thermal Updraft Center Prediction Method Based on Ordinary Least Squares. Drones. 2023; 7(10):603. https://doi.org/10.3390/drones7100603
Chicago/Turabian StyleAn, Weigang, Tianyu Lin, and Peng Zhang. 2023. "An Autonomous Soaring for Small Drones Using the Extended Kalman Filter Thermal Updraft Center Prediction Method Based on Ordinary Least Squares" Drones 7, no. 10: 603. https://doi.org/10.3390/drones7100603
APA StyleAn, W., Lin, T., & Zhang, P. (2023). An Autonomous Soaring for Small Drones Using the Extended Kalman Filter Thermal Updraft Center Prediction Method Based on Ordinary Least Squares. Drones, 7(10), 603. https://doi.org/10.3390/drones7100603





