Strapdown Celestial Attitude Estimation from Long Exposure Images for UAV Navigation
Abstract
1. Introduction
2. Methods
- Estimate the theoretical curve of the star trail on the image plane by using INS measurements.
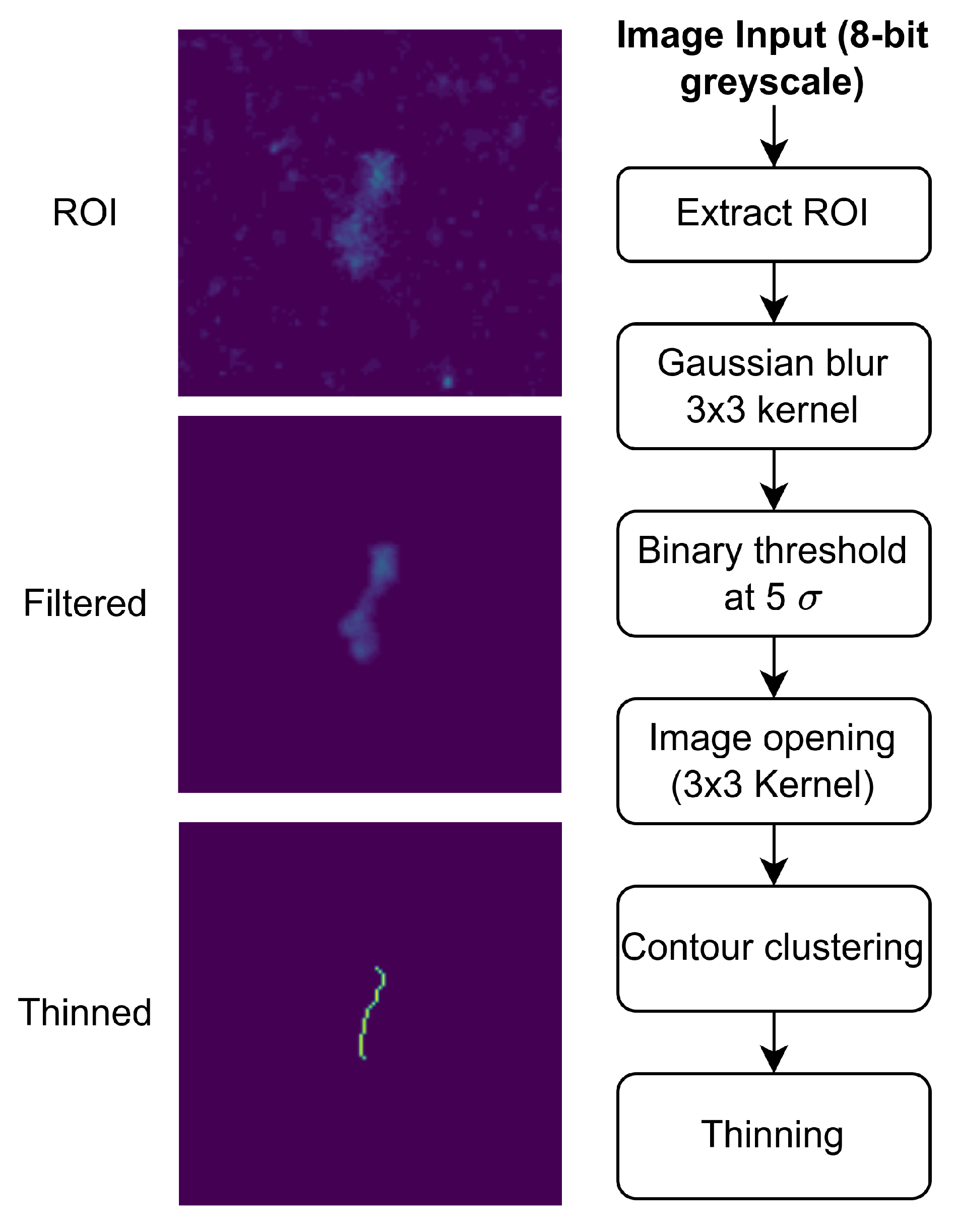
- Apply a smoothing filter, morphological operations, and clustering to extract the star trail for each star with brightness above a given magnitude threshold.
- Apply a thinning algorithm on each star trail to remove the effects of Gaussian point-spread diffusion.
- Identify the endpoints of each star trail given the INS-simulated approximation.
- Use the endpoints of the thinned star trails, along with the endpoints of the INS approximation, to compute the weighted least squares approximation for the mean attitude offset throughout the exposure window.
- For each point in the mean-error corrected INS approximation, compute the least squares approximation of the precise attitude offset.
2.1. Image Processing
2.2. Orientation Estimation
- The INS sampling period, , is constant.
- The photon flux density incident on the sensor from a given luminary is constant.
- The path taken by the airframe results in a simple curve on the image plane (i.e., the star trail does not cross itself at any point).
| Algorithm 1 Mapping from INS points to real image points. |
|
3. Results
- A random-valued constant offset, and
- Perlin noise.
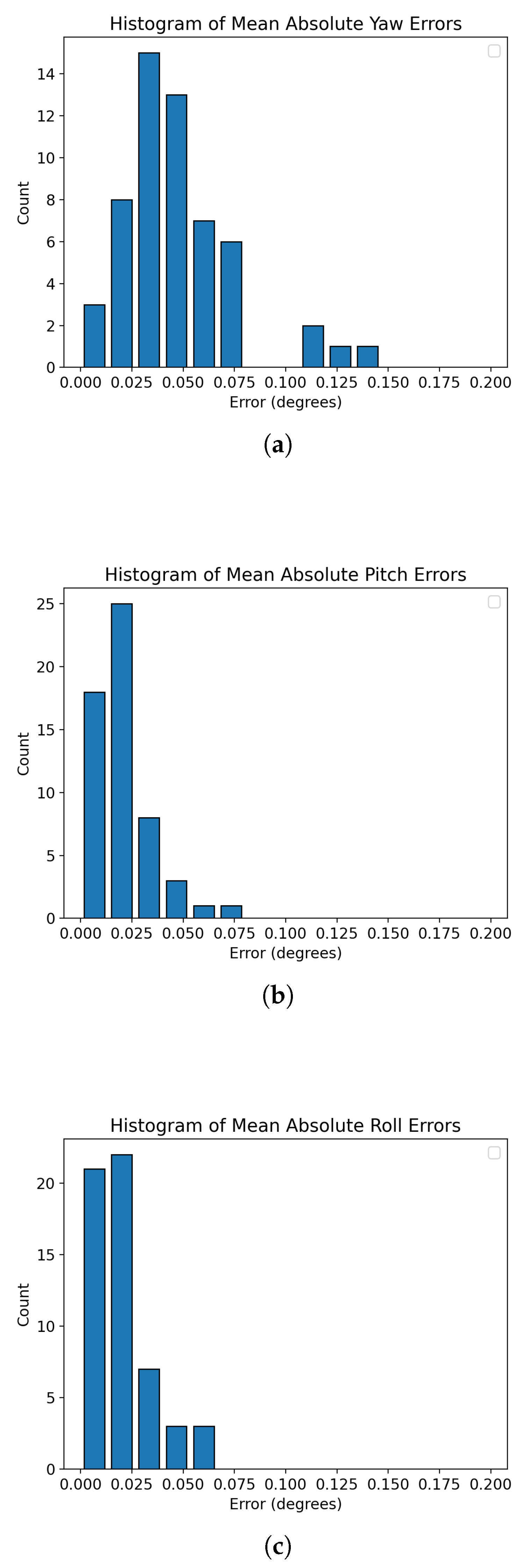
3.1. Simulation Results
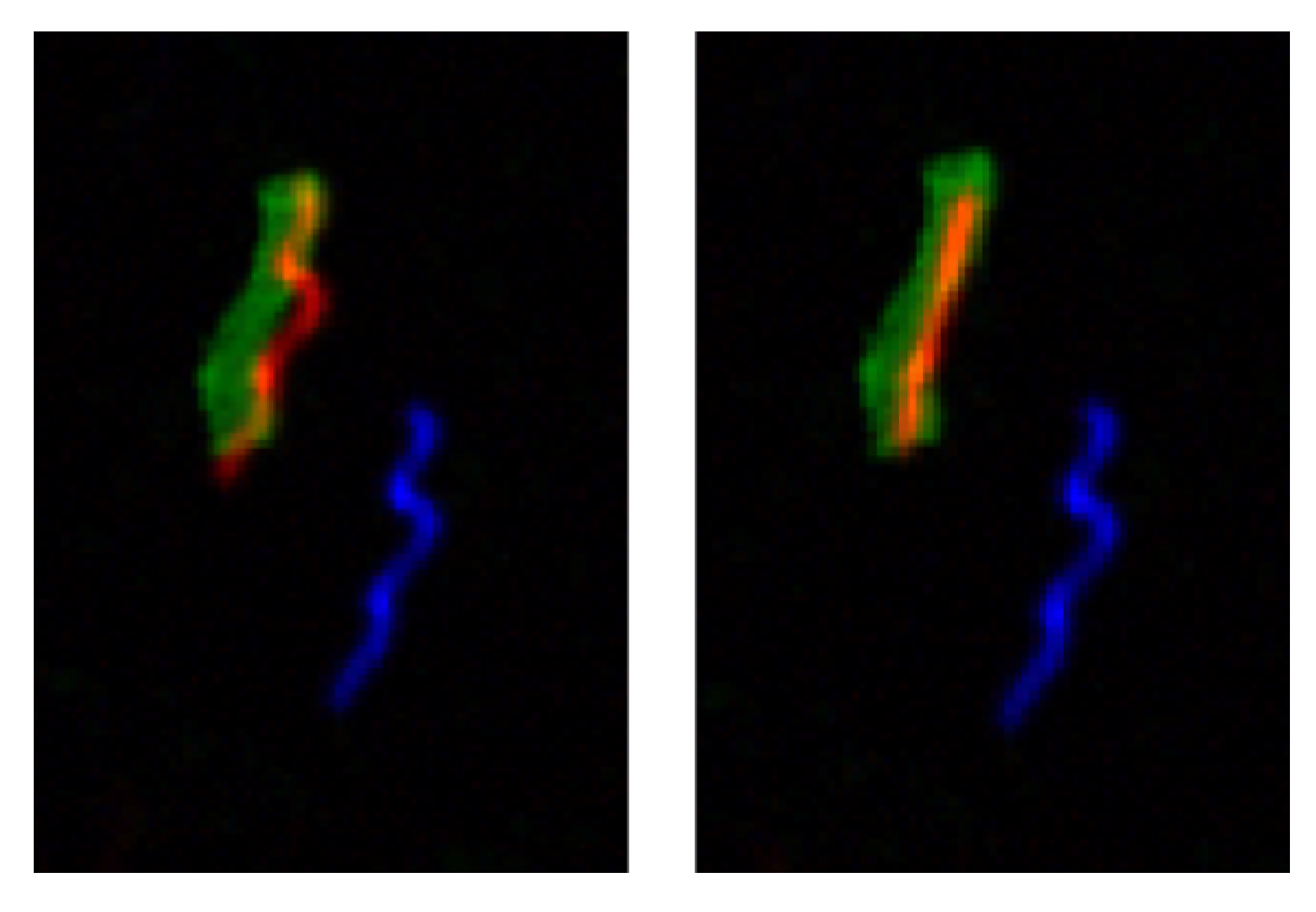
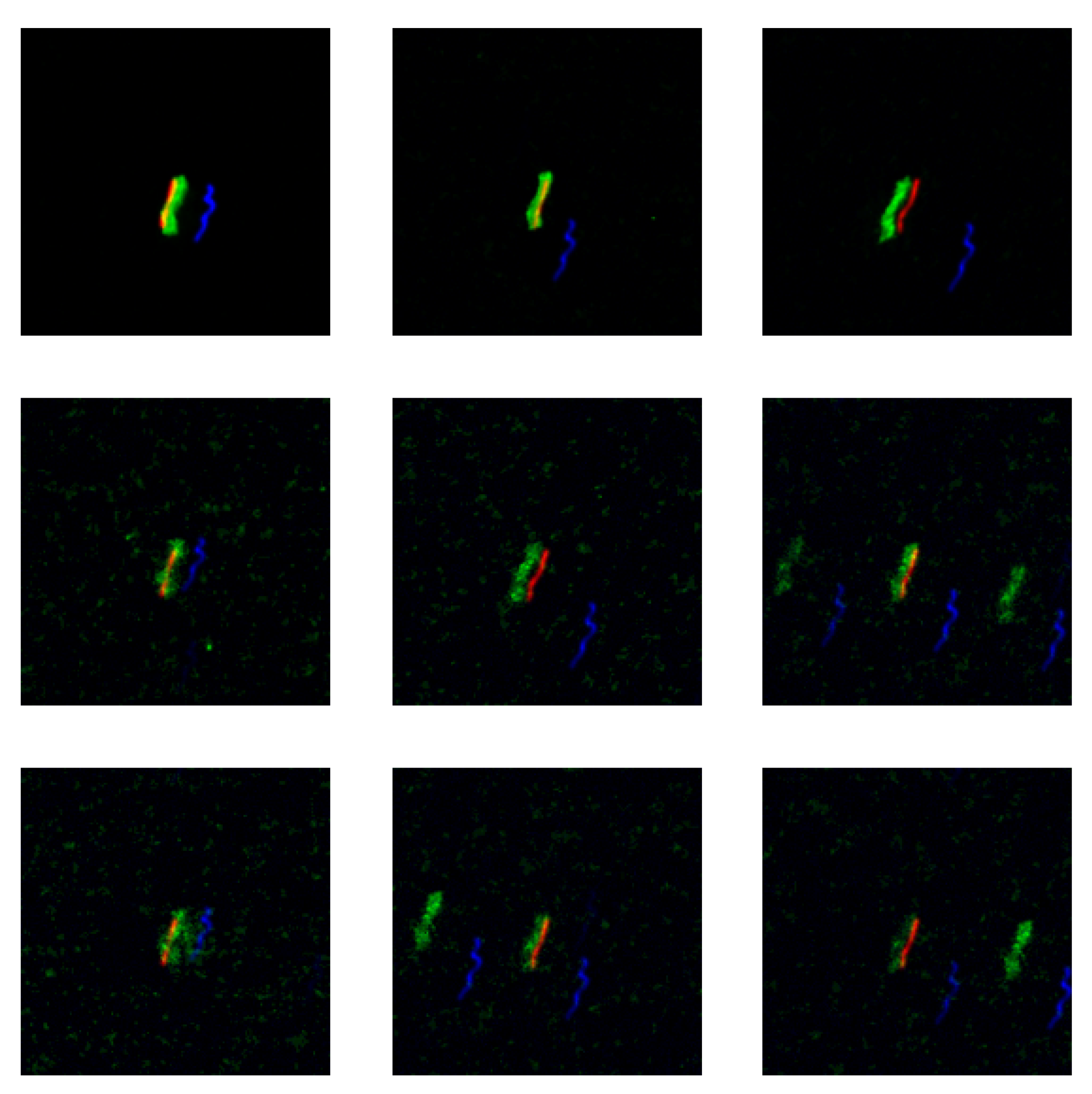
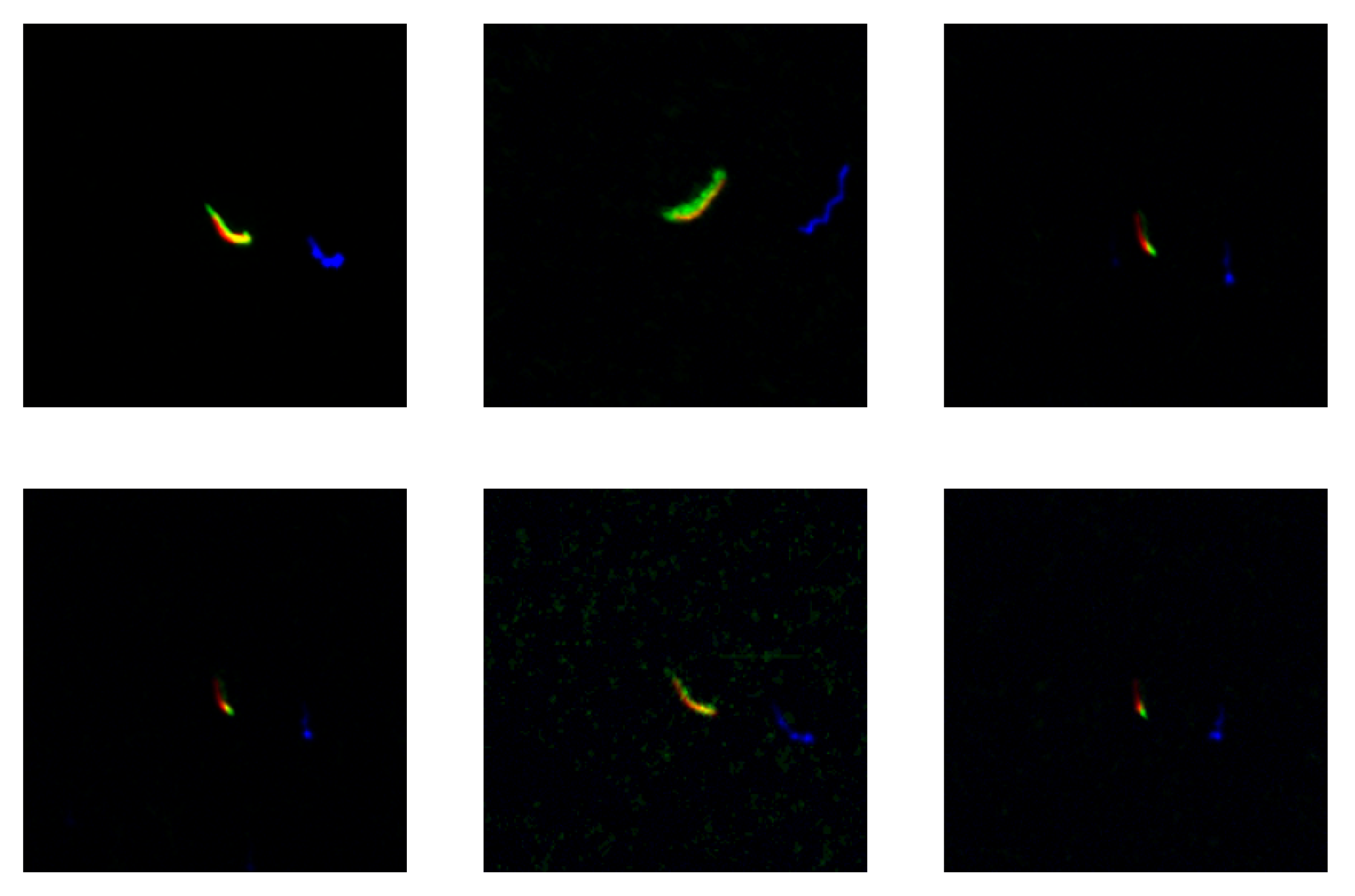
3.2. Real Imagery
4. Discussion
- The camera calibration matrix, does not perfectly characterize the camera.
- Unmodeled sources of noise caused the image processing techniques not to transfer from simulation to reality.
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Jacobian Matrix Entries
References
- Kayton, M.; Fried, W.R. Avionics Navigation Systems; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Titterton, D.; Weston, J.L.; Weston, J. Strapdown Inertial Navigation Technology; IET: Stevenage, UK, 2004; Volume 17. [Google Scholar]
- Teague, S.; Chahl, J. Imagery Synthesis for Drone Celestial Navigation Simulation. Drones 2022, 6, 207. [Google Scholar] [CrossRef]
- Chen, X.; Liu, D.; Zhang, Y.; Liu, X.; Xu, Y.; Shi, C. Robust motion blur kernel parameter estimation for star image deblurring. Optik 2021, 230, 166288. [Google Scholar] [CrossRef]
- Wei, Q.; Weina, Z. Restoration of motion-blurred star image based on Wiener filter. In Proceedings of the 2011 Fourth International Conference on Intelligent Computation Technology and Automation, Shenzhen, China, 28–29 March 2011; Volume 2, pp. 691–694. [Google Scholar]
- Wang, S.; Zhang, S.; Ning, M.; Zhou, B. Motion blurred star image restoration based on MEMS gyroscope aid and blur kernel correction. Sensors 2018, 18, 2662. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Quan, W.; Guo, L. Blurred star image processing for star sensors under dynamic conditions. Sensors 2012, 12, 6712–6726. [Google Scholar] [CrossRef] [PubMed]
- Sun, T.; Xing, F.; You, Z.; Wei, M. Motion-blurred star acquisition method of the star tracker under high dynamic conditions. Opt. Express 2013, 21, 20096–20110. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Zhan, D.; Jiang, G.; Fu, S.; Jia, H.; Wang, X.; Huang, Z.; Zheng, J.; Hu, F.; Wu, W.; et al. Attitude-correlated frames approach for a star sensor to improve attitude accuracy under highly dynamic conditions. Appl. Opt. 2015, 54, 7559–7566. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Wang, H.; Feng, L.; You, S. Motion-blurred star image restoration based on multi-frame superposition under high dynamic and long exposure conditions. J. Real-Time Image Process. 2021, 18, 1477–1491. [Google Scholar] [CrossRef]
- Klaus, A.; Bauer, J.; Karner, K.; Elbischger, P.; Perko, R.; Bischof, H. Camera calibration from a single night sky image. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2004. CVPR 2004, Washington, DC, USA, 27 June–2 July 2004; Volume 1, p. I. [Google Scholar]
- Rijlaarsdam, D.; Yous, H.; Byrne, J.; Oddenino, D.; Furano, G.; Moloney, D. A survey of lost-in-space star identification algorithms since 2009. Sensors 2020, 20, 2579. [Google Scholar] [CrossRef] [PubMed]
- Liebe, C.C. Accuracy performance of star trackers-a tutorial. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 587–599. [Google Scholar] [CrossRef]
- Zhang, T.Y.; Suen, C.Y. A fast parallel algorithm for thinning digital patterns. Commun. ACM 1984, 27, 236–239. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]




| Mean | Median | Std | Mean + 3 | |
|---|---|---|---|---|
| Max yaw error | 0.1053 | 0.0903 | 0.0856 | 0.2828 |
| Max pitch error | 0.0503 | 0.0414 | 0.0317 | 0.1453 |
| Max roll error | 0.0506 | 0.0418 | 0.0286 | 0.1366 |
| Mean absolute yaw error | 0.0428 | 0.0442 | 0.0274 | 0.1294 |
| Mean absolute pitch error | 0.0205 | 0.0167 | 0.0128 | 0.0591 |
| Mean absolute roll error | 0.0217 | 0.0207 | 0.0129 | 0.0604 |
| Mean yaw error | 0.0118 | 0.01076 | 0.0322 | - |
| Mean pitch error | −0.0080 | −0.0061 | 0.0138 | - |
| Mean roll error | −0.0078 | −0.0061 | 0.02124 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teague, S.; Chahl, J. Strapdown Celestial Attitude Estimation from Long Exposure Images for UAV Navigation. Drones 2023, 7, 52. https://doi.org/10.3390/drones7010052
Teague S, Chahl J. Strapdown Celestial Attitude Estimation from Long Exposure Images for UAV Navigation. Drones. 2023; 7(1):52. https://doi.org/10.3390/drones7010052
Chicago/Turabian StyleTeague, Samuel, and Javaan Chahl. 2023. "Strapdown Celestial Attitude Estimation from Long Exposure Images for UAV Navigation" Drones 7, no. 1: 52. https://doi.org/10.3390/drones7010052
APA StyleTeague, S., & Chahl, J. (2023). Strapdown Celestial Attitude Estimation from Long Exposure Images for UAV Navigation. Drones, 7(1), 52. https://doi.org/10.3390/drones7010052









