Cotton Yield Estimation Using the Remotely Sensed Cotton Boll Index from UAV Images
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data
2.2.1. UAV Data
2.2.2. Field Survey Data
3. Methods
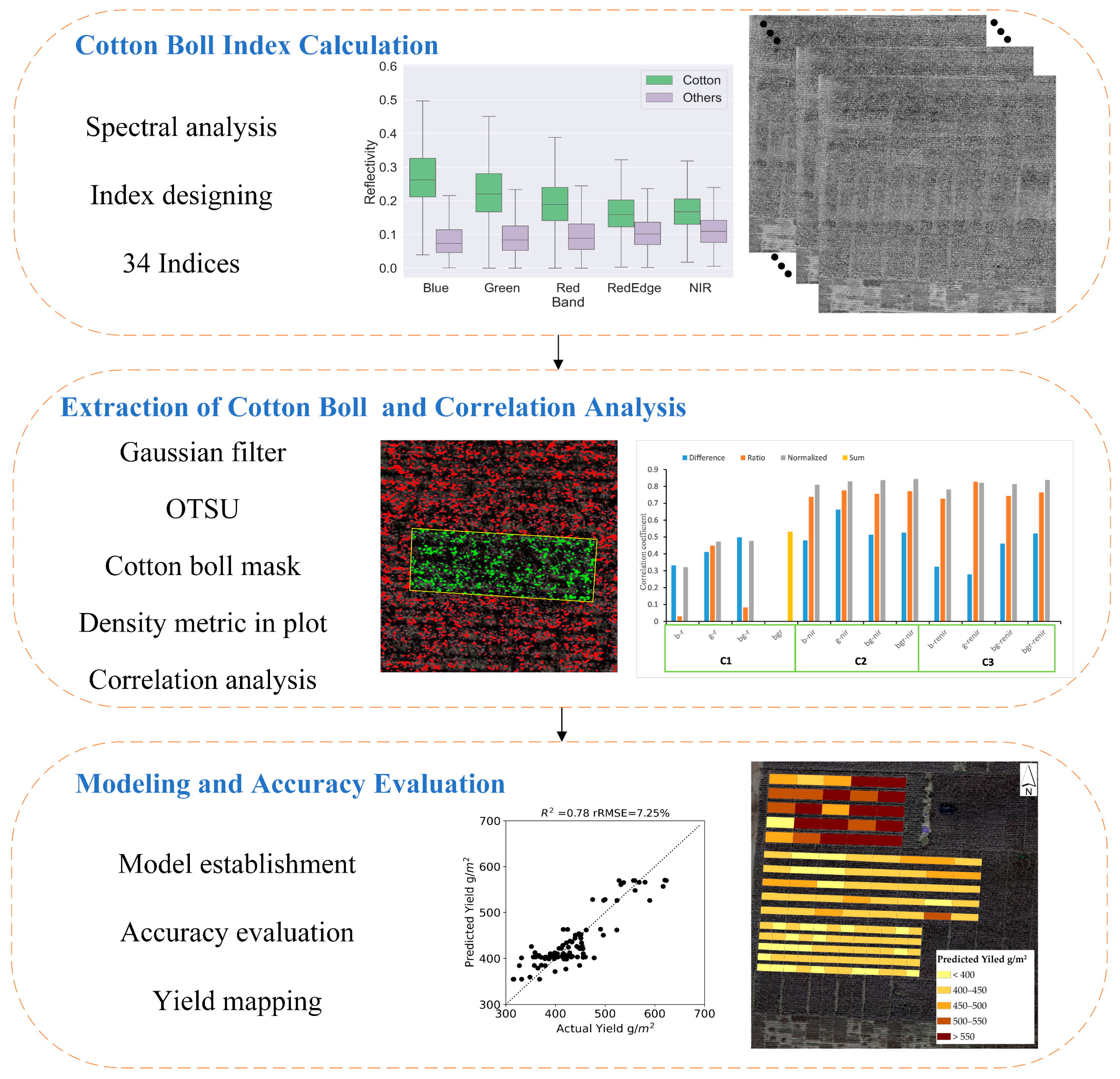
3.1. Cotton Boll Index Calculation
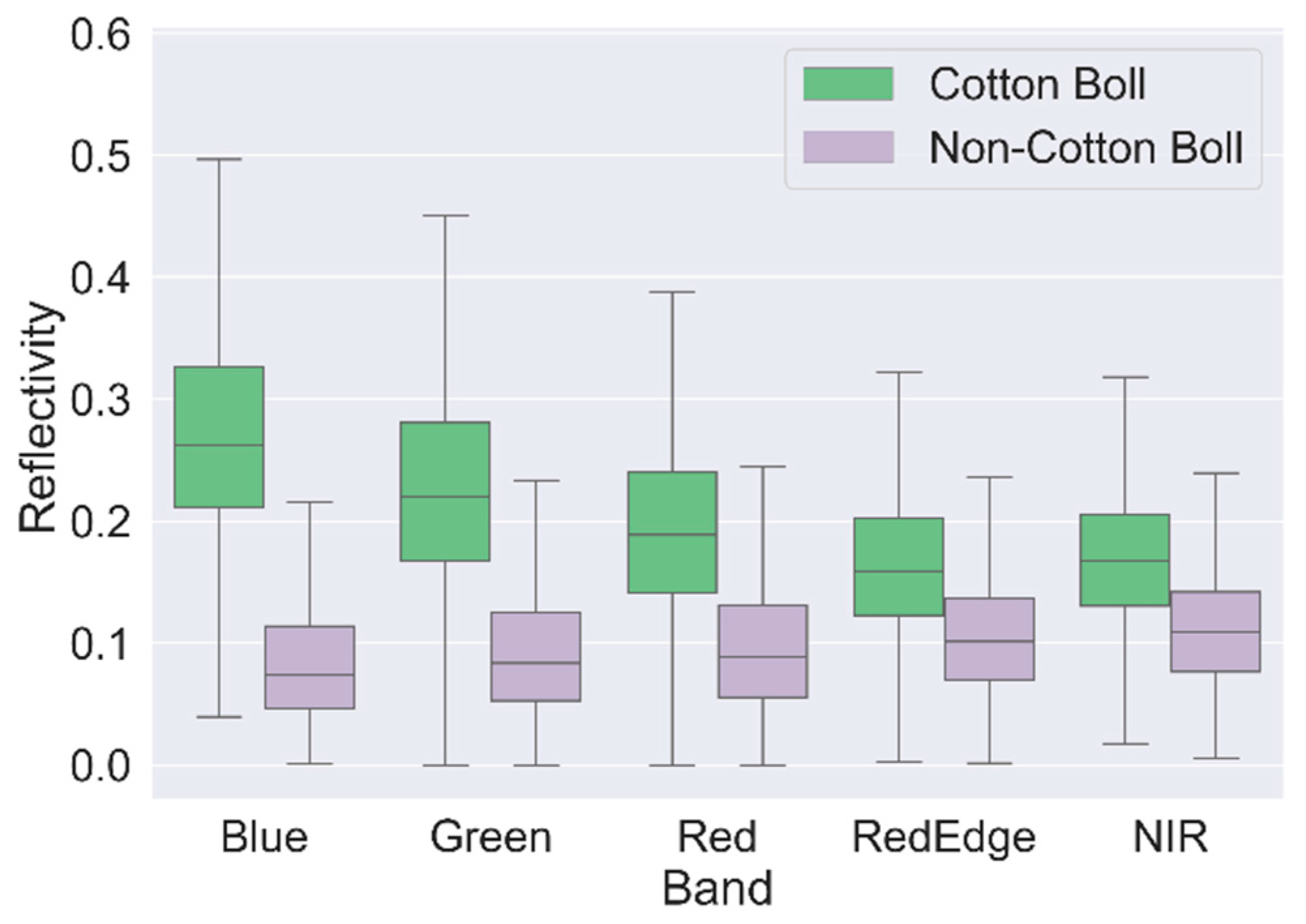
3.1.1. Spectral Analysis
3.1.2. Index Design
3.2. Extraction of Cotton Boll and Correlation Analysis
3.3. Modeling and Accuracy Evaluation
3.3.1. Linear Regression
3.3.2. Support Vector Regression
3.3.3. Classification and Regression Trees
3.3.4. Random Forest
3.3.5. K-Nearest Neighbors
3.3.6. Accuracy Evaluation
4. Results and Analysis
4.1. Extraction of Cotton Bolls
4.2. Correlation Analysis
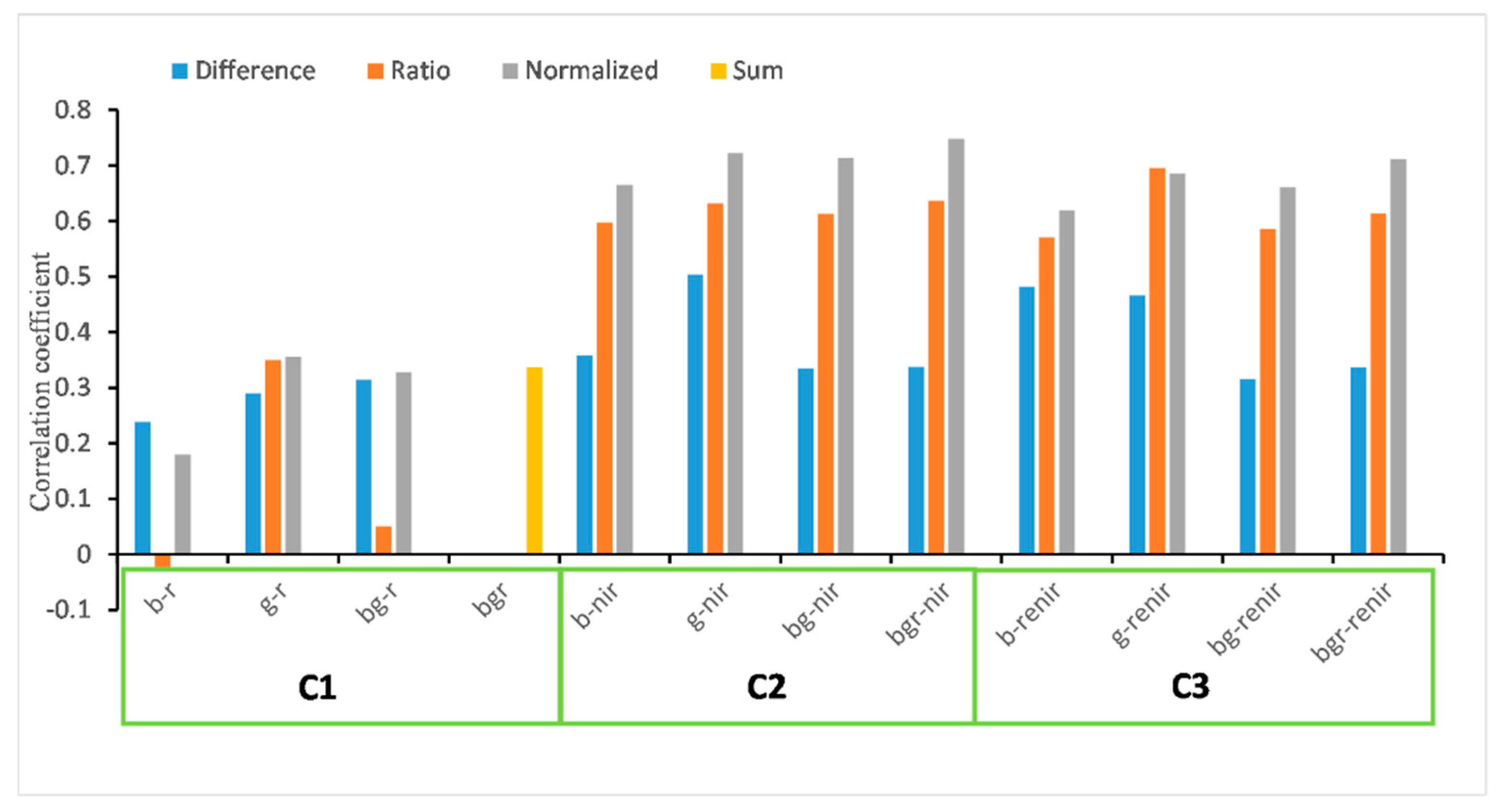
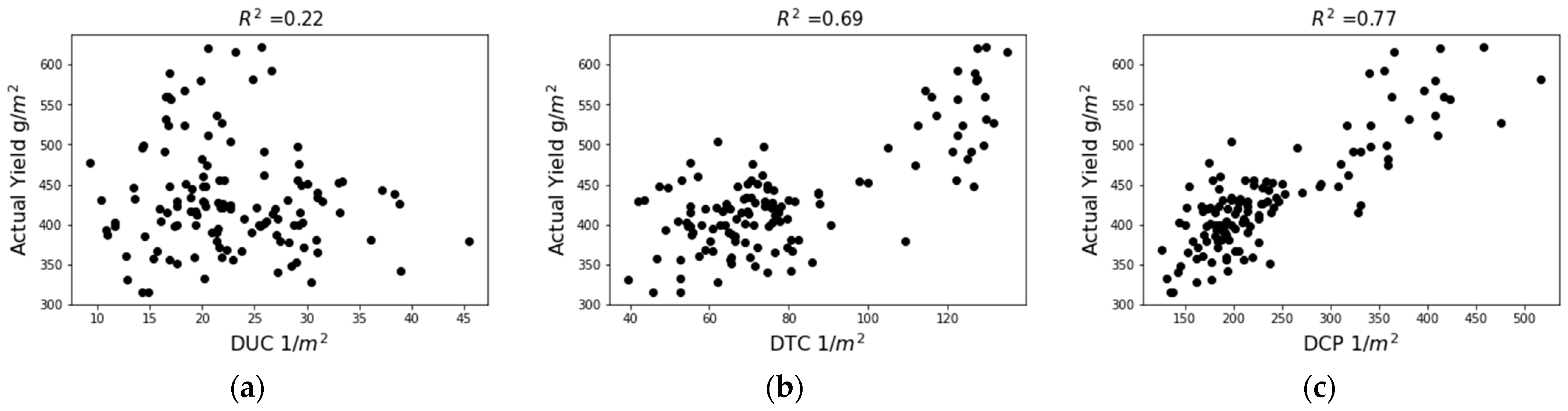
4.2.1. Correlation between DCP and DTC
4.2.2. Correlation between DCP and Yield
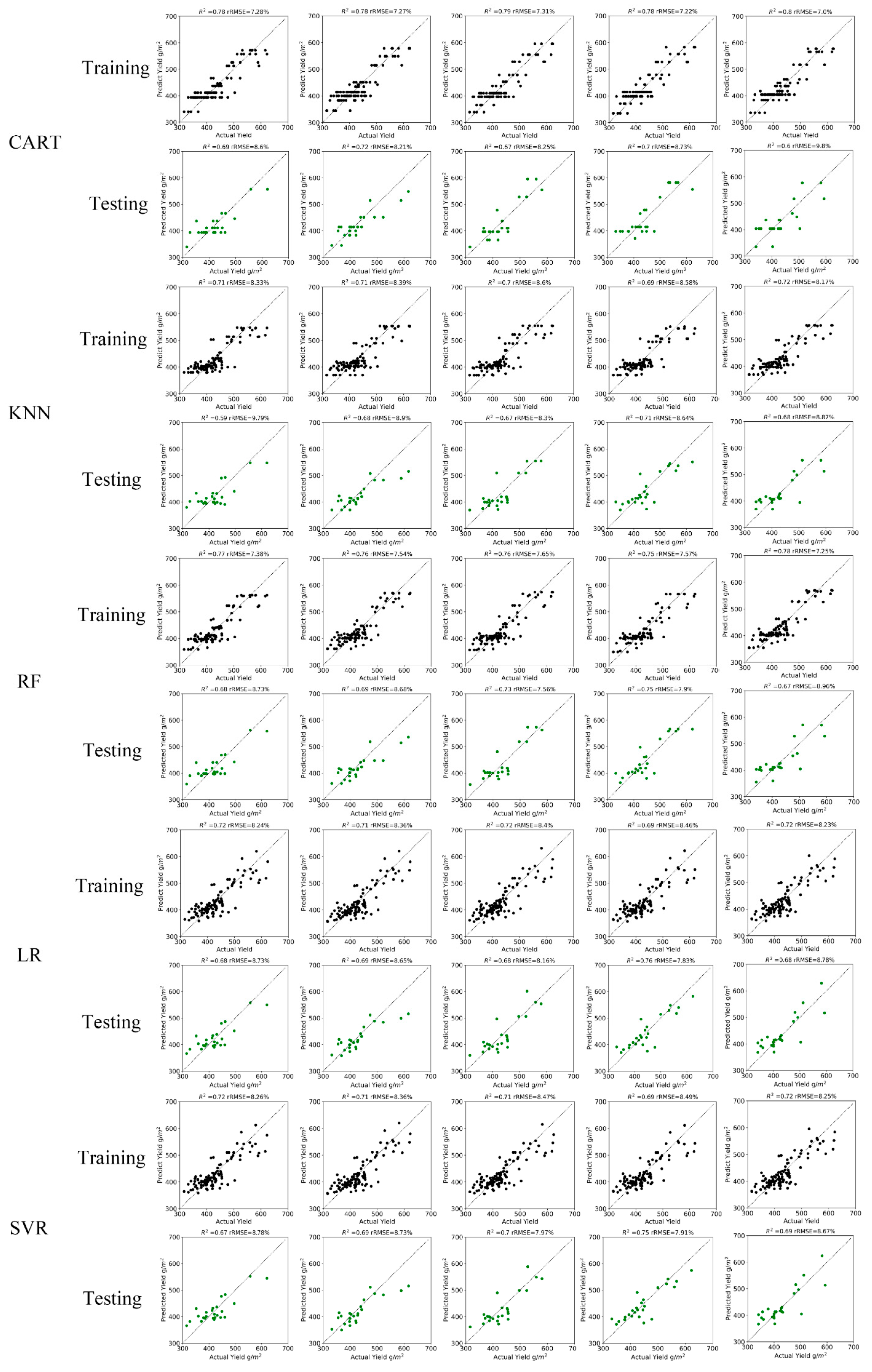
4.3. The Results of Model Establishment and Accuracy Evaluation
5. Discussion
6. Conclusions
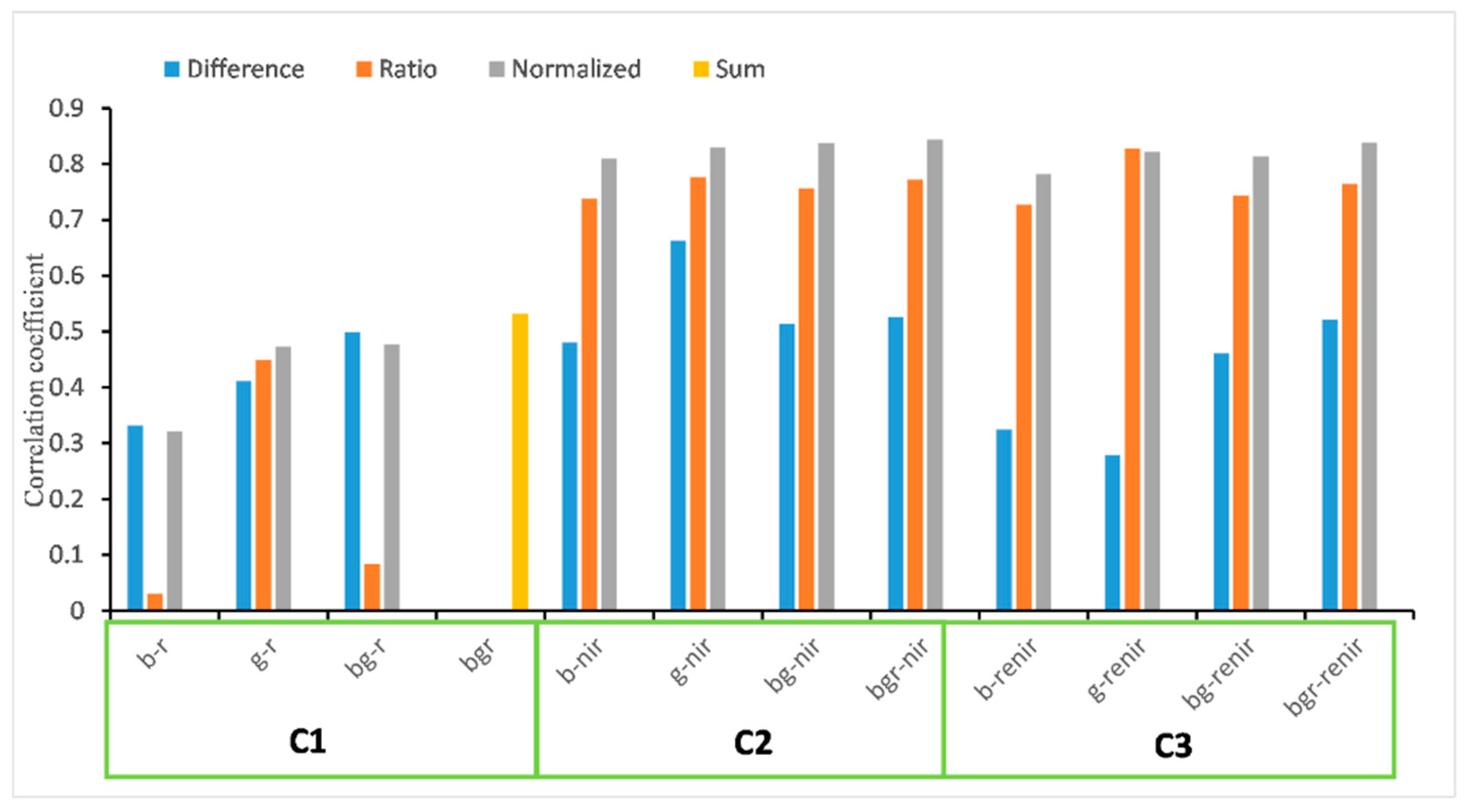
- Bgr-nir_n, an index that normalizes the NIR band by the sum of blue, green, and red bands, exhibited the best performance in highlighting information on open cotton bolls. The correlation coefficient between DCP extracted from this index and the measured yield was 0.84;
- DCP extracted from bgr-nir_n combined with the random forest methodology achieved an unbiased estimation of cotton yield on the plot scale; the average R2 based on five-fold cross-validation was 0.77, and the average rRMSE was 7.5%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| ID | NTC | Actual Production/g |
|---|---|---|
| A1 | 5663.87 | 22,140.00 |
| A2 | 5493.60 | 20,500.00 |
| A3 | 5057.60 | 23,550.00 |
| A4 | 5819.67 | 25,170.00 |
| A5 | 5140.80 | 25,570.00 |
| A6 | 5031.00 | 21,360.00 |
| A7 | 5627.53 | 21,680.00 |
| A8 | 5925.33 | 23,750.00 |
| A9 | 5704.67 | 26,530.00 |
| A10 | 5510.27 | 25,060.00 |
| A11 | 5804.93 | 22,480.00 |
| A12 | 5279.60 | 24,160.00 |
| A13 | 4728.00 | 22,330.00 |
| A14 | 5738.53 | 26,160.00 |
| A15 | 5720.40 | 26,110.00 |
| A16 | 5691.73 | 20,180.00 |
| A17 | 5516.00 | 23,050.00 |
| A18 | 5211.60 | 25,210.00 |
| A19 | 5514.13 | 26,690.00 |
| A20 | 5831.20 | 28,030.00 |
| A21 | 5456.07 | 22,080.00 |
| A22 | 5566.25 | 23,570.00 |
| A23 | 5842.60 | 23,920.00 |
| A24 | 5740.00 | 27,900.00 |
| A25 | 6072.00 | 27,750.00 |
| ID | NTC | Actual Production/g |
|---|---|---|
| B1 | 1645.00 | 10,381.76 |
| B2 | 2094.20 | 9973.11 |
| B3 | 1953.00 | 9536.92 |
| B4 | 1911.60 | 11,298.52 |
| B5 | 2739.10 | 12,377.12 |
| B6 | 1938.00 | 13,010.75 |
| B7 | 1968.00 | 12,341.12 |
| B8 | 2212.50 | 10,028.61 |
| B9 | 1887.60 | 10,331.08 |
| B10 | 2352.00 | 9645.34 |
| B11 | 2042.40 | 9332.29 |
| B12 | 2074.60 | 11,015.15 |
| B13 | 1829.00 | 11,137.88 |
| B14 | 1903.50 | 12,335.85 |
| B15 | 1834.00 | 12,233.03 |
| B16 | 2002.00 | 12,635.14 |
| B17 | 1864.20 | 11,373.58 |
| B18 | 2065.00 | 11,612.64 |
| B19 | 2989.60 | 10,365.61 |
| B20 | 2038.20 | 12,290.72 |
| B21 | 2673.20 | 12,416.68 |
| B22 | 1753.80 | 11,543.43 |
| B23 | 1512.80 | 10,899.73 |
| B24 | 2204.60 | 10,413.39 |
| B25 | 2201.90 | 9340.95 |
| B26 | 2256.00 | 10,398.35 |
| B27 | 2401.60 | 11,656.75 |
| B28 | 2390.10 | 12,038.14 |
| B29 | 2394.40 | 12,011.73 |
| B30 | 2081.20 | 12,116.70 |
| B31 | 1686.40 | 11,516.07 |
| B32 | 2186.80 | 11,802.84 |
| B33 | 1800.00 | 10,589.28 |
| B34 | 1152.40 | 11,754.78 |
| B35 | 1292.00 | 12,231.23 |
| B36 | 2232.10 | 11,724.94 |
| B37 | 1898.00 | 11,873.73 |
| B38 | 1928.00 | 12,451.56 |
| B39 | 2016.90 | 13,596.48 |
| B40 | 2175.40 | 11,160.55 |
| ID | NTC | Actual Production/g |
|---|---|---|
| C1 | 928.20 | 5110.38 |
| C2 | 967.60 | 4517.57 |
| C3 | 854.90 | 4372.02 |
| C4 | 809.10 | 4613.21 |
| C5 | 658.00 | 4892.43 |
| C6 | 834.20 | 5264.71 |
| C7 | 674.50 | 4704.62 |
| C8 | 782.00 | 5184.57 |
| C9 | 868.00 | 5201.47 |
| C10 | 529.30 | 5246.20 |
| C11 | 669.90 | 5809.46 |
| C12 | 671.50 | 5138.40 |
| C13 | 676.80 | 4737.80 |
| C14 | 638.40 | 4323.09 |
| C15 | 569.50 | 4344.34 |
| C16 | 790.50 | 4739.49 |
| C17 | 696.60 | 4376.91 |
| C18 | 930.60 | 5008.68 |
| C19 | 907.80 | 5400.04 |
| C20 | 693.60 | 5593.89 |
| C21 | 761.40 | 4861.65 |
| C22 | 754.80 | 6119.89 |
| C23 | 940.50 | 5043.02 |
| C24 | 643.20 | 5541.37 |
| C25 | 756.00 | 3979.26 |
| C26 | 639.60 | 4034.90 |
| C27 | 481.00 | 4030.50 |
| C28 | 768.00 | 5069.61 |
| C29 | 739.50 | 4459.73 |
| C30 | 846.00 | 5057.83 |
| C31 | 717.80 | 5099.76 |
| C32 | 943.40 | 4919.87 |
| C33 | 1100.00 | 4863.21 |
| C34 | 921.50 | 5200.45 |
| C35 | 897.60 | 5133.75 |
| C36 | 789.60 | 4736.87 |
| C37 | 916.70 | 5116.49 |
| C38 | 795.60 | 4361.68 |
| C39 | 791.70 | 4330.99 |
| C40 | 875.50 | 4513.94 |
| C41 | 797.90 | 4274.79 |
| C42 | 897.60 | 5219.46 |
| C43 | 911.80 | 4838.37 |
| C44 | 949.40 | 5150.25 |
| C45 | 865.20 | 4860.50 |
| C46 | 738.00 | 4792.67 |
| C47 | 632.40 | 4907.05 |
| C48 | 777.60 | 4858.27 |
| C49 | 717.80 | 4474.98 |
| C50 | 556.80 | 3831.51 |
| C51 | 639.00 | 3843.09 |
| C52 | 671.60 | 5055.71 |
| C53 | 703.10 | 4854.22 |
| C54 | 809.60 | 4684.16 |
| C55 | 595.90 | 4780.87 |
| C56 | 791.20 | 5104.70 |
| C57 | 838.30 | 4868.06 |
| C58 | 855.60 | 5268.38 |
| C59 | 600.60 | 5418.95 |
| C60 | 662.40 | 4837.42 |
References
- FAO. Recent Trends and Prospects in the World Cotton Market and Policy Developments; FAO: Rome, Italy, 2021; ISBN 978-92-5-133951-0. [Google Scholar]
- Liu, Q.-S.; Li, X.-Y.; Liu, G.-H.; Huang, C.; Guo, Y.-S. Cotton Area and Yield Estimation at Zhanhua County of China Using HJ-1 EVI Time Series. ITM Web Conf. 2016, 7, 09001. [Google Scholar] [CrossRef]
- Alganci, U.; Ozdogan, M.; Sertel, E.; Ormeci, C. Estimating Maize and Cotton Yield in Southeastern Turkey with Integrated Use of Satellite Images, Meteorological Data and Digital Photographs. Field Crops Res. 2014, 157, 8–19. [Google Scholar] [CrossRef]
- Leon, C.T.; Shaw, D.R.; Cox, M.S.; Abshire, M.J.; Ward, B.; Iii, M.C.W. Utility of Remote Sensing in Predicting Crop and Soil Characteristics. Precis. Agric. 2003, 4, 359–384. [Google Scholar] [CrossRef]
- Dalezios, N.R.; Domenikiotis, C.; Loukas, A.; Tzortzios, S.T.; Kalaitzidis, C. Cotton Yield Estimation Based on NOAA/AVHRR Produced NDVI. Phys. Chem. Earth Part B Hydrol. Ocean. Atmos. 2001, 26, 247–251. [Google Scholar] [CrossRef]
- Prasad, N.R.; Patel, N.R.; Danodia, A. Cotton Yield Estimation Using Phenological Metrics Derived from Long-Term MODIS Data. J. Indian Soc. Remote. Sens. 2021, 49, 2597–2610. [Google Scholar] [CrossRef]
- Yang, G.; Liu, J.; Zhao, C.; Li, Z.; Huang, Y.; Yu, H.; Xu, B.; Yang, X.; Zhu, D.; Zhang, X.; et al. Unmanned Aerial Vehicle Remote Sensing for Field-Based Crop Phenotyping: Current Status and Perspectives. Front. Plant Sci. 2017, 8, 1111. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Sui, R.; Thomson, S.J.; Fisher, D.K. Estimation of Cotton Yield with Varied Irrigation and Nitrogen Treatments Using Aerial Multispectral Imagery. Biol. Eng. 2013, 6, 5. [Google Scholar]
- Yeom, J.; Jung, J.; Chang, A.; Maeda, M.; Landivar, J. Landivar Cotton Growth Modeling Using Unmanned Aerial Vehicle Vegetation Indices. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017. [Google Scholar]
- Feng, A.; Zhou, J.; Vories, E.; Sudduth, K.; Zhang, M. Yield Estimation in Cotton Using UAV-Based Multi-Sensor Imagery. Biosyst. Eng. 2020, 193, 101–114. [Google Scholar] [CrossRef]
- Feng, A.; Zhang, M.; Sudduth, K.A.; Vories, E.D.; Zhou, J. Cotton Yield Estimation from UAV-Based Plant Height. Trans. ASABE 2019, 62, 393–404. [Google Scholar] [CrossRef]
- Chu, T.; Chen, R.; Landivar, J.A.; Maeda, M.M.; Yang, C.; Starek, M.J. Cotton Growth Modeling and Assessment Using Unmanned Aircraft System Visual-Band Imagery. J. Appl. Remote Sens 2016, 10, 036018. [Google Scholar] [CrossRef]
- Ma, Y.; Ma, L.; Zhang, Q.; Huang, C.; Yi, X.; Chen, X.; Hou, T.; Lv, X.; Zhang, Z. Cotton Yield Estimation Based on Vegetation Indices and Texture Features Derived From RGB Image. Front. Plant Sci. 2022, 13, 925986. [Google Scholar] [CrossRef] [PubMed]
- Yi, L.; Lan, Y.; Kong, H.; Kong, F.; Huang, H.; Han, X. Exploring the Potential of UAV Imagery for Variable Rate Spraying in Cotton Defoliation Application. Int. J. Precis. Agric. Aviat. 2019, 2, 42–45. [Google Scholar] [CrossRef]
- Huang, Y.; Brand, H.J.; Sui, R.; Thomson, S.J.; Furukawa, T.; Ebelhar, M.W. Cotton Yield Estimation Using Very High-Resolution Digital Images Acquired with a Low-Cost Small Unmanned Aerial Vehicle. Trans. ASABE 2016, 59, 1563–1574. [Google Scholar]
- Yeom, J.; Jung, J.; Chang, A.; Maeda, M.; Landivar, J. Automated Open Cotton Boll Detection for Yield Estimation Using Unmanned Aircraft Vehicle (UAV) Data. Remote Sens. 2018, 10, 1895. [Google Scholar] [CrossRef]
- Kadeghe, F.; Glen, R.; Wesley, P. Real-Time 3-D Measurement of Cotton Boll Positions Using Machine Vision Under Field Conditions. In Proceeding of Beltwide Cotton Conference, San Antonio, TX, USA, 3–5 January 2018. [Google Scholar]
- Wei, J.; Fei, S.; Wang, M.; Yuan, J. Research on the Segmentation Strategy of the Cotton Images on the Natural Condition Based upon the Hsv Color-Space Model. Cotton Sci. 2008, 20, 34–38. [Google Scholar]
- Rodriguez-Sanchez, J.; Li, C.; Paterson, A.H. Cotton Yield Estimation From Aerial Imagery Using Machine Learning Approaches. Front. Plant Sci. 2022, 13, 870181. [Google Scholar] [CrossRef]
- Li, Y.; Cao, Z.; Lu, H.; Xiao, Y.; Zhu, Y.; Cremers, A.B. In-Field Cotton Detection via Region-Based Semantic Image Segmentation. Comput. Electron. Agric. 2016, 127, 475–486. [Google Scholar] [CrossRef]
- Sun, S.; Li, C.; Paterson, A.H.; Chee, P.W.; Robertson, J.S. Image Processing Algorithms for Infield Single Cotton Boll Counting and Yield Prediction. Comput. Electron. Agric. 2019, 166, 104976. [Google Scholar] [CrossRef]
- Xu, W.; Chen, P.; Zhan, Y.; Chen, S.; Zhang, L.; Lan, Y. Cotton Yield Estimation Model Based on Machine Learning Using Time Series UAV Remote Sensing Data. Int. J. Appl. Earth Obs. Geoinf. 2021, 104, 102511. [Google Scholar] [CrossRef]
- Analysis of the Agrogeological Background and Climate of Main Golden Silk Jujube Production Area in Cangzhou. Available online: https://www-webofscience-com-443.webvpn.las.ac.cn/wos/alldb/full-record/CSCD:3472745 (accessed on 14 June 2022).
- Hubert, M.; Vandervieren, E. An Adjusted Boxplot for Skewed Distributions. Comput. Stat. Data Anal. 2008, 52, 5186–5201. [Google Scholar] [CrossRef]
- Wu, W.; Li, Q.; Zhang, Y.; Du, X.; Wang, H. Two-Step Urban Water Index (TSUWI): A New Technique for High-Resolution Mapping of Urban Surface Water. Remote Sens. 2018, 10, 1704. [Google Scholar] [CrossRef]
- Candiago, S.; Remondino, F.; De Giglio, M.; Dubbini, M.; Gattelli, M. Evaluating Multispectral Images and Vegetation Indices for Precision Farming Applications from UAV Images. Remote Sens. 2015, 7, 4026–4047. [Google Scholar] [CrossRef]
- Rouse Jr, J.W.; Haas, R.H.; Schell, J.; Deering, D. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation; NASA: Washington, DC, USA, 1973.
- Jordan, C.F. Derivation of Leaf-area Index from Quality of Light on the Forest Floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Richardson, A.J.; Wiegand, C. Distinguishing Vegetation from Soil Background Information. Photogramm. Eng. Remote Sens. 1977, 43, 1541–1552. [Google Scholar]
- Lindeberg, T. Feature Detection with Automatic Scale Selection. Int. J. Comput. Vis. 1998, 30, 79–116. [Google Scholar] [CrossRef]
- Otsu, N. Threshold Selection Method from Gray-Level Histograms. Ieee Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation Coefficients: Appropriate Use and Interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef]
- Jung, Y.; Hu, J. A K -Fold Averaging Cross-Validation Procedure. J. Nonparametric Stat. 2015, 27, 167–179. [Google Scholar] [CrossRef]
- Song, R.; Cheng, T.; Yao, X.; Tian, Y.; Zhu, Y.; Cao, W. Evaluation of Landsat 8 Time Series Image Stacks for Predicitng Yield and Yield Components of Winter Wheat. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016. [Google Scholar]
- Fu, Z.; Jiang, J.; Gao, Y.; Krienke, B.; Wang, M.; Zhong, K.; Cao, Q.; Tian, Y.; Zhu, Y.; Cao, W.; et al. Wheat Growth Monitoring and Yield Estimation Based on Multi-Rotor Unmanned Aerial Vehicle. Remote Sens. 2020, 12, 508. [Google Scholar] [CrossRef]
- Qian, J.P.; Li, M.; Yang, X.T.; Wu, B.; Zhang, Y.; Wang, Y.A. Yield estimation model of single tree of Fuji apples based on bilateral image identification. Trans. Chin. Soc. Agric. Eng. 2013, 29, 132–138. [Google Scholar]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A Training Algorithm for Optimal Margin Classifiers; ACM: New York, NY, USA, 1992; pp. 144–152. [Google Scholar]
- Loh, W. Classification and Regression Trees. WIREs Data Mining Knowl Discov 2011, 1, 14–23. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R.; Dixon, B. GIS-Based Groundwater Potential Mapping Using Boosted Regression Tree, Classification and Regression Tree, and Random Forest Machine Learning Models in Iran. Environ. Monit. Assess 2016, 188, 44. [Google Scholar] [CrossRef] [PubMed]
- Felicísimo, Á.M.; Cuartero, A.; Remondo, J.; Quirós, E. Mapping Landslide Susceptibility with Logistic Regression, Multiple Adaptive Regression Splines, Classification and Regression Trees, and Maximum Entropy Methods: A Comparative Study. Landslides 2013, 10, 175–189. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Khaledian, Y. Selecting Appropriate Machine Learning Methods for Digital Soil Mapping. Appl. Math. Model. 2020, 18, 401–418. [Google Scholar] [CrossRef]
- Bakay, M.S. Electricity Production Based Forecasting of Greenhouse Gas Emissions in Turkey with Deep Learning, Support Vector Machine and Artificial Neural Network Algorithms. J. Clean. Prod. 2021, 285, 125324. [Google Scholar] [CrossRef]
- Chatpatanasiri, R.; Kijsirikul, B. Bayesian Evidence Framework for Decision Tree Learning. In Proceedings of the Bayesian Inference and Maximum Entropy Methods in Science and Engineering; Knuth, K.H., Abbas, A.E., Morris, R.D., Castle, J.P., Eds.; Amer Inst Physics: Melville, Australia, 2005; Volume 803, pp. 88–95. [Google Scholar]








| Parameter | Multispectral Bands | Thermal Infrared Band |
|---|---|---|
| Resolution | 2064 × 1544 | 160 × 120 |
| Field of View (FOV) | 48° × 36.8° | 57° × 44.3° |
| Flight altitude | 50 m | 50 m |
| Ground sampling (GSD) | 2.16 cm/px | 13.56 cm/px |
| Imaging band | B (475 nm), G (560 nm), R (668 nm), RE(717 nm), NIR (840 nm) | 8–14 μm |
| Blue | Green | Red | Red-Edge | NIR | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| C | O | C | O | C | O | C | O | C | O | |
| Mean | 0.27 | 0.08 | 0.23 | 0.09 | 0.19 | 0.10 | 0.16 | 0.10 | 0.17 | 0.11 |
| STD | 0.08 | 0.05 | 0.08 | 0.05 | 0.07 | 0.05 | 0.06 | 0.05 | 0.05 | 0.05 |
| 25% | 0.21 | 0.05 | 0.17 | 0.05 | 0.14 | 0.06 | 0.12 | 0.07 | 0.13 | 0.08 |
| 50% | 0.26 | 0.07 | 0.22 | 0.08 | 0.19 | 0.09 | 0.16 | 0.10 | 0.17 | 0.11 |
| 75% | 0.33 | 0.11 | 0.28 | 0.13 | 0.24 | 0.13 | 0.20 | 0.14 | 0.21 | 0.14 |
| C1 | C2 | C3 | |||
|---|---|---|---|---|---|
| b-r_d | b-nir_d | b-renir_d | |||
| b-r_r | b-nir_r | b-renir_r | |||
| b-r_n | b-nir_n | b-renir_n | |||
| g-r_d | g-nir_d | g-renir_d | |||
| g-r_r | g-nir_r | g-renir_r | |||
| g-r_n | g-nir_n | g-renir_n | |||
| bg-r_d | bg-nir_d | bg-renir_d | |||
| bg-r_r | bg-nir_r | bg-renir_r | |||
| bg-r_n | bg-nir_n | bg-renir_n | |||
| bgr_sum | bgr-nir_d | bgr-renir_d | |||
| bgr-nir_r | bgr-renir_r | ||||
| bgr-nir_n | bgr-renir_n | ||||
| Model | Optimal Hyperparameters after Research Grid |
|---|---|
| Support Vector Machines | Kernel: linear, C: 22 |
| Random Forest | max_depth: 3, max_features: auto, min_samples_leaf: 4, n_estimators: 60 |
| CART | max_depth: 4, min_samples_leaf: 4, splitter: best |
| KNN | n_neighbors: 14 |
| Model | Average | Best | ||||||
|---|---|---|---|---|---|---|---|---|
| rRMSE Training | rRMSE Testing | R2 Training | R2 Testing | rRMSE Training | rRMSE Testing | R2 Training | R2 Testing | |
| CART | 7.213 | 8.719 | 0.784 | 0.678 | 6.997 | 8.215 | 0.796 | 0.724 |
| KNN | 8.411 | 8.898 | 0.706 | 0.664 | 8.167 | 8.297 | 0.722 | 0.707 |
| RF | 7.478 | 8.367 | 0.767 | 0.704 | 7.250 | 7.560 | 0.781 | 0.755 |
| LR | 8.322 | 8.428 | 0.712 | 0.699 | 8.235 | 7.831 | 0.718 | 0.759 |
| SVR | 8.365 | 8.410 | 0.709 | 0.700 | 8.251 | 7.907 | 0.717 | 0.754 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, G.; Du, X.; Du, M.; Li, Q.; Tian, X.; Ren, Y.; Zhang, Y.; Wang, H. Cotton Yield Estimation Using the Remotely Sensed Cotton Boll Index from UAV Images. Drones 2022, 6, 254. https://doi.org/10.3390/drones6090254
Shi G, Du X, Du M, Li Q, Tian X, Ren Y, Zhang Y, Wang H. Cotton Yield Estimation Using the Remotely Sensed Cotton Boll Index from UAV Images. Drones. 2022; 6(9):254. https://doi.org/10.3390/drones6090254
Chicago/Turabian StyleShi, Guanwei, Xin Du, Mingwei Du, Qiangzi Li, Xiaoli Tian, Yiting Ren, Yuan Zhang, and Hongyan Wang. 2022. "Cotton Yield Estimation Using the Remotely Sensed Cotton Boll Index from UAV Images" Drones 6, no. 9: 254. https://doi.org/10.3390/drones6090254
APA StyleShi, G., Du, X., Du, M., Li, Q., Tian, X., Ren, Y., Zhang, Y., & Wang, H. (2022). Cotton Yield Estimation Using the Remotely Sensed Cotton Boll Index from UAV Images. Drones, 6(9), 254. https://doi.org/10.3390/drones6090254











