Abstract
As one of the key issues in aviation safety, loss-of-control in the form of adverse aircraft-pilot couplings is attracting attention increasingly. Dynamic-pitch-control envelope shows to be a promising means to evaluate the loss-of-control related to pilot-induced oscillations. To mitigate this issue, this paper develops a human pilot model with the dynamic-pitch-control envelope cue. A key feature of the model is the capability to afford the characteristics of the pilot’s behavior through analyzing the cue of envelope boundaries in different areas. The fuzziness and adaption of the human are introduced into the model to describe the behavior of the human pilot. Fuzzy control logic is designed to reflect the fuzziness of the human’s response to the envelope cue. Time-varying parameters are adjusted to embody the adaptive characteristics of the human pilot to different regional envelope cues. Furthermore, three metrics methods, including error metric, envelope boundaries metric, and scalogram-based pilot-induced oscillation (PIO) metric, are proposed to design the dynamic-pitch-control envelope cues. The assessment results obtained by pilot–aircraft system simulation are compared with the pilot-in-the-loop flight experiment in-ground simulator to validate the effectiveness of the model. Simulation and experimental results show that the proposed human pilot model and envelope cue method can be applied to mitigate the loss-of-control events caused by the pilot–aircraft system oscillations.
1. Introduction
Aircraft loss-of-control (LOC) has been a major factor in aviation fatal accidents and it has resulted in more fatalities than other factors during the past 10 years [1,2]. One of the key issues is the loss-of-control related to the unfavorable interaction between the pilot and the aircraft system, including pilot-induced oscillations (PIO) [3,4,5]. Loss-of-control related to pilot-induced oscillations has become a persistent aviation safety problem [6].
Currently, the Boeing Company and the NASA Langley Research Center have jointly developed a set of metrics for defining loss-of-control, which are composed of five flight envelopes [7], that is, adverse aerodynamics envelope, unusual attitude envelope, structural integrity envelope, dynamic-pitch-control envelope, and dynamic roll control envelope. These envelopes can reliably identify key upset characteristics in a flight test or event time history [8,9,10,11]. The function of the flight envelope protection is that it is an augmentation of the flight control system to monitor and maintain the aircraft within its flight envelopes [12,13,14,15]. It requires that the aircraft stays within a predefined safe flight envelope through the adjustment of the flight parameters [16,17,18,19,20,21]. The existing aircraft upset prevention methods mainly focus on the design of flight envelope protection systems and lack of human control behavior with the envelope cues investigation. The flight envelope can be as an auxiliary cue system to inform pilots of the current flight envelope information via haptic or visual displays. The advantage of this approach is that pilot–aircraft interaction mechanisms are considered with the flight envelope cues. Among the flight envelopes above-mentioned, the dynamic-pitch-control envelope is related to the pitch axis PIO prediction [11]. With regard to the issues of the loss-of-control events caused by adverse aircraft–pilot couplings, the study of dynamic-pitch-control envelope cue design is of importance to improve the pilot–aircraft system characteristics so as to mitigate such issues.
In the research of pilot–aircraft system analysis with the flight envelope cues, the existing investigations mainly focus on analyzing the effect of flight envelope protection systems on human pilots through the flight test [22,23,24]. For example, Van Baelen proposed a new haptic feedback concept with a flight envelope protection system to limit the inputs of pilot control [25,26]. Then the results of an experimental evaluation were discussed to validate the feasibility and correctness of the design [27,28]. Ackerman developed an interface system display in the simulator, which was conceived to improve pilot situation awareness with respect to a flight envelope protection system [29,30]. Stepanyan combined the aural, visual, and tactile cues to predict loss-of-control safety margins as the aircraft gets closer to the edge of the safe operating envelope through the flight test simulation [31]. However, the flight test results above may vary with individuals, it is necessary to evaluate the effects of the flight envelope cues by establishing a parametric model of the pilot behavior that covers a broad range of behavior. Previously, we have developed an intelligent human pilot model based on a smart inceptor for the aircraft [32,33]. The feature of the model is its capability to reflect the interaction between the smart inceptor and the human pilot. The model provides a feasible way to predict the characteristics of a pilot–aircraft system including a smart inceptor for mitigating loss-of-control. As for the human pilot behavior with the flight envelope cues, the distinction from the above-mentioned model lies in the differences in the cue path, feedback signal, and the pilot’s control strategy between the smart inceptor and flight envelope cue system. The flight envelope cue provides the flight information for the human pilot via a display cue and the human pilot control strategy will be adjusted according to the position of flight state parameters in the flight envelope. Thus it is worth studying the human pilot behavior of the aircraft with the flight envelope cue.
A human pilot model is developed for the aircraft with the dynamic pitch control envelope cue, which aims to mitigate the pilot–aircraft system loss-of-control. The envelope cue boundaries take the dynamic pitch attitude and pitch-axis control authority into consideration. We focus on the analysis of the human pilot behavior with different regional boundaries via the visual display cue. The human pilot model emphasizes intelligent and adaptive characteristics to the flight envelope cue. The pilot model adopts time-varying parameters to accommodate different regional cues and utilizes the fuzzy logic to describe the fuzziness of human’s response to cues. Furthermore, three metrics evaluation methods, including error metric, envelope boundaries metric, and scalogram-based PIO metric, are put forward to design the dynamic-pitch-control envelope cues. The assessment results of dynamic-pitch-control flight envelope cue design are compared with the pilot-in-the-loop flight simulation experiments. Numerical simulation and experimental results are given to investigate the validity of the human pilot model and the dynamic-pitch-control envelope cue design method in mitigating the pilot–aircraft system loss-of-control.
2. Pilot–Aircraft System with Dynamic-Pitch-Control Envelope Cue
2.1. Dynamic-Pitch-Control Flight Envelope
The dynamic-pitch-control flight envelope is proposed by the Boeing Company and the NASA Langley Research Center [7]. The quantitative definition of this envelope is given relating to critical flight parameters that account for aircraft flight dynamics and flight control use. The dynamic-pitch-control envelope gives the limits of the protected envelope to ensure, on one hand, that the aircraft always stays in a safe flight condition. On the other hand, the envelope is related to the pitch axis PIO prediction, which is an effective means to evaluate the pilot–aircraft system loss-of-control. Here, we will use this dynamic-pitch-control envelope to cue and guide the human pilot to perform effective maneuvers.
The dynamic-pitch-control envelope can be shown in Figure 1. This envelope defines the relation between the dynamic pitch attitude and pitch-axis control authority. The x-axis represents the percent elevator deflection. The y-axis, that is, the dynamic pitch attitude represents the sum of the current pitch attitude angle and its expected change after one second in Equation (1). It reflects the trend of the pitch attitude angle. It can be used to analyze the prediction of the future states of the aircraft.
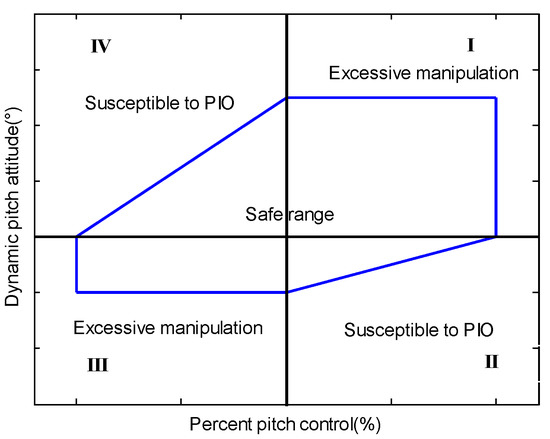
Figure 1.
Dynamic-Pitch-Control Envelope reproduced by reference [7].
The boundaries of this envelope reflect whether the trend in is consistent with the current motion of the aircraft or not. It exposes consistency or opposition between the pitch control commands and the longitudinal aircraft motion. For example, an aircraft that is nose-high but pitching down (or an aircraft that is nose-low but pitching up) may recover properly, while another aircraft may exceed the envelope even at an appropriate pitch attitude if its pitch angle rate is high and deviates from the direction of the aircraft motion.
Thus, the envelopes in quadrant I and quadrant III (in Figure 1) allow the normal control. For example, an aircraft-nose-up pitch control command may result in an aircraft-nose-up pitch attitude trend. The envelopes in quadrant II and quadrant IV (in Figure 1) represent the cases in which the aircraft is pitching in one direction while the control is in the opposite direction. In this case, the limits on and pitch control authority interact with each other. It needs to apply more pitch control to reduce the level of adverse . In this situation, it is easy to cause the aircraft to fall into oscillations or divergences, which may trigger the pilot-induced oscillation (PIO).
It represents the safe range within the dynamic-pitch-control envelope. When the flight states of the aircraft exceed the envelope boundary in quadrant II or quadrant IV, it is susceptible to causing PIO. When the flight states of the aircraft exceed the envelope boundary in quadrant I or quadrant III, it is excessive manipulation of the aircraft. Furthermore, a three-dimensional dynamic-pitch-control envelope graph with a time variable is developed in Figure 2, which is used to analyze the point of time when the aircraft states exceed the envelope boundary. It is helpful to analyze the occurrence time including the PIO tendency of the aircraft and the excessive control of the human pilot.
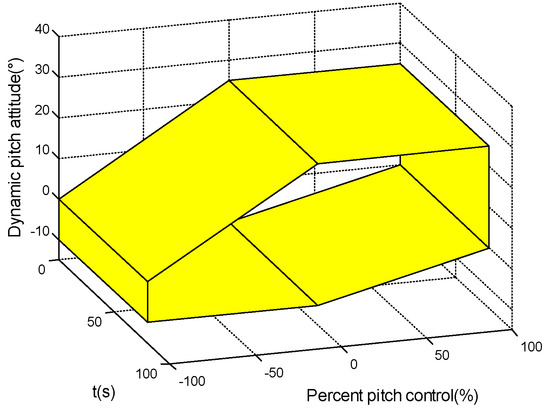
Figure 2.
Three-dimensional dynamic-pitch-control envelope graph with time variable.
2.2. Pilot–Aircraft System Model with Dynamic-Pitch-Control Envelope Cue
The pilot–aircraft system consists of the human pilot, the aircraft system, and the pilot–aircraft interface (including the display interface and inceptor). Here, the dynamic-pitch-control envelope cue is an auxiliary system to inform the human pilot of the current flight information via the visual display of the pilot–aircraft interface. Figure 3 provides a block diagram of pilot–aircraft system with dynamic-pitch-control envelope cue. As shown, the human pilot on one hand perceives the flight information from the error signals, on the other hand, obtains the information from the flight envelope cue. The human pilot model reflects the fact that the pilot needs to change his/her control behavior due to the cue of the dynamic-pitch-control envelope. According to the framework of the intelligent human pilot model, the human pilot model contains the perception module, adaptation module and neuromuscular module, as shown in Figure 3.
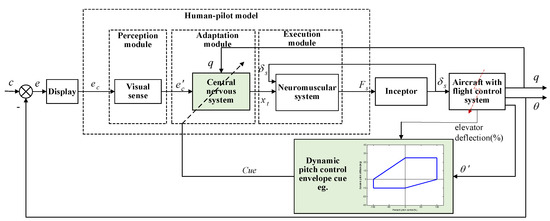
Figure 3.
Block diagram of pilot–aircraft system with dynamic-pitch-control envelope cue.
It can be seen from Figure 3 that the system input signal is c (here, it represents the pitch angle ), and the output signal is q and . The human pilot control behavior is motivated by an error e, which is the difference between c and . The display conveys the information ec to the visual sense module. Meanwhile, the dynamic-pitch-control envelope cue is perceived by the human pilot through visual feedback to guide him/her to change the control strategy. Here, the human pilot can see the flight envelope boundary and real-time flight data curve on it, which is similar to the flight display in reference [29]. The information and cue is processed through the central nervous system of the adaptation module to generate a desired control action xt. The actual control action Fs is obtained by the neuromuscular system of the execution module and exerted on the inceptor. The neuromuscular system and the inceptor interact with each other through inceptor displacement .
3. Human Pilot Model
The human pilot model describes the control behavior of the human pilot with the dynamic-pitch-control envelope cue. The perception module, adaptation module, and execution module of this human pilot model are depicted in this section. Among them, the adaptation module is the key part that is related to the changes in the control strategies based on the dynamic-pitch-control envelope cue.
3.1. Adaptation Module
The adaptation module of the human pilot involves the activities in which the human pilot needs to change the control behavior to adapt to the controlled element. The pilot adaptation behavior means the control action can be changed according to the dynamic-pitch-control envelope cue. If the state of the aircraft reaches or exceeds the dynamic-pitch-control envelope boundaries, the pilot will receive a cue message to remind him/her to change the control strategy; otherwise, the pilot will remain the same behavior.
The adaptation module of the human pilot model can be seen in Figure 4 and Figure 5. The initial structure of the module refers to the Hess adaptive human pilot model [34,35,36]. There are two gain parameters Kp and Kr in each control loop of the adaptation module. Here, the envelope cue is separated into two parts: the envelope cue for exceeding quadrant II or quadrant IV and the envelope cue for exceeding quadrant I or quadrant III. Among them, the envelope cue of exceeding quadrant II or quadrant IV will remind the pilot that the aircraft is prone to PIO (as shown in Figure 4). This cue signal is set as Kcue1. In this situation, the human pilot will mitigate the control magnitude and increase the damping. Here, Kp is the control gain of the error signal, which affects the magnitude of the human pilot manipulation. Kr reflects the damping of the inner closed-loop system. Through the analysis of aircraft configuration, Kr decreases with the increase of damping ratio. Therefore, both the inner loop gain Kr and outer loop gain Kp will decrease in the envelope cue exceeding the quadrant II or quadrant IV. Furthermore, the envelope cue exceeding quadrant I or quadrant III will warn the pilot that the manipulation is large and inappropriate (as shown in Figure 5). This cue signal is set as Kcue2. Then the human pilot will reduce the control magnitude, namely, decreasing the outer loop gain Kp.
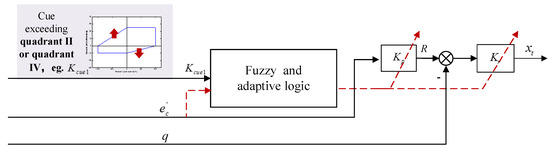
Figure 4.
Adaptation module of the human pilot model with cue exceeding quadrant II or quadrant IV.
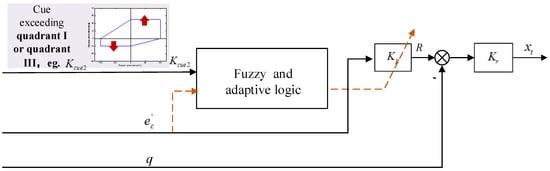
Figure 5.
Adaptation module of the human pilot model with cue exceeding quadrant I or quadrant III.
In Figure 4 and Figure 5, the fuzzy logic reflects that the pilot’s strategy change is not a sudden change process. The pilot needs a certain response process to understand the cue information. There is certain fuzziness in the pilot’s judgment and decision-making. Therefore, the fuzzy logic can be used to modify the changes in the pilot model parameters.
The fuzzy and adaptive logic is described as follows. First, the criterion signal z is defined as the cue signal Kcue, which reflects the cue information of the flight states beyond the flight envelope.
where, Kcue represents Kcue1 or Kcue2. If the envelope cue exceeds quadrant II or quadrant IV, Kcue1 = 1; else, Kcue1 = 0. Similarly, if the envelope cue exceeds quadrant I or quadrant III, Kcue2 = 1; else, Kcue2 = 0.
z = Kcue
Here, z is defined as the input variables of the fuzzy logic model. The output variables of the fuzzy logic model are defined as the strategy variation coefficient of the human pilot with the range of [0, 1]. It reflects the probability of whether the human pilot can change his/her control behavior. The membership function of fuzzy logic is shown in Table 1.

Table 1.
Fuzzy sets.
A central value 3 of the fuzzy-set input range [2.72, 3.28] is chosen as it can represent an instantaneous “” value. It indicates that human judgment of things obeys the normal distribution. It is evident that a too-small trigger value would cause normal system disturbances (e.g., turbulence) to initiate the unnecessary adaptation, whereas a too-large value would inhibit the adaptation when it is needed. The variable range [2.72, 3.28] is based on the human pilot’s perception error characteristics [37].
In Table 1, the fuzzy sets “RS” and “NS” represent the “short” and “long” of human reaction time individually. “RT” and “NT” represent “small” and “large” of the pilot’s strategy variation coefficient , respectively. The employed fuzzy rule sets are asserted in IF-THEN form as,
IF x is RS, THEN y is RT.
IF x is NS, THEN y is NT.
For the adaptive logic, the human pilot control strategy can be motivated based on the dynamic-pitch-control envelope cue. Here, the two category cues are differentiated.
When the human pilot obtains the cue of envelope exceeding quadrant II or quadrant IV (Figure 4), the parameters Kp and Kr will change. The changes in human pilot behavior in Kr and Kp (defined as and ) are shown:
Among them, is the undetermined coefficient, which is determined according to different aircraft configurations, flying tasks, and failure conditions, etc. The purpose is to ensure the rationality of parameters (Kr and Kp) variations and the stability of the pilot–aircraft system.
When the human pilot obtains the cue of envelope exceeding quadrant I or quadrant III (Figure 5), the parameters Kp will change. The change of human pilot behavior in Kp (defined as ) is as follows.
where, is the undetermined coefficient, similar with .
Then the changes in the gains Kr and Kp (defined as and ) during the whole process can be seen in Equation (5).
3.2. Perception and Execution Modules
The perception and execution modules represent the visual sense and neuromuscular system, and their parameters are fixed. The model structures and parameters can be found in reference [32]. Here, the visual sense perceives the error information for the human pilot to make judgments and for decision-making.
In the executive module, the correlation between the neuromuscular system and the inceptor is taken into account. The model is combined with models for the skin flexibility and the limb inertia, and neural feedback in the control of the neuromuscular system. The neural feedback enables the human pilot to modify the effective properties. The model of the neuromuscular system is based on the models available in reference [33].
4. Simulation Results
In order to test the feasibility and effectiveness of the dynamic pitch envelope cue, the flight tasks and aircraft failures are set in the simulation. The performances of the human pilot model and the evaluations of the flight envelope cue are calculated. Then the results are analyzed and discussed.
4.1. Pilot–Aircraft System Parameters Description
The inceptor is described as the feel system dynamics. They can be modeled as a second-order system. The characteristic parameters of the feel system are provided in Table 2 as follows.

Table 2.
Feel system characteristic parameters.
The aircraft configuration was based on NASA flight test configurations that were used in the past PIO evaluation programs [23]. The linear configuration dynamics are as follows.
The key control system elements are identified in Table 3. They mainly include surface rate limit, surface actuator, and surface position limit. The surface rate limit is the key element that causes nonlinear PIO events.

Table 3.
Parameters of flight control system.
The flight envelope ranges are set as: the limits on in these cases are , and the limits on pitch control authority are ±100%. These data are based on a statistical analysis of past LOC events by Wilborn and Foster. They recognized that these flight parameters were sufficient to address 95% of the causes attributed to the LOC data set.
The parameters of the human pilot model are set as follows. In the adaptation module, the initial value of inner loop gain Kr is chosen as the gain value that results in a minimum damping ratio of for any oscillatory mode in the inner closed-loop transfer function . The outer loop gain Kp is chosen to provide a desired, open-loop crossover frequency for the entire pilot model. The nominal value of this crossover frequency will be 2.0 rad/s. Figure 6 represents the bode plot of the open-loop system in the initial state, which indicates that the crossover frequency is 2.0 rad/s. Besides this, the parameters of the perceptual module and executive module in the human pilot model can be found in reference [32].
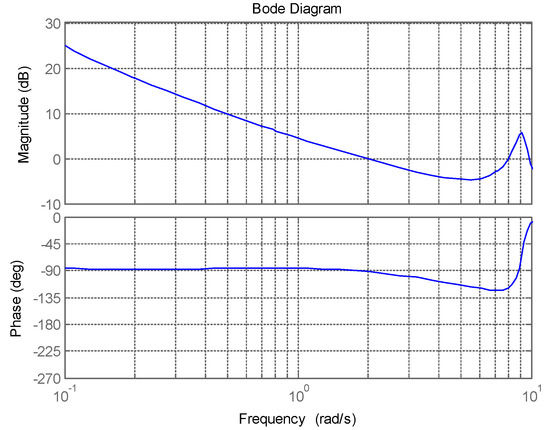
Figure 6.
Bode plot of the open-loop system in the initial state.
4.2. Simulation Results Analysis
In the simulation, a pitch tracking task is used to verify that the human pilot can track the displayed attitude command and attempt to keep errors within the specified tolerances. Sum-of-sines (SOS) command signals are selected as these force the human pilot to continuously apply control inputs. Failure scenarios are set as the control surface rate saturation is reduced from 100°/s to 10°/s at the time of 10 s. In order to investigate the effectiveness of the dynamic pitch envelope cue using the human pilot model, the related results of the human pilot model and the evaluations of flight envelope boundaries are simulated and analyzed. The simulation results with dynamic pitch envelope cue and without envelope cue are given as follows.
- (1)
- Simulation results without envelope cue
Figure 7 represents the evaluation results without the dynamic-pitch-control envelope cue. It shows that the result exceeds the dynamic-pitch-control envelope boundaries in quadrants II, III, and IV. Three-dimensional evaluation results with time variables can be seen in Figure 8. The projection in quadrant I and quadrant III boundaries without envelope cue is depicted in Figure 9, and Figure 10 is the projection in quadrant II and quadrant IV boundaries. It can be seen that the evaluation result exceeds the quadrant III boundary between 32 s and 51 s. The results exceed the quadrant II boundary at around 20 s and exceed the quadrant IV boundary between 25 s and 41 s.
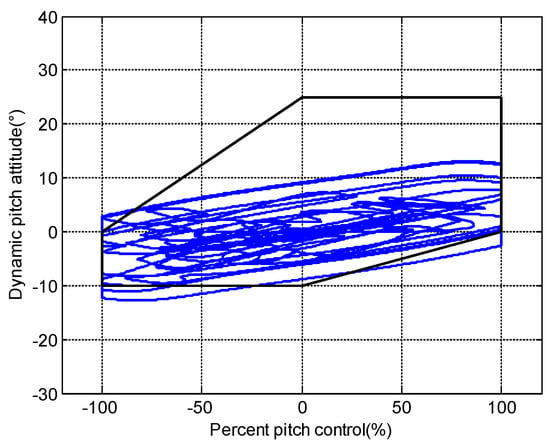
Figure 7.
Evaluation results without envelope cue.
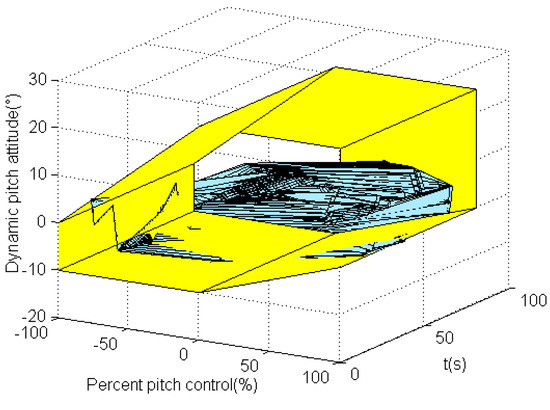
Figure 8.
Three-dimensional evaluation results with time variables.
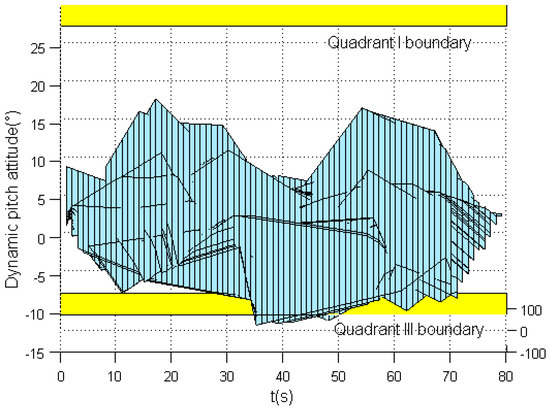
Figure 9.
Quadrants I, III boundary projection result without envelope cue.
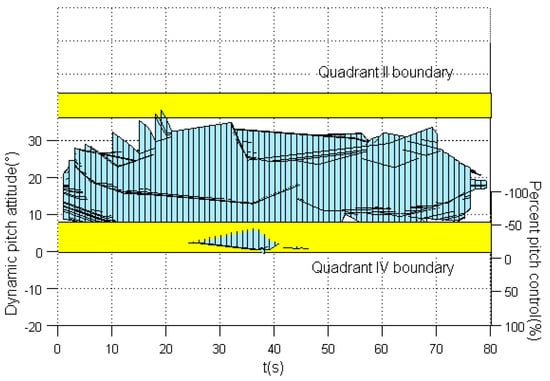
Figure 10.
Quadrants II, IV boundary projection result without envelope cue.
- (2)
- Simulation results with envelope cue
The time-domain tracking response can be shown in Figure 11. Figure 12 is the human pilot input signals, which are also the tracking errors of the pilot–aircraft system. Figure 13 shows the pilot output results, which also represent the signals of inceptor force. Figure 14 represents the parameter changes of the human pilot model with the dynamic-pitch-control envelope cue.
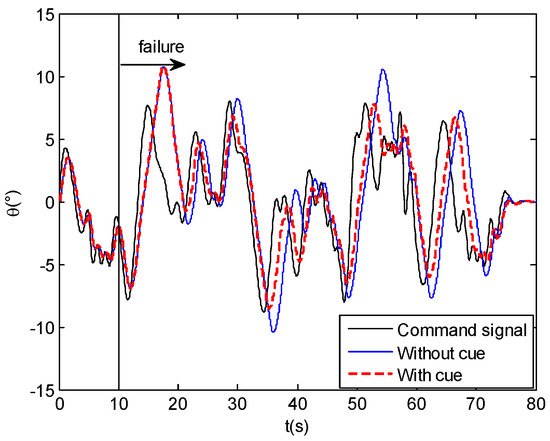
Figure 11.
Time-domain tracking performance.
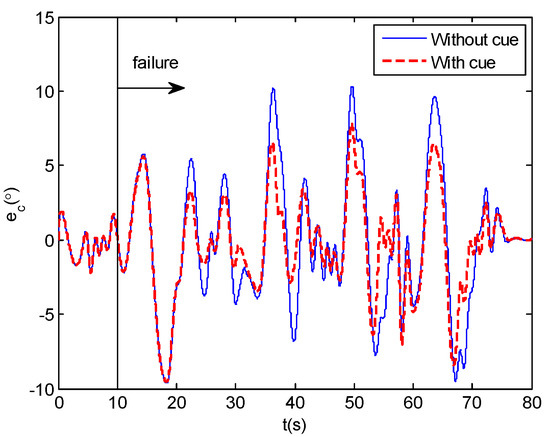
Figure 12.
Pilot input signals (tracking errors).
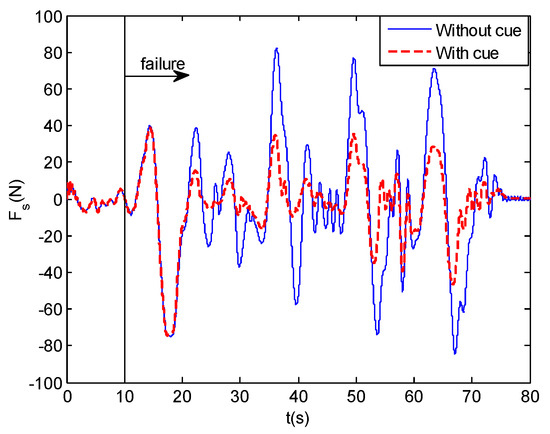
Figure 13.
Pilot output results (Inceptor force).
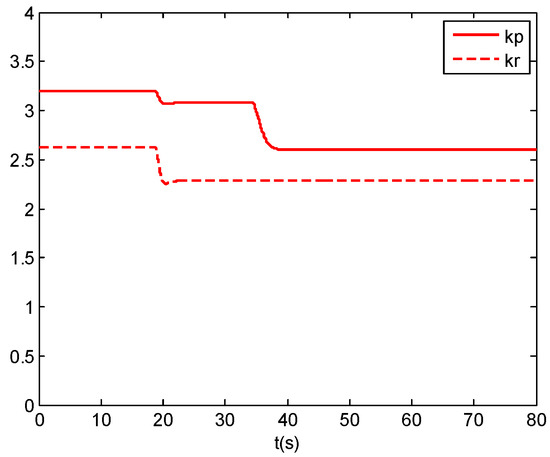
Figure 14.
Parameters changes of human pilot model.
In Figure 13, we can see that time-domain tracking results with envelope cue are essentially in agreement with the results without envelope cue before 20 s. After 20 s, the human pilot changes his/her control behavior so as to cause the differences in the tracking performance between the results with and without envelope cue. The human changing the control strategy in 20 s indicates that the envelope boundaries cue is triggered at that time. The tracking errors reflect that the range and fluctuation of the tracking errors with envelope cue are smaller than those without envelope cue after 20 s. Similarly, the inceptor force exerted by the human pilot with envelope cue is smaller than that without envelope cue after 20 s. In Figure 14, the parameters Kr and Kp of the human pilot model show that both Kr and Kp reduce simultaneously at the time of 20 s, and only Kp changes at the time of 35 s. The process of the reductions is continuous. Figure 15 represents the bode plot of the open-loop system after parameters tuning. It indicates that the crossover frequency is reduced to 1.5 rad/s. The damping ratio increases to . This also reflects the characteristics of parameters Kp and Kr decreasing, which is consistent with the analysis in Section 4.1.
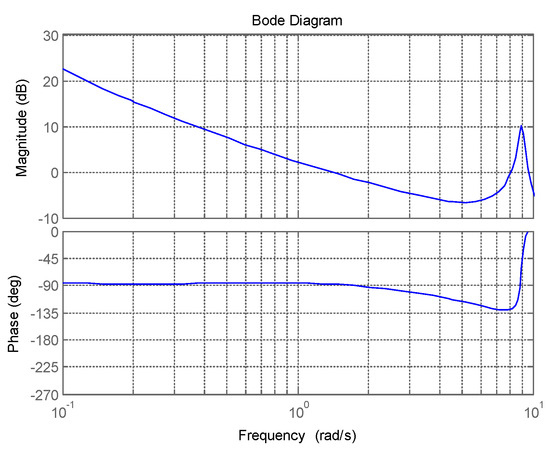
Figure 15.
Bode plot of the open-loop system after parameters tuning.
Figure 16 shows the evaluation results with the envelope cue. It can be seen that the results also exceed the dynamic-pitch-control envelope boundaries in quadrant II and quadrant III. Figure 17 gives three-dimensional evaluation results with time variables. The projections in quadrants I, III boundaries and quadrants II, IV boundaries with envelope cue are depicted in Figure 18 and Figure 19. They indicate that the evaluation result exceeds the quadrant III boundary around 35 s. Combined with Figure 14, we can see that Kp changes at the same time of 35 s. The results exceed the quadrant II boundary at nearly 20 s, and the Kr and Kp equally change at the time of 20 s. Compared with the evaluation results of the no envelope cue, the results with the envelope cue have improved. In order to obtain a more effective cue, the design of different envelope cues will be discussed in the next section.
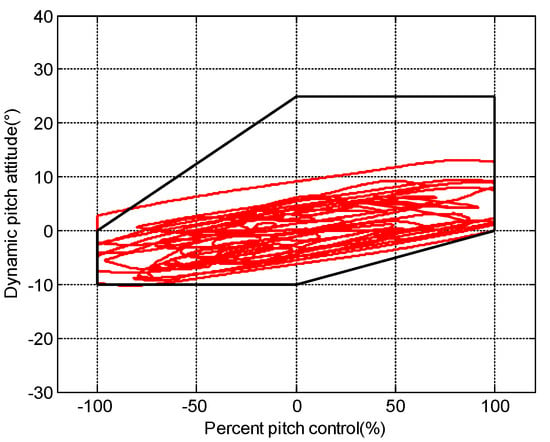
Figure 16.
Evaluation results with envelope cue.
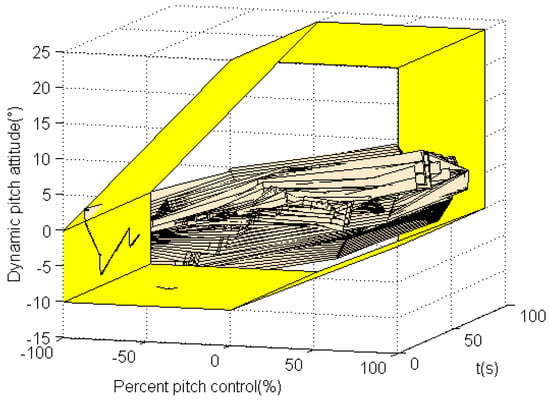
Figure 17.
Three-dimensional evaluation results with time variables.
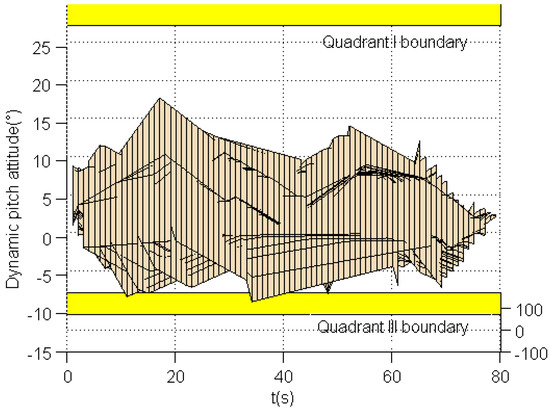
Figure 18.
Quadrants I, III boundary projection result with envelope cue.
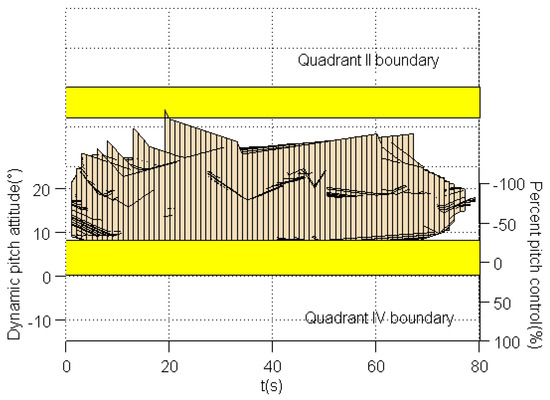
Figure 19.
Quadrants II, IV boundary projection result with envelope cue.
5. Design of the Dynamic-Pitch-Control Envelope Cue
Based on the pilot–aircraft system analysis using fuzzy and adaptive human pilot models, different dynamic-pitch-control envelope cues in this section are designed. In order to evaluate the effectiveness of the design, three metrics, namely, error metric, envelope boundaries metric, and scalogram-based PIO metric are utilized to assess the performance of dynamic-pitch-control envelope cues.
5.1. Dynamic-Pitch-Control Envelope Cue Design
The evaluation results with dynamic-pitch-control envelope cue (Figure 16) show that the simulation curves exceed the standard envelope boundary limits. This is because the control effects have reached the boundaries when the human pilot received the cues of the dynamic-pitch-control envelope. In order to improve this situation, the different envelope boundaries are designed to help the human pilot be aware that the control is close to the boundaries in time. The new reduced cue envelopes are shown in Figure 20, including envelope cue 1, envelope cue 2, and envelope cue 3. They are located in a place 95%, 90%, and 80% from the upper and lower boundaries, respectively.
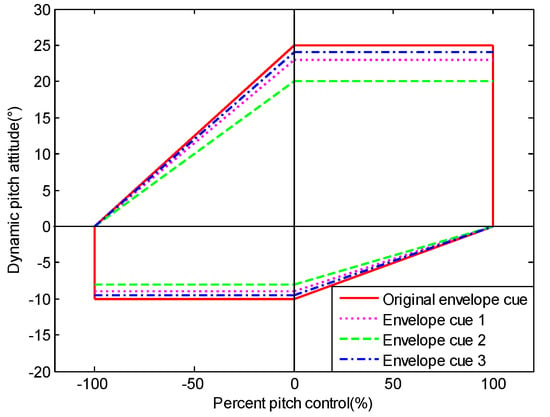
Figure 20.
Dynamic-pitch-control envelope cue design.
Through the pilot–aircraft system is modeled with different dynamic-pitch-control envelope cues, the time-domain simulation results are obtained as follows. Figure 21 gives the time-domain tracking performance for the human pilot model simulation with different envelope cues. The inceptor force results are shown in Figure 22. The tracking errors with the different envelope cues can be seen in Figure 23. Compared with the original envelope cue, the control magnitudes of the human pilot model with envelope cues 1, 2, and 3 have reduced, the tracking results have improved, and the errors are lower, relatively.
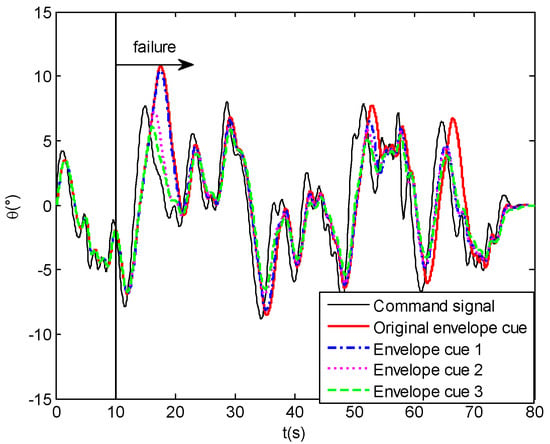
Figure 21.
Time-domain tracking performance.
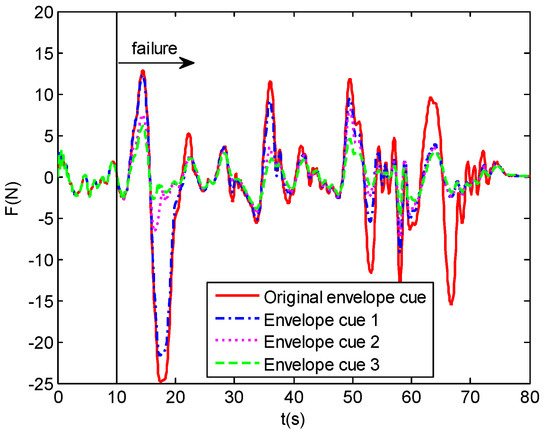
Figure 22.
Pilot output results (Inceptor force).
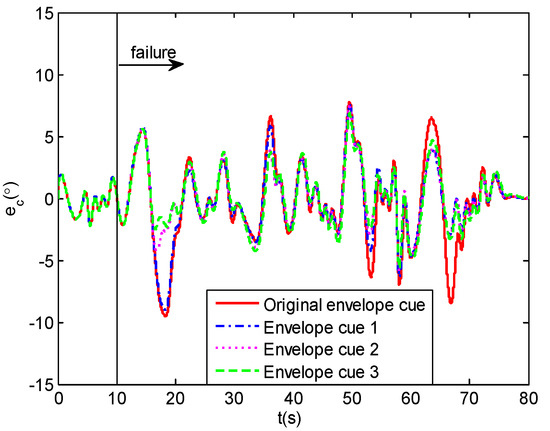
Figure 23.
Pilot input signals (tracking errors).
Figure 24 shows the change in parameters Kr and Kp in the human pilot model with different envelope cues. It can be seen that the Kr and Kp reduce simultaneously at a time of 10 s under the envelope cue 2 and envelope cue 3, while the Kr and Kp reduce at a time nearly 20 s under the envelope cue 1 and the original envelope cue. This indicates that reduced envelope boundaries will make the human pilot aware that the control is close to the boundaries timely. Furthermore, the changed amounts of Kr and Kp increase with the envelope boundaries range decreasing. The bode plot of the open-loop system after parameters tuning with different cue boundaries can be seen in Figure 25. It shows that crossover frequency decreases with the envelope boundaries range decreasing.
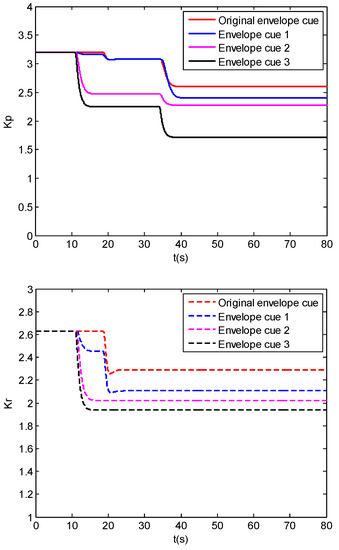
Figure 24.
Parameters (Kp, Kr) changes of human pilot.
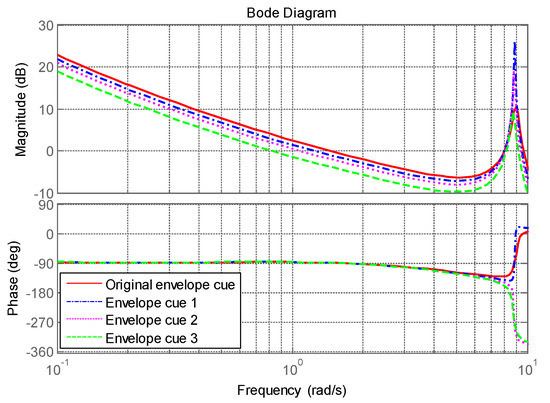
Figure 25.
Bode plot of the open-loop system after parameters tuning with different cue boundaries.
5.2. Assessment Metrics
To evaluate the design effects, three different metrics are chosen to assess the performance of dynamic-pitch-control envelope cues in the above-mentioned.
- (1)
- Error metric
In order to analyze the task completion of different envelope cues, an evaluation metric of task quality is developed according to the tracking error of the human pilot. Here, the relative increment can be used as the measurement of the task cost loss. The root mean square error and the relative increment caused by failure are taken as the metrics to evaluate the quality of the pilot’s task.
First, the root mean square of error before failure is calculated.
where, RMS represents root mean square and represents the error signal before the failure occurs. tf is the failure occurrence time and t1 is the starting time of the simulation task. Then, the root mean square of error after failure is obtained.
where, represents the error signal after the failure occurs, and t2 is the end time of the simulation task. Then the error metric is defined as the relative change of the root mean square of the error before and after the failure, as shown in Equation (9).
- (2)
- Envelope boundaries metric
The original dynamic-pitch-control envelope is also used as a metric to validate the effects of different envelope cues, as shown in Figure 1. If both pitch control percent and the dynamic pitch attitude are located in the safe range, the results are satisfying. If they are located in the regions susceptible to PIO or excessive manipulation, the dynamic pitch envelope control cue needs to be improved. The details can be seen in Section 2.
- (3)
- Scalogram-based PIO metric
A scalogram-based PIO metric is utilized here to identify the PIO cases of different envelope cues. In this metric, the control inceptor force is F(t). The wavelet-based scalogram of the inceptor force F(t) is the scalogram . The inceptor peak amplitude of is calculated as follows.
where, ωmax(t) is the main frequency of the human pilot controlling. The phase lag of the aircraft dynamics Yc(ω) at the frequency ωmax(t) is
In order to present a better visual comparison using inceptor peak amplitude Pmax versus weighted phase lag ϕmax, a weighted form of phase is taken into account.
The two parameters, and , are used as the prediction boundary of PIO. The metric is divided into two regions. One region is prone to PIO, and the other region is not prone to PIO. The details of the PIO metric are described in reference [33].
5.3. Results and Discussions
The error metric results with different envelope cues can be seen in Figure 26. They are obtained through the root mean square of errors calculation, which is indicated in Figure 27. It can be seen that the RMS and error index of the original envelope cue is the largest. The error indexes of the other envelope cues were reduced to reflect the effectiveness of reducing the envelope boundaries. However, it can be seen that the error index of envelope cue 3 is larger than that of envelope cue 2. This reflects that if the envelope boundaries are small enough, the quality of the task completion will be reduced. It is necessary to select suitable envelope boundaries.
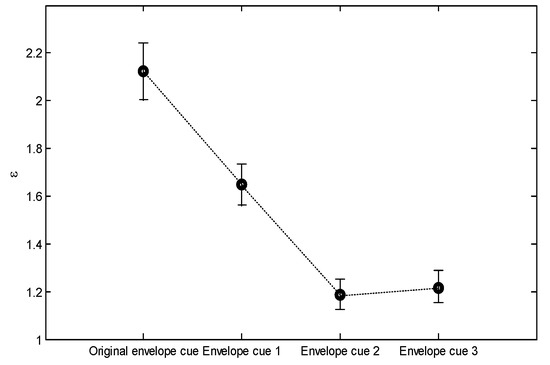
Figure 26.
Error index.
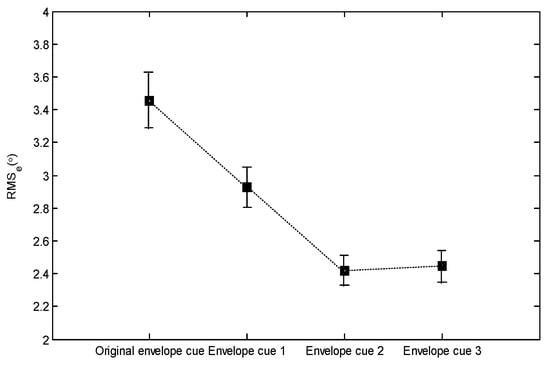
Figure 27.
Root mean square (RMS) of errors.
The envelope boundaries metric results with different envelope cues are shown in Figure 28. The results with envelope cue 2 and envelope cue 3 are within the envelope boundaries, while the evaluations of the original envelope cue and envelope cue 1 are beyond the envelope boundaries. It also reveals that the suitable envelope cue is helpful for mitigating the loss-of-control events caused by the pilot–aircraft system oscillations.
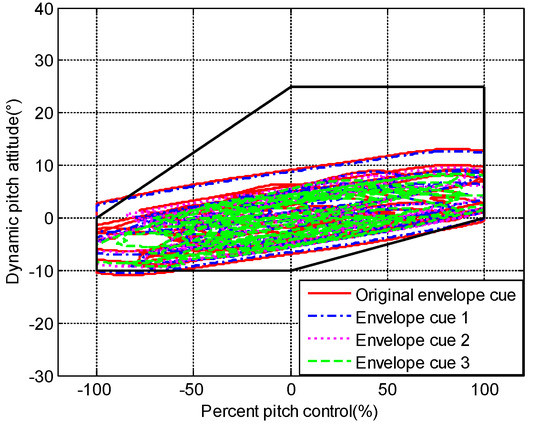
Figure 28.
Evaluation results with different envelope cues.
Figure 29 represents the results of the scalogram-based PIO metric applied to different dynamic-pitch-control envelope cues. The prediction of the PIO metric without envelope cue is located in the susceptible PIO region, and the inceptor peak amplitude reached nearly 0.7(12/(rad/s)). Even though the prediction result with the envelope cue still exceeds the PIO boundaries, the inceptor peak amplitude decreases compared with the result without the envelope cue. Moreover, the results of PIO metric prediction with reduced envelope cue 2 and envelope cue 3 are within the unsusceptible PIO region, which reveals the effectiveness of the appropriate envelope cue. These cases’ results agree with the results of the evaluations of envelope boundaries metric.
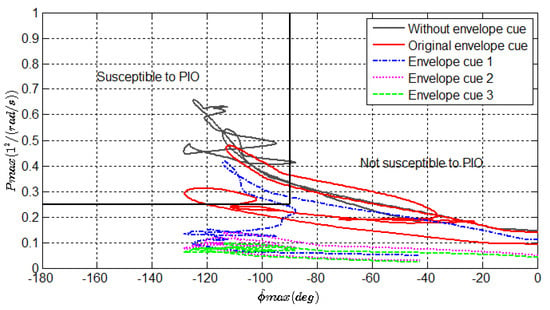
Figure 29.
Results of scalogram-based PIO metric.
The above results are summarized in Table 4. The assessment metrics results under different envelope cues are given as follows. It can be seen that the assessment results of envelope cue 2 are better than others, which indicates that the flight envelope cue near the place of 90% from the upper and lower boundaries is the most helpful for mitigating the loss-of-control related to pilot induced oscillations.

Table 4.
Synthesis of the assessment results.
6. Experimental Validation and Results Comparison
In order to validate the design of the dynamic-pitch-control envelope cue, a pilot-in-the-loop flight simulation experiment is conducted in this section. The simulation results are also compared with smart inceptor cues results.
6.1. Experimental Setup
In the pilot-in-the-loop flight simulation experiment, the pilot–aircraft system is shown in Figure 30. The pilot system is composed of the actual human pilot, the aircraft system, and the display interface. The human pilot can perceive the dynamic-pitch-control envelope cue information from the visual display.
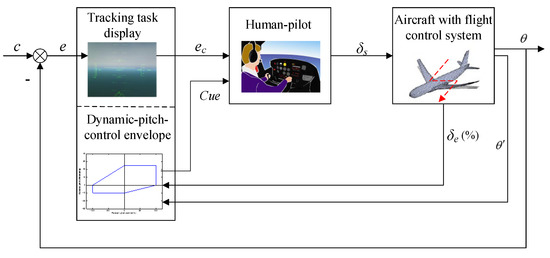
Figure 30.
Pilot–aircraft system in the experiment.
The experiment was conducted in the Flight Mechanics Laboratory of Beihang University, using the fixed-base flight simulator shown in Figure 31a. A control inceptor was used as the control device, and three high-resolution displays of the visual system were used for the visual environment for the human pilot. Among them, the display on the left reveals the model of the aircraft system and the connections of various pilot–aircraft system signals. The display on the right provides additional aircraft information such as the variation curves of aircraft states. The key tracking task display is located in the middle of the visual system. Here, the error e is presented on the visual display with a simplified artificial horizon indicator, as can be seen in Figure 31b.

Figure 31.
Flight simulator and tracking task display. (a) Pilot-in-the-loop flight simulator (b) Tracking task display.
The dynamic-pitch-control envelope cue is shown in the top right-hand corner of Figure 31b. Herein, the number 0 represents that the flight parameters are within the safe range, while numbers 1, 2, 3, and 4 represent that the flight parameters exceed quadrants I, II, III, and IV, respectively. Thus the human pilot can adjust his/her control strategy according to this information cue of visual display. In the experiment, the experiment task, controlled element, and failure scenarios are all consistent with the computer simulations. The experimental data were gathered and processed to be used for comparison with the simulations. The results are as follows.
6.2. Experimental Results Analysis
- (1)
- Results of no envelope cue
Figure 32 compares the time-domain tracking performance of the no envelope cue for the human pilot model simulation and pilot-in-the-loop experiment. The tracking trend of both is basically the same, especially 30 s after the failure. In comparison with the experiment, the simulation tracking is smoother. Figure 33 indicates the dynamic-pitch-control envelope evaluation results between the simulation and pilot-in-the-loop experiment. It can be seen that both evaluations exceed the envelope boundaries in quadrants II, III, and IV. These indicate that the human pilot model and actual human pilot are able to reach the consistent evaluation results in the case of no envelope cue.
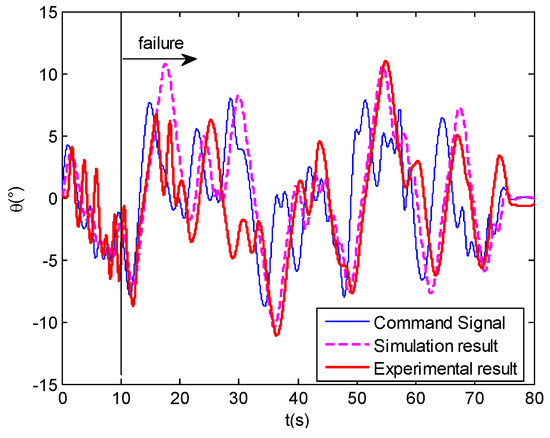
Figure 32.
Comparison of experimental and simulation results in time-domain tracking performance.
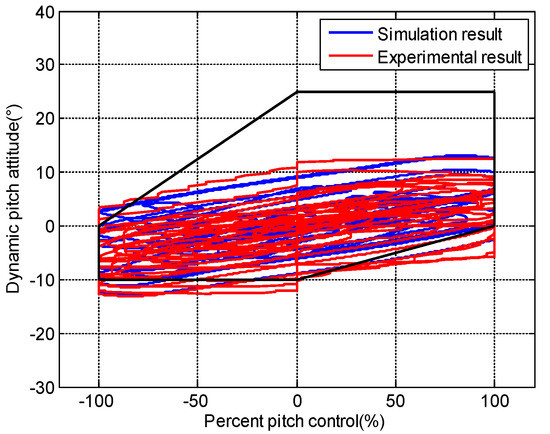
Figure 33.
Comparison of experimental and simulation evaluation results of no envelope cue.
- (2)
- Results of the original envelope cue
The time-domain tracking performances of the original envelope cue for the simulation and experiment are shown in Figure 34. The tracking results are almost consistent. The phase lags for the experiment are slightly larger than simulation. Figure 35 represents the dynamic-pitch-control envelope evaluation results of the original envelope cue between the simulation and experiment. It can be seen that the two results are basically the same. Compared with the evaluation results of no envelope cue (Figure 33), both the simulation and experimental results of the original cue are improved.
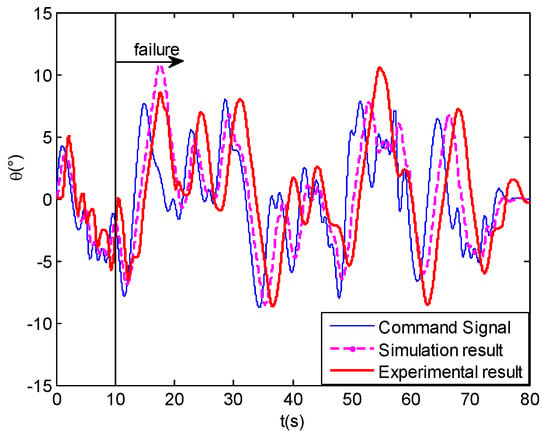
Figure 34.
Comparison of experimental and simulation results in time-domain tracking performance.
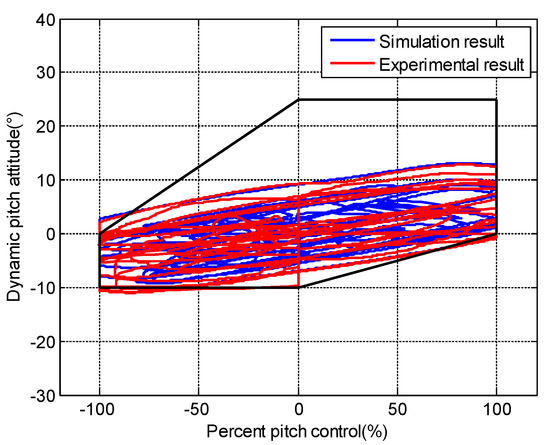
Figure 35.
Comparison of experimental and simulation evaluation results with original envelope cue.
- (3)
- Results of the designed envelope cue
According to the design of the dynamic-pitch-control envelope cue using the pilot–aircraft system model, envelope cue 2 received the best assessment results. In order to validate this design effect, the experimental evaluation results of envelope cue 2 are represented in Figure 36. Three-dimensional evaluation results with time variables can be seen in Figure 37. The projection in quadrant I and quadrant III boundaries is depicted in Figure 38, and Figure 39 reveals the projection in quadrant II and quadrant IV boundaries. It can be seen that the experimental evaluation results are within the envelope boundaries, which reveals the effectiveness of the designed envelope cue.
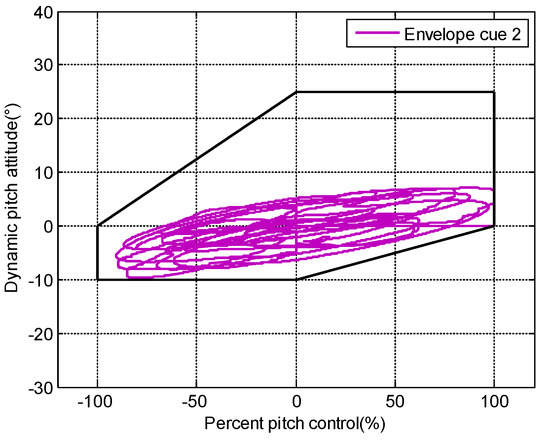
Figure 36.
Experimental Evaluation results with envelope cue 2.
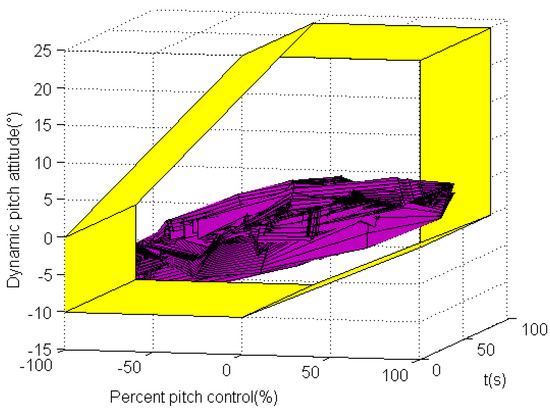
Figure 37.
Experimental results of three-dimensional evaluation with time variables.
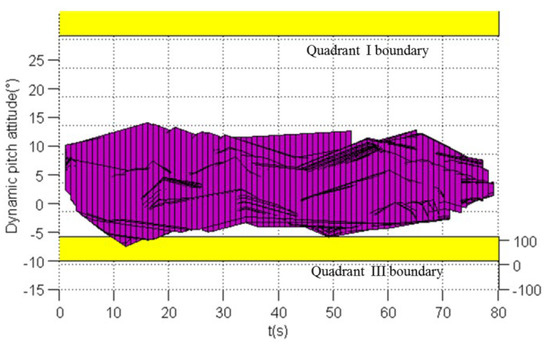
Figure 38.
Quadrants I, III boundary projection result.
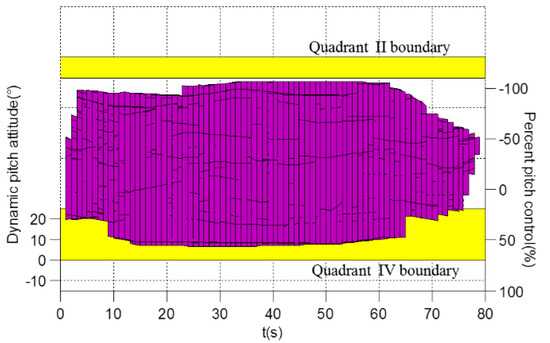
Figure 39.
Quadrants II, IV boundary projection result.
Figure 40 represents the experimental results of the scalogram-based PIO metric. It can be seen that the predictions of PIO metric without envelope cue and original envelope cue are located in the susceptible PIO region, while the predictions with envelope cue 2 are within the unsusceptible PIO region. These results are essentially in agreement with the simulations.
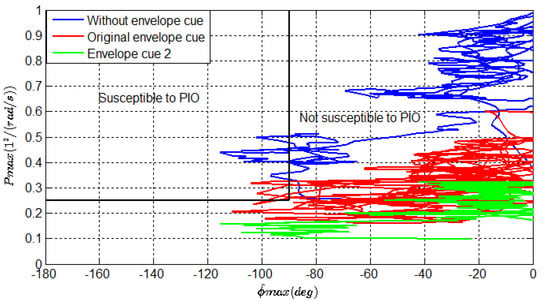
Figure 40.
Results of scalogram-based PIO metric.
In addition, the assessment results of other envelope cues including experimental and simulation assessments are summarized in Table 5. In the error metric evaluation, there exists a difference between the human pilot model and the actual pilot. But the trends are almost consistent. For the envelope boundaries metric and scalogram-based PIO metric, the evaluation results of the two are basically the same. Envelope cue 2 obtained the best results in both experimental and simulation assessments. It also indicates that the flight envelope cue near the place of 90% from the upper and lower boundaries is the most effective for mitigating the loss-of-control due to the adverse aircraft-pilot couplings.

Table 5.
Synthesis of the experimental and simulation assessment results.
6.3. Results Comparison
The pilot model simulation results with envelope cues are compared to the result of a pilot model with smart inceptor cues. According to reference [33], the scalogram-based PIO metric result of the smart inceptor cue is shown in Figure 41. Combined with Figure 29, it can be seen that both dynamic-pitch-control envelope cue and smart inceptor cue can mitigate the pilot–aircraft system oscillations. However, dynamic-pitch-control envelope cue via a visual display is easier to implement than the smart inceptor cue via haptic feedback.
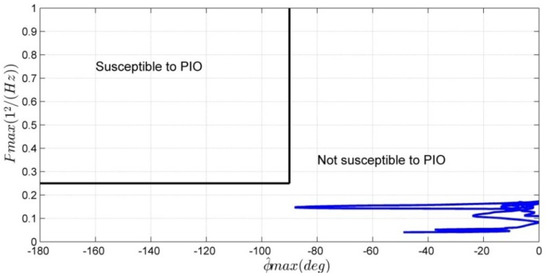
Figure 41.
Scalogram-based PIO metric result of smart inceptor cue [33].
7. Conclusions
In this paper, a fuzzy and adaptive behavior model of the human pilot with a flight envelope cue is proposed to mitigate the pilot–aircraft system loss-of-control events.
- (1)
- Based on the behavior characteristics of a human pilot with the dynamic-pitch-control envelope cue, a fuzzy and adaptive human pilot model is developed. The envelope cue provides the PIO or excessive manipulation information for the human pilot via the visual display. The model is different from other models that fail to consider the effect of different envelope cues information. The model can reflect fuzzy, adaptation, and variable strategy characteristics to the flight envelope cue. It utilizes fuzzy logic to describe the fuzziness of a human’s response to the cue and adopts time-varying parameters to accommodate different regional boundaries cues.
- (2)
- Based on the pilot–aircraft system analysis, three metrics assessment methods, including error metric, envelope boundaries metric, and scalogram-based PIO metric, are put forward to design the dynamic-pitch-control envelope cues. Note that the error metric reflects the qualities of task completion, envelope boundaries metric, and scalogram-based PIO metric reflect the prediction of adverse aircraft-pilot couplings. The comparison of the simulation and the experiment demonstrated that the assessments are basically consistent. The simulation and experimental results indicate that the evaluations of small boundary cues are easy to maintain within the envelope boundaries and unsusceptible to the PIO region. While if the envelope boundaries are small enough, the quality of the task completion will be reduced. In this study, the flight envelope cue near the place of 90% from the upper and lower boundaries is effective for mitigating the loss-of-control related to pilot-induced oscillations.
- (3)
- In addition, further investigation of this study is needed. First of all, the investigations of dynamic roll control envelope cues are expected to study the evaluation and mitigation of adverse aircraft-pilot couplings in the roll-axis. Secondly, more experienced human pilots are expected to be introduced into the verification of the human pilot modeling and flight envelope cue design.
Author Contributions
Conceptualization, S.X. and W.T.; methodology, S.X.; software, S.X.; validation, Y.W. and L.S.; formal analysis, Y.W.; investigation, L.S.; resources, L.S.; data curation, Y.W.; writing—original draft preparation, S.X. and W.T.; writing—review and editing, S.X. and W.T.; visualization, S.X.; supervision, W.T. and L.S.; project administration, W.T. and L.S.; funding acquisition, S.X. and W.T. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the China Postdoctoral Science Foundation (No. 2021M690288) and the Aeronautical Science Foundation of China (No. 20185702003).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Squalli, J. Mutual forbearance, the representativeness heuristic and airline safety. Transp. Res. Part F Traffic Psychol. Behav. 2010, 13, 143–152. [Google Scholar] [CrossRef]
- Smaili, M.H.; Breeman, J.; Lombaerts, T.J.J.; Mulder, J.A.; Chu, Q.P.; Stroosma, O. Intelligent flight control systems evaluation for loss-of-control recovery and prevention. J. Guid. Control Dyn. 2017, 40, 890–904. [Google Scholar] [CrossRef]
- Pavel, M.D.; Masarati, P.; Gennaretti, M.; Jump, M.; Zaichik, L.; Dang-Vu, B.; Lu, L.; Yilmaz, D.; Quaranta, G.; Ionita, A.; et al. Practices to identify and preclude adverse Aircraft-and-Rotorcraft-Pilot Couplings–A design perspective. Prog. Aerosp. Sci. 2015, 76, 55–89. [Google Scholar] [CrossRef]
- Pavel, M.D.; Jump, M.; Dang-Vu, B.; Masarati, P.; Gennaretti, M.; Ionita, A.; Zaichik, L.; Smaili, H.; Quaranta, G.; Yilmaz, D.; et al. Adverse rotorcraft pilot couplings—Past, present and future challenges. Prog. Aerosp. Sci. 2013, 62, 1–51. [Google Scholar] [CrossRef]
- Ji, M.; Xu, Q.; Xu, S.; Du, Q.; Li, D. Proactive personality and situational judgment among civil flying cadets: The roles of risk perception and cognitive flexibility. Transp. Res. Part F Traffic Psychol. Behav. 2018, 59, 179–187. [Google Scholar] [CrossRef]
- Klyde, D.H.; McRuer, D. Smart-cue and smart-gain concepts to alleviate loss of control. J. Guid. Control Dyn. 2009, 32, 1409–1417. [Google Scholar] [CrossRef]
- Wilborn, J.; Foster, J. Defining commercial transport loss-of-control: A quantitative approach. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Providence, RI, USA, 16–19 August 2004; p. 4811. [Google Scholar]
- Lombaerts, T.; Schuet, S.; Acosta, D.; Kaneshige, J.; Shish, K.; Martin, L. Piloted simulator evaluation of safe flight envelope display indicators for loss of control avoidance. J. Guid. Control Dyn. 2017, 40, 948–963. [Google Scholar] [CrossRef]
- Garone, E.; Di Cairano, S.; Kolmanovsky, I. Reference and command governors for systems with constraints: A survey on theory and applications. Automatica 2017, 75, 306–328. [Google Scholar] [CrossRef]
- Zheng, W.; Li, Y.; Zhang, D.; Zhou, C.; Wu, P. Envelope protection for aircraft encountering upset condition based on dynamic envelope enlargement. Chin. J. Aeronaut. 2018, 31, 1461–1469. [Google Scholar] [CrossRef]
- Sun, D.; Jafarnejadsani, H.; Hovakimyan, N. Command Limiting for Aerial Vehicles with Rate Control Augmentation Systems. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1702–1712. [Google Scholar] [CrossRef]
- Yuan, G.; Li, Y. Determination of the flight dynamic envelope via stable manifold. Meas. Control 2019, 52, 244–251. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, Y.; Chu, Q.; de Visser, C.C. Database-Driven Safe Flight-Envelope Protection for Impaired Aircraft. J. Aerosp. Inf. Syst. 2021, 18, 14–25. [Google Scholar] [CrossRef]
- Norouzi, R.; Kosari, A.; Sabour, M.H. Investigating Impaired Aircraft’s Flight Envelope Variation Predictability Using Least-Squares Regression Analysis. J. Aerosp. Inf. Syst. 2020, 17, 3–23. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Q.; Dong, C.; Gong, L. Closed-loop fault detection for full-envelope flight vehicle with measurement delays. Chin. J. Aeronaut. 2015, 28, 832–844. [Google Scholar] [CrossRef]
- Maciejowski, J.M.; Hartley, E.N.; Siaulys, K. A longitudinal flight control law to accommodate sensor loss in the reconfigure benchmark. Annu. Rev. Control 2016, 42, 212–223. [Google Scholar] [CrossRef][Green Version]
- Sun, D.; Hovakimyan, N.; Jafarnejadsani, H. Design of command limiting control law using exponential potential functions. J. Guid. Control Dyn. 2021, 44, 441–448. [Google Scholar] [CrossRef]
- Venkataraman, R.; Bauer, P.; Seiler, P.; Vanek, B. Comparison of fault detection and isolation methods for a small unmanned aircraft. Control Eng. Pract. 2019, 84, 365–376. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y. Fuzzy adaptive tracking control within the full envelope for an unmanned aerial vehicle. Chin. J. Aeronaut. 2014, 27, 1273–1287. [Google Scholar] [CrossRef]
- Rohith, G. An investigation into aircraft loss of control and recovery solutions. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 4509–4522. [Google Scholar] [CrossRef]
- Lombaerts, T.; Looye, G.; Seefried, A.; Neves, M.; Bellmann, T. Proof of concept simulator demonstration of a physics based self-preserving flight envelope protection algorithm. Eng. Appl. Artif. Intell. 2018, 67, 368–380. [Google Scholar] [CrossRef]
- Hughes, J.S.; Jamie, S.; Trafimow, D.; Clayton, K. The automated cockpit: A comparison of attitudes towards human and automated pilots. Transp. Res. Part F Traffic Psychol. Behav. 2009, 12, 428–439. [Google Scholar] [CrossRef]
- Klyde, D.H.; Schulze, P.C.; Mello, R.S.F.D.; Mitchell, D.G.; Cameron, N.; Cunliffe, C.; White, M.D. Assessment of a Scalogram-Based Pilot-Induced Oscillation Metric with Flight-Test and Simulation Data. J. Guid. Control Dyn. 2020, 43, 2058–2072. [Google Scholar] [CrossRef]
- Koglbauer, I.; Reinhard, B. Ab initio pilot training for traffic separation and visual airport procedures in a naturalistic flight simulation environment. Transp. Res. Part F Traffic Psychol. Behav. 2018, 58, 1–10. [Google Scholar] [CrossRef]
- Van Baelen, D.; van Paassen, R.; Ellerbroek, J.; Abbink, D.; Mulder, M. Evaluating Stick Stiffness and Position Guidance for Feedback on Flight Envelope Protection. In Proceedings of the AIAA Scitech 2021 Forum, Online, 11–15 January 2021; p. 1013. [Google Scholar]
- Van Baelen, D.; van Paassen, M.M.; Ellerbroek, J.; Abbink, D.A.; Mulder, M. Flying by Feeling: Communicating Flight Envelope Protection through Haptic Feedback. Int. J. Hum.–Comput. Interact. 2021, 37, 655–665. [Google Scholar] [CrossRef]
- Benloucif, M.A.; Sentouh, C.; Floris, J.; Simon, P.; Popieul, J.C. Online adaptation of the level of haptic authority in a lane keeping system considering the driver’s state. Transp. Res. Part F Traffic Psychol. Behav. 2019, 61, 107–119. [Google Scholar] [CrossRef]
- Van Baelen, D.; Ellerbroek, J.; van Paassen, M.M.; Abbink, D.; Mulder, M. Using Asymmetric Vibrations for Feedback on Flight Envelope Protection. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 0409. [Google Scholar]
- Ackerman, K.A.; Talleur, D.A.; Carbonari, R.S.; Xargay, E.; Seefeldt, B.D.; Kirlik, A.; Hovakimyan, N.; Trujillo, A.C. Automation situation awareness display for a flight envelope protection system. J. Guid. Control Dyn. 2017, 40, 964–980. [Google Scholar] [CrossRef]
- Nguyen, T.; Lim, C.P.; Nguyen, N.D.; Gordon-Brown, L.; Nahavandi, S. A review of situation awareness assessment approaches in aviation environments. IEEE Syst. J. 2019, 13, 3590–3603. [Google Scholar] [CrossRef]
- Stepanyan, V.; Krishnakumar, K.; Dorais, G.; Reardon, S.; Barlow, J.; Lampton, A.; Hardy, G. Loss-of-control mitigation via predictive cuing. J. Guid. Control Dyn. 2017, 40, 831–846. [Google Scholar] [CrossRef]
- Xu, S.; Tan, W.; Qu, X. Modeling human pilot behavior for aircraft with a smart inceptor. IEEE Trans. Hum.-Mach. Syst. 2019, 49, 661–671. [Google Scholar] [CrossRef]
- Xu, S.; Tan, W.; Qu, X.; Zhang, C. Prediction of nonlinear pilot-induced oscillation using an intelligent human pilot model. Chin. J. Aeronaut. 2019, 32, 2592–2611. [Google Scholar] [CrossRef]
- Hess, R.A. A model for pilot control behavior in analyzing potential loss-of-control events. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2014, 228, 1845–1856. [Google Scholar] [CrossRef]
- Hess, R.A. Modeling pilot control behavior with sudden changes in vehicle dynamics. J. Aircr. 2009, 46, 1584–1592. [Google Scholar] [CrossRef]
- Xu, S.; Wu, Y. Modeling multi-loop intelligent pilot control behavior for aircraft-pilot couplings analysis. Aerosp. Sci. Technol. 2021, 112, 106651. [Google Scholar] [CrossRef]
- Entzinger, J.O.; Suzuki, S. Modeling of the visual approach to landing using neural networks and fuzzy supervisory control. Aerosp. Sci. Technol. 2010, 14, 118–125. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).