Abstract
Multi-UAV cooperative systems are highly regarded in the field of cooperative multi-target localization and tracking due to their advantages of wide coverage and multi-dimensional perception. However, due to the similarity of target visual characteristics and the limitation of UAV sensor resolution, it is difficult for UAVs to correctly distinguish targets that are visually similar to their associations. Incorrect correlation matching between targets will result in incorrect localization and tracking of multiple targets by multiple UAVs. In order to solve the association problem of targets with similar visual characteristics and reduce the localization and tracking errors caused by target association errors, based on the relative positions of the targets, the paper proposes a globally consistent target association algorithm for multiple UAV vision sensors based on triangular topological sequences. In contrast to Siamese neural networks and trajectory correlation, the relative position relationship between targets is used to distinguish and correlate targets with similar visual features and trajectories. The sequence of neighboring triangles of targets is constructed using the relative position relationship, and the feature is a specific triangular network. Moreover, a method for calculating topological sequence similarity with similar transformation invariance is proposed, as well as a two-step optimal association method that considers global objective association consistency. The results of flight experiments indicate that the algorithm achieves an association accuracy of 84.63%, and that two-step association is 12.83% more accurate than single-step association. Through this work, the multi-target association problem with similar or even identical visual characteristics can be solved in the task of cooperative surveillance and tracking of suspicious vehicles on the ground by multiple UAVs.
1. Introduction
Multi-UAV cooperative technology has advanced rapidly in recent years. UAVs have been widely used in the fields of surveillance [1], reconnaissance [2], tracking and positioning [3,4,5,6,7] due to their superior remote perception capabilities. In the multi-target localization problem, the triangulation method [8] is a frequently used method, which first matches the line of sight of the UAV platform pointing at the target [9]. When the view axis is incorrectly matched, it inevitably leads to incorrect positioning results. In real application scenarios, the limitations of high UAV flight altitude and low sensor resolution add the difficulties to target detection and classification. In particular, targets with relatively similar visual features cannot be distinguished and classified by conventional vision-based detection algorithms. These reasons can lead to a large number of incorrect associations, which can produce incorrect targeting results [10,11]. Due to the importance of multi-target correlation problem in the field of localization and tracking, the multi-target association problem has become a key problem to be solved in the field of cooperative multi-UAV detection [12,13]. The main objective of this work is to solve the association problem of targets with similar visual features, and to propose an association method that does not use the visual features of the targets but only the relative position relationship between the targets to improve the accuracy of association of such targets.
Three primary methods can be used to solve the target association problem in UAV sensors: image, trajectory, and relative position [14]. The image-based methods require clear images of the target and a variety of image features [15]. Since UAVs are so maneuverable, the difficulty of extracting target trajectories is also significantly increased [16]. To distinguish and associate targets, relative position-based methods rely heavily on the topological and geometric relationships between them. This method does not require a high-resolution image and does not make use of other data from the UAV [17]. In this paper, we propose a method for constructing a specific topological network using the relative position relationship between targets, which is inspired by topological association methods used in the field of radar detection technology [18]. As illustrated in Figure 1, the method distinguishes and associates the targets based on their adjacent triangular topological sequences. This method does not require the extraction of target image and trajectory features and does not make use of the background of the images or the UAV’s attitude information.
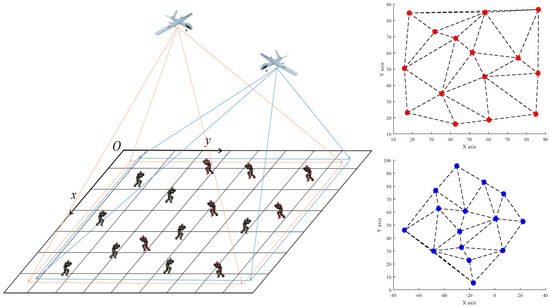
Figure 1.
A schematic diagram of multi-UAV target association based on a triangular topological sequence.
Considering the issues raised in this paper and the shortcomings of existing multi-target association algorithms, this paper proposes a globally consistent two-step multi-target association algorithm that solves the multi-sensor multi-target association problem solely using the relative position features of multiple targets. First, this paper triangulates all targets and determines their triangular topological characteristics based on their connectivity relationships in the triangular network. Second, to avoid the dependence of features on the coordinate system, this paper calculates the similarity of two triangles using the difference in triangle angles. Meanwhile, the feature similarity with similar transformation invariance is determined by calculating the weighted mean of all neighboring triangles’ similarity. Finally, considering the global goal association’s consistency, a two-step completion association is proposed. The partial correlation results from the first step are used to solve the transformation relationship between the two sensor coordinate systems. After eliminating the incorrect association in the first step, the transformation matrix is used to investigate possible associations in the unassociated results. The two-step association method not only improves the algorithm’s correct association rate, but also enables it to perform better when some targets are not detected. These benefits are confirmed in simulation experiments.
The method’s primary contribution to innovation is that it augments the geometric topology-based association method with the following three enhancements. The first is consistency of global association, which is achieved by combining knowledge about multi-view geometry, which has the same mapping relationship for two photos taken from the same viewpoint, and which is considered in this paper. The second is to rely on specific rules rather than empirical thresholds for the construction of topological features. Ref. [18] used thresholds to determine which neighbors should be included in the constructed features, which is not an easy task in practice. By comparison, the structure formed through triangular dissection is more scientific. Thirdly, because the method for calculating feature similarity is similar in terms of transformation invariance, i.e., the same structure remains unchanged after rotation, translation, and scaling, the similarity values obtained using this method are identical. The algorithm’s primary contributions are as follows:
- (1)
- Rather than relying on image and trajectory features, it distinguishes and associates identical targets within a single context using their relative positions.
- (2)
- The method for calculating similarity exhibits similar transformation invariance. The method used to generate feature sequences is a non-empirical one.
- (3)
- The association process considers the target coordinates’ global consistency.
- (4)
- The algorithms are applicable to vision and vision sensors, as well as vision and infrared sensors, as well as infrared and infrared sensors.
The remainder of this paper is organized as follows: Section 2 discusses some recent research on multi-objective association algorithms. Section 3 describes the multi-objective association algorithm proposed in this paper, which entails the construction of target detection, triangular topological networks, the calculation of the target similarity matrix using neighboring triangular sequences, and a two-step optimal association algorithm based on global consistency. Section 4 conducts simulation experiments to determine the algorithm’s association accuracy under various conditions and comparison tests to determine the algorithm’s association accuracy in comparison to various other algorithms. Section 5 summarizes the entire paper and provides an outlook on future work.
2. Related Works
Three primary algorithms for multi-objective association are described in the published work [14]. They include methods for associating trajectory similarity [16,19], image matching algorithms based on deep neural networks [20,21], and methods for associating reference topology [18]. Additionally, some researchers have attempted to process target trajectories using neural networks [22]. Trajectory-based association, in general, necessitates fixed sensor positions and high-quality extracted trajectories. Correlating images based on their clarity and feature density is difficult for drones flying at high altitudes to accomplish.
The methods for trajectory correlation primarily analyze data using probabilistic and statistically relevant methods. The Nearest Neighbor method was proposed by Singer and Kanyuch [23]. Then, Singer et al. [24] advanced the idea of trajectory association by introducing the concept of hypothesis testing and establishing a weighted trajectory association algorithm under the assumption that the estimation errors are mutually independent. On this basis, Bar-Shalom [25] modified this algorithm’s distance metric to remove the requirement that the estimation errors of trajectory sequences be independent of one another and proposed a modified weighted method. Chang et al. [26] introduced the concept of allocation to operations research to extend the weighted method and proposed the classical allocation method for solving the trajectory association problem. The outcomes of trajectory association-based methods are significant and widely applied in the field of visual perception [14]. However, extracting high-quality target trajectories from maneuverable UAV image sensors is challenging.
In terms of Siamese neural network research, Ref. [27] pioneered the concept of a Siamese network based on dual target–environment data streams. Ref. [15] proposed a Siamese network architecture with dual data streams capable of extracting spatial and temporal information from RGB frames and optical flow vectors, respectively, to match pedestrians to distinct data frames. Ref. [28] achieved vehicle association between cameras at various locations by utilizing a license plate-body dual data stream Siamese neural network. Ref. [29] proposed a novel relative geometry-aware Siamese neural network that improves the performance of deep learning-based methods by exploiting the relative geometric constraints between images explicitly. To address the issue of target association robustness, Ref. [30] added a SE-block and a temporal attention mechanism to the framework of the Siamese neural network to enhance the network’s discriminative ability and the tracker’s recognition ability. The preceding conclusions are predicated on the assumption that the sensor images are of high quality and that the image features of the targets are distinguishable.
The reference topology-based approach solves the multi-target association problem in terms of different trajectories and images, without relying on any image features and without requiring a consistent sensor coordinate system [18,31]. Yue et al. [32] pioneered the reference topology association method. On this basis, Ref. [33] switched to a topological sequence rather than a single reference topology. Zhang et al. [34] correlated topological sequences using the gray correlation method. Instead of a sequence, Wu et al. [35] attempted to construct a more complex target topological matrix. Hao et al. [36] used triangles as the basic topology instead of all neighboring targets in cases such as dense multi-target and formation targets. Hasan et al. [37] used the reference topology to solve the asynchronous trajectory association problem. In other words, Li et al. [38] proposed a topological sequence association method based on a one-dimensional position distribution of multiple targets for determining the characteristics of visual sensors in air-ground systems and applied the method to air-ground systems for the first time. You et al. [39] recovered lost objects using temporal topological constraints based on the continuity and consistency of the multi-target topology in continuous frames. Ref. [17] groups targets according to their positions and velocities before applying a topology-based group target tracking algorithm to the tracking problem of dense target groups. Ref. [35] proposes a method for target association based on the target mutual support topology model, in which the mutual support matrix is defined, and the correct target relationship is determined using the optimal method with constraints. While research on reference topology is expanding, the following issues persist with the current results: (1) since topological features cannot adapt to coordinate system transformations, the reference target must be determined empirically; (2) existing work is primarily concerned with local topology and neglects global consistency; (3) in practice, the correlation error rate is significantly less than the simulation effect.
3. Materials and Methods
The algorithm described in this paper is divided into three sections: (1) detecting the target and constructing a triangular network; (2) computing topological similarity; and (3) a two-step optimal association algorithm. The algorithm’s main flow is depicted in Figure 2, and this paper will use TTS as an abbreviation for proposed association algorithm based on Triangular Topological Sequence. The targets are first detected using vision images from and , and then their pixel coordinates and are extracted. Their pixel coordinates and are used to construct a specific triangular network, and their target’s topological triangular sequence and are extracted. Then, using a similarity calculation method based on the triangle angle, the similarity of the target triangular topological sequence is calculated, and the similarity matrix , which contains the degree of similarity between all combinations of m targets in and n targets in , is obtained. Finally, in two steps, the target association is completed. The first step processes the similarity matrix and extracts the global consistency matrix to obtain partial target association results R. The second step employs the global consistency matrix to eliminate incorrect associations discovered in the first step’s association results R and to identify possible new associations with the remaining unassociated targets under the new law. is the result obtained by eliminating the wrong association in R.
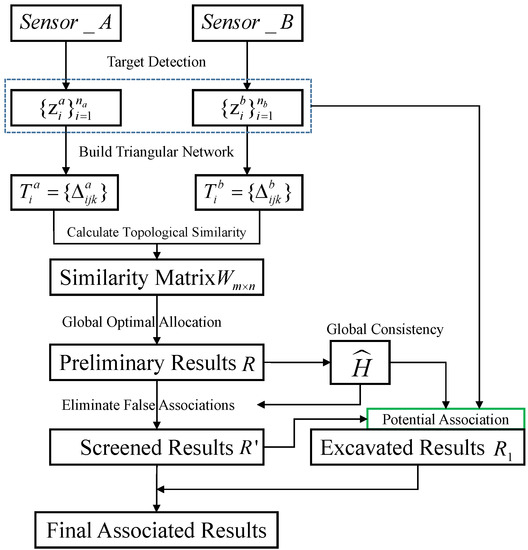
Figure 2.
The overall flow chart of multi-objective two-step association algorithm based on triangular topological sequence.
3.1. Constructing Triangular Topological Sequences
The input raw data are the visual image of the UAV, and an efficient target detection algorithm is needed to extract the relative position relationship of multiple targets. Many object detection algorithms are introduced in survey [40,41,42,43]. Considering the detection speed and accuracy of the algorithms mentioned in the above survey, this paper chooses yolov5 [44] as the target detection algorithm. Figure 3 illustrates the results of two UAV vision sensors’ multi-target detection. The results are parsed to extract the set of target points, and a triangular topology network is constructed.
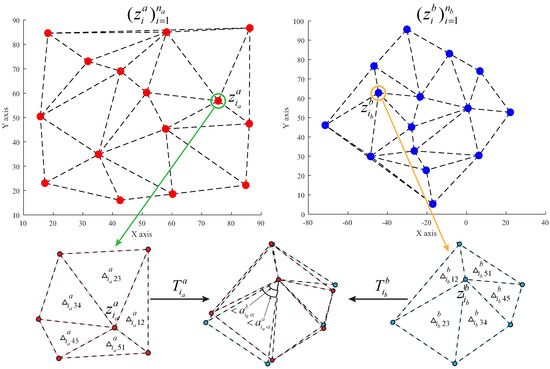
Figure 3.
Construction of triangular topological features for a multi-target point set and calculation of topological similarity.
In this paper, the Cartesian coordinate systems and are established with reference to the pixel coordinate system of the vision sensor. Meanwhile, the real coordinates of target i in the coordinate system at time t can be expressed as . Due to the image resolution and the detection algorithm, the target pixel coordinates typically carry an observation error . Thus, the target coordinates of the detected target in sensor s in the coordinate system with observation error can be expressed as:
where is the observation error of the target i pixel coordinates in sensor s. Let be the set of pixel coordinates of all targets in sensor s at moment t, where denotes the total number of targets detected in sensor s. According to [45], pictures taken at various angles for the same scene have a unique perspective transformation relationship, i.e.,
where is the optimal estimate transformation matrix from to .
The following topological features are constructed for . Ref. [18] used empirical thresholds to determine neighboring nodes based on their distance, which can be used only within the same coordinate system. This paper employs a method of feature construction that is not dependent on empirical thresholds or coordinate systems. First, Delaunay triangulation [46] is used to create a unique triangular network from . Due to the nature of Delaunay triangulation, which is closest, unique, and regional, each point in the constructed triangular network forms a triangle with only the nearest finite point. When a point is removed from the mesh, it affects only the triangles associated with that point. Due to the uniqueness of the result of Delaunay triangulation and the fact that the similarity transformation does not alter the ratio of angles and side lengths of any triangle in the network, the similarity transformation has no effect on the connectivity of points in the triangular network.
In the constructed network, let L be the set of all connected lines in the network and denote the line connecting and . For target i, all triangles adjacent to constitute the triangular topological features of target i:
where denotes the total number of reference points connected to target i in sensor s, and denotes the triangle composed of , , .
3.2. Calculate the Similarity of the Triangular Topological Sequence
For the triangular topological sequence depicted in Figure 3, we introduce a method for calculating the similarity between a single triangle and the triangular topological sequence . To calculate triangle similarity, Ref. [36] devised a method based on triangle side lengths, but this method is inapplicable when the scales of the two coordinate systems are different. To address this issue, this paper develops a more discriminating similarity calculation function based on the difference in triangle angles. A function for calculating triangle similarity that has a high degree of differentiation should exhibit the following characteristics: (1) The similarity value decreases monotonically as the difference between the two triangles increases. (2) The smaller the triangle difference, the larger the change in similarity caused by the unit change in the triangle. That is, a concave function that decreases monotonically. Let the three angles of be , , and . Then, the difference between and can be expressed as . Thus, the similarity of the xth triangle of and is calculated as:
where adjusts the range of values of . In this paper, we take . is the similarity association matrix of m targets in sensor a and n targets in sensor b, where is the element of the th row and th column of , the similarity between and :
where is the of the xth triangle in . This method can be described as taking a weighted average of the similarity of the neighboring triangles. The angle occupied by the neighboring triangle around the point is used as the weight of .
3.3. Two-Step Global Constraint-Based Association Algorithm
This section discusses the two-step association algorithm based on the similarity association matrix and the consistency of global association, where the consistency of global association has not been considered in previous works. The global association consistency entails that all association targets in and satisfy Equation (2).
In the first step of association, the similarity matrix that contains local feature information is processed, and the association result of the first step is derived. The principle of global optimal allocation is as follows: (1) only one element from each row of the matrix is chosen; (2) only one element is chosen from each column of the matrix; (3) the greatest possible sum of all selected elements’ values. In the first step, all selected pairs in form the global optimal association result R in the first step.
As shown in Figure 4, in practice, the triangular topological sequence of some targets produces local variations due to partial target occlusion and the influence of observation errors . For the case of multi-target formation, the targets have a similar relative position relationship with each other, so the triangular topological features of the targets are similar, and the similarity difference is small. These factors are not conducive to distinguishing the triangular topological sequence, so that the result of the global optimal assignment principle contains some wrong matches. Among the total association results, the wrong match has the different from the other associations. For the case where most of the correct association results contain a few incorrect associations, the Ransac algorithm can be used to compute the transformation matrix based on R and eliminate the incorrect associations. The result that contains only the correct association after algorithm processing is denoted as .
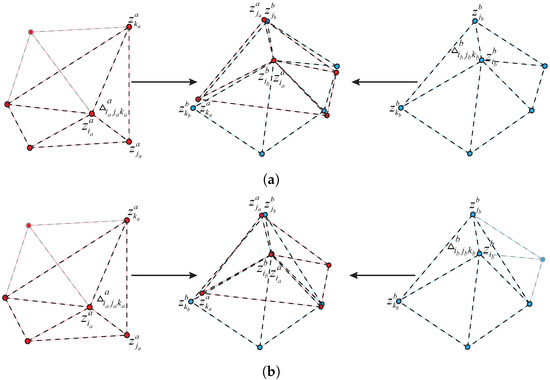
Figure 4.
(a) Topological sequences when a few targets are missing; (b) topological sequence when most targets are missing.
The second association step is to find potential associations among unassociated target points using and . indicates that and are accurately associated. Considering the effect of observation error , for ,, if is the closest point in at distance and satisfies the following formula:
and are determined as the new correct association, when , denotes the similarity of and .
In the next experiment part, this paper uses association precision and accuracy as metrics for evaluating the experimental results:
where is the number of correct associations predicted as correct associations, is the number of incorrect associations predicted as incorrect associations, is the number of incorrect associations predicted as associations, and is the number of correct associations predicted as incorrect associations.
4. Results
This section simulates and tests the proposed algorithm, with the simulation test consisting of three major sections. The first section contains a series of tests to determine the correlation’s precision under various experimental conditions. Several experimental conditions were established in the following manner: (1) the sensor coordinate systems have a similar transformation relationship; (2) specific targets are obscured or missed; (3) the experimental area contains a variable number of targets; and (4) errors in observation. The second section compares the correlation accuracy of the proposed TTS, the neighboring reference topological feature association algorithm (RTF) [18], and the triangle topological feature association algorithm (TTF) [36,47] under the four experimental conditions mentioned previously. The third part compares the proposed TTS to the RTF [18], TTF [36,47], and the Siamese neural network method [48,49] for the association accuracy and precision in a physical flight test.
Figure 5 shows the experiments of target detection using yolov5 [44] for UAV vision images in this paper, and the algorithm is fast and accurate for UAV platforms. However, the algorithm also cannot achieve the detection of all targets at all times. Figure 5a shows vehicles moving at high speed on the road, and Figure 5b shows a dense and neatly distributed vehicle in a square, where there are two undetected targets.

Figure 5.
Two scenarios for testing the target detection algorithm, (a) is high-speed moving vehicles, and (b) is dense and neatly distributed targets.
4.1. Testing on the Proposed Algorithm
The first section examines the effect of various experimental conditions on association accuracy and compares the accuracy of single-step and two-step association in this algorithm. As illustrated in Figure 1, multiple targets are randomly distributed throughout the scene and are monitored by two UAV sensors. We set a square area with a shape of 100 m × 100 m, and then fly drones equipped with visual sensors over it. Considering the effect of the number of targets on the association algorithm, we varied the number of targets in the experimental region at intervals of ten in the range of 10 to 100. We created a set of basic tests with a total of 12 combinations for each target quantity setup, which included three different rotation angles of 30°, 75°, and 135°, two scale transformations of 0.5× and 50×, and two translational transformations of 10 m and 50 m.
Figure 6a shows the results of the experiments on the algorithm’s similar invariance. The experiments were repeated several times with the same experimental setup, and 10% of the targets were not detected simultaneously by both sensors in each experiment due to occlusion or other factors. The two-step association algorithm’s experimental results were analyzed statistically (shown in Table 1), and the mean values of association precision were 98.40%, 98.39%, and 98.34% for three different rotation angles, 98.44% and 98.28% for two scale transformations, and 98.37% and 98.39% for two translational transformation experiments. The mean value of association precision for all results was 98.38%, with 58.90% of experiments achieving 100% correct association. The data indicate that the association precision under different similar transformations is within the overall mean (shown in Figure 6c), indicating that the similar transformation relationship between coordinates has no significant effect on the association precision and that the algorithm has similar transformation invariance. The effect of single-step and double-step association is depicted in Figure 6b, with single-step precision significantly lower than double-step precision. Single-step associations have an average precision of 63.3%, which is significantly less than that of two-step associations. Single-step association precision decreases as the number of targets increases and is greatest when the number of targets is small. The experimental results demonstrate that the association method proposed in this paper has comparable transformation invariance and that the two-step association significantly outperforms the single-step association.
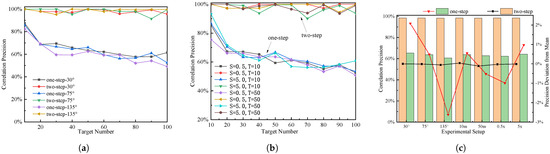
Figure 6.
(a) The effect of the number of targets in the region on the correlation precision at three rotation angles; (b) the effect of the number of targets in the experimental area on the correlation precision under different scale transformation and translational transformation conditions; (c) association precision histogram and standard deviation curve of the proposed TTS under various conditions.

Table 1.
Statistics of association precision under different similarity transformation experiments.
Figure 7 presents the experimental results of this paper for some target loss conditions. Target loss occurs when a target is not detected due to obstructions or the detection algorithm, most commonly certain randomly existing undetected targets and targets in a portion of the area obscured by obstacles. We repeated the 12 base experiments several times at 5% intervals, varying each of the 11 loss rates from 0% to 50%. The statistical data of the results of the two-step correlation experiment are depicted in Figure 7a. When the target is obscured within the local area, the experimental precision exceeds 98% and remains stable when the missing rate is less than 20%. When the missing rate exceeds 20%, the precision of the correlation decreases linearly. When the target is missed by 40%, the correlation precision falls below 30%. The experimental precision is greater than 98% for randomly distributed undetected targets and remains stable at a missing rate of 10% or less. When the rate of missing data exceeds 10%, the correlation precision decreases linearly. Correlation precision decreases to less than 30% at a target missing rate of 30%. In this case, a missing rate of less than 10% has little effect on the association algorithm’s precision, whereas the random presence of undetected targets has a greater effect on the algorithm’s precision when the missing rate exceeds 10%. In Figure 7a, the precision of the single-step association is significantly lower than the precision of the two-step association, and the two-step association has a significant improvement in association precision. The results of one experiment are depicted in Figure 7b, where the precision of two-step correlation is either extremely high or extremely low. To ensure that the algorithm maintains a higher correlation precision more frequently, the following analysis of this phenomenon is made: The critical step in the two-step association is to identify the global association consistency and estimate the value of . When the value of is estimated accurately, incorrect associations are eliminated, correct associations are increased, and association precision are improved. When the value of is estimated incorrectly, the correct association is reduced, and the incorrect association is increased. Analysis of the experimental data reveals that the two-step association algorithm has 88.10% probability of finding the correct when the single-step association precision is more than 30%.
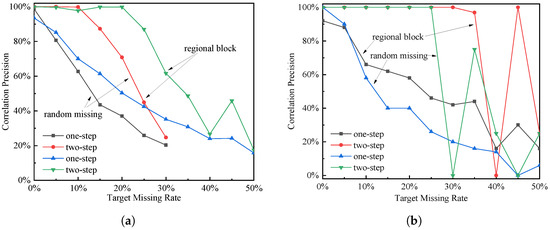
Figure 7.
(a) The effect of target missing rate of statistical results on correlation precision; (b) the effect of target missing rate on association precision in a specific experiment.
The effect of uniformly distributed observation error on the correlation precision is illustrated in Figure 8. In this paper, we set 31 values of in the range of 0 3 m at 0.1 m intervals and conduct 12 basic experiments used in Figure 6 under each value to study the trend of algorithm association precision with observation errors. Assuming that the size of the target is 1.5 m, the multiplier of the error relative to the target is used for the horizontal axis. Figure 8a depicts the effect of observation error on average correlation precision. When the observation error is less than 1.5 times, the correlation precision fluctuates steadily above 90% with no decreasing trend. When the observation error exceeds 1.5 times, the correlation precision rapidly decreases to approximately 70%, and the fluctuation increases. In comparison, the precision of the single-step correlation was always around 60%, indicating a slowing trend with insignificant fluctuations. Obviously, the two-step correlation algorithm has advantages. Figure 8b illustrates the effect of observation error on the correlation’s precision in one experiment. According to the data in the figure, the two-step association algorithm maintains an association precision close to 100% for observation errors less than 1.5 times, whereas the single-step association algorithm maintains an association precision of around 60%, which is always less than the two-step association. When observation errors exceed 1.5 times, the two-step correlation method begins to exhibit increased fluctuation and the correlation precision decreases further. The experimental results indicate that, while smaller observation errors have a smaller effect on the correlation method proposed in this paper, observation errors greater than 1.5 times have a greater effect on correlation precision, which may be due to observation errors causing estimation errors.
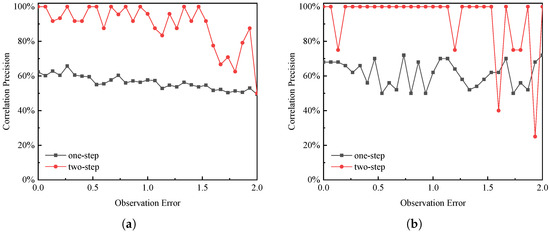
Figure 8.
(a) The effect of observation error on correlation precision; (b) the effect of observation error on correlation precision in a specific experiment.
4.2. Simulation Comparison Experiments
The second section compares TTS’s association accuracy to proposed TTS, RTF, and TTF under the same experimental conditions. We conducted another series of experiments on three different dimensions: (1) certain components are not detected; (2) the error associated with the observation is encoded in the coordinates; (3) the coordinate system of the sensor is scaled differently. The association accuracy variation curves for the three algorithms in different scale sensor coordinate systems are depicted in Figure 9a. Because all three algorithms compared in this paper are rotation and translation invariant, this experiment considers only cases with different scales. According to the experimental results, the correlation accuracy of the current algorithm remains stable at around 98% across a range of scales, whereas the accuracy of the other two algorithms decreases significantly as the coordinate system scales change. This demonstrates that the present algorithm possesses similar transformation invariance to that of other algorithms. Figure 9b illustrates the performance of the three algorithms in the presence of missing targets due to occlusion by a local obstacle. The experiments demonstrate that, as the occluded area increases, the association accuracy decreases. However, the algorithm described in this paper always maintains a high association accuracy, which is on average 19.88% and 27.46% higher than the association accuracy of the other two algorithms. The trend of association accuracy for the three algorithms with varying observation errors is depicted in Figure 9c. The results indicate that, when the observation error is less than 0.73 times of target size, the algorithm in this paper maintains the highest association accuracy. When the observation error is greater than 0.73 times, the results of TTS are lower than the results of TTF. Within the range of observation error distributions of 0 to 2 times, this algorithm’s association accuracy is always greater than that of RTF, by an average of 5.2%. When compared to the data in Figure 9, the TTS algorithm outperforms the other algorithms in all three experimental conditions, and its overall performance is optimal.
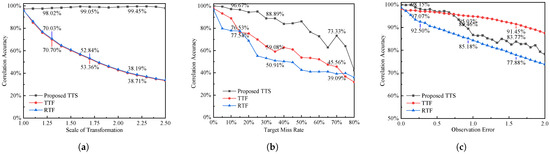
Figure 9.
The proposed TTS comparison experiments with other algorithms, (a) is the variation curve of the effect on association accuracy at different scale transformations (b) the variation curve of the effect of target occlusion rate on association accuracy (c) is the variation curve of the effect of different observation errors on association accuracy.
4.3. Physical Comparison Experiments
The third section compares the proposed TTS to the RTF [18], TTF [36,47], and the Siamese neural network method [48,49] for the association accuracy and precision in the scenario shown in Figure 10.

Figure 10.
The results of target detection and triangular network construction in three flight test scenarios. (a) is a scenario with a large number of randomly distributed moving targets. (b) is a scenario with a large number of neatly arranged stationary targets. (c) is a scene with a small number of neatly arranged stationary targets.
Figure 10a depicts the algorithm described in this article being tested on a road with heavy traffic and vehicles traveling at high speeds. Two DJI drones are used in this article to capture video above the road. The two drones flew continuously between 80 m and 100 m in altitude, following a predetermined trajectory to observe the vehicles on the road from various angles. The targets are associated using the proposed TTS, RTF [18], TTF [36,47] and Siamese neural networks [49], respectively, and the association precision and accuracy are analyzed (shown in Figure 11). To develop the Siamese neural network’s recognition model, we collected training data on the opposite road.
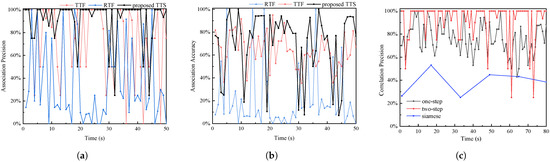
Figure 11.
(a,b) is the comparison of the proposed TTS with TTF and RTF in the scene shown in Figure 10a. (c) is precision curves of the association between the proposed TTS and Siamese neural networks in real flight experiments.
The proposed TTF, RTF, and TTF are compared in Figure 10a scenario in Figure 11a,b, with experimental data for 50 s shown in Table 2. The RTF algorithm must implement the specified threshold value, and Table 3 contains information about the threshold value and association results obtained during the experiments. The proposed two-step TTF achieves an association accuracy of 84.63%, while RTF and TTF achieve only 63.51% and 68.63%, respectively. The proposed two-step TTF achieves a correlation accuracy of 67.87%, while the RTF and TTF achieve only 20.31% and 61.81%, respectively. The proposed TTS’s single-step association accuracy and accuracy are 71.80% and 79.99%, respectively, which are higher than the RTF and TTF algorithms’ corresponding data. The experimental data demonstrate that the proposed algorithm outperforms comparable algorithms implemented in this paper in terms of association accuracy and association accuracy, with a significant improvement in association accuracy for the second-step association. The curves in Figure 11a,b demonstrate how significantly the association results of all three algorithms vary in actual flight experiments. While the algorithm performs better most of the time, there are times when it performs poorly.

Table 2.
Statistical data of experimental results of proposed TTF, RTF, and TTF comparative experiments.

Table 3.
Correlation result for different thresholds in the RTF method.
The algorithm’s association results are depicted in Figure 10 and Table 4. The precision of two-step association is generally greater than that of single-step association, and the Siamese neural network does not perform as well in practical tests as the algorithm described in this paper. The mean precision of two-step associations is 84.63%, single-step associations are 71.80%, and Siamese neural network associations are 38.25%. The algorithm described in this paper outperforms the Siamese neural network-based approach in terms of association precision. In terms of association accuracy, the algorithm in this paper achieves an average of 67.87%, while the Siamese neural network achieves an average of 38.25%, indicating that the algorithm in this paper outperforms the Siamese neural network. They demonstrate that the indicators produced by this algorithm are superior to those produced by the Siamese neural network, and that the two-step association results produced by this algorithm are superior to the single-step association results.

Table 4.
Statistical table of flight test results of proposed TTS and Siamese neural network in two typical scenarios.
Table 5 summarizes the major advantages and disadvantages of the four algorithms used in this paper based on the analysis of the aforementioned experimental results. Figure 6 and Figure 9a demonstrate that TTS transforms similarly to RTF and TTF without distortion. As illustrated in Table 3, RTF must rely on empirical thresholds, whereas TTS does not. To demonstrate the validity of global consistency, the improved correctness of two-step correlation is obtained. In comparison to Siamese neural networks, TTS, RTF, and TTF do not require consideration of the target’s image features to complete the association. Among them, this paper considers non-empiricality, similar transformation invariance, and global consistency for the first time, which is a novel contribution to the field.

Table 5.
Comparison of advantages and disadvantages of proposed TTS, RTF, and TTF and Siamese neural networks.
Additionally, the algorithm described in this paper has some limitations. In the scenario depicted in Figure 10b, where targets are densely aligned within the scene, the topological features constructed by the peripheral targets are more extreme and unsuitable for association, and small changes in the features can result in large changes. Indeed, this paper’s algorithm is applicable to a more decentralized target. The Siamese neural network outperforms the algorithm in this paper in terms of association for the two columns of neatly aligned targets shown in Figure 10c. In addition, this algorithm is influenced by global consistency matrix , in which, when solved incorrectly, the association effect of this method significantly decreases.
The preceding experiments are divided into three sections: the algorithm’s association precision is evaluated in simulation experiments under a variety of experimental conditions, and the association accuracy of multiple topological association methods is compared. Additionally, the results of this algorithm’s association with Siamese neural networks are compared under flight test conditions. Experiments demonstrate that the algorithm described in this article has a high correlation accuracy and correctness, similar transformation invariance, and performs well when the observation contains an error, and the target is true. The present algorithm associates significantly better than the Siamese neural network in the flight test and performs admirably in practical applications. Simultaneously, the experiment revealed several flaws in the algorithm described in this paper. First, when the global consistency matrix is solved incorrectly, the algorithm’s association effect is weakened. Second, due to the law of triangular dissection’s limitation, the topological characteristics of the target construction with neatly aligned boundaries are more extreme and unsuitable for target association.
5. Conclusions
The paper proposes a new multi-target association algorithm based on triangular topology sequences that utilizes global consistency and a two-step process to improve association accuracy. The algorithm constructs the feature sequence using a specific triangular network and exhibits similar transformation invariance. The experimental results demonstrate that the proposed multi-target association method achieves a high level of accuracy and precision, and that the two-step association method improves the association effect significantly. Under three experimental conditions, this algorithm had the best association effect when compared to other algorithms. However, the algorithm described in this paper has some limitations. When targets are neatly aligned, association results for targets on the periphery are poor. The results of the association are strongly influenced by the global consistency matrix, and any error in solving the consistency matrix results in a significant reduction in the association’s accuracy.
The work presented in this paper can be applied to problems involving correlation in UAV cluster reconnaissance of multiple ground targets, particularly when the visual characteristics of the targets are very similar. For instance, drones are used in conjunction to monitor many suspicious vehicles that share similar characteristics. The following will be improved in future work: We will consider the category information associated with the targets, and we will construct topological networks containing various types of targets and associate them using topological sequences containing various types of targets.
Author Contributions
X.L. was the main author of the work in this paper. X.L. conceived the methodology of this paper, designed the experiments, collected and analyzed the data, and wrote the paper; L.W. was responsible for directing the writing of the paper and the design of the experiments; Y.N. was responsible for managing the project and providing financial support; A.M. was responsible for assisting in the completion of the experiments. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant No. 61876187.
Acknowledgments
Thanks to the UAV Teaching and Research Department, Institute of Unmanned Systems, College of Intelligent Science, National University of Defense Technology for providing the support of the experimental platform.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yeom, S.; Nam, D.H. Moving Vehicle Tracking with a Moving Drone Based on Track Association. Appl. Sci. 2021, 11, 4046. [Google Scholar] [CrossRef]
- Zheng, Y.J.; Du, Y.C.; Ling, H.F.; Sheng, W.G.; Chen, S.Y. Evolutionary Collaborative Human-UAV Search for Escaped Criminals. IEEE Trans. Evol. Comput. 2019, 24, 217–231. [Google Scholar] [CrossRef]
- Wang, J.; Han, L.; Dong, X. Distributed sliding mode control for time-varying formation tracking of multi-UAV system with a dynamic leader. Aerosp. Sci. Technol. 2021, 111, 106549. [Google Scholar] [CrossRef]
- Bayerlein, H.; Theile, M.; Caccamo, M. Multi-UAV path planning for wireless data harvesting with deep reinforcement learning. IEEE Open J. Commun. Soc. 2021, 2, 1171–1187. [Google Scholar] [CrossRef]
- Ali, Z.A.; Zhangang, H. Multi-unmanned aerial vehicle swarm formation control using hybrid strategy. Trans. Inst. Meas. Control 2021, 43, 2689–2701. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, X.; Cui, J.; Meng, W. Multi-UAV Area Coverage Based on Relative Localization: Algorithms and Optimal UAV Placement. Sensors 2021, 21, 2400. [Google Scholar] [CrossRef]
- Wang, X.; Yang, L.T.; Meng, D.; Dong, M.; Ota, K.; Wang, H. Multi-UAV Cooperative Localization for Marine Targets Based on Weighted Subspace Fitting in SAGIN Environment. IEEE Internet Things J. 2021, 9, 5708–5718. [Google Scholar] [CrossRef]
- Bai, G.B.; Liu, J.H.; Song, Y.M.; Zuo, Y.J. Two-UAV intersection localization system based on the airborne optoelectronic platform. Sensors 2017, 17, 98. [Google Scholar] [CrossRef] [Green Version]
- Hinas, A.; Roberts, J.M.; Gonzalez, F. Vision-Based Target Finding and Inspection of a Ground Target Using a Multirotor UAV System. Sensors 2017, 17, 2929. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, B.; Wu, L.; Niu, Y. End-to-end vision-based cooperative target geo-localization for multiple micro UAVs. J. Intell. Robot. Syst. 2022. accepted. [Google Scholar]
- Sheng, H.; Zhang, Y.; Chen, J.; Xiong, Z.; Zhang, J. Heterogeneous Association Graph Fusion for Target Association in Multiple Object Tracking. IEEE Trans. Circuits Syst. Video Technol. 2018, 29, 3269–3280. [Google Scholar] [CrossRef]
- Lee, M.H.; Yeom, S. Multiple target detection and tracking on urban roads with a drone. J. Intell. Fuzzy Syst. 2018, 35, 6071–6078. [Google Scholar] [CrossRef]
- Shekh, S.; Auton, J.C.; Wiggins, M.W. The Effects of Cue Utilization and Target-Related Information on Target Detection during a Simulated Drone Search and Rescue Task. Proc. Hum. Factors Ergon. Soc. Annu. Meet. 2018, 62, 227–231. [Google Scholar] [CrossRef]
- Rakai, L.; Song, H.; Sun, S.; Zhang, W.; Yang, Y. Data association in multiple object tracking: A survey of recent techniques. Expert Syst. Appl. 2022, 192, 116300. [Google Scholar] [CrossRef]
- Chung, D.; Tahboub, K.; Delp, E.J. A Two Stream Siamese Convolutional Neural Network for Person Re-identification. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 1992–2000. [Google Scholar]
- Angle, R.B.; Streit, R.L.; Efe, M. Multiple Target Tracking With Unresolved Measurements. IEEE Signal Process. Lett. 2021, 28, 319–323. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, M.; Liu, X.; Wu, T. A group target tracking algorithm based on topology. J. Phys. Conf. Ser. 2020, 1544, 012025. [Google Scholar] [CrossRef]
- Tian, W.; Wang, Y.; Shan, X.; Yang, J. Track-to-Track Association for Biased Data Based on the Reference Topology Feature. IEEE Signal Process. Lett. 2014, 21, 449–453. [Google Scholar] [CrossRef]
- Tokta, A.; Hocaoglu, A.K. Sensor Bias Estimation for Track-to-Track Association. IEEE Signal Process. Lett. 2019, 26, 1426–1430. [Google Scholar] [CrossRef]
- An, N.; Qi Yan, W. Multitarget Tracking Using Siamese Neural Networks. ACM Trans. Multimid. Comput. Commun. Appl. 2021, 17, 75. [Google Scholar] [CrossRef]
- Valmadre, J.; Bertinetto, L.; Henriques, J. End-to-end representation learning for correlation filter based tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2805–2813. [Google Scholar]
- Yoon, K.; Kim, D.; Yoon, Y.C. Data Association for Multi-Object Tracking via Deep Neural Networks. Sensors 2019, 19, 559. [Google Scholar] [CrossRef] [Green Version]
- Kanyuck, A.J.; Singer, R.A. Correlation of Multiple-Site Track Data. IEEE Trans. Aerosp. Electron. Syst. 1970, 180–187. [Google Scholar] [CrossRef]
- Singer, R.A.; Kanyuck, A.J. Computer control of multiple site track correlation. Automatica 1971, 7, 455–463. [Google Scholar] [CrossRef]
- Bar-Shalom, Y. On the track-to-track correlation problem. IEEE Trans. Autom. Control 1981, 26, 571–572. [Google Scholar] [CrossRef]
- Chang, C.; Youens, L. Measurement correlation for multiple sensor tracking in a dense target environment. IEEE Trans. Autom. Control 1982, 27, 1250–1252. [Google Scholar] [CrossRef]
- Zagoruyko, S.; Komodakis, N. Learning to compare image patches via convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 4353–4361. [Google Scholar]
- de Oliveira, I.O.; Fonseca, K.V.O.; Minetto, R.A. A Two-Stream Siamese Neural Network for Vehicle Re-Identification by Using Non-Overlapping Cameras. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 669–673. [Google Scholar]
- Li, Q.; Zhu, J.; Cao, R. Relative geometry-aware Siamese neural network for 6DOF camera relocalization. Neurocomputing 2021, 426, 134–146. [Google Scholar] [CrossRef]
- Pang, H.; Xuan, Q.; Xie, M.; Liu, C.; Li, Z. Research on Target Tracking Algorithm Based on Siamese Neural Network. Mob. Inf. Syst. 2021, 2021, 6645629. [Google Scholar] [CrossRef]
- Qi, L.; He, Y.; Dong, K.; Liu, J. Multi-radar anti-bias track association based on the reference topology feature. Iet Radar Sonar Navig. 2018, 12, 366–372. [Google Scholar] [CrossRef]
- Yue, S.; Yue, W.; Shu, W.; Xiu, S. Fuzzy Data Association based on Target Topology of Reference. J. Natl. Univ. Def. Technol. 2006, 28, 105–109. [Google Scholar]
- Ze, W.; Shu, R.; Xi, L. Topology Sequence Based Track Correlation Algorithm. Acta Aeronaut. Astronaut. Sin. 2009, 30, 1937–1942. [Google Scholar]
- Yu, Z.; Guo, W.; Cheng, G.; Lei, C. Gray Track Correlation Algorithm Based on Topology Sequence Method. Electron. Opt. Control 2013, 20, 1–5. [Google Scholar]
- Wu, H.; Li, L.; Zhang, K. Track Association Method Based on Target Mutual-Support of Topology. In Proceedings of the 2020 IEEE 9th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 11–13 December 2020; Volume 9, pp. 2078–2082. [Google Scholar]
- Hao, Z.; Chula, S. Algorithm of Multi-feature Track Association Based on Topology. Command. Inf. Syst. Technol. 2020, 11, 83–88. [Google Scholar]
- Sönmez, H.H.; Hocaoğlu, A.K. Asynchronous track-to-track association algorithm based on reference topology feature. Signal Image Video Process. 2021, 16, 789–796. [Google Scholar] [CrossRef]
- Li, X.; Wu, L.; Niu, Y.; Jia, S.; Lin, B. Topological Similarity-Based Multi-Target Correlation Localization for Aerial-Ground Systems. Guid. Navig. Control 2021, 1, 2150016. [Google Scholar] [CrossRef]
- You, S.; Yao, H.; Xu, C. Multi-Object Tracking with Spatial-Temporal Topology-based Detector. IEEE Trans. Circuits Syst. Video Technol. 2015, 14, 12. [Google Scholar] [CrossRef]
- Oliveira, B.D.A.; Pereira, L.G.R.; Bresolin, T. A review of deep learning algorithms for computer vision systems in livestock. Livest. Sci. 2021, 253, 104700. [Google Scholar] [CrossRef]
- Jiang, P.; Ergu, D.; Liu, F.; Cai, Y.; Ma, B. A Review of Yolo Algorithm Developments. Procedia Comput. Sci. 2022, 199, 1066–1073. [Google Scholar] [CrossRef]
- Liu, L.; Ouyang, W.; Wang, X.; Fieguth, P.; Chen, J.; Liu, X.; Pietikäinen, M. Deep Learning for Generic Object Detection: A Survey. Int. J. Comput. Vis. 2020, 128, 261–318. [Google Scholar] [CrossRef] [Green Version]
- Zou, Z.; Shi, Z.; Guo, Y.; Ye, J. Object Detection in 20 Years: A Survey. arXiv 2019, arXiv:1905.05055. [Google Scholar]
- Ultralytics/yolov5. Available online: https://github.com/ultralytics/yolov5 (accessed on 31 March 2022).
- Hartley, R.; Zisserman, R. 2D Projective Geometry and Transformations. In Multi View Geometry in Computer Vision; Machinery Industry Press: Beijing, China, 2020; pp. 28–33. [Google Scholar]
- De Berg, M.T.; Van Kreveld, M.; Overmars, M.; Schwarzkopf, O. Delaunay Triangulation: Height Interpolation. In Computational Geometry: Algorithms and Applications, 3rd ed.; Springer: Dordrecht, The Netherlands, 2008; pp. 241–264. [Google Scholar]
- Zhe, Y.; Chong, H.; Chen, L.; Min, C. Data Association Based on Target Topology. J. Syst. Simul. 2008, 20, 2357–2360. [Google Scholar]
- Chopra, S.; Hadsell, R.; LeCun, Y. Learning a Similarity Metric Discriminatively, with Application to Face Verification. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition(CVPR), San Diego, CA, USA, 20–25 June 2005; pp. 539–546. [Google Scholar]
- Bubbliiiing, Bubbliiiing/Siamese-Keras. Available online: https://github.com/bubbliiiing/Siamese-keras (accessed on 10 March 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).