Abstract
Communication is the cornerstone of UAV swarms to transmit information and achieve cooperation. However, artificially designed communication protocols usually rely on prior expert knowledge and lack flexibility and adaptability, which may limit the communication ability between UAVs and is not conducive to swarm cooperation. This paper adopts a new data-driven approach to study how reinforcement learning can be utilized to jointly learn the cooperative communication and action policies for UAV swarms. Firstly, the communication policy of a UAV is defined, so that the UAV can autonomously decide the content of the message sent out according to its real-time status. Secondly, neural networks are designed to approximate the communication and action policies of the UAV, and their policy gradient optimization procedures are deduced, respectively. Then, a reinforcement learning algorithm is proposed to jointly learn the communication and action policies of UAV swarms. Numerical simulation results verify that the policies learned by the proposed algorithm are superior to the existing benchmark algorithms in terms of multi-target tracking performance, scalability in different scenarios, and robustness under communication failures.
1. Introduction
Multi-target tracking (MTT) is an important application of unmanned aerial vehicle (UAV) swarms, which is widely applied to environmental monitoring, border patrol, anti-terrorism, emergency response, etc. [1,2,3]. However, due to constraints, such as flight distance, endurance, sensor coverage, etc., the individual abilities are usually insufficient to meet the task requirements, so UAVs need to communicate to achieve information sharing and better cooperation [4,5], then improve the MTT capability.
Currently, the communication between UAVs mainly follows the manually designed communication protocol, and UAVs transmit specific messages in accordance with specific formats and prescriptions [6,7,8]. However, the design of the communication protocol requires prior knowledge and is highly task-relevant [9], and manually customized protocols may bring side effects, such as insufficient flexibility and versatility, which may affect the communication capabilities of UAVs and are not conducive to their efficient cooperation in highly dynamic environments.
With the development of multi-agent deep reinforcement learning (MADRL), many works using MADRL to learn the complex cooperative action policies of UAVs have appeared. This also provides a new idea for learning cooperative communication, that is, applying this advanced artificial intelligence technique to learn the effective communication between UAVs to achieve efficient cooperation. Different from those methods using manually customized communication protocols, such as value function decomposition [10,11] and reward shaping [8,12,13], communication learning is a more general and exploratory cooperation enhancement method. It empowers UAVs to learn how to actively share knowledge to achieve cooperation without requiring expert domain knowledge and experience [14,15]. In addition, the learned communication policy enables the UAV to independently decide the content according to its real-time status, so as to improve the autonomy and adaptability of the UAVs. Therefore, this method can easily be extended to different multi-agent systems, such as unmanned transportation networks, logistics robots, etc., but is not limited to the MTT scenarios in this paper.
This paper no longer follows the traditional idea of manually designing the communication protocol, but adopts a new data-driven idea to model the communication protocol as the communication policy, then uses a deep neural network (DNN) to approximate and fit the policy. On that basis, this paper proposes an MADRL algorithm to learn the communication and action policies of a UAV simultaneously; thus, the UAV learns how to communicate with others for better cooperation, thereby improving the overall MTT capability of UAV swarms. Then, the effectiveness of the proposed algorithm is verified through numerical simulation experiments, and the performance of the learned policies is further tested.
The major contributions and innovations of this paper include:
- (1)
- Different from the manually designed communication protocol, the communication learning in this paper enables the UAV to independently decide the message content to be published according to its current state and endows the UAV with the ability of active communication and autonomous cooperation.
- (2)
- The communication policy of a UAV is parameterized as a function from its input variable to the published message. Then, two neural networks based on an attention mechanism are designed to approximate the communication and action policies, respectively, which can not only automatically distinguish the important messages received but also scale to the dynamic changes of the local communication topology.
- (3)
- To maximize the rewards of neighboring UAVs, a gradient optimization procedure for deterministic communication policy over continuous space is derived. Then, a MADRL algorithm for UAV swarms is proposed to jointly learn the continuous communication and discrete action policies of the UAVs.
The paper is organized as follows. Section 2 summarizes the related works. In Section 3, the background and some definitions about reinforcement learning are introduced. Section 4 analyzes the MTT problem and establishes the mathematician models. Then, the communication settings of UAV swarms are configured. Next, the specific methods are proposed in Section 5, including the models of communication and action policies, the derivations of policy gradient, and the corresponding algorithm. Then, numerical simulation experiments are implemented in Section 6 to verify the effectiveness of the proposed algorithm. A discussion of the proposed algorithm and numerical simulation experiments is presented in Section 7. Finally, Section 8 gives the summary and outlook of the paper.
2. Related Works
As an emerging research hotspot, the MADRL-based communication learning research in recent years can be classified into several categories, including communication protocol, communication structure, communication object, and communication timing, etc.
2.1. Communication Protocol
The communication protocol specifies the textual content that agents communicate with each other. Foerster et al. [16] firstly proposed two communication learning methods: reinforced inter-agent learning (RIAL) and differentiable ning (DIAL) to learn the communication protocol between two agents. Although they can only learn the simple low-dimensional communication protocols between two agents, their findings inspired a lot of follow-up works. Similarly, grounded semantic network (GSN) [15] was proposed to encode high-dimensional observation information and transmit it to other agents to realize information sharing. Experiments verified that GSN can reduce the limitations caused by the individual partial observability and improve the cooperation between agents. Pesce and Emanuele [17] proposed a memory-shared communication mechanism in which each agent can generate a belief state about its local observation and store it in a shared memory, and all agents can access and update the memory to achieve message passing between agents. However, in complex and drastically dynamic scenarios, the belief states generated by different agents may be all kinds of strange, which is not conducive to establishing a stable cooperative relationship between agents.
2.2. Communication Structure
Communication structure focuses on how the communication messages flow between agents. Peng et al. [18] modeled the communication link between agents as the bidirectionally-coordinated nets (BiCNet), which can not only transfer information between agents but also store local memory. However, the chain relationship in BiCNet is not necessarily suitable and accurate to capture the interactions between agents. In addition, BiCNet can be extremely complex and fragile when the scale of the agents is large. Therefore, BiCNet cannot be scaled well to the large-scale and highly dynamic UAV swarms. CommNet [14] assumed that each agent can globally receive and average the messages from the hidden layers of all other agents’ neural networks. It can scale well to the population changes of agents but cannot distinguish the importance of the messages from different agents, which may overwhelm some important ones. Moreover, global communication is usually impractical for swarms. With the introduction of graph neural networks (GNNs), communication learning methods based on graph attention network (GAT) have been proposed, such as ATOC [19], GA-Comm and GA-AC [20]. The graph attention network can adaptively assign the weight of neighbor nodes, which improves the flexibility and adaptability of the communication of agents.
2.3. Communication Object
In the study of communicating object, an agent learns to choose which adjacent agent(s) to communicate with peer-to-peer rather than broadcast. Ding et al. [21] proposed the individually inferred communication (I2C) algorithm to train a neural network that maps an agent’s local observation to others’ index codes to determine who to communicate with. Similarly, targeted multi-agent communication (TARMAC) [22] was proposed to learn the communication objects of each agent and the message to be sent. The simulation verified that TARMAC can learn effective communication in a simple discrete environment, enabling effective cooperation among agents.
2.4. Communication Timing
In some competition and confrontation scenarios, an agent may only need to communicate with neighbors at certain important moments, thereby reducing the communication frequency and bandwidth requirements. To learn when to communicate, the individualized controlled continuous communication model (IC3Net) [23] assumed that each agent’s action variable set includes a physical movement and a discrete communication switch signal. The later one is modeled as a gating unit that controls whether the agent publishes its communication message to the outside.
Although there are many related studies on communication learning, there are few works applicable to UAV swarms. Aiming at the MTT problem of UAV swarms, how to learn the efficient, scalable and robust communication between UAVs to achieve active cooperation and improve the MTT capability of UAVs is the focus of this paper.
3. Preliminary
3.1. Decentralized Partially Observable Markov Decision Process (Dec-POMDP)
Dec-POMDP [24] is a model of a Markov decision process (MDP) for multi-agents in which each one can only partially observe the environment and make its action decision accordingly. For n agents, each one is indexed by ; the Dec-POMDP at every step (the subscript t is omitted for convenience) can be described as:
where is the collective set of all agents, S is the global state space denoting all agents’ and the environment’s configurations, and denotes the current and specific state. The joint action space of all agents is denoted as in which is agent i’s specific action; denotes all agents’ joint observation space; denotes the individual observation model of agent i given the global state s, and is agent i’s local observation. denotes the probability of s transiting to new state executing joint action ; R is the reward function; is the constant discount factor.
In Dec-POMDP, each agent makes its action decision following individual policy , and the joint policy is denoted as . Then, all agents execute the joint action to refresh the environment. Given a specific joint observation and all agents’ joint policy , if each agent can access its private reward at every time step t, denotes the state-value function of all agents. Furthermoremore, executing the joint action , their action-value function is denoted as .
3.2. Actor–Critic (AC)
AC combines the policy gradient and value function approximation methods in which each actor is a policy function to predict the agent’s action, and each critic is a value function to evaluate the performance of the policy function [25]. Thus, the policy function , which is parameterized with , can be optimized via maximizing the value function, and the policy gradient with respect to is:
where the value function can be optimized via minimizing the square of the temporal-difference (TD) error [25].
3.3. Deep Deterministic Policy Gradient (DDPG)
DDPG is an extended version of AC in which the policy function directly outputs a deterministic action value () instead of a probability distribution over the action space (). Then the gradient of the policy function is:
The value function in DDPG is updated with the frozen network trick, and in addition to the two networks appearing in AC, the target-policy function and the target-value function are used to improve training stability [26].
4. Problem Formulation
4.1. Problem Description
The research focus of this paper is to explore a communication and action policies joint learning method to achieve swarm cooperation. To reduce the learning difficulty, we make reasonable assumptions and simplifications of the models of both the UAV and the target. As shown in Figure 1, a large number of homogeneous small fixed-wing UAVs track an unknown number of moving targets on the ground. Each UAV can only perceive the targets below it but cannot distinguish the specific identities or indices of the tracked targets. It is assumed that the UAVs move at a uniform constant speed in a two-dimensional plane and rotate their headings according to the local communication messages and observation information. However, since the targets are non-cooperative and there is no explicit target assignment, a single UAV may track multiple aggregated targets, or multiple UAVs may cooperatively track one or multiple targets simultaneously. Therefore, the UAVs should cooperate in a decentralized manner to keep targets within their field of view and track as many targets as possible. In addition, the UAVs should also satisfy the safety constraints, such as avoiding collisions, crossing boundaries, etc.
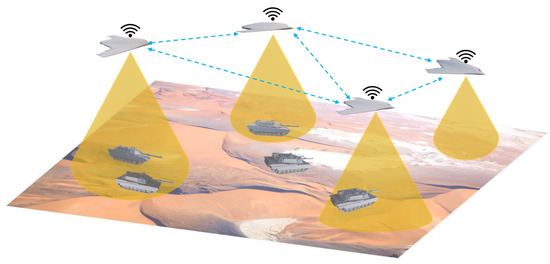
Figure 1.
MTT scenario for UAV swarms.
4.1.1. Kinematic Model
There are n UAVs and m targets in the two-dimensional mission area. The motions of these UAVs and targets can be modeled with two-dimensional plane motion models. For any UAV i, , its speed is denoted as , the heading angular is denoted as , and the control variable is its heading angular rate . Then, the kinematic model is described by its position and heading, that is:
where the subscription t is denoted as the current time, is the discrete time step, is the UAV’s maximum heading angular rate, and and are the maximum boundaries.
Similarly, for any target k, , its kinematic model can also be described with the position and heading angular , and the difference is that the target’s heading angular rate is assumed to be a bounded random variable.
4.1.2. Target Observation Model
Shown in Figure 2, each UAV can only observe these targets in a circle with radius below it and can resolve the position, speed and other information of the tracked targets from the raw observation but cannot identify their specific indexes. The ground projection distance between UAV i and target k is denoted as , and target k is tracked by UAV i when . The observation is denoted as . Furthermore, the observation information should be transformed from a global coordinate to UAV i’s local coordinate considering partial observability, denoted as .

Figure 2.
Target observation diagram.
Suppose UAV i can obtain the relative location information between itself and the boundaries of the task area through its GEO-fencing system and its partial observation of the targets. Then, the environment is denoted as .
4.1.3. Action Space
The purpose of this paper is to learn the cooperative policy of UAV swarms rather than the precise control of each individual. To facilitate the learning process, the action space of each UAV can be discretized into a limited number of action primitives as follows:
where is the cardinality of the discrete action set.
4.1.4. Reward Shaping
In MTT, UAVs are expected to track as many targets as possible. Therefore, each UAV should keep the tracked targets within its field of view as much as possible, while maximizing observation benefits by avoiding observation outside the boundaries and repeated tracking. Thus, the reward of each UAV i is shaped as the sum of multiple items, including:
- (1)
- Target Tracking Reward: Since the observation range of a UAV is limited, a naive idea is that the target should be as close as possible to the UAV’s observation center. Accordingly, the target tracking reward of UAV i to target k is defined as:When UAV i tracks multiple targets, its target tracking reward is . Specifically, the constant bias 1 in Equation (6) can encourage the UAV to track more targets rather than just obsessing over a single target. For example, when tracking two targets, , but when tracking a single target, .
- (2)
- Repeated Observation Penalty: Repeated observation of a target by multiple UAVs may not increase the number of tracked targets but may increase the risk of collision due to the proximity of the UAVs. Therefore, to improve the observation efficiency and track more targets, a penalty item is defined to guide the UAV i and to avoid repeated observations, that is:and . In Equation (7), if , there is no observational overlap between UAV i and j, and UAV i’s repeated observation penalty is .
- (3)
- Boundary Penalty: To effectively capture and track targets, UAV i’s observation area should always be within the boundaries. When the observation range is outside the boundaries, the outside part is invalid. To this end, the minimum distance from UAV i to all boundaries is , and the boundary penalty item is defined as:
To sum up, the individual reward of UAV i is shaped as:
4.2. Communication Settings
To cooperate among UAVs, they need to follow certain communication protocols to exchange information, and communication within a UAV swarm should meet the following requirements:
- (1)
- Local communication: In a large-scale UAV swarm, each one is both the communication receiving and output nodes, and all the nodes constitute a complex network. Considering the limitation of communication power, each one only communicates with the neighbors within its maximum communication range, which can effectively reduce the complexity of the communication network;
- (2)
- Direct communication: The MTT problem requires high timeliness of communication between UAVs. Therefore, to reduce the communication delay, it is assumed that each UAV only communicates with adjacent ones in a single-hop, and multi-hop bridge communication with ones outside the communication range is not considered;
- (3)
- Broadcast communication: To reduce bandwidth requirements and avoid communication congestion, each UAV broadcasts the same message to its neighbors once, instead of sending one-to-one multiple times;
- (4)
- Dynamic communication: The rapid movement of UAVs leads to dramatic changes in communication network and asymmetry between uplink and downlink. To this end, it is assumed that all neighbors within the communication range can receive the messages sent by a UAV to improve the dynamics and reliability of the communication network;
- (5)
- Autonomous communication: In complex scenarios, UAVs should be able to autonomously decide the content of messages to be sent based on their local observations, so as to promote efficient cooperation between them;
- (6)
- Safe communication: To improve the survivability of UAVs in the confrontation scenarios, the anti-jamming and anti-interception capabilities of communication should be improved to protect communication messages from being deciphered by non-receivers and improve communication security, etc.
5. Methods
5.1. Communication and Action Policies Modeling
Based on the above settings, the set of UAV i’s neighbors that can communicate locally with it at time t is denoted as . Its communication and action decision-making processes is shown in Figure 3. Specifically, , is its heading angular rate ; indicates the continuous and deterministic message that is about to be published to the neighbors. Here, UAV i can receive the messages from itself and all neighbors in the last moment; is denoted as . UAV i makes its action and communication decisions based on its local observation and the messages received. Then, the action policy is defined as:
and the communication policy is defined as:
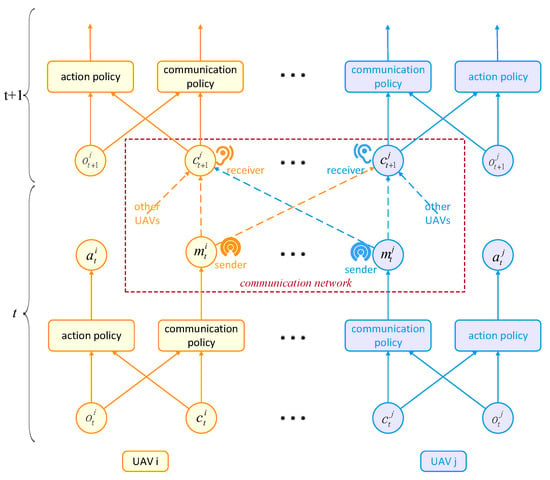
Figure 3.
Communication and action decision-making processes.
The communication and action decision process of UAV i is as follows:
- (1)
- At each time t, UAV i accesses its local observation and receives message set ;
- (2)
- (3)
- Execute joint action to refresh the environment and publish message to the neighboring UAVs, then receive the reward from the environment;
- (4)
- , and continue to step (1).
The input variables of both UAV i’s action and communication policies are the local observation and the received messages. As the UAVs and targets move continually, both the number of objects observed and the number of messages received by UAV i are dynamically changing accordingly. However, the input dimension of a neural network is usually fixed at initialization, and input variables with uncertain cardinality cannot be directly input into the neural network.
In MTT, each UAV can interpret the precise physical features of the tracked targets, such as their speeds, positions, etc. These explicit feature sets can be encoded as a dimension-determined input variable using feature embedding methods in [27]. Unfortunately, the message received from a neighbor is usually high-dimensional and often cryptic, i.e., its content composition may be time-varying, depending on the context of the sender, and has no definite physical properties. Therefore, the received messages cannot be easily encoded as a fixed-dimensional feature embedding. To this end, we adopt the graph attention mechanism [28] (GAT) to aggregate the received messages for each UAV, and its ability to extract and aggregate variable-length messages has been verified by [29,30].
Thus, the communication and action policies of UAV i can be approximated with neural networks. Take communication policy as an example, the overview of its neural network is shown in Figure 4, and the aggregation process of its communication messages in the dashed box on the right is as follows:
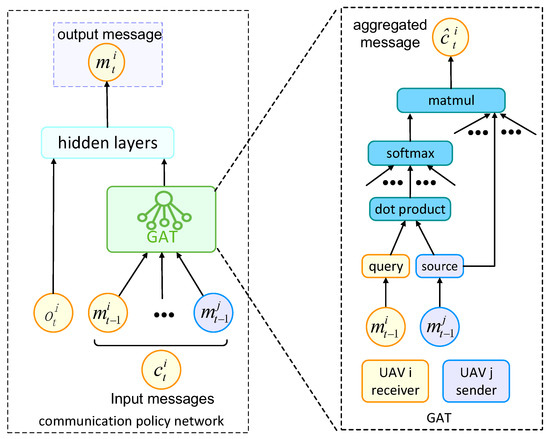
Figure 4.
The overview of communication policy neural network.
- (1)
- At time t, transform the communication messages with function F whose parameters can be learned to obtain the high-level feature [28], and denote as query, which represents the prior knowledge of UAV i, while are the set of sources, and each one indicates the received message to be aggregated;
- (2)
- The correlation coefficient from any adjacent UAV to the central UAV i is defined as:the inner product represents a parameter-free calculation, which outputs a scalar that measures the correlation;
- (3)
- Use the softmax function to normalize the similarity set to obtain the weight set in which
- (4)
- Weighted summation over the source set yields the aggregated message :
Then, and are concatenated and input into the following hidden layers to calculate the output message , and Equation (11) is redefined as:
where is the parameter of the communication neural network, and the GAT component is a part of the network.
Similarly, the action policy could also be approximated by a neural network, only the output layer should be modified accordingly. Then, the discrete actions of each UAV i obey the distribution:
where is the parameter of the action neural network.
5.2. Policy Gradient Optimization
Assuming that the action and communication policies of a UAV are independent of each other, the latter is frozen when training the action neural network and vice versa.
5.2.1. Action Policy Gradient
To learn the action policy , the action-value function is defined as , and is its parameter, which is updated by minimizing the following loss function:
where , is the parameter of the corresponding target network, is the next action, and are the local observations and the set of received messages at the next moment, respectively. The time-difference(TD) error is denoted as , and the gradient of this loss function with respect to performing gradient descent is:
Then, the action policy is updated via maximizing the action-value function:
and the policy gradient is:
5.2.2. Communication Policy Gradient
In local communication topography, all the adjacent UAVs receive the message that is an input variable of their next action and communication decisions. Given the action policy , the parameter of the action-value function , and UAV i’s current input variables , the communication objective is denoted as:
where is the set of UAV j’s received messages except .
Then, the communication policy gradient is derived according to the policy gradient theorem and the chain derivation rule as:
For simplicity, the conditional term in Equation (21) is omitted. Thus, given the input variables of UAV i at the current moment t and that of all adjacent UAVs at the next moment , the communication policy gradient can be calculated via Equation (22). Then, the policy can be updated accordingly.
Note that the objective functions, Equations (17), (19) and (21), are non-convex when using neural networks to approximate them, respectively. The common optimizers, such as MBSGD (mini-batch stochastic gradient descent) or Adam (adaptive moment estimation) in PyTorch, are usually adopted to solve these optimization problems.
5.2.3. Joint Communication and Action Policies Learning
As mentioned above, when calculating UAV i’s action policy gradient, its observation and messages received are required. However, for the communication policy gradient, in addition to these variables, it is necessary to further obtain the relevant variables of each adjacent UAV at the next moment. Employing the experience-sharing training mechanism [27] to train the communication and action policy neural networks, the action experience is denoted as , and the communication experience is denoted as . Utilizing the centralized-training decentralized-execution (CTDE) framework, an algorithm for jointly learning the communication and action policies for UAV swarms is proposed, and its pseudo-code is as follows.
In Algorithm 1, the two policy networks are not coupled with each other. During centralized training, they both have private experience buffers, and when one network is updated, the other one is frozen. However, communication policy gradient can backpropagate across UAVs, which enables closed-loop feedback updates of the communication policy. In decentralized execution, each UAV can decide its action and what to publish to its adjacent UAVs based on its own observation and received messages.
| Algorithm 1 Joint communication-action multi-agent deep reinforcement learning |
| Initialize: Neural network parameter: action policy, ; communication policy, ; action-value function and its target function, and . Action experience buffer: . Communication experience buffer: |
| //Centralized-Training: |
| 1: for epi = 1: episodes do |
| 2: Environment Reset |
| 3: for do |
| 4: for i = 1: n do |
| 5: Access observation and message set , and execute policy and policy to output action and message , respectively |
| 6: end for |
| 7: Execute joint action to update immediate rewards and joint observation at next moment |
| 8: for i = 1: n do |
| 9: Publish message , receive the neighbors’ messages to form |
| 10: Push action experience into buffer |
| 11: Push communication experience into buffer |
| 12: end for |
| 13: Randomly sample experiences from |
| 14: Minimize loss function to update the action-value function:
|
| 15: if Update target network then |
| 16: end if |
| 17: Update parameter with gradient:
|
| 18: Randomly sample experiences from |
| 19: Perform Equation (22), and update communication policy network parameter with gradient:
|
| 20: end for |
| 21: end for |
| //Decentralized-Execution: |
| 22: Environment Reset |
| 23: Load shared action policy and communication policy for each UAV |
| 24: for do |
| 25: For each UAV i, access and , and execute and to output its action and message , respectively |
| 26: Execute joint action to update environment, and each UAV i publishes message |
| 27: end for |
6. Experiments
6.1. Benchmark Algorithms
In this paper, the proposed Algorithm 1 is named Att-Message for simplification, and we hardly see from the existing literature that techniques other than MADRL can achieve the similar goal of solving communication and action policies for large-scale UAV swarms to cooperate. Thus, we select and adopt several benchmark algorithms that are commonly used by researchers from [14,19], and the non-communication one, including:
- (1)
- No-Comm. Literally, in No-Comm, each UAV can only receive local observation and selfishly maximize its individual rewards. There is no clear communication channel between UAVs and naturally no explicit cooperation or competition. Thus, the communication policy is , and the action policy is:
- (2)
- Local-CommNet. In CommNet [14], it is assumed that each agent can receive all agents’ communication messages. It should be adapted to the local communication configuration of UAV swarms in this paper, named Local-CommNet. Specifically, each UAV publishes the hidden layer information h of its action policy network to its adjacent UAVs, i.e., , Then, the messages received by UAV i are denoted as:Next, is aggregated using the average pooling method to obtain:
- (3)
- Att-Hidden. In addition to the average pooling method, the GAT can also be used to aggregate [12,19]. Then:The message of each UAV is its hidden layer information of the action policy network, and there is no separate communication policy network. So GAT, as an encoder, could be a component of the action policy network. The network can be updated according to the input variable following Equation (20).
6.2. Settings
In this section, the effectiveness of the proposed algorithm is verified by numerical simulation experiments. According to the problem description (Section 4.1), the training environmental parameters are set in Table 1. These parameters have been used in our previous work [8,27], and the rationality has been verified. During testing, the environment size and the numbers of UAVs and targets may change. The hyper-parameters of those algorithms are configured in Table 2.

Table 1.
Environmental parameters.

Table 2.
Hyper-parameters configuration.
To evaluate the tracking performance of UAV swarms, the following metrics are defined:
- (1)
- Average Reward:where has been defined in Equation (9), which comprehensively evaluates the performance of UAV swarms from the aspects of target tracking, repeated observation, safe flight, etc.
- (2)
- Average Target:which evaluates the number of targets tracked from the perspective of each UAV.
- (3)
- Collective Target:which evaluates the number of targets tracked by all the UAVs.
- (4)
- Coverage:which is denoted as the proportion of the tracked targets to all targets.Furthermore, the coverage rate, as a normalized indicator, can evaluate the tracking capability of UAV swarms in different scenarios from the perspective of targets.
6.3. Validity Verification
The neural networks in the four algorithms are randomly initialized and trained, and the curves of the defined metrics are plotted in Figure 5. Overall, the MTT performance of the Att-Message is the best, followed by Att-Hidden and Local-CommNet; the last one is No-Comm. Again, there is no explicit communication and cooperation between the UAVs in No-Comm, and each UAV greedily maximizes its private interest.

Figure 5.
The metric curves during the training process of the four algorithms.
Looking at specifics, (1) the three algorithms using explicit communication outperform No-Comm without communication, which indicates that communication can effectively promote the cooperation between UAVs, thereby improving the tracking performance of UAV swarms; (2) the comprehensive performance of Att-Hidden using GAT is better than that of Local-CommNet, but the UAV in both algorithms transmits the hidden layer of the action policy network. The reason may be that GAT can better aggregate the received messages, then effectively improve the action policy of UAVs and the cooperation between them; (3) furthermore, the comprehensive performance of the Att-Message is superior to that of Att-Hidden, indicating that compared with the hidden layer of the action policy neural network, the communication message can better capture the information that is helpful for cooperation. It is also proved that the communication policy in Att-Message can be optimized based on feedback from other UAVs to facilitate cooperation between UAVs.
Furthermore, Figure 6 intuitively visualizes the tracking process of the UAVs using the four algorithms, respectively, and the snapshots verify the previous conclusions again. In addition, it can be seen that executing the policies learned by Att-Message, the UAVs emerge with obvious cooperative behaviors. For example, when a target escapes the observation range of a UAV, the adjacent UAVs can quickly track and recapture the target again. Alternatively, there is a tendency to avoid getting too close between the UAVs to avoid repeated tracking as much as possible and to improve the observation coverage to capture more targets.
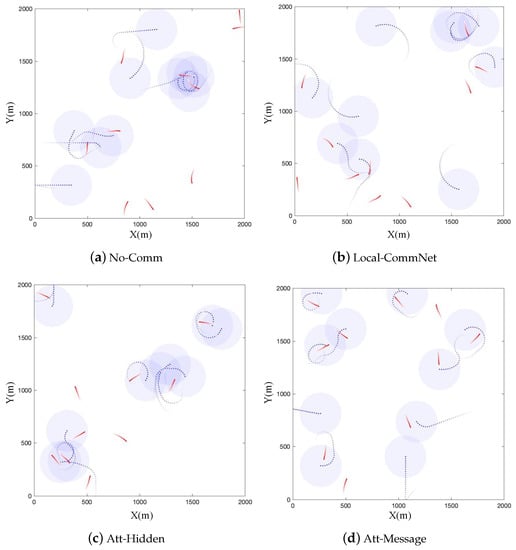
Figure 6.
Visualization of MTT executing different algorithms.
6.4. Scalability Test
To test whether the policies learned by the above four algorithms can be scaled to other scenarios beyond the training one, these policies were executed for 100 rounds in different scenarios, and the metrics of single-step are counted in Table 3.

Table 3.
Result statistics of scalability test.
The statistical results generally indicate that the average reward and coverage of the three algorithms that introduce explicit communication in different scenarios are significantly better than No-Comm without communication, which once again verify the effectiveness of the communication. Specifically, Att-Message performs better than other algorithms in terms of average reward and coverage, which directly reflects that the UAVs adopting the action and communication policies learned with Att-Message can better cooperate to track more targets in different scenarios. However, in the scenario with dense UAVs and targets, the average targets of No-Comm and Local-CommNet are higher, indicating that the individual performance of a single UAV is excellent, while the cooperation between UAVs is much lower. This also reveals the importance of cooperation for the emergence of swarm intelligence.
Combined with the visualization in Figure 6, the numerical results verify that UAV swarms can learn more efficient communication and action policies by using Att-Message and can scale these policies to different scenarios and achieve better performance.
6.5. Communication Failure Assessment
The above experiments assume perfect communication between UAVs; that is, the messages can always be received correctly by the adjacent UAVs. However, how does the performance of the UAVs change if there is a communication failure, while the UAVs still execute the policies learned while communicating perfectly? In this paper, two communication failures are assumed here: message loss and message error. The former refers to the message not being received due to communication disconnection or delay; and the later refers to the received message being inconsistent with the sent one due to electromagnetic interference or other reasons. Here, the error message is assumed to be a random noise signal. Under different failure probabilities, such as , the UAVs execute the policies learned by the four algorithms, respectively.
The variation trends of the metrics with the failure probability under the two failures are plotted in Figure 7 and Figure 8, respectively. At first glance, the corresponding statistical metric curves in both the two failure cases have similar trends; that is, when the probability gradually increases, the average reward and collective target curves of the three explicit communication-based algorithms gradually decrease, while the average target curve gradually increases, and the metric curves of No-Comm (without communication) is approximately flat. For the same failure probability, the descending order of comprehensive performance of the four algorithms is: Att-Message > Att-Hidden > Local-CommNet > No-Comm, which is consistent with the training results.
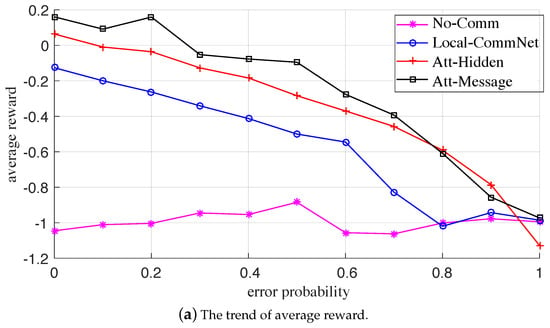
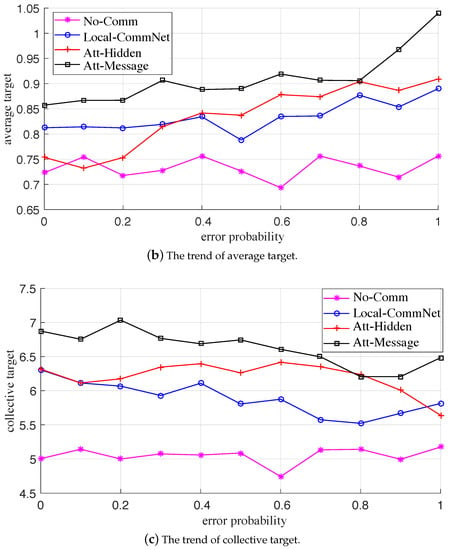
Figure 7.
The variation trends of the metrics with communication error probability.
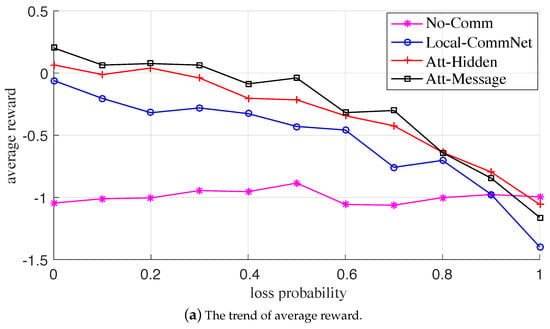
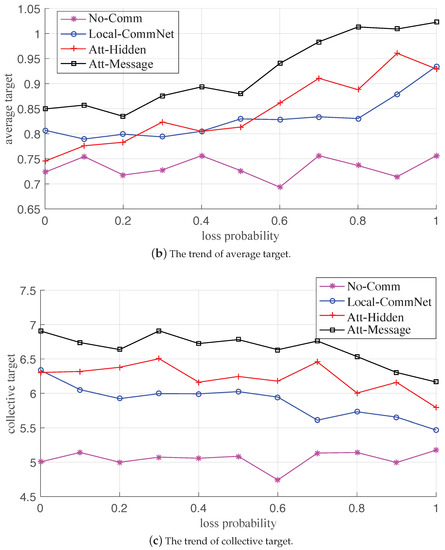
Figure 8.
The variation trends of the metrics with communication loss probability.
It is conceivable that when the probability increases, the available messages gradually dwindle, and the comprehensive performance of the former three algorithms with communication gradually deteriorates. The reason is that the reduction of useful messages leads to increased conflicts between UAVs and a decrease in cooperation. Moreover, as the probability increases, the average targets of the former three algorithms gradually increase, indicating that the UAVs shortsightedly maximize the number of targets tracked by individuals. In addition, when the communication is paralyzed, each UAV makes a completely independent decision. It can be seen that the comprehensive performance of Att-Message is the best, which reveals that while learning the communication policy, the UAVs can also learn a better action policy for tracking targets. Therefore, even the communication fails, and the improvement of the individual MTT capability can also feed back the overall capability of the swarm to a certain extent.
In summary, when there is a communication failure, such as message loss or error, the comprehensive performance of the communication and action policies learned by the proposed algorithm would be affected to a certain extent, but it is also better than the other three benchmark algorithms. The numerical results also demonstrate the robustness of the learned policies.
7. Discussion
As mentioned earlier, the research object of this paper is large-scale UAV swarms in which each UAV can only communicate and interact locally with the adjacent ones when making decisions. In local topology and ignoring other factors, the computational complexity of the action and communication policies for processing (aggregating) a message is assumed to be a unit, denoted as , and the average cardinal number of the message set is denoted as .
Then, in the decentralized execution, the computational complexity of the action and communication policies of each UAV is according to Equations (16) and (15), respectively. In centralized training, the computational complexity of updating action policy is also according to Equation (20), and that of the communication policy is since a message can influence the communication and action decisions at the next step of all adjacent UAVs according to Equation (22).
Therefore, similar to most MADRL algorithms adopting the CTDE framework, the training of the proposed algorithm requires more computational resources than execution, which is suitable for offline implementation. The offline training in this paper was deployed on the computer equipped with Intel (R) Xeon E5 CPU (Manufacturer: Intel Corporation, Santa Clara, CA, USA) and GTX Titan X GPU (Manufacturer: ASUS, Taiwan), the operating system was Ubuntu 16.04 LTS, and the algorithm was implemented by Pytorch. Then the learned policies can be performed online without retraining. The specific requirement of computational resources should comprehensively take the constraints, such as computing platform, neural network design and optimization, decision frequency and so on, into consideration.
Moreover, in the observation of a target, we only consider the simple numerical information, such as its location and speed, but not the real-time image, and the communication policy can also compress and encode the high-dimensional information to realize lightweight embedding interaction. These can further improve the feasibility of the algorithm in real-world scenarios.
8. Conclusions and Future Works
Communication is an important medium for transferring information and realizing cooperation between UAVs. This paper adopts a data-driven approach to learn the cooperative communication and action policies of UAV swarms and improve their communication and MTT capabilities. Specifically: (1) The communication policy of a UAV is mapped from the input variables to the message sent out, so that the UAV can autonomously decide the content of the message according to its real-time status. (2) The neural networks based on the attention mechanism are designed to approximate the communication and action policies, where the attention mechanism can distinguish the importance of different messages and aggregate the variable number of messages into a fixed-length code to adapt to the dynamic changes of the local communication topology. (3) To maximize the cumulative reward of the adjacent UAVs, the gradient optimization process of the continuous communication policy is derived. (4) Based on the CTDE framework, a reinforcement learning algorithm is proposed to jointly learn the communication and action policies of UAV swarms. The numerical simulation verifies that the proposed algorithm can learn effective cooperative communication and action policies to conduct the cooperation of UAV swarms, thereby improving their MTT ability, and the learned policies are robust to communication failures.
Although the communication policy in this paper can extract the message that is beneficial to cooperation, the physical meaning of the message cannot be explicitly parsed. Therefore, the interpretability of the message remains to be further explored. How to reasonably set the output dimension of the communication policy neural network, that is, the length of the message, also needs to be further solved. If the output dimension is too small, it may limit the communication capability of the UAV; otherwise, it may increase the difficulty of learning, which is not conducive to learning an effective communication policy. In addition, it is necessary to take more complex scenarios into consideration and establish more accurate models to investigate how the physical aspects of both the UAVs and targets would affect the MTT performance.
Author Contributions
Conceptualization, W.Z.; data curation, J.L.; formal analysis, W.Z.; funding acquisition, J.L.; investigation, W.Z.; methodology, W.Z.; project administration, Q.Z.; software, W.Z.; supervision, J.L.; validation, W.Z.; visualization, W.Z.; writing—original draft, W.Z.; writing—review and editing, W.Z., J.L. and Q.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Innovation 2030-Key Project of “New Generation Artificial Intelligence” under Grant 2020AAA0108200.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Goldhoorn, A.; Garrell, A.; Alquezar, R.; Sanfeliu, A. Searching and tracking people in urban environments with static and dynamic obstacles. Robot. Auton. Syst. 2017, 98, 147–157. [Google Scholar] [CrossRef][Green Version]
- Senanayake, M.; Senthooran, I.; Barca, J.C.; Chung, H.; Kamruzzaman, J.; Murshed, M. Search and tracking algorithms for swarms of robots: A survey. Robot. Auton. Syst. 2016, 75, 422–434. [Google Scholar] [CrossRef]
- Abdelkader, M.; Güler, S.; Jaleel, H.; Shamma, J.S. Aerial Swarms: Recent Applications and Challenges. Curr. Robot. Rep. 2021, 2, 309–320. [Google Scholar] [CrossRef] [PubMed]
- Emami, Y.; Wei, B.; Li, K.; Ni, W.; Tovard, E. Joint Communication Scheduling and Velocity Control in Multi-UAV-Assisted Sensor Networks: A Deep Reinforcement Learning Approach. IEEE Trans. Veh. Technol. 2021, 9545, 1–13. [Google Scholar] [CrossRef]
- Maravall, D.; de Lope, J.; Domínguez, R. Coordination of Communication in Robot Teams by Reinforcement Learning. Robot. Auton. Syst. 2013, 61, 661–666. [Google Scholar] [CrossRef]
- Kriz, V.; Gabrlik, P. UranusLink—Communication Protocol for UAV with Small Overhead and Encryption Ability. IFAC-PapersOnLine 2015, 48, 474–479. [Google Scholar] [CrossRef]
- Khuwaja, A.A.; Chen, Y.; Zhao, N.; Alouini, M.S.; Dobbins, P. A Survey of Channel Modeling for UAV Communications. IEEE Commun. Surv. Tutor. 2018, 20, 2804–2821. [Google Scholar] [CrossRef]
- ZHOU, W.; LI, J.; LIU, Z.; SHEN, L. Improving multi-target cooperative tracking guidance for UAV swarms using multi-agent reinforcement learning. Chin. J. Aeronaut. 2022, 35, 100–112. [Google Scholar] [CrossRef]
- Bochmann, G.; Sunshine, C. Formal Methods in Communication Protocol Design. IEEE Trans. Commun. 1980, 28, 624–631. [Google Scholar] [CrossRef]
- Rashid, T.; Samvelyan, M.; Schroeder, C.; Farquhar, G.; Foerster, J.; Whiteson, S. QMIX: Monotonic value function factorisation for deep multi-agent reinforcement learning. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 4295–4304. [Google Scholar]
- Son, K.; Kim, D.; Kang, W.J.; Hostallero, D.; Yi, Y. QTRAN: Learning to factorize with transformation for cooperative multi-agent reinforcement learning. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 10329–10346. Available online: https://arxiv.org/abs/1905.05408 (accessed on 20 September 2022).
- Wu, S.; Pu, Z.; Qiu, T.; Yi, J.; Zhang, T. Deep Reinforcement Learning based Multi-target Coverage with Connectivity Guaranteed. IEEE Trans. Ind. Inf. 2022, 3203, 1–12. [Google Scholar] [CrossRef]
- Xia, Z.; Du, J.; Wang, J.; Jiang, C.; Ren, Y.; Li, G.; Han, Z. Multi-Agent Reinforcement Learning Aided Intelligent UAV Swarm for Target Tracking. IEEE Trans. Veh. Technol. 2022, 71, 931–945. [Google Scholar] [CrossRef]
- Sukhbaatar, S.; Szlam, A.; Fergus, R. Learning multiagent communication with backpropagation. In Proceedings of the 30th Conference on Neural Information Processing Systems (NIPS 2016), Barcelona, Spain, 5–10 December 2016. [Google Scholar] [CrossRef]
- Hausknecht, M.; Stone, P. Grounded semantic networks for learning shared communication protocols. In Proceedings of the International Conference on Machine Learning (Workshop), New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Foerster, J.; Assael, Y.M.; de Freitas, N.; Whiteson, S. Learning to Communicate with Deep Multi-Agent Reinforcement Learning. Adv. Neural Inf. Process. Syst. 2016, 29, 2137–2145. [Google Scholar]
- Pesce, E.; Montana, G. Improving coordination in small-scale multi-agent deep reinforcement learning through memory-driven communication. Mach. Learn. 2020, 109, 1–21. [Google Scholar] [CrossRef]
- Peng, P.; Wen, Y.; Yang, Y.; Yuan, Q.; Tang, Z.; Long, H.; Wang, J. Multiagent Bidirectionally-Coordinated Nets: Emergence of Human-Level Coordination in Learning to Play StarCraft Combat Games. 2017. Available online: https://arxiv.org/abs/1703.10069 (accessed on 20 September 2022).
- Jiang, J.; Lu, Z. Learning attentional communication for multi-agent cooperation. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; Volume 18, pp. 7265–7275. [Google Scholar]
- Liu, Y.; Wang, W.; Hu, Y.; Hao, J.; Chen, X.; Gao, Y. Multi-agent game abstraction via graph attention neural network. In Proceedings of the AAAI 2020—34th AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 December 2020; pp. 7211–7218. [Google Scholar] [CrossRef]
- Ding, G.; Huang, T.; Lu, Z. Learning Individually Inferred Communication for Multi-Agent Cooperation. In Proceedings of the 34th Conference on Neural Information Processing Systems (NeurIPS2020), Vancouver, BC, Canada, 6–12 December 2020; Volume 33, pp. 22069–22079. [Google Scholar]
- Das, A.; Gervet, T.; Romoff, J.; Batra, D.; Parikh, D.; Rabbat, M.; Pineau, J. TarMAC: Targeted multi-agent communication. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 1538–1546. [Google Scholar]
- Singh, A.; Jain, T.; Sukhbaatar, S. Learning when to Communicate at Scale in Multiagent Cooperative and Competitive Tasks. arXiv 2018, arXiv:1812.09755. [Google Scholar]
- Dibangoye, J.S.; Amato, C.; Buffet, O.; Charpillet, F. Optimally Solving Dec-POMDPs as Continuous-State MDPs. J. Artif. Intell. Res. 2016, 55, 443–497. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Temporal-difference learning. In Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998; pp. 133–160. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Zhou, W.; Liu, Z.; Li, J.; Xu, X.; Shen, L. Multi-target tracking for unmanned aerial vehicle swarms using deep reinforcement learning. Neurocomputing 2021, 466, 285–297. [Google Scholar] [CrossRef]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Lee, J.B.; Rossi, R.A.; Kim, S.; Ahmed, N.K.; Koh, E. Attention Models in Graphs: A Survey. ACM Trans. Knowl. Discov. Data 2019, 13, 1–25. [Google Scholar] [CrossRef]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).