A Distributed Task Rescheduling Method for UAV Swarms Using Local Task Reordering and Deadlock-Free Task Exchange

Abstract

Distributed task scheduling is an ongoing concern in the field of multi-vehicles, especially in recent years; UAV swarm performing complex tasks endows it with new characteristics, such as self-organization, scalability, reconfigurability, etc. This requires the swarm to have distributed rescheduling capability to dynamically include as many unassigned tasks or new tasks as possible, while satisfying tight time constraints. As one of the most advanced rescheduling methods, the Performance Impact (PI)-MaxAss algorithm provides an important reference for this paper. However, its task exchange-based strategy faces the deadlock problem, and the task rescheduling method should not be limited to this. To this end, a new distributed rescheduling method is proposed for UAV swarms, which combines the local task reordering strategy and the improved task exchange strategy. On the one hand, based on the analysis of the fact that the scheduler is unreasonable for individuals, this paper proposes a local task reordering strategy denoted as PI-Reorder, which simply adds the reordering strategy to the recursive inclusion phase of the PI-MinAvg algorithm, so that unassigned tasks or new tasks can be included without relying on the task exchange. On the other hand, from the phenomenon that two or more vehicles occasionally get caught in an infinite cycle of exchanging the same tasks, the deadlock problem of PI-MaxAss is analyzed, which is then solved by introducing a deadlock-free task exchange strategy, where some defined counters are used to detect and isolate the deadlocks. Then, a rescue scenario is used to demonstrate the performance of the proposed methods, PI-Hybrid compared with PI-MaxAss. Monte Carlo simulation results show that, compared with PI-MaxAss, this method can not only increase the number of allocations to varying degrees, but also reduce the average waiting time, while ensuring deadlock avoidance. The methods can be used not only for the secondary optimization of the existing task exchange scheduling algorithms to escape local optima, but also for task reconfiguration of swarm tasks after adding or removing tasks.

1. Introduction

In recent years, UAV swarms have attracted much attention due to their low cost, scalability, wide-area distribution, etc. [1,2,3]. A team of homogeneous or heterogeneous specialized UAVs can cover more ground and be more resilient to failures than a single all-purpose UAV [4]. They have broad application prospects in post-disaster search and rescue, pollution traceability, pick-up and delivery, logistics, and any scenario that requires many urgent jobs to be completed in a minimum time by multiple UAVs. Different from simple clustering behavior, which can be achieved with a stigmergy-based approach, the complex tasks cannot be accomplished by a swarm without the assignment of tasks and the arrangement of their timing, that is, multi-vehicle scheduling. It is nothing new, but the swarm boom in recent years activates it again [5,6], and endows it with new characteristics, such as self-organization, scalability, reconfigurability, etc.

Multi-vehicle scheduling is a proven NP-hard combinatorial optimization problem; therefore, obtaining the global optimal solution is computationally intensive [7]. Earlier studies used a centralized approach to generate and distribute plans for all vehicles by using a central server capable of gathering system-wide information (situational awareness), either on the ground (the fleet’s ground control terminal) or on one of the vehicles selected as the master. In this approach, the overall objective function of the problem concerned can be explicitly minimized or maximized based on the collection of all vehicle information on a central server. Therefore, the main advantage lies in the ability to optimize the overall objective function (and thus obtain the approximate optimal solution) by some heuristic algorithms (such as genetic algorithm, ant colony algorithm, etc.). However, there are several disadvantages [8]: First, the computational requirements are high because the computational operations are placed on a central server for global optimization of the multi-vehicle scheduling problem; second, each vehicle is required to communicate with the central server, and all vehicles need to communicate their situational awareness (SA) to the central server, which will bring a heavy communication burden. Third, centralized approaches are prone to single points of failure.

Given the individual low cost and self-organization of the swarm, the individual cannot afford the computationally expensive centralized scheduling, and the central server faces the communication pressure brought by information collection. To this end, the swarm can only resort to distributed task scheduling [9,10,11], which is roughly divided into three implementation approaches: redundant central computing, distributed parallel optimization and market-based bidding. Redundant central computing instantiates the centralized scheduler on each vehicle in order to achieve distribution, as well as eliminate the single point of failure [12,13,14]. These approaches often assume perfect communication links with unlimited bandwidth, since every vehicle must have the same SA. Inconsistencies in SA can lead to allocation conflicts because each vehicle will perform a centralized optimization using a different information set. Distributed parallel optimization divides the global optimization problem into sub-problems, which are solved by parallel computation to obtain higher optimization performance and computational efficiency [14,15,16,17,18]. These methods rely on high-frequency and high-speed data exchange and seem to be more suitable for gigabit connected server farms. Market-based bidding is where vehicles bid on tasks in a greedy strategy, the higher bidder wins the task, and the suboptimal solution can be obtained through multiple rounds of bidding [7,19,20]. In these types of algorithms, vehicles bid on tasks with values based solely on their own SA. Even if there are inconsistencies in their SA, they can naturally converge to a conflict-free solution. In comparison, market-based bidding is more suitable for the low cost, self-organization, and wide-area distribution of swarms.

The scalability of the swarm cannot be ignored; it means that the UAV can flexibly join or withdraw. As the number of tasks and UAVs increases, it is usually too computationally expensive to consider each combination of tasks for each UAV in order to find the optimal solution. The computational limitations are particularly relevant in search and rescue scenarios in which time and resources could be limited. Thus, heuristic methods are employed to speed up the process of task scheduling while maintaining an efficient and scalable algorithm. Consensus-Based Bundle Algorithm (CBBA) [19] and Performance Impact (PI-MinAvg) [7,21] are two of the most representative heuristic methods, and many methods are derived from them. CBBA is a popular solution that utilizes a heuristic greedy strategy locally to select tasks and resolves task conflicts among multiple agents through consensus rules. It has been shown that CBBA produces the same solution as the centralized sequential greedy procedures, and guarantees 50% optimality, which means that CBBA is still trapped into local optimization where each robot is striving for its own optimal scheduling and cannot give up some local optimal tasks for the global optimization. PI-MinAvg is an extension of CBBA, which introduces the ‘significance’ to prioritize task assignments and updates the significance of the follow-up tasks in the respective task list after any task is included or removed. It was shown empirically to solve time-critical task scheduling problems that CBBA could not, and was shown to find a lower average start time compared with CBBA. Despite the improved performance, PI-MinAvg still fails to solve some problems that are solvable due to converging to locally optimal but globally suboptimal solutions. It can be seen that heuristic methods to solve combinational optimization problems are prone to finding a local optimum and lack the flexibility to escape from it [22]; nonetheless, a second search can perturb the first phase solution out of local optima to reach an enhanced solution closer to a nondominated global optimum. The procedure follows a two-phase task scheduling strategy that starts from a solution generated with an existing scheduling algorithm that minimizes average waiting time; a rescheduling method needs to be used in the second stage for maximizing task allocations.

In addition to the above features, the reconfigurability of swarms is meant to support the dynamic addition or removal of tasks, which also requires the swarm to have the ability to reschedule tasks. For instance, CBBA with Partial Replanning (CBBAPR) [20] enables CBBA to respond quickly to new tasks that appear online. PI-MaxAss [23] can increase the allocation number by exchanging tasks among robots and creating a feasible time slot for unallocated tasks. Moreover, preliminary experiments running PI-MaxAss showed that two or more UAVs occasionally get caught in an infinite cycle of exchanging the same tasks, i.e., a deadlock problem. This phenomenon is intolerable for the swarm and will cause the system to stagnate. Still taking search and rescue as an example, when multiple UAVs conduct distributed scheduling, without the truncation of the algorithm, they will not be able to jump out of the infinite loop of the algorithm, resulting in the failure to obtain and execute the schedules in time, and ultimately leading to the failure of survivors obtaining rescue. The paper [22] proposed a solution to limit the number of times that a robot can remove the same task before it no longer attempts to include it. However, this method relies heavily on the reasonableness of the maximum number of removals, with a lower limit causing premature truncation of the algorithm, and a higher limit causing multiple invalid bids. The above facts indicate that solving the deadlock problem arising from the exchange mechanism and further improving the performance of task rescheduling methods are worthy of research.

It can be seen that task rescheduling can be used not only for the secondary optimization of the algorithm to escape local optima, but also for task reconfiguration after adding or removing tasks. This paper proposes a novel distributed rescheduling method for UAV swarms using local task reordering and deadlock-free task exchange. First, in terms of the search and rescue scenario, a distributed tasks rescheduling problem is formulated as a mathematical optimization problem coupled with some time, space or task constraints. Second, based on suboptimal solutions obtained with a scheduling method such as PI-MinAvg, a novel local task reordering strategy denoted as PI-Reorder is designed, which simply adds the strategy to the recursive inclusion phase of PI-MinAvg, so that unassigned tasks or new tasks can be included as soon as possible without relying on the task exchange strategy (such as PI-MaxAss). Third, from the phenomenon that shifting tasks occasionally falls into an infinite cycle, the deadlock problem of PI-MaxAss is analyzed, which is then solved by introducing a deadlock-free task exchange strategy, where a removed task set, an included task set, a task removed counter, a task included counter and a collection of task included counters are introduced together to detect and isolate deadlocks. Fourth, the local task reordering strategy and the deadlock-free task exchange strategy is integrated into an algorithm called PI-Hybrid. Monte Carlo simulation results show that the proposed local task reordering strategy PI-Reorder and the improved exchanging strategy PI-Hybrid can both increase the number of allocated tasks and reduce the total task waiting time to different degrees in the swarm search and rescue task. Pi-Reorder provides a new boost to the result performance of the PI-MinAvg algorithm. Compared with PI-MaxAss method, PI-Hybrid has a small improvement in the results, and overcomes the intolerable deadlock problem of swarm distributed scheduling.

The rest of this paper is organized as follows. In Section 2, a formal description of a typical task rescheduling problem is given and a classical distributed scheduling algorithm is introduced. Section 3 presents a distributed rescheduling method—Section 3.1 presents a local task reordering strategy, Section 3.2 presents an improved task exchange strategy and Section 3.3 presents an integrated reordering and exchange method. Numerical simulation and analysis are presented in Section 4. Finally, some conclusions are drawn in Section 5, followed by expectations for the future.

2. Preliminaries

2.1. Problem Formulation

Consider a variety of heterogeneous UAVs performing a search and rescue mission; the purpose is to cooperate with each other to rescue a number of survivors discovered, who require food supplies or medical provisions [22,24]. Each survivor must be visited by one UAV in order to be deemed rescued. Every UAV always follows a minimum time path to visit all of the unvisited survivors allocated to it, while not being required to return to its initial location. The scenarios have similarities with the traveling salesman problem (TSP), a well-known NP-hard combinatorial optimization problem. The objectives considered here are comparable to the constraints of two variants of the TSP: the team orienteering problem with time windows (TOPTW) [25] and the K-traveling repairmen problem (K-TRP) [26]. These objectives and constraints are applicable to a variety of scenarios such as those found in target tracking, pick-up and delivery, logistics and any scenario that requires many urgent jobs to be completed in a minimum time by multiple drones. One challenge in using a swarm is to schedule them to perform tasks while optimizing one or more objectives, for example, to minimize the average waiting time before their rescue, and to maximize the number of rescued survivors.

To formulate the problem mathematically, a set of n heterogeneous UAVs is defined by $\mathbf{V}=\left[v_1,v_2,\dots ,v_n\right]$, and a set of m tasks waiting to be conducted is defined by $\mathbf{T}=\left[t_1,t_2,\dots ,t_m\right]$. Each UAV $v_i$ selects its appropriate tasks from the task set T and arranges them in sequence to form its scheduler ${\mathbf{p}}_i$ respecting time constraints. Whether a task is appropriate for a UAV depends on two aspects: one is whether the UAV can undertake this type of task, which is limited by the fact that low cost UAVs usually only have single task capability; another aspect is whether the task is within the limited range of the drone. The optimization objective J of the scheduling problem shown in the following formula is to minimize the total waiting time C as much as possible under the premise of allocating as many tasks N as possible.

$$\begin{array}{c}\hfill J=minC\left(maxN\right)\end{array}$$

(1)

where

$$\begin{array}{c}C={\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{k=1}^{\left|{\mathbf{p}}_i\right|}}{c}_{i,k}\left({\mathbf{p}}_i\right),N={\displaystyle \sum _{i=1}^n}\left|{\mathbf{p}}_i\right|\end{array}$$

(2)

in which the time cost of a task $t_k$ in ${\mathbf{p}}_i$, defined as $c_{i,k}\left({\mathbf{p}}_i\right)$, is the predicted waiting time taken by the drone to arrive at the location of the task $t_k$. This time includes the duration of earlier tasks in ${\mathbf{p}}_i$ and travel time to and from those earlier tasks, but does not include the duration of the execution of $t_k$. The objective of minimizing waiting time measures the cost of a task scheduling as the time it takes to start serving the task from the start of the drone’s schedule, i.e., the total time the survivor must wait before being attended to. $\left|{\mathbf{p}}_i\right|$ is the number of assigned tasks for $v_i$. Maximizing N measures the number of tasks assigned, that is, the number of survivors rescued.

The corresponding constraints are listed below:

$$\left\{\begin{array}{c}\begin{array}{cc}\left|{\mathbf{p}}_i\right|\le N_i,& \forall i\in \left\{1,\dots ,n\right\}\end{array}\hfill \\ \begin{array}{cc}{\mathbf{p}}_i\cap {\mathbf{p}}_j=\varnothing ,& \forall i\ne j\in \left\{1,\dots ,n\right\}\end{array}\hfill \\ \begin{array}{cc}{\bigcap }_i^z{\mathbf{p}}_i\subseteq \mathbf{T},& \forall i,z\in \left\{1,\dots ,n\right\}\end{array}\hfill \\ \begin{array}{cc}{c}_{i,k}\left({\mathbf{p}}_i\right)\le s_{{\mathbf{p}}_{i,K}},& \forall i\in \left\{1,\dots ,n\right\},\forall k\in \left\{1,\dots ,m\right\}\end{array}\hfill \\ \begin{array}{cc}{h}_{i,k}\in H,& \forall i\in \left\{1,\dots ,n\right\},\forall k\in \left\{1,\dots ,m\right\}\end{array}\hfill \end{array}\right.$$

(3)

where the first constraint represents the capacity $N_i$ at which the UAV $v_i$ can perform tasks. The second constraint ensures that each task is assigned to at most one UAV, or is left unassigned because it is beyond the capabilities of all UAVs. The validity of scheduling is promised by the third constraint where any scheduler’s combination is a subset of the task set T. The fourth constraint guarantees that the time $c_{i,k}\left({\mathbf{p}}_i\right)$ UAV $v_i$ to initiate the kth task in its scheduler ${\mathbf{p}}_i$ would be before their tasks’ deadlines $s_{{\mathbf{p}}_{i,K}}$, after which it is too late for the task to be executed successfully. It is therefore necessary to determine whether a drone can arrive at the location of a task $t_k$ before the latest start time $s_{{\mathbf{p}}_{i,K}}$. The last constraint in the form of a compatibility matrix H expresses that each UAV can only undertake one corresponding type of task, where $h_{i,k}$ is a Boolean variable.

Assume that a suboptimal solution in which additional tasks cannot be directly included without violating time constraints is obtained with the scheduling method; the UAVs rely on a decentralized rescheduling method to coordinate a rescue plan over multiple iterations to increase the allocation number simply. The main challenge is to reach an optimal allocation where the allocation number is maximized and the waiting time minimized while respecting time constraints.

2.2. Scheduling with PI-MinAvg

Whitbrook et al. [21] and Zhao et al. [7] proposed a distributed scheduling method as an extension of CBBA; it was shown empirically to solve time-critical task allocation problems such as search and rescue. In this method, a quantity called performance impact is introduced to determine the priority of task allocation for the robot, which takes into account not only the cost of task allocation, but also the impact of the task allocation on other allocation costs in the robot scheduler. The method employs a heuristic greedy strategy to enable robots to build a bundle of tasks sequentially and to optimize one or more objectives indirectly with a consensus rule; for instance, the average waiting time can be reduced by shifting tasks between robots. With PI-MinAvg, a robot does not release a task until it is reassigned elsewhere at a lower cost; i.e., once a task is assigned it does not become unassigned. Like CBBA, PI-MinAvg iterates over a task inclusion phase, a communication and conflict resolution phase.

During the task inclusion phase, robots select a task at a time to include in their schedulers until no more tasks can be added. Before including a task, the algorithm computes the inclusion performance impacts (abbreviated as IPI-MinAvg) of all candidate tasks $t_q$ at each position l according to Equation (4), where candidate tasks are those compatible with $v_i$’s capabilities and not already in ${\mathbf{p}}_i$. Here, the IPI-MinAvg of a task represents the minimum impact of a task addition on the average waiting time of the existing tasks in ${\mathbf{p}}_i$.

$${\omega }_q^{\oplus }\left({\mathbf{p}}_i,t_q\right)=\underset{l=1}{\overset{\left|{\mathbf{p}}_i\right|+1}{min}}\left\{\sum _{z=l}^{\left|{\mathbf{p}}_i\right|+1}{c}_{i,z}\left({\mathbf{p}}_i{\oplus }_l{t}_q\right)-\sum _{z=l}^{\left|{\mathbf{p}}_i\right|}{c}_{i,z}\left({\mathbf{p}}_i\right)\right\}$$

(4)

where $c_{i,z}\left({\mathbf{p}}_i\right)$ denotes the start time of the task at position z in $v_i$’s scheduler; ${\oplus }_l$ indicates that the task $t_q$ is inserted into the $l_{th}$ position of ${\mathbf{p}}_i$. Since the inserted task $t_q$ only affects the start times of its subsequent tasks in ${\mathbf{p}}_i$, the formula calculates the cumulative time delay of the $l_{th}$ task and the tasks after it. A list to store the IPI-MinAvg of each task is kept on each robot and is defined as ${\mathbf{\gamma }}_i^{\oplus }=\left[w_1^{\oplus },\dots ,w_m^{\oplus }\right]$ for robot $v_i$.

After the IPI-MinAvg of all candidate tasks have been computed, $v_i$ selects for inclusion the task whose IPI-MinAvg can improve upon the task’s removal performance impacts (abbreviated as RPI-MinAvg) the most. The maximum difference between the RPI-MinAvg of all tasks and the IPI-MinAvg of all tasks is computed as ${max}_{q=1}^m\{{\mathbf{\gamma }}_{i,q}-{\mathbf{\gamma }}_{i,q}^{\oplus }\}>0$. An IPI-MinAvg of $t_q$ in ${\mathbf{p}}_i$ lower than $t_q$’s RPI-MinAvg in another robot’s task list ${\mathbf{p}}_j$ indicates that the global cost can be reduced if $t_q$ is reallocated to $v_i$.

$$w_k^{\ominus }\left({\mathbf{p}}_i,t_k\right)=\sum _{z=b}^{\left|{\mathbf{p}}_i\right|}{c}_{i,z}\left({\mathbf{p}}_i\right)-\sum _{z=b+1}^{\left|{\mathbf{p}}_i\right|}{c}_{i,z}\left({\mathbf{p}}_i\ominus t_k\right)$$

(5)

where b is the position of task $t_k$ in $v_i$’s task list, $c_{i,z}\left({\mathbf{p}}_i\right)$ denotes the time cost of the task at position z in ${\mathbf{p}}_i$’s scheduler and ${\mathbf{p}}_i\ominus t_k$ denotes ${\mathbf{p}}_i$ with $t_k$ removed. The RPI-MinAvg of a task $t_k$ is referred to formally as $w_k^{\ominus }$ and each robot stores the vector ${\mathbf{\gamma }}_i=\left[w_1^{\ominus },\dots ,w_m^{\ominus }\right]$.

During the communication and conflict resolution phase, robots share their schedulers with neighboring robots and resolve conflicting allocations. As two or more robots may be assigned the same task, the consensus procedure introduced in [19] is used to resolve these conflicting assignments. A lower RPI-MinAvg indicates a more optimal schedule; therefore robots with a higher RPI-MinAvg for a conflicting assignment release the task. The above two phases are alternately repeated until the task assignment is agreed upon within the swarm.

2.3. Rescheduling with PI-MaxAss

Turner et al. [22] proposed a distributed rescheduling method called PI-MaxAss as an extension of PI-MinAvg. Starting from a suboptimal assignment in which additional tasks cannot be directly included without violating time constraints, PI-MaxAss is able to reschedule tasks to increase the allocation number simply through the cost-independent allocation. The idea is to attribute a high cost to an assigned task when the release of this task can permit an additional task to be inserted within the free time created. A schedule is considered optimal and without cost if the release of any task does not permit another task to be scheduled within the free time created.

PI-MaxAss follows the same algorithm process of PI-MinAvg, iterating over a task inclusion phase, a communication and conflict resolution phase. However, it adopts different definitions of inclusion performance impact and removal performance impact, which are denoted as IPI-MaxAss and RPI-MaxAss, respectively. A task’s IPI-MaxAss is set to be without cost if it can be included in a scheduler and satisfy time constraints.

$$\begin{array}{c}\begin{array}{cc}{w}_q^{\oplus }\left({\mathbf{p}}_i,t_q\right)=0,& \exists l\forall t_z\in \left\{{\mathbf{p}}_i{\oplus }_l{t}_q\right\},c_{i,z}\left({\mathbf{p}}_i{\oplus }_l{t}_q\right)\le min\left(s_z,f_i\right),t_q\in {\mathbf{\psi }}_i\end{array}\hfill \end{array}$$

(6)

where the candidate tasks for inclusion in ${\mathbf{p}}_i$ are formally defined as ${\mathbf{\psi }}_i=\left\{t_q\right|t_q\notin {\mathbf{p}}_{\mathrm{i}},w_q^{\ominus }>0\}$, which are those compatible with the robot’s capabilities and not already in ${\mathbf{p}}_i$, and with an RPI-MaxAss greater than 0. The RPI-MaxAss of a task is formally defined as:

$$w_q^{\ominus }=\left\{\begin{array}{c}\begin{array}{cc}U,& \begin{array}{cc}if& t_q\notin {\mathbf{p}}_i\end{array}\end{array}\hfill \\ \begin{array}{cc}0,& \begin{array}{cc}if& t_q\in {\mathbf{p}}_i\end{array}\end{array}\hfill \end{array}\right.$$

(7)

where the formula shows that unassigned tasks are initially set to have a fixed highest RPI-MaxAss, a constant defined as U, and the assigned tasks $t_k$ are initially set to have 0.

3. Proposed Rescheduling Method

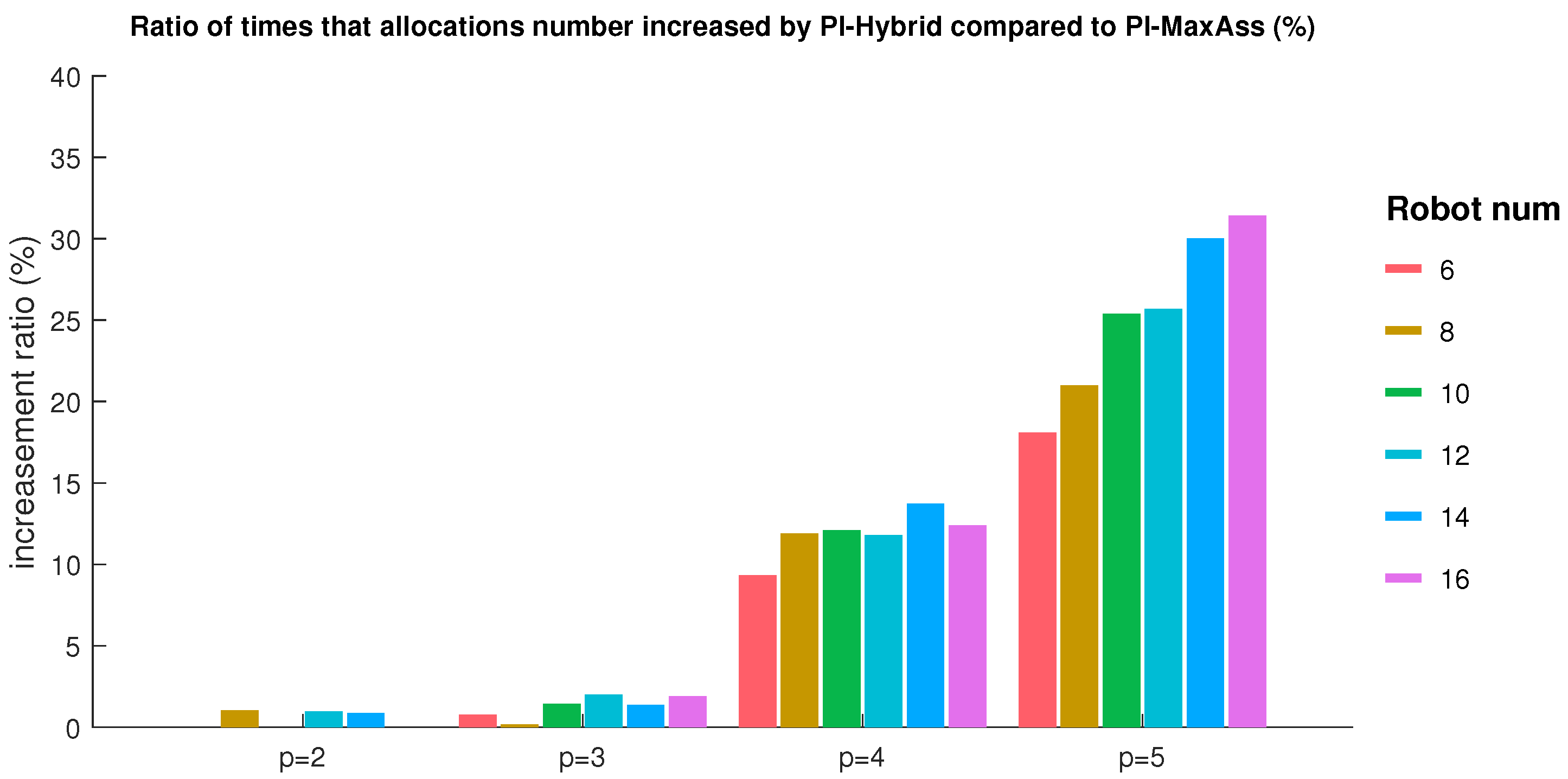
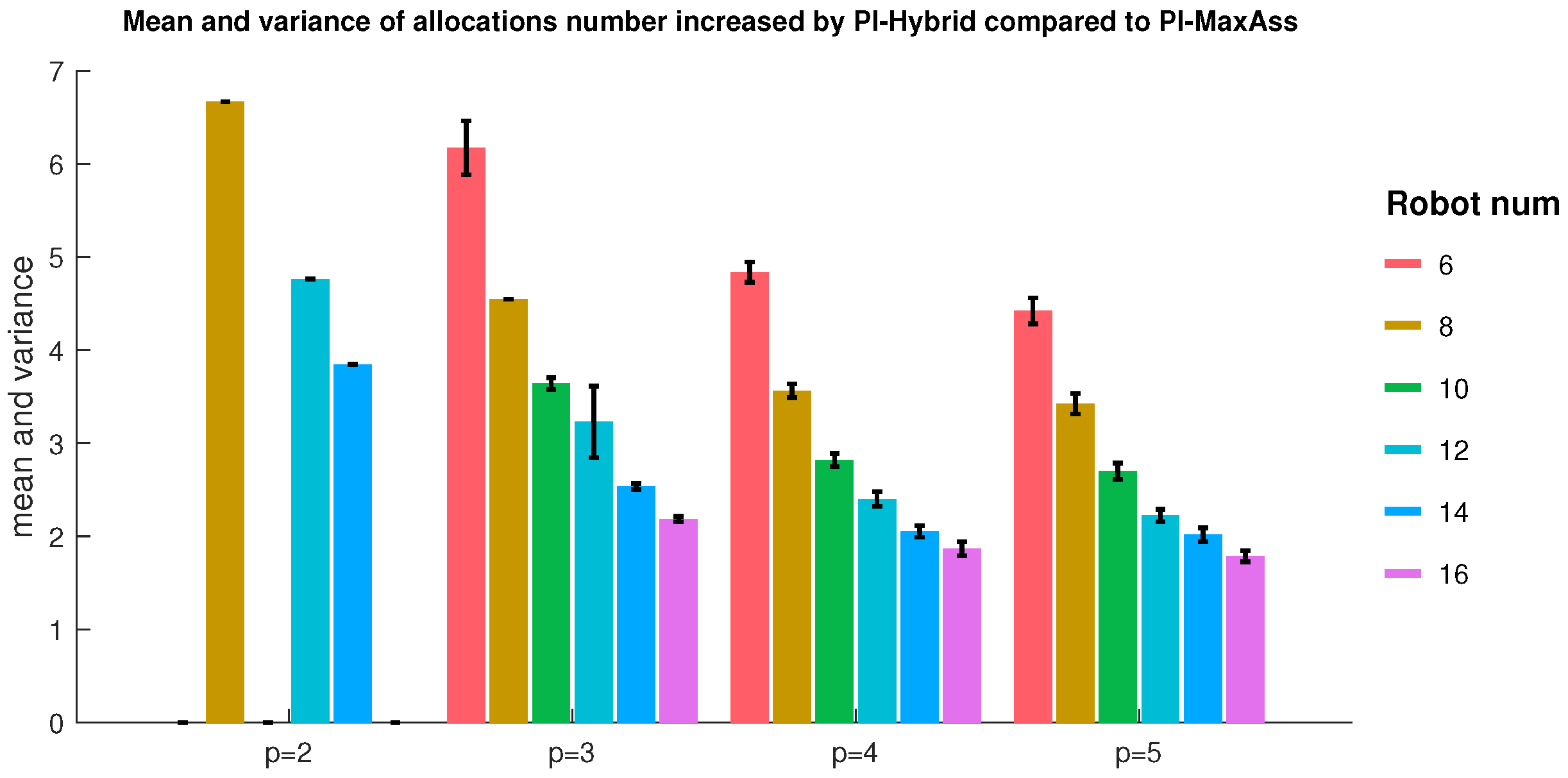
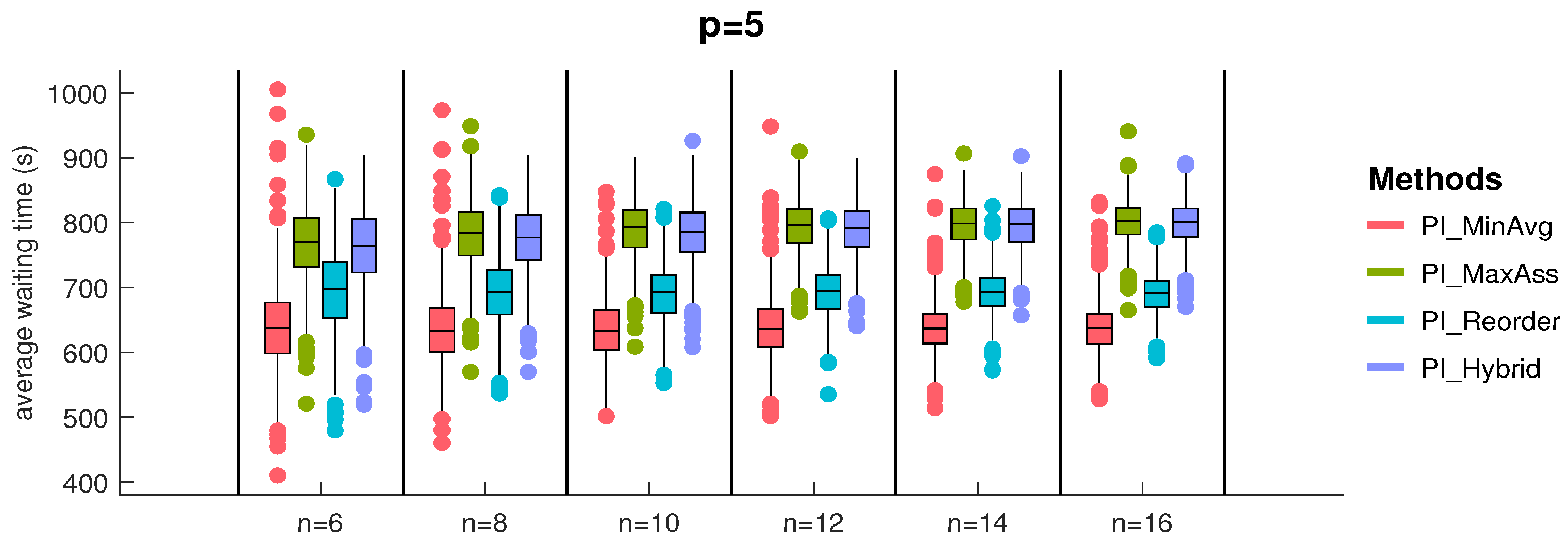
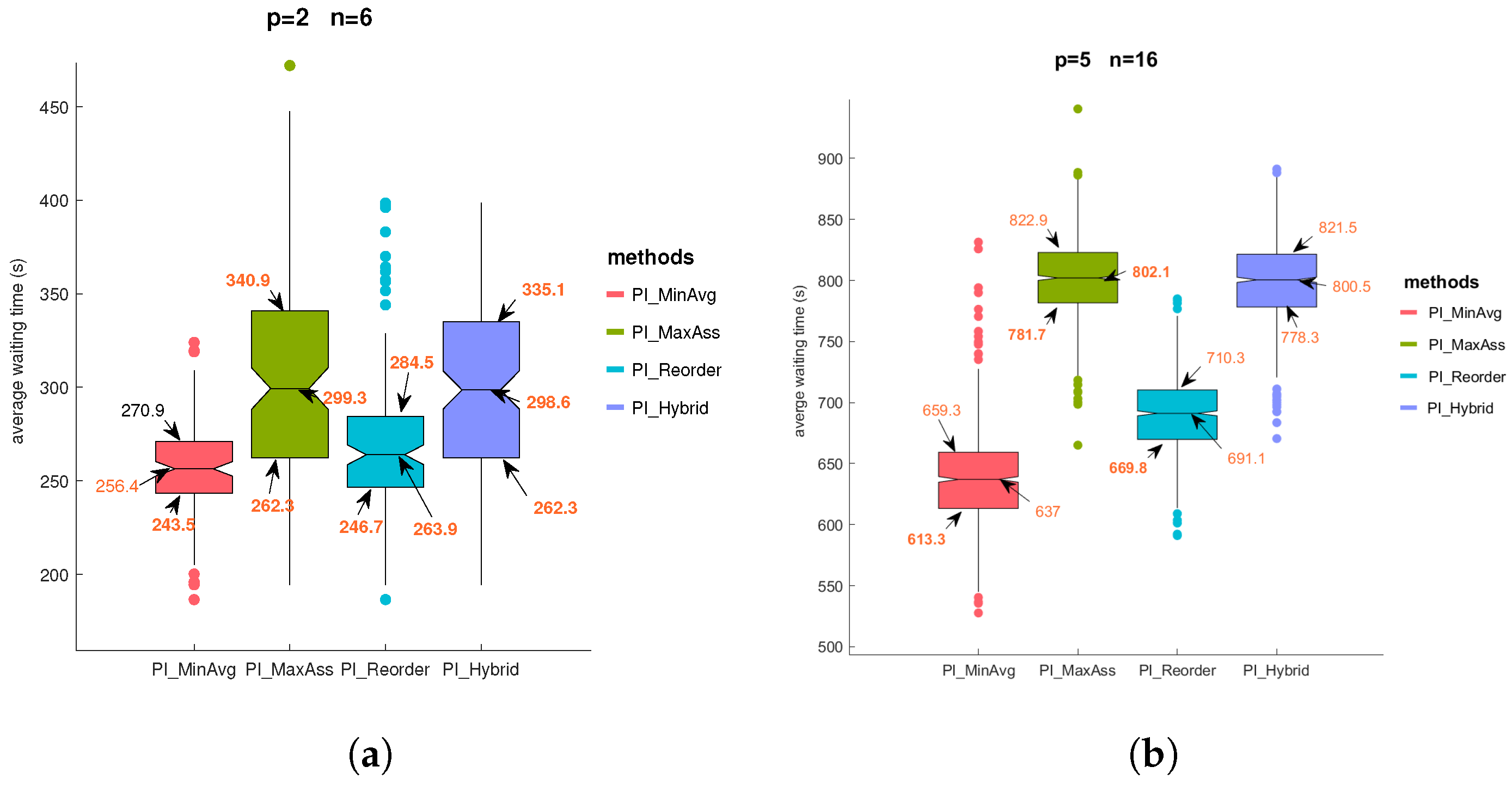
In general, distributed scheduling is not necessarily reasonable for individuals; it sacrifices local optimization to obtain a conflict-free global suboptimal solution while limiting the number of assigned tasks. Moreover, the exchange strategy is prone to deadlock, which is intolerable for the swarm and must be resolved. Below, we propose solutions to the above two aspects. In this section, we apply two rescheduling strategies to improve these problems: (1) One is the cost-dependent rescheduling strategy, which simply adds a local task reordering strategy in the recursive inclusion phase of PI-MinAvg to include unassigned tasks or new tasks directly; (2) the other is the cost-independent rescheduling strategy, that is, the improved deadlock-free PI-MaxAss method, which relies on the task exchange strategy without cost to create free time slots to contain unassigned tasks or new tasks indirectly. Finally, we incorporate the task reordering mechanism of strategy 1 into the recursive inclusion phase of strategy 2 to form a hybrid task rescheduling method.

3.1. A Novel Local Task Reordering Strategy

For search and rescue missions, PI-MinAvg prioritizes minimizing the average start time of all tasks, and then considers the number of tasks that can be accommodated, which makes it difficult to further increase the total number of allocated tasks and is not the most desirable for rescue. In order to achieve a consistent schedule, there is a mutual compromize among agents, although each adopts a heuristic greedy strategy. This may lead to the local scheduler possibly not being reasonable for individuals; either there is a task to look far away, or there is a necessity to wait. In other words, on the individual level, there is room for improvement in the local scheduler. Moreover, exchange-based methods, such as CBBA and PI-MinAvg, have a common feature that once included tasks that are not removed from the swarm in subsequent bidding rounds; they will only be exchanged within the swarm and obtained by other UAVs at a lower price. Actually, it is possible for the UAVs to form new slots to contain unassigned tasks or new tasks simply by rearranging their respective tasks without violating time constraints. To this end, we propose a novel distributed rescheduling method (denoted as PI-Reorder), which simply adds the local task reordering strategy to the recursive inclusion phase of PI-MinAvg, so that unassigned tasks or new tasks can be included as soon as possible without relying on the task exchange strategy (such as PI-MaxAss). The following is an example where the heuristic greedy strategy leads to non-ideal individual scheduling, and PI-MaxAss is unable to further improve the scheduling results through cost-independent task exchange.

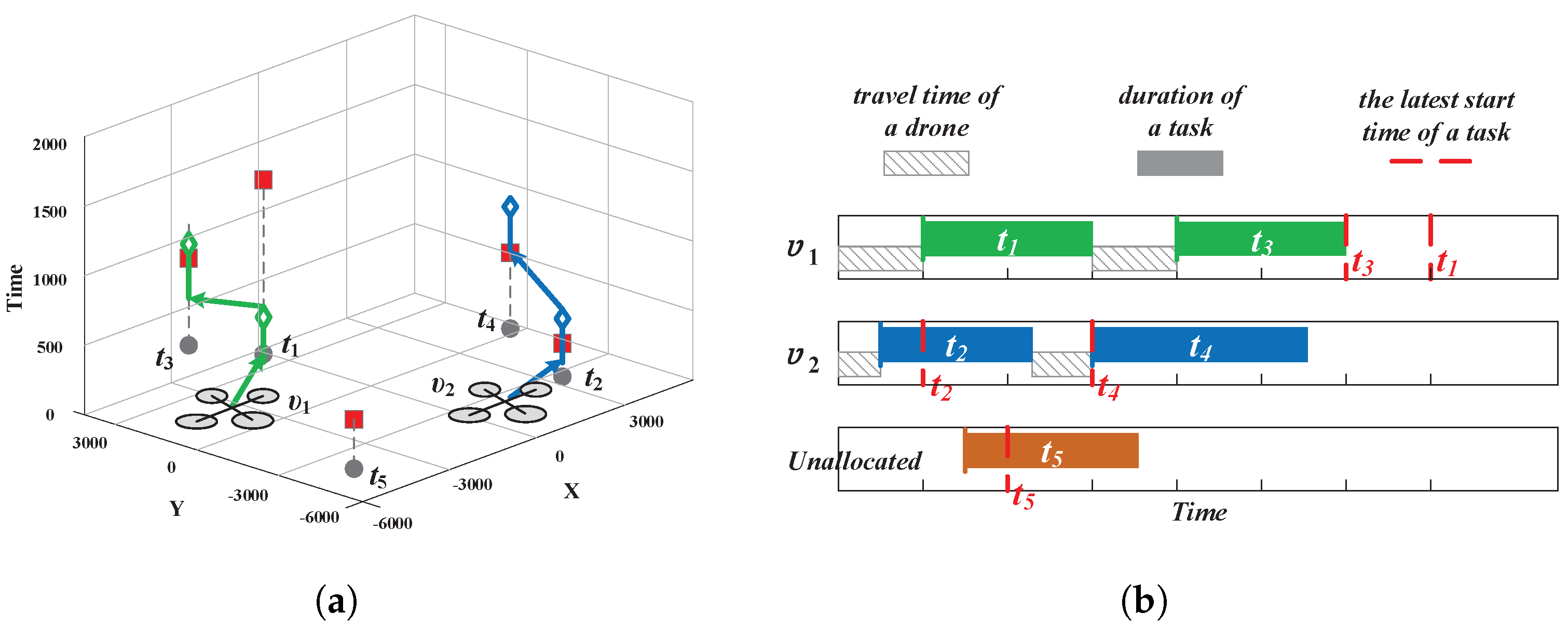
Example 1.

An illustrative example of two mobile UAVs $v_1,v_2$ and five tasks $t_1,\dots ,t_5$ distributed in a common partitioned workspace is depicted in Figure 1a. Driven by the greedy strategy of PI-MinAvg running on $v_1$, the UAV will firstly select $t_1$ due to its lower IPI-MinAvg and then $t_3$. Similarly, $v_1$ will choose to undertake $t_2$ and $t_4$ subsequently. However, the remaining task $t_5$ will not be selected by any UAV because neither $v_1$ nor $v_2$ can contain task $t_5$ without abandoning the existing task. Figure 1b depicts the timeline corresponding to the scheduling result in the left figure. Intuitively, it is not possible to create a feasible slot containing $t_5$ with a task exchange mechanism such as PI-MaxAss. For example: $v_1$ tries to pass $t_1$ to $v_2$ by raising $t_1$’s significance, thereby creating a slot that can contain $t_5$; however, $v_2$ is currently unable to take on additional tasks, and $t_5$ cannot be inserted into $v_2$’s task list. That is, there is no way to obtain a boost in the number of tasks by swapping methods.

The following describes the basic principles of the task reordering strategy, and the specific procedure is shown in Algorithm 1.

First, the UAV $v_i$ tries to sort its local scheduler in ascending order, according to the deadlines of tasks in the scheduler (Algorithm 1, line 2).

$$\begin{array}{c}{\tilde{\mathbf{p}}}_i=sort\left({\mathbf{p}}_i\right),s.t.\forall j\in \left\{1,\dots ,\left|{\mathbf{p}}_i\right|\right\},s_{j,K}<s_{j+1,K}\end{array}$$

(8)

Second, the UAV $v_i$ updates the time costs $c_{i,k}\left({\mathbf{p}}_i\right)$ of tasks in ${\tilde{\mathbf{p}}}_i$ (Algorithm 1, line 2). By adding $t_q$ to ${\mathbf{p}}_i$, $v_i$ will perform its remaining task assignments later. The time cost of tasks in the task list earlier than $t_q$ is not affected by increasing $t_q$.

Next, following PI-MinAvg, mentioned in Section 2.2, the UAV $v_i$ selects a task at a time to include in its updated task lists ${\tilde{\mathbf{p}}}_i$ until no more tasks can be added (Algorithm 1, lines 4–8).

Once tasks are recursively included, subsequent work follows the same method as PI-MinAvg, which is not described here.

Algorithm 1 Task Inclusion Procedure with Reordering running on $v_i$.

1: while$\left|{\mathbf{p}}_i\right|\le N_i$do 2:    Reorder ${\mathbf{p}}_i$ according to tasks’ deadlines: ${\tilde{\mathbf{p}}}_i\leftarrow sort\left({\mathbf{p}}_i\right)$. 3:    Update the time costs $c_{i,k}\left({\tilde{\mathbf{p}}}_i\right)$ for the tasks in ${\tilde{\mathbf{p}}}_i$. 4:    Compute the marginal significance list ${\mathbf{\gamma }}_{i,q}^{\oplus },\forall q\in \left\{1,\dots ,m\right\}$. 5:    if ${max}_{q=1}^m\{{\mathbf{\gamma }}_{i,q}-{\mathbf{\gamma }}_{i,q}^{\oplus }\}>0$ then 6:       Insert the task $t_{q^{\ast }}$ into ${\tilde{\mathbf{p}}}_i$ at position $l^{\ast }$. 7:       Update ${\mathbf{\gamma }}_{i,q^{\ast }},{\mathbf{\beta }}_{i,q^{\ast }},c_{i,\kappa }\left({\tilde{\mathbf{p}}}_i\right)$. 8:    end if 9:    ${\mathbf{p}}_i\leftarrow {\tilde{\mathbf{p}}}_i$. 10: end while 11: Update significance list ${\mathbf{\gamma }}_{i,k},\forall t_k\in {\mathbf{p}}_i$.

Continuing on Example 1, it is explained how the task reordering strategy achieves the further incorporation of $t_5$ while keeping the existing tasks $t_1,\dots ,t_4$ unchanged when PI-MinAvg and PI-MaxAss are incapable.

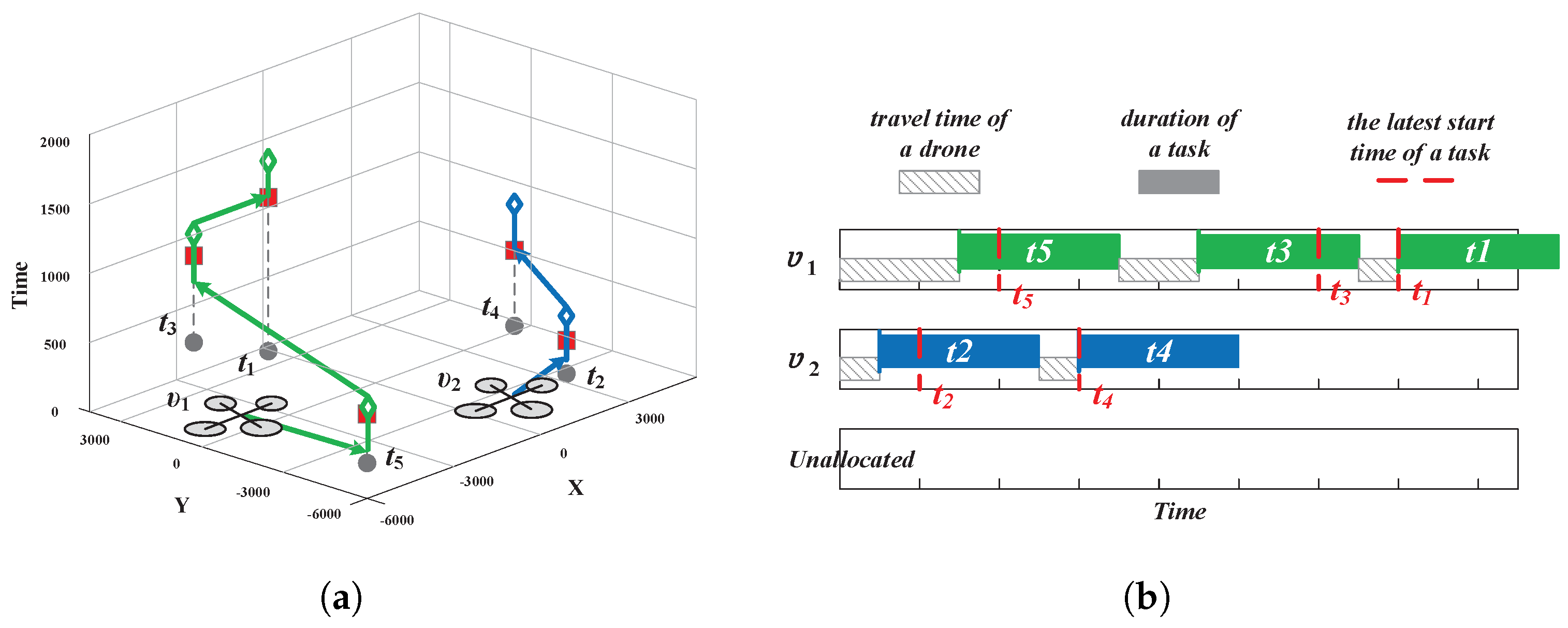
Example 2.

Based on the schedulers $\left\{t_1,t_3\right\}$ generated by PI-MinAvg, the UAV $v_1$ reorders its local scheduler according to tasks’ deadlines as shown in Figure 2a and it can create a new feasible slot for $t_5$. Thus, $v_1$ is able to add $t_5$ into its scheduler, increasing the allocation numbers further. The task timelines corresponding to Example 1 (continued) are illustrated in Figure 2b. Intuitively, utilizing the task reordering strategy, $v_1$ reorders its local scheduler from $\left\{t_1,t_3\right\}$ to $\left\{t_3,t_1\right\}$, despite increasing time cost. The change can create a feasible slot for unassigned tasks, so that $v_1$ adds a task into its scheduler as $\left\{t_5,t_3,t_1\right\}$.

The above example shows that without a swapping task, it is possible for each UAV to further increase the allocation number by exploiting its local schedule potential.

3.2. A Deadlock-Free Task Exchange Strategy

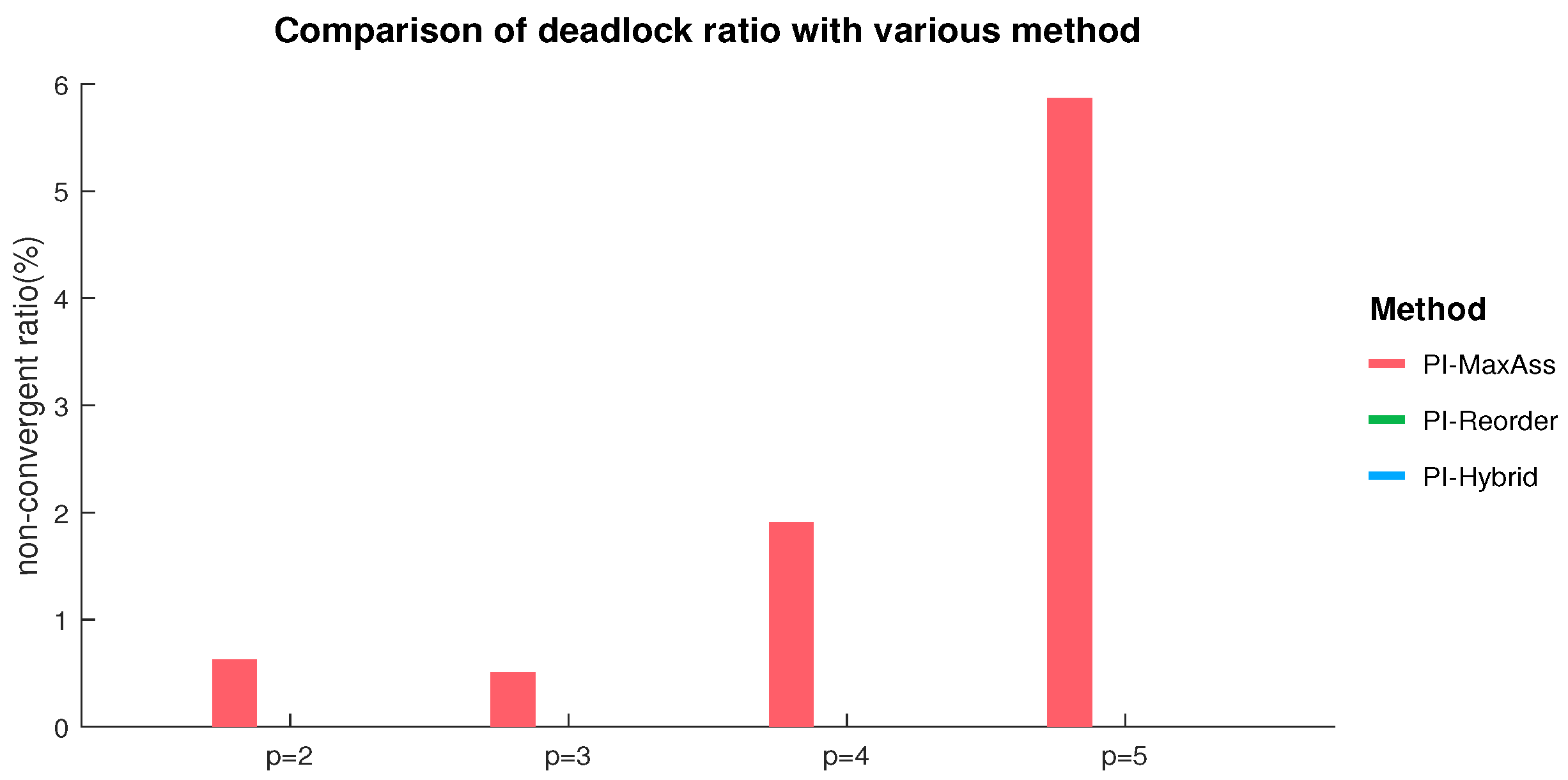
The effect of simply using the task reordering strategy is limited, and the task exchange strategy is still needed to obtain better schedules. Starting from a suboptimal assignment in which additional tasks cannot be directly included without violating time constraints, PI-MaxAss presented in [22] is able to reschedule tasks to increase the allocation number simply through the cost-independent allocation. The idea is to attribute a high cost (RPI-MaxAss) to an assigned task when the release of this task can permit an additional task to be inserted within the free time created, to further increase the total allocation number. However, PI-MaxAss occasionally falls into an infinite cycle of shifting the same task, i.e., the deadlock problem. In this section, we first analyze the deadlock phenomenon, and then propose a deadlock-free task exchange strategy.

(1) Deadlock Analysis for PI-MaxAss. To explain the deadlock problem for PI-MaxAss intuitively here an example of deadlock is exhibited in

Table 1. Deadlock phenomenon for PI-MaxAss.

Rounds	Phases	${\mathit{v}}_1$	${\mathit{v}}_2$	${\mathit{v}}_3$	Unassigned
0	— 1	$t_5\left(0\right),t_3\left(0\right)$	$t_2\left(0\right),t_4\left(0\right)$	$t_6\left(0\right)$	$t_1\left(U\right)$
1	TC	$t_1^{\varnothing }\left(U\right),t_2^2\left(0\right),t_3^1\left(0\right),t_4^2\left(0\right),t_5^1\left(0\right),t_6^3\left(0\right)$
	RU	$t_5\left(U-r\right),t_3\left(0\right)$	$t_2\left(0\right),t_4\left(0\right)$	$t_6\left(U-r\right)$	$t_1\left(U\right)$
2	TC	$t_1^{\varnothing }\left(U\right),t_2^2\left(0\right),t_3^1\left(0\right),t_4^2\left(0\right),t_5^1\left(U-r\right),t_6^3\left(U-r\right)$
	RU	$t_5\left(U-r\right),t_3\left(0\right)$	$t_2\left(U-2r\right),t_4\left(U-2r\right)$	$t_6\left(U-r\right)$	$t_1\left(U\right)$
3	TC	$t_1^{\varnothing }\left(U\right),t_2^2\left(U-2r\right),t_3^1\left(0\right),t_4^2\left(U-2r\right),t_5^1\left(U-r\right),t_6^3\left(U-r\right)$
	TI	~ 2	~	$+t_2\left(U-3r\right)$	~
	RU	$t_5\left(U-r\right),t_3\left(0\right)$	$t_2\left(U-2r\right),t_4\left(U-2r\right)$	$t_6\left(U-3r\right),t_2\left(U-3r\right)$	$t_1\left(U\right)$
4	TC	$t_1^{\varnothing }\left(U\right),t_2^3\left(U-3r\right),t_3^1\left(0\right),t_4^2\left(U-2r\right),t_5^1\left(U-r\right),t_6^3\left(U-3r\right)$
	TR	~	$-t_2\left(U-2r\right)$	~	~
	TI	~	$+t_2\left(0\right)$	~	~
	RU	$t_5\left(U-r\right),t_3\left(0\right)$	$t_2\left(0\right),t_4\left(0\right)$	$t_6\left(U-3r\right),t_2\left(U-3r\right)$	$t_1\left(U\right)$
5	TC	$t_1^{\varnothing }\left(U\right),t_2^2\left(0\right),t_3^1\left(0\right),t_4^2\left(0\right),t_5^1\left(U-r\right),t_6^3\left(U-3r\right)$
	TR	~	~	$-t_2\left(U-3r\right)$	~
	RU	$t_5\left(U-r\right),t_3\left(0\right)$	$t_2\left(0\right),t_4\left(0\right)$	$t_6\left(U-r\right)$	$t_1\left(U\right)$
6	G2	$t_1^{\varnothing }\left(U\right),t_2^2\left(0\right),t_3^1\left(0\right),t_4^2\left(0\right),t_5^1\left(U-r\right),t_6^3\left(U-r\right)$

¹ Not applicable. ² No tasks have been removed or included.

and a similar situation remains problematic.

Example 3.

A representative example of three mobile UAVs $v_1,v_2,v_3$ suffering from the deadlock problem when bidding for six tasks $t_1,\dots ,t_6$ with PI-MaxAss is depicted in Table 1, wherein each bidding round task consensus (abbreviated as TC), task removal (abbreviated as TR), task’s RPI-MaxAss update (abbreviated as RU) and task inclusion (abbreviated as TI) work in turn, but the stage in which the intermediate results do not change is omitted here for simplification. With PI, $v_1$ obtains two tasks $t_5,t_3$, $v_2$ also obtains two tasks $t_2,t_4$, $v_3$ obtains the task $t_6$ and the remaining task $t_1$ cannot be executed by any UAV. Next, the rescheduling process of PI-MaxAss is shown in Table 1, where the symbol in the form of $t_k\left(c\right),k\in \left\{1,\dots ,m\right\}$ indicates that $t_k$ is rescheduled to a UAV with its RPI-MaxAss equal to c. For an unassigned task (abbreviated as Un task), such as $t_1$, its RPI-MaxAss is set to a high value $U-n·r$, where r is a decay factor; that is, each time a task is rescheduled, its RPI value is subtracted by r. A task is regarded as an unassigned task if its RPI is larger than a preset value such as $U-3r$; that is, rescheduling is allowed for $t_1$ at most three times.

According to the schedules of PI-MinAvg given in the first row of Table 1, the rescheduling process of three UAVs bidding for six tasks is described in detail, which leads to an infinite deadlock loop.

In round 1, since $v_1$ and $v_2$ can add the unassigned task $t_1$ to their local scheduler on the premise that their tasks $t_5$ and $t_6$ are removed, respectively, they both actively increase $t_1$’s RPI-MaxAss to $U-r$, so that $t_1$ may be bid by other UAVs in the next round. The RPI-MaxAss of the remaining tasks in the individual UAV schedulers remain the same because even if they intend to remove any tasks from their schedulers, they cannot add any unassigned tasks.

In round 2, after communicating with each other, $v_2$ will find that the RPI-MaxAss of tasks $t_5$ and $t_6$ belonging to $v_1$ and $v_3$, respectively, have increased. At this point, $v_2$ has the opportunity to bid $t_6$ by removing $t_2$ or $t_4$, while $t_5$ is not considered because it cannot satisfy $v_2$’s time constraints. Similar to round 1, the RPI-MaxAss of $t_2$ and $t_4$ need to be raised to $U-2r$, so that they can be outbid by other UAVs.

In round 3, after communication and consistency, $v_3$ finds that $v_2$ increases the RPI of $t_2$, so it can add $t_2$ to its scheduler without removing any tasks. In the RPI-MaxAss update stage, $v_3$ finds that $t_4$ can be added on the premise of removing $t_6$, so $t_6$’s RPI-MaxAss is updated to $U-3r$.

In round 4, $v_2$ has to remove $t_2$ which was outbid by $v_3$. After removing $t_2$, $v_2$ selects the task with the lowest cost among the current candidate tasks, which happens to be still $t_2$ here. Then, when $v_2$ updates the RPI-MaxAss, it can still obtain $t_6$ by increasing the RPI-MaxAss of $t_2$ or $t_4$ as in round 2, but at this time, since $t_6$’ RPI-MaxAss for $v_3$ has reached the threshold value $U-3r$, for this reason $v_2$ cannot obtain $t_6$ with a lower RPI-MaxAss.

In round 5, $v_3$ has to remove $t_2$ which was outbid by $v_2$. After removing $t_2$, $v_3$ finds that there is a time margin to include $t_1$, so it updates $t_6$’s RPI-MaxAss to $U-r$, which goes back to round 2 (abbreviated as G2) and gets stuck in an endless loop.

Preliminary experiments running PI-MaxAss show that two or more UAVs occasionally get caught in an infinite cycle shifting the same tasks. For a swarm system, this phenomenon is intolerable and will cause the system to stagnate. For example, in a search and rescue mission, when multiple UAVs perform distributed task scheduling, in the absence of algorithm truncation, they will not be able to get out of the algorithm’s infinite loop, resulting in the inability to obtain schedules in time to carry out actions, and ultimately causing survivors to be unable to obtain rescue. Therefore, it is necessary to find a way to avoid this deadlock problem.

(2) A Deadlock-free Task Exchange Strategy. Ref. [22] proposed a solution to limit the number of times that a UAV can remove the same task from its list before it no longer attempts to include it. A removal task set ${\mathbf{Y}}_i\in {\mathbb{Z}}_{+}$ is created to record removed tasks, and a counter vector ${\varpi }_i$ is used to store the times each task has been removed from a UAV $v_i$’s task list. The precaution ${\varpi }_{i,k}\le \sigma ,\forall t_k\in {\mathbf{p}}_i$ can prevent those tasks that are being repeatedly swapped from being scheduled optimally, but it ensures that the system can converge. However, this method relies heavily on the reasonableness of the maximum number $\sigma$ of removals, with a lower limit causing premature truncation of the algorithm, and a higher limit causing multiple invalid bids. Here, based on the exchange mechanism of PI-MaxAss, we introduce a removed task set ${\mathbf{Y}}_i$, an included task set ${\mathbf{\Gamma }}_i$, a task removed counter ${\varpi }_{i,q}$, a task included counter ${\vartheta }_{i,q}$ and a collection of task included counters ${\mathbf{\Xi }}_i$ to achieve deadlock-free task exchange. The specific process is as follows:

As with PI-MaxAss, unallocated tasks are set initially to have a fixed highest RPI-MaxAss, a constant defined as U, such that if $t_q$ is unassigned then $w_q^{\ominus }=U$. The RPI-MaxAss of assigned tasks $t_k$ are initially set to 0, such that $w_k^{\ominus }=0$.

In the task inclusion phase as shown in Algorithm 2, UAVs select tasks to include in their schedulers until no more tasks can be added. The candidate task $t_q$ is the one compatible with the functionality of $v_i$ and not already in ${\mathbf{p}}_i$, and with an RPI-MaxAss greater than 0. In addition, $t_q$ either does not belong to the removed task set ${\mathbf{Y}}_i$, or it belongs to ${\mathbf{Y}}_i$ but ${\varpi }_{i,q}<\sigma$ (Algorithm 2, line 4). This condition indicates that $t_q$ has never been removed in the previous iteration, or the task removed counter ${\varpi }_{i,q}$ is less than the set threshold $\sigma$. The candidate tasks for inclusion in ${\mathbf{p}}_i$ are formally defined as

$$\begin{array}{ccc}{\mathbf{\psi }}_i=\left[t_1,\dots ,t_{\varsigma }\right],t_q\notin {\mathbf{p}}_i,w_q^{\ominus }>0,& if& t_q\notin {\mathbf{Y}}_{i}or\left(t_q\in {\mathbf{Y}}_{i}and{\varpi }_{i,q}<\sigma \right)\end{array}$$

(9)

If the condition in Algorithm 2, line 6, returns true for at least one position l, the IPI-MaxAss $w_q^{\oplus }$ of $t_q$ in ${\mathbf{p}}_i$ is recorded such that,

$$\begin{array}{c}\begin{array}{cc}{w}_q^{\oplus }\left({\mathbf{p}}_i,t_q\right)=0,& \exists l\forall t_z\in \left\{{\mathbf{p}}_i{\oplus }_l{t}_q\right\},c_{i,z}\left({\mathbf{p}}_i{\oplus }_l{t}_q\right)\le min\left(s_z,f_i\right),t_q\in {\mathbf{\psi }}_i\end{array}\hfill \end{array}$$

(10)

Next, $v_i$ selects for inclusion the task whose IPI-MaxAss can improve upon the task’s current RPI-MaxAss the most as shown in the following formula. An IPI-MaxAss of $t_q$ in ${\mathbf{p}}_i$ lower than $t_q$’s RPI-MaxAss in another UAV’s task list ${\mathbf{p}}_j$ indicates that the global cost can be reduced if $t_q$ is reallocated to $v_i$.

$$\underset{q=1}{\overset{m}{max}}\{{\mathbf{\gamma }}_{i,q}-{\mathbf{\gamma }}_{i,q}^{\oplus }\}>0$$

(11)

After the most appropriate task $t_{q^{\ast }}$ is included (Algorithm 2, line 11), $t_{q^{\ast }}$ needs to be added to the included task set ${\mathbf{\Gamma }}_i$ if $t_{q^{\ast }}\notin {\mathbf{\Gamma }}_i$, the corresponding task which included counter ${\vartheta }_{i,q^{\ast }}$ is instantiated with its initial value to be 1; otherwise, only the task which included count needs to be incremented by one (Algorithm 2, line 13).

$$\left\{\begin{array}{c}\begin{array}{cc}{\mathbf{\Gamma }}_i\leftarrow {\mathbf{\Gamma }}_i\cup \left\{t_{q^{\ast }}\right\}and{\vartheta }_{i,q^{\ast }}\leftarrow 1,& if{t}_{q^{\ast }}\notin {\mathbf{\Gamma }}_i\end{array}\hfill \\ \begin{array}{cc}{\vartheta }_{i,q^{\ast }}\leftarrow {\vartheta }_{i,q^{\ast }}+1,& if{t}_{q^{\ast }}\in \end{array}{\mathbf{\Gamma }}_i\hfill \end{array}\right.$$

(12)

Before the end of the task inclusion procedure, the RPI-MaxAss list, which keeps track of which UAV is assigned to which task, needs to be updated; this differs from PI-MaxAss in that additional conditions need to be met (Algorithm 2, line 15). Refer to Algorithm 3 for the specific process.

Algorithm 2 Task Inclusion Procedure running on $v_i$.

1: while$\left|{\mathbf{p}}_i\right|\le N_i$do 2:    $w_q^{\oplus }$← highest permissible cost, $w_q^{\oplus }\in {\mathbf{\gamma }}_i^{\oplus }$. 3:    Identify candidate tasks ${\mathbf{\psi }}_i$ satisfying $t_q\notin Y_{i}or\left(t_q\in Y_{i}and{\varpi }_{i,q}<\sigma \right)$ according to (11). 4:    for each task $t_q$ in ${\mathbf{\psi }}_i$ do 5:        if ${\mathbf{p}}_i{\oplus }_l{t}_q$ is feasible then 6:          Record the IPI-MaxAss $w_q^{\oplus }$ of $t_q$ in ${\mathbf{p}}_i$ according to (10). 7:        end if 8:    end for 9:    if ${max}_{q=1}^m\{{\mathbf{\gamma }}_{i,q}-{\mathbf{\gamma }}_{i,q}^{\oplus }\}>0$ then 10:     Insert task $t_{q^{\ast }}$ into ${\mathbf{p}}_i$ at position $l^{\ast }$. 11:     Update ${\mathbf{\gamma }}_{i,q^{\ast }},{\mathbf{\beta }}_{i,q^{\ast }},c_{i,\kappa }\left({\mathbf{p}}_i\right)$. 12:     ${\mathbf{\Gamma }}_i\leftarrow {\mathbf{\Gamma }}_i\cup \left\{t_{q^{\ast }}\right\}$ and ${\vartheta }_{i,q^{\ast }}\leftarrow 1$ if $t_{q^{\ast }}\notin {\mathbf{\Gamma }}_i$, else ${\vartheta }_{i,q^{\ast }}\leftarrow {\vartheta }_{i,q^{\ast }}+1$. 13:    end if 14: end while 15: Update significance ${\mathbf{\gamma }}_{i,k}$ with Algorithm 3 satisfying ${\vartheta }_{i,k}>\lambda$ or ${\varpi }_{i,k}=0$, $\forall t_k\in {\mathbf{p}}_i$.

In this paper, task $t_k$’s RPI-MaxAss ${\mathbf{\gamma }}_{i,k}$ is the maximum significance change brought by the insertion of a candidate task $t_q\in {\mathbf{\Omega }}_{i,k}$ shifted from other UAVs in local scheduler ${\mathbf{p}}_i$ after $t_k$ is removed, where ${\mathbf{\Omega }}_{i,k}$ is the candidate tasks set consisting of unassigned tasks, and tasks that would be released from other UAVs’ schedulers.

$$\begin{array}{c}{\mathbf{\Omega }}_{i,k}=\left\{t_q\in {\overline{\mathbf{\psi }}}_i|\exists l\forall t_z\in \left\{{\mathbf{p}}_i^{\ominus k}{\oplus }_l{t}_q\right\},c_{i,z}\left({\mathbf{p}}_i^{\ominus k}{\oplus }_l{t}_q\right)\le min(s_z,f_i)\right\}\hfill \end{array}$$

(13)

where ${\overline{\mathbf{\psi }}}_i$ is a list of the candidate tasks defined as follows:

$$\begin{array}{ccc}{\overline{\mathbf{\psi }}}_i=\left[t_1,\dots ,t_{\zeta }\right],& t_q\notin {\mathbf{p}}_i,0<\delta <{\gamma }_{i,q},& if{\mathbf{\Xi }}_{i,k}>\lambda or{\varpi }_{i,k}=0\end{array}$$

(14)

The candidate tasks follow the same constraints as the candidates in (11) with the added constraint that the candidate task’s RPI-MaxAss is greater than $\delta$. This constraint is used to limit the number of reassignments permissible to allocate an additional task. In addition, tasks that do not belong to the removed task set ${\mathbf{Y}}_i$ or with a task included counter ${\vartheta }_{i,k}$ greater than the threshold $\lambda$ can only be updated with the RPI-MaxAss. That is, if a task $t_k$ has never been removed, it can be freely updated with the RPI-MaxAss; if a task $t_k$ has a removed record and the task included counter ${\mathbf{\Xi }}_{i,k}$ exceeds the threshold $\lambda$ after being included in ${\mathbf{\Gamma }}_i$, then the task can be updated with the RPI-MaxAss.

If a task $t_k$ in ${\mathbf{p}}_i$ can be replaced by two or more candidate tasks $t_q$ with different RPI-MaxAss, the highest RPI-MaxAss is recorded. The RPI-MaxAss of $t_q$ in ${\mathbf{p}}_i$ is formally defined as

$$\begin{array}{cc}{w}_k^{\ominus }\left({\mathbf{p}}_i,t_k\right)=\underset{q=1}{\overset{|{\mathbf{\Omega }}_{i,k}|}{max}}\left\{w_q^{\ominus }-r\right\},& t_q\in {\mathbf{\Omega }}_{i,k},r\in {\mathbb{R}}_{+}\end{array}$$

(15)

where the decay factor r subtracted is used for limiting the number of reschedules.

Algorithm 3 Significance Update Procedure running on $v_i$.

1: Maintain tasks in ${\mathbf{p}}_i$ with the lowest RPI-MaxAss to 0: ${\mathbf{\gamma }}_{i,k}\leftarrow 0,if{t}_k\in q_i$. 2: Identify Candidate Tasks ${\overline{\mathbf{\psi }}}_i$ satisfying ${\mathbf{\Xi }}_{i,k}>\lambda$ or ${\varpi }_{i,k}=0$ according to (14). 3: for each task $t_k$ in ${\mathbf{p}}_i$ do 4:    Create a temporary scheduler ${\mathbf{p}}_i^{\ominus k}={\mathbf{p}}_i\ominus t_k$. 5:    Update $c_{i,z}\left({\mathbf{p}}_i^{\ominus k}\right)$ for tasks after $t_k$. 6:    Identify the list of candidate tasks ${\mathbf{\Omega }}_{i,k}$ according to (13). 7:    Compute $t_k$’s RPI-MaxAss $w_k^{\ominus }({\mathbf{p}}_i,t_k)$ according to (15). 8: end for

In the communication and conflict resolution phase as shown in Algorithm 4, except for the following differences, this paper follows the same task removal process for PI-MinAvg introduced in Section 2.2. When a task $t_{k^{\ast }}$ has been removed from the UAV $v_i$’s scheduler ${\mathbf{p}}_i$ for the first time, it will be added to ${\mathbf{Y}}_i$, and ${\varpi }_{i,k^{\ast }}$ is initialized to 1; otherwise, only the removal count needs to be incremented by one.

$$\left\{\begin{array}{cc}{\mathbf{Y}}_i\leftarrow {\mathbf{Y}}_i\cup \left\{t_{k^{\ast }}\right\}and{\varpi }_{i,k^{\ast }}\leftarrow 1,& if{t}_{k^{\ast }}\notin {\mathbf{Y}}_i\\ {\varpi }_{i,k^{\ast }}\leftarrow {\varpi }_{i,k^{\ast }}+1,& if{t}_{k^{\ast }}\in {\mathbf{Y}}_i\end{array}\right.$$

(16)

Once the current round of removal while-cycle ends, the tasks just removed need to be immediately deleted from the inclusion set ${\mathbf{\Gamma }}_i$.

$$\begin{array}{cc}{\mathbf{\Gamma }}_i\leftarrow {\mathbf{\Gamma }}_i-\left\{t_k\right\},& \forall t_k\in {\mathbf{\Gamma }}_i\cap {\mathbf{Y}}_i\end{array}$$

(17)

The corresponding task included counter ${\vartheta }_{i,k}\in {\mathbf{\Xi }}_i$ also needs to be cleared.

$$\begin{array}{cc}{\mathbf{\Xi }}_i\leftarrow {\mathbf{\Xi }}_i-\left\{{\vartheta }_{i,k}\right\},& \forall {\vartheta }_{i,k}\in {\mathbf{\Xi }}_{i}and{t}_k\notin {\mathbf{\Gamma }}_i\end{array}$$

(18)

For the detailed removal process of PI-MinAvg, please refer to [7].

Algorithm 4 Task Removal Procedure running on $v_i$.

1: UAV $v_i$ forms its conflict tasks set ${\mathbf{d}}_i\leftarrow {\mathbf{p}}_i\left[{\mathbf{\beta }}_i\left[{\mathbf{p}}_i\right]\ne i\right]$. 2: while${max}_{k=1}^{|{\mathbf{d}}_i|}\{{\mathbf{\gamma }}_i^{◊}\left[{\mathbf{d}}_i\right]-{\mathbf{\gamma }}_i\left[{\mathbf{d}}_i\right]\}>0$ and ${\mathbf{d}}_i\ne \varnothing$ do 3:    Remove task $t_{k^{\ast }}\leftarrow arg{max}_{k=1}^{|{\mathbf{d}}_i|}\{{\mathbf{\gamma }}_i^{◊}\left[{\mathbf{d}}_i\right]-{\mathbf{\gamma }}_i\left[{\mathbf{d}}_i\right]\}$ from ${\mathbf{p}}_i$ and ${\mathbf{d}}_i$. 4:    Update costs $c_{i,\kappa }\left({\mathbf{p}}_i\right)$ and significance ${\mathbf{\gamma }}_i^{◊}$ for the rest of the tasks in ${\mathbf{p}}_i$ and ${\mathbf{d}}_i$. 5:    ${\mathbf{Y}}_i\leftarrow {\mathbf{Y}}_i\cup \left\{t_{k^{\ast }}\right\}$ and ${\varpi }_{i,k^{\ast }}\leftarrow 1$ if $t_{k^{\ast }}\notin {\mathbf{Y}}_i$, else ${\varpi }_{i,k^{\ast }}\leftarrow {\varpi }_{i,k^{\ast }}+1$. 6: end while 7: Remove task $t_k$ from the included task set ${\mathbf{\Gamma }}_i$ for any $t_k\in {\mathbf{\Gamma }}_i\cup {\mathbf{Y}}_i$. 8: Remove the task included counter ${\vartheta }_{i,k}$ from ${\mathbf{\Xi }}_i$ satisfying $t_k\notin {\mathbf{\Gamma }}_i$. 9: Update the local list ${\mathbf{\beta }}_i\left({\mathbf{d}}_i\right)\leftarrow i$ belongs to UAV $v_i$.

3.3. The Integrated Method with Task Reordering and Task Exchange

Here, a decentralized rescheduling method for each UAV running independently is presented, denoted as PI-Hybrid, which combines the local reordering strategy with the modified task exchange strategy to improve optimization and avoid deadlocks. The pseudocode of the entire iterative process is shown in Algorithm 5.

Before entering the loop iteration, the parameters ${\mathbf{Y}}_i,{\varpi }_{i,k},\sigma ,{\mathbf{\Gamma }}_i,{\vartheta }_{i,k},{\mathbf{\Xi }}_i,\lambda$ need to be initialized. After entering the while loop, Algorithm 1 is called to reorder the tasks in the respective scheduler ${\mathbf{p}}_i$, and the unassigned tasks are added according to the greedy strategy to allocate as many tasks as possible. Next, Algorithm 2 is called to try to exchange the local task to other UAVs to free time slots for unassigned tasks. Subsequently, through mutual communication, the UAV $v_i$ obtains the consistent assignments of its scheduler ${\mathbf{\beta }}_i$ and significance list ${\mathbf{\gamma }}_i$ using consensus rules [19]. This information is used to guide the call to Algorithm 4 to remove local conflicting tasks. The above phases repeatedly alternate until a global conflict-free task allocation is agreed upon by all UAVs.

Algorithm 5 Distributed Scheduling Method running on $v_i$

1: Initialize timer $T\leftarrow 1$ and $converged\leftarrow false$. 2: Initialize parameters ${\mathbf{Y}}_i,{\varpi }_{i,k},\sigma ,{\mathbf{\Gamma }}_i,{\vartheta }_{i,k},{\mathbf{\Xi }}_i,\lambda$. 3: while$converged$ is false do 4:    Call Task Reordering Procedure with Algorithm 1. 5:    Call Task Inclusion Procedure with Algorithms 2 and 3, in which. 6:    Communication and Conflict Resolution using consensus rules. 7:    Call Task Removal Procedure with Algorithm 4. 8:    $converged\leftarrow CheckConvergence$. 9:    $T\leftarrow T+1$. 10: end while

4. Numerical Results

This section presents the numerical simulations conducted to test the performance of the proposed PI-Hybrid compared with that of PI-MinAvg and PI-MaxAss. In addition, PI-Reorder is also compared to independently reflect its impact on the overall performance. Among the above methods, PI-MaxAss, PI-Reorder and PI-Hybrid are all initialized with the PI-MinAvg solution. The results of simulations are analyzed from optimization and deadlock-free, respectively.

4.1. Scenario and Simulation Setup

The scenarios adopted in this paper are consistent with those of the literature [7,21]. The setup uses a rescue team equally split into two UAVs rescuing two types of survivors, who are likewise equally split into those requiring food and those requiring medicine. Parameters related to the scenario are summarized in

Table 2. Parameters related to the simulation scenario.

Properties	Medicine	Food
UAV speed	30$\mathrm{m}·{\mathrm{s}}^{-1}$	50 $\mathrm{m}·{\mathrm{s}}^{-1}$
UAV initial position	Random distribution in 10 km × 10 km × 0 km
Task duration	300 s	500 s
Task deadline	Random distribution between 0 s and 2000 s
Task location	Random distribution in 10 km ×10 km × 1 km

and are illustrated as follows. The UAVs are randomly distributed in 10 km × 10 km × 0 km ground space, where the UAVs’ speeds are assumed to be constant and are set to 30 $\mathrm{m}·{\mathrm{s}}^{-1}$ and 50 $\mathrm{m}·{\mathrm{s}}^{-1}$, respectively. The tasks take place in a 3D space spanning 10 km × 10 km × 1 km, with coordinates drawn from uniform distributions randomly. The medicine tasks last for a duration of 300 s and the food tasks last 350 s. The deadlines for starting each rescue are uniformly distributed on a timeline between 0 and 2000 s. Given the random initialization of tasks and UAV locations and deadlines, it is sometimes impossible for some tasks to be started by any UAV before their deadline. In these simulations, all task information is available to all UAVs up front.

4.2. Results and Analysis

As elaborated here, the paper uses the Monte Carlo method to implement random simulations, where each method is tested 1000 times for each pair of $p\in \left\{2,3,4,5\right\}$ and $n\in \left\{2,4,\dots ,16\right\}$. p is the ratio of the number of tasks to the number of UAVs, and n is the number of UAVs.

4.2.1. Optimization

First of all, the total allocation number obtained with four methods is compared and analyzed, which can be said to be the most important optimization indicator. For example, in search and rescue missions, saving one more survivor may be more important than other things. Figure 3 depicts the allocation numbers using four methods in the same scenario. When the proportion p is the same, as n increases, the total number of assigned tasks tends to increase. PI-MinAvg as a scheduling method has the lowest allocation number, and other rescheduling methods initialized with the PI-MinAvg solution all produce a boost in the allocation numbers. PI-Reorder can increase the limited allocation number by reordering UAVs’ local scheduler. PI-MaxAss as a typical task-swap method is able to obtain an appreciable effect on the allocation number. PI-Hybrid has the best improvement for the allocation numbers. Moreover, it should be explained that the deadline is randomly distributed between 0 and 2000 s, which means that some tasks have a short random deadline and it is impossible to complete them. Therefore, it is impossible to schedule all the tasks in such a situation.

Since Figure 3 can only present the variation trend of the number of scheduled tasks as increases and the approximate differences between methods, Figure 4 shows the box plots of the allocation numbers under the conditions of two groups of $p=2,n=6$ and $p=5,n=16$, respectively.

It can be seen from Figure 4a that PI-Reorder cannot increase the number of scheduled tasks through local reordering based on the solution of PI-MinAvg, while PI-MaxAss allocates one more task as a whole through task exchange. Similarly, PI-Hybrid’s total allocation number is the same as PI-MaxAss. The reason for the above phenomenon is that when the total number of tasks to be assigned is low and the number of UAVs is small, the optimization of the PI-MinAvg solution is close to optimal, and the room for improvement is small. At this time, since the local task switching cannot obtain a better solution, PI-Hybrid actually works only by its task switching, which is equivalent to PI-MaxAss. It can be seen from Figure 4b that as p and n increase, the median task assignment of PI-Reorder increases from 66 to 69 compared to PI-MinAvg, which is due to the fact that more UAVs have more tasks that can be chosen so that the total number of tasks for the problem has more room for improvement. Of course, PI-Reorder that only relies on local tasks reordering cannot obtain the effect of the PI-MaxAss method using task exchange, but PI-Hybrid combining the two mechanisms can obtain a better solution than PI-MaxAss. For example, the median assigned tasks increased from 73.5 to 74.

Since the solution performance of PI-MinAvg and PI-MaxAss is already very good, it is not obvious from the improvement of the allocation numbers obtained in the above experiments. Next, the number of times increasing allocation numbers in 1000 tests with different combinations of p and n is counted as shown in Figure 5. Removing unnecessary elaboration, here mainly PI-Hybrid and PI-MaxAss are compared. It can be found that, when p is larger, more solutions of PI-MaxAss can be improved by PI-Hybrid. This is because the larger p is, the larger the space for reordering tasks will be, and the hybrid mechanism can achieve a better optimization effect that cannot be reached with a solo task swap.

Figure 6 summarizes the average increase of scheduled tasks in the improved solutions in which the mean and standard deviation are shown. Obviously, PI-Hybrid has a good effect on the increase of the number of allocated tasks compared with PI-MaxAss, where the increase rate has reached about 7% when p and n are equal to 3 and 6, respectively. When the number of UAVs increases, the space for swapping tasks is also enlarged, making the difference between the two methods smaller. That is why PI-Hybrid has a weaker effect compared with PI-MaxAss under the condition of n increasing but p remaining unchanged, which can be seen in Figure 6.

Next, let us look at another important indicator. Under the same total number of tasks scheduled, the shorter the average waiting time, the better the method. Figure 7 is a graph about the average waiting time of various methods to complete tasks in the same scenarios. It is observed that PI-MinAvg has the shortest completion time because it also completes the least number of tasks. PI-Reorder has the second short travel time, which is also reasonable for its completed task number exceeds PI-MinAvg but not others. In addition, carefully comparing PI-MaxAss and PI-Hybrid, whether it is the upper quartile, the median or the lower quartile, PI-Hybrid is lower than PI-MaxAss to varying degrees, which fully shows that the proposed method not only increases the total number of the scheduled tasks but also reduces the average waiting time.

Figure 8 shows the boxplot statistics of the average waiting time of the four methods under the conditions of $p=2,n=6$, and $p=6,n=16$, respectively. It shows the boxplot statistics of the average waiting time of the four methods under the conditions of $p=2,n=6$, and $p=6,n=16$, respectively. As the number of assigned tasks increases, the average waiting time of PI-MinAvg, PI-Reorder and PI-MaxAss also increases. It is worth remembering that from the median, upper quartile and lower quartile of average waiting time, PI-Hybrid is able to obtain less average waiting time while allocating more total tasks. This performance improvement is obtained by mixing two strategies of the task reordering and the task exchange, which is bound to be crucial for the swarm search and rescue.

From the above analyses, it can be seen that the combination of the local task reordering and the task exchange can not only improve the allocation number but also have better average waiting time.

4.2.2. Deadlock Avoidance

Another important issue addressed in this paper is to avoid the algorithm occasionally falling into an infinite cycle of shifting the same task. Figure 9 shows the statistical deadlock situation of different methods with various values of p, where the abscissa is the ratio of task and UAV numbers, and the ordinate is the deadlock rate. The deadlock rate of a method with each is its average under various conditions of n from 6 to 16, where each situation is tested 1000 times with random initialization of UAVs and tasks.

It can be found that the deadlock situation only occurs in PI-MaxAss, and all the other proposed methods do not exist in any deadlock. For the PI-MaxAss algorithm, when p is equal to 2 or 3, its deadlock rate is very low, having not reached 1%. However, its deadlock rate increases rapidly with the increase of p, which comes up to 6% approximately at the condition of $p=5$. This is because more participating UAVs and tasks will lead to more conflict between UAVs, while PI-MaxAss does not consider the potential deadlock avoidance. By contrast, PI-Hybrid is completely deadlock-free no matter what the values of p and n are.

5. Conclusions

Aiming at the new characteristics of multi-vehicle scheduling given by UAV swarm, such as self-organization, scalability and reconfiguration, this paper proposes a task rescheduling method that integrates local task reordering and improved task exchange strategy, with the goal of secondary optimization of task scheduling suboptimal solution and task reconfiguration. As a supplement to the task exchange-based strategy, local task reordering is a new cost-related strategy to increase the number of allocation tasks. To improve the task exchange-based strategy, deadlock detection and isolation mechanism are introduced to avoid occasional task exchange falling into the deadlock problem. Based on the swarm rescue mission, a large number of numerical simulation experiments show that the integrated method can not only improve the number of allocation tasks but also have a better average waiting time.

In the future, we will carry out research on scheduling and rescheduling methods under the condition of ad hoc network communication. For large-scale clusters, we will focus on architecture design, interaction mechanisms and algorithms. Field experiments will be conducted in combination with the real UAV swarm system.