Identification of INS Sensor Errors from Navigation Data Based on Improved Pigeon-Inspired Optimization
Abstract
1. Introduction
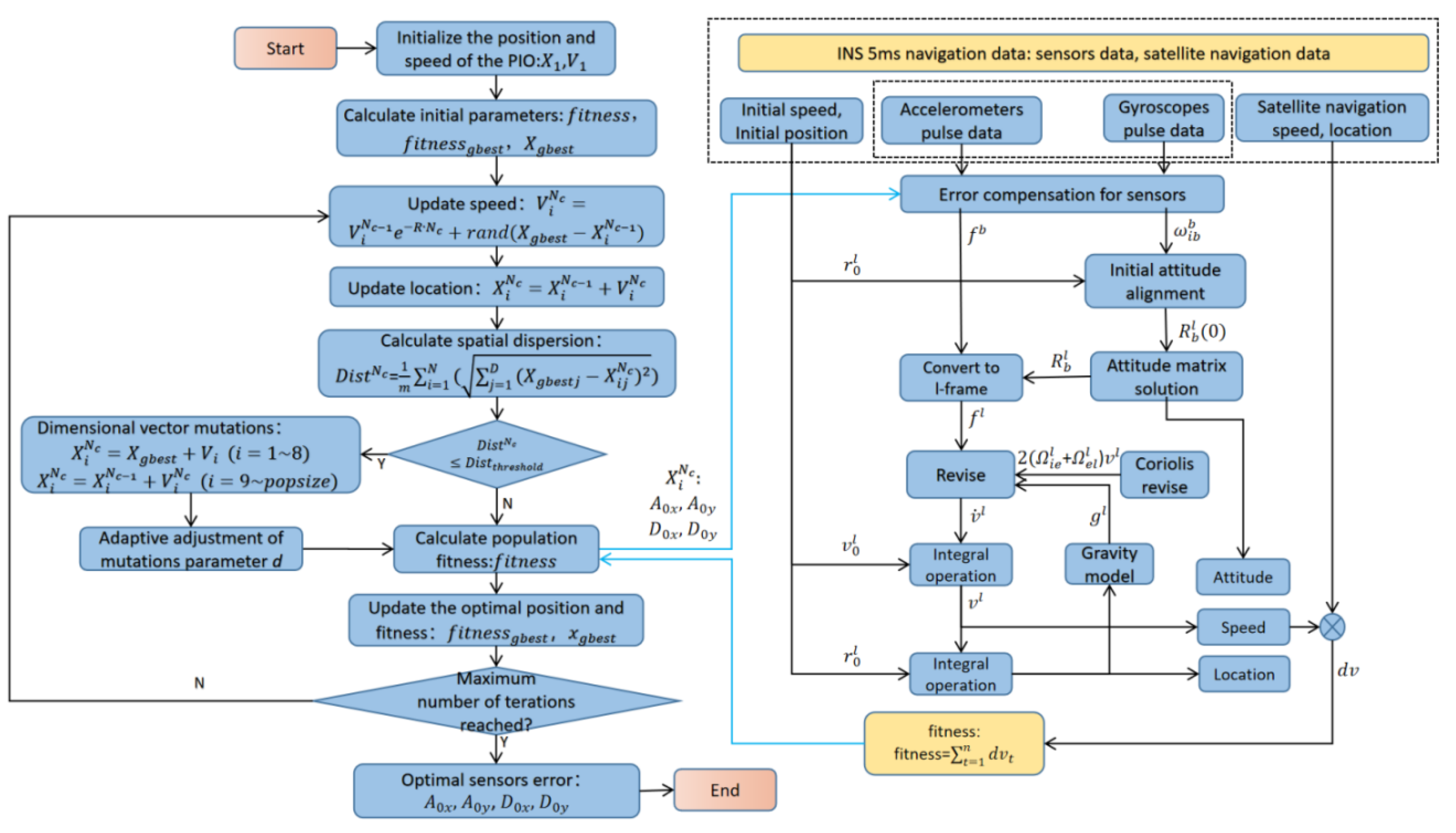
2. Method for Identifying Sensor Errors from Navigation Data Based on DVPIO
2.1. Principles and Error Effects of Inertial Navigation
2.1.1. Principles of Inertial Navigation
2.1.2. Error Effects of Inertial Navigation
2.2. DVPIO Method
- Premature judgment based on position:
- 2.
- Dimension vectors mutations:
- 3.
- Adaptive adjustment of mutations parameter d:
2.3. Identification of INS Sensor Errors Based on DVPIO
- The initial value of particle swarm is generated randomly, and the fitness function is calculated to find the global optimum.
- Calculation process of the fitness function:
- The sensor data collected during the flight compensate for errors according to the position data of the particle swarm;
- Obtain the initial parameters of inertial navigation: the initial velocity and position are obtained from the collected satellite navigation data, and the initial attitude is obtained from the initial alignment calculation;
- Execute inertial navigation solution and obtain the difference between the velocity calculated, , and the satellite navigation velocity at the time, i, which is the velocity error, ;
- Calculate the fitness function according to Formula (15).
- Update the particle swarm velocity and position according to Formulas (8) and (9), and recalculate the fitness function to update the global optimization.
- Judge whether the particle swarm has started prematurely according to Formula (10); if not, continue to execute (3). If it has started prematurely, execute (5).
- The particle swarm is sorted according to its fitness, and natural selection is carried out. The eight particles with the largest fitness are randomly mutated according to Formula (12), and the number of mutations is self-adaptively adjusted according to Formulas (13) and (14).
- Judge whether the convergence condition is reached. If so, the optimization calculation ends. If not, go to step 5 to continue the optimization calculation.
3. Results
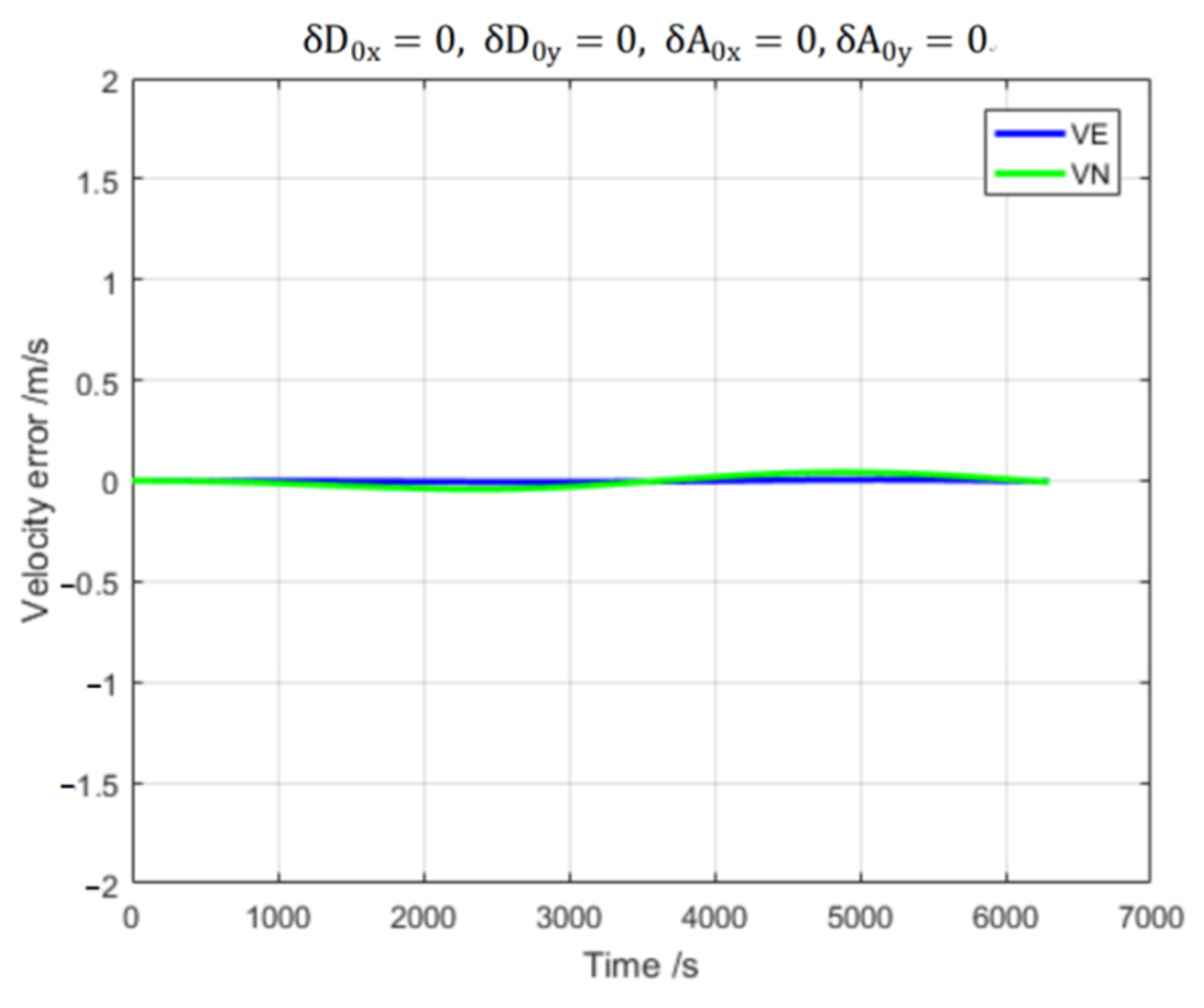
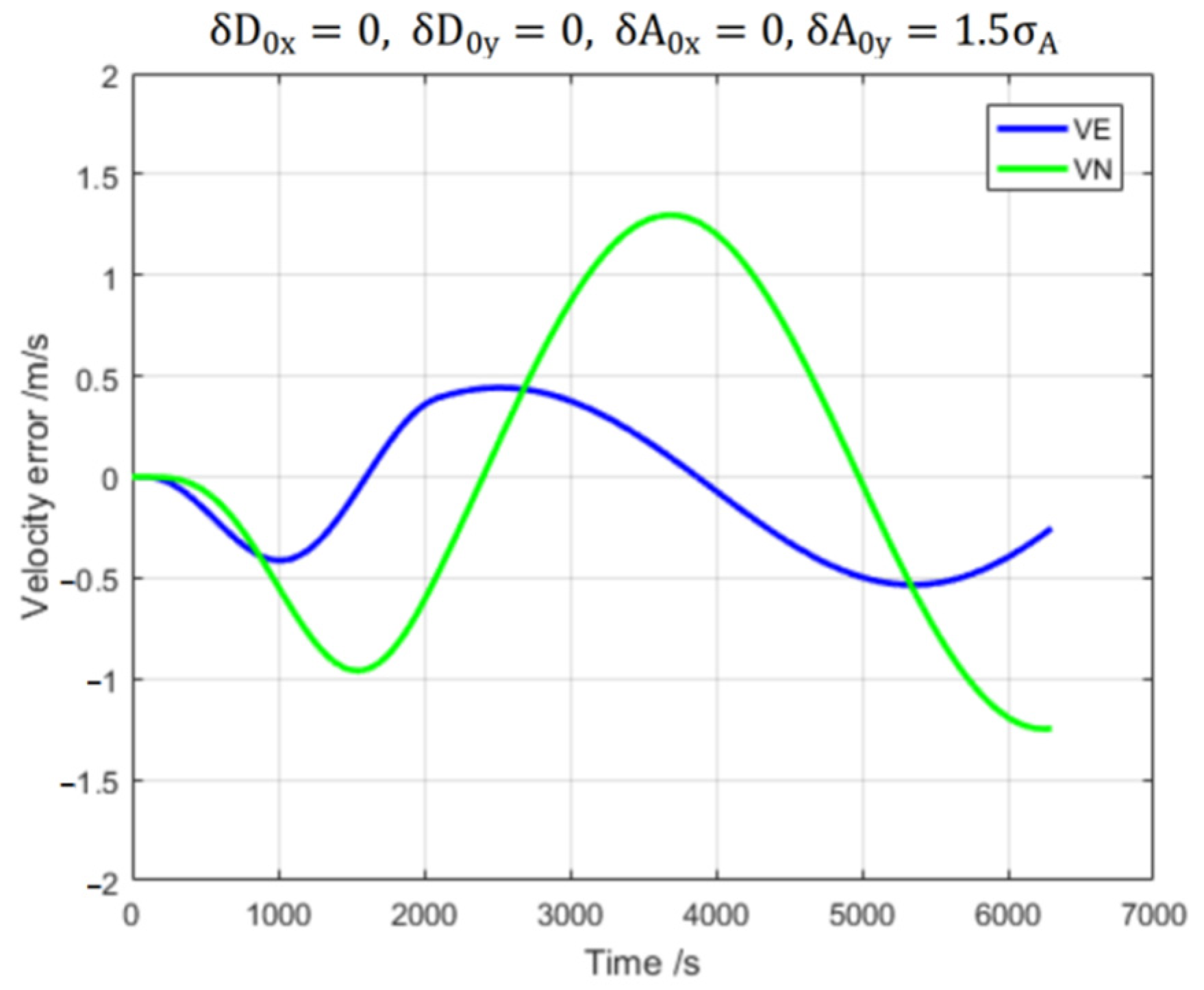
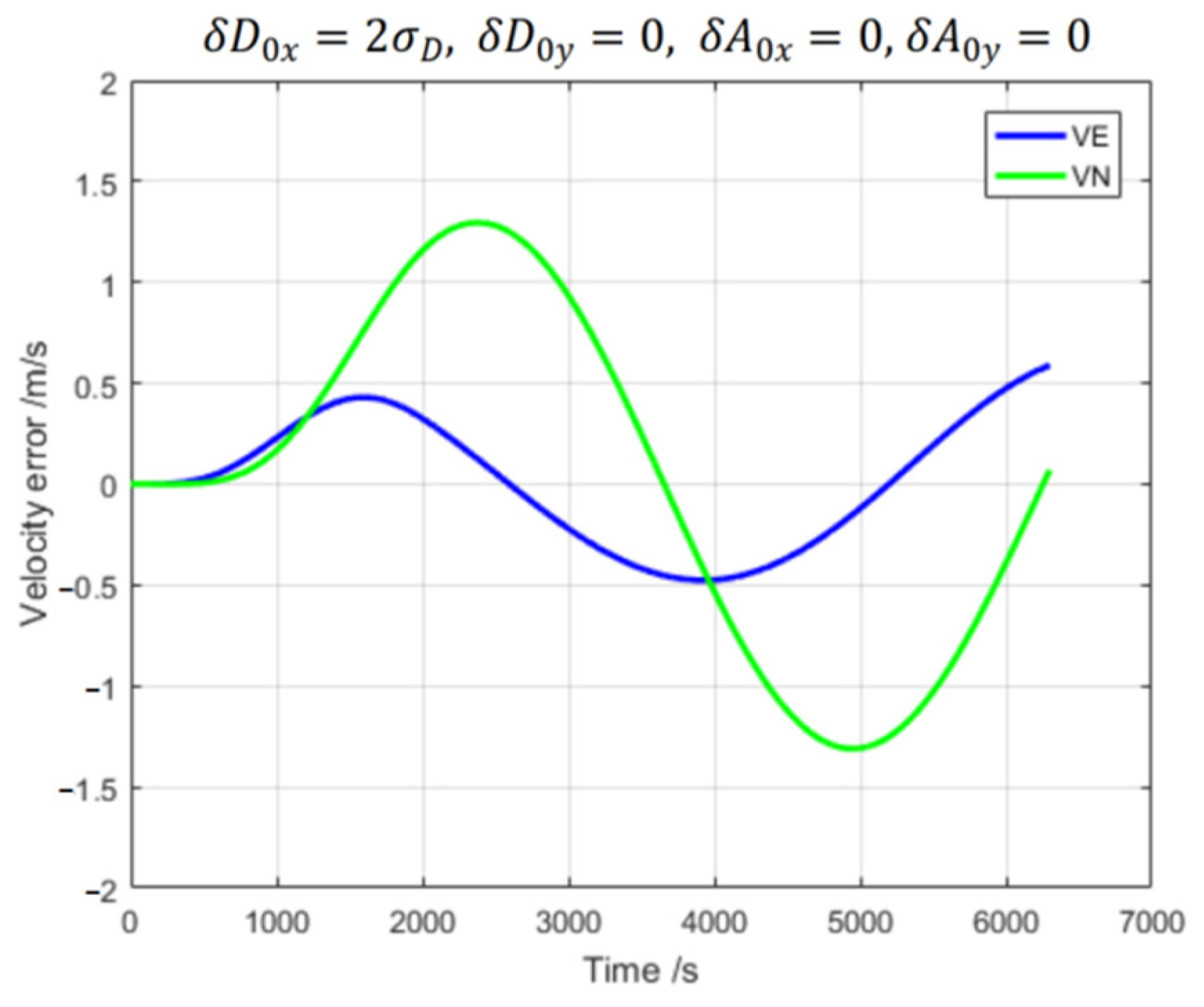
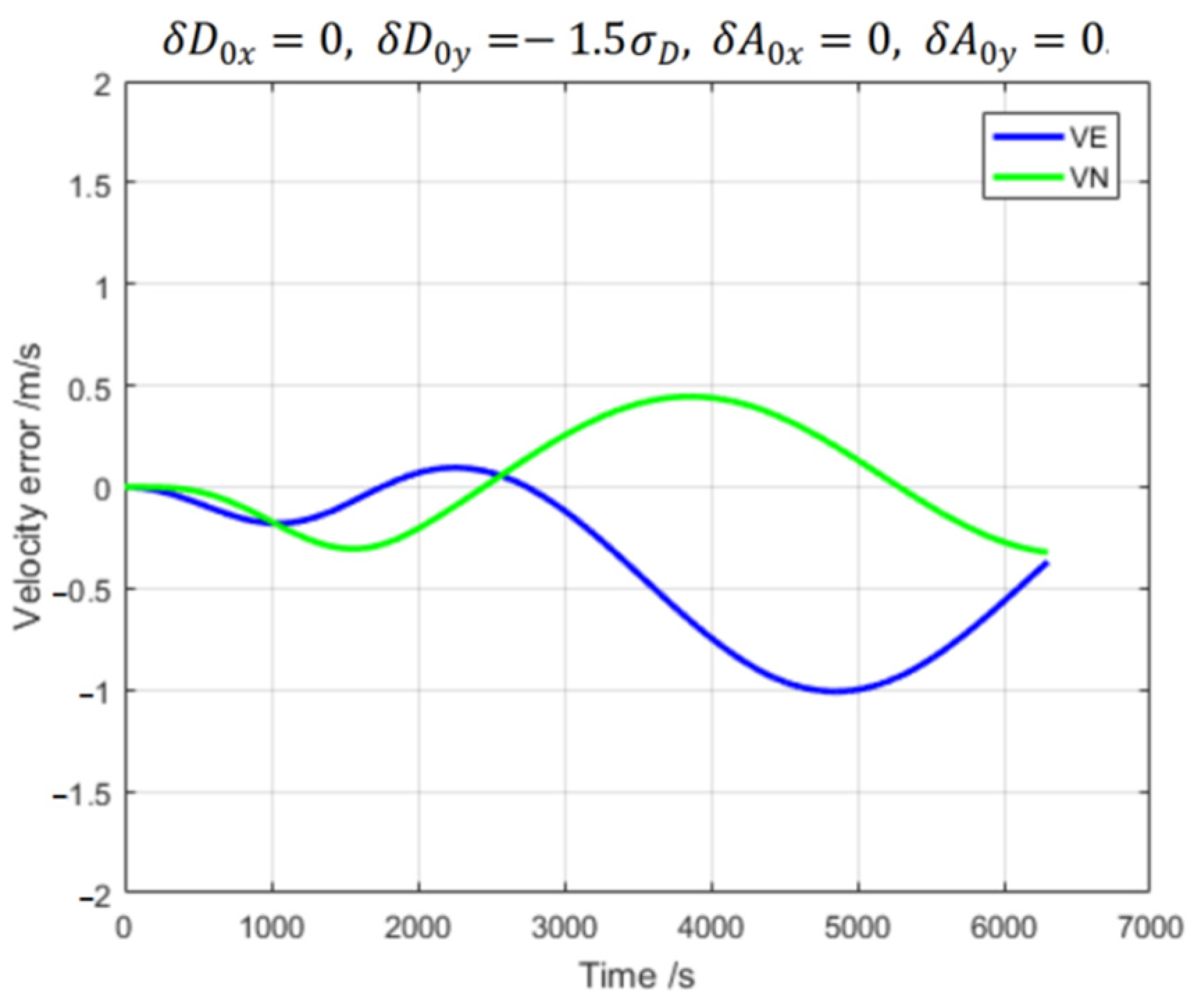
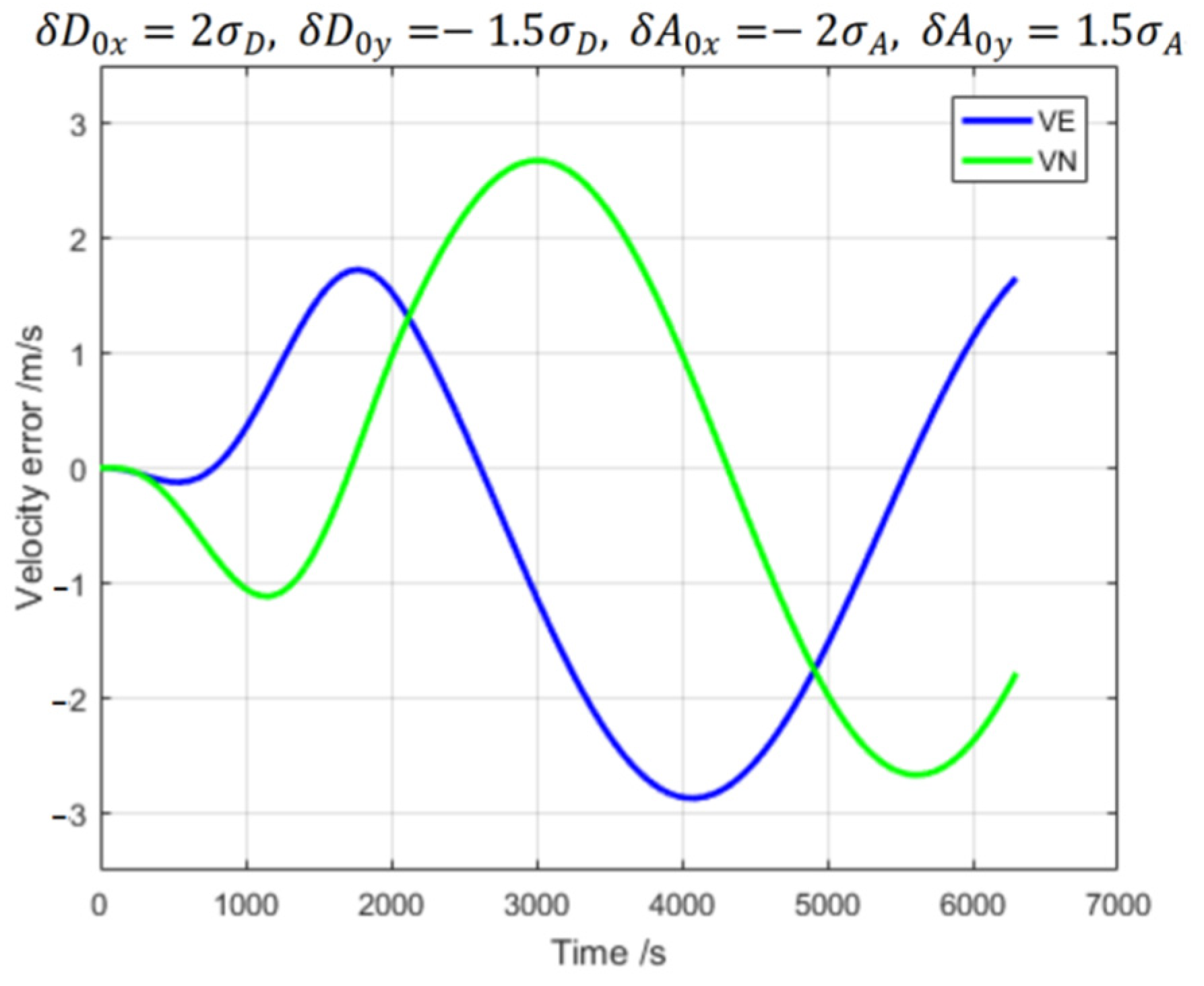
3.1. Error Effects Results of Inertial Navigation
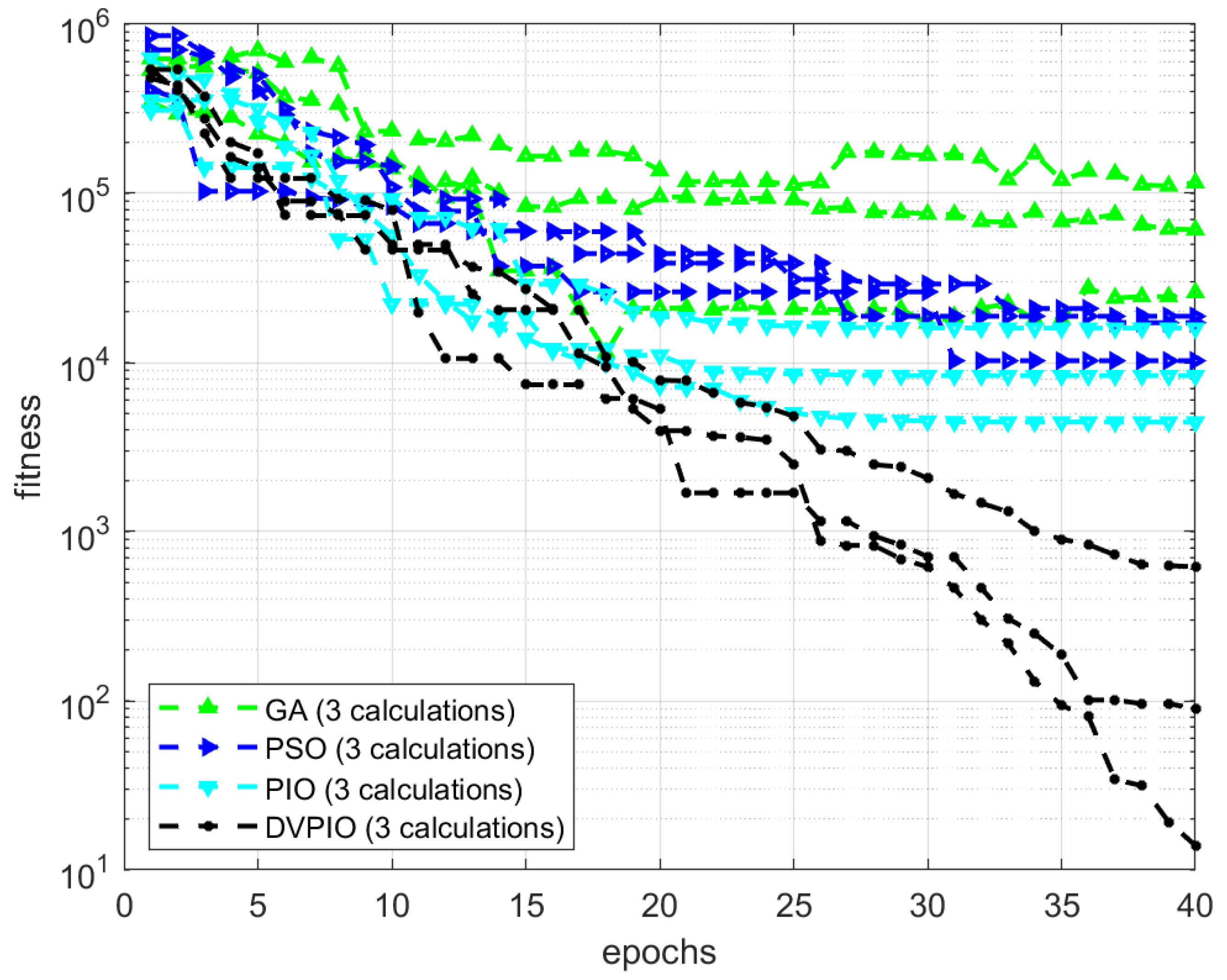
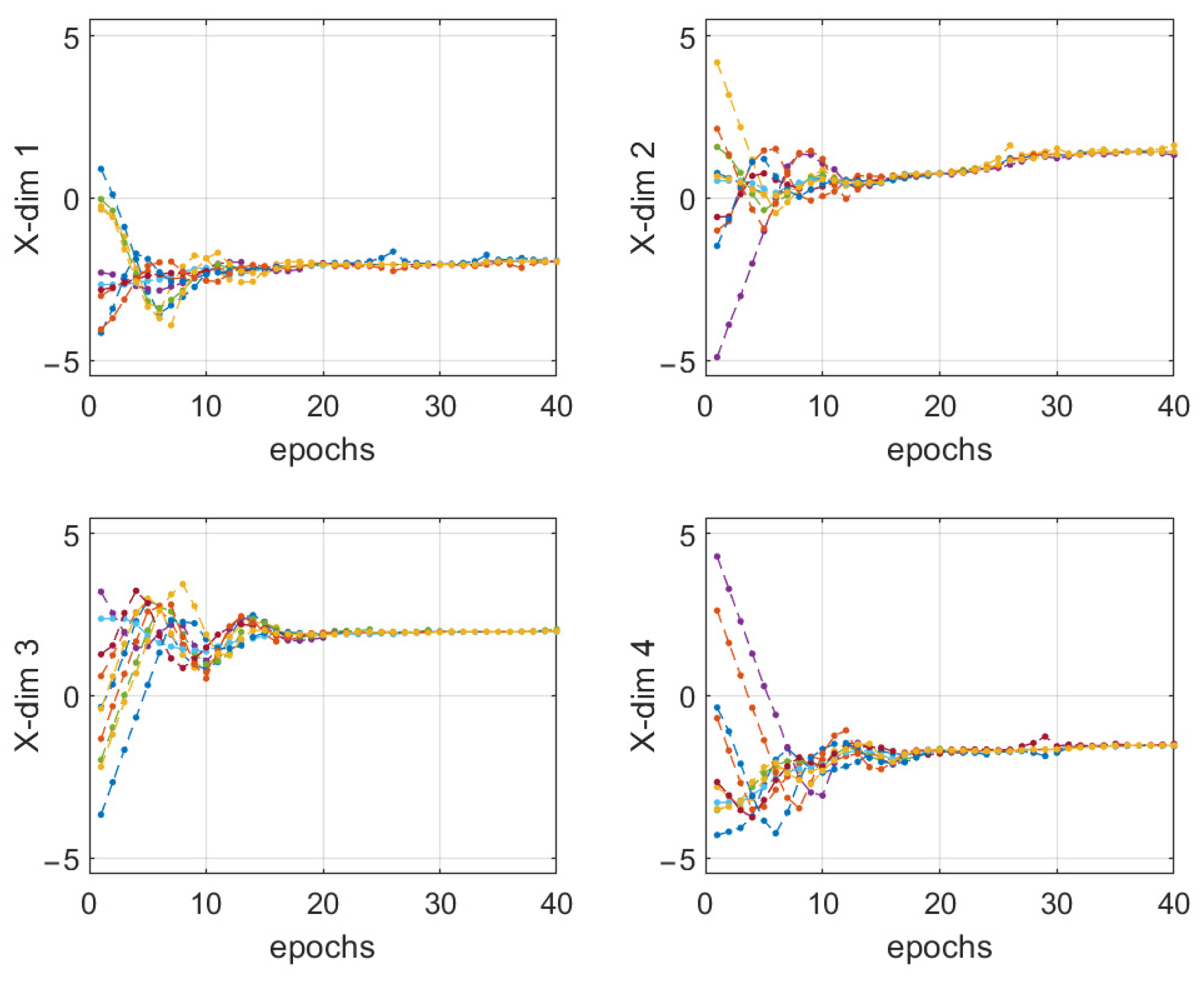
3.2. Identification Results of INS Sensor Errors Based on DVPIO
- The GA, PSO, PIO, and DVPIO methods can all be used to identify sensor errors from navigation data;
- Compared with the GA, PSO, and PIO methods, the PIO method has a faster convergence speed and a higher accuracy;
- The PIO method can easily fall into the local optimum in the later stage, while the DVPIO solves the problem of avoiding the local optimum and obtains more precise results.
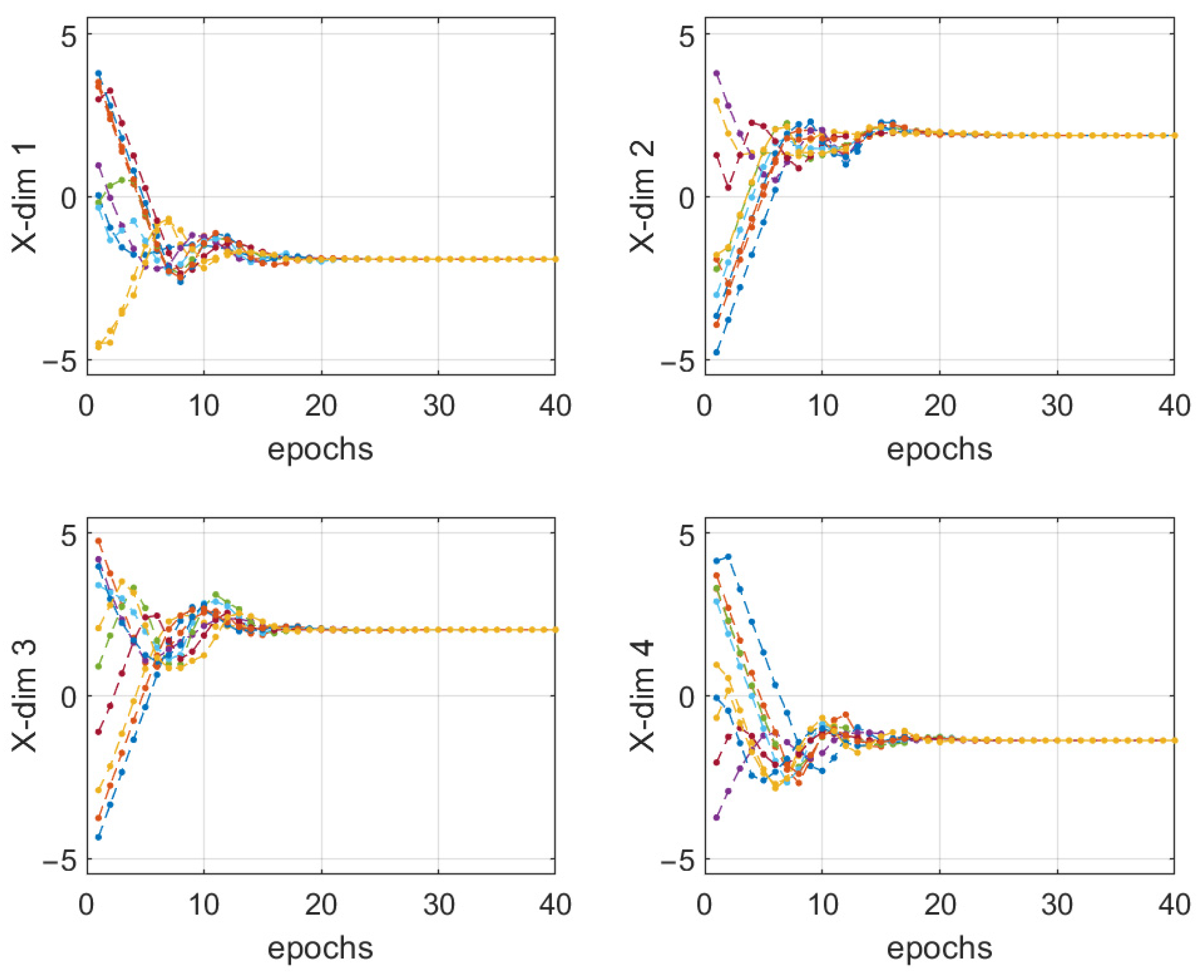
3.3. Improve Analytics of DVPIO
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| l | represents l-frame, the geographic coordinate system |
| b | represents b-frame, the vehicle coordinate system |
| i | represents i-frame, the inertial reference frame |
| e | represents e-frame, the earth coordinate system |
| the vector of latitude, longitude, and altitude of the l-frame | |
| the conversion matrix from b-frame to l-frame; is its constituent element | |
| an antisymmetric matrix of the angular rate vector that is expressed in the l-frame, where the angular rate vector is a vector for the l-frame relative to the e-frame | |
| the specific force of b-frame | |
| , , | the velocity in the east, north, and up directions, respectively |
| , , | the specific forces in the east, north, and up directions, respectively |
| the gravitational acceleration of the l-frame | |
| , | the height and the latitude |
| , | the radius of meridional section and the radius of curvature in the prime vertica |
| ) | an angular rate vector expressed in the b-frame, where the angular rate vector is a vector for the l-frame relative to the b-frame |
| , , | the coordinate component of |
| the quaternion of rotation | |
| , , | the carrier specific force errors |
| , , | the velocity errors in the east, north, and up directions, respectively |
| , , | the pitch angle error, roll angle error, and azimuth angle error, respectively |
| , , | the angular rate errors |
| , , | the zero bias errors of the accelerometers |
| , , | the zero bias errors of the gyroscopes |
| , , , , , | the installation errors of the accelerometers, where means the installation error of the z accelerometer relative to the x axis |
| , , , , , | the installation errors of the gyroscopes, where means the installation error of the z gyroscope relative to the x axis |
| , , | the scale factors of the accelerometers |
| , , | the scale factors of the gyroscopes |
| the position of the particle swarm | |
| the velocity of the particle swarm | |
| the number of iterations | |
| the global optimal position of the particle swarm |
References
- Kim, Y.; An, J.; Lee, J. Robust navigational system for a transporter using GPS/INS fusion. IEEE Trans. Ind. Electron. 2017, 65, 3346–3354. [Google Scholar] [CrossRef]
- Gao, P.; Li, K.; Song, T. An accelerometers-size-effect self-calibration method for triaxis rotational inertial navigation system. IEEE Trans. Ind. Electron. 2017, 65, 1655–1664. [Google Scholar] [CrossRef]
- Lee, J.; Lim, J.; Lee, J. Compensated heading angles for outdoor mobile robots in magnetically disturbed environment. IEEE Trans. Ind. Electron. 2017, 65, 1408–1419. [Google Scholar] [CrossRef]
- Poddar, S.; Kumar, V.; Kumar, A. A comprehensive overview of inertial sensor calibration techniques. J. Dyn. Syst. Meas. Control 2017, 139, 011006. [Google Scholar] [CrossRef]
- Hodas, S.; Izvoltova, J.; Rekus, D. Trends in Inertial Navigation Technologies. Earth Environ. Sci. 2021, 906, 012069. [Google Scholar] [CrossRef]
- Al-Radaideh, A.; Al-Jarrah, M.; Jhemi, A. UAV testbed building and development for research purposes at the american universityof sharjah. In Proceedings of the ISMA’10 7th International Symposium on Mechatronics and Its Applications, Sharjah, United Arab Emirates, 20–22 April 2010. [Google Scholar]
- Al-Radaideh, A. Guidance, Control and Trajectory Tracking of Small Fixed Wing Unmanned Aerial Vehicles (UAV’s). Master’s Thesis, American University of Sharjah, Sharjah, United Arab Emirates, 2009. [Google Scholar]
- Laupré, G.; Khaghani, M.; Skaloud, J. Sensitivity to time delays in VDM-based navigation. Drones 2019, 3, 11. [Google Scholar] [CrossRef]
- Bassolillo, S.R.; D’Amato, E.; Notaro, I. Enhanced Attitude and Altitude Estimation for Indoor Autonomous UAVs. Drones 2022, 6, 18. [Google Scholar] [CrossRef]
- Papafotis, K.; Sotiriadis, P.P. Exploring the Importance of Sensors’ Calibration in Inertial Navigation Systems. In Proceedings of the 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 12–14 October 2020. [Google Scholar]
- Grewal, M.S.; Andrews, A.P.; Bartone, C.G. Global Navigation Satellite Systems, Inertial Navigation, and Integration, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2013; pp. 54–103. [Google Scholar]
- Groves, P.D. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems. IEEE Aerosp. Electron. Syst. Mag. 2015, 30, 26–27. [Google Scholar] [CrossRef]
- Wang, X.J.; Li, D.; Zhang, X.; Sheng, D.Y.; Li, Z. Research and experiment on system level calibration method of fiber optic strapdown inertial navigation system. In Proceedings of the 2019 2nd International Conference on Information Systems and Computer Aided Education (ICISCAE), Dalian, China, 28–30 September 2019. [Google Scholar]
- Han, S.; Meng, Z.; Omisore, O. Random Error Reduction Algorithms for MEMS Inertial Sensor Accuracy Improvement—A Review. Micromachines 2020, 11, 1021. [Google Scholar] [CrossRef]
- Wang, Y.; Lin, Y.W.; Askari, S.; Jao, C.S.; Shkel, A.M. Compensation of systematic errors in ZUPT-aided pedestrian inertial navigation. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020. [Google Scholar]
- Xiao, Y.; Ruan, X.; Chai, J.; Zhang, X.; Zhu, X. Online IMU self-calibration for visual-inertial systems. Sensors 2019, 19, 1624. [Google Scholar] [CrossRef]
- Abro, G.E.M.; Zulkifli, S.A.B.; Asirvadam, V.S. Dual-loop single dimension fuzzy-based sliding mode control design for robust tracking of an underactuated quadrotor craft. Asian J. Control 2022, 1–26. [Google Scholar] [CrossRef]
- Abro, G.E.M.; Zulkifli, S.A.B.; Asirvadam, V.S.; Ali, Z.A. Model-free-based single-dimension fuzzy SMC design for underactuated quadrotor UAV. Actuators 2021, 10, 191. [Google Scholar] [CrossRef]
- Chen, C.; Zhao, P.; Lu, C.X. Deep-learning-based pedestrian inertial navigation: Methods, data set, and on-device inference. IEEE Internet Things J. 2020, 7, 4431–4441. [Google Scholar] [CrossRef]
- Wang, J.; Lou, W.; Liu, W. Calibration of MEMS Based Inertial Measurement Unit Using Long Short-Term Memory Network. In Proceedings of the 2019 IEEE 14th International Conference on Nano, Bangkok, Thailand, 11–14 April 2019. [Google Scholar]
- Weber, D.; Gühmann, C.; Seel, T. Neural networks versus conventional filters for Inertial-Sensor-based attitude estimation. In Proceedings of the 2020 IEEE 23rd International Conference on Information Fusion (FUSION), Rustenburg, South Africa, 6–9 July 2020. [Google Scholar]
- Li, Q.; Ma, Z. A Hybrid Dynamic Probability Mutation Particle Swarm Optimization for Engineering Structure Design. Mob. Inf. Syst. 2021, 2021, 6648650. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, M.; Liang, Y. A novel particle swarm optimization based on prey–predator relationship. Appl. Soft Comput. 2018, 68, 202–218. [Google Scholar] [CrossRef]
- Zaman, H.R.; Gharehchopogh, F.S. An improved particle swarm optimization with backtracking search optimization algorithm for solving continuous optimization problems. Eng. Comput. 2021, 1–35. [Google Scholar] [CrossRef]
- Batista, P.; Silvestre, C.; Oliveira, P.; Cardeira, B. Accelerometer calibration and dynamic bias and gravity estimation: Analysis, design, and experimental evaluation. IEEE Trans. Control Syst. Technol. 2010, 19, 1128–1137. [Google Scholar] [CrossRef]
- Beravs, T.; Podobnik, J.; Munih, M. Three-axial accelerometer calibration using Kalman filter covariance matrix for online estimation of optimal sensor orientation. IEEE Trans. Instrum. Meas. 2012, 61, 2501–2511. [Google Scholar] [CrossRef]
- Xiang, S.; Xing, L.N.; Wang, L.; Zhou, K. Comprehensive learning pigeon-inspired optimization with tabu list. Sci. China Inf. Sci. 2019, 62, 07028. [Google Scholar] [CrossRef]
- Li, C.; Duan, H.B. Target detection approach for UAVs via improved pigeon-inspired optimization and edge potential function. Aerosp. Sci. Technol. 2014, 39, 352–360. [Google Scholar] [CrossRef]
- Zhan, Z.H.; Zhang, J.; Li, Y.; Chung, H.S. Adaptive particle swarm optimization. IEEE Trans. Syst. Man Cybern. Part B 2009, 39, 1362–1381. [Google Scholar] [CrossRef] [PubMed]
- Tian, D.; Shi, Z. MPSO: Modified particle swarm optimization and its applications. Swarm Evol. Comput. 2018, 41, 49–68. [Google Scholar] [CrossRef]
- Duan, H.B.; Qiao, P. Pigeon-inspired optimization: A newswarm intelligence optimizer for air robot path planning. Int. J. Intell. Comput. Cybern. 2014, 7, 24–37. [Google Scholar] [CrossRef]
- Duan, H.B.; Qiu, H.X.; Fan, Y.M. Unmanned aerial vehicle formation cooperative control based on predatory escaping pigeon-inspired optimization. Sci. Sin. Technol. 2015, 45, 559–572. [Google Scholar]
- Yuan, G.S.; Xia, J.; Duan, H.B. A continuous modeling method via improved pigeon-inspired optimization for wake vortices in UAVs close formation flight. Aerosp. Sci. Technol. 2022, 120, 107259. [Google Scholar] [CrossRef]
- Yang, Z.Y.; Duan, H.B.; Fan, Y.M. Automatic carrier landing system multilayer parameter design based oncauchy mutation pigeon-inspired optimization. Aerosp. Technol. 2018, 79, 518–530. [Google Scholar] [CrossRef]
- Herdianti, W.; Gunawan, A.A.; Komsiyah, S. Distribution cost optimization using pigeon inspired optimization method with reverse learning mechanism. Procedia Comput. Sci. 2021, 179, 920–929. [Google Scholar] [CrossRef]




| Acronyms | Full Forms |
|---|---|
| INS | inertial navigation system |
| IMU | inertial navigation unit |
| MEMS | microelectromechanical system |
| GNSS | global navigation satellite system |
| EA | evolutionary algorithms |
| BSA | backtracking search optimization algorithm |
| GA | genetic algorithm |
| PSO | particle swarm optimization |
| PIO | pigeon-inspired optimization |
| DVPIO | pigeon-inspired optimization with dimension vectors adaptive mutation |
| LSTM | long-short-term memory neural network |
| UAV | unmanned aerial vehicle |
| Methods Involved | Limitations | References |
|---|---|---|
| Kalman filter estimation method to identify sensor errors through inertial navigation data and velocity errors during motion | The algorithm is complex, and the motion trajectory and the motion time of the inertial navigation system are strictly required; | [25,26] |
| PSO | It is easy to fall into local optimum, or it is difficult to further improve the accuracy in the later stage of iteration. | [27,28] |
| PIO | Although it has better convergence performance, it is easy to fall into local optimum, or it is difficult to further improve the accuracy in the later stage of iteration. | [29,30] |
| Parameters | Value and Unit |
|---|---|
| Navigation interruption time | 10 ms |
| Initial gravitational acceleration | |
| Initial latitude | |
| Initial longitude | |
| Initial height | 50 m |
| Angular rate of the earth’s rotation | 7.292115147 × 105 rad/s |
| Long radius of the earth | 6378245 m |
| Align time | 10 min |
| EA Methods | EA Parameters |
|---|---|
| GA | Number of particles: 20. Iteration steps: 40. Mating probability: 0.5. Mutation probability: 0.2. |
| PSO | Number of particles: 10. Iteration steps: 40. W = 0.8, C1 = 2, C2 = 2. |
| PIO | Number of particles: 10. Iteration steps: 40. R = 0.05, C = 1. |
| DVPIO | Number of particles: 10. Iteration steps: 40. R = 0.05, C = 1, d = 0.05 (initial value) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Deng, Y.; Liu, W. Identification of INS Sensor Errors from Navigation Data Based on Improved Pigeon-Inspired Optimization. Drones 2022, 6, 287. https://doi.org/10.3390/drones6100287
Li Z, Deng Y, Liu W. Identification of INS Sensor Errors from Navigation Data Based on Improved Pigeon-Inspired Optimization. Drones. 2022; 6(10):287. https://doi.org/10.3390/drones6100287
Chicago/Turabian StyleLi, Zhihua, Yimin Deng, and Wenxue Liu. 2022. "Identification of INS Sensor Errors from Navigation Data Based on Improved Pigeon-Inspired Optimization" Drones 6, no. 10: 287. https://doi.org/10.3390/drones6100287
APA StyleLi, Z., Deng, Y., & Liu, W. (2022). Identification of INS Sensor Errors from Navigation Data Based on Improved Pigeon-Inspired Optimization. Drones, 6(10), 287. https://doi.org/10.3390/drones6100287





