Abstract
Recently, interest in mission autonomy related to Unmanned Combat Aerial Vehicles(UCAVs) for performing highly dangerous Air-to-Surface Missions(ASMs) has been increasing. Regarding autonomous mission planners, studies currently being conducted in this field have been mainly focused on creating a path from a macroscopic 2D environment to a dense target area or proposing a route for intercepting a target. For further improvement, this paper treats a mission planning algorithm on an ASM which can plan the path to the target dense area in consideration of threats spread in a 3D terrain environment while planning the shortest path to intercept multiple targets. To do so, ASMs are considered three sequential mission elements: ingress, intercept, and egress. The ingress and egress elements require a terrain flight path to penetrate deep into the enemy territory. Thus, the proposed terrain flight path planner generates a nap-of-the-earth path to avoid detection by enemy radar while avoiding enemy air defense threats. In the intercept element, the shortest intercept path planner based on the Dubins path concept combined with nonlinear programming is developed to minimize exposure time for survivability. Finally, the integrated ASM planner is applied to several mission scenarios and validated by simulations using a rotorcraft model.
1. Introduction
Air-to-surface missions (ASMs) are becoming increasingly dangerous in modern warfare, where the successful performance of ASMs is strategically important. To deal with this issue, missions are carried out using stealth aircraft to avoid threats on recent battlefields. However, developing an aircraft with stealth capabilities is costly and does not exclude threats to pilots’ lives altogether. Performing ASMs using Unmanned Combat Aerial Vehicles (UCAVs) is an effective approach to handling these difficulties. For this reason, many studies have been conducted to perform missions using UCAVs. Through these efforts, several approaches are proposed to efficiently plan ASMs [1,2,3,4,5,6,7,8,9,10,11,12,13,14] in Table 1. Randal W Beard et al. [1] proposed an ASM planning algorithm for multiple UCAVs. The proposed algorithm plans the path based on the Voronoi-diagram concept and assigns the targets to UCAVs to minimize the prescribed objective function. Path planning based on the Voronoi diagram concept is advantageous for planning a path, which bypasses threats to the maximum extent. However, with the cost of creating unnecessary detours. Yeonju Eun et al. [2] proposed a path planner which combines the Voronoi-diagram concept and potential field concept to address this issue for Suppression to Enemy Air Defenses(SEAD) mission planning. There is a limitation that these algorithms are only applied to two-dimensional environments. H.H Triharminto et al. [3], proposed a path planner for moving target intercept on dynamic 3D environments, but the algorithm focuses only on local environments. Meanwhile, several path planners using Dubins path concept for target intercept were proposed [4,5,6]. These approaches have the advantage of being able to consider the dynamic constraints of aircraft and simply generate an optimal path. However, it has not been verified in a three-dimensional environment. Most of the proposed studies focus on generating paths to approach targets in a 2D global environment or generate only a path to pursue and intercept a target in a 3D environment. To contribute to this issue, an ASM planning technique that can simultaneously plan the path to approach the targets and the path to hit the targets while considering both threats and obstacles in the 3D environment is addressed in this paper.

Table 1.
ASM Planner’s characteristics of the literature [1,2,3,4,5,6,7,8,9,10,11,12,13,14].
ASMs are classified into several detailed missions, depending on the mission’s environment and goals as follows: Air Interdiction (AI), Close Air Support (CAS), Suppression to Enemy Air Defenses (SEAD), and Attack Operations (AO). According to the U.S. Air Force Doctrine [15,16], AO and SEAD missions fall under the category of Offensive Counterair(OCA) missions, while AI and CAS missions belong to the category of counterland missions. AO is intended to destroy, disrupt, or degrade counterair targets including enemy air and missile threats, their command and control, and their support infrastructure on the ground such as airfields, launch sites, launchers, fuel, supplies, etc. The SEAD missions aim to neutralize, destroy, or degrade enemy surface-based air defenses by destructive or disruptive means. While AO focuses on preventive measures to strike the enemy air defense assets before they are deployed, there is a difference that the SEAD mission aims to neutralize the already deployed enemy air defense assets. On the other hand, the AI missions’ goal is to preemptively disrupt, delay, or destroy the enemy’s military potential before it responds effectively to friendly forces. Whereas the CAS mission aims to strike against hostile targets that are near close to friendly forces. Since the enemy targets are near friendly forces, tracking of friendly forces’ movements and careful firing on targets are more crucial than in the case of the AI missions. However, since the targets of AI missions are usually within enemy territory, the number of interspersed threats within the mission environment is likely to be greater than that of CAS missions.
These ASMs have in common that they basically perform consecutive mission elements of ingress, intercept, and egress. The ingress mission element is the phase of approaching the intercept mission area while avoiding the various threats that appear when entering a hostile area. Then, the aircraft intercepts the target quickly and accurately in the intercept mission element. Lastly, the egress mission element is the phase of escaping the hostile area while avoiding scattered threats. Since the ASM planner can be designed through a strategy of sequential planning on each mission element. For ingress and egress missions, avoiding enemy radar detection and air defense threats are foremost important. Stealth aircraft may be a solution, but detection avoidance through low-fly flight maneuvers which is called hedgehop can also be a good approach. Therefore, a terrain flight path planner is proposed to generate a contour chasing flight path for the ingress and egress mission element maneuver path planning. In the intercept phase, it is important to strike the target as quickly as possible rather than avoiding the threats. Thus, an algorithm is proposed that can generate the shortest target intercept path in this paper.
The paper is structured as follows. In Section 2, terrain and threat modeling techniques are treated to describe the real-world battlefield environments. Terrain flight path planner based on RRT* algorithm that can generate asymptotic global optimal path is addressed in Section 3. The shortest target intercept path planner is addressed in Section 4. In Section 5, several test scenarios are presented for the validation of the presented mission planner. In Section 6, The integrated mission planner is validated through applications on the proposed scenarios. Furthermore, simulations are performed using a rotorcraft model to track the generated trajectories. Section 7 provides the important details and analysis of the results are summarized in the conclusion.
2. Mission Environment Construction
Building a virtual mission environment is crucial when designing path planning algorithms for ASMs. Therefore, this section treats the techniques used to increase the applicability of the designed path planner when building the real battlefield environment including terrain threat models. The terrain height model of the real world is inserted into the planning environment to describe actual battlefields such as in Figure 1. The maximum height of the terrain is 591 m while both the X-axis and Y-axis are 13,745.58 m wide. The terrain map was generated based on the terrain heightmap near 37°25′20.2” N, 127°01′21.9” E.
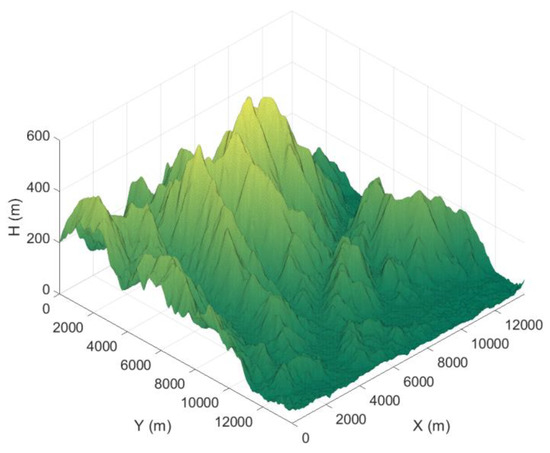
Figure 1.
Terrain model.
In addition, a spherical threat model is proposed which has a radius of maximum threat reach and Radial Basis Function (RBF) based threat strength distribution in the inner domain of the sphere to describe common threat types. Equation (1) shows the threat strength distribution in the inner domain of the threat:
where represents the position vector of a node, and represents the position vector of a threat. The strength of the threat center is , and the proportion of the threat varies according to the distance from the center of the threat and the RBF shape factor . Furthermore, the threat disappears when it is outside of the maximum threat distance. In this paper, the Gaussian function shown in Equation (2) is selected as the threat distribution [17]. Other types of RBF can also be adopted depending on the mission environment. Figure 2 represents an example of a terrain map with five threat models.
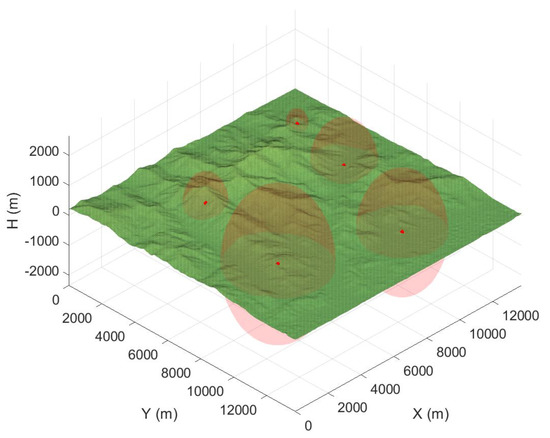
Figure 2.
An example of terrain map with five threat models.
3. Terrain Flight Path Planner
UCAVs must avoid multiple threats in the hostile area to perform ingress and egress mission elements. Therefore, there is a need for a Terrain Flightpath planner which is capable of avoiding threats while avoiding detection of enemy radar through a low approach. There are a number of path planning algorithms that can be applied to this problem. Path Planning algorithms are commonly classified into five different categories [18]: sampling-based algorithms, node-based algorithms, mathematic model-based algorithms, bio-inspired algorithms, and multifusion-based algorithms. Among them, the sampling-based algorithm can be used in both static and dynamic environments, with high time efficiency. The Rapidly-exploring Random Tree (RRT) algorithm [19] is one of the active sampling-based algorithms which is well-known for its fast convergence in multidimensional environments. However, the RRT algorithm has the shortcoming that it cannot guarantee an optimal path. To overcome this shortcoming, the RRT* algorithm [20] has been proposed. In the RRT* algorithm, an asymptotic optimal path can be reached through sufficient iterations by adding a routine to update the tree considering the path cost. However, its slow convergence rate became another issue. The RRT*-smart [21] algorithm was proposed to improve this weakness by accelerating the convergence rate to the asymptotic optimal path using intelligent sampling. In addition, the P-RRT* [22] algorithm with a potential-guided sampling technique was proposed to increase the convergence rate for the initial path. There are many other recent approaches to improve performance and overcome shortcomings of the RRT-based algorithms [23,24,25,26,27,28]. However, analyzing and applying all these algorithms requires a high excessive workload. Therefore, the P-RRT*-smart algorithm is selected and applied which is a fusion of classical P-RRT* and RRT*-smart to cover the applicability of a wide range of the path planning algorithms.
The following additional approaches are also applied when planning the terrain flight path. Areas over a certain distance from the surface are treated as obstacles. To do so, the generated path is always located near the surface. In addition, the cost due to threats between two nodes is calculated as follows:
where is the total number of threats in the environment and is the total number of steps between two nodes. In Equation (3), the step cost in each step is calculated using the cost function presented in Equation (1) while advancing between nodes by the prescribed step size. By summing all the calculated step costs, the cost due to threats between the nodes can be calculated. Since the cost due to threats continues to add up while the aircraft is within the threat range (i.e., ), it is possible to account for the cost change depending on the flight time consumed within the threat range. A geometrical schematic of the step cost concept at an arbitrary j-th step between two nodes in the presence of two existing threats is shown in Figure 3.
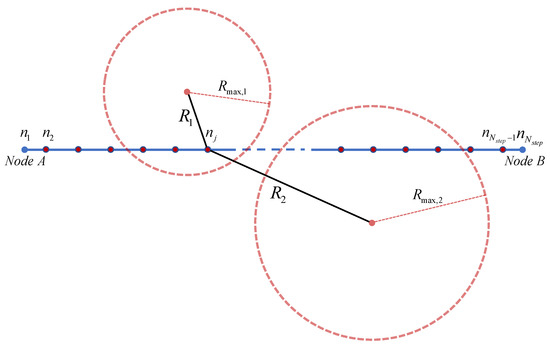
Figure 3.
Geometrical schematic of the step cost concept.
The node-to-node cost can then be calculated by additionally considering the distance cost between nodes as:
where and are the position vectors of nodes A and B, respectively.
Figure 4 represents an example case of terrain path planning. The path planning and all the other simulations are performed by Visual Fortran, Window 10 home, with the help of Intel Core i7-6700K CPU (4.0 GHz) with 32 GB of RAM. The total running time is 2.251 s with the 5000 total number of samplings. However, both the initial path convergence and the optimal path convergence times are quite short, 0.096 s and 0.7344 s, respectively. As shown in Figure 4a, the planned path avoids a threat with relatively strong strength to minimize the path cost. In addition, the planned path is generated within 100 m of the vertical distance from the surface as shown in Figure 5.
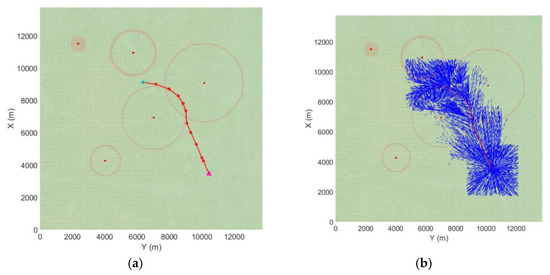
Figure 4.
An example of terrain path planning: on map (a) Planned path; (b) Generated tree.
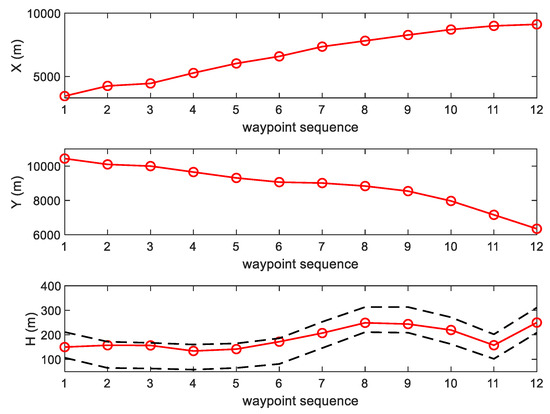
Figure 5.
An example of terrain path planning: Graph.
4. Shortest Target Intercept Path Planner
The target areas are likely to be interspersed with threats that take hostile actions. To increase the chances of completing a successful mission, the aircraft must survive during the intercept process. Accordingly, it is necessary to generate the shortest distance path from the vicinity of the target area so that the mission can be carried out as quickly as possible. Furthermore, in order to attack the target point, the aircraft’s heading angle should be aligned with the target point before the action takes place. Considering two necessary conditions, the Dubins circle can provide reliable results. Dubins [29] presented a method to generate the shortest path to reach the final position and heading while satisfying the constraint that vehicles must move along the arcs of a minimal turning radius while proceeding in the initially prescribed heading. The path generated by this approach may not be an obstacle-free path, and therefore can only be used in an environment undisturbed by obstacles. However, this approach is useful since it can generate a simple and fast flyable path. Based on this advantage, a planner was designed to plan the path of the target intercept mission element.
The concept of a target intercept path planning strategy is shown in Figure 6. First, the position and entry angle of the target and position and heading angle of the UCAV is prescribed. Furthermore, the height of the intercept mission plane is set to an XY plane high enough from the highest terrain height in the intercept mission area. The UCAV aims at the target while flying straight in the direction of the given entry angle . Thus, the aiming start position and weapon release point are defined as points separated by certain distances and in the direction of the entry angle from the target. Next, the path is generated by connecting the initial position of the UCAV, the aiming start position, and the weapon release point based on the Dubins path concept [30]. The same process is repeated until the path is generated which intercepts all the targets. Finally, the rest of the path is generated with the prescribed exit point and exit angle from the last target location. In this concept, can be determined by the aircraft’s dynamic characteristics and speed, and , can be determined by the missile’s aiming capability.
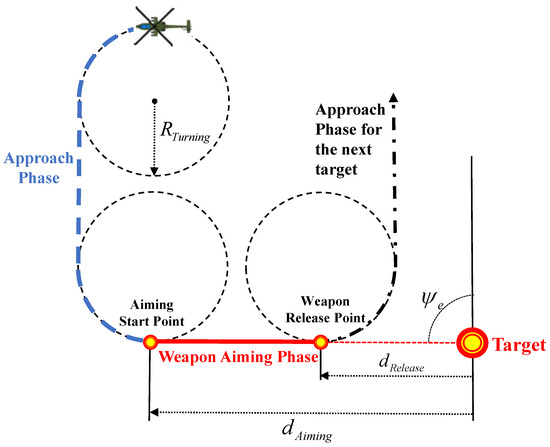
Figure 6.
Target intercept path planning strategy.
The length of the path generated by the presented process varies according to the intercept entry angles and the target intercept sequence. Therefore, the entry angles are needed to be optimized to obtain the shortest path. The optimization problem can be formulated as Equation (5). The object function is the total length of the generated path and the design variables are the intercept entry angles of each target. The formulated problem can be solved using an NLP solver and the robust SQP method [31] is applied in this paper.
However, the target intercept sequence is another factor that determines the length of the path. Accordingly, the target intercept sequence in which the path length is minimized should be determined. Therefore, optimization is performed on all possible combinations of target intercept sequences, and a combination having the shortest path length is selected.
Figure 7 illustrates an example case of the proposed planner. The square points represent the location of the targets. Furthermore, each of the parameters , , and were set to 300 m, 100 m, and 300 m, respectively. The solid line represents the planned path, and the dash lines describe the turning radius. The total consumed time to optimizing was 3.524 s. Figure 7 shows that the target entry angles, and target intercept sequence are properly optimized.
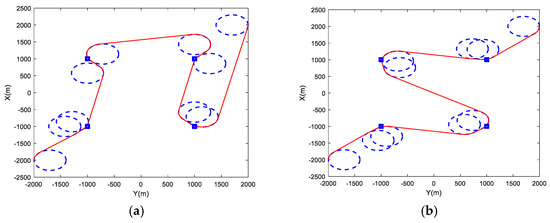
Figure 7.
An example of target intercept path planning: (a) Initial path; (b) Optimized path
The computation time seems unsuitable for real-time computation. However, this time is the time it takes when optimization is performed with the initial value set to 0 for all possible intercept sequences. When in flight, a strategy of updating the path in real-time can be taken while setting the initial value to the previously optimized value and performing optimization for a single intercept sequence. To validate this strategy, optimization was performed by changing each target position shown in Figure 7 by 100 m, setting the previously optimized entry angles to the initial values, and performed for the previously optimized intercept sequence. The time required for optimization was 0.2190 s, confirming the possibility of real-time application.
5. Application on Mission Scenarios
ASMs consist of AI, CAS, SEAD, and AO missions depending on the mission environment and its goal. The major differences between these four missions are the density and distribution of threats on the environment and the property of the targets.
First, in the environmental perspective view, AI and AO missions require the UCAVs to penetrate deep into the enemy territory. Therefore, there is a possibility of many scattered threats along UCAVs’ path. In SEAD missions, most targets are located on highlands since air defense assets are already deployed. CAS missions generally aim to strike targets located on the border between enemy and friendly territories where the number of threats increases when approaching the target intercept area.
Second, in the target property perspective view, all hostile assets can be targeted in counterland missions, including the enemy’s military potential, whereas only enemy air defense assets are targeted in counterair missions. However, there is no difference when planning the path of the two missions since there is a commonality that the targets are located on the surface. For this reason, the proposed planner validation for AI, AO, and CAS missions can be performed together in a single mission scenario. Considering that the targets of the SEAD mission are located on the highlands, another mission scenario is also constructed.
5.1. AI Mission Scenario
The targets in the AI mission scenario are shown in Figure 8 with the detailed location coordinates are represented in Table 2. The targets are assumed to be parked enemy vehicles.
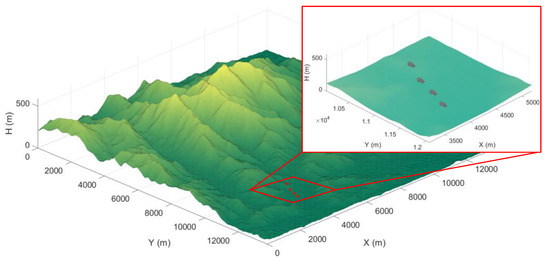
Figure 8.
Targets for AI mission.

Table 2.
Targets’ coordinate of the AI mission scenario.
Figure 9 illustrates the planned path of the AI mission scenario. The red transparent spherical area represents randomly placed threats, and the transparent cube area represents the target intercept mission area. The mission proceeds in order, starting with the triangle point and passing through the square point, the pentagonal point, and the hexagonal point, while the exact coordinates are shown in Table 3. The targets are represented by x points and the threat properties are shown in Table 4.
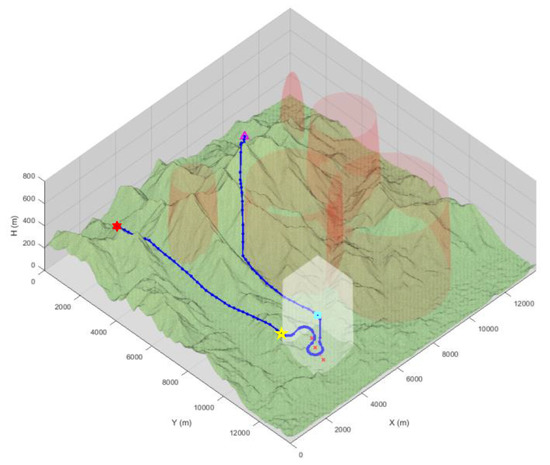
Figure 9.
Planned path of the AI mission scenario.

Table 3.
SEAD mission scenario’s waypoint locations.

Table 4.
Threats’ properties of the AI mission scenario.
The total consumed time is 30.6 s, and the number of samplings is set as 5000 for each terrain flight path planning for AI mission planning. As shown in Figure 9, the path is appropriately generated to avoid the threats while intercepting targets with the shortest length. Furthermore, the path is generated within 100 m above the surface in the terrain flight phase.
5.2. SEAD Mission Scenario
Figure 10 shows the targets of the SEAD mission scenario. The targets are assumed as already deployed enemy air defense assets on the highlands. The total number of targets is four and the locations of the targets are shown in Table 5.
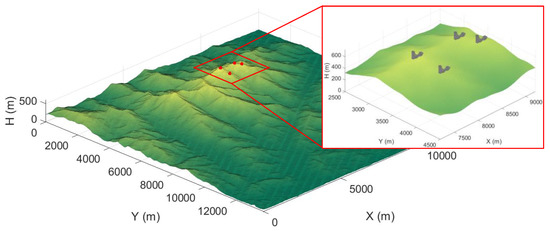
Figure 10.
Targets for the SEAD mission scenario.

Table 5.
Targets’ coordinate of the SEAD mission scenario.
Figure 11 represents the planned path of the SEAD mission scenario. The red transparent spherical area represents randomly placed threats, and the transparent cube area represents the target intercept mission area. The mission proceeds in the following order: the triangle point, the square point, the pentagonal point, and the hexagonal point while the exact coordinates are shown in Table 6. The targets are represented by x points and the threats’ properties are shown in Table 7.
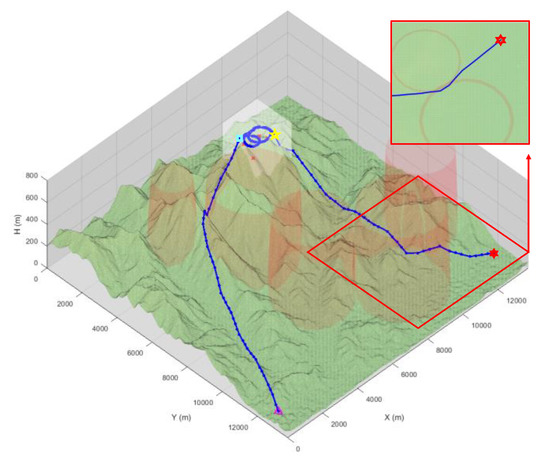
Figure 11.
Planned path of the SEAD mission scenario.

Table 6.
SEAD mission scenario’s waypoint locations.

Table 7.
Threats’ properties of the SEAD mission scenario.
The total consumed time is 16.85 s, and the number of samplings is set as 5000 for each terrain flight path planning for SEAD mission planning. The path shown in Figure 11 avoids a threat with relatively strong strength near the hexagonal point. Furthermore, the path is generated within 100 m above the surface in the terrain flight phase. One can find that the highlighted path in Figure 11 goes between threat #1 and threat #2 while bypassing a greater threat. This result occurs when it is more cost-effective to go through a threat than to avoid it.
6. Trajectory Tracking Simulation
Simulation of the planned trajectory tracking is essential to confirm the practical applicability of the proposed algorithm. Therefore, simulations are performed to track the flight trajectory as a function of time generated based on the planned path.
The waypoints represented in Section 5 only contain the sequence of position vectors. However, the Flight Control System (FCS) which will be mentioned later, requires heading angle information as well as position vectors. Furthermore, this information must be given as a function of time. For these reasons, a series of processes of allocating time and heading angle to the waypoint and converting the path into functions of time is required. Arrival time at each waypoint is allocated by assuming that UCAV is flying in a straight line between each waypoint at a prescribed constant speed. Moreover, the heading angle at each waypoint is assigned to face the next waypoint. Additional waypoints can be assigned to describe the original path more precisely where the waypoints can be expressed as a function of time through 7th-order spline interpolation [32]. The predicted arrival time may not be precise since the interpolated curve is not a straight line. To solve this problem, a simple iterative method is used to estimate the exact arc length and travel time simultaneously. Further details about trajectory generation are represented in Ref [33].
In order to design an appropriate trajectory tracking flight control system, trajectory tracking performance, robustness against disturbances and uncertainties, and the operating range of the aircraft must be considered. Incremental Backstepping Control (IBSC) guarantees stability across all Operational Flight Envelopes (OFE) based on the Lyapunov stability theory and is not affected by mismatched uncertainty. For this reason, there have been many approaches to design a controller based on the IBSC concept [34,35,36,37,38,39,40], and this paper also uses an IBSC-based tracking controller [33]. The reference trajectory was directly used as a feedback signal to obtain excellent tracking performance. For the completeness of this paper, the controller presented in Ref. [33] will be briefly described.
The main feature of the incremental control method is its stronger robustness compared to the conventional model-based control approaches. Rather than solely depending on the model dynamics, incremental controllers use the measurements of any aerodynamic changes through available sensors. Therefore, changes due to external disturbances or modeling errors can be measured and compensated directly to the controller, making the controller insensitive to such unfavorable effects. The aircraft’s equation of motion and the kinematic relations are defined as follows:
where and represent linear and angular velocity vector with respect to the aircraft’s body-fixed frame, and represent force and moment vector, and and represent the position and attitude vector of the aircraft. Furthermore, and are represented using the definition of the trigonometric functions like and for as.
The second-order dynamics for () are derived as:
which can be represented as following second-order nonlinear equation:
where is the primary control vector of a conventional helicopter consisting of the main rotor collective (), lateral-cyclic (), longitudinal-cyclic (), and tail rotor collective(. Let us define the dynamics in Equation (9) represented at as:
By applying the Taylor’s series expansion to Equation (10) at , and assuming is small enough, the incremental dynamics can be derived as:
Since the rank the control effectiveness matrix is less than the dimension of the system output , the system is underactuated. To cope with such difficulty, the slack variable approach is adopted as in Ref. [29] as follows:
where and are defined using the slack variable matrix and the slack variable vector as:
If is selected to make nonsingular, standard nonlinear control design methods can be applied to Equation (12).
The IBSC design starts by defining the trajectory tracking errors with the desired trajectory as:
where is the virtual control vector. Now, a control Lyapunov function is defined.
Without further derivation, the IBSC law that stabilizes the above Lyapunov function () can be selected as:
where, and are diagonal, positive definite matrices composing controller gains, and is a diagonal, positive definite matrix composing updating law gains. If you need further details of the controller, referring to Ref [33] is recommended.
Rotorcrafts are more appropriate to perform low-flying contour chasing maneuvers than fixed-wing aircraft for their low-speed flyability. For this reason, the BO-105 helicopter nonlinear model, modeled using the HETLAS program [41,42], is utilized.
The trajectories are generated based on the AI mission and the SEAD mission paths in Section 5. Figure 12 and Figure 13 represent the generated trajectories to fly at a constant speed of 40 m/s. The dashed line represents the height limit boundary of the terrain flight. That is, the lower boundary indicates the ground surface, and the upper boundary indicates a line of 100 m above the surface. As shown in Figure 12a, the height of the terrain flight trajectory was generated within 100 m from the surface. Meanwhile, the intercept maneuver trajectory was not affected the height constraint.
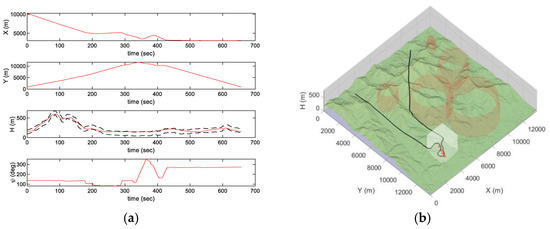
Figure 12.
Generated trajectory in the AI mission scenario: Trajectory (a) for time; (b) on 3D map.
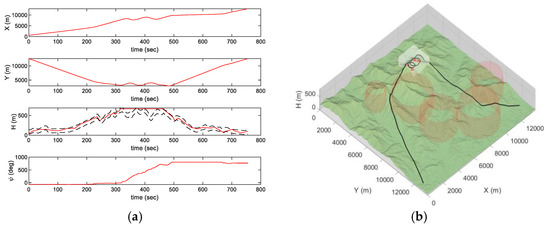
Figure 13.
Generated trajectory in the SEAD mission scenario: Trajectory (a) for time; (b) on 3D map.
Figure 14 and Figure 15 show tracking results and its error. Both results represent highly accurate tracking performance while showing position error within 1 m and heading angle error within 0.2 degrees. Through such high-accuracy tracking performance, the terrain flight missions can be performed without any collision.
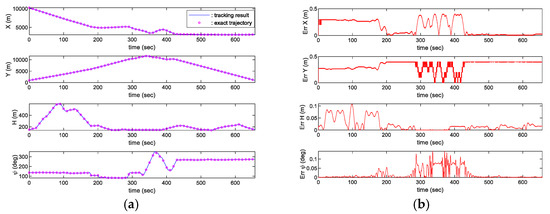
Figure 14.
Trajectory tracking result in the AI mission scenario: (a) Tracking result; (b) Tracking error.
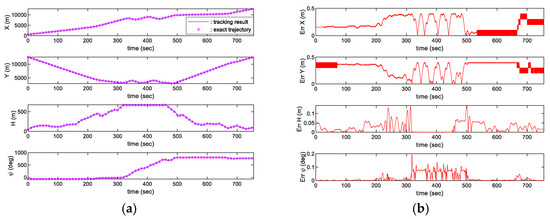
Figure 15.
Trajectory tracking result in the SEAD mission scenario: (a) Tracking result; (b) Tracking error.
The control inputs and states during the simulation are represented in Figure 16, Figure 17 and Figure 18. In the AI mission scenario, the lateral velocity varies over 40 m/s at about 300 s. Furthermore, the roll attitude temporally reaches over −30 degrees during intercept maneuver flight and the variation over 10 degrees in the pitch angle is represented at about 300 s. In the SEAD mission scenario, the lateral velocity varies over 40 m/s at about 650 s. Moreover, the roll attitude temporally reaches over 20 degrees during intercept maneuver flight and the variation over −15 degrees in the pitch angle is represented at about 320 s. The results in both simulations prove that the presented controller can maintain continuous tracking performance even with the aggressive maneuver. Furthermore, SEAD missions can be successfully performed with large height variations, where the maximum rate of climb reaches more than 10 m/s and the minimum rate of climb reaches near −20 m/s. In addition, the result is visualized in Figure 19 and Figure 20 to help discernible understanding.
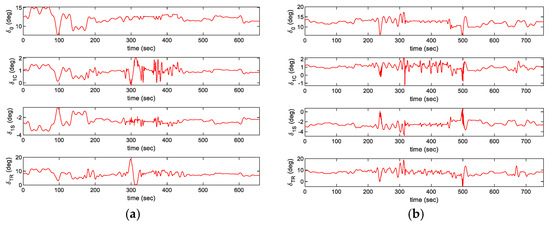
Figure 16.
Trajectory tracking result: control inputs for (a) the AI mission scenario; (b) for the SEAD mission scenario.
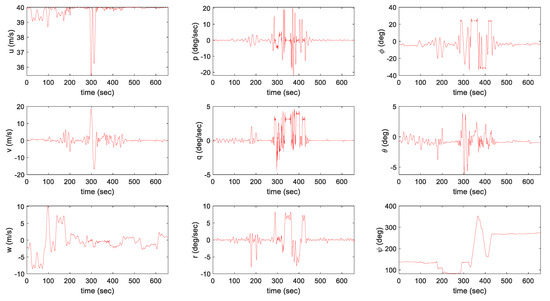
Figure 17.
Trajectory tracking result in the AI mission scenario: states.
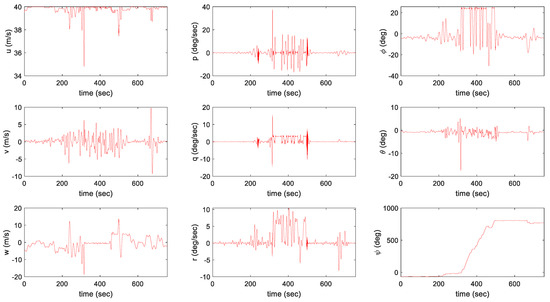
Figure 18.
Trajectory tracking result in the AI mission scenario: states.
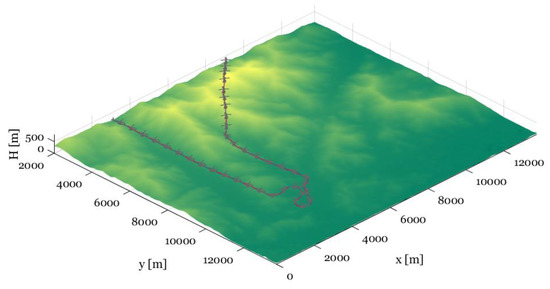
Figure 19.
Trajectory tracking result in the AI mission scenario: visualization.
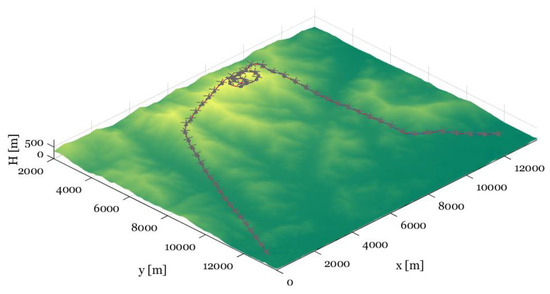
Figure 20.
Trajectory tracking result in the SEAD mission scenario: visualization.
7. Conclusions
A mission planner that enables effective ASM performance while considering the risk factors of the mission environment has been proposed and validated in this paper. First, ASMs were considered to consist of three sequential mission elements. The P-RRT*-smart algorithm was used to plan the ingress and egress mission element paths to quickly find the asymptotic global optimal path. The algorithm made it possible to find a path that could fly within 100 m of the surface. In addition, the concept of step cost was developed to account for the threats spread in the mission area. In order to increase the survivability of the UCAV and properly attack multiple targets, Dubins path was adopted in the intercept phase to generate short distance path near targets, taking into account the aircraft’s dynamic characteristics and the aiming capability of the mounted missiles. However, since the total length of the path still depends on target entry angles and the order of interception, the NLP was formulated to minimize the total length of the intercept path considering both the intercept entry angles and target intercept sequences. In return, the shortest intercept path could be obtained through the robust SQP. The integrated planner was then demonstrated in several test scenarios using a 3D terrain model with randomly placed threats. Finally, tracking simulations of the given path were successfully performed through a nonlinear rotorcraft model, confirming the method’s effectiveness.
Although the proposed planner has been confirmed to be an effective approach, questions about its real-time applicability remain. Therefore, there are several possible directions for the real-time applicability of this method. Since the proposed terrain path planner focuses on global planning, many samplings were performed in order to obtain the asymptotic optimal path. For this reason, the time consumed it takes to plan the terrain flight path shown in the results may seem quite long. In fact, the convergence time to the initial path and the optimal path was extremely short with in a few seconds. This characteristic shows the possibility of improvement as a real-time local planner sufficiently with a little improvement. The real-time local planner is focused on avoiding dynamic obstacles and threats during missions. To perform this task, the RT-RRT* [43] which is advanced for real-time application can be applied to the proposed planner. Furthermore, PQ-RRT [26] and bidirectional approaches [44] may also be useful to accelerate the convergence rate. Additionally, Line-of-Sight Path Optimization (LoSPO) technique [33] is a preferable option as a strategy to shorten the convergence time to the optimal path. Likewise, other RRT-based approaches can be applied to further improve the algorithm for real-time local planners.
The shortest intercept path planning may seem unsuitable for real-time applications. However, the time consumed shown in the results is the time required for optimization by setting the initial values to 0. In this case, it may take a long time to converge. Therefore, a strategy of planning the path with the previously optimized value as the initial value during the flight may be effective.
The results show that the proposed planner can generate the optimal path to approach the targets and the shortest path to intercept targets on the 3D global map which is the major difference from the previous studies. Furthermore, the presented simulation results show that the applied controller tracks the planned trajectory with high tracking performance, which proves that the generated trajectories from the proposed planner are flyable. In addition, the robust controller is adopted to cope with uncertainties such as the instantaneous weight reduction that occurs during an armed drop. Therefore, the method proposed in this paper can greatly contribute to planning air-to-surface missions of autonomous UCAVs.
Author Contributions
Supervision, C.-J.K.; Validation, J.-Y.A.; Writing—original draft, J.-W.W.; Writing—review & editing, Y.-S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not available.
Informed Consent Statement
Not available.
Data Availability Statement
Not available.
Acknowledgments
This paper was written as part of Konkuk University’s research support program for its faculty on sabbatical leave in 2021. Furthermore, this research was supported by Basic Science Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Education(No. 2020R1A6A1A03046811).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Radial distance | |
| Radial distance of maximum threat reach | |
| Function of threat distribution in the inner domain of threat | |
| RBF shape factor | |
| Strength of threat | |
| Radial basis function | |
| Cost due to threats | |
| Distance cost | |
| Node-to-node cost | |
| Target intercept entry angle | |
| Distance from target to aiming point | |
| Distance from target to weapon release point | |
| Turning radius | |
| Objective function | |
| vector of target intercept entry angles | |
| Position tracking error | |
| Velocity tracking error | |
| Desired trajectory | |
| UCAV | Unmanned Combat Aerial Vehicles |
| ASM | Air-to-Surface Mission |
| SEAD | Suppression to Enemy Air Defenses |
| AI | Air Interdiction |
| CAS | Close Air Support |
| AO | Attack Operations |
| RRT | Rapidly exploring Random Tree |
| RBF | Radial Basis Function |
| NLP | Nonlinear Programming |
| SQP | Sequential Quadratic Programming |
| IBSC | Incremental Backstepping Control |
| OFE | Operational Flight Envelope |
| HETLAS | Helicopter Trim Linearization and Simulation |
References
- Beard, R.W.; McLain, T.W.; Goodrich, M.A.; Anderson, E.P. Coordinated target assignment and intercept for unmanned air vehicles. IEEE Trans. Robot. Autom. 2002, 18, 911–922. [Google Scholar] [CrossRef] [Green Version]
- Eun, Y.; Bang, H. Cooperative control of multiple UCAVs for suppression of enemy air defense. In Proceedings of the AIAA 3rd ‘Unmanned Unlimited’ Technical Conference, Workshop and Exhibit, Chicago, IL, USA, 20–23 September 2004; Volume 20–23, pp. 1–14. [Google Scholar]
- Triharminto, H.H.; Adji, T.B.; Setiawan, N.A. Dynamic uav path planning for moving target intercept in 3D. In Proceedings of the IEEE 2nd International Conference on Instrumentation Control and Automation, Shiraz, Iran, 27–29 December 2011; Volume 15–17, pp. 157–161. [Google Scholar] [CrossRef]
- Shanmugavel, M.; Tsourdos, A.; White, B.; Zbikowski, R. Co-operative path planning of multiple UAVs using Dubins paths with clothoid arcs. Control Eng. Pract. 2010, 18, 1084–1092. [Google Scholar] [CrossRef]
- Manyam, S.G.; Casbeer, D.; Von Moll, A.; Fuchs, Z. Optimal dubins paths to intercept a moving target on a circle. Proc. Am. Control Conf. 2019, 2019, 828–834. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, Z.; Shao, X.; Zhao, W. Time-optimal guidance for intercepting moving targets by Dubins vehicles. Automatica 2021, 128, 109557. [Google Scholar] [CrossRef]
- Ridder, J.P.; HandUber, J.C. Mission planning for joint suppression of enemy air defenses using a genetic algorithm. In Proceedings of the Genetic and Evolutionary Computation Conference, GECCO 2005, Washington, DC, USA, 25–29 June 2005; pp. 1929–1936. [Google Scholar] [CrossRef]
- Griggs, B.J.; Parnell, G.S.; Lehmkuhl, L.J. An air mission planning algorithm using decision analysis and mixed integer programming. Oper. Res. 1997, 662–676. [Google Scholar] [CrossRef]
- Lan, Y. Multiple mobile robot cooperative target intercept with local coordination. CCDC 2012, 2012, 145–151. [Google Scholar]
- Sharma, A.; Shoval, S.; Sharma, A.; Pandey, J.K. Path Planning for Multiple Targets Interception by the Swarm of UAVs based on Swarm Intelligence Algorithms: A Review. IETE Tech. Rev. (Institution Electron. Telecommun. Eng. India) 2021, 0, 1–23. [Google Scholar] [CrossRef]
- Zhong, M.; Yang, R.N.; Wu, J.; Zhang, H. Multi-Target Strike Path Planning Based on Improved Decomposition Evolutionary Algorithm. Math. Probl. Eng. 2019, 2019, 7205154. [Google Scholar] [CrossRef] [Green Version]
- Wu, W.; Wang, X.; Cui, N. Fast and coupled solution for cooperative mission planning of multiple heterogeneous unmanned aerial vehicles. Aerosp. Sci. Technol. 2018, 79, 131–144. [Google Scholar] [CrossRef]
- Huang, H.; Zhuo, T. Multi-model cooperative task assignment and path planning of multiple UCAV formation. Multimed. Tools Appl. 2019, 78, 415–436. [Google Scholar] [CrossRef]
- Baspinar, B.; Koyuncu, E. Survivability Based Optimal Air Combat Mission Planning with Reinforcement Learning. In Proceedings of the 2018 IEEE Conference on Control Technology and Applications, CCTA 2018, Copenhagen, Denmark, 21–24 August 2018; pp. 664–669. [Google Scholar] [CrossRef]
- U.S Airforce. U.S Air Force Doctrine, AFDP 3-01, Counterair Operations. Available online: https://www.doctrine.af.mil/Doctrine-Publications/AFDP-3-01-Counterair-Ops/ (accessed on 5 July 2021).
- U.S Airforce. U.S Air Force Doctrine, AFDP 3-03, Counterland Operations. Available online: https://www.doctrine.af.mil/Doctrine-Publications/AFDP-3-03-Counterland-Ops/ (accessed on 5 July 2021).
- Morse, B.S.; Yoo, T.S.; Rheingans, P.; Chen, D.T.; Subramanian, K.R. Interpolating implicit surfaces from scattered surface data using compactly supported radial basis functions. In Proceedings of the International Conference on Shape Modeling and Applications, SMI 2001, Genova, Italy, 7–11 May 2001; pp. 89–98. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Qi, J.; Song, D.; Xiao, J.; Han, J.; Xia, Y. Survey of Robot 3D Path Planning Algorithms. J. Control Sci. Eng. 2016, 2016, 22. [Google Scholar] [CrossRef] [Green Version]
- LaValle, S.M. Rapidly-Exploring Random Trees: A New Tool for Path Planning. Report No. TR 98-11, Computer Science Department, Iowa State University. 1998. Available online: http://janowiec.cs.iastate.edu/papers/rrt.ps (accessed on 5 July 2021).
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Nasir, J.; Islam, F.; Malik, U.; Ayaz, Y.; Hasan, O.; Khan, M.; Muhammad, M.S. RRT*-SMART: A rapid convergence implementation of RRT*. Int. J. Adv. Robot. Syst. 2013, 10, 299–310. [Google Scholar] [CrossRef] [Green Version]
- Qureshi, A.H.; Ayaz, Y. Potential functions based sampling heuristic for optimal path planning. Auton. Robot. 2016, 40, 1079–1093. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Meng, M.Q.H.; Khatib, O. EB-RRT: Optimal Motion Planning for Mobile Robots. IEEE Trans. Autom. Sci. Eng. 2020, 17, 2063–2073. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, T.; Cheng, H.; Liang, F. Collision Avoidance of Fixed-Wing UAVs in Dynamic Environments Based on Spline-RRT and Velocity Obstacle. In Proceedings of the IEEE 2020 International Conference on Unmanned Aircraft Systems, ICUAS, Athens, Greece, 1–4 September 2020; Volume 2020, pp. 48–58. [Google Scholar] [CrossRef]
- Jeong, I.B.; Lee, S.J.; Kim, J.H. Quick-RRT*: Triangular inequality-based implementation of RRT* with improved initial solution and convergence rate. Expert Syst. Appl. 2019, 123, 82–90. [Google Scholar] [CrossRef]
- Li, Y.; Wei, W.; Gao, Y.; Wang, D.; Fan, Z. PQ-RRT*: An improved path planning algorithm for mobile robots. Expert Syst. Appl. 2020, 152, 113425. [Google Scholar] [CrossRef]
- Chiang, H.T.L.; Hsu, J.; Fiser, M.; Tapia, L.; Faust, A. RL-RRT: Kinodynamic Motion Planning via Learning Reachability Estimators from RL Policies. IEEE Robot. Autom. Lett. 2019, 4, 4298–4305. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Chi, W.; Li, C.; Wang, C.; Meng, M.Q.H. Neural RRT∗: Learning-Based Optimal Path Planning. IEEE Trans. Autom. Sci. Eng. 2020, 17, 1748–1758. [Google Scholar] [CrossRef]
- Dubins, L.E. On Curves of Minimal Length with a Constraint on Average Curvature, and with Prescribed Initial and Terminal Positions and Tangents. Am. J. Math. 1957, 79, 497. [Google Scholar] [CrossRef]
- Lugo-Cardenas, I.; Flores, G.; Salazar, S.; Lozano, R. Dubins path generation for a fixed wing UAV. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems, ICUAS, Orlando, FL, USA, 27–30 May 2014; Volume 79, pp. 339–346. [Google Scholar] [CrossRef] [Green Version]
- Kim, C.J.; Sung, S.; Shin, K.C. Pseudo-spectral application to nonlinear optimal trajectory generation of a rotorcraft. Adv. Sci. Lett. 2012, 9, 204–209. [Google Scholar] [CrossRef]
- Kim, C.J.; Lee, D.H.; Hur, S.W. Efficient and Robust Inverse Simulation Techniques Using Pseudo-Spectral Integrator with Applications to Rotorcraft Aggressive Maneuver Analyses. Int. J. Aeronaut. Sp. Sci. 2019, 20, 768–780. [Google Scholar] [CrossRef]
- Woo, J.W.; An, J.; Cho, M.G.; Kim, C. Integration of path planning, trajectory generation and trajectory tracking control for aircraft mission autonomy. Aerosp. Sci. Technol. 2021, 1, 107014. [Google Scholar] [CrossRef]
- Wang, X.; van Kampen, E.J. Incremental Backstepping Sliding Mode Fault-Tolerant Flight Control. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; Volume 118, p. 107014. [Google Scholar] [CrossRef]
- Jeon, B.J.; Seo, M.G.; Shin, H.S.; Tsourdos, A. Understandings of incremental backstepping controller considering measurement delay with model uncertainty. Aerosp. Sci. Technol. 2021, 109, 106408. [Google Scholar] [CrossRef]
- van Gils, P.; van Kampen, E.; de Visser, C.C.; Chu, Q.P. Adaptive Incremental Backstepping Flight Control for a High-Performance Aircraft with Uncertainties. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, San Diego, CA, USA, 4–8 January 2016; Volume 118, p. 107014. [Google Scholar] [CrossRef]
- Cho, M.G.; Jung, U.; An, J.-Y.; Choi, Y.-S.; Kim, C.-J. Adaptive Trajectory Tracking Control for Rotorcraft Using Incremental Backstepping Sliding Mode Control Strategy. Int. J. Aerosp. Eng. 2021, 2021, 1–15. [Google Scholar] [CrossRef]
- Cordeiro, R.A.; Azinheira, J.R.; Moutinho, A. Cascaded Incremental Backstepping Controller for the Attitude Tracking of Fixed-Wing Aircraft. In Proceedings of the 5th CEAS Conference on Guidance, Navigation and Control, Milano, Italy, 3–5 April 2019. [Google Scholar]
- Guerreiro, N.M.; Moutinho, A. Robust incremental backstepping controller for the attitude and airspeed tracking of a commercial airplane. In Proceedings of the 2019 IEEE 10th International Conference on Mechanical and Aerospace Engineering, ICMAE 2019, Brussels, Belgium, 22–25 July 2019; pp. 607–611. [Google Scholar] [CrossRef]
- Van Gils, P. Adaptive Incremental Backstepping Flight Control; Delft University of Technology: Delft, The Netherlands, 2015. [Google Scholar]
- Yun, Y.H.; Kim, C.-J.; Shin, K.C.; Yang, C.D.; Cho, I.J. Building the flight dynamic analysis program, HETLAS, for the development of helicopter FBW system. In Proceedings of the 1st Asian Australian Rotorcraft Forum and Exhibition, Busan, Korea, 12–15 February 2012. [Google Scholar]
- Kim, C.-J.; Shin, K.C.; Yang, C.D.; Cho, I.J. Interface Features of Flight Dynamic Analysis Program, HETLAS, for the Development of Helicopter FBW System. In Proceedings of the 1st Asian Australian Rotorcraft Forum and Exhibition, Busan, Korea, 12–15 February 2012. [Google Scholar]
- Naderi, K.; Rajamaki, J.; Hamalainen, P. RT-RRT∗: A real-time path planning algorithm based on RRT∗. In Proceedings of the 8th ACM SIGGRAPH Conference on Motion in Games, Paris, France, 16–18 November 2015; pp. 113–118. [Google Scholar]
- Jordan, M.; Perez, A. Optimal Bidirectional Rapidly-Exploring Random Trees; MIT: Cambridge, MA, USA, 2013. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).